Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Apr 23;3(5):2336–2340. doi: 10.1021/acsapm.1c00321

Concentrating Vapor Traces with Binary Brushes of Immiscible Polymers

Leon A Smook 1, Guido C Ritsema van Eck 1, Sissi de Beer 1,*
PMCID: PMC8154206  PMID: 34056613

Abstract

graphic file with name ap1c00321_0005.jpg

Vapors in the air around us can provide useful information about our environment, but we need sensitive vapor sensors to access this information, especially because those vapors are often present at very low concentrations. We report molecular dynamics simulations of a concept that can significantly increase the sensitivity of vapor sensors at low concentrations. By coating the sensor surfaces with end-anchored immiscible polymers, surface-bound polymer blends are formed that can concentrate vapors, reaching sorption enhancements of more than one order of magnitude, especially at low vapor concentrations.

Keywords: polymer brushes, vapor solvation, vapor sensing, molecular dynamics simulations, adsorption

Recognizing components of the air that surrounds us is more important than ever. Whether it is monitoring emissions, ensuring food safety, recognizing infectious diseases, or regulating air quality, the first step is a sensitive detection of molecular components in the atmosphere, preferably with accurate and portable sensors.1 To this end, vapor sensors have been developed with transduction mechanisms that operate based on a change in adsorbed mass2 or optical and dielectric properties3−5 at the sensor surface. The response of these sensors strongly depends on the number of adsorbed molecules on the sensor, and the sensitivity of these types of sensors is typically limited to concentrations of several ppm, even though some compounds are important to detect at sub-ppm levels.6

To enhance specific adsorption of vapor molecules, surface functionalizations can be applied to modify the chemical properties of a sensor surface.7 Moreover, polymer-brush-based coatings can add to this effect even further:8−10 Next to adsorption of vapors onto their surface, they can absorb vapors into their bulk based on the chemical makeup of the vapor and polymer.11−13 In other words, brushes can concentrate vapors near surfaces. Nevertheless, in affordable sensing platforms, sub-ppm resolutions have not yet been achieved with these brushes. Thus there is a strong need for optimized designs that can further increase the vapor concentration at sensor surfaces to fabricate sensitive and affordable sensors. We propose that vapor sorption on a surface can be strongly enhanced with binary polymer brushes.

Molecular dynamics (MD) simulations14 are an excellent tool to study the sorption in binary polymer brushes. In such simulations, the freedom to choose both the initial configuration of particles as well as their interactions enables us to isolate the effect of a single variable on the behavior of the system, which has resulted in new insights into polymer solvation15−17 as well as the interaction-dependent structure of polymers in brushes.18−21 Even more importantly, these simulations offer insight into details that are difficult to obtain with experimental techniques, such as the nanoscale spatial distribution of particles in the system.22−24

In this Letter, we study different brush coatings and show via MD simulations that surfaces coated with binary brushes can display an enhanced vapor sorption compared with a bare surface. In our simulations, we expose structurally different brushes to a vapor with a specified vapor pressure maintained via a Monte Carlo particle-exchange procedure.23,24 We show that enhanced absorption is most pronounced at low vapor pressures, enabling the concentration of vapor traces near sensor surfaces.

To assess the influence of the brush composition on vapor sorption, we study three different brush types: pure, striped, and mixed brushes. The insets in Figure 1 show the morphologies of these different brush types. In the pure brushes, the grafted chains are all of the same type (A). In the striped brushes, the chains are of two distinct types (A and B), and the anchor points of the different polymer types are segregated in strips on the grafting surface, ensuring a localized separation between A-rich and B-rich phases. In the mixed brushes, the chains are of two distinct types (A and B), and the anchor points of the different polymer types are distributed throughout the grafting surface, creating a homogeneous distribution of both polymer types at the grafting surface. As a result of the interactions between different polymer types, these brushes phase-separate, which leads to an inhomogeneous distribution of the different polymers in the brush.

Figure 1.

Figure 1

Open in a new tab

Average solvent density profile sampled over 8 M time steps along the x direction of the simulation box for (from left to right) (a) a pure brush, (b) a striped brush, and (c) a mixed brush at a relative vapor pressure of 68.5% and a cross-interaction strength between different polymer types of 0.453ϵ. The insets show a snapshot of the vapor-swollen brushes. (d) Absorption in each of the brushes normalized by the substrate area.

The brushes in this work consist of polymers anchored to a substrate on a hexagonal lattice with a grafting density of 0.25σ–2 in a simulation box of approximately 30σ × 30σ × 50σ.25 The polymers are modeled using a bead-chain with 30 beads forming Kremer–Grest chains.26 All beads on one chain are of the same type, giving A chains and B chains. The striped and mixed brushes consist of A and B chains in a 1:1 ratio. We expose these brushes to a vapor of Lennard-Jones particles. This vapor is generated in a 20σ region near the top of the simulation box. The vapor is kept at a constant vapor pressure by regular insertion/deletion of vapor particles from a virtual reservoir using a Grand-Canonical Monte Carlo procedure23,24 implemented in LAMMPS.27

In our simulation setup, two types of interactions dominate the system behavior: nonbonded and bonded interactions. The nonbonded interactions are based on 12-6 Lennard-Jones potentials characterized by their zero crossing at a pair distance of σ and a minimum value of ϵ, the interaction strength. All nonbonded interactions have an interaction strength of 1ϵ, except between different monomer types (ϵAB), where the variable strength ranges from 0.2 to 1.4ϵ. This means that for ϵAB < 1, the self-interaction of the polymers is stronger than the cross-interaction, and for ϵAB > 1, the cross-interaction is stronger than the self-interaction. All bonded interactions are identical and based on a finite extensible nonlinear elastic potential with parameters that have been proven to prevent nonphysical behavior.26 More details of the setup are given in the Supporting Information (SI).

After exposing the different brushes to the Lennard-Jones vapor, we monitor the distribution of this vapor in the brushes as well as the amount of vapor absorbed in the brush compared with a bare attractive surface (9-3 Lennard-Jones potential with a potential minimum of 1ϵ; for more detail see the SI). Figure 1 summarizes the results of these simulations: From left to right, it shows the projected solvent distribution in a pure (a), striped (b), and mixed brush (c) as well as the excess absorption for each of these surfaces (d). Here excess absorption is defined as the number of particles in the simulation box minus the number of particles in a (hypothetical) similarly sized box filled only with vapor. These simulations are performed under conditions that result in a preference in the monomers to interact with monomers of the same rather than a different type because their self-interaction is stronger than the cross-interaction (ϵAB = 0.453). The left three panels in the figure show the distribution of absorbed vapor, and we can observe three types of absorption (Figure 2). First, we observe adsorption at the polymer–vapor interface, which results from the surface energy of the free brush surface. Second, we observe absorption in the bulk of the brush, which results from favorable interactions between the monomers and vapor.23 Finally, we observe adsorption at the A–B polymer–polymer interface, which results from the interfacial energy between the different polymer phases created by the unfavorable interaction between polymers A and B. (ϵAB is low compared with ϵAA and ϵBB.) All types of brushes display the first two types of sorption. Hence, differences between single-component and binary brushes mostly result from the adsorption at the polymer–polymer interface; this is especially apparent in the striped brush (see Figure 1), where the brighter color indicates higher concentrations of vapor at this interface.

Figure 2.

Figure 2

Open in a new tab

Schematic depiction of the different types of sorption in binary brushes.

A quantification of the additional sorption is shown in Figure 1d. For a bare surface, the absorption is 0.05σ–2, and this increases for surfaces that are coated with brushes. The absorption in the pure brush is 0.12σ–2, whereas for the striped and mixed brush, this value increases to 0.18 and 0.25σ–2, respectively. This difference can be explained from a free-energy perspective: The entropic freedom of the vapor molecules contributes to the free energy of the system and can be compensated by the absorption energy when particles absorb.28 At the unfavorable interfaces, the energy of adsorption is higher than the energy of absorption in the pure brush due to the interfacial energy associated with this AB contact area. Hence more vapor will sorb at those interfaces.

To explore this effect in more detail, we perform simulations for varying cross-interaction strengths (ϵAB) ranging from 0.2 to 1.4ϵ. We calculate the absorption for each system by sampling the excess absorption at equilibrium. Figure 3a displays the excess factor (the factor by which the absorption increases compared with a bare surface) for the striped and mixed brushes at a relative vapor pressure of 68.5% and a self-interaction energy (ϵAA and ϵBB) of 1.0. Enhanced absorption is observed when the cross-interaction is weaker than the self-interactions, and the effect is stronger in the mixed brush than in the striped brush. More specifically, at a very unfavorable cross-interaction (ϵAB = 0.2), the absorption is enhanced by a factor 4.1 for the striped brush and 6.2 for the mixed brush with respect to the adsorption on a bare surface.

Figure 3.

Figure 3

Open in a new tab

(a) Absorption is enhanced with respect to a single-component brush when the cross-interaction strength (ϵAB) is reduced. (b) The ratio of the enhanced absorption compared with a pure brush (U) between the mixed (M) and striped (S) brushes ((ΓM – ΓU)/(ΓS – ΓU)) directly correlates with the ratio between the surface areas of both brushes between the nano-phase-separated A and B phases (AM/AS).

The excess factor relates almost linearly to the strength of the cross-interaction for both binary brushes when the brushes nano-phase-separate. We note that the slope of this effect is steeper for the mixed brush than for the striped brush. This results from the contact area between the A and B phases of the different systems, which is different for striped and mixed brushes. (For details of this surface analysis, we refer to the SI.) In a mixed brush, the system tends to nano-phase-separate into A and B phases that depend on the incompatibility between the polymers (cross-interaction),29 the anchoring30 and annealing31 conditions, and the temperature,32 creating an interfacial area between the A and B phases where adsorption takes place. Similarly, an AB interfacial area exists in the striped brush. However, here this area is limited by the spatial segregation of the A and B polymers, leading to a smaller AB interface compared with the mixed (phase-separated) brush. Because the interfacial area in both brushes depends only weakly on the cross-interaction strength in the nano-phase-separated domain, the linear increase in the excess factor results from the adsorption energy associated with these interfaces, which increases as cross-interactions become more unfavorable.

Figure 3b shows the ratio of this interfacial area in the mixed and striped brushes and compares it with the ratio in absorption in both binary brushes in excess of the absorption in homopolymer brushes. The interfacial area ratio and the absorption ratio correlate well, which indicates that the interfacial area is one of the main contributors to the enhanced absorption in binary brushes. Nevertheless, we observe a discrepancy between both ratios for cross-interaction strengths that are similar to the self-interaction strength (0.8 < ϵAB < 1.1). This discrepancy results from a difference in the mixing transitions between the striped and mixed brush. Interfaces between different domains soften when cross-interactions are similar to self-interactions due to limited blending of the different phases. Mixed brushes blend at lower cross-interaction strengths than striped brushes due to the additional chain stretching required for forming a homogeneous blended phase in the latter. (See Figure S1 in the SI.) For these small differences, nanophase separation is not complete, and hence there are more AB contacts in the brush, leading to the discrepancy.

At cross-interactions stronger than self-interactions (ϵAB > 1.1), the difference in absorption between striped and mixed brushes disappears because the interfacial interactions no longer introduce an additional driving force for absorption. The unfavorable interactions become favorable, leading to blending of the A and B polymers. Enhanced absorption is no longer present. In fact, these cross-interactions now reduce the absorption because they are favored over polymer–vapor interactions. The dimensions chosen for the simulations allow for near-complete blending of the polymers, effectively removing the difference between the striped and mixed brushes.

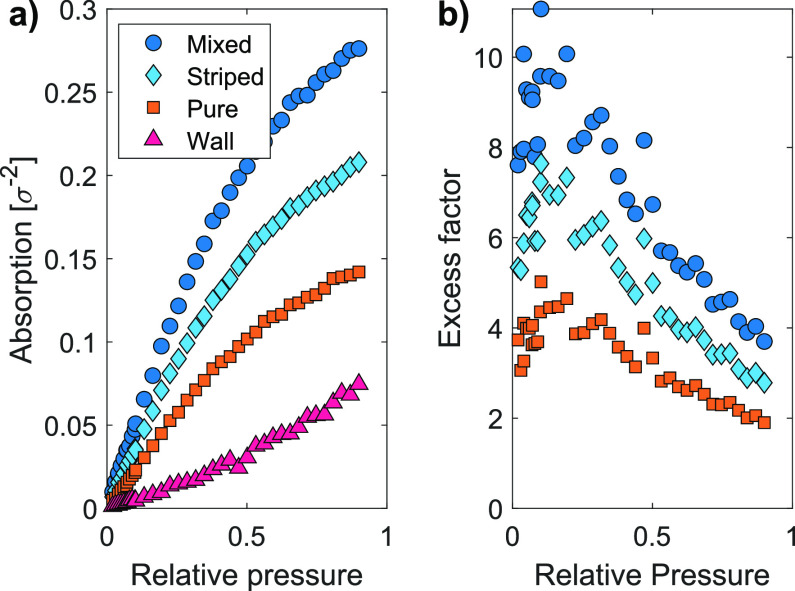
To investigate the absorption at low vapor concentrations, we vary the vapor pressure. Figure 4a shows absorption isotherms of the three systems for ϵAB = 0.453ϵ and for the bare surface: The excess absorption is presented versus the relative vapor pressure. The absorption isotherm of the pure brush (orange squares) is in line with isotherms found in solvophilic brushes.23 We note that the isotherm of the bare surface (wall) has a concave rather than convex shape and that this difference contributes to the enhanced absorption, especially at low concentrations. Vapor adsorbing on a bare surface forms fewer attractive interactions with neighboring particles compared with vapor absorbing in brushes: For surfaces, these neighboring particles are located on the surface underneath the adsorbing particle, whereas for brushes, they are present around the absorbing particle.

Figure 4.

Figure 4

Open in a new tab

(a) Absorption isotherm for a pure, a mixed, and a striped brush at a cross-interaction of 0.453ϵ and for a bare surface (wall). (b) The enhanced absorption relative to the pure brush increases at low vapor pressures and is relatively constant at higher vapor pressures.

Figure 4b shows the excess factor versus the relative pressure. For all evaluated pressures, absorption increases with a factor of at least 1.9, 2.8, and 3.7 for a pure, striped, and mixed brush, respectively. More importantly, the enhanced absorption effect increases upon lowering the vapor pressures; at a relative pressure of 0.1, a maximum excess factor of 5.0, 7.6, and 11.1 is reached for a pure, striped, and mixed brush, respectively. We observe that the solvent density profiles for brushes at vapor pressures of 0.1 and 0.685 show no qualitative differences. (See Figure S2 in the SI.) This indicates that at low vapor pressures, the vapor concentration near the surface can be enhanced using brushes, indicating a potential for increasing the sensitivity of brush-based vapor sensors.

The enhancement in binary brushes compared with homopolymer brushes is the result of a reduced sorption of vapor in the bulk of the brush. At low vapor pressures (<0.3), the entropic freedom of the vapor molecules contributes more to the free energy of the system than can be compensated by the absorption energy.28 However, at unfavorable interfaces, this energy of adsorption is higher than that in the bulk, so vapor still absorbs in the coating at low pressures. Consequently, the ratio between molecules absorbed inside the microdomains and those at the AB interfaces changes, leading to an increase in enhanced absorption. At even lower pressures (<0.1), the energy of adsorption at the AB interfaces can no longer balance the loss of entropy of the vapor; at very low pressures, no adsorption takes place.

Enhanced absorption has several promising implications for systems using polymer brushes in sensing applications. First, the enhanced absorption leads to more analyte in the brush, increasing the signal strength of the sensor. This improves the sensitivity of the sensor and will allow for more accurate measurements of vapors. Second, the absorption at low relative vapor pressures is significantly increased in pure brushes compared with the bare surface. For mixed brushes, this effect is even stronger. For many applications, a vapor sensor needs to measure very small traces of gases, and this enhanced sensitivity at low vapor pressures introduces new possibilities for the use polymer brushes.

In addition to an increased sensitivity, the presence of brushes on sensor surfaces can also create more selectivity, which is important for sensing particular (groups of) molecules and in developing artificial noses.10 The simulations presented in this Letter show the behavior of mixed brushes exposed to a single-component vapor, so we can only draw conclusions on the sensitivity of the coating. Nevertheless, in a recent paper,24 we explored the selectivity of vapor sorption in single-component brushes using MD simulations with a two-component Lennard-Jones vapor using a double grand-canonical Monte Carlo scheme. We intend to perform similar simulations on mixed brushes to gain insight into the specificity of these mixed brushes.

Whereas our work focuses on coatings of mixed polymer brushes, we hypothesize that the enhanced absorption effect is not limited to these systems. Other coatings may show similar behavior if one can introduce unfavorable interactions between components in the coating. Such coatings may include spincast random copolymers, block copolymers, or mixed polymer gels, yet these alternative coatings require the stabilization of a nano-phase-separated system, which may prove difficult for coatings that are not anchored to the substrate. In contrast, binary polymer brushes can be stably attached to substrates by well-established synthesis techniques such as grafting to33 and grafting from34,35 and therefore hold great potential for application in sensor technologies.

In summary, we have performed MD simulations of pure, striped, and mixed polymer brushes exposed to a Lennard-Jones vapor and compared the vapor absorption in these systems to the adsorption on a bare surface. At low vapor pressures, brushes can concentrate these vapor traces. The sorption can be increased by a factor of up to 5.0 for pure brushes and up to 11.1 for nanophase-separated mixed brushes. We show that this increase from pure to mixed brushes is due to adsorption of vapor at the interface between the immiscible polymer types. Enhanced absorption in binary brushes shows great potential for coatings in highly sensitive vapor sensors. These coatings, when applied to existing sensing platforms, may lower the detection limit of these platforms by concentrating vapors near the sensor surface, especially at low vapor pressures.

Acknowledgments

We thank Kris Kim for a careful reading of the manuscript and acknowledge NWO and SURFsara for HPC resources and support (project refs 45666 and EINF-700). This work is part of the research programme “Mechanics of Moist Brushes” with project number OCENW.KLEIN.020, which is financed by the Dutch Research Council (NWO).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsapm.1c00321.

  • Simulation procedures, procedure to determine the area between polymer nanophases, snapshots around the mixing transition of striped and mixed brushes, and vapor density profiles at selected pressures (PDF)

The authors declare no competing financial interest.

Supplementary Material

ap1c00321_si_001.pdf (1.5MB, pdf)

References

  1. Pelosi P.; Zhu J.; Knoll W. From gas sensors to biomimetic artificial noses. Chemosensors 2018, 6, 32. 10.3390/chemosensors6030032. [DOI] [Google Scholar]
  2. Nazemi H.; Balasingam J. A.; Swaminathan S.; Ambrose K.; Nathani M. U.; Ahmadi T.; Lopez Y. B.; Emadi A. Mass Sensors Based on Capacitive and Piezoelectric Micromachined Ultrasonic Transducers—CMUT and PMUT. Sensors 2020, 20, 2010. 10.3390/s20072010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Fan X.; White I. M.; Shopova S. I.; Zhu H.; Suter J. D.; Sun Y. Sensitive optical biosensors for unlabeled targets: A review. Anal. Chim. Acta 2008, 620, 8–26. 10.1016/j.aca.2008.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Jiang X.; Gao H.; Zhang X.; Pang J.; Li Y.; Li K.; Wu Y.; Li S.; Zhu J.; Wei Y.; Jiang L. Highly-sensitive optical organic vapor sensor through polymeric swelling induced variation of fluorescent intensity. Nat. Commun. 2018, 9, 1–9. 10.1038/s41467-018-06101-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Megahd H.; Lova P.; Comoretto D. Universal Design Rules for Flory–Huggins Polymer Photonic Vapor Sensors. Adv. Funct. Mater. 2021, 31 (9), 2009626. 10.1002/adfm.202009626. [DOI] [Google Scholar]
  6. Perkins J.; Gholipour B. Optoelectronic Gas Sensing Platforms: From Metal Oxide Lambda Sensors to Nanophotonic Metamaterials. Adv. Photonics Res. 2021, 2000141. 10.1002/adpr.202000141. [DOI] [Google Scholar]
  7. Zuo G.; Li X.; Zhang Z.; Yang T.; Wang Y.; Cheng Z.; Feng S. Dual-SAM functionalization on integrated cantilevers for specific trace-explosive sensing and non-specific adsorption suppression. Nanotechnology 2007, 18, 255501. 10.1088/0957-4484/18/25/255501. [DOI] [Google Scholar]
  8. Li L.; Li J.; Lukehart C. M. Graphitic carbon nanofiber-poly(acrylate) polymer brushes as gas sensors. Sens. Actuators, B 2008, 130, 783–788. 10.1016/j.snb.2007.10.050. [DOI] [Google Scholar]
  9. McCaig H. C.; Myers E.; Lewis N. S.; Roukes M. L. Vapor Sensing Characteristics of Nanoelectromechanical Chemical Sensors Functionalized Using Surface-Initiated Polymerization. Nano Lett. 2014, 14, 3728–3732. 10.1021/nl500475b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Horst R. J.; Brió Pérez M.; Cohen R.; Cirelli M.; Dueñas Robles P. S.; Elshof M. G.; Andreski A.; Hempenius M. A.; Benes N. E.; Damen C.; de Beer S. Swelling of Poly(methyl acrylate) Brushes in Acetone Vapor. Langmuir 2020, 36, 12053–12060. 10.1021/acs.langmuir.0c02510. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Galvin C. J.; Genzer J. Swelling of Hydrophilic Polymer Brushes by Water and Alcohol Vapors. Macromolecules 2016, 49, 4316–4329. 10.1021/acs.macromol.6b00111. [DOI] [Google Scholar]
  12. Brió Pérez M.; Cirelli M.; de Beer S. Degrafting of Polymer Brushes by Exposure to Humid Air. ACS Applied Polymer Materials 2020, 2, 3039–3043. 10.1021/acsapm.0c00474. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Aliyev E.; Shishatskiy S.; Abetz C.; Lee Y. J.; Neumann S.; Emmler T.; Filiz V. SI-ATRP Polymer-Functionalized Graphene Oxide for Water Vapor Separation. Adv. Mater. Interfaces 2020, 7, 2000443. 10.1002/admi.202000443. [DOI] [Google Scholar]
  14. Frenkel D.; Smit B.. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press: New York, 2002. [Google Scholar]
  15. Mukherji D.; Marques C. M.; Kremer K. Polymer collapse in miscible good solvents is a generic phenomenon driven by preferential adsorption. Nat. Commun. 2014, 5, 4882. 10.1038/ncomms5882. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Mukherji D.; Marques C. M.; Stuehn T.; Kremer K. Depleted depletion drives polymer swelling in poor solvent mixtures. Nat. Commun. 2017, 8, 1374. 10.1038/s41467-017-01520-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Sachar H. S.; Pial T. H.; Desai P. R.; Etha S. A.; Wang Y.; Chung P. W.; Das S. Densely Grafted Polyelectrolyte Brushes Trigger Water-in-Salt-like Scenarios and Ultraconfinement Effect. Matter 2020, 2, 1509–1521. 10.1016/j.matt.2020.02.022. [DOI] [Google Scholar]
  18. Dimitrov D. I.; Milchev A.; Binder K. Polymer brushes in solvents of variable quality: Molecular dynamics simulations using explicit solvent. J. Chem. Phys. 2007, 127, 084905. 10.1063/1.2768525. [DOI] [PubMed] [Google Scholar]
  19. Klushin L. I.; Skvortsov A. M.; Polotsky A. A.; Qi S.; Schmid F. Sharp and Fast: Sensors and Switches Based on Polymer Brushes with Adsorption-Active Minority Chains. Phys. Rev. Lett. 2014, 113, 068303. 10.1103/PhysRevLett.113.068303. [DOI] [PubMed] [Google Scholar]
  20. Bos I.; Merlitz H.; Rosenthal A.; Uhlmann P.; Sommer J.-U. Design of binary polymer brushes with tuneable functionality. Soft Matter 2018, 14, 7237–7245. 10.1039/C8SM01108G. [DOI] [PubMed] [Google Scholar]
  21. Wang L.; Zhong T.; Quan X.; Zhou J. Solvent-responsiveness of PS-PEO binary mixed polymer brushes: A coarse-grained molecular dynamics study. Mol. Simul. 2017, 43, 1322–1330. 10.1080/08927022.2017.1350662. [DOI] [Google Scholar]
  22. Opferman M. G.; Coalson R. D.; Jasnow D.; Zilman A. Morphology of Polymer Brushes Infiltrated by Attractive Nanoinclusions of Various Sizes. Langmuir 2013, 29, 8584–8591. 10.1021/la4013922. [DOI] [PubMed] [Google Scholar]
  23. Ritsema van Eck G. C.; Veldscholte L. B.; Nijkamp J. H. W. H.; de Beer S. Sorption Characteristics of Polymer Brushes in Equilibrium with Solvent Vapors. Macromolecules 2020, 53, 8428–8437. 10.1021/acs.macromol.0c01637. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Smook L. A.; Ritsema van Eck G. C.; de Beer S. Friends, Foes, and Favorites: Relative Interactions Determine How Polymer Brushes Absorb Vapors of Binary Solvents. Macromolecules 2020, 53, 10898–10906. 10.1021/acs.macromol.0c02228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. The units in this work (unless stated otherwise) are reduced units based on the Lennard-Jones potential function: σ for length, ϵ for energy, and τ for time. 1σ in our simulations is equivalent to lengths of <1 nm in real systems, and 1ϵ is ∼30 meV.26
  26. Kremer K.; Grest G. S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. 10.1063/1.458541. [DOI] [Google Scholar]
  27. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  28. Birshtein T. M.; Lyatskaya Y. V. Theory of the Collapse-Stretching Transition of a Polymer Brush in a Mixed Solvent. Macromolecules 1994, 27, 1256–1266. 10.1021/ma00083a028. [DOI] [Google Scholar]
  29. Wang J.; Müller M. Microphase separation of mixed polymer brushes: Dependence of the morphology on grafting density, composition, chain-length asymmetry, solvent quality, and selectivity. J. Phys. Chem. B 2009, 113, 11384–11402. 10.1021/jp903161j. [DOI] [PubMed] [Google Scholar]
  30. Santer S.; Kopyshev A.; Donges J.; Rühe J.; Jiang X.; Zhao B.; Müller M. Memory of Surface Patterns in Mixed Polymer Brushes: Simulation and Experiment. Langmuir 2007, 23, 279–285. 10.1021/la0629577. [DOI] [PubMed] [Google Scholar]
  31. Price A. D.; Hur S.-M.; Fredrickson G. H.; Frischknecht A. L.; Huber D. L. Exploring Lateral Microphase Separation in Mixed Polymer Brushes by Experiment and Self-Consistent Field Theory Simulations. Macromolecules 2012, 45, 510–524. 10.1021/ma202542u. [DOI] [Google Scholar]
  32. He G.-L.; Merlitz H.; Sommer J.-U.; Wu C.-X. Microphase Separation of Mixed Binary Polymer Brushes at Different Temperatures. Macromolecules 2009, 42, 7194–7202. 10.1021/ma901093u. [DOI] [Google Scholar]
  33. Li M.; Pester C. W. Mixed polymer brushes for ”smart” surfaces. Polymers 2020, 12, 1553. 10.3390/polym12071553. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Sui X.; Zapotoczny S.; Benetti E.; Memesa M.; Hempenius M.; Vancso G. Grafting mixed responsive brushes of poly(N-isopropylacrylamide) and poly(methacrylic acid) from gold by selective initiation. Polym. Chem. 2011, 2, 879–884. 10.1039/c0py00393j. [DOI] [Google Scholar]
  35. Wei W.; Kim T. Y.; Balamurugan A.; Sun J.; Chen R.; Ghosh A.; Rodolakis F.; McChesney J. L.; Lakkham A.; Evans P. G.; Hur S. M.; Gopalan P. Phase Behavior of Mixed Polymer Brushes Grown from Ultrathin Coatings. ACS Macro Lett. 2019, 8, 1086–1090. 10.1021/acsmacrolett.9b00501. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ap1c00321_si_001.pdf (1.5MB, pdf)

Articles from ACS Applied Polymer Materials are provided here courtesy of American Chemical Society

RESOURCES