Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Apr 7;60(15):5588–5599. doi: 10.1021/acs.iecr.1c00159

Liquid–Liquid Extraction of Formic Acid with 2-Methyltetrahydrofuran: Experiments, Process Modeling, and Economics

Antero T Laitinen †, Vyomesh M Parsana ‡, Olli Jauhiainen †, Marco Huotari †, Leo J P van den Broeke §, Wiebren de Jong ∥, Thijs J H Vlugt §, Mahinder Ramdin §,*
PMCID: PMC8154433  PMID: 34054211

Abstract

graphic file with name ie1c00159_0011.jpg

Formic acid (FA) is an interesting hydrogen (H2) and carbon monoxide (CO) carrier that can be produced by the electrochemical reduction of carbon dioxide (CO2) using renewable energy. The separation of FA from water is challenging due to the strong (cross)association of the components and the presence of a high boiling azeotrope. For the separation of dilute FA solutions, liquid–liquid extraction is preferred over conventional distillation because distilling large amounts of water is very energy-intensive. In this study, we use 2-methyltetrahydrofuran (2-MTHF) to extract FA from the CO2 electrolysis process, which typically contains <20 wt % of FA. Vapor–liquid equilibrium (VLE) data of the binary system 2-MTHF–FA and liquid–liquid equilibrium (LLE) data of the ternary system 2-MTHF–FA–water are obtained. Continuous extraction and distillation experiments are performed to test the extraction power and recovery of 2-MTHF from the extract. The VLE and LLE data are used to design a hybrid extraction and distillation process to produce a commercial grade product (85 wt % of FA). A detailed economic analysis of this hybrid extraction–distillation process is presented and compared with the existing FA separation methods. It is shown that 2-MTHF is a cost-effective solvent for FA extraction from dilute streams (<20 wt % FA).

Introduction

Formic acid (FA) is an important base chemical, which can play an important role in the energy transition and the related decarbonization of the chemical industry.1 FA is an interesting molecule because depending on the reaction conditions, it can be decomposed to hydrogen (decarboxylation, HCOOH ↔ CO2 + H2) or carbon monoxide (decarbonylation, HCOOH ↔ CO + H2O).2 FA is often discussed in the context of hydrogen storage (hydrogen carrier),3 but it is a far better carbon monoxide carrier.4 Theoretically, FA contains 14 times more CO than hydrogen on a mass basis. Currently, FA is produced from fossil fuel-based feedstocks, but it can also be obtained from fermentation processes or the electrochemical reduction of CO2 according to the cathodic reaction:5

graphic file with name ie1c00159_m001.jpg 1

The electrochemical conversion of CO2 to FA is an example of carbon capture and utilization (CCU) through the so-called power-to-X concept, where (excess) intermittent renewable energy is used to produce chemicals and fuels.6 FA is one of the few CO2 electroreduction products that can be obtained with a high Faraday efficiency (>90%) and current density (>150 mA/cm2).5 Typical concentrations of FA in an electrochemical cell are lower than 20 wt %, which requires a cost-effective downstream separation process.7,8 The separation of FA from water is not an easy task due to the presence of a high boiling azeotrope containing 77.6 wt % FA at atmospheric conditions.9 The FA content in the azeotrope can be increased to 85% by elevating the pressure to 3–4 bar. The consequence of this is that the boiling point is increased as well, which has a huge impact on the energy requirements of the distillation column and results in some decomposition of FA. In practice, liquid–liquid extraction has been shown to be more economical than distillation for dilute FA streams (<30 wt %).10 In liquid–liquid extraction, a selective solvent (extractant) is used to extract FA from the aqueous solution (carrier solvent). Note that liquid–liquid extraction is typically accompanied by a distillation step to recover the product and extraction solvent. However, the recovery of FA from the extraction solvent is often less energy-intensive than the distillation of water. Many different types of chemical and physical solvents have been investigated for FA extraction, for example, phosphorous compounds, amines, alcohols, aromatics, esters, ethers, ketones, hydrocarbons, and halogenated compounds.11−13 Chemical solvents are generally more efficient in extracting FA, but the solvent recovery step is often more challenging. Recently, we have performed an extensive screening of physical solvents for FA extraction.14 High boiling solvents like ionic liquids (ILs) and deep eutectic solvents (DESs) were excluded in this study because the raffinate treatment is more complex for these solvents. In this screening study, 2-methyltetrahydrofuran (2-MTHF) was identified as an interesting solvent. In our previous work, a hybrid process based on liquid–liquid extraction and azeotropic distillation (AD) was proposed.14 Unfortunately, the process design was seriously hindered by the lack of experimental liquid–liquid equilibrium (LLE) and vapor–liquid equilibrium (VLE) data for the systems 2-MTHF–FA–water and FA–2-MTHF, respectively.

In this work, we have measured the VLE and LLE of the binary and ternary systems 2-MTHF–FA and 2-MTHF–FA–water. In addition, we performed continuous extraction experiments in a counter-current Kühni column and tested the feasibility of recovering 2-MTHF from the extract phase using continuous distillation. The LLE measurements were performed at atmospheric pressures for three different temperatures (298.15, 313.2, and 328.2 K). For the VLE measurements, an ebulliometer was used to obtain the boiling points of the 2-MTHF–FA mixtures at seven different pressures between 40 and 101.2 kPa. We have fitted the LLE and VLE data to the universal quasi-chemical (UNIQUAC) model,15 which was used in Aspen Plus to design a liquid–liquid extraction process including solvent recovery. Aspen is a simulation software widely used by the engineering community and industry to design, optimize, and analyze chemical processes. A wide range of thermodynamic models, property databases, and regressed parameters are available in Aspen Plus, which significantly reduce the workload of the process designer. The hybrid extraction–distillation process is optimized in Aspen Plus, and a detailed techno-economic evaluation is presented. The economics of the proposed process is compared with the downstream separation costs of conventional distillation processes. We show that 2-MTHF is a cost-effective solvent for FA extraction from feeds containing concentrations less than 20 wt %.

The article is organized as follows: In the next section, we will present the experimental details of the LLE and VLE measurements and the continuous extraction and distillation tests. In a subsequent section, the details of the process design and modeling in Aspen Plus will be discussed. In the Economic Analysis section, an in-depth economic analysis of the hybrid extraction–distillation process will be presented. We will summarize our findings in the Conclusions section.

Experimental Section

In this section, we will provide the details of the LLE and VLE experiments of the systems 2-MTHF–water–FA and 2-MTHF–FA, respectively. In addition, the details of the continuous extraction experiments and the recovery of 2-MTHF from the extract phase using continuous distillation are presented. The LLE data are relevant for the extraction step, while the VLE data will be used to design the solvent recovery section.

VLE Measurements

For the VLE experiments, analytical grades of 2-Methyltetrahydrofuran (2-MTHF, >98%), FA (98–100%), and acetone (>99.5%) were purchased (Loba Chemie, Mumbai) and used without further purification.

The VLE experiments were carried out using a modified ebulliometer.16,17 The ebulliometer was cleaned with acetone to remove impurities of any other chemical. Traces of acetone were also removed by keeping the system under vacuum for a few hours. The heating chamber of the ebulliometer was charged with 60 mL of the sample. The heating rate was controlled by a voltage regulator to avoid superheating of vapor or subcooling of liquid. The ebulliometer was insulated to minimize the heat loss to surroundings. The condensation of the vapor was effected by a double-wall condenser with a jacket outside and a coil inside. The continuous flow rate of cooling water was ensured and maintained by an electric pump. The temperature was measured by a calibrated Pt-100 sensor with a precision of 0.1 K. The VLE was achieved in approximately 30–40 min. The equilibrium state was indicated by constant temperature and constant drop rate of condensate vapor for about 10 min. The drop counter is provided in the ebulliometer. The low pressure was maintained by a vacuum pump, which was connected to the ebulliometer through a ballast tank. The purpose of providing the ballast tank was to avoid fluctuations, while maintaining low pressure. The pressure was measured by a mercury manometer. The isobaric vapor–liquid experiments were carried out at 7 different pressures, that is, 101.2, 89.82, 79.86, 69.91, 59.95, 50, and 40.04 kPa. The samples were analyzed by a gas chromatograph–mass spectrometer (Shimadzu, GC-2010 with GCMS-TQ8040 columns).

LLE Measurements

Methyltetrahydrofuran (2-Methyltetrahydrofuran, anhydrous ≥99%, inhibitor free) and FA (Reag. Ph. Eur. ≥ 98%) were purchased from Sigma-Aldrich and used without further purifications. Sodium hydroxide solution (Reag. Ph. Eur., 0.1 M) for the analyses was obtained from Fluka Analytical. Ion-exchanged water was used in the experiments.

LLE experiments were carried out to determine the composition of FA, water, and 2-MTHF in the extract and raffinate phases at temperatures 298.2, 313.2, and 328.2 K and atmospheric pressure. Aqueous solutions, initially containing FA mass fractions of 0.01–0.3, were first prepared by dissolving an appropriate amount of the acid into ion-exchanged water. Equal masses (50 g) of the aqueous phase and 2-MTHF solvent phase were poured into a glass cell (150 mL) equipped with an external heating jacket to maintain constant temperature during measurement and sampling. The temperature was measured by a calibrated probe (VWR digital thermometer ±0.1 °C) placed inside the glass cell. After the temperature stabilization, the mechanical stirrer (Heidolph RZR 2102 control) was turned on, and the mixture was vigorously (350 rpm) stirred for 1 h. The stirrer was then turned off, and the formation of two clear phases was noticed to take place within a few minutes. Two settling times (30 and 90 min) were initially tested, and 30 min was proven to be long enough time to reach equilibrium. The bottom valve of the glass cell was very carefully opened and the phases were separated, collected, and weighed. The mass balance deviation of the amount of loaded and analyzed FA was within 1%. The mass balance deviation values for water computed in a similar way were within 2%. It was assumed that no chemical reactions took place during the experiments, and the third component in the mixture is the solvent (2-MTHF). The reproducibility of the LLE data was tested by carrying out three trials, and the results were almost identical. The concentration of FA in the extract and raffinate phases was analyzed by titration (799 GPT Titrino Metrohm) with 0.1 M sodium hydroxide, and the amount of water in each sample was analyzed by a Karl-Fischer titrator (Mettler-Toledo). In Karl-Fischer titration, the weighed samples were injected to titration solvent (ASTM D 203 chloroform/methanol 1:3). The titration reagent contained 2-methoxyethanol, sulfur dioxide, iodine, and pyridine to keep the pH at the optimal range (Karl-Fischer reagent 5).

Continuous Counter-Current Extraction

Extraction experiments were carried out for the system FA–H2O–2-MTHF at 25 °C in a continuously operated counter-current Kühni ECR60/50G (Sulzer Chemtech) column. The aqueous phase was the continuous phase, and 2-MTHF was dispersed in the solution. The column applied contains 50 agitated compartments, and the active column height is 1860 mm. The inside diameter of the column is 60 mm, and it is equipped with a heating jacket in order to control the extraction temperature inside the column. Two experiments were performed, and each experiment lasted approximately 4 h. Three to four raffinate and extract samples were taken during each run to make sure that the column reached equilibrium. Concentration relative standard deviations in the consecutive extract and raffinate samples were within 3.7%, and the average deviation of the mass balance around the column was 1.5%, whereas the average deviation of FA balance was 2.9%. The concentration of FA in the extract and raffinate phases was analyzed by titration (799 GPT Titrino Metrohm) with 0.1 M sodium hydroxide. In the first run, 11.1 kg/h aqueous feed initially containing 2.90 wt % FA was pumped to the extraction column, and FA was extracted with 8.2 kg/h 2-MTHF solvent (S/F = 0.74). The raffinate contained 0.012 wt % FA, while the recovery of FA in the extract was 99.6% FA. In the second run, the feed contained 3.02 wt % FA, and the flow rate was 14.1 kg/h. The solvent flow rate was 12.2 kg/h (S/F = 0.87). The raffinate contained 0.003 wt % FA, while the recovery of FA in the extract was 99.9%. The stirred speed was 150 rpm in both runs.

Continuous Distillation for Solvent Recovery from the Extract

The recovery of the 2-MTHF solvent was tested in a continuously operated distillation unit made of glass. The inner diameter of the stripping section and rectifying section columns is 26 mm. The packed length of the stripping column and the rectifying columns are 1170 and 550 mm, respectively. In the bottom of both columns, there is a spiral-shaped wire mesh to support the random packing. As packing, a 6 mm Raschig ring made from borosilicate glass was applied. The condenser and feed section are each equipped with a conical-shaped part that directs the liquid flow to the center line of the column to avoid liquid flow along the column wall. The feed location connects the rectifying and stripping sections. A Labview and National Instruments cRIO-9045 system with eight modules was used to control the unit and collect input/output data, such as temperature, absolute pressure, differential pressure, electrical balance readings, peristaltic pumps, and relay for the reflux rate controller among others. The tested feed composition was 0.037 FA/0.102 H2O/0.861 2-MTHF (mass fraction). This composition corresponds approximately to the composition of the extract of a feed containing around 6 wt % FA. The column was operated at atmospheric pressure. The feed rate to the column was around 0.15 g/s, and the feeding time was 4.2 h. The reflux ratio was 4. The bottom product boiled at 108 °C and contained 78 wt % FA, the rest being water. 2-MTHF was not detected in the bottom product. The distillation experiments confirmed that the bottom product is close to the maximum temperature boiling azeotrope of FA and water, and the distillate is the heterogeneous minimum temperature boiling azeotrope that splits in an aqueous-rich phase and organic 2-MTHF-rich phase. The bottom product flow rate was very small compared to the organic distillate because the feed contained mostly 2-MTHF.

Results

VLE and LLE Measurements

The VLE data of the system 2-MTHF-FA are provided in the Supporting Information. The VLE data are plotted in Figure 1. The system 2-MTHF–FA shows a high-boiling azeotrope near a 2-MTHF mole fraction of 0.25 and 104 °C at 101.2 kPa. The azeotropic composition does not change significantly upon reducing the pressure in the studied pressure range. This information is extremely valuable for the process design. In principle, it is not desired to select a solvent for extraction that shows an azeotrope with the solute because the recovery step is more complicated. However, 2-MTHF and water also forms an azeotrope around 10.6 wt % water and 71 °C at 1 bar.18 Therefore, distilling a mixture of 2-MTHF–water–FA will yield an azeotropic mixture of 2-MTHF and water as distillate and a concentrated FA stream as bottoms. The concentration of FA in the bottom stream depends on the water content in the feed, but it will be not higher than the FA–water azeotropic composition (77.6 wt % at 1 bar). For this reason, a secondary distillation column will be required for higher FA concentrations.

Figure 1.

Figure 1

Open in a new tab

VLE data of the system FA and 2-MTHF. Symbols are experiments from this work at different pressures; 101.2 kPa (closed circles), 89.82 kPa (closed squares), 79.86 kPa (closed diamonds), 69.91 kPa (closed triangles), 59.95 kPa (open circles), 50.0 kPa (open triangles), and 40.04 kPa (open squares). Lines are UNIQUAC modeling results; see the Supporting Information for the parameters used at different pressures.

The LLE data of the system 2-MTHF-FA-water are provided in Table 1. The distribution coefficient of FA (KFA) is calculated from the mass concentrations of FA in the organic (worgFA) and aqueous phase (wH2O)19

graphic file with name ie1c00159_m002.jpg 2

Table 1. LLE Data (Mass Fraction) for the System Formic Acid (1) + Water (2) + 2-MTHF (3) at Different Temperatures.

overall composition
 extract composition
 raffinate composition
      
w1 w2 w3 w1 w2 w3 w1 w2 w3 K1 K2 α1/2
T = 298.15 K
0.080 0.420 0.500 0.093 0.142 0.765 0.063 0.821 0.116 1.476 0.173 8.53
0.080 0.420 0.500 0.092 0.141 0.767 0.063 0.813 0.124 1.460 0.173 8.42
0.030 0.470 0.500 0.038 0.081 0.881 0.022 0.861 0.117 1.727 0.094 18.36
0.007 0.493 0.500 0.009 0.053 0.938 0.005 0.884 0.111 1.800 0.060 30.02
0.143 0.357 0.500 0.151 0.213 0.636 0.124 0.737 0.139 1.218 0.289 4.21
0.005 0.495 0.500 0.007 0.052 0.941 0.004 0.868 0.128 1.750 0.060 29.21
0.015 0.485 0.500 0.020 0.063 0.917 0.011 0.876 0.113 1.818 0.072 25.28
0.060 0.440 0.501 0.073 0.120 0.808 0.046 0.833 0.121 1.587 0.144 11.02
0.150 0.350 0.500 0.159 0.223 0.618 0.132 0.738 0.130 1.205 0.302 3.99
T = 313.15 K
0.080 0.420 0.500 0.090 0.125 0.787 0.070 0.826 0.104 1.279 0.151 8.45
0.030 0.470 0.500 0.035 0.077 0.888 0.025 0.881 0.094 1.400 0.087 16.02
0.007 0.493 0.500 0.008 0.054 0.938 0.006 0.894 0.100 1.333 0.060 22.07
0.143 0.357 0.500 0.150 0.192 0.658 0.134 0.755 0.111 1.119 0.254 4.40
0.015 0.485 0.500 0.018 0.061 0.921 0.013 0.882 0.105 1.385 0.069 20.02
0.060 0.440 0.500 0.069 0.106 0.826 0.051 0.834 0.115 1.353 0.127 10.64
0.150 0.350 0.500 0.157 0.200 0.643 0.142 0.739 0.119 1.106 0.271 4.09
0.005 0.495 0.500 0.006 0.051 0.943 0.004 0.909 0.087 1.500 0.056 26.74
T = 328.15 K
0.080 0.420 0.500 0.089 0.119 0.793 0.070 0.852 0.078 1.271 0.140 9.10
0.030 0.470 0.500 0.033 0.075 0.893 0.028 0.903 0.070 1.179 0.083 14.19
0.007 0.493 0.500 0.008 0.055 0.937 0.007 0.927 0.066 1.143 0.059 19.26
0.143 0.357 0.500 0.146 0.182 0.672 0.143 0.762 0.095 1.021 0.239 4.27
0.015 0.485 0.500 0.016 0.062 0.922 0.014 0.911 0.075 1.143 0.068 16.79
0.060 0.440 0.500 0.064 0.101 0.835 0.057 0.864 0.079 1.123 0.117 9.61
0.150 0.350 0.500 0.153 0.189 0.658 0.151 0.743 0.106 1.013 0.254 3.98
0.005 0.495 0.500 0.005 0.052 0.943 0.005 0.926 0.069 1.000 0.056 17.81
Open in a new tab

Often, the distribution coefficient in Bancroft coordinates (KB) is used in shortcut calculations, which is defined as20

graphic file with name ie1c00159_m003.jpg 3

where worgFA,wfb is the mass concentration of FA in the organic phase on a water-free basis and wH2O is the mass concentration of FA in the aqueous phase on a solvent-free basis. The selectivity or the separation factor (αi/j) is calculated as the ratio between the distribution coefficients of FA and water

graphic file with name ie1c00159_m004.jpg 4

where KH2O is the distribution coefficient of water defined as the ratio of the mass fractions of water in the extract and raffinate.

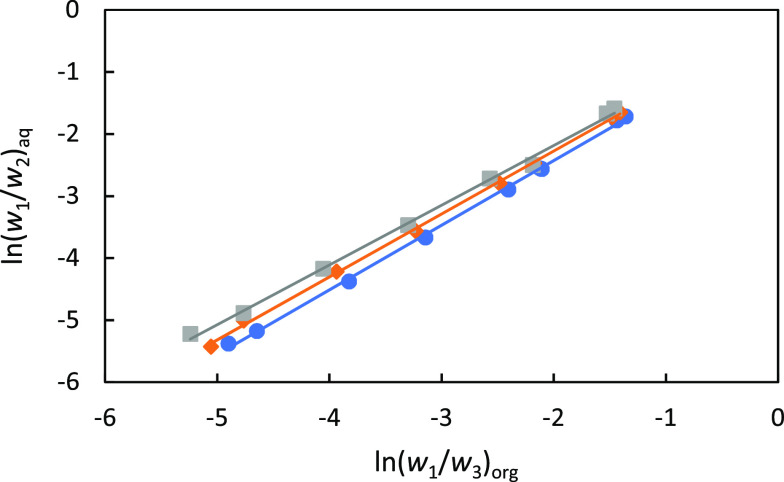
In Figure 2, the distribution coefficients and separation factors are plotted as a function of the FA concentration in the extract. The results show that the distribution coefficients of FA and the separation factor decrease, as the concentration of FA in the extract is increased. Furthermore, the distribution coefficient of FA and the separation factors are lower at higher temperatures. Nevertheless, the distribution coefficient of FA in 2-MTHF and the selectivities are among the highest observed so far for physical solvents. Figure 3a shows that the amount of co-extracted water increases as a function of the FA concentration in the extract, but the temperature effect is small. As we will show later, the amount of co-extracted water is important for the solvent recovery step. The amount of co-extracted water should be sufficient for the distillation of the water-2-MTHF azeotrope as tops and the water-FA azeotrope as bottoms. The desired amount of water can be calculated from the water contents of the water–2-MTHF and the water–FA azeotropes. The solid horizontal line in Figure 3a shows that the amount of co-extracted water is sufficient for a FA concentration of 10 wt % or higher in the extract, but water needs to be added for lower concentrations. In Figure 3b, the solubility of 2-MTHF in the aqueous phase is plotted as a function of the FA concentration in the raffinate. The solubility of 2-MTHF in the raffinate increases with the increasing FA concentration, but decreases with increasing temperature. Therefore, it may be interesting to operate the extractor at elevated temperatures, but the distribution coefficient is slightly lower at higher temperatures. The reliability of tie-line data is often checked by making a Hand plot, which describes the system in Bancroft coordinates.20 In Figure 4, a Hand plot is presented for the ternary system FA + water + 2-MTHF. The linearity of the plots gives an indication of the reliability of the measured LLE data.

Figure 2.

Figure 2

Open in a new tab

Distribution coefficients (a) and selectivities (b) of FA as a function of the FA concentration in the extract at different temperatures; 298.15 K (circles), 313.15 K (squares), and 328.15 K (diamonds). Lines are used to guide the eye.

Figure 3.

Figure 3

Open in a new tab

(a) Co-extraction of water as a function of the FA concentration in the extract and (b) solubility of 2-MTHF in the raffinate as a function of the FA concentration in the raffinate at different temperatures; 298.15 K (circles), 313.15 K (squares), and 328.15 K (diamonds). Lines are used to guide the eye.

Figure 4.

Figure 4

Open in a new tab

Hand plot for the ternary system FA (1) + water (2) + 2-MTHF (3) at different temperatures; 298.15 K (circles), 313.15 K (squares), and 328.15 K (diamonds). The subscripts org and aq refer to the organic phase and aqueous phase, respectively. The r2 values for the linear fits at 298.15, 313.15, and 328.15 K are 0.999, 0.999, and 0.997, respectively.

Clearly, 2-MTHF is an interesting solvent from the extraction point of view, but its recovery should be considered as well. The 2-MTHF–FA system shows an azeotrope, which is not desired from a solvent recovery point of view. However, as explained earlier, 2-MTHF and water form an azeotrope at much lower temperatures than the other two binary azeotropes (i.e., FA–water and 2-MTHF-FA) in the system. The consequence of this is that 2-MTHF will function like an entrainer for the azeotropic dehydration of FA. The bottom stream can only be concentrated up to the azeotropic point (77.6 wt % FA) because the FA–water mixture has the highest boiling point in the system. Therefore, a second distillation column will be required if a more concentrated FA stream is required. Here, we have used distillation at higher pressures (4 bar) to concentrate the FA stream from 75 to 85 wt %. Clearly, the separation of FA is an optimization problem governed by the interplay between capital and operating costs of different processes (e.g., extraction and pressure swing distillation). A selection between these separation methods can only be made by a detailed process design and economic evaluation.

Process Design and Modeling

An overview of the proposed process is presented in Figure 5. The process will be designed for a capacity of 1000 kg/h of FA, which is a reasonable scale for FA production from CO2 electrolysis. A feed containing 5, 10, or 20 wt % FA is introduced into the extractor, where 2-MTHF is used to extract FA from the aqueous phase. The extract containing FA, 2-MTHF, and co-extracted water is fed to the AD column. The raffinate containing water and dissolved 2-MTHF is sent to the stripper for water purification. In the AD column, a mixture of water and 2-MTHF is distilled over the top, while an azeotropic mixture of water and FA is obtained as bottoms. At atmospheric pressure, the water content and the boiling point of the 2-MTHF–water azeotrope and FA–water azeotrope are 10.6 wt % and 71 °C and 22.4 wt % and 107.7 °C, respectively. The distillate is condensed in a decanter into a water-rich stream (which is sent to the stripper) and a solvent-rich stream (which is recycled to the extractor). As explained earlier, the amount of water in the extract is very important for obtaining a concentrated FA stream, which is free of 2-MTHF, in the AD column. The amount of co-extracted water is not enough for a feed containing 5 and 10 wt % of FA in the extractor. In this case, a part of the water-rich phase from the decanter was recycled to the AD column. The amount of water that needs to be added to the extract can be calculated from the desired concentration of FA in the bottom stream (75 wt %) and the composition of the water–2-MTHF azeotrope. The amount of co-extracted water is enough for a feed containing 20 wt % of FA and no water addition was required. The raffinate and the aqueous phase of the decanters are fed to the steam stripper to purify water and recover the solvent. The organic phase from the decanters is recycled to the extractor. The FA–water azeotropic mixture from the AD column is sent to a HPD column to increase the FA concentration to 85 wt %. The concentrated FA stream leaves the HPD column as bottoms, while water is distilled over the top. In our previous work, we have used vacuum distillation (VD) to increase the FA concentration from 75 to 85 wt %. Both distillation schemes, HPD and VD, have their own advantages and disadvantages. In VD, the product containing 85 wt % FA is obtained as distillate, while in the HPD scheme, the product is obtained as bottoms. In practice, it is often preferred to have products in distillate streams because impurities tend to accumulate in bottoms. The operating cost of the VD column is relatively low because the boiling point of the FA and water azeotrope is reduced significantly at vacuum conditions. However, the drawback of the VD scheme is that the bottom stream, which contains a near-azeotropic mixture of FA and water, needs to be recycled to the AD column. As a consequence, the utility cost of the AD column increases significantly. In the HPD scheme, no recycling is required, but the utility cost of the HP column is higher due to the increased boiling points at elevated pressures. The main advantage of the VD scheme is that any concentration between 75 and 100 wt % can be achieved, while the HPD scheme only allows for a FA concentration of 85 wt % at 3 to 4 bar. Commercial processes operate according to both schemes,9 and hence the selection of one scheme over the other is not obvious and might depend on other factors (e.g., operational flexibility, stability, and on-site availability of steam) as well. Next, we will present the details of the Aspen Plus modeling.

Figure 5.

Figure 5

Open in a new tab

Hybrid extraction–distillation process. A dilute FA stream is fed at the top of the extractor, which uses 2-MTHF to extract FA. The extract is sent to an AD column where water and 2-MTHF is distilled over the top and FA is concentrated up to 75 wt % in the bottom. This FA stream is upgraded to 85 wt % in a high pressure distillation (HPD) column. The raffinate stream from the extractor and the aqueous phase from the decanters are sent to a steam stripper to recover the solvent and to purify water. The organic phase from the decanters is recycled to the extractor.

We will follow the procedure reported by Shah et al.21 for the design and modeling of the hybrid liquid–liquid extraction and AD process. The selection of a suitable thermodynamic model in Aspen Plus is crucial for the process modeling. We have selected the UNIQUAC model for the extraction, AD, and stripping columns, while the NRTL-HOC model was used for the HPD column. In principle, other thermodynamics models like PC-SAFT could be used as well, but for the process design, it is important that all systems are represented well by the selected model. It is well-known that the PC-SAFT model has difficulty in representing the VLE of the system FA and water, which shows a complex phase behavior including strong self-association and cross-association.22−24 In our previous work,14 we have shown that the NRTL-HOC model is more accurate than the UNIQUAC-HOC model for the separation of water–FA mixtures at high pressures. However, the HOC parameters for the systems containing 2-MTHF are not available in the Aspen database. The NRTL model was not able to accurately describe the ternary liquid–liquid equilibria. Therefore, we have decided to use the UNIQUAC model for the units containing 2-MTHF and NRTL-HOC for the separation of water and FA. The UNIQUAC parameters for the system 2-MTHF–water and 2-MTHF–FA were fitted to the LLE data reported by Glass et al.25 and the VLE data of this work, respectively. The NRTL-HOC parameters for the FA–water system were taken from the Aspen database. The optimized binary parameters used in the modeling at 1 bar can be found in Table 2.

Table 2. UNIQUAC Parameters Used in the Aspen Modeling.

component i water FA water
component j FA 2-MTHF 2-MTHF
temperature units °C °C °C
Aij 11.077 –0.328 –1.868
Aji –1.798 2.099 1.640
Bij –4056.980 329.832 585.150
Bji 900.666 –832.982 –924.812
Open in a new tab

Binary parameters for other pressures (not used in the process modeling) can be found in the Supporting Information. Note that we have measured the VLE of FA and 2-MTHF at isobaric conditions. Therefore, the parameters can be fitted to the VLE data at any of these pressures. For the modeling, the parameters were fitted to the VLE data at 1 bar because the azeotropic column operates at 1 bar. The binary parameters were used to calculate the LLE of the ternary 2-MTHF–water–FA system. A comparison of the modeling results and the experimental data for the binary and ternary systems is provided in Figures 6 and 7. VLE data for the system water and 2-MTHF are not available, but the UNIQUAC model can reproduce the LLE and the boiling temperature of the azeotrope (70.9 °C compared to the experimental value of 71 °C). The UNIQUAC model slightly overestimates the water content in the azeotrope (12 wt % compared to the experimental value of 10.6 wt %). The UNIQUAC model is able to accurately correlate the experimental data and is suitable for the design of separation processes containing these mixtures.

Figure 6.

Figure 6

Open in a new tab

Validation of the UNIQUAC model. (a) Comparison of experimental data of this work (symbols) with modeling results (lines) for the binary system FA and 2-MTHF at 1 bar. (b) Comparison of experimental data from Gmehling26 (symbols) with modeling results (lines) for the binary system FA and water at 1 bar. (c) Comparison of experimental data reported by Glass et al.25 (symbols) with modeling results for the binary system water and 2-MTHF.

Figure 7.

Figure 7

Open in a new tab

Prediction of the ternary LLE at 313.15 K and 1 bar using the UNIQUAC model. Mass fractions of the components are plotted on the axes.

The design of liquid–liquid extractors is not trivial and often requires pilot plant data for scale-up. The extraction column was modeled on a high level with the EXTRACT unit block in Aspen Plus. The extractor was operated at 40 °C and 1 bar. The solvent flow rate and the number of stages in the extractor were optimized to have an FA recovery of 99.9%. For designing extraction columns, as a rule of thumb, the extraction factor (E) is typically set between 1.5 and 2. The extraction factor is defined as20

graphic file with name ie1c00159_m005.jpg 5

where KB is the partition coefficient in Bancroft coordinates, and S/F is the solvent to feed ratio. The recovery (R) is defined as

graphic file with name ie1c00159_m006.jpg 6

where mFAext. and mFA are the mass flow of FA in the extract and feed, respectively. The column can be optimized by calculating the extraction factor and recovery for different solvent flow rates and stages. In Figure 8, the performance of the extractor in terms of FA recovery as a function of solvent flow rate is provided. The combination of the solvent flow rate and number of stages that resulted in an extraction factor of 1.5–2 and a recovery of at least 99.9% was selected for the design. In the modeling, we have used a solvent flow of 22,000, 11,000, and 5500 kg/h for a feed containing 5, 10, and 20 wt % FA, respectively. We have used 12 theoretical stages in the extractor for all feed concentrations.

Figure 8.

Figure 8

Open in a new tab

Mass recovery of FA in the extractor as a function of solvent flow to feed flow for different stages and feed concentrations; (a) 5 wt % FA in the feed, (b) 10 wt % FA in the feed, and (c) 20 wt % FA in the feed. The green box shows the range where the extraction factor is between 1.5 and 2.

The distillation columns and the stripper were modeled with the RADFRAC unit in Aspen Plus. The AD column was optimized using two design specifications, that is, the bottom stream should contain 75 wt % of FA and a FA mass recovery of 0.9999. The design specifications were met varying the reflux ratio and the bottoms rate. The number of stages and the feed stage were optimized by reducing the reboiler duty using the Model Analysis Tool in Aspen Plus. The distillate from the AD column was condensed in a decanter into an organic-rich phase, which was recycled to the extraction process, and a water-rich phase, which was sent to the stripper. The stripper was optimized to produce nearly pure (99.98 wt %) water as bottoms. The reboiler duty of the stripper was varied to achieve the desired water purity. The distillate from the stripper was after cooling condensed in a decanter into two liquid phases. The water-rich phase is completely refluxed to the stripper, while the organic-rich phase is recycled to the extractor. The HPD column was designed to produce at least 85 wt % FA as bottoms with a recovery of 99.99 wt % of FA. The reflux ratio and the bottom rates were varied to meet the design specifications. Similarly, the number of stages and the feed stage were optimized by reducing the reboiler duty. The tray efficiency of the distillation columns and the stripper were set to 0.75 and 0.5, respectively. The optimized parameters (number of stages, feed stage, reflux ratio, amount of water addition to the AD column, and the reboiler duty of the stripper) for the different units and different feed concentrations are provided in the Supporting Information.

The capital and operating costs of the optimized extraction–distillation process were evaluated with the Aspen Process Economic Analyzer. The assumptions and details of the economic analysis are presented next.

Economic Analysis

The optimal process design was used in Aspen Plus to determine the capital and operating costs. The built-in costing tool was used for equipment sizing and costing, and the calculation of the utilities. It is not trivial to size and scale-up extraction columns because this typically requires pilot plant data. For sizing the extractor, the empirical equations reported by Todd27 were used; see the Supporting Information for more details. The capital cost of the extractor was estimated from the correlations of Woods.28 The operating cost of the extractor is typically very small compared to the solvent recovery units and was neglected in the economic analysis. The utility prices and other parameters used in the economic analysis are listed in Table 3. The prices for cooling water and low pressure steam were taken from the report by Shah et al.21 The price of medium pressure steam was assumed to be 1/3 more expensive than the price of low pressure steam. It is important to note that utility prices can have a significant influence on the economics of a process because the operating cost is typically dominant.

Table 3. Utility Prices Used in the Aspen Modeling.

Utility unit value
Cooling water $/GJ 1.5
LP steam $/GJ 6
MP steam $/GJ 8
Open in a new tab

The basis for the economic evaluation is presented in Table 4. The capital and operating costs of the optimized hybrid extraction–distillation process for the different feed concentrations are reported in Table 5. As expected, the separation cost increases significantly with decreasing FA concentration in the feed. The costs of separating 5, 10, and 20 wt % FA are 0.382, 0.245, and 0.193 $/kg of FA. Note that these costs are reported on the basis of pure FA. For 85 wt % FA, the costs should be multiplied by 0.85. Recently, da Cunha et al.29,30 and Chua et al.31 estimated the costs of the BASF and Kemira–Leonard process for FA production, respectively. These authors estimated the costs of FA separation for the BASF process at $115/ton and around $145/ton for the Kemira–Leonard process. However, care should be taken to compare the costs of these commercial processes with our cost estimates because the process conditions are not the same. In the study of Chua et al.,31 the feed of the separation section contained 55 wt % FA, which is much higher than the concentration in our process. It is obvious that the separation cost of the Kemira–Leonard process is lower because the cost scales with the concentration. The higher the concentration, the lower the separation cost. In Figure 9, the costs of FA concentration up to 85 wt % using the proposed extraction–distillation process and the conventional HPD process is compared. The conventional HPD process was optimized in Aspen Plus for different feed concentrations. In the Supporting Information, we have reported the optimized parameters (reflux ratio, number of stages, feed stage, capital, and operating costs) for the conventional HPD process. Figure 9a clearly shows that the hybrid extraction–distillation process is much cheaper than conventional distillation for feed concentrations lower than 20 wt %. Figure 9b shows a log–log (Sherwood) plot of the costs as a function of the feed concentration. This plot also shows that extraction is an economically better option for FA concentration than conventional distillation when the concentration in the feed is low. Considering the market price of 85 wt % FA of 500 to 700 $/ton, the cost of concentrating 5 wt % FA to 85 wt % using the hybrid extraction–distillation process is relatively high. The process is most efficient in the range of 10 to 20 wt % FA in the feed because for lower concentrations, the utility cost increases significantly due to the relatively high solvent flows and the need for water addition in the extract for a proper operation of the AD column.

Table 4. Basis of Economic Evaluationa.

production capacity (kg/h) 1000
plant lifetime (y) 20
plant operation (h/y) 8000
plant location US
currency (2020) USD
Open in a new tab
a

Maintenance, depreciation, interest, and taxes are excluded.

Table 5. Capital and Operating Costs of the Hybrid Extraction–Distillation Process for Different Feed Concentrations.

feed concentration (wt %) 5 10 20
capital cost (M$) 10.584 8.987 8.373
utility cost (M$/y) 2.530 1.508 1.129
normalized CAPEX ($/kg FA) 0.066 0.056 0.052
normalized OPEX ($/kg FA) 0.316 0.189 0.141
total cost ($/kg FA) 0.382 0.245 0.193
Open in a new tab

Figure 9.

Figure 9

Open in a new tab

(a) Cost of FA separation using the proposed hybrid extraction–distillation process (squares) and conventional HPD (circles) for different feed concentrations. (b) Sherwood plot showing a typical concentration effect on the separation cost.

We have shown that 2-MTHF is a cost-effective solvent for FA extraction. However, from an application point of view, the stability of 2-MTHF in the presence of acids should be considered as well. Concentrated FA solutions are known to pose a challenge for the stability of organic compounds. According to Aycock,18 2-MTHF is very stable to bases and is stable to acids at concentrations that are typically found in most synthetic processes. Like most ethers, 2-MTHF can be cleaved at high concentrations of HCl or with many strong Lewis acids, but the cleavage rate is less than that with THF. With a 50:50 weight mixture of 2 N HCl at 60 °C, THF degrades about nine times faster than 2-MTHF, which is at least partly explained by the solubility differences of THF and 2-MTHF in the acidic aqueous phase. After 45 h mixing, 0.03% of 2-MTHF was degraded in 2 N HCl solution at 60 °C. 2-MTHF is contacted with concentrated FA in the AD column reboiler in particular. Reducing the distillation pressure in order to reduce the distillation temperature as well as short contact time should be beneficial in terms of solvent stability. It should also be pointed out that 2-MTHF will form peroxides when exposed to oxygen if no stabilizer is present. A small amount of butylated hydroxyl toluene (50 ppm) prevents peroxide formation for at least 1 year under normal storage conditions if exposed to air.18 With no stabilizer, 2-MTHF forms about 275 ppm peroxide measured as hydrogen peroxide when stirred at room temperature for 70 h.

Conclusions

FA is an interesting energy carrier that can be obtained from electrochemical reduction of CO2. Unfortunately, the FA concentration in the electrochemical reactor is typically below 20 wt %, which makes conventional distillation extremely expensive for concentrating the solution to comply with market specifications. Here, we used a hybrid extraction–distillation process to concentrate dilute FA feed streams (5, 10, and 20 wt %) to 85 wt % of FA. The solvent 2-MTHF was used to extract FA from the feed. The solvent was recovered as tops in an AD column, while 75 wt % of FA was produced as bottoms. Subsequently, a HPD column was used to concentrate the FA stream to 85 wt %. The raffinate stream from the extractor was treated in a steam stripper to recover the solvent and to purify water. To design the process, VLE data of the binary system 2-MTHF–FA and LLE data of the ternary system 2-MTHF–FA–water were measured. In addition, we have performed continuous extraction and distillation experiments to test the feasibility of 2-MTHF as extraction solvent and its recovery. The VLE and LLE data were fitted to the UNIQUAC model, which was used in Aspen Plus to simulate the hybrid extraction–distillation process and to perform a detailed economic analysis. We show that 2-MTHF is an effective solvent for FA extraction, but its recovery in the AD column is highly influenced by the amount of water in the extract. The reason for this is that water forms an azeotrope with FA and 2-MTHF, and hence the amount of water in the extract should exceed the amount of water present in the FA–water and water–2-MTHF azeotropes. The economic analysis shows that the hybrid extraction–distillation process is approximately a factor of 2 cheaper than conventional distillation for FA concentrations < 20 wt % in the feed. However, the process is most efficient in the range of 10 to 20 wt % FA in the feed because for lower concentrations, the utility costs increase significantly due to the huge solvent flows and the need for water addition in the extract to adjust the water–2-MTHF and water–FA ratios.

Acknowledgments

T.J.H.V. acknowledges NWO-CW (Chemical Sciences) for a VICI grant.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.iecr.1c00159.

  • VLE data of the system 2-MTHF and FA, UNIQUAC parameters for the binary system FA and 2-MTHF, optimized parameters for the hybrid extraction–distillation process, sizing and costing of the extractor, and optimized parameters of high pressure FA distillation at 4 bar (PDF)

The authors declare no competing financial interest.

Supplementary Material

ie1c00159_si_001.pdf (203.6KB, pdf)

References

  1. Eppinger J.; Huang K.-W. Formic Acid as a Hydrogen Energy Carrier. ACS Energy Lett. 2017, 2, 188–195. 10.1021/acsenergylett.6b00574. [DOI] [Google Scholar]
  2. Rahbari A.; Ramdin M.; van den Broeke L. J. P.; Vlugt T. J. H. Combined Steam Reforming of Methane and Formic Acid To Produce Syngas with an Adjustable H2:CO Ratio. Ind. Eng. Chem. Res. 2018, 57, 10663–10674. 10.1021/acs.iecr.8b02443. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Moret S.; Dyson P. J.; Laurenczy G. Direct synthesis of formic acid from carbon dioxide by hydrogenation in acidic media. Nat. Commun. 2014, 5, 4017. 10.1038/ncomms5017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Yu Z.; Yoshida A.; Shi J.; Wang T.; Yang S.; Ye Q.; Hao X.; Abudula A.; Fang Y.; Guan G. Formic Acid as a Bio-CO Carrier: Selective Dehydration with γ–Mo2N Catalysts at Low Temperatures. ACS Sustain. Chem. Eng. 2020, 8, 13956–13963. 10.1021/acssuschemeng.0c03269. [DOI] [Google Scholar]
  5. Ramdin M.; Morrison A. R. T.; de Groen M.; van Haperen R.; de Kler R.; van den Broeke L. J. P.; Trusler J. P. M.; de Jong W.; Vlugt T. J. H. High Pressure Electrochemical Reduction of CO2 to Formic Acid/Formate: A Comparison between Bipolar Membranes and Cation Exchange Membranes. Ind. Eng. Chem. Res. 2019, 58, 1834–1847. 10.1021/acs.iecr.8b04944. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Rego de Vasconcelos B.; Lavoie J.-M. Recent Advances in Power-to-X Technology for the Production of Fuels and Chemicals. Front. Chem. 2019, 7, 392. 10.3389/fchem.2019.00392. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Yang H.; Kaczur J. J.; Sajjad S. D.; Masel R. I. Performance and long-term stability of CO2 conversion to formic acid using a three-compartment electrolyzer design. J. CO2 Util. 2020, 42, 101349. 10.1016/j.jcou.2020.101349. [DOI] [Google Scholar]
  8. Kaczur J. J.; McGlaughlin L. J.; Lakkaraju P. S. Investigating Pervaporation as a Process Method for Concentrating Formic Acid Produced from Carbon Dioxide. C 2020, 6, 42. 10.3390/c6020042. [DOI] [Google Scholar]
  9. Hietala J.; Vuori A.; Johnsson P.; Pollari I.; Reutemann W.; Kieczka H.. Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp 1–22. [Google Scholar]
  10. Gentry J. C.; Solazzo A. J. Recovery of Carboxylic Acids From Aqueous Streams. Environ. Prog. 1995, 14, 61–64. 10.1002/ep.670140123. [DOI] [Google Scholar]
  11. Belova V. V.; Zakhodyaeva Y. A.; Voshkin A. A. Extraction of carboxylic acids with neutral extractants. Theor. Found. Chem. Eng. 2017, 51, 786–794. 10.1134/s0040579517050037. [DOI] [Google Scholar]
  12. Sprakel L. M. J.; Schuur B. Solvent developments for liquid-liquid extraction of carboxylic acids in perspective. Sep. Purif. Technol. 2019, 211, 935–957. 10.1016/j.seppur.2018.10.023. [DOI] [Google Scholar]
  13. Brouwer T.; Blahusiak M.; Babic K.; Schuur B. Reactive extraction and recovery of levulinic acid, formic acid and furfural from aqueous solutions containing sulphuric acid. Sep. Purif. Technol. 2017, 185, 186–195. 10.1016/j.seppur.2017.05.036. [DOI] [Google Scholar]
  14. Ramdin M.; Morrison A. R. T.; de Groen M.; van Haperen R.; de Kler R.; Irtem E.; Laitinen A. T.; van den Broeke L. J. P.; Breugelmans T.; Trusler J. P. M.; Jong W. d.; Vlugt T. J. H. High-Pressure Electrochemical Reduction of CO2 to Formic Acid/Formate: Effect of pH on the Downstream Separation Process and Economics. Ind. Eng. Chem. Res. 2019, 58, 22718–22740. 10.1021/acs.iecr.9b03970. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Prausnitz J.; Lichtenthaler R.; Gomes de Azevedo E.. Molecular Thermodynamics of Fluid-phase Equilibria, 3rd ed.; Prentice Hall PTR: New York, 1999. [Google Scholar]
  16. Olson J. D. Measurement of vapor-liquid equilibria by ebulliometry. Fluid Phase Equilib. 1989, 52, 209–218. 10.1016/0378-3812(89)80327-9. [DOI] [Google Scholar]
  17. Parsana V. M.; Parekh U.; Dabke S. P.; Ziniya K.; Joshi K.; Vlugt T. J. H.; Ramdin M. Isobaric Vapor–Liquid Equilibrium Data of Binary Systems Containing 2-Ethoxyethanol, 2-Ethoxyethyl Acetate, and Toluene. J. Chem. Eng. Data 2020, 65, 4798–4804. 10.1021/acs.jced.0c00291. [DOI] [Google Scholar]
  18. Aycock D. F. Solvent Applications of 2-Methyltetrahydrofuran in Organometallic and Biphasic Reactions. Org. Process Res. Dev. 2007, 11, 156–159. 10.1021/op060155c. [DOI] [Google Scholar]
  19. Müller E.; Berger R.; Blass E.; Sluyts D.; Pfennig A.. Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008; pp 1–31. [Google Scholar]
  20. Robbins L. A.; Cusack R. In Perry’s Chemical Engineers’ Handbook; Green D., Perry R., Eds.; McGraw-Hill, 1999; Chapter 15, pp 15-1–15-47. [Google Scholar]
  21. Shah V. H.; Pham V.; Larsen P.; Biswas S.; Frank T. Liquid–Liquid Extraction for Recovering Low Margin Chemicals: Thinking beyond the Partition Ratio. Ind. Eng. Chem. Res. 2016, 55, 1731–1739. 10.1021/acs.iecr.5b03914. [DOI] [Google Scholar]
  22. Román-Ramírez L. A.; García-Sánchez F.; Leeke G. A. Evaluation of association schemes in the CPA and PC-SAFT equations of state in modeling VLE of organic acids + water systems. Chem. Eng. Commun. 2020, 1–13. 10.1080/00986445.2020.1771323. [DOI] [Google Scholar]
  23. Kontogeorgis G.; Folas G.. Thermodynamic Models for Industrial Applications: From Classical and Advanced Mixing Rules to Association Theories; John Wiley & Sons: Chichester, 2010. [Google Scholar]
  24. Ramdin M.; Jamali S. H.; van den Broeke L. J. P.; Buijs W.; Vlugt T. J. H. CO2 solubility in small carboxylic acids: Monte Carlo simulations and PC-SAFT modeling. Fluid Phase Equilib. 2018, 458, 1–8. 10.1016/j.fluid.2017.11.001. [DOI] [Google Scholar]
  25. Glass M.; Aigner M.; Viell J.; Jupke A.; Mitsos A. Liquid-liquid equilibrium of 2-methyltetrahydrofuran/water over wide temperature range: Measurements and rigorous regression. Fluid Phase Equilib. 2017, 433, 212–225. 10.1016/j.fluid.2016.11.004. [DOI] [Google Scholar]
  26. Formic acid-Water Azeotropic Data: Datasheet from ’Dortmund Data Bank (DDB)–Thermophysical Properties Edition. In Springer Materials; Gmehling J., Ed.; Springer-Verlag Berlin Heidelberg & DDBST GmbH: Oldenburg, Germany, 2014, Copyright 2010-2014 Springer-Verlag Berlin Heidelberg & DDBST GmbH, Oldenburg, Germany. [Google Scholar]
  27. Todd D. B.Fermentation and Biochemical Engineering Handbook: Principles, Process Design and Equipment, 2nd ed.; Elsevier, 2014; pp 225–238. [Google Scholar]
  28. Woods D. R.Rules of Thumb in Engineering Practice; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2007; pp 376–436. [Google Scholar]
  29. da Cunha S.; Rangaiah G. P.; Hidajat K. Design, Optimization, and Retrofit of the Formic Acid Process II: Reactive Distillation and Reactive Dividing-Wall Column Retrofits. Ind. Eng. Chem. Res. 2018, 57, 14665–14679. 10.1021/acs.iecr.8b03031. [DOI] [Google Scholar]
  30. da Cunha S.; Rangaiah G. P.; Hidajat K. Design, Optimization, and Retrofit of the Formic Acid Process I: Base Case Design and Dividing-Wall Column Retrofit. Ind. Eng. Chem. Res. 2018, 57, 9554–9570. 10.1021/acs.iecr.8b00883. [DOI] [Google Scholar]
  31. Chua W. X.; da Cunha S.; Rangaiah G. P.; Hidajat K. Design and optimization of Kemira-Leonard process for formic acid production. Chem. Eng. Sci.: X 2019, 2, 100021. 10.1016/j.cesx.2019.100021. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ie1c00159_si_001.pdf (203.6KB, pdf)

Articles from Industrial & Engineering Chemistry Research are provided here courtesy of American Chemical Society

RESOURCES