Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Apr 9;143(15):5745–5754. doi: 10.1021/jacs.1c00331

Diphenylanthracene Dimers for Triplet–Triplet Annihilation Photon Upconversion: Mechanistic Insights for Intramolecular Pathways and the Importance of Molecular Geometry

Axel Olesund †, Victor Gray †,‡, Jerker Mårtensson †, Bo Albinsson †,*
PMCID: PMC8154513  PMID: 33835789

Abstract

graphic file with name ja1c00331_0010.jpg

Novel approaches to modify the spectral output of the sun have seen a surge in interest recently, with triplet–triplet annihilation driven photon upconversion (TTA-UC) gaining widespread recognition due to its ability to function under low-intensity, noncoherent light. Herein, four diphenylanthracene (DPA) dimers are investigated to explore how the structure of these dimers affects upconversion efficiency. Also, the mechanism responsible for intramolecular upconversion is elucidated. In particular, two models are compared using steady-state and time-resolved simulations of the TTA-UC emission intensities and kinetics. All dimers perform TTA-UC efficiently in the presence of the sensitizer platinum octaethylporphyrin. The meta-coupled dimer 1,3-DPA2 performs best yielding a 21.2% upconversion quantum yield (out of a 50% maximum), which is close to that of the reference monomer DPA (24.0%). Its superior performance compared to the other dimers is primarily ascribed to the longer triplet lifetime of this dimer (4.7 ms), thus reinforcing the importance of this parameter. Comparisons between simulations and experiments reveal that the double-sensitization mechanism is part of the mechanism of intramolecular upconversion and that this additional pathway could be of great significance under specific conditions. The results from this study can thus act as a guide not only in terms of annihilator design but also for the design of future solid-state systems where intramolecular exciton migration is anticipated to play a major role.

Introduction

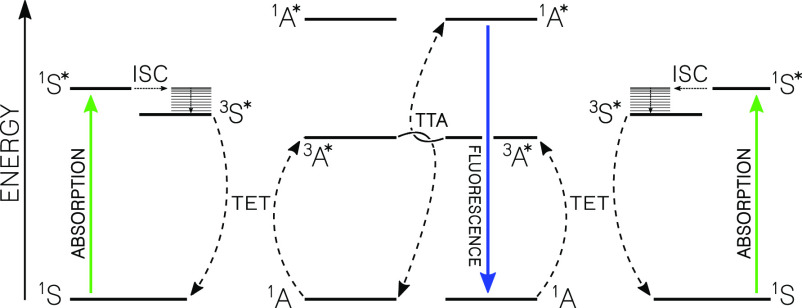
The ability to manipulate incoming sunlight to improve the spectral matching for different applications has seen great progress in recent years. Shockley and Queisser famously derived the intrinsic limit for p–n junction solar cell efficiencies more than 50 years ago,1 and two different ways of breaking this limit have gained extensive attention. To mitigate thermalization losses due to excess energy in the photons arriving at the junction, singlet fission (SF), a process in which a singlet excited state may be converted into two triplet excited states, has been proposed.2 The reverse of SF, that is, combining two low-energy photons into one high-energy excited state (exciton), is referred to as photon upconversion.3,4 This could be used to manage the losses associated with insufficient photon energy, thus expanding the spectral range of the solar cell.5,6 The process may operate by several different mechanisms, and triplet–triplet annihilation upconversion (TTA-UC) is one possible mechanism (Figure 1) that may proceed utilizing low-intensity, noncoherent light. Thus, TTA-UC is of special interest not only for photovoltaics7−10 but also in other solar energy conversion applications, such as photocatalysis11−13 and photochemistry.14−16 Two compounds are needed in this process: a sensitizer (S) and an annihilator (A). The sensitizer molecule absorbs one long wavelength photon and undergoes rapid intersystem crossing (ISC). Dexter-type triplet energy transfer (TET)17 from the sensitizer subsequently populates the first triplet excited state (3A*) of the annihilator molecule. This is then followed by TTA between two triplet excited annihilators, forming one ground-state (1A) and one singlet excited-state (1A*) annihilator, of which the latter may emit one shorter-wavelength photon.

Figure 1.

Figure 1

Open in a new tab

Jablonski diagram depicting the energy levels and transfer steps involved in photon upconversion by triplet–triplet annihilation (TTA-UC). S = sensitizer; A = annihilator.

The most efficient systems developed to date are liquid solutions of S and A,18 allowing for swift diffusion of long-lived triplets and thus promoting the short-range Dexter-type events. For practical applications solid-state solutions are however needed, introducing obstacles in terms of inefficient energy transfer due to spatial separation between the molecules.19 One way to mitigate these obstructions is by allowing the TTA event to proceed in an intramolecular fashion in addition to the intermolecular counterpart, which would require excitons to diffuse within the annihilator instead of relying on molecular diffusion.20−33 Our group has previously studied dendrimeric and oligomeric frameworks of covalently bonded 9,10-diphenylanthracene (DPA) units, showing that intramolecular TTA-UC in rigid environments is promoted by large annihilator frameworks.23 This behavior was further investigated using porphyrin–anthracene complexes, showing that parasitic back energy transfer from the anthracene unit to the covalently attached porphyrin is subdued as the anthracene unit increases in size.24,32 Several recent contributions have investigated different types of dimeric annihilators based on DPA29,31 and tetracene,22,33 respectively, in which intramolecular TTA (intra-TTA) is hypothesized to occur. A full mechanistic picture of intramolecular upconversion is however lacking, and different models for the energy transfer events have been proposed.23,29,31,33

In this study, four novel dimeric compounds based on DPA have been synthesized and investigated. The dimeric nature allows these annihilators to hold two triplets (triplet excited states) simultaneously, thus enabling intra-TTA in addition to conventional intermolecular TTA. The importance of structure and molecular geometry has been thoroughly investigated for SF and has been shown to play an important role in governing the SF efficiency and rate.34−40 In contrast, the structural effects of intra-TTA have not been fully understood. These dimers allow us not only to investigate the mechanism of intramolecular upconversion but also to draw conclusions with regard to how structural motifs of the annihilators relate to the upconversion performance.

Results and Discussion

Design and Synthesis of DPA Dimers

Synthesis details (Figure S1) as well as the proton and carbon NMR spectra for the dimers (Figures S2–S9) are found in the Supporting Information. The dimers consist of two anthracene units which are connected in four different ways. Three of the dimers, 1,2-bis(10-phenylanthracen-9-yl)benzene (1,2-DPA2), 1,3-bis(10-phenylanthracen-9-yl)benzene (1,3-DPA2), and 1,4-bis(10- phenylanthracen-9-yl)benzene (1,4-DPA2), have a central phenyl ring, and the numeric indices indicate at which positions the anthracenes connect to the ring. In comparison, 10,10′-diphenyl-9,9′-bianthracene (9,9′-PA2) lack the central phenyl ring connector, and instead the anthracene moieties are directly connected at their respective 9-positions.

Photophysical Characterization

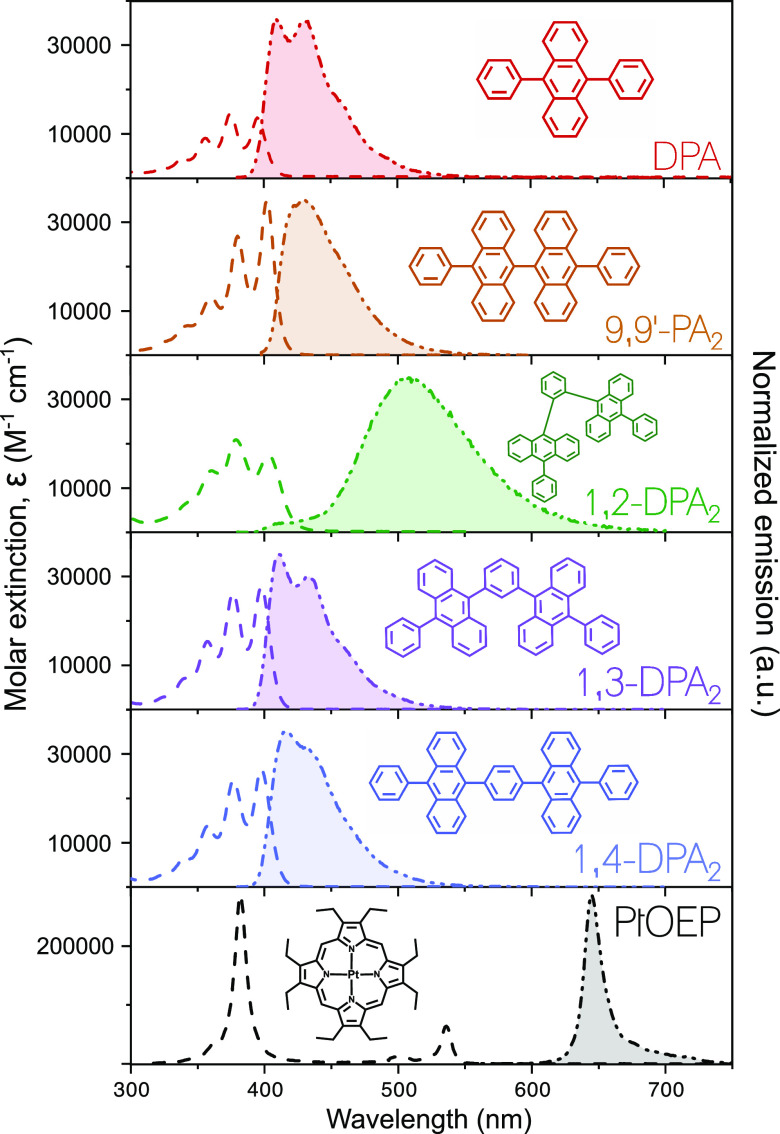
Figure 2 presents the absorption and fluorescence spectra of DPA and the dimer compounds, alongside that of platinum octaethylporphyrin (PtOEP). The latter was employed as the sensitizer during TTA-UC owing to its suitable energetics, strong absorption, and rapid intersystem crossing.41 The molar absorptivity of the dimers is roughly two times higher than for DPA, which is expected given the dimeric nature of these compounds. The vibronic progression is clearly visible in the absorption features of all dimers, with relative intensities of the vibronic peaks being the major difference between different spectra. Only minor shifts of the peak positions were observed. More pronounced differences were found upon investigation of the fluorescence properties. All compounds have a high fluorescence quantum yield close to unity in deaerated toluene, thus fulfilling one important prerequisite to perform well as an annihilator in TTA-UC.4 The fluorescence lifetimes are slightly shorter than for DPA for all dimers except 1,2-DPA2. Although not quantitatively reflected in the increased molar absorptivities, the faster radiative rates of the dimers show that the linked DPA chromophores interact electronically. Too weak emission at 410 nm from 1,2-DPA2 at room temperature hindered us from properly monitoring the lifetime of monomeric fluorescence, i.e., fluorescence originating from the isolated, noninteracting DPA moieties. The tabulated lifetime at 410 nm was instead measured at 93 K where short-wavelength fluorescence dominates. The findings are summarized in Table 1. A substantial red shift is seen for the fluorescence of 1,2- DPA2, with only a small fraction of the fluorescence taking place at shorter wavelengths at room temperature (Figure S11). This behavior is ascribed to the formation of an excited dimer, or excimer, upon excitation and has previously been observed for a number of different annihilator molecules.42−44 The creation of excimers is normally highly dependent on chromophore concentration as it is formed through interactions between a ground-state and an excited-state molecule. The fluorescence from 1,2-DPA2 does not show this dependence on concentration. The long-wavelength emission is dominating also for low-concentration samples, and thus, the excimer is believed to form by means of intramolecular interactions.42,45,46 The behavior and kinetics of 1,2-DPA2 were investigated thoroughly but are not the main focus of this paper, and the interested reader is referred to Section 3 of the Supporting Information. It is important to point out that, at room temperature, the lifetime of the initially excited singlet state of 1,2-DPA2 is very short (<10 ps) due to quantitative transformation into the singlet excited excimer, which is why all emission emanates from the excimer irrespectively if populated through TTA or direct excitation. A large fraction of this emission lies at longer wavelength than 532 nm and is, thus, not strictly speaking upconverted.

Figure 2.

Figure 2

Open in a new tab

Absorption (dashed) and emission (dot–dash) spectra of the investigated annihilators and the sensitizer PtOEP.

Table 1. Photophysical Properties of DPA and Dimers.

  E0–0 (nm)a λem (nm)b ϕf τf (ns)c
DPA 393 (13.6) 409 1.00 6.91
9,9′-PA2 402 (35.0) 431 1.00 6.56
1,2-DPA2 403 (17.3) 511 0.95 7.32d, 44.0e
1,3-DPA2 398 (27.7) 411 0.96 5.85
1,4-DPA2 398 (26.7) 416 0.95 4.56
Open in a new tab
a

Wavelength of 0 → 0 transition and molar absorptivity, ε (×103 M–1 cm–1).

b

Wavelength of maximum emission upon 377 nm excitation at 295 K.

c

Fluorescence lifetime probed at 410 nm and 295 K.

d

Probed at 410 nm and 93 K.

e

Probed at 510 nm and 295 K.

Upconversion Study

The upconversion potential of the four dimers has been evaluated in a series of experiments. The upconverting samples consisted of 6.6 μM PtOEP and 1 mM (DPA) or 0.5 mM (dimers) annihilator, which upon 532 nm excitation produced bright upconverted fluorescence (Figures S16–S17). No upconverted emission could be detected when PtOEP was absent from the samples.

A figure of merit which is of big importance when evaluating upconverting systems is the upconversion quantum yield, ϕUC. It is defined as the number of emitted high-energy photons compared with the number of absorbed low-energy photons and can thus take a maximum value of 50%.47 The efficiency is dependent on the quantum yield of all steps leading up to the emission of photons in accordance with eq 1:

graphic file with name ja1c00331_m001.jpg 1

Here, ϕISC is the intersystem crossing quantum yield of the sensitizer, ϕTET is the quantum yield of triplet energy transfer from sensitizer to annihilator, ϕTTA is the quantum yield of triplet–triplet annihilation, and ϕf is the fluorescence quantum yield of the annihilator. The spin statistical factor, f, defines the fraction of excited annihilator triplets that go on to create an emissive singlet excited state following TTA.18 Evaluating each of the terms in eq 1 is not viable, and instead the method of relative actinometry (eq 2) is used:

graphic file with name ja1c00331_m002.jpg 2

Here, ϕr is the known fluorescence quantum yield of a reference compound, Ai is the absorption at the excitation wavelength, Fi is the integrated emission intensity, and ηi is the refractive index. Subscripts r and UC denote reference sample and upconversion sample, respectively. Rhodamine 6G in air-saturated ethanol was employed as the reference compound (ϕf = 0.95)48 during UC measurements.

All dimers exhibit efficient upconversion upon 532 nm excitation (Table 2). 9,9′-PA2, 1,2-DPA2, and 1,4-DPA2 perform similarly, yielding a quantum yield of around 15%. Interestingly, 1,3-DPA2 outperforms the other dimers, showing an impressive 21.2% ϕUC which is comparable with 24.0% for DPA. Dimerization in the meta-position has previously yielded higher UC efficiencies than the corresponding para- and ortho-connected annihilators,31 and our results indicate that connections in the meta-position are beneficial at least for DPA-type dimer annihilators. The calculated thermodynamic driving forces for TTA, i.e., 2 × E(T1) – E(S1), are similar for all annihilators and do not explain the differences in our results.

Table 2. Experimentally and Computationally Determined Parameters Important to the Upconversion Process.

  ΦUCa Ithb (mW/cm2) kTETc (×109 M–1 s–1) kTTAd (×109 M–1 s–1) τTe (ms) kTf (×103 s–1) E(S1)g (eV) E(T1)h (eV) 2 × E(T1) – E(S1)j (eV)
DPA 0.240 15 1.78 3.01 5.5 0.18 3.05/3.15 1.72i 0.29
9,9′-PA2 0.150 605 0.99 3.73 0.56 1.79 2.86/3.08 1.72 0.36
1,2-DPA2 0.140 142 0.95 2.89 0.80 1.25 2.85/3.08 1.71 0.34
1,3-DPA2 0.212 44 1.04 2.81 4.7 0.21 3.04/3.12 1.72 0.32
1,4-DPA2 0.149 1343 0.96 4.00 0.29 3.44 3.06/3.12 1.72 0.32
Open in a new tab
a

Upconversion quantum yield relative to a theoretical maximum of 0.5 (50%).

b

Threshold intensity. Individual values have been normalized with respect to slight deviations in [S] between samples.

c

Rate constant for triplet energy transfer from PtOEP.

d

Rate constant for triplet–triplet annihilation.

e

First triplet excited-state lifetimes.

f

Rate constant for intrinsic triplet decay.

g

Energy of the first singlet excited state as calculated with TD-DFT (B3LYP/6-31G**)/calculated from the 0 → 0 transition of the absorption spectra. See the Supporting Information for calculation details.

h

Energy of the first triplet excited state as calculated with TD-DFT.

i

Experimental literature value50 is 1.77 eV.

j

Thermodynamic driving force for TTA.

In order to understand why 1,3-DPA2 exhibits a higher ϕUC than the other dimers, further experiments aimed at understanding the kinetics involved were performed. Efficient triplet energy transfer between sensitizer and annihilator is a feature present in all high-performing UC systems and may be investigated using Stern–Volmer quenching (eq 3):

graphic file with name ja1c00331_m003.jpg 3

I and I0 are the quenched and unquenched donor emission, respectively, kTET is the rate constant for TET from donor to acceptor, τ0 is the lifetime of the unquenched donor, and [A] is the quencher concentration. The quenching of PtOEP with the five different annihilators was determined by monitoring the phosphorescence of PtOEP, and the resulting Stern–Volmer plots are presented in Figure 3. The unquenched lifetime of PtOEP was determined to be 95 μs in deaerated toluene (Figure S20), and TET from PtOEP to the annihilators is found to be very efficient in all cases. The kTET rate constants of the dimers are roughly half that of DPA (measured in DPA subunit concentrations, Table 2), which is reasonable given that the lower diffusivity of the dimers is compensated for by a larger collision radius according to the Smoluchowski equation.49 All TET efficiencies are 99% or higher for DPA subunit concentrations of [A] = 1 mM, and it was concluded that the TET step is not the determining factor when evaluating these dimers against each other.

Figure 3.

Figure 3

Open in a new tab

Stern–Volmer plots of TET from PtOEP (3.4 μM) to the five annihilator compounds.

Another important figure of merit when evaluating upconverting systems is the threshold intensity, Ith. This is the excitation intensity at which ϕUC reaches 50% of a systems’ maximum and is related to system parameters as in eq 4:

graphic file with name ja1c00331_m004.jpg 4

The absorption cross section, α, and ground-state concentration, [1S], of the sensitizer are the same in all upconverting samples. Only the rate of intrinsic triplet decay of the annihilator, kT, and the rate of TTA, kTTA, will thus influence differences in Ith between annihilators. The Ith value defines the crossing point between a quadratic region where the supply of annihilator triplets is the limiting factor and a linear region where UC proceeds with the highest possible efficiency. For practical applications it is desirable to have as low an Ith as possible, as this facilitates possible applications using solar energy (the power density from the sun between 470 and 550 nm, i.e., the absorption range for the PtOEP Q-band, is approximately 15 mW/cm2 under AM1.5 solar irradiation). The excitation power density dependence on the UC emission intensity of our systems is presented in Figure 4. 1,2-DPA2 and 1,3-DPA2 have Ith values reasonably close to what is usually seen for compounds based on DPA (142 and 44 mW/cm2, respectively) but are significantly higher than the acquired value for DPA (15 mW/cm2, see also Table 2). The less congested dimers 9,9′-PA2 and 1,4-DPA2 have Ith values of 605 and 1343 mW/cm2, respectively, which is more than 1 order of magnitude higher than that of DPA. At closer examination of Figure 4B it becomes obvious that the linear regime (slope 1) has not been fully reached by either 9,9′-PA2 or 1,4-DPA2 at our setups maximum power density, and the presented values thus represent a lower estimate of their respective Ith value. The spread in Ith values is a bit surprising given that other studies on DPA-based molecules have shown a narrow distribution of threshold intensities and often close to that of DPA.29,31,51 These unexpected results were further analyzed by examining eq 4 and seeking to determine the parameters involved.

Figure 4.

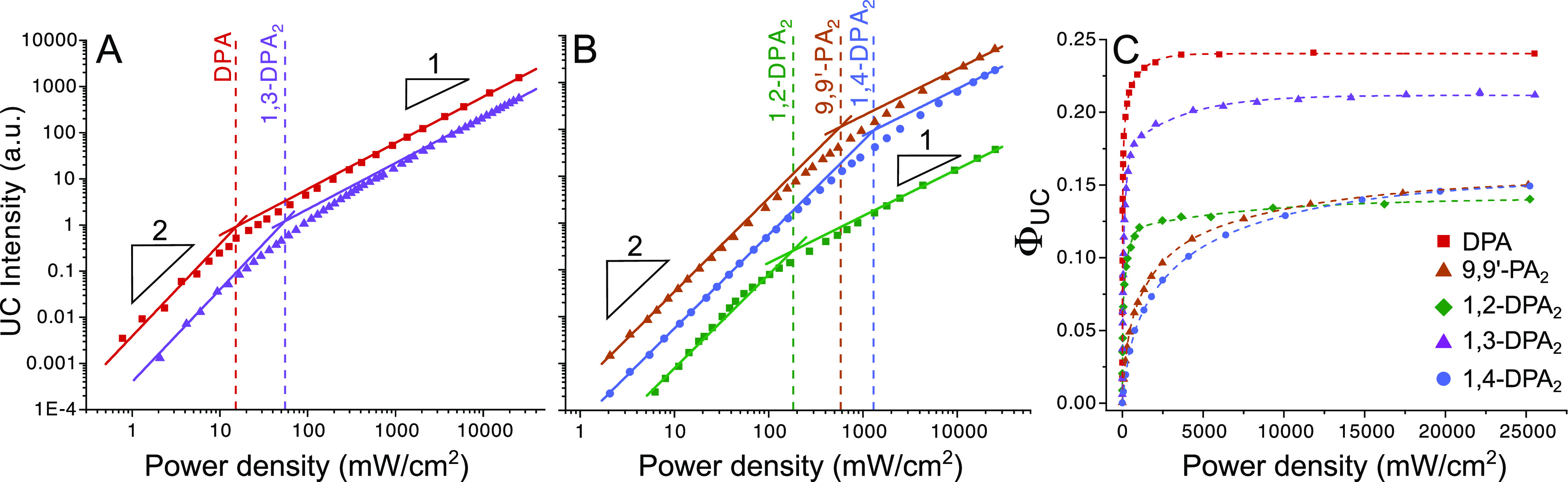
Figure 4

Open in a new tab

(A, B) Double-logarithmic plots of upconversion emission intensity versus excitation power density (532 nm). The threshold intensity Ith for each annihilator is indicated by vertical dashed lines, and quadratic and linear slopes (solid lines) for each compound are included for facile evaluation of Ith. Individual plots have been vertically shifted for clarity purposes. (C) UC quantum yield versus excitation power density for the annihilators.

Vital to an efficient upconversion process are long-lived annihilator triplet states, as this allows for diffusion-mediated annihilation to proceed more efficiently. Using time-resolved emission measurements and a fitting procedure based on eq 5, the annihilator triplet lifetimes, τT, and related kT rate constants could be determined (Table 2). The annihilator triplet state may decay by both first- and second-order channels, and the observed kinetics of the upconverted fluorescence will thus depend on the annihilator triplet concentration:52

graphic file with name ja1c00331_m005.jpg 5

Here, I(t) is the emission intensity, β is a dimensionless parameter between 0 and 1 expressing what fraction of initial decay is governed by second-order channels (with β = 1 meaning all initial decay is of second order), and t is time. Full details are found in the Supporting Information. As was the case with Ith, these compounds show a rather broad distribution of triplet lifetimes, ranging from 291 μs for 1,4-DPA2 to 5.5 ms for DPA (Figures S21–S24 and Table 2). 1,3-DPA2 (Figure 5) has the most long-lived triplet out of the dimers, which explains the high ϕUC as well as the relatively low Ith, while the shorter triplet lifetimes of 9,9′-PA2 and 1,4-DPA2 are consistent with higher Ith values. The longer lifetime of the triplet state in 1,3-DPA2 could potentially be explained by the decreased electronic coupling between the moieties due to linkage in the meta-position,31,53−55 thus better retaining the properties of the DPA monomer. This notion was strengthened by calculations of the electronic coupling between the triplet excited states of the dimers (see Supporting Information, Section 4.4). The second parameter that affects the threshold intensity is the rate of annihilation. kTTA was determined for all compounds using nanosecond transient absorption, monitoring UC samples at 430 nm and at 646 nm following 532 nm excitation. The transient signals are presented in Figures S26–S30, and a global fitting procedure was used to obtain the rate constants of interest (the full procedure is explained in the Supporting Information, Section 4.3). The kTTA rates are quite similar (see Table 2), but interestingly 9,9′-PA2 and 1,4-DPA2 show slightly elevated rates, even compared to DPA.

Figure 5.

Figure 5

Open in a new tab

Time-resolved, delayed upconverted fluorescence from 1,3-DPA2 in the presence of PtOEP. The emission is measured at 430 nm and at different pump excitation intensities (532 nm). Solid lines are best global fits to eq 5.

Intramolecular Upconversion in Solution

The design of our annihilators was in part based on the possibility of populating the molecules with two triplets simultaneously, as this enables intramolecular upconversion (hereon after referred to as intra-UC). Instead of relying on molecular diffusion, this mechanism may rely on the diffusion of excitons within a molecular system. Several recent studies exploiting dimeric,22,29,31,33 polymeric,20,21,26−28,30 and oligomeric23 structures have sought to investigate the influence of this additional pathway. In a recent study, Gao et al. studied structurally similar DPA derivatives which were separated with additional phenyl groups.31 The coupling pattern, para-, ortho-, meta-, was however the same as in the present study. Interestingly, the ϕUC trend follows what we observe here: DPA > meta- > ortho- and para-. However, in their case no significant difference in the triplet lifetime was observed between the derivatives and can thus not explain this trend. The difference was instead assigned to greater intra-TTA contributions for the meta-coupled dimer, which were indicated by means of magnetic-field-dependent measurements of the UC performance. It should be noted that their reported triplet lifetime of DPA was roughly five times shorter than that reported herein. This discrepancy is likely caused by differences in the type of measurement and fitting procedures, as Gao et al. used transient absorption without taking second-order channels into account during fitting. Figure S25 highlights that a single-exponential tail fit significantly underestimates the triplet lifetime, especially in systems with high TTA efficiencies.

In this section, the quest to fully understand intra-UC is continued, as there are still disagreements on how the actual mechanism of intra-UC proceeds in solution-based systems. Two different mechanisms are predominantly considered in the literature, and these are schematically presented in Scheme 1 alongside the intermolecular upconversion (inter-UC) route (pathway 1 in Scheme 1) always present in solution-based systems. The triplet energy transfer between annihilators model (TETA model, pathway 2a in Scheme 1) has been suggested by several authors29,31 and is based on the interactions between two multichromophoric triplet excited annihilators, 3A*–1A (in this section, annihilators are assumed to have the capacity of holding two triplets simultaneously and are then designated 3A*–3A*). Normally the interaction between two 3A* leads to an intermolecular TTA event where the f factor (see eq 1) determines the yield of singlet excited states. However, when two 3A*–1A interact there is the additional possibility of a triplet energy transfer step from the triplet moiety of one annihilator to the ground-state moiety of the other, creating one 3A*–3A* and one 1A–1A annihilator. An intra-TTA event between two triplets then rapidly gives the singlet excited state 1A*–1A and subsequent emission of an upconverted photon. It has been suggested that the TET step between two singly excited dimeric annihilators proceeds statistically, meaning that half of these interactions lead to 3A*–3A*, while only 25% proceeds through the common intermolecular TTA pathway to produce the singlet excited state 1A*–1A.31

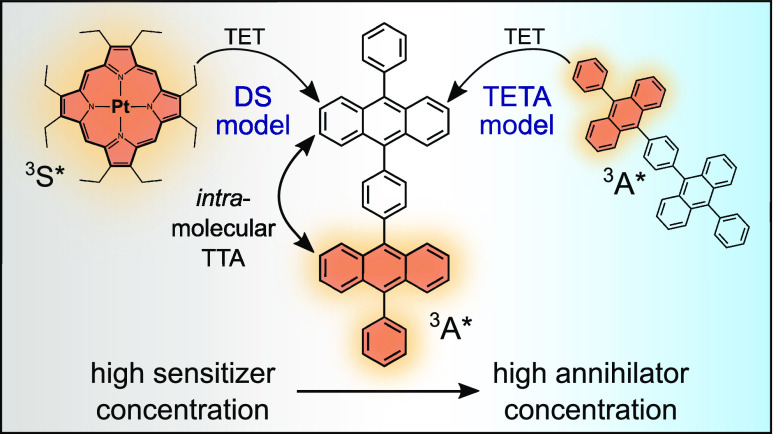
Scheme 1. Intermolecular Upconversion vs Two Suggested Models for Intramolecular Upconversion: TETA and DS.

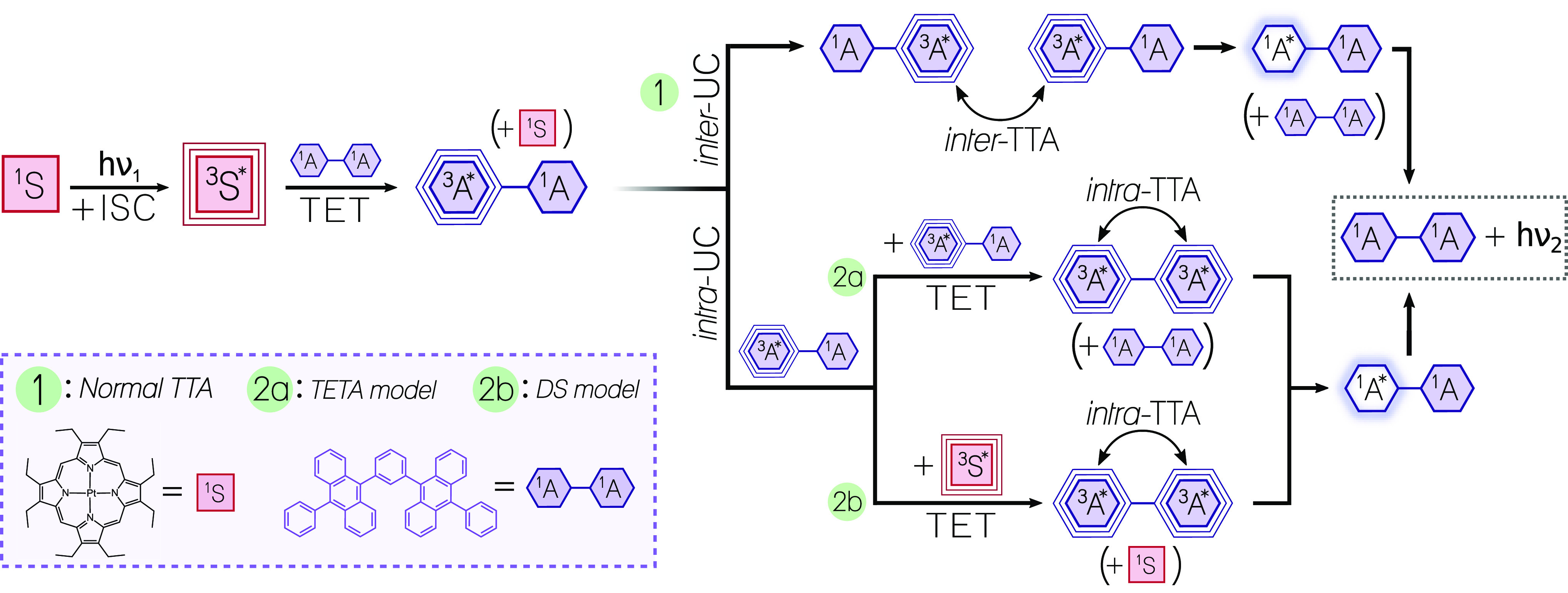
Scheme 1

Open in a new tab

Schematic of suggested pathways for triplet–triplet annihilation upconversion with dimeric annihilator compounds (here represented by 1,3-DPA2). Designations: S = sensitizer, A = annihilator moiety (spin multiplicity denoted by left superscript), * = excited state. Upon light absorption (hν1) and rapid intersystem crossing (ISC), the sensitizer populates the triplet excited state of one annihilator moiety through triplet energy transfer (TET). The TTA event forms a singlet excited state, and one high-energy photon (hν2, ν2 > ν1) is emitted. (1) Conventional intermolecular TTA between two triplet excited dimers. (2a) TET between annihilators (TETA) model: The triplet excited dimer becomes doubly excited following TET from another triplet excited annihilator. (2b) Double sensitization (DS) model: The ground-state moiety of the singly triplet excited dimer is populated with another triplet following TET from a sensitizer molecule.

The double-sensitization model (DS model, pathway 2b in Scheme 1) relies not on TET between annihilators but rather on a second TET step from a triplet excited sensitizer (3S*) to the ground-state moiety of 3A*–1A, ultimately leading to a 3A*–3A* annihilator which can proceed to perform intra-TTA. This model has been employed in a multitude of other studies,22,23,28,33 but the conclusions of different investigations in low-viscosity media vary significantly. In pursuit of elucidating the nature of intra-UC, steady-state and time-resolved simulations of the presented models were performed. The experimentally determined parameters for each annihilator (i.e., kTET, kT, and kTTA) were used during simulations, and the detailed description of the kinetic model is presented in the Supporting Information.

The two models have been evaluated for two different sample conditions: typical UC conditions (i.e., [1A]0 = 1 mM, [1S]0 = 5 μM), which will be referred to as high annihilator to sensitizer ratios ([1A]0/[1S]0), and conditions with low [1A]0/[1S]0 ratios (i.e., [1A]0 ≈ 10 μM, [1S]0 = 100 μM). This has been done in order to investigate the expected influence from each intra-UC mechanism separately and to draw conclusions on in which regimes each model is valid. Time-resolved simulations were performed, which are presented in Figure 6. At high [1A]0/[1S]0 ratios, the TETA model predicts that the dimer UC emission kinetics are slightly slower than in the DS model. However, both models predict that the kinetics get slower upon lowering [1A]0. The largest difference between the models is the evolution of early time kinetics, which are related to the TET events. No major difference between the models is discernible at high [1A]0/[1S]0 ratios (Figure 6A, B), but upon going to low [1A]0/[1S]0 it is clear that the DS model predicts that dimers will have a much faster rise time relative to that of DPA, a behavior not predicted by the TETA model (Figure 6E, F). Given the nature of the DS model, the faster early time kinetics would be expected as the intra-UC pathway depends on TET from 3S*, an event most likely to take place early on.

Figure 6.

Figure 6

Open in a new tab

Simulation results for the (A, E) TETA model, (B, F) DS model, (C, G) model where intra-TTA contributions are disallowed, and (D, H) experimental kinetic traces from delayed UC fluorescence emanating from (A–D) samples with [1S]0 = 5 μM and [1A]0 = 1 mM (i.e., [1A]0/[1S]0 = 100), and (E–H) samples with [1S]0 = 100 μM and [1A]0 = 5 μM (i.e., [1A]0/[1S]0 = 0.05). Emission monitored at 430 or 510 nm (for 1,2-DPA2).

To further elucidate the differences between the two models, steady-state simulations were also performed. Figure S33 shows the expected steady-state delayed UC fluorescence following 532 nm continuous-wave (cw) excitation for high [1A]0/[1S]0 ratios, with [1A]0 ranging from 0 to 5 mM. It is clear that the potential contribution from intra-UC is indiscernible at higher [1A]0 according to the DS model, which is expected as generated 3S* will quickly transfer their energy to surrounding ground-state 1A, thus swiftly depleting the 3S* population and hindering subsequent TET events needed to produce the doubly excited dimers (Figure S34). On the contrary, intra-UC contributions are expected to increase with [1A]0 in the TETA model, as this pathway ultimately depends mainly on [3A*–1A] (Figure S33B). Conversely, increasing [1S]0 to 100 μM gives rise to interesting behavior at lower [1A]0 (<10 μM), with the DS model predicting that intra-UC will dominate, allowing annihilator dimers to exhibit stronger UC fluorescence than their corresponding monomer under such conditions (Figure S35A). The TETA model predicts the resulting UC intensity to be lower than that of DPA also under these conditions (Figure S35B).

Samples of low and high [1A]0/[1S]0 ratios were prepared, and the behavior observed experimentally was compared with that predicted by each model. Time-resolved measurements of the UC emission display a marked difference in the kinetics when going from high (Figure 6D) to low (Figure 6H) [1A]0/[1S]0. It is clearly seen that the rise time of the UC emission of the dimers at low [1A]0/[1S]0 is faster relative to that of DPA (red line), even to such an extent that some dimers develop the UC emission faster than DPA. The evolution of the rise time kinetics in the dimers is compatible with the DS model only, which indeed predicts that the dimer UC emission will develop faster than that of DPA at low [1A]0/[1S]0 (Figure 6F). Interestingly, the kinetic evolution of the individual dimers differs slightly as well, with 1,2-DPA2 in particular showing a substantial shortening of its rise time compared with the other annihilators, indicating a stronger influence from intra-UC. While this could potentially be ascribed to differences in the intra-TTA event, simulations firmly establish that the observed differences are in fact determined by the second sensitization step (Figure S37). We find no reason to believe that the ortho-coupling in 1,2-DPA2 would cause a more efficient second sensitization step and ascribe the observed differences between individual dimers to experimental uncertainty.

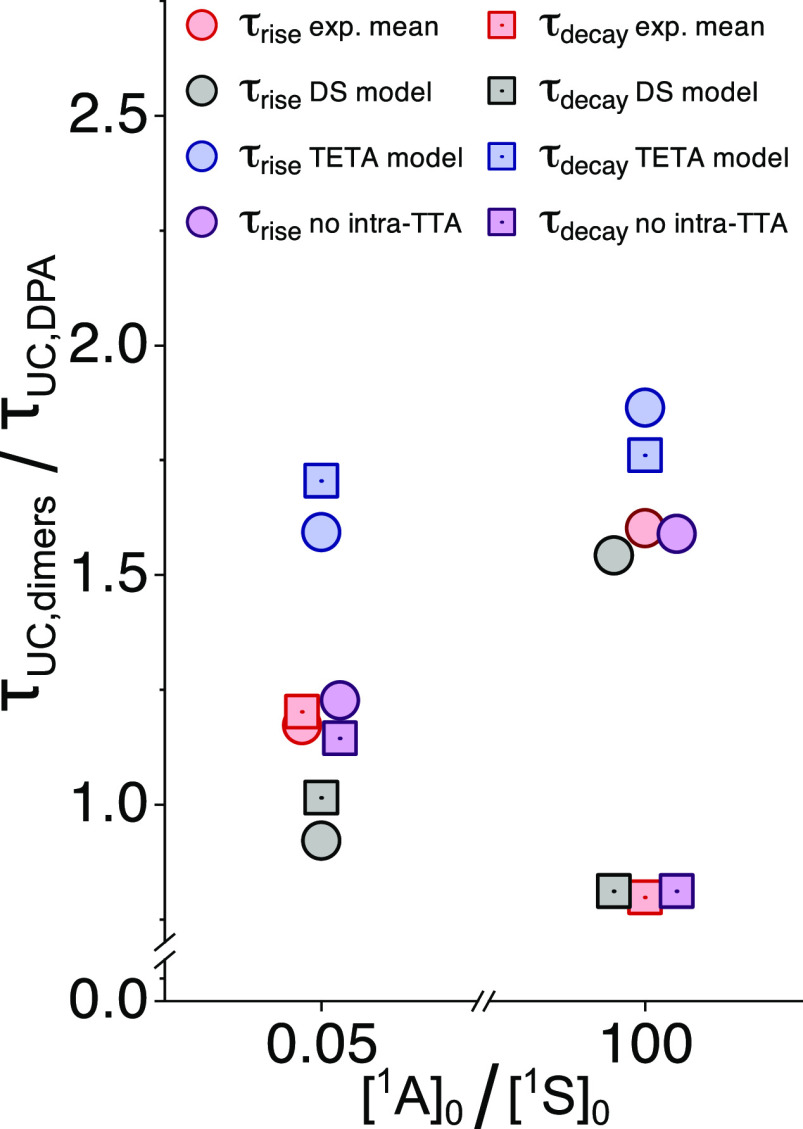
To quantify our analysis, the mean value of the rise times and decay times of our dimers was compared with that of DPA (Figure 7). The experimental ratios (red symbols) were then compared to the ratios predicted by the DS model (black symbols) and the TETA model (blue symbols) and for a scenario where intra-UC is disallowed (purple symbols). This was made at the two previously used [1A]0/[1S]0 ratios, and the results show a striking agreement between our experimental data and the model where no intra-UC occurs. The experimental data also show good agreement with the DS model, while the accordance to the TETA model is rather poor. Even though our quantified time-resolved data may be explained without involving the intra-UC pathway, such a description is not sufficient to explain the appearance of the kinetics in Figure 6H. Specifically, the immediate emergence of UC emission from the dimers during the first tens of microseconds is most likely a result of the DS mechanism and is particularly evident in the traces of 1,2-DPA2 (green) and 1,4-DPA2 (blue, see Figure 6F and 6G for a comparison of the DS model kinetics and the kinetics expected if no intra-UC contributions are present). It should be noted that the remarkable agreement between experimental data and the DS model at high [1A]0/[1S]0 ratios (Figure 7) is caused by the fact that no intra-UC is expected under such conditions, and the data is thus expected to coincide with that of the model where intra-UC is disallowed completely.

Figure 7.

Figure 7

Open in a new tab

Comparison of relevant time constants. The mean value for the dimeric annihilators is compared to the value of DPA at [1A]0/[1S]0 = 0.05 or 100. The rise times (τrise) and decay times (τdecay) are evaluated at the peak and 1/e values of the normalized emission traces, respectively.

Figure S38 shows the results from the steady-state measurements, where [1A]0 has been varied while keeping [1S]0 at 100 μM throughout, except for the rightmost data point which is given for [1A]0 = 1 mM, [1S]0 = 6.6 μM. No clear-cut interpretation is readily obtained from these data, with the only prominent feature being the relative 1,4-DPA2 emission increasing as the [1A]0/[1S]0 ratio gets lower. This could indicate that there are some contributions from intra-TTA in 1,4-DPA2 (given that the DS mechanism is active). However, 9,9′-PA2 and 1,3-DPA2 do also show signs of increased relative emission, although not as systematically as 1,4-DPA2, while 1,2-DPA2 exhibits similar behavior independent of [1A]0. The steady-state measurements are rather sensitive to experimental errors, with the evaluation of precise intensities being subject to substantial inner-filter effects, high sensitivity to exact sample concentrations, and possible oxygen contamination. Similar measurements on tetracene dimers by Pun et al. have however proved useful previously, specifically in contexts where low kTTA rates are measured for the upconverting materials.33 In this case the impact of the DS mechanism is manifested also at relatively high [1A]0/[1S]0 ratios, thus facilitating comparisons between annihilators where intra-TTA is allowed and forbidden, respectively.

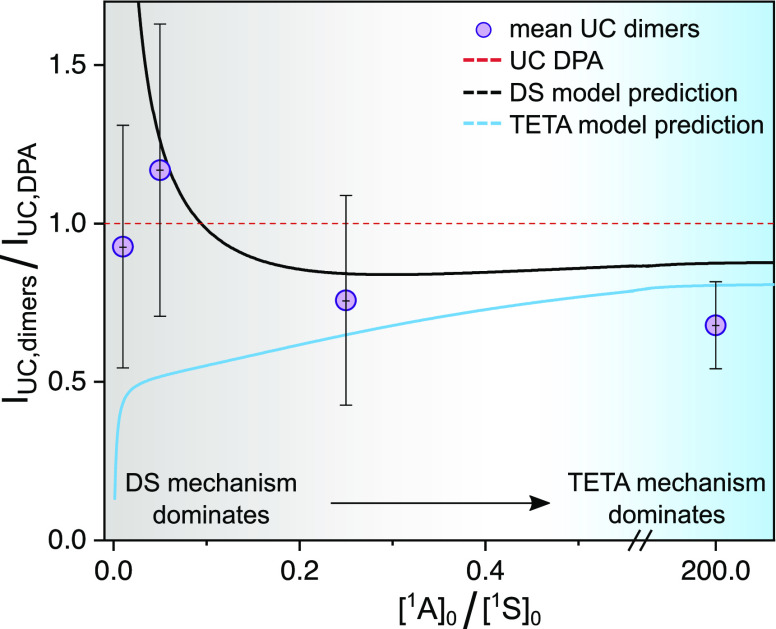
Despite the fact that our experiments did not yield any obvious signatures indicating the presence of the TETA mechanism, a closer examination of our steady-state data might shine some additional light on this matter. Although the data presented in Figure S38 show differences between the performances of individual dimers, our time-resolved measurements indicate that all investigated dimeric annihilators perform intra-TTA to some extent. It can therefore be helpful to look closer at the dimers as a group to understand the role of the intra-UC mechanism. Comparing the experimental mean performance of the dimers to the two proposed models then indicates which model explains the UC performance of the dimers as a group. We have previously established that the annihilator triplet lifetime is a crucial parameter which dictates much of the UC performance, but it cannot on its own explain the observed differences in UC efficiencies. In fact, the DS and TETA models predict slightly different UC efficiencies at different conditions, with the former complying better with our experimental findings at low [1A]0/[1S]0 ratios but the latter agreeing more with experiments at high [1A]0/[1S]0 ratios (Figure 8). Even though this transition from conditions under which the DS mechanism dominates to one where TETA dominates is not unambiguous, this change is expected given that the intra-UC mechanism in the DS and TETA models depends on [3S*] and [3A*-1A], respectively, which are high at each extreme of Figure 8. The correspondence between simulation and experiment is however not without fault, and the relatively low UC efficiencies of the dimers compared to DPA at high [1A]0/[1S]0 ratios (rightmost point in Figure 8) could possibly be due to differences in the intramolecular spin-statistical factor. This factor has not been included in our models but has been suggested to be rather low in compounds similar to ours.31 Moreover, the TETA mechanism which dictates intra-UC at high [1A]0/[1S]0 ratios will in fact be competing with the ubiquitous inter-UC pathway. If the efficiency of the intra-UC is lower than that of inter-UC, this would then be detrimental to UC performance, as indicated by our results.

Figure 8.

Figure 8

Open in a new tab

Comparison between the UC emission of DPA and dimers as a group. The abscissa signifies the ratio between ground-state annihilator and sensitizer concentrations, and the ordinate the mean relative UC emission of the dimers compared to that of DPA. Purple circles are the experimental mean values of dimer UC emission divided by that of DPA and are compared with the corresponding intensities predicted by the DS (black solid line) and TETA (blue solid line) models. The red dotted line represents the UC emission of DPA and is included as a reference point.

While these results are interesting on their own, one must consider in what settings intra-UC is anticipated to be of importance. As solid-state solutions are a desirable path moving forward, it is in the context of restricted molecular diffusion these results must be interpreted.19,56−61 With respect to this, it is improbable that the TETA mechanism will be active in future solid-state systems where interactions between multichromophoric annihilators are hampered. These implications are strengthened by the results from the study by Dzebo et al., where large DPA annihilator frameworks showed better UC performance than DPA when put inside a rigid polymer matrix.23 First, the performance of these compounds improved with molecular (dendrimeric/oligomeric) size and even outperformed a reference sample consisting of the DPA monomer, despite the fact that the molecular concentration of DPA was almost 10 times higher in the reference sample than in the oligomeric frameworks. Second, it was found that the best performance was achieved when the sensitizer concentration was on the same order as that of the annihilator. Together, this forms unequivocal proof that it is the DS mechanism that is active in such systems and that intra-UC in fact may enhance UC performance in solid-state systems. Major challenges in facilitating the energy transfer events that are needed remain, particularly how to precisely control the spatial association and interactions between the sensitizer and annihilator. Efforts to understand and control the complicated assembly of high-performing solid-state UC systems are currently undergoing in our lab.

Conclusions

In this study, four novel dimers based on DPA have been synthesized and evaluated as annihilators for TTA-UC. The upconversion efficiencies of these molecules are high throughout, with the meta-coupled 1,3-DPA2 in particular performing on par with DPA. This is primarily ascribed to the long triplet lifetime of this dimer, which is at least five times longer than that of the other dimers and similar to the triplet lifetime of DPA. The importance of the triplet lifetime to achieve efficient TTA-UC is thus reinforced, and a facile method to accurately measure this important parameter has been utilized. Furthermore, the mechanism of intramolecular upconversion has been investigated by comparison between simulations and experiments. Our results from time-resolved UC emission measurements firmly ascertain that the DS mechanism is active in systems with dimeric annihilators and that this additional pathway could be of great importance under specific conditions, e.g., at extremely low annihilator to sensitizer concentration ratios or in diffusionally restricted media. While the full picture of intra-UC is still lacking, especially in terms of how efficiently intra-UC may proceed, our results may act as a guide for future solid-state designs where exciton migration is envisioned as a crucial component.

Acknowledgments

Professor Kasper Moth-Poulsen and M. Sc. Fredrik Edhborg are gratefully acknowledged for valuable discussions. We are grateful to The Swedish Energy Agency (contracts 46526-1 and 36436-2) for providing financial support.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.1c00331.

  • Detailed description of the synthesis of novel compounds, proton and carbon NMR spectra, descriptions of experimental setups, additional spectroscopic and modeling data, full model descriptions, and full details on the temperature-dependent photophysics of 1,2-DPA2 (PDF)

The authors declare no competing financial interest.

Supplementary Material

ja1c00331_si_001.pdf (11.6MB, pdf)

References

  1. Shockley W.; Queisser H. J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510. 10.1063/1.1736034. [DOI] [Google Scholar]
  2. Smith M. B.; Michl J. Recent Advances in Singlet Fission. Annu. Rev. Phys. Chem. 2013, 64, 361–386. 10.1146/annurev-physchem-040412-110130. [DOI] [PubMed] [Google Scholar]
  3. Gray V.; Dzebo D.; Abrahamsson M.; Albinsson B.; Moth-Poulsen K. Triplet–triplet annihilation photon-upconversion: towards solar energy applications. Phys. Chem. Chem. Phys. 2014, 16, 10345–10352. 10.1039/C4CP00744A. [DOI] [PubMed] [Google Scholar]
  4. Singh-Rachford T. N.; Castellano F. N. Photon upconversion based on sensitized triplet-triplet annihilation. Coord. Chem. Rev. 2010, 254, 2560–2573. 10.1016/j.ccr.2010.01.003. [DOI] [Google Scholar]
  5. Gholizadeh E. M.; et al. Photochemical upconversion of near-infrared light from below the silicon bandgap. Nat. Photonics 2020, 14, 585–590. 10.1038/s41566-020-0664-3. [DOI] [Google Scholar]
  6. Albinsson B.; Olesund A. Untapping solar energy resources. Nat. Photonics 2020, 14, 528–530. 10.1038/s41566-020-0681-2. [DOI] [Google Scholar]
  7. Dilbeck T.; Hanson K. Molecular Photon Upconversion Solar Cells Using Multilayer Assemblies: Progress and Prospects. J. Phys. Chem. Lett. 2018, 9, 5810–5821. 10.1021/acs.jpclett.8b02635. [DOI] [PubMed] [Google Scholar]
  8. Cheng Y. Y.; et al. Improving the light-harvesting of amorphous silicon solar cells with photochemical upconversion. Energy Environ. Sci. 2012, 5, 6953–6959. 10.1039/c2ee21136j. [DOI] [Google Scholar]
  9. Monguzzi A.; et al. Broadband up-conversion at subsolar irradiance: Triplet-triplet annihilation boosted by fluorescent semiconductor nanocrystals. Nano Lett. 2014, 14, 6644–6650. 10.1021/nl503322a. [DOI] [PubMed] [Google Scholar]
  10. Hill S. P.; Dilbeck T.; Baduell E.; Hanson K. Integrated Photon Upconversion Solar Cell via Molecular Self-Assembled Bilayers. ACS Energy Lett. 2016, 1, 3–8. 10.1021/acsenergylett.6b00001. [DOI] [Google Scholar]
  11. Huang L.; et al. Highly Effective Near-Infrared Activating Triplet–Triplet Annihilation Upconversion for Photoredox Catalysis. J. Am. Chem. Soc. 2020, 142, 18460–18470. 10.1021/jacs.0c06976. [DOI] [PubMed] [Google Scholar]
  12. Yu T.; et al. Triplet–Triplet Annihilation Upconversion for Photocatalytic Hydrogen Evolution. Chem. - Eur. J. 2019, 25, 16270–16276. 10.1002/chem.201904025. [DOI] [PubMed] [Google Scholar]
  13. Ravetz B. D.; et al. Photoredox catalysis using infrared light via triplet fusion upconversion. Nature 2019, 565, 343–346. 10.1038/s41586-018-0835-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Awwad N.; Bui A. T.; Danilov E. O.; Castellano F. N. Visible-Light-Initiated Free-Radical Polymerization by Homomolecular Triplet-Triplet Annihilation. Chem. 2020, 6, 3071–3085. 10.1016/j.chempr.2020.08.019. [DOI] [Google Scholar]
  15. Börjesson K.; Dzebo D.; Albinsson B.; Moth-Poulsen K. Photon upconversion facilitated molecular solar energy storage. J. Mater. Chem. A 2013, 1, 8521–8524. 10.1039/c3ta12002c. [DOI] [Google Scholar]
  16. Khnayzer R. S.; et al. Upconversion-powered photoelectrochemistry. Chem. Commun. 2012, 48, 209–211. 10.1039/C1CC16015J. [DOI] [PubMed] [Google Scholar]
  17. Dexter D. L. A theory of sensitized luminescence in solids. J. Chem. Phys. 1953, 21, 836–850. 10.1063/1.1699044. [DOI] [Google Scholar]
  18. Hoseinkhani S.; Tubino R.; Meinardi F.; Monguzzi A. Achieving the photon up-conversion thermodynamic yield upper limit by sensitized triplet–triplet annihilation. Phys. Chem. Chem. Phys. 2015, 17, 4020–4024. 10.1039/C4CP03936J. [DOI] [PubMed] [Google Scholar]
  19. Gray V.; Moth-Poulsen K.; Albinsson B.; Abrahamsson M. Towards efficient solid-state triplet-triplet annihilation based photon upconversion: Supramolecular, macromolecular and self-assembled systems. Coord. Chem. Rev. 2018, 362, 54–71. 10.1016/j.ccr.2018.02.011. [DOI] [Google Scholar]
  20. Lee S. H.; Ayer M. A.; Vadrucci R.; Weder C.; Simon Y. C. Light upconversion by triplet-triplet annihilation in diphenylanthracene-based copolymers. Polym. Chem. 2014, 5, 6898–6904. 10.1039/C4PY00920G. [DOI] [Google Scholar]
  21. Sittig M.; et al. Fluorescence upconversion by triplet-triplet annihilation in all-organic poly(methacrylate)-terpolymers. Phys. Chem. Chem. Phys. 2020, 22, 4072–4079. 10.1039/D0CP00232A. [DOI] [PubMed] [Google Scholar]
  22. Imperiale C. J.; Green P. B.; Miller E. G.; Damrauer N. H.; Wilson M. W. B. Triplet-Fusion Upconversion Using a Rigid Tetracene Homodimer. J. Phys. Chem. Lett. 2019, 10, 7463–7469. 10.1021/acs.jpclett.9b03115. [DOI] [PubMed] [Google Scholar]
  23. Dzebo D.; Börjesson K.; Gray V.; Moth-Poulsen K.; Albinsson B. Intramolecular Triplet–Triplet Annihilation Upconversion in 9,10-Diphenylanthracene Oligomers and Dendrimers. J. Phys. Chem. C 2016, 120, 23397–23406. 10.1021/acs.jpcc.6b07920. [DOI] [Google Scholar]
  24. Gray V.; et al. Porphyrin-Anthracene Complexes: Potential in Triplet-Triplet Annihilation Upconversion. J. Phys. Chem. C 2016, 120, 19018–19026. 10.1021/acs.jpcc.6b06298. [DOI] [Google Scholar]
  25. Gao C.; et al. Tetraphenylethene 9,10-Diphenylanthracene Derivatives – Synthesis and Photophysical Properties. ChemPlusChem 2019, 84, 746–753. 10.1002/cplu.201900100. [DOI] [PubMed] [Google Scholar]
  26. Boutin P. C.; Ghiggino K. P.; Kelly T. L.; Steer R. P. Photon upconversion by triplet-triplet annihilation in Ru(bpy)3- and DPA-functionalized polymers. J. Phys. Chem. Lett. 2013, 4, 4113–4118. 10.1021/jz402311j. [DOI] [Google Scholar]
  27. Lee S. H.; Thévenaz D. C.; Weder C.; Simon Y. C. Glassy poly(methacrylate) terpolymers with covalently attached emitters and sensitizers for low-power light upconversion. J. Polym. Sci., Part A: Polym. Chem. 2015, 53, 1629–1639. 10.1002/pola.27626. [DOI] [Google Scholar]
  28. Tilley A. J.; Robotham B. E.; Steer R. P.; Ghiggino K. P. Sensitized non-coherent photon upconversion by intramolecular triplet-triplet annihilation in a diphenylanthracene pendant polymer. Chem. Phys. Lett. 2015, 618, 198–202. 10.1016/j.cplett.2014.11.016. [DOI] [Google Scholar]
  29. Matsui Y.; Kanoh M.; Ohta E.; Ogaki T.; Ikeda H. Triplet–Triplet Annihilation-Photon Upconversion Employing an Adamantane-linked Diphenylanthracene Dyad Strategy. J. Photochem. Photobiol., A 2020, 387, 112107. 10.1016/j.jphotochem.2019.112107. [DOI] [Google Scholar]
  30. Simon Y. C.; Weder C. Low-power photon upconversion through triplet-triplet annihilation in polymers. J. Mater. Chem. 2012, 22, 20817–20830. 10.1039/c2jm33654e. [DOI] [Google Scholar]
  31. Gao C.; et al. Intramolecular versus Intermolecular Triplet Fusion in Multichromophoric Photochemical Upconversion. J. Phys. Chem. C 2019, 123, 20181–20187. 10.1021/acs.jpcc.9b07098. [DOI] [Google Scholar]
  32. Edhborg F.; Küçüköz B.; Gray V.; Albinsson B. Singlet Energy Transfer in Anthracene–Porphyrin Complexes: Mechanism, Geometry, and Implications for Intramolecular Photon Upconversion. J. Phys. Chem. B 2019, 123, 9934–9943. 10.1021/acs.jpcb.9b07991. [DOI] [PubMed] [Google Scholar]
  33. Pun A. B.; Sanders S. N.; Sfeir M. Y.; Campos L. M.; Congreve D. N. Annihilator dimers enhance triplet fusion upconversion. Chem. Sci. 2019, 10, 3969–3975. 10.1039/C8SC03725F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Papadopoulos I.; et al. Perylene-Monoimides: Singlet Fission Down-Conversion Competes with Up-Conversion by Geminate Triplet-Triplet Recombination. J. Phys. Chem. A 2020, 124, 5727–5736. 10.1021/acs.jpca.0c04091. [DOI] [PubMed] [Google Scholar]
  35. Chen M.; et al. Quintet-triplet mixing determines the fate of the multiexciton state produced by singlet fission in a terrylenediimide dimer at room temperature. Proc. Natl. Acad. Sci. U. S. A. 2019, 116, 8178–8183. 10.1073/pnas.1820932116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Tayebjee M. J. Y.; et al. Quintet multiexciton dynamics in singlet fission. Nat. Phys. 2017, 13, 182–188. 10.1038/nphys3909. [DOI] [Google Scholar]
  37. Basel B. S.; et al. Unified model for singlet fission within a non-conjugated covalent pentacene dimer. Nat. Commun. 2017, 8, 1–8. 10.1038/ncomms15171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Korovina N. V.; et al. Singlet Fission in a Covalently Linked Cofacial Alkynyltetracene Dimer. J. Am. Chem. Soc. 2016, 138, 617–627. 10.1021/jacs.5b10550. [DOI] [PubMed] [Google Scholar]
  39. Sanders S. N.; et al. Quantitative Intramolecular Singlet Fission in Bipentacenes. J. Am. Chem. Soc. 2015, 137, 8965–8972. 10.1021/jacs.5b04986. [DOI] [PubMed] [Google Scholar]
  40. Lukman S.; et al. Tuneable Singlet Exciton Fission and Triplet-Triplet Annihilation in an Orthogonal Pentacene Dimer. Adv. Funct. Mater. 2015, 25, 5452–5461. 10.1002/adfm.201501537. [DOI] [Google Scholar]
  41. Bansal A. K.; Holzer W.; Penzkofer A.; Tsuboi T. Absorption and emission spectroscopic characterization of platinum-octaethyl-porphyrin (PtOEP). Chem. Phys. 2006, 330, 118–129. 10.1016/j.chemphys.2006.08.002. [DOI] [Google Scholar]
  42. Benniston A. C.; Harriman A.; Howell S. L.; Sams C. A.; Zhi Y. G. Intramolecular excimer formation and delayed fluorescence in sterically constrained pyrene dimers. Chem. - Eur. J. 2007, 13, 4665–4674. 10.1002/chem.200601498. [DOI] [PubMed] [Google Scholar]
  43. Zhao W.; Castellano F. N. Upconverted Emission from Pyrene and Di-tert-butylpyrene Using Ir(ppy) 3 as Triplet Sensitizer. J. Phys. Chem. A 2006, 110, 11440–11445. 10.1021/jp064261s. [DOI] [PubMed] [Google Scholar]
  44. Ye C.; Gray V.; Mårtensson J.; Börjesson K. Annihilation Versus Excimer Formation by the Triplet Pair in Triplet-Triplet Annihilation Photon Upconversion. J. Am. Chem. Soc. 2019, 141, 9578–9584. 10.1021/jacs.9b02302. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Chandross E. A.; Dempster C. J. Dempster. Intramolecular Excimer Formation and Fluorescence Quenching in Dinaphthylalkanes. J. Am. Chem. Soc. 1970, 92, 3586–3593. 10.1021/ja00715a010. [DOI] [Google Scholar]
  46. Nishiuchi T.; Uno S.; Hirao Y.; Kubo T. Intramolecular Interaction, Photoisomerization, and Mechanical C–C Bond Dissociation of 1,2-Di(9-anthryl)benzene and Its Photoisomer: A Fundamental Moiety of Anthracene-Based π-Cluster Molecules. J. Org. Chem. 2016, 81, 2106–2112. 10.1021/acs.joc.6b00134. [DOI] [PubMed] [Google Scholar]
  47. Zhou Y.; Castellano F. N.; Schmidt T. W.; Hanson K. On the Quantum Yield of Photon Upconversion via Triplet–Triplet Annihilation. ACS Energy Lett. 2020, 5, 2322–2326. 10.1021/acsenergylett.0c01150. [DOI] [Google Scholar]
  48. Kubin R. F.; Fletcher A. N. Fluorescence quantum yields of some rhodamine dyes. J. Lumin. 1982, 27, 455–462. 10.1016/0022-2313(82)90045-X. [DOI] [Google Scholar]
  49. Lakowicz J. R.Principles of Fluorescence Spectroscopy; Springer: New York, 2006. [Google Scholar]
  50. Chattopadhyay S. K.; Kumar C. V.; Das P. K. Triplet-related photophysics of 9,10-diphenylanthracene. A kinetic study of reversible energy transfer from anthracene triplet by nanosecond laser flash photolysis. Chem. Phys. Lett. 1983, 98, 250–254. 10.1016/0009-2614(83)87160-7. [DOI] [Google Scholar]
  51. Gray V.; et al. Photophysical characterization of the 9,10-disubstituted anthracene chromophore and its applications in triplet-triplet annihilation photon upconversion. J. Mater. Chem. C 2015, 3, 11111–11121. 10.1039/C5TC02626A. [DOI] [Google Scholar]
  52. Kondakov D. Y.; Pawlik T. D.; Hatwar T. K.; Spindler J. P. Triplet annihilation exceeding spin statistical limit in highly efficient fluorescent organic light-emitting diodes. J. Appl. Phys. 2009, 106, 124510. 10.1063/1.3273407. [DOI] [Google Scholar]
  53. Arroyo C. R.; et al. Quantum interference effects at room temperature in OPV-based single-molecule junctions. Nanoscale Res. Lett. 2013, 8, 234. 10.1186/1556-276X-8-234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Solomon G. C.; et al. Understanding quantum interference in coherent molecular conduction. J. Chem. Phys. 2008, 129, 054701. 10.1063/1.2958275. [DOI] [PubMed] [Google Scholar]
  55. Gantenbein M.; et al. Quantum interference and heteroaromaticity of para-and meta-linked bridged biphenyl units in single molecular conductance measurements. Sci. Rep. 2017, 7, 1–9. 10.1038/s41598-017-01903-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Vadrucci R.; et al. Nanodroplet-Containing Polymers for Efficient Low-Power Light Upconversion. Adv. Mater. 2017, 29, 1702992. 10.1002/adma.201702992. [DOI] [PubMed] [Google Scholar]
  57. Gharaati S.; et al. Triplet–Triplet Annihilation Upconversion in a MOF with Acceptor-Filled Channels. Chem. - Eur. J. 2020, 26, 1003–1007. 10.1002/chem.201904945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Barbosa de Mattos D. F.; et al. Covalent incorporation of diphenylanthracene in oxotriphenylhexanoate organogels as a quasi-solid photon upconversion matrix. J. Chem. Phys. 2020, 153, 214705. 10.1063/5.0029307. [DOI] [PubMed] [Google Scholar]
  59. Sakamoto Y.; Tamai Y.; Ohkita H. Sensitizer-host-annihilator ternary-cascaded triplet energy landscape for efficient photon upconversion in the solid state. J. Chem. Phys. 2020, 153, 161102. 10.1063/5.0025438. [DOI] [PubMed] [Google Scholar]
  60. Saenz F.; et al. Nanostructured Polymers Enable Stable and Efficient Low-Power Photon Upconversion. Adv. Funct. Mater. 2021, 31, 2004495. 10.1002/adfm.202004495. [DOI] [Google Scholar]
  61. Perego J.; et al. Engineering Porous Emitting Framework Nanoparticles with Integrated Sensitizers for Low-Power Photon Upconversion by Triplet Fusion. Adv. Mater. 2019, 31, 1903309. 10.1002/adma.201903309. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja1c00331_si_001.pdf (11.6MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES