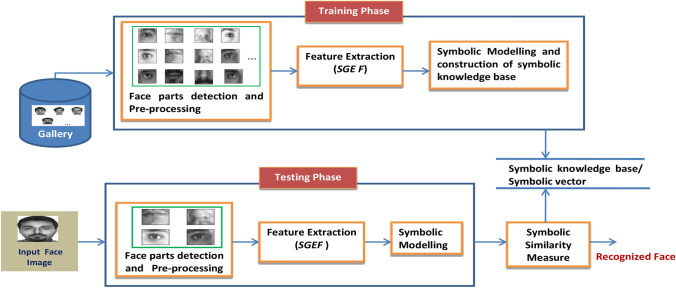
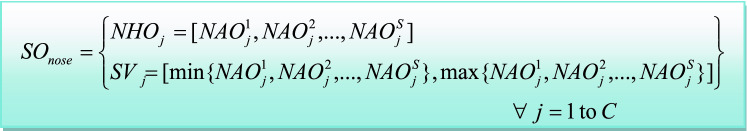Abstract
Face recognition is a well-researched domain however many issues for instance expression changes, illumination variations, and presence of occlusion in the face images seriously affect the performance of such systems. A recent survey shows that COVID-19 will also have a considerable and long-term impact on biometric face recognition systems. The work has presented two novel Savitzky–Golay differentiator (SGD) and gradient-based Savitzky–Golay differentiator (GSGD) feature extraction techniques to elevate issues related to face recognition systems. The SGD and GSGD feature descriptors are able to extract discriminative information present in different parts of the face image. In this paper, an efficient and robust person identification using symbolic data modeling approach and similarity analysis measure is devised and employed for feature representation and classification tasks to address the aforementioned issues of face recognition. Extensive experiments and comparisons of the proposed descriptors experimental results indicated that the proposed approaches can achieve optimal performance of 96–97, 92–96, 100, 84–93, and 87–96% on LFW, ORL, AR, IJB-A datasets, and newly devised VISA database, respectively.
Keywords: Face Recognition, Savitzky–Golay filter, Symbolic Modeling, Similarity Analysis, Face Parts
Introduction
Face recognition is used as a key tool for early revealing, patient screening and monitoring, in an attempt to control the spread of COVID-19 disease. Border control, banking, mobile lock, security monitoring, and signing systems, quarantine, and healthcare and so on are the key applications introducing biometric technology into infectious disease monitoring and control protocols [1–3]. Recent application of face recognition systems includes, passenger can get on a plane with a simple smile, and the fight against COVID-19 in blend with body temperature measurement devices [4]. Significant efforts have been made to devise new biometric systems for person identification using face trait and they have achieved substantial levels of identification accuracy. However, performances (recognition accuracy) of such biometric systems are influenced by various problems related to variations in expression, pose, non-uniform illumination, and presence of occlusion in face images. Recent study also reveals that COVID-19 will also have a substantial and enduring impact on performance of biometric face recognition systems [1]. The key point of these systems/face recognition methods is how to deal with the high dimensional dataset to get stable and efficient facial features. Most of these techniques offer satisfactory results under controlled circumstances (restricted environment) over comprehensive face datasets. Conversely, face image samples acquired in uncontrolled conditions will affect the recognition accuracy of such approaches. Face recognition operations are being retrofitted with newly devised screening software to find persons who are not wearing protective masks. In this context, new AI and ML face recognition algorithms are developed to handle any identification issues due to partial face disguise, which remains a major challenge for any face recognition system [1]. Current advancements in computer vision approaches show that deep learning-based techniques perform well for face recognition task [5, 6]. Several Deep Neural Network (DNN) models such as AlexNet, VGGNet, ResNet, Inception-ResNet and SENet are developed to perform face recognition [7, 8].What leftovers to be seen is how existing face recognition systems will prove to be clinically useful in the current scenario, where complete information is not available for recognition (especially in COVID-19, the person wearing mask and face shield) [9].
In general, the problems associated with such biometric recognition systems include non-uniform light conditions, pose variations, expression changes, and presence of occlusion. To elevate these problems, the proposed face techniques employ Savitzky–Golay [10] spectral domain filter to compute face features under various imaging conditions. The features required for person identification are estimated by employing a weighted Savitzky–Golay (SG) moving filter. SG filter was initially used to smooth the noisy information which is acquired from a chemical spectrum analyzer [10]. In which, for a given input data set, at each point, the smoothed coefficients are estimated [11]. The Savitzky–Golay filter uses a polynomial fitting method by employing least squares techniques for smoothing the given input signal (data) to reduce the mean square error [11]. The Savitzky–Golay filter preserves the peak shape property and reduces the signal-to-noise ratio. Hence, to take advantage of this property, it has been employed in various fields including the area of image processing for image enhancement [12] and enhancing the signal-to-noise ratio, video signals [13–16]. It has been devised to retain edge/texture information, which is required in the classification stage [17]. The major benefits of the SG smoothing moving filter are its speed and its ability to establish higher-order derivatives namely edges for the given input image data at the same time [18]. Yanping Liu et al. (2016) show that the performance of SG moving filter is better over Wiener filter and wavelet denoising techniques [19]. The recent techniques using SG filter for ECG signal denoising have shown impending results in comparison with other wavelet-based methods [20, 21]. By taking into account the edge/line preserving property of Savitzky–Golay filter, in this paper, it is employed. Savitzky–Golay filter is used to obtain an optimal set of features, which will effectively handle various imaging conditions such as pose variations, expression changes, non-uniform illumination and presence of occlusion present in the faces. Another issue for person identification using face trait is the representation of those estimated facial features in lower feature space to reduce the computation burden.
In the last recent years, much importance has been given to the development techniques that will reduce the dimensionality of feature space. In this direction, the symbolic modeling approach [22] provides a formal methodology to represent the features. The symbolic modeling approach offers an alternative way of representing obtained feature value/information about a subject. The methodology is found to be good in different applications including Postal Address Representation and Address Validation [23–25], face recognition technique through symbolic modeling of face graphs and texture, face recognition techniques like symbolic PCA, symbolic KPCA and symbolic LDA and character recognition [25]. Hence, the symbolic data modeling approach for person identification is introduced in this research work to investigate the flexibility and benefits of the modified form of symbolic similarity analysis approach. The proposed methods also explore the advantages of SG filter in feature extraction for a classification task.
Face image samples may be degraded partially or the complete face image may not be presented for person identification task due to variations in face images. There is also a need for artificial intelligence (AI)-based face recognition systems to facilitate COVID-19 preparedness and the tracking and monitoring of patient, and so the spread of COVID-19 virus infection can be reduced [2, 26].
In order to handle such problems, the proposed research introduces two feature extraction techniques namely Savitzky–Golay differentiator (SGD) and Gradient-based Savitzky–Golay differentiator (GSGD). In the Savitzky–Golay differentiator (SGD) feature extraction approach, initially eye, mouth, and nose face parts are segmented from a given image. Further, each segmented part is partitioned into four non-overlapping zones and from each zone, the edge/corner information is computed using Savitzky–Golay filter. The smoothing coefficient values of four zones are combined and are considered as facial SGEF feature values (Savitzky–Golay filter energy feature) for person identification. Based on the proposed feature extraction technique, this paper explores different classifiers namely symbolic data modeling, NNC (Nearest Neighbor Classifier), multiclass SVM (Support Vector Machine), and PNN (Probabilistic Neural Network).
The extracted SGEF (Savitzky–Golay filter energy feature) is represented in a lower dimension using symbolic modeling method. In this research, a symbolic data modeling approach for face recognition is introduced which will explore the symbolic data modeling of face Savitzky–Golay filter energy features and symbolic similarity analysis technique. The proposed face recognition techniques with SGEF are evaluated on standard face datasets like AR, ORL, LFW, IJB-A [6], and the newly constructed VISA face dataset [27]. Symbolic modeling approach with SGEF feature achieves recognition rates of 95.75% (AR), 99.75% (ORL), 97.22% (LFW), and 96.34% (VISA Face). NN classifier with SGEF feature achieves recognition rates of 97.67% (AR), 100% (ORL), 98.06% (LFW), and 94.17% (VISA Face). Multiclass SVM with SGEF feature achieves recognition rates of 94.67% (AR), 89.65% (ORL), 92.30% (LFW), and 79.33% (VISA Face). PNN classifier with SGEF feature achieves recognition rates of 92.92% (AR), 100% (ORL), 98.04% (LFW), and 89.28% (VISA Face).
In the Gradient-based Savitzky–Golay Differentiator (GSGD) feature extraction approach, initially, face parts such as mouth, eyes, and nose are extracted from the given face image. The gradient mean change in each face part in vertical and horizontal directions is determined and smoothing coefficient values are estimated independently by employing Savitzky–Golay filter. Based on the Gradient-based Savitzky–Golay filter energy feature (GSGEF) features, the current research work explores the advantage of gradient information along with Savitzky–Golay filter in person identification. The work also describes symbolic data modeling, NNC, multiclass SVM, and PNN classifiers for face recognition. The performance of proposed methods is evaluated on AR, ORL, LFW, and VISA Face databases. Symbolic modeling approach with GSGEF feature values achieves recognition rates of 92.34% (AR), 99.75% (ORL), 96.20% (LFW), and 87.14% (VISA Face). NN classifier with SG smoothing coefficient values achieves recognition rates of 93.30% (AR), 100% (ORL), 98.03% (LFW), and 90.23% (VISA Face). Multiclass SVM with GSGEF achieves recognition rates of 91.23% (AR), 88.25% (ORL), 91.60% (LFW), and 77.99% (VISA Face). PNN classifier with GSGEF feature values achieves recognition rates of 92.99% (AR), 100% (ORL), 98.04% (LFW), and 89.39% (VISA Face).
All the proposed symbolic modeling, NNC, SVM, and PNN classifiers for face recognition are deployed using MATLAB R2017b in Intel(R) Pentium(R) i5-8250U CPU@1.60Ghz and 8 GB RAM Laptop machine. In general, the main contributions of the anticipated research work are as follows:
A new efficient and robust symbolic data modeling approach based on spectral domain feature extractors for person identification is devised and presented to address issues related to different light conditions, expression variations, and inclusion of occlusion during face recognition.
This is the first approach to use Savitzky–Golay low-pass filter to get facial features in different imaging conditions.
Transformation of 1D-Savitzky–Golay filter to 2D, suitable for face recognition.
Symbolic modeling and symbolic similarity analysis, nearest neighbor (NN) classifier, support vector machine (SVM), and probabilistic neural network (PNN) face recognition techniques have been implemented using PFFT, DGM, SGEF, and GSGEF features and evaluated on AR, ORL, LFW, IJB-A, and a newly devised VISA face database.
The rest of the paper is divided into six sections as follows: The proposed Savitzky–Golay differentiator (SGD) and Gradient-based Savitzky–Golay differentiator (GSGD) feature extraction techniques are presented in Sect. 2. The symbolic data representation of the obtained features is described in Sect. 3. In Sect. 4, face recognition techniques based on proposed feature extraction approaches are described. The experimental results are illustrated and described in Sect. 5. Conclusions are presented in Sect. 6.
Savitzky–Golay Differentiator (SGD) and gradient-based Savitzky–Golay Differentiator (GSGD) for person identification
The section describes the representation of face image features and the methodology employed in the proposed face recognition works.
Savitzky–Golay Differentiator (SGD) for Face Recognition
The Savitzky–Golay (SG) filter is a unique type of low-pass moving filter and is a technique for computing smoothing coefficients of a given input noisy data by using local least squares polynomial estimate technique [12]. It reduces the noise present in the given data, while retaining the original shape property and features of waveform peaks. SG filter is superior to average moving filters that is it tends to retain relative maxima, minima, and width properties of the distribution, which are generally overlooked by moving average filter techniques. Because of these properties, Savitzky–Golay filter has established substantial attention in various applications in the domain of digital image processing [28, 29]. In the proposed face recognition works, SG filter has been employed for feature extraction from face images which are affected by different light conditions, change of expressions, pose variations, and occlusion.
To a given f(x, y) (2D-image data) or f(i) (1D-data), the SG filter aims to smooth and compute its dnth order derivative by employing moving filter window of Tpoints size and an α degree polynomial. The least squares polynomial can be defined as:
| 1 |
where (xi, yi) represents the location of the gray level value in the given face image f.
In the SG filter, dn indicates a non-negative integer having α < Tpoints. To estimate all smoothing coefficient values of an input face image f, the least squares polynomial equation can be rewritten in the form of a matrix as follows:
| 2 |
In Eq. (2), Y = [y1, y2,…,yTpoints]T is a column vector of computed coefficients in the filtering window, A = [a1,a2,…,a]T represents the column vector consisting of the coefficient values of polynomial function and only depends on polynomial order and the number of points in the mask (filter window size), i.e., depends on α and Tpoints and is independent of f (input data). Let ε represents the estimation error and X denotes an (Tpoints × (α + 1)) size Vandermonde matrix, which can be expressed as:
To reduce the sum of the squared errors that exist between given face image f and mask of Tpoints size, the least squared approximation technique is employed [28, 29]. In the proposed research work, to determine all the smoothing coefficient values of an input face image f, Eq. (2) can be rewritten and expressed as in Eq. (3).
| 3 |
In Eq. (3), A = (XT X)−1 XT Y and the matrix W represents the moving window’s (mask) coefficients and used to determine the smoothing coefficient values at the ith point in the mask window W. The nth order derivative of ith location in the given input face image data can be estimated as:
| 4 |
where indicates the nth order derivative of the ith location, vector represents the moving window’s coefficient values of the nth order derivative and is the coefficient value of the nth order derivative.
In general, integer-order form of the SG moving filter at ith location can be defined as:
| 5 |
The moving window which is employed to determine smoothing coefficient values of the input face image f can be expressed as:
| 6 |
where .
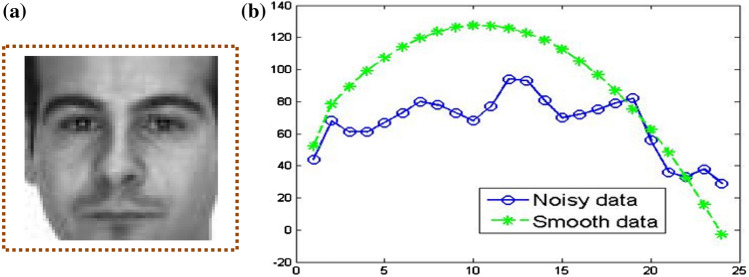
The mathematical form expressed in Eq. (5) will reduce the number of multipliers needed in computing the smoothing coefficients of an input face image. In general, degree polynomial with αth to the filter window size of (2Tpoints + 1) is fitted and can be deployed with only Tpoints-α/2 multiplications (polynomial degree α) per output value instead of 2Tpoints + 1 multiplication operations [14]. Demonstration of determining smoothing coefficient values of given input face image employing (5) is depicted in Fig. 1. In Fig. 1, the input face image is taken from the AR dataset [30].
Fig.1.
Computation of smoothing coefficient values using SG filter (a) face image (b) estimated smoothing coefficient values vs noisy input face image data
In the proposed research work, moving window of Tpoints size with α order of the derivative is used as a filter mask. The size of SG moving filter is (2Tpoints + 1) which approximates the input image information between − Tpoints and + Tpoints. In this technique, initially, each face image (face part such as mouth, nose, and eyes) is partitioned into four non-overlapping segments and SG filter is applied on each segment independently. Further, all the estimated smoothed coefficient values are pooled to obtain a complete set of smoothing coefficient values of an input face part data.
Finally, the smoothing coefficient values of size N × N are represented as 1D feature vector FV1 of size 1 × N2 and expressed as:
where values v1, v2, v3, …,vN×N represents smoothing coefficients of an input face part.
In general, the computed SG smoothing coefficient values of each face component are expressed as FV1 and used in NN, SVM, and PNN classifiers for classification.
Once the smoothing coefficient values of all the face parts are determined in xyth direction, Savitzky–Golay filter energy feature (SGEF) is computed using Eq. (7).
| 7 |
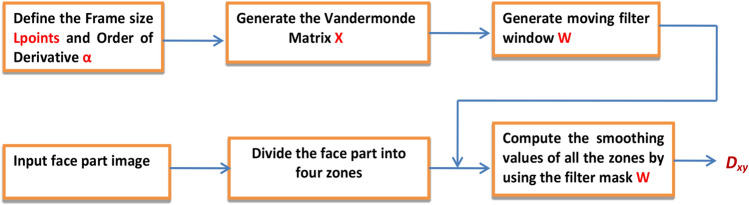
In summary, in the proposed Savitzky–Golay differentiator (SGD) methodology, the four face parts from the given image are partitioned into four segments. The smoothing coefficient values of each segment are estimated by applying the SG filter W mask. The SG filter mask W is designed by defining the order of derivative α and window of size Tpoints. Smoothing coefficient values of all the segments are combined to get Savitzky–Golay filter energy feature Dxy (SGEF). The block diagram computing Savitzky–Golay filter energy feature is shown in Fig. 2.
Fig.2.
Estimation of Savitzky–Golay filter energy feature of a face part
Another gradient-based descriptor proposed in this paper for face recognition is presented in the next section.
Gradient-based Savitzky–Golay Differentiator (GSGD) for face recognition
Savitzky–Golay filter with image gradient information-based feature extraction technique called Gradient-based Savitzky–Golay differentiator (GSGD) is explored in this section.
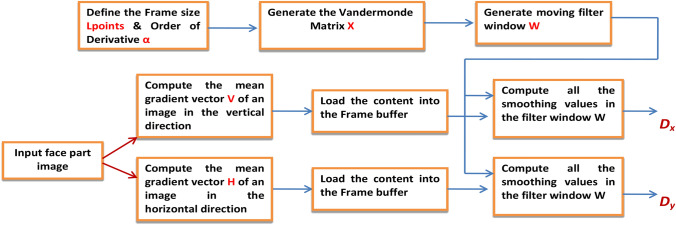
Savitzky–Golay filter is generally employed to fit 1D polynomial and estimate its numerical derivatives. On the other hand, given input face image is a function of two variables; as a result, 1D Savitzky–Golay filter differentiator is designed by using Eq. (1). The least squares technique is applied to determine the smoothing coefficient values of the face image precisely as expressed in Eq. (3). In this method, α = 2 as an order of the polynomial and the filter window of size 3 × 3 are employed (selection is empirical). In general, the procedure involved in obtaining the face part Dx and Dy features is demonstrated in Fig. 3.
Fig.3.
Computation of Dx and Dy features
In the proposed Gradient-based Savitzky–Golay Differentiator (GSGD) approach, initially, face parts are obtained from a face image and mean gradient of each face part is calculated independently in vertical and horizontal directions. The mean gradient vector Iav_v(V) and Iav_h(H) of face component f(x, y) in vertical and horizontal directions is computed using Eqs. (8) and (9) as follows:
| 8 |
| 9 |
The moving filtering window W using Vandermonde matrix is computed as described in Sect. 2.1 and employed to find Dx and Dy features of a gray scale face part of size N × N.
Further, using 2D template W and Eq. (3), the entire gradient-based smoothing coefficients are computed. The obtained features are referred to as GSGEF (Gradient-based Savitzky–Golay filter energy features). The GSGEF is computed in vertical (x) and horizontal (y) directions in the filter window W and can be defined as:
| 10 |
and
| 11 |
In Eq. (10) and (11), t = N and α = 2.
In this paper, the smoothing coefficients obtained from Eqs. (10) and (11) are referred as Gradient-based Savitzky–Golay filter energy features (GSGEF).
The smoothing coefficients of GSGEFdx of size 1 × N and GSGEFdy matrix of size 1 × N are concatenated to generate a single feature vector FV2 of size 1 × 2 N and expressed as:
In general, the computed mean gradient-based SG smoothing coefficient values of each face component is expressed as FV2 and used in NN, SVM, and PNN classifiers for classification.
Further, for symbolic modeling of GSGEF features (obtained from Eq. (10)–(11)), Dx and Dy features are computed using Eqs. (12)–(13) as follows:
| 12 |
| 13 |
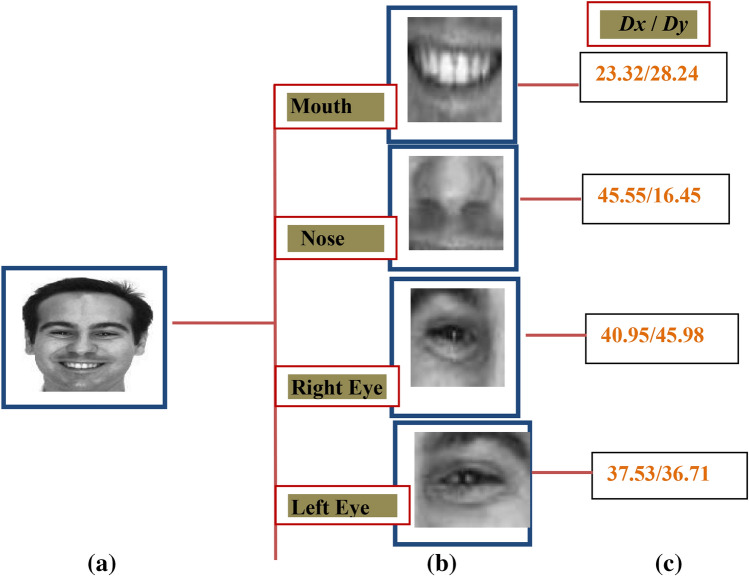
The obtained Dx and Dy features of the face part are further used for building the knowledge base required for symbolic data modeling and symbolic similarity analysis. Sample cropped face parts images and their computed respective Dx and Dy feature values are depicted in Fig. 4.
Fig.4.
AR database face sample a original image, b segmented face parts, c Dx and Dy feature values
The implementation of symbolic approach, NN, SVM, and PNN classifiers for person identification using SGEF/GSGEF feature values is described in subsequent sections.
Symbolic representation of SGEF and GSGEF features
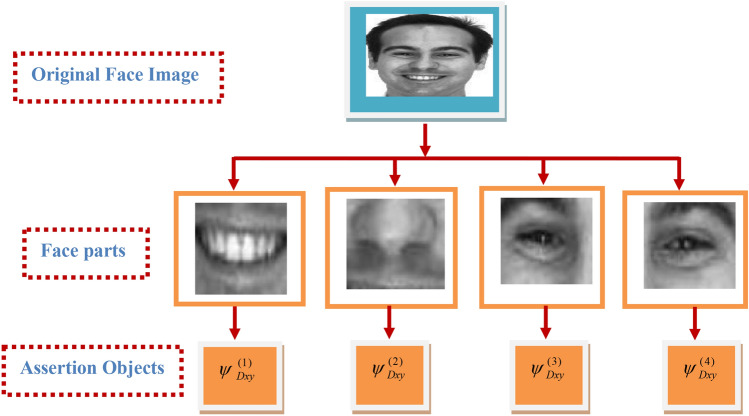
The various operations performed in symbolic data modeling and symbolic similarity measure analysis for recognition are depicted in Fig. 5. In the proposed approach, initially, face parts such as eye, mouth, and nose are segmented using the Viola–Jones algorithm [31, 32] from original face images. To reduce the computation burden, all the cropped images are resized into grayscale images of 64 × 64 pixel. In the second stage, Savitzky–Golay filter is applied to obtain the optimal set of Savitzky–Golay filter energy feature (SGEF) values from each face part. Further, in the symbolic data modeling step, the obtained features of face parts are represented as symbolic data objects (Assertion Object). The features extracted from the set of face images belong to a class are represented by a Hoard symbolic object, which is composed of Assertion symbolic data objects of face parts, respectively. In the classification stage, content-based symbolic similarity measure is devised and used to determine the utmost resemblance between trained and probe symbolic data objects. The index of the trained object class to which test Hoard symbolic data object belong yields the highest resemblance score and is considered as a known class.
Fig.5.
An illustration of proposed symbolic modeling with SGEF feature
Construction of knowledge base required for symbolic modeling of facial features is described in the next section.
Let N number of face image classes are used for training, let each class Ω = {Ѱ1,Ѱ2,Ѱ3 …. ѰM} composed of M number of training face images jth class that may vary in the pose, expression changes, presence of occlusion, and non-uniform light conditions. Then, U = {Ω1, Ω2,.., ΩN} represents the complete set of training face images of N classes.
Let Ѱmouth, Ѱnose, Ѱleft_eye, and Ѱright_eye denote the face part images of jth class of ith face Ѱ, i.e.,
| 14 |
In the proposed symbolic modeling approach, once nose, mouth, and eyes face parts are obtained from the face sample; by Eq. (7), Savitzky–Golay filter energy Dxy feature is computed from each part as shown in Fig. 6. The obtained features are represented as Assertion type of symbolic data objects as in Fig. 7a, i.e., four Assertion symbolic objects namely nose, mouth, and eyes of each image for M classes are created. Next, from M Assertion symbolic objects of each face piece, a Hoard symbolic object is created. In the symbolic modeling approach, each Hoard object is indicated by minimum and maximum (Min–Max) values of M Assertion objects of a face part. In general, each face class is composed of four Hoard objects such as nose, mouth, left eye and right eye Hoard symbolic objects of each face part, respectively. Fig. 7b depicts Hoard symbolic objects of jth face class, . Finally, the whole face dataset is represented by a single synthetic symbolic object which composed of N Hoard symbolic objects and illustrated in Fig. 7c, .
Fig.6.
Estimation of Savitzky–Golay filter energy feature Dxy (SGEF) of a face image
Fig.7.
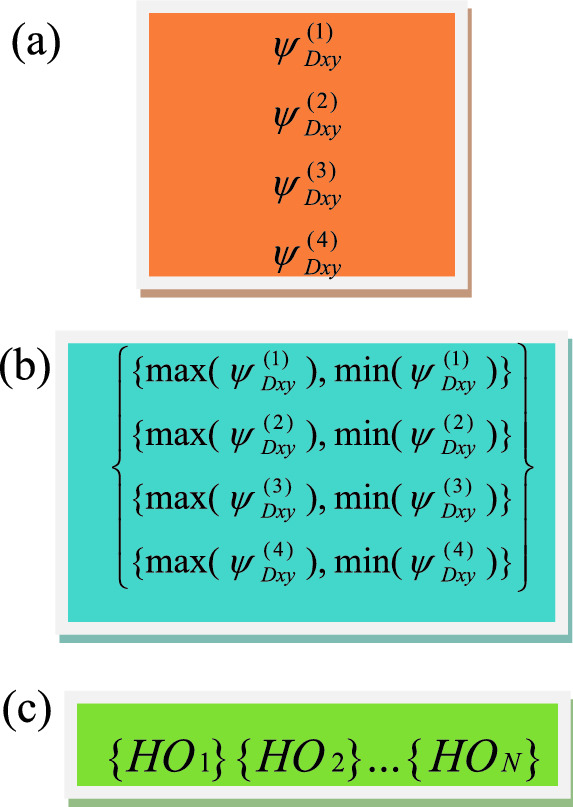
Creation of symbolic objects, a Assertion symbolic object (indicate a face sample) b Hoard symbolic object (denoted jth face class) c Synthetic symbolic object (indicate entire face database),
Similarly, symbolic objects of probe face image Ѱ can be reprinted as:
In Tob symbolic representation, Tobnose, Tobmouth, Tobleye,, and Tobreye indicate symbolic data objects of test face image (nose, mouth, and eyes parts), respectively.
In general, the entire face database is composed of C number of face classes and S number of images per class. In symbolic object modeling, each face part is represented as Assertion object AO = [Dxy] and the collection of such AO objects of a class constitutes the Hoard object HO. Synthetic object SO of each face component for entire face dataset is created. Synthetic objects consist of min and max value of Assertion objects (SVj) and Hoard objects of C classes. Figure 8 illustrates synthetic object creation of nose, where SOnose indicates synthetic object of nose, NAOij represents nose Assertion object of ith sample of jth class and NHOj is Hoard object of jth class.
Fig.8.
Synthetic object representation of SGEF features of face component
Finally, the knowledge base of entire face dataset consists of synthetic object of nose (SOnose), mouth (SOmouth), left eye (SOleye), and right eye (SOreye). Hence, the knowledge base can be expressed as: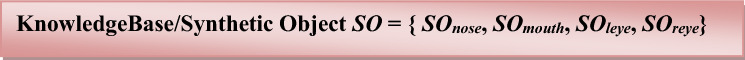
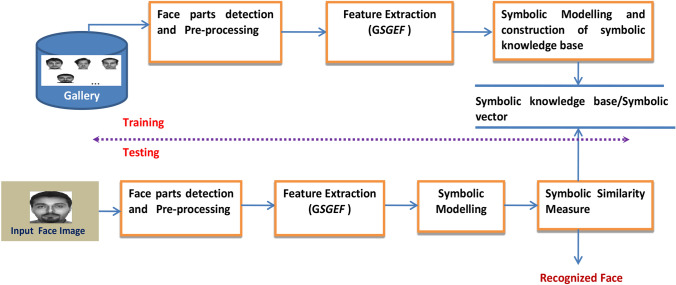
Similarly, the paper introduces a symbolic modeling approach for person identification using GSGEF features, which are obtained by applying Savitzky–Golay moving filter. All the operations involved in the symbolic modeling of GSGEF features for face recognition are shown in Fig. 9.
Fig.9.
The process involved in the proposed symbolic modeling of GSGEF features
In the proposed Gradient-based Savitzky–Golay Differentiator feature (GSGEF) extraction technique, initially, images from various databases are taken and face parts are obtained by employing the Viola–Jones algorithm [31, 32]. The segmented face parts are rescaled to 64 × 64 pixel grayscale images. From each face part, a mean gradient of the face image is computed in vertical and horizontal directions, respectively. Finally, based on gradient mean information, GSGEF features are computed by deploying Savitzky–Golay filter. Next, obtained facial feature of eyes, nose, and mouth parts is expressed as independent symbolic data objects which constitutes knowledge base for classification. During the classification, the modified form of content-based symbolic similarity measure presented in this paper is used to determine the symbolic similarity score between symbolic objects of knowledge base and test symbolic objects of an input test face image. The trained object class that has the utmost similarity score against probe symbolic objects is the recognized class of the test face image.
In general, the entire face dataset is composed of N face classes and M face images per class. In symbolic object modeling, each face part is represented as Assertion object AO = [Dx Dy] and collection of such AO objects of a class constitutes Hoard object HO. Gradient-based synthetic object GSO of each face component for entire face dataset is created. Synthetic objects consist of min and max value of Dx and Dy of Assertion objects (NSV) and Hoard objects of N classes. Figure 10 illustrates synthetic object creation of nose, where GSOnose indicates synthetic object of nose, Nose_AOij represents nose Assertion object of ith sample of jth class, and NHOj is Hoard object of jth class.
Fig.10.
Synthetic object representation of GSGEF features of face component
Finally, the knowledge base of entire face dataset contains synthetic symbolic object of nose (GSOnose), mouth (GSOmouth), left eye (GSOleye), and right eye (GSOreye). Hence, the knowledge base can be defined as: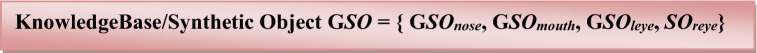
Face recognition techniques
This section describes the proposed face recognition methods based on SGEF and GSGEF features.
Symbolic similarity analysis
The symbolic similarity measure and analysis compute the maximum similarity score between probe symbolic object and trained symbolic objects. The symbolic similarity measure and analysis can be performed by considering content, span, and position as defined by Chidananda Gowda K. and Edwin Diday, 1992 [22]. In this section, the features extracted from the face images are represented as symbolic data objects having quantitative and interval type of values. During the symbolic similarity analysis, the content-based symbolic similarity measurement is more appropriate because of the type of data and gives the similarity score of the probe symbolic object against all the trained symbolic data objects and is described in the following:
The symbolic similarity between Hoard objects H(j) of jth class and test object Htest is computed using Eq. (15):
| 15 |
where
H(j)upper and H(j)lower denote upper and lower limits of symbolic object H(j) (maximum and minimum values). Tobtest_upper and Tobtest_lower represent the upper and lower limits of test symbolic object Tob (In this work Tobtest_upper = Tobtest_lower), inters(j) is the number of common elements of Assertion object pertaining to ith face image of jth face class and probe symbolic data object Tob. ls(j) represents the span length of H(j) and Tob symbolic objects.
In Eq. (15), overlap measure technique was devised and employed to estimate inters(j). Since in the symbolic data modeling technique for face recognition, Hoard object H(j) is a collection of Assertion data objects namely mouth, nose, right eye, and nose eye Hoard data objects and probe symbolic data object Tob is a set of Assertion objects such as mouth, nose, right eye, and nose eye Assertion data objects, thus the symbolic similarity measure score (H(j), Tob) of probe symbolic data object Tob and Hoard data object H(j) of jth face class can be determined using Eq. (16) by
| 16 |
where
Further, computed similarity scores of all N trained and test symbolic objects can be expressed as:
| 17 |
The index of the highest similarity score of Netsim vector gives the class id to which probe symbolic data object belongs and it can be computed as in Eq. (18).
| 18 |
The experimentation results of proposed techniques are discussed in Sect. 5.
Experimental results and discussion
The performance of the proposed face recognition methods is evaluated on publically available AR, ORL, LFW, IJB-A datasets, and the newly formed VISA Face database [27]. The VISA dataset is publically available for download using URL: https://vtu.ac.in/en/visa-multimodal-face-and-iris-biometrics-database/ [27]. The IJB-A dataset is publically available for download [6]. In the proposed works, face parts such as mouth, nose, and eyes are segmented from given face image using the Viola–Jones algorithm and are scaled down to 64 × 64 pixels grayscale face images. Further, using Savitzky–Golay filter, SGEF and GSGEF features of face image are computed and used for the classification tasks. The efficiency of the Savitzky–Golay smoothing filter is subjective to the choice of polynomial order and filter mask size factors. The detailed accomplishment of the projected face recognition algorithms with choice of polynomial order and filter mask size is discussed in Sect. 5.1.
Selection of polynomial order and filter mask size
The face image may vary due to illumination changes (non-uniform light condition) and expression change with light variations produce low quality /low contrast face samples. Due to the presence of occlusion (mask, scarf, and sunglass), the face sample appears to be dark (partially). The suitable choice of order of the derivative is significant while estimating smoothing coefficients from such face samples. For the dark face samples, choose the order of derivative as α < 0 and α > 0 for low contrast face samples [28, 32–34]. In the proposed works, several experiments were conducted for the selection of integer-order and fraction-order derivative values of α, among those, integer-order derivative value α = 2 and fraction-order derivative values of α = 0.3 result the best recognition accuracy rate. Hence, for the experimentation and comparative analysis, α = 2 and α = 0.3 are empirically considered.
The efficiency of the proposed face recognition methodologies also depends on the choice of polynomial order and mask window size when SG moving filter is used for smoothing and determining higher-order derivatives. Experiment results on AR, ORL, LFW datasets, and the new VISA Face database by considering the different combinations of polynomial order types (integer and fraction polynomial order types) and filter mask sizes are given in Tables 1, 2, 3. The computation times required by the proposed methods are listed in Tables 1, 2, 3. The proposed face recognition techniques are tested and evaluated for higher size masks like 3 × 3, 5 × 5, 7 × 7, and 11 × 11 along with integer polynomial order, and obtained results are illustrated in Tables 1 and 2.
Table 1.
Performance comparison of the proposed symbolic modeling approach with SGEF in different mask window size and integer polynomial order on AR, ORL, LFW, and VISA Face datasets
| Mask size | Computation time in seconds | Recognition accuracy at α = 2 in % | ||||||
|---|---|---|---|---|---|---|---|---|
| AR | ORL | LFW | VISA | AR | ORL | LFW | VISA Face | |
| F = 3 × 3 | 0.035 | 0.389 | 0.224 | 0.619 | 95.75 | 99.75 | 97.22 | 96.39 |
| F = 5 × 5 | 0.042 | 0.392 | 0.231 | 0.623 | 95.24 | 100 | 96.77 | 96.52 |
| F = 7 × 7 | 0.044 | 0.411 | 0.248 | 0.629 | 93.00 | 100 | 96.13 | 96.19 |
| F = 11 × 11 | 0.059 | 0.458 | 0.310 | 0.699 | 92.75 | 100 | 94.23 | 96.32 |
| F = 13 × 13 | 0.075 | 0.460 | 0.323 | 0.734 | 92.83 | 100 | 94.55 | 96.23 |
Bold values represents the best recognition rate and computation time for 3 × 3 mask size
Table 2.
Recognition performance of symbolic modeling approach with GSGEF features in low resolution face images with different mask window size and integer polynomial order
| Mask size | Computation time in seconds | Recognition accuracy at α = 2 in % | ||||||
|---|---|---|---|---|---|---|---|---|
| AR | ORL | LFW | VISA Face | AR | ORL | LFW | VISA Face | |
| F = 3 × 3 | 0.004 | 0.004 | 0.006 | 0.004 | 92.34 | 99.75 | 96.20 | 87.14 |
| F = 5 × 5 | 0.003 | 0.003 | 0.006 | 0.004 | 91.88 | 97.86 | 95.83 | 85.01 |
| F = 7 × 7 | 0.003 | 0.004 | 0.006 | 0.004 | 97.45 | 98.56 | 97.02 | 85.83 |
| F = 11 × 11 | 0.003 | 0.004 | 0.006 | 0.004 | 85.03 | 97.88 | 99.73 | 84.71 |
| F = 13 × 13 | 0.003 | 0.004 | 0.006 | 0.004 | 85.97 | 98.12 | 99.13 | 84.58 |
Bold values represents the best recognition rate and computation time for 3 × 3 mask size
Table 3.
Performance comparison of the symbolic data modeling with SGEF with different mask window size and fractional order polynomial on AR, ORL, LFW, and VISA Face datasets
| Mask size | Computation time in seconds | Recognition accuracy at α = 0.3 in % | ||||||
|---|---|---|---|---|---|---|---|---|
| AR | ORL | LFW | VISA | AR | ORL | LFW | VISA Face | |
| F = 3 × 3 | 0.032 | 0.340 | 0.222 | 0.625 | 95.17 | 99.75 | 97.03 | 96.59 |
| F = 5 × 5 | 0.035 | 0.356 | 0.224 | 0.626 | 95.08 | 100 | 96.90 | 96.52 |
| F = 7 × 7 | 0.038 | 0.364 | 0.226 | 0.703 | 94.92 | 100 | 96.75 | 96.19 |
| F = 11 × 11 | 0.045 | 0.451 | 0.239 | 0.734 | 94.83 | 100 | 94.00 | 96.59 |
| F = 13 × 13 | 0.054 | 0.356 | 0.241 | 0.738 | 94.92 | 100 | 94.15 | 96.23 |
Bold values represents best recognition rate and computation for 3 × 3 mask size
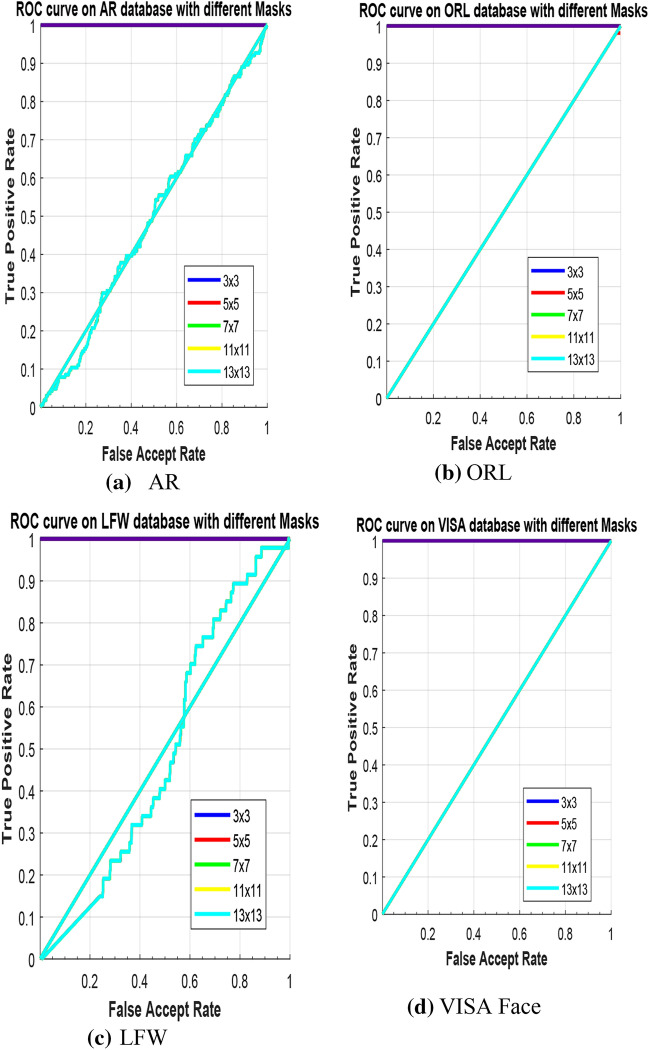
Tables 1 and 2 show that 3 × 3 mask is found to produce good results as compared to 5 × 5, 7 × 7, and 11 × 11; in most of the cases, as the computation time increases, the mask length is also increased. In this research work, to decrease the time needed for estimating smoothing coefficient values and to obtain finer details from each face part of the face sample, each face part is partitioned into four segments and from each segment, smoothing values are determined independently. The ROC curve analysis with different mask window size and polynomial order α = 2 on reported face datasets is illustrated in Fig. 11.
Fig. 11.
ROC curve on AR, ORL, LFW, and VISA Face datasets based on SGEF features with different mask size at α = 2
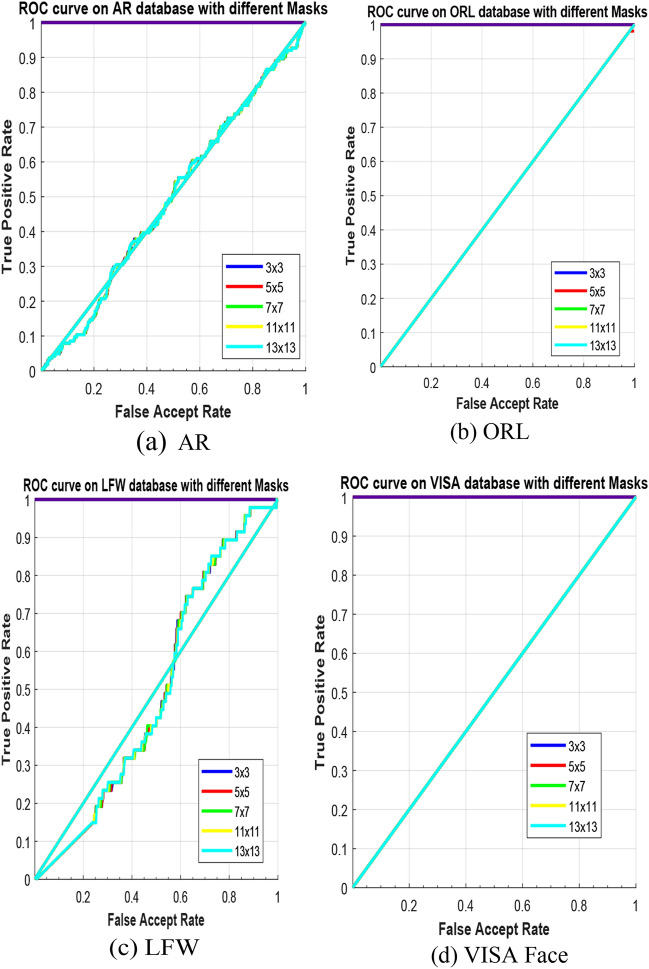
The efficiency of the Savitzky–Golay smoothing filter with fractional order polynomial and different mask window size is evaluated using SGEF feature set and obtained results are recorded in Table 3. The ROC curve analysis with different mask window size and polynomial order α = 0.3 on reported face datasets is illustrated in Fig. 12.
Fig. 12.
ROC curve on AR, ORL, LFW, and VISA Face datasets based on SGEF features with different mask size at α = 0.3
From Tables 1, 2, 3, it is observed that in most of the cases, as the length of the mask increases, the recognition accuracy of the proposed techniques is also reduced. The face sample with Wα at α < 0 suffers from the above exposition, which causes loss of information; hence, it is not appropriate in the presence of occlusion on face images. From Tables 1, 2, 3, it is seen that the efficiency of the proposed face recognition works has considerable excellence when α > 0 polynomial order derivative of SG is used for estimating the smoothing coefficient values. Hence, in this paper, for demonstration of fractional order polynomial with α = 0.3, and α = 2 integer-order polynomial with a mask window size 3 × 3 are empirically preferred on the computation of SGEF features. The experimentation results of Tables 1, 2, 3 also reveal that the mask Wα with integer polynomial order α produces superior efficiency than the fractional-order derivative and the same is chosen for computing GSGEF features.
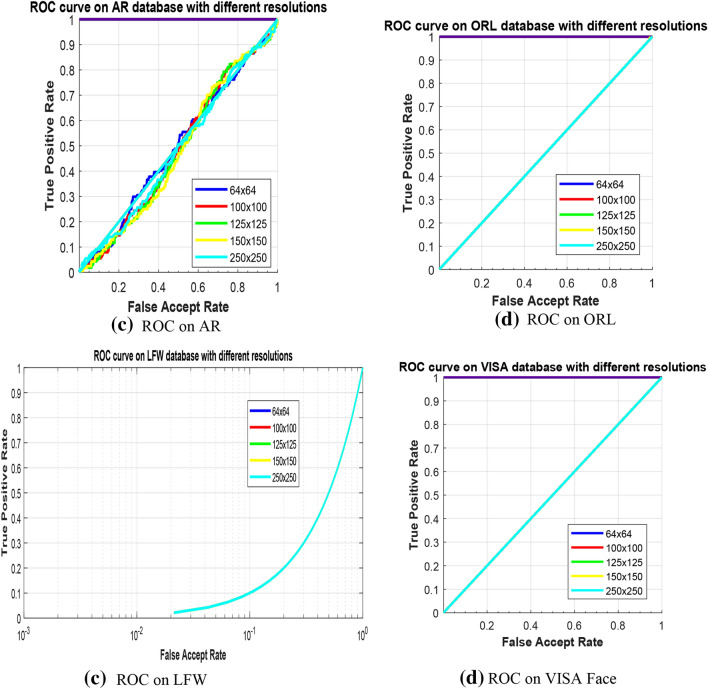
In this work, to test the robustness of the proposed techniques under the varying image resolutions, we downsample all the segmented face parts images into 64 × 64, 100 × 100, 125 × 125, 150 × 150, and 250 × 250 pixel dimensions and results obtained from the experiments on AR, ORL, LFW, and the new VISA Face databases with mask size 3 × 3 at α = 2 are given in Table 4 and ROC curve analysis is illustrated in Fig. 13. In Table 4, it is also noticed that the recognition accuracy of the proposed methods depends not only on mask size and polynomial order but also on image dimension. From Table 4, it may be understood that the face image resolution 64 × 64 and its corresponding mask of size 3 × 3 with α = 2 outperform the different resolutions and mask sizes. Hence, we empirically choose 3 × 3 mask size, α = 2, and 64 × 64 pixel dimensions for analysis of proposed works using SGEF and GSGEF features. To validate the performance of the proposed approach, K-Fold validation technique has been employed in this paper.
Table 4.
Recognition performance (%) of proposed face recognition techniques with SGEF features on different resolution face images
| Size of the face image | Symbolic Approach and Analysis | Nearest Neighbor | Support Vector Machine | Probabilistic Neural Network | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AR | ORL | LFW | VISA Face | AR | ORL | LFW | VISA Face | AR | ORL | LFW | VISA Face | AR | ORL | LFW | VISA Face | |
| 64 × 64 | 95.75 | 99.75 | 97.22 | 96.39 | 97.67 | 100 | 98.06 | 94.07 | 94.67 | 89.65 | 92.30 | 79.33 | 92.92 | 100 | 98.04 | 89.28 |
| 100 × 100 | 95.53 | 100 | 95.13 | 96.45 | 95.68 | 100 | 98.09 | 95.72 | 88.67 | 94.25 | 92.30 | 86.77 | 92.92 | 100 | 98.04 | 89.28 |
| 120 × 120 | 94.63 | 100 | 91.81 | 96.51 | 95.91 | 100 | 98.15 | 95.83 | 84.66 | 88.51 | 92.30 | 82.64 | 92.92 | 100 | 98.04 | 89.28 |
| 150 × 150 | 94.32 | 100 | 98.47 | 96.61 | 95.92 | 100 | 98.15 | 95.89 | 79.33 | 82.75 | 84.61 | 68.59 | 92.92 | 100 | 98.04 | 89.28 |
| 250 × 250 | 94.67 | 100 | 95.97 | 96.66 | 96.13 | 100 | 98.13 | 95.89 | 72.67 | 55.17 | 69.23 | 57.024 | 92.92 | 100 | 98.04 | 89.28 |
Bold values denotes best recognition rate
Fig.13.
ROC curve on AR, ORL, LFW, and VISA Face datasets based on SGEF features with different image sizes at α = 2
To investigate the efficiency of proposed face recognition techniques with SGEF and GSGEF features against non-uniform light conditions, expression, and occlusion on face images, AR dataset is considered for experimentations. 1200 face images of 120 individuals of the AR database are divided into five categories. The experimental results obtained on all the listed cases are given in Tables 5 and 6. The proposed methods can conquer the consequence of variations of face samples by segmenting the face into eyes, nose, and mouth face parts. The possible motive for such an observable fact is that the proposed approaches work well even if only a part of the face is obtainable in the recognition stage. Several experiments are conducted by taking into account different combinations of face parts, and results are shown in Tables 7 and 8.
Table 5.
Recognition accuracy (%) of proposed face recognition approaches with SGEF features on subsets of AR dataset
| Individuals/labels | Total number samples used for testing | Symbolic modeling and similarity | Nearest neighbor | Support vector machine | Probabilistic neural network | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | A | B | C | A | B | C | A | B | C | ||
| Illumination variation(Subset 1) | 480 | 463 | 17 | 96.46 | 469 | 11 | 97.71 | 458 | 22 | 95.42 | 449 | 31 | 93.54 |
| Expression (Subset 2) | 420 | 408 | 12 | 97.14 | 413 | 07 | 98.33 | 407 | 13 | 96.90 | 392 | 28 | 93.33 |
| Occlusion(Scarves + Sunglasses) (Subset 3) | (73 + 25) = 98 | 89 | 09 | 90.82 | 83 | 15 | 84.69 | 79 | 19 | 80.61 | 76 | 22 | 77.55 |
| Scarves-Illumination (Subset 4) | 244 | 231 | 13 | 94.67 | 239 | 05 | 97.95 | 226 | 18 | 92.62 | 224 | 20 | 91.80 |
| Sunglasses-Illumination (Subset 5) | 56 | 47 | 09 | 83.92 | 51 | 05 | 91.07 | 45 | 11 | 80.36 | 50 | 06 | 89.29 |
| Total number of images (Subset 1 + Subset 2 + Subset 4 + Subset 5) | 1200 | 1149 | 51 | 95.75 | 1172 | 28 | 97.67 | 1136 | 64 | 94.67 | 1115 | 85 | 92.92 |
A: Number of samples recognized correctly, B: Number of samples misclassified, C: Accuracy (%)
Table 6.
Recognition accuracy (%) of proposed face recognition approaches with GSGEF features on various combinations of AR
| Individuals/labels | Total number samples used for testing | Symbolic modeling and similarity | Nearest neighbor | Support vector machine | Probabilistic neural network | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | A | B | C | A | B | C | A | B | C | ||
| Illumination variation(Subset 1) | 480 | 463 | 17 | 96.46 | 443 | 37 | 92.29 | 431 | 49 | 89.80 | 437 | 43 | 91.05 |
| Expression (Subset 2) | 420 | 401 | 19 | 95.48 | 396 | 24 | 94.29 | 390 | 30 | 92.86 | 394 | 26 | 93.81 |
| Occlusion(Scarves + Sunglasses) (Subset 3) | (73 + 25) = 98 | 87 | 11 | 88.78 | 75 | 23 | 76.53 | 79 | 19 | 80.61 | 81 | 17 | 82.65 |
| Scarves-Illumination(Subset 4) | 244 | 234 | 10 | 95.90 | 233 | 11 | 95.49 | 223 | 21 | 91.39 | 221 | 23 | 90.57 |
| Sunglasses-Illumination(Subset 5) | 56 | 49 | 07 | 87.50 | 41 | 15 | 73.21 | 39 | 17 | 69.64 | 45 | 11 | 80.36 |
| Total number of images (Subset 1 + Subset 2 + Subset 4 + Subset 5) | 1200 | 1147 | 53 | 95.58 | 1113 | 87 | 92.75 | 1083 | 117 | 90.25 | 1097 | 103 | 91.42 |
A: Number of samples recognized correctly, B: Number of samples misclassified, C: Accuracy (%)
Table 7.
Recognition rate (%) of proposed symbolic approach + SGEF features on face parts
| Database | Face parts and recognition rate in % | ||||||
|---|---|---|---|---|---|---|---|
| Mouth, nose, and eyes | Eyes and mouth | Eyes and nose | Nose and mouth | Only eyes | Only mouth | Only nose | |
| AR | 95.75 | 74.22 | 74.80 | 90.17 | 79.08 | 64.33 | 66.66 |
| ORL | 99.75 | 81.19 | 78.68 | 62.87 | 61.35 | 36.32 | 41.08 |
| LFW | 97.22 | 91.95 | 93.47 | 70.41 | 92.36 | 72.64 | 72.51 |
| VISA | 96.39 | 90.13 | 89.95 | 96.39 | 90.40 | 67.00 | 66.87 |
Bold values represent the best recognition rate
Table 8.
Recognition rate (%) of symbolic modeling + GSGEF face features on different face parts
| Database | Face parts and recognition rate in % | ||||||
|---|---|---|---|---|---|---|---|
| Mouth, nose, and eyes | Eyes and mouth | Eyes and nose | Nose and mouth | Only eyes | Only mouth | Only nose | |
| AR | 92.34 | 86.19 | 75.62 | 54.87 | 59.89 | 27.28 | 20.55 |
| ORL | 99.75 | 94.61 | 93.76 | 91.31 | 80.94 | 70.74 | 66.62 |
| LFW | 96.20 | 94.27 | 93.33 | 90.62 | 89.58 | 67.13 | 62.01 |
| VISA | 87.14 | 85.88 | 85.20 | 83.70 | 82.15 | 61.00 | 60.90 |
Bold values represent the best recognition rate
Tables 7 and 8 show the recognition rate of the proposed methods with various combinations of segmented face parts are presented in recognition task and it is also noticed that when all the face parts are considered during the recognition process, the proposed approaches attain better recognition rate on AR, ORL, LFW, and the new VISA Face databases. The recognition accuracy of the proposed techniques is reduced when one or more of the face part features are not available for recognition.
In the proposed face recognition works, when individual face part or combination of segmented face parts is considered during the recognition process, the recognition rate of algorithms is unstable due to the useful regions such as eyes, nose, and mouth are affected by illumination variations, expression changes, and inclusion of occlusion on face images. Therefore, complete face sample representation for face recognition task is severely affected when these face parts vary and may not be obtainable during the recognition process. However, the biometric system based on the face, trait wishes to work fine even when part of the face sample is not accessible. The face parts representation-based approach can conquer the side effect of variations in face samples. To accomplish this objective, the proposed face recognition techniques cropped the face parts so that better details of face samples can be obtained using SG filter mask. The results of Tables 7 and 8 prove that the proposed techniques for face recognition achieve improved performance over some of the existing works even in the presence of variations in face images and if some part of the face image is not available. Tables 7and 8 show the implication of the left and right eye regions as they contain most of the valuable information required for recognition in comparison with nose and mouth regions. The performances of the anticipated works are also compared with some of the state-of-art works and are elaborated in Sect. 5.2.
Comparative analysis of face recognition techniques
The proposed approaches are evaluated for the performance analysis of face biometric techniques on freely available face datasets namely AR, ORL, LFW, IJB-A, and the newly constructed VISA Face dataset. The experimentation results obtained from SGEF and GSGEF features-based face recognition techniques are among the best and are comparable to some of the existing works such as symbolic modeling approach with Polar FFT features [24] and DGM (Directional Gradient Magnitude) feature-based techniques [25]. In the current research, nearest neighbor (NN) classifier, multiclass support vector machine (SVM), and probabilistic neural network (PNN) techniques have been implemented using PFFT, DGM, SGEF,, and GSGEF features and used for experimentation analysis.
The section describes the comparative investigation of the anticipated approaches with local approximation gradient descriptors and similar feature representation techniques proposed in [25, 35–37] on AR dataset because of their similarities with proposed methods. The proposed SGEF and GSGEF features-based face recognition techniques are compared with local gradient pattern descriptors [38], low rank feature representation techniques [39], and CNN approaches [40] on LFW public dataset. In this work, the efficiency of the proposed face recognition techniques is also evaluated and compared on the newly formed VISA Face dataset [27].
Performance comparison on AR dataset
For evaluating the accuracy of proposed face recognition techniques in different environments such as non-uniform illumination, variations in expression and occlusion, the AR dataset has been chosen for the experimentation. The experimentation results of the proposed methods are compared with existing techniques on the AR dataset. The experimentation results obtained from LAG–LDA, PFFT/DGM/SGEF/GSGEF feature-based symbolic approach, NN, SVM, and PNN methods are given in Table 9.
Table 9.
Comparison of proposed works with LAG –LDA and other works on AR dataset
| Method | Illumination variation (S1) | Expression change (S2) | Scarves-Illumination(S4) | Sunglasses-Illumination (S5) |
|---|---|---|---|---|
| LAG-LDA | 90.67 (Exp 6) | 93.25 (Exp 1) | 73.33 (Exp 8) | 92 (Exp 7) |
| Symbolic approach + PFFT | 98.54 | 98.81 | 89.79 | 95.08 |
| Symbolic approach + DGM | 91.67 | 95.24 | 93.03 | 98.21 |
| Symbolic approach + SGEF | 96.46 | 97.14 | 94.67 | 83.92 |
| Symbolic approach + GSGEF | 96.46 | 95.48 | 95.90 | 87.50 |
| NN + PFFT | 100 | 100 | 98.98 | 85.25 |
| NN + DG | 91.88 | 96.91 | 94.26 | 42.86 |
| NN + SGEF | 97.71 | 98.33 | 97.95 | 91.07 |
| NN + GSGEF | 92.29 | 94.29 | 95.49 | 73.21 |
| SVM + PFFT | 99.58 | 99.52 | 90.82 | 94.67 |
| SVM + DG | 95.00 | 99.05 | 95.90 | 83.93 |
| SVM + SGEF | 95.42 | 96.90 | 92.62 | 80.36 |
| SVM + GSGEF | 89.90 | 92.86 | 91.39 | 69.64 |
| PNN + PFFT | 93.54 | 96.19 | 72.45 | 88.93 |
| PNN + DG | 96.04 | 95.00 | 93.44 | 55.35 |
| PNN + SGEF | 93.54 | 93.33 | 91.80 | 89.29 |
| PNN + GSGEF | 91.05 | 93.81 | 90.57 | 80.36 |
Bold values highlights the best recognition rate of proposed techniques compared to LAG-LDA
Zhaokui Li. et al. (2015) proposed a local approximation gradient with LDA (LAG-LDA) approach for face recognition and evaluated using AR dataset referred to as exp1 to exp8 [24, 25, 35]. In LAG-LDA, experiments 1–4 use face samples number from 1–4 of session 1 and experiments 5–8 use face samples number from 8–13 of session 1 for training. In testing, different combinations of AR dataset samples are used. LAG-LDA technique attains the best recognition accuracy of 93.25, 89.33, and 67 to 67.33% on expression changes, non-uniform light conditions, and inclusion of occlusion with illumination variations in experiments 1–4, respectively. For experiments from 5–8, LAG-LDA method attains best recognition accuracy of 75.25, 90.67, and 92 to 73.33% on expression variations, illumination changes, and occlusion with different illumination conditions, respectively. Table 9 shows the best recognition rate of the proposed methods and LAG-LDA technique.
The results in Table 9 show the usefulness of PFFT/DGM/SGEF/GSGEF feature-based face recognition techniques. Most of the proposed face recognition techniques achieve superior performance than LAG–LDA technique on subsets of the AR dataset. The LAG operator computes more edge information by considering different gradient directions between 0° and 315°. Its performance reduces when non-uniform light conditions and presence of occlusion on face images. The condition becomes worst when partial information available in particular direction (part of the face/complete edge information is not available). To handle such issues, the proposed SGEF and GSGEF features-based face recognition techniques acquire the features from individual part of the face image for recognition task and the methods work well even if the information of all the parts is not completely available for recognition. In this regard, proposed SGEF and GSGEF feature-based techniques segment the face parts from the face sample. In the proposed feature extraction techniques, each segmented face part is partitioned into four zones. Further, the smoothing coefficient values of each zone are estimated and integrate gradient edge data of all the zones. The resultant feature information is used for the classification tasks, whereas as in GSGEF feature-based techniques, smoothing coefficients are obtained from the gradient mean of each face part. As a result, the performance of the proposed SG filter-based works is better compared to LAG-LDA operator, DGM features-based techniques methods in the cases of S1, S2, and S4 (except PFFT-based techniques). However, the performance of the proposed SG filter-based algorithms depends on the accuracy achieved during the segmentation of face parts. The Viola–Jones algorithm is sensitive to occlusion with lighting conditions, which leads to improper segmentation of face parts; hence, there is a large variation in accuracy on set S5. When the face images are occluded by sunglasses (denser edge information present in eye regions), the proposed SG filter-based feature extraction technique determines more gradient edge data from the eye regions (overestimation of smoothing coefficient values). And the proposed SG filter-based descriptors do underestimation of smoothing coefficient values of face images due to different light conditions (uneven edge information) at orientation angles in different directions (underestimation of smoothing coefficient values). Hence, the recognition accuracy of proposed SG filter-based face recognition techniques reduces against face images of set S5.
In Table 9, the recognition rate of the proposed face recognition techniques is better on subset 1 (illumination variations), subset 2 (expressions changes), and subset 4 (scarves with non-uniform illumination changes) over subset 5 (sunglass with illumination changes) of AR dataset, as most of the face parts namely nose, eye, and mouth features are available for feature extraction and classification (except in the case of scarves, mouth part is not available). Compared to other parts of the face image, left and right eye regions give most of the valuable information required for recognition. Due to sunglass and illumination changes, eye parts are not available from face images of subset 5 for feature extraction and classification tasks. The performance of NN, SVM and PNN classifiers is reduced when sunglasses with non-uniform light conditions on face images. It is also noticed that symbolic approach + PFFT and PNN + PFFT methods have reduced performance in case of occlusion along with illumination variations (S4). MLGD technique can accumulate more gradient edge information, which attains more robust feature dissimilarity between the face images.
Experimentation results of another similar face recognition technique called extended collaborative neighbor representation (ECNR) [36] and other works are compared with proposed methods on AR dataset [24, 25]. ECNR technique attained the best efficiency of 98.75, 88.33, 92.50, and 82.50% on face samples with non-uniform light conditions, change of expression, occlusion, and inclusion of occlusion with illumination variations, respectively. The experimental results of ECNR methods and proposed methods are given in Table 10.
Table 10.
Comparison of proposed works with ECNR technique and other works on AR dataset
| Method | Illumination variation(S1) | Expression changes (S2) | Occlusion (S3) | Occlusion and illumination (S4 + S5) |
|---|---|---|---|---|
| ECNR | 98.75 | 88.33 | 92.50 | 82.50 |
| Symbolic approach + PFFT | 98.54 | 98.81 | 89.79 | 95.67 |
| Symbolic approach + DGM | 91.67 | 95.24 | 96.94 | 94.00 |
| Symbolic approach + SGEF | 96.46 | 97.14 | 90.82 | 92.67 |
| Symbolic approach + GSGEF | 96.46 | 95.48 | 88.78 | 94.33 |
| NN + PFFT | 100 | 100 | 98.98 | 88.00 |
| NN + DG | 91.88 | 96.91 | 68.37 | 84.67 |
| NN + SGEF | 97.71 | 98.33 | 84.69 | 96.67 |
| NN + GSGEF | 92.29 | 94.29 | 76.53 | 91.33 |
| SVM + PFFT | 99.58 | 99.52 | 90.82 | 95.00 |
| SVM + DG | 95.00 | 99.05 | 90.82 | 93.67 |
| SVM + SGEF | 95.42 | 96.90 | 80.61 | 90.33 |
| SVM + GSGEF | 89.90 | 92.86 | 80.61 | 87.33 |
| PNN + PFFT | 93.54 | 96.19 | 72.45 | 87.33 |
| PNN + DG | 96.04 | 95.00 | 84.69 | 86.33 |
| PNN + SGEF | 93.54 | 93.33 | 77.55 | 91.33 |
| PNN + GSGEF | 91.05 | 93.81 | 82.65 | 88.67 |
From the study of Table 10, it can be concluded that the proposed face recognition methods give better results in case of expression changes (subset 2), presence of occlusion with non-uniform light conditions (subset 4 + subset 5) and almost equal on subset 1(illumination changes). When the face image is occluded by sunglass, most of the required information present in eye part is not available for the recognition (the information obtained from such occluded region is unwanted or irrelevant for classification task), as a result the performance of the proposed symbolic approach and PNN techniques is low on subset 3 compared to ECNR. As shown in Tables 9 and 10, the proposed symbolic similarity method with SGEF and GSGEF features for face recognition is an effective and more robust method to handle variations such as illumination, occlusion, and illumination and expression changes of face images and the proposed methods produce better results than the ECNR, LAG-LDA, and PFFT/DG/DGM/SGEF feature-based methods found in the literature. Due to the unavailability of eye and mouth features, the efficiency of the projected face recognition works is decreased on subset S3.
To compare and evaluate efficiency presented works over some of the supervised learning approaches, 25 men and 25 women face samples of AR dataset are uniformly selected to create a image gallery [37]. All the samples are rescaled to 32 × 32 size. Tenfold cross validation technique is chosen as evaluation protocol. The experimental outcome obtained from the proposed methods and others existing methods [24, 25, 37] are given in Table 11.
Table 11.
Recognition rate (%) of proposed methods and state-of-the-art techniques on AR dataset
| Sl. No | Methods | Recognition rate (%) | Sl. No | Methods | Recognition rate (%) | Sl. No | Methods | Recognition rate (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | GMD | 92.88 | 6 | SA-PFFT | 97.92 | 14 | SA-SGEF | 95.75 |
| 2 | SVM(P) | 38.30 | 7 | NN-PFFT | 96.92 | 15 | NN-SGEF | 97.67 |
| 3 | SVM(R) | 94.55 | 8 | SVM-PFFT | 98.42 | 16 | SVM-SGEF | 94.57 |
| 4 | KNN(E) | 95.64 | 9 | PNN-PFFT | 92.92 | 17 | PNN-SGEF | 92.92 |
| 5 | KNN(C) | 96.59 | 10 | SA-DGM | 97.50 | 18 | SA-GSGEF | 92.34 |
| 11 | NN-DG | 96.82 | 19 | NN-GSGEF | 93.30 | |||
| 12 | SVM-DG | 98.67 | 20 | SVM-GSGEF | 91.23 | |||
| 13 | PNN-DG | 93.25 | 21 | PNN-GSGEF | 92.99 |
Table 11 shows that the MLGD-based face recognition approaches have achieved better average recognition rates in comparison with methods proposed by Qiang Cheng et al. 2014 (GMD, SVM(P), SVM(R), KNN(E), and KNN(C)) and closer to SA-PFFT, NN-PFFT, SVM-PFFT, and PNN-PFFT methods [24, 25]. The experimental results of SGEF/GSGEF feature-based face recognition methods suggest the effectiveness to solve most of the issues related to class of variations on face images. From Tables 9, 10, 11, it can be seen that the proposed face recognition techniques with SGEF/GSGEF feature yield better recognition accuracy compared to some of the similar existing techniques. It is also noticed that the presented face recognition approaches are more robust to variations on face images (non-uniform illumination environment, expression, pose, and occlusion).
Performance comparison on LFW dataset
In this paper, more complex and publically available LFW dataset (evidently complex than AR database) is considered to evaluate the proposed techniques in unconstrained environment.
In order to prove the usefulness SGEF/GSGEF feature representation, the performances of proposed techniques are compared with low rank metric representation techniques called Discriminative Low-rank Metric Learning (DLML) over subset of LFW dataset [38]. The recognition accuracy of proposed works is also compared with CNN approach [39]. For evaluation, analogous experimental arrangements are made, i.e., segmented face images are down sampled to 120p × 120 size. The image restricted settings testing protocol is employed for validation. From 80 persons, 800 samples were selected to create a subset of LFW dataset. For training, 9 samples are randomly selected and remaining one for testing. The experimental outcome of proposed face recognition methods and some of the similar existing techniques [24, 25, 39] are recorded in Table12.
Table 12.
Comparison of recognition accuracy (%) of proposed methods over exiting techniques on LFW
| Sl. No | Methods | Recognition rate (%) | Sl. No | Methods | Recognition rate (%) | Sl. No | Methods | Recognition rate (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | 74.64—80.82 | 9 | SA-PFFT | 97.47 | 17 | SA-SGEF | 97.22 | |
| 2 | DML-eig | 82.28—87.94 | 10 | NN-PFFT | 98.04 | 18 | NN-SGEF | 98.06 |
| 3 | SILD | 80.07—86.04 | 11 | SVM-PFFT | 94.18 | 19 | SVM-SGEF | 92.30 |
| 4 | ITML | 79.98—85.94 | 12 | PNN-PFFT | 98.04 | 20 | PNN-SGEF | 98.04 |
| 5 | LDML | 80.65—86.64 | 13 | SA-DGM | 97.25 | 21 | SA-GSGEF | 96.20 |
| 6 | KISSME | 83.37—88.92 | 14 | NN-DG | 98.06 | 22 | NN-GSGEF | 98.03 |
| 7 | DLML | 85.35—91.15 | 15 | SVM-DG | 97.63 | 23 | SVM-GSGEF | 91.60 |
| 8 | FaceNet | 99.63 ± 0.09 | 16 | PNN-DG | 97.76 | 24 | PNN-GSGEF | 98.04 |
The experimentation results in Table 12 reveal that unconstrained conditions deteriorate the recognition rate of the reported works [39] compared to proposed face recognition techniques. It is also noticed that FaceNet deep learning technique achieves 99.63 ± 0.09% recognition rate by adopting standard testing protocol for unrestricted, labeled outside sample [39]. The face recognition techniques with DGM features meet nearly equal recognition rate to that of methods with PFFT features [24]. The experimentation outcomes also offer enough evidence that anticipated face recognition techniques-based SGEF/GSGEF features provide a robust system to address issues related to class of variation in an unconstrained environment (as LFW database represents).
In the experiments, the proposed methods are evaluated and compared with recent local pattern descriptors such as LVP, LBP, LDP, LTrP, LGHP, the methods proposed in [24, 25, 40, 41], SGEF and GSGEF features-based methods (Sl. No. 18–25) on LFW dataset. The experimentation results obtained from proposed techniques and the works from literature are given in Table 13.
Table 13.
Comparison of recognition rate (%) of proposed techniques over recent works on LFW dataset
| Sl. No | Methods | Recognition rate (%) | Sl. No | Methods | Recognition rate (%) | Sl. No | Methods | Recognition rate (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | LVP | 82.96 | 10 | SA-PFFT | 97.47 | 18 | SA-SGEF | 97.22 |
| 2 | LDP | 76.88 | 11 | NN-PFFT | 98.04 | 19 | NN-SGEF | 98.06 |
| 3 | LTrP | 80.84 | 12 | SVM-PFFT | 94.18 | 20 | SVM-SGEF | 92.30 |
| 4 | LBP | 83.16 | 13 | PNN-PFFT | 98.04 | 21 | PNN-SGEF | 98.04 |
| 5 | LGHP | 87.71 | 14 | SA-DGM | 97.25 | 22 | SA-GSGEF | 96.20 |
| 6 | MDML-DCPs + PLDA + Score averaging | 94.57 ± 0.30 | 15 | NN-DG | 98.06 | 23 | NN-GSGEF | 98.03 |
| 7 | MDML-DCPs + PLDA + SVM | 95.13 ± 0.33 | 16 | SVM-DG | 97.63 | 24 | SVM-GSGEF | 91.60 |
| 8 | MDML-DCPs + JB + SVM | 95.40 ± 0.33 | 17 | PNN-DG | 97.76 | 25 | PNN-GSGEF | 98.04 |
| 9 | MDML-DCPs + PLDA + JB + SVM | 95.58 ± 0.34 |
From Table 13, it is observed that the proposed techniques with GSGEF feature values outperform almost all the local pattern descriptors [40, 41]. The experimentation outcomes in Tables 9, 10, 11, 12, 13 show that the presented face recognition approaches achieve better recognition rates compared to some of the existing methods under uncontrolled environment. However, their performance is inferior to other methods proposed in Sl. Nos from 10 to 17.
Performance comparison on VISA face dataset
Further, to evaluate and investigate the effectiveness of proposed face recognition techniques with SGEF and GSGEF features, several experiments were conducted on the newly formed VISA face dataset. The performances of proposed techniques namely SA-GSGEF, NN-GSGEF, SVM-GSGEF, and PNN-GSGEF are compared with other approaches [24, 25]. In this paper, the performance of proposed face recognition methods with GSGEF features is also compared against methods with SGEF features on new VISA Face database and experimental results obtained are recorded in Table 14.
Table 14.
Comparison of recognition rate (%) of proposed works on VISA Face dataset
| Sl. No | Methods | Recognition rate (%) | Sl. No | Methods | Recognition rate (%) |
|---|---|---|---|---|---|
| 1 | SA-PFFT | 96.66 | 9 | SA-SGEF | 96.39 |
| 2 | NN-PFFT | 94.73 | 10 | NN-SGEF | 94.17 |
| 3 | SVM-PFFT | 96.15 | 11 | SVM-SGEF | 79.33 |
| 4 | PNN-PFFT | 89.28 | 12 | PNN-SGEF | 89.28 |
| 5 | SA-DGM | 95.40 | 13 | SA-GSGEF | 87.14 |
| 6 | NN-DG | 93.89 | 14 | NN-GSGEF | 90.23 |
| 7 | SVM-DG | 91.83 | 15 | SVM-GSGEF | 77.99 |
| 8 | PNN-DG | 89.33 | 16 | PNN-GSGEF | 89.39 |
From Table 14, it is noticed that recognition rate of proposed techniques is encouraging; however, it is comparatively low to that of the methods (Sl. Nos 1–4), (Sl. Nos 5–8), and (Sl. Nos 9–16). The new VISA Face dataset is more complex compared to AR, ORL, and LFW datasets. The anticipated face recognition approaches based on SGEF and GSGEF features are efficient and robust to illumination changes, expression, and pose variations. The proposed techniques maintain excellent performance on LFW dataset.
Performance comparison on IJB-A face dataset
Further to evaluate and investigate the effectiveness of the proposed symbolic modeling approach with SGEF and GSGEF features, several experiments were conducted on IJB-A database. In order to make a direct comparison of our face recognition techniques with state-of-the-art approaches [5], in this work, similar experimentation settings are made. The performances of proposed techniques are compared with deep learning-based techniques (Sl. Nos 9–11) and experimental results obtained are recorded in Table 15.
Table 15.
Comparison of recognition rate (%) of proposed works on IJB-A Face dataset
| Sl. No | Methods | Recognition rate (%) | Sl. No | Methods | Recognition rate (%) |
|---|---|---|---|---|---|
| 1 | SA-PFFT | 92.87 | 12 | SA-SGEF | 92.90 |
| 2 | NN-PFFT | 90.08 | 13 | NN-SGEF | 90.10 |
| 3 | SVM-PFFT | 88.10 | 14 | SVM-SGEF | 84.67 |
| 4 | PNN-PFFT | 89.20 | 15 | PNN-SGEF | 89.20 |
| 5 | SA-DGM | 90.17 | 16 | SA-GSGEF | 90.44 |
| 6 | NN-DG | 89.91 | 17 | NN-GSGEF | 87.17 |
| 7 | SVM-DG | 88.84 | 18 | SVM-GSGEF | 84.34 |
| 8 | PNN-DG | 83.98 | 19 | PNN-GSGEF | 89.18 |
| 9 | DCNN matching | 90.30 | |||
| 10 | VGG Face DCNN | 90.34 | |||
| 11 | FM + DCNN | 91.23 |
From Table 15, it is observed that proposed face recognition techniques achieved improvement in performance by using Savitzky–Golay filter-based features on IJB-A dataset. The Savitzky–Golay filter-based methods on IJB-A [5] show low performance because the database is relatively larger and more challenging than other reported datasets (ref. Tables [9–15]). However, our experimental results on IJB-A database (Sl. Nos 12 and 16) in Table 15 show that symbolic modeling approach with SGEF/GSGEF-based face recognition techniques provides higher recognition rate. Compared to the state-of-the-art technique (Sl. No. 11) on IJB-A, the proposed SA-SGEF (Sl. No. 12) achieved 1.67% performance improvement.
From the experimentation outcomes and performance analysis, it is noticed that Polar FFT-based face recognition techniques do consistently better compared to SG filter-based techniques. PFFT features of face images obtained using the PFFT algorithm are invariant to scale, and rotation and insensitive to noise, expression change, pose variations, inconsistent light conditions, and occlusion, whereas Savitzky–Golay filter is unable to estimate suitable smoothing coefficients, when the face images covered by mask, accessories, sunglass, other subjects, etc. The condition becomes even worst in the presence of combination of occlusion and non-uniform light on face samples. Hence, the performance of Savitzky–Golay moving filter-based face recognition techniques is reduced in the presence of illumination and occlusion on face samples. In AR dataset, face images are occluded by sunglass or masks and poses illumination variations. The VISA and IJB-A datasets face images are obtained from both indoor and outdoor conditions of different sessions, different occasions, etc., and face images are complex in terms of illumination changes and occlusion compared to AR, LFW, and ORL datasets. Hence, the SG filter-based face recognition techniques underperform on IJB-A, AR, and VISA Face datasets compared to performance on LFW and ORL datasets.
Conclusion
Efficient and robust face recognition techniques are presented based on Savitzky–Golay filter energy feature (SGEF) and Gradient-based Savitzky–Golay filter energy features (GSGEF) descriptors. In the proposed work, instead of considering complete face image, face parts are cropped from the given face image by employing Viola–Jones technique. From the cropped face parts set of feature, values are estimated by applying Savitzky–Golay filter. Further, based on SGEF and GSGEF feature values, symbolic modeling classifiers are presented. In symbolic modeling approach, feature values of each face part are represented as independent symbolic data objects. The symbolic representation of obtained features uses exceptionally small dimensional feature space, which reduces the computational time. The performance of proposed techniques is evaluated on face databases namely AR, ORL, LFW, IJB-A, and the new VISA Face. From experimentation results, it has been found that the proposed face recognition methods offer high recognition accuracy under uncontrolled environments. It is hoped that the proposed partial face recognition methods using new texture descriptors can pave the way to design and develop a standard application to take into account of new challenges faced by facial recognition technology in COVID-19.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Vishwanath C. Kagawade, Email: vishwanath.1312@gmail.com
Shanmukhappa A. Angadi, Email: vinay_angadi@yahoo.com
References
- 1.Carlaw S. (2020) Impact on biometrics of Covid-19(2020) Biometric Technol Today. 2020;4:8–9. doi: 10.1016/S0969-4765(20)30050-3. [DOI] [Google Scholar]
- 2.Whitelaw S, Mamas MA, Topol E, Van Spall HGC. Applications of digital technology in COVID-19 pandemic planning and response. Lancet Digit Health. 2020;2(8):e435–e440. doi: 10.1016/S2589-7500(20)30142-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.He L, Li H, Qi Z, Sun Z. Dynamic feature matching for partial face recognition. IEEE Trans Image Process. 2019;28(2):791–802. doi: 10.1109/TIP.2018.2870946. [DOI] [PubMed] [Google Scholar]
- 4.Madzou L, Louradour S. (2020) Building a governance framework for facial recognition. Biometric Technol Today. 2020;6:5–8. doi: 10.1016/S0969-4765(20)30083-7. [DOI] [Google Scholar]
- 5.Riaz S, Park U, Natarajan P. Improving face verification using facial marks and deep CNN: IARPA Janus benchmark-A. Image Vis Comput. 2020;104:104020. doi: 10.1016/j.imavis.2020.104020. [DOI] [Google Scholar]
- 6.Chen J, Patel VM, Chellappa R. Unconstrained face verification using deep CNN features; Lake Placid, NY, USA: IEEE; 2016. pp. 1–9. [Google Scholar]
- 7.Jin B, Cruz L, Gonçalves N. Deep facial diagnosis: deep transfer learning from face recognition to facial diagnosis. IEEE Access. 2020;8:123649–123661. doi: 10.1109/ACCESS.2020.3005687. [DOI] [Google Scholar]
- 8.Choi JY, Lee B. Ensemble of Deep Convolutional Neural Networks With Gabor Face Representations for Face Recognition. IEEE Trans Image Process. 2020;29:3270–3281. doi: 10.1109/TIP.2019.2958404. [DOI] [PubMed] [Google Scholar]
- 9.Bachtiger P, Peters NS, Walsh SLF. Machine learning for COVID-19-asking the right questions. Lancet Digit Health. 2020;2(8):e391–e392. doi: 10.1016/S2589-7500(20)30162-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Savitzky, Golay MJE. Soothing and differentiation of data by simplified least squares procedures. Anal Chem. 1964;36:1627–1639. doi: 10.1021/ac60214a047. [DOI] [Google Scholar]
- 11.Schafer Ronald W. What Is a Savitzky-Golay Filter? IEEE Signal Process Mag. 2011;28(4):111–117. doi: 10.1109/MSP.2011.941097. [DOI] [Google Scholar]
- 12.Agarwal S, Rani A, Singh V, Mittal AP. EEG signal enhancement using cascaded S-Golay filter. Biomed Signal Process Control. 2017;36:194–204. doi: 10.1016/j.bspc.2017.04.004. [DOI] [Google Scholar]
- 13.Kim S-R, Prasad AK, El-Askary H, Lee W-K, Kwak D-A, Lee S-H, Kafatos M. Application of the Savitzky-Golay filter to land cover classification using temporal MODIS vegetation indices. Photogramm Eng Remote Sens. 2014;80(7):675–685. doi: 10.1016/j.jcis.2014.11.033. [DOI] [Google Scholar]
- 14.Candan Ç, Inan H. A unified frame work for derivation and implementation of Savitzky-Golay filters. Signal Process. 2014;104:203–211. doi: 10.1016/j.sigpro.2014.04.016. [DOI] [Google Scholar]
- 15.Larson EC, Goel M, Boriello G, Heltshe S, Rosenfeld M, Patel SN (2012) SpiroSmart: using a microphone to measure lung function on a mobile phone. In: Proceedings of the 2012 ACM Conference on ubiquitous computing. Pittsburgh, USA, pp. 280–289. 10.1145/2370216.237026
- 16.Sameni R. Online filtering using piecewise smoothness priors: application to normal and abnormal electrocardiogram denoising. Signal Process. 2017;133(2017):52–63. doi: 10.1016/j.sigpro.2016.10.019. [DOI] [Google Scholar]
- 17.Gowri BG, Hariharan V, Thara S, Sowmya V, Kumar SS, Soman KP. 2013 International mutli-conference on automation, computing, communication, control and compressed sensing. Kottayam, India: IEEE; 2013. 2D image data approximation using Savitzky Golay filter - smoothing and differencing. [Google Scholar]
- 18.Acharya D, Rani A, Agarwal S. Vijander Singh (2016) Application of adaptive Savitzky Golayfilter for EEG signal processing. Perspect Sci. 2016;8:677–679. doi: 10.1016/j.pisc.2016.06.0562213-0209. [DOI] [Google Scholar]
- 19.Yanping LIU, Bo DANG, Yue LI, Hongbo LIN, Haitao MA. Applications of Savitzky-Golay Filter for Seismic Random Noise Reduction. Acta Geophys. 2016;64(1):101–124. doi: 10.1515/acgeo-2015-0062. [DOI] [Google Scholar]
- 20.Krishnan S, Seelamantula C. On the selection of optimum savitzky-golay filters. IEEE Trans Signal Process. 2013;61(2):80–391. doi: 10.1109/TSP.2012.2225055. [DOI] [Google Scholar]
- 21.Sadasivan J, Mukherjee S, Seelamantula CS. 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) Florence, Italy: IEEE; 2014. An optimum shrinkage estimator based on minimum-probability-of-error criterion and application to signal denoising. [Google Scholar]
- 22.Chidananda GK. Edwin Diday (1991) Symbolic clusters using a new dissimilarity measure. Pattern Recogn. 1991;24(6):567–578. doi: 10.1016/0031-3203(91)90022-W. [DOI] [Google Scholar]
- 23.Nagabhushan P, Angadi SA, Anami BS. A Fuzzy Symbolic Inference System for Postal Address Component Extraction and Labelling. In: Wang L, Jiao L, Shi G, Li X, Liu J, editors. Fuzzy Systems and Knowledge Discovery. FSKD 2006. Lecture Notes in Computer Science. Heidelberg: Springer, Berlin; 2006. [Google Scholar]
- 24.Angadi SA, Kagawade VC. A robust face recognition approach through symbolic modeling of polar FFT features. Pattern Recogn. 2017;71C(2017):235–248. doi: 10.1016/j.patcog.2017.06.014. [DOI] [Google Scholar]
- 25.Kagawade VC, Angadi SA. Multi-directional local gradient descriptor: A new feature descriptor for face recognition. Image Vis Comput. 2019;83–84:39–50. doi: 10.1016/j.imavis.2019.02.001. [DOI] [Google Scholar]
- 26.Chidambaram S, Erridge S, Kinross J, Purkayastha S. Observational study of UK mobile health apps for COVID-19. Lancet Digit Health. 2020;2(8):e388–e390. doi: 10.1016/S2589-7500(20)30144-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kagawade VC, Angadi SA. VISA: a multimodal database of face and iris traits. Multimed Tools Appl. 2021 doi: 10.1007/s11042-021-10650-4. [DOI] [Google Scholar]
- 28.Suman S, Jha RK. A new technique for image enhancement using digital fractional-order Savitzky-Golay differentiator. Multidim Syst Sign Process. 2017;28:709–733. doi: 10.1007/s11045-015-0369-9. [DOI] [Google Scholar]
- 29.Chen D, Chen YQ, Xue D. 1-D and 2-D digital fractional-order Savitzky-Golay differentiator. SIViP. 2012;6(503–511):2012. doi: 10.1007/s11760-012-0334-0. [DOI] [Google Scholar]
- 30.Martinez AM, Benavente R (1998) The AR face database, CVC technical report, 24 june 1998
- 31.Viola P, Jones M. (2004) Robust real-time face detection. Int J Comput Vision. 2004;57(2):137–154. doi: 10.1023/B:VISI.0000013087.49260.fb. [DOI] [Google Scholar]
- 32.Angadi SA, Kagawade VC. In: 2018 international conference on electrical, electronics, communication, computer, and optimization techniques (ICEECCOT) Msyuru, India: IEEE; 2018. Face and Iris wavelet feature fusion through canonical correlation analysis for person identification; pp. 172–178. [Google Scholar]
- 33.Angadi SA, Kagawade VC. 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI) Udupi: IEEE; 2017. Iris recognition using savitzky-golay filter energy feature through symbolic data modeling. [Google Scholar]
- 34.Angadi SA, Kagawade VC. 2017 International conference on smart technologies for smart nation (SmartTechCon) Bangalore, India: IEEE; 2017. Iris recognition: a symbolic data modeling approach using Savitzky-Golay filter energy features. [Google Scholar]
- 35.Li Z, Wang Y, Fan C, He J. Image Preprocessing Method based on Local Approximation Gradient with Application to Face Recognition. Pattern Anal Applic. 2015;20:101–112. doi: 10.1007/s10044-015-0470-6. [DOI] [Google Scholar]
- 36.Jadoon W, Zhang L, Zhang Y. Extended Collaborative Neighbor Representation for Robust Single-sample Face Recognition. Neural Comput Appl. 2015;26(8):1991–2000. doi: 10.1007/s00521-015-1843-x. [DOI] [Google Scholar]
- 37.Peng C, Cheng J, Cheng Q. A supervised learning model for high-dimensional and large-scale data. ACM Trans Intell Syst Technol (TIST) 2017;8(2):1–23. doi: 10.1145/2972957. [DOI] [Google Scholar]
- 38.Ding Z, Suh S, Han JJ, Choi C, Fu Y. 2015 11th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition (FG) Ljubljana, Slovenia: IEEE; 2015. Discriminative low-rank metric learning for face recognition. [Google Scholar]
- 39.Schroff F, Kalenichenko D, Philbin J. 2015 IEEE conference on computer vision and pattern recognition (CVPR) Boston, MA, USA: IEEE; 2015. FaceNet: a unified embedding for face recognition and clustering; pp. 815–823. [Google Scholar]
- 40.Fan KC, Hung TY. A novel local pattern descriptor- local vector pattern in high-order derivative space for face recognition. IEEE Trans Image Process. 2014;23(7):2877–2891. doi: 10.1109/TIP.2014.2321495. [DOI] [PubMed] [Google Scholar]
- 41.Chakraborty S, Singh SK, Chakraborty P. Local gradient hexa pattern: a descriptor for face recognition and retrieval. IEEE Trans Circuits Syst Video Technol. 2018;28(1):171–180. doi: 10.1109/TCSVT.2016.2603535. [DOI] [Google Scholar]