Interaction of Aromatic Molecules with Forsterite: Accuracy of the Periodic DFT-D4 Method

Abstract

Density functional theory (DFT) has provided deep atomic-level insights into the adsorption behavior of aromatic molecules on solid surfaces. However, modeling the surface phenomena of large molecules on mineral surfaces with accurate plane wave methods (PW) can be orders of magnitude more computationally expensive than localized atomic orbitals (LCAO) methods. In the present work, we propose a less costly approach based on the DFT-D4 method (PBE-D4), using LCAO, to study the interactions of aromatic molecules with the {010} forsterite (Mg₂SiO₄) surface for their relevance in astrochemistry. We studied the interaction of benzene with the pristine {010} forsterite surface and with transition-metal cations (Fe²⁺ and Ni²⁺) using PBE-D4 and a vdW-inclusive density functional (Dion, Rydberg, Schröder, Langreth, and Lundqvist (DRSLL)) with LCAO methods. PBE-D4 shows good agreement with coupled-cluster methods (CCSD(T)) for the binding energy trend of cation complexes and with PW methods for the binding energy of benzene on the forsterite surface with a difference of about 0.03 eV. The basis set superposition error (BSSE) correction is shown to be essential to ensure a correct estimation of the binding energies even when large basis sets are employed for single-point calculations of the optimized structures with smaller basis sets. We also studied the interaction of naphthalene and benzocoronene on pristine and transition-metal-doped {010} forsterite surfaces as a test case for PBE-D4. Yielding results that are in good agreement with the plane wave methods with a difference of about 0.02–0.17 eV, the PBE-D4 method is demonstrated to be effective in unraveling the binding structures and the energetic trends of aromatic molecules on pristine and transition-metal-doped forsterite mineral surfaces. Furthermore, PBE-D4 results are in good agreement with its predecessor PBE-D3(BJM) and with the vdW-inclusive density functionals, as long as transition metals are not involved. Hence, PBE-D4/CP-DZP has been proven to be a robust theory level to study the interaction of aromatic molecules on mineral surfaces.

Introduction

Astronomical observations have revealed a rich and diverse inventory of molecules in interstellar space. The observed different species range from simple molecules such as H₂, H₂O, and NH₃, identified in the birthplace of stars (molecular clouds), to ions and radicals detected in regions with high UV radiations as well as complex and stable aromatic molecules.¹ Furthermore, complex aromatic molecules along with prebiotic building blocks of life, e.g., amino acids and sugars, have been detected in asteroids and meteorites.² Polycyclic aromatic hydrocarbons (PAHs) are a class of abundant aromatic molecules in our galaxy and beyond. They have been identified through their vibrational signature in infrared spectra and thought to be involved in many important processes that regulate the physical conditions of star-forming regions.³ Specifically, PAHs have been extensively studied as catalysts for interstellar H₂ formation.⁴⁻¹⁰ They may also play a role as reagents in many reactions involving atoms, ions, and molecules that contribute to the rich organic inventory of space.¹¹ Finally, it has been suggested that PAHs may be more directly involved in the origin of life by providing a convenient assemblage structure for RNA.¹²

The coexistence and high abundance of both simple and complex species in space are indicative of the presence of at least two and potentially more chemical routes toward molecular complexity.¹ One chemical route is a bottom-up approach, where atoms and small molecules react to form larger species, one or a few atoms at a time. As densities and temperatures are low, this buildup is slow, and only relatively small molecules are formed this way. Much of this chemistry is thought to take place on submicron-sized grains, where CO can be hydrogenated on icy surfaces by H atoms to form H₂CO and CH₃OH.¹³ The latter can be the feedstock for further complex chemistry.¹⁴⁻¹⁷ The other chemical route starts in the high-density and -temperature regimes associated with stellar outflow. The stellar conditions will lead to soot formation, and large molecules such as PAHs are formed and injected into the interstellar medium (ISM).¹⁸⁻²⁰ Exposed to harsh environments, these molecules can fragment or isomerize due to interaction with UV photons and/or energetic ions.²¹ PAHs and their daughter products can also interact with simple species on ice surfaces in space.^22,23 Eventually, the products of both bottom-up and top-down chemistry as well as the prevalent mineral grains can become part of planetesimals in planet-forming disks. During the early stages of their evolution, planetesimals will go through a warm (∼500 K), aqueous phase, and large-scale transport within these bodies will allow direct interaction of PAHs with mineral surfaces, opening up new reaction channels. Eventually, these planetesimals will contribute to the organic inventory of terrestrial planets in the habitable zone of new planetary systems.¹

Chemistry on mineral surfaces may thus be of great relevance to molecular astrophysics. However, studies on astronomically relevant mineral surfaces are sorely lacking.²⁴ Specifically, while quantum chemistry and in particular density functional theory (DFT) are well established as important tools in assessing the relevance of gas-phase reactions of PAHs to space,^5−7,25 studies on the interaction of molecular species with mineral species have lagged due to the prohibitive computational costs and the challenges in employing hybrid functionals that correct the self-interaction error of standard (semilocal) DFT methods.²⁶ In material sciences, plane wave (PW) codes such as VASP have been widely employed as they ensure robust and accurate results.²⁷⁻³⁰ However, plane wave codes allow modeling of molecules of limited size due to their computational cost.³¹ Codes such as SIESTA³² make profitable use of localized atomic orbitals (LCAO) basis sets that allow the study of larger systems than plane wave by employing periodic DFT. Unfortunately, LCAO methods suffer from the so-called basis set superposition error (BSSE), which leads to an overestimation of the binding and adsorption energy.³³ This is the “price to be paid” for computational efficiency. This issue can be overcome using the counterpoise method developed by Boys et al.,³⁴ which is a pragmatic solution to the problem. Another challenge is that DFT methods describe bond formation well, thanks to a good description of the electronic correlation in the region of orbital overlapping between atoms to form the bond, but their weak spot is the lack of an accurate description of the London dispersion, i.e., density transfer between two long-distance orbitals.³⁵ One of the approaches to overcome this issue is to compute an interatomic potential named the DFT-D method.^36,37 This method is a posteriori empirical correction to the Kohn–Sham (KS) energy. Hence, the dispersion energy is calculated independently and is summed up to the KS energy (E_KS + E_D).³⁵ An alternative method to take the London dispersion into account is through the use of nonlocal correlation functionals such as vdW-DF³⁸ and vdW-DF2,³⁹ which depend directly on the electron density. However, this method results in significant BSSE issues when calculating the binding energy of organics on metal surfaces.⁴⁰

Few studies have benchmarked DFT functionals that model the interactions of molecules on forsterite surfaces.⁴¹ Here, we test an accurate, yet cheap method based on LCAO that employs the Perdew, Becke, and Ernzerho (PBE)⁴² exchange–correlation functional and the DFT-D4 method developed by Grimme et al.³⁷ (PBE-D4). The aim of this work is to compute accurate binding energies that can be used in astronomical grain surface models^43,44 to predict the abundance of large aromatic molecules such as PAHs interacting with a mineral surface under interstellar conditions, specifically the {010} forsterite surface, because of its relevance in astrophysics.⁴⁵⁻⁴⁷ The proposed theoretical approach is focused on systems of interest in astronomy, but its validity applies equally well to systems of interest in planetary science and material science. In fact, PAHs were detected in martian and carbonaceous chondrite meteorites,⁴⁸ and in the terrestrial environment; they are relevant because of their carcinogenic properties as well as their pollution properties.⁴⁹ The general problem in removing PAHs from contaminated soils makes materials such as minerals worthy of investigations.

Theoretical Methods and Models

In the present work, we model a 4 × 3 {010} forsterite surface ({010}-fo) with the molecular formula Mg₉₆O₁₉₂Si₄₈ (Figure 1), which is the most studied and stable forsterite surface under dry conditions⁵⁰⁻⁵² as well as the most studied one for the interaction of organic compounds.^53,54 Along with the pure {010}-fo (Figure 1a and 1c), we study its defective surfaces with a single doped Fe²⁺ (Fe-{010}-fo) and single doped Ni²⁺ (Ni-{010}-fo), as shown in Figure 1b and 1d. The defective surfaces are generated by the substitution of a transition-metal atom, Fe or Ni in this case, for a Mg atom on the surface of 4 × 3 {010}-fo.

Figure 1.

Top view (a) and (b) and lateral view (c) and (d) of the optimized structure of the 4 × 3 {010} forsterite surface with the corresponding atomic labels (Mg, O, Si, and M = Fe or Ni). The vacuum region is located along the z-axis.

The nonpolar {010}-fo is generated by cutting the fully optimized bulk with the METADISE code, which ensures a zero dipole moment along the z-axis.⁵⁵ The generated surface has a thickness of 9.28 Å to preserve the bulk properties and a vacuum region of 25 Å to avoid the interactions between the slab images. Finally, we create a 4 × 3 supercell of the nonpolar {010}-fo, which is large enough (18.996 Å x 17.938 Å) to minimize lateral interactions between adsorbed molecules in neighboring image cells.

In view of the large computational cost involved in modeling the interaction of large aromatic molecules with the supercell of {010}-fo, we employ SIESTA as the LCAO code³² with core pseudopotentials. We use PBE⁴² as the generalized-gradient approximation (GGA) exchange–correlation functional and the Dion, Rydberg, Schröder, Langreth, and Lundqvist⁵⁶ (DRSLL) vdW-DF exchange–correlation functional along with a polarized double-zeta (DZP) basis set. We set the radii for the split-valence type of the basis of hydrogen atoms to 0.50. Furthermore, the PBE/DZP method was already tested to reproduce correctly the adsorption properties of small molecules on {010}-fo.⁴¹ To have comparable results, we use the same pseudopotentials for both the PBE and DRSLL functionals. For the case of DRSLL, we set the maximum angular momentum of the Kleinman–Bylander projectors for the H atoms to zero to avoid ghost states for high values of angular momentum. We employ the Monkhorst–Pack⁵⁷ scheme to sample the Brillouin zone using 7 × 3 × 7 K-points for the bulk and 2 × 2 × 1 for the {010}-fo supercell along with the spin-unrestricted formalism for all calculations. The structures are considered optimized when the Hellmann–Feynman forces are less than 10^–3 eV Å^–1. The mesh cutoff grid density converges to 200 Ry (convergence test reported in the SI). We apply the counterpoise scheme to correct the total energy for the BSSE.^34,58

When a non-vdW-inclusive functional such as PBE is employed, the London dispersion energy (E_D) is calculated a posteriori with DFT-D4^37,59,60 and DFT-D3³⁶ codes due to the lack of implementation of these methods in SIESTA code. Therefore, the E_D is computed separately and summed up to the E_KS estimated at the PBE level. We use the revised Becke–Johnson damping (BJM)^61,62 for the DFT-D3 method for a fair comparison with DFT-D4 that uses the same damping function³⁷ and the nonadditive Axilrod–Teller–Muto three-body dispersion correction for both methods.⁶³

The electronic structure of bulk forsterite is characterized by the projected density of states (PDOS) generated with the LDAU + U method as implemented in SIESTA.⁶⁴ The Hubbard U value is set to 15.3 eV to include the strong on-site Coulombic interaction of the 2p orbitals of oxygen atoms and reproduce the experimental band gap⁶⁵ of 8.4 eV with a tolerance population of 4 × 10^–4 and a threshold tolerance of 10^–2. The PDOS is generated by a single-point calculation from the optimized structure of PBE/DZP employing a polarized triple-zeta (TZP) basis set. We set the radii for the split-valence type of basis to 0.30 for all atoms besides the hydrogen, in which we use the same setup as for the case of DZP (see SI). This approach is necessitated by the need to converge correctly the empty states that require expensive and larger basis sets. An extra grid of 4 × 4 × 1 K-points of Monkhorst–Pack⁵⁷ is employed for all PDOS calculations. The peak width is generated using 5000 points and a broadening eigenvalue of 0.05 in the energy window between −60 and 200 eV.

To accurately compute the binding energy, the Hubbard U value needs to be retro-corrected based on experimental data but these are currently lacking in the literature. Our adopted approach allows us to compute the electronic structure without interfering with the binding energy trend while avoiding computational expensive calculations.

For all calculations involving the organics on the {010} forsterite surfaces, an electric field is applied to compensate for the dipole moment at the vacuum region on every self-consistent field (SCF) cycle. The structure and reference energy of the gas-phase molecules are obtained in a cubic cell of dimensions (15 Å × 15 Å × 15 Å) using a 1 × 1 × 1 Monkhorst–Pack K-point mesh.⁵⁷

In this study, we refer to binding energy (E_b) as the difference between the energy of the reagents (the slab or the transition-metal cation, and the molecule in the gas phase) and the energy of the product (the molecule adsorbed on the slab or complexes with a transition-metal cation). A positive value of binding energy indicates an exoergic process. The adsorption energies reported in other studies are converted, for simplicity, into binding energies that are the opposite of the adsorption energy by definition.

Results and Discussion

Forsterite Bulk Properties

The bulk of forsterite (Mg₂SiO₄) has an orthorhombic structure and Pbnm as the space group;⁶⁶ see the inset of Figure 2. The forsterite structure is characterized by octahedral Mg atoms bound with six O atoms and tetrahedral Si atoms bound with four O atoms. This ionic system is formed by cations (Mg²⁺) and an equivalent number of anions (SiO₄^2–) that maintain the system’s electroneutrality.

Figure 2.

Hubbard-corrected total and projected density of states, PDOS, and optimized structure of the bulk (PBE/DZP) of forsterite with atomic labels reported on the corresponding atoms.

From a geometry optimization using the PBE/DZP functional, the unit cell parameters are predicted at a = 4.80 Å, b = 10.28 Å, c = 6.01 Å, and α = β = γ = 90°, which compared closely with known experimental values and plane wave code results (Table 1). Including dispersion corrections using a vdW-inclusive functional such as DRSLL or an empirical method such as DFT-D3 does not change significantly the unit cell parameters of the bulk structure of forsterite. Also, the unit cell parameters obtained using PBE/DZP are in close agreement with the hybrid functional B3LYP.

Table 1. Optimized Unit Cell of the Bulk of Forsterite at Different Levels of Theory Along with the Experimental Values and the Elapsed Time Per SCF Cycle (E.T.^scf) Where Applicable.

methods	a (Å)	b (Å)	c (Å)	E.T.scf (s)
PBE/DZPa	4.80	10.28	6.01	23.068
PBE-D3/PWb	4.77	10.25	6.01	41.993
DRSLL/DZPa	4.83	10.34	6.04	27.318
PBE/PW72	4.76	10.24	6.00
PBE/DZP73	4.80	10.28	6.02
B3LYP/GTO46	4.80	10.25	6.01
experiments66	4.76	10.21	5.98
experiments70	4.75	10.19	5.98

^aThis work employing SIESTA.

^bThis work employing VASP (see SI).

Table 1 also reports the elapsed time for the two different methods employed in this work, i.e., PW and LCAO methods. PBE seems slightly faster than DRSLL, but both methods are about 15–19 s (Table 1) faster than plane wave methods for the optimization of the bulk of forsterite.

Perusing the projected density of states (PDOS) spectra, shown in Figure 2, the insulating behavior of Mg₂SiO₄ is also well reproduced with a band gap of 8.4 eV in accordance with commonly reported band gaps of 7.5–9.5 eV.^65,67,68 The valence band is dominated by electrons of the 2p orbitals of O atoms, whereas the conduction band is dominated by electrons of 3p orbitals of Mg and Si atoms in conformity with theoretical studies making use of plane wave methods.⁶⁹ The electron density is centered around Mg–O and Si–O bonds with average bond distances of 2.09 and 1.69 Å, respectively, in agreement with the previous experimental⁷⁰ and theoretical calculations.^46,71 Therefore, PBE/DZP can reproduce the bulk properties of forsterite.

Benzene Adsorption on the Mg₂SiO₄ {010} Surface

The {010}-fo surface is characterized by an external layer, the interface between the mineral and vacuum region, of undercoordinated Mg atoms with a square pyramidal geometry above the inner layer of fully coordinated atoms in accordance with previous studies.⁴⁶ Here, we focus on the level of theory for the adsorption of a small aromatic molecule, benzene, on {010}-fo.^53,54

The binding energies of benzene interaction on {010} forsterite (Figure 3) are reported in Table 2 for different levels of theory. PBE-D4 is consistent with the PW method using PBE-D2.⁵⁴ The interatomic distances, calculated with PBE-D4, between the center of the ring and the Mg atom are in good agreement with the B3LYP-D2 calculation.⁵³ However, the binding energy calculated at the PBE-D4/CP-DZP level differs from B3LYP-D2/TZP//B3LYP-D2/DZP⁵³ by 0.45 eV. The difference between the two methods (PBE-D4 and B3LYP-D2) can be attributed to the lack of BSSE correction in the B3LYP-D2 calculation.

Figure 3.

Optimized structure (PBE/DZP) of benzene adsorbed on the {010} forsterite surface. The colored balls correspond to the following atoms: hydrogen (white), carbon (gray), magnesium (green), silicon (yellow), and oxygen (red). Atomic labels are reported on the corresponding atoms.

Table 2. Binding Energy (E_b), at Various Levels of Theory, of Benzene on the {010} Forsterite Surface^a.

level of theory	Eb (eV)	dcm (Å)	E.T.scf (s)
DRSLL/CP-DZPb	0.75	3.17
DRSLL/DZPb	1.80	3.17	78.711
PBE-D4/CP-DZPb	0.84	2.45
PBE-D4/DZPc	1.81	2.45	66.304d (1381.018e)
PBE-D4/CP-TZP//PBE-D4/DZPb	0.70	2.45
PBE-D4/TZP//PBE-D4/DZPc	1.70	2.45
PBE-D2/PW54	0.87
B3LYP-D2/TZP//B3LYP-D2/DZP53	1.29	2.42

^ad_cm is the distance between the center of the ring and the near Mg atom on the surface. .../TZP//.../DZP indicates a single-point calculation of the optimized geometry at the DZP level, whereas CP indicates a counterpoise-corrected basis set. Elapsed time per SCF cycle (E.T.^scf), only for the adsorbate on the surface, is reported for the corresponding theoretical level.

^bThis work.

^cAs a without CP correction.

^dElapsed time per SCF cycle without D4 correction.

^eElapsed time at PBE/PW (VASP).

For a fair comparison, we calculated the binding energy for the adsorption of benzene on {010}-fo, using a TZP basis set as a single-point calculation on the optimized geometry of PBE-D4/CP-DZP, in line with the calculation carried out by Rimola et al.⁵³ at the B3LYP-D2/TZP//B3LYP-D2/DZP level of theory. The binding energies are reported in Table 2, with (e.g., CP-TZP//DZP) and without (e.g., TZP//DZP) BSSE correction. The estimated BSSE error is about 1 eV for both PBE-D4/DZP and PBE-D4/TZP//PBE-D4/DZP. In other words, a TZP single-point calculation on the optimized geometry of DZP does not reduce the BSSE since a full optimization with a TZP basis set would be required.

The vdW-inclusive density functional DRSLL shows a slightly lower binding energy than PBE-D4/CP-DZP and PBE-D2/PW. Without accounting for the counterpoise correction, DRSLL/DZP is in agreement with PBE-D4/DZP. However, DRSLL underestimates the distance between the Mg atom and the center of the benzene ring by 0.72 Å compared to the other methods. Moreover, as shown in Table 2, both DRSLL and PBE-D4 in the LCAO approach are faster by about a factor of 20 with respect to plane wave methods.

Benzene Complexes of Transition-Metal Cations

Forsteritic olivine grains in meteorites contain a low amount, about 1%, of transition metals as point defects.^74,75 Specifically, Rimola et al.⁴⁶ already studied the structure of forsterite with Fe²⁺ atoms, showing that Fe is more stable on the surface when it is undercoordinated and in its most stable electronic configuration (quintet state). Atomic Ni has chemical properties similar to those of atomic Fe and it has been detected in chondrite meteorites with an abundance of about 1% and in olivinic grains analyzed by NASA’s Stardust mission.^76,77 Therefore, in preparation for studies of metal-doped forsterite surfaces and in view of their astronomical relevance, we have studied the effect of Fe²⁺, in quintet state, and Ni²⁺, in triplet state, on the adsorption geometry and energetics of benzene, Benz-Fe²⁺ and Benz-Ni²⁺, respectively, as shown in Figure 4.

Figure 4.

Top view and side view of the optimized geometry (PBE/DZP) of benzene coordinated with (a) Fe²⁺ (Benz-Fe²⁺) in quintet state and (b) Ni²⁺ (Benz-Ni²⁺) in triplet state.

Table 3 reports the interaction energy of benzene coordinated with Fe²⁺ and Ni⁺² at different levels of theory. The interatomic distances at PBE-D4 are consistent with MP2 calculations.⁷⁸ The obtained results suggest that all DFT methods overbind by about 1 eV compared to more accurate Post–Hartree–Fock methods (MP2 and CCSD(T)). The overbinding nature of DFT methods might be caused by the lack of an accurate description of the electronic localization over delocalization, e.g., describing the localization of the electrons of the d and f orbitals of transition metals as electronically delocalized and vice versa. In fact, hybrid functionals, even though energetically and geometrically more accurate than pure GGA ones, have problems in accurately describing the electronic localization of metal–carbon bonds.⁸⁰

Table 3. Binding Energy (E_b), Distances between the Center of the Aromatic Ring and the Transition Metal (d_cm), and the Carbon–Carbon Distance (d_C–C) of Benzene Coordinated with Fe²⁺ (Benz-Fe²⁺), in Quintet State, and Ni²⁺ (Benz-Ni²⁺), in Triplet State.

system (level of theory)	Eb (eV)	dcm (Å)	dC–C (Å)
Benz-Fe2+ (PBE-D4/CP-DZP)a	6.80	1.77	1.44
Benz-Fe2+ (DRSLL/CP-DZP)a	7.01	2.74	1.43
Benz-Fe2+ (CCSD(T)/6-311++G(2d,2p))78	5.61
Benz-Fe2+(MP2/6-311++G(2d,2p))78	5.55	1.85	1.41
Benz-Fe2+ (B3LYP-D2/6-311++G(2d,2p))78	6.71
Benz-Fe2+ (B3LYP-D2/6-31G**)79	6.78	1.80
Benz-Fe2+(ωB97X-D/6-311++G(2d,2p))78	6.38
Benz-Ni2+ (PBE-D4/CP-DZP)a	9.19	1.61	1.44
Benz-Ni2+ (DRSLL/CP-DZP)a	7.52	2.63	1.44
Benz-Ni2+ (CCSD(T)/6-311++G(2d,2p))78	8.14
Benz-Ni2+(MP2/6-311++G(2d,2p))78	8.39	1.69	1.42
Benz-Ni2+ (B3LYP-D2/6-311++G(2d,2p))78	9.68
Benz-Ni2+ (ωB97X-D/6-311++G(2d,2p))78	9.53

^aThis work.

PBE-D4 provides results in good agreement with B3LYP-D2 and ωB97X-D, for Benz-Fe²⁺. For Benz-Ni²⁺, PBE-D4 is about 0.4 eV lower in energy than the other DFT methods. For clarity, we report the B3LYP-D2 binding energy calculated using both double-zeta (6-311++G(2d,2p)) and triple-zeta (6-31G**) basis sets as well as DRSLL/CP-DZP. Note that the basis set does not significantly change the adsorption energy trend. For the case of DRSLL/CP-DZP, the binding energies are in agreement with the general trend, with only slight overbinding for the Fe²⁺ complex and underbinding for the Ni²⁺ one with respect to the other DFT methods. As for the benzene on the forsterite surface, the distance between the center of the ring and the transition-metal cations is larger by about 1 Å compared to PBE-D4 and MP2 calculations.

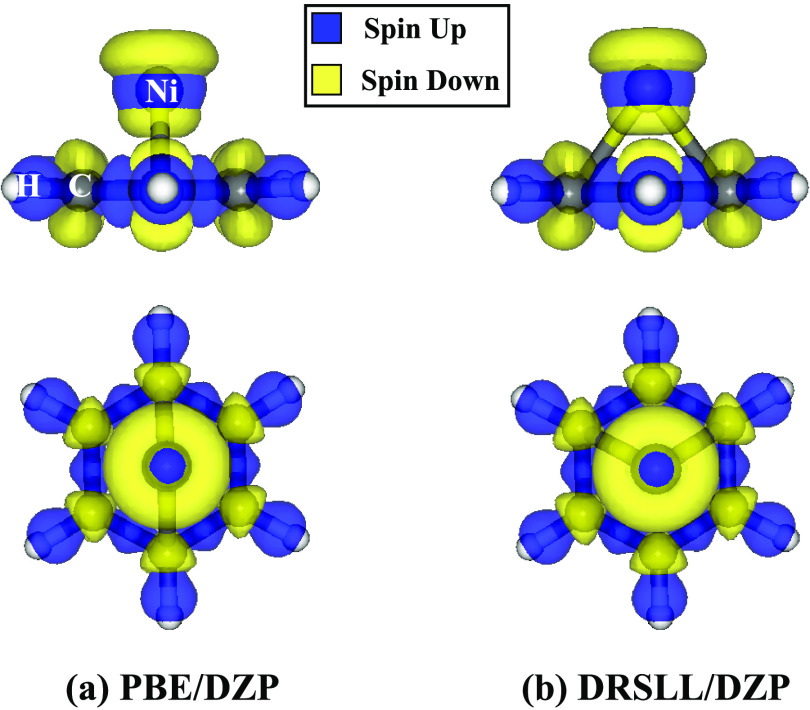
The binding energy trend is defined as the difference of the binding energy between Benz-Ni²⁺ and Benz-Fe²⁺; the results are reported in Table 4. The PBE-D4 estimate for the binding energy difference is in much better agreement with CCSD(T) than with other methods. MP2 overestimates the binding energy trend by about 0.29 eV. Furthermore, the deviation in the interaction energy between CCSD(T) and PBE-D4 is comparable to or better than that for the hybrid functionals. Hence, the use of hybrid functionals or large basis sets does not necessarily improve the quality of the trend. DRSLL, instead, underestimates the trend by 2.02 eV compared to CCSD(T). To understand the binding energy stabilization estimated using PBE and DRSLL, we computed the spin density isosurfaces for both complexes at PBE and DRSLL levels, shown in Figures 5, 6. A large population of spin-down localized on the transition metals and a small population in the carbon atoms confirm the donation of density from the p orbitals to d orbitals of the transition metal, whereas a large fraction of the spin-up population is localized in the region of C–C and C–H bonds. These effects explain the overstabilization of the binding energy compared to Post–Hartree–Fock methods. Furthermore, dispersion energy does not play an important role in spin localization and, therefore, the electronic structure. In fact, PBE and DRSLL show the same spin population, and, therefore, the spin density does not explain the trend divergence compared to the other methods. The next section will further focus on this topic.

Table 4. Binding Energy Trend (E_b^Ni2+ – E_b), Using Different Levels of Theory, of Benzene Coordinated with Fe²⁺ and Ni²⁺.

level of theory	EbNi2+ - Eb (eV)
B3LYP-D2/6-311++G(2d,2p)78	2.97
ωB97X-D/6-311++G(2d,2p)78	2.82
MP2/6-311++G(2d,2p)78	2.84
PBE-D4/CP-DZPa	2.39
DRSLL/CP-DZPa	0.51
CCSD(T)/6-311++G(2d,2p)78	2.53

^aThis work.

Figure 5.

Side view and top view of the spin density isosurface (isovalue 0.007 e/A³) of Benz-Fe²⁺ computed in quintet state at PBE/DZP and DRSLL/DZP levels. Spin population and atomic labels are reported.

Figure 6.

Side view and top view of the spin density isosurface (isovalue 0.005 e/A³) of Benz-Ni²⁺ computed in triplet state at PBE/DZP and DRSLL/DZP levels. Spin population and atomic labels are reported.

Dispersion Energy and the BSSE Effect

We studied the interaction of a small PAH, naphthalene, and a large one, benzocoronene, on three {010} forsterite surfaces. The three considered forsterite surfaces are optimized at the most stable spin configuration, singlet for the {010}-fo, quintet for Fe-{010}, and triplet for Ni-{010}. Figure 7 shows the calculated binding energies for benzocoronene and naphthalene using PBE-D4 and its predecessor PBE-D3(BJM)⁸¹ along with non-dispersion-corrected PBE. The latter allows us to understand how the dispersion correction affects these systems.

Figure 7.

Binding energies of benzocoronene and naphthalene chemisorbed on {010}-fo (singlet state), Fe (quintet state), and Ni-{010}-fo (triplet state) surfaces using different levels of theory (PBE-D4, PBE-D3(BJM), and PBE) with the CP-DZP basis set. The order of the labels corresponds to the order of the bars. Note: Numerical values are reported in the SI.

Figure 7 demonstrates that the trend and the absolute value of binding energies, using PBE-D4 and PBE-D3(BJM), are consistent with each other. However, the binding energies for naphthalene are higher than those for benzocoronene at the bare PBE level. This conflicts with the common assumption that larger molecules have a stronger interaction with the surface.⁸² Benzocoronene has eight aromatic rings and naphthalene has only two; the high electronic delocalization of the π-system of benzocoronene must contribute significantly to its adsorption to the surface through long-range interactions. However, PBE seems to poorly describe the long-range density transfer.^82,83 The difference in energy between PBE and PBE-D4/D3(BJM) is the dispersion energy, which we calculate to be large for these aromatic systems. Therefore, it is evident that noncovalent bonds play an important role in binding PAHs on the surface through van der Waals interactions between the π-system and the surface. Furthermore, including the van der Waals interaction results in a different trend in the binding energy as compared to the PBE-only calculations. Specifically, the energy trend calculated with DFT-D methods follows the order Fe > Ni > Mg. However, when DFT-D methods are not applied, the trend is Fe > Mg > Ni. Hence, it is important to use a method that can describe the dispersion interaction of PAHs on a surface well.

To test the performance of the LCAO method in comparison to the PW method, we have computed the dispersion-corrected binding energies of naphthalene on {010}-fo, Fe-{010}-fo, and Ni-{010}-fo using VASP,²⁷⁻³⁰ as shown in Table 5. The LCAO method underestimates the binding energy of naphthalene on {010}-fo by about 0.17 eV, which is consistent with previous theoretical investigations by Lee et al.⁸⁴ that estimate a difference of about 0.25 eV between the two methods. The authors stated that this energy difference cannot be removed easily even by increasing the orbital-confining cutoff radii of the basis set. Instead, there is good agreement between the LCAO and PW methods for the case of naphthalene on Fe-{010}-fo and Ni-{010}-fo by about 0.02–0.09 eV, where a strong bond formation occurs between the carbon atoms and the transition-metal one. The discrepancies between LCAO and PW might be attributed to the weak interaction between naphthalene and the pristine surface, which is partially overcorrected by the counterpoise energy, whereas these differences might not be important for small systems such as benzene, in which the dispersion energy is less important.

Table 5. Dispersion-Corrected Binding Energies (E_b), in eV, at Different Levels of Theory Using PW (See SI for Details) and LCAO Methods of Napthalene (Napht) on {010}-fo, Fe-{010}-fo, and Ni-{010}-fo.

	EbPBE-D4/PW	EbPBE-D4/CP-DZP
Napht ({010}-fo)	1.31	1.14
Napht (Fe-{010}-fo)	1.55	1.46
Napht (Ni-{010}-fo)	1.15	1.17

Therefore, we have also evaluated the binding energy trend using a vdW-inclusive density functional (DRSLL) taking into account the BSSE effect. The results are summarized in Figure 8. We conclude that DRSLL is not consistent with PBE-D4 in terms of absolute binding energy values since it shows a different energy trend: Ni > Fe > Mg. Finally, both PBE-D4 and DRSLL largely overestimate the binding energies, when they are not corrected for the BSSE, with respect to the counterpoise-corrected values.

Figure 8.

Binding energies of benzocoronene and naphthalene chemisorbed on {010}-fo (singlet), Fe (quintet), and Ni-{010}-fo (triplet) surfaces using PBE-D4 and DRSLL with the CP-DZP basis set and with the corresponding counterpoise-noncorrected values at the back. The order of the labels of the forsterite surfaces corresponds to the order of the bars. Note: Numerical values are reported in the SI.

Specifically, we analyzed the optimized geometries using both PBE and DRSLL functionals. Figure 9 shows the Mg, Ni, and Fe–C distances. We noticed that DRSLL tends to provide larger Ni–C and Fe–C distances by about 0.10 Å; in contrast, this effect is not so evident for the case of Mg–C bonds. This is in accordance with the studies carried out by Buimaga-Iarinca et al.⁴⁰ that confirm the presence of a BSSE effect in combination with an overestimation of the metal–C distances when vdW-DF functionals are employed to study aromatic molecules on a gold surface.

Figure 9.

Atomic labels and optimized structures of naphthalene and benzocoronene chemisorbed on Ni-{010}-fo (a) and (b) and Fe-{010}-fo (c) and (d). Table of carbon and metal distances (d_cc/mc) between the PAH and the surfaces using PBE and DRSLL. Note: As we are reporting only the geometric parameters and not the energy, we have not included the D3(BJM) and D4 correction (see the Theoretical Methods and Models section).

The spin density of PAHs on forsterite surfaces is reported in the SI and, as for the case of transition-metal complexes, it did not show any differences between DRSLL and PBE. DRSLL diverges from PBE-D4 since the dispersion energy is computed as the inclusive nonlocal dispersion energy (E_nld) at each SCF cycle, whereas PBE-D4 makes use of empirical formalism, the DFT-D4 method,⁵⁹ that has been computed a posteriori. Further differences between DRSLL and PBE-D4 are related to the exchange–correlation energy (E_xc) that, for the case of DRSLL,⁵⁶ is computed at the revPBE⁸⁵ level. We believe that the difference between DRSLL (E_xc^revPBE + E_nld) and PBE-D4 (E_xc + E_D4^PBE) is caused by the nonlocal dispersion energy and to justify this, we calculated the dispersion energy computed at the DRSLL level. We optimized the structures, for only the case in which the inversion trend is significant as for the case of benzocoronene, with revPBE estimating the nonlocal dispersion as the difference between the DRSLL and revPBE absolute energies as shown in Table 6. revPBE overcorrects the BSSE for the adsorption of benzocoronene on both transition-metal-doped surfaces, whereas revPBE and PBE functionals do not consistently use the counterpoise correction and exclude the dispersion energies. However, the revPBE counterpoise correction energy overcorrects about 1 eV more with respect to PBE, resulting in negative binding energies. In contrast, the dispersion energies (E_D4 and E_nld) for the adsorption on the Fe-doped surface computed at DFT-D4 and DRSLL levels are in good agreement, whereas this difference becomes larger for the case of the Ni-doped surface. This is consistent with the binding energy accuracy of benzene on transition-metal cation complexes at the DRSLL level, which shows a larger agreement with the other DFT methods for the adsorption on Fe²⁺ with respect to Ni²⁺ (Table 3). We also computed the counterpoise-corrected binding energy at the revPBE-D4 level that is consistent in the binding energy trend with PBE-D4. Therefore, the trend inversion among the functionals observed in Figure 8 can be attributed to the overestimation of nonlocal dispersion energy operated by DRSLL for the case of Ni-{010}-fo.

Table 6. Binding Energy (E_b) and Counterpoise-Corrected Binding Energy (E_CP-b) at Different Levels of Theories^a.

	EbPBE	EbrevPBE	ECP-bPBE	ECP-brevPBE	ECP-brevPBE-D4	ED4PBE	ED4revPBE	EnldDRSLL
Fe-{010}-fo:
Benzoco	4.23	3.20	0.42	–0.42	3.12	2.18	3.53	2.28
Ni-{010}-fo:
Benzoco	4.11	3.10	0.15	–0.48	3.08	2.22	3.56	3.23

^aD4 dispersion energy (E_D4) and nonlocal dispersion energy (E_nld) calculated as the difference between the binding energy computed at the DRSLL level and revPBE (E_nld^DRSLL = E_b – E_b^revPBE) for the benzocoronene (Benzoco) adsorbed on Fe and Ni-{010}-fo. The energies are reported in eV.

Conclusions

Understanding the organic inventory of regions of planet formation is key in astrophysics. The delivery of prebiotic organic species to Earth, and terrestrial planets in general, has direct links to the origin of life on Earth and elsewhere in the universe. Chemistry on mineral surfaces is thought to play an important role in astrochemistry both in molecular clouds and protoplanetary disks as also in planetesimals, the first steps in planet formation, but this chemistry is poorly understood. Quantum chemical methods can play an important role in identifying chemical routes and reaction products.^5,6,86,87 However, due to the large computational cost, little has been done to study the chemical and physical properties of PAHs on minerals.^53,54 In this work, we identified a DFT method that can accurately compute the binding energy of aromatic molecules on a mineral surface. The PBE-D4/DZP binding energies are accurate enough to be used in astronomical gas-grain models to predict the abundance of aromatic species in some regions of interstellar medium. We focused on the {010} forsterite surface as the most abundant and best-studied mineral surface composition of the rocky parts of our universe, such as submicron-sized silicate grains, and benzene as the smallest example of aromatic species. We conclude that to accurately describe the binding and, therefore, the adsorption energies, London dispersion forces have to be taken into account as currently available GGA functionals cannot accurately describe the electronic delocalization at long-range distances.

The interaction of aromatic molecules on a mineral surface in which transition metals are present requires an accurate description of localized electrons in the d and f orbitals along with an accurate description of the electronic delocalization at long-range distances. The BSSE-corrected PBE-D4/CP-DZP using local atomic orbitals describes the binding energy of benzene on {010}-fo with the same accuracy as that of plane wave methods. We found that a full optimization using a large basis set, e.g., TZP, is necessary to reduce the BSSE, whereas a TZP single-point calculation on the optimized geometry with DZP does not reduce the BSSE.

For the complexes of aromatic molecules interacting with transition-metal ions, DFT overbinds by about 1 eV with respect to CCSD(T). However, the binding energy difference between the Ni²⁺ and Fe²⁺ benzene complexes at the PBE-D4/CP-DZP level provides results in good agreement with the binding energy trend estimated by CCSD(T), while hybrid functionals overestimate this difference.

Finally, as a test case for PBE-D4, we studied the interaction of PAHs on three different {010} forsterite surfaces: pure Mg, single doped Fe, and Ni surfaces. We found that the interaction of PAHs with the surfaces is driven by important dispersion interactions and BSSE effects that need to be taken into account for a correct description of the aromatic systems on a mineral surface. We conclude that PBE-D4 is in good agreement with the predecessor PBE-D3(BJM). We also took into account London dispersion using DRSLL as the vdW-DF functional. DRSLL estimates slightly lower binding energies than PBE-D4 if transition metals are not present on the surface.

For the case of transition metals on forsterite surfaces, DRSLL does not provide consistent trend results with respect to PBE-D4. This is caused by the nonlocal dispersion energy computed on each SCF cycle. Moreover, DRSLL tends to overestimate the carbon–metal bond distance with respect to PBE.

This study provides a robust theoretical method to describe the interaction of aromatic molecules with forsterite mineral surfaces for astronomical and planetary science applications, applicable equally well to similar systems for material science applications. We showed that indeed, our proposed method, using PBE-D4/CP-DZP, is ideally suited to model the adsorption of aromatic molecules on a silicate mineral surface. This work will provide a solid springboard necessary for future experimental and computational studies and, in the follow-up work in preparation, we will apply our proposed method to the binding and molecular structure of a sample of PAHs on various forsterite surfaces.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.1c02326.

• Plane wave methods; mesh cutoff energy convergence test; table of binding energies of PAHs binding on {010} forsterite surfaces; spin density population; SIESTA keyword; and Cartesian coordinates of all studied systems (PDF)

The authors declare no competing financial interest.