A continuous flow cell culture system for precision cell stimulation and time-resolved profiling of cell secretion

Abstract

Cells exchange substances with their surroundings during metabolism, signaling, and other functions. These fluxes are dynamic, changing in response to external cues and internal programs. Static cultures are inadequate for measuring these dynamics because the environments of the cells change as substances accumulate or deplete from medium, unintentionally affecting cell behavior. Static cultures offer limited time resolution due to the impracticality of frequent or prolonged manual sampling, and cannot expose cells to smooth, transient changes in stimulus concentrations. In contrast, perfusion cultures constantly maintain cellular environments and continuously sample the effluent stream. Existing perfusion culture systems are either microfluidic, which are difficult to make and use, or macrofluidic devices built from custom parts that neglect solute dispersion. In this study, a multiplexed macrofluidic perfusion culture platform was developed to measure secretion and absorption rates of substances by cells in a temporally controlled environment. The modular platform handles up to 31 streams with automated fraction collection. This paper presents the assembly of this dynamic bioreactor from commercially available parts, and a method for quantitatively handling the effects of dispersion using residence time distributions. The system is then applied to monitor the secretion of a circadian clock gene-driven reporter from engineered cells.

Graphical Abstract

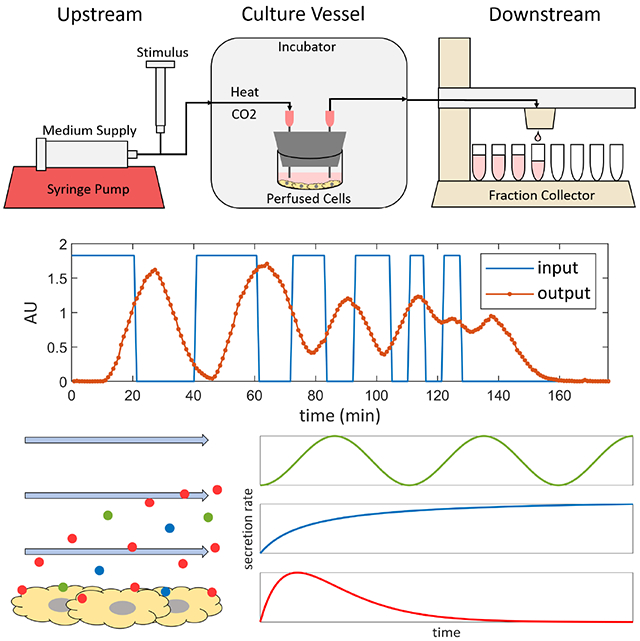
1. Introduction

The rates at which cells secrete and absorb substances to and from their environments are dynamic, changing with time. The absorptive and secreted fluxes are, respectively, inputs and outputs that govern cell metabolism and tissue growth, cell-to-cell signaling via soluble factors, and even genetically engineered constructs that reflect intracellular processes. Despite the importance of this class of phenomena, commonly used static cell culture methods are inadequate to study them. Static cultures do not allow for fine-tuned dynamic inputs; researchers must manually add and remove stimulus-containing medium to and from cultures and can only subject cells to step changes in solute concentrations. Manual medium changes expose cells to unintended step changes in medium components and accumulated secreted factors. Furthermore, medium changes and manual sampling can disturb cells with temperature and pH changes, and uncontrolled shear stresses from handling, all of which can affect cell behavior. In between medium changes, the composition of the culture medium varies with time as secreted substances accumulate and absorbed substances are depleted, and these uncontrolled changes can have unintended effects on cell behavior. Finally, it is difficult to obtain high-resolution time series of solute concentrations due to the requirement of frequent manual sampling, and it is impractical for researchers to take timepoints overnight.

A perfusion cell culture system with continuous measurements can address these issues and enable new insight into cell function. Fluidic systems can continuously replenish medium and keep cells exposed to a constant environment, while avoiding the unintended disturbances to cells caused by manual medium changes. Concentrations of stimuli can be modulated at the inlets to perfusion culture vessels to precisely control the transient concentration profile that cells are exposed to over time. Cells secrete substances into the flow, which can be collected and monitored continuously and automatically, giving a high-resolution measurement of concentrations over time without impractical manual efforts. Microfluidic systems can meet these criteria [1–5] but introduce additional problems. Labs require specialized, expensive equipment to design and fabricate microfluidic devices, and personnel must be trained to gain the expertise required to use them. In addition, cells must be seeded using special techniques, air bubbles can enter these systems and water can permeate out, and samples collected from effluent streams of microfluidic devices are on microliter scales and require specialized microanalytical methods to analyze [6]. Microfluidic devices may also not be suitable for perfusion cultures of large tissue slices or constructs. Alternatively, macrofluidic devices may be used, but previously published macrofluidic perfusion culture systems also have shortcomings. Existing devices may be constructed from custom, in-house parts that are difficult for other labs to reproduce [7, 8], may require multiple pumps or fraction collectors [9], and fail to account for the effects of solute dispersion on measured solute signals [7–10].

This paper presents a modular, macrofluidic perfusion bioreactor inspired by the design of Yamagishi et. al [8], and a method for quantitatively handling the effects of solute dispersion on measured signals, and improves upon the design of Yamagishi in the following ways: The system presented in this paper is capable of collecting samples from multiple independently perfused cell cultures in parallel for the measurement of secretion and absorption rates of arbitrary solutes and controlling dynamic cellular environments. This system preserves the ease and familiarity of static culture methods while providing the benefits of perfusion culture. This dynamic bioreactor can be constructed entirely from low-cost commercial parts, and improved further with a simple custom modification laser-cut from a single sheet of acrylic. This paper presents the dynamic bioreactor system setup and a method for characterizing and mitigating effects of solute dispersion in the flow using residence time distribution (RTD) analysis, and demonstrates the system applied to monitor the secretion of a circadian clock gene-controlled luciferase reporter from transduced U2-OS cells.

2. Results

2.1. Modular design and prototype of a dynamic bioreactor system

This dynamic bioreactor system consists of three sections: an upstream, culture vessel, and downstream sections (Figure 1 A–B). The upstream section used here supplies medium from a syringe pump at a constant rate to culture vessels through silicone tubing. Valves can be included in each stream to allow for multiple medium sources from different pumps to supply the same culture vessel. A medium source can contain a chemical stimulus, and by switching a valve, an experimenter can expose cells to the stimulus for desired periods of time. Alternatively, bursts chemical stimuli can be injected by needle directly into upstream flows through the tubing. Once the upstream tubing is fed through a port into an incubator, enough tubing length must be inside the incubator upstream of any culture vessels to allow heat and CO₂ to diffuse through the silicone walls of the tubing into the medium stream to bring the stream to the appropriate temperature and pH before it enters the culture vessels. It was found that 0.5 m of tubing inside an incubator is sufficient to allow medium at a flow rate of 1 ml/hour to reach 37 °C before entering the culture vessel (Appendix Figure A.1).

Figure 1. A dynamic bioreactor system.

A schematic overview of the system (A) shows its three major sections: an upstream section consisting of medium supplied from a syringe pump with a constant flow rate and a port for the input of a stimulus, and silicone tubing that is long enough to allow the medium stream to reach the necessary temperature and CO₂ concentration inside an incubator before entering a culture vessel; a perfused culture vessel, in this case a plugged well; and a downstream section of tubing that leaves the incubator and leads to a fraction collector, which distributes the effluent stream into a series of collection tubes over time. (B) A photo of the real system without an incubator. In addition to a single plugged well, two simple culture vessels that can be used include a hollow fiber bioreactor (C), or two plugged wells in series that act as a one-way co-culture (D). More complex setups can also be perfused, such as a circulating loop between a bioreactor and a medium reservoir, with and inlet for fresh medium and outlet for continuous sample collection (E), which can reproduce the dynamics of a compartmental pharmacokinetic model.

Culture vessels can have any number of designs. In this paper, a 12-well plate plugged with a silicone stopper with two needles traversing the stopper to serve as inlet and outlet ports for medium flow is used (Figure 1 B). This plugged well plate design allows for cell cultures to initially be prepared in the well plate using standard static culture methods, and then be incorporated easily into a perfusion system without disturbing the cells simply by plugging the well. Multiple wells of the same plate can be plugged and perfused in parallel. The well has enough space to accommodate large 3-D tissue constructs or tissue slices, and the height of the medium can be adjusted simply by adjusting the height of the outflow needle. In addition to accommodating adherent cells, suspension cells can be perfused in well plates at slow flow rates if the outlet needle is raised high enough to prevent cells from flowing out. Furthermore, well plates can be placed on plate rockers to keep culture medium throughout its volume well-mixed, exposing all the cells to equivalent environmental conditions. Another simple culture vessel is a hollow fiber bioreactor (Figure 1 C), in which medium flows through the reactor in permeable hollow fibers that allow for exchange of medium components between the medium stream and the cells seeded in one of the compartments. Simple culture vessels can be used in combinations, such as two plugged wells in series to create a dynamic, one-way perfusion co-culture (Figure 1 D). Finally, more complex systems can take the position of the culture vessel such as a circulating loop between a bioreactor and a medium reservoir, with an inlet for fresh medium and outlet for continuous sample collection, that can reproduce the solute concentration dynamics of compartmental pharmacokinetic models (Figure 1 E) [11].

The downstream section used in this paper consists of tubing leading out from culture vessels to a fraction collector outside the incubator (Figure 1 A–B). Without a custom modification, each fraction collector can receive one culture vessel effluent stream and distribute it over time along a series collection tubes. The fraction collector can collect fractions into a variety of pre-programmed collection containers, including commercially available test tube racks and well plates. The fraction collector settings can be programmed to fill each fraction for a desired length of time, fraction volume, or number of drops.

2.2. Multi-stream customization using laser-cut parts

Simple parts were designed and fabricated that can be easily attached to a fraction collector dispensing head to allow the fraction collector to collect samples from multiple streams simultaneously, instead of just one (Figure 2). These multi-head dispensers can be laser-cut from single sheets of acrylic and attached to fraction collector dispensing heads using their existing set of screws. 200 μl pipette tips fit snugly into rows of holes in the multi-head dispensers, and the ends of culture vessel effluent tubing can be pushed into the wide ends of the pipette tips and held in place by friction (Figure 2 C). The fraction collector can then be programmed as if it were collecting from a single stream, and the additional effluent streams are dispensed through the pipette tips into parallel rows of a collection container. One multi-head dispenser was designed that can collect fractions from up to 31 simultaneous effluent streams into a set of 96-well plates (Figure 2 A), and another was designed that can collect from up to 11 effluent streams into F1 tube racks (Figure 2 B–C). The latter design was tested, and it was found that it can consistently dispense equal volume fractions for six simultaneous streams (Figure 2 D). These multi-head dispenser modifications greatly increase the throughput of a single fraction collector at almost no cost, improving experimental rigor by allowing multiple replicates of experimental and control cultures to be perfused simultaneously.

Figure 2. Custom modifications increase the throughput of fraction collectors.

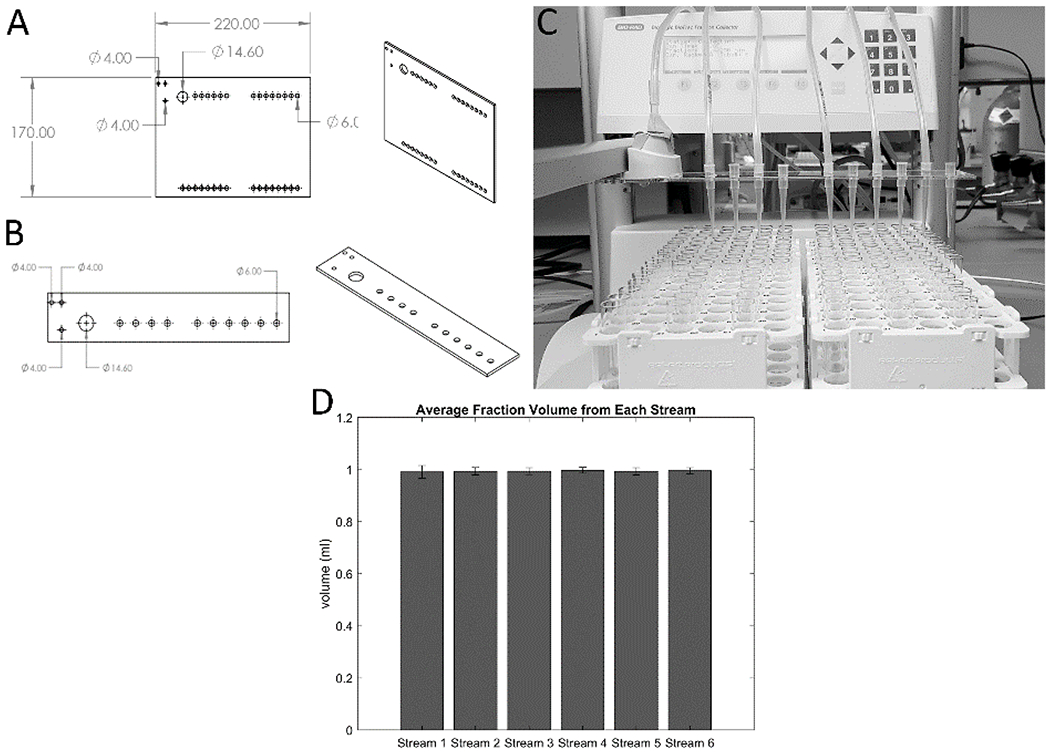
Two laser-cut, easy-to-integrate fraction collector modifications were designed to allow each fraction collector to collect from multiple effluent streams simultaneously. 2-D and 3-D schematics of multi-head dispensing modifications for collecting into 96-well plates (A) and into F1 tube racks (B) are shown with relevant dimensions. Either modification can be attached to a fraction collector by removing three screws holding the fraction collector dispensing head to the moving arm, and re-attaching the head by replacing the screws through the three 4.00 mm diameter holes in the upper-left area of the laser-cut parts, attaching the part to the dispensing head (C). These modifications have a 14.60 mm diameter hole that opens beneath the original dispensing head so it may continue to be used. The remaining 6.00 mm diameter holes hold 200 pL pipette tips which act as additional dispensing heads by receiving downstream tubing from culture vessels and directing their effluent streams into parallel rows of collection wells or tubes. (D) Fractions were collected from the six streams shown in (C) at a rate of 1 fraction/hour and a flow rate of 1 ml/hour for 20 hours. The volumes collected in the 20 fractions for each stream were averaged and graphed with their standard deviations. The data confirm that there was no difference in the fractions collected from each of the 6 streams.

2.3. Solute dispersion smears signals predictably according to convolution with residence time distributions

Concentration profiles of solutes along flow axes, such as input signals generated by researchers or secretion signals from cells, become “smeared” as they move through flow systems due to dispersion in the flow (Figure 3). This is an unavoidable phenomenon resulting from a combination fluid velocity gradients and diffusion that occur in fluid flows [12]. As a consequence, any solute signal at the entrance to a flow system will be distorted by the time it exits the flow system, and thus the solute concentration profiles collected in effluent fractions will be smeared representations of the original input signal. To study this effect, a flow system was set up consisting of 1 m of tubing leading to a fraction collector. At the system inlet, a valve was used to manually switch the flow source between pure water and water with a tracer, both at 10 ml/hour, to create an input signal consisting of a series of step changes in tracer concentration. Fractions were collected and the tracer concentrations in the fractions were measured to produce the smeared output signal (Figure 3 A).

Figure 3. Signals passing through a flow system are smeared by dispersion according to the residence time distribution of the system.

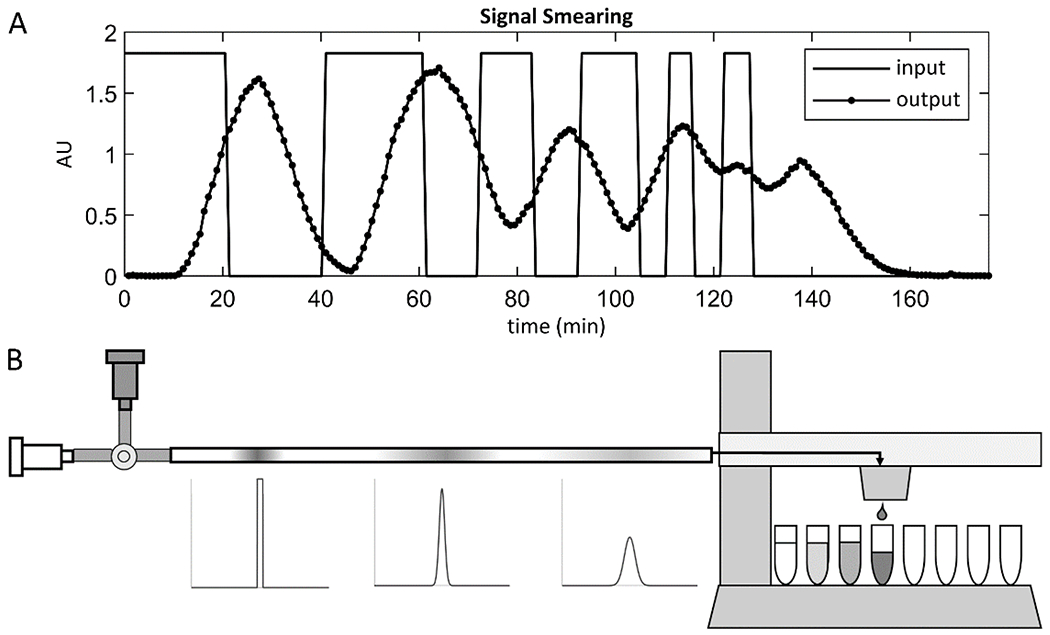
A concentration vs. time signal at the inlet of a flow system, such as a signal generated by dynamic cell secretion or manual input of solute pulses, becomes “smeared” due to dispersion as it passes through the flow system. This is demonstrated in the graph (A), where the rectangular concentration vs. time signal generated at the inlet of a 1 m length of tubing by switching the flow source between pure water and tracer is smeared by the time it is measured at the outlet. The shape and extent of smearing are determined by the residence time distribution (RTD) of the flow system, which can be measured using the method shown in the schematic (B). A valve at the system inlet is switched to allow a brief pulse of tracer solution to flow into the system, approximating an infinitesimal impulse. The valve is then switched back to pure water, and as the tracer pulse flows through the system, it spreads and takes the shape of the RTD of the system. Fractions are collected until all the tracer has exited the system, and the concentration vs. time signal is measured to reveal the RTD.

The shape and intensity of signal smearing can be quantified by the residence time distribution (RTD) of the given flow system [12]. An RTD is the impulse response of a flow system, and is measured by injecting an impulse of a tracer into the system to approximate a Dirac delta function, and measuring the concentration of the tracer at the outlet of the flow system over time (Figure 3B) [12]. The resulting normalized tracer concentration vs. time curve is a measurement of the distribution of residence times of all the tracer molecules that entered the flow system simultaneously, and it captures all diffusion and dispersion effects in the flow system [12]. Knowledge of the RTD of the given flow system can inform how input signals should be shaped upstream of culture vessels to expose cells to the desired transient solute concentrations, and can allow for partial or complete undoing of the effects of smearing on signals, using methods of signal convolution and deconvolution (Figure 5).

Figure 5. Application of residence time distributions for signal processing.

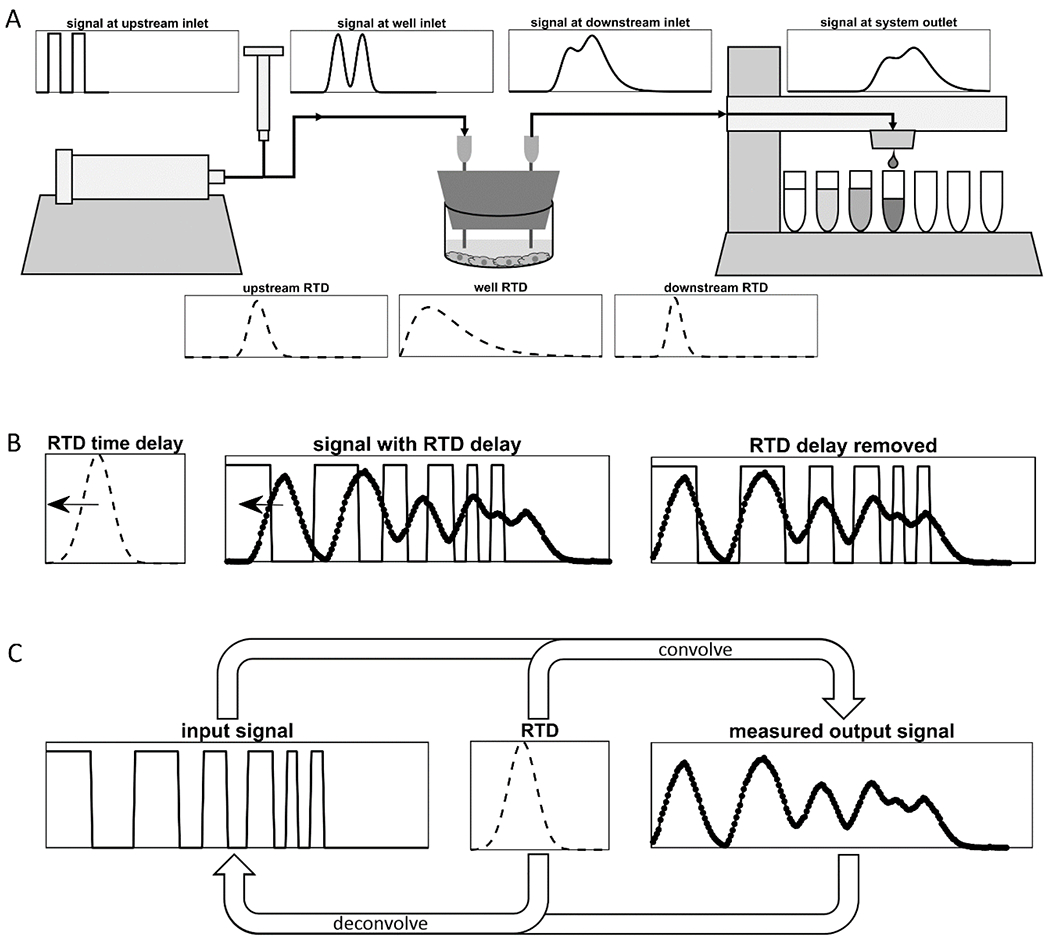
(A) Smearing of an arbitrary input signal in a given flow system can be predicted by convolving the input signal with the residence time distribution (RTD) of the flow system. If the RTDs of multiple flow units in series are known, then the shape of the signal can be predicted at the outlet of each unit by convolving the signal at the outlet of the previous unit with the RTD of the unit. (B) If the RTD of a flow system is approximately symmetrical, then the time of the peak of the RTD curve can be defined as the time delay. A measured output signal can be shifted backwards in time by the time delay to align its peaks with those of the input signal, as is shown here with the experimental data from Figure 3. (C) Signal deconvolution is the natural method to use to remove the smearing effects of the RTD from an output signal to recover its corresponding input signal. However, numerical deconvolution methods are highly sensitive to noise and imperfections in RTD measurements, and thus deconvolution is not always feasible.

The RTDs of modular units commonly used in dynamic bioreactor experiments were measured at flow rates of 1 ml/hour and 10 ml/hour, using 10 minute dye pulses and 1 minute dye pulses, respectively (Figure 4). If the RTDs of all the units of a flow system are known, then the RTD of the overall flow system of units in series can be calculated as the convolution of the RTDs of its components [13]. The RTD of a given flow system varies with any factor that affects fluid velocity profiles and the diffusion coefficient of the solute of interest within the system [12]. It was found that fluid temperature and solute diffusion coefficient had little effect on the RTDs of commonly used flow system units within the ranges used in cell culture applications (Appendix Figure A.2), but unit geometry and volumetric flow rate had large effects. Therefore, the RTDs of a range of relevant flow system geometries and flow rates were measured (Figure 4).

Figure 4. Residence time distributions of tracers in different components of integrated flow system.

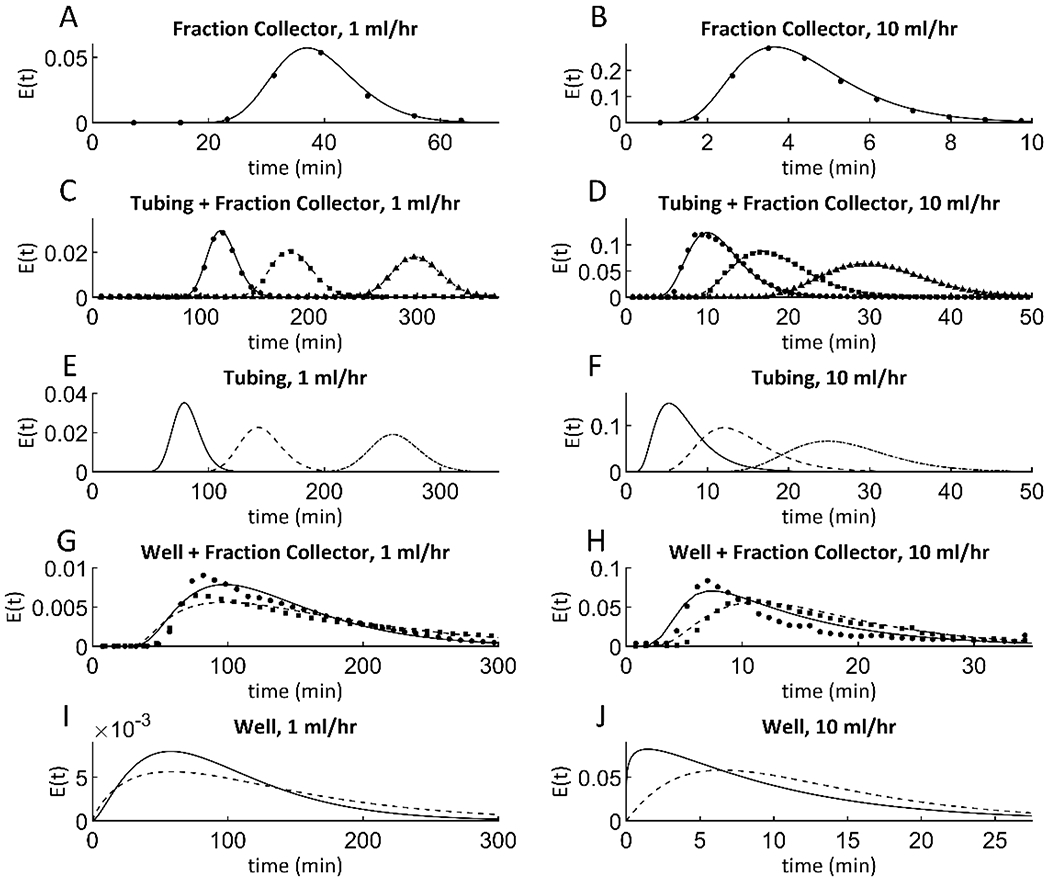
The residence time distributions (RTDs) of several basic flow system units were measured at relevant flow rates of 1 and 10 ml/hour, and models were fit to the data. (A) and (B) show RTD data of a fraction collector (circles), along with fit axial dispersion models (solid line). (C) and (D) show RTD data for tubing connected to a fraction collector. Tubing lengths used were 0.5 m, 1 m, and 2 m, which are represented by measured data (circles, squares, and triangles, respectively), and their corresponding fit axial dispersion models (solid, dashed, and dot-dashed lines, respectively). (E) and (F) show fit axial dispersion models for tubing of length 0.5 m, 1 m, and 2 m (solid, dashed, and dot-dashed lines, respectively). RTDs of plugged wells with fraction collectors attached do not fit simple models. However, the RTDs of wells alone were fit loosely to n-CSTR models, so for each well condition, an n-CSTR model was found that, when convolved with the fraction collector model of the same flow rate, best fit the data of the well with a fraction collector attached. (G) and (H) show data for wells attached to fraction collectors for both static wells and wells on a plate rocker (circles and squares, respectively), along with their fit models (solid and dashed lines, respectively). (I) and (J) show fit n-CSTR models for static and rocked wells (solid and dashed lines, respectively).

Fitting mathematical models to RTDs is useful. Demonstrating that a particular theoretical model fits the RTD data of a system well gives physical insight into the nature of the fluid flow in that system, and can yield useful system parameters such as the contact time (τ) and the Péclet number (Pe). Understanding these physical models and their defining parameters can aid in designing new flow systems by allowing researchers to predict their RTDs. Performing convolution and deconvolution operations at desired resolutions may require interpolation of RTD data, but if a good RTD model is available, it is easier and more accurate to query the model for points instead. Finally, there are cases in which it may not be possible to measure the RTD of a particular flow system unit in isolation, and so the RTD of the unit must be inferred and represented by a theoretical model.

RTDs of systems composed of cylindrical tubes are well approximated by an axial dispersion model [12] (Equation 1). The value of the RTD at time t, denoted E(t), is dependent upon two parameters, Pe and τ, which are found by fitting Equation 1 to RTD measurements using nonlinear regression.

$$E\left(t\right)=\left(\frac{1}{\tau }\right){\left(\frac{Pe\tau }{4\pi t}\right)}^{\frac{1}{2}}\exp \left(-\frac{{\left(1-\frac{t}{\tau }\right)}^{2}Pe\tau }{4t}\right)$$ (1)

The RTDs of system components were then evaluated. Fraction collectors themselves have RTDs, which were measured using tracer studies and fit by Equation 1 (Figure 4 A–B). The RTDs for the tubing + fraction collector systems exposed to tracer studies were fit by axial dispersion models (Figure 4 C–D) and represent the convolution of the RTD of the tubing with the RTD of the fraction collector. Nonlinear regression was used to find parameters for an axial dispersion model that could predict the RTD data for the tubing + fraction collector (Figure 4 E–F). All fit Pe and τ values are listed in Appendix Table A.1.

The cell culture vessel was also assessed in terms of impact on RTD by modeling a simple well plate as a continuous stirred tank reactor (CSTR). CSTRs and similar, non-ideal reactors are well approximated by the n-CSTR model [14] (Equation 2). It was assumed that well plate culture vessels may behave similarly to stirred tank reactors with large amounts of bypass due to lack of mixing, and so their RTDs may be fit by the n-CSTR model. In the n-CSTR model, E(t) is dependent upon two system parameters: n and τ, where n is any real number greater than zero, and τ is the contact time. In this model, n represents the amount of backmixing or bypass in the reactor. When n = 1 it indicates that the reactor is perfectly mixed and behaves like an ideal CSTR. When n > 1, the reactor behaves like n CSTRs in series, similar to the tanks-in-series model [12], extended to non-integer numbers of tanks. When n < 1, the reactor exhibits bypass and is less well-mixed than a CSTR due to fluid exiting before it is properly mixed. The Bodenstein number (Bo) is related to the parameter n by Equation 3, and can be used interchangeably with Pe in this context [14].

$$E\left(t\right)=\frac{t^{n-1}}{\Gamma \left(n\right)}{\left(\frac{n}{\tau }\right)}^n\exp \left(-\frac{tn}{\tau }\right)$$ (2)

$$n=\frac{Bo}{2}+1$$ (3)

Having a culture vessel that behaves like a CSTR (has an n = 1) comes with two advantages. First, being well-mixed ensures that all cells in the vessel experience the same environment at every point in time, as opposed to in an un-mixed culture vessel where poor mixing and non-uniform flow could lead to cells in different locations experiencing different environments [12]. Similarly, mixing eliminates effects that the spatial distribution of the cells may have on secreted signals [12]. If two cells in different parts of a culture vessel secrete the same type of molecule simultaneously, those two molecules will exit the culture vessel at different times because they will follow different streamlines to the exit, which affects the shape of the overall secretion dynamic signal. If the culture vessel is well-mixed, then the effects of spatial distribution of cells is eliminated. Furthermore, in a perfectly mixed well, any molecule that cells secrete into the flow can be treated as if it had entered the vessel from the culture medium inlet, and thus the RTD of the vessel can be included in the deconvolution calculation of the final measured secretion signal to give a more clear picture of the original secretion signal. For these reasons, the RTDs of plugged 12-well plates were measured both sitting still and on a plate rocker for increased mixing.

As with tubing, the RTDs of wells themselves cannot be measured directly, and so n-CSTR models for wells must be found that, when convolved with known fraction collector RTDs for the same flow rate, fit RTD data for the well + fraction collector (Figure 4 I–J). While tubing + fraction collector systems can be fit with an axial dispersion model directly, well + fraction collector systems do not fit a simple function, and so measured RTD data points of these systems are overlaid with functions resulting from numerical convolution of n-CSTR models with known RTDs of fraction collectors (Figure 4 G–H). All fit n and τ values are listed in Appendix Table A.1.

Once a flow system RTD is known, it has several uses. Note that for each of the following methods, measured RTD data itself should be used in numerical calculations, and fit models should only be used if the RTD cannot be measured or if the measurement is too noisy and the model is a very accurate fit. The RTDs of any individual flow systems connected in series can be convolved together to compute the RTD of the overall system [13]. In a similar manner, the smearing of any arbitrary input signal can be predicted by convolving the signal with the flow system RTD (Figure 5 A). Thus, for any signal generated upstream of a culture vessel, the signal that the cells in the culture vessel will experience as a result can be predicted. There are also several approaches to undoing effects of smearing on the measured secretion signals generated by cells. As a simple, first-order approximation, the RTD can be assumed to be merely a time delay, which can be subtracted from the time values of the measured signal to recover the original locations of peaks and troughs (Figure 5 B). If a flow system RTD downstream of a culture vessel has a symmetrical shape, the time coordinate of the RTD peak can be considered to be the time delay, which is the amount of time it takes a peak in solute secretion from cells to be seen in collected fractions. By subtracting the time delay from time values of data points in measured secretion signals, the times at which the secretion of solute by the cells peaked and troughed can be recovered. The natural, more powerful technique for undoing smearing is called signal deconvolution which can undo both time delays and the signal smearing (Figure 5 C). Deconvolution is the inverse of signal convolution and it removes the effects of RTDs on measured signals to recover the original signals [13]. However, in practice deconvolution requires signal smoothing and is highly sensitive to noise and inaccuracies in measured secretion signals and RTDs, and thus is not always feasible [13].

2.4. Precision measurements of circadian oscillations of a secreted reporter from virally transduced U2-OS cells

In this study, circadian clock gene-driven secretion rates of luciferase from transduced U2-OS cells were measured (Figure 6). In studies of cellular circadian rhythms, it is common to engineer cells to secrete reporter proteins, the expression of which are driven by circadian clock gene promoters [7–9, 15–17]. We have made a synthetic circadian promoter called Circa2 that contains abbreviated portions of the Per1 promoter which was used in this study [15]. Gaussia princeps luciferase (GLUC) was used as the secreted reporter, the concentration of which is measured by measuring its bioluminescence after addition of its substrate, coelenterazine. U-2 OS osteosarcoma cells were plated into four wells of a 12-well plate and transduced by lentiviral vectors containing either GLUC driven by the Circa2 promoter (Circa2-GLUC), or GLUC driven by a constitutively active promoter EF1α (EF1α-GLUC). After 1 week, the cells were synchronized with dexamethasone for 30 minutes, then the wells were immediately plugged with silicone stoppers with inlet and outlet needles and perfused with medium at 0.5 ml/hour. The effluent streams of the wells were collected by the modified fraction collector, collecting 1 fraction/hour. Batches of fractions were frozen every 24 hours, and after 74 hours, flow was stopped and the luciferase in every other thawed fraction was measured. For each curve, each point is presented as its fold difference over the average luminosity of that curve, with the time delay of the downstream RTD subtracted from the time values of the curve. The measurements reveal that the system is able to capture both the constant expression of EF1α-GLUC and the circadian expression of Circa2-GLUC in the biological replicates (Figure 6).

Figure 6. Precision measurements of circadian oscillations of a secreted reporter from transfected U2-OS cells.

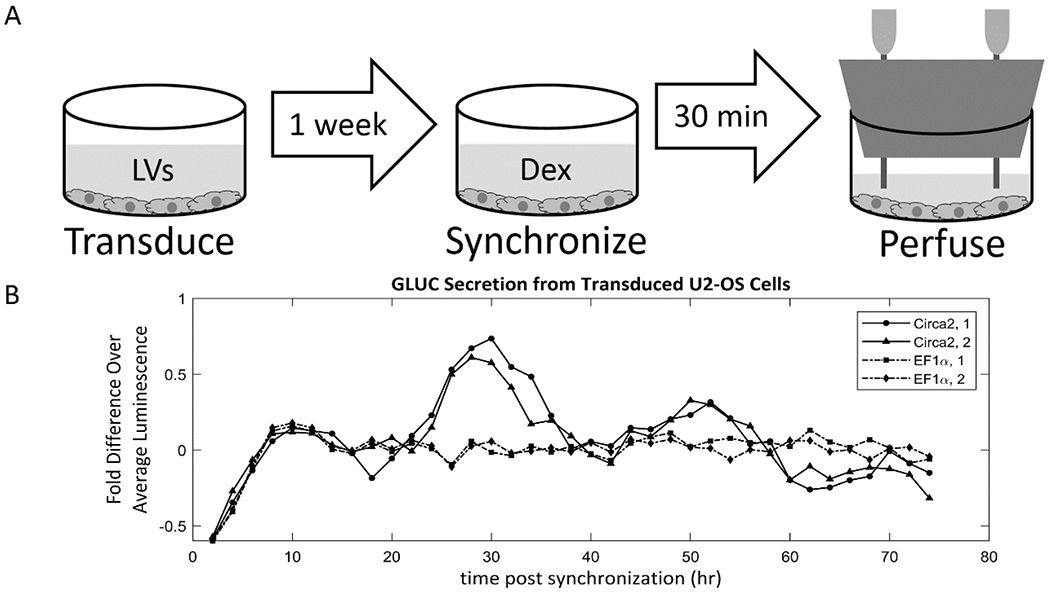
(A) U2-OS cells were seeded into a 12-well plate and transduced by lentiviral vectors containing Gaussia princeps luciferase (GLUC) driven by either a synthetic circadian promoter (Circa2) or a constitutively expressed promoter (EF1α). After 1 week, the circadian clocks of the cells were synchronized with dexamethasone for 30 minutes, after which the wells were perfused at 0.5 ml/hour for 74 hours while effluent fractions were collected at 1 fraction/hour. (B) The dynamic bioreactor platform was able to capture both the constant expression rate of EF1α-GLUC and the circadian expression rate of Circa2-GLUC.

3. Discussion

In this paper, a design of a simple, low-cost dynamic bioreactor for transient cell stimulation and monitoring of secretion and absorption rates with the use of a fraction collector was demonstrated. It was shown that a 12-well plate can be easily converted into a perfusion culture vessel and that this and other culture vessel modules can be used to accommodate a multitude of culture conditions in the system. A method to measure RTDs of bioreactor units was developed, and the RTDs of several relevant bioreactor units were measured. Furthermore, the uses of RTDs to inform culture vessel design, and to predict and potentially undo the effects of dispersion and diffusion on the smearing of solute signals using convolution and deconvolution were discussed. Finally, the bioreactor was used to measure circadian oscillations in the secretion rate of a reporter from transduced U2-OS cells.

The present study and the platform itself have several limitations. Depending on its operation, the system can consume large volumes of culture medium, increasing the costs of experiments. For the cell culture experiments in this paper, a flow rate of 0.5 ml/hour was chosen arbitrarily; however, the flow rate of each experiment can be optimized to minimize the volume of medium needed while ensuring that the culture vessel is replenished at an adequate rate and the RTD smearing effect does not become too large. Thinner tubing and smaller culture vessels, such as plugged 48-well plates, can reduce the system volume while maintaining ease of use. It is possible for solutes to adsorb and desorb to and from the walls of tubing and culture vessels which can remove the solutes from flow and affect signals. Prior to performing experiments, the adsorption capacity of flow systems should be measured by flowing samples of medium containing the solute of interest through the systems and measuring the changes in concentration of the solute.

The problem of signal smearing can in some cases result in the loss of signal features altogether. High-frequency components of signals, i.e. the signal features that change rapidly relative to the width of an RTD that smears it, such as a pair of spikes, can become smeared together before they are measured to the point that they cannot be recovered by deconvolution. However, cell secretion dynamics typically take place on timescales slow enough with low frequency components to not be affected in this way, and if signals with faster features need to be measured, flow system RTD widths can be reduced by changing flow rates and tubing lengths. The n-CSTR model does not closely fit well + fraction collector RTD data. However, the n-CSTR model was somewhat close, and was chosen due the simplicity and physical interpretability of its two parameters. In particular, the parameter n, which serves as a measure of mixing within wells, can indicate when the system behaves like a well-mixed tank. If necessary, more complex models can be fit to RTD data, but for most signal processing purposes, RTD data itself should be used for calculations when possible. It was expected that rocked wells with a flow rate of 1 ml/hour would have the most CSTR-like behavior of all the conditions because each particle that enters these vessel has a long residence time, allowing it to be exposed to mixing effects of the plate rocker for a long time. Furthermore, RTD data for the rocked well + fraction collector at 1 ml/hour perfectly fits an exponential decay function following its initial peak, which indicates CSTR behavior. Surprisingly, however, when n-CSTR models were found that, when convolved with the fraction collector axial dispersion models, fit the well + fraction collector data, the static well at 10 ml/hour condition was reported to have the most CSTR-like behavior with the n closest to 1, which was the opposite of expected. This calls into question the validity of the parameter n as an indicator of the mixing in these culture vessels, or the validity of the model fitting approach. RTD measurements for some culture vessels, like the hollow fiber bioreactors, are more difficult to measure because some tracers adsorb to the hollow fibers and some of the particles that enter the system do not exit, leading to inaccurate measurements. To overcome this, alternative tracers that do not adsorb to these surfaces must be identified. Ideally, the tracer should be the solute of interest itself, although these are not always easy or inexpensive to measure.

The in vitro experiment demonstrates that cells can survive in the bioreactor for over 3 days and that the system can clearly resolve differences between constant gene expression and circadian-oscillating gene expression. While numerical signal deconvolution was not performed on the measured signals, the low-pass filtering effects of the RTD would have had little smearing effect on the low-frequency circadian signal, so shifting the measured signal by the delay time was sufficient to recover an accurate signal. Interestingly, after analyzing the signals using BioDare2 circadian analysis software, Circa2, 1 was found to have a period of 21.48 hours, while Circa2, 2 had a period of 23.09 hr. However, after smoothing the signals with a three-point moving mean, the periods were 21.64 hours for Circa2, 1, and 21.70 hours for Circa2, 2. The cause of this <24 hours period could be due to unique genetic features of the cell line used, and this requires further investigation. Also notable is the initial rise in all signals up to a peak around hour 10, which is likely due to signal smearing. When perfusion begins, the downstream tubing is full of fresh medium, and plugging the culture vessel in-line is similar to a step-change signal in GLUC concentration at the inlet to the downstream tubing. When a step-change is convolved with the downstream tubing RTD of this system, the signal at the downstream tubing outlet takes about 6.67 hours to reach 99% of the signal at the inlet. The remaining 3.33 hours can be accounted for by movement of GLUC originating from different points within the culture vessel, which cannot be captured by the RTD. The fact that the signal peaks at hour 10 and then decreases slightly is likely due to an initially high GLUC concentration in the culture vessel due to accumulation of GLUC during the time between the medium change after the dexamethasone shock and the start of the perfusion.

Further improvements can be made to this dynamic bioreactor system. The upstream section can be improved by automating the modulation of the flow rate and solute concentrations at the inlet to generate pre-programmed signal waveforms, possibly in a similar manner to previous attempts with microfluidic devices [16], to further improve user-friendliness. New cell culture vessels can be designed to culture cells and tissues in different environments with different substrates, modulate their interactions with the flow, and to create more complex dynamics with interacting compartments. In particular, plugged 48-well plates can be used, which operate in the same manner as the plugged 12-well plates but have smaller volumes and less surface area, requiring a lower volume of culture medium and reducing the effects of the spatial distribution of cells throughout the well. Downstream of culture vessels, in-line sensing capabilities can be included. Emerging chemometric approach used as process analytical technologies in bioprocess engineering, such as in-line IR and Raman spectroscopy, are solid-state devices that could provide nearly continuous measurements of the effluent stream compositions in the form of spectra that can be coupled with machine learning methods to reveal dynamics of individual components [17].

Future applications of this dynamic bioreactor platform are broad. It will be useful for advancing research in circadian rhythms of peripheral clocks, especially for studying dynamics of perturbations to clocks, secretion and absorption activity dependent on clock state, and coupling of clocks between cell types controlled by secreted signals. Existing methods in which luciferase-secreting cells are cultured in photomultiplier tubes in medium that contains luciferase substrate provide near-instantaneous, high-resolution measurements of circadian gene expression [18]. However, studies using these methods are restricted to undisturbed static cultures and they require the purchase of photomultiplier tube devices. Under these experimental conditions, the culture medium cannot be changed because doing so causes the circadian clocks to reset [19–22], and so culture medium components can accumulate or deplete, and these uncontrolled changes can affect cell behavior. Furthermore, because culture medium cannot be changed, cells cannot be cultured long-term. It is also difficult to input any dynamic signals to cells to intentionally perturb or reset their clocks without manually replacing medium and potentially disturbing cells in unintended ways, and it is difficult to collect samples to measure secretion and absorption dynamics of substances other than the reporter molecules that depend on the clock dynamics. The dynamic bioreactor in this paper overcomes all of these issues. Beyond circadian rhythms, this dynamic bioreactor can be used to measure cytokine secretion dynamics in response to timed stimuli, and enables multi-compartment interactions for cell-to-cell cytokine and endocrine signaling. The device will enable the characterization of the secretion rates of larger particles like secreted exosomes [23, 24] or mitochondria [25], or viral vectors or biologics secreted by cells engineered for biomanufacturing [26]. This bioreactor can measure cellular metabolic rates in response to different stimuli, dynamically modulate nutrient availability to cells. The system can even be used as a diagnostic device, culturing patient samples and monitoring their dynamics to screen for disorders or characterize patients for personalized medicine. This platform can be adopted by researchers and adapted to their needs as a simple and affordable means to study secretion and absorption dynamics in a wide variety of contexts.

4. Materials and Methods

4.1. Multi-head dispenser design and fabrication

Each multi-head dispenser was composed of a 1/8” acrylic base (McMaster-Carr) that was laser-cut (Epilog Zing 24 Laser) according to layouts made using design software (SolidWorks). 200 μl pipette tips (Fisherbrand cat # 02-707-410) were fitted into holes in the acrylic base of the multi-head at sites aligned with the desired fraction collection rack. The downstream ends of silicone tubing (Masterflex 96410-14) carrying medium streams from culture vessels were pushed tightly into the pipette tips to allow effluent to flow out through the tips into the collection tubes or wells on the rack. Benchmarking metrics such as collection volume were used to assess the accuracy and reliability of the multi-head dispenser.

4.2. Flow system assembly

All cell culture and residence time distribution experiments were conducted using a multi-channel syringe pump (New Era Pump Systems NE-1600) with 20 ml syringes (Fisherbrand cat # 14955460). All tubing was 1.6 mm ID platinum cured silicone (Masterflex 96410-14) which was used to connect all parts using Luer connectors (Cole-Parmer). Optionally, 4-way stopcocks (Cole-Parmer) could be placed in-line to aid in filling the system with medium and to switch between medium sources and serve as a port for injection. The plugged well plate culture vessels consisted of a 12-well plate (Corning) plugged with a size 4 versilic silicone stopper (Saint Gobain cat # 142-55017) with the excess material at the bottom cut off, and two 18-gauge needles (BD PrecisionGlide) inserted directly through the stopper to the bottom of the well. This culture vessel could optionally be placed on a plate rocker (Labquake cat # T400110). The multi-head dispensers were attached to the BioFrac fraction collector (Bio-Rad cat # 7410002) underneath the native dispensing head by removing three screws, inserting them through the designated holes on the multi-head base, and replacing them in their sockets to attach the multi-head base.

4.3. Residence time distribution measurements

Blue food dye containing Brilliant Blue FCF (Wilton Color Right Base Blue) was used as a tracer. An absorption spectrum for the dye diluted in tap water was obtained using a microplate reader (Varioskan LUX) and it was found to have a peak absorbance at 628 nm. The tracer solution for the RTD measurement was prepared at the maximum concentration of the dye’s linear absorption range. The tracer solution was loaded into a syringe and placed in a syringe pump and attached by silicone tubing to one opening of a 4-way stopcock. The pump was run until the tubing was full and the tracer solution started to flow out of the stopcock, at which point the tracer inlet of the stopcock was shut. A second syringe filled with tap water was placed in a second syringe pump and similarly attached to a second opening on the stopcock. The downstream end of the flow system to be measured was then attached to a fraction collector, and the upstream end was attached to the third port of the stopcock. The tap water syringe pump was run to fill the entire system with tap water until water started dripping out of the fraction collector. The fraction collector was then loaded with 96-well plates (Greiner Bio-One cat # 655101) to collect fractions and was programmed to collect 3 drops/fraction.

The length of the pulse duration was chosen to be 1 minute when the flow rate was 10 ml/hour and was scaled for all other flow rates to keep the pulse volume constant between experiments. The stopcock was then opened to the tracer inlet and shut to the water inlet. The tracer syringe pump was set to the desired flow rate, and the tracer pump and fraction collector were started simultaneously, with the time noted as initial time. After the pulse duration had elapsed, the tracer pump was stopped, the stopcock was quickly switched to shut off the tracer and open to water, and the water pump was started at the desired flow rate. The water pump was run until all of the tracer had passed through the system and been collected in the fractions, after which the system was stopped, and the final time was noted. The absorbance values of the fractions were immediately read at 628 nm in a microplate reader.

The data was then processed using a MATLAB script to produce the final RTD. Through this algorithm, the absorbance values of all fractions were loaded as a vector, along with the initial time, final time, and the pulse duration. The assumption was made that each fraction took an equal length of time to collect, and each fraction was assigned a time point corresponding to the midpoint of the collection interval of that fraction, with time zero assigned to the midpoint of the pulse duration. The background absorbance value of tap water without dye was subtracted from each absorbance value. The area under the absorbance vs. time curve was computed using the trapz function built into MATLAB, and each absorbance value was divided by the area to normalize the area under the curve to 1, producing the final RTD points.

4.4. Fitting residence time distribution models to data

All RTD models were fit to data using the MATLAB nlinfit function to perform nonlinear regression. For fraction collectors and tubing + fraction collectors, nonlinear regression was used to find the Pe and τ values that fit the axial dispersion model directly to the RTD points. For all other flow system units, nonlinear regression was used to find models that, when convolved with the RTD of the fraction collector for the same flow rate, fit the measured data. Specifically, initial parameter values were guessed for the RTD model of the flow system unit were guessed, and this model was convolved numerically with the previously measured RTD of the fraction collector. The error between the resulting curve and the data was calculated and the model parameters were adjusted accordingly using the nlinfit function. These steps of adjustment and error calculation were iterated until the best fit model was found. For tubing, this convolution and nonlinear regression method was used to find the Pe and τ values for an axial dispersion model. For wells, the method was used to find the n and τ values for an n-CSTR model.

4.5. Signal convolution in MATLAB

The RTD of one flow system can be convolved with the RTD of another flow system to produce the overall RTD of the flow systems in series. In a similar manner, any solute signal can be convolved with an RTD to predict how the signal will smear as it passed through the given flow system. RTDs can be prepared in MATLAB as described above. Solute signals can be loaded into MATLAB in terms of a vector containing a series of concentration values, and a vector with the corresponding time points. The concentration vectors of the solute signal and/or the RTD curves are then convolved using the conv function built into MATLAB. The corresponding time vector of the curve produced by convolution is then calculated using a MATLAB script. Note that, in order to convolve two curves, the size of the time steps between points in both of the curves must be equivalent. For this reason, it is useful to either fit a function to the RTD that can be sampled at arbitrary time points, or to interpolate between values in the RTD, to produce a corresponding curve with time intervals that match the signal it is being convolved with.

4.6. Monitoring U2-OS circadian reporter secretion

U-2 OS cells (ATCC cat # HTB-96) were passaged as indicated by the vendor in McCoy’s 5a Medium modified with 10% FBS (Gibco) and 1% Antibiotic Antimycotic Solution (Corning). Passage 7 cells were plated in a Costar 12-well plate (Corning cat # 3512) at 1x10⁴ cells/well. The next day, cells were transduced with lentiviral vectors carrying either Circa2-GLUC or EF1α-GLUC at a multiplicity of infection of 150. After 1 week, the medium was replaced with fresh medium containing 1 μM dexamethasone (Sigma-Aldrich D2915) for 30 minutes to synchronize the circadian clocks of the cells, followed by 3 washes with PBS and finally fresh medium. The wells were immediately plugged with size 4 silicone rubber stoppers (Saint Gobain), the bottoms of which were cut off such that the bottoms of the stoppers were just below the top of the well to leave room for air above the medium. Prior to plugging the wells, two 18-gauge needles (BD PrecisionGlide) were inserted vertically through each stopper far enough for the tips of the needles to touch the bottom of the well once inserted. Medium-filled 60 ml syringes were loaded into a syringe pump outside the incubator (Panasonic MCO-5ACL-PA) and were attached to the inlet needles of each well by 1 m of silicone tubing fed through a port in the incubator, which allowed heat and CO₂ to enter the medium stream before reaching the cells. The outlet needles of the wells were each connected by silicone tubing fed out through the incubator port to one dispensing head of the modified fraction collector outside the incubator. To initially fill all of the tubing, medium was pumped from the syringe pump at 1 ml/minute until medium started dispensing out of the fraction collector, at which point the flow rate was switched to 0.5 ml/hour, and the syringe pumps began collecting 1 fraction/hour into glass tubes (Fisherbrand cat # 14-961-26) in F1 racks (Bio-Rad cat # 741-0100). The cells were perfused at a constant rate for 74 hours, and every 24 hours, every-other fraction from each stream was transferred to a microfuge tube and frozen at −20 °C until assayed.

To measure GLUC, medium fractions were thawed and mixed by vortexing, and 20 μl of each fraction was loaded into each of two wells of a black-walled 96-well plate (Corning cat # 3915). GLUC substrate solution was prepared fresh by mixing 1 μl of 100 μM coelenterazine (Alfa Aesar J66823) for every 1 ml of PBS. The plate was loaded into the microplate reader tray, and 100 μl GLUC substrate was added to all the wells of one row simultaneously using a multichannel pipette immediately before starting the luminescence read for that row, after which each well in the row was read 10 times. This was repeated for each row of samples, with duplicate rows of samples read in opposite directions so that duplicates could be averaged and cancel out the effects of luminescence decay of the flash assay.

The 10 reads of each well were averaged to report the luminescence in terms of the kinetic reduction, and the luminescence values of the duplicate samples were averaged. The average value for each curve was calculated, and the points of each curve were reported as the fold difference over the average of that curve and were plotted versus time, shifted backwards in time by the time delay of the downstream RTD.

Linear detrending and period analysis of circadian oscillations were performed using BioDare2 [27].

Highlights.

• A simple, low-cost, and modular perfusion bioreactor was created.

• Can transiently stimulate cells and measure secretion rates in parallel cultures.

• Method developed to measure the residence time distributions of bioreactor parts.

• Residence time distributions used to predict signal smearing using convolution.

• Bioreactor used to measure the secretion rate of a circadian clock-driven reporter.

Abbreviations:

RTD

Residence time distribution

CSTR

continuous stirred tank reactor

Pe

Péclet number

Bo

Bodenstein number

GLUC

Gaussia princeps luciferase

FBS

fetal bovine serum

EDTA

Ethylenediaminetetraacetic acid

9. Appendix

Figure A.1. Steady state temperature of water in a representative culture vessel as a function of flow rate for a system with 0.5 m of upstream tubing in an incubator.

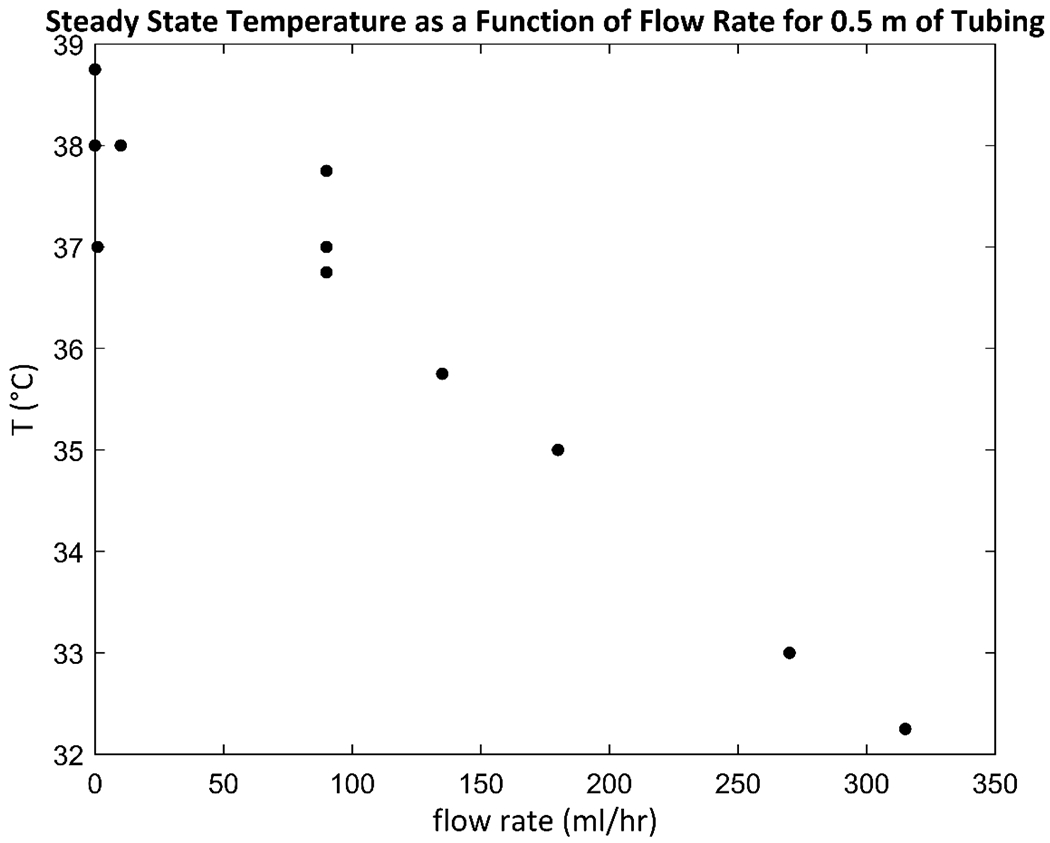
A culture medium reservoir is kept outside the incubator at room temperature (20 °C), and as medium flows through upstream tubing within an incubator, it must heat up to 37 °C before it enters a culture vessel. Both increasing the length of upstream tubing or decreasing the flow rate increase the residence time of medium in the upstream tubing, giving it more time to thermally equilibrate. To measure the effect of flow rate on the steady state exit temperature for a fixed upstream tubing length of 0.5 m, a measurement apparatus was constructed consisting of the bottom part of a 15 ml conical tube with the rest of the tube cut off, placed at the bottom of a 50 ml conical tube. A reservoir of tap water was kept outside an incubator at 20 °C and water was pumped into the 37 °C incubator at a chosen flow rate, and for each experiment, the last 0.5 m of tubing was kept inside the incubator. The end of the tubing was placed at the bottom of the cut 15 ml conical tube, and the water that flowed out was allowed to pool in the cut tube before spilling over into the 50 ml conical tube, where it was removed by a second length of tubing that drew the water back out of the incubator to a waste bottle. A mercury thermometer was placed in the pool in the cut tube, and water was allowed to flow for at least 1 hour at the specified flow rate to allow the system to reach steady state, after which the temperature was recorded. The data show that the temperature did not drop off below 37 °C until flow rates were used that are impractically high for cell culture applications, indicating that an upstream tubing length of 0.5 m is sufficient to allow the temperature of medium to reach 37 °C before entering a culture vessel.

Figure A.2. Flow system factors that do not affect residence time distribution.

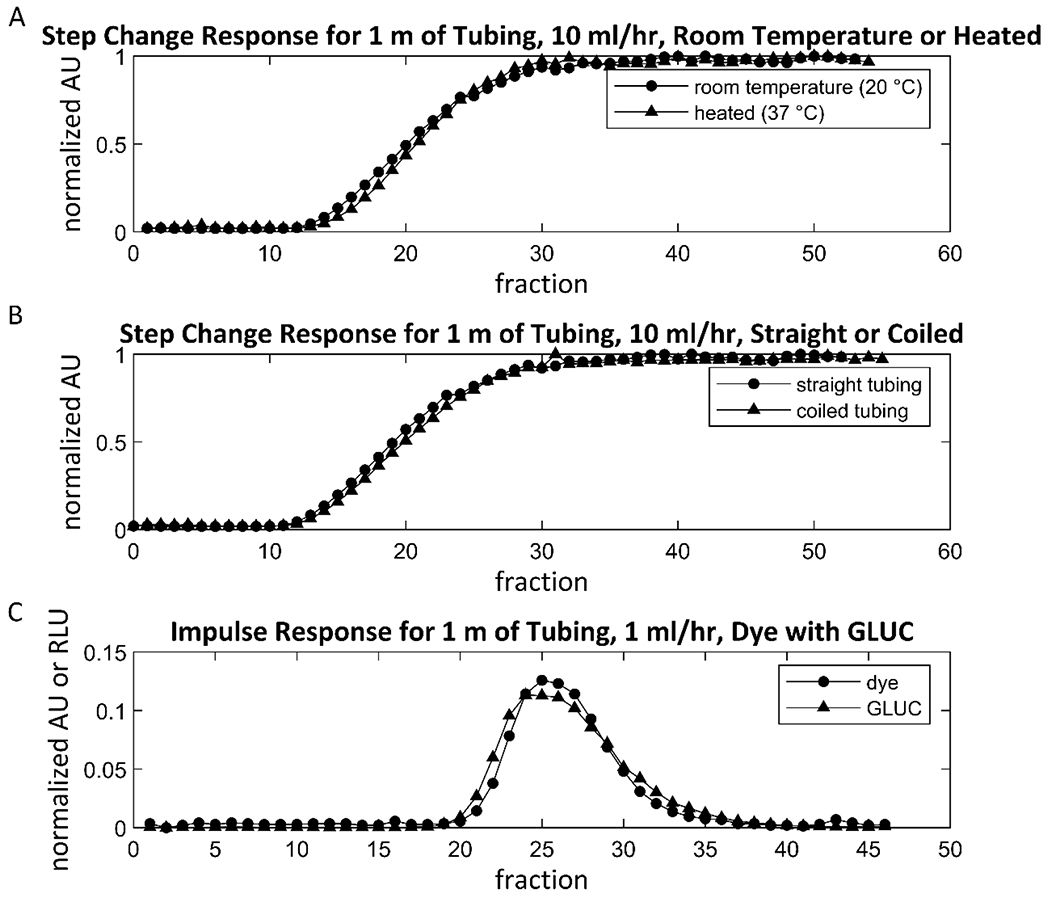
Several flow system factors were found to have no significant effect on flow system RTDs. (A) A step-change tracer experiment was performed, in which the same setup was used as in the RTD measurement experiments, except instead of injecting an impulse of dye into the flow, the flow source was instead switched from water to dye at time zero, creating a step change in concentration. For 1 m of tubing and a flow rate of 10 ml/hour, the step-change response of the flow system was nearly indistinguishable between the case where tubing was kept at 20 °C, and the case where the tubing was run through a water bath at 37 °C. Note that water flowed through the tubing while it was submerged in the water bath for 30 minutes prior to the step change, to allow the temperature to reach steady state. (B) The step-change response was nearly indistinguishable between the default case where the tubing was laid straight and the case where the entire length of the tubing was coiled around a 50 ml conical tube. (C) To measure the effect of solute diffusion coefficient on the RTD of that solute, the impulse responses of a simultaneous pulse of both dye and GLUC were measured. First, a population of Jurkat cells that were modified to constitutively secrete GLUC were cultured in a flask with RPMI medium for 5 days, after which the GLUC-containing supernatant was collected and stored at −20 °C until use. For the impulse response experiment, 1 m of tubing was filled with fresh RPMI. Dye was mixed into the GLUC-containing RPMI, and an impulse of this mixture was injected into the flow following the RTD measurement method at time zero. The dye is a small molecule, and GLUC is a protein, and the two molecules should have very different diffusion coefficients. The dye concentrations of the fractions from this experiment were measured in a plate reader, and the GLUC concentrations were measured by the bioluminescence produced upon addition of its substrate, coelenterazine. The measurement shows that the impulse response for both solutes do not differ greatly.

Table A.1. Parameters for fit RTD models.

Values for all model parameters found to fit experimental RTD data.

Flow System Unit	Model	Flow Rate (ml/hr)	τ (min)	Pe	n	Bo
Fraction Collector	Axial Dispersion	1	37.67	57.83
Fraction Collector	Axial Dispersion	10	3.895	15.49
0.5 m Tubing + Fraction Collector	Axial Dispersion	1	119.0	155.1
0.5 m Tubing + Fraction Collector	Axial Dispersion	10	10.51	20.57
1 m Tubing + Fraction Collector	Axial Dispersion	1	182.9	183.4
1 m Tubing + Fraction Collector	Axial Dispersion	10	17.27	28.41
2 m Tubing + Fraction Collector	Axial Dispersion	1	298.9	362.1
2 m Tubing + Fraction Collector	Axial Dispersion	10	29.98	45.68
0.5 m Tubing	Axial Dispersion	1	79.96	98.65
0.5 m Tubing	Axial Dispersion	10	5.890	9.063
1 m Tubing	Axial Dispersion	1	143.8	132.7
1 m Tubing	Axial Dispersion	10	12.73	17.99
2 m Tubing	Axial Dispersion	1	259.9	306.5
2 m Tubing	Axial Dispersion	10	25.51	35.62
Static Well	n-CSTR	1	96.81		2.488	2.976
Static Well	n-CSTR	10	9.540		1.180	0.3600
Rocked Well	n-CSTR	1	128.9		1.822	1.644
Rocked Well	n-CSTR	10	12.70		2.049	2.098