Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Mar 18;11(7):2667–2674. doi: 10.1021/acs.jpclett.0c00247

Polariton Transitions in Femtosecond Transient Absorption Studies of Ultrastrong Light–Molecule Coupling

Courtney A DelPo †, Bryan Kudisch †, Kyu Hyung Park †, Saeed-Uz-Zaman Khan ‡, Francesca Fassioli †,#, Daniele Fausti †,⊥,, Barry P Rand ‡,§, Gregory D Scholes †,*
PMCID: PMC8154840  PMID: 32186878

Abstract

graphic file with name jz0c00247_0005.jpg

Strong light–matter coupling is emerging as a fascinating way to tune optical properties and modify the photophysics of molecular systems. In this work, we studied a molecular chromophore under strong coupling with the optical mode of a Fabry–Perot cavity resonant to the first electronic absorption band. Using femtosecond pump–probe spectroscopy, we investigated the transient response of the cavity-coupled molecules upon photoexcitation resonant to the upper and lower polaritons. We identified an excited state absorption from upper and lower polaritons to a state at the energy of the second cavity mode. Quantum mechanical calculations of the many-molecule energy structure of cavity polaritons suggest assignment of this state as a two-particle polaritonic state with optically allowed transitions from the upper and lower polaritons. We provide new physical insight into the role of two-particle polaritonic states in explaining transient signatures in hybrid light–matter coupling systems consistent with analogous many-body systems.

The field of light–matter coupling has evolved to include various degrees of coupling ranging from weak to ultrastrong; various types of coupling, including electronic, vibrational, and vibronic; and various media through which the coupling occurs, including solid semiconductor architectures and liquid flow cells.1 Accompanying this large range are exciting applications, including room-temperature polariton lasing and Bose–Einstein condensation,2,3 modification of ground-state and chemical reactivity,4,5 mediated and enhanced rate of energy transfer,6,7 and adjustment of work-function.8 These applications are possible due to the formation of hybrid light–matter polaritonic states that change the energetic landscape of the coupled material.

Realizing additional applications as well as improving current applications requires a fundamental understanding of the properties of polaritonic states. When an electronic or vibrational transition is resonant with the cavity mode in a Fabry–Perot cavity, the energy level of the transition is split into an upper polariton and a lower polariton. The energy splitting between the two polaritons is called the Rabi splitting, ΩR, and its magnitude is approximately:1

graphic file with name jz0c00247_m001.jpg 1

where g is the strength of the coupling between the molecules and the cavity, μ is the magnitude of the transition dipole moment of the material, N is the number of molecules coupled to the cavity, ω is the frequency of the transition, ε0 is the vacuum permittivity constant, and v is the cavity mode volume.

If there are N molecules coupled to the cavity mode, then a ladder of states that comprises a superposition of molecular excitations and cavity photons is generated. The eigenvalues of these states are grouped into “rungs” of an energy ladder, where each rung comprises an upper polariton (UP) and a lower polariton (LP) state with a high density of intervening dark states (DS). Transitions from the ground state to these dark states are forbidden.9

As hybrid light–matter states, polaritons adopt both photonic and molecular characteristics. While there are well-established methods for characterizing the dispersive steady-state features of polaritons, there remains ambiguity in assigning the excited state transitions in a cavity system. Within the vibrational strong coupling regime, the presence of overtones of the dark states complicates excited state absorption assignments. For example, the positive absorptive feature close to the lower polariton energy observed in transient absorption spectroscopy has been discussed as an excited state absorption to the second vibrational overtone from either the upper polariton or the dark states.10−12 In the electronic strong coupling regime, electronic overtones of the molecular states generally do not obfuscate assignments; however, available reports feature overlapping molecular and polaritonic features with similar spectral shapes that can make distinct assignments difficult.13,14 This blurring of spectral features occurs as a result of the small Rabi splitting but can be overcome by using materials with high energy electronic transitions and strong oscillator strengths that make the ultrastrong coupling regime feasible. The transition dipole moment term in eq 1 is scaled by the transition energy leading to larger Rabi splitting for molecules with high energy transitions.15 Thus, with a stronger coupled cavity, we can avoid the blurring of polaritonic and molecular features.

In this study, we use the organic light emitting diode (OLED) material 1,2,3,5-tetrakis(carbazol-9-yl)-4,6-dicyanobenzene (4CzIPN) to achieve ultrastrong electronic coupling, allowing us to distinctly separate and observe the excited state features of a cavity system. Using pump–probe spectroscopy, we propose a new interpretation of the spectral features in a cavity system and use this framework to investigate polaritonic dynamics (Figure 1).

Figure 1.

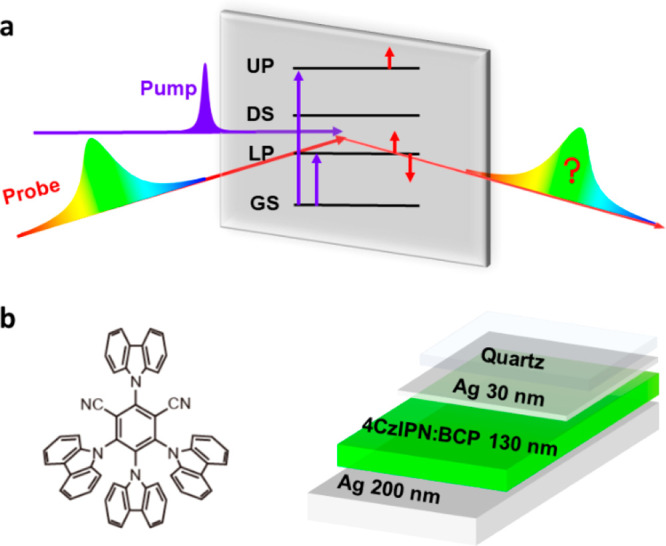
Figure 1

Open in a new tab

Fabry–Perot cavity description. (a) Pump–probe spectroscopy reveals excited state features attributed to the UP, LP, and DS. (b) Cavity architecture is shown next to the 4CzIPN structure.

The allowed absorption transitions of 4CzIPN have significant charge-transfer character, so the maximum peaks of absorption and fluorescence are concentration dependent and sensitive to the polarity of the surrounding medium (SI Figure 1).16−18 In bathocuproine (BCP), 4CzIPN has a lowest energy absorption maximum around 385 nm and a fluorescence maximum at 570 nm. As a vacuum-evaporated film, BCP has a maximum absorption peak at 281 nm and a fluorescence peak at 384 nm.19 We embedded 4CzIPN in a BCP host such that the 4CzIPN lowest energy singlet transition, highlighted in blue in Figure 2, is apparent as a shoulder at 460 nm.

Figure 2.

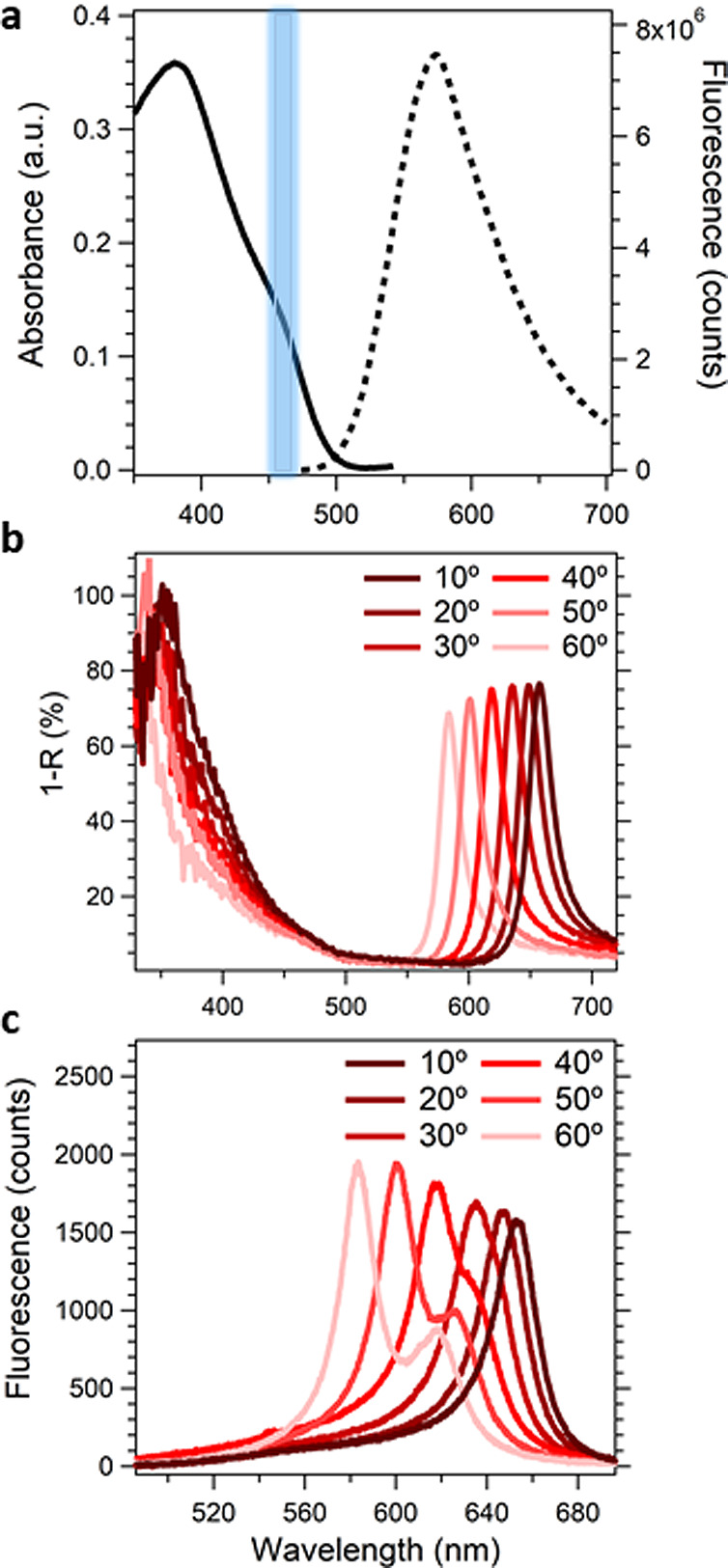
Figure 2

Open in a new tab

Steady-state measurements of the bare film and cavity system. (a) Absorption and fluorescence (ex. 380 nm) of a bare film of 4CzIPN in BCP with the singlet transition at 460 nm highlighted in blue. Angle-dependent reflectance (b) and photoluminescence (ex. 406 nm) (c) measurements of the 4CzIPN cavity system.

To prepare the cavities, 4CzIPN:BCP (10:1) was thermally evaporated between two silver layers of thicknesses 30 and 200 nm. The thickness of the 4CzIPN:BCP layer was tuned with nanometer precision to maximize Rabi splitting. The magnitude of the Rabi splitting was estimated using the separation of the maxima of the polaritonic peaks in the angle-dependent reflection measurements displayed in Figure 2, yielding a Rabi splitting of 1.6 eV. We find an upper polariton peak centered around 360 nm and a lower polariton at 660 nm. At nearly 60% of the energy of the 460 nm transition, the magnitude of this Rabi splitting places the system in the ultrastrong coupling regime.20 As the angle-dependent fluorescence spans from 660 nm at 10° to 550 nm at 90°, the color of the fluorescence changes from red to green. The Q-factor for this cavity is approximately 15 (SI Figure 2), which is in agreement with the reported Q-factors for similar optical cavity systems.14 The double peaks observed at angles 40° to 60° are a result of transverse electric (TE) and transverse magnetic (TM) polarization (SI Figure 3).21,22

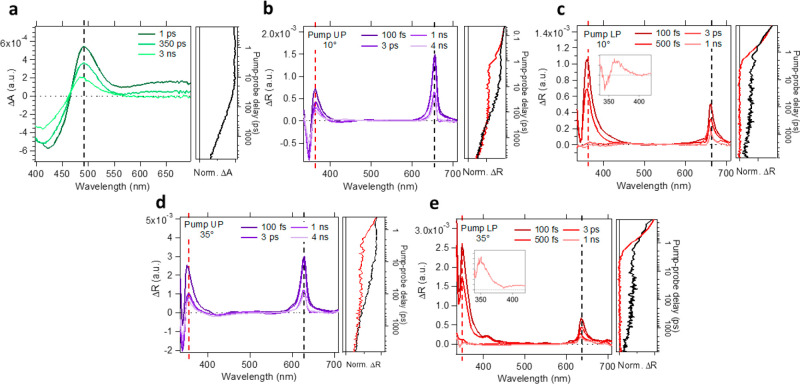
Ultrafast pump–probe spectroscopy at room temperature reveals differences in the spectral features of the cavity system as compared to a bare film of 4CzIPN in BCP. In BCP, 4CzIPN has an excited-state absorption (ESA) at 485 nm and a ground state bleach (GSB) at 420 nm (Figure 3a). These spectral features are attributed to photoinduced charge transfer from the carbazole donor groups to the dicyanobenzene center in 4CzIPN, as confirmed by spectroelectrochemistry measurements (SI Figure 4). The bare film spectrum is consistent with pump–probe measurements performed on 4CzIPN in solution.23 The kinetic trace of the ESA shows a multiexponential decay with three time constants outlined in Table 1. To the best of our knowledge, the ultrafast dynamics of this molecule have not been previously reported, but the final time constant is in agreement with the reported time constant of prompt fluorescence.24

Figure 3.

Figure 3

Open in a new tab

Pump–probe spectroscopy of the bare film and angled cavity. (a) Bare film (no cavity) transient absorption spectrum pumped at 370 nm. Transient reflection spectra pumping the UP (b, d) and LP (c, e) at 10° (b,c) and 35° (d, e). The angle is relative to normal incidence of the probe. The UP and LP were pumped at 370 and 650 nm at 10° and at 360 and 635 nm at 35°, respectively. Pump power for the bare film, the UP at 10°, the LP at 10°, the UP at 35°, and the LP at 35° was 60, 10, 20, 20, and 25 μW, respectively. All experiments were conducted within a linear power regime (SI Figure 5). Kinetic traces are displayed in red and black with the corresponding wavelength indicated on the spectrum. Insets in c and e enhance the UP energy feature at 1 ns when pumping the LP. Note that white light generation below 330 nm was not efficient enough to reveal the entire feature in the inset of e, but it is predicted to be a derivative-like feature as that observed in the inset of c.

Table 1. Time Constants for the Excited State Spectral Features of the Bare Filma.

  τ1 τ2 τ3
bare film 19 ps 530 ps 14 ns
Open in a new tab
a

Time constants for the excited state spectral features of the cavity were fit using these constants (SI Figure 9 and SI Figure 10).

The 4CzIPN spectral features are notably absent in the cavity spectra (Figure 3b, c). Upon resonant photoexcitation of the UP, we observe a derivative-like shape at 360 nm and a positive Lorentzian shaped response at 660 nm. Due to the common ground state for UP and LP transitions, we expect a GSB response at the lower polariton energy. Note that in Figure 3, the linear response is subtracted from the transient measurement, and therefore, the GSB is expected to appear as a negative feature in the transient spectra. Instead, we observe a sharp ESA at 660 nm, appearing as mentioned above as a positive Lorentzian-shaped feature. In contrast, upon resonant excitation of the LP (Figure 3c), we observe a strong ESA at 360 nm and a smaller ESA at 660 nm.

Within the electronic strong coupling regime, many studies have focused on probing the excited state dynamics of J-aggregate systems. Derivative shaped transient spectra are observed for the J-aggregate system both inside and outside of the cavity, making it difficult to distinguish molecular and polaritonic features.13,25−27 In the vibrational strong coupling regime, a transient response featuring a derivative-like shape at a higher energy and an ESA at a lower energy has also been reported.10,11,28

Rotating the incident angle in a polaritonic system results in changes of the relative contribution of photonic and molecular character in each of the polariton bands.1,9 As a result of these contributions, angle-dependent pump–probe spectroscopy can reveal differences in the relative intensities of the spectral features at various angles. At larger angle (35°, Figure 3d), we confirm a derivative-like feature at 350 nm and a sharp ESA at 635 nm when pumping the UP. Upon excitation of the LP (Figure 3e), there is an ESA at 350 nm and an ESA at 635 nm.

Differences in the relative intensities of the spectral features are observed at a larger angle. When pumping the UP at 35°, the ratio of the intensities of the features at 350 and 635 nm is 0.83:1 which is closer to unity than the 0.5:1 ratio of the intensities of the 360 and 660 nm features when pumping the UP at 10°. In contrast, when pumping the LP at 35°, the difference in the ratio of the intensities of the two spectral features is more drastic at 1:0.33 compared to the 1:0.5 ratio observed when pumping the LP at 10°.

Importantly, while the intensities and position of the spectral features change with the angle, the transient population kinetics remain the same. When pumping the UP, the 660 nm ESA at 10° and 635 nm ESA at 35° decay very similarly to the 4CzIPN 485 nm ESA outside the cavity. Comparing the black traces in Figure 3a, b, and d highlights this similarity. The 360 nm feature at 10° and 350 nm feature at 35° show an initial sharp decay with a time constant of approximately 1 ps. After the first few ps, they further decay with the same dynamics as each corresponding longer wavelength ESA (as shown by the overlap between the red and black traces at long times in Figure 3b and d). Upon excitation of the LP, the 360 nm ESA at 10° and 350 nm ESA at 35° undergo a fast decay to nearly baseline with a time constant of approximately 1 ps. The signal that remains at these wavelengths following the decay of each ESA is the same derivative-like feature observed when photoexciting the UP (see inset in Figure 3c or SI Figure 8). The 660 nm ESA at 10° and 635 nm ESA at 35° undergo an initial decay on the same 1 ps time scale but conversely do not decay to baseline. Compare the red trace of normalized change in reflectance versus pump–probe time delay in Figure 3b to the corresponding black trace in Figure 3c. When we pump the UP and probe the ESA at the UP energy, we observe, surprisingly, the same kinetics as when we pump the LP and probe the ESA at the LP energy. Similarly, we can compare the red trace in Figure 3d to the black trace in Figure 3e. Time constants for each of the traces obtained from Global Analysis are presented in the Supporting Information(29) (SI Figure 9 and SI Figure 10).

We now discuss assignments for the transient spectra recorded under the various experimental conditions. A derivative-like feature in the pump–probe spectra of cavity polaritons, like the one appearing at the UP energy, has often been rationalized as a contraction of the Rabi splitting that occurs when a population of the system is excited by the pump pulse.28,30 The contraction is the consequence of the photoinduced reduction of the number of ground state molecules effectively coupled to the cavity and results in a red-shift of the transition from the ground state to UP (because the LP-UP splitting is proportional to the square root of the number of molecules coupled to the cavity mode). When the spectrum arising from the red-shifted transition is subtracted from the ground-state spectrum, a derivative feature is expected in this description (Figure 4b). In this picture, a derivative-like feature is also expected at the LP energy as the contraction leads to a slight blue-shift of the LP absorption.

Figure 4.

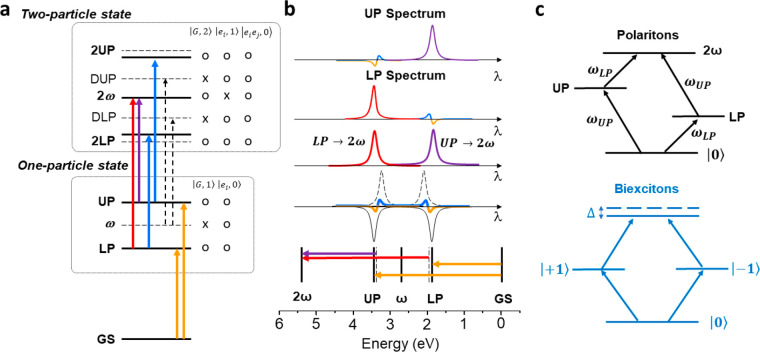
Figure 4

Open in a new tab

Spectral feature assignments for polaritonic states. (a) Ladder of states predicted using the Tavis–Cummings model including two-particle states. G, ei, and eiej designations are representative of the ground, one, and two-exciton molecular states, respectively. The number of photons in the cavity is 0, 1, or 2. Contributing terms to each state are marked with an O, while absent terms are marked with an X. Optically allowed transitions between the GS and one-particle states and between one- to two-particle states are indicated by arrows. Note that transitions from the one-particle dark states at energy ω to optically bright DUP and DLP states are allowed and indicated with black dashed arrows. Other two-particle states without predicted optical transitions are omitted for clarity (see Supporting Information). (b) Excited and ground state contributions to the transient response. The UP (LP) to 2ω ESA overlaps with the LP (UP) derivative feature. (c) Comparison of the energy level schematic for the 2ω state in the polariton framework to the classic biexciton diagram in semiconductors. In semiconductors, excitons of opposite spin (+1, −1) can combine to form the biexciton state. Exciton binding energy, Δ, results from phase-space filling and causes a slight difference in energy between the biexciton state and the state at twice the energy of a single exciton (dashed).

While there is nothing wrong with this as a phenomenological description of the transient spectra, we propose that the derivative-like shape in electronic strong coupling should be better regarded as phase-space filling—that is, the transition frequency of one-particle states to two-particle states of many body systems tends to be shifted compared to that of ground state to one-particle states because of differences in the one-particle versus two-particle wave functions.31,32 In this picture, the derivative-like feature is the result of the quantum mechanical energy structure predicted by the simplest Hamiltonian that treats strong light–matter coupling with many molecules, namely the Tavis–Cummings Hamiltonian33,34 (Supporting Information).

The Tavis–Cummings Hamiltonian (TCH) is given by

graphic file with name jz0c00247_m002.jpg 2

where σi+(−) are the rising (lowering) operators of the ith two level system, ω is the frequency of the bosonic optical mode, and a⧧ (a) describe the creation (annihilation) operators of the bosonic field and g measures the strength of the interaction. Since the Hamiltonian in eq 2 conserves the total number of particles Np = ∑i=1Nσiσi– + a⧧a (either molecular or photonic excitations), i.e., [H,Np ] = 0, its eigenstates are a superposition of states with the same number of particles. We assume the case of resonance (ω = E) and focus on the solution of the eigenstates for the Np = 1 and Np = 2 particle cases. The collective matter–photon states are labeled as {|G,n⟩, |ei,n⟩ and |eiej,n⟩ (I≠ j)}. G, ei, and eiej label the molecular states and represent all molecules in the ground state, only a single molecule i excited and two molecules i and j excited, respectively. The n instead labels the number of photons on each state. The results are summarized in Figure 4a.

As depicted in Figure 4a, the TCH predicts optically allowed transitions from the LP and UP one-particle states to three different two-particle polaritons, which we label as 2LP, 2ω and 2UP. While the energy of the 2ω state is fixed at twice the cavity resonance frequency, the energy of 2LP and 2UP depend on the number of molecules coupled to the cavity (see Supporting Information). The ESA from UP (LP) to the 2UP (2LP) states is predicted at an energy that is lower (higher) than the UP (LP) GSB, leading to a derivative-like feature in the transient spectra, analogous to the contraction of the Rabi splitting. We note, however, that the expected derivative-like feature at the LP energy when pumping the LP is absent. This may be due to the ESA dominating at the LP energy which arises from the UP to 2ω transition. The TCH also predicts allowed transitions from the dark states to the upper (DUP) and lower (DLP) polaritons in the two-particle manifold which we will discuss with the kinetics of the UP to DS transition.

We now turn to the ESA at 660 nm (the LP energy) when pumping the UP. The vibrational strong coupling literature reported a similar ESA feature appearing at the LP energy, which was assigned to a transition from the dark states to the first vibrational overtone.11,28 The TCH model we employ does not necessarily involve an overtone of the molecular transition. We instead attribute this sharp ESA to the transition from the UP to the two-particle polaritonic state at 2ω (Figure 4a). By the nature of the symmetry of the Rabi splitting in a resonant cavity, the energy of the transition from the UP (LP) to the second mode of the cavity (2ω) is equal to the energy of the LP (UP) (Figure 4a). The derivative-like features expected to appear at both the UP and LP energies become obscure when the transition from UP or LP to 2ω overlaps.

The existence of the 2ω state and the possibility for transitions to this state can be understood in analogy to a semiconductor spectroscopic framework. Semiconductors are well-known to have ladders of excitonic states: excitons, biexcitons, triexcitons, etc.35−37 The transient excited state absorptions in this work are similar to transitions within the exciton-to-biexciton fine structure states (Figure 4c, bottom diagram).32 Essentially, each two-particle state comprises two one-particle states. In nonlinear spectroscopy, we can sequentially add these two one-particle states in either order to produce a two-particle state. In the polaritonic framework, these two-particle states at 2ω correspond to a quantum superposition of the states with two photons and no molecular excitations and two molecular excitations with no photons (Figure 4c, top diagram, see details in the Supporting Information).

The relative intensities of the spectral features are indicative of polariton character. Comparing the spectra for pumping the LP in the cavity angled at 35° (Figure 3e) to the cavity angled at 10° (Figure 3c) reveals a higher intensity of the LP to 2ω transition, as indicated by the increased signal intensity of the 360 and 350 nm features relative to the signal intensity of the 660 and 635 nm features at early times. Similarly, the spectra when pumping the UP with the cavity angled at 35° reveals a stronger intensity LP to 2ω transition as compared to the cavity angled at 10°. The detuning-dependent intensity of the spectral features has been reported.28 We speculate the change in photonic character of the lower polariton with increasing angle increases the strength of the transition to 2ω, as has previously been proposed.30

When the sample is angled at 35° (Figure 3d, e), the spectral shapes remain consistent with the explanation provided. The states at ω and 2ω change by the same amount of energy as the UP and LP, leading to the same spectral assignments at the new angle. The change in relative energy levels is reflected in the new position of the spectral features at 360 and 635 nm corresponding to the energies of the UP and LP at this angle, respectively. The spectral feature assignments are also supported in detuned cavities and off-resonant excitation (SI Figure 6 and SI Figure 7).

According to our spectral assignments, it appears that both UP and LP are photoexcited at early times, despite the fact that our pump pulse is only resonant with one of their transitions. When we pump only the LP, both LP and UP spectral features initially decay with a time constant of 1 ps. The 360 nm ESA corresponding to the transition from the LP to 2ω decays completely on this time scale, leaving a very small UP derivative-like signal (see inset in Figure 3c or SI Figure 8). The 1 ps time constant is assigned to the lifetime of the LP. This same initial time constant is observed in the 360 nm feature when pumping the UP because the LP ESA overlaps the UP derivative-like signal at 360 nm. This indicates that when pumping the UP, there is population of the LP before 1 ps. When pumping the LP, the 660 nm ESA survives beyond the lifetime of the LP. Within our proposed scheme, the energy of this signal corresponds to an excited state transition from the UP to 2ω. This is further supported by comparing the kinetic trace of the 360 nm feature when pumping the UP to the 660 nm ESA when pumping the LP. These kinetic traces are the same because they both contain contributions from the UP and LP.

In the vibrational strong coupling regime, the energy difference between the LP and the dark state reservoir is small enough to allow thermal population of the dark states by the LP. In the case of the system studied in our work, the energy difference between the LP and the dark states is on the order of 800 meV, which prevents this same thermal population. We propose two-photon absorption to the UP when pumping the LP to account for the spectral similarities when pumping the UP and the LP. The GS to UP transition energy (3.44 eV) is roughly twice that of the GS to LP (1.87 eV) transition in this particular cavity. Absorption of two photons of LP energy when pumping the LP can lead to two-photon absorption to the UP state, thus populating the UP. While we were operating at low powers where the power dependence appears to be in the linear regime, we tested the power dependence to higher powers where a superlinear dependence becomes evident and is indicative of two-photon absorption (SI Figure 5). While not negligible, two-photon absorption is not strong at lower powers, which can explain the small intensity of the UP spectral features when pumping the LP as compared to the signal intensity when directly pumping the UP.

The UP likely populates the dark states on the time scale of tens of picoseconds. Comparing the kinetic trace for the bare film ESA at 485 nm in Figure 3a to the trace for the cavity ESA at 660 nm in Figure 3b reveals slight differences between the two traces up to 100 ps. For clarity, these traces have been reproduced on the same plot in SI Figure 11. We also note that the kinetic traces are identical in the nanosecond time scale, which likely reflect dark state population in accordance with other similar investigations.10,11,28 It appears that the cavity kinetic trace has a faster decaying component on the tens of picoseconds time scale that is not present in the bare film trace. However, fitting with multiexponential functions yields similar time constants for both traces, which makes it difficult to characterize the exact time constant for the UP to DS transition. Additionally, the predicted ESA’s from the dark states at ω to the DUP and DLP overlap spectrally with the energies of the UP and LP, respectively. As a result of this overlap, the dark state spectrum, expected to be present in the nanosecond time scale (as a result of the similarity of the darks state decay to the bare molecule decay),10,11,28 can appear spectrally similar to the polaritonic spectrum in the earlier time regime when pumping either the UP or the LP. The spectral similarity increases the difficulty of assigning the time scale on which the UP populates the dark states. Due to the common ground state when pumping either the UP or LP, an overlapping bleach feature also adds complexity in disentangling the kinetics.

Although extracting the lifetime of the UP from the entangled kinetics may be difficult, we anticipate the UP lifetime to be greater than the 1 ps LP lifetime.10,11,28,38 As mentioned earlier, the transient features we observe in the 4CzIPN cavity system are very similar to those reported in the vibrational strong coupling regime. Within the vibrational strong coupling regime, the lifetime of the UP has been reported to range from 10 to 30 ps, which is longer than the corresponding LP lifetime of 5 ps.10 Within the electronic strong coupling regime, the UP and LP lifetimes are much shorter—on the order of hundreds of femtoseconds. According to the model by Agranovich et al, the UP lifetime is determined by an intricate interplay of the UP–DS energy gap and the energy broadening of the DS.27 The coupling in our electronic strong coupling system reaches the ultrastrong regime with an UP–DS energy difference that is four times as large as the reported J-aggregate microcavity cases, which brings the UP lifetime in our system into the picosecond time scale (see SI Figure 11 for more details).

Characterization of the excited states of polaritonic systems is necessary for the advancement of optoelectronic applications of hybrid light–matter coupling, particularly in nonlinear optics, but has remained ambiguous in the current state of the field. We have proposed a rigorous interpretation of excited state spectral features in cavity coupled systems. To avoid difficulties in distinguishing between vibrational overtone transitions and spectral crowding in less strongly coupled electronic cavity systems, we studied an ultrastrong electronic cavity coupled system. We compared experimental pump–probe data to predictions from a quantum mechanical model. The spectral assignments we have proposed may be used to uncover details of polariton dynamics in other systems or for the purposes of quantum control. Taking advantage of the multiple pathways available to arrive at the 2ω state, coherent control experiments can provide additional avenues for polariton exploration.39 The design of experiments to probe states within the three-particle manifold and higher as well as fluorescence upconversion studies that can capture the fast emission from the LP also provide suitable platforms for further polariton investigation. One other significant area of interest that remains to be explored is the presence and role of dark states in electronically coupled systems; moving beyond the ultrafast time scale to observe dynamics within the cavity system at later times will provide information about the long-lived states within the cavity, including the elusive dark states.

Acknowledgments

This research was funded by the Gordon and Betty Moore Foundation through Grant GBMF7114. C.A.D. acknowledges acknowledge the use of Princeton’s Imaging and Analysis Center, which is partially supported by the Princeton Center for Complex Materials, a National Science Foundation (NSF)-MRSEC program (DMR-1420541). B.K. acknowledges support by the National Science Foundation Graduate Research Fellowship under Grant DGE-1656466. S.U.Z.K. and B.P.R. acknowledge funding from the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award DE-SC0012458. F.F. acknowledges financial support from the European Union’s H2020 Marie Skłodowska Curie actions, Grant 799408. D.F. was supported by the European Commission through the European Research Council (ERC), Project INCEPT, Grant 677488. This research made use of the PRISM Cleanroom at Princeton University.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c00247.

  • Experimental details, bare film absorption, Q-factor calculation, power dependent experiments, off-resonant cavity excitation, detuned cavity transient spectra, global analysis, and Tavis–Cummings Hamiltonian (PDF)

Author Contributions

∇ B.K. and K.H.P. contributed equally.

The authors declare no competing financial interest.

Supplementary Material

jz0c00247_si_001.pdf (860.6KB, pdf)

References

  1. Hertzog M.; Wang M.; Mony J.; Börjesson K. Strong Light–Matter Interactions: A New Direction within Chemistry. Chem. Soc. Rev. 2019, 48 (3), 937–961. 10.1039/C8CS00193F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Kéna-Cohen S.; Forrest S. R. Room-Temperature Polariton Lasing in an Organic Single-Crystal Microcavity. Nat. Photonics 2010, 4 (6), 371–375. 10.1038/nphoton.2010.86. [DOI] [Google Scholar]
  3. Plumhof J. D.; Stöferle T.; Mai L.; Scherf U.; Mahrt R. F. Room-Temperature Bose–Einstein Condensation of Cavity Exciton–Polaritons in a Polymer. Nat. Mater. 2014, 13 (3), 247–252. 10.1038/nmat3825. [DOI] [PubMed] [Google Scholar]
  4. Hutchison J. A.; Schwartz T.; Genet C.; Devaux E.; Ebbesen T. W. Modifying Chemical Landscapes by Coupling to Vacuum Fields. Angew. Chem. 2012, 124 (7), 1624–1628. 10.1002/ange.201107033. [DOI] [PubMed] [Google Scholar]
  5. Thomas A.; George J.; Shalabney A.; Dryzhakov M.; Varma S. J.; Moran J.; Chervy T.; Zhong X.; Devaux E.; Genet C.; Hutchison J. A.; Ebbesen T. W. Ground-State Chemical Reactivity under Vibrational Coupling to the Vacuum Electromagnetic Field. Angew. Chem., Int. Ed. 2016, 55 (38), 11462–11466. 10.1002/anie.201605504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Zhong X.; Chervy T.; Wang S.; George J.; Thomas A.; Hutchison J. A.; Devaux E.; Genet C.; Ebbesen T. W. Non-Radiative Energy Transfer Mediated by Hybrid Light–Matter States. Angew. Chem., Int. Ed. 2016, 55 (21), 6202–6206. 10.1002/anie.201600428. [DOI] [PubMed] [Google Scholar]
  7. Coles D. M.; Somaschi N.; Michetti P.; Clark C.; Lagoudakis P. G.; Savvidis P. G.; Lidzey D. G. Polariton-Mediated Energy Transfer between Organic Dyes in a Strongly Coupled Optical Microcavity. Nat. Mater. 2014, 13 (7), 712–719. 10.1038/nmat3950. [DOI] [PubMed] [Google Scholar]
  8. Hutchison J. A.; Liscio A.; Schwartz T.; Canaguier-Durand A.; Genet C.; Palermo V.; Samorì P.; Ebbesen T. W. Tuning the Work-Function Via Strong Coupling. Adv. Mater. 2013, 25 (17), 2481–2485. 10.1002/adma.201203682. [DOI] [PubMed] [Google Scholar]
  9. Ebbesen T. W. Hybrid Light–Matter States in a Molecular and Material Science Perspective. Acc. Chem. Res. 2016, 49 (11), 2403–2412. 10.1021/acs.accounts.6b00295. [DOI] [PubMed] [Google Scholar]
  10. Xiang B.; Ribeiro R. F.; Chen L.; Wang J.; Du M.; Yuen-Zhou J.; Xiong W. State-Selective Polariton to Dark State Relaxation Dynamics. J. Phys. Chem. A 2019, 123 (28), 5918–5927. 10.1021/acs.jpca.9b04601. [DOI] [PubMed] [Google Scholar]
  11. Dunkelberger A. D.; Spann B. T.; Fears K. P.; Simpkins B. S.; Owrutsky J. C. Modified Relaxation Dynamics and Coherent Energy Exchange in Coupled Vibration-Cavity Polaritons. Nat. Commun. 2016, 7 (1), 13504. 10.1038/ncomms13504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Xiang B.; Ribeiro R. F.; Li Y.; Dunkelberger A. D.; Simpkins B. B.; Yuen-Zhou J.; Xiong W. Manipulating Optical Nonlinearities of Molecular Polaritons by Delocalization. Sci. Adv. 2019, 5 (9), eaax5196 10.1126/sciadv.aax5196. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Schwartz T.; Hutchison J. A.; Léonard J.; Genet C.; Haacke S.; Ebbesen T. W. Polariton Dynamics under Strong Light-Molecule Coupling. ChemPhysChem 2013, 14 (1), 125–131. 10.1002/cphc.201200734. [DOI] [PubMed] [Google Scholar]
  14. George J.; Wang S.; Chervy T.; Canaguier-Durand A.; Schaeffer G.; Lehn J.-M.; Hutchison J. A.; Genet C.; Ebbesen T. W. Ultra-Strong Coupling of Molecular Materials: Spectroscopy and Dynamics. Faraday Discuss. 2015, 178, 281–294. 10.1039/C4FD00197D. [DOI] [PubMed] [Google Scholar]
  15. Hilborn R. C. Einstein Coefficients, Cross Sections, f Values, Dipole Moments, and All That. Am. J. Phys. 1982, 50 (11), 982–986. 10.1119/1.12937. [DOI] [Google Scholar]
  16. Ishimatsu R.; Matsunami S.; Shizu K.; Adachi C.; Nakano K.; Imato T. Solvent Effect on Thermally Activated Delayed Fluorescence by 1,2,3,5-Tetrakis(Carbazol-9-Yl)-4,6-Dicyanobenzene. J. Phys. Chem. A 2013, 117 (27), 5607–5612. 10.1021/jp404120s. [DOI] [PubMed] [Google Scholar]
  17. Noda H.; Chen X.-K.; Nakanotani H.; Hosokai T.; Miyajima M.; Notsuka N.; Kashima Y.; Brédas J.-L.; Adachi C. Critical Role of Intermediate Electronic States for Spin-Flip Processes in Charge-Transfer-Type Organic Molecules with Multiple Donors and Acceptors. Nat. Mater. 2019, 18 (10), 1084–1090. 10.1038/s41563-019-0465-6. [DOI] [PubMed] [Google Scholar]
  18. Northey T.; Stacey J.; Penfold T. J. The Role of Solid State Solvation on the Charge Transfer State of a Thermally Activated Delayed Fluorescence Emitter. J. Mater. Chem. C 2017, 5 (42), 11001–11009. 10.1039/C7TC04099G. [DOI] [Google Scholar]
  19. Pelczarski D.; Grygiel P.; Falkowski K.; Klein M.; Stampor W. Electromodulation and Magnetomodulation of Exciton Dissociation in Electron Donor (Starburst Amine): Electron Acceptor (Bathocuproine) System. Org. Electron. 2015, 25, 362–376. 10.1016/j.orgel.2015.06.050. [DOI] [Google Scholar]
  20. Frisk Kockum A.; Miranowicz A.; De Liberato S.; Savasta S.; Nori F. Ultrastrong Coupling between Light and Matter. Nat. Rev. Phys. 2019, 1 (1), 19–40. 10.1038/s42254-018-0006-2. [DOI] [Google Scholar]
  21. Stelitano S.; De Luca G.; Savasta S.; Patané S. Polarized Emission from High Quality Microcavity Based on Active Organic Layered Domains. Appl. Phys. Lett. 2008, 93 (19), 193302. 10.1063/1.3026534. [DOI] [Google Scholar]
  22. Kéna-Cohen S.; Maier S. A.; Bradley D. D. C. Ultrastrongly Coupled Exciton-Polaritons in Metal-Clad Organic Semiconductor Microcavities. Adv. Opt. Mater. 2013, 1 (11), 827–833. 10.1002/adom.201300256. [DOI] [Google Scholar]
  23. Lu J.; Pattengale B.; Liu Q.; Yang S.; Shi W.; Li S.; Huang J.; Zhang J. Donor–Acceptor Fluorophores for Energy-Transfer-Mediated Photocatalysis. J. Am. Chem. Soc. 2018, 140 (42), 13719–13725. 10.1021/jacs.8b07271. [DOI] [PubMed] [Google Scholar]
  24. Hosokai T.; Matsuzaki H.; Furube A.; Tokumaru K.; Tsutsui T.; Nakanotani H.; Yahiro M.; Adachi C. 58–2: Revealing the Excited-State Dynamics of Thermally Activated Delayed Flourescence Molecules by Using Transient Absorption Spectrospy. Dig. Tech. Pap. - Soc. Inf. Disp. Int. Symp. 2016, 47 (1), 786–789. 10.1002/sdtp.10790. [DOI] [Google Scholar]
  25. Wang S.; Chervy T.; George J.; Hutchison J. A.; Genet C.; Ebbesen T. W. Quantum Yield of Polariton Emission from Hybrid Light–Matter States. J. Phys. Chem. Lett. 2014, 5 (8), 1433–1439. 10.1021/jz5004439. [DOI] [PubMed] [Google Scholar]
  26. Wang H.; Wang H.; Sun H.; Cerea A.; Toma A.; Angelis F.; Jin X.; Razzari L.; Cojoc D.; Catone D.; Huang F.; Proietti Zaccaria R. Dynamics of Strongly Coupled Hybrid States by Transient Absorption Spectroscopy. Adv. Funct. Mater. 2018, 28 (48), 1801761. 10.1002/adfm.201801761. [DOI] [Google Scholar]
  27. Agranovich V. M.; Litinskaia M.; Lidzey D. G. Cavity Polaritons in Microcavities Containing Disordered Organic Semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 67 (8), 085311. 10.1103/PhysRevB.67.085311. [DOI] [Google Scholar]
  28. Xiang B.; Ribeiro R. F.; Dunkelberger A. D.; Wang J.; Li Y.; Simpkins B. S.; Owrutsky J. C.; Yuen-Zhou J.; Xiong W. Two-Dimensional Infrared Spectroscopy of Vibrational Polaritons. Proc. Natl. Acad. Sci. U. S. A. 2018, 115 (19), 4845–4850. 10.1073/pnas.1722063115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Snellenburg J. J.; Laptenok S. P.; Seger R.; Mullen K. M.; Stokkum I. H. M. v.. Glotaran: A Java -Based Graphical User Interface for the R Package TIMP. J. Stat. Soft. 2012, 49 ( (3), ). 10.18637/jss.v049.i03. [DOI] [Google Scholar]
  30. F. Ribeiro R.; Dunkelberger A. D.; Xiang B.; Xiong W.; Simpkins B. S.; Owrutsky J. C.; Yuen-Zhou J. Theory for Nonlinear Spectroscopy of Vibrational Polaritons. J. Phys. Chem. Lett. 2018, 9 (13), 3766–3771. 10.1021/acs.jpclett.8b01176. [DOI] [PubMed] [Google Scholar]
  31. Schäfer W.; Kim D. S.; Shah J.; Damen T. C.; Cunningham J. E.; Goossen K. W.; Pfeiffer L. N.; Köhler K. Femtosecond Coherent Fields Induced by Many-Particle Correlations in Transient Four-Wave Mixing. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 53 (24), 16429–16443. 10.1103/PhysRevB.53.16429. [DOI] [PubMed] [Google Scholar]
  32. Salvador M. R.; Sreekumari Nair P.; Cho M.; Scholes G. D. Interaction between Excitons Determines the Non-Linear Response of Nanocrystals. Chem. Phys. 2008, 350 (1–3), 56–681. 10.1016/j.chemphys.2007.12.020. [DOI] [Google Scholar]
  33. Tavis M.; Cummings F. W. Exact Solution for an N -Molecule—Radiation-Field Hamiltonian. Phys. Rev. 1968, 170 (2), 379–384. 10.1103/PhysRev.170.379. [DOI] [Google Scholar]
  34. Garraway B. M. The Dicke Model in Quantum Optics: Dicke Model Revisited. Philos. Trans. R. Soc., A 2011, 369 (1939), 1137–1155. 10.1098/rsta.2010.0333. [DOI] [PubMed] [Google Scholar]
  35. Chemla D. S.; Shah J. Many-Body and Correlation Effects in Semiconductors. Nature 2001, 411 (6837), 549–557. 10.1038/35079000. [DOI] [PubMed] [Google Scholar]
  36. Binder R.; Koch S. W. Nonequilibrium Semiconductor Dynamics. Prog. Quantum Electron. 1995, 19 (4–5), 307–462. 10.1016/0079-6727(95)00001-S. [DOI] [Google Scholar]
  37. Schäfer W.; Wegener M.. Semiconductor Optics and Transport Phenomena; Springer: Berlin, London, 2011. [Google Scholar]
  38. Virgili T.; Coles D.; Adawi A. M.; Clark C.; Michetti P.; Rajendran S. K.; Brida D.; Polli D.; Cerullo G.; Lidzey D. G. Ultrafast Polariton Relaxation Dynamics in an Organic Semiconductor Microcavity. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83 (24), 245309. 10.1103/PhysRevB.83.245309. [DOI] [Google Scholar]
  39. Franco I.; Spanner M.; Brumer P. Quantum Interferences and Their Classical Limit in Laser Driven Coherent Control Scenarios. Chem. Phys. 2010, 370 (1–3), 143–150. 10.1016/j.chemphys.2010.02.016. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz0c00247_si_001.pdf (860.6KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES