Abstract
Cs2AgBiBr6 is a promising metal halide double perovskite offering the possibility of efficient photovoltaic devices based on lead-free materials. Here, we report on the evolution of photoexcited charge carriers in Cs2AgBiBr6 using a combination of temperature-dependent photoluminescence, absorption and optical pump–terahertz probe spectroscopy. We observe rapid decays in terahertz photoconductivity transients that reveal an ultrafast, barrier-free localization of free carriers on the time scale of 1.0 ps to an intrinsic small polaronic state. While the initially photogenerated delocalized charge carriers show bandlike transport, the self-trapped, small polaronic state exhibits temperature-activated mobilities, allowing the mobilities of both to still exceed 1 cm2 V–1 s–1 at room temperature. Self-trapped charge carriers subsequently diffuse to color centers, causing broad emission that is strongly red-shifted from a direct band edge whose band gap and associated exciton binding energy shrink with increasing temperature in a correlated manner. Overall, our observations suggest that strong electron–phonon coupling in this material induces rapid charge-carrier localization.
Metal halide perovskite materials have achieved remarkable success as photovoltaic active layers over the past decade,1,2 with the record power conversion efficiency (PCE) of perovskite solar cells now exceeding 25%.3 This success has resulted from the excellent optoelectronic properties of these materials, including their strong absorption across the visible spectrum and high charge-carrier mobilities.1,4 The presence of toxic lead in a readily water-soluble form in the principal perovskite photovoltaic materials, such as methylammonium lead triiodide (MAPbI3, MA = CH3NH3), is however a concern from a health and environmental perspective.5 Although attempts at homovalent replacement of the lead cation (Pb2+) by Ge2+ or Sn2+ have suffered from instability against oxidation,6 heterovalent substitution by monovalent and trivalent cations offers a larger compositional space of possible materials.7 Perhaps the most prominent6 of the resultant family of double perovskite materials is Cs2AgBiBr6, the extensive study of which has resulted in its successful fabrication in the form of single crystals,8,9 nanocrystals,10 and thin films through both solution-processing and vapor-deposition routes.11,12 Cs2AgBiBr6 has demonstrated a better thermodynamic stability than MAPbI3,10 but power conversion efficiencies in solar cells based on the former lag behind, having reached only 2.84% at best.13 The indirect band gap of this material is a hindrance to its photovoltaic performance,14 since the large film thicknesses thus required to substantially improve photocurrent generation would also necessitate very long charge-carrier diffusion lengths: of the order of tens of micrometers rather than the current tens of nanometers.12 Nonetheless, Cs2AgBiBr6 also possesses more positive optoelectronic properties for photovoltaic purposes, such as a long-lived component to the charge-carrier lifetime9,15,16 and a band gap that is relatively narrow for a double perovskite, being in the visible range.6 This material has also shown promise as a photocatalyst,17 in photodetectors,18 and in X-ray detectors.19,20
Understanding the nature of the coupling between the lattice and the charge carriers in Cs2AgBiBr6, and its influence on charge-carrier dynamics, is crucial for the optimization of this material in a variety of optoelectronic applications and to further the understanding of a wide range of related silver–bismuth–halide semiconducting materials.21,22 Such electron–phonon coupling may limit the charge-carrier mobility of a material, as is the case for MAPbI3.1,23 Because the electron–phonon coupling in Cs2AgBiBr6 is even stronger than in MAPbI3,24−26 it may potentially cause self-trapping of charge carriers. The phenomenon of self-trapping occurs when the local lattice distortion caused by a photoexcited charge carrier is sufficiently strong that the charge carrier rapidly relaxes into the energetic state associated with this local deformation,27 such that its localization length may approach the length of a single unit cell of the lattice.28 Self-trapping of charge carriers has been reported in related materials, whether for electrons in CsPbI329 or for holes in CsPbBr3,30 in other bismuth-based materials such as Rb4Ag2BiBr931 and Cs3Bi2Br9,32 and layered metal halide perovskites.33 For Cs2AgBiBr6, the proposed self-trapping34 has also been synonymously35 described as the formation of small polarons24 or color centers,25 with broad photoluminescence (PL) emission25,34 and low charge-carrier mobility24 attributed to its occurrence. The mobility of charge carriers has however alternatively been interpreted in terms of large polarons,26 which are shallow bound states of charge carriers associated with a lattice distortion extended over tens to hundreds of unit cells and result from weaker electron–phonon coupling.28,36 Proponents of this interpretation argue that the energetic barrier37 to small polaron formation in three-dimensional materials is too great.26,37 However, Cs2AgBiBr6 has in fact been described as having 0D electronic dimensionality because of the spatial isolation between the [AgBr6]5– and [BiBr6]3– octahedra that respectively determine its valence band maximum and conduction band minimum,21,22,38,39 which causes localization of photoexcited charge carriers24,38 and consequently high charge-carrier effective masses and low mobilities.22 Thus, in Cs2AgBiBr6 the existence of charge-carrier self-trapping to form small polarons remains a plausible proposal, but one that has not yet been either convincingly proven or directly observed.
In this work, we investigate the optoelectronic properties of Cs2AgBiBr6 and report the direct observation of ultrafast charge-carrier self-localization from an initially highly mobile delocalized state to a self-trapped, small polaronic state, which ultimately diffuses to an emitting color center. Through a combination of temperature-dependent PL and absorption spectroscopy, we can identify the electronic states occupied before and after localization and characterize their relation to the direct and indirect gap transitions in this material. The localization of charge carriers with time is directly traced by using PL upconversion spectroscopy and optical pump terahertz probe (OPTP) measurements, and we interpret its influence on the charge-carrier mobility in terms of a quantitative model that allows us to identify a temperature-invariant localization rate of 0.99 ps–1. We therefore conclude that the electron–phonon coupling in this material is sufficiently strong to lead to the formation of intrinsically self-trapped charge carriers and consider the consequent implications on the application of Cs2AgBiBr6 and other double perovskites in photovoltaic and other optoelectronic devices.
To explore the nature of the electronic states in Cs2AgBiBr6, we first measured the temperature dependence of the absorption and PL spectra of vapor-deposited thin films of this material between 4 and 295 K (see sections 1 and 2 of the Supporting Information for details of the sample fabrication and experimental setup). The spectra measured at 4 and 295 K are shown in Figures 1a and 1b, respectively. At room temperature, the PL spectrum peaks at 1.95 eV, in line with previous studies.9,24,25,40 Cs2AgBiBr6 has been reported to be an indirect band gap semiconductor,6,8,25,41 and this PL emission has in the past been assigned to phonon-assisted recombination across the indirect band gap;8,9,24,41 however, more recent PL excitation measurements have indicated that it may instead result from spatially localized color centers.25 Meanwhile, previous calculations38,41−44 and experimental measurements8−10,12,16,24,25,34,40,44,45 have reported the room temperature indirect gap to lie in the range 1.79–2.25 eV. This range is also consistent with the value of 1.9 eV obtained by our quadratic fit to the absorption spectrum at energies below the direct gap, as detailed in section 3.1 of the Supporting Information. The temperature dependence of the PL spectrum is shown in Figure 1c, while that of its peak energy is compared with the indirect gap energy in Figure 2b. The position of the PL peak at energies above the indirect gap energy, and their opposite trends in energy shifts with temperature, suggests that the PL does not originate from a band-to-band transition across the indirect gap but is rather linked to a different transition, albeit with a similar energy, involving bound excitons localized at a color center.25,42 A bound exciton refers to a Coulombically bound electron–hole pair which is localized to a particular point on the lattice. The ≈20 meV red-shift of the PL peak between 4 and 295 K may result from the enhanced relaxation of charge carriers between color-center states, whose energetic spread is indicated by the red-shift. At higher temperatures, more thermal energy is available for the charge carriers to activate over the energetic barriers between these states, which could allow them to reach deeper color centers before recombining.46
Figure 1.
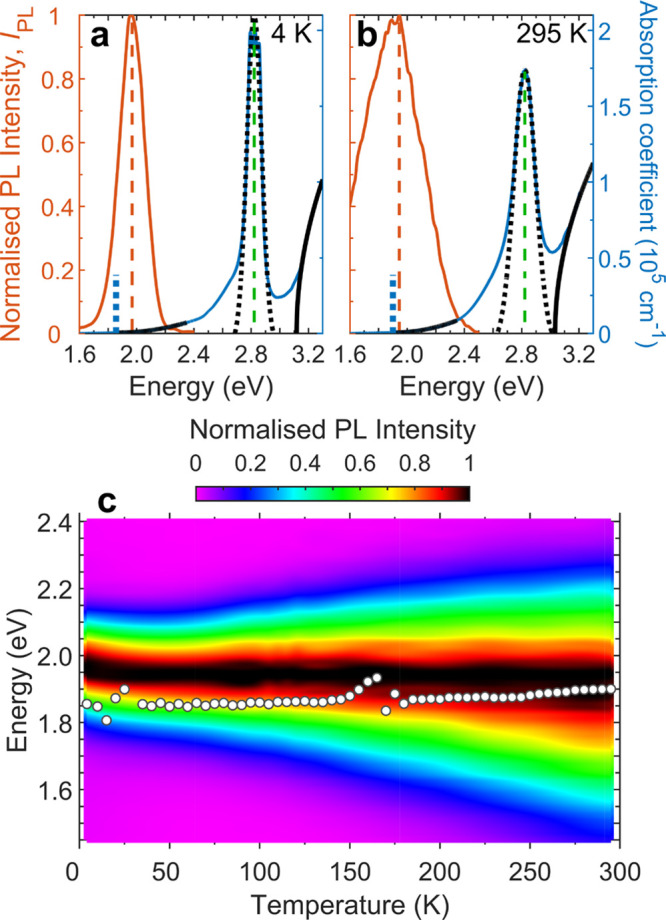
Temperature-dependent absorption and PL spectra of Cs2AgBiBr6. (a) Steady-state PL (solid red line) and absorption spectra (solid blue line) at 4 K as a function of photon energy for a Cs2AgBiBr6 thin film. A Gaussian fit to the excitonic absorption peak at around 2.8 eV is plotted as a dotted black line, with its central energy corresponding to the dashed green line. The dashed red line indicates the energy at the maximum PL intensity. Quadratic and square-root fits to the lower-energy indirect absorption onset and higher-energy direct absorption onset respectively are plotted as solid black lines. Close-up views of the absorption spectrum in the regions of the fits are shown in Figure S1. The dotted blue line indicates Egi, which provides an estimate of the indirect band gap energy from the quadratic fit. (b) Corresponding spectra and fits at 295 K. (c) Color plot of the normalized PL spectra at temperatures between 4 and 295 K. The white circles show Egi as a function of temperature.
Figure 2.
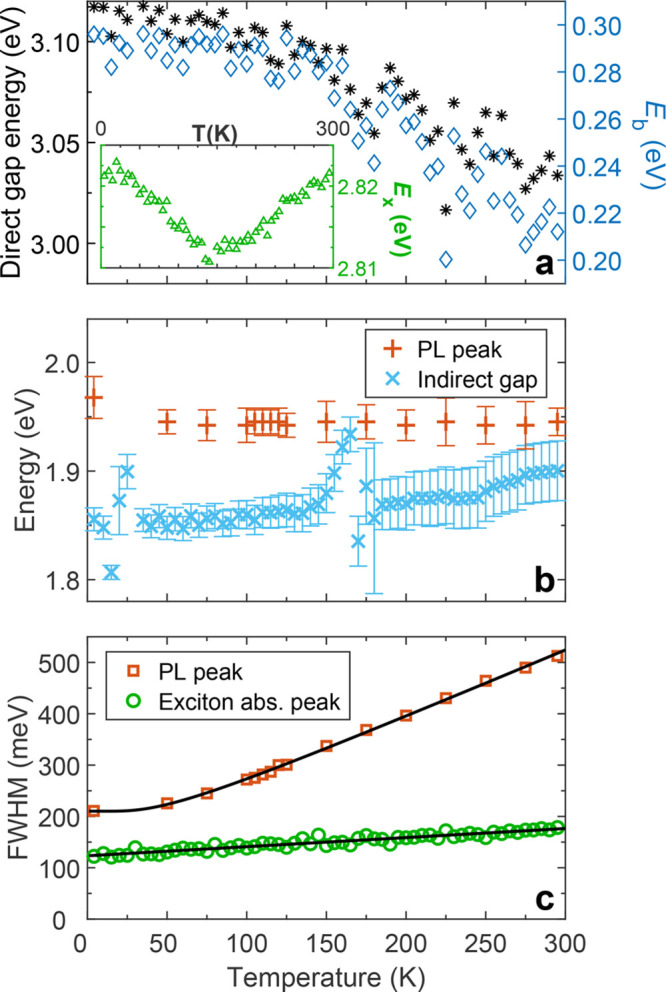
Temperature-dependence of transition energies and peak widths of Cs2AgBiBr6. (a) Direct band gap energy (black asterisks, left axis) and direct exciton binding energy (Eb, blue diamonds, right axis) of Cs2AgBiBr6 as a function of temperature, as obtained from fits to absorption spectra. The inset shows the temperature dependence of the direct exciton energy (Ex, green triangles), obtained from Gaussian fits to the peak evident in absorption spectra. (b) Temperature dependence of the peak of the PL spectra (red plus signs) and the indirect band gap energy (light blue crosses) as determined from the absorption spectra. (c) Temperature-dependent line width (full width at half-maximum, FWHM) of the PL peak (red squares) and excitonic absorption peak (green circles). The solid black lines are fits that account for Fröhlich coupling with LO phonons, as described in the main text.
The absorption spectra in Figures 1a and 1b are dominated by a strongly absorbing feature at ∼2.8 eV, which has usually been described as an excitonic peak,9,25,34,47 although alternative explanations have attributed it to one or more transitions between atomic orbitals either within the Bi3+ ion or involving the Ag+ ion as well.10,48,49 Attributing an excitonic nature to the absorption peak has faced contentions that the resultant exciton line width and binding energy values are too large for what should be expected of Cs2AgBiBr6.48,49 However, the resonance in the reflectance spectrum of Cs2AgBiBr6 at 2.8 eV is characteristic of a band-edge, free-exciton absorption,9,25 while Kentsch et al.34 noted that similar excitonic absorption features are common features of bismuth-containing perovskites and their relatives and found evidence from Raman and transient absorption spectroscopy for a considerable excitonic contribution to the feature in Cs2AgBiBr6. Furthermore, Palummo et al.42 were able to ascribe the absorption peak to a bound direct exciton using ab initio methods, noting that the large exciton binding energy compared to MAPbI3 could be explained by the reduced ionic contribution to dielectric screening in Cs2AgBiBr6. Dey et al.50 also attribute this peak to a bound exciton, whereas Lv et al.51 attribute it to a free exciton, i.e., a Coulombically bound electron–hole pair which may move freely throughout the lattice. A further objection to describing the absorption peak as excitonic is based on the apparent invariance of its energy with temperature,10,48 which would not be expected behavior for an excitonic emission that would normally shift with temperature according to the band gap trend. However, as we reveal below, the absorption peak energy actually varies slightly with temperature, but with the magnitude of the shift being reduced because the associated exciton binding energy shifts with temperature in close correlation with the direct band gap energy. We therefore consider this absorption feature to be an excitonic peak and fit it with a Gaussian function to parametrize its central energy and line width.
The temperature dependence of the excitonic absorption peak line width is compared with that of the PL peak in Figure 2c, in which both data sets are quantitatively assessed by using the function23 Γ(T) = Γ0 + ΓLO, where ΓLO = γLO/(eELO/kBT – 1) , which is commonly employed to describe the temperature dependence of the PL or absorption line width. Here, Γ0 is a temperature-independent inhomogeneous scattering term arising from disorder and imperfections, whereas the temperature-dependent homogeneous scattering from longitudinal optical (LO) phonons via the Fröhlich interaction contributes with charge-carrier coupling strength γLO for a representative LO phonon energy ELO.52 Fits of Γ(T) (solid black lines in Figure 2c) to the excitonic absorption and PL peak line widths describe the data well, resulting in output parameters of Γ0 = 123 meV, γLO = 0.12 meV, and ELO = 0.06 meV for the excitonic peak and Γ0 = 210 meV, γLO = 175 meV, and ELO = 11.5 meV for the PL peak. Even without accounting for the acoustic phonon contribution to homogeneous scattering, it is clear that the PL peak broadens much more with temperature than does the direct gap excitonic peak, perhaps indicative of a stronger coupling to the lattice by the self-trapped state responsible for the former compared with the direct excitons responsible for the latter. The LO phonon coupling strength and energy obtained from the PL peak are comparable to those previously reported,24 with the coupling strength several times that of MAPbI3 (for which γLO = 40 meV),23 in agreement with the strong electron–phonon coupling that has been attributed to Cs2AgBiBr624−26 and which is likely to be responsible for the self-localization of the excitons therein.
Figure 2a shows the temperature dependence of the direct gap Eg, obtained from a square-root fit to the absorption spectrum as detailed in section 3.1 of the Supporting Information. The direct gap energy red-shifts from 3.12 to 3.03 eV between 4 and 295 K, which is unlike the corresponding blue-shift of the direct gap in MAPbI3 but is, however, in accordance with the typical behavior of semiconductors such as Si, Ge, and GaAs.53 Tauc plots to absorption spectra have often underestimated the room-temperature direct gap of Cs2AgBiBr6 by several hundred millielectronvolts8,24,54 by placing it between 2.2 and 2.41 eV, possibly as a result of mistaking the excitonic peak for the direct gap onset. There have nonetheless also been reports placing the direct gap energy in the range 2.85–3.20 eV at 295 K,9,34,48 which is consistent with our measured value. The direct exciton binding energy Eb is also plotted in Figure 2a, obtained by subtracting the central energy of the Gaussian fit to the excitonic absorption peak (plotted in the inset to Figure 2a) from the direct gap energy. In section 3.2 of the Supporting Information we alternatively apply a fit based on Elliott’s theory55 to the direct gap onset to obtain Eb by a more sophisticated method but find that the overlap between the excitonic and continuum contributions to the absorption is sufficiently small that our original approach of obtaining the excitonic and direct gap energies separately is in excellent agreement with the Elliott fitting approach. We find that Eb also decreases as the temperature increases from 4 to 295 K, reaching 210 meV at room temperature, which is slightly smaller than previous estimates that have placed it between 268 and 340 meV.34,42 As mentioned above, such values of Eb are relatively large compared to MAPbI3 (for which Eb ∼ 10 meV4,56) but are typical for similar bismuth-based materials.34 We note that the prominence of the direct excitonic absorption peak at room temperature in Cs2AgBiBr6 compared to MAPbI3 can be attributed to the much larger value of Eb for the former. The apparent positive correlation between the temperature dependences of Eb and the direct gap energy in Cs2AgBiBr6 is an example of a relationship that has been empirically shown to hold more generally for 3D semiconductors.57,58 Such a correlation ultimately derives from both band gap energies and exciton binding energies being dependent on factors such as effective charge-carrier masses and values of the dielectric function, which may vary for example with material composition or temperature. We note that unlike Eb, the excitonic absorption peak energy (Ex = Eg – Eb, plotted in the inset to Figure 2a) shows only minor changes with temperature, of the order of 10 meV, largely because the temperature dependences of Eg and Eb almost completely cancel. However, within these minor shifts the excitonic absorption peak energy Ex is seen to undergo a reversal in its temperature trend at around 130 K, roughly corresponding to the phase transition between the low-temperature tetragonal phase and the high-temperature cubic phase.9 These changes in excitonic peak position Ex around the phase transition may result from a corresponding shift in the dielectric constant9 affecting the band gap and exciton binding energy to a slightly different extent. In any case, the observed positive correlation between the exciton binding energy Eb and the direct gap energy supports our interpretation that the prominent absorption peak arises from a direct exciton.
Having established the nature of the electronic states in Cs2AgBiBr6, we investigated the charge-carrier dynamics and mobility therein. Figure 3a shows temperature-dependent OPTP photoconductivity transients (plotted as the photoinduced transmission change −ΔT/T ) measured out to 40 ps after excitation, under the experimental conditions detailed in section 2.4 of the Supporting Information. The sample was excited at 400 nm (3.1 eV), which corresponds to a transition above the direct band gap. As shown in section 5.3 of the Supporting Information, the photoconductivity spectra across the measured energy range (0.5–10 meV) are Drude-like, in accordance with the presence of free charge carriers. The photon-to-charge branching ratio is thus likely to be close to 1, though we cannot rule out the formation of free excitons by the initial excitation. As discussed in section 5.3 of the Supporting Information, the high Eb of this material means that any intraexcitonic transitions would in any case be too large to be probed by our OPTP spectroscopy.
Figure 3.
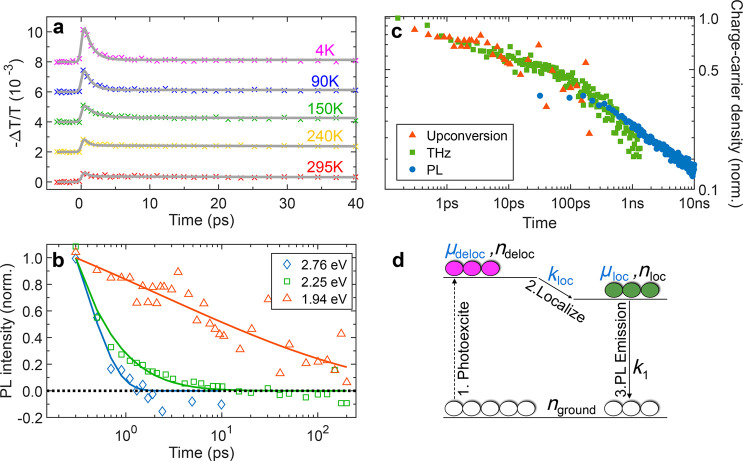
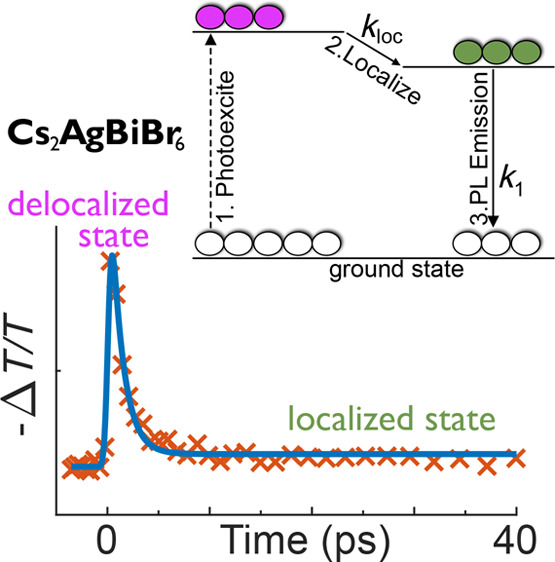
Dynamics of charge-carrier localization in Cs2AgBiBr6. (a) OPTP photoconductivity transients for a Cs2AgBiBr6 thin film, measured at the temperatures shown in the legend under an excitation fluence of 10.1 μ J cm–2. For clarity, transients at successively decreasing temperatures are offset vertically by 2 × 10–3. The gray lines depict fits based on a two-level charge-carrier mobility model, as described in the main text. (b) Room-temperature normalized PL upconversion transients measured at 2.76 eV (blue diamonds), 2.25 eV (green squares), and 1.94 eV (red triangles). The solid lines are stretched exponential fits to the transients (empty markers) of the corresponding colors. The dotted black line indicates zero intensity; negative intensities are an artifact of background subtraction. (c) Time dependence of charge-carrier density, n, after photoexcitation, as derived from OPTP photoconductivity (green squares), PL upconversion (red triangles), and TCSPC (blue circles) measurements. The latter two transients are scaled to line up with the terahertz transient, which is normalized at its maximum intensity point. (d) Schematic of the two-level mobility model used to fit the OPTP decays in (a). The fixed parameters are shown in black, while parameters that are fitted and extracted from the model are shown in blue. After being initially photoexcited to the delocalized state (pink), the charge carriers localize to the localized state (green) before recombining.
A fast decay component is evident in all the photoconductivity transients, though more prominent at lower temperatures, followed by a long-lived decay. Such behavior is qualitatively consistent with the fast localization of charge carriers from an initial state with high mobility (reflected in the value of −ΔT/T at the peak of the transient) to a state whose lower mobility is indicated by the lower value of −ΔT/T on longer time scales. Localization is also evident in Figure 3b, in which room-temperature ultrafast PL transients measured at emission wavelengths of 2.76, 2.25, and 1.94 eV (using PL upconversion59−61 as described in section 2.5 of the Supporting Information) are plotted, following the charge carriers as they rapidly shift downward in energy over subpicosecond time scales to progressively longer-lived states: the transients for the three excitation energies were phenomenologically parametrized by average lifetimes of 0.34, 0.65, and 340 ps, respectively, obtained by fitting stretched exponential functions. The short-lived, high-energy PL transient measured at 2.76 eV corresponds to the direct exciton state identified in the absorption spectrum shown in Figure 1b, while the longer-lived, low-energy transient measured at 1.94 eV results from the principal PL emission also plotted in that figure and which was attributed to a color center.25 Meanwhile, the transient measured at 2.25 eV captures the emission from excitons at an intermediate stage between the direct exciton and color center states. Because PL derives from the bimolecular recombination of free carriers, or the recombination of excitons formed in bimolecular fashion from free carriers, its intensity is directly proportional to n2, whereas the −ΔT/T in OPTP transients is directly proportional to n. By plotting the normalized charge-carrier densities, n, derived from the 1.94 eV PL upconversion transient and the 295 K OPTP transient on the same graph (Figure 3c), their overlap demonstrates that the charge-carrier behavior captured by the two techniques is consistent, with the recombination of the charge carriers at the principal PL peak48 driving the decay in the total charge-carrier density measured by OPTP spectroscopy, once the initial localization has taken place. Using PL measured at 1.95 eV by time-correlated single photon counting (TCSPC), the time dependence of n is extended to later times, though this technique lacks the time resolution to capture the initial fast localization of charge carriers. The temperature-dependent dynamics of the TCSPC transients are presented in section 4 of the Supporting Information, extending to much longer time scales than the PL upconversion transients and thus providing more meaningful estimates of the PL lifetime. Although charge-carrier dynamics in metal halide perovskites often depend on how the sample was processed,62 the shape of these transients is in fact similar to those measured for single crystals of Cs2AgBiBr6,9,40 which suggests that charge-carrier recombination in this material is dominated by intrinsic factors. In combination, the three measurement techniques follow the charge carriers as they localize over ultrafast time scales from an incipient delocalized state to more localized states that are downshifted in energy.
To quantitatively interpret the OPTP terahertz photoconductivity transients in Figure 3a in terms of localization of charge carriers upon transitioning from one state to another, we developed a simple two-level model of the early time charge-carrier dynamics (depicted in Figure 3d and described in detail in section 5.1 of the Supporting Information) which was used to fit the transients. In brief, the model allows for two excited states of the charge carriers: a delocalized state associated with a high mobility, μdeloc, and a localized state associated with a low mobility, μloc. Photoexcitation occurs into the delocalized state, from which charge carriers may localize at rate kloc to the localized state. The initial delocalized state determines the initial terahertz photoconductivity response, while its ultrafast emission was evident in the PL upconversion transient measured at 2.76 eV in Figure 3b. Charge carriers in the localized state then diffuse to color centers and recombine to the ground state with recombination rate k1, producing the PL peak which we observed in Figure 1c and the TCSPC transients in Figure S3, the lifetimes of which we used to estimate k1. By assuming that only these transitions between states are permitted, we can describe the time evolution of the charge-carrier density in each state in terms of the aforementioned rate constants and hence relate these densities to the measured −ΔT/T in the OPTP transients via the sheet conductivity, which is given by
| 1 |
We find that the early time charge-carrier dynamics of Cs2AgBiBr6 can indeed be well-described by a two-state localization model, as evidenced by the good fits of the resultant model function to the OPTP transients in Figure 3a. Such fits to the temperature-dependent transients yield the corresponding localization rate and charge-carrier mobilities, which are respectively plotted in Figures 4a and 4b. At low temperatures, the transients rapidly decay almost to zero as the localized state becomes populated, indicating that its mobility (≈ 0.5 cm2 V–1 s–1) is far lower than the charge-carrier mobility of the initial delocalized state (≈ 12 cm2 V–1 s–1). In contrast, the high-temperature transients do not drop as sharply, possessing a long tail which indicates an increased charge-carrier mobility (≈ 1.3 cm2 V–1 s–1 at 295 K) of the localized state at higher temperatures, approaching that of the delocalized state (≈ 3 cm2 V–1 s–1 at 295 K). It is thus apparent that the difference between the mobilities of the delocalized and localized states becomes smaller with increasing temperature, as quantified in Figure 4b, which shows the mobilities obtained from the two-state model. Notably, the localization rate seems largely temperature-independent, with a mean value of kloc = 0.99 ± 0.43 ps–1 across all temperatures, suggesting that the process is barrier-free rather than temperature-activated. In contrast, the mobilities of both states vary with temperature, with that of the delocalized state decreasing at higher temperatures, while the localized state mobility exhibits the opposite trend. These trends may be quantified by fitting a power-law dependence, μ ∝ Tp to the data, yielding exponents of p = −0.47 ± 0.13 for μdeloc and p = 0.64 ± 0.32 for μloc. For the delocalized state, we neglect the two lowest temperature data points, since the power-law model diverges unphysically in this region.63 The temperature dependence of charge-carrier mobility is strongly influenced by the type of lattice coupling or scattering experienced by charge carriers, with potentially multiple contributions involved.64,65 As discussed further below, the negative exponent for μdeloc clearly suggests bandlike transport as expected for delocalized charge carriers, while the positive exponent for μloc is commensurate with the temperature-activated hopping transport associated with localized, self-trapped states.66
Figure 4.
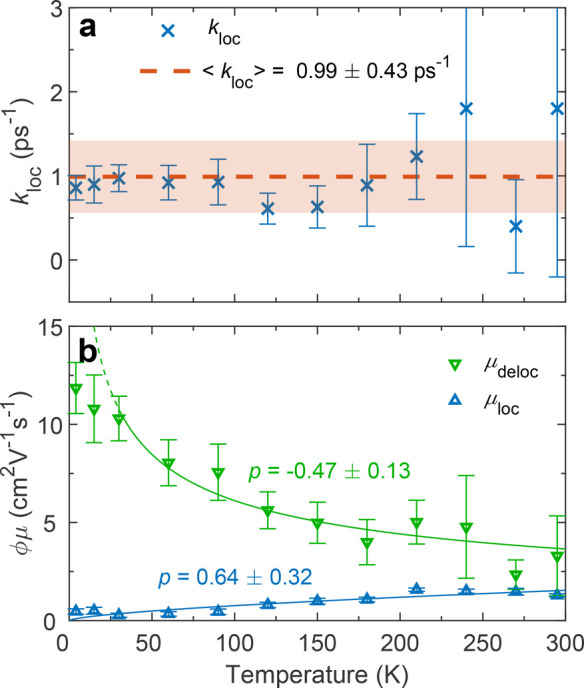
Charge-carrier mobility changes indicative of excited-state localization. (a) Temperature dependence of the localization rate (kloc, blue crosses) within the two-state mobility model for Cs2AgBiBr6. The red dashed line indicates the mean value, with its uncertainty represented by the red shaded area. (b) Temperature dependence of the effective charge-carrier mobilities associated with the delocalized (μdeloc, green) and localized (μloc, blue) states. Power-law fits are plotted as solid lines in the corresponding colors, with their exponents (p) displayed alongside. The data points for μdeloc at the lowest two temperatures were not included in the fit as the power-law model becomes unphysical in this region, indicated by the dashed green line. The mobilities are “effective” since the photon-to-charge branching ratio, ϕ, is not necessarily 1.
Overall, our detailed investigation based on multiple complementary techniques and across a wide temperature range allows us to provide a holistic explanation of the electronic states and charge-carrier dynamics in Cs2AgBiBr6. Our analysis of the OPTP transients strongly supports the notion that a fast charge-carrier localization process exists in this material, through which charge carriers transition from an initially excited delocalized state to a subsequent self-trapped state. The mobility of the initial delocalized state varies with temperature according to a power law with p = −0.47, an exponent which is not as negative as that commonly measured for MAPbI3,62 but whose sign is still indicative of bandlike transport limited by phonon scattering.63,67 We associate this state with the direct band gap (of 3.03 eV at 295 K) observed in the absorption spectra. From the OPTP transients, we detected a lower-energy state to which the charge-carriers relax, whose mobility varies with a positive exponent, p = 0.64, which is highly indicative of the temperature-activated hopping transport typical of localized charge carriers.68,69 The low energetic barrier to the formation of this localized state (indicated by the temperature invariance of the localization rate) is consistent with the formation of intrinsically self-trapped excitons, which have also been observed to form in a quasi-barrierless manner in 2D metal halide perovskites.70 We thus propose that this localized state is a self-trapped or small polaronic state, formed through an intrinsic process involving relaxation of the lattice around the excited state, rather than mediated by defects, given that localization is ultrafast and temperature-independent. This picture is consistent with the strong electron–phonon coupling we observe in Cs2AgBiBr6. This self-trapped state is clearly still mobile, but its motion is akin to that of a small polaron, which carries significant lattice distortion with it and therefore has a temperature-activated mobility.
We note that the self-trapped state we observe to form on a picosecond time scale is unlikely to be the final state leading to the principal emission observed from Cs2AgBiBr6 near 1.95 eV at room temperature. As discussed above, we confirm that the lack of correlation between the temperature dependence of this PL peak with the lower-energy indirect band gap means that the PL emission does not result from band-to-band transitions across the indirect gap but rather from a color center. Such color-center emission is also consistent with our observations of strong electron–phonon coupling in the temperature-dependent PL broadening of Cs2AgBiBr6 and a large energetic shift of the PL peak from the direct gap. However, the ultrafast initial localization step we observe in the photoconductivity transients is unlikely to be associated with the trapping of charge carriers at color centers, for the following reasons. First, the self-trapped state still has a respectable associated mobility of ≈1.3 cm2 V–1 s–1 at 295 K, which cannot originate from color centers that trap charge carriers relatively tightly.27 Second, the relaxation to the self-trapped state is ultrafast, meaning that the density of color centers would have to be incredibly high, which is unlikely given that our Cs2AgBiBr6 thin films are highly crystalline.12 Finally, the relaxation rate is also temperature-independent, which is inconsistent with diffusion of charge carriers to color centers.
Altogether, we report evidence for ultrafast localization of charge carriers in the Cs2AgBiBr6 double perovskite. We observed rapid decays in OPTP transients, which we were able to interpret in terms of a two-state model involving relaxation of free carriers to a localized state on the time scale of 1.0 ps. By combining temperature-dependent PL and absorption measurements, we were able to interpret the localized state as intrinsically self-trapped, or small polaronic, in nature. Such self-trapped charge carriers subsequently diffuse to color centers that account for the broad and strongly red-shifted emission. Because this material is the flag bearer for its class, developing our understanding of its electronic transitions and charge-carrier dynamics is helpful in guiding the search for better such materials or optimizing Cs2AgBiBr6 for such applications as in solar cells or X-ray detectors. The finding of intrinsic self-trapping of charge carriers in this material may intuitively suggest that Cs2AgBiBr6 is not an ideal material to choose for optoelectronic devices that rely on high charge-carrier mobilities, even if all defects were eliminated. However, we note that such self-trapping is less severe at room temperature because temperature-activated hopping processes lead to a relatively benign reduction in charge-carrier mobility, with the mobilities of both delocalized and localized states exceeding a respectable 1 cm2 V–1 s–1. Thus, while intrinsic self-trapping is clearly present in Cs2AgBiBr6, temperature activation of charge motion at room temperature still renders this material a promising candidate for lead-free photovoltaic applications. In addition, self-trapping effects may potentially be tuned through factors such as electronic dimensionality and composition,66 which opens up prospects of optimized material design through further computational simulation and optoelectronic characterization.
Acknowledgments
The authors thank the Engineering and Physical Sciences Research Council (EPSRC), UK, for financial support. L.R.V.B. thanks the Centre for Doctoral Training in New and Sustainable Photovoltaics and the Oxford-Radcliffe Scholarship for financial support. K.J.S. thanks the Rhodes Trust for financial support through a Rhodes Scholarship. L.M.H. thanks the Institute for Advanced Study at the Technical University of Munich for support through a Hans Fischer Senior Fellowship.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.1c00653.
Experimental details and sample fabrication methods, temperature-dependent photoluminescence transients, terahertz photoconductivity and dark conductivity spectra, details of fits to the absorption spectra and terahertz photoconductivity traces (PDF)
Author Present Address
G.L.: Department of Mathematics, Physics and Electrical Engineering, Northumbria University, Newcastle upon Tyne NE1 8ST, UK.
The authors declare no competing financial interest.
Supplementary Material
References
- Johnston M. B.; Herz L. M. Hybrid Perovskites for Photovoltaics: Charge-Carrier Recombination, Diffusion, and Radiative Efficiencies. Acc. Chem. Res. 2016, 49, 146–154. 10.1021/acs.accounts.5b00411. [DOI] [PubMed] [Google Scholar]
- Kojima A.; Teshima K.; Shirai Y.; Miyasaka T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
- Green M.; Dunlop E.; Hohl-Ebinger J.; Yoshita M.; Kopidakis N.; Hao X. Solar Cell Efficiency Tables (Version 57). Prog. Photovoltaics 2021, 29, 3–15. 10.1002/pip.3371. [DOI] [Google Scholar]
- Herz L. M. Charge-Carrier Dynamics in Organic-Inorganic Metal Halide Perovskites. Annu. Rev. Phys. Chem. 2016, 67, 65–89. 10.1146/annurev-physchem-040215-112222. [DOI] [PubMed] [Google Scholar]
- Meyer E.; Mutukwa D.; Zingwe N.; Taziwa R. Lead-Free Halide Double Perovskites: A Review of the Structural, Optical, and Stability Properties as Well as Their Viability to Replace Lead Halide Perovskites. Metals 2018, 8, 667. 10.3390/met8090667. [DOI] [Google Scholar]
- Xiao Z.; Song Z.; Yan Y. From Lead Halide Perovskites to Lead-Free Metal Halide Perovskites and Perovskite Derivatives. Adv. Mater. 2019, 31, 1803792. 10.1002/adma.201803792. [DOI] [PubMed] [Google Scholar]
- Filip M. R.; Giustino F. The Geometric Blueprint of Perovskites. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, 5397–5402. 10.1073/pnas.1719179115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slavney A. H.; Hu T.; Lindenberg A. M.; Karunadasa H. I. A Bismuth-Halide Double Perovskite with Long Carrier Recombination Lifetime for Photovoltaic Applications. J. Am. Chem. Soc. 2016, 138, 2138–2141. 10.1021/jacs.5b13294. [DOI] [PubMed] [Google Scholar]
- Schade L.; Wright A. D.; Johnson R. D.; Dollmann M.; Wenger B.; Nayak P. K.; Prabhakaran D.; Herz L. M.; Nicholas R.; Snaith H. J.; et al. Structural and Optical Properties of Cs2AgBiBr6 Double Perovskite. ACS Energy Lett. 2019, 4, 299–305. 10.1021/acsenergylett.8b02090. [DOI] [Google Scholar]
- Bekenstein Y.; Dahl J. C.; Huang J.; Osowiecki W. T.; Swabeck J. K.; Chan E. M.; Yang P.; Alivisatos A. P. The Making and Breaking of Lead-Free Double Perovskite Nanocrystals of Cesium Silver-Bismuth Halide Compositions. Nano Lett. 2018, 18, 3502–3508. 10.1021/acs.nanolett.8b00560. [DOI] [PubMed] [Google Scholar]
- Greul E.; Petrus M. L.; Binek A.; Docampo P.; Bein T. Highly Stable, Phase Pure Cs2AgBiBr6 Double Perovskite Thin Films for Optoelectronic Applications. J. Mater. Chem. A 2017, 5, 19972–19981. 10.1039/C7TA06816F. [DOI] [Google Scholar]
- Longo G.; Mahesh S.; Buizza L. R. V.; Wright A. D.; Ramadan A. J.; Abdi-Jalebi M.; Nayak P. K.; Herz L. M.; Snaith H. J. Understanding the Performance-Limiting Factors of Cs2AgBiBr6 Double-Perovskite Solar Cells. ACS Energy Lett. 2020, 5, 2200–2207. 10.1021/acsenergylett.0c01020. [DOI] [Google Scholar]
- Yang X.; Chen Y.; Liu P.; Xiang H.; Wang W.; Ran R.; Zhou W.; Shao Z. Simultaneous Power Conversion Efficiency and Stability Enhancement of Cs2AgBiBr6 Lead-Free Inorganic Perovskite Solar Cell Through Adopting a Multifunctional Dye Interlayer. Adv. Funct. Mater. 2020, 30, 2001557. 10.1002/adfm.202001557. [DOI] [Google Scholar]
- Chatterjee S.; Pal A. J. Influence of Metal Substitution on Hybrid Halide Perovskites: Towards Lead-Free Perovskite Solar Cells. J. Mater. Chem. A 2018, 6, 3793–3823. 10.1039/C7TA09943F. [DOI] [Google Scholar]
- Hoye R. L. Z.; Eyre L.; Wei F.; Brivio F.; Sadhanala A.; Sun S.; Li W.; Zhang K. H. L.; MacManus-Driscoll J. L.; Bristowe P. D.; et al. Fundamental Carrier Lifetime Exceeding 1 μs in Cs2AgBiBr6 Double Perovskite. Adv. Mater. Interfaces 2018, 5, 1800464. 10.1002/admi.201800464. [DOI] [Google Scholar]
- Bartesaghi D.; Slavney A. H.; Gélvez-Rueda M. C.; Connor B. A.; Grozema F. C.; Karunadasa H. I.; Savenije T. J. Charge Carrier Dynamics in Cs2AgBiBr6 Double Perovskite. J. Phys. Chem. C 2018, 122, 4809–4816. 10.1021/acs.jpcc.8b00572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z.; Liang Y.; Huang H.; Liu X.; Li Q.; Chen L.; Xu D. Stable and Highly Efficient Photocatalysis With Lead-Free Double-Perovskite of Cs2AgBiBr6. Angew. Chem., Int. Ed. 2019, 58, 7263–7267. 10.1002/anie.201900658. [DOI] [PubMed] [Google Scholar]
- Yang J.; Bao C.; Ning W.; Wu B.; Ji F.; Yan Z.; Tao Y.; Liu J. M.; Sum T. C.; Bai S.; et al. Stable, High-Sensitivity and Fast-Response Photodetectors Based on Lead-Free Cs2AgBiBr6 Double Perovskite Films. Adv. Opt. Mater. 2019, 7, 1801732. 10.1002/adom.201801732. [DOI] [Google Scholar]
- Pan W.; Wu H.; Luo J.; Deng Z.; Ge C.; Chen C.; Jiang X.; Yin W.-j. J.; Niu G.; Zhu L.; et al. Cs2AgBiBr6 Single-Crystal X-Ray Detectors With a Low Detection Limit. Nat. Photonics 2017, 11, 726–732. 10.1038/s41566-017-0012-4. [DOI] [Google Scholar]
- Zhang Z.; Chung C.-C.; Huang Z.; Vetter E.; Seyitliyev D.; Sun D.; Gundogdu K.; Castellano F. N.; Danilov E. O.; Yang G. Towards Radiation Detection Using Cs2AgBiBr6 Double Perovskite Single Crystals. Mater. Lett. 2020, 269, 127667. 10.1016/j.matlet.2020.127667. [DOI] [Google Scholar]
- Zhao X. G.; Yang D.; Ren J. C.; Sun Y.; Xiao Z.; Zhang L. Rational Design of Halide Double Perovskites for Optoelectronic Applications. Joule 2018, 2, 1662–1673. 10.1016/j.joule.2018.06.017. [DOI] [Google Scholar]
- Xiao Z.; Meng W.; Wang J.; Mitzi D. B.; Yan Y. Searching for Promising New Perovskite-Based Photovoltaic Absorbers: The Importance of Electronic Dimensionality. Mater. Horiz. 2017, 4, 206–216. 10.1039/C6MH00519E. [DOI] [Google Scholar]
- Wright A. D.; Verdi C.; Milot R. L.; Eperon G. E.; Pérez-Osorio M. A.; Snaith H. J.; Giustino F.; Johnston M. B.; Herz L. M. Electron–Phonon Coupling in Hybrid Lead Halide Perovskites. Nat. Commun. 2016, 7, 11755. 10.1038/ncomms11755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steele J. A.; Puech P.; Keshavarz M.; Yang R.; Banerjee S.; Debroye E.; Kim C. W.; Yuan H.; Heo N. H.; Vanacken J.; et al. Giant Electron-Phonon Coupling and Deep Conduction Band Resonance in Metal Halide Double Perovskite. ACS Nano 2018, 12, 8081–8090. 10.1021/acsnano.8b02936. [DOI] [PubMed] [Google Scholar]
- Zelewski S.; Urban J.; Surrente A.; Maude D. K.; Kuc A. B.; Schade L.; Johnson R. D.; Dollmann M.; Nayak P.; Snaith H.; et al. Revealing the Nature of Photoluminescence Emission in the Metal-Halide Double Perovskite Cs2AgBiBr6. J. Mater. Chem. C 2019, 7, 8350–8356. 10.1039/C9TC02402F. [DOI] [Google Scholar]
- Keshavarz M.; Debroye E.; Ottesen M.; Martin C.; Zhang H.; Fron E.; Küchler R.; Steele J. A.; Bremholm M.; Van de Vondel J.; et al. Tuning the Structural and Optoelectronic Properties of Cs2AgBiBr6 Double-Perovskite Single Crystals Through Alkali-Metal Substitution. Adv. Mater. 2020, 32, 2001878. 10.1002/adma.202001878. [DOI] [PubMed] [Google Scholar]
- Williams R. T.; Song K. S. The Self-Trapped Exciton. J. Phys. Chem. Solids 1990, 51, 679–716. 10.1016/0022-3697(90)90144-5. [DOI] [Google Scholar]
- Morrissey F. X.; Mance J. G.; Van Pelt A. D.; Dexheimer S. L. Femtosecond Dynamics of Exciton Localization: Self-Trapping From the Small to the Large Polaron Limit. J. Phys.: Condens. Matter 2013, 25, 144204. 10.1088/0953-8984/25/14/144204. [DOI] [PubMed] [Google Scholar]
- Neukirch A. J.; Nie W.; Blancon J.-C.; Appavoo K.; Tsai H.; Sfeir M. Y.; Katan C.; Pedesseau L.; Even J.; Crochet J. J.; et al. Polaron Stabilization by Cooperative Lattice Distortion and Cation Rotations in Hybrid Perovskite Materials. Nano Lett. 2016, 16, 3809–3816. 10.1021/acs.nanolett.6b01218. [DOI] [PubMed] [Google Scholar]
- Santomauro F. G.; Grilj J.; Mewes L.; Nedelcu G.; Yakunin S.; Rossi T.; Capano G.; Al Haddad A.; Budarz J.; Kinschel D.; et al. Localized Holes and Delocalized Electrons in Photoexcited Inorganic Perovskites: Watching Each Atomic Actor by Picosecond X-Ray Absorption Spectroscopy. Struct. Dyn. 2017, 4, 044002. 10.1063/1.4971999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma M.; Yangui A.; Whiteside V. R.; Sellers I. R.; Han D.; Chen S.; Du M.-H.; Saparov B. Rb4Ag2BiBr9: A Lead-Free Visible Light Absorbing Halide Semiconductor With Improved Stability. Inorg. Chem. 2019, 58, 4446–4455. 10.1021/acs.inorgchem.8b03623. [DOI] [PubMed] [Google Scholar]
- Liu C.; Wang Y.; Geng H.; Zhu T.; Ertekin E.; Gosztola D.; Yang S.; Huang J.; Yang B.; Han K.; et al. Asynchronous Photoexcited Electronic and Structural Relaxation in Lead-Free Perovskites. J. Am. Chem. Soc. 2019, 141, 13074–13080. 10.1021/jacs.9b04557. [DOI] [PubMed] [Google Scholar]
- Li J.; Wang H.; Li D. Self-Trapped Excitons in Two-Dimensional Perovskites. Front. Optoelectron. 2020, 13, 225–234. 10.1007/s12200-020-1051-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kentsch R.; Scholz M.; Horn J.; Schlettwein D.; Oum K.; Lenzer T. Exciton Dynamics and Electron-Phonon Coupling Affect the Photovoltaic Performance of the Cs2AgBiBr6 Double Perovskite. J. Phys. Chem. C 2018, 122, 25940–25947. 10.1021/acs.jpcc.8b09911. [DOI] [Google Scholar]
- Emin D.; Seager C. H.; Quinn R. K. Small-Polaron Hopping Motion in Some Chalcogenide Glasses. Phys. Rev. Lett. 1972, 28, 813–816. 10.1103/PhysRevLett.28.813. [DOI] [Google Scholar]
- Zheng F.; Wang L. W. Large Polaron Formation and Its Effect on Electron Transport in Hybrid Perovskites. Energy Environ. Sci. 2019, 12, 1219–1230. 10.1039/C8EE03369B. [DOI] [Google Scholar]
- Emin D.; Holstein T. Adiabatic Theory of an Electron in a Deformable Continuum. Phys. Rev. Lett. 1976, 36, 323–326. 10.1103/PhysRevLett.36.323. [DOI] [Google Scholar]
- Savory C. N.; Walsh A.; Scanlon D. O. Can Pb-Free Halide Double Perovskites Support High-Efficiency Solar Cells?. ACS Energy Lett. 2016, 1, 949–955. 10.1021/acsenergylett.6b00471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan W.; Niu G.; Xian Y.; Wu H.; Wang H.; Yin H.; Liu P.; Li W.; Fan J. In Situ Regulating the Order–Disorder Phase Transition in Cs2AgBiBr6 Single Crystal Toward the Application in an X-Ray Detector. Adv. Funct. Mater. 2019, 29, 1900234. 10.1002/adfm.201900234. [DOI] [Google Scholar]
- Wright A. D. Electronic Processes in Metal Halide Perovskites. Ph.D. Thesis, University of Oxford, 2018. [Google Scholar]
- Filip M. R.; Hillman S.; Haghighirad A.-A.; Snaith H. J.; Giustino F. Band Gaps of the Lead-Free Halide Double Perovskites Cs2BiAgCl6 and Cs2BiAgBr6 From Theory and Experiment. J. Phys. Chem. Lett. 2016, 7, 2579–2585. 10.1021/acs.jpclett.6b01041. [DOI] [PubMed] [Google Scholar]
- Palummo M.; Berrios E.; Varsano D.; Giorgi G. Optical Properties of Lead-Free Double Perovskites by Ab Initio Excited-State Methods. ACS Energy Lett. 2020, 5, 457–463. 10.1021/acsenergylett.9b02593. [DOI] [Google Scholar]
- Xiao Z.; Meng W.; Wang J.; Yan Y. Thermodynamic Stability and Defect Chemistry of Bismuth-Based Lead-Free Double Perovskites. ChemSusChem 2016, 9, 2628–2633. 10.1002/cssc.201600771. [DOI] [PubMed] [Google Scholar]
- McClure E. T.; Ball M. R.; Windl W.; Woodward P. M. Cs2AgBiX6 (X = Br, Cl): New Visible Light Absorbing, Lead-Free Halide Perovskite Semiconductors. Chem. Mater. 2016, 28, 1348–1354. 10.1021/acs.chemmater.5b04231. [DOI] [Google Scholar]
- Wu C.; Zhang Q.; Liu Y.; Luo W.; Guo X.; Huang Z.; Ting H.; Sun W.; Zhong X.; Wei S.; et al. The Dawn of Lead-Free Perovskite Solar Cell: Highly Stable Double Perovskite Cs2AgBiBr6 Film. Adv. Sci. 2018, 5, 1700759. 10.1002/advs.201700759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright A. D.; Milot R. L.; Eperon G. E.; Snaith H. J.; Johnston M. B.; Herz L. M. Band-Tail Recombination in Hybrid Lead Iodide Perovskite. Adv. Funct. Mater. 2017, 27, 1700860. 10.1002/adfm.201700860. [DOI] [Google Scholar]
- Yang B.; Chen J.; Yang S.; Hong F.; Sun L.; Han P.; Pullerits T.; Deng W.; Han K. Lead-Free Silver-Bismuth Halide Double Perovskite Nanocrystals. Angew. Chem., Int. Ed. 2018, 57, 5359–5363. 10.1002/anie.201800660. [DOI] [PubMed] [Google Scholar]
- Schmitz A.; Leander Schaberg L.; Sirotinskaya S.; Pantaler M.; Lupascu D. C.; Benson N.; Bacher G. Fine Structure of the Optical Absorption Resonance in Cs2AgBiBr6 Double Perovskite Thin Films. ACS Energy Lett. 2020, 5, 559–565. 10.1021/acsenergylett.9b02781. [DOI] [Google Scholar]
- Connor B. A.; Leppert L.; Smith M. D.; Neaton J. B.; Karunadasa H. I. Layered Halide Double Perovskites: Dimensional Reduction of Cs2AgBiBr6. J. Am. Chem. Soc. 2018, 140, 5235–5240. 10.1021/jacs.8b01543. [DOI] [PubMed] [Google Scholar]
- Dey A.; Richter A. F.; Debnath T.; Huang H.; Polavarapu L.; Feldmann J. Transfer of Direct to Indirect Bound Excitons by Electron Intervalley Scattering in Cs2AgBiBr6 Double Perovskite Nanocrystals. ACS Nano 2020, 14, 5855–5861. 10.1021/acsnano.0c00997. [DOI] [PubMed] [Google Scholar]
- Lv C.; Yang X.; Shi Z.; Wang L.; Sui L.; Li Q.; Qin J.; Liu K.; Zhang Z.; Li X.; et al. Pressure-Induced Ultra-Broad-Band Emission of a Cs2AgBiBr6 Perovskite Thin Film. J. Phys. Chem. C 2020, 124, 1732–1738. 10.1021/acs.jpcc.9b11187. [DOI] [Google Scholar]
- Wright A. D.; Volonakis G.; Borchert J.; Davies C. L.; Giustino F.; Johnston M. B.; Herz L. M. Intrinsic Quantum Confinement in Formamidinium Lead Triiodide Perovskite. Nat. Mater. 2020, 19, 1201–1206. 10.1038/s41563-020-0774-9. [DOI] [PubMed] [Google Scholar]
- Varshni Y. Temperature Dependence of the Energy Gap in Semiconductors. Physica 1967, 34, 149–154. 10.1016/0031-8914(67)90062-6. [DOI] [Google Scholar]
- Pantaler M.; Cho K. T.; Queloz V. I.; García Benito I.; Fettkenhauer C.; Anusca I.; Nazeeruddin M. K.; Lupascu D. C.; Grancini G. Hysteresis-Free Lead-Free Double-Perovskite Solar Cells by Interface Engineering. ACS Energy Lett. 2018, 3, 1781–1786. 10.1021/acsenergylett.8b00871. [DOI] [Google Scholar]
- Elliott R. J. Intensity of Optical Absorption by Excitions. Phys. Rev. 1957, 108, 1384–1389. 10.1103/PhysRev.108.1384. [DOI] [Google Scholar]
- Davies C.; Filip M.; Patel J.; Crothers T.; Verdi C.; Wright A.; Milot R.; Giustino F.; Johnston M.; Herz L. Bimolecular Recombination in Methylammonium Lead Triiodide Perovskite Is an Inverse Absorption Process. Nat. Commun. 2018, 9, 293. 10.1038/s41467-017-02670-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi J. H.; Cui P.; Lan H.; Zhang Z. Linear Scaling of the Exciton Binding Energy Versus the Band Gap of Two-Dimensional Materials. Phys. Rev. Lett. 2015, 115, 066403. 10.1103/PhysRevLett.115.066403. [DOI] [PubMed] [Google Scholar]
- Haug H.; Koch S. W.. Quantum Theory of the Optical and Electronic Properties of Semiconductors, 4th ed.; World Scientific: Singapore, 2004; p 176. [Google Scholar]
- Savill K. J.; Klug M. T.; Milot R. L.; Snaith H. J.; Herz L. M. Charge-Carrier Cooling and Polarization Memory Loss in Formamidinium Tin Triiodide. J. Phys. Chem. Lett. 2019, 10, 6038–6047. 10.1021/acs.jpclett.9b02353. [DOI] [PubMed] [Google Scholar]
- Herz M.; Daniel C.; Silva C.; Hoeben M.; Schenning H. J.; Meijer W.; Friend H.; Phillips T. Fast Exciton Diffusion in Chiral Stacks of Conjugated p-Phenylene Vinylene Oligomers. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 68, 045203. 10.1103/PhysRevB.68.045203. [DOI] [Google Scholar]
- Chang M. H.; Frampton M. J.; Anderson H. L.; Herz L. M. Intermolecular Interaction Effects on the Ultrafast Depolarization of the Optical Emission From Conjugated Polymers. Phys. Rev. Lett. 2007, 98, 027402. 10.1103/PhysRevLett.98.027402. [DOI] [PubMed] [Google Scholar]
- Herz L. M. Charge-Carrier Mobilities in Metal Halide Perovskites: Fundamental Mechanisms and Limits. ACS Energy Lett. 2017, 2, 1539–1548. 10.1021/acsenergylett.7b00276. [DOI] [Google Scholar]
- Yu P. Y.; Cardona M.. Fundamentals of Semiconductors; Springer-Verlag: Berlin, 2010. [Google Scholar]
- Poncé S.; Schlipf M.; Giustino F. Origin of Low Carrier Mobilities in Halide Perovskites. ACS Energy Lett. 2019, 4, 456–463. 10.1021/acsenergylett.8b02346. [DOI] [Google Scholar]
- Herz L. M. How Lattice Dynamics Moderate the Electronic Properties of Metal-Halide Perovskites. J. Phys. Chem. Lett. 2018, 9, 6853–6863. 10.1021/acs.jpclett.8b02811. [DOI] [PubMed] [Google Scholar]
- Buizza L. R.; Herz L. M. Polarons and Charge Localisation in Metal-Halide Semiconductors for Photovoltaic and Light-Emitting Devices. Adv. Mater. 2021, 33, 2007057. [DOI] [PubMed] [Google Scholar]
- Hutter E. M.; Gélvez-Rueda M. C.; Bartesaghi D.; Grozema F. C.; Savenije T. J. Band-Like Charge Transport in Cs2AgBiBr6 and Mixed Antimony-Bismuth Cs2AgBi1–XSbxBr6 Halide Double Perovskites. ACS Omega 2018, 3, 11655–11662. 10.1021/acsomega.8b01705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emin D. Lattice Relaxation and Small-Polaron Hopping Motion. Phys. Rev. B 1971, 4, 3639–3651. 10.1103/PhysRevB.4.3639. [DOI] [Google Scholar]
- Holstein T. Studies of Polaron Motion: Part II. the “small” Polaron. Ann. Phys. (Amsterdam, Neth.) 1959, 8, 343–389. 10.1016/0003-4916(59)90003-X. [DOI] [Google Scholar]
- Hu T.; Smith M. D.; Dohner E. R.; Sher M. J.; Wu X.; Trinh M. T.; Fisher A.; Corbett J.; Zhu X. Y.; Karunadasa H. I.; et al. Mechanism for Broadband White-Light Emission From Two-Dimensional (110) Hybrid Perovskites. J. Phys. Chem. Lett. 2016, 7, 2258–2263. 10.1021/acs.jpclett.6b00793. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.