Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2021 Mar 24;7(4):603–612. doi: 10.1021/acscentsci.1c00110

Spontaneous Patterning during Frontal Polymerization

Evan M Lloyd †,‡, Elizabeth C Feinberg †,§, Yuan Gao †,∥, Suzanne R Peterson †,∥, Bhaskar Soman ⊥,#, Julie Hemmer †, Leon M Dean †,#, Qiong Wu †,§, Philippe H Geubelle †,∥,*, Nancy R Sottos †,#,*, Jeffrey S Moore †,§,*
PMCID: PMC8155460  PMID: 34056090

Abstract

graphic file with name oc1c00110_0005.jpg

Complex patterns integral to the structure and function of biological materials arise spontaneously during morphogenesis. In contrast, functional patterns in synthetic materials are typically created through multistep manufacturing processes, limiting accessibility to spatially varying materials systems. Here, we harness rapid reaction-thermal transport during frontal polymerization to drive the emergence of spatially varying patterns during the synthesis of engineering polymers. Tuning of the reaction kinetics and thermal transport enables internal feedback control over thermal gradients to spontaneously pattern morphological, chemical, optical, and mechanical properties of structural materials. We achieve patterned regions with two orders of magnitude change in modulus in poly(cyclooctadiene) and 20 °C change in glass transition temperature in poly(dicyclopentadiene). Our results suggest a facile route to patterned structural materials with complex microstructures without the need for masks, molds, or printers utilized in conventional manufacturing. Moreover, we envision that more sophisticated control of reaction-transport driven fronts may enable spontaneous growth of structures and patterns in synthetic materials, inaccessible by traditional manufacturing approaches.

Short abstract

Competition between reaction and thermal transport during frontal polymerization drives the emergence of complex thermal profiles that are harnessed to spontaneously pattern material properties.

Introduction

Throughout nature, patterns of various shapes, sizes, and colors adorn biological materials. These multiscale patterns impart organisms with unique characteristics that are critical to their survival. Patterns serve a diverse array of functions, including extraordinary fracture toughness (e.g., the layering of hard and soft domains in glass sea sponge spicules1 and nacre2,3), tactile sensing (e.g., the textured surface of a fingertip4), intimidation (e.g., the coloration of an emperor angel fish), and camouflage (e.g., the spots on a cheetah) (Figure 1a). Structural complexity and function in natural systems are derived from initial states of high symmetry and emerge during the growth and development of an organism.5−9 In great contrast, patterns and structures in synthetic materials are generated by multistep manufacturing processes such as layer-by-layer assembly,10 lithography,11 or molding and casting. In lieu of traditional manufacturing processes, we seek autonomous routes of patterning synthetic structural materials more akin to biological patterning.

Figure 1.

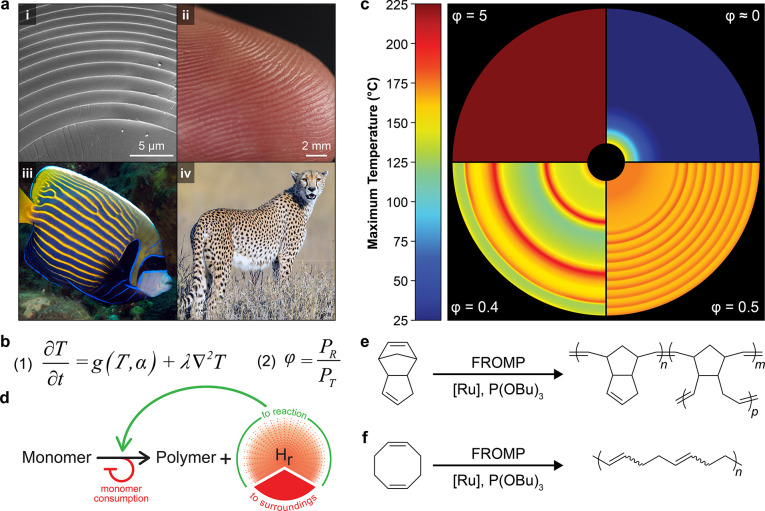
Figure 1

Open in a new tab

Conceptual design of patterning with frontal polymerization. (a) Complex patterns in nature that enable functional properties: (i) microstructure of a glass sea sponge spicule (adapted with permission from ref (1). Copyright 2005 Science), (ii) textured surface of a fingertip (photograph provided by Travis Ross, Imaging Technology Group, Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana–Champaign), (iii) adult emperor angel fish (adapted with permission from Florent Charpin, Copyright 2020, reefguide.org), and (iv) spots of a cheetah (adapted with permission from Brian Jones, Copyright 2018, flickr.com). (b) Equation 1: coupled reaction and thermal transport (only diffusion considered for simplicity) inherent to frontal polymerization, where T, α, and λ represent the temperature, extent of reaction, and thermal diffusivity of the resin, respectively. Equation 2: ratio of power density generated by reaction (PR) and spread by thermal transport (PT) during frontal polymerization. (c) Computed thermal profiles of frontal polymerization with different values of φ. The inner and outer radii of the circular area are 0.5 mm and 5 mm, respectively. (d) Feedback mechanism for spontaneous patterning during frontal polymerization via competition between thermal transport and chemical reaction. Using the heat generated by the reaction (Hr), thermal transport spontaneously heats unreacted monomer, activating the initiator toward polymerization. Once the polymerization reaction consumes the available monomer within the activated zone, the rate of heat release decreases, inhibiting further activation. Competition between reaction and transport generates thermal patterns that are exploited for material property variations. (e, f) Frontal ring-opening metathesis polymerization (FROMP) of dicyclopentadiene (e) and 1,5-cyclooctadiene (f) by a thermally activated ruthenium catalyst (Grubbs 2nd generation, GC2) inhibited by tributyl phosphite.

Coupled reaction-transport processes are versatile yet underexplored methods for manufacturing as they exhibit unique opportunities to control the spatial properties of materials, achieving order through spontaneous symmetry breaking events.12 Elegant and controllable multiscale patterns and structures have been created in a variety of media with reaction-mass transport processes.12−20 These initial demonstrations are limited to solutions, gels, or thin membranes as mass transport is prohibitively slow in solid media. Thermally driven reaction-transport networks provide an unexplored yet promising route to the autonomous formation of patterns in structural materials since thermal transport is orders of magnitude faster than mass transport. In this report, we exploit frontal polymerization as an alternative to traditional reaction-mass transport networks and demonstrate spontaneous pattern development during the frontal ring-opening metathesis polymerization of strained cyclic olefins.

During frontal polymerization (FP), a small energetic input activates a thermally latent initiator, and transport of heat (through diffusion, convection, or advection) from the highly exothermic polymerization reaction drives the propagation of the polymerization front. In the absence of propagation instabilities, uniform temperature profiles and a homogeneous final state are obtained.21−24 Unstable front propagation, however, spontaneously generates complex thermal instabilities.25−31 We hypothesize that, when combined with orthogonal chemistries, the undulations in temperature which emerge in the presence of propagation instabilities can be harnessed to pattern material properties.

Results and Discussion

To guide experimental design, we sought to numerically determine the key parameters governing propagation stability. Previous models of propagating reaction fronts (e.g., combustion and self-propagating high-temperature synthesis) utilize the Zeldovich number to describe the transition into instability.32−35 However, the Zeldovich number considers only the initial temperature, maximum front temperature, and activation energy. Our numerical simulations (Figure 1b,c and Figure S1) revealed that the spatial and temporal balance of thermal power density (expressed by the ratio φ in eq 2 in Figure 1b and in Figure S1b) generated by the polymerization reaction (PR, J m–3 s–1) and diffused by thermal transport (PT, J m–3 s–1) dictates the development of thermal instabilities during frontal propagation (detailed description of φ included in Methods). Under typical conditions, the power generated during polymerization far exceeds that diffused by thermal transport (φ ≫ 1), and the polymerization front propagates with constant velocity and temperature (Figure 1c, φ = 5). When transport is dominant (φ ≪ 1), heat diffuses away from the reaction zone faster than it is locally supplied by polymerization, and the front quenches immediately after initiation (Figure 1c, φ ≈ 0). In either limiting case, homogeneity is preserved in the system. However, when reaction and transport powers are similar in value (φ ≈ 1), undulations in reaction temperature are observed (Figure 1c, φ = 0.4 or 0.5), indicating that frontal instabilities result from a competition between reaction and transport.

Spontaneous patterning with a reaction-thermal transport process is summarized in Figure 1d. After an initial energy input, liquid monomer is converted to solid polymer with an accompanying release of energy (Hr, Figure 1d). The rapid transport (through diffusion, convection, or advection) of the energy supplied by the reaction (Hr) spontaneously heats unreacted monomer, leading to local activation according to Arrhenius kinetics. Consumption of the activated monomer during polymerization depletes the latent chemical energy, preventing further activation by thermal transport. Following complete consumption of the activated monomer, propagation rates slow, transport becomes dominant again, and the process repeats cyclically to generate the undulations in reaction temperature shown in Figure 1c. In the absence of competition (φ ≫ 1), monomer is consumed before significant local activation occurs due to the greater reaction power, and a homogeneous final state is obtained. Conversely, as φ approaches zero, the heat from Hr is lost to the surroundings faster than it is supplied to the reaction, inhibiting the polymerization reaction and quenching fronts immediately after initiation.

Experimentally, we leverage the competition between reaction rate and thermal transport during the frontal ring-opening metathesis polymerization (FROMP) of dicyclopentadiene (DCPD) and 1,5-cyclooctadiene (COD) (Figure 1e,f) to break symmetry and generate emergent patterns. Competition between reaction rate and thermal transport is observed in an open-mold geometry with a free surface (Figure S2), which allows for increased rates of thermally driven advective and convective transport22 in addition to thermal diffusion. Precise control over this competition and the resulting temperature profiles is achieved by tuning the reaction rate through altering the chemistry (e.g., monomer, catalyst concentration, inhibitor concentration) or the ambient temperature, where higher ambient temperatures result in accelerated reaction kinetics. Spatial variations in reaction temperature are exploited to drive changes in polymer morphology, chemistry, and mechanical properties.

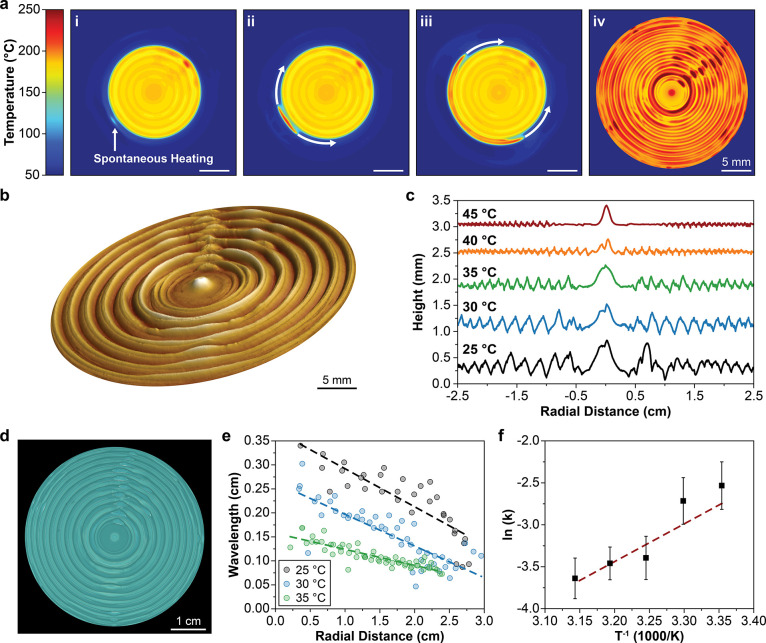
During free-surface FROMP of DCPD, the polymerization front propagates outward from the central initiation point and thermal transport away from the reaction zone spontaneously heats a localized region of monomer ahead of the polymerization front (Figure 2a,i and Video S1). Once this preheated region reaches ca. 80 °C, a new front initiates and propagates circumferentially, rapidly consuming the available preheated monomer (Figure 2a, ii–iii). The onset of initiation is in agreement with the polymerization onset temperature measured during dynamic differential scanning calorimetry (DSC) traces (Figure S3a). Peak front temperatures as high as 270 °C and as low as 180 °C are recorded in circular patterns with radial periodicity (Figure 2a, iv). These undulations in reaction temperature lead to significant differences in thermal expansion of the liquid monomer, which is confined by the polymerization reaction, generating circumferential surface ridges (Figure 2b,d). On the basis of thermal expansion alone (assuming a coefficient of thermal expansion of 0.001 °C–1,36 and initial resin depth of 5 mm), a height difference of 450 μm is expected for a 90 °C difference in maximum reaction temperature, in good agreement with the experimentally measured maximum amplitude of 485 μm for an ambient temperature of 30 °C (Figure 2b,c).

Figure 2.

Figure 2

Open in a new tab

Radial patterning during FROMP of dicyclopentadiene. (a) Thermal images revealing circumferential propagation in an open circular mold with an initial temperature of 30 °C: (i) spontaneous heating ahead of the polymerization front at t = 15 s after initiation; (ii, iii) frontal propagation around the circumference following spontaneous heating; and (iv) maximum local temperature during polymerization. (b) Topographic profile of sample shown in a, obtained by optical profilometry; the vertical axis is scaled by 150% for clarity. (c) Surface height measurements of samples prepared with varied initial temperature. Profiles are offset for clarity. (d) Optical image obtained under UV light (365 nm) of the sample in a; 0.25 wt % of 1,1,2,2-tetraphenylethylene was incorporated into the resin prior to frontal polymerization to enhance the fluorescence of resulting samples. (e) Feature wavelength as a function of radial distance from the center of samples prepared with varied initial temperature, determined from optical images of fluorescent samples. (f) Temperature dependence of the wavelength decay constant obtained from the linear fit of wavelength vs radial distance. Reported values and error bars represent the average and standard deviation, respectively (n = 3).

The amplitude and wavelength of the ridges are systematically varied by adjusting the initial temperature of the resin immediately prior to initiation (Figure 2c). As the initial temperature increases, the undulations in reaction temperature damp (Figure S4a), leading to decreased differences in thermal expansion and smaller ridge amplitudes (Figure 2c). When the initial temperature reaches 50 °C, no undulations in reaction temperature were observed (Figure S4a), suggesting that PR is greater than PT. Additionally, the initial wavelength of the ridges, determined by analysis (Figure S4b–e) of fluorescent images of the samples (Figure 2d), decreases with increasing initial temperature. Interestingly, the pattern wavelength decays with radial distance (Figure 2e). Thermal imaging (Video S1 and Figure S4f) reveals that the unreacted monomer ahead of the front steadily increases in temperature, resulting in the subsequent decay in wavelength. This temperature rise is likely due to advective motion induced by thermal expansion during polymerization. The zeroth-order wavelength decay constant, k (Figure 2f), is defined as the negative slope of the linear fits in Figure 2e and roughly follows Arrhenius behavior.

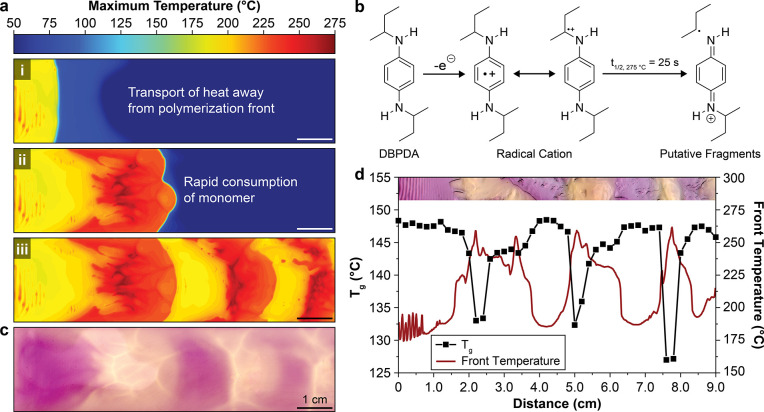
To further explore the decay in wavelength and extend the length scale of study, we adopted a rectangular channel geometry (Figure S2b). Free-surface FROMP of DCPD in a channel (Video S2) results in similar circumferential propagation as in radial geometries. As the wavelength of circumferential propagation tends toward zero, a large zone (∼1 cm) of heated monomer accumulates spontaneously ahead of the front (Figure 3a, i). Analogous to the short-range experiments in radial geometries, this large preheated zone is subsequently consumed in a rapid, high-temperature polymerization reaction that exceeds 270 °C (Figure 3a, ii). Following the consumption of all of the available preheated monomer, reaction rates slow, and reaction temperatures decrease to around 200 °C. This process repeats cyclically to generate the striped thermal profiles shown in Figure 3a, iii. The size and the spacing of the features are controlled by varying the initial temperature, again demonstrating the utility of tuning the boundary conditions to generate distinct thermal profiles (Figure S5).

Figure 3.

Figure 3

Open in a new tab

Color patterning with a thermochrome. (a) Evolution of maximum temperature profiles during FROMP of DCPD in a rectangular channel: (i) a zone of spontaneously heated monomer, (ii) rapid, high-temperature polymerization encountered during consumption of the preheated monomer, and (iii) large thermal gradients encountered during unstable propagation. Scale bar = 1 cm. (b) Putative single electron transfer oxidation of DBPDA to form a highly colored and stable radical cation and subsequent temperature-dependent cleavage of the radical cation to form colorless species. Reported half-life determined during ex situ bleaching at 275 °C (Figure S6). (c) Optical image of the sample after the frontal polymerization in a; 2 wt % DBPDA was incorporated into the resin prior to frontal polymerization (sample was polished to remove surface features and enhance visualization of the DBPDA thermochrome). (d) Glass transition temperature (Tg, determined by DSC analysis) and maximum front temperature as a function of distance from the initiation location for a polymerized sample containing 2 wt % DBPDA. Inset is an optical image of the tested sample.

The presence of large, spatially defined regions of high and low reaction temperatures provides an opportunity to produce permanent patterns by the application of a secondary chemical reaction, the rate of which varies widely over the observed range of peak temperatures. Specifically, the incorporation of a phenylenediamine-based thermochrome enables patterning of the optical and thermomechanical properties of pDCPD. Substituted phenylenediamines, such as N,N′-di-sec-butyl-p-phenylenediamine (DBPDA), readily undergo single electron transfer oxidation (EOX ≈ 0.2 V vs SCE37) to form stable and highly colored radical cations, known as Wüster’s dyes38 (Figure 3b). We postulate that while stable at modest temperatures, the radical cations undergo mesolytic cleavage at high temperature to form colorless species. When DBPDA is incorporated into DCPD resins cured at room temperature, we observe a slow transition from faint red to deep purple over the course of several hours, indicating formation of radical cation species in the presence of Grubbs catalyst 2nd generation (GC2) (Figure S6b,c). The presence of DBPDA (2 wt %) has minimal impact on frontal propagation; resins with DBPDA exhibit nearly identical front velocities to those without DBPDA (Figure S6d). Importantly, the deep purple color is retained at modest front temperatures, ca. 200 °C. Heating the resulting samples on a hot stage at temperatures in excess of 250 °C results in rapid (t1/2 = 25 s at 275 °C), complete, and irreversible bleaching to the innate color of pDCPD, supporting our conjecture that the radical cation dye serves as a permanent thermochrome (Figure S6e,f).

In addition to ex situ bleaching, DBPDA displays highly selective thermochromism in situ, enabling a permanent visual indication of the local front temperature (Figure 3c). Decay of the radical cation results in visible bleaching at front temperatures near 250 °C, and bleaching increases with increasing front temperature, up to ca. 270 °C. Further, the decay of radical cations may generate reaction byproducts, altering the thermomechanical properties of the resulting polymer. The bleached regions exhibit a 20 °C decrease in the glass transition temperature (Tg) compared to the unbleached regions (Figure 3d). The undulations in Tg correlate to trends in both bleaching and front temperature. In the absence of DBPDA, a similar thermal profile is obtained, but only a modest 8 °C change in Tg is observed (Figure S7c), indicating that DBPDA reaction products are responsible for the large changes in thermomechanical properties.

While the DCPD-DBPDA system exhibits interesting optical and thermomechanical patterning, we sought to apply this concept to other materials. Inspired by the impressive fracture toughness that results from patterning hard and soft domains which differ in stiffness by several orders of magnitude in biological materials such as glass sea sponges1 and nacre,2,3 we targeted material systems that would generate significant differences in material stiffness in response to front temperature. We recently demonstrated that frontally polymerized 1,5-cyclooctadiene (COD) has a propensity to crystallize due to high trans content.39 We suspected that the cis/trans ratio would vary with reaction temperature, resulting in patterned regions of amorphous and crystalline material. During free-surface FROMP of COD (Video S3), we observe significant thermal transport ahead of the reaction zone, generating a large region of heated monomer, which upon initiation (at ca. 70 °C) is rapidly consumed in a high-temperature polymerization reaction. As with the DCPD systems, this process repeats cyclically until all monomer is consumed (Figure 4a, top image).

Figure 4.

Figure 4

Open in a new tab

Spontaneous patterning with cyclooctadiene. (a) Maximum temperature profile during free-surface FROMP of 1,5-cyclooctadiene (top) and optical image (bottom) of the resulting pattern showing crystalline (white) and amorphous (yellow) domains. The numbered markers represent measurement locations in subsequent characterization. (b) WAXS profiles obtained at the locations indicated in a. (c) Raman spectra obtained at the locations indicated in a. (d) Reduced modulus as a function of distance from the initiation point obtained via nanoindentation. The indentation profile follows the same trajectory as the numbered locations in a. (e) Reduced modulus as a function of maximum front temperature obtained through spatial correlation of nanoindentation scans and thermal profiles. The reported raw data (gray) represents the average of spatial correlations for the nanoindentation curves shown in d and Figure S8. The smoothed curve (black) was obtained from adjacent averaging 100 points of raw data (gray).

After polymerization, the sample is cooled and held at room temperature for 24 h. During this time, the areas that experienced low front temperatures (ca. 120 °C) crystallize to form a white opaque material (Figure 4a, bottom image), while regions with front temperatures greater than 145 °C remain a transparent yellow. Wide-angle X-ray scattering (WAXS) analysis of the white opaque material shows a sharp peak centered at 16.5 nm–1 (Figure 4b, region 1), confirming the presence of crystalline pCOD domains. The intensity of the crystalline peak decreases significantly through the transition region (Figure 4b, region 2), until only an amorphous halo remains (Figure 4b, region 3), indicating a fully amorphous phase. Raman spectroscopy of region 1 (Figure 4c) indicates high trans content in the crystalline domains40 that were exposed to lower maximum front temperatures. The high trans content suggests that chain transfer is rapid on the time scale of frontal polymerization. In regions with higher peak temperatures, a mixture of cis and trans pCOD is produced (Figure 4c, regions 2 and 3), indicating either that trans-selectivity of the chain transfer reaction decreases above 145 °C or that polymerization kinetics become competitive with chain transfer at higher temperature. The trans content of the crystalline (Tmax ≈ 130 °C) and amorphous (Tmax ≈ 165 °C) domains as measured by 1H NMR is 88% and 76%, respectively (Figure S8d). Additionally, we observe that the amorphous domains are only partially soluble, suggesting some degree of cross-linking, possibly a result of radical formation at high temperatures. Together, the higher cis content and cross-linking contribute to the formation of an amorphous domain.

The temperature-responsive crystallization of pCOD yields our target result: spontaneously patterned materials with hard and soft domains. The changes in stiffness between the crystalline and amorphous domains are measured by nanoindentation. The reduced modulus varies by several orders of magnitude, reaching a maximum of 1.3 GPa and a minimum of 3 MPa in a representative example (Figure 4d). The stiffness correlates well with the physical characteristics, spectroscopic properties, and the maximum front temperature, where higher front temperature results in lower stiffness. Correlation between front temperature and stiffness reveal three distinct stiffness regimes (Figure 4e): (1) a hard domain with moduli ranging from 200 MPa to 1 GPa, where front temperatures remain less than 143 °C; (2) a transitional domain with moduli near 30 MPa; and (3) a soft domain with moduli of approximately 5 MPa, where front temperatures remain above 160 °C. The relationship between stiffness and front temperature is a key design principle when developing patterns for engineering applications such as high-toughness polymer matrices or architected materials.

The low ring-strain of cyclooctadiene limits PR generated during the ring-opening reaction, leading to a system that displays a weak, transport-dominated imbalance. As a result, pattern control with COD is significantly more challenging than with DCPD. To address this issue, future work will center on measuring the thermal expansion driven advection associated with free-surface FROMP and development of strategies to accurately modulate and predict thermal transport. Further, we anticipate that modification of boundary conditions may enable spatiotemporal control of the resin temperature and produce more highly controlled patterns such as those predicted in Figure S9.

Conclusions

We have demonstrated that thermally driven reaction-transport during frontal polymerization produces spontaneous patterns in structural materials. Patterning of surface morphology, color, and Tg was realized in pDCPD resins. Control of boundary conditions such as the initial temperature of the monomer enabled fine-tuning of pattern development and evolution. Application of this patterning technique to frontal polymerization of COD resulted in materials with clearly defined regions varying more than two orders of magnitude in stiffness. The ability to create and control large thermal gradients creates opportunities for new chemical and physical transformations in response to temperature such as liquid crystal mesogens, thermochromes, catalyst inhibition schemes, and cross-linking reactions. Provided that the transformation kinetics are competitive with frontal polymerization, we anticipate that this patterning strategy can be combined with the wide variety of thermally responsive materials and chemistries that have been developed to date. The reaction-thermal transport processes of frontal polymerization are analogous to the reaction-mass transport processes in Turing’s model of biological morphogenesis5 and may have significant impacts on the design and manufacture of macroscale functional materials by enabling the autonomous growth of structures and patterns.

Methods

Numerical Simulations

Frontal polymerization in a two-dimensional concentric fan-shape domain (Figure 1c) and in a two-dimensional channel (Figure S9) was modeled by solving the following partial differential equations:

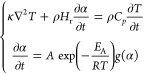graphic file with name oc1c00110_m001.jpg

The variables of interest are the temperature T (K) and the degree of cure α (nondimensional), both evolving with time and position. The first equation describes thermal conservation with the power density transported by diffusion (κ∇2T) and the power density generated by polymerization (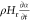Inline graphic). The associated material properties are the thermal conductivity, κ (W m–1 K–1); the specific heat capacity, Cp (J kg–1 K–1); the density, ρ (kg m–3); and the heat of reaction, Hr (J kg–1). The second equation models the cure kinetics of the considered material, where the parameters (pre-exponential factor, A (s–1); activation energy EA (J mol–1); and the evolution of the degree of cure, g(α)) are determined by performing nonlinear fitting optimization with the data obtained from dynamics DSC tests performed on the resins. R (8.314 J mol–1 K–1) represents the ideal gas constant.

The initial and boundary conditions used to solve the governing equations in the adiabatic fan-shape domain are

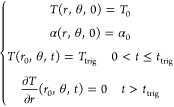graphic file with name oc1c00110_m003.jpg

where T0, α0, Ttrig and r0 are the initial temperature, initial degree of cure, triggering temperature, and the inner radius of the fan-shape domain. Figure S1a depicts the initial mesh adopted for the finite element analysis. The inner and outer radii of the domain were 0.5 and 5.0 mm, respectively. A total of 11 712 four-node quadrilateral elements uniformly distributed in the angular direction were used to discretize the domain at the beginning of the simulation, and a maximum refinement level of 5 was applied to adapt the mesh and capture the sharp gradients in T and α in the vicinity of the advancing front.

In the channel with glass boundaries (Figure S9a), the governing equations were solved in two subdomains. The first subdomain, where no chemical reaction is considered, consisted of glass with Cp = 840 J kg–1 K–1, ρ = 2500 kg m–3, κ = 1.14 W m–1 K–1, and Hr = 0 J kg–1. The second subdomain consisted of cyclooctadiene resin. The initial and boundary conditions are described as follows:

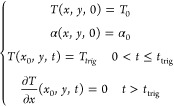graphic file with name oc1c00110_m004.jpg

where x0 = 0 represents the left boundary of the channel where polymerization is triggered. Since there is no chemical reaction in the glass, only thermal diffusion is considered in this subdomain. The domain (Figure S9a), representing the top view of an adiabatic channel, is 75 mm long and 7 mm width with an additional 0.5 mm of glass at top and bottom boundaries. The overall domain is divided into 32 000 four-node quadrilateral elements with a maximum refinement level of 3 near the front vicinity.

The numerical analysis was conducted using the Multiphysics Object-Oriented Simulation Environment (MOOSE),41 an open source C++ finite element solver that includes robust mesh adaptivity capability. The implicit Euler time stepping scheme and a preconditioned Jacobian-free Newton–Krylov method were adopted to solve the transient, nonlinear equations.42,43 The ratio of power densities, φ, was computed as follows:

graphic file with name oc1c00110_m005.jpg

where T̅ and Lθ represent the average of the initial and maximum temperature and the width of the thermal front, respectively. Parameters for computing the cases discussed in Figure 1c and Figure S9 are summarized in Figure S1c,e,f.

Materials

Dicyclopentadiene (DCPD), 5-ethylidene-2-norbornene (ENB), Grubbs catalyst 2nd generation (GC2), tributyl phosphite (TBP), 1,1,2,2-tetraphenylethylene (TPE), and cis-polybutadiene (Mw = 200 000–300 000 Da) were purchased from Sigma-Aldrich and used without further purification. TBP was stored under inert atmosphere to prevent hydrolysis of the phosphite. 1,5-Cyclooctadiene (COD) and N,N′-di-sec-butyl-p-phenylenediamine (DBPDA) were purchased from TCI America. DBPDA was used as received and stored under inert atmosphere. COD was passed through a 1 cm plug of basic alumina to remove the octadecyl 3-(3′,5′-di-tert-butyl-4′-hydroxylphenyl)propionate stabilizer, which was found to interact negatively with GC2, preventing frontal polymerization. RTV630 silicone rubber compound was purchased from Momentive and used as received. 26-Gauge Kanthal wire (D = 0.40 mm, resistivity = 1.4 × 10–4 Ω cm) was used to initiate FROMP. Polyurethane rubber gaskets, laminated glass plates, and aluminum plates were purchased from McMaster-Carr.

Free-Surface Frontal Ring-Opening Metathesis Polymerization

To depress the freezing point of DCPD, 5 wt % ENB was blended with DCPD at 35 °C. The liquid mixture was then degassed overnight at room temperature and 15 kPa with stirring. Unless otherwise noted, all references to DCPD refer to the 95:5 DCPD/ENB mixture. To enhance the fluorescence and aid in visualization of radial samples, 0.25 wt % TPE was dissolved in DCPD and degassed for an additional 12 h at room temperature and 15 kPa. In a typical experiment, 30 mg of GC2 (0.0353 mmol) was weighed out in a vial. In a separate container, TBP (9.6 μL, 0.0353 mmol) was added to DCPD (46.6 g, 10 000 mol equiv to GC2) or COD (38.4 g, 10 000 mol equiv to GC2). The monomer/inhibitor solution was then added to the vial containing GC2, and the resulting mixture was sonicated for 10 min to ensure complete dissolution of GC2. The solution was then filtered through a 0.22 μm PVDF membrane to remove any particulates. Filtered solutions were added to either a radial or channel mold to give a resin depth of 5 mm and incubated until the desired initial monomer temperature was achieved. Frontal polymerization was then initiated by local heating with a resistive wire. Polymerized samples were stored under a continuous flow of nitrogen gas to prevent surface oxidation.

Radial (D = 100 mm) and channel (150 mm × 25 mm) molds were fabricated by compressing an 8 mm thick polyurethane rubber gasket, cut into the desired geometry by waterjet, between a 1 mm thick laminated glass plate and a 3 mm thick aluminum plate. The top aluminum plate was machined to match the geometry of the rubber gasket and coated with Krylon ultraflat black spray paint prior to assembly to simulate a blackbody during thermal imaging. Initiation was achieved by heating a portion of the mold surface at 200 °C for 5 s with a resistive heater. Radial molds were heated in the center (Dinitiation = 3.0 mm), and channel molds were heated along one 25 mm edge. Schematics of the molds and initiation schemes employed for individual experiments are summarized in Figure S2. Front temperatures were monitored from overhead with a FLIR T1020 thermal infrared camera focused at the liquid surface. The initial resin temperature and the ambient temperature were maintained in a custom-built environmental chamber equipped with an AC-162 Peltier module, TC-720 temperature controller, and PS-24–25 power supply from TE Technology, Inc. Resin temperature was monitored with a thermocouple and the overhead infrared camera.

Materials Characterization

3D surface profiles as shown in Figure 2b were obtained with a Keyence VK-X1000 3D laser scanning confocal microscope equipped with a 5× objective and 405 nm laser. Because of the fluorescence of polymerized samples, inverse molds of the circumferential ridges were generated by casting degassed silicone resin onto the sample surface and curing for 24 h at room temperature and 1 h at 100 °C. Surface profiles of the silicone molds were then inverted to quantify the pDCPD surface.

Differential scanning calorimetry (DSC) traces were obtained with a Discovery 250 DSC equipped with an RCS 90 cooling system and an autosampler. Disks (D = 1.5 mm) were punched from the samples at 2 mm intervals, weighed on an analytical balance (XPE205, Mettler-Toledo), and transferred to Tzero aluminum pans. Traces were obtained between 25 and 250 °C at 10 °C min–1. Glass transition temperatures were defined as the inflection point in DSC traces (Figure S7a,b). Dynamic curing traces were obtained for 2–3 mg samples of freshly prepared resin sealed in Tzero aluminum pans with hermetic lids. Traces were obtained between −50 and 250 °C at various ramp rates.

Nanoindentation was performed with a Hysitron TI-950 TriboIndenter equipped with a Hysitron 3D Omniprobe high load transducer and Berkovich tip from Bruker. Samples were loaded at 3 mN s–1 up to a maximum load of 15 mN, which was held for 2 s, and subsequently unloaded at 3 mN s–1. Reduced moduli were extracted from the unloading curves utilizing the Oliver-Pharr method.44 Prior to indentation, samples were ground and polished to ensure a uniform surface on a MetPrep 3 polisher from Allied High Tech Products, Inc., equipped with a series of silicon carbide grinding papers (with a minimum grit of 1200) from Buehler.

Raman spectra were obtained with a Horiba LabRAM HR 3D Raman confocal imaging microscope equipped with an 830 nm laser, a 300 groove mm–1 grating (blazed at 600 nm), a long working distance 20× objective from Leica, and a Horiba Synapse back-illuminated deep depletion CCD camera. 1H NMR spectra were obtained in chloroform-d with a Carver 500 MHz spectrometer provided by the School of Chemical Sciences NMR laboratory at the University of Illinois at Urbana–Champaign. UV–vis spectra were obtained with a Shimadzu UV-2401PC spectrometer and quartz cuvettes were purchased from Starna Cells.

Transmission wide-angle X-ray scattering was conducted with a Xenocs GeniX3D Cu Kα X-ray source (1.54 Å) and a Pilatus 2D detector. A rod beam stop placed in front of the detector was used to attenuate the primary beam, and the sample-to-detector distance was calibrated with silver behenate powder. Scattering patterns were collected with a 10 min exposure time under ambient conditions. The 2D diffraction data were radially averaged using FIT2D software, and the intensity was plotted as a function of scattering vector q.

Ex situ bleaching of DBPDA was evaluated in pDCPD panels containing 2 wt % DBPDA. The panels were prepared by pouring DCPD resin containing 2 wt % DBPDA into cell casting molds (t = 1.0 mm) and allowing the samples to cure for 3 days at room temperature. Disks (D = 5.0 mm) were punched from the panels and placed on a Linkam THMS600 heating stage which was preheated to the desired temperature. The disks were then imaged optically, and the intensity of the yellow channel was averaged over the sample area. The degree of bleaching was calculated according to the following relation:

graphic file with name oc1c00110_m006.jpg

where I0 and It represent the average intensity of the yellow channel prior to and after thermal treatment, respectively.

Image Analysis

All image analysis was performed using FIJI (ImageJ 1.49v). The wave features of radial (D = 100 mm) pDCPD samples were analyzed by converting full color optical image to binary using the default color threshold function. Noise was removed by 2–3 pixel erosion steps, followed by an equal number of pixel dilation steps. After denoising, a radial profile function was run, centered at the sample initiation point, to provide a 2-D plot of feature intensity as a function of radial distance. Peak picking afforded the radii at maximum feature intensity, which was then used to calculate the feature wavelength.

All data are available in the main text or the Supporting Information. Numerical simulations were performed using the Multiphysics Object-Oriented Simulation Environment (MOOSE), an open-source C++ finite element framework developed at Idaho National Laboratory (https://mooseframework.inl.gov

Acknowledgments

The authors gratefully acknowledge the support of the Air Force Office of Scientific Research through the Center of Excellence in Self-Healing and Morphogenic Manufacturing (Award FA9550-20-1-0194). E.M.L. and J.H. thank the Arnold and Mabel Beckman Foundation, L.M.D. thanks the National Science Foundation, and S.R.P. thanks the Illinois Space Grant Consortium for financial support. The authors thank Dorothy Loudermilk and Jose Vazquez for assistance with graphics, Travis Ross for assistance with imaging, Kathy Walsh for assistance with nanoindentation, and Omar Alshangiti for preparing materials for NMR spectroscopy. Finally, the authors thank the Beckman Institute for Advanced Science and Technology, the Frederick Seitz Materials Research Laboratory, and the School of Chemical Sciences NMR Laboratory for the facilities and support to effectively conduct this research.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.1c00110.

  • Videos S1–S3 (MP4-1, MP4-2, MP4-3)

  • Additional computational details and characterization data; video captions (PDF)

Author Contributions

∇ E.M.L. and E.C.F. contributed equally. J.S.M., N.R.S., and P.H.G. directed this research. J.S.M., N.R.S., P.H.G., E.M.L., E.C.F., and J.H. conceived the idea. E.M.L., E.C.F., S.R.P., B.S., L.M.D., and Q.W. performed the experiments. Y.G. and J.H. performed the numerical calculations. E.M.L. and E.C.F. analyzed the experimental data. All authors participated in writing this manuscript.

This work is dedicated to the memory of Prof. Scott White, who initially conceived the idea and whose guidance and enthusiasm formed the foundation of this work. Prof. White was an excellent mentor, world-leading scientist, and constant inspiration.

The authors declare no competing financial interest.

Supplementary Material

oc1c00110_si_001.mp4 (12MB, mp4)
oc1c00110_si_002.mp4 (8.9MB, mp4)
oc1c00110_si_003.mp4 (11.7MB, mp4)
oc1c00110_si_004.pdf (3.9MB, pdf)

References

  1. Aizenberg J.; Weaver J. C.; Thanawala M. S.; Sundar V. C.; Morse D. E.; Fratzl P. Skeleton of Euplectella Sp.: Structural Hierarchy from the Nanoscale to the Microscale. Science 2005, 309, 275–278. 10.1126/science.1112255. [DOI] [PubMed] [Google Scholar]
  2. Deville S.; Saiz E.; Nalla R. K.; Tomsia A. P. Freezing as a Path to Build Complex Composites. Science 2006, 311, 515–518. 10.1126/science.1120937. [DOI] [PubMed] [Google Scholar]
  3. Huang W.; Restrepo D.; Jung J.-Y.; Su F. Y.; Liu Z.; Ritchie R. O.; McKittrick J.; Zavattieri P.; Kisailus D. Multiscale Toughening Mechanisms in Biological Materials and Bioinspired Designs. Adv. Mater. 2019, 31, 1901561. 10.1002/adma.201901561. [DOI] [PubMed] [Google Scholar]
  4. Prevost A.; Scheibert J.; Debrégeas G. Effect of Fingerprints Orientation on Skin Vibrations during Tactile Exploration of Textured Surfaces. Commun. Integr. Biol. 2014, 2, 422–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Turing A. M. The Chemical Basis of Morphogenesis. Philos. Trans. R. Soc. London, Ser. B 1952, 237, 37–72. 10.1098/rstb.1952.0012. [DOI] [Google Scholar]
  6. Gierer A.; Meinhardt H. A Theory of Biological Pattern Formation. Kybernetik 1972, 12, 30–39. 10.1007/BF00289234. [DOI] [PubMed] [Google Scholar]
  7. Meinhardt H.Models of Biological Pattern Formation; Academic Press: London, 1982. [Google Scholar]
  8. Melton D. Pattern Formation during Animal Development. Science 1991, 252, 234–241. 10.1126/science.1672778. [DOI] [PubMed] [Google Scholar]
  9. Murray J. D.Mathematical Biology, I: An Introduction, 3rd ed.; Springer: New York, 2002. [Google Scholar]
  10. Richardson J. J.; Cui J.; Björnmalm M.; Braunger J. A.; Ejima H.; Caruso F. Innovation in Layer-by-Layer Assembly. Chem. Rev. 2016, 116, 14828–14867. 10.1021/acs.chemrev.6b00627. [DOI] [PubMed] [Google Scholar]
  11. Thompson L. F. in An Introduction to Lithography; Thompson L. F., Willson C. G., Bowden M. J., Eds.; American Chemical Society: Washington D. C., 1983; pp 1–13. [Google Scholar]
  12. Epstein I. R.; Pojman J. A.. An Introduction to Nonlinear Chemical Dynamics; Oxford University Press: New York, 1998. [Google Scholar]
  13. Zaikin A. N.; Zhabotinsky A. M. Concentration Wave Propagation in Two-Dimensional Liquid-Phase Self-Oscillating System. Nature 1970, 225, 535–537. 10.1038/225535b0. [DOI] [PubMed] [Google Scholar]
  14. Noszticzius Z.; Horsthemke W.; McCormick W. D.; Swinney H. L.; Tam W. Y. Sustained Chemical Waves in an Annular Gel Reactor: A Chemical Pinwheel. Nature 1987, 329, 619–620. 10.1038/329619a0. [DOI] [Google Scholar]
  15. Ouyang Q.; Swinney H. L. Transition from a Uniform State to Hexagonal and Striped Turing Patterns. Nature 1991, 352, 610–612. 10.1038/352610a0. [DOI] [Google Scholar]
  16. Lengyel I.; Epstein I. R. A Chemical Approach to Designing Turing Patterns in Reaction-Diffusion Systems. Proc. Natl. Acad. Sci. U. S. A. 1992, 89, 3977–3979. 10.1073/pnas.89.9.3977. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Campbell C. J.; Fialkowski M.; Klajn R.; Bensemann I. T.; Grzybowski B. A. Color Micro- and Nanopatterning with Counter-Propagating Reaction–Diffusion Fronts. Adv. Mater. 2004, 16, 1912–1917. 10.1002/adma.200400383. [DOI] [Google Scholar]
  18. Campbell C. J.; Klajn R.; Fialkowski M.; Grzybowski B. A. One-Step Multilevel Microfabrication by Reaction–Diffusion. Langmuir 2005, 21, 418–423. 10.1021/la0487747. [DOI] [PubMed] [Google Scholar]
  19. Tan Z.; Chen S.; Peng X.; Zhang L.; Gao C. Polyamide Membranes with Nanoscale Turing Structures for Water Purification. Science 2018, 360, 518–521. 10.1126/science.aar6308. [DOI] [PubMed] [Google Scholar]
  20. Karig D.; Martini K. M.; Lu T.; DeLateur N. A.; Goldenfeld N.; Weiss R. Stochastic Turing Patterns in a Synthetic Bacterial Population. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, 6572–6577. 10.1073/pnas.1720770115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Mariani A.; Fiori S.; Chekanov Y.; Pojman J. A. Frontal Ring-Opening Metathesis Polymerization of Dicyclopentadiene. Macromolecules 2001, 34, 6539–6541. 10.1021/ma0106999. [DOI] [Google Scholar]
  22. Pojman J. A. In Polymer Science: A Comprehensive Reference; Matyjaszewski K., Möller M., Eds.; Elsevier: Amsterdam, 2012; Vol. 4 , pp 957–980. [Google Scholar]
  23. Goli E.; Robertson I. D.; Geubelle P. H.; Moore J. S. Frontal Polymerization of Dicyclopentadiene: A Numerical Study. J. Phys. Chem. B 2018, 122, 4583–4591. 10.1021/acs.jpcb.7b12316. [DOI] [PubMed] [Google Scholar]
  24. Robertson I. D.; Yourdkhani M.; Centellas P. J.; Aw J. E.; Ivanoff D. G.; Goli E.; Lloyd E. M.; Dean L. M.; Sottos N. R.; Geubelle P. H.; Moore J. S.; White S. R. Rapid Energy-Efficient Manufacturing of Polymers and Composites via Frontal Polymerization. Nature 2018, 557, 223–227. 10.1038/s41586-018-0054-x. [DOI] [PubMed] [Google Scholar]
  25. Pojman J. A.; Ilyashenko V. M.; Khan A. M. Spin Mode Instabilities in Propagating Fronts of Polymerization. Phys. D 1995, 84, 260–268. 10.1016/0167-2789(95)00022-V. [DOI] [Google Scholar]
  26. Masere J.; Pojman J. A. Free Radical-Scavenging Dyes as Indicators of Frontal Polymerization Dynamics. J. Chem. Soc., Faraday Trans. 1998, 94, 919–922. 10.1039/a707270h. [DOI] [Google Scholar]
  27. Masere J.; Stewart F.; Meehan T.; Pojman J. A. Period-Doubling Behavior in Frontal Polymerization of Multifunctional Acrylates. Chaos 1999, 9, 315–322. 10.1063/1.166408. [DOI] [PubMed] [Google Scholar]
  28. Ilyashenko V. M.; Pojman J. A. Single-Head Spin Modes in Frontal Polymerization. Chaos 1998, 8, 285–289. 10.1063/1.166308. [DOI] [PubMed] [Google Scholar]
  29. Pojman J. A.; Masere J.; Petretto E.; Rustici M.; Huh D.-S.; Kim M. S.; Volpert V. The Effect of Reactor Geometry on Frontal Polymerization Spin Modes. Chaos 2002, 12, 56–65. 10.1063/1.1445436. [DOI] [PubMed] [Google Scholar]
  30. Huh D. S.; Kim H. S. Bistability of Propagating Front with Spin-mode in a Frontal Polymerization of Trimethylopropane Triacrylate. Polym. Int. 2003, 52, 1900–1904. 10.1002/pi.1269. [DOI] [Google Scholar]
  31. Inamdar S. R.; Pujari N. S.; Karimi I. A.; Ponrathnam S.; Tayal R. K.; Kulkarni B. D. Spinning Wave Motion in Frontal Polymerization. Chem. Eng. Sci. 2007, 62, 1448–1455. 10.1016/j.ces.2006.11.037. [DOI] [Google Scholar]
  32. Aldushin A. P.; Malomed B. A.; Zeldovich Ya. B. Phenomenological Theory of Spin Combustion. Combust. Flame 1981, 42, 1–6. 10.1016/0010-2180(81)90137-1. [DOI] [Google Scholar]
  33. Strunin D. V.; Strunina A. G.; Rumanov E. N.; Merzhanov A. G. Chaotic Reaction Waves with Fast Diffusion of Activator. Phys. Lett. A 1994, 192, 361–363. 10.1016/0375-9601(94)90219-4. [DOI] [Google Scholar]
  34. Solovyov S. E.; Ilyashenko V. M.; Pojman J. A. Numerical Modeling of Self-Propagating Polymerization Fronts: The Role of Kinetics on Front Stability. Chaos 1997, 7, 331–340. 10.1063/1.166248. [DOI] [PubMed] [Google Scholar]
  35. Pojman J. A. Mathematical Modeling of Frontal Polymerization. Math. Model. Math. Modell. Nat. Phenom. 2019, 14, 604. 10.1051/mmnp/2019059. [DOI] [Google Scholar]
  36. Smith W. T.; Greenbaum S.; Rutledge G. P. Correlation of Critical Temperatures with Thermal Expansion Coefficients of Organic Liquids. J. Phys. Chem. 1954, 58, 443–447. 10.1021/j150515a016. [DOI] [Google Scholar]
  37. Chung Y.-C.; Su Y. O. Effects of Phenyl- and Methyl-Substituents on p-Phenylenediamine, an Electrochemical and Spectral Study. J. Chin. Chem. Soc. 2009, 56, 493–503. 10.1002/jccs.200900074. [DOI] [Google Scholar]
  38. Michaelis L.; Schubert M. P.; Granick S. The Free Radicals of the Type of Wurster’s Salts. J. Am. Chem. Soc. 1939, 61, 1981–1992. 10.1021/ja01877a013. [DOI] [Google Scholar]
  39. Dean L. M.; Wu Q.; Alshangiti O.; Moore J. S.; Sottos N. R. Rapid Synthesis of Elastomers and Thermosets with Tunable Thermomechanical Properties. ACS Macro Lett. 2020, 9, 819–824. 10.1021/acsmacrolett.0c00233. [DOI] [PubMed] [Google Scholar]
  40. Cornell S. W.; Koenig J. L. The Raman Spectra of Polybutadiene Rubbers. Macromolecules 1969, 2, 540–545. 10.1021/ma60011a018. [DOI] [Google Scholar]
  41. Gaston D.; Newman C.; Hansen G.; Lebrun-Grandié D. MOOSE: A Parallel Computational Framework for Coupled Systems of Nonlinear Equations. Nucl. Eng. Des. 2009, 239, 1768–1778. 10.1016/j.nucengdes.2009.05.021. [DOI] [Google Scholar]
  42. Pernice M.; Walker H. F. NITSOL: A Newton Iterative Solver for Nonlinear Systems. SIAM J. Sci. Comput. 1998, 19, 302–318. 10.1137/S1064827596303843. [DOI] [Google Scholar]
  43. Knoll D. A.; Keyes D. E. Jacobian-Free Newton-Krylov Methods: A Survey of Approaches and Applications. J. Comput. Phys. 2004, 193, 357–397. 10.1016/j.jcp.2003.08.010. [DOI] [Google Scholar]
  44. Oliver W. C.; Pharr G. M. An Improved Technique for Determining the Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments. J. Mater. Res. 1992, 7, 1564–158. 10.1557/JMR.1992.1564. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc1c00110_si_001.mp4 (12MB, mp4)
oc1c00110_si_002.mp4 (8.9MB, mp4)
oc1c00110_si_003.mp4 (11.7MB, mp4)
oc1c00110_si_004.pdf (3.9MB, pdf)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES