Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2021 Apr 13;7(4):658–670. doi: 10.1021/acscentsci.0c01699

Computational and Experimental Approaches to Controlling Bacterial Microcompartment Assembly

Yaohua Li †,‡, Nolan W Kennedy §,⊥, Siyu Li †, Carolyn E Mills §, Danielle Tullman-Ercek §,*, Monica Olvera de la Cruz †,‡,§,∥,*
PMCID: PMC8155464  PMID: 34056096

Abstract

graphic file with name oc0c01699_0007.jpg

Bacterial microcompartments compartmentalize the enzymes that aid chemical and energy production in many bacterial species. They are postulated to help bacteria survive in hostile environments. Metabolic engineers are interested in repurposing these organelles for non-native functions. Here, we use computational, theoretical, and experimental approaches to determine mechanisms that effectively control microcompartment self-assembly. We find, via multiscale modeling and mutagenesis studies, the interactions responsible for the binding of hexamer-forming proteins in a model system, the propanediol utilization bacterial microcompartments from Salmonella enterica serovar Typhimurium LT2. We determine how the changes in the microcompartment hexamer protein preferred angles and interaction strengths can modify the assembled morphologies. We demonstrate that such altered strengths and angles are achieved via amino acid mutations. A thermodynamic model provides guidelines to design microcompartments of various morphologies. These findings yield insight in controlled protein assembly and provide principles for assembling microcompartments for biochemical or energy applications as nanoreactors.

Short abstract

A combination of multiscale modeling and experimental validation shows that hexamer−hexamer interactions can control morphologies produced by self-assembly and microcompartment assembly.

Introduction

Compartmentalization of cell components enables a variety of functions and ensures that biochemical processes happen without interfering with one another. Proteins play a crucial role in compartmentalization. Examples of closed compartments formed by protein components include viral capsids, which protect enclosed nucleic acids,1,2 and bacterial microcompartments (MCPs), which aid in the breakdown of chemicals and energy production that allow bacteria to thrive in various environments.3 MCPs, which are polyhedral structures capable of controlling the transport of specific molecules, are found in a large variety of bacterial species.4−6 Due to their native ability to enhance chemical transformations within cells, synthetic biologists are working to repurpose MCPs for non-native, industrially relevant purposes.5,7 Therefore, determining and understanding assembly mechanisms of MCPs are relevant to industry, life, and physical sciences problems.

The envelopes of MCPs are assembled from proteins, much like some viral capsids. Viral capsids that form closed crystalline shells are usually smaller than MCPs and mostly made of isomeric subunits that adopt spherical shapes with icosahedral symmetry or have an icosahedral shape.8−10 In contrast, MCP shells are often irregular in shape, contain multiple types of proteins, and enclose specific enzymes as cargo.11 Three types of shell protein components form the envelope of 1,2-propanediol utilization (Pdu) MCPs, ethanolamine utilization (Eut) MCPs, and many other MCPs.12 These three MCP shell components are composed entirely of two different protein domains, the bacterial microcompartment (BMC) domain (which comprises the hexameric and trimeric proteins) and the bacterial microcompartment vertex (BMV) domain (which comprises the pentameric proteins). Six BMC-domain monomers form the flat, six-sided, hexameric structures (BMC-H); three tandem BMC-domain dimers form the flat, six-sided, pseudohexameric trimers (BMC-T), and five BMV-domain monomers form the flat, five-sided, pentameric structures (BMC-P) (see Scheme S1 in the SI). When hexagonal shape components (BMC-H and BMC-T) assemble with pentagonal components (BMC-P) into closed shells, the topological constraints of Euler’s polyhedron formula are obeyed.13 This formula states that 12 pentagonal components (BMC-P) are needed to form a topologically closed shell. The position of the 12 pentagonal components in a crystalline shell is determined by the “quasiequivalent” triangulations of an icosahedron, which are all possible regular triangulations with 12 pentagonal (5-fold) disclinations.8 The 5-fold disclinations reside at the vertices of an inscribed icosahedron on a sphere,14,15 illustrating the ubiquitous icosahedral symmetry of spherical shells in viruses.8 These disclinations seed the buckling into an icosahedral shape when the shells are large, sufficiently inextensible, and/or highly bendable.16−18 Various models of the BMC-P, BMC-T, and BMC-H components’ assembly into icosahedral MCPs have been proposed in the literature (see Scheme S1 in the SI). However, these models are not always consistent with the observations, which attest that closed shells formed by many MCP systems, including the Pdu MCP system, have complex polyhedral geometries19−21 in which shell protein components are present at different ratios.22,23 Polyhedral MCPs have been predicted in multicomponent closed shells using elasticity theory,24−27 yet the conditions, including protein size, shape, and interactions, to achieve specific structures are unknown. In certain conditions, these MCP proteins assemble to produce extended cylindrical structures.19 A recent study demonstrated that open “icosahedral cages” can be formed in the absence of BMC-P proteins;23 these cages contain open spaces that enable BMC-P binding such that Euler’s polyhedron formula is still obeyed when the shell closes.

While genetic and crystallographic studies have increased the understanding of shell formation and MCP architecture, shell protein mutation studies have also provided information on specific shell protein functionality3 including structure and transport.28 Recent mutation studies that alter the charge of pore amino acids in Pdu MCPs, for example, showed how these mutations affect growth of bacteria harboring these altered MCPs on 1,2-propanediol as a sole carbon source, demonstrating their metabolic importance.7 Moreover, due to the high abundance of BMC-H proteins in the MCP shell,29 the mutations of hexamers that affect interhexamer interactions play a crucial role in determining the MCP assembly.30

Here, we develop a multiscale computational approach and a thermodynamic model combined with mutagenesis studies and experimental observations to analyze the assembly of native and mutated Pdu MCP shell proteins. As an experimental model system, we study the PduA BMC-H protein of Salmonella enterica serovar Typhimurium LT2.31 By computationally studying specific interactions between PduA hexamers, we find the conditions for assembly into closed polyhedral or extended shapes and examine a specific mutation site on these hexamers that affects the assembly of MCPs into different morphologies. We use all-atom (AA) molecular dynamics (MD) simulations to determine the interaction energy and equilibrium bending and twisting angles of native and mutated hexamers and predict what mutations can lead to self-assembly of MCPs or extended shapes. Experimental results with mutated PduA hexamers qualitatively corroborate the simulation predictions. Our study reveals that electrostatic and hydrogen bonding interactions between the arginine and valine residues on the edge of PduA are key to the self-assembly of PduA hexamers and MCP formation, as the majority of the mutations to this residue negatively impact MCP formation.32 We use the structural information and interaction energy from AA MD simulations to construct a coarse-grained (CG) model for PduA self-assembly. Moreover, we determine what assembled geometries are accessible given a different stoichiometric ratio of the 3 major MCP component proteins. Finally, we use this CG framework in combination with a theoretical thermodynamic model to explore how modulating BMC-H/BMC-H and BMC-H/BMC-P interactions can permit access to an array of assembled morphologies. Simulation and theoretical findings agree with in vivo experiments of MCPs with encapsulated green florescent protein (GFP). These findings will help guide future studies that seek to repurpose MCPs with specific morphologies and shed light onto the rules governing MCP assembly in general.

Results

Molecular Dynamic Simulations

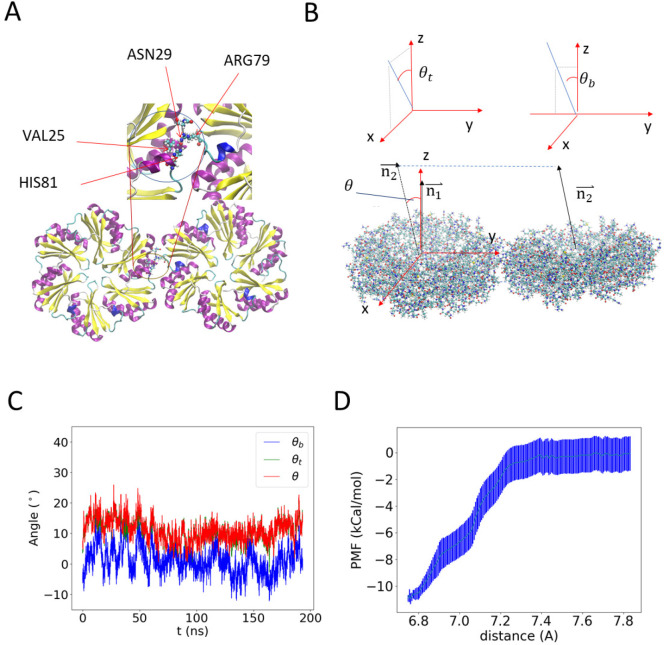
We first investigate the interaction between two native BMC-H subunits using AA MD simulations of the PduA crystal structure from S. enterica LT2 (PDB id: 3ngk).33 BMC-H proteins are found at high abundance in the MCP shell29 and play a crucial role in MCP assembly,30 raising the importance of interhexamer interactions in the molecular layer presumed to comprise the facets of the shell. The two PduA hexamers bind into a highly stable dimer (see Figure 1A and Video S1) as a result of the complementary shape and hydrogen bonding (see Table 1), in which the arginine at the 79th position (ARG79) binds to the backbone carbonyl oxygen of VAL25. The side chain of ARG79 fits in the pocket formed by the residues ASN29, VAL25, HIS81, and LYS26 (Figure 1A, inset). This result agrees with previous studies indicating that ARG79 plays a role in interhexamer binding.32,34−36 To better quantify the relative orientation of the two hexamers, we calculated the angle between the normal vector of the hexagonal planes (Figure 1B), which are determined by the α carbon (the first carbon atom on the amino acid) on 3 residues (ARG79 for the wild type and the corresponding mutated residue for the mutants listed in Table 1) on alternated positions in the hexameric unit (see Figure 1A). The angle is projected onto the y–z plane and x–z plane to decompose into a bending angle θb = 0.4 ± 4° (error bars are standard deviations) and a twisting angle θt = 10 ± 3° at equilibrium (Figure 1C), with a mean total angle θ = 11 ± 4°. (Histograms of the bending and twisting angles are shown in Figure S1.) This calculation suggests that in solution the PduA hexamer complex mostly adopts a near coplanar configuration, corresponding to a near-zero preferred curvature. In the assembled MCP, there is another configuration with the hexamers at a 30° angle relative to each other35 (see Figure S2). The latter bent configuration is likely due to collective interactions among other proteins and enzymes, as shown in our coarse-grained model described below, and therefore, it is not observed in simulations of two proteins.

Figure 1.

Figure 1

Open in a new tab

All-atom (AA) molecular dynamics (MD) simulation results of a pair of PduA hexamers. (A) Equilibrium configuration. The arginine residue on each edge sticks out to form a hydrogen bond with the backbone of valine in the neighboring PduA hexamer. The two arginine residues are highlighted by increased bead size. Water and ions are hidden for visual clarity. (B) Illustration of the reference frame and angle between the two PduA hexamers. The angle θ is decomposed into the twisting angle θt and bending angle θb by projecting the normal of the neighboring protein (n2) onto the X–Z plane and the Y–Z plane, respectively (see Figure S1 for a different representation). (C) MD simulation values of θ, θs, and θb. Negative θb indicates bending toward the concave side of PduA hexamers. (D) The potential of mean force between two PduA hexamers shows an attractive binding energy of about 11 kcal/mol.

Table 1. Hydrogen Bond Analysis of Selected PduA Mutants (Listed as a Percentage of Time during the Simulation).

residue residue 1 residue 2 average
native ARG79-Side; VAL25-Main; 67.16% ARG79-Side; VAL25-Main; 63.93% 65.50%
R79K LYS79-Side; VAL25-Main; 41.54% LYS79-Side; VAL25-Main; 31.34% 36.40%
R79C 0 0 0.00%
R79N ASN79-Side; ALA28-Main; 8.21% ASN79-Side; LYS26-Main; 3.98% 6.10%
R79S SER79-Side; LYS26-Main; 47.51% SER79-Side; LYS26-Main; 27.36% 37.45%
R79T THR79-Side; ASN29-Side; 4.23% THR79-Side; LYS26-Main; 4.73% 4.48%
R79W TRP79-Side; ASN29-Side; 2.24% 0 1.12%
R79Y TYR79-Side; VAL25-Main; 1.74% ASN29-Side; TYR79-Side; 6.97% 4.36%
Open in a new tab

We study the potential of mean force (PMF) of two PduA hexamers using umbrella sampling MD simulations (Figure 1D). The binding energy (εhh,AA) is estimated to be 11 ± 2 kcal/mol. This binding energy falls in the range of reported values of hydrogen bonds,37 further indicating that hydrogen bonds are a major contributor to PduA binding. The calculated binding energy and bending and twisting angles from atomistic simulations provide semiquantitative guidance for building larger-scale models.

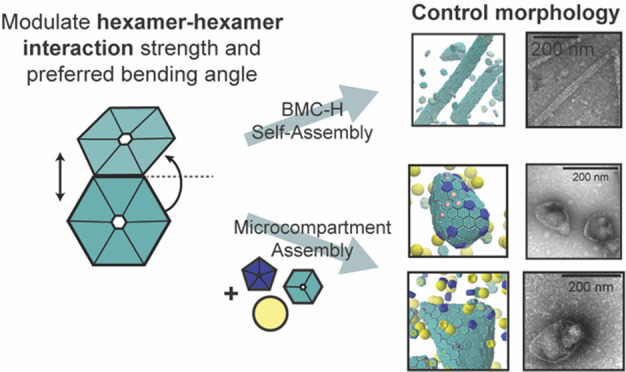
Since AA simulations cannot include many proteins and cover the time scales required to assemble the proteins into different MCP morphologies, we use CG modeling to study the assembly of MCPs at larger time and length scales. CG simulations have been used to follow the assembly of simplified protein models into MCPs or viral capsids.38,39 CG models have also elucidated the initial faceting process40 and the formation of a complete MCP.38,39 However, these models have not investigated how interactions between multiple shell components result in various MCP morphologies such as cylinders, and the molecular origin of spontaneous curvature has not been explained. We hypothesize that the stoichiometric ratio of different components and the interaction strength between them control the morphology of assembly products.12,20,41 We construct a CG model using the approximate shapes and charge distributions of the aforementioned PduA structure (PDB: 3ngk(33)) for the BMC-H model, the PduB homologue from Lactobacillus reuteri (PDB: 4fay(42)) for the BMC-T model, and the PduN homologue GrpN from Rhodospirillum rubrum (PDB: 4i7a(43)) for the BMC-P model. We validate this model by comparing assembled morphologies against known experimental observations of various MCP and cylinder shapes.12,19,20

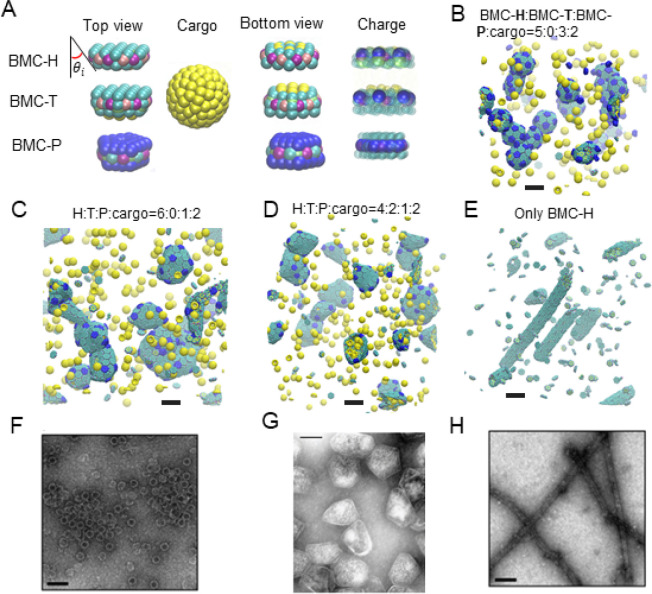
The components of our CG model are shown in Figure 2A. In the CG simulations, the charges of the BMC-H, BMC-T, and BMC-P proteins are computed from the AA structures (see Figure S3); the mechanical properties such as the spontaneous curvature of BMC-H assemblies result from the inclined edge shape, that is, the inclination angle θi ∼ 25° obtained from the PDB (see CG simulation results using other inclination angles in Figures S4 and S5 in the SI). We first explore the various geometries with a different stoichiometric ratio of BMC-H and BMC-P. We find shells with icosahedral symmetry (that is, with 12 pentamers in the position of an inscribed icosahedron on a sphere) assembled with BMC-H:BMC-P = 5:3, which resemble the shape of in vitro MCPs from Haliangium ochraceum(19,35) (Figure 2B). When we reduce the content of BMC-P to BMC-H:BMC-P = 6:1, the addition of hexameric proteins allows the shell to assemble into the irregular shapes of Pdu MCPs reported in the literature,12,20,41 illustrating how varying shell protein contents can control the morphology of MCP structures formed. When a small portion of BMC-H is replaced by BMC-T, similar structures are found (Figures 2C,D). However, when the content of BMC-T further increases, the asphericity increases (see Figure S6), and the BMC-T units seem to segregate, as predicted by elasticity theory of multicomponent shells.25 A detailed structural analysis of assembled MCPs is available in Table S1. The impact of BMC-T on the assembly can be understood by the difference in bending angle and rigidity of the BMC-H and BMC-T (a bending angle analysis is given in the SI). We note that the BMC-H:BMC-P ratio used in these simulations is lower than that typically observed for Pdu MCPs in vivo, and the MCPs simulated are about 20–40 nm in diameter, compared to typical reported Pdu MCP diameters of 40–600 nm.21,41,44,45 These smaller MCPs equilibrate faster, allowing more efficient exploration of parameter space while still qualitatively reproducing the characteristic polyhedral shapes of MCPs observed in experiments.19,20 Simulations with BMC-H:BMC-P ratios of 8:1 produced bigger, more aspherical shells (Figure S7), similar to the shapes found in CG simulations of the MCP assembly.39

Figure 2.

Figure 2

Open in a new tab

Coarse-grained (CG) model and MD simulation results. (A) Illustration of the CG model. The sides of BMC-H and BMC-T are inclined at an angle θi = 25° according to their PDB structures (PDB id 3ngk(33) and 4fay(42)). The green beads interact via excluded volume (changed to blue for pentamers); the purple and pink beads are short-range attractive sites representing the arginine hydrogen bonds. The sphere of yellow beads is the cargo, and the yellow beads on the BMC-H and BMC-T proteins are the residues that bind to the cargo. To show the negative (blue) and positive (green) charged sites clearly, all the noncharged sites are shown as semitransparent and in smaller size on the right column. (B–E) Snapshots of CG simulations (the hexamers, pentamers, and cargo are in green, blue, and yellow, respectively): a red dot is marked on the center of BMC-T to distinguish them from BMC-H. Scale bars are 14 nm. (B) A system without BMC-T and with a ratio BMC-H:BMC-P:cargo = 5:3:2 forms shells with icosahedral symmetry (T = 3) resembling in vitro electron micrographs of compartments from Haliangium ochraceum (F) which also form spherical shells with icosahedral symmetry (T = 9). (C, D) Increasing the number of BMC-H or adding BMC-T can enable assembly into polyhedral shapes that resemble the shape of purified MCPs shown in part F. (E) BMC-H proteins alone form cylinders, reproducing observations of the in vitro BMC-H assembly shown in part D. Detailed model parameters for these simulation results are provided in Table S1. Part G is reprinted with permission from ref (20). Copyright 2010 National Academy of Sciences. Parts F and H are reprinted with permission from ref (19). Copyright 2018 American Chemical Society.

Long cylinders are obtained when only BMC-H proteins are in the assembly, as shown in Figure 2E. The shape is consistent with both in vivo and ex vivo experiments,34,46 in which overexpressing PduA proteins resulted in the assembly of long cylindrical tubes, and in vitro experiments in which the BMC-H from H. ochraceum spontaneously assembled into tubes in the absence of other shell proteins.19 The ability to reproduce vastly different shapes (cylinders and polyhedra) suggests that this simple CG model captures the key interactions of Pdu MCP proteins.

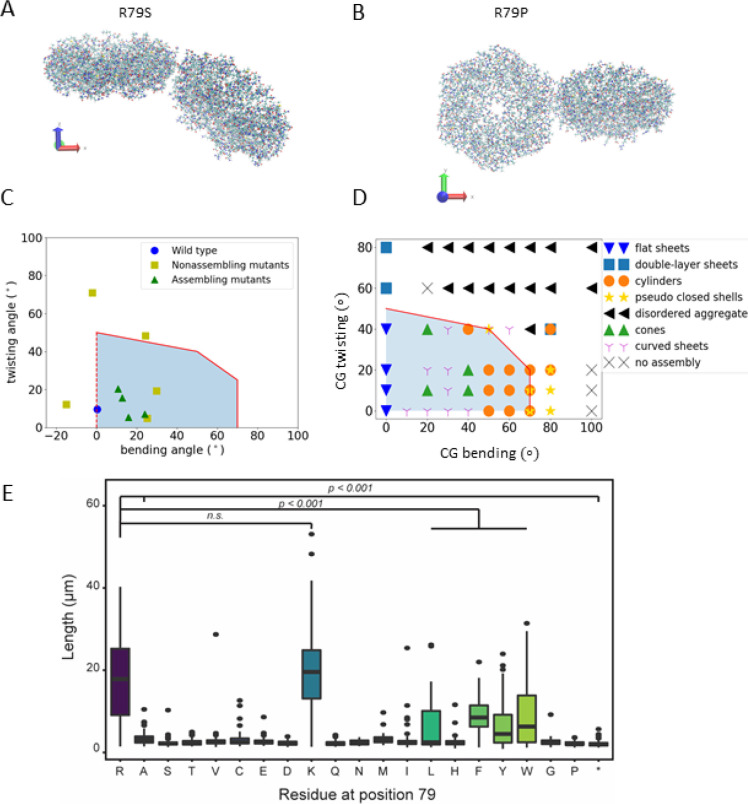
After validating our CG model by comparing the results with experimentally observed morphologies at different stoichiometries, we explore how the docking angle of BMC-H proteins impacts MCP assembly. AA MD simulations reveal (Table 2) that the docking angle of BMC-H can be tuned by mutating the arginine at the binding site. To this end, we use a combination of AA MD simulations, mutation experiments, and CG modeling to determine the role of hexamer–hexamer interactions on BMC-H assembly. AA MD simulations, the PduA conservation score (Figure S8), and prior work in the field11,32,34,35 indicate that the arginine at the 79th position (ARG79) is a key residue for controlling PduA interactions. Thus, we hypothesized that mutations to ARG79 of PduA could impact PduA and, subsequently, MCP assembly. We perform AA simulations of the hexamer–hexamer interface on 14 PduA mutants. Of these, 11 mutants retain some degree of hexamer–hexamer interfacial contact for the duration of the simulations, and their bending and twisting angles are shown in Figure 3A–C. Three mutants result in hexamers that entirely dissociate from each other, completely eliminating interfacial contacts (Table 2 and Figure S9 in the SI provide further details). The hexamer–hexamer dissociation arises when ARG79 is replaced by a negatively charged residue or hydrophilic residue with low isoelectric point (aspartic acid, glutamic acid, and glutamine), indicating that Coulombic interactions play an important role in stabilizing the hexamer–hexamer interface in PduA. The α helix of the opposite hexamer has a negative partial charge, which is thought to complement the native, positively charged ARG79 residue.36 Therefore, mutating ARG79 to the opposite charge results in total dissociation of the PduA.

Table 2. Summary of All-Atom Molecular Dynamics Simulation Resultsa.

mutation hydrophobicity or charge bending/deg twisting/deg assemble cylinder binding energy (kcal/mol)
native positive charge 0.4 10 Y –11 ± 2
R79K positive charge 24 7 Y –11 ± 2
R79D negative charge detach detach N N/A
R79E negative charge detach detach N N/A
R79Q hydrophilic (5.65) detach detach N N/A
R79N hydrophilic 25 4.8 N N/A
R79S hydrophilic 24 48 N N/A
R79T hydrophilic 30 19 N N/A
R79Y hydrophilic 12 15 Y N/A
R79C hydrophilic –15 12 N N/A
R79A hydrophobic 8 35 N N/A
R79P hydrophobic –2 71 N –15 ± 2
R79L hydrophobic 11 20 Y N/A
R79F hydrophobic 16 5 Y N/A
R79W hydrophobic 8 27 Y –17 ± 2
Open in a new tab
a

Negative bending angles indicate bending towards the outside of PduA. In the binding energy column, negative values correspond to attractive interactions.

Figure 3.

Figure 3

Open in a new tab

PduA mutant orientation studies. An example of a mutation with large bending angle is shown in part A, and one with a large twisting angle is shown in part B. (C) Twisting and bending angle calculated for the 11 R79 mutation from AA simulations (corresponding to the data in Table 2). The PMF for 3 mutations and WT are calculated and shown in Table 2. The red line indicates the critical angle to form extended structures as predicted by CG simulations. Triangle and square markers indicate whether the mutants self-assemble in experiments (part E and Figure S10). (D) Morphologies formed in CG simulation of 256 PduA proteins with given bending and twisting angles. The shaded area below the solid red lines in parts C and D indicates that the system can form extended structures, which we predict to cause long chains of cells to form in experiments. At bending angles of 70° and 80°, the pseudoclosed shells (yellow stars) resemble quasi-icosahedra of T = 1 in that each hexamer has 5 neighbors (Figure S11). (E) Distribution of cell length populations for each PduA variant. R79R (WT) and R79K were significantly longer than other PduA variants (p < 0.001, t test).

Mutagenesis Experiment Comparison with Simulations of the Hexamer Assembly

We turned to an experimental approach to assess the assembly of PduA mutants and validate the above-described AA MD simulations. When PduA is overexpressed in E. coli cells, it naturally assembles into long cylinders that span the length of the cell body. The assembled protein structures form bundles within the cell cytoplasm, preventing cell division and leading to extended chains of cells30 (Figure S10). This allows for cell length to be used as a proxy for protein assembly and allows us to rapidly assess the assembly state of different PduA mutants. We hypothesized that mutants which formed stable dimers and had limited bending and twisting angles in AA MD simulations would be more likely to lead to the linked cell phenotype, indicative of protein self-assembly into cylinders. Indeed, the two PduA variants predicted to form hydrogen bonds (the native ARG79 and the R79K mutant, where “R79K” indicates that the arginine (R) at 79th position in the protein sequence is mutated to a lysine (K)) have among the lowest bending and twisting angles in simulations (Figure 3C, Table 2), and overexpression of both proteins leads to highly elongated cells (Figure 3E, Figure S10) compared to the negative control mutants (R79A and R79*, where “*” indicates a stop codon) (p < 0.0001). We also verified that the expression level of various PduA mutants did not correlate strongly with cell length, indicating that differences in assembly state are not likely to be due to differences in expression (Figure S11). These results indicate successful assembly of wild-type (WT) PduA and PduA-R79K into cylinders. Surprisingly, we found that substitution of ARG79 with large hydrophobic residues (R79L) or aromatic residues (R79F, R79Y, R79W) also enabled some amount of assembly, as indicated by the presence of linked cells during overexpression (Figure 3E, Figure S10), although to a lesser degree than the native ARG79 (p < 0.001). While initially surprising, this assembly is predicted by the low bending and twisting angles calculated for these mutants from our simulations (Figure 3C). Free energy calculations for the binding energy of select mutants are also provided (R79K, R79W, and R79P; see Table S2), but these do not correlate as well with cell length as bending and twisting angles—while hydrophobic residues tryptophan (R79W) and proline (R79P) have similar binding energies, experiments indicate that they do not exhibit a similar self-assembly behavior. Overall, two residues that form hydrogen bonds (R79R and R79K) and aromatic residues (R79W, R79F, and R79Y) both confer small bending and twisting angles between hexamers. Together, these results imply that bending and twisting angles as determined by our AA MD simulations can provide insight into the assembly of PduA.

The combination of experimental and AA simulation results described above suggests that PduA assembly is largely influenced by the inclination angle θi and twisting angle θt between hexamers. To understand what assembled morphologies may be accessed by these different PduA mutants, we performed CG MD simulations on PduA alone (no other proteins and no cargo) using the BMC-H model described above and documented how preferred inclination and twisting angle between hexamers impacts the morphology of PduA-only structures formed (Figure 3D). From the inclined geometry assumed in the CG model, the resulting bending angle between two hexamer planes is approximately 2θi (see Figure 2A and Figure S4A). The CG model predicts that, at small θi, the mutated PduA assemble into extended structures (flat/curve sheet, cylinder/cone) with low curvature, whereas at large θi, the hexamers form structureless aggregates or nonextended pseudoclosed shells with high curvature (see Figure S12 for snapshots of assembled morphologies). The flat or curved sheets are expected to roll into cylinders or cones in the confinement of the cell. The predicted critical angles for self-assembly into extended structures from CG simulations are given by the red line in Figure 3C,D. We note that several nonassembling mutants have bending and twisting angles (calculated by AA simulations) below this line. This quantitative discrepancy is because AA simulations have detailed interatomic interactions omitted in the CG model that overestimate the CG critical bending and twisting angle. That is, agreement with the in vivo experiments is found if we take into account this shift by moving the red line to the lower left. Taken together, the AA and CG simulations indicate that pure PduA hexamers that form interfaces with small bending and twisting angles can assemble into extended structures. Mutations with big angles, despite having comparable attractive interaction strength, tend to form pseudoclosed shells, unstructured aggregates, and stacked layers (see Figure S12 in the SI).

Multicomponent Microcompartment Assembly: Thermodynamic Model Comparison with Coarse-Grained Simulations and Experiments

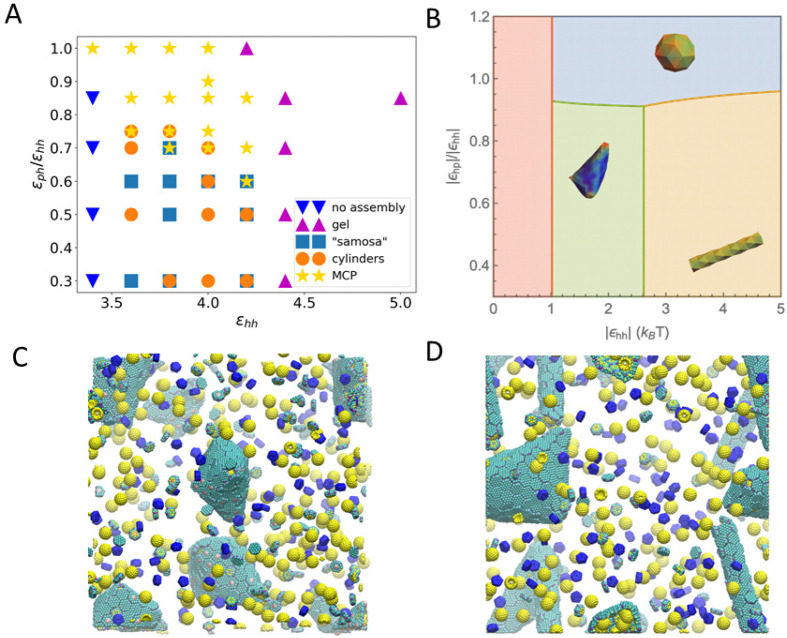
Extending our exploration of how shell protein interactions impact MCP assembly, we next used CG MD simulations and thermodynamic modeling to explore how hexamer–hexamer and pentamer–hexamer interaction strengths impact assembled morphologies. We hypothesized that modulating these interaction strength ratios would allow us to tune the morphologies of MCPs formed, enabling downstream engineering efforts. The thermodynamic model is constructed by numerically minimizing a free energy that includes protein–protein binding, protein–cargo interaction, elastic penalty of shell bending, and chemical potentials (see the Materials and Methods section), using parameters consistent with the CG model described in the previous section. Based on the hexamer–hexamer binding energies calculated in our R79 mutation simulations, we specified a range of accessible BMC-H/BMC-H (εhh) and BMC-H/BMC-P (εph) interaction energies. We used a protein ratio of BMC-H:BMC-T:BMC-P:cargo = 4:2:1:2 for CG simulations (Figure 4A). For simplicity, the interaction parameters for BMC-T/BMC-T and BMC-T/BMC-H were set equal to the BMC-H/BMC-H interaction energy, because PduB trimers have conserved arginines in positions analogous to the arginines on PduA hexamers, and these are thought to be critical for binding35 (in Figure S6D, we discuss the effect of changing these values). The data shown in Figure 4A are for a BMC-H and BMC-T inclination angle of θi = 25°; however, data taken for an inclination angle of 15° produce qualitatively similar morphologies and trends (Figure S4B), suggesting that the observed trends hold for a variety of inclination angles.

Figure 4.

Figure 4

Open in a new tab

(A) Phase diagram of assembled shapes from CG MD simulations. The axes are the ε parameters defined in eq 1. The simulation box is constructed from a unit of 4 μBC–H, 2 μBC-T, 2 enzymes, and 1 μBC–P, replicated 5 times in x, y, and z directions. (B) Phase diagram from thermodynamics analysis (see parameters used in Table S5 in the SI). When the hexamers’ binding energy is weak, there is no assembly (red region). With stronger hexamer–hexamer interaction εhh, MCP, cylindrical, and samosa shaped shells are formed, corresponding to the blue, yellow, and green regions, respectively. (C, D) Snapshots of CG simulations (the hexamers, pentamers, and cargo are in green, blue, and yellow, respectively; a red dot is marked on the center of BMC-T to distinguish them from BMC-H). (C) The “samosa” shape (εhh = 3.8, εph = 1.9) is a quasiclosed surface without BMC-P proteins. They are different from MCPs in that they have no pentamers, and the vertices are sharp cones with a hole or defect at the tip. An example of a 4-fold defect is shown in the center. (D) Coexistence of cylinders and “samosas” at (εhh = 3.8, εph = 2.28).

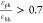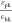The different morphologies predicted by the CG simulation and by the thermodynamic theory as a function of pentamer–hexamer and hexamer–hexamer interactions are shown Figure 4A,B, respectively. The phase diagram constructed using CG MD simulations shows that closed MCP structures form when Inline graphic, and εhh is between 3.6 and 4.2. This range of energy values corresponds to a hexamer–hexamer attraction energy between 4 and 6 kcal/mol, obtained using eq 1, which does not include the repulsion caused by screened electrostatics (adding this screened Coulomb energy contribution, the overall attractive energy is between 3.6 and 5.6 kcal/mol). When hexamer–hexamer interaction strength is increased beyond this MCP-forming range (εhh > 4.4), the proteins bind irreversibly and assemble into gel-like structures. When hexamer–hexamer attractions are weakened (εhh < 3.4), no assembled morphologies are observed. When εph is small compared to εhh (Inline graphic < 0.7), assembled structures do not contain pentamers. These structures include cylinders and structures resembling “samosas” with 4-fold coordinated defective holes at the corners (Figure 4C). We note that these samosa-like structures are also observed when inextensible sheets are folded to form a quasiclosed surface, for example, in macroscopic inelastic membranes.47

The thermodynamic theory (described in the Materials and Methods section) predicts changes in morphology with changing pentamer–hexamer (ϵph) and hexamer–hexamer (ϵhh) interaction energies. By comparing the formation energy of each tested morphology, we obtain the phase diagram shown in Figure 4B. In the region of ϵhh < 1.0kBT (in red), the nucleation barrier is large, and as a result, no shells could be formed. At a moderate value of ϵhh, the shells can assemble into multiple shapes depending on the value of ϵph. When ϵph is sufficiently high, a small, closed shell (MCP) (blue region) results. In the lower pentamer–hexamer interaction region, hexamers aggregate without pentamers, and in such a case, cargo is required to provide the curvature to close the shell. The competition between the cargo–hexamer interaction and the bending energy decides whether a cylindrical shape or a “samosa” shape is assembled. While the cylindrical shells can encapsulate dense cargo at a considerable bending energy cost, the “samosa” shell can encapsulate loose cargo at a smaller bending energy penalty. These results are in qualitative agreement with the CG simulations in Figure 4A, except that the CG simulations for large εhh values produce gels of connected sheets trapped in a local minimum. The lack of quantitative agreement can be explained by the fact that the thermodynamic model assumes equilibrium and constant reservoir concentrations during the assembly.

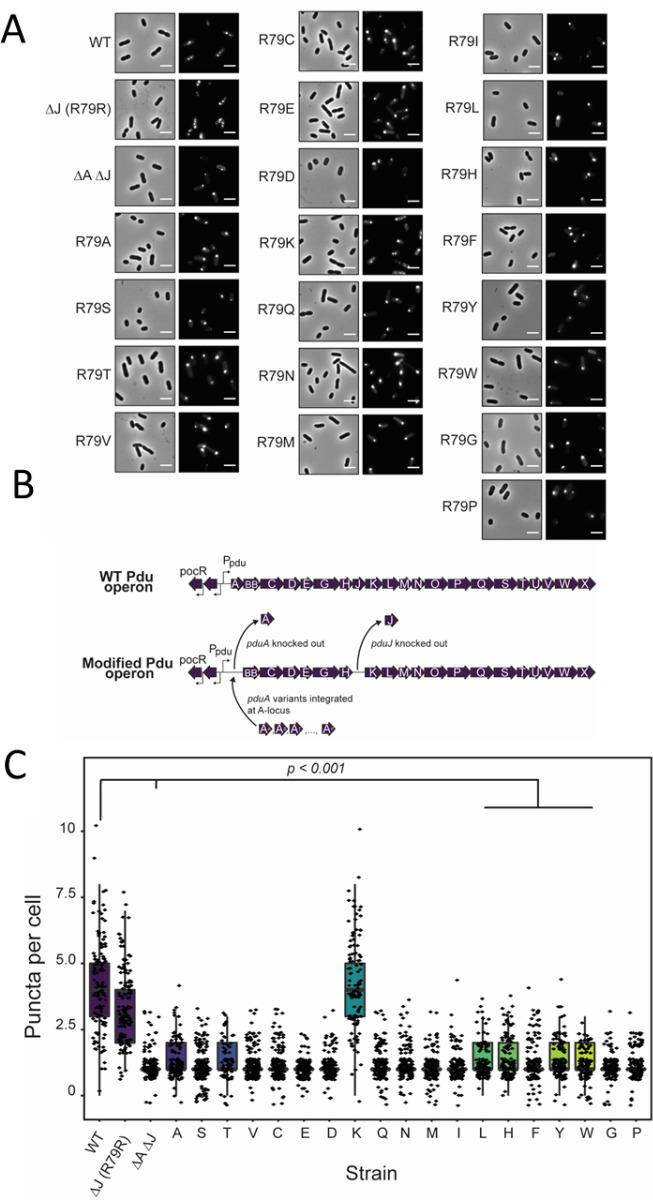
Many of the morphologies observed in our CG simulations (Figure 4) have been observed in the literature for different MCP systems assembled under various conditions (Figure 5),20,34,43,46 supporting our hypothesis that shell protein interaction strength plays an important role in determining MCP morphology. To provide experimental support for the observed effects of changing hexamer–hexamer binding energy on MCP assembly in our models, we used a green fluorescent protein (GFP) encapsulation assay to probe MCP formation in strains expressing the PduA mutants characterized above. In this assay, GFP is fused to an N-terminal signal sequence that is sufficient for targeting GFP to the lumen of MCPs.20,48 This results in bright, fluorescent puncta in the cell cytoplasm if MCPs are present (Figure 6A). However, if MCPs do not form properly, fluorescence will be observed instead at one or both poles of the cells; these are termed polar bodies (Figure 6A). In this way, it is possible to determine if a strain is capable of forming MCPs.

Figure 5.

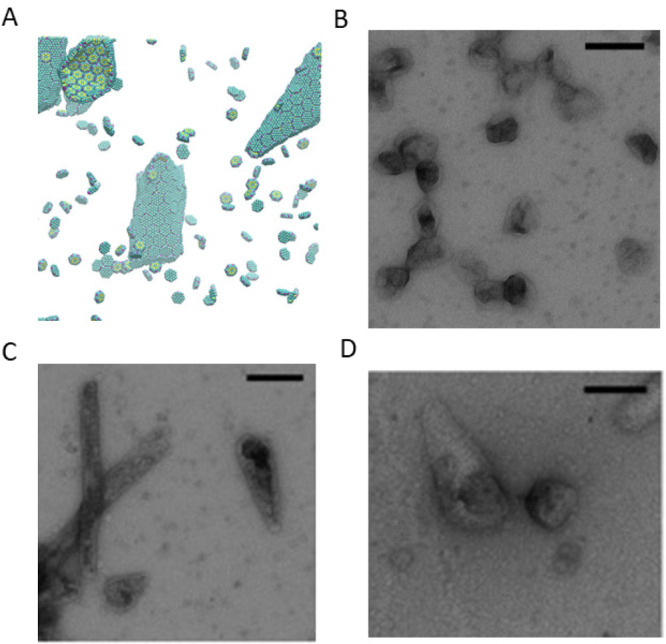
Figure 5

Open in a new tab

Additional morphologies formed in the CG model and comparisons to morphologies observed by TEM in experiments. (A) With a slightly smaller tilting angle, a system of only BMC-H can form cones similar to the ones observed in parts C and D. (B) Native MCP shells have a similar shape compared to simulated MCPs with BMC-H, BMC-T, and BMC-P in Figure 2C,D. When BMC-P has weaker interactions (εhh = 3.8, εph = 2.28) as shown in Figure 4D the proteins form coexisting cylinders and “samosas”, similar to those observed in parts C and D. Parts B–D are reprinted with permission from ref (22). Copyright 2020 Elsevier.

Figure 6.

Figure 6

Open in a new tab

(A) GFP encapsulation assay for PduA variant strains. Phase contrast microscopy (left) and fluorescence (right) micrographs of modified Salmonella strains. GFP-containing MCPs appear as bright puncta in the cell cytoplasm (see the WT image), while malformed MCPs appear as polar bodies (see the ΔA ΔJ image). Scale bar = 3 μm. (B) Pdu operon modification strategy. Schematic representation of strains with a modified Pdu operon. WT PduA is replaced with PduA variants, and PduJ is knocked out in all variant strains. (C) Population distribution of puncta (MCPs) per cell for each strain. ΔJ and ΔA::R79K ΔJ had significantly more puncta per cell than other variant strains and the negative control ΔA ΔJ strain (p < 0.001, t test).

To this end, we constructed 19 mutant strains of Salmonella enterica serovar Typhimurium LT2 to test the effect of altering PduA assembly on overall MCP assembly. Alterations were made to the pdu operon as shown in Figure 6B. Because PduJ is capable of overcoming loss of PduA function,30 we have knocked out the pduJ open reading frame from these strains. Thus, the WT and ΔJ strains serve as positive controls, as these both contain functional, WT PduA. Note that fluorescent puncta are visible throughout the cytoplasm of these strains, as expected when MCPs form (Figure 6A). The ΔA ΔJ strain, in which both the pduA and pduJ open reading frames have been knocked out, serves as a negative control. Only polar bodies are observed in this strain, indicating improper MCP assembly (Figure 6A). In the experimental strains, a point mutant of PduA is encoded at the pduA locus (Figure 6A), and puncta were counted in each cell to determine the effect of these mutants on MCP assembly. Notably, only strains containing PduA mutants capable of forming hydrogen bonds (R79R and R79K) are also capable of forming MCPs (Figure 6C). These strains had significantly more puncta than all other mutant strains (p < 0.001) (Figure 6C). This includes strains that were demonstrated to have lower, but detectable, levels of assembly (R79L, R79F, R79Y, R79W) (Figure 3E). This is likely due to the fact that these strains are not able to form hydrogen bonds with the adjacent hexamer and therefore have lower binding stabilities. To confirm these results, we attempted to purify MCPs from a number of the PduA point mutant strains which did not show MCP assembly in the GFP encapsulation assay. However, we were unable to purify MCPs from these strains, as evidenced by the lack of the standard MCP banding pattern by sodium dodecyl sulfate gel electrophoresis (SDS-PAGE) (Figure S13). Together, these results demonstrate that only PduA variants capable of forming hydrogen bonds enable MCP assembly. This validates the results shown in Figure 4A which indicates that reduction of εhh disrupts MCP assembly and leads to no assembly.

Discussion and Conclusion

Combined multiscale MD simulations and in vivo mutation experiments show that hydrogen bonding and Coulomb interactions of arginine residues on the hexamer edges (ARG79) of PduA play a crucial role in native PduA self-assembly. In our experiments, mutations of ARG79 to most other residues negatively affect the assembly of Pdu proteins into tubes, cones, or polyhedral compartments. From the 14 mutations tested by AA MD simulations, we find that those that have smaller bending and twisting angles are shown experimentally to be more likely to assemble into extended structures.

We determine the shape of these extended structures (tubes or cones) and confirm that small twisting and bending angles promote their formation by performing coarse-grained (CG) MD simulations. The CG model also determines the conditions to form polyhedral and icosahedral shells. MCPs contain hexamers, pseudohexameric trimers, and pentamers, which are incorporated in our CG model. Our CG model includes twisting and bending by considering the shape, the position of the charges, and specific short-range interaction (including hydrogen bonding and hydrophobic interaction) of Pdu proteins in the form of BMC-H, BMC-T, and BMC-P structures. In agreement with our experimentally observed trends, the CG model predicts that small bending and twisting angles facilitate PduA self-assembly into extended cylinders. However, the agreement is only qualitative because the CG bending angle used in our CG simulations is overestimated; that is, it tends to be larger than the equilibrium bending angle obtained in the AA simulations, which include more detailed interactions.

According to our CG MD simulations, BMC-H proteins that maintain proper bending and twisting angles can form MCPs when BMC-P proteins and BMC-T proteins are present, and BMC-P interactions with BMC-H are strong enough. For BMC-P/BMC-H mixtures that can form MCPs, the number ratio of BMC-H to BMC-P determines the size and asphericity of assembled shells, with a higher ratio of BMC-H leading to larger, more elongated shells. We find that increasing the content of BMC-T increases the asphericity of assembled structures (Figure S6) because BMC-T prefers smaller bending angles. All crystalline closed shells should have 12 pentamers required by Euler’s theorem.13 However, we see fluctuations in the number of pentamers in some MCPs. Moreover, in some assemblies, pentameric units are stuck in 6-coordinated sites. This may be due to local kinetic traps that are not overcome by annealing (see the Materials and Methods section). Only in a few cases, when BMC-H and BMC-P units coassemble without BMC-T units, are the 12 pentamers further away from each other forming spherical shells with icosahedral symmetry, which are too small and/or too rigid to buckle into icosahedral shapes.16

Other morphologies including “samosas” and cylinders arise in our CG simulations and theoretical arguments by modifying the hexamer and pentamer interactions. These morphologies are robust in simulations using other CG bending angles (see Figures S4 and S5) and are also observed using a thermodynamic model that includes interactions, bending energies, and concentrations of the components via chemical potentials. Our experiments demonstrate that reducing the hexamer–hexamer interaction strength abolishes MCP assembly in GFP encapsulation assays, as predicted by our CG MD simulations and theory. Our work explains the necessary conditions for BMC domain proteins to assemble into closed MCPs, as well as cylinders, and suggests that it is possible to systematically modify the shape of the resulting assembled structures.

Materials and Methods

All-Atom (AA) Molecular Dynamics (MD) Simulations

The PduA hexamers (PDB id: 3ngk) in the AA MD simulations are downloaded from the PDB and solvated in water containing 100 mM NaCl and 4 mM MgCl2. Afterward, the system undergoes a short constant volume, temperature (NVT) equilibration of 100 ps with the backbone restrained. Then, restraints are released for one PduA hexamer, while the other still has a backbone restraint, and constant pressure, temperature (NPT) production simulations of 100 ns and umbrella sampling simulations are performed. For native PduA, an NPT extended simulation of 200 ns is performed; the PduA–PduA angle calculated is similar to 100 ns simulations. More details for AA MD simulations are in the SI.

Coarse-Grained (CG) MD Simulations

The BMC-H, BMC-T, and BMC-P models include short-range attractive interactions modeled by a Lennard-Jones–Gauss potential on a pair of attractive sites on the side of CG proteins (Figure 2A), given by

graphic file with name oc0c01699_m003.jpg 1

where σ = 1.0 nm is the bead size; r0 is 1.2 nm roughly corresponding to the length of arginine side chain; ij refers to the three species, p for pentamer (BMC-P), h for hexamer (BMC-H), and t for trimer (BMC-T); and εij is the binding energy between species i and j, where we choose the hexamer–hexamer interaction based on the AAMD simulation (εhh = εhh,AA + μ, μ is the CG chemical potential). To reduce the enormous parameter space, the value of εij is set equal for the BMC-H and BMC-T proteins. The consequence of this assumption is discussed in the SI. εph is unknown and left as a free parameter (see Table S2). In addition to the hydrogen bonding, the proteins’ charges (Figure 2A, right column) interact via a screened Coulomb potential with Debye length of 0.91 nm. The resulting total hexamer–hexamer interaction from two sites is then about −7kBT (or −4.4 kcal/mol) per edge. The spherical cargo is a generic model for enzymes encapsulated in MCPs; they are attracted to BMC-H and BMC-T proteins at six sites by a standard 12–6 Lennard-Jones (LJ) potential with ε = 1.8, resulting in a total cargo/shell protein binding energy of ∼−7.5 kBT. The energy scale for this LJ potential was selected such that the cargo can bind to BMC-H and BMC-T, but the MCP structures are not heavily deformed by the strength of the cargo/shell protein attraction. Note that the hexamer–hexamer interaction energy in the CG model is smaller than that calculated from AA simulations because the protein concentration in CG simulations is higher (See the appendix in the SI for details of MD simulations).

Plasmid and Strain Creation

All plasmids and strains used in this study are listed in Tables S3 and S4. For modifications to the Pdu operon in LT2, λ red recombineering was used as previously described (see the Extended Materials and Methods section in the SI).

PduA Self-Assembly Assay

The PduA self-assembly assay was carried out as previously described (see the Extended Materials and Methods section in the SI). Once cultures were grown to saturation, strains were imaged using phase contrast microscopy. All images were adjusted equally for brightness and contrast and were cropped to an area of 500 × 500 pixels. Measurements of cell length were done using the segmented line tool in ImageJ as described previously.30

Western Blot

Western blots were done on cell cultures expressing FLAG-tagged PduA variants (see the Extended Materials and Methods section in the SI).

GFP Encapsulation Assay

The GFP encapsulation assay was carried out to measure differences in MCP assembly between PduA variant strains as described in previous manuscripts (see the Extended Materials and Methods section in the SI20).

Thermodynamic Theory

In this section, we describe the thermodynamic model that explains the morphologies observed in CG MD simulations. Consider Ns protein monomers (corresponding to BMC-H hexamers in the MD simulations) and Nc enzyme cargo initially placed in the simulation box. When the system reaches equilibrium, the monomers are distributed either as free monomers (N0) or as subunits of an oligomer (Nq) that contains q monomers. The total number of monomers is conserved by the relation Ns = N0 + qNq. Similarly, the free (Ncf) and encapsidated (Nce) cargo is subject to the conservation constraint Nc = Ncf + Nce. The free energy thus can be written as a sum of ideal free energy of each component and the interaction energy arising from shell bending energy, monomer–monomer binding energy, and the cargo–monomer interaction:

graphic file with name oc0c01699_m004.jpg 2

where v0 denotes the standard volumetric cell size (a3), with a approximated by the monomer size; and ϵbend, ϵbond, and ϵc represent the bending energy, binding energy per monomer, and cargo–monomer interaction, respectively. Note that we have assumed that the total internal energies for monomers (U0 + Uq) and cargo (Uc) are constant.

Minimizing the free energy with respect to the number of free monomers, we obtain the equilibrium condition

graphic file with name oc0c01699_m005.jpg 3

and the law of mass action for the particle density49

graphic file with name oc0c01699_m006.jpg

where ΔG = qϵ – qμ0 – Nceμc is the formation energy with the excess energy given by 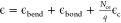Inline graphic, and the monomer and cargo chemical potentials are μ0 = kBT ln(ρ0ν0) and μc = kBT ln(ρcfν0), respectively.

To investigate the formation of the shell, we incorporate the line tension50,51 so that

graphic file with name oc0c01699_m008.jpg 4

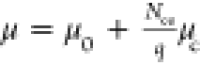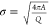where Inline graphic and Inline graphic, Q is the monomer number of a complete shell, and 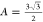Inline graphic is the area factor of hexamer. Since the main contribution to the bending energy comes from the block geometry, it is reasonable to set the corresponding rigidity (kb) as a piece-wise function, i.e., kb = 0 when no geometry overlaps, and kb is finite when overlap occurs. In such a case, only the corners of samosa shape and cylinder shape assemblies are subject to the bending penalty, with the local curvature defined by the cargo size (rc). Thus, we write the formation energy for each morphology as

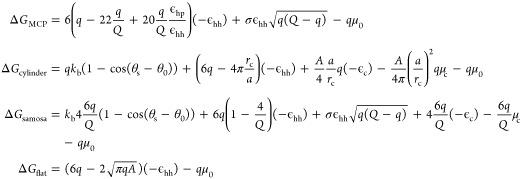graphic file with name oc0c01699_m012.jpg

where θs is the angle between normal vectors of connected subunits, and θ0 is the spontaneous angle determined by the intrinsic properties of the protein. (see Table S5 for the list of thermodynamic parameters).

Acknowledgments

Y.L., S.L., and M.O.d.l.C. were supported by Department of Energy Award DE-FG02-08ER46539 and thank the Sherman Fairchild Foundation for computational support and Baofu Qiao for helpful discussions. D.T.-E. and C.E.M. were supported by Army Research Office Award W911NF-19-1-0298. N.W.K. was supported by the National Science Foundation Graduate Research Fellowship Program (DGE-1842165), and by the National Institutes of Health Training Grant (T32GM008449) through Northwestern University’s Biotechnology Training Program.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.0c01699.

  • Additional schematics, figures, tables, details of MD simulation, and experimental methods (PDF)

  • Video S1: Constant pressure, temperature all-atom simulation of native 2 PduA hexamer proteins (pdb id 3ngk) in an aqueous solution with 100 mM NaCl and 4mM MgCl2 (MPG)

  • Video S2: Coarse-grained system of 500 BMC-H, 250 BMC-T, 125 BMC-P, and 250 cargo quickly assembling into polyhedral MCPs, followed by slow relaxation of correcting malformed units such as flipped BMC-T or BMC-P with incorrect coordination number (MPG)

Author Contributions

# Y.L. and N.W.K. contributed equally to this work

The authors declare no competing financial interest.

Supplementary Material

oc0c01699_si_001.pdf (1.3MB, pdf)
oc0c01699_si_002.mpg (19.3MB, mpg)
oc0c01699_si_003.mpg (39.7MB, mpg)

References

  1. Zandi R.; Dragnea B.; Travesset A.; Podgornik R. On virus growth and form. Phys. Rep. 2020, 847, 1–102. 10.1016/j.physrep.2019.12.005. [DOI] [Google Scholar]
  2. Garmann R. F.; Goldfain A. M.; Manoharan V. N. Measurements of the self-assembly kinetics of individual viral capsids around their RNA genome. Proc. Natl. Acad. Sci. U. S. A. 2019, 116 (45), 22485–22490. 10.1073/pnas.1909223116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Kerfeld C. A.; Aussignargues C.; Zarzycki J.; Cai F.; Sutter M. Bacterial microcompartments. Nat. Rev. Microbiol. 2018, 16 (5), 277. 10.1038/nrmicro.2018.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Jorda J.; Lopez D.; Wheatley N. M.; Yeates T. O. Using comparative genomics to uncover new kinds of protein-based metabolic organelles in bacteria. Protein Sci. 2013, 22 (2), 179–195. 10.1002/pro.2196. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chowdhury C.; Chun S.; Pang A.; Sawaya M. R.; Sinha S.; Yeates T. O.; Bobik T. A. Selective molecular transport through the protein shell of a bacterial microcompartment organelle. Proc. Natl. Acad. Sci. U. S. A. 2015, 112 (10), 2990–2995. 10.1073/pnas.1423672112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Axen S. D.; Erbilgin O.; Kerfeld C. A. A taxonomy of bacterial microcompartment loci constructed by a novel scoring method. PLoS Comput. Biol. 2014, 10 (10), e1003898 10.1371/journal.pcbi.1003898. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Slininger Lee M. F.; Jakobson C. M.; Tullman-Ercek D. Evidence for improved encapsulated pathway behavior in a bacterial microcompartment through shell protein engineering. ACS Synth. Biol. 2017, 6 (10), 1880–1891. 10.1021/acssynbio.7b00042. [DOI] [PubMed] [Google Scholar]
  8. Caspar D. L.; Klug A. In Physical principles in the construction of regular viruses; Cold Spring Harbor symposia on quantitative biology; Cold Spring Harbor Laboratory Press, 1962; pp 1–24. [DOI] [PubMed]
  9. Waltmann C.; Asor R.; Raviv U.; Olvera de la Cruz M. Assembly and stability of simian virus 40 polymorphs. ACS Nano 2020, 14 (4), 4430–4443. 10.1021/acsnano.9b10004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Li S.; Roy P.; Travesset A.; Zandi R. Why large icosahedral viruses need scaffolding proteins. Proc. Natl. Acad. Sci. U. S. A. 2018, 115 (43), 10971–10976. 10.1073/pnas.1807706115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Tsai S. J.; Yeates T. O.. Bacterial microcompartments: insights into the structure, mechanism, and engineering applications. In Progress in molecular biology and translational science; Elsevier, 2011; Vol. 103, pp 1–20. [DOI] [PubMed]
  12. Cheng S.; Liu Y.; Crowley C. S.; Yeates T. O.; Bobik T. A. Bacterial microcompartments: their properties and paradoxes. BioEssays 2008, 30 (11–12), 1084–1095. 10.1002/bies.20830. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Euler L. Elementa doctrinae solidorum. Novi commentarii academiae scientiarum Petropolitanae 1758, 109–140. [Google Scholar]
  14. Bowick M.; Cacciuto A.; Nelson D. R.; Travesset A. Crystalline order on a sphere and the generalized Thomson problem. Phys. Rev. Lett. 2002, 89 (18), 4. 10.1103/PhysRevLett.89.185502. [DOI] [PubMed] [Google Scholar]
  15. Zandi R.; Reguera D.; Bruinsma R. F.; Gelbart W. M.; Rudnick J. Origin of icosahedral symmetry in viruses. Proc. Natl. Acad. Sci. U. S. A. 2004, 101 (44), 15556–15560. 10.1073/pnas.0405844101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lidmar J.; Mirny L.; Nelson D. R. Virus shapes and buckling transitions in spherical shells. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2003, 68 (5), 051910. 10.1103/PhysRevE.68.051910. [DOI] [PubMed] [Google Scholar]
  17. Vernizzi G.; Olvera de la Cruz M. Faceting ionic shells into icosahedra via electrostatics. Proc. Natl. Acad. Sci. U. S. A. 2007, 104 (47), 18382–18386. 10.1073/pnas.0703431104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Emanuel M. D.; Cherstvy A. G.; Metzler R.; Gompper G. Buckling transitions and soft-phase invasion of two-component icosahedral shells. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2020, 102 (6), 26. 10.1103/PhysRevE.102.062104. [DOI] [PubMed] [Google Scholar]
  19. Hagen A. R.; Plegaria J. S.; Sloan N.; Ferlez B.; Aussignargues C.; Burton R.; Kerfeld C. A. In vitro assembly of diverse bacterial microcompartment shell architectures. Nano Lett. 2018, 18 (11), 7030–7037. 10.1021/acs.nanolett.8b02991. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Fan C.; Cheng S.; Liu Y.; Escobar C. M.; Crowley C. S.; Jefferson R. E.; Yeates T. O.; Bobik T. A. Short N-terminal sequences package proteins into bacterial microcompartments. Proc. Natl. Acad. Sci. U. S. A. 2010, 107 (16), 7509–7514. 10.1073/pnas.0913199107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kennedy N. W.; Hershewe J. M.; Nichols T. M.; Roth E. W.; Wilke C. D.; Mills C. E.; Jewett M. C.; Tullman-Ercek D. Apparent size and morphology of bacterial microcompartments varies with technique. PLoS One 2020, 15 (3), e0226395 10.1371/journal.pone.0226395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Nichols T. M.; Kennedy N. W.; Tullman-Ercek D. A genomic integration platform for heterologous cargo encapsulation in 1, 2-propanediol utilization bacterial microcompartments. Biochem. Eng. J. 2020, 156, 107496. 10.1016/j.bej.2020.107496. [DOI] [Google Scholar]
  23. Sutter M.; McGuire S.; Ferlez B.; Kerfeld C. A. Structural characterization of a synthetic tandem-domain bacterial microcompartment shell protein capable of forming icosahedral shell assemblies. ACS Synth. Biol. 2019, 8 (4), 668–674. 10.1021/acssynbio.9b00011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Vernizzi G.; Sknepnek R.; Olvera de la Cruz M. Platonic and Archimedean geometries in multicomponent elastic membranes. Proc. Natl. Acad. Sci. U. S. A. 2011, 108 (11), 4292–4296. 10.1073/pnas.1012872108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Sknepnek R.; Vernizzi G.; Olvera de la Cruz M. Buckling of multicomponent elastic shells with line tension. Soft Matter 2012, 8 (3), 636–644. 10.1039/C1SM06325A. [DOI] [Google Scholar]
  26. Bowick M. J.; Sknepnek R. Pathways to faceting of vesicles. Soft Matter 2013, 9 (34), 8088–8095. 10.1039/c3sm51729b. [DOI] [Google Scholar]
  27. Haselwandter C. A.; Phillips R. Elastic energy of polyhedral bilayer vesicles. Phys. Rev. E 2011, 83 (6), 17. 10.1103/PhysRevE.83.061901. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Tanaka S.; Sawaya M. R.; Yeates T. O. Structure and mechanisms of a protein-based organelle in Escherichia coli. Science 2010, 327 (5961), 81–84. 10.1126/science.1179513. [DOI] [PubMed] [Google Scholar]
  29. Yang M.; Simpson D. M.; Wenner N.; Brownridge P.; Harman V. M.; Hinton J. C.; Beynon R. J.; Liu L.-N. Decoding the stoichiometric composition and organisation of bacterial metabolosomes. Nat. Commun. 2020, 11 (1), 1976. 10.1038/s41467-020-15888-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kennedy N. W.; Ikonomova S. P.; Slininger Lee M.; Raeder H. W.; Tullman-Ercek D. Self-assembling shell proteins PduA and PduJ have essential and redundant roles in bacterial microcompartment assembly. J. Mol. Biol. 2021, 433 (2), 166721. 10.1016/j.jmb.2020.11.020. [DOI] [PubMed] [Google Scholar]
  31. Bobik T. A.; Havemann G. D.; Busch R. J.; Williams D. S.; Aldrich H. C. The Propanediol Utilization (pdu) Operon of Salmonella enterica serovar Typhimurium LT2 Includes Genes Necessary for Formation of Polyhedral Organelles Involved in Coenzyme B12-Dependent 1, 2-Propanediol Degradation. J. Bacteriol. 1999, 181 (19), 5967–5975. 10.1128/JB.181.19.5967-5975.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Sinha S.; Cheng S.; Sung Y. W.; McNamara D. E.; Sawaya M. R.; Yeates T. O.; Bobik T. A. Alanine scanning mutagenesis identifies an asparagine-arginine-lysine triad essential to assembly of the shell of the Pdu microcompartment. J. Mol. Biol. 2014, 426 (12), 2328–2345. 10.1016/j.jmb.2014.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Crowley C. S.; Cascio D.; Sawaya M. R.; Kopstein J. S.; Bobik T. A.; Yeates T. O. Structural insight into the mechanisms of transport across the Salmonella enterica Pdu microcompartment shell. J. Biol. Chem. 2010, 285 (48), 37838–37846. 10.1074/jbc.M110.160580. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Pang A.; Frank S.; Brown I.; Warren M. J.; Pickersgill R. W. Structural insights into higher order assembly and function of the bacterial microcompartment protein PduA. J. Biol. Chem. 2014, 289 (32), 22377–22384. 10.1074/jbc.M114.569285. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Sutter M.; Greber B.; Aussignargues C.; Kerfeld C. A. Assembly principles and structure of a 6.5-MDa bacterial microcompartment shell. Science 2017, 356 (6344), 1293–1297. 10.1126/science.aan3289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Tsai Y.; Sawaya M. R.; Cannon G. C.; Cai F.; Williams E. B.; Heinhorst S.; Kerfeld C. A.; Yeates T. O. Structural analysis of CsoS1A and the protein shell of the Halothiobacillus neapolitanus carboxysome. PLoS Biol. 2007, 5 (6), e144 10.1371/journal.pbio.0050144. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Desiraju G. R.; Steiner T.. The weak hydrogen bond: in structural chemistry and biology; International Union of Crystal, 2001; Vol. 9. [Google Scholar]
  38. Mohajerani F.; Hagan M. F. The role of the encapsulated cargo in microcompartment assembly. PLoS Comput. Biol. 2018, 14 (7), e1006351 10.1371/journal.pcbi.1006351. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Rotskoff G. M.; Geissler P. L. Robust nonequilibrium pathways to microcompartment assembly. Proc. Natl. Acad. Sci. U. S. A. 2018, 115 (25), 6341–6346. 10.1073/pnas.1802499115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Mahalik J.; Brown K. A.; Cheng X.; Fuentes-Cabrera M. Theoretical study of the initial stages of self-assembly of a carboxysome’s facet. ACS Nano 2016, 10 (6), 5751–5758. 10.1021/acsnano.5b07805. [DOI] [PubMed] [Google Scholar]
  41. Tanaka S.; Sawaya M. R.; Phillips M.; Yeates T. O. Insights from multiple structures of the shell proteins from the β-carboxysome. Protein Sci. 2008, 18 (1), 108–120. 10.1002/pro.14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Pang A.; Liang M.; Prentice M. B.; Pickersgill R. W. Substrate channels revealed in the trimeric Lactobacillus reuteri bacterial microcompartment shell protein PduB. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2012, 68 (12), 1642–1652. 10.1107/S0907444912039315. [DOI] [PubMed] [Google Scholar]
  43. Wheatley N. M.; Gidaniyan S. D.; Liu Y.; Cascio D.; Yeates T. O. Bacterial microcompartment shells of diverse functional types possess pentameric vertex proteins. Protein Sci. 2013, 22 (5), 660–665. 10.1002/pro.2246. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Price G. D.; Badger M. R. Evidence for the role of carboxysomes in the cyanobacterial CO2-concentrating mechanism. Can. J. Bot. 1991, 69 (5), 963–973. 10.1139/b91-124. [DOI] [Google Scholar]
  45. Nichols T. M.; Kennedy N. W.; Tullman-Ercek D.. Cargo encapsulation in bacterial microcompartments: Methods and analysis. In Methods in enzymology; Elsevier, 2019; Vol. 617, pp 155–186. [DOI] [PMC free article] [PubMed]
  46. Havemann G. D.; Sampson E. M.; Bobik T. A. PduA is a shell protein of polyhedral organelles involved in coenzyme B12-dependent degradation of 1, 2-propanediol in Salmonella enterica serovar Typhimurium LT2. J. Bacteriol. 2002, 184 (5), 1253–1261. 10.1128/JB.184.5.1253-1261.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Paulsen J. D.; Démery V.; Santangelo C. D.; Russell T. P.; Davidovitch B.; Menon N. Optimal wrapping of liquid droplets with ultrathin sheets. Nat. Mater. 2015, 14 (12), 1206–1209. 10.1038/nmat4397. [DOI] [PubMed] [Google Scholar]
  48. Kim E. Y.; Tullman-Ercek D. A rapid flow cytometry assay for the relative quantification of protein encapsulation into bacterial microcompartments. Biotechnol. J. 2014, 9 (3), 348–354. 10.1002/biot.201300391. [DOI] [PubMed] [Google Scholar]
  49. Morozov A. Y.; Bruinsma R. F.; Rudnick J. Assembly of viruses and the pseudo-law of mass action. J. Chem. Phys. 2009, 131 (15), 155101. 10.1063/1.3212694. [DOI] [PubMed] [Google Scholar]
  50. Zandi R.; van der Schoot P.; Reguera D.; Kegel W.; Reiss H. Classical nucleation theory of virus capsids. Biophys. J. 2006, 90 (6), 1939–1948. 10.1529/biophysj.105.072975. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Luque A.; Reguera D.; Morozov A.; Rudnick J.; Bruinsma R. Physics of shell assembly: Line tension, hole implosion, and closure catastrophe. J. Chem. Phys. 2012, 136 (18), 184507. 10.1063/1.4712304. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc0c01699_si_001.pdf (1.3MB, pdf)
oc0c01699_si_002.mpg (19.3MB, mpg)
oc0c01699_si_003.mpg (39.7MB, mpg)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES