Non-Negative Spherical Deconvolution (NNSD) for Estimation of Fiber Orientation Distribution Function in Single-/Multi-Shell Diffusion MRI

Abstract

Spherical Deconvolution (SD) is commonly used for estimating fiber Orientation Distribution Functions (fODFs) from diffusion-weighted signals. Existing SD methods can be classified into two categories: 1) Continuous Representation based SD (CR-SD), where typically Spherical Harmonic (SH) representation is used for convenient analytical solutions, and 2) Discrete Representation based SD (DR-SD), where the signal profile is represented by a discrete set of basis functions uniformly oriented on the unit sphere. A feasible fODF should be non-negative and should integrate to unity throughout the unit sphere ${\mathbb{S}}^2$. However, to our knowledge, most existing SH-based SD methods enforce non-negativity only on discretized points and not the whole continuum of ${\mathbb{S}}^2$. Maximum Entropy SD (MESD) and Cartesian Tensor Fiber Orientation Distributions (CT-FOD) are the only SD methods that ensure non-negativity throughout the unit sphere. They are however computational intensive and are susceptible to errors caused by numerical spherical integration. Existing SD methods are also known to overestimate the number of fiber directions, especially in regions with low anisotropy. DR-SD introduces additional error in peak detection owing to the angular discretization of the unit sphere. This paper proposes a SD framework, called non-negative SD (NNSD), to overcome all the limitations above. NNSD is significantly less susceptible to the false-positive peaks, uses SH representation for efficient analytical spherical deconvolution, and allows accurate peak detection throughout the whole unit sphere. We further show that NNSD and most existing SD methods can be extended to work on multi-shell data by introducing a three-dimensional fiber response function. We evaluated NNSD in comparison with Constrained SD (CSD), a quadratic programming variant of CSD, MESD, and an L1-norm regularized non-negative least-squares DR-SD. Experiments on synthetic and real single-/multi-shell data indicate that NNSD improves estimation performance in terms of mean difference of angles, peak detection consistency, and anisotropy contrast between isotropic and anisotropic regions.

1. Introduction

Diffusion MRI (dMRI) non-invasively reveals the microstructure of white matter by capturing the diffusion patterns of water molecules. The most widely used dMRI approach, Diffusion Tensor Imaging (DTI), captures one fiber direction per voxel and is incapable of describing complex diffusion processes due to its Gaussian diffusion assumption (Johansen-Berg and Behrens, 2009). In view of this, many High Angular Resolution Diffusion Imaging (HARDI) (Tuch et al., 2002) methods, have been developed in recent years to characterize non-Gaussian diffusion and compute quantities such as the Ensemble Average Propagator (EAP) (Wedeen et al., 2005; Descoteaux et al., 2010; Cheng et al., 2010b; Özarslan et al., 2009; Cheng et al., 2012), diffusion Orientation Distribution Function (dODF) (Tuch, 2004; Hess et al., 2006; Descoteaux et al., 2007; Aganj et al., 2010; Cheng et al., 2010a, 2012), and fiber Orientation Distribution Function (fODF) (Tournier et al., 2004, 2007; Alexander, 2005; Jian and Vemuri, 2007; Dell’Acqua et al., 2007, 2010; Landman et al., 2012; Weldeselassie et al., 2012).

Spherical Deconvolution (SD) has been shown to be effective for estimating the fODF by assuming that the measured diffusion-weighted signal can be obtained via spherically convolving a latent fODF with a fiber response function estimated from voxels known to be traversed by a single fascicle (Tournier et al., 2004, 2007; Jian and Vemuri, 2007; Johansen-Berg and Behrens, 2009). The fODF can hence be recovered via an inverse problem by deconvolving the signal with the estimated fiber response function. The local peaks (maxima) of the fODF give the corresponding fiber directions. SD methods can be classified into two categories, 1) Continuous Representation based SD (CR-SD), which is normally based on the Spherical Harmonic (SH) basis (Tournier et al., 2004, 2007; Anderson, 2005), and 2) Discrete Representation based SD (DR-SD), which is based on a discrete mixture of rotated versions of the fiber response function (Jian and Vemuri, 2007; Dell’Acqua et al., 2007, 2010; Landman et al., 2012).

Existing SD methods in both continuous and discrete representation categories share some common limitations. First, they often result in false-positive fiber directions (Tournier et al., 2004, 2007; Alexander, 2005; Johansen-Berg and Behrens, 2009; Jian and Vemuri, 2007; Landman et al., 2012; Weldeselassie et al., 2012), especially in low-anisotropy gray matter and cerebrospinal fluid (CSF) regions. Second, they normally fall short in ensuring that the estimated fODF is a proper probability density function, because non-negativity and unit integral throughout the unit sphere are not explicitly enforced. Most SD methods, including the popular Constrained SD (CSD) (Tournier et al., 2007) and all DR-SD methods (Jian and Vemuri, 2007; Dell’Acqua et al., 2007, 2010; Landman et al., 2012), consider non-negativity only on discretized points but not the whole continuum of the unit sphere ${\mathbb{S}}^2$. To the best of our knowledge, Maximum Entropy SD (MESD) (Alexander, 2005) and Cartesian Tensor Fiber Orientation Distributions (CT-FOD) (Weldeselassie et al., 2010, 2012) are the only existing methods that ensure non-negativity throughout ${\mathbb{S}}^2$. However, they are computationally inefficient and rely on the error-prone process of numerical spherical integration. Ad-hoc normalization is also employed in these methods to obtain fODFs with unit integral. Some methods estimate continuously non-negative dODFs (Schwab et al., 2012; Cheng et al., 2012; Krajsek and Scharr, 2012) and EAPs (Cheng et al., 2012) using eigenvalue distribution of spherical functions and square root representation. But to our knowledge, none of these methods has been proposed to estimate continuously non-negative fODF in a SD framework. Third, for estimation of the fODF with reasonable accuracy, DR-SD methods (Jian and Vemuri, 2007; Dell’Acqua et al., 2007, 2010; Landman et al., 2012) require a significant amount of rotated fiber response functions along directions that are distributed densely on the unit sphere, significantly increasing the dimensionality and the time cost of the optimization problem. Furthermore, since for DR-SD methods (Jian and Vemuri, 2007; Dell’Acqua et al., 2007, 2010; Landman et al., 2012) the local peaks (maxima) of the fODF are detected from discretized points on the unit sphere, the angular resolution is limited.

To our knowledge, existing SD methods deal only with single-shell data (i.e., single b-value) and do not consider the radial component of diffusion. With advances in dMRI, multi-shell data are increasingly available (e.g., Human Connectome Project (HCP)¹ (Sotiropoulos et al., 2013)). For example, the HCP Q1 data² come with three b-values (b = 1000/2000/3000s/mm²). Recent estimation methods such as the ball-stick model (Jbabdi et al., 2012), Q-Ball Imaging (Aganj et al., 2010), and other multi-shell HARDI methods (Assemlal et al., 2011; Cheng et al., 2010b,a; Descoteaux et al., 2010; Özarslan et al., 2009) demonstrated that ODF, EAP as well as fiber directions can be estimated with greater accuracy from multi-shell data compared with single-shell data. However, there is currently no existing work on how to perform SD on multi-shell data.

In this paper, we propose a method called Non-Negative Spherical Deconvolution (NNSD) to estimate fODF from both single- and multi-shell data. The main contributions of this paper are summarized as follows:

• NNSD is the first SH-based SD method to guarantee non-negativity throughout ${\mathbb{S}}^2$, not only on discretized points on the unit sphere, as in CSD (Tournier et al., 2007). In NNSD, non-negativity is achieved by representing the square root of the fODF as a linear combination of SH basis functions. Compared with non-SH methods like MESD and CT-FOD, which also guarantee non-negativity on the whole ${\mathbb{S}}^2$, NNSD is significantly faster due to the use of closed-form expression for spherical convolution. Compared with CSD which suppresses negative values in discrete samples using iteratively re-weighted regularization, the non-negativity constraint in NNSD is built into its fODF representation and hence NNSD works well even without any regularization.

• In addition to the non-negativity constraint, NNSD reduces spurious peaks by implementing Riemannian gradient descent with an adaptive stopping condition. As a result, the anisotropy values of the fODFs estimated by NNSD in gray and white matter regions exhibit large contrast. Existing SD methods result in many false-positive peaks and hence high anisotropy in regions that are less anisotropic.

• Compared with traditional single-shell methods, we show that multi-shell data can be used for fODF estimation with greater robustness.

• Performance evaluation using real data is difficult due to the lack of ground truth. We propose in this paper a measure called Peak Consistency (PC) for quantitative fODF evaluation without exact knowledge of the ground truth.

Part of this work has been reported in our conference paper (Cheng et al., 2013b,a). Herein, we provide additional examples, results, derivations, and insights that are not part of this conference publication.

The rest of the paper is organized as follows. SD theory and algorithms are reviewed in Section 2. Section 2.1 provides an overview of existing SD methods using single-/multi-shell data, i.e. CSD (Tournier et al., 2007), a variant of CSD based on quadratic programming, MESD (Alexander, 2005), and DR-SD via L1 regularized non-negative least-squares fitting (L1-NNLS) (Jian and Vemuri, 2007; Landman et al., 2012). Section 2.2 describes NNSD and the associated Riemannian gradient descent algorithm. Two stopping strategies for Riemannian gradient descent are discussed. Section 3 furnishes evaluation details, including fiber response function estimation (Section 3.1), peak detection (Section 3.2), synthetic data generation (Section 3.3), and peak consistency evaluation (Section 3.4). In Section 4, NNSD is evaluated in comparison with the methods discussed in Section 2.1. Section 5 provides additional discussions on various aspects of NNSD. Section 6 concludes this paper.

2. Theory

2.1. Spherical Deconvolution Revisited

In this section, we describe CSD, MESD, and L1-NNLS, which were originally proposed for single-shell data, and generalize them for multiple-shell data. We also proposed a new implementation of CSD using quadratic programming.

Constrained SD (CSD).

SD (Tournier et al., 2004; Anderson, 2005) methods assume that the measured signal in each voxel is the product of convolving a latent fODF with an axisymmetric fiber response function. For $u\in {\mathbb{S}}^2$, the fODF is represented as

$$\Phi (u)=\sum _{l=0}^L\sum _{m=-l}^l{f}_{lm}{Y}_l^m(u),$$ (1)

and the axisymmetric 3D fiber response function along the z-axis is represented as

$$H(qu\mid (0,0,1))=\sum _{l=0}^L{h}_l(q)Y_l^0(u),$$ (2)

where $Y_l^m(u)$ is the l order m degree real SH basis function (Johansen-Berg and Behrens, 2009; Descoteaux et al., 2007) defined in spherical coordinates as

$$Y_l^m(\theta ,\varphi )=\{\begin{array}{ll}\sqrt{2}\text{Re}\left(y_l^{\left|m\right|}(\theta ,\varphi )\right)\hfill & \text{ if }-l\le m<0,\hfill \\ y_l^m(\theta ,\varphi )\hfill & \text{ if }m=0,\hfill \\ \sqrt{2}\text{Im}\left(y_l^m(\theta ,\varphi )\right)\hfill & \text{ if \hspace{1em}}0<m\le l,\hfill \end{array}$$ (3)

$$y_l^m(\theta ,\varphi )=\sqrt{\frac{2l+1}{4\pi }\frac{(l-m)!}{(l+m)!}}{e}^{im\varphi }{P}_l^m(\text{cos\hspace{0.17em}}\theta ).$$ (4)

Re(·) and Im(·) denote respectively the real and imaginary parts of a complex number. $P_l^m(\cdot )$ is the associated Legendre polynomial. Since the fODF is antipodal symmetric, only even l’s are used. Based on the property of spherical convolution and spherical harmonics (Tournier et al., 2004; Anderson, 2005), the diffusion signal can be represented in closed form as the convolution of the fiber response function with the fODF (Tournier et al., 2004) using

$$E(qu)={\int }_{{\mathbb{S}}^2}H(qu\mid r)\Phi (r)\text{d}r=\sum _{l=0}^L\sum _{m=-l}^l\sqrt{\frac{4\pi }{2l+1}}{f}_{lm}{h}_l(q)Y_l^m(u).$$ (5)

Note that in the original formulation (Tournier et al., 2004), signal measurements are performed on a single-shell in the q-space³, fixing q at a certain value. In the current work, we let q vary and define the fiber response function in ${ℝ}^3$, hence allowing the coefficients {h_l(q)} to vary across shells. This generalization allows us to extend CSD to work with multi-shell data. Based on Eq. (1) and Eq. (2), the SH coefficient vector f = (f₀₀, …, f_LL)^T of the fODF can be estimated via

$$\underset{\mathit{f}}{\text{min}}\Vert M\mathit{f}-E{\Vert }_2^2,$$ (6)

where $M=\left[\sqrt{\frac{4\pi }{2l+1}}{h}_l\left(q_i\right)Y_l^m\left(u_i\right)\right]$ is an $N\times \frac{(L+1)(L+2)}{2}$ basis matrix that is the element-wise product between the SH basis matrix $\left[Y_l^m\left(u_i\right)\right]$ and the radial basis matrix $\left[\sqrt{\frac{4\pi }{2l+1}}{h}_l\left(q_i\right)\right]$, and E = (E₁, …, E_N)^T is the measured signal vector, including samples from single shell or multiple shells. The least-squares solution is (M^TM)⁻¹M^TE (Tournier et al., 2004). Due to the smoothness of H(qu), h_l(q) decreases to zero as l increases, causing instability in estimating f_lm when l is large. Therefore, Tournier et al. (2004) proposed a low-pass Filtered SD (FSD) by down-weighting the high-order SH coefficients. However, FSD is known to result in many false-positive peaks because fODF non-negativity is not considered. In view of this, Constrained SD (CSD) (Tournier et al., 2007) attempts to iteratively suppress the negative values by a discrete reconstruction of each fODF estimate, i.e.

$${\mathit{f}}^{(k+1)}=\underset{\mathit{f}}{\text{argmin}}\parallel M\mathit{f}-E{\parallel }_2^2+{\lambda }_{\text{CSD}}^2{\Vert L^{(k)}\mathit{f}\Vert }_2^2,$$ (7)

where $L_{i,j}^{(k)}=P_{i,j}\text{ if }{\left(P{\mathit{f}}^{(k)}\right)}_i<\tau$, $L_{i,j}^{(k)}=0\text{ if }{\left(P{f}^{(k)}\right)}_i>\tau$, and P is a matrix for reconstructing the fODF at discretized points on ${\mathbb{S}}^2$. τ is a threshold normally chosen as 0.1 (Tournier et al., 2007). Note that non-negativity is only imposed on a set of discretized points, not throughout the whole unit sphere. Although CSD reduces significantly the negative values compared with FSD (Tournier et al., 2004), a significant amount of negative values still exist, even at points where non-negativity is imposed. An implementation of CSD for single shell data is available via MRtrix⁴ (Tournier et al., 2012).

Maximum Entropy SD (MESD).

MESD is a CR-SD method that involves solving a non-linear least-squares problem using the Levenberg-Marquardt algorithm (Alexander, 2005). Based on the maximum entropy principle, the fODF is represented as an exponential function of the mixture of fiber response functions, i.e.,

$$\underset{{\left\{{\lambda }_j\right\}}_{i=0}^K}{\text{min}}\sum _{i=1}^N{\left({\int }_{{\mathbb{S}}^2}H\left(q_i\mid r\right)\Phi \left(r\mid {\left\{{\lambda }_j\right\}}_{j=0}^K\right)\text{d}r-E_i\right)}^2,$$ (8)

$$\Phi \left(r\mid {\left\{{\lambda }_j\right\}}_{j=0}^K\right)=\text{exp}\left({\lambda }_0+\sum _{j=1}^K{\lambda }_{j}H\left(q_j\mid r\right)\right),$$ (9)

where N is the number of diffusion-weighted samples. The exponential representation naturally ensures non-negativity on ${\mathbb{S}}^2$. However, without any closed-form expression for spherical convolution as in Eq. (5), the spherical integration in Eq. (8) needs to be approximated numerically. Based on the method of Lagrange multipliers and the maximum entropy principle, K should ideally be equal to N and the sampling points ${\left\{q_j\right\}}_{j=1}^K$ should correspond to the N sampling points of the diffusion-weighted signal (Alexander, 2005). However, as a trade-off between accuracy and speed, only K < N evenly distributed points are used⁵. After estimating ${\left\{{\lambda }_j\right\}}_{j=0}^K$, ad-hoc normalization of the fODF needs to be performed for unit integral. CT-FOD (Weldeselassie et al., 2010, 2012), which achieves non-negativity by representing the fODF using a sum of squares of homogeneous polynomials, share the same limitations as MESD by relying on numerical spherical integral and ad-hoc normalization.

L1-NNLS.

DR-SD uses a discrete representation of the fODF: {w_i = Φ(u_i)} (Jian and Vemuri, 2007; Landman et al., 2012; Yap and Shen, 2012).

The SD problem in this case is typically formulated as

$$\underset{\mathit{w}}{\text{min}}\parallel A\mathit{w}-E{\parallel }_2^2+{\lambda }_{L1}\parallel \mathit{w}{\parallel }_1,\text{\hspace{1em} s.t. \hspace{1em}}\mathit{w}\ge 0,$$ (10)

where A is a matrix with columns containing rotated versions of the fiber response function, and λ_L1 is the sparsity tuning parameter. We refer to this method as L1 regularized Non-Negative Least Squares (L1-NNLS). The problem in Eq. (10) can be solved using efficient algorithms, such as those reported in (Lee et al., 2006; Kim et al., 2007). When λ_L1 = 0, Eq. (10) becomes the Non-Negative Least Squares (NNLS) (Landman et al., 2012; Jian and Vemuri, 2007; Dell’Acqua et al., 2007). The Richardson-Lucy SD (Dell’Acqua et al., 2007), another DR-SD method, was shown to converge to the solution of NNLS in the case of Gaussian noise (De Pierro, 1993). The sparsity of the solution increases as λ_L1 increases. If λ_L1 is large enough, all elements in w are zero. Landman et al. (2012) proposed to determine λ_L1 based on the so-called breakdown parameter ${\lambda }_{L1}^{*}={\Vert 2A^{\text{T}}E\Vert }_{\infty }$, which is the minimal λ_L1 that causes w = 0 (Kim et al., 2007). Experimentally, Landman et al. (2012) set ${\lambda }_{L1}=0.1{\lambda }_{L1}^{*}$. We followed this approach for experiments performed in this paper. Since the fODF in L1-NNLS is represented using discretized points, peak detection is restricted to these points instead of the whole ${\mathbb{S}}^2$, limiting the angular resolution.

QP-CSD.

We propose a quadratic programming implementation of CSD (QP-CSD) for imposing non-negativity in a manner that is more similar to NNLS, i.e.,

$$\underset{f}{\text{min}}\parallel M\mathit{f}-E{\parallel }_2^2,\text{\hspace{1em} s.t. \hspace{1em}}{f}_{00}=\frac{1}{\sqrt{4\pi }},P\mathit{f}\ge 0,$$ (11)

where $f_{00}=\frac{1}{\sqrt{4\pi }}$ ensures unit integral

$${\int }_{{\mathbb{S}}^2}\Phi (u)\text{d}u={\int }_{{\mathbb{S}}^2}\sum _{l=0}^L\sum _{m=-l}^l{f}_{lm}{Y}_l^m(u)\text{d}u=1.$$ (12)

QP-CSD, unlike CSD, produces the global solution and guarantees non-negativity on fODF points specified by matrix P. Compared with L1-NNLS, QP-CSD works in a low dimension space thanks to the SH representation and allows peak detection to be performed on the continuous sphere.

2.2. Non-Negative Spherical Deconvolution (NNSD)

SH-based SD methods are able to leverage the nice property of having a closed-form solution to spherical deconvolution. But currently they fall short in enforcing non-negativity throughout the unit sphere. To address this issue, we propose a new approach called Non-Negative Spherical Deconvolution (NNSD), which we will describe next.

2.2.1. Square Root Representation of the fODF

The square root representation has been proposed for the dODF (Cheng et al., 2009) and the EAP (Cheng et al., 2011), and it has been used for non-negative dODF and EAPs estimation (Cheng et al., 2012). In this work, we propose to utilize the square root representation for non-negative fODF estimation by letting

$$\begin{gathered} \Phi (u\mid \mathit{c})={\left(\sum _{l=0}^L\sum _{m=-l}^l{c}_{lm}{Y}_l^m(u)\right)}^2 \\ =\sum _{\alpha =0}^{2L}\sum _{\beta =-\alpha }^{\alpha }\underset{f_{\alpha \beta }}{\underbrace{\left(\sum _{l,m}^L\sum _{l^{\prime },m^{\prime }}^L{c}_{lm}{c}_{l^{\prime }{m}^{\prime }}{Q}_{l{l}^{\prime }\alpha }^{m{m}^{\prime }\beta }\right)}}{Y}_{\alpha }^{\beta }(u), \end{gathered}$$ (13)

where

$$Q_{l{l}^{\prime }\alpha }^{m{m}^{\prime }\beta }={\int }_{{\mathbb{S}}^2}{Y}_l^m(u)Y_{l^{\prime }}^{m^{\prime }}(u)Y_{\alpha }^{\beta }(u)\text{d}u.$$ (14)

The notation ${\sum }_{l,m}^L$ is a shorthand for ${\sum }_{l=0}^L{\sum }_{m=-l}^l$. $Q_{l{l}^{\prime }\alpha }^{m{m}^{\prime }\beta }$ is a constant resulting from the integration of three real SH functions (Cheng et al., 2012), which can be calculated from the Wigner 3-j symbol and Eq. (3). Note that the sum over α is up to 2L, because when α > 2L, $Q_{l{l}^{\prime }\alpha }^{m{m}^{\prime }\beta }=0$, based on the property of the Wigner 3-j symbol⁶.

Note that 1) a SH representation of $\sqrt{\Phi (u)}$ with maximum order L corresponds to a SH representation of Φ(u) with maximum order 2L. Therefore compared with Eq. (1), the square root representation Eq. (13) is more compact in representing high angular resolution information. This is also contributive to reducing the Gibbs ringing artifact associated with the truncation of the SH series (Raffelt et al., 2012); 2) the fODF is naturally non-negative throughout ${\mathbb{S}}^2$ due to the square root representation.

Based on Eq. (2), Eq. (5) and Eq. (13), the diffusion signal can be represented using convolution as

$$\begin{gathered} E(qu)=\sum _{\alpha =0}^{2L}\sum _{\beta =-\alpha }^{\alpha }\sqrt{\frac{4\pi }{2\alpha +1}}{f}_{\alpha \beta }{h}_{\alpha }(q)Y_{\alpha }^{\beta }(u) \\ =\sum _{\alpha =0}^{2L}\sum _{\beta =-\alpha }^{\alpha }\sum _{l,m}^L\sum _{l^{\prime },m^{\prime }}^L\sqrt{\frac{4\pi }{2\alpha +1}}{c}_{lm}{c}_{l^{\prime }{m}^{\prime }}{Q}_{l{l}^{\prime }\alpha }^{m{m}^{\prime }\beta }{h}_{\alpha }(q)Y_{\alpha }^{\beta }(u) \\ ={\mathit{c}}^{\text{T}}K(qu)\mathit{c}, \end{gathered}$$ (15)

where for any fixed qu, K(qu) is a square matrix of dimension (L+1)(L+2)/2 with elements

$$K_{l{l}^{\prime }}^{m{m}^{\prime }}(qu)=\sum _{\alpha =0}^{2L}\sum _{\beta =-\alpha }^{\alpha }\sqrt{\frac{4\pi }{2\alpha +1}}{Q}_{l{l}^{\prime }\alpha }^{m{m}^{\prime }\beta }{h}_{\alpha }(q)Y_{\alpha }^{\beta }(u).$$ (16)

2.2.2. Riemannian Gradient Descent

Based on Eq. (15), we propose to estimate c from the measured ${\left\{E_i\right\}}_{i=1}^N$ by minimizing

$$J(\mathit{c})=\frac{1}{2}\sum _{i=1}^N{\left({\mathit{c}}^{\text{T}}K\left(q_i{u}_i\right)\mathit{c}-E_i\right)}^2+\frac{1}{2}{\mathit{c}}^{\text{T}}\Lambda \mathit{c},\text{\hspace{1em} s.t. \hspace{1em}}\parallel \mathit{c}{\parallel }_2=1$$ (17)

where Λ is a diagonal matrix with elements Λ_lm = λ_NNSDl²(l + 1)² for Laplace-Beltrami regularization (Descoteaux et al., 2007), penalizing the high-order coefficients. The constraint ∥c∥₂ = 1 is a result of the unit integral, i.e. ${\int }_{{\mathbb{S}}^2}\Phi (u)\text{d}u=1$, and the orthogonality of the SH basis:

$${\int }_{{\mathbb{S}}^2}\Phi (u)\text{d}u=\sum _{l,m}^L\sum _{l^{\prime },m^{\prime }}^L{c}_{lm}{c}_{l^{\prime }{m}^{\prime }}{\int }_{{\mathbb{S}}^2}{Y}_l^m(u)Y_{l^{\prime }}^{m^{\prime }}(u)\text{d}u=\parallel c{\parallel }_2^2=1,$$ (18)

which is equivalent to $f_{00}=\frac{1}{\sqrt{4\pi }}$, as in Eq. (11). The influence of the unit integral constraint on NNSD will be discussed in Section 5.3.

We propose a Riemannian gradient descent method on the sphere ∥c∥₂ = 1 to minimize Eq. (17). The Euclidean gradient of J(c) is

$$\frac{\partial J(\mathit{c})}{\partial \mathit{c}}=\sum _{i=1}^{N}2\left({\mathit{c}}^{\text{T}}K\left(q_i{u}_i\right)\mathit{c}-E_i\right)K\left(q_i{u}_i\right)\mathit{c}+\Lambda \mathit{c}$$ (19)

and the Riemannian gradient is the projection of Euclidean gradient onto the tangent space of c, i.e.,

$$\nabla J(\mathit{c})=\frac{\partial J(\mathit{c})}{\partial \mathit{c}}-\left({\mathit{c}}^{\text{T}}\frac{\partial J(\mathit{c})}{\partial \mathit{c}}\right)\mathit{c}.$$ (20)

The Riemannian gradient descent associated with J(c) is

$${\mathit{c}}^{(k+1)}={\text{exp}}_{{\mathit{c}}^{(k)}}\left(-\text{d}t\frac{\nabla J(\mathit{c})}{\parallel \nabla J(\mathit{c}){\parallel }_2}\right),$$ (21)

$${\text{Exp}}_{\mathit{c}}(\mathit{v})=\mathit{c}\text{cos}\parallel \mathit{v}{\parallel }_2+\frac{\mathit{v}}{\parallel \mathit{v}{\parallel }_2}\text{sin}\parallel \mathit{v}{\parallel }_2,$$ (22)

where c^(k) is the estimated c in the k-th step, dt is the step size chosen from inexact line search in (0, dt₀], and Exp_c(v) is the exponential map on the sphere (Cheng et al., 2009). See Algorithm 1 for a summary of the whole process. We use the isotropic fODF with c⁽⁰⁾ = (1, 0, …, 0)^T for initialization and choose dt₀ = 0.1 based on experimental observations and the fact that ∥c∥₂ = 1. We found that NNSD is robust to noise and λ_NNSD = 0 works well in the experiments. The stopping condition is described next.

2.2.3. Adaptive Stopping Condition

The stopping condition for Algorithm 1 is

$$\tilde{J}(k)=\frac{J\left({\mathit{c}}^{(k-1)}\right)-J\left({\mathit{c}}^{(k)}\right)}{J\left({\mathit{c}}^{(k-1)}\right)}<\delta .$$ (23)

Parameter δ should be chosen as a small number such that the algorithm converges to a local minimum of Eq. (17). Experimentally δ = 10⁻² works well in most cases. If δ is further reduced beyond 10⁻², the fODFs in regions with high anisotropy will increase in sharpness, but the fODFs in regions with low anisotropy will however suffer from spurious peaks due to over-fitting. Therefore, we propose to adaptively stop the algorithm if GFA(c^(k)) < T and $\tilde{J}(k)<{\delta }_0$ or if GFA(c^(k)) ≥ T and $\tilde{J}(k)<0.01{\delta }_0$, where δ₀ = 10⁻² and

$$\text{GFA}(\mathit{c})=\sqrt{1-\frac{c_{00}^2}{\parallel \mathit{c}{\parallel }_2^2}}=\sqrt{1-c_{00}^2}$$ (24)

is the Generalized Fractional Anisotropy (GFA) (Tuch, 2004) of the square root of the fODF $\sqrt{\Phi (u\mid \mathit{c})}$, and T ∈ [0, 1] is a threshold depending on the noise level. We call the NNSD implementation with this adaptive stopping condition ASC-NNSD. Since gradient descent is initialized using the isotropic fODF, GFA(c^(k)) < T is satisfied for all voxels during the early stage of optimization. As k increases, $\tilde{J}(k)$ decreases such that for a certain step k₀ we have $\tilde{J}\left(k_0\right)<{\delta }_0$. If for a voxel $\tilde{J}\left(k_0\right)<{\delta }_0$ and $\text{GFA}\left({\mathit{c}}^{\left(k_0\right)}\right)<T$, we consider the voxel insufficiently anisotropic to proceed further and hence stop the algorithm early at step k₀. If $\tilde{J}\left(k_0\right)<{\delta }_0$ and $\text{GFA}\left({\mathit{c}}^{\left(k_0\right)}\right)\ge T$, we consider the voxel anisotropic and further refine the solution by proceeding with gradient descent. When T = 0, ASC-NNSD becomes NNSD with δ = 0.01δ₀ = 10⁻⁴; when T = 1, ASC-NNSD becomes NNSD with δ = δ₀ = 10⁻². Both NNSD and ASC-NNSD converge quickly, normally in a dozen of steps. Based on our C++ implementation, if L = 6, 1000 fODFs can be estimated within 5 seconds using an ordinary laptop, significantly faster than MESD as implemented in Camino (Alexander, 2005).

3. Methods

3.1. Estimation of Fiber Response Function

SD methods require an estimate of the fiber response function, which is essentially the diffusion signal profile of a single-directional highly-coherent fiber bundle. Anderson (2005) computed a SH representation of the fiber response function using the diffusion signal generated from a tensor model. Tournier et al. (2007) proposed to first fit the tensor model to the data of voxels with high Fractional Anisotropy (FA) and then rotate the diffusion-weighted measurements such that the principal directions coincide with the z-axis. From the rotated measurements, the SH coefficients of the fiber response function are computed. Although these two methods described above were originally proposed for single-shell data, they can be generalized for multi-shell data using two different approaches:

• First fit diffusion models, such as DTI (Basser et al., 1994) or Spherical Polar Fourier Imaging (Assemlal et al., 2009; Cheng et al., 2010b), to high-anisotropy diffusion signal E(q) in ${ℝ}^3$. Then, reconstruct the signal in each shell and compute the SH representation (Anderson, 2005; Cheng et al., 2010b).

• If a sufficiently large number of measurements are collected for each shell, the fiber response function can be estimated independently for each shell using the approach described in (Tournier et al., 2007).

Both approaches were used in the experiments (see Section 4.1).

3.2. Peak Detection

At each voxel, fiber orientations are given by the peaks or local maxima of each fODF. For L1-NNLS, the peaks are determined based on the local maxima of 321 points evenly distributed on a hemisphere, generated by subdividing the faces of an icosahedron. We discard local maxima with low fODF value and consider only peaks with fODF values greater than the mean of the minimal and maximal fODF values. We assume that the fiber crossing angle is no smaller than θ_Δ = 15° and within this angle only one peak with the greatest fODF value is retained. The choice θ_Δ = 15° is motivated by the fact the angle is approximately twice the minimal angular separation (i.e., 7.9°) between the 321 points.

For all CR-SD methods, including NNSD, CSD, QP-CSD, and MESD, we first determine candidate local maxima from the same 321 points. Then, using the continuous representation associated with these methods, a gradient ascent method, also implemented in MRtrix (Tournier et al., 2012), is performed to give a set of refined peaks.

3.3. Synthetic Data Simulation and Evaluation

For evaluation, synthetic data were generated by a mixture of tensor models:

$$E(qu)=\frac{S(u)}{S(0)}=\sum _{k=1}^K{p}_k\text{exp}\left(-q^2{u}^{\text{T}}{D}_{k}u\right),b=q^2,$$ (25)

where D_k is a 3 × 3 matrix representing a diffusion tensor and K = 1, 2 corresponds to the single-direction case and the crossing case, respectively. The baseline signal is S(0) = 1 and b is the diffusion weighting (Johansen-Berg and Behrens, 2009). For the crossing case, the tensors share the same eigenvalues (λ₁, λ₂, λ₂) and are equally weighted with p₁ = p₂ = 0.5. We generated Rician noise corrupted signal by

$$E_i=\sqrt{{\left(E\left(q_i{u}_i\right)+s_1\right)}^2+s_2^2}$$ (26)

where s₁ and s₂ are the Gaussian distributed noise with zero mean and standard deviation σ. The signal-to-noise ratio (SNR) is defined as $\frac{1}{\sigma }$ (Descoteaux et al., 2007). The methods used for comparison might not necessarily detect the correct number of peaks (2 in this case). Therefore, we report the success ratio, which tells us the proportion of trials that correctly detect the number of peaks. The Mean Difference of Angles (MDA) (Descoteaux et al., 2007) is then computed only for the successful trials.

3.4. Real Data Evaluation via Peak Consistency

Real data evaluation is challenging due to the lack of ground truth. To make comparison possible, we gauge the correctness of the fiber directions at each voxel based on the agreement of different datasets and methods. We assume that if a certain direction is widely agreed upon, then there is a high possibility that the direction reflects the true direction. Based on this assumption, we propose here a novel measure, called Peak Consistency (PC), to evaluate peak estimation accuracy. Assuming we have N datasets (e.g., resulting from different sampling schemes) pertaining to the same subject, then M methods will yield MN fODFs at each voxel, resulting in more than MN peaks (at least one peak for each fODF).

Two peaks are said to be consistent if the angle between them is no more than threshold θ_C. Our choice of angular threshold θ_C = 5° is based on the empirical observation that, for moderate Rician noise, the peak detection error of the algorithms is around 2°. This angular threshold gives a good tolerance to cover the variability caused by noise.

For voxel x, we denote $p_{i,k}^x$ as the k-th peak from the i-th fODF (i ∈ [1 : MN], [a : b] denotes {a, a + 1, …, b}). Since θ_C < θ_Δ, for peak $p_{i,k}^x$, at most one consistent peak can be found from peaks ${\left\{p_{j,l}^x\right\}}_{l=1}^{K_j^x}$ for a given j ∈ [1 : MN], j ≠ i, where $K_j^x$ denotes the number of peaks for the j-th fODF at voxel x. The maximum number of possible matches for all j ≠ i is hence MN − 1. For each peak, we define the Single-Peak Consistency (SPC)

$$\text{SPC}(i,k,\mathit{x})=\frac{|\Gamma (i,k,x)|}{MN-1},$$ (27)

where Γ(i, k, x) = {j | j ≠ i, j ∈ [1 : NM], $l\in \left[1:K_j^x\right]$, $d\left(p_{i,k}^x,p_{j,l}^x\right)\le {\theta }_{\text{C}}\}$, $d\left(p_{j,l}^x,p_{i,k}^x\right)$ is the angle between the two peaks, and | · | denotes the number of elements in a set. SPC = 0 indicates that no peak is consistent with the reference peak $p_{i,k}^x$. SPC = 1 indicates that the reference peak $p_{i,k}^x$ is fully consistent with all other MN − 1 peaks. For concurrent consistency evaluation of multiple peaks, we define the Multi-Peak Consistency (MPC) as

$$\text{MPC}(i,x)=\frac{\left|{\cap }_{k\in \left[1:K_i^x\right]}\Gamma (i,k,x)\right|}{MN-1}.$$ (28)

See Fig. 1 for a visual summary of the single- and multi-peak consistency measures. Given a field of fODFs with voxels {x|x ∈ Ω}, we define for a threshold PC_T ∈ (0, 1) (0.5 in the current work) the overall single- and multi-peak consistency measures as

$$\overline{\text{SPC}}(i)=\frac{{\sum }_{\mathit{x}\in \Omega }|\left\{k\mid \text{SPC}(i,k,x)\ge {\text{PC}}_{\text{T}},k\in \left[1:K_i^x\right]\right\}|}{{\sum }_{\mathit{x}\in \Omega }{K}_i^x}$$ (29)

and

$$\overline{\text{MPC}}(i)=\frac{{\sum }_{\mathit{x}\in \Omega }|\left\{\mathit{x}\mid MPC(i,\mathit{x})\ge {\text{PC}}_{\text{T}}\right\}|}{|\Omega |}.$$ (30)

Figure 1: Peak Consistency.

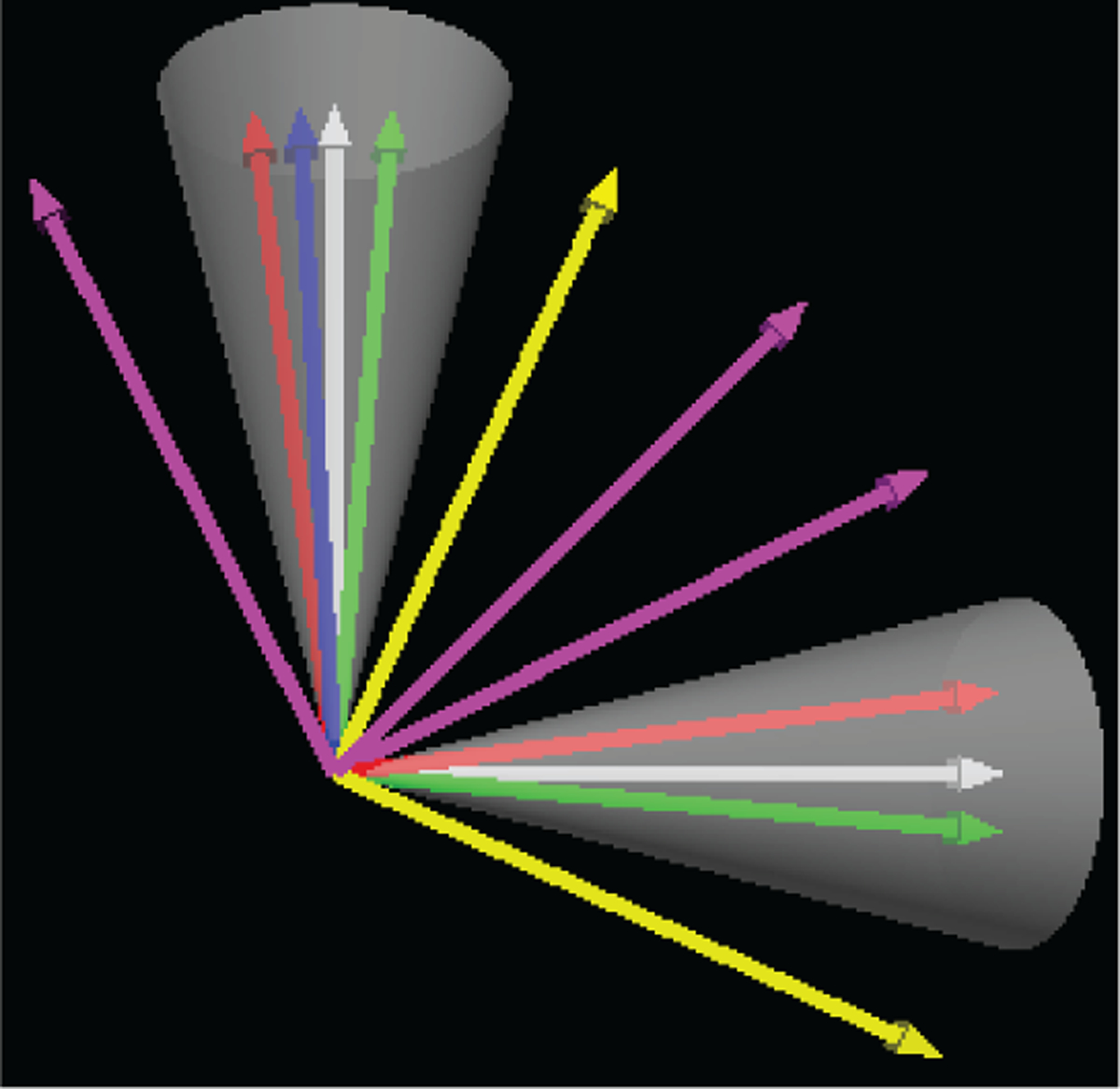
The peaks detected from each fODF are indicated by identically colored arrows. The cones cover peak orientations subtending an angle θ_C with the white arrows. The white peaks are said to be consistent with the peaks within these cones. In this case, SPC = 3/5 and SPC = 2/5, respectively for the vertical and horizontal white peaks, and MPC = 2/5.

4. Experiments

4.1. Parameters

We compared NNSD and ASC-NNSD with CSD, QP-CSD, MESD, and L1-NNLS, using both synthetic and real data. For CSD, MRtrix (Tournier et al., 2012) was used in all experiments involving single-shell data (Tournier et al., 2007), and an in-house implementation of CSD was used in experiments involving multi-shell data. The default parameters specified in (Tournier et al., 2007) and 321 orientations evenly distributed in a hemisphere were used to generate L^(k) in Eq. (7) for CSD (Tournier et al., 2007) and P in Eq. (11) for QP-CSD. Accelerated MESD with K = 16 in Eq. (8) was used as suggested in Camino. Following (Landman et al., 2012), we set ${\lambda }_{L1}=0.1{\lambda }_{L1}^{*}$ for L1-NNLS. To demonstrate the robustness of NNSD, we intentionally set λ_NNSD = 0 to switch off Laplace-Beltrami regularization and set T = 0.5 for ASC-NNSD. For the synthetic data experiments, the fiber response function for all methods was set according to the signal from the tensor model with eigenvalues [1.7, 0.2, 0.2] × 10⁻³ mm²/s. For the real data experiments, the response function was estimated by MRtrix (Tournier et al., 2012) using voxels with FA greater than 0.7.

4.2. Synthetic Data

Evaluation with SNR=1000.

We would like to investigate how the different methods behave when the anisotropy of the signal changes and when there is a mismatch between the fiber response function and the data. Diffusion signal was first generated from the mixture of tensor models in Eq. (25) with b = 1500s/mm², crossing angle 60°, mean diffusivity 0.7 × 10⁻³ mm²/s, and different FA values (Johansen-Berg and Behrens, 2009) by varying tensor eigenvalues (λ₁, λ₂, λ₃ = λ₂). Fig. 2 (SNR=1000) shows the estimated fODFs when λ₁ increases from 0.7 × 10⁻³ mm²/s (left with FA= 0) to 1.7 × 10⁻³ mm²/s (right with FA= 0.87). For all methods, the fiber response function was the tensor model with eigenvalues [1.7, 0.2, 0.2] × 10⁻³ mm²/s. Therefore, the response function matches the data on the far right but not on the left. The results indicate that CSD, QP-CSD and L1-NNLS result in many spurious peaks for data with low anisotropy, even when the SNR is high. NNSD and ASC-NNSD work well when the signal is anisotropic or less so. The fODFs estimated by NNSD with δ = 10⁻² are a little smoother than the fODFs estimated by NNSD with δ = 10⁻⁴. Note that for isotropic signal, the fODFs given by NNSD and ASC-NNSD are close to being isotropic.

Figure 2: Synthetic Data.

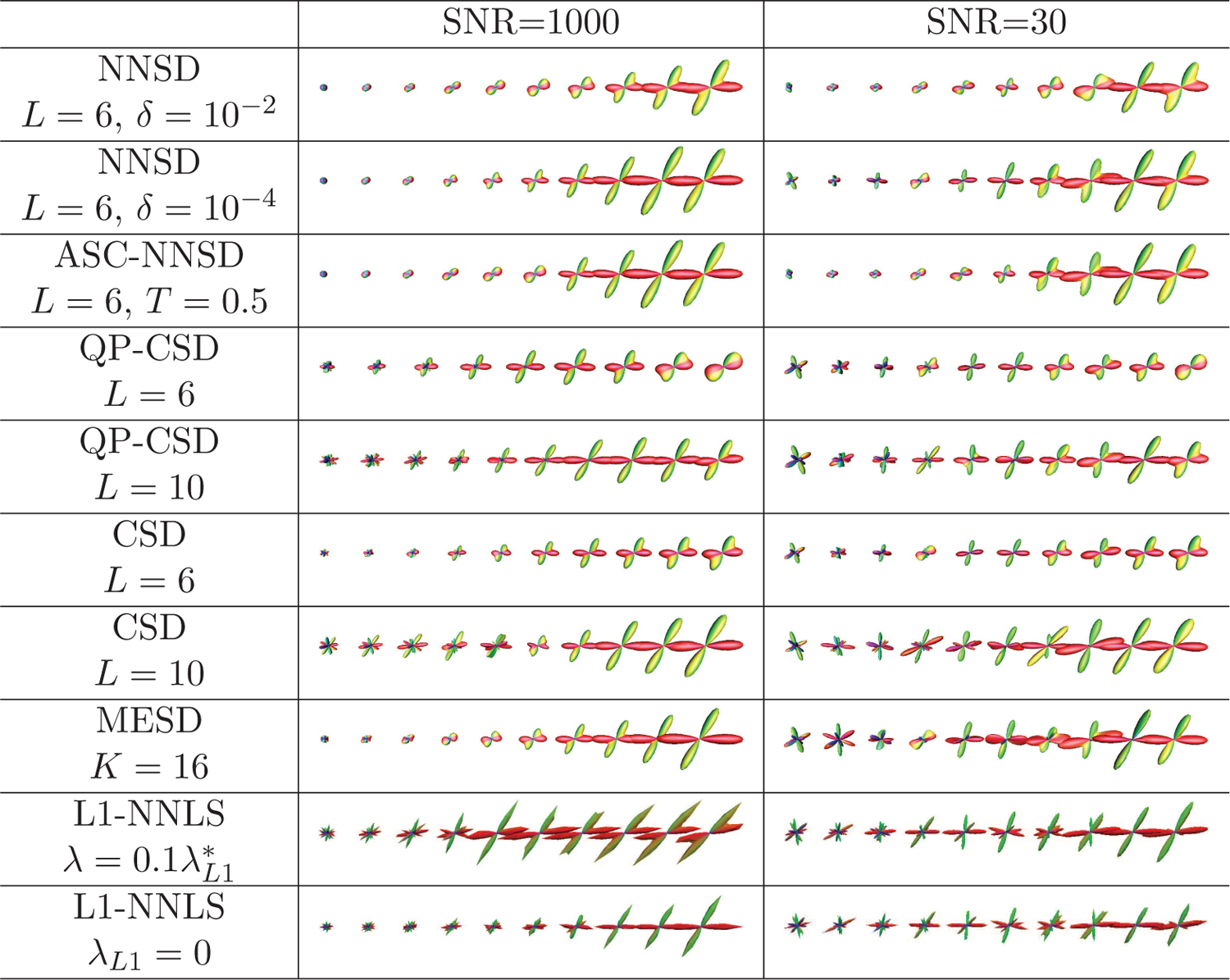
fODF estimation results given by different methods under different parameter settings for synthetic data with varying anisotropy.

Evaluation with SNR=30.

The estimation results when the noise level is increased are shown in Fig. 2 (SNR=30). Despite the noise, both NNSD and ASC-NNSD obtain significantly smoother results for signal that is more isotropic when compared with other methods. ASC-NNSD works best among all methods in obtaining sharper fODFs for anisotropic signal and smoother fODFs for isotropic signal. The results given by ASC-NNSD can be seen as a combined outcome of NNSD with δ = 10⁻² for the less anisotropic signal and NNSD with δ = 10⁻⁴ for the anisotropic signal.

Evaluation of Non-Negativity and Anisotropy.

1000 Rician-noise realizations of isotropic signal with eigenvalues [0.7, 0.7, 0.7] × 10⁻³ mm²/s and anisotropic signal with eigenvalues [1.7, 0.2, 0.2] × 10⁻³ mm²/s were generated at SNR=15 and 30 for b = 1500s/mm² and 60 evenly distributed directions. From the estimated fODFs, we recorded the GFA values (Tuch, 2004) and the proportion of directions (among 5121 points uniformly distributed on the unit sphere) with negative fODF values. We ignored negative values close to zero and only took into consideration negative values with absolute values larger than 1% of the maximal fODF value. The top subfigure in Fig. 3 indicates that CSD is still susceptible to negative values despite its non-negativity constraint. QP-CSD results in a significantly lower number of negative values than CSD because it enforces a stricter non-negativity requirement than CSD. ASC-NNSD and MESD guarantee non-negativity throughout ${\mathbb{S}}^2$. Note that the fODFs estimated by L1-NNLS are non-negative on the 321 points used during optimization; however, since fODF values on the other points are unknown, we cannot compute the proportion of negative values for L1-NNLS. The bottom subfigure indicates the GFA values of the fODFs given by CSD, QP-CSD, MESD and L1-NNLS are high even for isotropic signal, indicating overestimation of the number of fiber directions. Only ASC-NNSD yields significant contrast between anisotropic and isotropic signals.

Figure 3: Nonnegativity and Anisotropy.

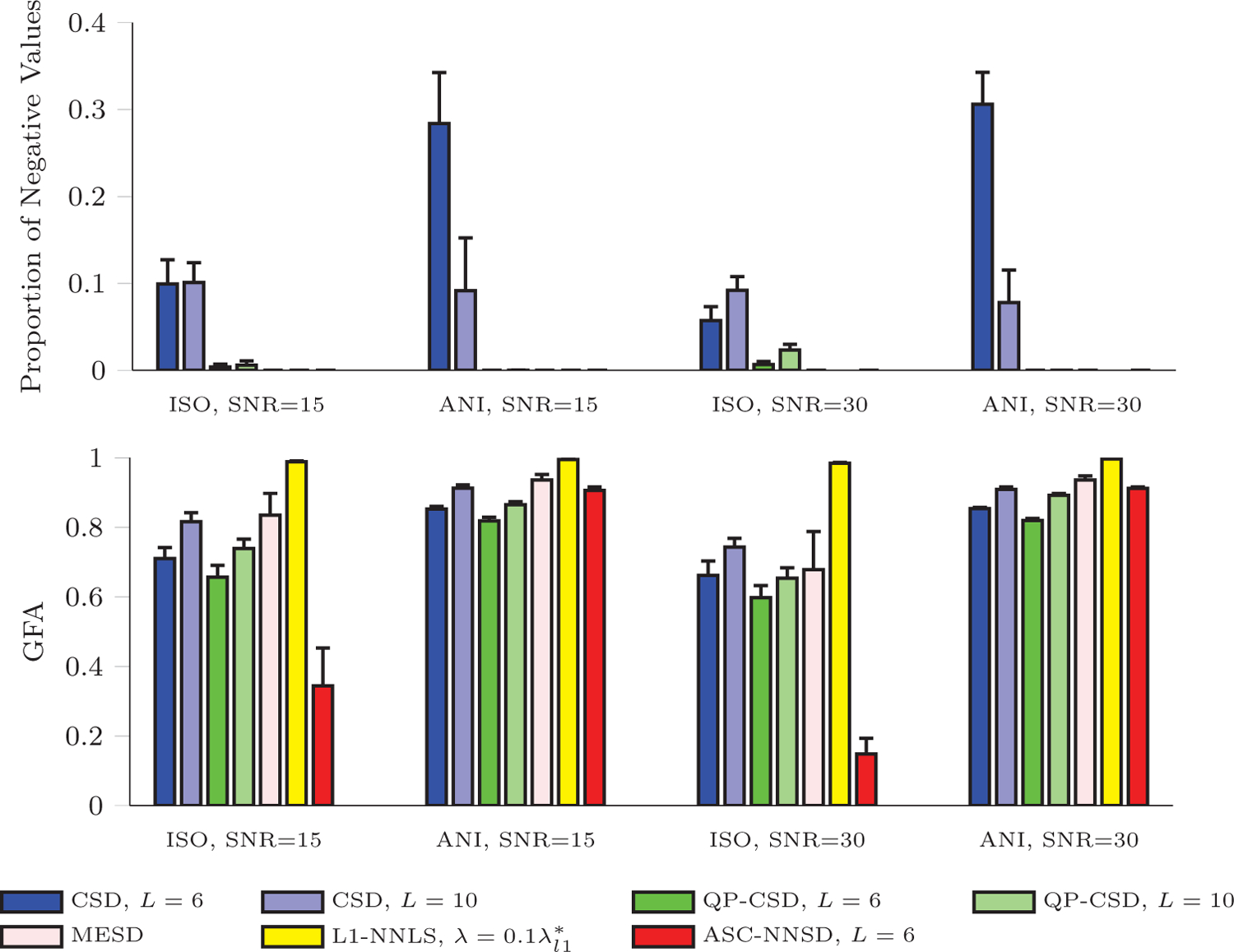
Proportions of negative values and GFA values of fODFs estimated from isotropic (ISO) and anisotropic (ANI) data. The error bars indicate standard deviations.

Evaluation of Peak Accuracy – Single Shell.

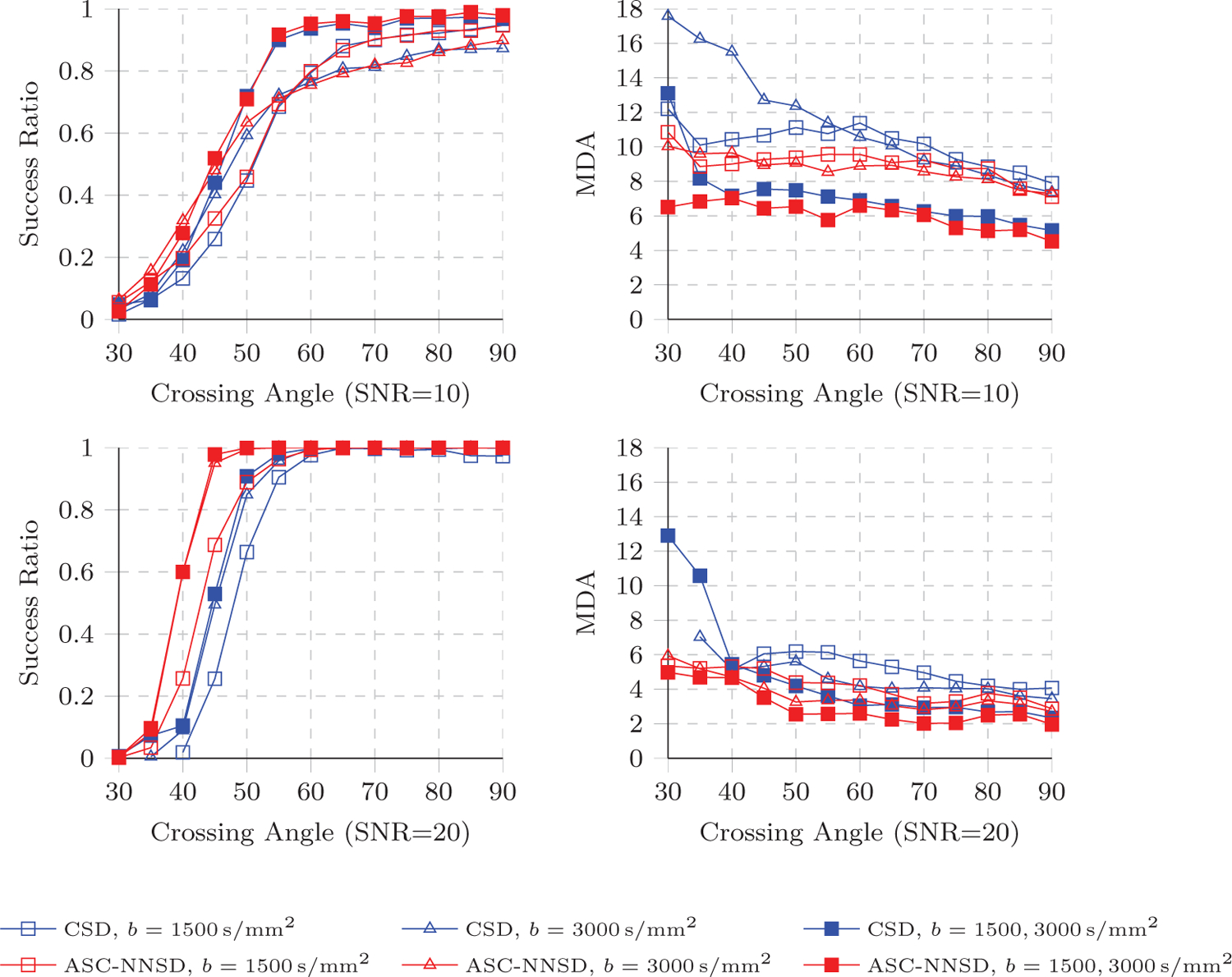
Noise-corrupted signals were generated from a two-tensor model with b = 1500s/mm², eigenvalues [1.7, 0.2, 0.2] × 10⁻³ mm²/s, different crossing angles in the range of [30°, 90°], and at SNR=10 and 20. For peaks detected from the fODFs estimated by each method, we recorded the success ratio and the MDA as described in Section 3.3. The results are shown in Fig. 4 for both SNR=10 and SNR=20. When SNR=10, MESD, CSD, and NNSD with L = 10 give low success ratios for small crossing angles, but high success ratios for the large crossing angles. With L = 6, when the crossing angle is larger than 55°, ASC-NNSD generally gives higher success ratio than CSD and lowest MDA among all methods. When SNR=20, MESD, CSD, and NNSD with L = 10 give higher success ratios for both small and large crossing angles. CSD, QP-CSD NNSD with L = 10 give better performance than their counterparts with L = 6. This implies that, if SNR is high, CSD and NNSD benefit from using a higher order representation. It is interesting to see that the success ratio of L1-NNLS is high for small crossing angle but low for large crossing angle. This indicates that L1-NNLS has high sensitivity, but low specificity due to false-positive peaks. Partially due to limited angular resolution, L1-NNLS yields larger MDA values than CSD and NNSD. The MDA performance of MESD can potentially be improved by increasing parameter K.

Figure 4: Peak Accuracy – Single Shell.

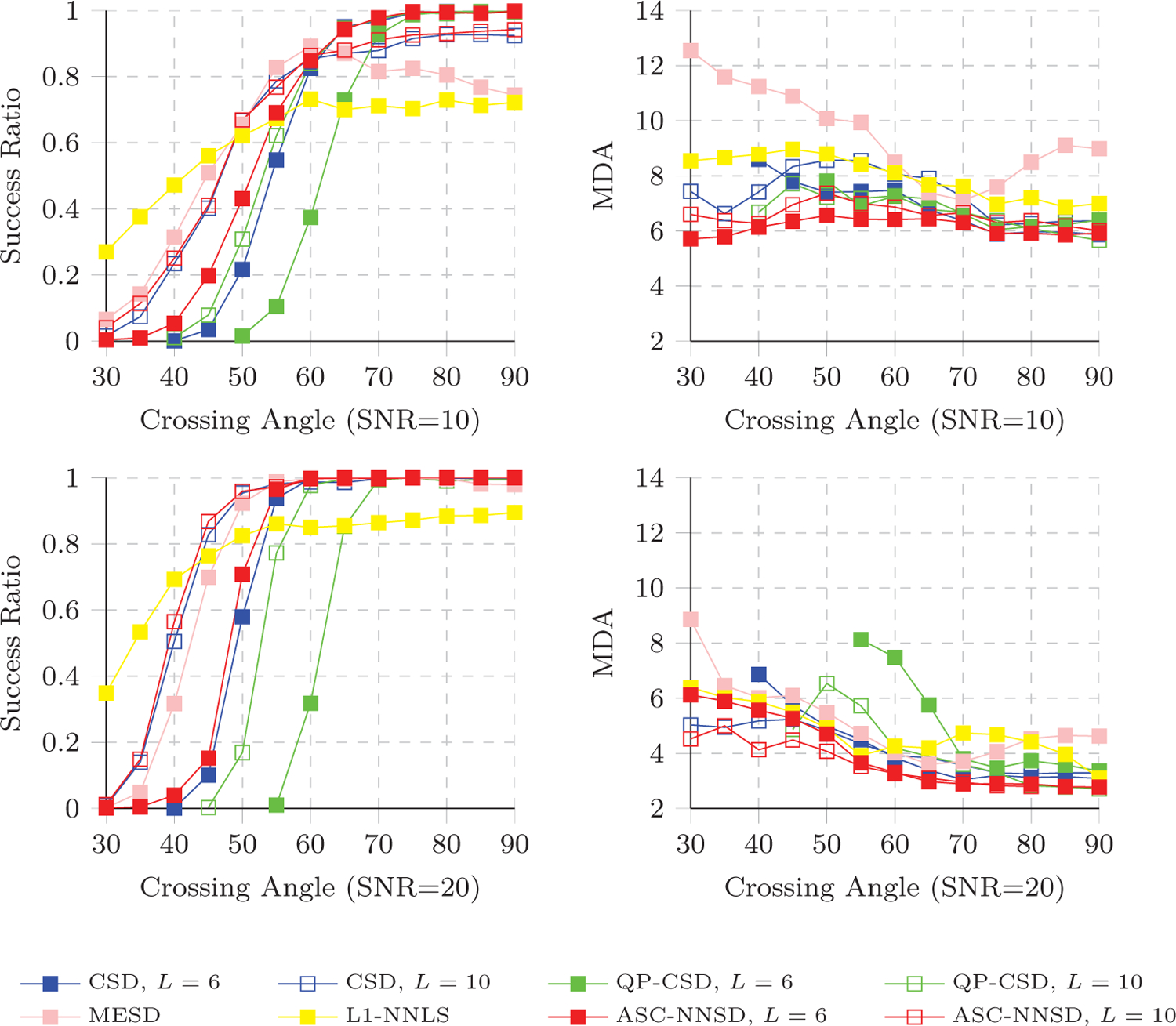
Success ratios and MDA values for different crossing angles at SNR=10 and SNR=20.

Evaluation of Peak Accuracy – Multiple Shells.

We performed an evaluation similar to the previous section using multi-shell data. Since the results reported in the previous section indicate that CSD and NNSD generally give better performance than QP-CSD, MESD, and L1-NNLS, we focus our comparison in this section on CSD and NNSD. We chose L = 8, which is good a trade-off between angular resolution and robustness. This is also suggesed in MRtrix (Tournier et al., 2012). The data were generated by sampling from a mixture of tensor models (Caruyer et al., 2011) using b = 1500s/mm², 3000s/mm² in 30 staggered directions per shell. Fig. 5 shows the success ratios and MDA values given by CSD and NNSD using samples respectively from the outer b = 3000s/mm² shell (30 samples) and from two shells (60 samples) concurrently. When SNR=10, ASC-NNSD and CSD give similar success ratios, but ASC-NNSD generally gives lower MDA than CSD for both single- and two-shell cases. For both ASC-NNSD and CSD, the two-shell data generally result in higher success ratios and lower MDA values than single-shell data. When SNR=20, ASC-NNSD gives better performance than CSD both in terms of success ratio and MDA. For both ASC-NNSD and CSD, the two-shell data result in success ratios similar to the single-shell data with b = 3000s/mm², but lower MDA values.

Figure 5: Peak Accuracy – Multiple Shells.

Success ratios and MDA values for different crossing angles at SNR=10 and SNR=20.

4.3. Real Data

4.3.1. Single-Shell Data

Evaluation was performed using real human data with b = 2000s/mm², 120 gradient directions, 2mm isotropic resolution, and TR/TE=12400/116ms. We set L = 8 for CSD, QP-CSD, NNSD, and ASC-NNSD. MRtrix was used for the estimation of the fiber response function from voxels with FA > 0.7 (Tournier et al., 2004, 2007). The results are shown in Fig. 6. NNSD with δ = 10⁻⁴ and ASC-NNSD with T = 0.5 give similar results, implying that the result is insensitive to T for this data. For each method, the GFA map computed from the estimated fODFs is displayed as the background image. Consistent with the results in Fig. 3, the results in Fig. 6 for CSD, QP-CSD, MESD, and L1-NNLS show a significant amount of false-positive peaks, which are especially evident in the regions with low anisotropy, as indicated by the high GFA values in gray matter and cerebrospinal fluid regions. NNSD and ASC-NNSD dramatically reduced the spurious peaks of the estimated fODFs. See for example the region marked by the yellow circles in Fig. 6. Compared with CSD, NNSD and ASC-NNSD yield sharper fODFs in anisotropic regions and more isotropic fODFs in isotropic regions. This gives high GFA contrast between these regions. Note that existing work (Tournier et al., 2004, 2007; Jian and Vemuri, 2007; Landman et al., 2012; Weldeselassie et al., 2012) attempts to avoid such low GFA contrast by computing FA or GFA using some other models, such as the tensor model.

Figure 6: Real Data – Single Shell.

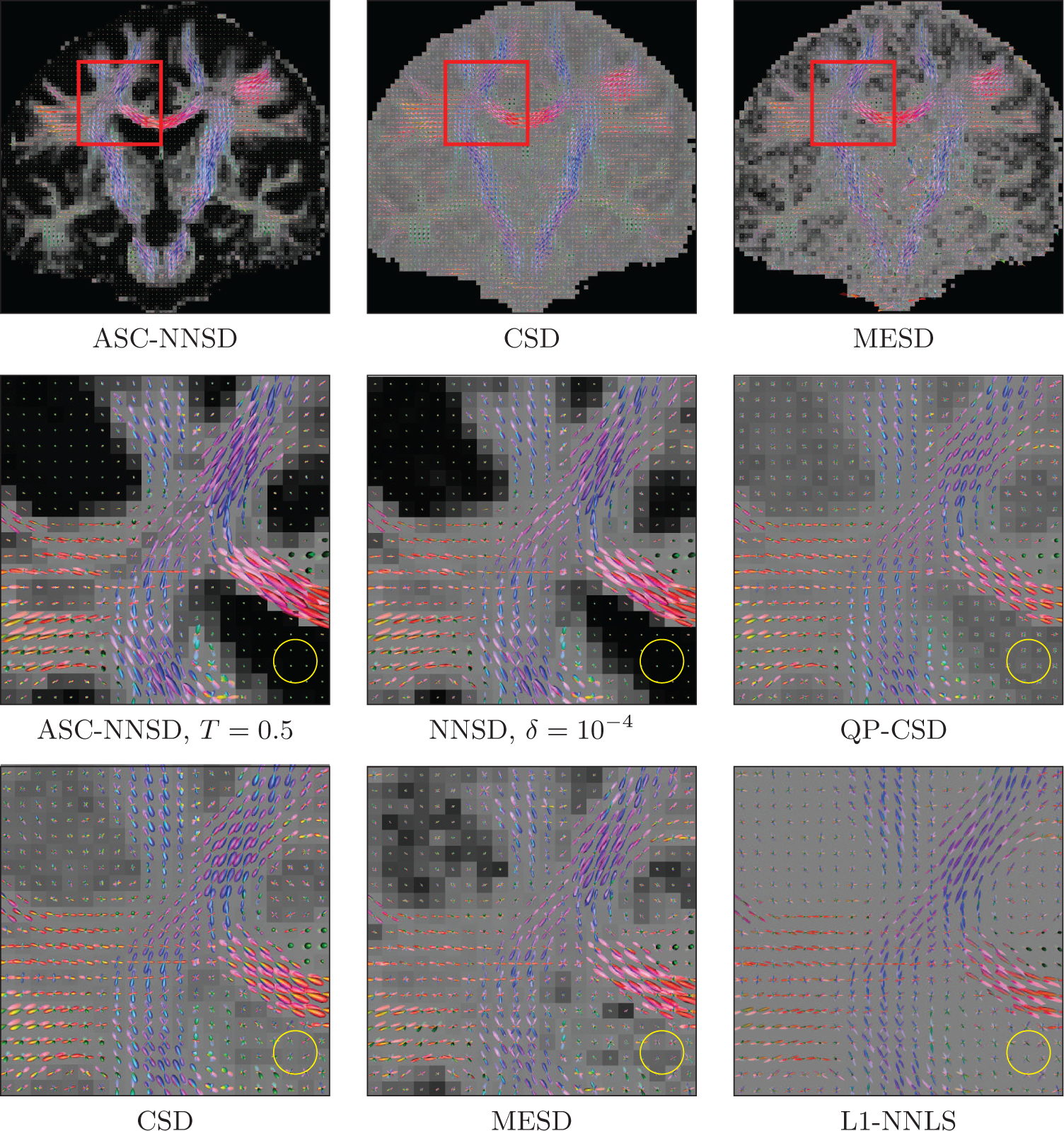
Coronal views and close-up views of the fODF fields generated by various methods. The background is the GFA map.

4.3.2. High Spatial Resolution Multi-Shell HCP Data

Evaluation was also performed using a high-resolution dataset (1.25mm in all dimensions) obtained from the Human Connectome Project (HCP)⁷. fODF estimation from this dataset is challenging because the SNR is low due to the small voxel size. This dataset was acquired using three shells, with 90 staggered directions per shell, and at b = 1000, 2000, 3000s/mm².

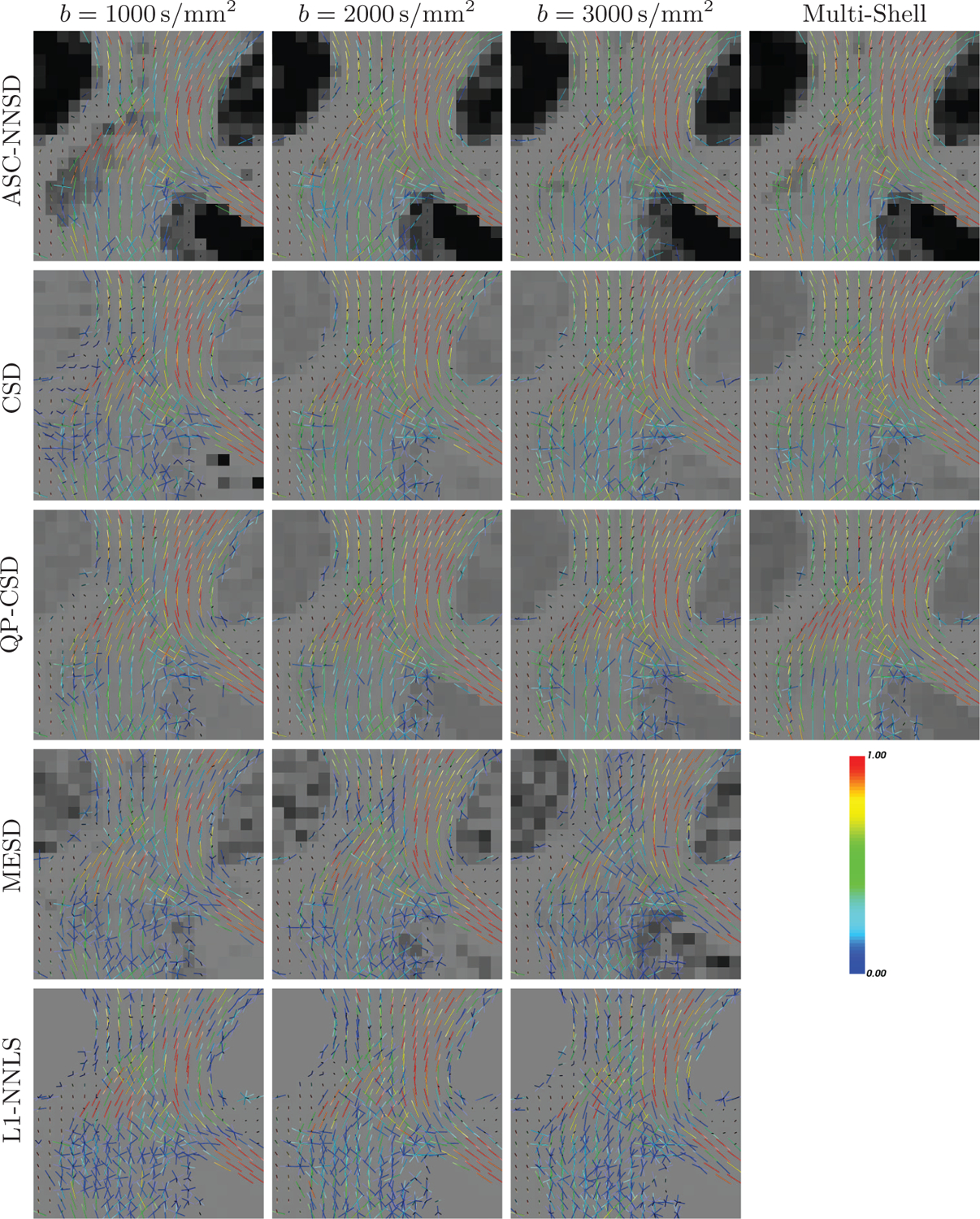
First, we performed a single-shell evaluation (b = 2000s/mm²) using NNSD with δ = 10⁻⁴, ASC-NNSD with T = 0.5, CSD, QP-CSD, MESD, and L1-NNLS. L = 8 was used in all SH-based methods. The results shown in Fig. 7 demonstrate the effectiveness of NNSD and ASC-NNSD. In isotropic regions, only NNSD and ASC-NNSD give isotropic fODFs, while other methods result in a significant amount of false-positive peaks. See for example the region marked by the yellow circles. In anisotropic regions, NNSD and ASC-NNSD yield the sharpest fODFs. In particular, the fODFs estimated by CSD are not as sharp as those estimated by NNSD, ASC-NNSD, and MESD. This can be seen in the region marked by the yellow squares. Spurious peaks can be observed for L1-NNLS, as indicated by the high anisotropy values, even in regions with isotropic diffusion.

Figure 7: HCP Data – Single Shell.

Coronal views and close-up views of the fODF fields generated by various methods from single shell data with b = 2000s/mm². The background is the GFA map.

Second, we included the two other shells (b = 1000, 3000s/mm²) in the estimation, totaling up to 90 × 3 samples. The results are shown in Fig. 8. For ASC-NNSD, the b = 1000s/mm² data give fODFs that are not as sharp as the results given by the two other b-values. The b = 3000s/mm² data give fODFs that are the sharpest but with more false-positive peaks. The b = 2000s/mm² data seem to yield more moderate results than among all b-values.

Figure 8: Single Shell vs. Multiple Shells.

Estimation results for different methods using data from each shell (90 samples) and concurrently from the three shells (90 × 3 samples). See Fig. 7 for the b = 2000s/mm² results.

Third, we detected the peaks from the fODFs estimated using the 4 sampling schemes (the individual shells and all three shells) and 5 methods⁸(ASC-NNSD, CSD, QP-CSD, MESD, and L1-NNLS) and then computed the corresponding peak consistency values defined in Section 3.4. Note that fODF peaks detected in isotropic regions are not reliable and are hence not included in the evaluation. Only voxels with GFA greater than 0.5, estimated based on ASC-NNSD using all three shells, were used for consistency evaluation. The detected peaks, color-coded with SPC values, are shown in Fig. 9, indicating that 1) peak consistency is high anisotropic and single directional regions; 2) peak consistency is low in fiber crossing regions; and 3) the lowest peak consistency occurs at boundaries between white matter and gray matter or cerebrospinal fluid regions. It can also be observed that for ASC-NNSD, CSD, and QP-CSD, the multi-shell data result in higher SPC than single-shell data. For both single- and multi-shell data, ASC-NNSD yields higher SPC values than other methods. These observations are confirmed by the overall peak consistency values ($\overline{\text{SPC}}$ and $\overline{\text{MPC}}$) shown in Table 1.

Figure 9: Single Peak Consistency.

Single Peak Consistency (SPC) for different methods and different sampling schemes. Cool and warm colors indicate low and high SPC, respectively.

Table 1:

$\overline{\text{SPC}}$ and $\overline{\text{MPC}}$ values for fODF fields estimated by different methods for different sampling schemes.

	b = 1000 s/mm2		b = 2000 s/mm2		b = 3000 s/mm3		Multi-Shell
	$\overline{\text{SPC}}$	$\overline{\text{MPC}}$	$\overline{\text{SPC}}$	$\overline{\text{MPC}}$	$\overline{\text{SPC}}$	$\overline{\text{MPC}}$	$\overline{\text{SPC}}$	$\overline{\text{MPC}}$
ASC-NNSD	0.2411	0.2503	0.2839	0.2931	0.2857	0.2995	0.3845	0.3745
CSD	0.1533	0.1870	0.2245	0.2569	0.2359	0.2793	0.2779	0.3236
QP-CSD	0.1811	0.2319	0.2158	0.2720	0.1938	0.2593	0.2597	0.3218
MESD	0.1347	0.1752	0.1399	0.1815	0.1600	0.2102
L1-NNLS	0.1080	0.1571	0.1148	0.1650	0.1030	0.1653

5. Discussion

5.1. Multi-Shell SD

Existing fODF estimation methods such as CSD only can be applied to single-shell data. We have generalized SD to work with multi-shell data by defining the fiber response function in ${ℝ}^3$. Data with low diffusion weighting have high SNR but low angular resolution, whereas data with high diffusion weighting data have low SNR but high angular resolution. Our method takes advantage of the whole spectrum of the data. Evaluation based on both synthetic and real data, as shown in Figs. 5, 6, 8, 9, and Table 1, indicate that multi-shell data improve peak estimation accuracy compared with single-shell data.

It should be noted that for the HCP data, the multi-shell SD methods use all 90 × 3 diffusion-weighted images for estimation. This is 3 times the number of samples used by single-shell SD methods. It will be interesting to fix the total number of samples and evaluate the advantages of the two different sampling schemes, e.g., a multi-shell sampling scheme with 90 samples per shell against a single-shell scheme with 270 samples. However, choosing a good sampling scheme (Cheng et al., 2014) with proper consideration of the tradeoff between angular resolution and SNR is still an open problem beyond the scope of this paper. The proposed multi-shell SD framework can be used as a tool to evaluate different sampling schemes in the future.

5.2. Non-Local NNSD (NL-NNSD)

In practice, denoising methods such as non-local mean (Buades et al., 2005; Descoteaux et al., 2008; Yap et al., 2014) and spatial regularization (Goh et al., 2009) can significantly improve SNR and hence fODF estimation accuracy. Our initial implementation of a non-locally regularized (Buades et al., 2005) version of NNSD, called non-local NNSD (NL-NNSD) (Cheng et al., 2013a), supports this idea. In the ISBI 2013 HARDI Reconstruction Challenge⁹, which considered DTI, HARDI, and DSI-like sampling schemes and SNR=10,20,30, NL-NNSD was ranked the best technique in terms of local fiber orientation estimation for all sampling categories and all SNRs¹⁰.

5.3. Unit Integral Constraint

Unlike NNSD, existing SD methods, such as FSD, CSD, MESD and L1-NNLS, do not explicitly incorporate the unit integral constraint. In Appendix A, we show that the solutions given by FSD in Eq. (6) with and without the constraint differ only by the isotropic component, and under some conditions the results given by NNSD with and without the constraint also differ only by the isotropic component. The constraint is beneficial for fODF estimation as explained below:

1. As a probability distribution function of orientations, fODF should naturally have unit integral.

2. The constraint helps mitigate the representation error inherent in SD-based fODF estimation methods. Based on Eq. (5) and Eq. (15), the spherical means of E(qu) and H(qu) are respectively

   $$\overline{E}(q)=\frac{1}{4\pi }{\int }_{{\mathbb{S}}^2}E(qu)\text{d}u=f_{00}{h}_0(q),\overline{H}(q)=\frac{1}{\sqrt{4\pi }}{h}_0(q).$$ (31)

   The value of f₀₀ should ideally be adaptive to the values of these means in order to minimize the representation error. For example, if the diffusion signal and fiber response function have the same spherical mean, then one should set $f_{00}=\frac{1}{\sqrt{4\pi }}$ to avoid representation error. This requirement is obvious for q = 0, where we expect $\overline{E}(0)=\overline{H}(0)=1$ and $h_0(0)=\sqrt{4\pi }$, especially when the fiber response function is based on the tensor model. If the spherical means differ, our analysis in Appendix A shows that under some conditions setting $f_{00}=\frac{1}{\sqrt{4\pi }}$ will result in an fODF with the same anisotropic component.

3. Due to the constraint, the solution space of SD methods with the constraint is one dimension smaller than the solution space of SD methods without this constraint. This reduces the feasible solutions to a smaller space, effectively reducing the complexity of the associated non-convex optimization, and focuses the optimization on the anisotropic components of the fODF.

NNSD without the constraint can be solved by traditional gradient descent with inexact line search. The stopping condition Eq. (23) and its adaptive version can be used to terminate the algorithm. Our experiments indicate that δ = 10⁻⁴ gives the best results. Fig. 10 shows the fODF results given by NNSD without the constraint using the synthetic data shown in Fig. 2. The glyphs are normalized by ∥c∥ = 1 for visualization. Compared with the results given by NNSD in Fig. 2 with δ = 10⁻⁴, the fODFs given by NNSD without the constraint are generally similar, but not as sharp. It should be noted that when δ varies, the fODFs given by NNSD without the constraint vary more dramatically than NNSD with the constraint, indicating that the latter is more robust to the choice of δ.

Figure 10: NNSD without unit integral constraint.

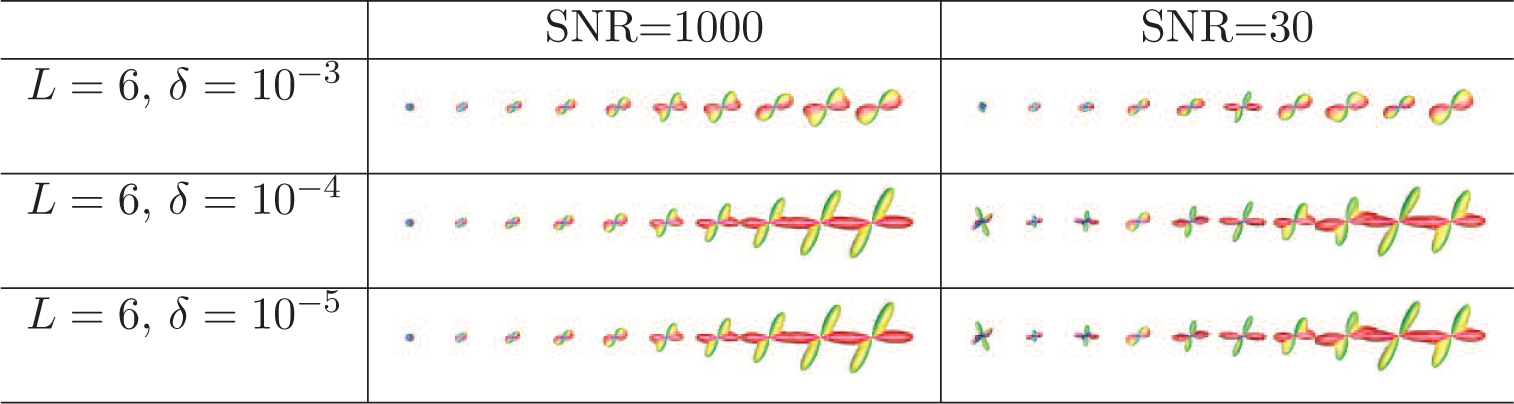
Estimation results for NNSD without unit integral constraint for mixture of tensor models with varying anisotropy.

6. Conclusion

The contribution of this paper is threefold. First, by introducing a ${ℝ}^3$ fiber response function, we have generalized the existing single-shell SD framework to cater to multi-shell data. The experimental results indicate that, compared with single-shell data, multi-shell data give lower MDA, higher success ratios and more consistent peaks. Second, we have proposed a novel SD method, called Non-Negative SD (NNSD), which utilizes a square root representation to impose non-negativity. Comparisons with existing SD methods, including CSD, MESD, and L1-NNLS, demonstrate the advantages of NNSD: 1) NNSD guarantees non-negativity with unit integral of the fODF throughout the whole ${\mathbb{S}}^2$; 2) NNSD significantly reduces false-positive peaks and yields high GFA contrast between isotropic and anisotropic regions; 3) Due to the SH representation, NNSD is efficient and allows accurate peak detection on ${\mathbb{S}}^2$. Third, we have proposed a new metric called peak consistency for evaluation of the different methods in the absence of ground truth. Using this metric, we demonstrated that NNSD gives better estimates of peak orientations in real data. Improvements in fODF estimation obtained with NNSD will be helpful for applications such as fiber tractography (Yap et al., 2011b,c), fiber clustering (Wang et al., 2013), and brain connectomics (Yap et al., 2010, 2011a; Wee et al., 2010, 2012; Shi et al., 2012).

Highlights.

1. Improved fODF estimation with non-negative and unit integral constraints.

2. Significantly increased anisotropy contrast between WM and GM/CSF regions.

3. Improvements over state-of-the-art methods, such as constrained spherical deconvolution.

Appendix A. fODF estimation with and without the unit integral constraint

Since for each shell the matrix $\left[Y_l^m\left(u_i\right)\right]$ has orthonormal columns, Eq. (6), in continuous form, is equivalent to

$$\underset{f}{\text{min}}\sum _{s=1}^S{\int }_{{\mathbb{S}}^2}{\left(\sum _{l,m}^L\sqrt{\frac{4\pi }{2l+1}}{f}_{lm}{h}_l\left(q_s\right)Y_l^m(u)-E\left(q_{s}u\right)\right)}^2\text{d}u$$ (A.1)

The minimization is quadratic with respect to f_lm and the optimal coefficients can be found at the point where the derivative vanishes as

$$f_{lm}^{*}=\sqrt{\frac{2l+1}{4\pi }}\frac{{\sum }_{s=1}^S{h}_l\left(q_s\right)e_{lm}\left(q_s\right)}{{\sum }_{s=1}^S{h}_l{\left(q_s\right)}^2},$$ (A.2)

where e_lm(q_s) is the SH coefficients of E(q_su). With the unit integral constraint, we have $f_{00}^{*}=\frac{1}{\sqrt{4\pi }}$, but this does not alter $f_{lm}^{*}$ for l > 0. Thus the difference between the fODFs with and without the constraint is only the isotropic component.

The NNSD formulation can be seen as an extension of FSD because based on Eq. (15) we can write E(q_iu_i) = c^TK(q_iu_i)c = M(q_iu_i)f, where M(q_iu_i) is the row in basis matrix M corresponding to the sample q_iu_i. Without taking unit integral constraint into consideration, the unconstrained version of NNSD solves the following problem:

$$\underset{\mathit{c}}{\text{min}}\sum _{s=1}^S{\int }_{{\mathbb{S}}^2}{\left(\sum _{\alpha ,\beta }^{2L}\sqrt{\frac{4\pi }{2\alpha +1}}{f}_{\alpha \beta }{h}_{\alpha }\left(q_s\right)Y_{\alpha }^{\beta }(u)-E\left(q_{s}u\right)\right)}^2\text{d}u$$ (A.3a)

$$\text{ s.t. \hspace{1em}}{f}_{\alpha \beta }=\sum _{l,m}^L\sum _{l^{\prime },m^{\prime }}^L{c}_{lm}{c}_{l^{\prime }{m}^{\prime }}{Q}_{l{l}^{\prime }\alpha }^{m{m}^{\prime }\beta }.$$ (A.3b)

Note that by setting α = β = 0 in Eq. (A.3b) we have $f_{00}=\frac{\parallel \mathit{c}{\parallel }^2}{\sqrt{4\pi }}$. Without loss of generality, we let, for optimal solution c*, $\frac{1}{\sqrt{4\pi }}{\Vert c^{*}\Vert }^2=f_{00}^{*}=\frac{1}{\sqrt{4\pi }}+\Delta$. The problem given by Eq. (A.3a) and Eq. (A.3b) then becomes

$$\underset{c}{\text{min}}\sum _{s=1}^S{\int }_{{\mathbb{S}}^2}{\left(\sum _{\alpha ,\beta }^{2L}\sqrt{\frac{4\pi }{2\alpha +1}}{f}_{\alpha \beta }{h}_{\alpha }\left(q_s\right)Y_{\alpha }^{\beta }(u)-E\left(q_{s}u\right)\right)}^2\text{d}u$$ (A.4a)

$$\text{ s.t. \hspace{1em}}{f}_{\alpha \beta }=\sum _{l,m}^L\sum _{l^{\prime },m^{\prime }}^L{c}_{lm}{c}_{l^{\prime }{m}^{\prime }}{Q}_{l{l}^{\prime }\alpha }^{m{m}^{\prime }\beta },f_{00}=\frac{1}{\sqrt{4\pi }}+\Delta .$$ (A.4b)

If Δ = 0, then Eq. (A.4a) is just the NNSD with unit integral in Eq. (17). If Δ ≠ 0, we let $f_{00}^1=\frac{1}{\sqrt{4\pi }}$, and $f_{\alpha \beta }^1=f_{\alpha \beta }$ for α > 0. Then Eq. (A.4a) is equivalent to

$$\sum _{s=1}^S{\int }_{{\mathbb{S}}^2}{\left(\Delta h_0\left(q_s\right)+\sum _{\alpha ,\beta }^{2L}\sqrt{\frac{4\pi }{2\alpha +1}}{f}_{\alpha \beta }^1{h}_{\alpha }\left(q_s\right)Y_{\alpha }^{\beta }(u)-E\left(q_{s}u\right)\right)}^2\text{d}u=\sum _{s=1}^S{\int }_{{\mathbb{S}}^2}{\left(\sum _{\alpha ,\beta }^{2L}\sqrt{\frac{4\pi }{2\alpha +1}}{f}_{\alpha \beta }^1{h}_{\alpha }\left(q_s\right)Y_{\alpha }^{\beta }(u)-E\left(q_{s}u\right)\right)}^2\text{d}u+2\sum _{s=1}^S\Delta h_0\left(q_s\right)\sqrt{4\pi }\left(h_0\left(q_s\right)-e_{00}\left(q_s\right)\right)+\sum _{s=1}^{S}4\pi {\Delta }^2{h}_0{\left(q_s\right)}^2.$$ (A.5)

Since e₀₀(q_s), {h_α(q_s)} and Δ are known constants, the problem given by Eq. (A.4a) and Eq. (A.4b) is equivalent to

$$\underset{c}{\text{min}}\sum _{s=1}^S{\int }_{{\mathbb{S}}^2}{\left(\sum _{\alpha ,\beta }^{2L}\sqrt{\frac{4\pi }{2\alpha +1}}{f}_{\alpha \beta }^1{h}_{\alpha }\left(q_s\right)Y_{\alpha }^{\beta }(u)-E\left(q_{s}u\right)\right)}^2\text{d}u$$ (A.6a)

$$\text{ s.t. \hspace{1em}}{f}_{\alpha \beta }^1=\sum _{l,m}^L\sum _{l^{\prime },m^{\prime }}^L{c}_{lm}{c}_{l^{\prime }{m}^{\prime }}{Q}_{l{l}^{\prime }\alpha }^{m{m}^{\prime }\beta },f_{00}^1=\frac{1}{\sqrt{4\pi }}$$ (A.6b)

which is exactly the NNSD with unit integral constraint. The conditions for this equivalence are (a) ${\text{min}}_{u\in {\mathbb{S}}^2}{\sum }_{lm}{f}_{lm}^{*}{Y}_l^m(u)\ge \frac{\Delta }{\sqrt{4\pi }}$ and (b) L is large enough. Condition (a) is to ensure that the fODF as represented by $\left\{f_{lm}^1\right\}$ is nonnegative; this can be satisfied if Δ ≤ 0. Condition (b) is to ensure representation of this nonnegative fODF using $\left\{c_{lm}^{*}\right\}$ without error. With these two conditions satisfied, the difference between the fODF solutions given by NNSD with and without the unit integral constraint is an isotropic component. In practice, since obtaining the solutions involves non-convex optimization, local minima might cause differences even in the anisotropic component.