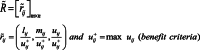An integrated fuzzy sustainable supplier evaluation and selection framework for green supply chains in reverse logistics

Abstract

Green supply chain management considers the environmental effects of all activities related to the supply chain, from obtaining raw materials to the final delivery of finished goods. Selecting the right supplier is a critical decision in green supply chain management. We propose a fuzzy green supplier selection model for sustainable supply chains in reverse logistics. We define a novel hierarchical fuzzy best-worst method (HFBWM) to determine the importance weights of the green criteria and sub-criteria selected. The fuzzy extension of Shannon’s entropy, a more complex evaluation method, is also used to determine the criteria weights, providing a reference comparison benchmark. Several hybrid models integrating both weighting techniques with fuzzy versions of complex proportional assessment (COPRAS), multi-objective optimization by ratio analysis plus the full multiplicative form (MULTIMOORA), and the technique for order of preference by similarity to ideal solution (TOPSIS) are designed to rank the suppliers based on their ability to recycle in reverse logistics. We aggregate these methods’ ranking results through a consensus ranking model and illustrate the capacity of relatively simple methods such as fuzzy COPRAS and fuzzy MOORA to provide robust rankings highly correlated with those delivered by more complex techniques such as fuzzy MULTIMOORA. We also find that the ranking results obtained by these hybrid models are more consistent when HFBWM determines the weights. A case study in the asphalt manufacturing industry is presented to demonstrate the proposed methods’ applicability and efficacy.

Introduction

Environmental issues related to waste and toxic gas emissions have raised concerns over the environment and public health (Khor and Udin 2013). Globalization and legal environmental provisions have forced companies and organizations to promote environmental performance (Abdel-Basset et al. 2019). One of the critical matters in this area is recycling, which begs attention. The pressures posed by regulators and stakeholders for recycling benefit the environment and lead to a sustainable competitive advantage (Bai et al. 2019). The principal goal of recycling is to reduce the waste and efficient use of resources, which has both economic and environmental benefits. Due to severe environmental impacts, manufacturers have been encouraged to change their reverse logistics (RL) networks into green concepts and reduce harmful ecological impacts (Haji et al. 2015).

RL refers to operations collecting used goods for reuse, repair, remanufacturing, recycling, or disposal to produce new products (Alkahtani et al. 2021; Chen et al. 2021). Also, RL is a process of moving a typical product in an inverse path from the mainstream logistics to retrieve value or ensure proper disposal (Hansen et al. 2018; Tavana et al. 2016a, b). Furthermore, it is a tool to recover and recycle or green disposal of goods to reduce pollution (Zarbakhshnia et al. 2019). RL helps companies gain a competitive advantage by creating economic value through reuse and retrieval. Being the main step in green supply chain initiatives, RL allows manufacturers to enter the reused products into the production cycle (Mavi et al. 2017). In RL, materials used can be transformed into new products that could return to the same market or other markets (Ribeiro et al. 2021). The core objectives of RL are cost minimization, profit maximization, and environmental benefits (Liao 2018). Companies pursue three main activities in RL: (i) gathering, where consumers discard their used products; (ii) reconstruction, where separation, rehabilitation, or recycling is done; and (iii) demand centers, where restored products are sold (Ravi 2014).

Many manufacturing companies with limited capabilities outsource some of their reconstruction activities to their suppliers. Suppliers rebuild, repair, and recycle the collected products and reconstruct the final products that can be reused in the manufacturing process within RL companies. As environmental agencies and organizations control the industry activities, suppliers play a critical role in the RL companies. Hence, evaluating suppliers and assessing their impacts on the company’s productivity are of great importance for RL companies.

In the tire industry, companies operate RL processes to recycle worn-out tires as raw material. In tire and rubber recycling, the process takes place on worn or ruptured tires, which are not repairable and not suitable for use. There are crucial concerns about this process as worn-out tires are among the leading causes of environmental contamination. The spoiled tires are considered hazardous wastes since burning them emanate black and harmful smoke causing air pollution. Burying tires is also detrimental to the environment as they produce dangerous gas bubbles (also known as cavitation), which contaminates underground water resources. Tires can be recycled for different types of products; for instance, they can be used in the hot asphalt production process, where they improve the asphalt durability and increase the asphalt compressive strength. Moreover, recycled tires can also be used in Portland cement, production of new tires, sports fields, shoe industry, flooring, and artificial grass. This study aims to shed light on the waste recycling processes and the environmental pollution concerns in the asphalt manufacturing companies. In this regard, the main empirical contribution of this research focuses on the recycling process of worn-out tires and their use as raw material.

The model proposed to evaluate and rank the set of potential green suppliers incorporates two main novel features. First, it extends the fuzzy best-worst method (BWM) into a hierarchical structure, defining a relatively simple weighting technique whose performance is more consistent than that of more complex methods such as the fuzzy version of Shannon’s entropy. Second, we design a hybrid ranking model that incorporates the previous weights into the fuzzy extensions of evaluation techniques such as the complex proportional assessment of alternatives (COPRAS), multi-objective optimization on the basis of ratio analysis (MOORA), MOORA plus full multiplicative form (MULTIMOORA), and the technique for order of preference by similarity to ideal solution (TOPSIS). The empirical results obtained allow for a direct comparison of the rankings provided by these techniques and their aggregation into a unique consensus ranking via the maximize agreement heuristic (MAH) method.

The main contributions of this research can be summarized as follows:

• Our study case focuses on tire recycling and the use of recycled tires as raw materials, an important problem that has received relatively little attention in the literature. Tires are made of polymeric materials that do not decompose easily in nature, constituting a severe long-term problem that cannot be initially solved by burning or burying them. Two main sets of consequences follow from their correct re-utilization. From an environmental viewpoint, worn-out recycling tires reduce waste and reinforces the material cycle in nature. From a financial viewpoint, recycled tires can be incorporated into production cycles, becoming a source of economic profitability and helping industrial development; a particularly important feature is less developed countries.

• We develop a novel hierarchical extension of the fuzzy best-worst method, denoted by HFBWM, which allows for the simultaneous determination of the weights of criteria and sub-criteria within a fuzzy environment.

• We propose several enhanced hybrid ranking models that incorporate HFBWM and fuzzy Shannon’s entropy, allowing for direct comparisons across methods and resulting in more accurate aggregate results.

The rest of this research is arranged in the following order: In the second section, this study reviews the current literature on RL, tire recycling, and evaluation and assortment of green suppliers. The literature review generates the supplier evaluation criteria for tire recycling in RL. In the third section, this research presents the suggested fuzzy green supplier selection model. In the fourth section, a case study in the asphalt manufacturing industry is presented to stress the proposed method’s applicability and efficacy. In the final section, we conclude with a discussion and conclusions.

Literature review

In this part, the present study provides a concise review of the literature on RL, tire recycling, and green supplier evaluation and selection.

Reverse logistics

Today, RL has attracted many manufacturers (Ramírez and Morales 2014), and the RL operations refer to all restructuring actions in which the factory directly or indirectly benefits from the changes. RL is related to the process of retrieval of goods at the final stage of the lifecycle for regeneration, recycling, or green disposal (Zarbakhshnia et al. 2019). RL is the efficient control of raw materials, finished goods, and in-process inventory from production to consumption to regain value from the disposed goods (Rogers and Tibben-Lembke 1999). Figure 1 presents an RL system. A typical RL system involves product acquisition, collection, examination and classification, disposal, and redistribution processes. The disposition process includes five steps of repair, refurbish, remanufacture, cannibalize, and recycle. In this research, the focus is on the recycling step of the disposition process. Next, this study presents the RL processes from a literature perspective (Agrawal et al. 2016a, b; Rachih et al. 2019).

Fig. 1.

The process flow in RL

Reverse logistic processes encompass different stages that include product acquisition (gatekeeping), collection (gathering), inspection and sorting, disposition, and redistribution, all of which are described below.

Product acquisition (gatekeeping)

Product acquisition refers to operations in which goods are collected and returned from the end-users (Jayaraman et al. 2008). In this process, companies use agents in the purchasing sector to identify the market for consumer goods and buy the used or returned products (Agrawal et al. 2016b).

Collection (gathering)

Collection or gathering refers to goods received from the interior and exterior end-users and includes the processes of delivery of the returned goods and their transport (Lambert et al. 2011). In this process, the company takes ownership of the products by purchasing them from retailers (Agrawal et al. 2016a). After the purchase, products are harvested and prepared for recycling, repair, or disposal (Agrawal et al. 2016b). Three methods of the collection include direct contact with customers, retailers, or a third party.

Inspection and sorting

The collected products often have different qualities and appearances. Therefore, inspection and isolation are needed to sort these products. In this step, a separate inspection is carried out to categorize these products accordingly (Agrawal et al. 2016b). Generally, sorting involves deciding on the goods and products returned (Lambert et al. 2011). This process can be complex when hazardous goods are being sorted.

Disposition

Disposition refers to goods that are either defective or have reached the end of their lifetime so that they can be re-produced and enter the consumption cycle. Returned products can also be used as raw material in the production of new products (Jayaraman et al. 2008). Generally, this process involves deciding whether to repair, refurbish, remanufacture, cannibalize, or recycle the product.

Redistribution

Redistribution is the process of diverting reusable goods to a market for resale purposes. Reusable goods can be traded through redistribution on a secondary market (Agrawal et al. 2016a).

Tire recycling

The primary consumers of tire products are asphalt manufacturing and automotive industries. Tire waste is usually obtained from the tire production process or products consumed by customers (Fukumori et al. 2002). Tire waste recycling is an example of recycled solids that has received considerable attention due to its environmental benefits (Price and Smith 2015). The natural destruction of tires is often time-consuming, expensive, and causes environmental pollution. The environmentally conscious approach to tackle this problem is recycling and reusing the tire waste (Adhikari 2000). These tire recycling approaches lead to economic and social benefits such as reducing energy consumption, diminishing production cost by combining rubber powder from recycled rubber, and reducing rubber waste (Fang et al. 2001).

Tire recycling methods are divided into mechanical and chemical approaches. In the mechanical approach, tires are divided into smaller pieces. This process is done in several steps by shredder and granulator machines. Each step produces different products, which are used in various industries. Some industries use coarse granules, and others use a very soft tire powder. In the chemical approach, the tire is burned, and the metal wires or the tire become pyrolyzed. In pyrolysis, the tire is burned in a vacuum, and several products are extracted, such as diesel fuel and oil. Recycled tire products vary based on the mechanical or chemical recycling: rubber granulate, rubber powder, recycled metal, reclaimed tire, asphalt and bitumen polymer, gasoline fuel, and the car battery.

Green supplier assessment and assortment

Supplier assessment and assortment have a significant role in creating an impressive and competitive chain (Freeman and Chen 2015; Ghadimi et al. 2019). Due to outsourcing activities, companies’ dependence on suppliers has increased; thus, supplier evaluation and selection have become of great importance. The supplier evaluation and selection procedure are done with different objectives (Govindan et al. 2015b). In addition, as public awareness about the environmental impacts increases, principles and strategies for green supply chain activities happen to be the key success factors for companies (Liao et al. 2016). One of the critical principles in green activities is removing or reducing wastes, which causes hazardous solid waste, energy losses, and greenhouse gas emissions. Improving waste management can turn into a core competency for suppliers (Torabzadeh Khorasani 2017). This research conducted a thorough literature review to explore the environmental dimensions and the primary standards for assessing and selecting the best suppliers for tire recycling presented in Table 1.

Table 1.

Environmental dimensions and criteria for green supplier selection

Environmental dimensions	Environmental criteria		Objective	References
Pollution controls C1	C11	Energy consumption	MIN	Cao et al. 2015; Kannan et al. 2015; Datta et al. 2012; Lee et al. 2009; Noci 1997; Fallahpour et al. 2016; Qin et al. 2017; Shaik and Abdul-Kader 2011; Yeh & Chuang, 2011
	C12	Use of harmful material	MIN	Kannan et al. 2015; Datta et al. 2012; Lee et al. 2009; Govindan et al. 2015a
	C13	Pollution control initiatives	MAX	Kannan et al. 2015
	C14	Pollution decrease capability	MAX	Kannan et al. 2015; Humphreys et al. 2006; P. Humphreys et al. 2003
Green product C2	C21	Recycle	MAX	Kannan et al. 2015; Datta et al. 2012; Lee et al. 2009; Büyüközkan and Çifçi 2012; Govindan and Sivakumar 2016; Jabbour and Jabbour 2009; Shaik and Abdul-Kader 2011; P. Humphreys et al. 2006; P. K. Humphreys et al. 2003
	C22	Reuse	MAX	Jabbour and Jabbour 2009; Shaik and Abdul-Kader 2011; P. Humphreys et al. 2006
	C23	Remanufacture	MAX	Hashemi et al. 2015; Kannan et al. 2015; Jabbour and Jabbour 2009; Datta et al. 2012; Shaik and Abdul-Kader 2011; P. Humphreys et al. 2006; P. K. Humphreys et al. 2003
Environment protection/environment management C3	C31	The capability of preventing pollution	MAX	Kannan et al. 2015
	C32	Continuous pursuit and regulatory compliance		Kannan et al. 2015
	C33	Environmental management system	MAX	Kannan et al. 2015; Çifçi and Büyüközkan 2011; Rezaei et al. 2016; Yazdani 2017
	C34	Environmental protection plans	MAX	Kannan et al. 2015
Pollution production C4	C41	Production of polluting agents	MIN	Bai and Sarkis 2010
	C42	Production of toxic products	MIN	Bai and Sarkis 2010
	C43	Waste production	MIN	Bai and Sarkis 2010

Different approaches have been suggested and applied for green supplier assessment and assortment, including grey-based Decision-Making Trial and Evaluation Laboratory (DEMATEL) (Fu et al. 2012), grey analytic network process (ANP) (Dou et al. 2014), data envelopment analysis (DEA) (Dobos and Vörösmarty 2014), fuzzy additive ratio assessment and multi-segment goal programming (Liao et al. 2016), the qualitative flexible multiple method (Wang et al. 2017), DEMATEL-ANP (Jiang et al. 2018), TOPSIS (Shafique 2018), elimination and choice expressing reality (Gitinavard et al. 2018), Visekriterijumska Optimizcija I Kaompromisno Resenje (VIKOR) (Demir et al. 2018), TOPSIS-VIKOR-grey relational analysis (Banaeian et al. 2018), the preference ranking organization technique for improving assessments (Abdullah et al. 2018), fuzzy analytic hierarchy process (AHP) (Zafar et al. 2019), BWM and TOmada de Decisao Interativa Multicriterio (TODIM) (Bai et al. 2019), and hybrid FUll COnsistency Method (FUCOM) and rough simple additive weighting (SAW) techniques (Durmić et al. 2020).

Prakash and Barua (2015) studied RL obstacles and used AHP and TOPSIS to rank barriers. Similarly, Bouzon et al. (2016) investigated RL obstacles in Brazil’s electronic industry, identified barriers based on expert opinion using the fuzzy Delphi method, and ranked them by applying the AHP approach. Govindan et al. (2016) used a model of multi-objective particle swarm optimization for an effective and viable RL network outline considering the environmental, social, and economic domains. Moreover, Mangla et al. (2016) used DEMATEL and AHP approaches to examine the RL critical success elements in Indian industries. Ravi and Shankar (2017) investigated RL principles in the automobile industry using interpretive structural modeling.

COPRAS, MULTIMOORA, and TOPSIS

MCDM models are applied to identify and select the best possible solution from a set of alternatives based on different decision criteria. For example, prior research has used COPRAS to plan water transfer between basins (Roozbahani et al. 2020), rank hybrid wind farms (Dhiman and Deb 2020), select green suppliers (Kumari and Mishra 2020), evaluate the performance of contractors (Jasim 2021), assess construction project safety (Wei et al. 2021), rank effective risks in natural gas supply projects (Balali et al. 2021), and evaluate COVID-19 regional safety (Hezer et al. 2021). In addition, previous studies have used MULTIMOORA for selecting suppliers (Tavana et al. 2020a, b) and logistic service providers (Sarabi and Darestani 2021), examining the barriers to the adoption of renewable energy (Asante et al. 2020), selecting car subscription station sites (Lin et al. 2020a, b), choosing stable battery suppliers (Wang et al. 2021a, b), and evaluating technology project review experts (Wang et al. 2021c, d). A similar range of applications arises when considering previous research works that implement TOPSIS, including supplier selection (Lei et al. 2020), the evaluation of unusual emergency events (Zhan et al. 2020), the assessment of lake eutrophication levels (Lin et al. 2020a, b), sustainable supply chain risk management (Abdel-Basset and Mohamed 2020), risk analysis of cutting system (Kushwaha et al. 2020), transportation management (Sarkar and Biswas 2021), risk prioritization in self-driving vehicles (Bakioglu and Atahan 2021), and the evaluation of renewable energy production capabilities (Wang et al. 2021a, b, c, d).

BWM and fuzzy Shannon’s entropy

BWM, proposed by Rezaei (2016), is an MCDM technique used to determine the weights of criteria. BWM has been developed and applied by researchers across several disciplines. For instance, Bonyani and Alimohammadlou (2019) integrated BWM with ANP to improve pair-wise comparison processes. Amiri et al. (2020) developed a group BWM and integrated it with a fuzzy preference programming method to examine hospital performance. Other studies have also used BWM for evaluation purposes, including the performance of solid waste management (Behzad et al. 2020), insurance companies (Dwivedi et al. 2021), and healthcare departments (Torkayesh et al. 2021), driver’s behavior in road safety (Moslem et al. 2020), the green performance of airports (Kumar et al. 2020), selection of providers (Muravev and Mijic 2020), and ship recycling (Soner et al. 2021). Similarly, the method based on Shannon’s entropy is an appropriate technique for specifying the relevance of weights in multiple attribute decision-making methods. For instance, this method has been used to rank cities (Storto 2016), assess flood vulnerability (Yang et al. 2018a, b), analyze barriers to the implementation of continuous improvement (Tavana et al. 2020a, b), study surface air temperature and rainfall (Ray and Chattopadhyay 2021), and rank the structural analysis of software applications (Jarrah et al. 2021).

Methodology

This study uses a fuzzy green supplier selection model for sustainable supply chains in RL. To prioritize those green suppliers with a robust ability to recycle in RLs, we use fuzzy extensions of COPRAS, MULTIMOORA, and TOPSIS. COPRAS, MULTIMOORA, and TOPSIS are robust MCDM techniques applied to evaluate the performance of a series of alternatives according to different criteria. The relative importance assigned to these criteria is determined by the separate implementation of the fuzzy extension of Shannon’s entropy and our proposed approach, namely, HFBWM. This latter method constitutes one of the main contributions of the current study. We extend FBWM into HFBWM to evaluate the weights of the criteria and sub-criteria used to rank alternatives through COPRAS, MULTIMOORA, and TOPSIS. Integrating these MCDM methods into hybrid evaluation techniques aims to improve the accuracy and robustness of the results compared to those obtained when applying a single method. We also use fuzzy Shannon’s entropy to determine the weights of the criteria and sub-criteria of the different hybrid models, allowing us to compare the rankings derived from both weighting techniques. The comparisons performed both across hybrid MCDM models and between weighting techniques aim at improving the quality of decision-making and the reliability of the results obtained.

As depicted in Fig. 2, the procedure of the current research entails six phases. First, this research reviews the literature and identifies the green supplier assortment benchmarks. In addition, the green supplier assortment benchmarks for the tire recycling industry are classified accordingly. Second, this research uses fuzzy Shannon’s entropy and HFBWM to compute the importance weight of the green supplier assessment benchmarks. Third, this study uses fuzzy COPRAS in phase 3, fuzzy MULTIMOORA in phase 4, and fuzzy TOPSIS in phase 5 to rank the suppliers. We compare the rankings provided by the set of methods implemented throughout the evaluation procedure, illustrating fuzzy COPRAS and fuzzy MOORA’s capacity to deliver sufficiently robust rankings relative to more complex techniques such as fuzzy MULTIMOORA. Finally, in phase 6, this research aggregates the rankings obtained from the fuzzy COPRAS, fuzzy MULTIMOORA, and fuzzy TOPSIS techniques using the maximize agreement heuristic (MAH) method proposed by Beck and Lin (1983) to reach an agreement for the rankings produced by the different hybrid methods. Several consensus ranking methods, such as the Copeland approach, exist. MAH is commonly used since it provides an effective consensus ranking framework that maximizes agreement in decision-making. It is a practical method that has been introduced to motivate the application of our integrated model by future researchers. We conclude by highlighting the hybrid models’ capacity based on HFBWM to provide consistent ranking results while requiring a simpler evaluation framework than those based on the fuzzy extension of Shannon’s entropy.

Fig. 2.

Proposed framework

In phase 1, this study conducted a rigorous literature review and explored the benchmarks and environmental dimensions to assess and assort the best suppliers for tire recycling. As depicted in Fig. 3, the green supplier selection benchmarks chosen in this study were classified into the four environmental dimensions of pollution control, green product, environment management, and pollution production.

Fig. 3.

The green supplier selection criteria

Fuzzy Shannon’s entropy method

Entropy refers to the quantitative measure of information (Shannon 1948), leading to a higher degree of compression (Naidu et al. 2018). According to Pourhamidi (2013), the entropy approach has its roots in the Boltzmann entropy of conventional statistical methods. Fuzzy entropy refers to the fuzzy information obtained from the fuzzy system (Al-Sharhan et al. 2001), and it differs from Shannon entropy, which is an estimate of unpredictability. The difference is mainly the probabilistic nature of Shannon entropy. According to Lotfi and Fallahnejad (2010), it is a good technique in specifying the relevant weights in multiple attribute decision-making methods. Previous research improved this method for fuzzy data (Lotfi and Fallahnejad 2010). The steps of the fuzzy Shannon’s entropy approach are presented as follows:

• Step 1:
  This step involves transforming the fuzzy numbers to set-level data. In a fuzzy variable $\widetilde{x_{\mathit{ij}}}$, the α-level set indicates a class of intervals that has a participation of minimum value α, i.e., ${\left(\widetilde{x_{\mathit{ij}}}\right)}_{\alpha }=\left\{X_{\mathit{ij}}\in Rl{u}_{\widetilde{x_{\mathit{ij}}}}\left(X_{\mathit{ij}}\right)\ge \alpha \right\}$. The following formula indicates the α-level set:

  $$\left[{\left(\widetilde{x_{\mathit{ij}}}\right)}_{\alpha }^l,{\left(\widetilde{x_{\mathit{ij}}}\right)}_{\alpha }^u\right]=\left[{\mathit{Min}}_{x_{\mathit{ij}}}\left\{x_{\mathit{ij}}\in R\left|u_{x_{\mathit{ij}}}\right)\left(X_{\mathit{ij}}\right)\ge \alpha \right\},{\mathit{Max}}_{x_{\mathit{ij}}}\left\{x_{\mathit{ij}}\in R\left|u_{x_{\mathit{ij}}}\right)\left(X_{\mathit{ij}}\right)\ge \alpha \right\}\right]$$

  in which 0 < α ≤ 1.

Through the different levels of confidence interval limits in terms of 1-α, the fuzzy data is transformed to the different interval set values of $\left\{{\left({\tilde{x}}_{\mathit{ij}}\right)}_{\alpha }\left|0<\alpha \le 1\right)\right\}$.

• Step 2:
  In this step, the $p_{\mathit{ij}}^l$ and $p_{\mathit{ij}}^u$ values are calculated through the parameters of Eq. (1):

  $$p_{\mathit{ij}}^l=\frac{x_{\mathit{ij}}^l}{{\sum }_{j=1}^m{x}_{\mathit{ij}}^u},p_{\mathit{ij}}^u=\frac{x_{\mathit{ij}}^u}{{\sum }_{j=1}^m{x}_{\mathit{ij}}^u},j=1,\dots ,m;i=1,\dots ,n$$ 1
• Step 3:
  In the following stage, the $h_i^l$ and $h_i^u$ formulas as min and max interval values are computed through Eq. (2):

  $$\begin{array}{cc}{h}_i^l=\mathit{Min}\left\{-h_0{\sum }_{j=1}^m{p}_{\mathit{ij}}^l.ln{p}_{\mathit{ij}}^l,-h_0{\sum }_{j=1}^m{p}_{\mathit{ij}}^u.ln{p}_{\mathit{ij}}^u\right\},& i=1,\dots ,n\\ h_i^u=\mathit{Max}\left\{-h_0{\sum }_{j=1}^m{p}_{\mathit{ij}}^l.ln{p}_{\mathit{ij}}^l,-h_0{\sum }_{j=1}^m{p}_{\mathit{ij}}^u.ln{p}_{\mathit{ij}}^u\right\},& i=1,\dots ,n\end{array}$$ 2

  in which h₀ = (lnm)⁻¹ and $p_{\mathit{ij}}^l.ln{p}_{\mathit{ij}}^l$ or $p_{\mathit{ij}}^u.ln{p}_{\mathit{ij}}^u$ are zero in case $p_{\mathit{ij}}^l=0$ or $p_{\mathit{ij}}^u=0$.
• Step 4:
  In this step, the $d_i^l$ and $d_i^u$ diversification interval values are assigned in Eq. (3):

  $$d_i^l=1-h_i^u,d_i^u=1-h_i^l,i=1,\dots ,n$$ 3
• Step 5:
  In this step, the $w_i^l$ and $w_i^u$ values are assigned as the base and upward value limits of the interim weights of the attribute i, where i = 1, …, n, as shown in Eq. (4):

  $$w_i^l=\frac{d_i^l}{{\sum }_{s=1}^n{d}_s^u},w_i^u=\frac{d_i^u}{{\sum }_{s=1}^n{d}_s^l}$$ 4
• Step 6:
  This research calculates $w_i^{\text{'}}=\frac{w_i^l+w_i^u}{2},$, then computes ${\sum }_i^n{w}_i^{\text{'}}$, and finally calculates w_i using Eq. (5) to obtain the final weight:

  $$w_i=\frac{w_i^{\text{'}}}{{\sum }_i^n{w}_i^{\text{'}}}$$ 5

Hierarchical fuzzy best-worst method

Rezaei (2015) proposed the best-worst method as an MCDM technique used to determine the weights of criteria via pair-wise comparisons of the best criterion relative to all the other criteria and all the criteria relative to the worst criterion (Bonyani and Alimohammadlou 2019). Immediate extensions were developed by Tabatabaei et al. (2019), who introduced the Hierarchical BWM, and Guo and Zhao (2017), who proposed a fuzzy version of the BWM. The HBWM allows considering the weights of the criteria and sub-criteria within a simultaneous programming model so as to calculate the global weights of the set of sub-criteria (Ren and Toniolo 2021).

We propose the Hierarchical Fuzzy Best-Worst Method (HFBWM) based on the fuzzy BWM (FBWM) introduced by Guo and Zhao (2017) and the HBWM defined by Tabatabaei et al. (2019). The steps of the HFBWM can be summarized as follows:

• Step 1:

  Identify the set of criteria {C₁, C₂, …, C_n} and sub-criteria {C_1S, C_2S, …, C_nS}.

• Step 2:

  Identify the best (most important) criteria and sub-criteria, B, and the worst (least important) criteria and sub-criteria, W.

• Step 3:
  Determine the fuzzy preference for the best criterion over each of the other criteria on a scale from 1 to 5. The fuzzy best-to-others criteria are defined as follows:

  $${\tilde{A}}_B=\left({\tilde{a}}_{B1},{\tilde{a}}_{B2},\dots ,{\tilde{a}}_{\mathit{Bn}}\right)$$ 6

  where ${\tilde{a}}_{\mathit{Bj}}$ is the fuzzy preference of B over C_j (j = 1, 2, …, n) and ${\tilde{a}}_{\mathit{BB}}=\left(1,1,1\right)$.
• Step 4:
  Determine the fuzzy preference of all the criteria over the worst criterion on a scale from 1 to 5. The fuzzy others-to-worst criteria are defined as follows:

  $${\tilde{A}}_W=\left({\tilde{a}}_{1W},{\tilde{a}}_{2W},\dots ,{\tilde{a}}_{\mathit{nW}}\right)$$ 7

  where ${\tilde{a}}_{\mathit{jW}}$ is the fuzzy preference of C_j (j = 1, 2, …, n) over W and ${\tilde{a}}_{\mathit{WW}}=\left(1,1,1\right)$.
• Step 5:
  Determine the fuzzy preference of the best sub-criterion over each of the other sub-criteria in a scale from 1 to 5. The fuzzy best-to-others sub-criteria are defined as follows:

  $${\tilde{A}}_{\mathit{BS}}=\left({\widetilde{a^j}}_{B1},{\widetilde{a^j}}_{B2},\dots ,{\widetilde{a^j}}_{\mathit{Bn}}\right)$$ 8

  where ${\widetilde{a^j}}_{\mathit{BS}}$ is the fuzzy preference of the best sub-criterion over the S-th sub-criterion within the j-th criterion and ${\widetilde{a^j}}_{\mathit{BB}}=\left(1,1,1\right)$.
• Step 6:
  Determine the fuzzy preference of all sub-criteria over the worst sub-criterion on a scale from 1 to 5. The fuzzy others-to-worst sub-criteria are defined as follows:

  $${\tilde{A}}_{\mathit{SW}}=\left({\widetilde{a^j}}_{1W},{\widetilde{a^j}}_{2W},\dots ,{\widetilde{a^j}}_{\mathit{nW}}\right)$$ 9

  where ${\widetilde{a^j}}_{\mathit{SW}}$ is the fuzzy preference of the S-th sub-criterion over the worst sub-criterion within the j-th criterion and ${\widetilde{a^j}}_{\mathit{WW}}=\left(1,1,1\right)$.
• Step 7:
  Calculate the weights of the criteria (w^c₁, w^c₂, …, w^c_n) and sub-criteria (w^j₁, w^j₂, …, w^j_S), and then calculate the final weights of the sub-criteria as Gw^j_S = w^c_j × w^sj_S:

  $$\begin{array}{c}min\tilde{\xi }+\sum _j\widetilde{{\xi }_j}\\ s.t:\\ \left|\raisebox{1ex}{$w_B$}\!\left/ \!\raisebox{-1ex}{$w_j$}\right.-{\tilde{a}}_{\mathit{Bj}}\right|\le \tilde{\xi },\forall j=1,\dots ,n\\ \left|\raisebox{1ex}{$w_j$}\!\left/ \!\raisebox{-1ex}{$w_W$}\right.-{\tilde{a}}_{\mathit{jW}}\right|\le \tilde{\xi },\forall j=1,\dots ,S\\ \left|\raisebox{1ex}{$w_B^j$}\!\left/ \!\raisebox{-1ex}{$w_S^j$}\right.-\widetilde{a_{\mathit{BS}}^j}\right|\le \widetilde{{\xi }_j},\forall j=1,\dots ,S\\ \left|\raisebox{1ex}{$w_S^j$}\!\left/ \!\raisebox{-1ex}{$w_W^j$}\right.-{\tilde{a}}_{\mathit{SW}}^j\right|\le \widetilde{{\xi }_j},\forall j=1,\dots ,n\\ G{w}_S^j=w_j\times w_S^j\\ \sum _{j=1}^{n}R\left(w_j\right)=1,\\ \sum _{j=1}^{n}R\left(w_S^j\right)=1,\\ l_j^w\le m_j^w\le u_j^w,\forall j=1,\dots ,n\\ l_j^w,m_j^w,u_j^w\ge 0,\forall j=1,\dots ,n\end{array}$$ 10-1

  $$\begin{array}{c}min\tilde{\xi }+\sum _j\widetilde{{\xi }_j}\\ s.t:\\ \left|w_B-{\tilde{\mathrm{a}}}_{\mathit{Bj}}{w}_j\right|\le \tilde{\xi },\forall j=1,\dots ,n\\ \left|w_j-{\tilde{a}}_{\mathit{jW}}{w}_W\right|\le \tilde{\xi },\forall j=1,\dots ,S\\ \left|w_B^j-\widetilde{a_{\mathit{BS}}^j{w}_S^j}\right|\le \widetilde{{\xi }_j},\forall j=1,\dots ,S\\ \left|w_S^j-{\tilde{a}}_{\mathit{SW}}^j{w}_W^j\right|\le \widetilde{{\xi }_j},\forall j=1,\dots ,n\\ G{w}_S^j=w_j\times w_S^j\\ \sum _{j=1}^{n}R\left(w_j\right)=1,\\ \sum _{j=1}^{n}R\left(w_S^j\right)=1,\\ l_j^w\le m_j^w\le u_j^w,\forall j=1,\dots ,n\\ l_j^w,m_j^w,u_j^w\ge 0,\forall j=1,\dots ,n\end{array}$$ 10-2

  $$R\left(w_j\right),R\left(w_S^j\right)=\frac{l_j^w+4m_j^w+u_j^w}{6}$$ 11

In Model (10-2), R(w_j) and $R\left(w_S^j\right)$ are the average weights of the criteria and sub-criteria, w_j and $w_S^j$, respectively:

The consistency ratio of the comparisons is calculated according to Eq. (12) and Table 2 as follows:

$$\mathit{\text{Consistency\hspace{0.17em}Ratio}}=\frac{{\xi }^{\ast }}{\mathit{\text{Consistency\hspace{0.17em}Index}}}$$ 12

Table 2.

Consistency index in BWM

aBW, $a_{\mathit{BW}}^j$	Exactly equal (E)	Slightly strong (SS)	Fairly strong (FS)	Very strong (VS)	Absolutely strong (AS)
CI	3.00	3.80	5.29	6.69	8.04

where ${\xi }^{\ast }=\tilde{\xi }+\sum _j\widetilde{{\xi }_j}$ for all criteria and sub-criteria.

Fuzzy COPRAS

COPRAS is a multiple attribute decision-making approach developed by Zavadskas et al. (1994). The COPRAS approach calculates the solution by considering the best solution ratio. This approach surmises the proportionate and direct association between the importance-efficiency measures of checked versions and a system of criteria in which it explains the alternatives, weights, and values of the criteria accordingly (Yazdani et al. 2015). Zavadskas and Antucheviciene (2007) developed the fuzzy COPRAS approach. The phases of the ranking process used for fuzzy COPRAS (Zarbakhshnia et al. 2018) are appended below:

• Step 1:
  According to Table 3, the fuzzy decision matrix (DM) is built in this step:

  $$\tilde{X}=\left[\begin{array}{ccc}\left[x_{11}^l,x_{11}^m,x_{11}^u\right]& \left[x_{12}^l,x_{12}^m,x_{12}^u\right]& \dots \\ \begin{array}{c}.\\ .\\ .\end{array}& \begin{array}{c}.\\ .\\ .\end{array}& \dots \\ \left[x_{m1}^l,x_{m1}^m,x_{m1}^u\right]& \left[x_{m2}^l,x_{m2}^m,x_{m2}^u\right]& \dots \end{array}\begin{array}{c}\left[x_{1n}^l,x_{1n}^m,x_{1n}^u\right]\\ \begin{array}{c}.\\ .\\ .\end{array}\\ \left[x_{\mathit{mn}}^l,x_{\mathit{mn}}^m,x_{\mathit{mn}}^u\right]\end{array}\right]$$ 13

Table 3.

Linguistic variables for fuzzy COPRAS, fuzzy MULTIMOORA, fuzzy BWM, and Shannon’s entropy methods

Linguistic variables for rating the suppliers		Linguistic variables for the weighting of each criterion				Interval values for linguistic variables
Linguistic variables	Triangular fuzzy number for fuzzy COPRAS and fuzzy MULTIMOORA	Linguistic variables (priority weights)	Triangular fuzzy numbers of the fuzzy BWM (Guo and Zhao 2017)	Linguistic variables (priority weights)	Triangular fuzzy number for fuzzy Shannon	Interval data at 0.3α
Very low (VL)	(0,0,0.25)	Equally importance (EI)	(1,1,1)	Unimportant (UI)	(0,0,0.2)	[0,0.17]
Low (L)	(0,0.25,0.5)	Weakly importance (WI)	(2/3,1,3/2)	Slightly important (SI)	(0,0.2,0.4)	[0.07,0.42]
Medium (M)	(0.25,0.5,0.75)	Fairly importance (FI)	(3/2,2,5/2)	Fairly important (FI)	(0.2,0.4,0.6)	[0.32,0.67]
High (H)	(0.5,0.75,0.1)	Very importance (VI)	(5/2,3,7/2)	Important (I)	(0.4,0.6,0.8)	[0.57,0.92]
Very high (VH)	(0.75,1,1)	Absolutely importance (AI)	(7/2,4,9/2)	Very important (VI)	(0.6,0.8,1)	[0.82,1]

The m parameter in the matrix outlines how many alternatives are assigned, and the n parameter highlights the existing benchmarks, and the xmn parameter indicates the efficiency of alternative i in criteria j. Table 3 shows the guidelines used for the conversion process of fuzzy membership functions (M. P. Amiri 2010; Zarbakhshnia et al. 2018).

• Step 2:
  In this stage, the fuzzy normalization DM is calculated for estimating its analogous sufficiency. As $\widetilde{X_{\mathit{ij}}^{\ast }}=\left(x_{\mathit{ij}}^{l\ast },x_{\mathit{ij}}^{m\ast },x_{\mathit{ij}}^{u\ast }\right)$ and ∀i, j,

  $$x_{\mathit{ij}}^{l\ast }=x_{\mathit{ij}}^l/\sqrt{{\sum }_{i=1}^m\left[{\left(x_{\mathit{ij}}^l\right)}^2+{\left(x_{\mathit{ij}}^m\right)}^2+{\left(x_{\mathit{ij}}^u\right)}^2\right]}$$ 14

  $$x_{\mathit{ij}}^{m\ast }=x_{\mathit{ij}}^{\mathrm{m}}/\sqrt{{\sum }_{i=1}^m\left[{\left(x_{\mathit{ij}}^l\right)}^2+{\left(x_{\mathit{ij}}^m\right)}^2+{\left(x_{\mathit{ij}}^u\right)}^2\right]}$$ 15

  $$x_{\mathit{ij}}^{u\ast }=x_{\mathit{ij}}^u/\sqrt{{\sum }_{i=1}^m\left[{\left(x_{\mathit{ij}}^l\right)}^2+{\left(x_{\mathit{ij}}^m\right)}^2+{\left(x_{\mathit{ij}}^u\right)}^2\right]}$$ 16
• Step 3:

  In this stage, the weight of the benchmarks that were calculated utilizing the fuzzy Shannon is computed.

• Step 4:

  In this stage, the weighted normalized DM is calculated.

• Step 5:
  In this stage, higher values of the sum of attributes $\widetilde{p_j}$ are preferred for each alternative (optimization direction is maximization), with k representing the number of attributes that must be maximized:

  $$\widetilde{p_j}=\sum _{i=1}^k\widetilde{x_{\mathit{ij}}}$$ 17
• Step 6:
  In this stage, lower values of the sum of attributes $\widetilde{R_j}$ are preferred for each alternative (optimization direction is minimization), with (m−k) representing the number of attributes that must be minimized:

  $$\widetilde{R_j}=\sum _{i=K+1}^m\widetilde{x_{\mathit{ij}}}$$ 18
• Step 7:
  In this stage, the lower bound of $\widetilde{R_j}$ as $\tilde{R}$ minimum is calculated:

  $$\widetilde{R_{\min }}={min}_j\widetilde{R_j};j=1,2,\dots ,n$$ 19
• Step 8:
  In this stage, the comparative importance of every variable is calculated:

  $$\widetilde{Q_i}=\widetilde{p_j}+\frac{\widetilde{R_{\min }}{\sum }_{j=1}^n\widetilde{R_j}}{\widetilde{R_j}{\sum }_{j=1}^n\frac{\widetilde{R_{\min }}}{\widetilde{R_j}}};j=1,2,\dots ,n$$ 20
• Step 9:
  In this stage, the 푄 ~_푗 function to a non-fuzzy value using Eq. (21) is defuzzified:

  $$x_{\mathit{ij}}=\frac{\left(x_{\mathit{ij}}^u-x_{\mathit{ij}}^l\right)+\left(x_{\mathit{ij}}^m-x_{\mathit{ij}}^l\right)}{3}+x_{\mathit{ij}}^l$$ 21
• Step 10:
  In this stage, the best alternative is chosen according to Eq. (22) in which the upper weight limit of the alternatives is calculated according to the preference value:

  $$K={max}_j{Q}_j;j=1,2,\dots ,n$$ 22
• Step 11:
  In this stage, the scope of parameters in every variable is computed with Eq. (23). Furthermore, all numbers are defuzzified in this phase:

  $$K_j=\frac{Q_j}{Q_{\max }}\times 100\%;j=1,2,\dots ,n$$ 23

In this equation, Q_j and Q_max are referred to as the non-fuzzified comparative importance of each alternative as well as the best alternative value. With regard to the K_j parameter, the alternative values are classified and graded downward so that the superior value of K_j is the best alternative.

Fuzzy MULTIMOORA

The MULTIMOORA approach is a combination of multi-objective optimization with ratio analysis (MOORA) and the full multiplicative form (FMF) of multiple objectives. MULTIMOORA is a vigorous method in multiple objective optimizations (Brauers and Zavadskas 2011). Previous studies had applied the MULTIMOORA approach in various disciplines such as risk assessment (Fattahi and Khalilzadeh 2018), project management initiatives (Dorfeshan et al. 2018), automobile selection (Wu et al. 2017), choosing home structure and fabric (Zavadskas et al. 2017), logistics (Awasthi and Baležentis 2017), supplier selection (Liu et al. 2018a), recycling (Ding and Zhong 2018), entertainment (Wu et al. 2018), automobile design (Liu et al. 2018b), ERP (Tian et al. 2017), robotics (You et al. 2018), agriculture (Hafezalkotob et al. 2018), and housing industry (Zavadskas et al. 2017).

Fuzzy MOORA

Brauers and Zavadskas (2006) initially recommended the MOORA for improving two or more contradicting attributes that are bound to specific limitations. The MOORA approach is a multicriteria decision-making method commonly used to solve business challenges such as manufacturing, gas and oil industry, process design, or every flawless decision that considers several other contradicting attributes (Akkaya et al. 2015). According to Ceballos et al. (2016), the MOORA method builds a ranking system that is resorted to three computations: the reference point (RP), the ratio system, and the FMF of multiple objectives (Ceballos et al. 2016). The fuzzy MOORA approach as a multicriteria decision-making technique for privatization research in a subsistence economy is proposed by Brauers and Zavadskas (2006). The stages of the fuzzy ratio approach used in this research are identical in the previous applications of this method by Karande and Chakraborty (2012), Gupta et al. (2017), and Akkaya et al. (2015):

• Step 1:
  In this stage, a DM is formed using triangular fuzzy numbers:

  $$\tilde{X}=\left[\begin{array}{ccc}\left[x_{11}^l,x_{11}^m,x_{11}^u\right]& \left[x_{12}^l,x_{12}^m,x_{12}^u\right]& \dots \\ \begin{array}{c}.\\ .\\ .\end{array}& \begin{array}{c}.\\ .\\ .\end{array}& \dots \\ \left[x_{m1}^l,x_{m1}^m,x_{m1}^u\right]& \left[x_{m2}^l,x_{m2}^m,x_{m2}^u\right]& \dots \end{array}\begin{array}{c}\left[x_{1n}^l,x_{1n}^m,x_{1n}^u\right]\\ \begin{array}{c}.\\ .\\ .\end{array}\\ \left[x_{\mathit{mn}}^l,x_{\mathit{mn}}^m,x_{\mathit{mn}}^u\right]\end{array}\right]$$ 24
• Step 2:

  In this stage, the DM is changed to a normalized fuzzy DM (FDM) utilizing Eqs. (25), (26), and (27):

  As $\widetilde{X_{\mathit{ij}}^{\ast }}=\left(x_{\mathit{ij}}^{l\ast },x_{\mathit{ij}}^{m\ast },x_{\mathit{ij}}^{u\ast }\right)$ and ∀i, j,

  $$x_{\mathit{ij}}^{l\ast }=x_{\mathit{ij}}^l/\sqrt{{\sum }_{i=1}^m\left[{\left(x_{\mathit{ij}}^l\right)}^2+{\left(x_{\mathit{ij}}^m\right)}^2+{\left(x_{\mathit{ij}}^u\right)}^2\right]}$$ 25

  $$x_{\mathit{ij}}^{m\ast }=x_{\mathit{ij}}^m/\sqrt{{\sum }_{i=1}^m\left[{\left(x_{\mathit{ij}}^l\right)}^2+{\left(x_{\mathit{ij}}^m\right)}^2+{\left(x_{\mathit{ij}}^u\right)}^2\right]}$$ 26

  $$x_{\mathit{ij}}^{u\ast }=x_{\mathit{ij}}^u/\sqrt{{\sum }_{i=1}^m\left[{\left(x_{\mathit{ij}}^l\right)}^2+{\left(x_{\mathit{ij}}^m\right)}^2+{\left(x_{\mathit{ij}}^u\right)}^2\right]}$$ 27
• Step 3:
  In this stage, the weighted normalized FDM is determined by using Eqs. (28), (29), and (31):

  $$V_{\mathit{ij}}=\left(v_{\mathit{ij}}^l,v_{\mathit{ij}}^m,v_{\mathit{ij}}^u\right);$$

  $$v_{\mathit{ij}}^l=w_j{\chi }_{\mathit{ij}}^{l\ast }$$ 28

  $$v_{\mathit{ij}}^m=w_j{\chi }_{\mathit{ij}}^{m\ast }$$ 29

  $$v_{\mathit{ij}}^u=w_j{\chi }_{\mathit{ij}}^{u\ast }$$ 30

This research used the weights calculated previously by the fuzzy Shannon entropy to compute the weighted normalized FDM.

• Step 4:
  In this stage, Eq. (31) is used to compute the normalized performance measures where the total cost measures are deducted from overall benefit measures as follows:

  $$\begin{array}{c}{V}_{\mathit{ij}}=\left(v_{\mathit{ij}}^l,v_{\mathit{ij}}^m,v_{\mathit{ij}}^u\right);\\ y_i=\sum _{j=1}^g{V}_{\mathit{ij}}-\sum _{j=g+1}^n{V}_{\mathit{ij}}\end{array}$$ 31

  where $\sum _{j=1}^g{V}_{\mathit{ij}}$ shows the benefit measures (for 1,…,g) and $\sum _{j=g+1}^n{V}_{\mathit{ij}}$ indicates the cost measure (for g+1,…,n), where g and (n − g) show the maximum and the minimum number of measures, respectively. For the benefit measures, the total ratings of an alternative can be computed for the low, center, and high limits of the triangular membership function, which are appended below:

  $$y_i^{+l}=\sum _{j=1}^n{v}_{\mathit{ij}}^l\left|j\in J^{\max }\right)$$ 32

  $$y_i^{+m}=\sum _{j=1}^n{v}_{\mathit{ij}}^m\left|j\in J^{\max }\right)$$ 33

  $$y_i^{+u}=\sum _{j=1}^n{v}_{\mathit{ij}}^u\left|j\in J^{\max }\right)$$ 34
  In addition, the cost measures are computed in the same way for the entire ratings of an objective, as shown below:

  $$y_i^{-l}=\sum _{j=1}^n{v}_{\mathit{ij}}^l\left|j\in J^{\max }\right)$$ 35

  $$y_i^{-m}=\sum _{j=1}^n{v}_{\mathit{ij}}^m\left|j\in J^{\max }\right)$$ 36

  $$y_i^{-u}=\sum _{j=1}^n{v}_{\mathit{ij}}^u\left|j\in J^{\max }\right)$$ 37
• Step 5:
  In this stage, the entire performance index (y_i) for each objective is identified by computing the defuzzified boundaries of the total ratings of the benefit and cost measures for all the alternatives utilizing the vertex approach appended below:

  $$\begin{array}{l}{y}_i=\left(y_i^l,y_i^m,y_i^u\right);\\ \mathit{BN}{P}_i\left(y_i\right)=\frac{\left(y_i^u-y_i^l\right)+\left(y_i^m-y_i^l\right)}{3}+y_i^l\end{array}$$ 38

  within which Eq. (38) indicates the total performance value of the i-th alternative (objective).
• Step 6:

  In this stage, the total performance index is arranged from high to low values, and this study ranks all the alternatives from the excellent to the inferior. Among the alternatives, the most preferred choice is the alternative with the highest total performance index.

Fuzzy reference point method

Equations (25), (26), and (27) compute the RP method. This method utilizes the normalized performance of the i-th objective on the j-th measure based on the aforementioned equations. In addition, a maximum measure RP is identified between the normalized performances as a non-subjective and feasible to the coordinates (r_j). In Eq. (39), the minimum–maximum metric formula is described, and previous research highlights that this is the appropriate formula for the RP (Adalı and Işık 2017) as follows:

$$\left\{\begin{array}{c}{\tilde{r}}_j^{+}=\left(\underset{i}{max}{x_{\mathit{ij}}}^{l\ast },\underset{i}{max}{x_{\mathit{ij}}}^{m\ast },\underset{i}{max}{x_{\mathit{ij}}}^{u\ast }\right),j\le g;\text{for criteria to}\mathrm{be}\text{maximized}\\ {\tilde{r}}_j^{=}=\left(\underset{i}{min}{x_{\mathit{ij}}}^{l\ast },\underset{i}{min}{x_{\mathit{ij}}}^{m\ast },\underset{i}{min}{x_{\mathit{ij}}}^{u\ast }\right),j\rangle g;\text{for criteria to}\mathrm{be}\text{minimized}\end{array}\right)$$ 39

On condition that decision-makers decide to assign a higher value to a particular measure, Eq. (39) is recalculated through examining the weights of the measures as follows:

$$\underset{i}{min}\left(\underset{j}{max}{W}_j\times \left|{\tilde{r}}_j-{\tilde{x}}_{\mathit{ij}}^{\ast }\right|\right)$$ 40

The objectives are eventually ranked based on Eq. (38), and the most attractive objective is selected based on the lowest overall distance from the RPs (Adalı and Işık 2017).

Fuzzy full multiplicative form

The third phase of the MULTIMOORA approach is FMF. This approach was initially proposed by Miller and Starr (1969), and it is both consisted of max and min values of a completely multiplicative utility formula. The key features of the FMF include not using attribute weights, being non-additive, and non-linear (Adalı and Işık 2017). The appended formula, based on the guidelines of Hafezalkotob et al. (2019), calculates the FMF’s utility function as a fraction of the weighted normalized alternatives’ ratings on the benefit measures over the weighted normalized alternatives’ ratings on the cost measures:

$${\widetilde{U^{\prime }}}_i=\frac{{\tilde{A}}_i}{{\tilde{B}}_i}$$ 41

where ${\tilde{A}}_i=\left(A_{i1},A_{i2},A_{i3}\right)={\prod }_{j=1}^g{\left({x^{\ast }}_{\mathit{ij}}\right)}^{w_j}$ represents the result of the number of objectives of the i-th alternative to get augmented with terms of g = 1, 2, …, n and ${\tilde{B}}_i=\left(B_{i1},B_{i2},B_{i3}\right)={\prod }_{j=g+1}^m{\left({x^{\ast }}_{\mathit{ij}}\right)}^{w_j}$ represents the result of the objectives for the i-th alternative to get reduced with the condition of n − g. In Eq. (41), propagating the weights with the normalized ratings is conducive to a similar outcome in which no weights are evaluated. Therefore, weights need to be referred to as the exponents of Eq. (41) in the FMF. Since the result of the overall utility function $\left({\widetilde{U^{\prime }}}_i\right)$ has a fuzzy digit, defuzzification is required based on Eq. (38) to grade each of the alternatives. According to Akkaya et al. (2015), the rank of each of the i-th alternative is greater if the BNP_i receives a greater value.

According to the FMF, the most advantageous alternative contains the maximum utility (which is retrieved from Eq. (41)) $\left({\widetilde{U^{\prime }}}_i\right)$, and the ranking procedure for this approach is computed in the following formula:

$$R_{\mathit{FMF}}=\left\{A_{\left(i\right|\underset{i}{max{u}_i}}>\dots >A_{\left(i\right|\underset{i}{max{u}_i}}\right\}.$$ 42

Final ranking

The trio approaches of the MULTIMOORA method are equally important. Several approaches are applied to combine the rankings of the three supporting approaches. The final ranking of this research (in terms of measures used) is rooted in the dominance theory. This theory is a popular ranking aggregation method in MULTIMOORA related research (Hafezalkotob et al. 2019). As suggested by previous research, to get the final ranking of the measures, transitiveness principles, general dominance approaches, and absolute dominance are applied (Brauers and Zavadskas 2011).

Fuzzy TOPSIS

Hwang and Yoon (1981) proposed the TOPSIS method as an MCDM technique to rank alternatives by considering positive and negative ideal solutions. Chen (2000) was the first to extend TOPSIS into a fuzzy environment (Tavana et al. 2016a, b). We implement the fuzzy TOPSIS extension developed by Sun (2010), whose steps can be summarized as follows:

• Step 1:

  Determine the fuzzy decision matrix.

• Step 2:
  Calculate the normalized fuzzy decision matrix using Eqs. (43) and (44) below:

  43

  44
• Step 3:

  Calculate the weighted normalized fuzzy decision matrix.

• Step 4:

  Calculate the fuzzy positive ideal solution and the fuzzy negative ideal solution.

• Step 5:

  Calculate the fuzzy positive and fuzzy negative distances ${\tilde{d}}_i^{+}$ and ${\tilde{d}}_i^{-}$ for the different alternatives.

• Step 6:
  Calculate the closeness coefficients by applying Eq. (45) below:

  $$C{C}_i=\frac{d_i^{-}}{d_i^{-}+d_i^{+}}$$ 45

Consensus ranking: maximize agreement heuristic

In mathematics, the term consensus is ambiguous, susceptible to a myriad of explanations, and Emond and Mason (2002) indicate that little is known about consensus ranking. Beck and Lin (1983) showed that the maximization of rater agreement is considered as a rational measure for a consensus function, and they proposed the maximize agreement heuristic (MAH) method for representing consensus or collective agreement in decision-making problems. In ranking the objects, they also show how agreement and disagreement are achieved in the final consensus ranking (FCR). This study mainly resorts to Beck and Lin (1983)’s guidelines for consensus ranking. Emond and Mason (2002, p. 17) provide a solution to the consensus ranking problem by coming up with a measure of agreement between pairs of ranking and choosing those rankings which maximize overall average agreement. The MAH is an effective consensus ranking method used within a wide span of multi-criteria decision-making problems (Kengpol and Tuominen 2006; Tavana 2002, 2003, 2004; Tavana et al. 1996; Tavana and Banerjee 1995).

In this research, the MAH method is applied to arrive at a final ranking of the alternatives (objects) selected by different raters (methods, i.e., fuzzy FM rankings, fuzzy COPRAS, fuzzy RP rankings, and fuzzy ratio method rankings). Given k multi-criteria methods that have all ranked n alternatives, an agreement matrix, A, is defined, where a_ij indicates the number of methods which prefer alternative i over j. If the summation for each alternative i is calculated for all the columns, a column vector in which each element shows the total number of times alternative i is favored over all other alternatives are created. This vector is called the positive preference vector P:

$$P_i=\sum _{j=1}^n{a}_{\mathit{ij}},i=1,2,3,\dots ,n.$$ 46

In addition, if the summation for each alternative j is calculated for all rows, a row vector in which each element shows the total number of times alternative j isn’t favored over all other alternatives is created. This vector is called the negative preference vector N:

$$N_i=\sum _{j=1}^n{a}_{\mathit{ji}},i=1,2,3,\dots ,n.$$ 47

This study uses Eqs. (46) and (47) and formulate the following selection criterion. If alternative i receives a zero-value entry in the negative preference vector N, it indicates that alternative i isn’t ranked lower than other alternatives. Therefore, if alternative i is entered in the upcoming obtainable value from the uppermost of FCR, there is no disappointment when the result of the objective function is reached. However, suppose alternative i receives a zero-value entry in the positive preference vector P. In that case, this indicates that this alternative isn’t ranked ahead of other alternatives, following Beck and Lin’s (1983) guidelines. Thus, alternative i has no positive impact on the objective function and should be placed in the lowest available consensus ranking position, according to Beck and Lin (1983). The quantity (P_i − N_i) provides a reasonable selection criterion for cases in which there exist no zero entries in each negative and positive preference vectors. Therefore, it seems more logical to consider the max |P_i − N_i|. when concentrating on max |P_i − N_i|; if (P_i − N_i) is positive, alternative i should be put at the top of the FCR because alternative i has the greatest positive impact on the objective function. Similarly, if for the max |P_i − N_i|, the (P_i − N_i) gets a negative value, alternative i should be placed at the upcoming obtainable position at the bottom of the ranking because this placement of alternative i reduces that alternative’s negative effect on the objective function. The following algorithm formulates the discourse above:

• Step 1:

  In this step, the agreement matrix A is produced, and parameter n is set equal to the number of alternatives.

• Step 2:
  In this step, Eqs. (48) and (49) are used to compute the entries for the negative and positive preference vectors N and P:

  $$P_i=\sum _j^n{a}_{\mathit{ij}}$$ 48

  $$N_i=\sum _j^n{a}_{\mathit{ji}}$$ 49
• Step 3:

  In this step, any alternatives with zero-value entries in each of both negative and positive preference vectors are candidates for entry into the FCR. In line with the guidelines of Beck and Lin (1983), if the zero-value entry takes place in the positive preference vector P, this study enters alternative i in the upcoming obtainable value from the lowermost of consensus ranking. However, if the zero-value entry takes place in the negative preference vector N, current research enters alternative i in the upcoming obtainable value in the uppermost of the ranking. In either case, this research reduces the row and column effects of the alternatives in matrix A and subsequently moves to Step 5, as shown below.

• Step 4:

  In this step, this study examines the P_i − N_i difference for all i in case there is no zero-value entries in both N or P. Furthermore, alternative i is chosen with the largest absolute difference, and alternative i is entered in the upcoming obtainable value from the uppermost of the ranking in case a positive difference is achieved. In this step, alternative i is entered in the upcoming obtainable value from the lower level of the ranking if the difference is negative, according to Beck and Lin (1983). In case of a tie where more than one alternative is a candidate for the FCR, the tie is broken arbitrarily. In the next step, the row and column results of the agreement matrix A are subsequently removed for alternative i accordingly.

• Step 5:

  In this step, set n = n − 1

• Step 6:

  In this step, if n > 1, move to Step 2, and if n = 1, enter the last alternative in the upcoming obtainable position on the top of the ranking and stop.

Finally, the above exploratory process in this study is applied to solve both incomplete and complete ranking problems. In a complete ranking problem, all methods have ordinally or cardinally ranked every alternative. In contrast, in an incomplete ranking problem, each method ranks only a subset of the alternatives (Beck and Lin 1983).

Case study

In this section, this research presents a case study in the asphalt manufacturing industry to signify the adequacy and applicability of the suggested model of this study. Technopave1 is the largest asphalt manufacturing company in southern Pennsylvania using tire powder recycled by suppliers to produce road-paving asphalt. The tire powder is the main asphalt ingredient with several advantages, including increasing strength and stability, decreasing thickness, increasing life span, reducing maintenance costs, improving bitumen adhesion, reducing crack, and having more resistant to high temperatures. In summary, using tire powder in asphalt creates rubberized asphalt, which has much better quality than ordinary asphalt. Technopave is considering twelve alternative suppliers with tire recycling capabilities for their rubberized asphalt line. This research used the model proposed in this study to help Technopave choose the most preferred suppliers.

Fuzzy Shannon results

Technopave appointed six managers to this project. This study used their expert opinions to compute the weight of the green supplier assessment benchmarks, according to Eqs. (1) to (5) and the linguistic variables presented in Table 4. As tabulated in Table 4, this study used Eq. (1) to normalize the interval DM. In addition, this research used Eq. (2) to calculate the lower and upper limits, respectively. Next, Eq. (3) is utilized to assign the base and upper value limits of the diversification intervals. In the next step, this study used Eqs. (4) and (5) to compute the weights of the benchmark presented in Table 5. These benchmarks weights were applied in this research for the fuzzy COPRAS, fuzzy MULTIMOORA, and fuzzy TOPSIS methods for the sake of ranking the suppliers.

Table 4.

Interval DM for the fuzzy Shannon’s entropy method

Criteria	DM1	DM2	DM3	DM4	DM5	DM6	Aggregate DMs
C11	H	VH	H	VH	VH	VH	[0.7366 0.9733]
C12	VH	I	M	VH	H	H	[0.6116 0.9066]
C13	H	VI	H	H	H	H	[0.57 0.92]
C14	H	VH	H	VH	VH	VH	[0.7366 0.9733]
C21	VH	VH	VH	H	H	H	[0.659 0.96]
C22	VH	VH	H	H	H	H	[0.6533 0.946]
C23	VH	VH	VH	VH	H	VH	[0.7783 0.9866]
C31	H	H	H	H	H	H	[0.57 0.92]
C32	M	H	H	M	H	H	[0.4866 0.84]
C33	VH	H	H	H	H	VH	[0.6533 0.9466]
C34	H	H	VH	VH	H	H	[0.6533 0.9466]
C41	VH	H	VH	H	H	VH	[0.695 0.96]
C42	H	M	H	M	H	H	[0.4866 0.84]
C43	VH	H	H	H	H	M	[0.57 0.8933]
C11	H	VH	H	H	H	H	[0.6116 0.9333]

Note: Green supplier selection and evaluation (GSSE)

Table 5.

Final weights for the fuzzy Shannon entropy’s method

Criteria	[hl hu]	[dl du]	[w l W u]	w’i
C11	[0.0573 0.0686]	[0.9313 0.9426]	[0.0654 0.0673]	0.0664
C12	[0.0506 0.0656]	[0.9343 0.9493]	[0.0656 0.0678]	0.0667
C13	[0.0482 0.0662]	[0.9337 0.9517]	[0.0656 0.0679]	0.0668
C14	[0.0573 0.0686]	[0.9319 0.9426]	[0.0654 0.0673]	0.0664
C21	[0.0551 0.0686]	[0.9319 0.9448]	[0.0655 0.0676]	0.0665
C22	[0.0529 0.0674]	[0.9325 0.9470]	[0.0655 0.0676]	0.0666
C23	[0.0594 0.0691]	[0.9308 0.9405]	[0.0654 0.0671]	0.0663
C31	[0.0482 0.0662]	[0.9337 0.9517]	[0.0656 0.0679]	0.0668
C32	[0.0432 0.0624]	[0.9375 0.9567]	[0.0659 0.0683]	0.0671
C33	[0.0529 0.0674]	[0.9325 0.9470]	[0.0655 0.0676]	0.0666
C34	[0.0529 0.0674]	[0.9325 0.9470]	[0.0655 0.0676]	0.0666
C41	[0.0551 0.0680]	[0.9319 0.9448]	[0.0655 0.0674]	0.0665
C42	[0.0432 0.0624]	[0.9375 0.9567]	[0.0659 0.0683]	0.0671
C43	[0.0482 0.0649]	[0.9350 0.9517]	[0.0657 0.0679]	0.0668

HFBWM results

In this section, the weights of the criteria and sub-criteria are calculated using HFBWM. We asked several experts to identify the best and worst criteria and sub-criteria to determine the fuzzy preference of the best criterion relative to the other criteria and that of all criteria relative to the worst criterion on a scale from 1 to 5. The same procedure was applied to the different sub-criteria.

The resulting fuzzy preferences are presented in Tables 6 and 7. The model proposed in Eq. (10) is then applied to calculate the weights of the criteria and sub-criteria, as well as the global weights of the sub-criteria. These latter weights, described in Table 8, will be implemented within the fuzzy COPRAS, fuzzy MULTIMOORA, and fuzzy TOPSIS methods to rank the suppliers.

Table 6.

Linguistic terms for fuzzy preferences of the criteria by experts

		Criteria
Best criterion	Worst criterion	C1	C2	C3	C4
C1	-	(1,1,1)	(2.5,3,3.5)	(1.5,2,2.5)	(0.67,1,1.5)
-	C2	(2.5,3,3.5)	(1,1,1)	(0.67,1,1.5)	(1.5,2,2.5)

Table 7.

Linguistic terms for fuzzy preferences of the sub-criteria by experts

	Best criterion	Worst criterion	Sub-criteria
C1			C11	C12	C13	C14
	C11	-	(1,1,1)	(0.67,1,1.5)	(2.5,3,3.5)	(1.5,2,2.5)
		C13	(2.5,3,3.5)	(1.5,2,2.5)	(1,1,1)	(0.67,1,1.5)
C2			C21	C22	C23
	C21	-	(1,1,1)	(2.5,3,3.5)	(1.5,2,2.5)
	-	C22	(2.5,3,3.5)	(1,1,1)	(0.67,1,1.5)
C3			C31	C32	C33	C34
	C31	-	(1,1,1)	(0.67,1,1.5)	(2.5,3,3.5)	(1.5,2,2.5)
	-	C33	(2.5,3,3.5)	(1.5,2,2.5)	(1,1,1)	(0.67,1,1.5)
C4			C41	C42	C43
	C42	-	(1.5,2,2.5)	(1,1,1)	(0.67,1,1.5)
	-	C41	(1,1,1)	(1.5,2,2.5)	(0.67,1,1.5)

Table 8.

Weights of the sub-criteria determined by HFBWM

Sub-criteria	C11	C12	C13	C14	C21	C22	C23
GwjS	0.015852	0.012362	0.005945	0.007132	0.037442	0.013576	0.016744
Sub-criteria	C31	C32	C33	C34	C41	C42	C43
GwjS	0.012847	0.010018	0.004818	0.00578	0.026442	0.044879	0.034449

The consistency of the model is calculated using Eq. (12), with ξ^∗ determined by running the model in LINGO 18 software. The optimal ξ^∗ equals 0.56155, with CI = 6.69 (as described in Table 2) and CR = 0.0839. The CR is close to 0, implying that our model has high consistency.

Fuzzy COPRAS results

After determining the green supply chain criteria weights based on expert opinions, we used the fuzzy Shannon entropy approach, HFBWM, and the fuzzy COPRAS to rank the suppliers according to Eqs. (13) to (23). This study first used Eq. (13) to assess the FDM for every supplier (see Table 9). Equations (14) to (16) are then applied to normalize the FDM. Next, the fuzzy Shannon entropy weights presented in Table 5 and the HFBWM weights presented in Table 8 are utilized to calculate the weighted normalized FDM for each supplier.

Table 9.

Fuzzy DM results for each supplier

Criteria	Supplier
	S1			S2			S3			…	S11			S12
C11	0.3125	0.5625	0.8125	0.0625	0.3125	0.5625	0.0625	0.3125	0.5625	…	0.375	0.625	0.875	0.25	0.5	0.75
C12	0.25	0.5	0.75	0.0625	0.1875	0.4375	0.125	0.375	0.625	…	0.75	1	1	0.3125	0.5625	0.8125
C13	0.1875	0.4375	0.6875	0.625	0.875	1	0.3125	0.5625	0.8125	…	0.125	0.375	0.625	0.125	0.375	0.625
C14	0.0625	0.3125	0.5625	0.5	0.75	1	0.25	0.5	0.75	…	0.0625	0.3125	0.5625	0.125	0.375	0.625
C21	0.3125	0.5625	0.8125	0.5	0.75	1	0.5	0.75	1	…	0.0625	0.25	0.5	0.0625	0.25	0.5
C22	0.375	0.625	0.875	0.625	0.875	1	0.4375	0.6875	0.9375	…	0.0625	0.25	0.5	0.0625	0.3125	0.5625
C23	0.375	0.625	0.875	0.5	0.75	1	0.4375	0.6875	0.9375	…	0.0625	0.25	0.5	0.125	0.375	0.625
C31	0.1875	0.4375	0.6875	0.5625	0.8125	1	0.375	0.625	0.875	…	0.0625	0.1875	0.4375	0.0625	0.1875	0.4375
C32	0.1875	0.4375	0.6875	0.625	0.875	1	0.25	0.5	0.75	…	0.1875	0.4375	0.6875	0.0625	0.25	0.5
C33	0.25	0.5	0.75	0.5	0.75	1	0.25	0.5	0.75	…	0.25	0.5	0.75	0.0625	0.25	0.5
C34	0.125	0.375	0.625	0.5	0.75	1	0.4375	0.6875	0.9375	…	0.1875	0.4375	0.6875	0.1875	0.4375	0.6875
C41	0.4375	0.6875	0.9375	0.0625	0.25	0.5	0.125	0.375	0.625	…	0.4375	0.6875	0.9375	0.5625	0.8125	1
C42	0.3125	0.5625	0.8125	0.0625	0.125	0.375	0.0625	0.3125	0.5625	…	0.4375	0.6875	0.9375	0.5	0.75	1
C43	0.1875	0.4375	0.6875	0.0625	0.125	0.375	0.0625	0.125	0.375	…	0.25	0.5	0.75	0.4375	0.6875	0.9375

In the final step, Eqs. (17) to 23) and the fuzzy COPRAS method are applied to rank the suppliers utilizing the weighted normalized FDM tabulated. Equtations (17) and (18) were used to estimate the total of the aggregate values of the parameters for the maximum and minimum values, respectively. Next, Eq. (20) is used to calculate the comparative importance of every option, and Eq. (21) is computed to defuzzify them. To rank the suppliers, as the next step, Eqs. (20) and (23) are applied accordingly. The supplier rankings are tabulated in Tables 10 and 11. The findings of these tables, resulting from the fuzzy Shannon entropy and HFBWM-FCOPRAS approaches, suggest that supplier 2 is the most preferred provider.

Table 10.

Alternative rankings with fuzzy COPRAS-FShannon

Supplier	$\widetilde{p_j}$			$\widetilde{R_j}$			$\widetilde{Q_j}$			Non-fuzzy $\widetilde{Q_j}$	Kj	Fuzzy COPRAS ranking
1	0.0383	0.0801	0.1219	0.0279	0.0511	0.0744	0.0572	0.1201	0.182	0.1198	0.5158	7
2	0.0759	0.1105	0.1383	0.0048	0.0154	0.0346	0.1853	0.2436	0.2676	0.2322	1	1
3	0.0589	0.0996	0.1404	0.0079	0.0272	0.0499	0.1252	0.1748	0.2301	0.1767	0.7611	2
4	0.0438	0.0876	0.1314	0.017	0.0402	0.0645	0.0746	0.1385	0.2007	0.1379	0.5941	3
5	0.0254	0.0711	0.1168	0.0318	0.0572	0.0826	0.0419	0.1069	0.1709	0.1066	0.4591	8
6	0.0315	0.0705	0.1096	0.038	0.0597	0.0804	0.0453	0.1048	0.1652	0.1051	0.4527	9
7	0.0634	0.0942	0.119	0.0291	0.0463	0.0617	0.0814	0.1384	0.1915	0.1371	0.5906	5
8	0.0617	0.0934	0.1208	0.0282	0.0459	0.0609	0.0804	0.138	0.1942	0.1375	0.5925	4
9	0.0212	0.0614	0.1016	0.0448	0.0671	0.085	0.033	0.0919	0.1543	0.093	0.4008	10
10	0.0625	0.0929	0.1157	0.0321	0.049	0.0617	0.0789	0.1346	0.1882	0.1339	0.5768	6
11	0.0203	0.0572	0.1	0.0429	0.0668	0.0858	0.0325	0.0878	0.1521	0.0908	0.3912	11
12	0.0174	0.0559	0.1007	0.0411	0.066	0.0897	0.0302	0.0869	0.1506	0.0892	0.3844	12

Table 11.

Alternative rankings with fuzzy COPRAS-HFBWM

Supplier	$\widetilde{p_j}$			$\widetilde{R_j}$			$\widetilde{Q_j}$			Non-fuzzy $\widetilde{Q_j}$	Kj	Fuzzy COPRAS ranking
1	0.0086	0.0166	0.0245	0.0112	0.0205	0.0298	0.0158	0.0317	0.0482	0.0319	0.4489	7
2	0.0142	0.0208	0.0264	0.0019	0.0055	0.0132	0.0561	0.0773	0.0798	0.0711	1	1
3	0.0127	0.0205	0.0282	0.0029	0.0103	0.0194	0.0403	0.0506	0.0646	0.0518	0.7293	2
4	0.0108	0.0191	0.0275	0.0066	0.0158	0.0256	0.0229	0.0387	0.0551	0.0389	0.5475	3
5	0.005	0.0137	0.0224	0.0139	0.0241	0.0344	0.0108	0.0265	0.0429	0.0267	0.3763	8
6	0.0053	0.0128	0.0202	0.0159	0.0246	0.0328	0.0104	0.0254	0.0418	0.0258	0.3637	9
7	0.011	0.0169	0.0221	0.0105	0.0174	0.0239	0.0187	0.0347	0.0516	0.035	0.4924	5
8	0.0112	0.0173	0.0229	0.0096	0.0167	0.0232	0.0196	0.0358	0.0533	0.0363	0.5104	4
9	0.0039	0.0116	0.0193	0.0192	0.0281	0.0346	0.0082	0.0226	0.0397	0.0235	0.3305	10
10	0.0113	0.0171	0.0218	0.0114	0.0182	0.024	0.0184	0.0342	0.0512	0.0346	0.4868	6
11	0.003	0.0095	0.0176	0.0157	0.0253	0.034	0.0081	0.0217	0.0384	0.0227	0.3201	11
12	0.0029	0.01	0.0185	0.018	0.028	0.0375	0.0074	0.0211	0.0373	0.0219	0.3087	12

Fuzzy MULTIMOORA

This study applies the fuzzy MULTIMOORA approach in assessing the alternatives. Twelve different suppliers (S1, S2, S3, …, S11, and S12) were considered in the evaluation process. This research applied Eqs. (23), (24), and (25) to normalize the FDM. In addition, Eqs. (26), (27), and (28) are applied for the sake of computing the weighted normalized FDMs for the benefits and cost. Equation (29) is used to compute the total ratings of the benchmarks of the alternative. Furthermore, Eqs. (30), (31), and (32) are used for the benefit benchmarks to calculate the alternatives’ total ratings for the lower–middle–upper measures of the triangular membership formula. In addition, considering the cost measures, Eqs. (33), (34), and (35) are applied to calculate the total score of an alternative for the lower–middle–upper values of the triangular membership formula, respectively. Further, Eq. (36) is used to defuzzify the overall score of the measures. By virtue of the fuzzy ratio system approach, the results of the ranking for suppliers are tabulated in Tables 12 and 13. Based on both approaches, namely, fuzzy Shannon entropy and HFBWM, supplier 2 is shown as the distinguished alternative provider for the Technopave company.

Table 12.

Alternative rankings with the fuzzy ratio method-FShannon

Supplier	$y_i=\sum _{j=1}^g{\tilde{v}}_{\mathit{ij}}-\sum _{j=g+1}^n{\tilde{v}}_{\mathit{ij}}$									BNPi	Fuzzy ratio ranking
	Benefits			Cost			yi
	l	m	u	l	m	u	$y_i^l$	$y_i^m$	$y_i^u$
S1	0.1443	0.3155	0.4867	0.0965	0.1799	0.2633	−0.119	0.1356	0.3902	0.1356	7
S2	0.2355	0.3433	0.431	0.0434	0.1296	0.3032	−0.0677	0.2137	0.3875	0.1778	1
S3	0.1906	0.3273	0.4641	0.0459	0.153	0.2914	−0.1008	0.1744	0.4182	0.1639	2
S4	0.1487	0.3166	0.4844	0.0694	0.1704	0.277	−0.1283	0.1461	0.415	0.1443	6
S5	0.1056	0.3049	0.5042	0.0987	0.1804	0.2621	−0.1565	0.1245	0.4055	0.1245	9
S6	0.1293	0.3109	0.4925	0.1161	0.1852	0.2513	−0.1221	0.1257	0.3765	0.1267	8
S7	0.2275	0.3417	0.4356	0.1156	0.1864	0.2506	−0.0231	0.1553	0.32	0.1507	4
S8	0.2219	0.3387	0.4411	0.1108	0.1858	0.2522	−0.0303	0.1528	0.3303	0.1509	3
S9	0.1008	0.3033	0.5059	0.1254	0.1898	0.243	−0.1422	0.1136	0.3805	0.1173	10
S10	0.2284	0.3436	0.4331	0.122	0.1899	0.2439	−0.0156	0.1537	0.3111	0.1498	5
S11	0.0963	0.2862	0.5157	0.1181	0.1878	0.2471	−0.1508	0.0984	0.3976	0.1151	11
S12	0.086	0.2833	0.5201	0.1129	0.1845	0.2532	−0.1671	0.0987	0.4072	0.1129	12

Table 13.

Alternative rankings with the fuzzy ratio method-HFBWM

Supplier	$y_i=\sum _{j=1}^g{\tilde{v}}_{\mathit{ij}}-\sum _{j=g+1}^n{\tilde{v}}_{\mathit{ij}}$									BNPi	Fuzzy ratio ranking
	Benefits			Cost			yi
	l	m	u	l	m	u	$y_i^l$	$y_i^m$	$y_i^u$
S1	0.031	0.061	0.091	0.039	0.072	0.106	−0.075	−0.011	0.053	−0.011	7
S2	0.044	0.065	0.083	0.018	0.049	0.123	−0.078	0.016	0.064	0.001	1
S3	0.039	0.063	0.087	0.018	0.06	0.118	−0.079	0.003	0.069	−0.002	2
S4	0.032	0.061	0.09	0.028	0.068	0.111	−0.079	−0.007	0.062	−0.008	3
S5	0.021	0.058	0.096	0.042	0.073	0.104	−0.084	−0.015	0.054	−0.015	8
S6	0.023	0.059	0.095	0.047	0.075	0.1	−0.077	−0.016	0.047	−0.015	9
S7	0.041	0.064	0.085	0.044	0.074	0.102	−0.061	−0.01	0.041	−0.01	5
S8	0.041	0.064	0.085	0.041	0.073	0.104	−0.063	−0.01	0.044	−0.009	4
S9	0.019	0.058	0.097	0.052	0.077	0.096	−0.077	−0.019	0.044	−0.017	10
S10	0.043	0.065	0.084	0.046	0.075	0.101	−0.058	−0.01	0.038	−0.01	6
S11	0.016	0.052	0.1	0.045	0.074	0.101	−0.086	−0.022	0.055	−0.018	11
S12	0.015	0.053	0.1	0.047	0.075	0.101	−0.085	−0.022	0.053	−0.018	12

Next, utilizing the fuzzy RP method, Eqs. (37) and (38) are used to compute the overall performance measure of the alternatives (Adalı and Işık 2017). Equation (36) is then applied to compute the fuzzy RPs rankings presented in Tables 14 and 15. Based on the fuzzy RP approach, together with fuzzy Shannon entropy and HFBWM, supplier 2 is the distinguished alternative provider for the Technopave company.

Table 14.

Alternative rankings with fuzzy RP-FShannon

Supplier	$\left(\underset{j}{max}{W}_j\times \left|{\tilde{r}}_j-{\tilde{x}}_{\mathit{ij}}^{\ast }\right|\right)$			BNPi	Fuzzy reference point ranking
S1	0.0137	0.0155	0.0049	0.0124	4
S2	0.0022	0	0.0191	0.0053	1
S3	0.0048	0.0078	0.0147	0.0088	2
S4	0.0062	0.0124	0.0119	0.0107	3
S5	0.0156	0.0159	0.0038	0.0128	5
S6	0.0163	0.0178	0.004	0.0139	7
S7	0.0203	0.0125	0.0058	0.0128	8
S8	0.0203	0.0125	0.0058	0.0128	9
S9	0.0195	0.02	0	0.0149	11
S10	0.022	0.0137	0.0038	0.0133	10
S11	0.0248	0.0156	0	0.014	12
S12	0.0184	0.0164	0.0021	0.0134	6

Table 15.

Alternative rankings with fuzzy RP-HFBWM

Supplier	$\left(\underset{j}{max}{W}_j\times \left|{\tilde{r}}_j-{\tilde{x}}_{\mathit{ij}}^{\ast }\right|\right)$			BNPi	Fuzzy reference point ranking
S1	0.009	0.01	0.003	0.008	7
S2	0.003	0	0.01	0.003	1
S3	0	0.008	0.007	0.006	2
S4	0.003	0.009	0.006	0.007	3
S5	0.01	0.011	0.003	0.009	8
S6	0.012	0.011	0.001	0.009	10
S7	0.008	0.01	0.004	0.008	5
S8	0.008	0.01	0.004	0.008	4
S9	0.014	0.012	0	0.009	12
S10	0.009	0.01	0.003	0.008	6
S11	0.011	0.011	0.002	0.009	9
S12	0.012	0.011	0.001	0.009	11

In addition, the FMF of multi-criteria is computed using Eq. (39). The FMF is non-additive and non-linear, and the form doesn’t utilize the weights of the measures. The overall utility functions of the alternatives utilizing the FMF (${\widetilde{U^{\prime }}}_i$) are tabulated in Table 16. Considering the fact that the overall utility function has a fuzzy digit, defuzzification is required based on Eq. (36) for the sake of computing BNP_i values and grade each of the alternatives. Table 16 highlights the overall ranking for the suppliers. Based on the FMF approach, combined with fuzzy Shannon entropy and HFBWM, supplier 2 is the most distinguished alternative for the Technopave company.

Table 17.

Alternative rankings with the fuzzy full multiplicative form-HFBWM

Supplier	${\tilde{A}}_i$			${\tilde{B}}_i$			Non-fuzzy ${\tilde{A}}_i$	Non-fuzzy ${\tilde{B}}_i$	${\widetilde{U^{\prime }}}_i=\frac{{\tilde{A}}_i}{{\tilde{B}}_i}$	Fuzzy full multiplicative ranking
S1	0.856	0.931	0.975	0.845	0.921	0.969	0.921	0.911	1.01	7
S2	0.897	0.938	0.964	0.765	0.872	0.988	0.933	0.875	1.066	1
S3	0.882	0.934	0.969	0.76	0.895	0.983	0.929	0.879	1.056	2
S4	0.861	0.931	0.973	0.806	0.914	0.976	0.922	0.899	1.026	3
S5	0.819	0.926	0.98	0.854	0.922	0.967	0.908	0.914	0.994	8
S6	0.824	0.927	0.979	0.869	0.925	0.962	0.91	0.919	0.991	9
S7	0.889	0.936	0.966	0.86	0.923	0.965	0.931	0.916	1.016	5
S8	0.889	0.936	0.967	0.852	0.922	0.966	0.931	0.914	1.019	4
S9	0.811	0.925	0.981	0.88	0.929	0.956	0.906	0.922	0.983	10
S10	0.892	0.937	0.965	0.865	0.925	0.962	0.931	0.917	1.015	6
S11	0.793	0.914	0.985	0.863	0.924	0.963	0.897	0.917	0.979	11
S12	0.791	0.915	0.985	0.869	0.924	0.962	0.897	0.919	0.977	12

Table 16.

Alternative rankings with the fuzzy full multiplicative form-FShannon

Supplier	${\tilde{A}}_i$			${\tilde{B}}_i$			Non-fuzzy ${\tilde{A}}_i$	Non-fuzzy ${\tilde{B}}_i$	${\widetilde{U^{\prime }}}_i=\frac{{\tilde{A}}_i}{{\tilde{B}}_i}$	Fuzzy full multiplicative ranking
S1	0.4111	0.68	0.8819	0.6587	0.8138	0.924	0.6577	0.7988	0.8233	7
S2	0.5702	0.7154	0.8199	0.5036	0.7256	0.9685	0.7018	0.7325	0.9581	1
S3	0.5004	0.6955	0.8573	0.5102	0.767	0.9557	0.6844	0.7443	0.9195	2
S4	0.422	0.6814	0.8792	0.5786	0.7991	0.9397	0.6609	0.7725	0.8556	6
S5	0.3422	0.6664	0.901	0.6636	0.8146	0.9226	0.6365	0.8003	0.7954	8
S6	0.3726	0.6738	0.8881	0.7009	0.8216	0.9096	0.6448	0.8107	0.7954	9
S7	0.5564	0.7134	0.8249	0.7001	0.8233	0.9088	0.6983	0.8107	0.8613	4
S8	0.5489	0.7096	0.8312	0.6878	0.8224	0.9102	0.6966	0.8068	0.8634	3
S9	0.3297	0.6642	0.9028	0.7197	0.8282	0.8992	0.6322	0.8157	0.7751	10
S10	0.5571	0.7157	0.8218	0.7116	0.8283	0.9	0.6982	0.8133	0.8585	5
S11	0.3211	0.6399	0.913	0.7033	0.8252	0.9037	0.6247	0.8107	0.7705	11
S12	0.3055	0.6362	0.9179	0.6943	0.8207	0.9118	0.6199	0.8089	0.7663	12

In addition, being rooted in dominance theory, the final rankings presented in Tables 18 and 19 are computed for all the suppliers utilizing the fuzzy MULTIMOORA, together with fuzzy Shannon entropy and HFBWM. The results show that supplier 2 is the most preferred supplier.

Table 18.

Fuzzy MULTIMOORA rankings (aggregation and comparison)-FShannon

Supplier	Fuzzy ratio method rankings (Table 12)	Fuzzy reference point rankings (Table 14)	Fuzzy full multiplicative rankings (Table 16)	Fuzzy MULTIMOORA ranking
S1	7	4	7	7
S2	1	1	1	1
S3	2	2	2	2
S4	6	3	6	6
S5	9	5	8	8
S6	8	7	9	9
S7	4	8	4	4
S8	3	9	3	3
S9	10	11	10	10
S10	5	10	5	5
S11	11	12	11	11
S12	12	6	12	12

Table 19.

Fuzzy MULTIMOORA rankings (aggregation and comparison)-HFBWM

Supplier	Fuzzy ratio method rankings (Table 13)	Fuzzy reference point rankings (Table 15)	Fuzzy full multiplicative rankings (Table 17)	Fuzzy MULTIMOORA ranking
S1	7	7	7	7
S2	1	1	1	1
S3	2	2	2	2
S4	3	3	3	3
S5	8	8	8	8
S6	9	9	10	9
S7	5	5	5	5
S8	4	4	4	4
S9	10	10	12	10
S10	6	6	6	6
S11	11	11	9	11
S12	12	12	11	12

Fuzzy TOPSIS results

For comparative purposes, the fuzzy TOPSIS method is applied to assess the alternatives. Twelve different suppliers (S1, S2, S3, … , S11, and S12) were considered in the evaluation process, which applies the results described in Table 9 together with Eqs. (43) to (45) to generate a ranking. Based on the fuzzy TOPSIS approach, combined with fuzzy Shannon entropy and HFBWM, supplier 2 is the most preferred one. The corresponding results are presented in Tables 20 and 21.

Table 20.

Fuzzy TOPSIS rankings-FShannon

Supplier	d+	d-	Fuzzy full multiplicative rankings (Table 10)
S1	13.2678	0.014	7
S2	12.7863	0.0334	1
S3	13.0154	0.0232	5
S4	13.2215	0.0158	6
S5	13.3849	0.0102	9
S6	13.3533	0.0118	8
S7	12.9701	0.0271	2
S8	13.0294	0.0243	4
S9	13.4205	0.0097	10
S10	13.0087	0.0256	3
S11	13.4457	0.0091	11
S12	13.4521	0.009	12

Table 21.

Fuzzy TOPSIS rankings-HFBWM

Supplier	d+	d-	Fuzzy full multiplicative rankings (Table 10)
S1	13.814	0.001	7
S2	13.697	0.003	1
S3	13.735	0.003	2
S4	13.796	0.002	4
S5	13.85	0.001	8
S6	13.857	0.001	11
S7	13.773	0.002	3
S8	13.786	0.002	6
S9	13.863	0.001	10
S10	13.784	0.002	5
S11	13.869	0.001	12
S12	13.866	0.001	9

As illustrated in these tables, the ranking results delivered by FTOPSIS differ from those of FCOPRAS and FMULTIMOORA. These latter techniques focus on the maximum and minimum values of the attributes, as described within Eqs. (17), (18), and (20) and Eqs. (31), (40) and (41), respectively, to generate the corresponding rankings. On the other hand, FTOPSIS is based on comparisons relative to the positive and negative ideal solution benchmarks, increasing its susceptibility to the weights assigned to the criteria. As a result, the rankings delivered by these techniques are expected to differ whenever the weighting methods differ.

Consensus raking

Given the different results obtained, we use the MAH to reach a consensus raking of the alternative rankings proposed by fuzzy MULTIMOORA, fuzzy COPRAS, and fuzzy TOPSIS. The MAH evaluates alternatives simultaneously and builds agreement matrices until all alternatives are ranked without any prior ranked alternatives (Tavana et al. 2007). The MAH is conducted by constructing first the matrices given in Tables 22 and 23 to evaluate and compare all alternatives to each other through the ranking results suggested by the methods described in Tables 10–21. That is, Tables 22 and 23 summarize the rankings delivered by each technique.

Table 22.

The initial individual rankings-FShannon

Method	Supplier
	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12
Fuzzy COPRAS ranking (Table 10)	7	1	2	3	8	9	5	4	10	6	11	12
Fuzzy MULTIMOORA ranking (Table 18)	7	1	2	6	8	9	4	3	10	5	11	12
Fuzzy TOPSIS ranking (Table 20)	7	1	5	6	9	8	2	4	10	3	11	12

Table 23.

The initial individual rankings-HFBWM

Method	Supplier
	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12
Fuzzy COPRAS ranking (Table 11)	7	1	2	3	8	9	5	4	10	6	11	12
Fuzzy ratio method rankings (Table 13)	7	1	2	3	8	9	5	4	10	6	11	12
Fuzzy reference point rankings (Table 15)	7	1	2	3	8	10	5	4	12	6	9	11
Fuzzy full multiplicative rankings (Table 17)	7	1	2	3	8	9	5	4	10	6	11	12
Fuzzy TOPSIS ranking (Table 21)	7	1	2	4	8	11	3	6	10	5	12	9

Next, based on the MAH method, the number of preferences in each row is aggregated to obtain the total number of methods agreeing on each supplier (P_i).. The same procedure is applied to obtain the total number of methods disagreeing on each supplier (N_i).. In case any entry in the P column receives zero-value, the supplier with that entry is included at the top of the FCR. The opposite takes place (the supplier with that entry is included at the bottom of the FCR) in case any entry in the N row receives a zero-value. Then, the greatest positive difference (33 when considering the fuzzy Shannon entropy setting and 55 in the HFBWM case) placed supplier 2 at the top of the final consensus ranking. Following this placement, supplier 2 was deleted, and a new matrix was produced. As tabulated in the next matrix, (P_i), (N_i), and (P_i − N_i) are calculated for the remaining suppliers. The same procedure is applied to the remaining suppliers. Tables 24 and 25 outline the outcome of the MAH process and indicate the number of times each supplier is favored over the rest by each method, resulting in the final consensus ranking.

Table 24.

Consensus ranking calculations using MAH-FShannon

Supplier	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	Pi	Pi − Ni	Rank (Pi − Ni)
S1	0	0	0	0	3	3	0	0	3	0	3	3	15	−3	7
S2	3	0	3	3	3	3	3	3	3	3	3	3	33	33	1
S3	3	0	0	3	3	3	2	2	3	2	3	3	27	21	2
S4	3	0	0	0	3	3	1	1	3	1	3	3	21	9	6
S5	0	0	0	0	0	2	0	3	3	0	3	3	14	−5	8
S6	0	0	0	0	1	0	0	0	3	0	3	3	10	−13	9
S7	3	0	1	2	3	3	0	1	3	3	3	3	25	−7	3
S8	3	0	1	2	0	3	2	0	3	2	3	3	22	11	4
S9	0	0	0	0	0	0	0	0	0	0	3	3	6	−21	10
S10	3	0	1	2	3	3	0	1	3	0	3	3	22	11	4
S11	0	0	0	0	0	0	0	0	0	0	0	3	3	−27	11
S12	0	0	0	0	0	0	0	0	0	0	0	0	0	−33	12
Ni	18	0	6	12	19	23	8	11	27	11	30	33

Table 25.

Consensus ranking calculations using MAH-HFBWM

Supplier	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	Pi	Pi − Ni	Rank (Pi − Ni)
S1	0	0	0	0	5	5	0	0	5	0	5	5	25	−5	7
S2	5	0	5	5	5	5	5	5	5	5	5	5	55	55	1
S3	5	0	0	5	5	5	5	5	5	5	5	5	50	45	2
S4	5	0	0	0	5	5	4	5	5	5	5	5	44	33	3
S5	0	0	0	0	0	5	0	0	5	0	5	5	20	−15	8
S6	0	0	0	0	0	0	0	0	4	0	4	4	12	−31	9
S7	5	0	0	1	5	5	0	1	5	5	5	5	37	19	5
S8	5	0	0	0	5	5	4	0	5	4	5	5	38	21	4
S9	0	0	0	0	0	1	0	0	0	0	4	3	8	−39	10
S10	5	0	0	0	5	5	0	1	5	0	5	5	31	7	6
S11	0	0	0	0	0	1	0	0	1	0	0	4	6	−43	11
S12	0	0	0	0	0	1	0	0	2	0	1	0	4	−47	12
Ni	30	0	5	11	35	43	18	17	47	24	49	51

We conclude by highlighting an important argument developed throughout the manuscript. Figure 4 illustrates the substantial similarity exhibited by the rankings generated through the fuzzy versions of COPRAS, MOORA, and MULTIMOORA when implementing the HFBWM weights. This similarity contrasts with the lower one exhibited by these ranking techniques when implementing Shannon’s entropy’s fuzzy extension. A similar intuition follows from the analysis of the rankings delivered by the methods implemented to extend fuzzy MOORA into fuzzy MULTIMOORA, particularly the reference point one. The dissimilarities arising among the corresponding rankings under both weighting techniques are presented in Fig. 5.

Fig. 4.

Rank similarity among COPRAS, MOORA, and MULTIMOORA. a HFBWM framework. b Fuzzy Shannon entropy framework

Fig. 5.

Rank similarity among full multiplicative, MOORA, and reference point. a. HFBWM framework. b Fuzzy Shannon entropy framework

Thus, when implementing the HFBWM weights, fuzzy COPRAS suffices to generate rankings that display an identical order to fuzzy MULTIMOORA, a method requiring more elaborated and complex computations. Note also that the fuzzy MOORA and fuzzy MULTIMOORA techniques deliver identical rankings, that is, the procedure required to extend MOORA into MULTIMOORA is not always necessarily justified.

However, this is not the case when implementing the weights generated via fuzzy Shannon’s entropy. In this regard, notice how, particularly in the TOPSIS and reference point cases, the rankings obtained display higher variability than those generated using the HFBWM weights. These results are formally complemented through the Spearman rho correlation tests presented in Tables 26 and 27, highlighting that intuitively simpler techniques such as HFBWM can be implemented in more complex evaluation structures while preserving (indeed, improving) the consistency of the rankings obtained.

Table 26.

Correlations among the different rankings under FShannon

			COPRAS	MOORA	MULTIMOORA	Reference point	Full multiplicative	TOPSIS
Spearman’s rho	COPRAS	Correlation coefficient	1.000	0.951**	0.958**	0.622*	0.958**	0.867**
		Sig. (2-tailed)		0.000	0.000	0.031	0.000	0.000
		N	12	12	12	12	12	12
	MOORA	Correlation coefficient	0.951**	1.000	0.993**	0.483	0.993**	0.937**
		Sig. (2-tailed)	0.000		0.000	0.112	0.000	0.000
		N	12	12	12	12	12	12
	MULTIMOORA	Correlation coefficient	0.958**	0.993**	1.000	0.497	1.000**	0.930**
		Sig. (2-tailed)	0.000	0.000		0.101		0.000
		N	12	12	12	12	12	12
	Reference point	Correlation coefficient	0.622*	0.483	0.497	1.000	0.497	0.315
		Sig. (2-tailed)	0.031	0.112	0.101		0.101	0.319
		N	12	12	12	12	12	12
	Full multiplicative	Correlation coefficient	0.958**	0.993**	1.000**	0.497	1.000	0.930**
		Sig. (2-tailed)	0.000	0.000		0.101		0.000
		N	12	12	12	12	12	12
	TOPSIS	Correlation coefficient	0.867**	0.937**	0.930**	0.315	0.930**	1.000
		Sig. (2-tailed)	0.000	0.000	0.000	0.319	0.000
		N	12	12	12	12	12	12

**Correlation is significant at the 0.01 level (2-tailed).

*Correlation is significant at the 0.05 level (2-tailed)

Table 27.

Correlations among the different rankings under HFBWM

			COPRAS	MOORA	MULTIMOORA	Reference point	Full multiplicative	TOPSIS
Spearman’s rho	COPRAS	Correlation coefficient	1.000	1.000**	1.000**	0.965**	1.000**	0.916**
		Sig. (2-tailed)				0.000		0.000
		N	12	12	12	12	12	12
	MOORA	Correlation coefficient	1.000**	1.000	1.000**	0.965**	1.000**	0.916**
		Sig. (2-tailed)				0.000		0.000
		N	12	12	12	12	12	12
	MULTIMOORA	Correlation coefficient	1.000**	1.000**	1.000	0.965**	1.000**	0.916**
		Sig. (2-tailed)				0.000		0.000
		N	12	12	12	12	12	12
	Reference point	Correlation coefficient	0.965**	0.965**	0.965**	1.000	0.965**	0.902**
		Sig. (2-tailed)	0.000	0.000	0.000		0.000	0.000
		N	12	12	12	12	12	12
	Full multiplicative	Correlation coefficient	1.000**	1.000**	1.000**	0.965**	1.000	0.916**
		Sig. (2-tailed)				0.000		0.000
		N	12	12	12	12	12	12
	TOPSIS	Correlation coefficient	0.916**	0.916**	0.916**	0.902**	0.916**	1.000
		Sig. (2-tailed)	0.000	0.000	0.000	0.000	0.000
		N	12	12	12	12	12	12

**Correlation is significant at the 0.01 level (2-tailed).

*Correlation is significant at the 0.05 level (2-tailed)

Discussion

RL is one of the key factors determining the success of SC sustainability (Wang et al. 2021a, b, c, d). On the one hand, the worldwide existence of environmental pollution has increased the pressure on companies to consider sustainability in RL (Richnák and Gubová 2021). On the other hand, environmental protection has become a global issue (Daniels 2017), and concerns about environmental protection have stimulated researchers and practitioners to pay more attention to waste recycling. For instance, Yang et al. (2018a, b) investigated waste disposal and management to reduce poverty and pollution in low- and middle-income countries. Li et al. (2020) studied effective policy tools to recycle the waste of construction and demolition. Liu et al. (2020) considered the effect of construction and demolition waste and its recycling when minimizing waste and protecting natural resources. Wang et al. (2020) examined sustainable waste management for household solid waste to raise public awareness.

Even though these studies are informative, additional research is required focusing on each particular industry dealing with RL. Tire waste increases daily due to the increasing population and subsequent demand for tires, which are hazardous to the environment and public health due to the fact that tire waste is not biodegradable and is usually stored and disposed of improperly (Svoboda et al. 2018). The best way to protect the environment and prevent the improper burial of worn-out tires is recycling and the reuse of tire waste. One of the most important applications of tire recycling is its use in the production of asphalt. Several industries, including the asphalt manufacturing industry, have adopted green supply chain philosophy and used recycled tires to produce various products such as rubberized asphalt, rubberized bitumen, reclaim rubber, and rubber ground flooring. Suppliers play an important role in tire recycling as they mainly produce and deliver the tire powder and granule to produce rubberized asphalt. Therefore, finding the best supplier is critical for environmentally conscious.

Research on RL is in its infancy in developing countries, and there is a need for examining green RL initiatives in emerging economies (Bouzon et al. 2016). Companies can embark on RL initiatives by taking small steps and engaging in simple implementation strategies (Hammes et al. 2020). Recycling and green supply chain management are effective strategies for protecting the environment and reducing production costs (Zarbakhshnia et al. 2018). Choosing the right green supplier is a critical success factor in RL systems, and any initiative aimed at reducing production waste in the tire industry is beneficial to both the environment and manufacturing companies.

Conclusion, limitations, and future research

This study proposed a fuzzy green supplier selection model for sustainable supply chains in RL. The HFBWM was applied to determine the importance weights of the green criteria and sub-criteria. For comparative purposes, fuzzy Shannon’s entropy was also used to determine the weights of criteria. The fuzzy Shannon’s entropy approach and HFBWM were then integrated with fuzzy COPRAS, fuzzy MULTIMOORA, and fuzzy TOPSIS to prioritize and rank suppliers with a robust ability to recycle in RL.

Finally, this research used the MAH method to find the consensus ranking of the suppliers. A real-world case study in the asphalt manufacturing industry was presented to highlight the efficacy and show the applicability of the models suggested in this study. The results derived from the different hybrid models illustrate the higher ranking variability generated by the fuzzy Shannon’s entropy weighting method relative to HFBWM.

The main findings of the current paper are of substantial importance for manufacturing companies moving towards a closed-loop supply chain. Future research can extend the methods proposed in this study to industries other than tire recycling ones. Additional research is needed to integrate other relevant methods and expand the number of measures considered to strengthen the precision and accuracy of the proposed assessment and selection model.

We conclude by emphasizing that relatively simple ranking methods such as fuzzy COPRAS and fuzzy MOORA manage to provide sufficiently robust evaluations. In this regard, even though having a larger number of methods at their disposal may seem to endow managers with a complete picture of the evaluation procedure, the use of multiple techniques can also be confusing, particularly when dealing with complex ranking methods implemented through several technical steps.

Author contributions

Madjid Tavana: Conceptualization, formal analysis, methodology, writing — review and editing,and visualization. Akram Shaabani: Investigation, formal analysis, validation and data curation, and software. Francisco Javier Santos-Arteaga: Formal analysis, resources, and visualization. Naser Valaei: Investigation, resources, software, and project administration.

Funding

Dr. Madjid Tavana is grateful for the partial support he received from the Czech Science Foundation (GAˇCR19-13946S) for this research.

Availability of data and materials

Not applicable.

Declarations

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.