A solution to a sex ratio puzzle in Melittobia wasps

Significance

Many social interactions generate "a tragedy of the commons," where individuals would do better if everyone cooperated, but selfish interests can select against cooperation. Examples range from the production of extracellular enzymes by bacteria, to cooperative breeding in animals, to female-biased sex ratios in structured populations, where brothers compete for mates. We examined the offspring sex ratios produced by Melittobia wasps in natural populations and found that females adjust their offspring sex ratio in response to both the presence of other females and whether they had dispersed. Dispersal matters because it determines the genetic relatedness between interacting individuals, and so an analogous influence of dispersal would be predicted for a range of cooperative traits, including parasite virulence.

Abstract

The puzzling sex ratio behavior of Melittobia wasps has long posed one of the greatest questions in the field of sex allocation. Laboratory experiments have found that, in contrast to the predictions of theory and the behavior of numerous other organisms, Melittobia females do not produce fewer female-biased offspring sex ratios when more females lay eggs on a patch. We solve this puzzle by showing that, in nature, females of Melittobia australica have a sophisticated sex ratio behavior, in which their strategy also depends on whether they have dispersed from the patch where they emerged. When females have not dispersed, they lay eggs with close relatives, which keeps local mate competition high even with multiple females, and therefore, they are selected to produce consistently female-biased sex ratios. Laboratory experiments mimic these conditions. In contrast, when females disperse, they interact with nonrelatives, and thus adjust their sex ratio depending on the number of females laying eggs. Consequently, females appear to use dispersal status as an indirect cue of relatedness and whether they should adjust their sex ratio in response to the number of females laying eggs on the patch.

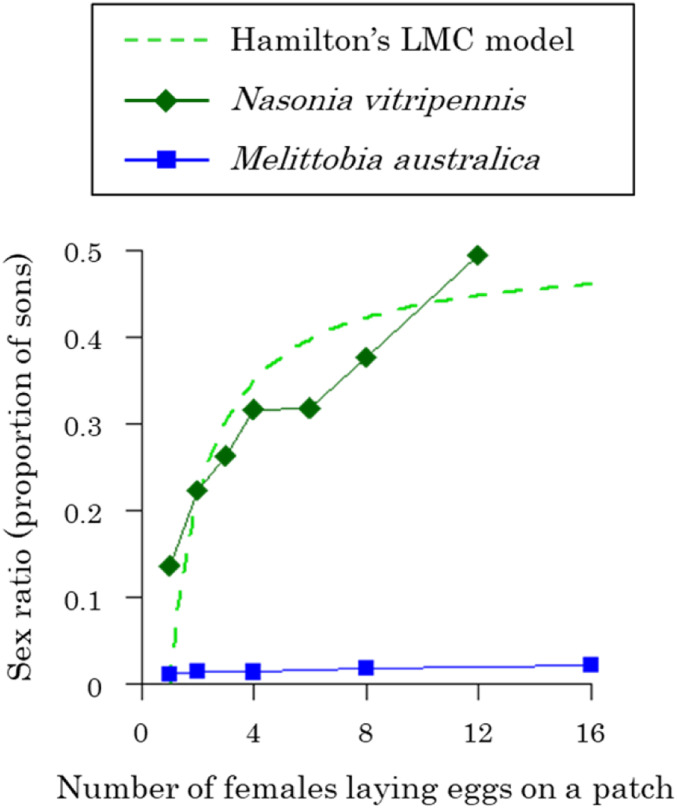
Sex allocation has produced many of the greatest success stories in the study of social behaviors (1–4). Time and time again, relatively simple theory has explained variation in how individuals allocate resources to male and female reproduction. Hamilton’s local mate competition (LMC) theory predicts that when n diploid females lay eggs on a patch and the offspring mate before the females disperse, the evolutionary stable proportion of male offspring (sex ratio) is (n − 1)/2n (Fig. 1) (5). A female-biased sex ratio is favored to reduce competition between sons (brothers) for mates and to provide more mates (daughters) for those sons (6–8). Consistent with this prediction, females of >40 species produce female-biased sex ratios and reduce this female bias when multiple females lay eggs on the same patch (higher n; Fig. 1) (9). The fit of data to theory is so good that the sex ratio under LMC has been exploited as a “model trait” to study the factors that can constrain “perfect adaptation” (4, 10–13).

Fig. 1.

LMC. The sex ratio (proportion of sons) is plotted versus the number of females laying eggs on a patch. The bright green dashed line shows the LMC theory prediction for the haplodiploid species (5, 39). A more female-biased sex ratio is favored in haplodiploids because inbreeding increases the relative relatedness of mothers to their daughters (7, 32). Females of many species adjust their offspring sex ratio as predicted by theory, such as the parasitoid Nasonia vitripennis (green diamonds) (82). In contrast, the females of several Melittobia species, such as M. australica, continue to produce extremely female-biased sex ratios, irrespective of the number of females laying eggs on a patch (blue squares) (15).

In stark contrast, the sex ratio behavior of Melittobia wasps has long been seen as one of the greatest problems for the field of sex allocation (3, 4, 14–21). The life cycle of Melittobia wasps matches the assumptions of Hamilton’s LMC theory (5, 15, 19, 21). Females lay eggs in the larvae or pupae of solitary wasps and bees, and then after emergence, female offspring mate with the short-winged males, who do not disperse. However, laboratory experiments on four Melittobia species have found that females lay extremely female-biased sex ratios (1 to 5% males) and that these extremely female-biased sex ratios change little with increasing number of females laying eggs on a patch (higher n; Fig. 1) (15, 17–20, 22). A number of hypotheses to explain this lack of sex ratio adjustment have been investigated and rejected, including sex ratio distorters, sex differential mortality, asymmetrical male competition, and reciprocal cooperation (15–18, 20, 22–26).

We tested whether Melittobia’s unusual sex ratio behavior can be explained by females being related to the other females laying eggs on the same patch. After mating, some females disperse to find new patches, while some may stay at the natal patch to lay eggs on previously unexploited hosts (Fig. 2). If females do not disperse, they can be related to the other females laying eggs on the same host (27–31). If females laying eggs on a host are related, this increases the extent to which relatives are competing for mates and so can favor an even more female-biased sex ratio (28, 32–35). Although most parasitoid species appear unable to directly assess relatedness, dispersal behavior could provide an indirect cue of whether females are with close relatives (36–38). Consequently, we predict that when females do not disperse and so are more likely to be with closer relatives, they should maintain extremely female-biased sex ratios, even when multiple females lay eggs on a patch (28, 35).

Fig. 2.

Host nest and dispersal manners of Melittobia. (A) Photograph of the prepupae of the leaf-cutter bee C. sculpturalis nested in a bamboo cane and (B) a diagram showing two ways that Melittobia females find new hosts. The mothers of C. sculpturalis build nursing nests with pine resin consisting of individual cells in which their offspring develop. If Melittobia wasps parasitize a host in a cell, female offspring that mate with males inside the cell find a different host on the same patch (bamboo cane) or disperse by flying to other patches.

We tested whether the sex ratio of Melittobia australica can be explained by dispersal status in a natural population. We examined how the sex ratio produced by females varies with the number of females laying eggs on a patch and whether or not they have dispersed before laying eggs. To match our data to the predictions of theory, we developed a mathematical model tailored to the unique population structure of Melittobia, where dispersal can be a cue of relatedness. We then conducted a laboratory experiment to test whether Melittobia females are able to directly access the relatedness to other females and adjust their sex ratio behavior accordingly. Our results suggest that females are adjusting their sex ratio in response to both the number of females laying eggs on a patch and their relatedness to the other females. However, relatedness is assessed indirectly by whether or not they have dispersed. Consequently, the solution to the puzzling behavior reflects a more-refined sex ratio strategy.

Results

Population Structure and Relatedness.

To obtain the natural broods of Melittobia, we placed about 200 bamboo traps, each with 20 bamboo canes, in the wild (Fig. 2). A total of 4,890 host wasps and bees developed in these bamboo traps, with an average of 4.7 ± 2.9 (SD) hosts per bamboo cane (SI Appendix, Table S2-1). Of these hosts, 0.94% were parasitized by M. australica, and we obtained data from 29 M. australica broods in which all of the emerging offspring were obtained (SI Appendix, Table S2-4). The adults and the dead bodies of Melittobia females in the host cells or cocoons could be regarded as mother that laid eggs in the broods and could be distinguished from emerging offspring based on the filled abdomen of offspring. We used microsatellite genotype analysis to check that all these potential mothers had actually contributed offspring to the brood and to determine whether there were other mothers that had departed (SI Appendix, Tables S2-5 and S2-6) (27).

We assessed whether the mothers that had laid these broods were from the same host patch (nondispersers) or had dispersed from different host patches (dispersers; SI Appendix, Fig. S1-1). If there was only one host parasitized in a bamboo trap (patch), we assumed that mothers were “dispersers” from different host patches. If there were multiple parasitized hosts and M. australica individuals had emerged from at least one host, the mothers at some of those parasitized hosts could potentially be nondispersers. A nondispersing mother would be the sister of the offspring emerging from one of the other hosts on the patch (i.e., the host from which they had also emerged). The emergence timing from a single brood is not synchronized in Melittobia, and emerging females mate and then start searching for a new host continuously. We assigned a mother as a “nondisperser” when their microsatellite genotype suggested that they were a sister of the offspring emerging from one of the other hosts on the patch (SI Appendix, Table S2-5) (27). Overall, we found that 8 broods were laid by only nondispersing females (5 to 36 mothers; 28% of broods), 19 broods were laid by only dispersing females (1 to 5 mothers; 66% of broods), and 2 broods were laid by mixture of nondispersers and dispersers (6 mothers; 7% of broods).

In nature, we found that 55.2% (16 of 29) of broods were produced by more than one female. The number of females producing a brood varied from 1 to 36, with an arithmetic mean of 6.7 and a harmonic mean of 1.7 (SI Appendix, Table S2-2D). Broods where multiple females lay eggs are therefore relatively common. Consequently, the lack of sex ratio adjustment when multiple females lay eggs on patch cannot be explained by multiple female broods not occurring or being extremely rare in nature (10). In the two mixed broods, produced by nondispersers and dispersers, single dispersers produced all-male clutches, and other females were nondispersers producing clutches containing both sexes. We carried out analyses below discarding the two all-male clutches because we were interested in the sex allocation behavior of mothers producing both sexes. However, we found the same qualitative results irrespective of whether we removed the two broods laid by a mixture of dispersers and nondispersers (SI Appendix, Supporting Information 1). Our genetic analyses found no genetic differentiation between dispersing and nondispersing females or between the females that produced all-male clutches and those that produced clutches containing both sexes (SI Appendix, Supporting Information 1).

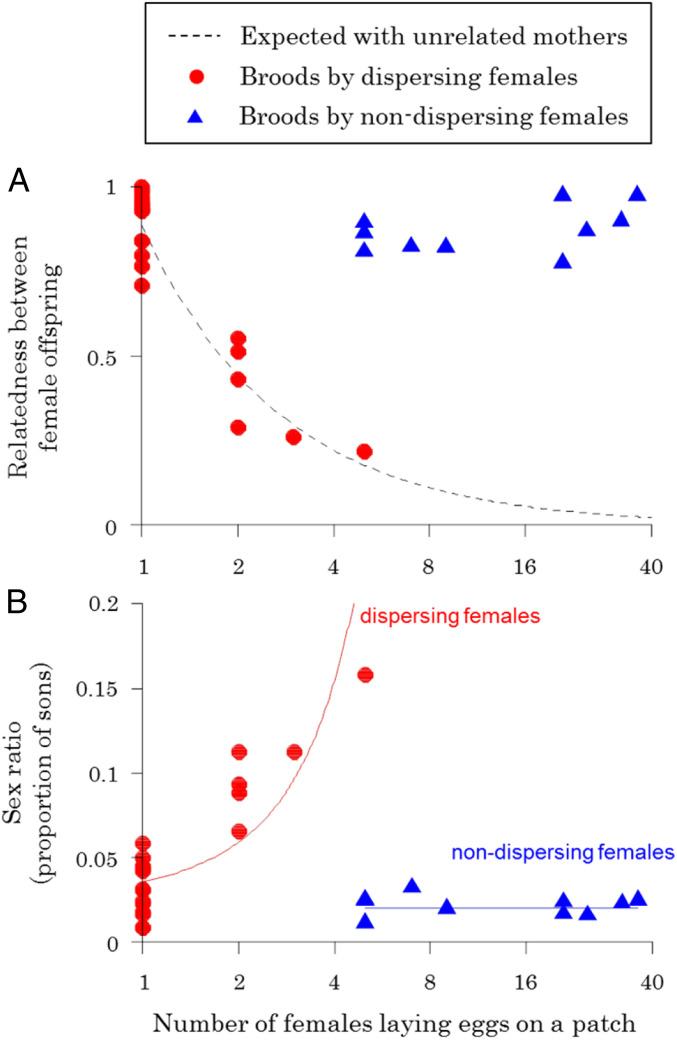
Our analysis of relatedness estimated by 16 polymorphic microsatellite loci suggests that dispersing females laying eggs on the same patch are unrelated but that nondispersing females laying eggs on the same patch are highly related. As the number of females laying eggs increased, the relatedness between females developing in a brood decreased when the brood was produced by dispersing females but not when the brood was produced by nondispersing females (Fig. 3A; dispersers: χ²₁ = 10.15, P = 0.001; nondispersers: χ²₁ = 0.93, P = 0.33; interaction between dispersal status and number of females laying eggs: χ²₁ = 12.34, P < 0.01). The pattern of relatedness for dispersers closely resembled that expected if unrelated females had produced the broods, while the pattern for nondispersers was clearly different from this expectation (Fig. 3A). The relatedness between the female offspring of nondispersers remained high regardless of the number of females laying eggs, suggesting that when multiple nondispersing females laid eggs on the same patch, they were inbred sisters. This was confirmed by our parentage analysis, which suggests that when multiple nondispersers contributed to a brood, they were offspring of a single female or very closely related females (SI Appendix, Table S2-5).

Fig. 3.

Sex ratios and relatedness in nature. The relationship between the number of females laying eggs on a patch and (A) the average relatedness between female offspring on a patch; (B) the offspring sex ratio (proportion males). The dashed black line in A shows the expected relatedness assuming that the mothers of the female offspring are not genetically related, (1 + 3f) / (2n(1 + f)), where n is the number of mothers and f is the inbreeding coefficient estimated as f = 0.631 from the microsatellite data. The solid red and blue lines in B represent the fitted lines of the generalized linear mixed models assuming binomial distribution for dispersing and nondispersing females, respectively. The x-axes are logarithmic. When females disperse (red circles), an increasing number of females laying eggs on a patch leads to a decrease in relatedness between female offspring (A) and an increase in the offspring sex ratio (B). In contrast, when females do not disperse, neither the relatedness between female offspring (A) nor the offspring sex ratio (B) significantly varies with the number of females laying eggs on a patch.

Sex Ratios.

There was a clear difference in the sex ratios (proportion of sons) produced by dispersing females compared with nondispersing females. As the number of females laying eggs on a patch increased, dispersers produced less female-biased sex ratios but nondispersers did not (Fig. 3B; dispersers: χ²₁ = 14.62, P < 0.001; nondispersers: χ²₁ = 0.56, P = 0.46; interaction between dispersal status and number of females laying eggs: χ²₁ = 18.69, P < 0.001). Consequently, while nondispersers always produced ∼2% males, dispersers produced from 3 to 16% males as the number of females laying eggs increased.

The pattern in nondispersers is consistent with laboratory experiments. In laboratory experiments, females were not given a chance to disperse, and as the number of females laying eggs was increased from 1 to 16, there was only a very small increase in offspring sex ratio, from 1 to 2% males (Fig. 1) (15). In contrast, the increasing sex ratios observed in broods produced by dispersers is consistent with the pattern predicted by Hamilton’s original LMC model (5, 39). The fit to Hamilton’s theory is qualitative, not quantitative, as the observed sex ratios were more female biased (Figs. 1 and 3B).

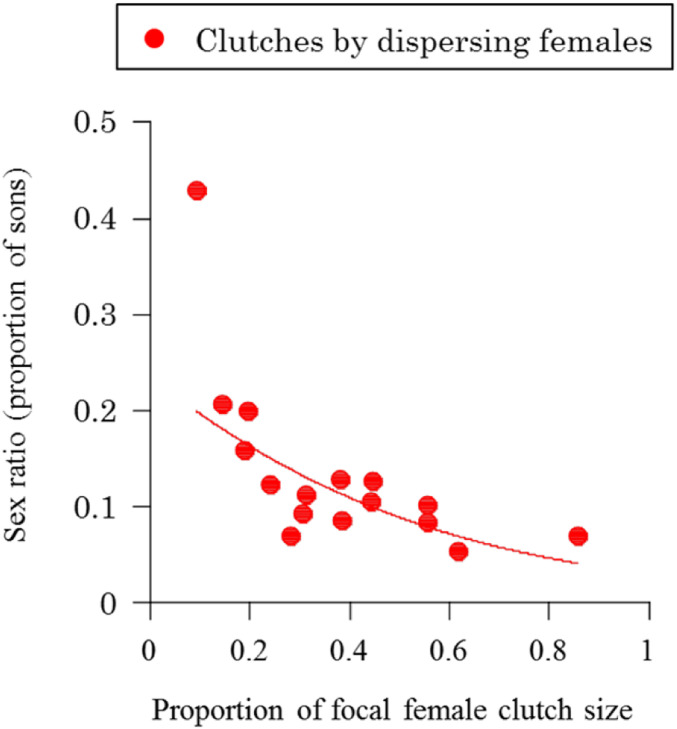
As also predicted by LMC theory, we found that when individual dispersing females produced more of the offspring on a patch, they produced more female-biased offspring sex ratios (40–42). The offspring sex ratios produced by a dispersing female were significantly negatively correlated with the proportion of the brood that she produced (Fig. 4; χ²₁ = 9.99, P = 0.002). This pattern is predicted by theory because when a female lays a greater proportion of the offspring on a patch, her sons are more likely to be competing for mates with their brothers and more likely to be mating with their sisters. Consequently, when females produce a greater proportion of offspring on the patch, their offspring will encounter greater LMC and so more female-biased sex ratios are favored (40–42). Analogous sex ratio adjustment in response to fecundity has been observed in a range of species including wasps, aphids, and cestodes (40, 43–46).

Fig. 4.

Sex ratios in response to relative clutch size. Sex ratios produced by dispersing females laying eggs with other dispersers decrease with an increasing proportion of focal female clutch size (focal female clutch size divided by the sum of clutch sizes produced on the same host), as predicted by theory (39–41). The solid red line represents the fitted line of the generalized linear mixed model assuming binomial distribution.

Sex Ratio and Relatedness.

Hamilton’s LMC theory can be rewritten to give the predicted sex ratio in terms of the relatedness between the offspring on a patch rather than the number of females laying eggs on a patch (2, 47). This is useful for examining Melittobia sex ratios because it can apply to cases where relatedness between offspring is influenced by multiple factors, including relatedness between mothers, and not just the number of mothers (2).

We extended existing theory to examine the scenario where a fraction of females does not disperse, and instead remain to lay eggs with related females (SI Appendix, Supporting Information 3) (28). We assumed the standard LMC scenario that n females lay eggs per patch and that all mating occurs between the offspring laid on a patch. However, we also assumed that patches survive into the next generation with a probability 1 − e. If the patch survives, a fraction of female offspring become nondispersers remaining on the natal patch to reproduce and others become dispersers. In contrast, with a probability e the patch does not survive (goes extinct), and all female offspring become dispersers. In the next generation, extinct patches were replaced with new patches, where dispersed females from other patches can reproduce.

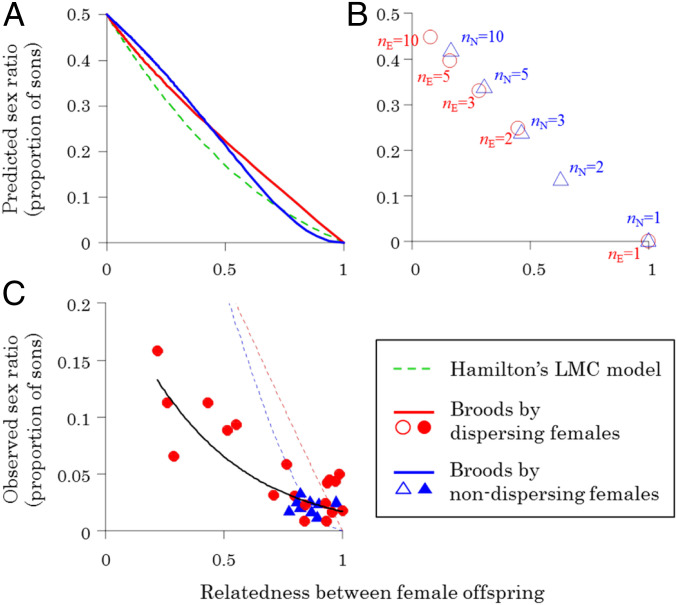
Our model predicts the following: 1) as relatedness between offspring increases, a more female-biased sex ratio is favored and 2) this predicted negative relationship is almost identical for dispersing and nondispersing females (Fig. 5A and SI Appendix, Fig. S3-1B). The relationship is almost identical because it is the increased relatedness between offspring on a patch that leads to competition and mating between relatives and hence favors biased sex ratios (2). Increased relatedness can come from either one or a small number of females laying eggs on a patch or multiple related females laying eggs. For a given number of females laying eggs on a patch, nondispersing females will be favored to produce a more-biased sex ratio (SI Appendix, Fig. S3-1A), but this can also be accounted for by the extent to which their offspring will be more related (Fig. 5B). Nondispersing females produce offspring that are more related, and so a more female-biased sex ratio is favored (Fig. 5A). For example, if five nondispersing females lay eggs on a patch, the relatedness between female offspring and offspring sex ratio are both predicted to be almost the same as those for three dispersing females (Fig. 5B).

Fig. 5.

Sex ratios and relatedness. The predicted (A and B) and observed (C) relationship between the offspring sex ratio and the relatedness between female offspring on a patch. Our model predicts that the evolutionarily stable sex ratio is negatively correlated with the relatedness between female offspring (A and B; assuming haplodiploid genetics, and e = 0.66, which is assigned from the proportion of broods by dispersing females in the field). (A) The predicted relationships are almost identical for dispersing females (red line) and nondispersing females (blue line), which are also equivalent to the prediction of Hamilton’s original LMC model (green dashed line) (2). (B) The predicted sex ratio is shown when a given number of dispersing females (n_E; open red circle) or nondispersing females (n_N; open blue triangle) lay eggs on a patch. When more than one (n > 1) female lays eggs on a patch, nondispersing females are predicted to exhibit more related females and lower sex ratios. However, the overall relationship between the sex ratio and relatedness is very similar for dispersing and nondispersing females because the prediction for each number of dispersing females (n_E) is approximately equivalent to that for a slightly lower number of nondispersing females (n_N). For example, compare the predictions for n_E = 3 and n_N = 5. (C) Compared across natural broods, the offspring sex ratio was negatively correlated with the relatedness between female offspring. While the sex ratios produced by dispersing females (solid red circle) decrease with relatedness, the broods of nondispersing females (solid blue triangles) were all clumped at high relatedness/low sex ratio. The solid black line in C represents the fitted line of the generalized linear mixed model assuming binomial distribution for dispersing and nondispersing females, and the red and blue dashed lines in C represent predicted sex ratios for dispersing and nondispersing females, respectively.

When we plotted the M. australica sex ratio data for both dispersers and nondispersers, there was a clear negative relationship between the sex ratio and the relatedness between female offspring (Fig. 5C; χ²₁ = 25.86, P < 0.001). Relatedness between female offspring explained 72.2% of the variance in the offspring sex ratio. This relationship is driven by relatively continuous variation across the broods produced by dispersing females and all the broods produced by nondispersing females being at one end of the continuum (Fig. 5C). When more dispersing females laid eggs on a patch, this led to the offspring being less related (Fig. 3A), and females produced a less female-biased sex ratio (Fig. 3B). In contrast, in the broods produced by nondispersers, neither the relatedness between offspring nor the offspring sex ratio varied significantly with the number of females laying eggs on the patch (Fig. 3). Consequently, the broods of nondispersers were all at the extreme end of the relationship between offspring sex ratio and relatedness between female offspring (Fig. 5C).

These results show that the sex ratio behavior of dispersing and nondispersing females lays on the same continuum and explains why nondispersers do not adjust their offspring sex ratios (Fig. 5C). Nondispersers are so related that the number of females laying eggs does not significantly influence the relatedness between their offspring (Fig. 3A). Consequently, nondispersers always encounter extreme LMC and are selected to produce consistently and highly female-biased offspring sex ratios (Fig. 5A).

Can Females Recognize Relatives?

Females could be assessing relatedness by either directly recognizing kin or indirectly by using whether or not they have dispersed as a cue of whether they are likely to be with nonrelatives (dispersing females) or relatives (nondispersing females) (35–38). We conducted a laboratory experiment to test whether females directly recognize the relatedness of other females laying eggs on the same host and adjust their sex ratio accordingly. We examined the sex ratio behavior of females who were either 1) laying eggs on a host alone, 2) laying eggs with a related female in the same inbred strain, or 3) laying eggs with an unrelated female from a different inbred strain.

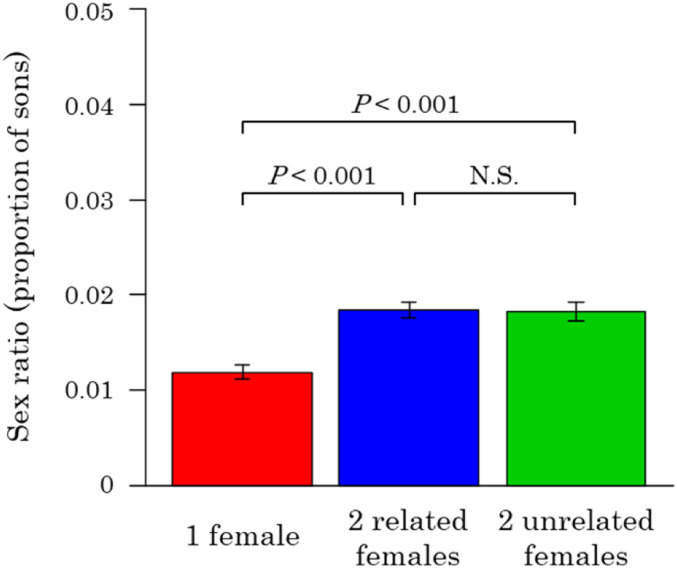
We found that there was no significant influence of relatedness between females on the offspring sex ratio that they produced. The sex ratio produced by females ovipositing with another female did not differ significantly depending upon whether the other female was related or not (Fig. 6 and SI Appendix, Fig. S1-2B; χ²₁ = 0.66, P = 0.42). As has been found previously (15–17), the sex ratio produced when two females laid eggs together was slightly higher than when a female was laying eggs alone (χ²₁ = 20.5, P < 0.001), but this shift was negligible compared to the predictions of Hamilton’s LMC theory (5). Consequently, it appears that females cannot assess relatedness directly, consistent with previous work on Melittobia species (16, 25).

Fig. 6.

Sex ratios in the laboratory experiment. The number of replicates was 24 for each treatment. The error bars represent SEs. The statistical values indicate the result of a pairwise comparison after correcting for multiple comparisons. Females show slightly increased sex ratios when they lay eggs with another female, as previously observed (15–17). However, they do not adjust their sex ratios in response to relatedness to the females.

Discussion

We found theoretically that when the offspring on a patch are more closely related, females should produce more female-biased offspring sex ratios (Fig. 5A) (2). In our model, the relatedness between offspring is determined by both how many females laid eggs on a patch and whether those females (mothers) had dispersed. Furthermore, we found that the predicted relationship between sex ratio and relatedness is relatively invariant to whether variation in relatedness is caused by the number of females laying eggs on a patch or their dispersal status. Frank has previously shown that one way of thinking about and analyzing LMC is that it is the relatedness between offspring that determines the extent to which relatives are competing for mates and mating siblings and hence the extent of LMC (2). Our results support Frank (2), showing that his prediction is very little altered when allowing for variable dispersal strategies.

We found that, in nature, M. australica females adjust their offspring sex ratio in the direction predicted by theory (Fig. 5C). Females appear to do this by adjusting their offspring sex ratio in response to two factors, the number of females laying eggs on a patch and whether they have dispersed (Fig. 3B). The influence of the number of females laying eggs has previously been demonstrated in numerous species (4). The more females lay eggs on a patch, the less related offspring will be (2, 5, 39). In contrast, the influence of dispersal status is relatively novel. Previous work on the thrip Hoplothrips pedicularius suggests that nondispersing females lay more female-biased sex ratios, but it is not known if the offspring sex ratio is also adjusted in response to the number of females laying eggs (28). What is special about the pattern in M. australica is that females appear to adjust their response to other females depending upon whether they have dispersed or not—only dispersed females lay less female-biased sex ratios when more females are laying eggs on a patch (Fig. 3B). Consequently, M. australica females appear to use a relatively sophisticated strategy to adjust their offspring sex ratios in response to the extent of LMC, as measured by the relatedness between the offspring that will develop on that patch (Fig. 5). Overall, the relatedness between female offspring was able to explain an impressive 72% of the variation in the sex ratio data, which is far higher than the average of 28% for studies on LMC (9).

M. australica females appear to assess their relatedness to other females indirectly, by their dispersal status, rather than directly by genetic cues. The optimal sex ratio depends upon relatedness to other females laying eggs on the same patch, and so females will be selected to assess relatedness. Our laboratory experiment suggests that females cannot assess relatedness directly (Fig. 6). The direct assessment of kin via genetic cues appears to be rare in parasitoids, with most studies finding that females do not use genetic cues to assess relatedness to other females (16, 25, 35–38, 48, 49). A possible reason for the rarity of direct genetic kin recognition is that it can sometimes be not evolutionarily stable. The reason for this is that selection will favor more common markers and hence eliminate the genetic variability required for kin recognition (50–53). In contrast, dispersal status appears to be an excellent indirect (environmental) cue of relatedness (28–30)—when females do not disperse, they are closely related to the other females laying eggs on a patch, leading to their offspring being highly related (Fig. 3A). It would be very useful to determine the exact cue that females use to determine their dispersal status. Our model examines context-dependent sex ratio adjustment, as has been observed in numerous species (4). Another possibility is that selection can lead to dispersal and social behaviors becoming linked (31).

While the pattern of sex ratio adjustment in M. australica is in the direction predicted by theory, the fit to theory is qualitative not quantitative. The offspring sex ratios are more female biased than predicted by theory (Fig. 5; the likelihood ratio test: χ²₁ = 817.9, P < 0.001). One possible explanation is that while our model assumes that females lay equal clutch sizes, our genetic analysis showed variation in clutch sizes between the females (Fig. 4). Variable clutch size increases average relatedness among interacting offspring and hence favors a more female-biased sex ratio (40–42). Another possible explanation is cooperative interactions between related females (6, 54–56). In Melittobia, females favor ovipositing on hosts parasitized by other females rather than intact hosts (56). In addition, a larger number of Melittobia females are likely to be advantageous to cooperatively make tunnels in host nests and to fight against mite species that live symbiotically with host species (57, 58). Cooperative female interactions have previously been suggested to favor an increased proportion of female offspring in a range of organisms, including other parasitoids, bees, beetles, and birds (38, 54, 59–63). A complication here is that although limited dispersal increases relatedness between encountering individuals, it can also increase competition between the related individuals and so reduce selection for female-biased sex ratios (33, 34, 47, 56, 64). However, in the case of Melittobia species, overlapping generations, inelasticity, dispersing with relatives, and open sites could negate this increased competition (34, 65–68) (SI Appendix, Supporting Information 3). Haystack models, as have been applied to some mites, offer another way of examining the interaction between competition and cooperation (69–71). Specific theory, which takes all these factors into account, would be very useful.

To conclude, our results provide a solution to the Melittobia sex ratio puzzle. Laboratory experiments on four Melittobia species have found that females produce lay extremely female-biased sex ratios (1 to 5% males) that change little with increasing number of females laying eggs on a patch (Fig. 1) (15, 18–20, 22). In these laboratory experiments, females were kept in vials and hence not able to disperse, and so they were likely to have behaved as nondispersers who would normally be on a patch with close relatives. We found that, in natural conditions, nondispersers behave as if other females are close relatives and show little response to the number of females laying eggs on the same patch (Fig. 3B). So, the solution to the puzzling sex ratio behavior of Melittobia appears to reflect a refined strategy that also takes account of indirect cues of relatedness.

Materials and Methods

Parasitoid Wasps.

M. australica (Hymenoptera: Eulophidae) is a gregarious parasitoid wasp that mainly parasitizes prepupae of various solitary wasp and bee species nesting above ground. The host species build nests containing brood cells, in which offspring develop separately while eating food provided by their mothers. Several generations (five or more on the main island of Japan) appear per year in Melittobia species, while most of the host species are mainly univoltine. Multiple generations of Melittobia may occur on a single host patch. Therefore, females laying eggs in Melittobia could be derived from other broods on the same host patch or disperse from other patches (Fig. 2). Once a female finds a host, she continues to lay eggs on the surface of the host and is potentially able to produce several hundred eggs on a single host as long as the host resources are sufficient. Similar to other hymenopteran species, Melittobia exhibits a haplodiploid sex determination, in which male and female individuals develop from unfertilized and fertilized eggs, respectively. Hatched larvae develop by sucking host haemolymph from the outside, and offspring sequentially emerge from previously laid eggs. The adults of males are brachypterous and do not disperse from their natal host cells, in which they mate with females that develop on the same host (21).

Field Sampling.

To collect the Melittobia broods from the field, we used bamboo traps, in which the host species build nests to develop their offspring. We set up 7 to 32 bamboo traps at the end of July or the beginning of August from 2011 to 2019 within an area with a 2-km radius in and around the campus of Kanagawa University in Hiratsuka, Kanagawa, Japan (SI Appendix, Table S2-1). The traps were horizontally fixed to the trunks or branches of trees at ∼1.5 m above the ground. Each bamboo trap consisted of a bundle of 20 dried bamboo canes. Each cane (200- to 300-mm long and 10- to 15-mm internal diameter) was closed with a nodal septum at one end and open at the other end. The traps were collected between December and the following March, when the individuals of the host wasps and bees in the cells were undergoing diapause at the prepupal stage. The traps were brought back to the laboratory, where all of the canes were opened to inspect the interior. Along with the traps that were set up in summer as described above, we conducted field sampling in the spring of 2015, 2017, and 2018. Bamboo canes containing nests with host prepupae that were collected in winter and kept in a refrigerator were exposed in the field for 1 to 2 mo.

In the laboratory, all individuals of the solitary wasps and bees and their kleptoparasites and parasitoids in the bamboo canes were counted and identified at the species level according to the morphology of the juveniles and the construction of the nests (SI Appendix, Table S2-2). If they were parasitized by Melittobia species, we recorded the host and Melittobia species (SI Appendix, Table S2-3). The adults and the dead bodies of Melittobia females in the host cells or cocoons could be regarded as mothers that laid eggs in the broods. We could distinguish female offspring from mothers based on the filled abdomen of emerged females. We collected the mothers and preserved them in 99.5% ethanol. After removing the mothers, the parasitized hosts were individually incubated at 25 °C until the offspring emerged. Emerged individuals were counted, sexed, and preserved in 99.5% ethanol.

Molecular Analysis.

For the analysis of sex ratios and molecular genetics, we only used the broods of M. australica among the two collected species (SI Appendix, Table S2-4) because this species was dominant in the present sampling area and most of the applied microsatellite markers indicated below were only valid for this species (27). We also only included broods in which all the individuals of the offspring generation had not yet started to emerge. The existence of emerged offspring in the host cells may indicate that some females had already dispersed. Finally, we excluded broods in which 16 or fewer individuals emerged, or the majority of juveniles were destroyed by an accidental event such as host haemolymph flooding. For genotyping, we analyzed 16 female offspring that were randomly selected from all emerged females in each brood. For mothers and male offspring, we genotyped all individuals if the number of individuals was less than 16; otherwise, 16 randomly selected individuals were analyzed.

We used the boiling method for DNA isolation (17). DNA was isolated from the whole body for male individuals or from the head and thorax for female individuals to prevent the contamination of spermatozoa from their mates. For the genomic analysis, we selected 16 microsatellite markers (SI Appendix, Table S2-5) out of 19 markers (27) to avoid the use of markers that might show genetic linkage with other loci. The detailed PCR methods are described elsewhere (27). The microsatellite genotypes of each individual were identified (SI Appendix, Table S2-5) from the amplified DNA fragments through fragment analysis with an ABI 3130 capillary sequencer (Life Technologies) and Peak Scanner software version 1.0 (Life Technologies). Based on the genotyping data, the average relatedness between the individuals on the broods and inbreeding coefficient were calculated using the software Relatedness version 4.2b (72). The broods were equally weighted in all analyses. Because we could obtain a sufficient number of female offspring from all the broods due to the female-biased sex ratio, we estimated relatedness from female offspring and used them for the analyses.

Although adult females that were captured in the broods of developing offspring could be regarded as females laying eggs (foundresses), all of these females might not necessarily have contributed eggs to the brood, and other foundress females who laid eggs might have departed before we collected them. To test for these possibilities, we conducted a parentage analysis to reconstruct the genotypes of females laying eggs (mothers) from the genotypic data of the offspring following the Mendelian rules under haplodiploidy (SI Appendix, Table S2-6) (46, 73). We first assigned the minimum number of captured adult females as the candidate mothers. If we could not identify the candidates from the captured females, we assumed that additional females produced offspring in the brood and rebuilt their genotypes. For assignment, we adopted the solution with the minimum number of mothers producing broods. We also assumed that mothers mated with multiple but minimal numbers of males. For dispersers, the genotypes of the mothers could be uniquely determined, and the number of mothers was strongly correlated with that of captured females (Pearson’s correlation: r = 0.84, t = 6.51, df = 17, P < 0.001). In contrast, we could not uniquely determine the genotypes of mothers for nondispersers because of the high similarity of the genotypes of the captured females. This suggests that nondispersers laying eggs on the same host were produced by a single female or very closely related females. Consequently, we used the number of captured females as the number of mothers for nondispersers, although this may be an overestimation.

Laboratory Experiment.

A female was introduced into a plastic case (86 mm in diameter and 20 mm in height) 1) alone, 2) with a related female from the same inbred strain, or 3) with an unrelated female from a different strain and allowed to lay eggs on a prepupa of Chalicodoma sculpturalis for 12 d. All the females of the same strains were collected from a single prepula of C. sculpturalis that was parasitized by eight females randomly chosen among the laboratory strains. The laboratory strains were the Amami strain (AM) and the Shonan 1 or 2 strain (SN1 or SN2), which were initiated by wild-caught wasps from single hosts collected from Amami Oshima Island in 2007 and from Hiratsuka in 2017, respectively. Amami Oshima and Hiratsuka are located ∼1,200 km away and are separated by sea. The SN 1 and 2 strains originated in the same population but were developed from individuals caught by different bamboo traps. The AM and SN 1 and 2 strains were maintained in the laboratory for ∼70 and 10 generations, respectively, during which several dozen females from previous generations were allowed to lay eggs on prepupae of C. sculpturalis to produce the subsequent generations. This procedure mimics the situation in which nondispersed females produce a new brood on another host in the same patch in the field. Before the experiment, a female was allowed to mate with a male from the same strain in the manner described elsewhere (17). The emerged offspring were counted and sexed. In the treatment involving two females from different strains, all male and 16 randomly collected female offspring were genotyped for one of the microsatellite loci (27), and the offspring sex ratios of the two ovipositing females were estimated separately using the ratio of the genotyped individuals. In the treatment involving females from the same strain, the two females were assumed to equally contribute to the broods. The experiment was conducted at a temperature of 25 °C and a photoperiod of L16:D8 h.

Statistical Analysis.

We analyzed all data using generalized linear mixed models implemented in statistical software R version 3.6.1 (74). The data on the number of females laying eggs or offspring, the sex ratio, the injury frequency, and relatedness were fitted with Poisson, binomial, binomial, and beta distributions, respectively. Because multiple broods in the same bamboo canes were estimated to be produced by females from the same hosts in some broods by nondispersers, we added the bamboo cane to the models as a random effect. In addition, we added the individual brood as a random effect for count data (the number of females laying eggs or offspring) or proportional data (sex ratio) to resolve the problem of overdispersion. We first ran full models including all fixed effects of interest and random effects and then simplified the models by removing nonsignificant terms (α > 0.05) from the least-significant ones to arrive at the minimum adequate models (75). The statistical significance was evaluated by using the likelihood ratio test comparing the change in deviance between the models. In multiple comparisons, significance thresholds were adjusted using the false discovery rate (76).

Theoretical Model.

We assume a population consisting of infinite discrete patches in which emerged male and female offspring mate at random (Wright’s island model of dispersal) (77). In Melittobia species, if there remain unparasitized hosts on the same patch where females emerged, the females can utilize them to produce next generation; otherwise, they need to disperse for other patches. We define the patch extinction rate e as the probability that patches will go extinct and assume that the same number of new patches are created in the next generation. If the patches go extinct (which occurs with a probability of e), all developed female offspring on the patches disperse to other patches. In contrast, if a patch has survived (with a probability of 1 − e), female offspring do not disperse with a probability of 1 − d or otherwise disperse with a probability of d. Nondispersers remain on their natal patch, in which n randomly selected females reproduce in the next generation. Dispersers from all the patches compete for reproduction on the newly created patches in which n randomly selected females reproduce. Although we assumed the situation above here, the fitness functions below (Eqs. 1 and 2) may also be applied to other situations (SI Appendix, Supporting Information 3).

We use the subscript i to denote dispersers (i = E) or nondispersers (i = N). Let x_i denote the sex ratio of a focal female, y_i denote the average sex ratio in the same patch as the focal female, and z_i denote the average sex ratio in the whole population. Then, the relative fitness of a daughter of the focal female $w_i^{\mathbf{F}}$ and the relative fitness of a son of the focal female $w_i^{\mathbf{M}}$ may be written as follows:

$$\begin{array}{l}{w}_i^{\mathbf{F}}=\left(1-x_i\right)[\left(1-e\right)\left(1-d\right)\frac{n}{\left(1-d\right)n\left(1-y_i\right)}+\left\{\left(1-e\right)d+e\right\}\frac{en}{\left\{\left(1-e\right)d+e\right\}n\left(1-\overline{z}\right)}]\\ \hspace{1em}=\left(1-x_i\right)\left\{\left(1-e\right)\frac{1}{1-y_i}+e\frac{1}{1-\overline{z}}\right\},\end{array}$$ [1]

$$\begin{array}{l}{w}_i^{\mathbf{M}}=x_i\frac{1-y_i}{y_i}[\left(1-e\right)\left(1-d\right)\frac{n}{\left(1-d\right)n\left(1-y_i\right)}+\left\{\left(1-e\right)d+e\right\}\frac{en}{\left\{\left(1-e\right)d+e\right\}n\left(1-\overline{z}\right)}]\\ \hspace{1em}=x_i\frac{1-y_i}{y_i}\left\{\left(1-e\right)\frac{1}{1-y_i}+e\frac{1}{1-\overline{z}}\right\},\end{array}$$ [2]

respectively, where $\overline{z}$ represents the metapopulation-wide average sex ratio

$$\overline{z}={\pi }_0{z}_{\text{E}}+{\displaystyle \sum }_{\tau =1}^{+\infty }{\pi }_{\tau }{z}_{\text{N}}$$ [3]

and π_τ is the frequency of patches that were recolonized during τ generations. Note that the parameter d is cancelled out as dispersers compete only with dispersers, while nondispersers only with nondispersers. By applying the neighbor-modulated fitness approach to kin selection methodology (2, 78–81), we find that an increased sex ratio is favored by natural selection for dispersers if

$$\begin{array}{l}e\left[c^{\mathbf{M}}\left(r_{\text{E}}^{\text{S}}-r_{\text{E}}^{\text{M}}\right)-\left(c^{\mathbf{M}}{r}_{\text{E}}^{\text{S}}+c^{\mathbf{F}}{r}_{\text{E}}^{\text{D}}\right)z_{\text{E}}\right]\left(1-z_{\text{E}}\right)\\ +\hspace{0.17em}\left(1-e\right)\left[c^{\mathbf{M}}\left(r_{\text{E}}^{\text{S}}-r_{\text{E}}^{\text{M}}\right)-\left\{c^{\mathbf{M}}\left(r_{\text{E}}^{\text{S}}-r_{\text{E}}^{\text{M}}\right)+c^{\mathbf{F}}\left(r_{\text{E}}^{\text{D}}-r_{\text{E}}^{\text{F}}\right)\right\}{z}_{\text{E}}\right]\left(1-\overline{z}\right)\hspace{0.17em}>\hspace{0.17em}0\end{array}$$ [4]

and for nondispersers if

$$\begin{array}{l}e\left[c^{\mathbf{M}}\left(r_{\text{N}}^{\text{S}}-r_{\text{N}}^{\text{M}}\right)-\left(c^{\mathbf{M}}{r}_{\text{N}}^{\text{S}}+c^{\mathbf{F}}{r}_{\text{N}}^{\text{D}}\right)z_{\text{N}}\right]\left(1-z_{\text{N}}\right)\\ +\hspace{0.17em}\left(1-e\right)\left[c^{\mathbf{M}}\left(r_{\text{N}}^{\text{S}}-r_{\text{N}}^{\text{M}}\right)-\left\{c^{\mathbf{M}}\left(r_{\text{N}}^{\text{S}}-r_{\text{N}}^{\text{M}}\right)+c^{\mathbf{F}}\left(r_{\text{N}}^{\text{D}}-r_{\text{N}}^{\text{F}}\right)\right\}{z}_{\text{N}}\right]\left(1-\overline{z}\right)\hspace{0.17em}>\hspace{0.17em}0,\end{array}$$ [5]

where c^M and c^F are the class reproductive values for females and males, respectively, $r_{\text{E}}^{\text{S}}$, $r_{\text{E}}^{\text{D}}$, $r_{\text{E}}^{\text{M}}$, and $r_{\text{E}}^{\text{F}}$ are the kin selection coefficients of relatedness for a daughter, a son, a random male offspring on the same patch, and a random female offspring on the same patch, respectively, from a perspective of a disperser, and $r_{\text{N}}^{\text{S}}$, $r_{\text{N}}^{\text{D}}$, $r_{\text{N}}^{\text{M}}$, and $r_{\text{N}}^{\text{F}}$ are the average kin selection coefficients of relatedness for a daughter, a son, a random male offspring on the same patch, and a random female offspring on the same patch, respectively, from a perspective of a nondisperser. Substituting the terms of reproductive values and relatedness, we may derive the convergence stable sex ratios for dispersers ($z_{\text{E}}^{\text{*}}$) and nondispersers ($z_{\text{N}}^{\text{*}}$). If we replace e with $1-{\left(1-d\right)}^2$, where d is female dispersal rate after mating, we recover Gandner et al.’s results (34). A full derivation is given in SI Appendix, Supporting Information 3.

Data Availability

All study data are included in the article and/or supporting information.