Maximizing power and velocity of an information engine

Significance

Around 100 y ago, Szilard imagined how to raise a weight without doing any work, just using the information gained by “looking” at a single gas molecule bouncing inside a box. Here, we designed an engine that stores energy by raising a bead against gravity, driven purely by information about the bead position. No work is done directly on the bead; instead, all dissipation occurs in the measuring apparatus. By choosing the right size of bead and through careful design, we improved information-engine performance by more than a factor of 10 over the best previous designs. We achieve a maximum velocity of 190 μm/s and maximum power of $10^3\hspace{0.17em}{k}_{\mathrm{B}}T/\mathrm{s}$, numbers comparable to those measured in microorganisms.

Abstract

Information-driven engines that rectify thermal fluctuations are a modern realization of the Maxwell-demon thought experiment. We introduce a simple design based on a heavy colloidal particle, held by an optical trap and immersed in water. Using a carefully designed feedback loop, our experimental realization of an “information ratchet” takes advantage of favorable “up” fluctuations to lift a weight against gravity, storing potential energy without doing external work. By optimizing the ratchet design for performance via a simple theory, we find that the rate of work storage and velocity of directed motion are limited only by the physical parameters of the engine: the size of the particle, stiffness of the ratchet spring, friction produced by the motion, and temperature of the surrounding medium. Notably, because performance saturates with increasing frequency of observations, the measurement process is not a limiting factor. The extracted power and velocity are at least an order of magnitude higher than in previously reported engines.

Over 150 y ago, Maxwell proposed a thought experiment to sharpen understanding of the second law of thermodynamics (1). He envisioned a “neat-fingered being” that could sort fast and slow molecules to create a temperature difference between two chambers, thereby converting the energy of a heat bath into a form that could be used to do work. In modern terms, Maxwell’s thought experiment was the first example of an information engine. In 1929, Leo Szilard proposed a simpler variant consisting of a single gas molecule in a chamber, partitioned by a wall (2, 3). If the particle is observed in the left half, the demon attaches a mass raised by motion to the right, and vice versa. Then, an isothermal expansion of the chamber raises the mass and stores potential energy. When run cyclically, the engine converts information about the state of the molecule into gravitational potential of a raised mass, seemingly without doing any work to lift the mass. This apparent violation of the second law of thermodynamics was later resolved by considering costs associated with the processing of information (4, 5), leading to a clearer understanding of the thermodynamics of information (6–8).

Recent advances in technology and theoretical developments in stochastic thermodynamics (9–12) have made it possible to experimentally realize information engines, based on the ideas of Maxwell and Szilard (13–19). They have been used to evaluate the Landauer cost of manipulating the associated measurement-memory device (20–23) and to explore the efficiency of information-to-work conversion (24–27).

Here, we create and study the performance of a useful information engine that not only extracts energy from heat but also stores energy by raising a weight, as initially imagined by Szilard. The “fuel” for the motor is the information gathered from favorable system fluctuations.

Our information engine consists of an optically trapped, micron-scale bead in water. The laser beam of the trap is horizontal, perpendicular to the vertical gravitational axis. The optical tweezers create a harmonic potential, where the bead fluctuates about an equilibrium that is lower because of the bead’s weight (Fig. 1B). The motion of the heavy bead can be modeled by a simple spring-mass system (Fig. 1A). The demon monitors the position of the mass and, when the mass fluctuates beyond a predefined threshold, raises the position of the spring anchor (top bar). Repeating the process, the mass is raised by exploiting favorable “up” fluctuations arising from thermal noise in the medium.

Fig. 1.

Schematic of the information engine. (A) Ratcheted spring-mass system under gravity. (B) Experimental realization using horizontal optical tweezers in a vertical gravitational field. Feedback operations on the right side in A and B are indicated by the small red “swoosh” arrows.

The experimental setup is similar to ref. 28, but here we store the extracted work in a reservoir. The ability to “spend” stored work on demand and for varying purposes greatly increases the utility of the engine. A previous experimental system introduced by Admon et al. (25) also stored work, but its design was based on a repulsive potential, which meant that the motor was always powered by a combination of external mechanical work and information. Here, with a design based on a trap potential having a local minimum, we ensure that no external work is done on the bead, which simplifies the physical picture.

In our study of this information engine we focus on understanding and then optimizing its performance: How much can it lift? How fast can it go? More precisely, what is the upper bound to the rate of gravitational energy storage and to the directed velocity? We reason that the value of the function of a motor can greatly exceed the cost of running it. For example, in biological applications such as chemotaxis, the metabolic costs of running cellular machinery (including information-processing costs) are usually unimportant compared to the benefit gained by the ability to move toward a new food source or away from a predator (29).

We thus seek to maximize performance, independent of the energy required. As we will show, there is a maximum achievable energy-storage rate and a maximum achievable directed velocity, even when the signal-to-noise ratio of the measuring system is arbitrarily high (with correspondingly high costs for information processing); knowing the maximum level of performance independent of information costs can provide a benchmark to evaluate trade-offs between performance and operational costs. We will also show that the performance of an information engine is limited by its material parameters. In our case, these parameters include trap stiffness and bead size, and we provide a systematic method of choosing their values to maximize the desired performance measure.

Theory

Equation of Motion.

The dynamics of an optically trapped bead are well described by an overdamped Langevin equation,

$$\gamma \dot{x}\left(t\right)=\underset{\text{restoring force}}{\underbrace{-\kappa \left(x\left(t\right)-\lambda \left(t\right)\right)}}-\underset{\text{grav. force}}{\underbrace{mg}}+\underset{\text{thermal noise}}{\underbrace{\sqrt{2k_{\mathrm{B}}T\gamma }\hspace{0.17em}\nu \left(t\right)}}\hspace{0.17em},$$ [1]

where $x\left(t\right)$ denotes the position of a bead of radius $r$ at time $t$, $\lambda \left(t\right)$ the center of the trap, $\kappa$ the trap stiffness, $\gamma$ the friction coefficient, and $g$ the gravitational acceleration, and $\nu \left(t\right)$ represents Gaussian white noise with zero mean and $⟨\nu \left(t\right)\hspace{0.17em}\nu \left(t^{\prime }\right)⟩=\delta \left(t-t^{\prime }\right)$. The effective mass $m=\left(4/3\right)\pi r^3\mathrm{\Delta }\rho$ of the bead depends on the relative density $\mathrm{\Delta }\rho ={\rho }_{\mathrm{b}\mathrm{e}\mathrm{a}\mathrm{d}}-{\rho }_{\mathrm{m}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{m}}$ (= 1.0 g/mL, for all bead diameters) and accounts for buoyancy. Scaling lengths by the equilibrium standard deviation $\sigma =\sqrt{k_{\mathrm{B}}T/\kappa }$ of the bead position and time by the bead relaxation time ${\tau }_r=\gamma /\kappa$, the overdamped Langevin equation becomes

$$\dot{x}\left(t\right)=-\left[x\left(t\right)-\lambda \left(t\right)\right]-{\delta }_{\mathrm{g}}+\sqrt{2}\hspace{0.17em}\nu \left(t\right)\hspace{0.17em},$$ [2]

where ${\delta }_{\mathrm{g}}\equiv mg/\kappa \sigma$ is a scaled effective mass that measures the sag of the bead due to gravity, relative to the scale of equilibrium fluctuations in the trap. The bead position is measured at discrete time intervals of $t_{\mathrm{s}}^{\prime }=20$ $\mathrm{\mu }$s, and the feedback on the trap position is applied after a delay of one time step. Integrating Eq. 2 over one time step gives discrete-time dynamics (30),

$$x_{n+1}={\text{e}}^{-t_{\mathrm{s}}}{x}_n+\left(1-{\text{e}}^{-t_{\mathrm{s}}}\right)\left({\lambda }_n-{\delta }_{\mathrm{g}}\right)+\sqrt{1-{\text{e}}^{-2t_{\mathrm{s}}}}\hspace{0.17em}{\xi }_n,$$ [3]

where $t_{\mathrm{s}}\equiv t_{\mathrm{s}}^{\prime }/{\tau }_{\mathrm{r}}$, $x_n\equiv x\left(n{t}_{\mathrm{s}}\right)$ denotes the position at time step number $n$, and ${\xi }_n$ is a Gaussian random variable, with zero mean and unit variance, satisfying $⟨{\xi }_m\hspace{0.17em}{\xi }_n⟩={\delta }_{mn}$.

The trap position ${\lambda }_n$ is updated according to a feedback algorithm,

$${\lambda }_{n+1}=\left\{\begin{array}{cc}{\lambda }_n+\alpha \left(x_n-{\lambda }_n\right),\hspace{1em}\hfill & \hspace{1em}{x}_n-{\lambda }_n>X_{\mathrm{T}}\hfill \\ {\lambda }_n,\hspace{1em}\hfill & \hspace{1em}\text{otherwise}.\hfill \end{array}\right.$$ [4]

Here, $X_{\mathrm{T}}$ is the threshold, and $\alpha$ is the feedback gain. Fig. 2, Bottom-Right Inset shows example time series of the upward motion $x\left(t\right)$ of the mass and $\lambda \left(t\right)$ of the trap.

Fig. 2.

Zero-work condition defining a pure information engine. Trap power $P_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{p}}$ as a function of feedback gain $\alpha$ for fixed threshold $X_{\mathrm{T}}=0$, scaled relaxation frequency ${\tau }_{\mathrm{r}}/t_{\mathrm{s}}^{\prime }=180$, scaled effective mass ${\delta }_{\mathrm{g}}=0.8$, relaxation time ${\tau }_{\mathrm{r}}$ = 3.6 ms, diffusion constant $D=0.16$ $\mathrm{\mu }{\mathrm{m}}^2$/s, trap stiffness $\kappa$ = 7.0 pN/$\mathrm{\mu }$m, and bead diameter of 3 $\mathrm{\mu }$m. (Bottom-Right Inset) Experimental trajectories of the bead [$x\left(t\right)$, gray] and trap [$\lambda \left(t\right)$, black] during continuous ratcheting. (Top-Left Inset) Naive zero-work condition for a harmonic potential is $\alpha =2$, equivalent to $X_{\mathrm{R}}=X_{\mathrm{T}}$. The black curve denotes the trap potential in the current step and gray curve in the previous step. Error bars here and in other figures are the standard error of the mean (SI Appendix, section M).

For an instantaneous measurement and shift of the trap center, Fig. 2, Top-Left Inset shows that choosing $\alpha =2$ would impose a zero-work condition (cf. SI Appendix, section B), where the stored potential energy results solely from the conversion of the information about the bead position; i.e., the work done by the trap is set to zero. In our experimental apparatus, there is a delay of 20 $\mathrm{\mu }$s (one time step) arising (mostly) from the acousto-optic deflector (AOD) that controls the position of the trap (31). If uncompensated, such a delay can lead to a significant amount of input-trap work. During the delay, the bead tends to move back toward the equilibrium, reducing the value of $\alpha$ needed to impose zero work. To compensate, $\alpha$ is set empirically to implement the zero-work condition, which occurs at $\alpha \approx 1.5$ in Fig. 2. Note that the reset position $X_{\mathrm{R}}$ illustrated in Fig. 2 is related to $\alpha$ by $X_{\mathrm{R}}=\left(\alpha -1\right)X_{\mathrm{T}}$.

Energy Storage and Directed Motion.

The input work is the change in energy of the bead that occurs when the position $\lambda$ of the trap center is moved. Since the trap center is moved only at the sampling times $\left\{t_{n+1}\right\}$ and since the shift happens at a faster time scale ($<1$ $\mathrm{\mu }$s, set by the response of the AOD) than bead motion, the work done at each update $t_{n+1}$ is

$$W_{n+1}=\frac{1}{2}\left[{\left(x_{n+1}-{\lambda }_{n+1}\right)}^2-{\left(x_{n+1}-{\lambda }_n\right)}^2\right].$$ [5]

Similarly, the gain in gravitational potential is

$$\mathrm{\Delta }{U}_{n+1}={\delta }_{\mathrm{g}}\left(x_{n+1}-x_n\right).$$ [6]

By convention, the trap work is positive if energy flows into the system and negative if it flows out.

We quantify the performance of the information engine by the (long-time average) directed velocity and stored power, ideally for an infinitely long trajectory. Each trajectory can be viewed as a sequence of independent ratchet events, each starting with the particle at position $\lambda -X_{\mathrm{R}}$ inside the trapping potential and ending when the particle fluctuates up and first reaches the position $\lambda +X_{\mathrm{T}}$. The displacement $\mathrm{\Delta }x=\left(\lambda +X_{\mathrm{T}}\right)-\left(\lambda -X_{\mathrm{R}}\right)=X_{\mathrm{R}}+X_{\mathrm{T}}$ is thus fixed for each event, but the time required for event $m$, the first-passage time ${\tau }_{\mathrm{F}\mathrm{P}}$, is stochastic (32).

Using the above definitions, we write the velocity

$$v=\underset{t_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}\to \infty }{lim}\frac{X_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}}{t_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}}\hspace{0.17em}=\underset{N_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}\to \infty }{lim}\frac{{\sum }_{m=1}^{N_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}}\mathrm{\Delta }x}{{\sum }_{m=1}^{N_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}}{\left({\tau }_{\mathrm{F}\mathrm{P}}\right)}_m}\hspace{0.17em}=\frac{X_{\mathrm{R}}+X_{\mathrm{T}}}{{\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}}},$$ [7]

where $X_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}$ and $t_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}$ are the total trajectory length and time and $N_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}$ is the number of ratcheting events. We used the law of large numbers to write ${\sum }_m{\left({\tau }_{\mathrm{F}\mathrm{P}}\right)}_m\to N_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}{\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}}$, with ${\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}}$ the mean first-passage time (MFPT), the average of ${\tau }_{\mathrm{F}\mathrm{P}}$ (cf. SI Appendix, section J).

The corresponding rate of energy extraction (power) is $v\hspace{0.17em}mg$, or, in scaled units,

$$P=v\hspace{0.17em}{\delta }_{\mathrm{g}}.$$ [8]

For each data point, typically 100 repeated trajectories are measured over a fixed distance of 340 nm. The velocity and power are estimated by replacing $X_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}$ and $t_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}$ in Eqs. 7 and 8 with their trajectory averages (Materials and Methods).

Predicted Maximum Output Power and Velocity.

To predict the maximum output power and velocity, we first calculate the MFPT (Fig. 2, Top-Left Inset). A standard calculation (32, 33) (SI Appendix, section C) gives, in scaled units,

$${\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}}\left(X_{\mathrm{T}}\right)={\int }_{-X_{\mathrm{T}}}^{X_{\mathrm{T}}}\text{d}{x}^{\prime }\hspace{0.17em}{\text{e}}^{V\left(x^{\prime }\right)}{\int }_{-\infty }^{x^{\prime }}\text{d}{x}^{″}\hspace{0.17em}{\text{e}}^{-V\left(x^{″}\right)}\hspace{0.17em},$$ [9]

for total potential $V\left(x\right)\equiv \frac{1}{2}{x}^2+{\delta }_{\mathrm{g}}\hspace{0.17em}x$. Although Eq. 9 in general must be solved numerically, a Taylor expansion for small threshold $X_{\mathrm{T}}$ gives

$${\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}}\left(X_{\mathrm{T}}\right)=\sqrt{2\pi }\hspace{0.17em}{\text{e}}^{{\delta }_{\mathrm{g}}^2/2}\hspace{0.17em}\left[1+\text{erf}\left(\frac{{\delta }_{\mathrm{g}}}{\sqrt{2}}\right)\right]X_{\mathrm{T}}+\mathcal{O}\left(X_{\mathrm{T}}^3\right),$$ [10]

with positive higher-order corrections.

The velocity is then maximized by taking $X_{\mathrm{T}}\to 0$:

$$v\left(X_{\mathrm{T}}\right)=\frac{2X_{\mathrm{T}}}{{\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}}\left(X_{\mathrm{T}}\right)}$$ [11a]

$$\stackrel{X_{\mathrm{T}}\to 0}{\to }\sqrt{\frac{2}{\pi }}\hspace{0.17em}{\text{e}}^{-{\delta }_{\mathrm{g}}^2/2}\hspace{0.17em}{\left[1+\text{erf}\left(\frac{{\delta }_{\mathrm{g}}}{\sqrt{2}}\right)\right]}^{-1}.$$ [11b]

Eq. 11b was derived previously using a different method and in a slightly different context (34).

In physical units and for large force constants ($\kappa \to \infty$), the velocity and power are

$$v^{\prime }=\left(\frac{\sigma }{{\tau }_{\mathrm{r}}}\right)v\hspace{0.17em}\stackrel{\kappa \to \infty }{\sim }\hspace{0.17em}\sqrt{\frac{2k_{\mathrm{B}}T}{\pi }}\frac{\sqrt{\kappa }}{\gamma }\hspace{0.17em},$$ [12a]

$$P^{\prime }=\left(\frac{k_{\mathrm{B}}T}{{\tau }_{\mathrm{r}}}\right)P\hspace{0.17em}\stackrel{\kappa \to \infty }{\sim }\hspace{0.17em}\sqrt{\frac{2k_{\mathrm{B}}T}{\pi }}\frac{\sqrt{\kappa }}{\gamma }mg.$$ [12b]

Results

To maximize the rate of gravitational-energy extraction (the power), we first studied its dependence on the sampling frequency. Fixing the trap stiffness $\kappa$ and hence the relaxation time ${\tau }_{\mathrm{r}}$, we varied the sampling time $t_{\mathrm{s}}^{\prime }$. Fig. 3A shows that the power saturates at large sampling frequencies ($f_{\mathrm{s}}={\tau }_{\mathrm{r}}/t_{\mathrm{s}}^{\prime }\gg 1$). Thus, making more measurements may not increase the extracted power. Indeed, measurements faster than the relaxation time ${\tau }_{\mathrm{r}}$ of the bead are correlated and thus provide less information than a single, isolated measurement (25). Nonetheless, sampling faster than ${\tau }_{\mathrm{r}}$ reduces the chance of missing a favorable fluctuation that reaches $X_{\mathrm{T}}$.

Fig. 3.

Optimization of ratcheting power. (A) Power as a function of sampling frequency $f_{\mathrm{s}}={\tau }_{\mathrm{r}}/t_{\mathrm{s}}^{\prime }$. The black solid curve denotes the semianalytic results (SI Appendix, section E) for the same material parameters, feedback gain $\alpha =1.8$, and threshold $X_{\mathrm{T}}=0$. The horizontal dotted line indicates the infinite-frequency limit (Eq. 11b multiplied by ${\delta }_{\mathrm{g}}$), and the dashed line denotes the low-frequency limit (SI Appendix, section D). (B) Power as a function of threshold $X_{\mathrm{T}}$ for fixed $\alpha =1.9$ and sampling frequency of 50 kHz. The gray markers show that the input trap power is small. The black curve follows from Eq. 11a. Red markers denote experimental values. For all data, scaled effective mass ${\delta }_{\mathrm{g}}=0.8$, relaxation time ${\tau }_{\mathrm{r}}$ = 3.5 ms, diffusion constant = 0.16 $\mathrm{\mu }{\mathrm{m}}^2$/s, trap stiffness $\kappa$ = 7.3 pN/$\mathrm{\mu }$m, and bead diameter = 3 $\mathrm{\mu }$m.

At low frequencies, the number of ratchet events is linearly proportional to the sampling frequency. The gray dotted line in Fig. 3A has slope $\approx 0.19$, which is consistent with a calculation assuming the particle position distribution equilibrates during each interval (SI Appendix, section D). The solid curve in Fig. 3A is based on semianalytic calculations (SI Appendix, section E) that use the measured material parameters and agree well with experiments, with no free parameters. Thus, sampling more slowly than the fluctuation time scale ${\tau }_{\mathrm{r}}$ of the dynamics misses possibly useful fluctuations; sampling more quickly eventually yields diminishing returns.

Having established that the extracted power is maximized for infinite sampling frequency, we henceforth use the fastest feedback time of 20 $\mathrm{\mu }$s, which typically corresponds to $f_{\mathrm{s}}\gtrsim 100$. Such a sampling frequency is high enough that analytic calculations based on the continuous-sampling limit ($f_{\mathrm{s}}\to \infty$) describe the data well.

We next explored how to set the position threshold $X_{\mathrm{T}}$. This parameter controls the magnitude of the fluctuation that is captured during each ratchet event. The experiments were performed for ${\delta }_{\mathrm{g}}=0.8$. The feedback gain $\alpha =1.9$ ensured that the input power was zero for the chosen threshold values, as confirmed by the gray solid markers in Fig. 3B.

Fig. 3B shows that the output power, under the constraint of zero input power, is maximized for $X_{\mathrm{T}}\to 0$ (“continuous ratcheting”). The trap position $\lambda \left(t\right)$ then either ratchets to accommodate up fluctuations or pauses when the bead fluctuates down, before reaching the threshold again (Fig. 2, Bottom-Right Inset). As $X_{\mathrm{T}}$ increases, the fluctuations that take the bead to the threshold become increasingly rare (exponentially in $X_{\mathrm{T}}$), leading to longer wait times between ratchet events; hence, the power tends to zero. The solid black curve is calculated by numerically integrating Eq. 9 to find ${\tau }_{\mathrm{M}\mathrm{F}\mathrm{P}}\left(X_{\mathrm{T}}\right)$.

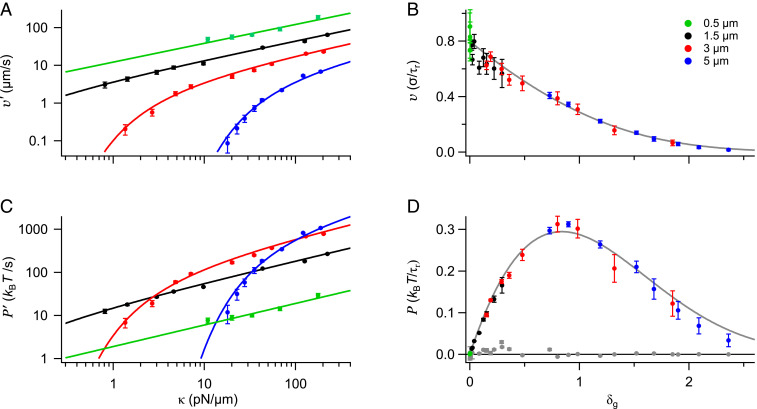
Having determined that continuous sampling and continuous ratcheting maximize the extracted power, we explored the role of bead mass in experiments using nominal bead diameters of 0.5, 1.5, 3, and 5 $\mathrm{\mu }$m. For each trap strength $\kappa$ (set by the trapping laser power) and for each trapped bead (whose size varies slightly from the nominal size listed by the manufacturer) we determine the value of feedback gain $\alpha$ that makes $P_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{p}}\approx 0$. The gray markers in Fig. 4D show that the trap power can be kept small, even though the required value of $\alpha$ is different for each value of ${\delta }_{\mathrm{g}}$.

Fig. 4.

Power and velocity for bead diameters 0.5 (green), 1.5 (black), 3 (red), and 5 (blue) $\mathrm{\mu }$m for threshold $X_{\mathrm{T}}=0$. Markers denote experimental data (see SI Appendix, Table S2 for experimental parameters). (A) Velocity as a function of trap stiffness $\kappa$. (B) Scaled velocity as a function of scaled effective mass ${\delta }_{\mathrm{g}}$. (C) Power as a function of $\kappa$. (D) Scaled power as a function of ${\delta }_{\mathrm{g}}$. Gray markers show that the corresponding $P_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{p}}$ values remain small. Solid curves in A and C are calculated from Eqs. 12a and 12b. Solid curves in B and D are calculated from Eq. 11b.

We then measured the extracted velocity (Fig. 4A) and power (Fig. 4C) for the four nominal bead sizes. For a fixed bead size, the power and velocity increase monotonically with trap stiffness, as increasing the trap stiffness reduces the MFPT. For fixed trap stiffness and bead density, the velocity decreases with bead size. By contrast, the power is maximized at an optimal intermediate bead size. Scaling the length, time, and energy by the trap standard deviation $\sigma$, trap relaxation time ${\tau }_{\mathrm{r}}$, and $k_{\mathrm{B}}T$, respectively, collapses the data onto single scaled power and velocity curves as a function of the scaled effective mass ${\delta }_{\mathrm{g}}$, Eq. 11b (Fig. 4 B and D). The power is maximized at $P^{*}\approx 0.295\hspace{0.17em}{k}_{\mathrm{B}}T/{\tau }_{\mathrm{r}}$ for ${\delta }_{\mathrm{g}}\approx 0.845$ and the velocity at $v^{*}\approx 0.8\hspace{0.17em}\sigma /{\tau }_{\mathrm{r}}$ for ${\delta }_{\mathrm{g}}\to 0$ (34). The maximum in extracted power at finite ${\delta }_g$ results from a competition between two effects: The potential energy of a raised object increases with mass, but so does the time to fluctuate beyond a threshold.

Finally, we explored the influence of gravity on directed motion. Our analysis suggests that gravitational effects should be quantified by the scaled effective mass, ${\delta }_{\mathrm{g}}$. To test this idea, we compared the measured directed velocity achieved for horizontal motion with that achieved for vertical motion (SI Appendix, section G). Horizontal velocities are consistent with predictions based on Eq. 12a or, equivalently, Eq. 11b for ${\delta }_{\mathrm{g}}\to 0$. Thus, when the bead is sufficiently light or small (1.5 $\mathrm{\mu }$m in this case), gravity becomes irrelevant: Particle speed is independent of direction (SI Appendix, Fig. S4). For heavier beads and smaller spring constants the motion is slower in the vertical direction.

Discussion

We have designed a simple information-fueled engine that can convert the heat of a surrounding bath into directed motion and hence store gravitational potential energy. A systematic study of conditions that optimize the performance limits of the engine shows that continuous measurements and continuous ratcheting are best. Fortunately, the analysis of the continuous-feedback limit is simpler than that for the corresponding discrete-time dynamics and can draw on well-known results from the analytic theory of MFPTs. From the optimization, we find simple expressions for extracted power and velocity establishing that the performance limits of the engine are set by material parameters such as the stiffness of the spring created by the optical tweezers.

Fig. 4 A and C and Eq. 12 show that smaller beads maximize directed motion, but larger beads maximize power extraction. That varying goals call for varying design principles is familiar in macroscopic applications. For example, the diesel engines used in trucks are optimized for power, whereas the turbocharged engines used in race cars are optimized for speed. More generally, systematic connections between material parameters and performance limits are common features of motors. Indeed, motors ranging from proteins to jet engines follow scaling laws whose form is determined by the failure modes of the materials used in the motor construction (35, 36).

By following optimal design principles, we have markedly improved performance relative to previous efforts, which focused instead on information-processing costs and the associated “information-to-work” efficiency of the engine (13, 24, 25, 28). The maximum extracted power is $10^4$ times higher than that reported in ref. 25), although comparable laser powers are used. Most of the improvement in extracted power is achieved through the trap design. In the present case, power is applied where needed, via a single trap; an array of traps was used in ref. 25. Our design may also be compared with ref. 28, which uses a single trap, as here, but does not store work. The power levels achieved here exceed those in ref. 26 by an order of magnitude. The improvement relative to ref. 26 arises from careful optimization of parameters (bead size, $X_{\mathrm{T}}$, etc.). Similarly, we increase the directed velocity by a factor of 30 compared to ref. 37 by choosing a smaller bead.

For our setup, the “best” values achieved for power and velocity are 1,066 $k_{\mathrm{B}}T$/s and 190 $\mathrm{\mu }$m/s, respectively. These values are significant: They are roughly 10 times faster than Escherichia coli and are comparable to the speeds of faster motile bacteria such as those found in marine environments (which need to outswim their algae prey) (38) and are also comparable to the power used to drive molecular motors such as kinesin (39).

For setups similar to the one used here, the laser power can in principle be increased significantly, which would increase the trap constant $\kappa$; however, in many applications, heating will limit the power that can be applied. Another route to increasing performance is to optimize the response properties of the trapped particle. Here, we limited our particle choice to dielectric spheres; more sophisticated core-shell particle designs can reduce beam reflection and scattering forces, thereby increasing the trap stiffness at fixed laser power by a factor of approximately 10 (40).

In our experiments, the optical-tweezer setup imposed a harmonic potential. Could more power or higher velocities be possible using a different potential shape? We numerically studied a potential with controllable asymmetry and found no improvement, given a fixed maximum stiffness. Additionally, we can show that, for symmetric traps, the harmonic shape is optimal (SI Appendix, section K).

Another route to higher rates of energy extraction and storage is via systems with intrinsically shorter dynamical time scales. Experimental setups using electronic circuits (15, 22) and superconducting qubits (16, 17) have been used to extract power. With modification, they could also store power and then be optimized by following the techniques introduced here.

Beyond technological limits set by the stiffness of the material used to build the motor, the dynamical model used in our optimization can break down. Naively, decreasing dynamical time scales (e.g., by increasing the trap stiffness $\kappa$) always improves information-engine performance. However, our analysis assumes Eq. 1, which describes a simple overdamped Langevin model with instantaneous damping and is characterized by the relaxation time ${\tau }_{\mathrm{r}}$. For the range of $\kappa$ and bead sizes that we explore, this assumption holds; however, as $\kappa$ increases, the time scale ${\tau }_{\mathrm{r}}$ of the trap dynamics decreases.

If short enough, other dynamical time scales, linked to inertial and memory effects in the surrounding fluid, can act to filter high-frequency fluctuations, thereby limiting the ratcheting achievable through feedback that is based solely on the most recent measurement. To capture inertial effects, the term $m\ddot{x}$ should be included in Eq. 1, which introduces the velocity relaxation time scale ${\tau }_v=m/\gamma$. To capture memory effects, the viscous friction term $\gamma \dot{x}$ generalizes to a convolution with a kernel that captures the effects of fluid rearrangements in response to bead motion. This introduces a time scale ${\tau }_{\mathrm{f}}=r^2/\nu$, the time it takes the fluid to diffuse one particle radius $r$, where $\nu$ is the kinematic viscosity. The combined effects of inertia and hydrodynamic memory are captured by the Basset-Boussinesq–Oseen equation (41).

We have made informal numerical studies of these two effects. On the one hand, we find that our proposed feedback algorithm (Eq. 4) leads to worse performance than implied by estimates based on the overdamped limit. The performance begins to degrade at trap dynamics time scales $\approx 3$ $\mathrm{\mu }$s, obtained by equating the overdamped relaxation time to the fluid memory time scale ${\tau }_{\mathrm{r}}={\tau }_{\mathrm{f}}$. This regime is achieved by the 5-$\mathrm{\mu }$m bead at a trap stiffness of $\kappa \approx \mathrm{6,000}$ pN/$\mathrm{\mu }$m, which is about an order of magnitude greater than our current setup is capable of; however, deviations are empirically already seen for $\kappa \approx 200$ pN/$\mathrm{\mu }$m (SI Appendix, Fig. S6). Nevertheless, “naively” extrapolating the overdamped theory to this time scale implies work extraction of $\approx 10^4\hspace{0.17em}{k}_{\mathrm{B}}T/\mathrm{s}$ (for a 5-$\mathrm{\mu }$m bead) and speeds of $\approx \mathrm{3,000}$ $\mathrm{\mu }$m/s (for a 0.5-$\mathrm{\mu }$m bead). See SI Appendix, section L.

On the other hand, these new physical effects are characterized by new dynamical variables that can be used to further optimize the feedback algorithm. When inertial effects are important, measuring the velocity $\dot{x}$ can improve feedback; likewise, when the hydrodynamic memory kernel is important, the history of positions can help. In principle, one could modify the feedback rule to incorporate the recent history rather than just the most recent measurement. Operating an information engine in a gas of reduced pressure (42) would make these scales more accessible experimentally, and it would be interesting to explore whether improved algorithms can capture some of the performance that would otherwise be lost in these regimes.

Although our focus here has been on maximizing either the rate of extracted work or the directed velocity, the energetic costs of running the engine are also of interest. For our macroscopic experimental apparatus, the operating costs dwarf the engine output; however, several studies have shown that the fundamental, unavoidable information costs in similar contexts can be much lower (43–47). In the limits of infinite sampling frequency and signal-to-noise ratio (SNR), different ways of estimating costs (24–26, 48) all lead to vanishing efficiency when applied to our setup. We have not here specified the details of our feedback controller, but one reasonable choice is to allow each new measurement to overwrite the previous one. For such an architecture, the appropriate measure of minimum costs is the information flow (46, 47). For our “typical” experiment with amplitude $\mathrm{S}\mathrm{N}\mathrm{R}\approx 10$ and scaled sampling frequency $f_{\mathrm{s}}\approx 180$, this measure implies an input–output efficiency of about 8% (SI Appendix, section N). Even at this relatively low efficiency, the power and velocity are indistinguishable experimentally from those found in the limit of infinite sampling frequency and SNR. In future work, it would be interesting to explore more systematically the trade-off between performance and information-processing costs, using the tools of multiobjective optimization (49).

Finally, our information-engine design exploits only the “up” fluctuations. In Szilard’s original proposal, the ability to change the connection between mass and partition as a function of the measurement outcome (the side on which the particle is found) allowed exploitation of all measurement outcomes. However, in our design “down” fluctuations lead to no feedback response. The information gathered in measuring those fluctuations cannot be exploited, reflecting a structural limitation of the engine (50). A design that could convert and store energy from all measurements would further enhance information-engine performance.

Materials and Methods

The experiments were performed using an optical-tweezer setup that can rapidly shift the beam position under feedback control (31, 51). For setup details, see SI Appendix, section A. To estimate the power and velocity from empirical data, we record trajectories over a fixed distance of 340 nm, a range set by the quadrant photodiode sensor, which records beam deflections due to bead movement. The measurement noise ${\sigma }_{\text{m}}^{\prime }$ ranged from 0.6 to 4.8 nm (see SI Appendix, Table S2); the amplitude SNR ranged from 1 to 60 and was typically about 10. Every time the bead reaches the upper bound, it is returned to the lower bound, and the ratchet protocol is repeated. Each 340-nm trajectory contains $N_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}\approx 80$ ratchet events when the threshold $X_{\mathrm{T}}=0$. Typically, the first relaxation time ${\tau }_{\mathrm{r}}$ of the trajectory is not included when estimating power and velocity, to allow the system to reach steady state. The total displacement and time for each trajectory $j$ is recorded, and then the procedure is repeated $N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}\approx 100$ times. The velocity and power are calculated from the average over the $N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}$ trajectories as $\overline{v}=\sum \left(x_n-x_{n-1}\right)/t_{\mathrm{s}}$ and $\overline{P}={\delta }_{\mathrm{g}}\overline{v}$, where the sum is over time steps within a trajectory and over the $N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}$ multiple trials. Because the total number of ratcheting events is large ($N_{\mathrm{t}\mathrm{o}\mathrm{t}}=N_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}\times N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}\approx 8\times 10^3$) and each first-passage time ${\tau }_{\mathrm{F}\mathrm{P}}$ is an independent random variable, we can aggregate the first-passage times from all $N_{\mathrm{t}\mathrm{o}\mathrm{t}}$ events. As $N_{\mathrm{t}\mathrm{o}\mathrm{t}}\gg 1$, the law of large numbers can be used to estimate the mean velocity and power. The approximation becomes exact when $N_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}},N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{j}}\to \infty$ (SI Appendix, section J).

Sample Preparation.

Four sizes of silica bead were used, with nominal diameters specified by the manufacturer of 1.49 $\pm$ 0.22 $\mathrm{\mu }$m (Bangs Laboratories), 0.50 $\pm$ 0.05 $\mathrm{\mu }$m, 3.00 $\pm$ 0.25 $\mathrm{\mu }$m, and 5.00 $\pm$ 0.35 $\mathrm{\mu }$m (Sigma-Aldrich). The properties (diffusion constant and force constant) associated with each bead were measured individually before each set of experiments done with the particular bead. The sphere solution from the manufacturer was diluted using deionized water. The sample chamber was prepared from a glass slide and a coverslip, which were separated by 100-$\mathrm{\mu }$m spacer wires and sealed by nail polish. For the 0.5-$\mathrm{\mu }$m-bead experiment, the sample chamber consisted of two coverslips, separated by 50-$\mathrm{\mu }$m spacer wires.

Data Availability

Code and experimental data have been deposited in Zenodo (DOI: 10.5281/zenodo.4697882) (52).