A spatial model of YAP/TAZ signaling reveals how stiffness, dimensionality, and shape contribute to emergent outcomes

Significance

The YAP/TAZ pathway plays a fundamental role in integrating a variety of cellular cues to control important physiological processes. Here, we develop a spatial model of this pathway that contributes quantitative understanding and disentangles the role various stimuli play that are difficult to distinguish experimentally. The model integrates key spatial and physical inputs, namely cell and nuclear shape, surface area-to-volume ratios of cytoplasmic and nuclear compartments, substrate dimensionality, substrate activation area, and substrate stiffness, through membrane-proximal, cytoskeletal, and nuclear mechanotransduction modules. The resulting model accounts for seemingly contradictory experimental trends and lends new insight into controlling YAP/TAZ signaling.

Abstract

YAP/TAZ is a master regulator of mechanotransduction whose functions rely on translocation from the cytoplasm to the nucleus in response to diverse physical cues. Substrate stiffness, substrate dimensionality, and cell shape are all input signals for YAP/TAZ, and through this pathway, regulate critical cellular functions and tissue homeostasis. Yet, the relative contributions of each biophysical signal and the mechanisms by which they synergistically regulate YAP/TAZ in realistic tissue microenvironments that provide multiplexed input signals remain unclear. For example, in simple two-dimensional culture, YAP/TAZ nuclear localization correlates strongly with substrate stiffness, while in three-dimensional (3D) environments, YAP/TAZ translocation can increase with stiffness, decrease with stiffness, or remain unchanged. Here, we develop a spatial model of YAP/TAZ translocation to enable quantitative analysis of the relationships between substrate stiffness, substrate dimensionality, and cell shape. Our model couples cytosolic stiffness to nuclear mechanics to replicate existing experimental trends, and extends beyond current data to predict that increasing substrate activation area through changes in culture dimensionality, while conserving cell volume, forces distinct shape changes that result in nonlinear effect on YAP/TAZ nuclear localization. Moreover, differences in substrate activation area versus total membrane area can account for counterintuitive trends in YAP/TAZ nuclear localization in 3D culture. Based on this multiscale investigation of the different system features of YAP/TAZ nuclear translocation, we predict that how a cell reads its environment is a complex information transfer function of multiple mechanical and biochemical factors. These predictions reveal a few design principles of cellular and tissue engineering for YAP/TAZ mechanotransduction.

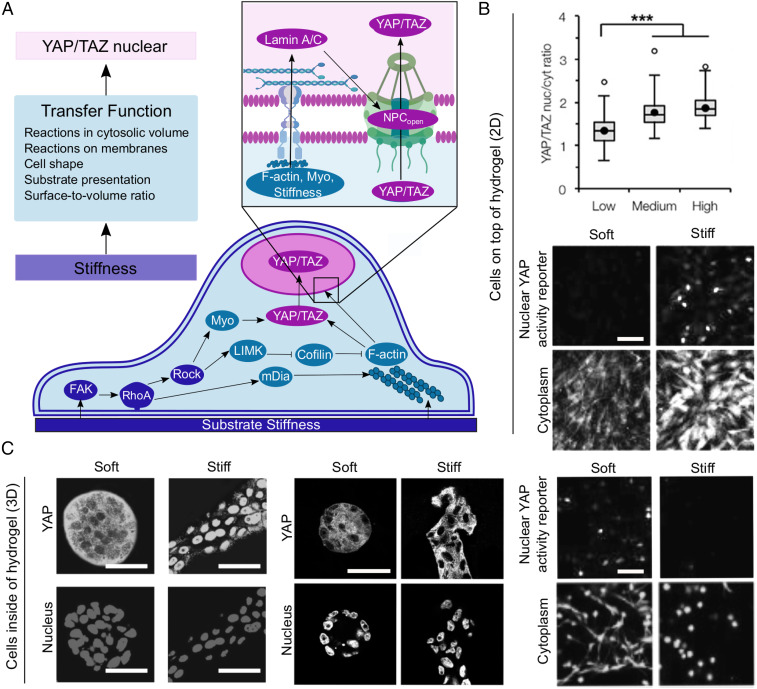
The interplay between cell shape, cell–substrate interaction, and nuclear translocation of transcription factors is critical for cellular homeostasis; misregulation of these relationships can often result in pathological states. An important example of this is the regulation of nuclear translocation of YES‐associated protein 1 (YAP1) and TAZ (YAP/TAZ), a cotranscriptional activator repressed in the Hippo tumor suppressor pathway, which regulates proliferation and cell differentiation to maintain organ size (1). While YAP/TAZ has been implicated as a key regulator of mechanotransduction by translating extracellular matrix (ECM) cues, specifically matrix stiffness, it remains unclear how other biophysical and biochemical features of the cell interact with substrate stiffness to initiate downstream signaling events all the way to nuclear translocation (2, 3) (Fig. 1A).

Fig. 1.

(A) A spatial model of the YAP/TAZ mechanochemical sensing network. Reactions that respond to substrate stiffness are carried out near the substrate-adjacent plasma membrane of the cell by integrins and propagated by FAK, RhoA, and ROCK (components in blue, module 1 of model). These signals are translated into cytoskeleton regulation by mDia, LIMK, cofilin, myosin, and F-actin (components in teal, module 2 of model). The cytoskeletal regulators then impinge on YAP/TAZ phosphorylation state, regulating the ability of YAP/TAZ to enter the nucleus (components in pink, module 3 of model). (Inset) The actin cytoskeleton also directly regulates YAP/TAZ nuclear import by transferring cytoskeletal stiffness to the nucleus by way of Lamin A/C, stretching NPCs (17). (B) Cells cultured in 2D conditions, on top of substrates, respond to increasing stiffness by increasing YAP localization to the nucleus. Adapted from ref. 8, with permission from Elsevier; and from ref. 57, which is licensed under CC by 4.0. ***P < 0.001. (C) Cells cultured in 3D conditions, inside of substrates, respond to increasing stiffness by increasing YAP nuclear localization (Left, mammary epithelial cells in Matrigel+collagen 1 gels), not changing YAP localization (Center, mammary epithelial cells in Matrigel+alginate gels), or decreasing nuclear YAP reporter (Right, mesenchymal stem cells in fibrin gels). Adapted from ref. 9, with permission from Elsevier; from ref. 57, which is licensed under CC by 4.0; and from ref. 46, which is licensed under CC by 4.0. (Scale bars, 100 μm.)

ECM stiffness is a key environmental input, instructing the cell about its pericellular space (4). However, the cell must interpret this input by regulating integrin clustering (5) and through cytoskeletal contractility, including both myosin and actin activities (6) through actin-binding proteins (7). Such interpretation likely involves sensing the dimensionality of stiffness cues through the spatial organization of the extracellular substrate as well as spatial restrictions on cell spreading imposed by the substrate format. Specifically, the presentation of two-dimensional (2D) versus three-dimensional (3D) ECM structure has revealed a critical need to unravel the information transfer function underlying the context-dependence of YAP/TAZ nuclear translocation (Fig. 1 B and C). In 2D cell culture, nuclear YAP/TAZ localization increases with increasing substrate stiffness (Fig. 1B) (3, 8). However, in 3D the trends of YAP/TAZ and stiffness are more complex (Fig. 1C). For example, while YAP/TAZ nuclear localization increased with increasing stiffness in 3D Matrigel/collagen matrices (9), no statistically significant relationship between YAP/TAZ nuclear translocation and stiffness was observed with physically cross-linked alginate hydrogels (10). Caliari et al. (8) observed that in 3D tunable hyaluronic acid gels that YAP/TAZ nuclear localization does not correlate with stiffness but does depend on the degradability of the scaffold in 3D.

While these results seem confounding, it is important to note that several features of the substrate and cells change in tandem with substrate dimensionality. Key factors that can be altered between 2D and 3D cell culture systems include cell shape, cell–substrate interaction, and nuclear shape. Specifically, cell volume and shape change as cells spread on 2D substrates (11), but 3D substrates are inherently confining and can restrict volume and shape changes due to fewer physical degrees of freedom (12). By the same token, cell–substrate contact area changes between 2D and 3D. When cells are cultured on 2D surfaces, cells display large focal adhesions (13, 14). Yet, cells grown in 3D soft matrix possess smaller, more nascent focal adhesions that diffuse not only in the basal side of the cell but across the apical surface of the cell (14). Additionally, nuclear shape and mechanical properties are also different between 2D and 3D. For example, in 2D, stress fibers link focal adhesions in the lamellipodia to linker of nucleoskeleton and cytoskeleton (LINC) complexes at the cell nucleus (15). LINC complexes are transmembrane protein complexes that bind Lamin A in the inner nuclear membrane side to stress fibers on the cytoplasmic side; interaction of stress fibers with LINC complexes forms a nuclear actin cap. In 3D, the number of stress fibers over the nucleus of the cell and the amount of Lamin A are both lower (16). It has been suggested that the interaction of stress fibers and the LINC complex may facilitate nuclear flattening, which stretches nuclear pores to increase YAP/TAZ nuclear localization (17). Thus, YAP/TAZ nuclear localization is linked to mechanical properties of the matrix through multiple layers of spatiotemporal integration of mechanochemical information (Fig. 1A). Therefore, how information transfer through multiple mechanical, spatial, and temporal scales ultimately orchestrates YAP/TAZ nuclear translocation remains poorly understood.

Given the complexity of the inputs in such a mechanotransduction system, computational modeling offers a systematic way to conduct multivariate experiments and generate experimentally testable predictions. Computational modeling of signal transduction has played a key role in identifying the emergent properties in signaling networks (18–20). Subsequently, spatial modeling of cell shape and signaling has revealed the importance of geometry, surface-volume effects, and the localization of kinases in modulating signal transduction (21–25). More recently, substantial advances in modeling the interaction between mechanical cues and biochemical signaling have resulted in shedding light on this intricate coupling, paving the way for modeling efforts that can integrate different inputs to the cell (26, 27).

Specifically, modeling YAP/TAZ translocation by Sun et al. (28) has revealed the dependence of YAP/TAZ response on stiffness as a function of multiple signaling pathways and the different molecule concentrations using a well-mixed model. Building on these technical and scientific advances, we sought to answer the following questions: How does cell shape and culture dimensionality affect the nuclear translocation of YAP/TAZ for different substrate stiffnesses? Does substrate contact area play a role in modulating these relationships? And finally, how does nuclear shape affect YAP/TAZ nuclear localization under these different conditions? To answer these questions, we used a systems biophysics approach to computationally model the different scenarios that may affect YAP/TAZ mechanotransduction. By doing so, we sought to build a transfer function: essentially, an input–output relationship, which can capture the impact of multiple cues on YAP/TAZ nuclear translocation.

Materials and Methods

Modular Construction of the Model.

We developed a 3D spatial model of YAP/TAZ nuclear localization as a function of substrate stiffness (Fig. 1A). The modules are divided as follows: 1) substrate stiffness sensing by a biochemical cascade, 2) biophysical regulation of the cytoskeleton in response to substrate stiffness, and 3) YAP/TAZ nuclear localization as a function of cytoskeletal and nuclear properties. Each module in detail is described below and the reactions and parameters are explained in detail in SI Appendix, Tables S1–S13.

Module 1: Substrate Stiffness Sensing.

In this module (Fig. 1A, blue components), we describe the events that connect the stiffness of the ECM to the upstream signaling events, including the activation of focal adhesion kinase (FAK), RhoA activation, and Rho kinase (ROCK) activation. All of these events are adapted from the well-mixed model in Sun et al. (28) and converted to a spatial model.

FAK activation.

Stiffness of the ECM activates clustering of integrins and associated proteins, which facilitates FAK phosphorylation (29). In this model, matrix stiffness is incorporated into the signaling pathway as a stimulus such that FAK is activated by the stiffness, E (SI Appendix, Table S1, rates 1 and 2), using kinetics similar to that of Michaelis–Menten kinetics (28, 30). The activation of FAK was implemented as a boundary condition at the plasma membrane in the spatial model using a position Boolean operator (SI Appendix, Fig. S1).

RhoA activation downstream of FAK.

RhoA is known to be activated downstream of FAK (31) and is also up-regulated with increasing rigidity of ECM in 3D environments (32). RhoA-GTP is modeled as a membrane species, while RhoA-GDP is modeled as a cytosolic species, consistent with experimental observation (33). The reaction flux of RhoA is modeled as a function of phospho-FAK, as shown in (SI Appendix, Table S1, rate 3) (28).

RhoA activates ROCK.

ROCK is a downstream target of RhoA (34) and increases myosin activity by phosphorylating myosin light chain and inhibiting myosin phosphatase (35) (SI Appendix, Table S1, rates 4 and 5). The activation of ROCK by RhoA-GTP is modeled as a boundary flux at the plasma membrane. Inactivation of ROCK is modeled as a first-order reaction in the cytoplasm.

Module 2: Cytoskeleton Regulation.

In this module (Fig. 1A, teal components), we modeled cytoskeletal reorganization, particularly F-actin dynamics through ROCK, mDia, and cofilin and stress fiber accumulation through the cumulative effects of myosin and F-actin. These events were modeled spatially building on the well-mixed model in Sun et al. (28) (Fig. 2).

Fig. 2.

Validation of the compartmental ODE model outcomes against published experiments. (A) The ratio of pFAK to total FAK as a function of stiffness was validated against data from Beamish et al. (51) for both normal human lung fibroblasts (NHLF) and renal proximal tubular epithelial cells (RPTECs) seeded on 2D PEG hydrogels of various stiffnesses and glass. (B) RhoA-GTP activation over stiffness model fit and comparison to experimental data from endothelial cells seeded on 2D polyacrylamide gels of various stiffnesses and glass (32). (C) Ratio of myosin activation over total myosin predicted by our model and a comparison with experimental data from endothelial cells seeded on 2D polyacrylamide gels of various stiffnesses and glass (32). (D) Validation of Lamin A activation as a function of tissue stiffness across various tissues including brain, kidney, and bone among others (43). (E) The ratio of nuclear YAP/TAZ to cytosolic YAP/TAZ as predicted by our model and a comparison with experimental data from multiple sources (17, 46–48) (six utilized 2D PA gels and eight utilized 2D hyaluronic acid gels) (6, 8, 17, 46–48). (F) Sensitivity analysis with respect to YAP/TAZ Nuc/Cyto ratio for 3.5 kPa. Additional sensitivity analyses for all of the variables to all of the parameters and all initial conditions can be found in SI Appendix, Supplemental Methods (SI Appendix, Figs. S4 and S5).

RhoA activates mDia.

In addition to the activation of ROCK, RhoA also activates mDia. mDia is a formin protein that nucleates actin filaments and accelerates the rate of actin elongation 5- to 15-fold (28, 36) (SI Appendix, Table S2, rates 7 and 8). Because RhoA-GTP is a membrane-bound protein and mDia is in the cytosol, the activation of mDia is modeled as a boundary flux. Inactivation of mDia is modeled as a first-order reaction in the cytosol.

ROCK activates myosin.

ROCK promotes myosin activity by phosphorylating myosin light-chain kinase, and inhibiting myosin phosphatase, which, in turn, regulates cellular contractility. To capture the nonlinear nature of these interactions, we model the activation of myosin using a hyperbolic tangent function similar to the one described in Sun et al. (28) (SI Appendix, Fig. S2 and Table S2, rate 9). Inactivation of myosin is modeled using first-order kinetics (SI Appendix, Table S2, rate 9).

ROCK activates LIM kinase.

ROCK is one of the key upstream regulators of LIM kinase (LIMK) and activation of ROCK further activates LIMK (28, 37). To capture the nonlinear interactions of ROCK and LIMK, we use a similar hyperbolic tangent function as described for myosin activation in our model (SI Appendix, Table S2, rate 10) and a first-order rate for LIMK inactivation (28, 38, 39).

Cofilin inhibits F-actin polymerization.

LIMK phosphorylates and inactivates cofilin, an F-actin severing protein (40). These relationships are incorporated into the model as shown in SI Appendix, Table S2, rate 11.

F-actin dynamics.

The polymerization of F-actin is modeled using two functions. The first function is an mDia-dependent polymerization of G-actin to F-actin and the second is a basal polymerization rate of F-actin. We assume that mDia must threshold to effectively polymerize F-actin and use a hyperbolic tangent function to model this thresholding (SI Appendix, Table S2, rate 12). Similar to the simplified polymerization model, we include a basal depolymerization rate of F-actin and a cofilin-mediated net depolymerization (28, 38, 39, 41).

Module 3: YAP/TAZ Nuclear Translocation.

Here (Fig. 1A, pink components), we designed a set of reactions to reflect the mechanochemical events that affect the nuclear translocation of YAP/TAZ. Nuclear translocation of YAP/TAZ depends on stress fibers, Lamin A activation in the nucleus, and nuclear shape and stiffness. Here we introduce two cytosolic species of YAP/TAZ: phosphorylated YAP/TAZ, called YAPTAZ_P, and dephosphorylated YAP/TAZ, called YAPTAZ, which can translocate to the nucleus. YAPTAZ_nuc represents the concentration of YAP/TAZ in the nucleus. We calculate the YAP/TAZ Nuc/Cyto ratio using the relative volumes of each compartment.

Stress fibers activate YAP/TAZ dephosphorylation.

YAP/TAZ dephosphorylation depends on stress fiber formation from F-actin and myosin (3, 42). In our model, the accumulation of stress fibers in the cell is incorporated as a product of F-actin and myosin (SI Appendix, Table S3, rate 13).

Lamin A activation due to stiffness.

Emerging evidence points to the importance of Lamin A in regulating YAP/TAZ nuclear localization (43, 44). Furthermore, Lamin A is sensitive to substrate stiffness. Lamin A molecules form a network of intermediate filaments in the inner nuclear lamina with complex dynamic and mechanosensitive regulation; Lamin A phosphorylation promotes meshwork disassembly and protein turnover. On stiff substrates, Lamin A is dephosphorylated and incorporated into the inner nuclear lamin, while on soft substrates Lamin A is significantly more phosphorylated (43). What is not yet clear is how Lamin A senses substrate stiffness. To simplify the interactions between Lamin A and substrate stiffness, we argue that substrate stiffness is read by the upstream events in modules 1 and 2 and alters cytosolic stiffness as a function of F-actin concentration. We propose a model in which the rate of Lamin A dephosphorylation is a function of cytosolic stiffness, where the cytosolic stiffness is a function of F-actin, which, in turn, is responsive to substrate stiffness. To develop this nested model, we first estimated the relationship between F-actin concentration and actin stiffness using data presented in Gardel et al. (45). Using these data, we propose that cytosolic stiffness increases as a function of F-actin using a power law with an exponent of 2.6 (see SI Appendix, Fig. S2 for fit) so that E_cytosol = p[F-actin]^2.6. Then, we propose Lamin A dephosphorylation as a function of cytosolic stiffness, similar to the mechanotransduction model for FAK (SI Appendix, Table S3, rate 14).

Stretching of nuclear pores.

The interaction between the cytoskeleton and nucleus through Lamin A and LINC complexes generates nuclear stress, which then induces stretching of nuclear pore complexes (NPCs), decreasing mechanical resistance and increasing YAP/TAZ nuclear import (17). We model the phenomenon of nuclear stress-induced stretching of NPCs using the relationship shown in SI Appendix, Table S3, rate 15 (16).

YAP/TAZ nuclear import and export.

In this step, YAP/TAZ nuclear import is controlled by basal level YAP/TAZ import and nuclear import due to stretching of NPC and the associated import and export proteins, including the state of Lamin A (6, 8, 17, 46–48). YAP/TAZ nuclear export is modeled using a simple first-order rate (SI Appendix, Table S3, rate 16) (6, 8, 17, 46–48). The transport of YAP/TAZ across the nuclear membrane is modeled as a boundary condition for both YAPTAZ_nuc flux into the nucleus and YAPTAZ transport in the cytoplasm (SI Appendix, Table S3, rate 16).

Validation with Published Experimental Results.

We validated the simulation output from the compartmental model against experiments in the published literature (Fig. 2). We focused on the relationship between stiffness of the substrate and the activation of key species including FAK, RhoA, myosin, Lamin A, and YAP/TAZ Nuc/Cyto ratio. The activation of FAK in response to stiffness, denoted by pFAK, was in good alignment between model and experiment (root mean square error [RMSE] = 0.03; R² = 0.88) (Fig. 2A). Good agreement was also observed between RhoA-GTP membrane species and experimental results from Lampi et al. (32) (RMSE = 2.4 × 10⁻¹⁷; R² = 0.68) (Fig. 2B). Our model also showed a good agreement between experiments and simulations for Lamin A activation as a function of substrate stiffness (Fig. 2D). Thus, our proposed multiscale model of substrate stiffness impacting cytosolic stiffness, which in turn alters Lamin A activation, was able to capture the experimentally observed relationship between substrate stiffness and Lamin A (RMSE = 0.34; R² = 0.66). On the other hand, there was good agreement with the model for myosin activation for low stiffness, but poor agreement for myosin activation at high stiffness, such as glass (RMSE = 0.047, R² = −0.65; the negative R² value indicates that mean value would have been a good fit) (Fig. 2C). This is probably because of missing biochemical interactions in the model. However, we prioritized the prediction of the myosin activation for low stiffnesses due to the importance of YAP/TAZ nuclear localization at physiologic stiffnesses. We also conducted parametric sensitivity analysis for three different values of stiffnesses, 0.1 kPa, 3.5 kPa, and 5.7 kPa (Fig. 2 E and F).

Translation from Well-Mixed to Spatial Models.

We next developed a spatial model of YAP/TAZ nuclear translocation. All simulations were conducted in 3D (Figs. 3–7) using the Virtual Cell modeling suite (49, 50) and results from the simulations are shown as a 2D cross-section for ease of interpretation. Even though the model parameters were constrained using the compartmental model, we note that the spatial averages of the different species at steady state conform to the same trend as shown in Fig. 2. Additional model details can be found in SI Appendix, Supplemental Methods.

Fig. 3.

Effect of substrate dimensionality and substrate stiffness on YAP/TAZ nuclear translocation. (A) Schematic showing the model setup for substrate dimensionality presentation. (B) Steady-state profiles at 4,000 s for (B) pFAK, (C) RhoA-GTP, (D) MyoA, (E) Lamin A, and (F) YAP/TAZ nuclear activation. In each row, (i) shows the effect of stiffness when the stimulus is presented in 2D, (ii) shows the effect of stiffness when the stimulus is presented in 3D, and (iii) shows a direct comparison between the 2D and 3D stimulus of the same values in a bar graph. All values are spatial averages at 4,000 s; RhoA-GTP and Lamin A are in number per square micrometer. For YAP/TAZ the nuclear to cytosolic ratio is shown in F, iii.

Fig. 7.

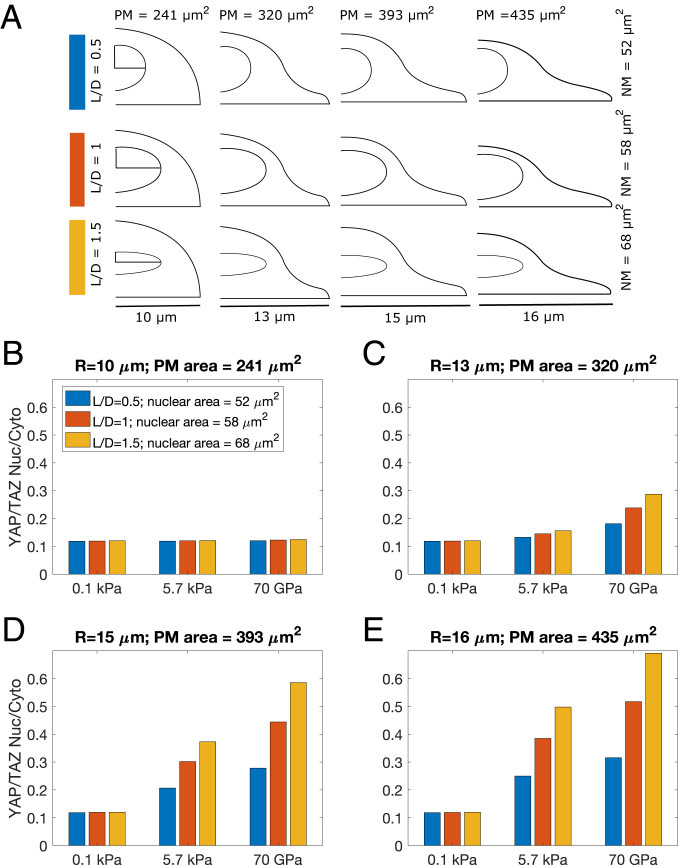
YAP/TAZ Nuc/Cyto is influenced by nuclear shape. YAP/TAZ Nuc/Cyto ratio for four different cell sizes and three different nuclear shapes. (A) The nuclear shapes were varied by changing the L/D ratio, while conserving the nuclear volume. (B) R = 10 μm, plasma membrane area = 241μm²; (C) R = 13 μm, plasma membrane area = 320 μm²; (D) R = 15 μm, plasma membrane area = 393 μm²; and (E) R = 16 μm, plasma membrane area = 435 μm². Blue bars L/D = 0.5, nuclear membrane area = 52 μm²; red bars L/D = 1, nuclear membrane area = 58 μm²; yellow bars L/D = 1.5, nuclear membrane area = 68 μm².

Results

Using the model developed above, we investigated how the shape of the cell and nucleus, as well as the localization of the stiffness signal could affect YAP/TAZ nuclear localization. To analyze these coupled effects, we have organized our simulations as follows. First, we investigated the effect of substrate dimensionality and substrate stiffness on YAP/TAZ nuclear localization (Figs. 3 and 4). Next, we investigate the effect of cell shape changes that maintain constant substrate activation area across different substrate dimensionalities and their impact on perceived stiffness in terms of YAP/TAZ Nuc/Cyto ratio (Figs. 5 and 6). Finally, we change the shape of the nucleus (Fig. 7).

Fig. 4.

YAP/TAZ nuclear localization depends on cell shape, substrate stiffness, and substrate dimensionality. (A) YAP/TAZ nuclear localization at 4,000 s for three different geometries representing increasing cell elongation and three different substrate stiffnesses: (i) R = 10 μm, plasma membrane area = 241 μm², (ii) R = 13 μm, plasma membrane area = 320 μm², and (iii) R = 15 μm, plasma membrane = 393 μm². (B) YAP/TAZ Nuc/Cyto ratio for the three different cell sizes for three different stiffness values (physiologic stiffness ∼0.1 kPa in blue, tumor stiffness ∼5.7 kPa in red, and glass ∼70 GPa in yellow).

Fig. 5.

Differences in substrate presentation and membrane reaction area alter responses to 2D and 3D stimulus. (A) The 2.xD substrate presentation where the substrate is present only on the bottom surface but the entire plasma membrane is available for membrane reactions. (B) The 3D substrate presentation where the substrate activation and the membrane reactions occur on the entire plasma membrane. (C) The 2D substrate presentation with the same area used for substrate presentation and for membrane reactions. (D) Increasing substrate activation area while keeping cytosolic volume constant forces cell shape changes dependent on stimulus presentation geometry. (E) pFAK, (F) RhoA-GTP, (G) F-actin, (H) E_cyto, and (I) Lamin A as a function of substrate presentation, substrate stiffness, and activation area.

Fig. 6.

Increasing substrate activation area changes YAP/TAZ Nuc/Cyto ratio as a function of substrate dimensionality. Nuclear YAP/TAZ for different activation areas for (A) 3D stimulus, (B) 2D stimulus, and (C) 2.xD dimensions. The black, pink, and green surface areas refer to the total plasma membrane surface area, the surface area activated by the substrate stiffness, and the surface area available for membrane reactions, respectively, as detailed in Fig. 5D. (D) YAP/TAZ Nuc/Cyto ratio for different activation areas and different stimuli.

YAP/TAZ Nuclear Localization Depends on Substrate Stiffness and Substrate Dimensionality.

Experimental evidence in the literature demonstrates that FAK phosphorylation, RhoA, MyoA, and Lamin A are all functions of substrate stiffness (32, 43, 51). Having demonstrated that the well-mixed model does indeed capture these experimental trends (Fig. 2), we next asked how this complex relationship is affected by cell shape and substrate dimensionality. We conducted simulations in three different geometries representing different spread states, 30-mm diameter cell with a thin lamellipodia, 20 mm with no thin lamellipodium, and an intermediary cell shape with 26-mm diameter (8, 52), and three different stiffness values representing normal tissue ∼0.1 kPa, tumorigenic stiffness at 5.7 kPa (53), and glass 70 GPa (54) (Fig. 3). The boundary conditions for the 2D versus 3D substrate presentation are shown in (Fig. 3A). For a given shape, we found that substrate stiffness does indeed increase the amount of pFAK in a cell and that this effect is somewhat increased in 3D compared to 2D (Fig. 3B). When the diffusivity of pFAK was reduced to mimic juxtamembrane localization, these trends remained the same with slightly larger differences between 2D and 3D pFAK levels (SI Appendix, Fig. S7 A and B). Downstream of FAK, RhoA-GTP (Fig. 3C) and MyoA (Fig. 3D) both show strong stiffness dependence, indicating that the effect of stiffness is propagated to the downstream membrane and cytosolic components in module 1. We also note that RhoA-GTP, which is membrane-bound, demonstrates a strong cell shape-dependent gradient along the membrane (SI Appendix, Fig. S8), consistent with our previous observations (21). Thus, stiffness dominates the response in module 1.

Downstream of FAK and RhoA-GTP, we looked at the different components in modules 1 and 2 (SI Appendix, Fig. S9) and noted that all components showed a stiffness and dimensionality proportional response (SI Appendix, Fig. S9 A–E). Interestingly, the cytosolic stiffness shows a dramatic change in response to increasing substrate stiffness for a given substrate dimensionality (SI Appendix, Fig. S9F). The power law dependence of cytosolic stiffness on actin concentration means that small changes in F-actin are magnified dramatically in the cytosolic stiffness. This is evident in Lamin A activation (module 3) (Fig. 3E). We observed that Lamin A activation integrates volumetric biochemical and mechanical signals onto the nuclear membrane surface and shows dependence on both substrate stiffness and substrate dimensionality. For a given substrate stiffness, Lamin A activation is slightly higher in 3D than in 2D. However, for a given substrate dimensionality, Lamin A activation increases with stiffness (Fig. 3E). Finally, the small changes in modules 1 and 2 integrate into larger changes in module 3 to result in both stiffness and dimensionality dependent YAP/TAZ nuclear activation (plotted as YAP/TAZ nuclear concentration in Fig. 3 F, i and ii, as YAP/TAZ nuclear-to-cytosolic ratio in Fig. 3 F, iii, and in SI Appendix, Fig. S7C). Interestingly, at the lower end of the substrate-stiffness spectrum modeled here, YAP/TAZ is more sensitive to stiffness changes than dimensionality changes (compare 0.1 kPa to 5.7 kPa in Fig. 3 B, iii). However, at the higher end of the substrate stiffness spectrum, YAP/TAZ is more sensitive to dimensionality changes than stiffness changes (compare 5.7 kPa to 70 GPa in Fig. 3 B, iii). In summary, each upstream component in the pathway responds strongly to stiffness changes, with little difference between the 2D versus 3D response. Dimensionality changes are sensed downstream, when YAP/TAZ integrates signals directly from the cytoskeleton and indirectly from the effect of cytosolic stiffness on the nucleus.

YAP/TAZ Nuclear Localization Integrates Cell Shape and Substrate Presentation Information.

Depending on the culture dimensions, cell shape can vary widely from elongated shapes in 2D culture to rounded shapes in 3D culture (55, 56). Given the mixed conclusions in the literature on the role of culture dimensions on YAP/TAZ nuclear localization (Fig. 1C), we next asked if we could use the 3D spatial model to dissect the effects of cell shape, substrate stiffness, and substrate dimensionality on YAP/TAZ nuclear localization. We systematically varied cell shape while conserving cell volume and nuclear dimensions and used 2D or 3D substrate stimulus for the same three stiffnesses as before (Fig. 4). We note that increasing cell elongation is the equivalent to increasing the surface area of the plasma membrane for activation by substrate stiffness and reaction of plasma membrane-associated components (i.e., an increase in the surface area-to-volume ratio of the cell). For a given cell shape, all components in the signaling networks in modules 1 and 2 showed the same stiffness-dependent response as expected (SI Appendix, Fig. S10), and in all cases the 3D responses were slightly larger than the 2D stimulus response. Low substrate stiffness values (0.1 kPa) did not elicit any noticeable shape-dependent effects, while the intermediate (5.7 kPa) and high (70 GPa) stiffnesses showed dependence on cell shape. Spread cells, with a larger radius, had a larger response for various signaling components for a given value of stiffness (SI Appendix, Fig. S10 A–G, with the exception of SI Appendix, Fig. S10B, Rho-GTP) and this effect was magnified in the readout of cytosolic stiffness (SI Appendix, Fig. S10H) and Lamin A activation (SI Appendix, Fig. S10I). As a result of these upstream effects, we found that for a given cell shape, increasing stiffness increased the YAP/TAZ Nuc/Cyto ratio and this response was always amplified in 3D versus 2D by module 3 of the pathway (Fig. 4), consistent with what we observed in Fig. 3. We also found that increased cell elongation, with an effectively larger plasma membrane surface area that could result from cell spreading or other effects of 2D culture, resulted in higher YAP/TAZ Nuc/Cyto ratio when compared to rounded cells. Thus, for a given stiffness stimulus, increased cell elongation leads to increased YAP/TAZ Nuc/Cyto ratio and this effect is more pronounced in 3D substrate presentation rather than 2D substrate presentation. Thus, cell elongation amplifies stiffness sensing and dimensionality sensing by the YAP/TAZ pathway.

Thus far, simulations from the model show that maintaining the same cell shape but changing the activation area so that stiffness is applied on the entire cell boundary (simulating 3D culture) increases YAP/TAZ nuclear localization relative to stimulus on the basal side only (simulating 2D culture) (Figs. 3F and 4). This result is not very surprising, since the total surface activation area, and thus the total signal, increases from 2D to 3D conditions. However, experimental data show that lower YAP/TAZ nuclear localization can sometimes occur in 3D compared to 2D culture in response to stiffness increases (46, 57). This reveals that a simple change in substrate dimensionality alone is insufficient to explain YAP/TAZ signaling differences observed experimentally. We note that there are major differences between 2D and 3D substrate presentation for a given cell shape. Currently, the literature in the field suggests that in 2D culture, adhesion signaling originates from the basal side of the cell, whereas in 3D culture, adhesion signaling is localized across the entire cell surface (14, 58–60). Our model captures this effect since the activation area for FAK, which is an immediate downstream readout of substrate stiffness, is different in each case because the surface area of the membrane that is exposed to the substrate in these two different culture conditions is different (Fig. 3A). However, the surface area available for the membrane-associated reactions downstream of FAK activation is the same in 2D and 3D and is the total surface area of the plasma membrane. For example, RhoA-GTP, which is membrane-bound, shows a different response from other components in the case of increasing cell elongation due to the differences in membrane activation downstream of FAK (SI Appendix, Fig. S10B). These results suggest that the differences in surface presentation of the stimulus to upstream components versus surface area available for all the downstream membrane reactions can lead to confounding results for nuclear localization of YAP/TAZ.

Differences in Surface-To-Volume Ratio for Substrate Activation vs. Surface-To-Volume Ratio for Plasma Membrane Reactions Dictate the Trends of YAP/TAZ Nuclear Translocation.

To investigate the role played by substrate activation area versus the total plasma membrane area in signal integration and amplification, we conducted the following simulations. We classified our geometries into three categories: 1) “2.xD” stimulus is defined by substrate activation of FAK on the basal side of the cell with membrane reactions occurring across the entire plasma membrane area (Fig. 5A; see SI Appendix, Supplemental Methods for details of boundary condition implementation); 2) “3D” stimulus is defined by substrate activation of FAK on the entire plasma membrane area as well as membrane reactions occurring across the entire plasma membrane surface area (Fig. 5B); and 3) “2D” stimulus is defined by substrate activation of FAK and all membrane reactions restricted to the basal side of the cell (Fig. 5C). All geometries had the same cytosolic volume and nuclear dimensions, as a result of which we could draw direct comparisons between the different stimuli presentation and interpretation effects. We conducted these simulations for five different values of substrate activation areas (Fig. 5D). Holding cytosolic volume constant while increasing substrate activation area and varying stimulus presentation geometry resulted in cell shape changes, as shown in Fig. 5D.

We found that for a given substrate activation area, pFAK was constant for the three different substrate and membrane area combinations and only depended on substrate stiffness (Fig. 5E). pFAK increased with substrate stiffness, consistent with our previous observations, and also increased with substrate area. Thus, the first interpretation of substrate stiffness by the cell appears to be independent of substrate dimensionality. Looking at RhoA-GTP, which uses both the pFAK signal and the membrane surface area, we found that the surface density of RhoA-GTP was higher in 3D than in 2D, where the membrane area and substrate activation area were held constant with our previous results (Fig. 5F). However, the 2D case where the substrate activation area was in the bottom only, but the entire plasma membrane area was available for membrane reactions and showed Rho-GTP density that was in between the 2D response and the 3D response (Fig. 5F, blue bars). We note that this response was between 2D and 3D, which supports our naming of this situation as 2.xD.

Downstream of RhoA-GTP, we found that the 2.xD case had higher F-actin than 3D or 2D stimulus (Fig. 5G). This can be understood by thinking about the two surface-to-volume ratios at play here. For FAK, the surface-to-volume ratio is the surface area of the membrane that senses the substrate stiffness to the cytosolic volume (which is the same across all conditions). For RhoA, the surface area is the total plasma membrane surface area in 2.xD, which is higher than the substrate presentation area. Therefore, in 2.xD, components in module 1 respond to a surface-to-volume ratio of 2D substrate presentation, while components in modules 2 and 3 respond to a surface-to-volume ratio of 3D substrate presentation (where the substrate sensing area is the same as the total plasma membrane area). This change in the trend of substrate dimensionality response of F-actin is further amplified in the cytosolic stiffness because of their power law dependence (Fig. 5H). As a result, Lamin A activation on the nuclear membrane is larger for 2.xD than for 3D or 2D (Fig. 5I).

All of these relationships hold true for a given substrate activation area. However, the differences between 2D, 2.xD, and 3D are much larger for smaller activation areas when compared to larger activation areas. For larger activation areas, the differences in the response of various signaling components are smaller for different substrate dimensionalities. This is because as the substrate activation area increases and the cytosolic volume is held constant, all substrate presentation geometries elicit a more elongated cell shape, where high surface area-to-volume effects dominate (Fig. 5D and SI Appendix, Fig. S7 D–F). In such shapes, the cytoskeleton module is impacted by the closer proximity of membrane reaction.

Finally, we looked at the effects of the differences in surface activation area and membrane reaction area on YAP/TAZ Nuc/Cyto ratio (Fig. 6). We found that at low stiffness values in 2.xD, 2D, and 3D, increasing surface activation area did not elicit any differences in YAP/TAZ nuclear localization (Fig. 6 A–C). At higher stiffness values, YAP/TAZ responded strongly to increasing surface activation area, with the strongest response occurring in 2.xD. As the activation area increased, the 2.xD conditions consistently had higher YAP/TAZ nuclear to cytosolic values for higher stiffness values than 3D or 2D (Fig. 6 C and D). These results suggest that each module in this mechanochemical network integrates not only the biophysical cues of substrate stiffness but also the geometric information of the cell, particularly the plasma membrane surface area and cytosolic volume to modulate the YAP/TAZ Nuc/Cyto ratio.

Nuclear Shape Influences YAP/TAZ Nuclear Localization.

Finally, we explored if alterations to nuclear shape would alter YAP/TAZ Nuc/Cyto ratio. In all of our previous simulations, we maintained the nuclear shape (both nuclear membrane area and nuclear volume) to be the same for all simulations. However, it has been reported that nuclear shape can change with cell shape (61, 62). Furthermore, nuclear flattening may drive stretching of the nuclear pore, which can stimulate an increase in YAP/TAZ nuclear import (17). It is thought that nuclear flattening as a result of the stress fibers interaction with LINC complexes has been shown to increase YAP/TAZ Nuc/Cyto in 2D, whereas 3D interaction between stress fibers and the nucleus is reduced (16). Therefore, we investigated how nuclear shape alone can alter the YAP/TAZ Nuc/Cyto ratio when a 2.xD stimulus is presented. To test the role of nuclear shape and its interaction with cell shape on YAP/TAZ Nuc/Cyto ratio, we set up the following simulations in 2.xD: we used four different cell shapes, ranging from rounded to elongated (R = 10 μm to R = 16 μm), and for each cell shape, varied the nuclear shape by changing the length to diameter ratio (L/D ratio) such that the nuclear volume was conserved but the nuclear membrane surface area was changed (Fig. 7A). Again, we observed an interesting dependence of cell shape and nuclear shape on YAP/TAZ Nuc/Cyto ratio (Fig. 7 B–E). First, for the small, rounded cell, there was no strong dependence of YAP/TAZ Nuc/Cyto ratio on nuclear shape or substrate stiffness (Fig. 7B). Second, for low stiffness, there was no cell or nuclear shape-dependent response (Fig. 7 B–E) (0.1 kPa). For tumor stiffness values, as the cell shape changes from rounded to elongated (through increasing values of R), we found that cells with elongated nuclei (i.e., larger nuclear membrane area) showed larger YAP/TAZ Nuc/Cyto ratio. For example, in the cell with R = 16 μm, at 5.7 kPa, there is approximately a twofold increase in YAP/TAZ Nuc/Cyto ratio when L/D changes from 0.5 to 1.5 (corresponding to an increase in the nuclear surface area). At the stiffness values of 70 GPa, this fold-change is greater than 2. Thus, our model predicts that in addition to the substrate activation area and the plasma membrane surface area, the nuclear membrane area also plays an important role in multiplexing the transfer of information from the substrate to the nucleus. Therefore, interpretation of substrate stiffness is fundamentally dependent on cell shape at both the cytosolic and the nuclear level.

Discussion

In this study, we have constructed a 3D spatial model of YAP/TAZ nuclear translocation in response to substrate stiffness to identify the transfer functions that govern this fundamental mechanotransduction pathway. Using a systematic approach to vary substrate stiffness and geometry, we found that upstream components in this transfer function respond to stiffness changes while dimensionality changes are sensed downstream, when YAP/TAZ integrates signals directly from the cytoskeleton and indirectly from the effect of cytosolic stiffness on the nucleus (Fig. 8). This highlights a need to investigate how other mechanotransduction circuits, like MRTF-SRF, which directly regulate cytoskeleton components, impinge on YAP/TAZ dimensionality sensing. Indeed, experimental evidence is emerging that demonstrates the codependence of MRTF-SRF and YAP/TAZ pathways (63).

Fig. 8.

YAP/TAZ nuclear localization outcomes rely on multiplexed signals integrated through the cellular transfer function.

We also systematically varied cell shape and nuclear shape in our model, since shape is an important cellular property associated with YAP/TAZ signaling (64), but often changes concomitantly with culture dimensionality and ECM stiffness, making these features difficult to decouple experimentally. This investigation revealed that how a cell senses stiffness is very tightly regulated by cell shape through different surface-to-volume relationships. Interestingly, we found that low stiffness, corresponding to physiological tissue stiffness, was fundamentally a robust state for YAP/TAZ nuclear translocation and changes in cell shape, substrate dimensionality, and nuclear shape did not affect this outcome. Separately, we note that rounded cells were fairly robust to changes in stiffness and substrate dimensionality. Thus, high substrate stiffness alone is not enough to generate a response in YAP/TAZ nuclear translocation, nor is 3D substrate dimensionality. Rather, cell shape and nuclear shape are major determinants of the YAP/TAZ response to substrate stiffness and dimensionality. Thus, experimental evidence that conflicts on the role of substrate stiffness and dimensionality (Fig. 1 B and C) would be better compared by considering cell and nuclear shape along with the plasma membrane area in contact with the substrate. For example, in 3D systems where nuclear YAP increases with stiffness (Fig. 1 C, Left), our model predicts that cells maintain the same shape and activation areas (Fig. 6A, compare cells from bottom to top of rightmost columns) or cells elongate and increase their activation area (Fig. 6A, compare cells on the diagonal across columns from bottom left to top right). However, for nuclear YAP to decrease with increasing substrate stiffness, cell shape must also become more rounded, decreasing the activation area (Fig. 6A, compare cells on the diagonal across columns from middle row, right column to top row, left column). This is consistent with the experimental data shown in Fig. 1 C, Right: when nuclear YAP activity decreases with stiffness (Fig. 1 C, Upper), cell shape also becomes more rounded (Fig. 1 C, Lower).

Our model also predicts that nuclear YAP will not change significantly under certain shape and activation area constraints with increasing stiffness, which has also been demonstrated experimentally (Fig. 1 C, Center). This is predicted to happen when cell shape remains very rounded, despite increasing stiffness (Fig. 6A, compare cells in the leftmost column from bottom to top) or when cells elongate slightly more in softer conditions than in stiffer conditions (Fig. 6A, compare cell at bottom right to cell at top left, or cell at 5.7kPa and 490 μm² to cell at 7GPa and 415 μm², or compare by identifying cells with similar nuclear color but located in different rows). Our model also allows us to compare culture dimensionalities, and predicts that cells in 3D will have less nuclear YAP at a given stiffness than cells in 2.xD when the substrate activation area is small, requiring cells in 3D to be more rounded than the cells in 2.xD. (Fig. 6 A and C, leftmost columns). Interestingly, our model also shows that membrane reactions must be allowed occur on the entire surface of the cell (2.xD), regardless of where stiffness is applied, to achieve higher nuclear YAP for 3D compared to 2D activation at equivalent stiffness (Fig. 6, compare A to B and A to C). Indeed, Rho biosensor experiments show that localization and activity is not biased to the basal surface of cells on 2D substrates (65–68), suggesting that our 2.xD model geometry is a more relevant representation of 2D culture.

Importantly, these findings also highlight that the multiple mechanisms regulating cell and nuclear shape, such as outside-in changes imposed by the ECM or inside-out changes directed by gene expression, will determine how stiffness and dimensionality are sensed by the cell, making the landscape of YAP/TAZ nuclear translocation quite complex. For example, nuclear shape is dysregulated in cancer (69, 70) and laminopathies (71). In cells with lamin mutations derived from laminopathies, YAP/TAZ actually tends to be constitutively nuclear. Experimentally, YAP/TAZ nuclear import increases with either nuclear pressure or substrate stiffness, where nuclear pore diameter increases with increasing substrate stiffness (9). Thus, one possibility is that constitutive YAP/TAZ nuclear import occurs through dysregulation of nuclear shape and nuclear pores that can occur in laminopathies (17, 72). Given the multitude of ways in which cell shape is regulated, additional variables may need to be considered in a comprehensive model in order to fully explain differences in YAP/TAZ nuclear localization due to dimensionality and stiffness.

In addition to cell shape, nuclear shape, and substrate activation area, our model suggests that the cell’s surface area that is available for membrane reactions is another dominant factor in YAP/TAZ mechanotransduction. Experimentally, it has been observed that increasing cell surface area corresponds to increasing YAP/TAZ Nuc/Cyto (73, 74). While membrane mechanotransduction is typically attributed to proteins, like integrins and ion channels in the plasma membrane and lamins associated with the nuclear membrane, cell surface area regulation depends on phospholipid and glycocalyx polymer trafficking (75). Most cells use membrane trafficking to continually rework their plasma membrane through ruffles, folds, endo- and exocytosis, and it has been suggested that cells sense and regulate their volume and surface area through plasma membrane tension (76). Recent evidence suggests that plasma membrane domains, such as clathrin-coated pits and caveolae, as well as lipid metabolism, are regulated by and provide feedback to YAP/TAZ (77, 78). Thus, additional insight will be gained by experiments and models that explore the role of membrane trafficking, membrane surface roughness, and membrane lipid metabolism on regulating YAP/TAZ mechanotransduction.

We note that our model, even though validated against data from the literature, is limited to certain components of the signaling pathway and that integration of other biochemical pathways will be important to build on this present work (79–83). For example, the model doesn’t capture the myosin fit as well as it captures other components. Even though myosin is critical for representing the upstream biochemical events in the model, the power law relationship of cytosolic stiffness in response to F-actin dominates the YAP/TAZ Nuc/Cyto ratio. Future work will involve a multiscale coupling of actomyosin contractility to capture the complex interactions between these components. Additionally, here we have only discussed the interaction between the ECM and single cells, yet cell–cell interactions are very important in vivo and may be responsible for some of the changes observed between 2D and 3D systems in vitro (84, 85). Cell–cell and cell–matrix adhesions can have synergistic and antagonistic effects (4), and regulation of YAP/TAZ by cell–cell communication through LATs and Merlin are additional key features to explore in future work. Incorporating cell type-specific protein expression levels and physiologically relevant activation areas, such as number, size, and localization of focal adhesions (86–91), will also offer further insight. Likewise, the timescale of YAP/TAZ nuclear localization could be important (92). Our model is also simplified in terms of the features we have compared across 2D and 3D culture geometries and the stiffness cells sense may not be equivalent to the stiffness that is measured (14, 93–95). To make direct comparisons, it was also necessary for us to hold cell shape constant across 2D and 3D systems. We anticipate that incorporating more realistic cell and matrix representations and time-dynamic behaviors will be important future directions for modeling.

Data Availability

All study data are included in the article and SI Appendix.