Atomic-scale insights into quantum-order parameters in bismuth-doped iron garnet

Significance

Substituted iron garnets, with a complex and diverse range of substitutional lattice sites, are widely used in magneto-optical devices. Atomic-scale investigations of local variations due to such substituents can give insights into the specific effects of elemental substitution, thereby helping to improve the functionality of magneto-optical materials. Here, via advanced electron microscopy techniques and theoretical calculations, we reveal how variations in the microstructure of Bi-substituted lutetium iron garnet are coupled to modulations in the lattice, electron, and spin structure. Our comprehensive approach provides a template for further improvement of materials through compositional design and shows how cooperative measurement of correlation characteristics between multiple quantum order parameters at the atomic scale can be beneficial for a wide range of functional materials.

Abstract

Bismuth and rare earth elements have been identified as effective substituent elements in the iron garnet structure, allowing an enhancement in magneto-optical response by several orders of magnitude in the visible and near-infrared region. Various mechanisms have been proposed to account for such enhancement, but testing of these ideas is hampered by a lack of suitable experimental data, where information is required not only regarding the lattice sites where substituent atoms are located but also how these atoms affect various order parameters. Here, we show for a Bi-substituted lutetium iron garnet how a suite of advanced electron microscopy techniques, combined with theoretical calculations, can be used to determine the interactions between a range of quantum-order parameters, including lattice, charge, spin, orbital, and crystal field splitting energy. In particular, we determine how the Bi distribution results in lattice distortions that are coupled with changes in electronic structure at certain lattice sites. These results reveal that these lattice distortions result in a decrease in the crystal-field splitting energies at Fe sites and in a lifted orbital degeneracy at octahedral sites, while the antiferromagnetic spin order remains preserved, thereby contributing to enhanced magneto-optical response in bismuth-substituted iron garnet. The combination of subangstrom imaging techniques and atomic-scale spectroscopy opens up possibilities for revealing insights into hidden coupling effects between multiple quantum-order parameters, thereby further guiding research and development for a wide range of complex functional materials.

The element bismuth has been chosen as a substituent, or major element, in a diverse range of functional materials, including multiferroics, superconductors, and catalysts (1–3). On account of the often significantly improved performance and various unique phenomena when bismuth is introduced in functional materials, investigations on the local order parameters underpinning such effects have attracted considerable attention. In the past few years, it has been verified that bismuth doping is also an effective method to enhance the performance of magneto-optical devices (4, 5). Among the iron oxides, ferrimagnetic insulators with the complex iron garnet structure R₃Fe₅O₁₂ (where R is an element with large radius) are already widely utilized in magneto-optic devices owing to their combination of small spin-wave damping, good optical transparency, and a pronounced Faraday effect (6–12). The strength of the Faraday effect, which describes a rotation of the plane of polarization of electromagnetic radiation in a magnetic field, is linearly proportional to the Verdet constant (13, 14) for a given material, which for magneto-optical materials such as substituted garnets depends strongly on the coupling effect of multiple quantum-order parameters (15, 16), including those of lattice, spin, and electronic orbitals (12, 17, 18). In particular, diverse polyhedral sites in the garnet structure are bridged via oxygen atoms with a strong exchange interaction effect, resulting in complex electronic and crystal structures (19–22). Although pure yttrium iron garnet (YIG) has several advantages in terms of magneto-optical response, it has not been widely applied in integrated devices due to its low Verdet constant, resulting in a limited Faraday rotation (23, 24). Due, however, to its chemical flexibility, selective substitution has been established as an effective method to tune various physical properties of iron garnets (7, 12, 25, 26), and it is noteworthy that Bi-substituted lutetium iron garnet films prepared via liquid phase epitaxy (LPE) demonstrate an appreciable enhancement in magneto-optical performance (8). Several models based on diamagnetic transitions have been proposed to explain the effect of Bi substitution on magneto-optical response (4, 12, 17, 19, 21, 27–30), in each case with a strong dependence on the crystal energy levels of the Fe³⁺ ions in differently coordinated lattice sites. There is still, however, a lack of experimental evidence to test these models, as this requires the distribution of substituent atoms to be characterized and related to their effect on the crystal lattice and electronic structure at different lattice sites. In this work, we address this limitation by the use of several advanced electron microscopy techniques (31–40) applied synergistically to a Bi-substituted lutetium iron garnet.

Results

Single-crystal (Bi_0.9Lu_2.1)Fe₃O₁₂ (BLIG) films were prepared by LPE. The films showed high crystallinity and a sharp interface with the substrate (SI Appendix, Figs. S1 and S2) with an obvious garnet structure, as verified by electron diffraction analysis along different zone axes (SI Appendix, Fig. S2). High-angle annular dark field (HAADF) imaging of the atomic structure along the [001] zone axis (Fig. 1A) shows a lattice structure consistent with the atomic model of iron garnet in Fig. 1B. Lattice constants a and b are defined as shown in the atomic model of Fig. 1B. HAADF image of the atomic structure was acquired in a region of thickness 19.85 ± 0.16 nm (SI Appendix, Fig. S3A) along the [001] zone axis (Fig. 1A). A two-dimensional (2D) Gaussian fitting of the positions and intensities of the central bright spots in the HAADF image, marked by red circles in Fig. 1A, reveals a variation in normalized intensity (Fig. 1C) of these spots, which in this projection correspond to an overlap of dodecahedral and tetrahedral lattice sites (see inset of Fig. 1B). As the intensity in HAADF images scales with atomic number, Z, (approximately proportional to Z²) (41), these differences in intensity suggest a nonsystematic variation in the substituted Bi atoms (Z = 83; cf. Z = 71 for Lu) in each atom column, presumably located at dodecahedral lattice sites. Energy-dispersion X-ray spectroscopy (EDS) maps showing the elemental distribution of Bi, Lu, and Fe (Fig. 1D) indeed confirm that Bi atoms are located at positions where dodecahedral and tetrahedral sites overlap in this projection. Further detailed examination shows that regions with higher intensities in Fig. 1B exhibit a higher bismuth content (as determined from the EDS data), while regions showing lower intensity in Fig. 1B tend to exhibit lower bismuth content by comparison (SI Appendix, Fig. S3). The values of the lattice constants over the same region also show an obvious spatial variation, where the local lattice constants are expanded in some regions, while they tend to be smaller in surrounding regions, thereby stabilizing the overall lattice structure.

Fig. 1.

Atomic structure analysis using STEM-HAADF images. (A) STEM-HAADF image projected along the [001] direction of the BLIG film. (B) An enlarged HAADF image extracted from panel A shows the atomic structure. Distances a and b_, along [100] and [010], respectively, are defined as lattice constants of the unit cell of garnet structure. The standard length of the unit cell in unsubstituted Lu₃Fe₅O₁₂ garnet is measured to be a = 12.33 ± 0.02 Å (SI Appendix, Fig. S2). (C) Colored dots correspond to bright spots in panel A marked by red circles and show the distribution of substituted bismuth atoms. A relative higher intensity dot (each representing an atomic column) means a higher fraction of Bi atoms. Variations of the lattice constants for unit cells over the region in panel A are mapped by the color of short lines drawn along the [010] and [100] directions and superposed on the map of normalized intensity. (D) Atomic-scale EDS mapping images of Lu, Fe, Bi corresponding region shown in panel A using the L-edge for (Bi, Lu) and the K-edge for Fe.

To confirm the position of the substituted Bi atoms the BLIG film was examined in a [111] projection, where the three different cation sublattice sites are well separated and nonoverlapping (Fig. 2A). A HAADF image viewed along the [111] direction is shown in Fig. 2 B, Upper Left. EDS analysis reveals a quantitative variation in composition consistent with the observed intensity variations in the HAADF images, further demonstrating a lack of any long-range order in the positions of the Bi and Lu atoms (SI Appendix, Fig. S3). Atomic-scale EDS mapping along the [111] direction shows that the Bi atoms and Lu atoms are both located at dodecahedral sites, with the Fe atoms located at octahedral and tetrahedral sites (Fig. 2B). The Bi EDS signal also shows a variation in intensity at equivalent dodecahedral sites, as seen in Fig. 2C, where the intensities for Bi and Lu at four dodecahedral sites within one unit cell are plotted. The Bi intensity in these equivalent dodecahedral sites is nonregular and varies in an opposing manner to the Lu EDS intensity. These structural observations show therefore that in the BLIG film the Bi atoms are substituted at dodecahedral sites without any long-range order, resulting in fluctuations in the local lattice constants due to the large difference in ionic radius between Bi³⁺ (1.11 Å) and Lu³⁺ (0.97 Å).

Fig. 2.

Atomic-scale structure and element distribution in (Bi_0.9Lu_2.1)Fe₅O₁₂ at different sites. (A) Projected atomic structure viewed along the [111] direction, showing the three nonoverlapping cation sublattice sites. (B) Atomic-scale EDS maps of (Bi_0.9Lu_2.1)Fe₅O₁₂ for Lu, Fe, and Bi. (C) EDS intensity of Bi and Lu at the different positions labeled by numbers in the unit cell.

In the following, the influence of the lattice distortions on changes in electronic structure and related order parameters is examined using electron energy loss spectroscopy (EELS) (35, 42, 43) and electron magnetic circular dichroism (EMCD) (37, 44), to investigate the spin, valence, and fine electronic structure of Fe in BLIG, using Lu₃Fe₅O₁₂(LuIG) and YIG as a reference.

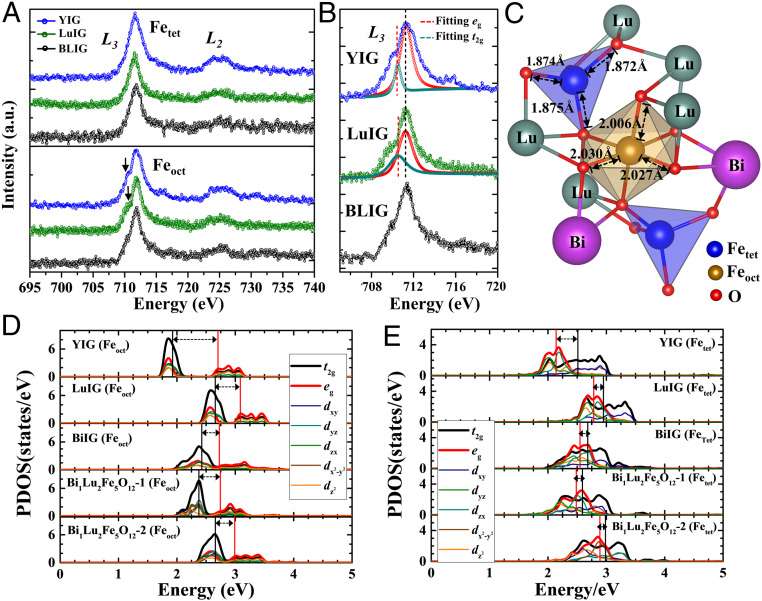
Fig. 3A shows EELS spectra corresponding to the Fe L_2,3 edges from octahedral and tetrahedral sites in BLIG, LuIG, and YIG. For transition metal oxides, both energy shifts and fine features in the L_2,3 edges are related to the valence state and coordination (e.g., octahedral or tetrahedral sites). Due to the octahedral crystal field effect, the Fe 3d orbital states usually split into t_2g and e_g states, appearing as a shoulder on the left side of the L₃ edge (43, 45). As shown in Fig. 3B, the L₃ edge for octahedral Fe sites in LuIG and YIG shows a distinct shoulder that can be fitted to the t_2g and e_g states. In contrast, for BLIG, no clear evidence for a crystal-splitting effect at the octahedral Fe sites is observed. The energy positions of the Fe L_2,3 edges for both octahedral and tetrahedral sites in BLIG remain the same as those in pure LuIG and YIG, indicating an unchanged +3 valence for Fe at octahedral and tetrahedral sites in both materials. It can be noted that no L_2,3 edge-shoulder is seen for Fe in tetrahedral sites in both BLIG, LuIG, and YIG, on account of the lower crystal-field splitting energy (CFE) compared to that at octahedral sites. Our observation of a significantly diminished shoulder in the Fe L₃ edge for BLIG can be strongly related to the variations in local structure described above that result in a distortion around octahedral sites and reveals the direct influence of the Bi distribution on the crystal field.

Fig. 3.

Site-specific resolved EELS and DFT calculations revealing the bonding length and orbital characteristics of Fe in octahedral and tetrahedral sites in BLIG, LuIG, and YIG films. (A) EELS of Fe L_2,3-edge from octahedral and tetrahedral sites in BLIG, LuIG, and YIG films. (B) Spectra from octahedral Fe sites in BLIG, LuIG, and YIG films are plotted in enlarged view—a clear shoulder that can be fitted with t_2g and e_g is seen for the octahedral Fe L₃ edge in LuIG and YIG, while this feature is not observed in BLIG. (C) Fe-O bonding lengths for diverse polyhedra connected via oxygen atoms. (D and E) Orbital-projected DOS for the Fe 3d orbital at octahedral and tetrahedral sites in BLIG, respectively; horizontal arrows highlight the difference of the CFE. When this energy gap is large enough, as in YIG, a fine shoulder can be seen in the Fe L₃ edge. Bi₁Lu₂Fe₅O₁₂-1 and Bi₁Lu₂Fe₅O₁₂-2 refer to specific atomic models with the same composition but different Bi arrangements (SI Appendix, Fig. S4).

Based on the experimental results for the lattice parameter in thin-film BLIG, a most probable approach for a unit cell structure of BLIG was determined from self-consistent lattice relaxation calculations using density functional theory for a series of BLIG primitive cells with different Bi arrangements (SI Appendix, Fig. S4). The energy of each relaxed structure only varies slightly, but the structure where Bi and Lu atoms are most clustered (labeled BLIG-2) has the lowest energy. The Fe-O bonding lengths at octahedral and tetrahedral sites in fully relaxed primitive cells with the BLIG-2 configuration are listed in SI Appendix, Fig. S4, together with those for YIG, unsubstituted LuIG and Bi₃Fe₅O₁₂ (BiIG). An important feature in BLIG-2 is the variation in both different Fe-O bond lengths, as indicated in Fig. 3C. In contrast all Fe-O bond lengths for tetrahedrally coordinated Fe remain very similar. Accordingly, Fe-O octahedra, which share edges with the Bi/Lu dodecahedral sublattice, undergo a much stronger crystal distortion arising from Bi substitution into dodecahedral sites than the Fe-O tetrahedra, which are only connected to the octahedra and dodecahedra via apical oxygen atoms. These variations in Fe-O bond lengths cannot be observed from real-space imaging. However, our atomic-column–resolved EELS data show how the resulting modulated electronic structure can be related to octahedral distortions arising from local structure variations due to substitution of Bi in this material.

To further investigate the effect of the distortions arising from Bi substitution, the CFE at octahedral and tetrahedral sites was determined. In unsubstituted compounds, the CFE values, represented by the energy difference between the black and red lines in Fig. 3 D and E, decrease from YIG to LuIG to BiIG, consistent with previous studies (46), showing that a larger ion radius leads to a decrease of hybridization strength and consequently a decreased CFE. Calculated values for a series of (Lu_3-xBi_x)Fe₅O₁₂ compounds (x = 0.5 to 2.5) all show a reduced CFE, though not varying monotonically with the Bi/Lu ratio (SI Appendix, Table S1). Regarding the tetrahedral Fe, the BLIG structures have a smaller CFE than all the unsubstituted compounds, as shown in Fig. 3E. These calculations therefore support the conclusion from the EELS spectra observations that the diminished shoulder in BLIG at the octahedral Fe L₃ edge can be attributed to a reduced CFE compared to that of YIG and highlight how substitution at dodecahedral sites without long-range order can lead to crystal-field fluctuations in the iron garnet structure.

Fig. 4A illustrates the electronic structure modulation in octahedral sites in BLIG either with or without substitution by Bi. In the undistorted lattice the 3d⁵ orbital energy levels are split into two degenerate levels, t_2g and e_g. Following partial Bi substitution at dodecahedral sites, partial density of states calculations show that the induced octahedral distortion leads to a lifted degeneracy of both the t_2g and e_g levels, thereby leading to the reduced CFE values (Fig. 4B).

Fig. 4.

Orbital energy and site-specific magnetic analysis of Fe at different sites. (A) Schematic diagram illustrating splitting of the Fe 3d energy level introduced by the CFE in octahedral sites. Due to Bi substitution, the degeneracy of the t_2g and e_g energy levels is lifted. (B) Energy levels of Fe 3d orbitals at octahedral sites in (Bi_xLu_3-x)Fe₅O₁₂. (C and D) Site-specific EMCD signals from octahedral and tetrahedral Fe sites, respectively. The schematic insets indicate the different diffraction geometry, and the circles represent the entrance aperture positions. Black and red lines represent EELS spectra acquired from the “+” and “−” aperture positions; blue lines represent the EMCD signals. The EMCD spectra in panels C and D are opposite, indicating that spin configuration is antiferromagnetically coupled between two sites. (E) In BLIG the antiparallel spin ordering of Fe³⁺ at octahedral and tetrahedral sites allows for cross-transfer transitions between these sites.

Another important aspect of the garnet structure is that the two differently coordinated Fe sites are coupled with each other via a strong exchange interaction, leading to ferrimagnetism. Accordingly, EMCD was used to investigate the site-specific magnetic structure of Fe in octahedral and tetrahedral sites (SI Appendix, Fig. S6), taking care to choose appropriate dynamic diffraction conditions.

Strongly enhanced EMCD signals from octahedral and tetrahedral sites are shown in Fig. 4 C and D, respectively, acquired from the aperture positions as indicated in each figure (see SI Appendix, Fig. S7 for further details). It is observed that the EMCD signal from octahedral sites is opposite to that from tetrahedral sites, implying that the magnetic moments of the Fe atoms are antiparallel in the two different sites. Accordingly, it can be concluded that an antiferromagnetic coupling of Fe atoms in the two differently coordinated sites is still maintained in BLIG, mediated by oxygen atoms through a strong superexchange interaction. Consequently, a description for its magnetic structure can be written as $\text{Bi}/{\text{Lu}}_3{[{\text{Fe}}_2^{3+},\downarrow ]}_{\text{oct}}{[{\text{Fe}}_3^{3+},\uparrow ]}_{\text{tet}}{\text{O}}_{12}$. Moreover, macroscopic moment-field loops for BLIG and YIG (SI Appendix, Fig. S8) show almost the same saturation magnetization, indicating that magnetic moments are not visibly modified after substitution of Lu by Bi. As illustrated in Fig. 4E, this unchanged magnetic configuration allows the ∆S_ζ = 0 spin selection rule (where ∆S_ζ is the change of total spin in the ζ-direction) for cross-transfer transitions within Fe³⁺(octahedral)–Fe³⁺(tetrahedral) pairs to be satisfied, due to the antiparallel Fe³⁺ spin ordering at octahedral and tetrahedral sites. These allowed transitions can be assigned to the optical transitions (19, 30, 47, 48) responsible for the remarkably enhanced magneto-optical response in the range of the visible and infrared bands.

These results show how multiple quantum-order parameters, including lattice, charge, spin, orbital, and CFE can be experimentally determined in Bi-substituted lutetium iron garnet. It is directly demonstrated that Bi substitution of Lu atoms at dodecahedral sites takes place in (Bi_0.9Lu_2.1)Fe₅O₁₂ without any long-range order of either atom type, resulting in a fluctuation of the local lattice constants and distorted Fe-O bonding at octahedral sites. These variations in local polyhedral structure decrease the CFE of the Fe 3d orbitals at both octahedral and tetrahedral sites, leading to a lifted degeneracy of the octahedral Fe 3d orbitals. Moreover, these changes result in a modification of the available energy transitions between different excited states (SI Appendix, Fig. S9) and promote magneto-optical transitions that contribute to the enhanced Verdet constant, thereby showing how the transition energies can be altered in iron garnets by Bi substitution. Furthermore, antiparallel spin ordering between octahedral and tetrahedral sites is preserved in the Bi-substituted lutetium iron garnet, thereby allowing satisfaction of spin-selection rules, facilitating the cross-transfer transitions that are part of the optical transitions responsible for magneto-optical response in the visible and near-infrared bands. With regard to the magneto-optical response, the contribution from octahedral Fe increase, where, due to the octahedral distortion, local symmetry at the Fe octahedra in BLIG is broken, resulting in a lifted orbital degeneracy. The lifted degeneracy can increase the oscillator strength of crystal-field transition in octahedral sites, which contributes to the magnetic-optical response in the lower-energy region.

With advances both in spherical correction and spectrometers, advanced EELS techniques with high-energy resolution can be used to resolve anion vacancies, charge ordering and charge transfer, and even interfacial bandgap variations (49–51). For transition elements in oxide materials, specific fine structures in EELS data can help to understand coordination transformations, such as those between octahedral and tetrahedral sites (43, 45), especially in unique interfaces of heterojunctions or boundaries. Furthermore, by using specific dynamic conditions, EMCD techniques based on EELS can be used to directly resolve magnetic variations across heterojunction interfaces (37, 38, 44). Motivated by these advantages of EELS with high spatial resolution, the present work sheds light on electronic structure variations at different sites in iron garnet, arising due to the hidden effect of substituent atoms. These investigations contribute significantly to an understanding of effect of substituent atoms on local structures.

Summary

In conclusion, our study shows that together with spin-orbital coupling effects in Bi-substituted iron garnet, local atomic/charge/spin/orbital structure modulation via element substitution should be taken into consideration in order to advance understanding of coupling effects on properties of functional materials.

By use of a suite of advanced electron microscopy techniques applied synergistically at the atomic scale, we are able to reveal experimentally how, in Bi-substituted lutetium iron garnet, substitution by Bi results in a distortion of Fe-O octahedra, leading to a lifting of the degeneracy in key electron levels in strongly coupled ferrimagnetic Fe atoms and to show how this results in changes in energy level transitions that can account for enhanced magneto-optical properties. Moreover, the results show the effectiveness and benefits of synergistic experimental measurements of lattice/charge/spin/orbital/topology order parameters at high resolution, enabling insights into hidden coupling effects between multiple quantum-order parameters, thereby further guiding research and development for a wide range of complex functional materials.

Materials and Methods

Film Synthesis.

Films of BLIG and of undoped pure YIG were grown on (1$\overline{1}$1)-oriented gadolinium gallium garnet Gd₃Ga₅O₁₂ (GGG) substrates by lead-free liquid phase epitaxy, with final thickness of 5 to 6 µm. For the BLIG film, Lu₂O₃, Fe₂O₃, and Bi₂O₃ were added to a crucible in the required molar ratio then heated at 1,000 ∼ 1,050 °C for 24 h, with stirring for 12 h. The molten liquid was then cooled to 803 °C to achieve a supersaturated condition. A cleaned GGG substrate was fixed on a bracket using platinum wire to achieve a small angle (3 to 15°) with the liquid surface. The substrate was then fully lowered into the molten liquid to start the film growth; at the same time, the substrate was rotated at a rate of 60 to 100 rpm, with the rotation direction changed once every 3 min. Finally, the film was cleaned in hot nitric acid to remove any residual Bi₂O₃ flux agent. Film of Lu₃Fe₅O₁₂ was grown on (1$\overline{1}$1)-oriented Gd₃Ga₅O₁₂ substrate.

Characterization of Structure and Physical Properties.

X-ray characterization was performed in using a Rigaku Smartlab X-ray diffractometer. X-ray photoelectron spectroscopy (XPS) was conducted using a PHI5300 instrument. The TEM specimen was a lamella extracted from the sample by focused-ion-beam (FIB) milling in a Zeiss Auriga FIB instrument and then thinned to reduce the thickness of the surface amorphization layer by using 5 kV 20 mA ion beam milling. Finally, the surface of the TEM sample was carefully thinned and polished by using a Nanomill instrument.

Atomic structure investigations and element mapping characterization were carried out by scanning transmission electron microscopy (STEM) in a FEI Titan Cubed Themis G2 300 operated at 300 kV and equipped with a high-brightness Schottky field emission gun and monochromator, a probe aberration corrector to provide a spatial resolution better than 0.6 Å in STEM mode, an energy dispersive EDS detector and a postcolumn imaging energy filter (Gatan Quantum 965 Spectrometer) for EELS analysis. Atomic number (Z) contrast imaging was conducted in HAADF mode with a probe convergence angle of 25 mrad and an inner collection angle of ∼80 mrad and outer collection angle of ∼240 mrad. HAADF imaging was combined with EDS to perform element mapping, and ADF imaging was combined with EELS to achieve atomic-resolved EELS by spectrum imaging (SI). The magnetic properties of the films were characterized by a superconducting quantum interference device (SQUID) magnetometer. Electron magnetic chiral dichroism (EMCD) was carried out in a FEI Titan 80-300 operated at 300 kV and equipped with field emission gun and a postcolumn Gatan Tridiem system. Diffraction patterns were acquired on a FEI G20 transmission electron microscope (TEM), equipped with a tilt-rotation holder (±35°). The sample area selected for electron diffraction was about 100 nm in diameter, corresponding to the use of a smallest selected area diffraction aperture of around 10 µm in diameter.

In the EMCD measurements, all TEM experimental conditions and the simulation of dynamical diffraction effects for (Bi_0.9Lu_2.1)Fe₃O₁₂ were optimized as discussed in previous work (52, 53). In summary, the calculations consisted of two parts: Firstly, the Bloch coefficients and momentum transfer based on the specific experimental diffraction conditions were calculated using a Bloch wave software package (54). Then we used a Matlab code to calculate the dynamical coefficients corresponding to nonmagnetic and magnetic components.

Atomic column positions in the HAADF images were determined using the 2D Gaussian fitting method embedded in MacTEMPAS (49). Next, the integrated intensity of atomic columns is extracted over defined ranges of the fitted 2D Gaussian peak centered at each peak position. Finally, these values are normalized, with intensity of 1 corresponding to the maximum value, allowing the plot of Fig. 1C to be made. A Matlab code was used to precisely determine the center of mass of the projected atomic columns in the STEM-HAADF images to derive the local lattice parameters.

Density Function Theory Calculation.

The electronic structure was calculated using density functional theory, implemented in the Vienna ab initio simulation package (VASP) (55, 56). Projector augmented wave pseudopotentials (57) and the generalized gradient approximation (GGA) for the exchange correlation interaction were used (20, 58). Due to the complexity and time consumption of density functional theory (DFT) calculations when substituent elements are considered in strongly correlated iron garnet with large numbers of atoms, Bi-substituted lutetium iron garnet of different Bi/Lu ratio, and unsubstituted samples were each built as a primitive unit cell containing 80 atoms. Self-consistent lattice relaxation calculations were carried out for Bi₁Lu₂Fe₅O₁₂ (where the ratio of Bi/Lu is 1:2, corresponding to the approximate average ratio of the experimental film), yielding a lattice constant of 12.377 Å. Primitive unit cells with different Bi/Lu ratios were also relaxed in the same manner, as well as for unsubstituted Y₃Fe₅O₁₂, Lu₃Fe₅O₁₂, and Bi₃Fe₅O₁₂, where lattice constants of 12.377 Å, 12.277 Å and 12.677Å, respectively, were obtained. The plane-wave cut off was chosen as 500 eV, and a 4 × 4 × 4 Monkhorst–Pack k-point mesh was employed in the Brillouin zone for convergence. To reproduce the measured energy gaps in these insulators, an on-site Coulomb interaction (GGA+U) was included. The Hubbard and Hund’s U and J parameters were chosen as U − J = 2.7 eV for YIG, 4.7 eV for LuIG, and 5 eV for BiIG and Bi_xLu_3-xFe₅O₁₂. By integrating the densities of the t_2g and e_g states of the total Fe 3d bands at these sites, the CFE of iron garnets with different composition was determined. The mean energy values of t_2g and e_g were obtained by integrating above the Fermi level weighted according to the calculated densities of states (DOS), and then normalized by the integrated DOS.

Data Availability

All data used in this study are included in the article and supporting information.