Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2021 May 12;6(20):13331–13340. doi: 10.1021/acsomega.1c01293

Novel Descriptors Derived from the Aggregation Propensity of Di- and Tripeptides Can Predict the Critical Aggregation Concentration of Longer Peptides

Saeed Zanganeh †,‡, Loghman Firoozpour §, Soroush Sardari ∥, Ali Afgar ⊥, Reza Ahangari Cohan †,*, Nasir Mohajel #,*
PMCID: PMC8158804  PMID: 34056481

Abstract

graphic file with name ao1c01293_0005.jpg

Self-assembling amphiphilic peptides have recently received special attention in medicine. Nonetheless, testing the myriad of combinations generated from at least 20 coded and several hundreds of noncoded amino acids to obtain candidate sequences for each application, if possible, is time-consuming and expensive. Therefore, rapid and accurate approaches are needed to select candidates from countless combinations. In the current study, we examined three conventional descriptor sets along with a novel descriptor set derived from the simulated aggregation propensity of di- and tripeptides to model the critical aggregation concentration (CAC) of amphiphilic peptides. In contrast to the conventional descriptors, the radial kernel model derived from the novel descriptor set accurately predicted the critical aggregation concentration of the test set with a residual standard error of 0.10. The importance of aromatic side chains, as well as neighboring amino acids in the self-assembly, was emphasized by analysis of the influential descriptors. The addition of very long peptides (70–100 residues) to the data set decreased the model accuracy and changed the influential descriptors. The developed model can be used to predict the CAC of self-assembling amphiphilic peptides and also to derive rules to apply in designing novel amphiphilic peptides with desired properties.

Introduction

In recent years, amphiphilic peptides have received great attention due to their ability to form a variety of nanostructures.1 These peptides are composed of distinct hydrophilic and hydrophobic parts and, depending on the sequence, they exhibit different physicochemical and biochemical properties.2,3 These peptides were first introduced by Zhang et al. at the Massachusetts Institute of Technology.4 Initial studies were focused on a better understanding of their physicochemical properties; however, in the following years, numerous potential applications have been suggested for these materials, including drug5 and gene delivery,6 vaccination,7 regenerative medicine,4 and stabilization of membrane proteins.8 Despite the proposed biomedical applications, there are still many obstacles that need to be addressed for their realization. For example, self-assembling peptides show a low efficiency for drug and gene delivery,9 and/or peptides with lower critical aggregation concentration (CAC) values are needed to reduce the cost for regenerative applications.10 Therefore, discovery or design strategies are still needed to obtain sequences that provide the desired physicochemical properties for each application of amphiphilic peptides.

Meeting this demand by testing all possible combinations of 20 coded and several hundreds of noncoded amino acids with different lengths is an impossible task at the laboratory level. Therefore, various design and discovery strategies have been tried by researchers. There are two approaches to discover self-assembling peptides. Either amino acids are rationally chosen based on their known properties (rational design strategy)4,11 or the desired characteristics of the final system are considered to achieve the desired attributes (directed discovery strategy).12 Directed discovery consists of three different methodologies, namely sequence editing, computation, and dynamic libraries. The computational methodology has been used by Frederix et al. They used Martini coarse-grained molecular dynamics (CG-MD) simulations to identify sequences with higher aggregation propensity (AP) values via screening of di- and tripeptides containing coded amino acids.13,14 Ultimately, they suggested several design rules by observing sequences with the highest AP values. However, extension of the computational methods to longer peptides or sequences containing noncoded amino acids is not currently achievable because of the computational cost. Quantitative structure–property relationship (QSPR) is a less computationally intensive method that uses statistical modeling to create a mathematical relationship between a measurable property and its molecular descriptors. This method has been extensively used with success for critical micelle concentration (CMC) prediction of surfactants.15 Since surfactants are structurally comparable to amphiphilic peptides and both of them have a similar property (named CAC), the same strategies were used for studying their self-assembly. Tian et al. employed QSPR for CAC modeling of 32 amphiphilic peptides. They concluded that their novel MD-based descriptor, named the molecular dynamics-based hydrophobic cross-field (MD-HCF), shows a better performance in model building than descriptors generated by the CODESSA package.16 In another study, Guo et al. developed two different models for studying the flexibility and CAC of self-assembling peptides.17 Their data showed a negative correlation between flexibility and self-assembling power. Although these initial attempts reported a high correlation coefficient between the predicted and experimental CAC values, the small size of the database prevented the authors from defining independent test sets. Moreover, testing various descriptor types and other modeling approaches like support vector machines are essential for finding the best model for accurate prediction.

Defining new descriptors having a high correlation with the desired property is a critical step to obtain an accurate predictive model. MD-driven descriptors have been shown to improve the performance of QSPR models in various areas.18−20 The computational expense of MD-driven descriptors has prevented their widespread use in QSPR models. This was the case in the Guo et al. study, where the authors omitted the use of MD-HCF descriptors mentioning their computational expense.17 This obstacle, along with a limited database of amphiphilic peptides, has restricted extensive investigations on QSPR models to predict the CAC of these peptides to just one report.16

Therefore, in the current study, we developed a novel set of MD-driven descriptors that did not require running simulation before descriptor definition and compared their performance to that of three conventional descriptor sets in different model-building methods to predict the CAC of amphiphilic peptides in the test set. The novel defined MD-driven descriptors, called AP scales, modeled with support vector machine with radial kernel showed the best performance in practice. Evaluation of influential descriptors indicated the importance of neighboring aromatic amino acids and aromatic side chains in the self-assembling phenomenon. The addition of long peptides (70–100 residues) changes the accuracy of the model as well as the influential descriptors.

Results

Here, we investigated different descriptor sets and statistical modeling approaches (Figure 1) to model the CAC of the amphiphilic peptides listed in Table 1. The first approach used descriptors derived from peptide structures (the structure-drawing commands are listed in Tables S1–S3 and the peptide structures are shown in Table S4) using the PaDEL-Descriptor (whole-peptide approach, which is depicted by the black line in Figure 1). The second approach used the principal components of PaDEL descriptors for each amino acid in the sequence (PCA approach, which is depicted by the red line in Figure 1). The third approach used z-scales for each amino acid in the sequence as defined by Jonsson et al.21 (z-scale approach, which is depicted by the blue line in Figure 1). The fourth approach used a novel set of descriptors driven from the coarse-grained simulation of di- and tripeptides (AP/APH scale approaches, which are depicted by the purple lines in Figure 1).13,14 These scales are listed in Table S5. For the last three sets, the matrix dimensions for peptides with various lengths were unified using auto cross-covariance (ACC) calculations.22 Four machine learning algorithms were applied to model the data, including the support vector machine with the radial kernel (svmRadial), support vector machine with the linear kernel (svmLinear), partial least square (PLS), and generalized boosted models (GBM). Descriptors and ACCs with the most influence in the best models were extracted and the ability of the best model to predict the CAC values of long peptides (70–100 residues) was also investigated.

Figure 1.

Figure 1

Open in a new tab

Schematic representation of different approaches used for CAC modeling of self-assembling amphiphilic peptides. Four different approaches of descriptor generation were used. Each approach is depicted by a colored line. Black line (whole-peptide): PaDEL descriptors defined for peptide structures; red line (PCA): principal components of PaDEL descriptors defined for each amino acid in the sequence; blue line (z-scale): z-scales defined for each amino acid in the sequence; and purple line (AP/APH scales): novel AP/APH scales defined for each amino acid in the sequence. The last approach consisted of three steps. In each step, more descriptors were added to the previous AP/APH scales. In brief, in the first step (indicated by ①) AP/APH scales for Ala-AAi and AAi-Ala (the structures and AP/APH scales for these peptides are presented in the first and second columns of Table S5) were used in model building. In the second step (indicated by ②) AP/APH scales for Ala-AAi-Ala (the structures and AP/APH scales for these peptides are presented in the third column of Table S5) were used in addition to the AP/APH scales defined in the previous step. In the third step (indicated by ④) AP/APH scales for Ala-Ala- AAi and AAiAla-Ala (the structures and AP/APH scales for these peptides are presented in the fifth and sixth columns of Table S5) were used in addition to the AP scales defined in the two previous steps. AAi is the ith amino acid in the peptide sequence. PCA: principal component analysis, ACC: auto cross-covariance.

Table 1. Amphiphilic Peptides and the Measured CAC Values Collected from the Literaturea.

peptides CAC (−log M) refs peptides CAC (−log M) refs peptides CAC (−log M) refs
V6K2GRGDS 4.83 (23) A10H6 6.64 (31) Ac-GAVILEE 3.15 (38)
Ac-A6K± 4.60 (24) RF 1.74 (32) Ac-GAVILEE-NH2 3.10  
Ac-L6K2-NH2 4.34 (25) [RF]2 4.40   Ac-I3D 2.96  
Ac-L6K3-NH2 3.60   [RF]3 2.64   Ac-L3D 2.92  
Ac-V6K2-NH2 3.48   [RF]4 3.52   Ac-L3K-NH2 2.92  
Ac-V6K3-NH2 3.08   [RF]5 4.70   Ac-V3K-NH2 2.80  
            Ac-V3D 2.64  
Ac-V6K4-NH2 2.33   A6YD 2.52 (33) Ac-V6K-NH2 3.35 (39)
Ac-L6K4-NH2 2.27   V4WD2 2.12   A3C 3.42 (40)
Ac-A6K2-NH2 2.10   V4D 2.70 (34) V3C 3.77  
Ac-V6D 3.30 (26) V4WD 2.32   I3C 4.15  
Ac-V6D2 2.96   I4WD2 2.39   I4K 3.60 (41)
A6RGD 1.74 (27) L4WD2 2.72   I5K 3.89  
G3A3V3I3K3 3.23 (28) RFL4FR 3.10 (35) LI2K 2.99  
K3I3V3A3G3 3.19   K60L30 10.19 (36) L4K 3.27  
I3V3A3G3K3 3.28   K60L20 6.17   L5K 3.85  
K3G3A3V3I3 3.55   E60L20 5.46   Ac-A6D 3.34 (42)
V3G3I3A3K3 3.01   K80L20 4.38   Ac-GAVILRR-NH2 3.09 (43)
K3A3I3G3V3 3.15   K60L10 4.01   K4X4-gAb 3.70 (44)
K-K8 2.10 (29) Ac-A9K-NH2 4.82 (37) K5X3-gA 3.68  
KK8 2.10   Ac-A6K-NH2b 3.70   K8-gA 3.66  
IK-K11 2.58   Ac-A3K-NH2 2.00   K6X2-gA 3.64  
IKK11 2.66   Ac-A6D 3.52 (38) K7X1-gA 3.62  
IK-K16 3.03   DA6-NH2 3.70   K3X5-gA 3.77  
IKK16 3.13   KA6-NH2 3.52        
GAAVILRR 1.52 (30) Ac-I3K-NH2 3.35        
Open in a new tab
a

The CAC values were measured by fluorimetry,23−36 conductivity,37−41 or dynamic light scattering (DLS) techniques42−44 in pure water. All concentrations are represented as −log M. The defined test set is presented in bold font. Long peptides are indicated by italic format. All peptide structures and molar concentrations can be found in the supporting information Table S4.

b

The value of CAC for Ac-A6K-NH2 was extracted from reference (38) as the techniques used there tended to be more accurate than those used in the other reports.

Model Performance

Model performance was assessed by residual standard error (RSE) calculation for the test and train sets (Figure 2). Among all models in all approaches, the model generated by svmRadial for the AP scale 2 (containing AP scales for AAi-Ala, Ala-AAi, and Ala-AAi-Ala) showed the best performance on the test set with an RSE of 0.1. The svmRadial model also showed the best performance in other approaches except for the z-scale approach, where the PLS model was the best. Generally, models fitted on APH scales, which are based on hydrophilicity-adjusted derivatives of AP scales,14 performed inferior to those fitted on the AP scale. Consequently, the svmRadial model on AP scale 2 is suitable for the CAC prediction of newly designed amphiphilic peptides.

Figure 2.

Figure 2

Open in a new tab

Performance of svmRadial, svmLinear, PLS, and GBM models on the training and test sets: model performance on the train (green dots) and test (orange dots) sets were measured using residual standard error (RSE) calculation and visualized by plotting predicted CAC values against experimental ones. The equation for the black lines is predicted CAC = experimental CAC.

Influential Descriptors

To identify the physicochemical properties that govern the self-assembling behavior of amphiphilic peptides, descriptors or ACCs with the most influence on the best model in each approach were extracted using the “varImp()” function of the CARET package (Table 3). Topological polar surface area (TopoPSA), centered Broto–Moreau autocorrelation—lag 7/weighted by van der Waals volumes (ATSC7v), and the number of hydrogen bond acceptors (nHBAcc3) were the most influential descriptors in the whole peptide approach (Table 3). The most influential ACC in the svmRadial model in the PCA approach consisted of the sum of products between PCs 1 and 3 with a lag of 1 (two adjacent amino acids in the peptide sequence), indicating the intensifying effect of neighboring amino acids on the self-assembly power of amphiphilic peptides. The other two influential ACCs contained the sum of products of PCs 4–5 and 3–8 with a lag of 1, respectively. In the PLS model in the z-scale approach, z-scale 1 was the most important z-scale as seen in ACC 1 and 3 (Table 3). This scale is related to the hydrophilicity of amino acids in the peptide sequence. Scales 3 and 2 are other influential z-scales that are related to the electronic and side-chain bulk properties of amino acids. The AP scale 3, which presented the aggregation propensity of the Ala-AAi-Ala peptide, was the most influential ACC in the AP-scale approach. Since the performance of all models in the APH-scale approach is poor, none of the APH scales can have physicochemical relevance. The aggregation propensity of the Ala-AAi-Ala peptide is the most influential descriptor in the best model; however, this descriptor provides no sensible information about physicochemical properties that drive the self-assembly of amphiphilic peptides.

Table 3. Correlation between AP and the PaDEL Molecular Descriptors for Ala-AAi-Ala Tripeptides Constructed by Replacing AAi with Amino Acids in the Data Seta.

number descriptor type definition correlation coefficient
1 SdsCH sum of atom-type E-state: =CH– 0.96
2 khs.aaCH counts the number of occurrences of the E-state fragments 0.95
3 ndsCH count of atom-type E-state: =CH– 0.95
4 nHother count of atom-type H E-state: H on aaCH, dCH2 or dsCH 0.95
5 nHdsCH count of atom-type H E-State: =CH– 0.95
6 HybRatio hybridization ratio (fraction of sp3 carbons to sp2 carbons) –0.87
7 GATS1i Geary autocorrelation—lag 1/weighted by first ionization potential –0.82
8 GATS1p Geary autocorrelation—lag 1/weighted by polarizabilities –0.81
9 SpMax1_Bhs largest absolute eigenvalue of Burden modified matrix—n 1/weighted by relative I-state –0.80
10 SpMax3_Bhs largest absolute eigenvalue of Burden modified matrix—n 3/weighted by relative I-state –0.80
Open in a new tab
a

Ten descriptors with the highest positive and negative correlations are presented.

Correlation Studies

Therefore, to find the molecular descriptors related to the aggregation propensity of Ala-AAi-Ala, a Pearson correlation study was conducted between this parameter and the PaDEL descriptors defined for Ala-AAi-Ala peptides. Table 3 lists 10 molecular descriptors that had a strong positive or negative correlation with the aggregation propensity of Ala-AAi-Ala peptides. The positively related descriptors were the sum of atom-type E-State: =CH–, count of the number of occurrences of the E-state fragments, count of atom-type E-State: =CH–, count of atom-type H E-State: H on aaCH, dCH2 or dsCH, and count of atom-type H E-State: =CH– belonging to electrotopological state indices, which measure the atom-type E-states or hydrogen atoms in =CH– or =CH2 fragments. These states are only present in aromatic amino acids among Ala-AAi-Ala peptides. The first negatively related descriptor was the fraction of sp3 carbons to sp2 carbon. The second and third negatively correlated descriptors were Geary autocorrelations with a lag of 1 weighted by first ionization potential and polarizability, respectively. The two last negatively correlated descriptors were the largest absolute eigenvalue of Burden modified matrix—n 1 and —n 3 weighted by the relative intrinsic state (I-state), respectively. All negatively correlated descriptors had their lowest values in Ala-AAi-Ala peptides containing aromatic amino acids (Table 2).

Table 2. Three Descriptors or ACCs with the Most Influence on the Best Model in Each Approach.

  order
approach 1 2 3
whole peptide-svmRadial TopoPSA ATSC7v nHBAcc3
PCA-svmRadial 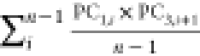Inline graphic Inline graphic Inline graphic
z-scale-PLS Inline graphic Inline graphic Inline graphic
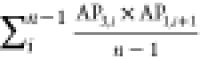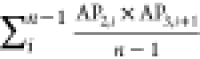AP-scale-svmRadial Inline graphic Inline graphic Inline graphic
APH-scale-svmRadial 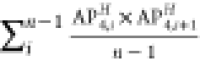Inline graphic Inline graphic Inline graphic
Open in a new tab

Effect of Peptide Length

To understand the effect of peptide length on the best model and the most influential ACCs, the data set was expanded to include peptides between 70 and 100 amino acids (peptides from ref (36), Table 1). Then, the AP approach with svmRadial was applied to generate models for the new data set, once with and once without the shortest peptide (RF) in the data set. Generally, the addition of longer peptides reduced the accuracy of the model as the RSE value for the test set increased from 0.1 to 0.29 (Figures 2 and 3). Although removing the shortest peptide in the data set decreased the RSE value from 0.29 to 0.23 for the test set (Figure 3), it cannot be concluded that this removal improved the accuracy of the model. As seen in Figure 3b, the CAC values of the test set were located in the region that had the best fit in the train set. In other words, if the test set was selected from the regions with a CAC value of more than 5.0 or less than 2.5, the RSE would have increased drastically. The addition of the long peptides also changed the most influential ACCs (Tables 3 and S6). All influential ACCs, whether for the model on the original data set or the data set containing longer peptides with or without RF, had a lag of 1. The most influential ACC in both the original data set and the data set including long peptides and RF was the same, while the other two influential ACCs for the data set with longer peptides contained AP scale 4. Removing RF from the data set containing long peptides changed all influential ACCs to contain AP scales 4. This AP scale is different from AP scale 3 just for terminal amino acids if they are capped with acetyl or amine groups. Therefore, it can be concluded that the physicochemical properties of amphiphilic peptides differ as the peptide sizes differ.

Figure 3.

Figure 3

Open in a new tab

Addition of long peptides to the data set reduced the model performance. Model performance was measured after (a) adding five long peptides from ref (35) to the data set and (b) after removing the shortest peptide (RF) from the data set. The model fitted on the data set containing RF and the five long peptides had an RSE value of 0.29 on the test set. However, removing RF from the data set reduced the RSE value to 0.23.

Discussion

Here we studied a novel set of descriptors (AP scale) along with three conventional sets in different model-building approaches regarding their ability to predict the CAC values of amphiphilic peptides. Model-building methods were selected based on their previous application in the CAC modeling of amphiphilic peptides16,17 or their performance in CMC modeling of surfactants.15,45 Our results showed that a svmRadial model fitted on AP scale step 2 showed the best performance on the test set. Influential ACCs in this model had AP scale 3 in their formula, indicating that AP for amino acids in a sequence of Ala-AAi-Ala peptides had the most influence on the model. APs for Ala-AAi-Ala peptides were positively correlated with several electrotopological indices and negatively correlated with the carbon hybridization ratio, two Geary autocorrelations weighted by ionization and polarizability, and two absolute eigenvalues of Burden modified matrix weighted by the relative I-state. The addition of longer peptides to the data set decreased the accuracy of the model and also changed the influential ACCs.

To our knowledge, the model built in this study is the most accurate model for CAC prediction of amphiphilic peptides to date. We noted two previous attempts to model the CAC of amphiphilic self-assembling peptides. In the first report, Tian et al.16 obtained their best-performing model by fitting a genetic algorithm feature selection-partial least-square model (GA-PLS) model on MD-HCF descriptors, which had an R2 value of 0.832 after fourfold cross-validation. In another report, Guo et al. used the same model on 680 conventional descriptors and reported an R2 value of 0.685 after 10-fold cross-validation. A comparison between the model presented here and those reported by Tian et al.16 and Guo et al.17 is not feasible, because they did not use a test set and the number of peptides in their data sets was lower than that in this study. Nonetheless, the reported R2 values are still lower than the R2 value of the test set in our study (0.9). Therefore, the best-performing model reported in our study can be used with higher reliability in designing novel self-assembling amphiphilic peptides.

Influential descriptors of the models can be more effectively harnessed in designing novel amphiphilic self-assembling peptides when they contain information about the contribution of each amino acid type at each position to their final values. This information is obtainable by the ACC technique. Tian et al.16 have suggested that the dynamic hydrophobicity of peptide atoms, which is reflected in MD-HCF descriptors, is the major determinant of the CAC value. The most influential descriptors in their model, which was developed using GA-PLS on CODESSA descriptors, were the octanol/water partition coefficient (log P), solvent-accessible molecular surface area (A), and molecular polarizability (α). A similar method was used here in the whole-peptide approach, where PaDEL descriptors for entire peptides were employed for modeling. The most influential descriptor for the best model in this approach, obtained by svmRadial, was the topological polar surface area (topoPSA),46 which is calculated by the summation of tabulated surface contributions of polar fragments. Regarding this observation, it can be suggested that the molecular surface area and also polarizability of the molecule are important determinants of the self-assembling tendency. Tian et al. also observed that CODESSA descriptors, representing the static state of the molecule, performed worse than MD-HCF descriptors, representing the dynamic state of the molecule. Here, the whole-peptide approach also performed worse than other approaches, indicating that amphiphilic peptide self-assembly cannot be adequately understood by the static molecular state. Guo et al.17 observed that a decrease in structural flexibility could decrease the CAC, which also emphasizes the influence of dynamic structural properties on the self-assembling tendency. None of these descriptors carry information about the importance of each amino acid type at a specific position in the self-assembly.

Interestingly, the PLS model in the z-scale approach performed better than both the whole-peptide and PCA approaches. The most important ACC in this model is the sum of products of z-scale 1 in two neighboring amino acids. z-scale 1 is related to amino-acid hydrophilicity as described by Jonsson et al.21 Therefore, it can be concluded that in this model, the hydrophobic interaction of two adjacent amino acids plays an important role in the CAC of the peptides. The other two z-scales are related to the side-chain bulk and electronic properties that are used to calculate the second influential ACC in the model. Therefore, one can increase the self-assembly tendency of an amphiphilic peptide by putting two highly hydrophobic amino acids in adjacent positions. The svmRadial model in the AP-scale approach outperformed the other models. The most influential ACC in this model was the sum of products of AP scales 1 and 3 with a lag of 1 (Table 3), meaning that the interaction between the aggregation propensities of Ala-AAi-Ala and AAi-Ala peptides in neighboring amino acids is crucial in determining the CAC value. The AP value for AAi-Ala dipeptides (AP scale 2) is equal to 1 for all dipeptides except those containing aromatic amino acids. This finding is in accordance with the observation by Frederix et al.14 on the computed AP values of tripeptides that neighboring aromatic amino acids have an intensifying effect on the aggregation propensity. The existence of AP for Ala-AAi-Ala peptides in two other influential ACCs makes it the most important descriptor in this model. However, the computed aggregation propensity of Ala-AAi-Ala peptides merely ranks amino acids based on the self-assembling tendency and does not provide physicochemical information.

To understand the physicochemical meaning of the calculated aggregation propensity, we carried out a Pearson correlation between these values and the PaDEL descriptors for Ala-AAi-Ala tripeptides. All electrotopological descriptors having a strong positive correlation with the aggregation propensity of Ala-AAi-Ala peptides had the highest values for aromatic amino acids. Also, descriptors having a strong negative correlation with this quantity had the lowest values for aromatic amino acids. This observation indicates the importance of aromatic amino acids in the self-assembling tendency. Moreover, as ACCs with a lag of 1 had a significant influence on the best-performing model, one can conclude that two adjacent aromatic amino acids can intensely drive amphiphilic peptide self-assembly. Our results are in accordance with the study by Frederix et al. They observed that two sequential aromatic amino acids increase the self-assembly tendency. They hypothesized that this phenomenon is due to the conformation of the backbone and aromatic interactions.14 However, more studies are needed to get a better physicochemical interpretation on the aggregation propensity of di- and tripeptides as descriptors.

To our knowledge, this is the first report on the modeling of CAC values for amphiphilic peptides that includes long peptides (70–100 amino acids). Reduction in the accuracy on adding long peptides indicates that principles governing the self-assembly of short peptides might be less applicable for the longer ones. However, it is not clear whether inclusion or exclusion of ultra-short peptides (RF) in the data set can improve the model performance because long and also ultra-short peptides had a low frequency in our data set. Therefore, future studies on data sets with a higher number of ultra-short and long peptides are needed to determine whether self-assembling principles change by peptide length.

Conclusions

The successful prediction of CAC for amphiphilic self-assembling peptides by the novel descriptor set, reported in this study, brings forward several opportunities in the field. Besides enabling better design and screening of the amphiphilic peptides containing coded amino acids, the relationship between the AP scale of AAi-Ala, Ala-AAi, and Ala-AAi-Ala peptides and the CAC of longer amphiphilic peptides suggests the possibility of CAC determination by CG-MD simulation of newly designed peptides that contain noncoded amino acids. Although screening of sequence space for di- and tripeptides has been reported, performing the same for longer peptides might exceed the current computational capacity. The model developed here could help us to reduce the computational burden in the screening of longer peptides for finding new self-assembling peptides.

Materials and Methods

General Strategy

Four different approaches were used for QSPR analysis of self-assembling amphiphilic peptides (Figure 1). In the first approach (whole-peptide approach, indicated by a black line), structures for the whole-peptide molecules were generated and descriptors were defined for these structures. In the second approach (PCA approach, indicated by a red line), peptide sequences were split into Ala-AAi-Ala peptides, where AAi was substituted for each amino acid in the sequence. Descriptors were defined for these tripeptides and their principal components were calculated and used for the next steps. In the other two approaches, indicated by blue (z-scale approach) and purple (AP/APH-scale approach) lines, no structure building or optimization was used. Instead, two different sets of scales were defined for each amino acid in the peptide structure.

Data Set

A database containing 74 amphiphilic peptides was constructed through a literature search. The CAC value of the included peptides was measured in pure water because the ionic strength of the solution can affect the CAC value. Moreover, when two or more reports existed for the same peptide sequence, the value measured by the more accurate method was included. Six peptides with noncoded amino acids and five long peptides (70–100 amino acids in length) were then removed to obtain a data set of 63 peptides. All CAC concentrations, which ranged from 0.01 to 2.3 × 10–7 M, were transformed into their negative logarithms before use in QSPR studies. The peptide data set is presented in Table 1 and their structures are shown in Table S4.

Structures

Peptide sequences were converted to two- and three-dimensional structures. All structures of amphiphilic peptides were built using Marvin software 19.17.0, 2019, ChemAxon (www.chemaxon.com). Briefly, the FASTA formats of peptide sequences were prepared and converted to images of one-dimensional (1D) structures by the Molconvert command. Terminal acetyl and amine groups were added manually where needed for the whole-peptide structures and also for all Ala-AAi-Ala tri-peptide structures. Charges were then applied to the structures at pH 7.00. The generated 1D structures were converted to two-dimensional (2D) and three-dimensional (3D) structures by Marvin software’s command-line options, where the MMFF94 force field was used to optimize the 3D structures. This step is presented as the “Structure Drawing” node in Figure 1. The commands used for the generation of peptide structures are summarized in Tables S1–S3. The generated structures are provided as a separate zip file.

Descriptors

Four sets of descriptors were defined for amphiphilic peptides in the data set. Descriptor sets for whole-peptide molecular structures and Ala-AAi-Ala tripeptides (whole-peptide and PCA approaches) were generated using PaDEL descriptors software (version 2.21).47 PaDEL generated 1875 descriptors including 1444 1D and 2D descriptors, 431 3D descriptors, and 12 types of molecular fingerprints.47 In the z-scale approach, each amino acid in the peptide sequence was replaced with the three extended z-scales introduced by Jonsson et al.,46 generating a 3 × n matrix for each peptide, where n is the length of the peptide. In the final approach, we used a novel set of descriptors that were derived from the AP of di- and tripeptides simulated in the MARTINI force field13,14 and its derivative normalized for solubility (APH). Similar to the z-scale approach, each amino acid in the peptide sequence was replaced with defined scales (Figure 1 and Table S5). In step 1, the scales were selected from the AP of AAi-Ala and Ala-AAi dipeptides, where AAi was substituted for the amino acid in the sequence. In step 2, the scales were APs for Ala-AAi-Ala peptides. In step 3, if the terminal amino acids were not capped (acetylated or aminated), AAi-Ala-Ala and Ala-Ala-AAi were selected for carboxyl and amine termini, respectively. The same process was performed for all APH scales. The matrices generated for all amphiphilic peptide sequences are provided in a zip file.

Data Processing

Different data preparation steps were taken for different QSPR approaches before fitting the same models on each data set. In the whole-peptide and PCA approaches, descriptors with near-zero variance and high correlation were removed from the data set. The resulting data set was directly used for model building in the whole-peptide approach. As for the PCA approach, principal components of the descriptor sets were calculated and 14 PCs that cover 90 percent of the variance were selected. A matrix for each peptide was constructed like matrices described for the z-scale and AP-scale approaches, by replacing 14 PCs for each amino acid in the peptide sequence. Since peptides with different sequence lengths produced matrices with different dimensions in the PCA, z-scale, and AP-scale approaches, the auto cross-covariance of each matrix was calculated according to eq 1 to produce a matrix for the model-building step,22 which was implemented in the RCPI package.48

graphic file with name ao1c01293_m001.jpg 1

where j and k are used for the scales (j = 1, 2, 3...,), n is the number of amino acids in a sequence, and i is the amino acid position (i = 1, 2... n...). Data sets were then split into the train and test sets. Four models were fitted on the train sets in each approach: namely, support vector machine with the radial kernel (svmRadial), support vector machine with the linear kernel (svmLinear), partial least square (PLS), and generalized boosted models (GBM). A 10-fold cross-validation was performed to evaluate the model fitted on the train sets. Finally, the best model was used to predict the CAC values in the test set. All model-building and evaluation steps were done using the CARET package of R. Calculation of RSE was performed using eq 2 to select the model with the best performance on the test set

graphic file with name ao1c01293_m002.jpg 2

where Yi is the experimental value of Y, Ŷi is the predicted value by model, n is the sample size, and df is the degree of freedom.

Influential Descriptors

Models were further studied by investigating their important descriptors. The important descriptors in the best model for each approach were extracted using the “VarImp()” function from the CARET package of R, which sorts descriptors with the most influence on the model. The correlation between the AP for Ala-AAi-Ala peptides and PaDEL descriptors was determined using standard R functions.

Peptide Length

To evaluate the ability of the best model to predict the CAC of longer peptides, these peptides were added to the data set before splitting into the train and test sets. Finally, the effect on model performance was evaluated once with and once without the shortest peptide in the data set (named RF).

Acknowledgments

We thank Dr. Pim W. J. M. Frederix for generously providing the calculated AP and APH values for the tripeptides. We also thank Dr. Amirhossein Sakhteman for the initial assistance in model building and Dr. Saeed Yousefinejad for suggesting the use of the PCA approach. This project was financially supported by Pasteur Institute of Iran (Grant Nos. 934 and 692 and thesis number BP-9583) and Iran National Science Fund (INSF) (Grant No. 98008933).

Glossary

Abbreviations

ACC

auto cross-covariance

AP

aggregation propensity

CAC

critical aggregation concentration

CG-MD

coarse-grained molecular dynamics

CMC

critical micelle concentration

DLS

dynamic light scattering

GA-PLS

genetic algorithm feature selection-partial least-square model

GBM

gradient boosting machine

I-state

intrinsic state

MD

molecular dynamics

MD-HCF

molecular dynamics-based hydrophobic cross-field

PCA

principal component analysis

PLS

partial least squares

QSPR

quantitative structure–property relationship

RSE

residual standard error

SVM

support vector machines

svmLinear

support vector machine with the linear kernel

svmRadial

support vector machine with radial kernel

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c01293.

  • Commands for generation of structures in Marvin; amphiphilic peptide data set with more detail; structures of di- and tripeptides used for AP/APH-scales calculations; and the effect of long peptides on influential ACCs (PDF)

  • 2D and 3D structures of peptide data set; 2D and 3D structures of di- and tripeptides; and AP-scale matrices (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ao1c01293_si_001.pdf (1.5MB, pdf)
ao1c01293_si_002.zip (461.4KB, zip)

References

  1. Dasgupta A.; Das D. Designer Peptide Amphiphiles: Self-Assembly to Applications. Langmuir 2019, 35, 10704–10724. 10.1021/acs.langmuir.9b01837. [DOI] [PubMed] [Google Scholar]
  2. Dehsorkhi A.; Castelletto V.; Hamley I. W. Self-Assembling Amphiphilic Peptides. J. Pept. Sci. 2014, 20, 453–467. 10.1002/psc.2633. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Santoso S. S.; Vauthey S.; Zhang S. Structures, Function and Applications of Amphiphilic Peptides. Curr. Opin. Colloid Interface Sci. 2002, 7, 262–266. 10.1016/S1359-0294(02)00072-9. [DOI] [Google Scholar]
  4. Zhang S.; Holmes T.; Lockshin C.; Rich A. Spontaneous Assembly of a Self-Complementary Oligopeptide to Form a Stable Macroscopic Membrane. Proc. Natl. Acad. Sci. U.S.A. 1993, 90, 3334–3338. 10.1073/pnas.90.8.3334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Liu J.; Zhang L.; Yang Z.; Zhao X. Controlled Release of Paclitaxel from a Self-Assembling Peptide Hydrogel Formed in Situ and Antitumor Study in Vitro. Int. J. Nanomed. 2011, 6, 2143. 10.2147/IJN.S24038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Yan X.; He Q.; Wang K.; Duan L.; Cui Y.; Li J. Transition of Cationic Dipeptide Nanotubes into Vesicles and Oligonucleotide Delivery. Angew. Chem. 2007, 119, 2483–2486. 10.1002/ange.200603387. [DOI] [PubMed] [Google Scholar]
  7. Zepeda-Cervantes J.; Vaca L. Induction of Adaptive Immune Response by Self-Aggregating Peptides. Expert Rev. Vaccines 2018, 17, 723–738. 10.1080/14760584.2018.1507742. [DOI] [PubMed] [Google Scholar]
  8. Zhao X.; Nagai Y.; Reeves P. J.; Kiley P.; Khorana H. G.; Zhang S. Designer Short Peptide Surfactants Stabilize G Protein-Coupled Receptor Bovine Rhodopsin. Proc. Natl. Acad. Sci. U.S.A. 2006, 103, 17707–17712. 10.1073/pnas.0607167103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Seow W. Y.; Yang Y.-Y. A Class of Cationic Triblock Amphiphilic Oligopeptides as Efficient Gene-Delivery Vectors. Adv. Mater. 2009, 21, 86–90. 10.1002/adma.200800928. [DOI] [Google Scholar]
  10. Ravichandran R.; Griffith M.; Phopase J. Applications of Self-Assembling Peptide Scaffolds in Regenerative Medicine: The Way to the Clinic. J. Mater. Chem. B 2014, 2, 8466–8478. 10.1039/C4TB01095G. [DOI] [PubMed] [Google Scholar]
  11. Yang S. J.Self-Assembly of Aurfactant-like Amphiphilic Peptides Made of Natural Amino Acids; Massachusetts Institute of Technology: Cambridge, USA, 2004. [Google Scholar]
  12. Lampel A.; Ulijn R.; Tuttle T. Guiding Principles for Peptide Nanotechnology through Directed Discovery. Chem. Soc. Rev. 2018, 47, 3737–3758. 10.1039/C8CS00177D. [DOI] [PubMed] [Google Scholar]
  13. Frederix P. W.; Ulijn R. V.; Hunt N. T.; Tuttle T. Virtual Screening for Dipeptide Aggregation: Toward Predictive Tools for Peptide Self-Assembly. J. Phys. Chem. Lett. 2011, 2, 2380–2384. 10.1021/jz2010573. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Frederix P. W.; Scott G. G.; Abul-Haija Y. M.; Kalafatovic D.; Pappas C. G.; Javid N.; Hunt N. T.; Ulijn R. V.; Tuttle T. Exploring the Sequence Space for (tri-) Peptide Self-Assembly to Design and Discover New Hydrogels. Nat. Chem. 2015, 7, 30. 10.1038/nchem.2122. [DOI] [PubMed] [Google Scholar]
  15. Hu J.; Zhang X.; Wang Z. A Review on Progress in QSPR Studies for Surfactants. Int. J. Mol. Sci. 2010, 11, 1020–1047. 10.3390/ijms11031020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Tian F.; Wu J.; Huang N.; Guo T.; Mao C. The Critical Aggregation Concentration of Peptide Surfactants Is Predictable from Dynamic Hydrophobic Property. SAR QSAR Environ. Res. 2013, 24, 89–101. 10.1080/1062936X.2012.742134. [DOI] [PubMed] [Google Scholar]
  17. Guo T.; Yang J.; Zeng L.; Wang H.; Tong Q.; Li X. Does There Exist an Intrinsic Relationship between the Flexibility and Self-Assembly of Pepfactants?. Mol. Simul. 2014, 40, 423–430. 10.1080/08927022.2013.817673. [DOI] [Google Scholar]
  18. Linati L.; Lusvardi G.; Malavasi G.; Menabue L.; Menziani M. C.; Mustarelli P.; Segre U. Qualitative and Quantitative Structure–Property Relationships Analysis of Multicomponent Potential Bioglasses. J. Phys. Chem. B 2005, 109, 4989–4998. 10.1021/jp046631n. [DOI] [PubMed] [Google Scholar]
  19. Jamal S.; Grover A.; Grover S. Machine Learning from Molecular Dynamics Trajectories to Predict Caspase-8 Inhibitors against Alzheimer’s Disease. Front. Pharmacol. 2019, 10, 780 10.3389/fphar.2019.00780. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Van Lommel R.; Zhao J.; De Borggraeve W. M.; De Proft F.; Alonso M. Molecular Dynamics Based Descriptors for Predicting Supramolecular Gelation. Chem. Sci. 2020, 11, 4226–4238. 10.1039/D0SC00129E. [DOI] [Google Scholar]
  21. Jonsson J.; Eriksson L.; Hellberg S.; Sjöström M.; Wold S. Multivariate Parametrization of 55 Coded and Non-Coded Amino Acids. Quant. Struct.-Act. Relat. 1989, 8, 204–209. 10.1002/qsar.19890080303. [DOI] [Google Scholar]
  22. Andersson P. M.; Sjöström M.; Lundstedt T. Preprocessing Peptide Sequences for Multivariate Sequence-Property Analysis. Chemom. Intell. Lab. Syst. 1998, 42, 41–50. 10.1016/S0169-7439(98)00062-8. [DOI] [Google Scholar]
  23. Liang J.; Wu W.-L.; Xu X.-D.; Zhuo R.-X.; Zhang X.-Z. pH Responsive Micelle Self-Assembled from a New Amphiphilic Peptide as Anti-Tumor Drug Carrier. Colloids Surf., B 2014, 114, 398–403. 10.1016/j.colsurfb.2013.10.037. [DOI] [PubMed] [Google Scholar]
  24. Qiu F.; Chen Y.; Zhao X. Comparative Studies on the Self-Assembling Behaviors of Cationic and Catanionic Surfactant-like Peptides. J. Colloid Interface Sci. 2009, 336, 477–484. 10.1016/j.jcis.2009.04.014. [DOI] [PubMed] [Google Scholar]
  25. Meng Q.; Kou Y.; Ma X.; Liang Y.; Guo L.; Ni C.; Liu K. Tunable Self-Assembled Peptide Amphiphile Nanostructures. Langmuir 2012, 28, 5017–5022. 10.1021/la3003355. [DOI] [PubMed] [Google Scholar]
  26. Yang S. J.; Zhang S. Self-Assembling Behavior of Designer Lipid-like Peptides. Supramol. Chem. 2006, 18, 389–396. 10.1080/10615800600658586. [DOI] [Google Scholar]
  27. Castelletto V.; Gouveia R.; Connon C.; Hamley I.; Seitsonen J.; Nykänen A.; Ruokolainen J. Alanine-Rich Amphiphilic Peptide Containing the RGD Cell Adhesion Motif: A Coating Material for Human Fibroblast Attachment and Culture. Biomater. Sci. 2014, 2, 362–369. 10.1039/C3BM60232J. [DOI] [PubMed] [Google Scholar]
  28. Cao M.; Lu S.; Zhao W.; Deng L.; Wang M.; Wang J.; Zhou P.; Wang D.; Xu H.; Lu J. R. Peptide Self-Assembled Nanostructures with Distinct Morphologies and Properties Fabricated by Molecular Design. ACS Appl. Mater. Interfaces 2017, 9, 39174–39184. 10.1021/acsami.7b11681. [DOI] [PubMed] [Google Scholar]
  29. Cao M.; Shen Y.; Wang Y.; Wang X.; Li D. Self-Assembly of Short Elastin-like Amphiphilic Peptides: Effects of Temperature, Molecular Hydrophobicity and Charge Distribution. Molecules 2019, 24, 202 10.3390/molecules24010202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kornmueller K.; Letofsky-Papst I.; Gradauer K.; Mikl C.; Cacho-Nerin F.; Leypold M.; Keller W.; Leitinger G.; Amenitsch H.; Prassl R. Tracking Morphologies at the Nanoscale: Self-Assembly of an Amphiphilic Designer Peptide into a Double Helix Superstructure. Nano Res. 2015, 8, 1822–1833. 10.1007/s12274-014-0683-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Hamley I. W.; Kirkham S.; Dehsorkhi A.; Castelletto V.; Adamcik J.; Mezzenga R.; Ruokolainen J.; Mazzuca C.; Gatto E.; Venanzi M.; et al. Self-Assembly of a Model Peptide Incorporating a Hexa-Histidine Sequence Attached to an Oligo-Alanine Sequence, and Binding to Gold NTA/nickel Nanoparticles. Biomacromolecules 2014, 15, 3412–3420. 10.1021/bm500950c. [DOI] [PubMed] [Google Scholar]
  32. Silva E. R.; Listik E.; Han S. W.; Alves W. A.; Soares B. M.; Reza M.; Ruokolainen J.; Hamley I. W. Sequence Length Dependence in Arginine/phenylalanine Oligopeptides: Implications for Self-Assembly and Cytotoxicity. Biophys. Chem. 2018, 233, 1–12. 10.1016/j.bpc.2017.11.005. [DOI] [PubMed] [Google Scholar]
  33. Kornmueller K.; Lehofer B.; Meindl C.; Fröhlich E.; Leitinger G.; Amenitsch H.; Prassl R. Peptides at the Interface: Self-Assembly of Amphiphilic Designer Peptides and Their Membrane Interaction Propensity. Biomacromolecules 2016, 17, 3591–3601. 10.1021/acs.biomac.6b01089. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Kornmueller K.; Lehofer B.; Leitinger G.; Amenitsch H.; Prassl R. Peptide Self-Assembly into Lamellar Phases and the Formation of Lipid-Peptide Nanostructures. Nano Res. 2018, 11, 913–928. 10.1007/s12274-017-1702-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Da Silva E. R.; Walter M. N. M.; Reza M.; Castelletto V.; Ruokolainen J.; Connon C. J.; Alves W. A.; Hamley I. W. Self-Assembled Arginine-Capped Peptide Bolaamphiphile Nanosheets for Cell Culture and Controlled Wettability Surfaces. Biomacromolecules 2015, 16, 3180–3190. 10.1021/acs.biomac.5b00820. [DOI] [PubMed] [Google Scholar]
  36. Holowka E. P.; Pochan D. J.; Deming T. J. Charged Polypeptide Vesicles with Controllable Diameter. J. Am. Chem. Soc. 2005, 127, 12423–12428. 10.1021/ja053557t. [DOI] [PubMed] [Google Scholar]
  37. Xu H.; Wang J.; Han S.; Wang J.; Yu D.; Zhang H.; Xia D.; Zhao X.; Waigh T. A.; Lu J. R. Hydrophobic-Region-Induced Transitions in Self-Assembled Peptide Nanostructures. Langmuir 2009, 25, 4115–4123. 10.1021/la802499n. [DOI] [PubMed] [Google Scholar]
  38. Wang X.; Corin K.; Baaske P.; Wienken C. J.; Jerabek-Willemsen M.; Duhr S.; Braun D.; Zhang S. Peptide Surfactants for Cell-Free Production of Functional G Protein-Coupled Receptors. Proc. Natl. Acad. Sci. U.S.A. 2011, 108, 9049–9054. 10.1073/pnas.1018185108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Pan F.; Zhao X.; Perumal S.; Waigh T. A.; Lu J. R.; Webster J. R. Interfacial Dynamic Adsorption and Structure of Molecular Layers of Peptide Surfactants. Langmuir 2010, 26, 5690–5696. 10.1021/la9037952. [DOI] [PubMed] [Google Scholar]
  40. Cao M.; Cao C.; Zhou P.; Wang N.; Wang D.; Wang J.; Xia D.; Xu H. Self-Assembly of Amphiphilic Peptides: Effects of the Single-Chain-to-Gemini Structural Transition and the Side Chain Groups. Colloids Surf., A 2015, 469, 263–270. 10.1016/j.colsurfa.2015.01.044. [DOI] [Google Scholar]
  41. Han S.; Cao S.; Wang Y.; Wang J.; Xia D.; Xu H.; Zhao X.; Lu J. R. Self-Assembly of Short Peptide Amphiphiles: The Cooperative Effect of Hydrophobic Interaction and Hydrogen Bonding. Chem. - Eur. J. 2011, 17, 13095–13102. 10.1002/chem.201101970. [DOI] [PubMed] [Google Scholar]
  42. Nagai A.; Nagai Y.; Qu H.; Zhang S. Dynamic Behaviors of Lipid-like Self-Assembling Peptide A6D and A6K Nanotubes. J. Nanosci. Nanotechnol. 2007, 7, 2246–2252. 10.1166/jnn.2007.647. [DOI] [PubMed] [Google Scholar]
  43. Khoe U.; Yang Y.; Zhang S. Self-Assembly of Nanodonut Structure from a Cone-Shaped Designer Lipid-like Peptide Surfactant. Langmuir 2009, 25, 4111–4114. 10.1021/la8025232. [DOI] [PubMed] [Google Scholar]
  44. de Bruyn Oubote D.Rational Design of Purely Peptidic Amphiphiles for Drug Delivery Applications; University of Basel, 2011. [Google Scholar]
  45. Katritzky A. R.; Pacureanu L. M.; Slavov S. H.; Dobchev D. A.; Shah D. O.; Karelson M. QSPR Study of the First and Second Critical Micelle Concentrations of Cationic Surfactants. Comput. Chem. Eng. 2009, 33, 321–332. 10.1016/j.compchemeng.2008.09.011. [DOI] [Google Scholar]
  46. Ertl P.; Rohde B.; Selzer P. Fast Calculation of Molecular Polar Surface Area as a Sum of Fragment-Based Contributions and Its Application to the Prediction of Drug Transport Properties. J. Med. Chem. 2000, 43, 3714–3717. 10.1021/jm000942e. [DOI] [PubMed] [Google Scholar]
  47. Yap C. W. PaDEL-Descriptor: An Open Source Software to Calculate Molecular Descriptors and Fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. 10.1002/jcc.21707. [DOI] [PubMed] [Google Scholar]
  48. Cao D.-S.; Xiao N.; Xu Q.-S.; Chen A. F. Rcpi: R/Bioconductor Package to Generate Various Descriptors of Proteins, Compounds and Their Interactions. Bioinformatics 2015, 31, 279–281. 10.1093/bioinformatics/btu624. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c01293_si_001.pdf (1.5MB, pdf)
ao1c01293_si_002.zip (461.4KB, zip)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES