Theoretical Study of Actinide(III)-DOTA Complexes

Abstract

1,4,7,10-Tetraazacyclododecane-N,N′,N″,N‴-tetraacetic acid (DOTA) is a prominent chelating ligand used in imaging contrast agents and radiopharmaceuticals. The present study explores the stabilities, structures, and bonding properties of its complexes with trivalent actinides (Ac, U, Np, Pu, Am, Cm, Cf) using density functional theory and relativistic multireference calculations. For reference purposes, the La- and Lu-DOTA complexes are also included. Similar to La³⁺, the large An³⁺ ions prefer the TSAP conformer of the ligand. The An–ligand bonding is mainly electrostatic, with minor charge transfer contributions to the An 6d orbitals. For the assessment of the thermodynamic stabilities in aqueous solution, PCM radii to use in conjunction with the SMD solvation model were developed. Basically, the thermodynamic stability of the DOTA complexes increases along the An row but with notable counteracting of spin–orbit coupling.

Introduction

1,4,7,10-Tetraazacyclododecane-N,N′,N″,N‴-tetraacetic acid (DOTA)^1,2 is a distinguished carrier of metal-based imaging contrast agents and radiopharmaceuticals³ on the basis of the high thermodynamic stabilities of these chelate complexes and their kinetic inertness in physiological conditions. Its compound with gadolinium is known as the MRI contrast agent Dotarem,⁴ while europium(III), ytterbium(III), and thulium(III) complexes with DOTA derivatives were considered as paramagnetic chemical exchange transfer (PARACEST) agents.⁵⁻⁷ DOTA was also tested with γ-emitting radiometals such as ^99mTc and ¹¹¹In for diagnostic tumor targeting.⁸ However, the most eminent recent application of this chelating agent emerged in targeted α-therapy (TAT).^9,10

TAT is based on the short range and high energy of α-particles emitted from radioactive isotopes. By appropriate biological targeting vectors (antibody or peptide), the chelate complexes can be carried to and thus selectively destroy solid tumors and metastates.¹¹⁻¹⁵ Prominent examples include the treatment of metastatic castration-resistant prostate cancer,¹⁶⁻¹⁸ acute myeloid leukemia,^19,20 neuroendocrine tumors,²¹ and tumors expressing mesothelin.²² Presently, DOTA (or its derivative) is a primary choice for chelating ²¹³Bi, ²²⁵Ac, and the β-emitting ¹⁷⁷Lu isotopes used in radiotherapy.^23,24 These agents passed successfully already the first clinical tests.^24,25 Aiming for further improvement, the field is the subject of intense current research.^{9,10,23,24,26,27}

New possibilities can emerge from the application of other actinide (An) radioisotopes. As the stability of DOTA complexes increases generally with decreasing metal size,^28,29 the smaller An ions in the middle of the An row can be expected to form more stable complexes with DOTA compared to Ac³⁺. From the actinides, the medical application of ²²⁷Th is already at an advanced clinical test level with the HOPO chelator.^{10,18,30−33} The α-emitting ²³⁰U isotope, due to its short half-life of 20.83 days, can be a promising agent for TAT.³⁴ However, a proper complexation of this An is challenging due to its reversible redox properties (a recent study of U-DOTA with axially bonded H₂O and hydroxide found the U^IV/U^III redox couple to be quasi-reversible³⁵) and the under in vivo conditions very stable UO₂²⁺ form.^36,37 Last but not the least, the slow neutron-emitting ²⁵²Cf isotope should be mentioned to be suitable for brachytherapy or internal radiation therapy.^38,39

The aim of the present study is to comparatively analyze DOTA complexes with trivalent An (U, Np, Pu, Am, Cm, Cf) and to elucidate the trend in their stability and bonding properties. For this reason, the other frequent oxidation states of U, Np, and Pu are not included here. On the other hand, data of La-DOTA and Lu-DOTA are included for reference purposes. For these latter complexes, reliable experimental data on their structures^40,41 and stability^28,42,43 are available, which are used to validate the theoretical methods chosen for the present study.

The DOTA complexes of lanthanides (Ln) are well explored in the literature.^2,28,42,44 In contrast, little is known about the An-DOTA complexes. Because of its TAT application, Ac-DOTA is the most known.⁴⁵⁻⁵¹ In addition, there are a few recent studies on the stability constants of Am- and Cm-DOTA,^47,52 water coordination in Cm-DOTA,^47,52 and on the aqueous chemistry of An(IV)-DOTA complexes (An = Th, U, Np, Pu).^35,53,54

Results and Discussion

Structure

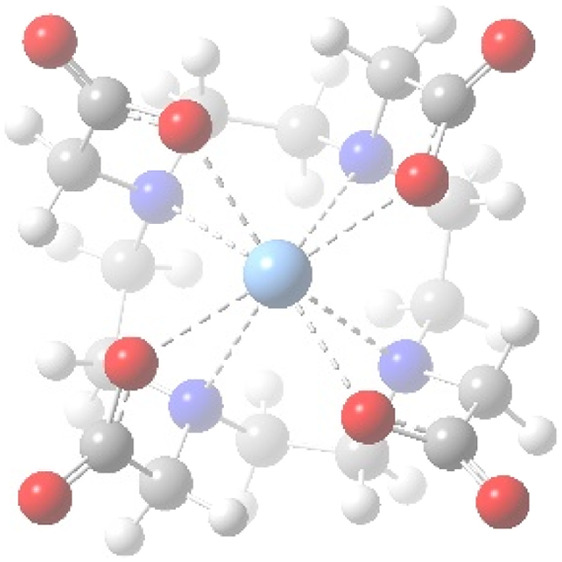
The DOTA ligand is a 12-membered tetraazamacrocycle containing four pendant carboxylate arms (Figure 1a). The structure of the chelate complex depends on the size of the metal centers.² Large metal ions (lanthanides and heavy metals) are coordinated to the four N atoms of the cyclen ring and to the four O atoms from the COO^– arms, leaving sufficient free space for a 9th coordination,^{40,41,55−60} e.g., to a H₂O molecule (Figure 1b). Other metals (e.g., Ca, Bi, and Sc) were shown to have a coordination number of CN = 8,^56,61,62 while the coordination of small transition metals is limited to the four N atoms and two or three carboxylates (CN = 6, 7).^57,63−65

Figure 1.

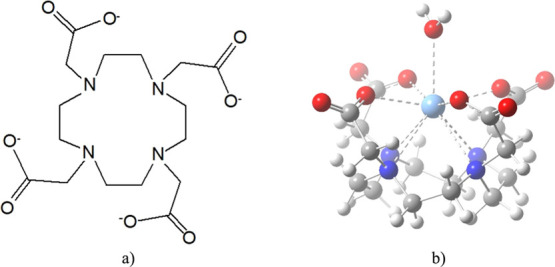
(a) DOTA^4– ligand and (b) structure of the Ac(DOTA)(H₂O)⁻ complex.

The DOTA ligand can appear as two diastereoisomeric pairs of enantiomers in its octacoordinated complexes.⁴⁴ One stereochemical element is the macrocycle, where the binding of the metal to the four N atoms fixes the four ethylene groups either in a δ- or a λ-gauche orientation (δδδδ or λλλλ, respectively). The four COO^– groups represent the other stereochemical element and can form two opposite helical arrangements, Δ and Λ. Thus, the diastereoisomeric pairs are Λ(δδδδ)/Δ(λλλλ) where the ring and the arms have opposite helicities and Δ(δδδδ)/Λ(λλλλ) with the same ring and acetate helicity. The former conformers possess a square antiprismatic coordination geometry (designated as SAP or M in the literature), while the latter ones give a twisted square antiprismatic structure (designated as TSAP or m).

The conformational properties of Ln-DOTA complexes have been studied extensively. The crystal structures have been determined for the La,⁴⁰ Ce, Pr, Nd, Dy, Ho,⁵⁶ Eu,^55,56 Gd,^57,66 Tm,⁵⁶ and Lu⁴¹ complexes. These studies revealed that the complexes from Pr to Lu (except for Tm) crystallize in the SAP geometry, while the complexes with the larger La and Ce crystallize in the TSAP geometry. The regular conformations and the switch between Ce and Pr were ascribed to the Ln³⁺-contraction, namely, how the Ln³⁺ ions match the different sizes and shapes of the cavities (determined primarily by the carboxylate arms) of the two DOTA conformers. The exceptional eight-coordinate TSAP crystal structure of Tm-DOTA was ascribed to the missing H₂O ligand,⁵⁶ which at the 9th coordination site supports the SAP geometry in the crystal. According to NMR studies, in solution, the Ln-DOTA complexes present mixtures of two conformers.^67,68 The ratio of the SAP and TSAP conformers depends somewhat on the concentration of inorganic salts in the solution, temperature, and pressure, but essentially, the trend in the crystal state was found in solution, too. The H₂O ligand at the 9th coordination site is involved in a rapid exchange process with the solvent H₂O molecules, hence the observed C₄ symmetry.^43,69

Early quantum chemical calculations performing geometry optimization at the Hartree–Fock (HF) level⁷⁰ and B3LYP single-point energy calculations on HF-optimized geometries⁷¹ reproduced the trend of the increasing SAP preference along the Ln row. The small free energy differences between the two conformers (within 10 kJ/mol in aqueous solution⁴³) could quite well be reproduced at the B3LYP/6-311G**//HF/3-21 level using the C-PCM solvation model.⁷² From the actinides, theoretical results are available only for Ac-DOTA: in these recent DFT calculations modeling the aqueous solution, the TSAP conformer proved to be the most stable one.^48,49 Accordingly, for the other large An³⁺ ions, the preference of the TSAP conformer can be expected.

The present TPSSh/TZ calculations using the SMD solvation model with PCM radii^73,74 reproduced well the experimental ΔG°₂₉₈ differences of the TSAP and SAP conformers for the La and Lu complexes⁴³ (Figure 2). They are also in accord with previous reports on solvent effects enhancing the stability of the TSAP conformer in water:^71,75 in the crystal, the switch from TSAP to SAP was observed between Ce and Pr,⁵⁶ while in solution, it was observed between Nd and Sm.⁴³ However, while being pleased about the shown performance of the present computational level, the possibility of fortuitous error cancellation of the theoretical models for this complex chemical system should be kept in mind. Nevertheless, the computed preference of the TSAP conformers for the large early actinides agrees with the expectations.

Figure 2.

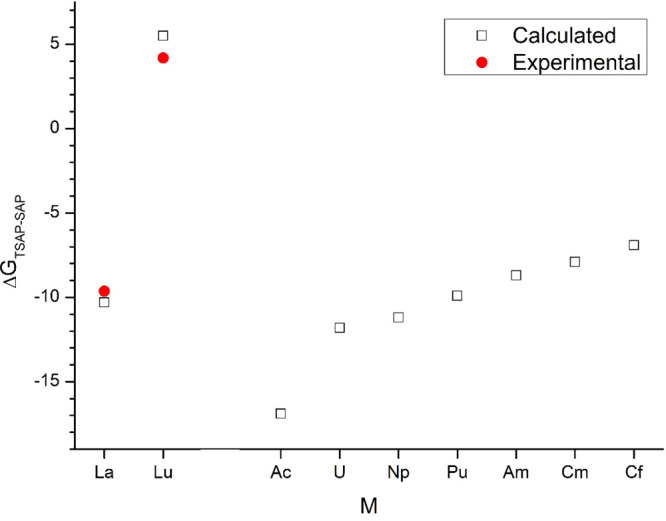
Calculated ΔG°₂₉₈ differences (kJ/mol) of the TSAP and SAP conformers of M(DOTA)(H₂O)⁻ complexes. Calculated at the TPSSh/TZ geometries using the SMD solvation model in conjunction with PCM ionic radii.

On the other hand, the marked preference of the TSAP geometry for the Cf complex is somewhat unexpected in view of its size. The ionic radius of six-coordinate Cf³⁺ is 1.09 Å, comparable to the one of Sm³⁺ (1.098 Å).⁷⁶ The Sm-DOTA complex is known to appear in the SAP form in aqueous solution.^43,71 Hence, strictly on the basis of the ionic size from the literature, Cf³⁺ would be expected to prefer the SAP conformer, too. However, the abovementioned radii refer to six-coordinate metal ions, while in the M-DOTA complexes, they are nine-coordinate (which M³⁺ radii are not available). Furthermore, the bonding interactions of lanthanides can somewhat deviate from those of the actinides; hence, a comparison on the basis of ionic radii alone does not apply.

Based on the found preference of the TSAP conformer for actinide complexes, the following analyses are restricted on these isomers using the TPSSh/TZ optimized structures.

Figure 3 demonstrates an excellent correlation between the M³⁺ ionic radii⁷⁶ and the computed M–O and M–N bond distances in the DOTA complexes. The H₂O ligand at the 9th coordination site has a small influence on the M–DOTA interaction, as seen in the slight increase (0.03–0.04 Å) of the M–O and M–N bond distances upon coordination of H₂O. The H₂O ligand is bonded relatively weakly to the metal: the M–OH₂ bonds are longer by 0.09–0.17 Å than the M–O bonds with DOTA. The main reason is the neutral nature of the H₂O oxygen, in contrast to the anionic carboxylate oxygens of DOTA. Another effect is the probable electrostatic repulsion with the adjacent carboxylate arms (cf. Figure 1b).

Figure 3.

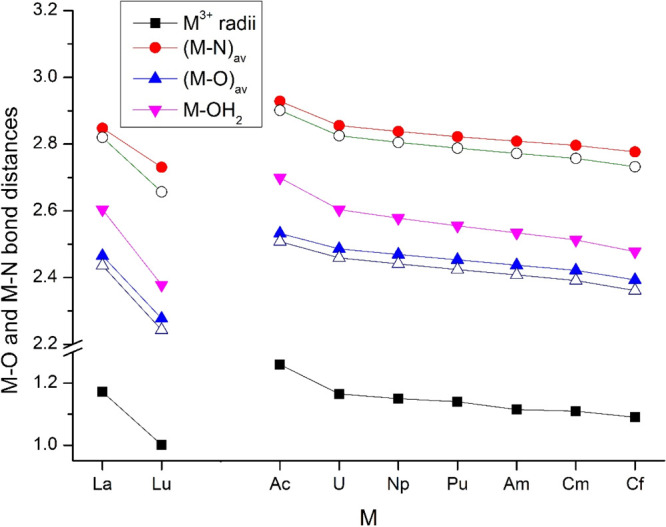
Comparison of M–O and M–N bond distances (Å) of M(DOTA)(H₂O)⁻ (filled symbols) and M(DOTA)⁻ (empty symbols) complexes optimized at the TPSSh/TZ level as well as the M³⁺ ionic radii.⁷⁶ The slightly differing values originating from the C₂ symmetry of M(DOTA)(H₂O)⁻ structures are averaged.

Obviously, the M–O interaction with the anionic carboxylate oxygens is the strongest component of the M–DOTA bonding. The Wiberg bond indices⁷⁷ are ca. 0.2 for this interaction (cf. Table S3 in the Supporting Information). The Wiberg indices for the M–N interactions are ca. 0.1, while those for the M–OH₂ interaction are around 0.14, in agreement with the relations of the respective bond distances in Figure 3.

Relativistic Multireference Calculations

In order to verify the multiconfigurational nature and the role of the 5f subshell in the metal–ligand interactions, CASSCF calculations were performed on the An(DOTA)(H₂O)⁻ and An(DOTA)⁻ TSAP structures. Selected characteristics of the spin–orbit (SO) and spin–orbit–free (SF) ground states are compiled in Table 1. In addition, the SO energies were utilized as correction terms in the evaluation of the thermodynamic stabilities (vide infra).

Table 1. Selected Characteristics of the Spin–Orbit (SO) and Spin–Orbit–Free (SF) Ground States of the An(DOTA)(H₂O)⁻ Complexes.

An	statea	SO composition (%)b	SF composition (%)c
Ac	1S0	1A (100)	1A (100)
U	4I9/2	4A (26) + 4B (25) + 4A (17) + 4B (14)	4A (83)
Np	5I4	5A (33) + 5A (29)	5A (82)
Pu	6H5/2	6B (29) + 6B (28) + 6A (15)	6B (71)
Am	7F0	6B (32) + 6B (31)	6B (100)
Cm	8S7/2	8A (100)	8A (100)
Cf	6H	-d	7A (55)

^aTerm symbol of the An state.

^bComposition of the SO ground state from the SF states (lowest-energy ones from the C₂ irreps).

^cSymmetry and contribution of the main electron configuration of the SF ground state.

^dThe hyphen means that SO calculation could not be performed with the Cf pseudopotential in MOLCAS.

The electronic characters (term symbols) of An in the SO ground states of the complexes correspond to those of the free An³⁺ ions.⁷⁸ The ligand splitting effects on the ground-state multiplet in An(DOTA)(H₂O)⁻ molecules in terms of SO-CASPT2 energies are given in Table S2 of the Supporting Information.

The SO ground states of Ac(DOTA)(H₂O)⁻ and Cm(DOTA)(H₂O)⁻ are composed entirely (100%) of the SF ground state. The other actinides form their SO ground state as mixtures of the lowest-energy SF states. In contrast, the SF ground states contain mostly one dominant (70–100%) electron configuration, the only exception being Cf(DOTA)(H₂O)⁻. The major electron configurations of the SF ground states are generally strongly mixed and cannot be characterized by specific magnetic quantum numbers of the 5f electrons.

Bonding

Table 2 presents selected results from the QTAIM analysis of CASSCF wave functions of the M(DOTA)(H₂O)⁻ complexes. Additional data are given in Table S3 of the Supporting Information. As Cf was modeled with a different (pseudopotential) basis, the data of Cf(DOTA)(H₂O)⁻ should be considered cautiously in the trends.

Table 2. Selected Results^a from the QTAIM Analysis of CASSCF Wave Functions of the M(DOTA)(H₂O)⁻ Complexes.

M3+	qM	CT1	CT2	DI1	DI2	DI3	ρ(M–O)	∇2ρ(M–O)
Ac	2.54	0.44	0.02	0.25	0.15	0.13	0.048	0.19
U	2.46	0.51	0.03	0.26	0.17	0.14	0.051	0.21
Np	2.45	0.52	0.03	0.26	0.17	0.14	0.051	0.22
Pu	2.43	0.54	0.03	0.26	0.17	0.14	0.052	0.23
Am	2.42	0.55	0.03	0.26	0.17	0.14	0.052	0.24
Cm	2.42	0.55	0.03	0.26	0.17	0.14	0.053	0.25
Cf	2.39	0.58	0.03	0.26	0.17	0.14	0.053	0.24
La	2.48	0.50	0.02	0.25	0.15	0.13	0.050	0.19
Lu	2.45	0.52	0.03	0.23	0.14	0.10	0.055	0.29

^aBader charge of M (q_M, e); charge transfer to M from DOTA (CT₁, e) and from H₂O (CT₂, e); delocalization indices between M–O_DOTA (DI₁, e), M – O_H2O (DI₂, e), and M–N_DOTA (CT₃, e), the ones with DOTA were averaged because of the C₂ symmetry. Averaged electron density (ρ, au) and Laplacian of this electron density (∇²ρ, au) at the bond critical points of the M–O_DOTA interactions. Additional topological data are given in Table S3.

The main bonding interaction between M and the ligands is the electrostatic attraction between the strongly positive M (Bader charges around +2.4 e) and the partially negative oxygens. Further evidences for this dominant ionic interaction are the very low electron densities (ρ) and the positive Laplacian values of ρ at the M–O and M–N bond critical points (BCPs) (cf. Table 2 and Table S3). The minor covalent part of the M–ligand bonding includes charge transfer interactions between M and Tp (CT) and energy-degeneracy-driven orbital overlap.^79,80 The former interaction can quantitatively be estimated from the Bader charges: the net CT from DOTA to M amounts to ca. 0.5 e, while that from H₂O to M amounts to 1 order of magnitude smaller (0.03 e). The considerable difference is determined by the anionic character and multiple number (four) of the DOTA carboxylate oxygen donors. The concept of energy-degeneracy-driven covalency is based on the mixing of metal and ligand orbitals on the basis of their close energies.^79,80 Recently, an increasing trend of 5f and ligand orbital mixing has been shown in various An compounds^79,81−85 due to decreasing 5f orbital energies across the An row. Unfortunately, the computational tools applied in the present study do not facilitate a straightforward analysis of energy-driven covalency in the title complexes.

The Bader charges of M correspond to a slightly decreasing ionic character along the An row (and between La and Lu). The same gentle trend appears also in the increasing electron densities at the BCPs.

Another important integral property is the delocalization index (DI), which corresponds to the number of electrons forming the covalent (donor–acceptor) bonding between M and the donor atoms of the ligands. The DI values of ca. 0.25, 0.16, and 0.14 e for M–O_DOTA, M–O_H2O, and M–N_DOTA, respectively (cf. Table 2), correlate well with the Wiberg bond indices⁷⁷ of ca. 0.21, 0.14 and 0.09 (given in detail in Table S3), respectively. As can be seen, despite the marginal charge transfer from the neutral H₂O ligand to M, a significant number of electrons are participating in its orbital interactions with M.

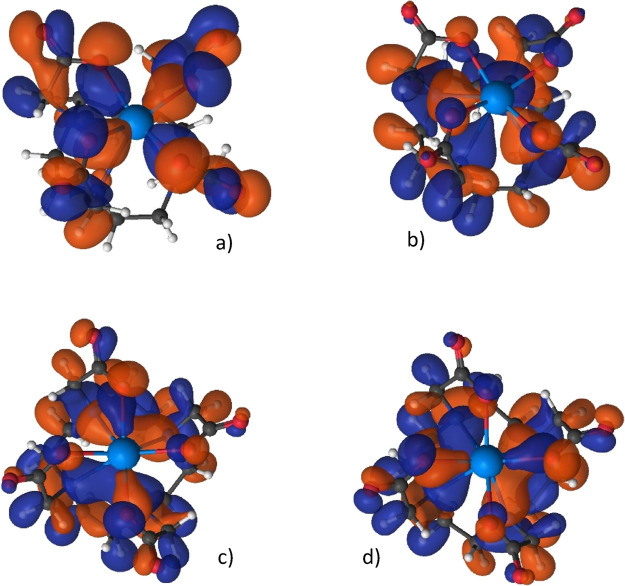
Inspection of the CASSCF orbitals indicated that the 5f electrons occupy nonbonding orbitals mostly with pure 5f (in few cases with minor 6d contributions) character. 5f populations could not be recognized as notable contributors in any bonding orbitals. The lack of 5f orbital participation in the bonding in the An-DOTA complexes justifies the applicability of 5f-in-core pseudopotentials. The An–ligand bonding is manifested by the 6d orbitals of An that, due to their symmetries, are better suited to interact with the deformed C₄-type DOTA ligand than 5f. It should be noted that there are no pure metal–ligand bonding molecular orbitals, but ones mixed with other intra-DOTA orbital interactions. The four characteristic molecular orbitals of the U(DOTA)⁻ complex containing significant U–DOTA bonding are shown in Figure 4.

Figure 4.

Characteristic molecular orbitals of U(DOTA)⁻ from CASSCF calculations: (a) U–O; (b) U–N; (c,d) U–O,N bonding.

Thermodynamics in Aqueous Solution

The relative thermodynamic stabilities are assessed with respect to the Lu-DOTA complexes according to the following reactions (utilizing the more stable SAP isomer for the Lu while the TSAP one for the other complexes):

1

2

Experimental data are available for DOTA complexes of La, Lu, Ac, Am, and Cm. For La- and Lu-DOTA, the values of the stability constants from potentiometric titration (lgK = 22.9 and 25.4, respectively)²⁸ and from a spectrophotometric study (20.7 and 23.5, respectively)⁴² differ considerably due to the differences in the experimental conditions. However, the relative stabilities calculated from these two sets of data are in reasonable agreement (ΔG°₂₉₈ = 14.3 and 16.0 kJ/mol, respectively). The stability constants of Am- and Cm-DOTA from solvent extraction experiments proved to be nearly the same; in fact, the difference is well within the experimental uncertainties (lgK = 23.95 ± 0.09 and 24.02 ± 0.11, respectively).⁵² The slightly larger value of Cm-DOTA is in agreement with the expected larger stability of the latter complex on the basis of ionic radii. A distinct decreasing trend in the stability along the An row was demonstrated by the thermodynamic data of Ac-DOTA and Cm-DOTA in ref (47) obtained from samples with various Cm³⁺:DOTA ratios using time-resolved laser fluorescence spectroscopy detection in the case of Cm-DOTA while separation of free Ac³⁺ and the complex by instant thin layer chromatography followed by detection using gamma spectroscopy in the case of Ac-DOTA. The lgK values (25 °C, I = 0.1 M, approximately comparable to the experimental conditions in ref (28)) were 16.4 and 19.0 for Ac- and Cm-DOTA, respectively. The reported corresponding ΔG°₂₉₈ values are −93.9±2.1 and −108.3±13.7 kJ/mol, respectively.

The ΔG°₂₉₈ values from the present TPSSh/DZ + SMD(aq) calculations are presented in Figure 5. The thermal contributions were calculated using the rigid rotor harmonic oscillator approximation and neglecting the electronic contributions. Because the electronic contributions are expected to be similar for the M³⁺ ions and the M-DOTA complexes, they should more or less cancel each other in eqs 1 and 2.

Figure 5.

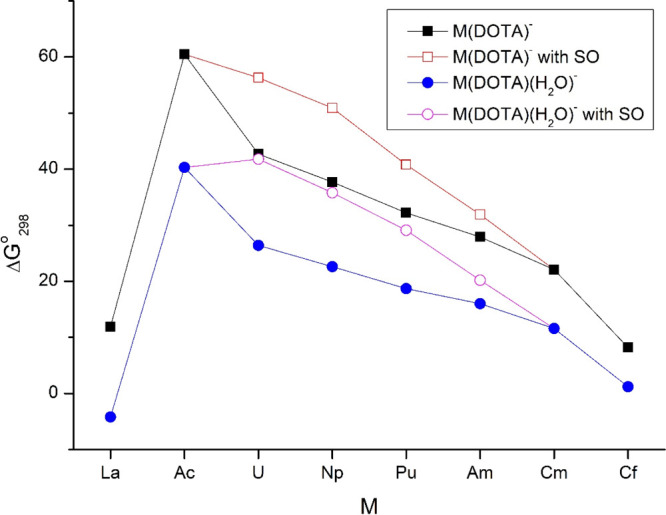
Relative thermodynamic stabilities of M(DOTA)⁻ and M(DOTA)(H₂O)⁻ complexes on the basis of the exchange reaction M-DOTA(TSAP) + Lu³⁺ → Lu-DOTA(SAP) + M³⁺. The data given by unfilled symbols include spin–orbit coupling.

The value of 11.9 kJ/mol for La(DOTA)⁻ from eq 1 is in good agreement with the experimentally obtained stability difference between the La- and Lu-DOTA complexes (vide supra). In contrast, the −4.2 kJ/mol value for the La(DOTA)(H₂O)⁻ model (eq 2) would correspond to a higher stability of the La complex with respect to the Lu one, which is in contradiction with experimental observations.^28,42 Hence, the M(DOTA)⁻ model structures (eq 1) seem to be more appropriate for assessment of the relative stabilities in aqueous solution. The better performance of this model can also be related to the observed reversible bonding of the H₂O molecule at the 9th coordination site, i.e., its rapid exchange with the solvent H₂O molecules.^43,69

The trend of increasing thermodynamic stabilities of the studied An-DOTA complexes along the An row (lower ΔG°₂₉₈) is in agreement with the abovementioned limited experimental information.^47,52 It should be noted that the SO corrections taken from the SO-CASPT2 calculations decrease the calculated relative stabilities: the reason is the larger stabilization of the An³⁺ ions than that of the respective complexes by the SO interaction. The SO effect could not be evaluated in the present study for the Cf-DOTA complexes, but it can be expected to increase its ΔG°₂₉₈ value, too.

The calculated ΔG°₂₉₈ difference of Ac(DOTA)⁻ and Cm(DOTA)⁻ is considerably overestimated compared to the experimental value from ref (47) (38.4 vs 14.4 ± 15.8 kJ/mol, vide supra), though the large experimental uncertainty smoothens the discrepancy. Part of the deviation may still stem from the neglect of electronic contribution in the calculated ΔG°₂₉₈ data. While this contribution should be negligible for La³⁺, Lu³⁺, and Ac³⁺ due to the lack of low-lying electronic states, it may have some relevance for Cm³⁺ where the excitation of the 5f⁷ configuration results in medium-energy excited states.

Computational Details

The density functional theory (DFT) computations were performed with the Gaussian09 suite of programs.⁸⁶ On the basis of the reported good experience with the TPSSh meta-hybrid functional⁸⁷ for the molecular geometries and relative stabilities of various lanthanide complexes,^73,74,88,89 this functional was considered at the first place in conjunction with the 4/5f-in-core (large-core) quasi-relativistic pseudopotentials of the Stuttgart–Cologne group (La-ECP46MWB, Lu-ECP60MWB,^90,91 Ac-ECP78MWB, U-ECP81MWB, Np-ECP82MWB, Pu-ECP83MWB, Am-ECP84MWB, Cm-ECP85MWB, Cf-ECP87MWB⁹²) and double-zeta valence basis sets ([7s6p5d]/[5s4p3d] for the lanthanides,⁹⁰ [7s6p5d]/[4s3p3d] for the actinides,⁹² and 6-31G** for the light atoms). This DFT level is denoted in the paper as TPSSh/DZ. Comparative calculations were performed with a larger basis set of triple-zeta quality using contracted [8s7p6d3f3g]/[6s5p5d3f2g] valence basis sets for the lanthanides,^90,93,94 [7s6p5d2f]/[5s4p4d2f] for the actinides,⁹² and 6-311+G** for the light atoms (denoted as TPSSh/TZ). In contrast to DZ, this basis set has f polarization functions, which can have relevance for the bonding and electronic properties, particularly of the An complexes. Calculations with 5f-in-valence (small-core) pseudopotentials (ECP60MWB)^95,96 failed because of SCF convergence problems already in the case of the Ac complex (with the simplest An electronic structure).

The performance of the above DFT levels was tested on the experimental X-ray diffraction structural data of the Lu- and La-DOTA complexes^40,41 taking advantage of their significantly different Ln³⁺ ion radii and the covered two DOTA conformers.⁴⁴ In addition, some other DFT functionals (B3PW91,^97,98 BH&HLYP,⁹⁹ B3LYP,^97,100 BP86,^101,102 PBE,¹⁰³ M062X,¹⁰⁴ and wB97XD¹⁰⁵) and basis sets for the light atoms (6-31+G**, cc-pVDZ, cc-pVTZ) were also probed.

The model structure selected for the present study required some considerations. The Lu-DOTA complex, similar to the other late small-sized Ln³⁺ ions, has a H₂O ligand in the first coordination sphere.^{41,55−58,66} In contrast, the nine-coordinate structure of solid La-DOTA (similar to Ce⁵⁶) is formed by bridging of a carboxylate O atom of a neighboring complex molecule.⁴⁰ Accordingly, La-DOTA has a polymeric structure in the crystal, yet the molecular structure of the La(DOTA)⁻ unit is expected to be close to the one in the La(DOTA)(H₂O)⁻ species. Therefore, for the present theoretical study, the M(DOTA)(H₂O)⁻ model was used for both the La and An complexes. The H₂O molecule was constrained in a vertical arrangement in order to facilitate C₂ symmetry (being, e.g., advantageous for the multireference calculations). Though this structure is a second-order saddle-point on the potential energy surface, due to the very weak interaction, it is only slightly higher in energy than the global minimum. Moreover, this arrangement resembles more that in the crystal and polar solvents, where this H₂O is involved rather in interactions with the environment than with the DOTA ligand in the same complex.

The computed La/Lu–O and La/Lu–N distances from the benchmark study are compiled in the Supporting Information (Table S1). The general feature of all tested levels is the underestimation of the M–O and overestimation of the M–N distances compared to the solid-phase data. Such deviations are understandable in view of the missing intermolecular interactions of both the carboxylate groups and the H₂O ligand in the computed isolated molecules. The stronger M–O interactions in the isolated molecule pull the metal away from the N donors toward the free site of DOTA, i.e., closer to the carboxylate O donors. The larger underestimation of the Lu–O_w distance is in agreement with the larger effect of intermolecular interactions on the weakly bonded H₂O ligand. The modeling of such effects is difficult: it required for solvated Gd(DOTA)(H₂O)⁻ a mixed cluster/continuum approach including explicitly two second-sphere water molecules.¹⁰⁶

Nevertheless, the data confirm the superior performance of the TPSSh functional over the other probed DFT ones as well as that of the 6-311+G** basis set. Comparison of the TPSSh/DZ and TPSSh/TZ levels revealed a slightly better performance of TPSSh/TZ for the geometry. However, calculations of basis set superposition error (BSSE) using the counterpoise method¹⁰⁷ failed for some complexes at the TPSSh/TZ level because of SCF convergence problems. There were no such problems with the smaller DZ basis; thus, the TPSSh/DZ level was used to assess the solution stability ratios (similar to previous studies on related complexes^73,74,89) where the BSSE corrections were shown to play an important role.

The solvent effects were taken into account using the polarizable continuum model (PCM)^108,109 with radii and nonelectrostatic terms for Truhlar and co-workers’ SMD solvation model.¹¹⁰ For La³⁺, Lu³⁺, Ac³⁺, and Cf³⁺, the PCM radii from the literature were used.^73,74 For the other An³⁺ ions, no such radii are available; therefore, they were developed in the present study (Table 3) on the basis of literature hydration free energies.¹¹¹ No scaling factor (α = 1.0) was applied for the PCM radii in the present study.

Table 3. PCM Radii (Å) of the M³⁺ Ions Used in Conjunction with the SMD Solvation Model.

M3+	PCM radii	ref
La	1.874	(73)
Lu	1.659	(73)
Ac	1.933	(74)
U	1.848	present studya
Np	1.826	present study
Pu	1.807	present study
Am	1.789	present study
Cm	1.773	present study
Cf	1.747	(74)

^aDeveloped according to the procedure described in ref (73). The reference values for hydration free energies of the actinides were taken from ref (111).

The multiconfigurational nature of the complexes was studied by single-point relativistic complete active space self-consistent field (CASSCF)¹¹² calculations in order to verify the ground electronic states and their character. For these single-point calculations, the TPSSh/TZ reference geometries were used taking advantage of their C₂ symmetry.

The scalar relativistic effects were taken into account with the second-order Douglas–Kroll–Hess Hamiltonian.^113,114 The used atomic natural orbital type all-electron basis sets developed for relativistic calculations (ANO-RCC) had the contraction schemes of [26s23p17d13f5g3h]/[8s7p5d3f1g] for Ac, U, Np, Pu, Am, and Cm,¹¹⁵ [8s4p3d1f]/[2s1p] for H,¹¹⁶ and [14s9p4d3f2g]/[3s2p1d] for C, N, and O¹¹⁷ corresponding to valence double-zeta plus polarization quality. As the ANO-RCC basis is not available for Cf, these calculations were performed using the small-core quasi-relativistic pseudopotential of the Stuttgart–Cologne group (ECP60MWB) in conjunction with a contacted [12s11p10d8f]/[8s7p6d4f] valence basis^95,96 and Dunning’s cc-pVDZ basis¹¹⁸ for the light atoms.

In conformity with the large size of the complex, the active space consisted of the seven 5f orbitals occupied by the 5f electrons of the An³⁺ ions. In the state-averaged calculations, all the states of the ground-state spin multiplicities were considered, i.e., 34, 35, 21, 7, 1, and 21 roots for U, Np, Pu, Am, Cm, and Cf, respectively.

Dynamic electron correlation was considered by second-order perturbation theory calculations on the basis of the CASSCF wave functions (CASPT2).^119,120 Spin–orbit (SO) effects were taken into account by using the complete active space state interaction (CASSI) method,¹²¹ which allows CASSCF wave functions for different electronic states to interact under the influence of a spin–orbit Hamiltonian. Dynamic electron correlation was represented by the CASPT2 energies used in the spin–orbit Hamiltonian (SO-CASPT2). The CASSI treatment was not applicable in the case of the quasi-relativistic pseudopotential of Cf. The above multireference calculations were performed by means of the MOLCAS 8.2 code.^122,123

Bonding analysis was performed on the basis of the CASSCF wave functions. The molecular orbitals were visualized using the Luscus software.¹²⁴ Bader atomic charges, delocalization indices, and topological properties in terms of Quantum Theory of Atoms in Molecules (QTAIM)¹²⁵ were obtained with the Multiwfn code using medium quality grid.¹²⁶ The wfn input files for the latter analyses were obtained with the Molden2AIM utility program¹²⁷ from the Molden input files generated by MOLCAS.

Conclusions

The DOTA ligand forms stable complexes with the studied trivalent actinides (Ac, U, Np, Pu, Am, Cm, Cf). The thermodynamic stability in aqueous solution increases along the An row, with the ΔG°₂₉₈ values without SO correction showing good correlation with the An³⁺ ionic radii. The SO effects stabilize the An³⁺ ions somewhat more than the An(DOTA)⁻ complexes, worsening the correlation but still keeping the gradual decreasing trend. The increasing stability across the An row is in line with results on An complexes with other chelating ligands.^79,81,83 The found trend supports the applicability of the DOTA ligand for heavy actinides.

A further characteristic of the solvated complexes is the preference of the TSAP conformers for all the An involved in the study. The above solution-phase results were achieved with PCM radii used in conjunction with the SMD solvation model, evaluated in the present study for U³⁺, Np³⁺, Pu³⁺, Am³⁺, and Cm³⁺.

The relativistic multireference calculations at the SO-CASPT2/DZ level confirmed the electronic ground states of the complexes to be the same as in the An³⁺ ions. Worthwhile, 5f populations were not found in the bonding molecular orbitals, justifying the applicability of 5f-in-core pseudopotentials. The An–ligand bonding is mainly electrostatic, with minor charge transfer contributions to the An 6d orbitals according to the (deformed) C₄ symmetric nature of the complexes.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c01292.

• Benchmark results using the X-ray diffraction reference data of La- and Lu-DOTA; SO-CASPT2 energy levels of the ground-state multiplets in An(DOTA)(H₂O)⁻ molecules (An = U, Np, Pu); selected Wiberg bond indices and electron density and Laplacian values of the electron density data at M–O and M–N bond critical points; input Gaussian09 file of the SMD solvation calculation on Pu(DOTA)⁻ using the PCM radii of Pu; Cartesian coordinates of the M(DOTA)⁻ and M(DOTA)(H₂O)⁻ complexes optimized at the TPSSh/TZ level (PDF)

The author declares no competing financial interest.