Abstract

We present a global optimization method to construct phase boundaries in multicomponent mixtures by minimizing the Gibbs energy. The minimization method is, in essence, an extension of the Maxwell construction procedure that is used in single-component systems. For a given temperature, pressure, and overall mixture composition, it reveals the mole fractions of the thermodynamically stable phases and the composition of these phases. Our approach is based on particle swarm optimization (PSO), which is a gradient-free, stochastic method. It is not reliant on good initial guesses for the phase fractions and compositions, which is an important requirement for the high-pressure applications considered in this study because data on phase boundaries at high pressures tend to be extremely limited. One practical use of this method is to create equation-of-state tables needed by continuum-scale, multiphysics codes that are ubiquitous in high-pressure science. Currently, there does not exist a method to generate such tables that rigorously account for changes in phase boundaries due to mixing. We have done extensive testing to demonstrate that PSO can reliably determine the Gibbs energy minimum and can capture nontrivial features like eutectic and peritectic temperatures to produce coherent phase diagrams. As part of our testing, we have developed a PSO-based Helmholtz-energy minimization procedure that we have used to cross-check the results of the Gibbs energy minimization. We conclude with a critique of our approach and provide suggestions for future work, including a PSO-based entropy-maximization method that would enable the aforementioned continuum codes to perform on-the-fly, phase-equilibria calculations of multicomponent mixtures.
1. Introduction
The thermodynamics of multicomponent mixtures at high pressures is a topic of great interest in a number of fields. By components, we mean “atom types” (elements) or possibly assumed indivisible “molecular units” in certain special cases. Planetary science is awash with such systems, and prominent examples include hydrogen/helium mixtures in giant planets;1−3 aqueous solutions of organic compounds, ammonia, carbon dioxide, and/or salts in icy moons and ocean planets;4−8 and mixtures that may form as a result of carbon dioxide dissociation in Earth’s mantle.9−11 Other examples are those produced from the detonation of diatomic and polyatomic species.12−14 Moreover, there is a growing need to understand the behavior of additively manufactured alloys under high-pressure static and dynamic loading in order to certify them for use in aerospace and automobile applications.15
Like their single-component counterparts, multicomponent mixtures do not necessarily exist as homogeneous substances and can instead split up into two or more phases. Therefore, determining the equilibrium state for a given set of conditions requires finding which phases are thermodynamically stable and the relative amounts (mole fractions) of each phase. This procedure in single-component systems is often referred to as a Maxwell construction. The key distinguishing feature of multicomponent mixtures is that the various components may segregate preferentially into different phases, so that determining the mixture’s equilibrium state also requires finding the composition (mole fraction of every component) of each of the stable phases. This may be done by minimizing a particular free energy or maximizing the entropy, depending on the conditions that are specified. We present an optimization procedure to minimize the Gibbs energy of a multicomponent mixture, which reveals the relative amounts of the different phases and the composition of each phase, when the temperature, pressure, and overall composition of the mixture are specified. Our minimization scheme is based on particle swarm optimization (PSO), which is a stochastic method introduced in its modern-day form over 25 years ago.16 PSO is highly versatile because it is a gradient-free method that places few requirements on the nature of the objective function that is to be minimized. As a result, it has since been applied to a wide variety of optimization problems.17,18 A crucial feature of PSO is that it is a global optimization method which, unlike local optimization methods, does not require good initial guesses for the phase mole fractions and compositions. This is an important requirement for mixtures at high pressures because under such conditions, experimental and theoretical data on the phase diagram will likely not be available. We apply our method—which may be thought of as a multicomponent extension of a Maxwell construction—to generate phase diagrams and construct equation-of-state tables that are compatible with continuum-scale, multiphysics codes19−21 that are widely used in high-pressure science.
We expand on the statements mentioned above by considering the case of single-component materials, for which a widely adopted thermodynamic formalism22−25 has already been established by the high-pressure science community. In this particular formalism, the equation of state (EOS) for each phase of a single-component material is represented with a separate Helmholtz-energy model, which is subsequently divided into three contributions: a cold energy that designates the energy of the phase at 0 K, an ion-thermal free energy that accounts for the motion of the nuclei, and an electron-thermal free energy that reflects electronic excitations and ionization processes. (In some cases, it may be important to also include terms representing phenomena such as magnetism or electron–phonon interactions,26 but this is not necessary for the vast majority of materials under most conditions.) Variants on this formalism have produced, for example, the large collection of EOSs that make up the LEOS27−29 and SESAME26,30,31 libraries maintained by Lawrence Livermore and Los Alamos National Laboratories, respectively. EOS construction is an iterative process that involves two distinct tasks: (1) development of phase-specific free-energy models and (2) generation of phase diagrams, the latter of which requires performing a minimization over the free-energy surface represented by the models. We focus on the second task in this study. Frequently, one is interested in a temperature–pressure diagram, but it is also common to produce a temperature–density diagram. The motivation behind making temperature–density diagrams often arises from the fact that the continuum-scale codes mentioned above read in the EOSs as two-dimensional tables of certain thermodynamic properties (such as Helmholtz energy) as a function of temperature and density, from which they can compute other properties through interpolation and numerical differentiation. These EOS tables are then used by the codes to simulate hydrodynamics, spall, and other nonequilibrium processes that may occur in materials subjected to strong disturbances like shock and ramp-compression waves.32 Even when the kinetics of phenomena like phase transitions33,94 or chemical reactions are sufficiently slow to preclude the establishment of local thermodynamic equilibrium, it is useful to have a capability to rigorously determine the equilibrium state because this would serve as a bounding limit for the case of infinitely fast kinetics. If the equilibrium state for a given temperature and density lies in a multiphase region, a free-energy minimization must be performed to determine the phase mole fractions, so that the total free energy of the multiphase state at that temperature and density may be tabulated. Reliable free-energy minimization methods are thus necessary for the construction of EOS tables.
In multicomponent mixtures at high pressures, the two tasks mentioned above—(1) development of free-energy models and (2) minimization over these free energies to construct phase diagrams and EOS tables—may both be sufficiently complicated that it is useful to draw a clear separation between them. High pressures naturally result in the formation of new (perhaps yet undiscovered) phases and compounds. Hence, producing a complete set of free-energy models for even a binary mixture can be extremely laborious because even before the models are to be developed, an exhaustive structure search (through experiments and/or ab initio quantum simulations) must be done to fully identify not only the fluid and terminal solid solutions, but also intermediate phases34—such as compounds and secondary solid solutions—that may exist over the conditions of interest. We do not intend to do that in this study for any particular mixture. Rather, our objective is to enable the second of the two tasks, namely, the construction of phase boundaries/diagrams and EOS tables via free-energy minimization. Although our focus is not necessarily on the development of free-energy models themselves, we do need such models in order to test/demonstrate our PSO-based minimization method, and for that purpose, we employ a formulation that applies well-established concepts from chemical thermodynamics35−39 to develop mixture models that are built from the high-pressure, single-component EOSs described in the preceding paragraph. We apply this formalism to develop different example models that we subsequently use in the minimization calculations. This is somewhat akin to how one might demonstrate a new free-energy minimization technique in classical molecular dynamics simulations with representative interatomic potentials.
We organize the rest of this study in the following manner. Section 2 and the Appendix provide a largely self-contained outline of key thermodynamic concepts and quantities relevant to mixtures that we refer to throughout the rest of the study, with an eye toward building on the very successful, high-pressure EOS framework encapsulated in the LEOS and SESAME tables. Details of our PSO algorithm and its suitability for high-pressure applications are explained in section 3. This is followed by section 4, which tests and demonstrates our PSO method with different example mixing models for the iron/gallium (Fe/Ga) system at high pressures. We show that it can reliably capture nontrivial features of the Fe/Ga phase diagrams dictated by the models, such as eutectic and peritectic points. We then demonstrate how PSO may be used to construct EOS tables of the type mentioned earlier. That is, we produce multiphase tables of Helmholtz energy as a function of temperature and density; for multicomponent mixtures, this means that each such table corresponds to a fixed overall composition. We produce tables for Fe/Ga mixtures and use them to perform EOS-related calculations (e.g., compute isentropes and Hugoniot curves), just like we may do with any table from the LEOS or SESAME libraries. Section 5 concludes with a summary of our study. This section also presents a critical evaluation of our approach, gives suggestions on future work, and compares our approach with others that have been developed for multiphase, multicomponent mixtures.
2. Thermodynamic Description of Mixtures
2.1. Overview
For a multiphase mixture
with  different
phases, its molar internal energy E, entropy S, and volume V are given by
different
phases, its molar internal energy E, entropy S, and volume V are given by
| 1 |
| 2 |
| 3 |
where χi is the mole fraction of phase i and denotes the moles of phase i divided by the moles of the mixture. In this work, we will introduce four different kinds of mole fractions, and so for the purposes of clarity, we will be very explicit when defining each of them. If phase i is at a temperature Ti and pressure Pi, we apply standard thermodynamic relations to define the molar Helmholtz energy, enthalpy, and Gibbs energy of the phase as
| 4 |
| 5 |
| 6 |
respectively. For the multiphase mixture as a whole, we have
| 7 |
| 8 |
| 9 |
If all phases are at a common temperature T and pressure P (which are fundamental requirements for the mixture to be in thermodynamic equilibrium35), eqs 1–9 lead to
| 10 |
| 11 |
| 12 |
To proceed further, we must have a prescription for the thermodynamic properties of the individual phases, so that we can compute Gi, Ei, Si, Vi, Fi, and Hi of each phase i. It is useful at this point to draw a distinction between solutions and compounds. A compound is a covalently or ionically bonded substance with a fixed stoichometric ratio between its constituent elements; it remains fixed in this ratio even when it is melted to a liquid or vaporized to a gas. In contrast, a solution—which includes fluid mixtures, substitutional alloys, and interstitial alloys—may have a variable composition. If Q denotes G, E, S, V, F, or H, then Q of a compound can be represented as a linear combination of the Q of its elements (with the weights coming from the stoichiometric ratios) plus ΔQf of formation. In practice, this representation is likely to be useful only at ambient pressure, where an abundance of experimental data tends to be available even for difficult-to-compute quantities like the entropy of formation ΔSf. If we are instead interested in the compound’s properties over a wide range of pressures where such data are no longer available, a better approach is to construct a multiphase EOS specific to that compound that is separate from the EOSs for the constituent elements. Thus, if i represents a particular phase of a compound, then Gi, Ei, Si, Vi, Fi, and Hi denote the properties extracted from the EOS corresponding to that phase. A prime example of a compound is water, for which the development of a wide-ranging, accurate EOS that covers its multiple solid and fluid phases is still an ongoing area of work. Because water has very different properties from a solution of hydrogen and oxygen, its EOS will bear little resemblance to those of its constituent elements and can be developed independently of the EOSs for those elements.
In contrast, if phase i is a solution (e.g., a fluid mixture or an alloy), a good approach is to represent Gi, Ei, Si, Vi, Fi, and Hi in terms of the corresponding properties of the constituent components, rather than developing a separate EOS altogether like in the case of a compound. A standard prescription from chemical thermodynamics is to model the properties of each solution phase as a linear combination of the properties of the pure components that make up the phase plus additional mixing terms.35−39 In the rest of this study, we neglect compounds and assume that each phase is a solution that is composed of up to c components. This implies that for the Fe/Ga mixture examples in section 4, our analysis excludes compounds like Fe3Ga, Fe6Ga5, Fe3Ga4, and FeGa3 that exist at ambient pressure40 and are presumably still stable at higher pressures. We have noted in the Introduction that the goal of the present study is not necessarily to develop a set of free-energy models for Fe/Ga or for any other mixture. Our objective is to instead demonstrate PSO as a reliable means to perform a free-energy minimization given a set of such models. Section 4 does this with different example Fe/Ga solution mixing models. Section 5.1 includes a discussion of how the PSO algorithm may be adapted in the future to handle compounds like the ones listed above, which can then be tested once an EOS has been developed for them. Although the present study does not focus on model development per se, the formulation we outline in the rest of this section builds on existing high-pressure, single-component EOS models (e.g., those in the LEOS and SESAME tables), and so, it can be an effective basis for future development of EOSs for a diverse selection of multicomponent mixtures.
Using the index j to label the c components of phase i, we can express the molar Gibbs energy of that phase as
| 13 |
where zij is the mole fraction of component j in phase i and is defined as the moles of j in i divided by the total moles of phase i. Here, μij is the chemical potential of component j in phase i, and it is clear from eq 13 why μij is also commonly referred to as the partial molar Gibbs energy of j in i. The concept of a partial molar Gibbs energy (or more generally, any partial molar property) appears prominently in the chemical thermodynamics of multicomponent solutions.35−39 A rather general expression for μij = μij(T,P,zi) is
| 14 |
in which zi = (zi1, zi2, ..., zic) denotes the composition (mole fractions of the c components) of phase i, R is the gas constant, and Gij(T,P) is the molar Gibbs energy of component j when it exists by itself as a pure substance but is evaluated at the same T and P of the mixture. The subscript i in Gij indicates that this pure-component property is to be evaluated in the same state of matter as phase i. For instance, if i is a liquid, Gij is the molar Gibbs energy of pure j in the liquid phase.
The second and third terms on the right-hand side of eq 14 represent contributions of mixing to the free energy. The second term, RT ln zij, is the ideal-mixing contribution of j in i, while G̅ijexcess(T,P,zi) is the excess partial molar Gibbs energy of j in i and represents the nonideal-mixing contribution. It is evident that G̅ij(T,P,zi) may in general be far more complicated than the ideal contribution RT ln zij. For instance, the former may depend on pressure, while the latter does not. Furthermore, RT ln zij depends only on the mole fraction zij, while G̅ijexcess(T,P,zi) may involve the mole fractions of the other components in phase i as well. As with any EOS, developing a model for G̅ij requires fitting a set of parameters to a combination of experimental and theoretical data. For high-pressure applications, this represents a great challenge because we must fit it to data that span an enormous range of temperatures, pressures, and potentially also compositions.
Substituting eqs 14 into 13 and 9, we obtain
| 15 |
| 16 |
The molar entropy and molar volume of each phase are given by
 |
17 |
 |
18 |
where Sij(T,P) = −(∂Gij/∂T)P and Vij(T,P) = (∂Gij/∂P)T are the molar entropy and volume of pure j evaluated in the same state of matter (solid, liquid, etc.) as phase i, and the quantities in the square brackets are referred to as the partial molar entropy and partial molar volume of component j in phase i. The derivatives in these brackets are the excess partial molar entropy S̅ijexcess = −(∂G̅ij/∂T)P,zi and the excess partial molar volume V̅ijexcess = (∂G̅ij/∂P)T,zi of j in i. From these equations, one may compute the internal energy Ei = Gi + TSi – PVi, Helmholtz energy Fi = Gi – PVi, and enthalpy Hi = Gi + TSi of the individual phases. The molar internal energy E, entropy S, volume V, Helmholtz energy F, and enthalpy H of the entire multiphase, multicomponent mixture may then be calculated from eqs 1–3 and 7 and 8, respectively. Other thermodynamic properties of interest, such as the sound speed, may be derived by taking one or more derivatives of G, E, S, V, F, or H. This seemingly straightforward task can actually be quite complicated for the reasons explained in the Appendix, where we suggest an approximation to greatly simplify the computation of these thermodynamic derivatives.
2.2. Ideal and Nonideal Mixtures
An ideal multiphase, multicomponent mixture is defined to be one in which G̅ijexcess = 0 for every component j and phase i over all conditions. The Gibbs energy G, Helmholtz energy F, and entropy S of such a mixture are
| 19 |
| 20 |
| 21 |
while its volume V, internal energy E, and enthalpy H are
| 22 |
| 23 |
| 24 |
An ideal mixture is imagined as being a lattice in which the components are randomly distributed on the lattice sites. An analysis of the number of additional lattice configurations in the mixture leads to the well-known terms of the form −Rzij ln zij (for entropy) or RTzij ln zij (for free energies).36,41 In addition, one assumes in an ideal mixture that a component experiences the same interatomic interactions, on average, in the mixture that it would experience if it were instead surrounded by other like components, that is, in the pure substance. This also implies that there is no short-range ordering (preferential mixing or bonding) or any other phenomena that lead to a deviation away from the idealized, random-distribution-on-a-lattice picture described above. As a result, V, E, and H of an ideal mixture depend only on the pure-component contributions, with no contribution from the mixing itself. [The additivity of volumes in eq 22 has been referred to in different contexts as the “linear mixing approximation”4,42 or as Amagat’s law.] Although the assumptions inherent in ideal mixing appear to be rather severe, if the components in the mixture are similar in nature, it can actually provide a fairly good approximation. For instance, a binary mixture of toluene and benzene (both of which are large, but similar organic molecules) behaves ideally,35 and a recent study has found that ideal mixing may also hold for certain shock-compressed mixtures in a particular range of conditions.42 We note that if a phase i is almost pure in a particular component j, so that zij ≈ 1, then G̅ijexcess ≈ 0 (though G̅ik for k ≠ j is not necessarily close to zero) because the environment that j experiences in this phase is very similar to what it would experience as a pure substance. In a largely phenomenological way, the goal of an accurate excess free energy model is to account for the aforementioned processes that are neglected in the ideal-mixing approximation.
We clarify that to be precise in our terminology, the definition of an ideal mixture that we have adopted is based on Raoult’s law and may be referred as an ideal Raoultian mixture.35,38,43 In this definition, the Gij that appears in eq 14, which is the molar Gibbs energy or chemical potential of pure j, may be thought of as a reference state onto which the mixing terms are added to obtain the true chemical potential μij of j when it is mixed with the other components that make up phase i. This is the most convenient reference state to adopt for our purposes because it allows us to directly use high-pressure-oriented EOSs that have already been developed for the individual components, like the EOS tables in the LEOS and SESAME libraries, to compute Gij and other pure-component properties. An alternative reference state is the chemical potential of j in the ideal-gas state, for which the analogues to the excess properties are called residual properties or departure functions. (These are associated with the concepts of fugacity and fugacity coefficients, while excess properties are more closely associated with activity and activity coefficients.35,36,44−46) While EOSs involving departure functions are more elegant in some ways than the formulation we have chosen here, they are not convenient for our purposes because under the conditions achieved in typical high-pressure applications (e.g., ramp-compression experiments), ideal gases are often times very far away in terms of their properties from the real mixture of interest.
3. Application of PSO to Phase Equilibria
3.1. Algorithm Details
The main objective
of this study is to develop an optimization method that enables one
to construct phase diagrams for multiphase, multicomponent mixtures
and produce EOS tables that can be used in high-pressure, continuum-scale
simulations. In order to achieve this goal, we aim to solve the following
problem: given the temperature T, pressure P, and overall composition 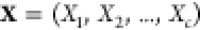 in a mixture of
in a mixture of 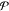 phases and c components
determine the mixture’s equilibrium state. The variable
phases and c components
determine the mixture’s equilibrium state. The variable 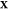 is the third
distinct set of mole fractions
that we have introduced so far; the other two sets defined earlier
are the phase mole fractions
is the third
distinct set of mole fractions
that we have introduced so far; the other two sets defined earlier
are the phase mole fractions 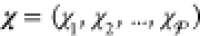 and phase compositions
and phase compositions 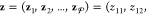
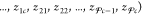 . The mole fraction
. The mole fraction 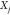 denotes the
total moles of component j in the mixture (moles
of j in each phase
summed over all
denotes the
total moles of component j in the mixture (moles
of j in each phase
summed over all 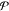 phases)
divided by the total moles in the
mixture. Constraining T, P, and
phases)
divided by the total moles in the
mixture. Constraining T, P, and 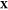 to some fixed
set of values provides a
complete thermodynamic specification of the mixture, corresponding
to a description of the system in the isothermal–isobaric ensemble,
and therefore, it should be possible in principle to determine the
mixture’s equilibrium state from this specification. The well-known
condition for equilibrium in this particular situation is that the
Gibbs energy G must attain a global minimum. From eq 19 for G of an ideal mixture or the more general expression in 16 for G of a nonideal mixture, it is clear
that if T and P are fixed, the only
freedom one has in adjusting the value of G is to
vary χ and z. Therefore, we find the
equilibrium state of a mixture by adjusting the relative amounts of
the different phases χ and the compositions of
the phases z to minimize G subject to
the constraints that all phases must remain fixed at T and P, and the following mole-balance (mass-conservation)
equations
to some fixed
set of values provides a
complete thermodynamic specification of the mixture, corresponding
to a description of the system in the isothermal–isobaric ensemble,
and therefore, it should be possible in principle to determine the
mixture’s equilibrium state from this specification. The well-known
condition for equilibrium in this particular situation is that the
Gibbs energy G must attain a global minimum. From eq 19 for G of an ideal mixture or the more general expression in 16 for G of a nonideal mixture, it is clear
that if T and P are fixed, the only
freedom one has in adjusting the value of G is to
vary χ and z. Therefore, we find the
equilibrium state of a mixture by adjusting the relative amounts of
the different phases χ and the compositions of
the phases z to minimize G subject to
the constraints that all phases must remain fixed at T and P, and the following mole-balance (mass-conservation)
equations
| 25 |
We will show later in this study that
the mole-balance constraints are much easier to enforce if we introduce an auxiliary set of mole fractions 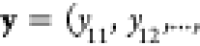
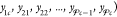 , where yij is defined as the moles of component j in
phase i divided by the total moles of the mixture.
The information content in y is the same as that in the
set (χ, z), so that we can obtain
the latter from the former, and vice-versa, through the following
relations
, where yij is defined as the moles of component j in
phase i divided by the total moles of the mixture.
The information content in y is the same as that in the
set (χ, z), so that we can obtain
the latter from the former, and vice-versa, through the following
relations
| 26 |
| 27 |
| 28 |
The mole-balance constraints, when expressed in terms of y, take on the simpler form
| 29 |
Thus, the maximum value that yij can take is 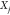 , corresponding
to the situation where all
of component j resides in phase i. In each iteration of our optimization process, we convert y to χ and z, so that we can
evaluate our objective function (the Gibbs energy G) according to eq 16, then we proceed to the next iteration by adjusting y via some prescription that obeys (29).
, corresponding
to the situation where all
of component j resides in phase i. In each iteration of our optimization process, we convert y to χ and z, so that we can
evaluate our objective function (the Gibbs energy G) according to eq 16, then we proceed to the next iteration by adjusting y via some prescription that obeys (29).
As stated in the Introduction, we perform
the Gibbs-energy minimization using PSO, which is a stochastic method
whose modern-day form is attributed to the seminal work by Kennedy
and Eberhart.16 PSO simulates the trajectory
of a large number Np of particles (points)
that reside in the search space. The particles together comprise the
swarm. (Kennedy and Eberhart were motivated by a desire to model collective
social behavior in animals, and they imagined the swarm as being a
flock of birds in their original study.) In the problem of interest
in this study, the search space is the Gibbs-energy surface, and each
of the particles in the swarm represents—in general—a
multiphase, multicomponent mixture that is fixed at the given T, P, and 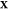 . If Np →
∞, the swarm signifies an isothermal–isobaric ensemble.
Each particle is initially assigned to a location on the Gibbs-energy
surface, meaning that it is assigned to some set of y and consequently also some set of χ and z. The y of each particle is then adjusted iteratively
in a manner that depends on the particle’s current y, its best ever y (corresponding to the lowest G it has ever achieved), the best ever y achieved
by any of the particles in the swarm, and potentially other quantities.
The iterations are carried out until a termination criterion is met.
PSO has enjoyed widespread usage since its introduction over 25 years
ago, and many variants have been developed.17,18 The assortment of PSO flavors may differ in their choice of particle
initialization, the method by which the particles are moved in the
search space, the termination criteria, and the various hyperparameters
that influence the optimization process. A perusal of the literature
reveals the perhaps obvious fact that there does not seem to be a
“magic bullet”; different variants work better for different
applications.
. If Np →
∞, the swarm signifies an isothermal–isobaric ensemble.
Each particle is initially assigned to a location on the Gibbs-energy
surface, meaning that it is assigned to some set of y and consequently also some set of χ and z. The y of each particle is then adjusted iteratively
in a manner that depends on the particle’s current y, its best ever y (corresponding to the lowest G it has ever achieved), the best ever y achieved
by any of the particles in the swarm, and potentially other quantities.
The iterations are carried out until a termination criterion is met.
PSO has enjoyed widespread usage since its introduction over 25 years
ago, and many variants have been developed.17,18 The assortment of PSO flavors may differ in their choice of particle
initialization, the method by which the particles are moved in the
search space, the termination criteria, and the various hyperparameters
that influence the optimization process. A perusal of the literature
reveals the perhaps obvious fact that there does not seem to be a
“magic bullet”; different variants work better for different
applications.
PSO has been used in a number of thermodynamic
modeling studies.
Cox and Christie report it to be an effective tool for optimizing
EOS parameters to fit experimental data, and they have applied it
to develop high-pressure-oriented, multiphase EOSs for four single-component
materials: aluminum, tantalum, lead, and titanium.47,48 PSO has also been tested along certain select  points under ambient
or near-ambient conditions
in multicomponent systems, including mixtures of energetic materials,49 petrochemical fluids,50,51 and complex microemulsions.52 Although
none of these studies have applied PSO toward our goal of producing
whole phase diagrams covering multiple phase boundaries of a mixture,
they suggest that if extensive and careful testing is done to properly
tune the optimization details, it can be a reliable method for achieving
our goal.
points under ambient
or near-ambient conditions
in multicomponent systems, including mixtures of energetic materials,49 petrochemical fluids,50,51 and complex microemulsions.52 Although
none of these studies have applied PSO toward our goal of producing
whole phase diagrams covering multiple phase boundaries of a mixture,
they suggest that if extensive and careful testing is done to properly
tune the optimization details, it can be a reliable method for achieving
our goal.
Now that we have provided an overview of PSO, the
rest of this
section focuses on the specific details of our particular algorithm.
The first step is to initialize the location of the particles (mixtures)
along the Gibbs-energy surface by assigning mole fractions y to each. Let yijkl denote the value
of the mole fraction yij for particle k at iteration l.
Initializing the particle locations entails setting the mole fractions yij for all phases 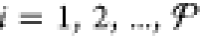 and all components j =
1, 2, ..., c for each particle k = 1, 2, ..., Np at l = 0. To do this, we first randomize the order of the
and all components j =
1, 2, ..., c for each particle k = 1, 2, ..., Np at l = 0. To do this, we first randomize the order of the 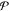 phases (so
as to not bias any particular
one) by creating the set
phases (so
as to not bias any particular
one) by creating the set 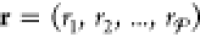 , in which ri is a random
integer between 1 and
, in which ri is a random
integer between 1 and 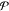 and
is different from the other
and
is different from the other  integers in r. For each particle k, its mole fractions in the
phase corresponding to r1 are assigned
as follows:
integers in r. For each particle k, its mole fractions in the
phase corresponding to r1 are assigned
as follows:
-
1
Calculate
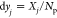 for each component j.
for each component j. -
2.
Set yr1jk0 to be a random real number between (k – 1)dyj and kdyj for each j.
Thus, the k = 1 particle
has mole fractions in
its r1 phase that lie between 0 and dyj for each component j, while the k = Np particle has mole fractions in that same phase that lie between
(Np – 1)dyj and 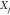 for each component j.
This ensures that, at least for the r1 phase, the particles in the swarm collectively provide a representative
sampling of the search space. Our initialization approach is adapted
from the Latin-hypercube sampling technique used in the recent study
by Sterbentz et al.,53 who have applied
another stochastic method called differential evolution optimization
to determine the input drive in high-pressure, ramp-compression experiments.
(Incidentally, we have also tried differential evolution optimization
for our problem, but we have not been able to get it to work as reliably
as PSO.) If we let
for each component j.
This ensures that, at least for the r1 phase, the particles in the swarm collectively provide a representative
sampling of the search space. Our initialization approach is adapted
from the Latin-hypercube sampling technique used in the recent study
by Sterbentz et al.,53 who have applied
another stochastic method called differential evolution optimization
to determine the input drive in high-pressure, ramp-compression experiments.
(Incidentally, we have also tried differential evolution optimization
for our problem, but we have not been able to get it to work as reliably
as PSO.) If we let 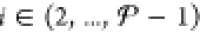 , so that we consider all of the remaining
phases except for the
, so that we consider all of the remaining
phases except for the 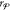 phase in the sequential order given by r, we set the
mole fractions of the ri phase in all Np particles in a similar
manner:
phase in the sequential order given by r, we set the
mole fractions of the ri phase in all Np particles in a similar
manner:
-
1.
Calculate
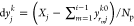 for each j and k.
for each j and k. -
2.
For each j and k, set the mole fraction yrijk0 to be a random real number between (q – 1)dyj and qdyjk, where q is a random integer between 1 and Np.
Finally, the mole fractions of the 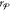 phase
in all Np particles are initialized by
setting
phase
in all Np particles are initialized by
setting 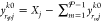 for each j and k. This enforces the mole-balance constraints in eq 29.
for each j and k. This enforces the mole-balance constraints in eq 29.
In every iteration, each particle’s fitness is examined by evaluating its Gibbs energy using eq 16. Evaluation of G requires converting each particle’s y to χ and z by applying eqs 26 and 27. As mentioned earlier, we track yk,best of every particle k and the best ever y achieved by any of the particles in the swarm, yswarm,best. In addition, we also track Gswarm,best, which is the lowest value of G ever achieved by any of the particles in the swarm and corresponds to yswarm,best. All of these quantities are updated, if necessary, in each iteration.
A critical part of any PSO algorithm is in
updating the locations
of the particles from one iteration to the next, and many of the studies
in the literature17,18,51,54 focus on proposing new ways to perform this
update. If we designate the mole fractions y for particle k at iteration l as 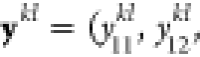
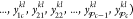 , then the mole
fractions at the next iteration
are given by yk,l+1 = ykl + Δykl, where we calculate Δykl according to the formula
, then the mole
fractions at the next iteration
are given by yk,l+1 = ykl + Δykl, where we calculate Δykl according to the formula
| 30 |
in which Δyk,l–1 from the previous iteration is set to zero for all Np particles if we are in the initialization step, where l = 0; and w, a, and b are weighting factors. All three weighting factors are based on real random numbers that lie between two specified bounds. After much testing, bounds that we have found to be effective are (−0.02, 0.05), (0, 1), and (0, 3) for w, a, and b, respectively. These random numbers are generated separately for each particle in every iteration, and so, w, a, and b will in general be different across particles and across iterations. The fact that w can be a negative number helps the algorithm escape local minima. In addition, we apply a “constriction factor”17,18,51 on w, so that the complete expression for w is
| 31 |
where lmax = 100 is the maximum number of iterations allowed (see below for a discussion on how we decided on this particular value), and rand(−0.02, 0.05) is a random number between the specified bounds. The constriction factor is always positive, and its role is to gradually decrease the magnitude of w, as PSO iterates and settles in on a minimum, with w becoming zero if l + 1 = lmax.
The mole fractions that we obtain from the sum yk,l+1 = ykl + Δykl may sometimes be unphysical because one or more of the resulting yijk,l+1 might be negative or might exceed the bounds set by the mole-balance constraints in eq 29. Some adjustment on yk,l+1 may therefore be necessary to make these mole fractions physically viable. For each particle k, we apply the following adjustment procedure on yk,l+1 that resembles the initialization procedure described above:
-
1
Randomize the order of the phases by creating the set
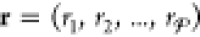 as discussed earlier. Carry out the steps
below for each component j.
as discussed earlier. Carry out the steps
below for each component j. -
2
Let
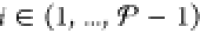 , so that we traverse through all but the
last phase in the order given by r and perform the following
for each phase ri. We
remind the reader that if the phase mole fractions are set in the
order dictated by r, the maximum possible value for yrijk,l+1 allowed by the mole-balance constraints
is
, so that we traverse through all but the
last phase in the order given by r and perform the following
for each phase ri. We
remind the reader that if the phase mole fractions are set in the
order dictated by r, the maximum possible value for yrijk,l+1 allowed by the mole-balance constraints
is 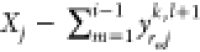 . We multiply
this maximum value by scaling
factors α and β—whose values we determine as explained
below—to obtain
. We multiply
this maximum value by scaling
factors α and β—whose values we determine as explained
below—to obtain 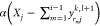 and
and 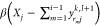 , which we subsequently use to adjust yrijk,l+1 as necessary in the
following manner:
, which we subsequently use to adjust yrijk,l+1 as necessary in the
following manner:If yrijk,l+1 < 0 (is negative), set yrij to a random number between 0 and
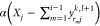 .
.If
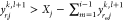 (exceeds the maximum), set yrijk,l+1 to a random
number between
(exceeds the maximum), set yrijk,l+1 to a random
number between 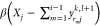 and
and 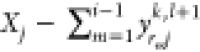 .
.
-
3.
Finally, in order to satisfy eq 29, the mole fractions of the
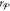 phase
are determined by setting
phase
are determined by setting 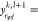
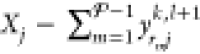 .
.
We have done extensive testing to determine
the most effective
values for the scaling factors α and β. From this testing,
we conclude that it is best to set α ≈ 0 and β
≈ 1. In retrospect, this seems reasonable because if yrijk,l+1 is found to be negative, it is an indication
that component j is likely not present in great amounts
in phase ri, and so,
its value should be adjusted to be close to zero. Likewise, if yrij exceeds the maximum 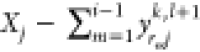 , it seems reasonable
to adjust it to a
number that is only slightly smaller than this maximum. Specifically,
we set β = 0.99 and α = 10–9. We find
that small values of α are required in single-phase regions
to prevent the spurious appearance of other phases that should not
be present. However, if α is too small, it reduces the efficiency
in two-phase regions, especially when significant amounts of both
phases are present. The value we have chosen appears to be a good
compromise between these two competing needs. We have tried setting
α closer to 1 and β closer to 0 and have found that this
choice does not lead to lower values of Gswarm,best; in fact, this choice only reduces the efficiency of the algorithm,
so that it requires more iterations to converge to the same Gswarm,best and yswarm,best.
, it seems reasonable
to adjust it to a
number that is only slightly smaller than this maximum. Specifically,
we set β = 0.99 and α = 10–9. We find
that small values of α are required in single-phase regions
to prevent the spurious appearance of other phases that should not
be present. However, if α is too small, it reduces the efficiency
in two-phase regions, especially when significant amounts of both
phases are present. The value we have chosen appears to be a good
compromise between these two competing needs. We have tried setting
α closer to 1 and β closer to 0 and have found that this
choice does not lead to lower values of Gswarm,best; in fact, this choice only reduces the efficiency of the algorithm,
so that it requires more iterations to converge to the same Gswarm,best and yswarm,best.
We terminate the optimization process if one of two criteria are met. One criterion is satisfied if the maximum number of iterations lmax is exceeded. For the Fe/Ga examples that we show in section 4, we have found that a good compromise between reliability and computational efficiency is to set the number of particles Np = 60. With this choice of Np, we have found that PSO always terminates in less than 100 iterations, which is why we have set lmax = 100 as stated above. In single-phase regions, it usually converges within 15–20 iterations, while in two-phase regions, it usually does so in under 40 iterations, but in rare instances can take up to 80 iterations. A second termination criterion we check is if the method stops producing meaningful improvements. We define this as having occurred when Gswarm,best at the current iteration minus the running average of this quantity over the past 10 iterations converges to within a very tight tolerance of 10–10RT. We evaluate whether or not this criterion is met starting in the 15th iteration.
Once the
optimization process has terminated, we use eqs 26 and 27 to
translate yswarm,best to χ and z, and we take the resulting set (χ, z) as being the equilibrium state that corresponds
to the given T, P, and 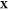 . If component j is insoluble
in phase i, this will be revealed by the fact that
the equilibrium value of the mole fraction zij will be a very small number, typically
10–9 or less. Likewise, if phase i is not present in the equilibrium state (this state may lie in a
single-phase region for instance), χi will be a negligibly small number. From knowledge of the equilibrium χ and z, one can compute other properties
of the mixture (internal energy, density, sound speed, etc.) by applying
the formulas in section 2 and the Appendix to the chosen EOS for the
mixture of interest.
. If component j is insoluble
in phase i, this will be revealed by the fact that
the equilibrium value of the mole fraction zij will be a very small number, typically
10–9 or less. Likewise, if phase i is not present in the equilibrium state (this state may lie in a
single-phase region for instance), χi will be a negligibly small number. From knowledge of the equilibrium χ and z, one can compute other properties
of the mixture (internal energy, density, sound speed, etc.) by applying
the formulas in section 2 and the Appendix to the chosen EOS for the
mixture of interest.
3.2. Suitability of PSO for High-Pressure Phase Equilibria
A key set of equations that we use in our testing
of PSO is the equality of chemical potentials in eq 32, which is a fundamental thermodynamic
requirement for equilibrium.35−39 Suppose that the equilibrium state for a given 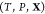 is an
is an 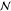 -phase
state, where
-phase
state, where 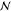 is an integer
that is less than or equal
to the maximum possible number of phases
is an integer
that is less than or equal
to the maximum possible number of phases 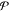 . The chemical
potentials across the various
phases must then satisfy
. The chemical
potentials across the various
phases must then satisfy
| 32 |
We may solve these equations
with a
direct numerical method (e.g., a Newton–Raphson solve) to obtain
the phase compositions 
 . A crucial
point we emphasize is that we
do not explicitly enforce these constraints in PSO, but the equilibrium
state that it converges to must nevertheless satisfy these equations
because they are necessary but not sufficient conditions for the Gibbs
energy to achieve a minimum. Thus, they serve as an important check
on the phase boundaries predicted by PSO.
. A crucial
point we emphasize is that we
do not explicitly enforce these constraints in PSO, but the equilibrium
state that it converges to must nevertheless satisfy these equations
because they are necessary but not sufficient conditions for the Gibbs
energy to achieve a minimum. Thus, they serve as an important check
on the phase boundaries predicted by PSO.
Direct numerical solutions
of eq 32 offer a potentially
simple and computationally efficient
means to infer phase boundaries and construct phase diagrams, but
they have certain limitations that a more sophisticated approach like
PSO is able to overcome. One limitation is that the direct solutions
reveal information only about the phase compositions z, but not the relative amounts of the different phases encapsulated
in the mole fractions χ, whereas PSO reveals the
complete set (χ, z). Another issue
is that a direct method for solving eq 32 will converge to a sensible solution only if there
actually are 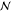 phases in
equilibrium at the given
phases in
equilibrium at the given 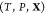 . It will
fail to converge if this is not
the case, especially if a gradient-based method is used. This means
that number of phases must be known a priori if using a direct method.
Contrast this with PSO, which requires input only about the maximum
possible number of phases
. It will
fail to converge if this is not
the case, especially if a gradient-based method is used. This means
that number of phases must be known a priori if using a direct method.
Contrast this with PSO, which requires input only about the maximum
possible number of phases 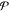 and
free-energy models for these phases.
Given this input, PSO will determine the actual number of phases
and
free-energy models for these phases.
Given this input, PSO will determine the actual number of phases 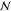 in the equilibrium
state and will thereby
eliminate much of the guesswork that would be required if one were
to instead piece together a mixture’s phase diagram from the
direct solutions alone.
in the equilibrium
state and will thereby
eliminate much of the guesswork that would be required if one were
to instead piece together a mixture’s phase diagram from the
direct solutions alone.
Furthermore, it is important to reiterate
that the equations in eq 32 represent necessary
but not sufficient conditions for equilibrium; they cannot distinguish
between local minima and the global minimum. Direct solutions of those
equations therefore cannot resolve ambiguities when there are multiple
different sets of 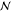 phases
that can be in equilibrium (each
set represents a different minimum) at the given T, P, and
phases
that can be in equilibrium (each
set represents a different minimum) at the given T, P, and 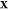 , meaning
multiple different ways for the
resulting phase boundaries to combine together to form the phase diagram.
An example of this kind of ambiguity will be presented in Figure 7. The direct solutions
tend to be useful only when the “right answer” is known
in some sense. For instance, we will apply them in this study as an a posteriori check on the PSO-predicted phase diagrams.
Direct solutions also enjoy usage when experimental data on the phase
diagram are readily available, which is the case for some mixtures
at ambient pressure. In such situations, eq 32 may be solved directly to verify whether
phase boundaries predicted by EOS models developed for these mixtures
can reproduce the experimental data. One of the authors of this paper
has in fact done this55,56 for condensed-phase mixtures
of unreacted high explosives57 at ambient
and near-ambient pressures. However, in the Introduction, we have alluded to a quite different reality that exists at higher
pressures, where data regarding phase boundaries are not available
for the vast majority of mixtures. For these mixtures, the only such
information that one may reasonably hope to obtain are predictions
from atomistic simulations at a few select points along a particular
phase boundary. Consequently, the free-energy models for these mixtures
will have to be fit to more readily available data, such as isotherms,
Hugoniot curves, and isentropes. Thus for high-pressure applications,
one must be able to reliably generate phase diagrams with little a
priori knowledge about the appearance of the phase diagram, that is,
how the phase boundaries are connected together. This is precisely
what a global optimization method like PSO, which does not require
one to specify good guesses for the phase fractions χ and compositions z, is intended to do. As long as it
is given EOS models for the different phases of the mixture that might
be present, it will automatically sort out the different possibilities
for the phase boundaries to find the one that minimizes the Gibbs
energy represented by those models.
, meaning
multiple different ways for the
resulting phase boundaries to combine together to form the phase diagram.
An example of this kind of ambiguity will be presented in Figure 7. The direct solutions
tend to be useful only when the “right answer” is known
in some sense. For instance, we will apply them in this study as an a posteriori check on the PSO-predicted phase diagrams.
Direct solutions also enjoy usage when experimental data on the phase
diagram are readily available, which is the case for some mixtures
at ambient pressure. In such situations, eq 32 may be solved directly to verify whether
phase boundaries predicted by EOS models developed for these mixtures
can reproduce the experimental data. One of the authors of this paper
has in fact done this55,56 for condensed-phase mixtures
of unreacted high explosives57 at ambient
and near-ambient pressures. However, in the Introduction, we have alluded to a quite different reality that exists at higher
pressures, where data regarding phase boundaries are not available
for the vast majority of mixtures. For these mixtures, the only such
information that one may reasonably hope to obtain are predictions
from atomistic simulations at a few select points along a particular
phase boundary. Consequently, the free-energy models for these mixtures
will have to be fit to more readily available data, such as isotherms,
Hugoniot curves, and isentropes. Thus for high-pressure applications,
one must be able to reliably generate phase diagrams with little a
priori knowledge about the appearance of the phase diagram, that is,
how the phase boundaries are connected together. This is precisely
what a global optimization method like PSO, which does not require
one to specify good guesses for the phase fractions χ and compositions z, is intended to do. As long as it
is given EOS models for the different phases of the mixture that might
be present, it will automatically sort out the different possibilities
for the phase boundaries to find the one that minimizes the Gibbs
energy represented by those models.
Figure 7.

Gibbs energy relative to the PSO-predicted results as a function of composition for Fe/Ga mixtures at different fixed temperatures and pressures: (a) 4500 K and 205 GPa; (b) same as in (a), except that the y-axis is on a linear scale; (c) 3450 K and 205 GPa; and (d) 7150 K and 700 GPa. The orange curves indicate the Gibbs energy of the fluid phase minus that of the PSO result, normalized by RT. The blue and green curves show the same ΔG/RT comparison for the Ga-III/Fe and Ga-IV/Fe phases, respectively. The black curves portray the Gibbs-energy difference between the various hypothetical scenarios described in the text and the PSO result. These scenarios access local minima along the Gibbs-energy surface. The vertical dashed lines represent boundaries between two-phase (fluid–solid or solid–solid) regions for the PSO (equilibrium/global minimum) result, while the vertical dotted lines show the same for the hypothetical scenarios. The dashed–dotted vertical lines in (d) show the left (hypoeutectic) branch of the fluid–solid phase boundaries in Figure 6; these boundaries are traversed in both the PSO and hypothetical scenarios.
4. Results and Discussion
Here, we demonstrate our PSO algorithm on the Fe/Ga system, using
LEOS tables for pure Fe and pure Ga combined with different example
models for the mixing free energy. We verify through different ways
that it can reliably locate the minimum on the Gibbs-energy surface
fashioned by these models. We illustrate this by producing temperature–composition
phase diagrams at different fixed pressures. (Although not shown in
this study, we could also apply the same algorithm to fix the temperature
and generate pressure–composition diagrams instead.) Finally,
we explain how PSO may be used to construct multiphase LEOS- or SESAME-style
tables for a mixture at a particular overall composition 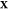 , again using
the Fe/Ga system to demonstrate
the construction process. In this process, we first produce a temperature–pressure
phase diagram for the mixture using PSO and then apply post-processing
steps to obtain a table of Helmholtz energy versus temperature and
density, which may be graphically visualized in the form of a temperature–density
diagram. We compare Hugoniot and isentrope curves obtained from the
resulting Fe/Ga tables with those from the pure Fe table.
, again using
the Fe/Ga system to demonstrate
the construction process. In this process, we first produce a temperature–pressure
phase diagram for the mixture using PSO and then apply post-processing
steps to obtain a table of Helmholtz energy versus temperature and
density, which may be graphically visualized in the form of a temperature–density
diagram. We compare Hugoniot and isentrope curves obtained from the
resulting Fe/Ga tables with those from the pure Fe table.
Before proceeding to the mixtures, we briefly introduce the EOSs we use for pure Fe and Ga, along with their phase diagrams. For Fe, we use a new two-phase EOS developed by Benedict et al.,58 which is intended for temperatures above roughly 3200 K and pressures above around 100 GPa. A recent study on shock-compressed Fe reports that the solid under these conditions is in the hexagonal closed-pack (hcp) phase.59 As a result, the two phases modeled by the EOS developed by Benedict et al. are fluid and hcp. To keep the nomenclature simple, we use “fluid” as a general term to indicate liquid or supercritical fluid or any other fluid-like phase, all of which are represented by the same set of free-energy models in the EOS. The temperature–pressure phase diagram predicted by this EOS is shown in Figure 1a. For Ga, we use the five-phase EOS developed by Wu et al.,60 though only three phases—the fluid plus two solids, Ga-III (which has a body-centered tetragonal [bct] structure) and Ga-IV (face-centered cubic [fcc])—are thermodynamically stable in the applicable temperature–pressure range of the Fe EOS developed by Benedict et al. The phase diagram of the Wu et al. Ga EOS is shown in Figure 1b–d.
Figure 1.

Temperature–pressure phase diagrams of iron (Fe) and gallium (Ga) constructed from the pure-component EOSs used in this study: (a) Fe; (b) Ga; (c) same as (b), except that here we have neglected the fluid phase, so that metastable extensions of the solid phases can be seen; and (d) magnified view of (c) near the lower end of the temperature and pressure range. Each “+” symbol denotes a point at which we have performed a free-energy minimization to determine the thermodynamically stable phase(s). The Fe phase diagram is produced from the two-phase EOS developed by Benedict et al.,58 where we have used blue and orange to indicate the hcp and fluid phases, respectively. We model Ga with the five-phase EOS developed by Wu et al.,60 though only three phases (Ga-III = blue, Ga-IV = green, and fluid = orange) are stable under the conditions in this figure. The fluid–solid (melt) phase boundary in all figures is illustrated by the dashed curves, while the dotted curves in (c) and (d) indicate the Ga-III/Ga-IV phase boundary.
4.1. Temperature–Composition Phase Diagrams
4.1.1. Ideal Mixtures
When considering
a mixture of two or more components, a question naturally arises as
to what are the possible number of phases 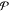 and the identity
of these phases. In the
Fe/Ga system at the pressures shown in Figure 1, obvious choices are the fluid phase, which
is a mixture of fluid Fe and fluid Ga, and three terminal solid solutions:
hcp, bct, and fcc. In the first of these solid solutions, Fe in the
hcp phase would serve as a solvent for Ga solutes in that same phase.
Likewise, the bct and fcc phases would be composed of Fe solute in
those phases dissolved in a Ga-III or Ga-IV solvent, respectively.
At intermediate compositions, there might also be compounds (e.g.,
Fe3Ga, Fe6Ga5, Fe3Ga4, and FeGa3) and potential secondary solid solutions—such
as a body-centered cubic (bcc) phase—that have yet to be discovered.
Developing a complete set of free-energy models to cover all of these
possibilities is not the purpose of this study, nor is it necessary
to demonstrate the efficacy of PSO. Given the lack of currently available
EOSs (e.g., high-pressure EOSs have not yet been developed for any
of the compounds, nor do we have a bcc-phase EOS for either Fe or
Ga that is usable under such conditions), we take
and the identity
of these phases. In the
Fe/Ga system at the pressures shown in Figure 1, obvious choices are the fluid phase, which
is a mixture of fluid Fe and fluid Ga, and three terminal solid solutions:
hcp, bct, and fcc. In the first of these solid solutions, Fe in the
hcp phase would serve as a solvent for Ga solutes in that same phase.
Likewise, the bct and fcc phases would be composed of Fe solute in
those phases dissolved in a Ga-III or Ga-IV solvent, respectively.
At intermediate compositions, there might also be compounds (e.g.,
Fe3Ga, Fe6Ga5, Fe3Ga4, and FeGa3) and potential secondary solid solutions—such
as a body-centered cubic (bcc) phase—that have yet to be discovered.
Developing a complete set of free-energy models to cover all of these
possibilities is not the purpose of this study, nor is it necessary
to demonstrate the efficacy of PSO. Given the lack of currently available
EOSs (e.g., high-pressure EOSs have not yet been developed for any
of the compounds, nor do we have a bcc-phase EOS for either Fe or
Ga that is usable under such conditions), we take  in which the three phases include the fluid
and two solid solutions that we refer to as the Ga-III/Fe and Ga-IV/Fe
phases. In both of these solid solutions, the properties of pure Fe
are modeled with the hcp-phase EOS from Benedict et al. We present
various mixing models and demonstrate that PSO may be used to reliably
locate the minimum on the Gibbs-energy surface represented by these
models to produce coherent phase diagrams.
in which the three phases include the fluid
and two solid solutions that we refer to as the Ga-III/Fe and Ga-IV/Fe
phases. In both of these solid solutions, the properties of pure Fe
are modeled with the hcp-phase EOS from Benedict et al. We present
various mixing models and demonstrate that PSO may be used to reliably
locate the minimum on the Gibbs-energy surface represented by these
models to produce coherent phase diagrams.
The simplest test of PSO is the case of ideal mixing. Under this assumption, the Gibbs energy that we minimize is taken from eq 19 and may be expressed as
| 33 |
where the phase index i covers the fluid, Ga-III/Fe, and Ga-IV/Fe phases (in that order), while the component index j = 1 stands for Fe and j = 2 denotes Ga. We have used PSO to produce temperature–composition diagrams at two different pressures: 205 GPa and 700 GPa; see Figure 2. The fluid–solid region (colored in red) in this figure is lens-shaped, which is a characteristic feature of ideal mixing. In these two-phase regions, the equilibrium conditions in eq 32 require that the chemical potentials satisfy
| 34 |
in Figure 2a,b, where the fluid (i = 1) is in equilibrium with Ga-III/Fe (i = 2), while they must satisfy
| 35 |
in Figure 2c,d, where the fluid is in equilibrium with Ga-IV/Fe (i = 3). The PSO-predicted two-phase regions in Figure 2 satisfy these equations, without requiring any explicit enforcement, to within 10–5RT (the left- and right-hand sides agree to about 0.00005% or better). We have also verified that the liquidus and solidus curves illustrated in the figure are essentially indistinguishable from what we would obtain if eq 34 or eq 35 were explicitly solved with a direct numerical method to a very tight tolerance of 10–9RT.
Figure 2.
Temperature–composition phase diagrams
of ideal Fe/Ga mixtures
in which the pressure P is fixed at some value in
each figure: (a) P = 205 GPa; (b) magnified view
of (a) in the Ga-rich side; (c) P = 700 GPa; and
(d) magnified view of (c) in the Ga-rich side. The x-axis refers to the overall mole fraction of Fe, which we symbolize
as 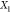 , so that the overall mole fraction
of Ga
is
, so that the overall mole fraction
of Ga
is 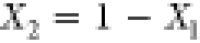 . Each “+” symbol therefore
denotes a particular set
. Each “+” symbol therefore
denotes a particular set 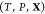 for which
we have carried out a Gibbs-energy
minimization using PSO. The Gibbs energy in all cases here is computed
from eq 33. We consider
three possible phases for the Fe/Ga mixtures: (1) fluid (orange),
(2) Ga-III/Fe (blue), and (3) Ga-IV/Fe (green). States that lie in
the two-phase, fluid–solid region are colored in red. The liquidus
and solidus curves that enclose this lens-shaped region are illustrated
by the black solid curves. These curves indicate the composition z of the fluid and solid phases. The phase mole fractions χ in each of the two-phase states are computed directly
by PSO but can also be determined graphically from the liquidus and
solidus curves by applying the lever rule. The horizontal dotted lines
in (a) and (b) reflect the transition temperature between pure Ga-III
and Ga-IV at 205 GPa.
for which
we have carried out a Gibbs-energy
minimization using PSO. The Gibbs energy in all cases here is computed
from eq 33. We consider
three possible phases for the Fe/Ga mixtures: (1) fluid (orange),
(2) Ga-III/Fe (blue), and (3) Ga-IV/Fe (green). States that lie in
the two-phase, fluid–solid region are colored in red. The liquidus
and solidus curves that enclose this lens-shaped region are illustrated
by the black solid curves. These curves indicate the composition z of the fluid and solid phases. The phase mole fractions χ in each of the two-phase states are computed directly
by PSO but can also be determined graphically from the liquidus and
solidus curves by applying the lever rule. The horizontal dotted lines
in (a) and (b) reflect the transition temperature between pure Ga-III
and Ga-IV at 205 GPa.
PSO is also able to correctly describe the solid-phase equilibria dictated by the Gibbs-energy surface in eq 33. We can see from Figure 1d that at 205 GPa, Ga-IV is more thermodynamically stable than Ga-III at low temperatures, but there is a relatively narrow temperature band of about 100 K directly below the melt temperature, where Ga-III is more stable than Ga-IV. Thus, we would expect both the Ga-III/Fe and Ga-IV/Fe phases to be present in the temperature–composition diagram at this pressure, and that is indeed what we observe in Figure 2a,b. These PSO-generated phase diagrams suggest that there is no two-phase, solid–solid region, and instead, there is an abrupt transition from Ga-IV/Fe to Ga-III/Fe or vice-versa. The absence of a solid–solid region may be understood from the following arguments. If such a region were to exist, all points in it would satisfy
| 36 |
which means that for Fe (j = 1), we have from eq 33 that
| 37 |
and because z22 = 1 – z21 and z32 = 1 – z31, we have for Ga (j = 2) that
| 38 |
Because the pure-component Gibbs energies of Fe in both solid solutions are described by the same free-energy model (see our discussion at the beginning of this subsection), we have G21 = G31, which therefore implies that z21 = z31 and G22 = G32. The last equality indicates that under the assumption of ideal mixing, the two solid solutions can be equilibrium only at the transition temperature between pure Ga-III and Ga-IV, which is represented by the dotted lines in Figure 2a,b. Moreover, at 700 GPa, the Ga-III/Fe phase is absent, as we would expect from Figure 1.
The phase diagrams that we generate in this study
are produced
through an iterative procedure that resembles the process of how one
might put together a jigsaw puzzle. In the first iteration, a set
of overall mole fractions 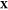 is chosen,
and for each
is chosen,
and for each 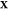 , we perform
PSO calculations over a coarsely
spaced set of temperatures. This produces a rough overview of the
phase diagram. In subsequent iterations, we refine it by performing
calculations over additional choices of
, we perform
PSO calculations over a coarsely
spaced set of temperatures. This produces a rough overview of the
phase diagram. In subsequent iterations, we refine it by performing
calculations over additional choices of 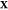 and/or homing
in on multiphase regions
with a more closely spaced temperature grid. Two iterations are sufficient
for the phase diagrams in Figure 2, but multiple rounds of refinement may be needed for
more complicated ones. Results for some of the points are omitted
in order to improve the visual appearance/clarity.
and/or homing
in on multiphase regions
with a more closely spaced temperature grid. Two iterations are sufficient
for the phase diagrams in Figure 2, but multiple rounds of refinement may be needed for
more complicated ones. Results for some of the points are omitted
in order to improve the visual appearance/clarity.
4.1.2. Nonideal Mixtures
If we relax the assumption of ideal mixing, the expression for the Gibbs energy G becomes
 |
39 |
It is conceptually useful to decompose 39 so that
| 40 |
in which ΔGipure = ΔGi(T,P,zi) is the change in Gibbs energy that occurs when the components of phase i are physically brought together in the proportions indicated by zi
| 41 |
and ΔGimix = ΔGi(T,P,zi) is the change in Gibbs energy that occurs when the components are chemically mixed together (dissolved) in phase i
| 42 |
In order for any functional form of ΔGimix to be physically valid, it must go to zero if phase i is pure in any component j, so that zij = 1 and zik = 0 for k ≠ j. Furthermore, the nonideal-mixing effects encapsulated in the excess Gibbs energy must vanish in the limit, as T → ∞. The excess Gibbs energy may be nonzero at T = 0, reflecting “cold” contributions to the mixing that may be computed from ab initio quantum simulations or inferred from high-pressure cell experiments conducted at low temperatures. For the Fe/Ga examples in this study, we employ the functional form
| 43 |
Here, nonideal mixing is represented in terms of a Margules model35,43 of the form GMzi1zi2, and we set the temperature and pressure dependence of the Margules coefficient GM as
| 44 |
where ηi, σi, and θi are phase-specific constants.
As a first step toward
nonideal mixing, we consider the situation
where the fluid phase is a nonideal mixture described by eqs 43 and 44, while the two solid solutions still undergo ideal mixing
(which essentially implies that for the time being, we set η2 = η3 = 0). We set η1 =
0.5 cm3/mol, σ1 = 100 GPa, and θ1 = 2000 K for the fluid. With this choice of σ1 and η1, the Margules coefficient GM is positive (negative) for all temperatures and compositions
if the pressure P is below (above) 100 exp(1) ≈
271.8 GPa. Therefore, we expect nonideal mixing to destabilize (and
thus contract the stability field of) the fluid at 205 GPa, while
it should have the opposite effect at 700 GPa. This is exactly the
behavior depicted in Figures 3 and 4, respectively. Again, we can
validate the results predicted by PSO with a direct numerical solution
of the equilibrium conditions in eq 34 or 35. The liquidus and solidus
curves that we obtain from this direct solution overlap with those
predicted by PSO. This includes the behavior on both sides of the
minimum at 700 GPa that occurs around an Fe mole fraction of 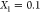 ,
which is a particular two-phase state
where the coexisting fluid and solid [Ga-IV/Fe] happen to have the
same composition.
,
which is a particular two-phase state
where the coexisting fluid and solid [Ga-IV/Fe] happen to have the
same composition.
Figure 3.
Temperature–composition phase diagrams of Fe/Ga mixtures at a fixed pressure of 205 GPa: (a) the entire composition range; (b) magnified view of the Fe-rich side; and (c) magnified view of the Ga-rich side. We have used the same coloring scheme for the different phases/regions as in Figure 2. Like in that figure, the two solid phases (Ga-III/Fe and Ga-IV/Fe) are modeled as ideal mixtures, but unlike in that figure, the fluid phase is not an ideal mixture but instead obeys the nonideal-mixing model in eqs 43 and 44. At the 205 GPa pressure represented in this figure, the resulting excess Gibbs energy in the fluid is positive, meaning that nonideal mixing destabilizes the fluid, making it less thermodynamically favorable. The boundaries of the fluid–solid region (the liquidus and solidus curves) are indicated by the solid curves. For comparison, we have superimposed these same boundaries from the ideal-mixing case of Figure 2a,b (see the dashed curves). The horizontal dotted lines in (a,c) again reflect the Ga-III/Ga-IV transition temperature at 205 GPa.
Figure 4.
Temperature–composition phase diagrams of Fe/Ga mixtures at a fixed pressure of 700 GPa: (a) the entire composition range; (b) magnified view of the Fe-rich side; and (c) magnified view of the Ga-rich side. Here, we have applied the same models and assumptions as in Figure 3, with the key difference being that now at 700 GPa, our nonideal-mixing model for the fluid stabilizes that phase and thereby expands its stability field. Again, the solid curves show the fluid–solid phase boundaries in the nonideal case, while the dashed curves are taken from Figure 2c,d and portray the same boundaries if we instead assume ideal mixing.
We may add a degree of complexity by allowing for nonideality in one of the two solid solutions, the Ga-IV/Fe phase. We model the Gibbs energy of mixing in Ga-IV/Fe with eqs 43 and 44, and we set two out of the three parameter values to be the same as in the fluid, so that σ3 = σ1 = 100 GPa and θ3 = θ1 = 2000 K. However, we choose η3 = −0.1 cm3/mol, and because η3 has a different sign and is smaller in magnitude than η1 = 0.5 cm3/mol, this particular nonideal-mixing model has the opposite, though weaker, effect as in the fluid. Therefore, nonideal mixing at 205 GPa increases the thermodynamic stability of Ga-IV/Fe, while it destabilizes Ga-IV/Fe at 700 GPa. Results at these two pressures are presented in Figures 5 and 6, respectively. Comparing Figures 5 with 3, both of which are at 205 GPa, we see that nonideal mixing in Ga-IV/Fe at this pressure results in a significant expansion in the stability field of that phase, to the extent that it almost entirely displaces Ga-III/Fe. The Ga-III/Fe phase appears in only a narrow range of low Fe concentrations (high Ga concentrations), as shown in Figure 5d. Ga-III/Fe and Ga-IV/Fe are separated by a two-phase, solid–solid region that we have colored in cyan. All points in this region satisfy the equality of chemical potentials in eq 36, which when we substitute the Margules model in eqs 43 and 44 for the excess Gibbs energy, may be written as
| 45 |
and
| 46 |
Figure 5.

Temperature–composition phase diagrams of Fe/Ga
mixtures
at a fixed pressure of 205 GPa: (a) the entire composition range;
(b) magnified view of the Fe-rich side; (c) magnified view of the
Ga-rich side; and (d) even more magnified view deep in the Ga-rich
side, near the peritectic point. The Ga-III/Fe phase is treated as
being ideal, while the fluid phase is described with the same excess
Gibbs energy model as in Figure 3. The difference with that figure is that we now model
the Ga-IV/Fe phase with the nonideal-mixing free energy described
in the text, which stabilizes that phase. (Contrast this with the
situation in the fluid, where nonideal mixing destabilizes it at 205
GPa.) The Ga-III/Fe and Ga-IV/Fe phases are separated by a two-phase,
solid–solid region that we have colored in cyan. The solvus
curves that represent the boundaries of this region are depicted by
the dashed lines. This particular phase diagram has a peritectic point
at a temperature and Fe overall mole fraction 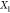 of about 3458 K and 0.0083, respectively.
This point represents a three-phase state, where Ga-III/Fe at that
composition is in equilibrium with both the fluid and Ga-IV/Fe. The
tie line connecting the three phases at the peritectic temperature
is illustrated by the dotted line in (d).
of about 3458 K and 0.0083, respectively.
This point represents a three-phase state, where Ga-III/Fe at that
composition is in equilibrium with both the fluid and Ga-IV/Fe. The
tie line connecting the three phases at the peritectic temperature
is illustrated by the dotted line in (d).
Figure 6.
Temperature–composition
phase diagrams of Fe/Ga mixtures
at a fixed pressure of 700 GPa: (a) the entire composition range;
(b) magnified view of the Fe-rich side; and (c) magnified view of
the Ga-rich side, near the eutectic point. At this pressure, the nonideal-mixing
model for Ga-IV/Fe (the same as the one we have used in Figure 5) destabilizes that phase,
so that it is displaced almost completely by the Ga-III/Fe phase.
Like in previous figures, the liquidus and solidus curves that enclose
the fluid–solid regions are represented by the solid curves,
while the solvus curves that form the boundaries of the solid–solid
region are illustrated by the dashed lines. This particular phase
diagram has a eutectic point at a temperature and  of about 7106 K and 0.188, respectively.
This point represents a three-phase state, where the fluid phase at
that composition is in equilibrium with both Ga-IV/Fe (which has a
slightly less Fe-rich composition) and Ga-III/Fe (which has a more
Fe-rich composition).
of about 7106 K and 0.188, respectively.
This point represents a three-phase state, where the fluid phase at
that composition is in equilibrium with both Ga-IV/Fe (which has a
slightly less Fe-rich composition) and Ga-III/Fe (which has a more
Fe-rich composition).
The behavior of the solid-phase equilibria in Figure 5 may be rationalized by considering the term GMz312 that appears in eq 46, which is negative at 205 GPa (because GM < 0 at this pressure) for all compositions. At very low Fe concentrations where z31 ≈ 0, this term is small in magnitude, and so, it cannot compensate for the fact that the Gibbs energy G32 of pure Ga-IV is larger than G22 of pure Ga-III for most temperatures at this pressure. This explains why Ga-III/Fe persists at very low Fe concentrations despite the stabilizing effect of nonideal mixing on Ga-IV/Fe. The opposite occurs at higher Fe concentrations, where GMz31 becomes too large in magnitude, such that Ga-IV/Fe is favored over Ga-III/Fe for all temperatures shown in the phase diagram. The solid–solid region lies in an intermediate range of compositions and represents states for which it is possible to simultaneously satisfy both eq 45 and eq 46. The intersection of the solid–solid and fluid–solid regions results in a peritectic point, which is a state where all three phases are in equilibrium. At temperatures above (below) the peritectic temperature [the dotted tie line in Figure 5d], the solid that is present along the solidus is the Ga-IV/Fe (Ga-III/Fe) phase.
Similar reasoning may be applied toward comparing Figures 6 and 4, both of which are at 700 GPa. Nonideal mixing at this pressure destabilizes Ga-IV/Fe, so that it gets displaced by Ga-III/Fe throughout most of the composition range. Ga-IV/Fe is present only at low Fe concentrations, where the magnitude of the excess mixing term GMz312 that appears in eq 46 is small. The liquidus curve in Figure 4 exhibits a minimum, and when combined with the two-phase, solid–solid region, the result is a eutectic point that can be seen in Figure 6c. This is a three-phase equilibrium state that represents lowest temperature where the fluid can exist at 700 GPa.
Like we have done for Figures 2–4, we can
compare the
PSO-predicted phase diagrams in Figures 5 and 6 against direct
numerical solutions of the equilibrium conditions in eqs 34–36. Solving those equations produces the liquidus, solidus, and solvus
curves that enclose the two-phase regions, and we have verified that
in all cases, results for these phase boundaries from the two methods
are indistinguishable from each other. However, because Figures 5 and 6 have a fair degree of complexity, and there are different possibilities
for these phase diagrams, it is worth doing a more thorough investigation
to ensure that PSO does indeed yield the true equilibrium state. For
example, Figure 5 shows
that above the peritectic temperature, Ga-IV/Fe dominates over Ga-III/Fe
due to the particular nonideal-mixing model we have chosen. If we
assume that the phase along the solidus is actually Ga-III/Fe instead
of Ga-IV/Fe, the phase boundaries that we obtain from a direct numerical
solution—which represent local minima in the Gibbs energy—turn
out to be similar (displaced toward higher Fe concentrations by about
2 mol % or less) to those displayed in the figure. Perhaps surprisingly,
the Gibbs energies along the liquidus and solidus in that hypothetical
scenario are actually lower for most conditions than
the Gibbs energies along those same boundaries in the figure. Thus,
based on the direct numerical solution alone, one might be led to
conclude that Ga-III/Fe is actually the true equilibrium phase along
the solidus. However, an examination of the Gibbs energy as a function
of composition at a fixed temperature reveals that this is not the
case. Figure 7a,b illustrates
results for the 4500 K isotherm in Figure 5. The hypothetical scenario that we have
laid out above, which is represented by the black solid curve, is
always equal to or higher in Gibbs energy than the PSO result. This
occurs because the liquidus and solidus in the PSO result (the vertical
dashed lines) are shifted to the left compared to those boundaries
in the hypothetical scenario (the vertical dotted lines). As a result,
for any set of  that lies
within both of these two-phase
regions, the solid phase fraction will be larger in the PSO case than
in the hypothetical scenario. The differing relative amounts of fluid
versus solid works out such that the two-phase state predicted by
PSO has a lower Gibbs energy than the two-phase state in the hypothetical
scenario, despite the fact that the latter may have lower free energies
along its liquidus and solidus. Figure 7c shows a similar analysis for 3450 K and 205 GPa,
which is slightly below the peritectic temperature of 3458 K at that
pressure. The black curve in this figure represents the hypothetical
scenario where we ignore the solid–solid transition and assume
that the phase that is present along the solidus is Ga-IV/Fe instead
of Ga-III/Fe. Figure 7d demonstrates results for the 7150 K isotherm at 700 GPa, which
lies a little above the eutectic temperature of 7106 K at that pressure
(see Figure 6). Here,
the black curve denotes the local minimum, where the branch of the
solidus that lies to the right of the eutectic point is composed of
Ga-IV/Fe rather than Ga-III/Fe. We note that in all the hypothetical
scenarios depicted in Figure 7, the free-energy differences are rather small; even well
into the two-phase regions, ΔG/RT for the black curves in most instances is less than 10–3RT. This suggests that PSO reliably yields the
true equilibrium state even when there are competing local minima
that are close in free energy to the equilibrium state. It illustrates
the point we mentioned in the previous section about how PSO, being
a global optimization scheme, is able to resolve ambiguities in phase
boundaries and diagrams, whereas direct numerical solutions of eqs 34–36 [and (32) in the general case] cannot
do this.
that lies
within both of these two-phase
regions, the solid phase fraction will be larger in the PSO case than
in the hypothetical scenario. The differing relative amounts of fluid
versus solid works out such that the two-phase state predicted by
PSO has a lower Gibbs energy than the two-phase state in the hypothetical
scenario, despite the fact that the latter may have lower free energies
along its liquidus and solidus. Figure 7c shows a similar analysis for 3450 K and 205 GPa,
which is slightly below the peritectic temperature of 3458 K at that
pressure. The black curve in this figure represents the hypothetical
scenario where we ignore the solid–solid transition and assume
that the phase that is present along the solidus is Ga-IV/Fe instead
of Ga-III/Fe. Figure 7d demonstrates results for the 7150 K isotherm at 700 GPa, which
lies a little above the eutectic temperature of 7106 K at that pressure
(see Figure 6). Here,
the black curve denotes the local minimum, where the branch of the
solidus that lies to the right of the eutectic point is composed of
Ga-IV/Fe rather than Ga-III/Fe. We note that in all the hypothetical
scenarios depicted in Figure 7, the free-energy differences are rather small; even well
into the two-phase regions, ΔG/RT for the black curves in most instances is less than 10–3RT. This suggests that PSO reliably yields the
true equilibrium state even when there are competing local minima
that are close in free energy to the equilibrium state. It illustrates
the point we mentioned in the previous section about how PSO, being
a global optimization scheme, is able to resolve ambiguities in phase
boundaries and diagrams, whereas direct numerical solutions of eqs 34–36 [and (32) in the general case] cannot
do this.
As an additional way to verify the results of the Gibbs-energy minimization, we have developed a separate version of PSO that minimizes the Helmholtz energy instead and have used it to cross-check the results of Gibbs-energy minimization. The details and motivation behind this second PSO method is best explained in the context of EOS table generation, which is the subject to which we now proceed.
4.2. Generation of EOS Tables
We have
discussed in the Introduction the practical
need for EOS tables in high-pressure science. An EOS table for a single-component
system is simply an array of numbers representing the Helmholtz energy
of the equilibrium (possibly multiphase) state on a grid of temperatures T and densities ρ. For a mixture, we would also have
to fix the overall composition 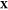 . Thus,
table construction involves finding
the equilibrium state for a given set of
. Thus,
table construction involves finding
the equilibrium state for a given set of 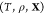 , much like how we have
used PSO to find
the equilibrium state for a given set of
, much like how we have
used PSO to find
the equilibrium state for a given set of 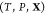 . Basic thermodynamics
dictates that one
must minimize the Helmholtz energy in the former situation. Currently,
there does not exist a method to rigorously produce multiphase EOS
tables for mixtures in this manner, and so, we have explored PSO as
a means to do that. Our algorithm for Helmholtz-energy minimization
is very similar to that for Gibbs-energy minimization outlined in section 3 (indeed, this flexibility
of PSO is one of the reasons we have chosen it in the first place),
with the swarm representing a canonical ensemble instead of an isothermal–isobaric
ensemble. The only procedural difference is that Helmholtz-energy
minimization requires one additional step, where the pressure P of each particle in the swarm—here, each particle
represents a multiphase, multicomponent mixture that is fixed at the
specified T, ρ, and
. Basic thermodynamics
dictates that one
must minimize the Helmholtz energy in the former situation. Currently,
there does not exist a method to rigorously produce multiphase EOS
tables for mixtures in this manner, and so, we have explored PSO as
a means to do that. Our algorithm for Helmholtz-energy minimization
is very similar to that for Gibbs-energy minimization outlined in section 3 (indeed, this flexibility
of PSO is one of the reasons we have chosen it in the first place),
with the swarm representing a canonical ensemble instead of an isothermal–isobaric
ensemble. The only procedural difference is that Helmholtz-energy
minimization requires one additional step, where the pressure P of each particle in the swarm—here, each particle
represents a multiphase, multicomponent mixture that is fixed at the
specified T, ρ, and 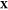 —must
be computed in every iteration.
This P is common to all
—must
be computed in every iteration.
This P is common to all 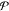 phases in
the particle and is the pressure
corresponding to the particle’s χ and z at the current iteration plus also the specified T and ρ. Unfortunately, while this additional step
is conceptually simple, it is computationally expensive. A minimization
over one set of
phases in
the particle and is the pressure
corresponding to the particle’s χ and z at the current iteration plus also the specified T and ρ. Unfortunately, while this additional step
is conceptually simple, it is computationally expensive. A minimization
over one set of 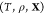 for the Fe/Ga examples is 2 orders of magnitude
slower than an equivalent calculation for a set
for the Fe/Ga examples is 2 orders of magnitude
slower than an equivalent calculation for a set 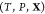 in Gibbs-energy minimization.
As a result,
our Helmholtz-energy minimization algorithm cannot, in its present
form, construct multiphase EOS tables for mixtures in a reasonable
amount of time. This may become possible with the speedup options
discussed in section 5.1, but its usage is currently limited to serving as a cross-check
for the Gibbs-energy minimization through the following process:
in Gibbs-energy minimization.
As a result,
our Helmholtz-energy minimization algorithm cannot, in its present
form, construct multiphase EOS tables for mixtures in a reasonable
amount of time. This may become possible with the speedup options
discussed in section 5.1, but its usage is currently limited to serving as a cross-check
for the Gibbs-energy minimization through the following process:
-
1
Select a particular
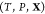 and perform a Gibbs-energy
minimization
with PSO to obtain the equilibrium values of the phase fractions χ and compositions z.
and perform a Gibbs-energy
minimization
with PSO to obtain the equilibrium values of the phase fractions χ and compositions z. -
2.
Input this χ and z, as well as T and P, into the given free-energy models to compute ρ.
-
3.
Perform a Helmholtz-energy minimization with PSO on
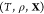 and verify that its predicted
equilibrium
state reproduces the P, χ, and z from step 1.
and verify that its predicted
equilibrium
state reproduces the P, χ, and z from step 1.
We have cross-checked
several 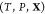 points with both ideal
and nonideal-mixing
models and have found that the two minimization procedures yield the
same equilibrium state for all the points that we have tested.
points with both ideal
and nonideal-mixing
models and have found that the two minimization procedures yield the
same equilibrium state for all the points that we have tested.
It is still possible to produce EOS tables with the more indirect
procedure that we now describe. In this procedure, we first produce
a temperature–pressure phase diagram for a fixed overall composition 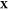 through Gibbs-energy
minimization with
PSO. Figure 8 shows
such diagrams for the case of a 90% Fe and 10% Ga mixture. A feature
we point out is that the one-dimensional melt curve in a single-component
system like pure Fe transforms to a two-dimensional, fluid–solid
region in the binary Fe/Ga mixture. (These two-phase regions in iron–silicate
alloys have practical importance in studying the structure of the
inner Earth.61) The increased dimensionality
compared to the single-component case is a natural consequence of
mixing and is manifested in the well-known Gibbs phase rule.35−39,95 Simple mixing protocols that
combine different single-component EOSs without properly accounting
for changes in phase boundaries would inherently not be able to capture
the increased dimensionality. After the temperature–pressure
diagrams are produced, we use our free-energy models to compute different
properties like the density ρ and Helmholtz energy F at each T and P point, and we
fit these results to two-dimensional splines of T and P. We find the lowest and highest densities
spanned by these diagrams, which are represented by the dashed curves
in Figure 8. We then
employ the splines over the temperature and density range to generate
a table of F as a function of T and
ρ for the specified
through Gibbs-energy
minimization with
PSO. Figure 8 shows
such diagrams for the case of a 90% Fe and 10% Ga mixture. A feature
we point out is that the one-dimensional melt curve in a single-component
system like pure Fe transforms to a two-dimensional, fluid–solid
region in the binary Fe/Ga mixture. (These two-phase regions in iron–silicate
alloys have practical importance in studying the structure of the
inner Earth.61) The increased dimensionality
compared to the single-component case is a natural consequence of
mixing and is manifested in the well-known Gibbs phase rule.35−39,95 Simple mixing protocols that
combine different single-component EOSs without properly accounting
for changes in phase boundaries would inherently not be able to capture
the increased dimensionality. After the temperature–pressure
diagrams are produced, we use our free-energy models to compute different
properties like the density ρ and Helmholtz energy F at each T and P point, and we
fit these results to two-dimensional splines of T and P. We find the lowest and highest densities
spanned by these diagrams, which are represented by the dashed curves
in Figure 8. We then
employ the splines over the temperature and density range to generate
a table of F as a function of T and
ρ for the specified 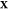 . This
table will necessarily be multiphase
and will properly reflect the increased dimensionality (in the Gibbs
phase rule sense) that arises from mixing.
. This
table will necessarily be multiphase
and will properly reflect the increased dimensionality (in the Gibbs
phase rule sense) that arises from mixing.
Figure 8.

Temperature–pressure
phase diagrams for a fixed overall
composition 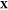 of 90% Fe and
10% Ga where (a) all three
solution phases form ideal mixtures and (b) the fluid and Ga-IV/Fe
phases are described by nonideal-mixing models in the previous section,
while Ga-III/Fe undergoes ideal mixing. The various regions are labeled
with the same coloring scheme used in all of the previous phase diagrams.
We follow the procedure explained in the text to convert these temperature–pressure
diagrams to multiphase EOS tables of Helmholtz energy vs temperature
and density. An additional round of PSO calculations could be performed
to more clearly refine the boundaries of the fluid–solid region
colored in red, but doing so is not necessary to demonstrate the table-construction
process. The left and right dashed curves indicate isochores representing
the lowest and highest density covered by the tables, respectively.
As we have discussed earlier, the nonideal-mixing model we have used
for Ga-IV/Fe in (b) stabilizes it at lower pressures and destabilizes
at higher pressures, which is why the two solid solutions nearly swap
stability fields from (a) to (b). Although not shown here, we have
also produced diagrams for the case of 95% Fe and 5% Ga, which look
qualitatively similar to those presented in this figure.
of 90% Fe and
10% Ga where (a) all three
solution phases form ideal mixtures and (b) the fluid and Ga-IV/Fe
phases are described by nonideal-mixing models in the previous section,
while Ga-III/Fe undergoes ideal mixing. The various regions are labeled
with the same coloring scheme used in all of the previous phase diagrams.
We follow the procedure explained in the text to convert these temperature–pressure
diagrams to multiphase EOS tables of Helmholtz energy vs temperature
and density. An additional round of PSO calculations could be performed
to more clearly refine the boundaries of the fluid–solid region
colored in red, but doing so is not necessary to demonstrate the table-construction
process. The left and right dashed curves indicate isochores representing
the lowest and highest density covered by the tables, respectively.
As we have discussed earlier, the nonideal-mixing model we have used
for Ga-IV/Fe in (b) stabilizes it at lower pressures and destabilizes
at higher pressures, which is why the two solid solutions nearly swap
stability fields from (a) to (b). Although not shown here, we have
also produced diagrams for the case of 95% Fe and 5% Ga, which look
qualitatively similar to those presented in this figure.
We may use the EOS tables produced by PSO to perform calculations, just like we can with any EOS from the LEOS or SESAME libraries mentioned in the Introduction. As an example, Figure 9 compares Hugoniot and isentrope predictions from the Fe/Ga mixture tables with those from the pure Fe table by Benedict et al.58 The initial pressure and density in all cases are 240 GPa and 12.15 g/cm3, respectively, which is in the fluid phase and could represent the result of a shock-melting experiment. The Hugoniot curves and isentropes in the figure might therefore represent double-shock or shock–ramp experiments, respectively. Interestingly, the effect of introducing Ga solute particles to the Fe solvent appears to be much more pronounced on the temperature than it is on the pressure or the shock speed–particle speed relation. Part of this is due to the ideal-mixing entropy terms of the form −Rzij ln zij, but nonideal contributions to the entropy and the heat capacity also have a noticeable effect. This suggests that obtaining reliable temperature measurements along dynamic-compression paths, which is an ongoing and extremely challenging area of work,62 could be important toward discerning the effect of impurities under relevant high-pressure conditions.
Figure 9.

Comparison of Hugoniot curves and isentropes of pure Fe vs those of Fe/Ga mixtures at two different overall compositions (90% Fe and 95% Fe) and described by different mixing models: (a–c) pressure, temperature, and shock speed along the Hugoniot and (d) temperature along the isentrope. (We have not included pressure–density results for the isentrope in the figure because the differences are even smaller than they are for the Hugoniot.) All of the curves are initiated at an initial pressure and density of 240 GPa and 12.15 g/cm3, respectively. As explained in the text, the results for Fe/Ga mixtures are calculated from the multiphase EOS tables for these mixtures that are produced from PSO-generated temperature–pressure phase diagrams like the ones shown in Figure 8.
5. Conclusions
5.1. Critical Evaluation of Our Approach and Future Work
Now that we have demonstrated the reliability and utility of PSO with the examples in the previous section, we are in a position to suggest future work to address the current limitations of our approach and expand its capabilities. We focus on limitations that we believe can be overcome in the near future. One topic that we do not dwell on at length here is chemical-reaction equilibria, which broadly includes ionic equilibria (salt solutions), acid–base equilibria, and other redox reactions that are of relevance to planetary science in particular. While PSO can describe chemical-reaction equilibria (e.g., Bonilla-Petriciolet and Segovia-Hernández51 have applied it to model equilibria in reacting fluid mixtures at low pressures), we anticipate that for high-pressure applications, this will be more of a long-term challenge than the other topics that we describe below. The main difficulty is that reactions tend to occur not in isolation, but in a complex network that can involve hundreds of species linked through several different reactions. Each reaction, whose mechanism will likely not be well characterized, introduces additional mass-conservation constraints and constraints on the chemical potentials due to the requirement for vanishing entropy production at equilibrium.63 These constraints will have to be verified, just like how we have verified that our PSO-predicted phase boundaries satisfy the equality of chemical potentials in eq 32. Moreover, EOS models will need to be supplied for each species in order to do a proper calculation of the equilibrium state. This will be a challenge for ionic and possibly also for acid–base equilibria because the charged species involved in them are notoriously difficult to model.64 All of these difficulties will be exacerbated at high pressures because the application of pressure can introduce additional reactions and species in the complex network and cause the species to become more closely packed (and thereby interact more strongly), so that, for example, simple electrolyte models like Debye–Hückel that work well for dilute mixtures are not applicable. Thermochemical codes such as Magpie13 and Cheetah12,65−67 are able to model high-pressure, chemical-reaction equilibria of certain select mixtures (see section 5.2), but they necessarily have to adopt some simplifications in order to make the problem tractable.
One
way to extend our algorithm, which is currently limited to solutions,
is to enable it to handle compounds of the type discussed in section 2. Because these
compounds have a fixed stoichiometry, each possible phase of the compound
brings in an additional phase mole fraction—but not an additional
set of phase compositions—whose value is to be adjusted during
the minimization process. For example, suppose that Fe3Ga is the first compound40 to appear on
the Fe-rich side of the Fe/Ga phase diagram and that it can exist
in 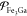 different possible phases. Then, for a
given T and P and for all Fe/Ga
mixtures where the Fe overall mole fraction
different possible phases. Then, for a
given T and P and for all Fe/Ga
mixtures where the Fe overall mole fraction 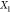 is greater than 0.75, we can generalize
the Gibbs energy that is to be minimized via PSO from its form in eq 39 to
is greater than 0.75, we can generalize
the Gibbs energy that is to be minimized via PSO from its form in eq 39 to
 |
47 |
where the double sum over i and j concerns the three solution phases (fluid,
Ga-III/Fe, and Ga-IV/Fe) considered in the previous section, and the
summation over k is performed over the 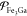 phases of Fe3Ga. Here, χk is the mole fraction of phase k of Fe3Ga, and Gk(T,P) is the Gibbs energy
of that phase obtained from the chosen multiphase EOS for Fe3Ga. Clearly, this EOS must be constructed beforehand if it is to
be used in eq 47, which
speaks to the issue we raised earlier about the challenging need to
construct separate multiphase EOSs for each compound of interest.
In order to account for the presence of the compound Fe3Ga, the mole-balance constraints in eq 25 must be modified to
phases of Fe3Ga. Here, χk is the mole fraction of phase k of Fe3Ga, and Gk(T,P) is the Gibbs energy
of that phase obtained from the chosen multiphase EOS for Fe3Ga. Clearly, this EOS must be constructed beforehand if it is to
be used in eq 47, which
speaks to the issue we raised earlier about the challenging need to
construct separate multiphase EOSs for each compound of interest.
In order to account for the presence of the compound Fe3Ga, the mole-balance constraints in eq 25 must be modified to
| 48 |
| 49 |
We may apply
PSO to minimize the Gibbs energy in eq 47 subject to these mole-balance
constraints to obtain the equilibrium state corresponding to the given T, P, and 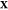 . The equilibrium
state indicates the mole
fractions χ and compositions z of
the three solution phases and the mole fractions of the
. The equilibrium
state indicates the mole
fractions χ and compositions z of
the three solution phases and the mole fractions of the 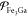 different phases of Fe3Ga. If
the PSO algorithm is working correctly, the equilibrium mole fraction
of all Fe3Ga phases except for that of the most stable
phase(s) at the given T and P should
be virtually zero, much like how PSO is able to select out and eliminate
all unstable solution phases, as illustrated in the previous section.
The same procedure may be followed for
different phases of Fe3Ga. If
the PSO algorithm is working correctly, the equilibrium mole fraction
of all Fe3Ga phases except for that of the most stable
phase(s) at the given T and P should
be virtually zero, much like how PSO is able to select out and eliminate
all unstable solution phases, as illustrated in the previous section.
The same procedure may be followed for 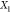 less than 0.75 with other compounds
(such
as Fe6Ga5, Fe3Ga4, and
FeGa3), as long as multiphase EOSs are available for these
compounds, so that we can compute their Gibbs energy.
less than 0.75 with other compounds
(such
as Fe6Ga5, Fe3Ga4, and
FeGa3), as long as multiphase EOSs are available for these
compounds, so that we can compute their Gibbs energy.
A limitation
of our PSO-based approach as presently designed is
the computational efficiency. This is true in general for global optimization
methods applied to phase-equilibria computations. For each set 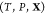 , the Fe/Ga examples we
have presented take
a few seconds to converge on a laptop equipped with a 2.8 GHz Intel
Core i7 processor. The exact amount of time varies due to the stochastic
nature of the optimization process, and it also depends on the number
of phases present in the equilibrium state; fewer iterations are generally
required to achieve convergence in single-phase regions than in two-phase
regions. Construction of the phase diagrams in Figures 2–6 typically
takes several hours because each diagram involves performing a Gibbs-energy
minimization for thousands of different sets of
, the Fe/Ga examples we
have presented take
a few seconds to converge on a laptop equipped with a 2.8 GHz Intel
Core i7 processor. The exact amount of time varies due to the stochastic
nature of the optimization process, and it also depends on the number
of phases present in the equilibrium state; fewer iterations are generally
required to achieve convergence in single-phase regions than in two-phase
regions. Construction of the phase diagrams in Figures 2–6 typically
takes several hours because each diagram involves performing a Gibbs-energy
minimization for thousands of different sets of 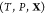 . While the speed could
certainly be improved
significantly along the lines suggested below, PSO is still a practical
means for Gibbs-energy minimization. It is significantly slower, however,
for Helmholtz-energy minimization. Each set
. While the speed could
certainly be improved
significantly along the lines suggested below, PSO is still a practical
means for Gibbs-energy minimization. It is significantly slower, however,
for Helmholtz-energy minimization. Each set 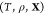 for the Fe/Ga examples
takes hundreds of
seconds to complete, which is 2 orders of magnitude slower than an
equivalent calculation for a set
for the Fe/Ga examples
takes hundreds of
seconds to complete, which is 2 orders of magnitude slower than an
equivalent calculation for a set 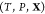 in Gibbs-energy minimization.
Part of the
computational inefficiency of our code may be attributed to the fact
that we are running a development version (not a production version)
that is written in Python, an interpreted language. If it were instead
to be optimized and rewritten in a compiled language like C++, it
is reasonable to expect a several-fold (perhaps even more than a 10-fold)
increase in efficiency. A more significant speedup could be achieved
through parallelization in which the particles of a swarm are divided
up among different processors. We note that PSO is amenable to architectures
involving graphics processing units because the particles move largely
independently of each other, with the only communication necessary
being the need to track yswarm,best, which
is the most optimal position in the search space ever accessed by
any of the particles. Once the necessary speedup has been achieved,
we aim to perform Helmholtz-energy minimization to construct temperature–density
phase diagrams (for a fixed overall
in Gibbs-energy minimization.
Part of the
computational inefficiency of our code may be attributed to the fact
that we are running a development version (not a production version)
that is written in Python, an interpreted language. If it were instead
to be optimized and rewritten in a compiled language like C++, it
is reasonable to expect a several-fold (perhaps even more than a 10-fold)
increase in efficiency. A more significant speedup could be achieved
through parallelization in which the particles of a swarm are divided
up among different processors. We note that PSO is amenable to architectures
involving graphics processing units because the particles move largely
independently of each other, with the only communication necessary
being the need to track yswarm,best, which
is the most optimal position in the search space ever accessed by
any of the particles. Once the necessary speedup has been achieved,
we aim to perform Helmholtz-energy minimization to construct temperature–density
phase diagrams (for a fixed overall 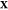 ) from which
we can readily obtain EOS tables.
This is a more direct way of producing these tables than the Gibbs-based
procedure followed in this study, which requires post-processing steps
to convert temperature–pressure phase diagrams to the desired
tabular format.
) from which
we can readily obtain EOS tables.
This is a more direct way of producing these tables than the Gibbs-based
procedure followed in this study, which requires post-processing steps
to convert temperature–pressure phase diagrams to the desired
tabular format.
Improving the computational efficiency will
also be a necessary
step toward developing a PSO capability for entropy maximization.
The goal of entropy maximization is to find the equilibrium state
of a multicomponent mixture for a given set of E,
ρ, and 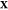 , where E is the total
molar internal energy of the mixture. The swarm in this case symbolizes
a microcanonical ensemble because each PSO particle represents a mixture
that is fixed at the specified E, ρ, and
, where E is the total
molar internal energy of the mixture. The swarm in this case symbolizes
a microcanonical ensemble because each PSO particle represents a mixture
that is fixed at the specified E, ρ, and 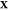 . The equilibrium
state reveals the compositions
of the solution phases and the mole fractions of all phases (both
solutions and compounds) and the temperature and pressure that are
common to all phases. Adapting the Gibbs-energy minimization to Helmholtz-energy
minimization requires only one additional step; the same is true for
entropy maximization, where the additional step in this case involves
a simultaneous determination of both temperature and pressure (instead
of only pressure like in Helmholtz-energy minimization) for each PSO
particle at every iteration. While conceptually simple, this additional
step will again be numerically expensive, even more so than the pressure-only
solution required in Helmholtz-energy minimization. One possible way
to ease the computational burden is to apply the scheme we have developed
for a related problem, where we map our chosen set of free-energy
models for the mixture onto a more simple EOS in which pressure depends
linearly on volume.68 The functional form
of this simple EOS is specifically designed, so that the T and P consistent with the given E and ρ can be found analytically. This mapping onto the analytically
invertible EOS would have to be performed for each PSO particle at
every iteration, but we expect that it will be much more computationally
efficient to do this than to carry out a direct numerical solve for T and P. The motivation for developing
an entropy-maximization capability comes from the needs of the continuum-scale,
multiphysics codes for high-pressure applications that we have mentioned
in the Introduction. These codes track and
update E, ρ, and
. The equilibrium
state reveals the compositions
of the solution phases and the mole fractions of all phases (both
solutions and compounds) and the temperature and pressure that are
common to all phases. Adapting the Gibbs-energy minimization to Helmholtz-energy
minimization requires only one additional step; the same is true for
entropy maximization, where the additional step in this case involves
a simultaneous determination of both temperature and pressure (instead
of only pressure like in Helmholtz-energy minimization) for each PSO
particle at every iteration. While conceptually simple, this additional
step will again be numerically expensive, even more so than the pressure-only
solution required in Helmholtz-energy minimization. One possible way
to ease the computational burden is to apply the scheme we have developed
for a related problem, where we map our chosen set of free-energy
models for the mixture onto a more simple EOS in which pressure depends
linearly on volume.68 The functional form
of this simple EOS is specifically designed, so that the T and P consistent with the given E and ρ can be found analytically. This mapping onto the analytically
invertible EOS would have to be performed for each PSO particle at
every iteration, but we expect that it will be much more computationally
efficient to do this than to carry out a direct numerical solve for T and P. The motivation for developing
an entropy-maximization capability comes from the needs of the continuum-scale,
multiphysics codes for high-pressure applications that we have mentioned
in the Introduction. These codes track and
update E, ρ, and 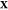 along the different
mesh points, but they
do not track T and P or the phase
mole fractions and compositions. Although this latter set of information
is not tracked, the codes do need to extract this information from
the given EOS models because it is of interest (especially T and P) to the various constitutive models
in these codes, like those for strength effects, kinetics, transport
coefficients, and so forth. If the computational efficiency can be
sufficiently improved, it may be possible to implement a PSO-based,
entropy-maximization procedure directly into these codes, so that
they can perform on-the-fly, phase-equilibria calculations of multicomponent
mixtures. This would be a thermodynamically rigorous alternative to
simplified, albeit more pragmatic, approaches that treat these mixtures
as if the components were homogeneously mixed (i.e., neglects the
fact that they can separate into multiple phases with different compositions).
along the different
mesh points, but they
do not track T and P or the phase
mole fractions and compositions. Although this latter set of information
is not tracked, the codes do need to extract this information from
the given EOS models because it is of interest (especially T and P) to the various constitutive models
in these codes, like those for strength effects, kinetics, transport
coefficients, and so forth. If the computational efficiency can be
sufficiently improved, it may be possible to implement a PSO-based,
entropy-maximization procedure directly into these codes, so that
they can perform on-the-fly, phase-equilibria calculations of multicomponent
mixtures. This would be a thermodynamically rigorous alternative to
simplified, albeit more pragmatic, approaches that treat these mixtures
as if the components were homogeneously mixed (i.e., neglects the
fact that they can separate into multiple phases with different compositions).
As the first demonstration in the literature of PSO on high-pressure
phase equilibria, we have chosen to work with a binary system (Fe/Ga)
of up to three phases because it is relatively easy to explain, validate,
and visualize the performance of our method on such a system. Our
algorithm is nonetheless designed to be applicable more generally
to mixtures with an arbitrary number of components c and (solution) phases  . Part
of our future work will be to test
its performance on true multicomponent mixtures. In anticipation of
this future testing, we have performed a computational-cost analysis
of Gibbs-energy minimization of ternary and quaternary mixtures. We
have mimicked the additional components in the cost analysis by creating
fictitious secondary Fe and Ga components with different molar masses. Table 1 indicates an approximately
linear scaling in both c and
. Part
of our future work will be to test
its performance on true multicomponent mixtures. In anticipation of
this future testing, we have performed a computational-cost analysis
of Gibbs-energy minimization of ternary and quaternary mixtures. We
have mimicked the additional components in the cost analysis by creating
fictitious secondary Fe and Ga components with different molar masses. Table 1 indicates an approximately
linear scaling in both c and  . The table
gives only a rough idea of the
scaling because the actual run time will vary due to the stochastic
nature of the method and the complexity of the Gibbs-energy surface.
It should also be pointed out that the table paints an incomplete
picture because we have kept the swarm size Np fixed in it, yet the free-energy surface will become more
complicated (will increase in dimensionality) as c increases, implying that Np will likely
need to increase with c to ensure that the swarm
successfully converges to the true minimum. Hence, we have performed
a second cost analysis in which Np is
varied while c and
. The table
gives only a rough idea of the
scaling because the actual run time will vary due to the stochastic
nature of the method and the complexity of the Gibbs-energy surface.
It should also be pointed out that the table paints an incomplete
picture because we have kept the swarm size Np fixed in it, yet the free-energy surface will become more
complicated (will increase in dimensionality) as c increases, implying that Np will likely
need to increase with c to ensure that the swarm
successfully converges to the true minimum. Hence, we have performed
a second cost analysis in which Np is
varied while c and  are kept fixed,
the results of which are
presented in Table 2. It indicates that the run time also scales linearly with Np. In summary, our analysis has demonstrated
that the PSO performance cost scales linearly with c,
are kept fixed,
the results of which are
presented in Table 2. It indicates that the run time also scales linearly with Np. In summary, our analysis has demonstrated
that the PSO performance cost scales linearly with c,  , and Np, which
is only a fairly modest increase. This suggests that PSO would continue
to be a suitable approach for more complicated mixtures than those
investigated in this study, especially taking into consideration the
fact that PSO is amenable to parallelization.
, and Np, which
is only a fairly modest increase. This suggests that PSO would continue
to be a suitable approach for more complicated mixtures than those
investigated in this study, especially taking into consideration the
fact that PSO is amenable to parallelization.
Table 1. Computational
Cost of PSO Calculations
as a Function of the Number of Components c and Maximum
Possible Number of Phases  in the
Mixture of Interesta.
in the
Mixture of Interesta.
| c = 1 | 1.00 | 1.35 | ||||
| c = 2 | 1.79 | 2.72 | 3.66 | |||
| c = 3 | 2.89 | 4.32 | 5.82 | |||
| c = 4 | 3.63 | 5.42 | 7.50 |
Each entry indicates
the average
time it takes to perform a Gibbs-energy minimization for a given 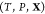 relative to the simplest
case of
relative to the simplest
case of 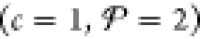 . Each listed time is an average over 20
PSO runs carried out with a fixed number of Np = 60 particles in the swarm. The
. Each listed time is an average over 20
PSO runs carried out with a fixed number of Np = 60 particles in the swarm. The 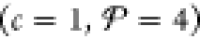 case is not examined because it is forbidden
by the Gibbs phase rule.35−39,95
case is not examined because it is forbidden
by the Gibbs phase rule.35−39,95
Table 2. Computational Cost of PSO Calculations
as a Function of Np for a Binary (c = 2) Mixture that can Exist in up to 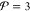 Phasesa.
Phasesa.
| Np = 50 | Np = 100 | Np = 200 | Np = 400 | Np = 800 |
|---|---|---|---|---|
| 1.00 | 2.06 | 3.82 | 7.56 | 15.20 |
Each entry indicates
the average
time (averaged over 20 runs) it takes to perform a Gibbs-energy minimization
for a given  relative to the fastest
case of Np = 50 particles.
relative to the fastest
case of Np = 50 particles.
5.2. Comparison with Other Approaches
Here, we briefly review three other approaches for modeling the thermodynamics of multiphase, multicomponent mixtures: (1) flash calculations,69−77 (2) the thermochemical code Cheetah,12,65−67 and (3) the CALculation of PHAse Diagrams (CALPHAD) methodology.78−88 All three are now mature capabilities that have benefited from decades of development. We cannot make an apples-to-apples comparison because they each have certain functions that the others are not designed to do, but by pointing out some of these differences, we hope to clarify how this work fits in the context of the others.
The objective of a flash calculation is the same as that of our PSO-based optimization: determine the equilibrium state of a multicomponent mixture for a specified set of conditions given an EOS for these mixtures. The name stems from the widespread need in the chemical and petroleum industries to perform phase separations like “flash distillations” of fluid mixtures, and as such, virtually all of the published studies on this topic feature examples with fluid mixtures described by EOSs specialized for the low-pressure conditions (typically well below 1 GPa) of industrial relevance. Nevertheless, the thermodynamic principles that underpin flash calculations are also applicable to solid solutions and to higher-pressure conditions. The conventional approach to a flash calculation is to divide it into two sequential steps: a stability analysis that determines the number of stable phases, followed by a phase-split calculation that determines the phase compositions. Most of the algorithms have been developed for Gibbs-energy minimization,69−71 though more recent work has also been done on Helmholtz-energy minimization72,73 and entropy maximization.74−77 The main advantage that these conventional flash methods offer over PSO is computational efficiency. This efficiency has allowed them to be implemented into the multiphysics simulation codes used by the chemical and petroleum industries. For Gibbs-energy minimization, a flash calculation tends to be several times faster than PSO. The disparity becomes even greater for Helmholtz-energy minimization and entropy maximization; the computational cost of a flash calculation for these more complicated problems increases by an order of magnitude or less, whereas it increases by at least 2 orders of magnitude for PSO. However, PSO offers distinct advantages that may make it a more attractive option under certain circumstances. First of all, it is far more suited to parallelization, which could potentially allow it to make up for a significant part of its extra computational requirements. It also does not perform the arbitrary separation into stability and phase-split steps. We have seen that going from Gibbs-energy minimization to Helmholtz-energy minimization to entropy maximization is conceptually a straightforward matter in PSO. In contrast, for flash calculations, these transformations often require a substantial reformulation of the algorithms. Perhaps most importantly, one does not need to supply PSO with a good initial guess for quantities like phase mole fractions and compositions (though the tradeoff for this robustness is the higher computational load). This is essential for high-pressure applications, as we have discussed in section 3.2. Flash calculations are the opposite in that they are very much reliant on a good initial guess for such quantities (this is especially true for Helmholtz-energy minimization and entropy maximization as explained in a recent study77), without which they are prone to failures like converging to an unphysical solution or not even converging to a solution at all. Correlations and recipes for initial guesses have been developed for a variety of fluid mixtures under low-pressure industrial conditions, but ultimately they are all based on trial-and-error and may not be applicable to higher pressures or to solid mixtures. As a result, it is not uncommon in a flash calculation to have to cycle through different initial guesses until finding one that works, which can significantly impact the robustness of these methods and add to the computational cost.
Cheetah65,66 is widely used for modeling thermodynamics under detonation, which includes chemical-reaction equilibria. It does this by representing the interatomic interactions between the different species in a mixture with exponential-six potentials,12,67 whose parameters are fit to experimental data. These interactions are translated to a free energy via the application of mixing rules and statistical–mechanical models, and the free energy is minimized to obtain the equilibrium state for a given set of conditions. Cheetah has been coupled with high-pressure continuum-scale codes, so that it can feed information directly to these codes. It can model systems ranging in complexity from monatomic materials to large organic molecules like high explosives and plastics. However, Cheetah cannot describe regimes where there is significant electronic ionization (recall from the Introduction that the LEOS and SESAME tables that we use for the pure components account for this through an electron-thermal term) and is limited in its applicable temperature and pressure range as a result. It is also not intended to model dense metals like pure Fe, pure Ga, and Fe/Ga mixtures because the exponential-six potentials are not expected to give accurate predictions for such materials over most conditions of interest.
CALPHAD78−83 is the most well-known methodology for multiphase, multicomponent mixtures in materials science. It follows the standard prescription from chemical thermodynamics35−39 outlined in section 2, in which the Gibbs energy of each solution phase is expressed as a linear combination of the Gibbs energies of the pure components that make up the phase plus some additional mixing terms. CALPHAD applies an optimization procedure (which could be a Newton-based method or a regression approach or a Bayesian technique84) to fit the parameters of the mixing models, and potentially also those of the pure-component Gibbs energies, to reproduce experimental data on the phase diagrams. Unlike Cheetah, it is designed to handle dense metallic systems, and in fact, producing phase diagrams for metallurgical applications is probably the most common use of CALPHAD. However, the vast majority of CALPHAD studies focus only on ambient pressure, where experimental phase-diagram data are far more readily available than at higher pressures. Some relatively recent studies have attempted to extend CALPHAD to higher pressures,85−88 in which most of the pressure dependence is introduced by adding a cold energy and an ion-thermal term (an Einstein model with a pressure-dependent Einstein temperature), but again no electron-thermal term, to the ambient pure-component Gibbs energies. These high-pressure extensions are tied to the legacy of the earlier, ambient-pressure database through the use of an ad hoc interpolation function, and this constraint to the ambient-pressure models can in some cases make it difficult to obtain agreement with experimental data at higher pressures, such as those pertaining to melt curves.87 While CALPHAD could be a good option for high-pressure applications, it is not widely used within high-pressure science at the moment because the details regarding the implementation of the underlying models and algorithms are obscured behind propietary software packages (e.g., Thermo-Calc, FactSage). Thus in practice, it requires an experienced user of these packages to make the modifications necessary to adapt the underlying databases to high pressures. Furthermore, to the best of our knowledge, the high-pressure CALPHAD-based models have remained as standalone objects in the sense that there has been no attempt to construct EOS tables from them or to otherwise connect CALPHAD to the continuum-scale codes mentioned in the Introduction.
5.3. Summary
This study is motivated by a number of practical needs for thermodynamic modeling of multicomponent mixtures at high pressures. One is the desire to have a framework for these mixtures that directly uses existing EOS models specifically designed for high-pressure conditions, with prominent examples being the EOSs that make up the LEOS and SESAME libraries. Section 2 and the Appendix outline such a formulation in which mixing terms are added onto the pure-component properties that are obtained from the existing high-pressure EOSs. Our study is also motivated by the fact that multicomponent systems, like their single-component counterparts, can exist in a multiphase state when in equilibrium. A complete determination of the equilibrium state therefore requires finding the relative amounts of the different phases and the composition of each phase. This may be achieved through a free-energy minimization procedure. Such a capability would also be needed to generate phase diagrams because a phase diagram is merely a visual depiction of the equilibrium states of a mixture across a range of conditions. A crucial point that we reiterate here is that unlike the situation at ambient pressure, available data on phase diagrams at high pressures tend to be extremely limited. A free-energy minimization method that is suitable for high-pressure conditions must therefore be able to generate phase diagrams with little information (minimal input from the user regarding initial guesses, actual number of phases in equilibrium, etc.) on how the phase boundaries are connected together.
Our PSO-based minimization scheme described in section 3 satisfies this
important criterion. Another key reason why we have chosen PSO is
because it is a simple method that does not require expertise in or
access to any specialized software. As long as it is given free-energy
models for each of the possible phases that might be present in the
equilibrium state, it will iteratively adjust the relative amounts
of these phases and the compositions of the individual solution phases
to find the minimum on the Gibbs-energy surface provided by the models.
In doing so, it will reveal the equilibrium state for a given temperature T, pressure P, and overall composition 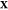 . If it turns
out, for example, that a particular
phase is not present in the equilibrium state at the specified
. If it turns
out, for example, that a particular
phase is not present in the equilibrium state at the specified 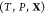 , PSO will determine its
mole fraction to
be very close to zero, typically 10–9 or less. Section 4 tests and demonstrates
the reliability of our method with different example mixing models
by generating temperature–composition phase diagrams. It is
able to capture the fact that the particular nonideal-mixing models
we have used for demonstration purposes in this study result in nontrivial
features like eutectic and peritectic points. Moreover, we have applied
PSO to produce EOS tables for mixtures that rigorously account for
changes in phase boundaries due to mixing. As far as we know, this
is the first demonstration of such a capability.
, PSO will determine its
mole fraction to
be very close to zero, typically 10–9 or less. Section 4 tests and demonstrates
the reliability of our method with different example mixing models
by generating temperature–composition phase diagrams. It is
able to capture the fact that the particular nonideal-mixing models
we have used for demonstration purposes in this study result in nontrivial
features like eutectic and peritectic points. Moreover, we have applied
PSO to produce EOS tables for mixtures that rigorously account for
changes in phase boundaries due to mixing. As far as we know, this
is the first demonstration of such a capability.
In addition to its reliable and readily accessible nature, PSO is also highly adaptable. We have discussed how our method, which is currently limited to mixtures involving fluid or solid (e.g., alloy) solutions, may be extended to also allow for stoichiometric compounds. This is a topic that we intend to work on in the near future. With minor modifications, the PSO algorithm may also be adapted to minimize the Helmholtz energy or maximize the entropy instead of minimizing the Gibbs energy. In fact, we have done this already for Helmholtz-energy minimization and have used it to cross-check results of the Gibbs-energy minimization. A limitation, however, is that our current Helmholtz-energy minimization procedure is too computationally inefficient to be used for its original intended purpose of constructing EOS tables in a direct manner through the generation of temperature–density phase diagrams. We have given suggestions on how to improve the efficiency in the previous section, though there are likely to be other avenues for speedup as well. We note that PSO is amenable to parallelization, and our tests show that it scales well (linearly) with respect to the number of components, phases, and particles in the swarm. With sufficient improvements in the efficiency, we hope to use PSO to produce multiphase EOS tables for mixtures via Helmholtz-energy minimization. It may also be possible to implement a PSO-based entropy-maximization procedure directly into continuum-scale codes for high-pressure applications to enable them to perform on-the-fly, phase-equilibria calculations of mixtures in a thermodynamically rigorous fashion.
Acknowledgments
This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. We thank A. Arsenlis, N. R. Barton, and W. J. Evans for financial support, and R. Bi, A. Firoozabadi, Y. Gao, and J. Kimko for helpful discussions.
Appendix
Quasistatic Phase Equilibrium in the Computation of Thermodynamic Derivatives
Section 2 describes how one may compute the molar Gibbs energy G, internal energy E, entropy S, volume V, Helmholtz energy F, or enthalpy H of a multiphase, multicomponent mixture. Other thermodynamic properties of interest, such as the sound speed and the heat capacity, may be obtained by taking derivatives of G, E, S, V, F, or H. However, we have mentioned that evaluating such derivatives can be complicated for mixtures. We illustrate this point by considering the sound speed cs. The definition of the bulk thermodynamic sound speed is
| 50 |
where M is the molar mass, BS = −V(∂P/∂V)S is the isentropic
bulk modulus, and ρ = M/V is
the mass density. Evaluating this derivative is a simple matter in
a single-phase, single-component system. However, in a multiphase,
multicomponent mixture, a complication arises when evaluating this
derivative: the passage of the sound wave disturbs the phase equilibrium
within the mixture. That is, when the sound wave propagates through
the mixture and changes its pressure from P to P + dP and temperature from T to T + dT, the phase mole fractions 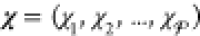 and compositions
and compositions 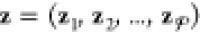
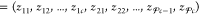 change from their values at T and P to some other set of values χ′ and z′ that correspond to the equilibrium
state at T + dT and P + dP.
change from their values at T and P to some other set of values χ′ and z′ that correspond to the equilibrium
state at T + dT and P + dP.
Even if a closed-form expression exists for the terms that account for the perturbation of the phase equilibrium, they may not be simple to compute. For instance, by adapting ideas from Kieffer,89 one may show that the square of the sound speed in a two-phase, single-component system is
 |
51 |
Here, ΔV = V1 – V2 and ΔS = S1 – S2 are the differences between the molar volumes and molar entropies of the two phases. It is straightforward to employ an EOS to compute all the quantities that appear in eq 51 except the last one in the denominator: (∂Si/∂P)S. The terms that depend on (∂Si/∂P)S account for the perturbation in the equilibrium phase mole fractions χ due to the sound wave. Perhaps the easiest approach to calculate (∂Si/∂P)S is through numerical finite differences in which we apply a small pressure perturbation ΔP and iteratively find what the temperature T of this perturbed state has to be, so that the total entropy S is the same as that of the original state. Determination of the pressure and temperature in this way will then allow us to find the entropy Si of phase i of the perturbed state. Studies that have derived multiphase, multicomponent extensions of eq 51 to the specialized case of fluid mixtures90,91 show that the calculations can become rather involved if one rigorously accounts for the changes in χ and z.
In light of the complications illustrated above, we suggest for practical purposes to hold χ and z fixed when evaluating the derivatives of G, E, S, V, F, or H. When applied to the sound speed, this assumption of quasistatic phase equilibrium implies that the timescale of the disturbance itself (the sound wave) is fast compared to any nonequilibrium process (phase-transition kinetics,33,94 diffusion, convection in fluids, dislocations in solids, etc.) that contributes to the re-establishment of equilibrium. If we redefine the isentropic bulk modulus as BS = −V(∂P/∂V)S,χ,z = −V/(∂V/∂P)S,χ,z, so that the sound speed becomes
| 52 |
| 53 |
The troublesome terms involving (∂Si/∂P)S no longer appear because the phase mole fractions χ are now fixed in the evaluation of the bulk modulus. Equations 51 and 53 are applicable to a two-phase, single-component system. In a multiphase, multicomponent mixture, we have from eqs 3 and 18 that
 |
54 |
where the pure-component
volumes Vij and bulk
moduli BS,ij are to be
evaluated at the same
temperature, pressure, and state of matter as phase i. Substitution of eq 54 into 52 yields a formula for the sound speed
of a multiphase, multicomponent mixture under the assumption of quasistatic
phase equilibrium, and this formula reduces to (53) if the number of phases 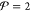 and the number of components c = 1 (remembering that all mixing free energies such as G̅ijexcess vanish when c = 1).
We have tested
this expression by using the Fe EOS developed by Benedict et al.58 described in section 4 to compute the two-phase (fluid–hcp
solid) sound speed with the full expression in eq 51 and with the quasistatic approximation in
(53). We have found that the two expressions
yield similar results and fall within the experimental error bars
from Nguyen and Holmes.92 (A slight caveat
is that we have to add a contribution from the shear modulus of the
solid93 when comparing the sound speed
in that phase to experimental data.) Thus, at least in this particular
example, the small errors that one incurs in making the quasistatic
approximation are well worth the practical benefit of greatly simplifying
the computations. Perhaps, this approximation may be valid for most
multiphase regions involving condensed phases, where processes that
re-establish equilibrium (e.g., diffusion) tend to be slow compared
to those in the gas phase.
and the number of components c = 1 (remembering that all mixing free energies such as G̅ijexcess vanish when c = 1).
We have tested
this expression by using the Fe EOS developed by Benedict et al.58 described in section 4 to compute the two-phase (fluid–hcp
solid) sound speed with the full expression in eq 51 and with the quasistatic approximation in
(53). We have found that the two expressions
yield similar results and fall within the experimental error bars
from Nguyen and Holmes.92 (A slight caveat
is that we have to add a contribution from the shear modulus of the
solid93 when comparing the sound speed
in that phase to experimental data.) Thus, at least in this particular
example, the small errors that one incurs in making the quasistatic
approximation are well worth the practical benefit of greatly simplifying
the computations. Perhaps, this approximation may be valid for most
multiphase regions involving condensed phases, where processes that
re-establish equilibrium (e.g., diffusion) tend to be slow compared
to those in the gas phase.
Other thermodynamic derivatives that are frequently of interest in various applications include the isochoric heat capacity CV and isobaric heat capacity CP. If we assume quasistatic phase equilibrium, we may combine eqs 2 and 17 to obtain the following expression for CV
 |
55 |
where CV,ij = T(∂Sij/∂T)V is CV of pure j evaluated at the same T, P, and state of matter as phase i. Similarly, it is easy to show that
 |
56 |
Because by definition all excess free energies of mixing vanish in an ideal mixture, these expressions for an ideal mixture simplify to
| 57 |
| 58 |
Thus, the heat capacity of an ideal mixture is a linear combination of the pure-component heat capacities, where the weighting coefficients come from χ and z, much like the case with V, E, and H in eqs 22–24. All other thermodynamic derivatives of a general multiphase, multicomponent mixture, such as the isobaric thermal-expansion coefficient (1/V)(∂V/∂T)P,χ,z and the Grüneisen parameter Γ = −V(∂V/∂T)P,χ,z(∂P/∂V)T,χ,z/CV, may be derived in the same manner as that illustrated above.
The authors declare no competing financial interest.
References
- Klepeis J. E.; Schafer K. J.; Barbee T. W. III; Ross M. Hydrogen–Helium Mixtures at Megabar Pressures: Implications for Jupiter and Saturn. Science 1991, 254, 986–989. 10.1126/science.254.5034.986. [DOI] [PubMed] [Google Scholar]
- Saumon D.; Chabrier G.; van Horn H. M. An Equation of State for Low-Mass Stars and Giant Planets. Astrophys. J. 1995, 99, 713–741. 10.1086/192204. [DOI] [Google Scholar]
- Militzer B. Equation of state calculations of hydrogen–helium mixtures in solar and extrasolar giant planets. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 014202. 10.1103/PhysRevB.87.014202. [DOI] [Google Scholar]
- Bethkenhagen M.; Meyer E. R.; Hamel S.; Nettelmann N.; French M.; Scheibe L.; Ticknor C.; Collins L. A.; Kress J. D.; Fortney J. J.; Redmer R. Planetary Ices and the Linear Mixing Approximation. Astrophys. J. 2017, 848, 67. 10.3847/1538-4357/aa8b14. [DOI] [Google Scholar]
- Journaux B.; Daniel I.; Petitgirard S.; Cardon H.; Perrillat J.-P.; Caracas R.; Mezouar M. Salt partitioning between water and high-pressure ices. Implication for the dynamics and habitability of icy moons and water-rich planetary bodies. Earth Planet. Sci. Lett. 2017, 463, 36–47. 10.1016/j.epsl.2017.01.017. [DOI] [Google Scholar]
- Abramson E. H.; Bollengier O.; Brown J. M. Water–carbon dioxide solid phase equilibria at pressures above 4 GPa. Sci. Rep. 2017, 7, 821. 10.1038/s41598-017-00915-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vance S. D.; Panning M. P.; Stähler S.; Cammarano F.; Bills B. G.; Tobie G.; Kamata S.; Kedar S.; Sotin C.; Pike W. T.; et al. Geophysical Investigations of Habitability in Ice-Covered Ocean Worlds. J. Geophys. Res.: Planets 2018, 123, 180–205. 10.1002/2017JE005341. [DOI] [Google Scholar]
- Kroonblawd M. P.; Lindsey R. K.; Goldman N. Synthesis of functionalized nitrogen-containing polycyclic aromatic hydrocarbons and other prebiotic compounds in impacting glycine solutions. Chem. Sci. 2019, 10, 6091–6098. 10.1039/C9SC00155G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Litasov K. D.; Goncharov A. F.; Hemley R. J. Crossover from melting to dissociation of CO2 under pressure: Implications for the lower mantle. Earth Planet. Sci. Lett. 2011, 309, 318–323. 10.1016/j.epsl.2011.07.006. [DOI] [Google Scholar]
- Teweldeberhan A. M.; Boates B.; Bonev S. A. CO2 in the mantle: Melting and solid–solid phase boundaries. Earth Planet. Sci. Lett. 2013, 373, 228–232. 10.1016/j.epsl.2013.05.008. [DOI] [Google Scholar]
- Wu C. J.; Young D. A.; Sterne P. A.; Myint P. C. Equation of state for a chemically dissociative, polyatomic system: Carbon dioxide. J. Chem. Phys. 2019, 151, 224505. 10.1063/1.5128127. [DOI] [PubMed] [Google Scholar]
- Bastea S.; Fried L. E. In Chemical Equilibrium Detonation; Zhang F., Ed.; Chapter 1 of Shock Waves Science and Technology Library; Springer: Berlin, 2012; Vol. 6: Detonation Dynamics, pp 1–31. [Google Scholar]
- Ticknor C.; Andrews S. A.; Leiding J. A. Magpie: A new thermochemical code. AIP Conf. Proc. 2020, 2272, 030033. 10.1063/12.0000785. [DOI] [Google Scholar]
- Lindsey R. K.; Goldman N.; Fried L. E.; Bastea S. Many-body reactive force field development for carbon condensation in C/O systems under extreme conditions. J. Chem. Phys. 2020, 153, 054103. 10.1063/5.0012840. [DOI] [PubMed] [Google Scholar]
- Gray G. T. III; Livescu V.; Rigg P. A.; Trujillo C. P.; Cady C. M.; Chen S. R.; Carpenter J. S.; Lienert T. J.; Fensin S. J. Structure/property (constitutive and spallation response) of additively manufactured 316L stainless steel. Acta Mater. 2017, 138, 140–149. 10.1016/j.actamat.2017.07.045. [DOI] [Google Scholar]
- Kennedy J.; Eberhart R.. Particle Swarm Optimization IEEE International Conference on Neural Networks, 1995; pp 1942–1948.
- Simon D.Evolutionary Optimization Algorithms; John Wiley & Sons: Hoboken, 2013; p 784. [Google Scholar]
- Bonyadi M. R.; Michalewicz Z. Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review. Evol. Comput. 2017, 25, 1–54. 10.1162/EVCO_r_00180. [DOI] [PubMed] [Google Scholar]
- Darlington R. M.; McAbee T. L.; Rodrigue G. A study of ALE simulations of Rayleigh–Taylor instability. Comput. Phys. Commun. 2001, 135, 58–73. 10.1016/S0010-4655(00)00216-2. [DOI] [Google Scholar]
- Noble C.; Anderson A.; Barton N. R.; Bramwell J.; Capps A.; Chang M.; Chou J.; Dawson D.; Diana E.; Dunn T.; et al. ALE3D: An Arbitrary Lagrangian-Eulerian Multi-Physics Code. Technical Report LLNL-TR-732040, 2017.
- Cook A. W. Enthalpy diffusion in multicomponent flows. Phys. Fluids 2009, 21, 055109. 10.1063/1.3139305. [DOI] [Google Scholar]
- Wallace D. C.Statistical Physics of Crystals and Liquids: A Guide to Highly Accurate Equations of State; World Scientific Publishing Company: Singapore, 2002; p 328. [Google Scholar]
- Kerley G. I.An Equation of State for Helium. Technical report KTS04-2, 2004.
- Benedict L. X.; Driver K. P.; Hamel S.; Militzer B.; Qi T.; Correa A. A.; Saul A.; Schwegler E. Multiphase equation of state for carbon addressing high pressures and temperatures. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 224109. 10.1103/PhysRevB.89.224109. [DOI] [Google Scholar]
- Wu C. J.; Myint P. C.; Pask J. E.; Prisbrey C. J.; Correa A. A.; Suryanarayana P.; Varley J. B. Development of a multiphase beryllium equation of state and physics-based variations. J. Phys. Chem. A 2021, 125, 1610–1636. 10.1021/acs.jpca.0c09809. [DOI] [PubMed] [Google Scholar]
- Chisolm E. D.; Crockett S. D.; Wallace D. C. Test of a theoretical equation of state for elemental solids and liquids. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 68, 104103. 10.1103/PhysRevB.68.104103. [DOI] [Google Scholar]
- More R. M.; Warren K. H.; Young D. A.; Zimmerman G. B. A new quotidian equation of state (QEOS) for hot dense matter. Phys. Fluids 1988, 31, 3059–3078. 10.1063/1.866963. [DOI] [Google Scholar]
- Young D. A.; Corey E. M. A new global equation of state model for hot, dense matter. J. Appl. Phys. 1995, 78, 3748–3755. 10.1063/1.359955. [DOI] [Google Scholar]
- Fritsch F. N.The LEOS Interpolation Package. Technical Report UCRL-ID-148554-REV-1, 2003; p 30.
- Lyon S. P.; Johnson J. D.. SESAME: the Los Alamos National Laboratory Equation of State Database. Technical Report LA-UR-92-3407, 1992.
- Chisolm E. D.; Wallace D. C. Dynamics of monatomic liquids. J. Phys.: Condens. Matter 2001, 13, R739–R769. 10.1088/0953-8984/13/37/201. [DOI] [Google Scholar]
- Zel’dovich Y. B.; Raizer Y. P. In Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena; Hayes W. D., Probstein R. F., Eds.; Dover Publications: Mineola, 2012; p 946. [Google Scholar]
- Myint P. C.; Chernov A. A.; Sadigh B.; Benedict L. X.; Hall B. M.; Hamel S.; Belof J. L. Nanosecond freezing of water at high pressures: nucleation and growth near the metastability limit. Phys. Rev. Lett. 2018, 121, 155701. 10.1103/PhysRevLett.121.155701. [DOI] [PubMed] [Google Scholar]
- Consiglio A.; Ukpai G.; Rubinsky B.; Powell-Palm M. J. Suppression of cavitation-induced nucleation in systems under isochoric confinement. Phys. Rev. Research 2020, 2, 023350. 10.1103/PhysRevResearch.2.023350. [DOI] [Google Scholar]
- Campbell F. C.Phase Diagrams: Understanding the Basics; ASM International: Materials Park, 2012; p 462. [Google Scholar]
- Prausnitz J. M.; Lichtenthaler R. N.; Gomes de Azevedo E.. Molecular Thermodynamics of Fluid-Phase Equilibria, 3rd ed.; Prentice Hall: Upper Saddle River, 1999. [Google Scholar]
- Sandler S. I.Chemical, Biochemical, and Engineering Thermodynamics, 4th ed.; John Wiley & Sons: Hoboken, 2006. [Google Scholar]
- Lupis C. H. P.Chemical Thermodynamics of Materials; Prentice Hall, Inc.: New York, North-Holland, 1983. [Google Scholar]
- Stølen S.; Grande T.; Allan N. L.. Chemical Thermodynamics of Materials: Macroscopic and Microscopic Aspects; John Wiley & Sons: Chichester, 2003. [Google Scholar]
- DeHoff R.Thermodynamics in Materials Science; CRC Press, Taylor & Francis Group: Boca Raton, 2006; p 624. [Google Scholar]
- Okamoto H. The Fe–Ga (Iron-Gallium) system. Bull. Alloy Phase Diagrams 1990, 11, 576–581. 10.1007/BF02841721. [DOI] [Google Scholar]
- Sandler S. I.An Introduction to Applied Statistical Thermodynamics; John Wiley & Sons: Hoboken, 2011. [Google Scholar]
- Militzer B.; González-Cataldo F.; Zhang S.; Whitley H. D.; Swift D. C.; Millot M. Nonideal mixing effects in warm dense matter studied with first-principles computer simulations. J. Chem. Phys. 2020, 153, 184101. 10.1063/5.0023232. [DOI] [PubMed] [Google Scholar]
- Anderson G. M.; Crerar D. A.. Thermodynamics in Geochemistry: The Equilibrium Model; Oxford University Press: New York, 1993. [Google Scholar]
- Sterner S. M.; Pitzer K. S. An equation of state for carbon dioxide valid from zero to extreme pressures. Contrib. Mineral. Petrol. 1994, 117, 362–374. 10.1007/BF00307271. [DOI] [Google Scholar]
- Elliott J. R.; Lira C. T.. Introductory Chemical Engineering Thermodynamics, 1st ed.; Prentice Hall: Upper Saddle River, 1999. [Google Scholar]
- Myint P. C.; Hao Y.; Firoozabadi A.. The CPA Equation of State and an Activity Coefficient Model for Accurate Molar Enthalpy Calculations of Mixtures with Carbon Dioxide and Water/Brine. Technical Report LLNL-TR-672077, 2015; p 43.
- Cox G. A.; Christie M. A. Fitting of a multiphase equation of state with swarm intelligence. J. Phys.: Condens. Matter 2015, 27, 405201. 10.1088/0953-8984/27/40/405201. [DOI] [PubMed] [Google Scholar]
- Cox G. Generating a multiphase equation of state with swarm intelligence. AIP Conf. Proc. 2018, 1979, 040002. 10.1063/1.5044780. [DOI] [Google Scholar]
- Myint P. C.; Gersten B. T.; McClelland M. A.; Nichols A. L. III; Springer H. K. Entropy maximization and free energy minimization of multiphase mixtures using particle swarm optimization. AIP Conf. Proc. 2018, 1979, 030006. 10.1063/1.5044776. [DOI] [Google Scholar]
- Rahman I.; Das A. K.; Mankar R. B.; Kulkarni B. D. Evaluation of repulsive particle swarm method for phase equilibrium and phase stability problems. Fluid Phase Equilib. 2009, 282, 65–67. 10.1016/j.fluid.2009.04.014. [DOI] [Google Scholar]
- Bonilla-Petriciolet A.; Segovia-Hernández J. G. A comparative study of particle swarm optimization and its variants for phase stability and equilibrium calculations in multicomponent reactive and non-reactive systems. Fluid Phase Equilib. 2010, 289, 110–121. 10.1016/j.fluid.2009.11.008. [DOI] [Google Scholar]
- Moreira L. A.; Firoozabadi A. Molecular thermodynamic modeling of droplet-type microemulsions. Langmuir 2012, 28, 1738–1752. 10.1021/la203909b. [DOI] [PubMed] [Google Scholar]
- Sterbentz D. M.; Gambino J. R.; Myint P. C.; Delplanque J.-P.; Springer H. K.; Marshall M. C.; Belof J. L. Drive-pressure optimization in ramp-wave compression experiments through differential evolution. J. Appl. Phys. 2020, 128, 195903. 10.1063/5.0023361. [DOI] [Google Scholar]
- Shi Y.; Eberhart R.. A Modified Particle Swarm Optimizer. IEEE International Conference on Evolutionary Computation, 1998; pp 69–73.
- Myint P. C.; McClelland M. A.; Nichols A. L. III Application of the Peng–Robinson equation of state to energetic materials RDX and TNT: pure components, liquid mixtures, and solid mixtures. Ind. Eng. Chem. Res. 2016, 55, 2252–2266. 10.1021/acs.iecr.5b04808. [DOI] [Google Scholar]
- Myint P. C.; Nichols A. L. III Thermodynamics of HMX and HMX/RDX Mixtures. Ind. Eng. Chem. Res. 2017, 56, 387–403. 10.1021/acs.iecr.6b03697. [DOI] [Google Scholar]
- Davis S. M.; Zerkle D. K. Short communication: Estimation of yield stress/viscosity of molten octol. AIP Adv. 2018, 8, 055202. 10.1063/1.5027397. [DOI] [Google Scholar]
- Benedict L. X.; Kraus R. G.; Hamel S.; Belof J. L.. A semi-empirical iron EOS for temperature predictions in high pressure shock–ramp experiments, 2019. https://meetings.aps.org/Meeting/MAR19/Session/H17.6 (accessed 2020-10-17).
- Turneaure S. J.; Sharma S. M.; Gupta Y. M. Crystal Structure and Melting of Fe Shock Compressed to 273 GPa: In situ X-Ray Diffraction. Phys. Rev. Lett. 2020, 125, 215702. 10.1103/PhysRevLett.125.215702. [DOI] [PubMed] [Google Scholar]
- Wu C. J.; Myint P. C.; Prisbrey C. J.; Bonev S. A.; Belof J. L.. Development of a multiphase equation of state for gallium with experiments and ab initio free-energy calculations. 2021, In preparation. [Google Scholar]
- Arveson S. M.; Deng J.; Karki B. B.; Lee K. K. M. Evidence for Fe–Si–O liquid immiscibility at deep Earth pressures. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 10238–10243. 10.1073/pnas.1821712116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brantley D. A.; Crum R. S.; Akin M. C. Comparing temperature convergence of shocked thin films of tin and iron to a bulk temperature source. J. Appl. Phys. 2021, 129, 015903. 10.1063/5.0026053. [DOI] [Google Scholar]
- Haase R.Thermodynamics of Irreversible Processes; Dover Publications: Mineola, 1990 [Google Scholar]
- Butler J. N.Ionic Equilibrium: Solubility and pH Calculations; John Wiley & Sons: New York, 1998; p 559. [Google Scholar]
- Fried L.; Souers P.. CHEETAH: A Next Generation Thermochemical Code. Technical Report UCRL-ID-117240, 1994.
- Fried L. E.; Howard W. M. An accurate equation of state for the exponential-6 fluid applied to dense supercritical nitrogen. J. Chem. Phys. 1998, 109, 7338–7348. 10.1063/1.476520. [DOI] [Google Scholar]
- Bastea S.; Fried L. E. Exp6-polar thermodynamics of dense supercritical water. J. Chem. Phys. 2008, 128, 174502. 10.1063/1.2913055. [DOI] [PubMed] [Google Scholar]
- Myint P. C.; Sadigh B.; Benedict L. X.; Sterbentz D. M.; Hall B. M.; Belof J. L. Coupling solidification kinetics with phase-behavior computations in hydrodynamic simulations of high-pressure, dynamic-compression processes. AIP Adv. 2020, 10, 125111. 10.1063/5.0032973. [DOI] [Google Scholar]
- Michelsen M. L. The isothermal flash problem. Part I. Stability. Fluid Phase Equilib. 1982, 9, 1–19. 10.1016/0378-3812(82)85001-2. [DOI] [Google Scholar]
- Michelsen M. L. The isothermal flash problem. Part II. Phase-split calculation. Fluid Phase Equilib. 1982, 9, 21–40. 10.1016/0378-3812(82)85002-4. [DOI] [Google Scholar]
- Firoozabadi A.Thermodynamics and Applications in Hydrocarbons Energy Production; McGraw-Hill: New York, 2015. [Google Scholar]
- Nichita D. V. New unconstrained minimization methods for robust flash calculations at temperature, volume and moles specifications. Fluid Phase Equilib. 2018, 466, 31–47. 10.1016/j.fluid.2018.03.012. [DOI] [Google Scholar]
- Cismondi M.; Ndiaye P. M.; Tavares F. W. A new simple and efficient flash algorithm for T–v specifications. Fluid Phase Equilib. 2018, 464, 32–39. 10.1016/j.fluid.2018.02.019. [DOI] [Google Scholar]
- Castier M. Solution of the isochoric–isoenergetic flash problem by direct entropy maximization. Fluid Phase Equilib. 2009, 276, 7–17. 10.1016/j.fluid.2008.10.005. [DOI] [Google Scholar]
- Smejkal T.; Mikyška J. Phase stability testing and phase equilibrium calculation at specified internal energy, volume, and moles. Fluid Phase Equilib. 2017, 431, 82–96. 10.1016/j.fluid.2016.09.025. [DOI] [Google Scholar]
- Paterson D.; Michelsen M. L.; Yan W.; Stenby E. H. Extension of modified RAND to multiphase flash specifications based on state functions other than (T, P). Fluid Phase Equilib. 2018, 458, 288–299. 10.1016/j.fluid.2017.10.019. [DOI] [Google Scholar]
- Bi R.; Firoozabadi A.; Myint P. C. Efficient and Robust Phase-split Computations at Specified Internal Energy, Volume, and Moles (UVN). Fluid Phase Equilib. 2020, 526, 112729. 10.1016/j.fluid.2020.112729. [DOI] [Google Scholar]
- Saunders N.; Miodownik A. P. In CALPHAD (Calculation of Phase Diagrams): A Comprehensive Guide; Cahn R. W., Ed.; Pergamon Materials Series; Pergamon Publications: Oxford, 1998; Vol. 1. [Google Scholar]
- Lukas H. L.; Fries S. G.; Sundman B.. Computational Thermodynamics: The Calphad Method; Cambridge University Press: New York, 2007. [Google Scholar]
- Turchi P. E. A.; Abrikosov I. A.; Burton B.; Fries S. G.; Grimvall G.; Kaufman L.; Korzhavyi P.; Rao Manga V.; Ohno M.; Pisch A.; et al. Interface between quantum-mechanical-based approaches, experiments, and CALPHAD methodology. CALPHAD: Comput. Coupling Phase Diagrams Thermochem. 2007, 31, 4–27. 10.1016/j.calphad.2006.02.009. [DOI] [Google Scholar]
- Perron A.; Turchi P. E. A.; Landa A.; Söderlind P.; Ravat B.; Oudot B.; Delaunay F.; Kurata M. Thermodynamic re-assessment of the Pu–U system and its application to the ternary Pu–U–Ga system. J. Nucl. Mater. 2014, 454, 81–95. 10.1016/j.jnucmat.2014.07.051. [DOI] [Google Scholar]
- Perron A.; Turchi P. E. A.; Landa A.; Söderlind P.; Ravat B.; Oudot B.; Delaunay F. The Pu–U–Am system: An ab initio informed CALPHAD thermodynamic study. J. Nucl. Mater. 2015, 458, 425–441. 10.1016/j.jnucmat.2014.12.101. [DOI] [Google Scholar]
- Moore E. E.; Turchi P. E. A.; Landa A.; Söderlind P.; Oudot B.; Belof J. L.; Stout S. A.; Perron A. Development of a CALPHAD Thermodynamic Database for Pu–U–Fe–Ga Alloys. Appl. Sci. 2019, 9, 5040. 10.3390/app9235040. [DOI] [Google Scholar]
- Königsberger E. Improvement of excess parameters from thermodynamic and phase diagram data by a sequential Bayes algorithm. CALPHAD: Comput. Coupling Phase Diagrams Thermochem. 1991, 15, 69–78. 10.1016/0364-5916(91)90027-H. [DOI] [Google Scholar]
- Brosh E.; Makov G.; Shneck R. Z. Application of CALPHAD to high pressures. CALPHAD: Comput. Coupling Phase Diagrams Thermochem. 2007, 31, 173–185. 10.1016/j.calphad.2006.12.008. [DOI] [Google Scholar]
- Karbasi A.; Saxena S. K.; Hrubiak R. The thermodynamics of several elements at high pressure. CALPHAD: Comput. Coupling Phase Diagrams Thermochem. 2011, 35, 72–81. 10.1016/j.calphad.2010.11.007. [DOI] [Google Scholar]
- Fei Y.; Brosh E. Experimental study and thermodynamic calculations of phase relations in the Fe–C system at high pressure. Earth Planet. Sci. Lett. 2014, 408, 155–162. 10.1016/j.epsl.2014.09.044. [DOI] [Google Scholar]
- Saxena S.; Eriksson G. Thermodynamics of Fe–S at ultra-high pressure. CALPHAD: Comput. Coupling Phase Diagrams Thermochem. 2015, 51, 202–205. 10.1016/j.calphad.2015.09.009. [DOI] [Google Scholar]
- Kieffer S. W. Sound speed in liquid–gas mixtures: Water–air and water–steam. J. Geophys. Res., Solid Earth Planets 1977, 82, 2895–2904. 10.1029/JB082i020p02895. [DOI] [Google Scholar]
- Firoozabadi A.; Pan H. Two-Phase Isentropic Compressibility and Two-Phase Sonic Velocity for Multicomponent-Hydrocarbon Mixtures. SPE Reservoir Eval. Eng. 2000, 3, 335–341. 10.2118/65403-PA. [DOI] [Google Scholar]
- Castier M. Thermodynamic speed of sound in multiphase systems. Fluid Phase Equilib. 2011, 306, 204–211. 10.1016/j.fluid.2011.04.002. [DOI] [Google Scholar]
- Nguyen J. H.; Holmes N. C. Melting of iron at the physical conditions of the Earth’s core. Nature 2004, 427, 339–342. 10.1038/nature02248. [DOI] [PubMed] [Google Scholar]
- Steinle-Neumann G.; Stixrude L.; Cohen R. E.; Gülseren O. Elasticity of iron at the temperature of the Earth’s inner core. Nature 2001, 413, 57–60. 10.1038/35092536. [DOI] [PubMed] [Google Scholar]
- Sun W.; Powell-Palm M. J.. Generalized Gibbs’ Phase Rule. arXiv, May 4, 2021, 2105.01337. https://arxiv.org/abs/2105.01337. [Google Scholar]






