Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 May 12;15(5):8525–8536. doi: 10.1021/acsnano.1c00166

Multivalent Affinity Profiling: Direct Visualization of the Superselective Binding of Influenza Viruses

Nico J Overeem †, P H (Erik) Hamming †, Malte Tieke ‡, Erhard van der Vries ‡,§,∥, Jurriaan Huskens †,*
PMCID: PMC8158855  PMID: 33978406

Abstract

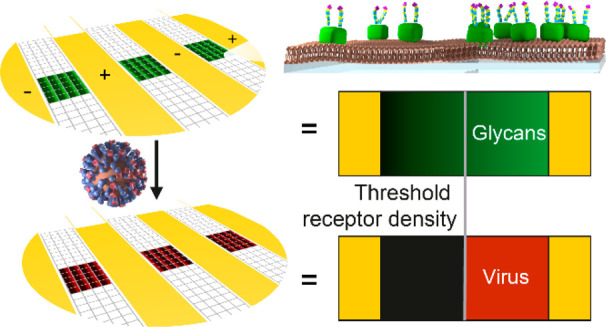
graphic file with name nn1c00166_0008.jpg

The influenza A virus (IAV) interacts with the glycocalyx of host cells through its surface proteins hemagglutinin (HA) and neuraminidase (NA). Quantitative biophysical measurements of these interactions may help to understand these interactions at the molecular level with the long-term aim to predict influenza infectivity and answer other biological questions. We developed a method, called multivalent affinity profiling (MAP), to measure virus binding profiles on receptor density gradients to determine the threshold receptor density, which is a quantitative measure of virus avidity toward a receptor. Here, we show that imaging of IAVs on receptor density gradients allows the direct visualization and efficient assessment of their superselective binding. We show how the multivalent binding of IAVs can be quantitatively assessed using MAP if the receptor density gradients are prepared around the threshold receptor density without crowding at the higher densities. The threshold receptor density increases strongly with increasing flow rate, showing that the superselective binding of IAV is influenced by shear force. This method of visualization and quantitative assessment of superselective binding allows not only comparative studies of IAV–receptor interactions, but also more fundamental studies of how superselectivity arises and is influenced by experimental conditions.

Keywords: multivalency, glycans, influenza viruses, microfluidics, lipid membranes, supramolecular chemistry, superselectivity

Influenza A viruses (IAVs) originate in wild waterfowl and have repeatedly caused outbreaks in livestock and deadly zoonotic infections.1 Adaptation to human hosts has led to four pandemics since 1918 followed by regular seasonal epidemics.2 The initiation of an infection is governed by complex interactions between the surface proteins of the virus and the glycocalyx of the host. Biophysical measurements of IAV can help to understand these interactions by quantifying physical parameters that contribute to the virus–host cell interactions.3−5 Effective use of these measurements requires an understanding of how the measured parameters relate to the interactions of IAV with the glycocalyx on the molecular level.6

The surface proteins of IAV are hemagglutinin (HA) and neuraminidase (NA). HA can bind sialic acid-terminated glycans with millimolar affinities.7 NA is an enzyme that binds the same receptors with comparable affinities and cleaves the bond between sialic acid and the penultimate sugar monomer, which is usually galactose.3,8,9 The opposing actions of HA and NA have a functional balance that ensures sufficient avidity while maintaining the dynamicity that the virus needs to proliferate.10−12 Avian influenza viruses bind preferentially to glycans where the sialic acid is linked to the penultimate galactose by an α2,3-linkage (2,3-SLN), whereas human influenza viruses favor the α2,6-linkage (2,6-SLN).13,14 Structural factors such as the length and branching of glycans also affect the specificity of the virus.15

The receptor density determines whether a virus can bind or not, as multiple glycan–HA interactions are needed for stable attachment.7,16 If a particle needs multiple interactions for stable attachment, its binding depends nonlinearly on the number of receptors that are available in the contact area.17 The resulting bias toward high receptor densities is called “superselectivity”, which is characterized by a sigmoidal increase in binding around a threshold receptor density.18−21

Biolayer interferometry (BLI) is an optical technique that is used to address both the receptor specificity of IAV and the receptor density dependence of the virus–surface interaction.7,22 BLI typically uses streptavidin (SAv)-modified sensor tips that are functionalized with biotinylated glycans, glycopolymers, or glycoproteins.7,12 The density of receptors is controlled by varying the loading time12 or concentration,7 or by diluting the receptors with a dummy receptor.15 The virus binding is measured in solutions with a single, fixed concentration of virus to obtain binding profiles as a function of relative receptor loading. The resulting BLI curves are used as a relative measure of IAV avidity. The insight that this technique can offer is limited by the limited control over the surface chemistry of the sensor tips and the constant virus concentration.

Glycan microarrays provide an efficient technique to evaluate the receptor specificity of IAV.23,24 Small islands of several to hundreds of different glycan types are printed on a surface in an array so that the binding to each glycan type can be measured relative to the others.25,26 The binding of IAV or recombinant HA is quantified using fluorescent labels.27,28 While this technique is more efficient in evaluating the receptor specificity than BLI, it offers even less control over the surface chemistry and does not address receptor density dependence.

Surface gradients of receptors allow evaluation of virus binding as a function of receptor density in a single image. Spatial gradients of physicochemical properties are widely used to improve the efficiency of analysis, design, and discovery.29−35 Our group developed methods using interdigitated electrodes on glass chips to form electrochemical surface density gradients in self-assembled monolayers36,37 and electrophoretic gradients in supported lipid bilayers (SLBs).38 By using lipids that are in the gel state at room temperature, gradients have been formed at elevated temperatures and locked-in by cooling.39 The resulting gradients were then post-functionalized and used as a receptor density gradient.33,40

Recently, we introduced a method, called “multivalent affinity profiling” (MAP), to measure the avidity of influenza viruses using receptor density gradients to obtain binding profiles as a function of receptor density.15 The equilibrium constant of the multivalent virus–surface interaction is a receptor density-dependent quantity reflected in the shape of the binding profile obtained by MAP. The binding profiles were acquired using fluorescence microscopy. The use of internal standards and normalization allow MAP to determine threshold receptor densities that can be compared with those obtained using other platforms. When the maximum receptor density on the sensor tips of BLI is known, this technique can be used to determine the threshold receptor density similar to MAP, though less efficiently.41 The binding profiles obtained with MAP were used to determine the threshold receptor density, and we applied a model to determine the number of interactions and their individual contributions. Broader application of MAP in dynamic measurements requires further understanding of how superselective binding is visualized and how the threshold receptor density depends on experimental conditions.

Here, we show that receptor density gradients can be used to make superselective binding of IAV visible in a single image. These images can be analyzed to quantitatively assess multivalent IAV binding and study the effect of shear force on the binding. First, we show that the broad and continuous range of receptor densities on a gradient allows visualization of superselective binding. Image analysis of fluorescence micrographs is a powerful method to construct binding profiles. The threshold receptor density is shown to be a characteristic quantity for a superselective particle–surface interaction. After that, the influence of flow cell design and experimental conditions on the accuracy of the measured binding profiles is studied. A model is described to account for the influence of flow rate on the threshold receptor density.

Results and Discussion

Visualization and Quantification of Virus Binding on Receptor Gradients

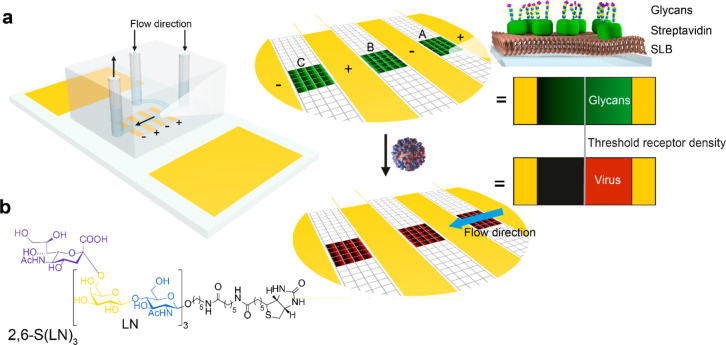
Receptor gradients for studying the binding of IAV were prepared in a microfluidic chip as shown in Figure 1a. The sensing area in the MAP chip is divided into three positions with a total of 21–48 corrals, depending on the chip layout and the alignment of the microchannel. Two inlets are used to decouple the SLB formation from the binding of receptors and viruses.40 Using a previously described method,40 we formed SLBs from vesicles of zwitterionic MPPC (1-myristoyl-2-palmitoyl-sn-glycero-3-phosphocholine) with 0.3–0.8% biotin-DOPE (1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(cap biotinyl)), which has a negative charge. Electrophoretic gradients were formed by applying a potential over the SLBs. The resulting biotin gradients were subsequently modified with fluorescently labeled streptavidin (SAv) and biotinylated glycans (2,6-S(LN)3, Figure 1b). The fluorescent SAv signals the presence of 2,6-S(LN)3, so that the colocalization of fluorescently labeled IAV and 2,6-S(LN)3 can be imaged to obtain binding profiles and determine the threshold receptor density (Figure 1a).

Figure 1.

Figure 1

Open in a new tab

Method for visualization of superselective binding of IAV. (a) Method to form gradients and visualize superselectivity. In SLBs between electrodes inside a microchannel (positions A, B, C), electrophoretic gradients of biotinylated lipids are formed. Fluorescently labeled SAv and 2,6-S(LN)3 are bound onto the biotinylated lipids to form a receptor gradient. Fluorescently labeled influenza virus is added, and the colocalization is imaged with fluorescence microscopy. (b) Structure of the biotinylated glycan receptor 2,6-S(LN)3. In the dummy receptor (LN)2, which is used as a negative control for 2,6-S(LN)3, the sialic acid group (purple) and one LN repeat are omitted.

Whereas previously, gradients were formed at low potential to avoid water splitting,38 we formed the biotin-DOPE gradients at 2.0 V for 30 min to address a wider range of receptor densities. The formation of bubbles at the electrodes was prevented by passing a solution of ferrocene methanol continuously through the flow cell at high flow rate while the gradient was formed.

After forming the receptor gradients, fluorescently labeled IAV Puerto Rico/8/34 Mt. Sinai (PR8) was passed over the chip in concentrations of (6.25 × 108)–(2.0 × 1010) virus particles (vp) per mL (1.04–33.2 pM) overnight at a flow rate of 1 μL/min in the presence of 200 mM Zanamivir to inhibit the receptor-cleaving activity of NA. When PR8 was imaged over the 2,6-S(LN)3 gradients, bright areas could be seen against a low-intensity background matching with the relatively brighter and darker areas of SAv (Figure 2a). The transition from dark to bright areas was sharper for IAV than for SAv, indicating that the binding was superselective.17 As a negative control for IAV binding, glycans without sialic acid (LN)2 were used as a dummy receptor. The same surfaces have been prepared in a quartz crystal microbalance (QCM) experiment where no significant virus binding was observed,15 showing that the SLBs are highly antifouling against IAV. Here, some binding was observed but only at the highest (LN)2 densities (Figure 2b). Possibly, PR8 retains some affinity for (LN)2.

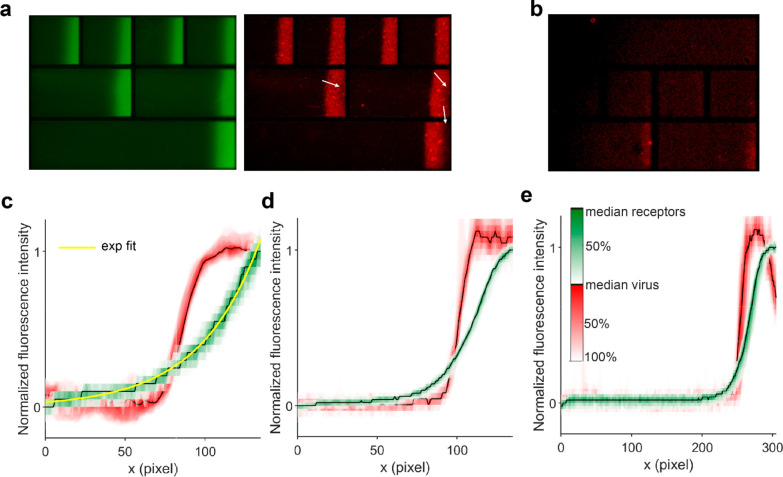
Figure 2.

Figure 2

Open in a new tab

Visualization of receptor gradients and superselective binding of IAV. (a) Fluorescent micrographs of receptor (green) and virus (red) gradients on SLBs with 0.5% biotin-DOPE. White arrows indicate areas where little virus bound despite sufficient SAv density. The square corrals at the top are 100 × 100 μm2. (b) Negative control for virus binding using a biotinylated glycan without sialic acid (LN)2 as a dummy receptor on SLBs with 0.5% biotin-DOPE. (c) Lateral intensity profiles of SAv (green) and virus (red) fluorescence on SLBs with 0.3% biotin-DOPE in a 100 μm corral (0.6 μm/pixel) with an exponential fit (yellow) through the SAv profile. The black lines show the median along the vertical direction. The colored contours around the median indicate the percentage of data points that fall within that contour; i.e., the 50% contour corresponds to the interquartile range of a boxplot. (d) Intensity profiles on SLBs with 0.5% biotin-DOPE in a 100 μm corral. (e) Intensity profiles on SLBs with 0.5% biotin-DOPE in a 210 μm corral.

To investigate the range of receptor densities at which superselective binding may be observed, we formed gradients from SLBs with 0.3% and 0.5% biotin-DOPE and studied the shape of the gradients and the colocalization of virus and receptors with fluorescence microscopy. We used 100 μm × 100 μm corral chips and multicorral chips that have alternatingly one corral of 430 μm long, two corrals of 210 μm, and four corrals of 100 μm, each with a width of 100 μm (Figure 2a). With 0.3% biotin-DOPE in 100 μm corrals, the SAv gradient had an exponential shape in accordance with the shape of the electric field as was previously described for lipid gradients (Figure 2c).38 The SAv gradients were not affected by flow direction. With 0.5% biotin-DOPE, the SAv fluorescence leveled off (Figure 2d). In the 210 and 430 μm corrals, the SAv fluorescence was more sharply divided, approaching a sigmoidal rather than exponential shape (Figure 2e), possibly indicating that steric crowding of SAv occurs at the higher biotin-DOPE densities.

The sigmoidal binding profile of IAV, characteristic of superselectivity, could be seen in all corral lengths for both 0.3% and 0.5% biotin-DOPE. In some binding studies, we found that the virus bound in lower amounts at the areas of the highest receptor densities in the 210 μm and 430 μm corrals (Figure 2a, indicated by arrows), whereas these artifacts occurred rarely in the 100 μm corrals. These defects manifested in a drop in the virus binding profile toward maximal SAv fluorescence (Figure 2e).

The digital imaging transforms continuous gradients into a finely meshed array of discrete samples. At 10× magnification and a resolution of 1360 × 1024 pixels, each pixel is 641 × 641 nm2. In binding studies of bacteria, the individual bacteria were counted to quantify their binding.33 Here, a visual inspection of the fluorescent micrographs (Figure 2a) shows that the fluorescence of the viruses is not clearly separated from neighboring viruses so that fluorescence intensity is more appropriate for quantification than counting the number of viruses. The viruses in this study have an average size of 112 nm.15 Assuming random deposition with a maximum coverage of 54.7%,42 up to 23 virus particles may bind on the area of one pixel. Each pixel is regarded as an individual measurement of receptor and virus density for the purpose of determining the binding profile and threshold receptor density with 1562 pixels for a 100 μm corral. These measurements are not strictly independent, as any degree of defocus causes a spillover of emitted light into neighboring pixels, which has a smoothing effect on the intensity. A not-too-high gradient steepness should therefore be chosen, as long as plateau values of virus binding can be determined on both sides of the transition.

To determine the colocalization of virus and receptors, fluorescence micrographs in appropriate colors are acquired at identical position and focus and saved as an image stack. The stacked micrographs are cropped into corrals by aligning a mask, using a custom-written MATLAB script (Figure 3a). Part of a corral outside the microchannel is selected as background. From the edges of the corrals, part of the image with a width of 10 pixels is discarded. The local receptor density in each pixel is calculated using

graphic file with name nn1c00166_m001.jpg 1

with ρ̅R the average receptor density based on the percentage of biotin-DOPE in the SLB and the lipid footprint, Ii the local fluorescence intensity, I̅bg the average fluorescence intensity of the background, and I̅ the average intensity of the corral. A lipid footprint of 60 Å2 was assumed,43,44 and a stoichiometry of 2 biotin-DOPE lipids and 2 receptors per SAv, so that ρ̅R = 2.77 × %biotin-DOPE.15 While the biotin-DOPE/SAv stoichiometry appeared constant in this study (see below), its absolute value was not verified. The local fluorescence intensities are typically approximately 4-fold lower than average at the minimum and 4-fold higher at the maximum. After the local receptor densities are calculated according to eq 1, these values are used on the x-axis in plots of virus intensity vs. receptor density (Figure 3b–d).

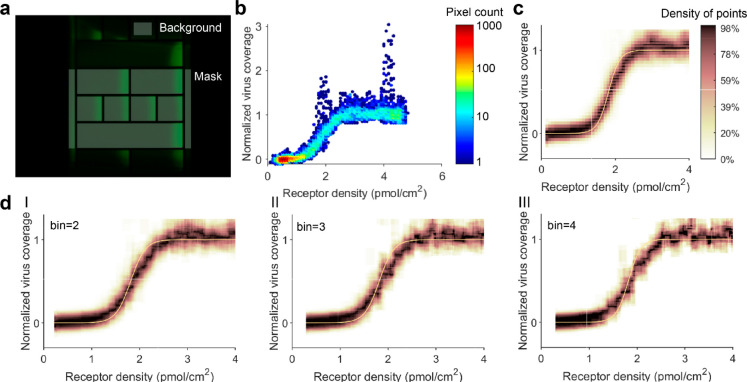
Figure 3.

Figure 3

Open in a new tab

Image processing of fluorescence micrographs to extract IAV binding profiles as a function of receptor density. (a) Corrals and background are selected from the receptor image using a mask. The same mask position is used for the corresponding IAV image. (b) “Point cloud” of one corral, having a receptor gradient from 0.5% biotin-DOPE, showing the normalized virus coverage as a function of receptor density. (c) Binding profile of one corral, fitted with eq 4. Data points are shown in a density map that was generated using a rolling window average that was evaluated at 2001 × 250 points with a window of 40 × 25 points. The fit is based directly on the point cloud and not on the density map. (d) Binding profiles and fits where the data was binned into superpixels with a size of 2 × 2 (I), 3 × 3 (II), and 4 × 4 (III) pixels.

The fluorescence intensity of the virus in the corresponding micrograph is normalized between 0 and 1 using

graphic file with name nn1c00166_m002.jpg 2

with θV,i the virus coverage, Ii the local fluorescence intensity, Imin the minimum fluorescence intensity, and Imax the maximum fluorescence intensity. The minimum fluorescence intensity is determined by finding the maximum of a 1D kernel estimation of the data points with the 50 lowest receptor densities. The maximum fluorescence intensity is determined using a 2D kernel estimation and the 10% highest receptor densities. These values to select the minimum and maximum showed a robust balance between ignoring outliers and finding the extremes in data sets of varying sizes.

The normalized virus coverage, calculated according to eq 2, is plotted against the receptor density of each pixel in a “point cloud” (Figure 3b). Groups of outliers having exceptionally high values for normalized virus coverage and low pixel count correspond to the bright red spots that can be seen on micrographs of bound virus (Figure 2a). These may be small aggregates or larger virus particles, which occur in varying amounts in IAV samples.45 The point cloud is unevenly distributed over the x-axis because the receptor density increases exponentially over the length of a corral. To visualize the discrete and unevenly distributed point cloud as a binding profile, we used a rolling window average. The average was evaluated at 2001 × 250 points with a window of 2% over the x-direction and 10% over the y-direction, in which we normalized the number of data points to the maximum within the window to obtain a continuous binding profile where the areas with the highest local density of data points are indicated with a dark color (Figure 3c). This binding profile forms a direct visualization of the superselective binding profiles that were predicted by Martinez-Veracoechea and Frenkel.17

The point cloud (Figure 3b), which is a representation of the IAV binding data as a function of receptor density and is represented in a binding profile, can be fitted using a theoretical binding model, based on the statistical thermodynamics of multivalent adsorption,26,30 that was described earlier:15

graphic file with name nn1c00166_m003.jpg 3

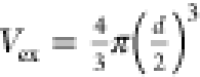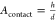where Kav is the multivalent equilibrium binding constant, NA is Avogadro’s number, Inline graphic the excluded volume of a virus particle with d = 112 nm the virus diameter as determined by nanoparticle tracking analysis,15Ki,eff the effective equilibrium constant of an individual HA–glycan interaction, Vexplore the volume accessible to a glycan, Inline graphic the surface area that can be reached by HA when the virus is bound with h = 3.5 nm the length of 2,6-S(LN)3 from molecular dynamics,15 and σR the receptor density. The product AcontactσR is the maximum number of possible simultaneous virus–receptor interactions a virus can form on average when σR is smaller than the density of binding sites on the virus. The resulting virus binding profile is described by

graphic file with name nn1c00166_m006.jpg 4

where θ is the virus coverage, Kav(σR) is the receptor density-dependent Kav (according to eq 3), and [V] the virus concentration. The threshold receptor density is the point where Kav(σR)[V] = 1.

This model is fitted to a point cloud using 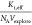Inline graphic as fitting parameter. With all other constants given, both the threshold receptor density and the steepness of the fit depend on 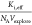Inline graphic. In Figure 3c, the fit is slightly steeper than the experimental binding profile for one corral. Point clouds obtained from multiple corrals in multiple micrographs are combined to obtain a more reliable binding profile and fit. For this virus–receptor combination, we used molecular dynamics to determine the length of a compressed or a stretched 2,6-S(LN)3 glycan and estimated that Vexplore = 140 nm3 using the volume spanned by two half-spheres having these lengths as inner and outer radii, respectively. We found Ki,eff = 409.1 ± 0.4 M–1, using 22 corrals from 3 pairs of micrographs.15 This value for Ki,eff is within experimental error identical with the value for Ki (476 ± 68 M–1) that was found in solution with NMR for influenza strain X-31,7 which has a highly similar binding profile to PR8 in biolayer interferometry studies.46

Because the pixel size is only 1 order of magnitude larger than the size of a virus, we investigated if binning adjacent pixels into larger superpixels would decrease the noise from stochastically adsorbed viruses (Figure 3d). Increasing the bin size progressively decreases the resolution of the binding profile around the threshold receptor density and broadens the confidence interval of the fit. While binning may generally help to suppress noise, in this case it also lowers the accuracy because the underlying properties of adjacent pixels (even above or below) are not necessarily the same and the virus binding depends nonlinearly on receptor density. This also suggests that increasing the resolution or color depth of the micrographs would further improve the precision of the binding profiles.

To assess the superselectivity, binding profiles are usually plotted against receptor density on a logarithmic axis (Figure 4a).17 The superselectivity can then be quantified using the superselectivity parameter α (Figure 4b):17

graphic file with name nn1c00166_m009.jpg 5

Binding is superselective when α > 1. The superselectivity parameter has a peak just before the threshold receptor density. For a threshold receptor density at 0.89 pmol/cm2, α has a maximum of 10.7 at 0.72 pmol/cm2.

Figure 4.

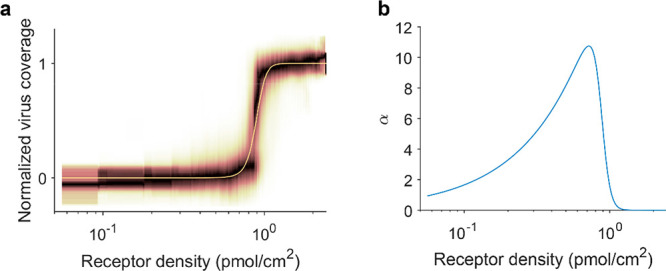
Figure 4

Open in a new tab

Quantitative assessment of the superselectivity of virus binding profiles. (a) Binding profile and fitted model as a function of receptor density (logarithmic axis). This binding profile was obtained using receptor gradients from 0.3% biotin-DOPE in 100 μm corrals, from a data set that was published previously.15 (b) Superselectivity parameter α as a function of receptor density (logarithmic axis).

Equation 4 assumes thermodynamic equilibrium. To test whether this applied, we passed a PR8 solution over the chip at a flow rate of 1 μL/min and acquired fluorescence micrographs at 30 min intervals over a period of 16 h. The shutter was closed between frames and no obvious differences in fluorescence intensity were observed between positions at which time series were acquired, and those where only the end point was imaged (data not shown). Over time, the fluorescence intensity increased toward a plateau that is not reached within the time of the measurement (Figure 5a). The fluorescence intensity increased at the same relative rate at the different glycan densities so that the shape of the binding profile did not change over time (Figure 5b). As soon as the signal-to-noise ratio was high enough, the fitted threshold receptor density stabilized so that the variance between corrals decreased (Figure 5c). From 360 min onward, the average threshold receptor density did not differ significantly from that of the last frame, which was long before the fluorescence intensity reached its plateau. This means that when the virus binding profiles are individually normalized (Figure 5d), the profiles from 360 min onward are identical to the profile at equilibrium. When the chip was washed with PBS with and without 200 mM Zanamivir at a flow rate of 10 μL/min for 30 min, the threshold receptor density did not change, but the fluorescence intensity dropped slightly (Figure 5a). While equilibrium was not reached after 16 h, the threshold receptor density reached a stable value much earlier (Figure 5c), suggesting that the shape of the binding profile of IAV is thermodynamically controlled. Yet, the overall binding rate of the virus is likely controlled by mass transport because the absolute fluorescence intensity appeared to increase faster at higher virus concentrations and flow rates (data not shown). We deduce from this that the maximum binding rate of IAV depends on mass transport, while the chance of successful binding depends on avidity.

Figure 5.

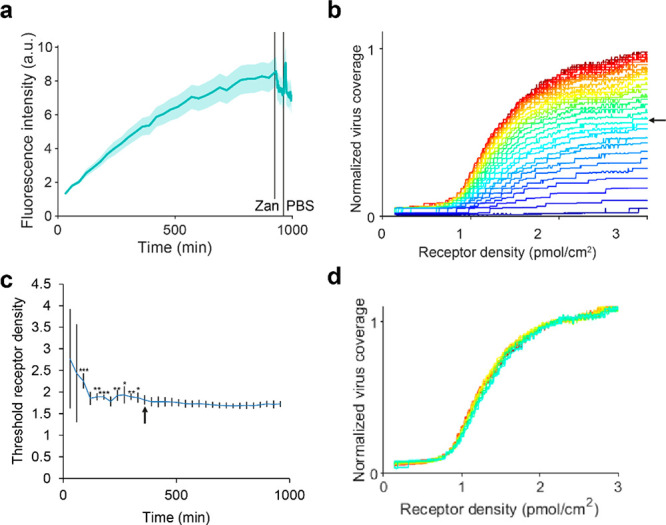
Figure 5

Open in a new tab

Threshold receptor density of IAV particles binding to receptor gradients as a function of time in 4 corrals. (a) Development of the average fluorescence intensity over time in 100 μm corrals of a mixed corral flow cell with 2,6-S(LN)3 gradients on 0.5% biotin-DOPE. The shaded area indicates the standard error between corrals. After 930 min of PR8, the solution was changed to 200 mM Zanamivir, the flow rate to 10 μL/min and micrographs were taken every min. After 960 min, the solution was changed to PBS without NA inhibitor. (b) Development of virus binding profile over time (from 30 to 930 min). The time between frames was 30 min. The median fluorescence intensity of the virus was normalized to the highest value in the last frame. (c) Development of the threshold receptor density over time. Error bars show the standard deviation between corrals. From 360 min onward, the threshold density does not differ significantly from that of the last frame. This point is indicated with an arrow in both a and b. *: p < 0.05, **: p < 0.01, ***: p < 0.001. (d) Individually normalized virus binding profiles from 360 min onward.

The actual threshold receptor density is expected to be independent from the layout of the receptor gradients. To test whether the layout of the gradients influenced the observed threshold receptor density, we compared the mean threshold receptor densities for different corral sizes and different positions in the microchannel, using a two-way ANOVA followed by a multiple comparison test. The threshold receptor density was significantly higher for 210 μm corrals than for 100 μm corrals (p < 0.05), and the variance within 430 μm corrals was high (Figure 6a). We compared the observed threshold receptor densities for gradients made from SLBs with different percentages of biotin-DOPE and found that the threshold densities differed strongly (p ≪ 0.001) (Figure 6b). We found no significant difference (p > 0.05) between the three positions in the microchannel or between the two gradient directions, with or against the flow direction (Figure 6c). This suggests that the differences in the observed threshold receptor density for different layouts and different percentages of biotin-DOPE do not arise from mass transport limitations of the virus but from differences in the gradients.

Figure 6.

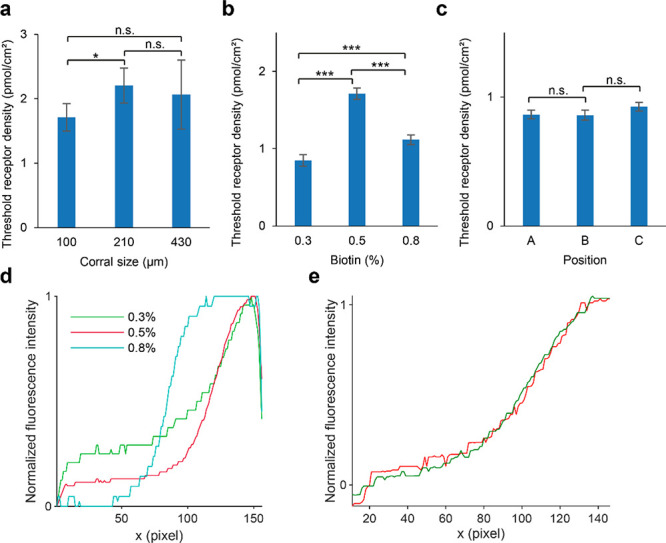
Figure 6

Open in a new tab

Threshold densities of IAV particles binding to receptor gradients observed for different chip layouts and biotin densities. (a) Mean threshold receptor density for corrals of different sizes on gradients from 0.5% biotin-DOPE, determined for 24, 11, and 4 corrals. Error bars indicate 95% confidence interval. n.s.: not significant, *: p < 0.05. (b) Mean threshold receptor density on gradients prepared from different percentages of biotin-DOPE in 100 μm corrals, determined for 36, 24, and 46 corrals. Error bars indicate 95% confidence interval. ***: p < 0.001. (c) Mean threshold receptor density on 0.3% biotin-DOPE in 100 μm corrals for different positions in the microchannel (A–C, Figure 1a), determined for 8, 6, and 8 corrals. Gradients in A and C are with the direction of the flow through the channel; B is against the flow. Error bars indicate 95% confidence interval. n.s.: not significant. (d) Median lateral intensity profiles of SAv on gradients prepared from different percentages of biotin-DOPE in a 100 μm corral, without the edges removed from the image. (e) Median lateral intensity profiles of SAv (green) and ATTO 565-biotin (red) fluorescence on 0.5% biotin-DOPE over four 100 μm corrals, normalized to the average of the first and last 20 points of the median.

Figure 6d shows the lateral intensity profiles of gradients from different percentages of biotin-DOPE. While the gradients from 0.3% biotin-DOPE have an exponential shape in accordance with the electric field (Figure 2c), the 0.5% gradients level off, and the 0.8% gradients have a distinct sigmoidal shape. This sigmoidal shape is more strongly pronounced in the longer 210 and 430 μm corrals (Figure 2e). At both ends of the intensity profiles, the fluorescence drops off near the edge of the corrals. The strong differences in fluorescence intensity between 0.3%, 0.5%, and 0.8% for x values below 50 pixels are an artifact of mask alignment (Figure 3a), which is mitigated by cropping 10 pixels off the edges (cf., Figure 2c). The deviation from an exponential shape for higher biotin-DOPE percentages suggests that the maximum density of SAv is reached. In studies with quartz crystal microbalance (QCM), SLBs are typically saturated with SAv at around 1% biotin-DOPE.43,47 This means that the number of biotin groups per SAv is not constant over the whole gradient for higher biotin percentages, and ρ̅R cannot be calculated directly from the percentage of biotin-DOPE in the SLB but is likely overestimated. If eq 1 is then used to calculate the local receptor densities ρR,i, the observed threshold receptor density will also be overestimated. This overestimation can be seen in Figure 3c, where the virus binding profile is stretched out with respect to the fitted model. In other experiments using the same receptor on 0.3% biotin-DOPE gradients, the binding profile was slightly steeper than the fitted model (Figure 4a). Because the normalization is unreliable when the SAv profile does not follow the biotin gradient, it is difficult to calculate how much the threshold receptor density is overestimated. Normalization is reliable only when the actual threshold receptor density is well below the density where the SLBs are saturated with SAv, which is achieved by using only 100 μm corrals and no more than 0.3% biotin-DOPE in the SLBs.

Dubacheva et al. reported that the residual valency of SAv increases with biotin density (between 1.12 and 1.74) in fluid-state SLBs but decreases with biotin density, but to a smaller extent (between 1.95 and 1.68), in self-assembled monolayers.43 We expect our gel-state SLBs, because of the lack of lipid mobility, to resemble self-assembled monolayers rather than fluid-state SLBs. To test whether the residual valency of SAv in the gradients on gel-state SLBs changes, we incubated SAv gradients on 0.5% biotin-DOPE with fluorescent ATTO 565-biotin (Figure 6e). The lateral intensity profiles of ATTO 565-biotin and SAv are highly similar, suggesting that the residual valency of SAv in the gradients is constant, and no additional constraints on the percentage of biotin-DOPE are necessary.

Effects of Virus Concentration and Flow Rate on Threshold Receptor Density

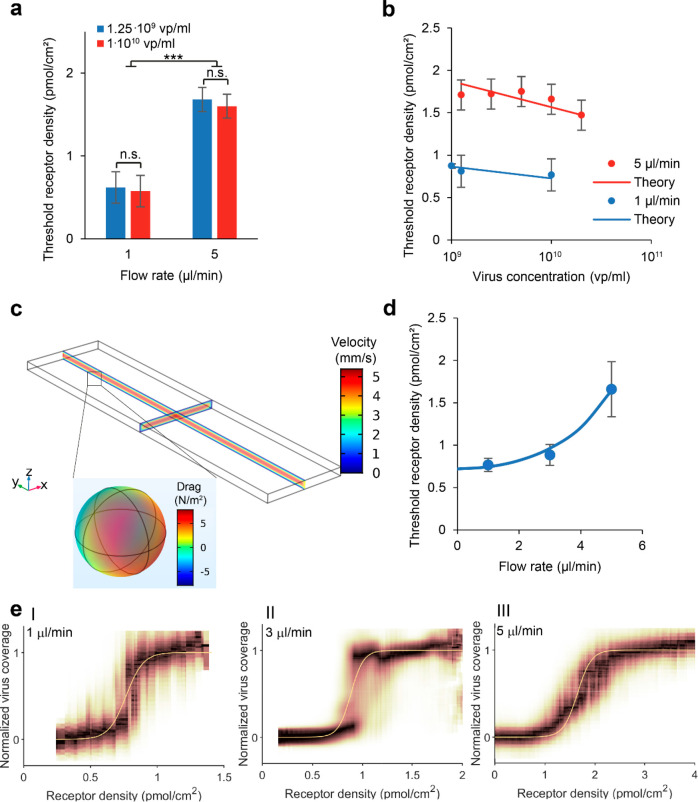
To study the influence of virus concentration and flow rate on the observed threshold receptor density, we measured the virus binding on gradients from 0.3% biotin-DOPE in 100 μm corrals at flow rates of 1 μL/min and 5 μL/min and titrated the virus concentration. We found no significant change in threshold density (p > 0.5) with an 8-fold increase in virus concentration (Figure 7a) but found a strong difference between 1 μL/min and 5 μL/min (p ≪ 0.001).

Figure 7.

Figure 7

Open in a new tab

Threshold receptor density of IAV particles binding to receptor gradients as a function of flow rate and virus concentration. (a) Mean threshold receptor density for different virus concentrations and flow rates, from 7 corrals for 1 μL/min and 12 for 5 μL/min. Error bars indicate 95% confidence interval. n.s.: not significant, ***: p < 0.001. (b) Measured and predicted threshold receptor density at different virus concentrations for different flow rates. The theoretical change in threshold receptor density with virus concentration is calculated separately for 1 μL/min and 5 μL/min using eq 6 with 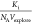Inline graphic as fit parameter. Experimental threshold receptor densities were evaluated over 12 corrals for 5 μL/min and over 22, 7, and 7 corrals for 1 μL/min. Error bars indicate 95% confidence interval. (c) Finite element simulation of laminar flow in a microchannel at a flow rate of 5 μL/min and the resulting drag force on a 112 nm particle. (d) Fitted threshold receptor density at different flow rates using eq 7 with the spring constant k as fit parameter, using 7, 20, and 12 corrals. Error bars indicate standard deviation. (e) Binding profiles and fits at flow rates of 1 μL/min (I), 3 μL/min (II), and 5 μL/min (III). For these profiles, point clouds from 7 (I), 20 (II), and 12 (III) corrals were combined.

From eqs 3 and 4, it follows that the threshold receptor density depends on virus concentration by

graphic file with name nn1c00166_m010.jpg 6

This relationship is plotted in Figure 7b over the experimentally determined threshold receptor densities. The difference in σR,threshold predicted by eq 6 with a change in virus concentration of 1 order of magnitude is small. While the experimentally determined σR,threshold appears to follow eq 6, the difference in σR,threshold between the highest and lowest virus concentrations remains not significant.

While there was a strong difference in threshold receptor density between flow rates of 1 μL/min and 5 μL/min, there was no significant difference in threshold density between gradients with or against the flow direction for either flow rate. This suggests that increased shear flow does not disrupt mass transport or “push” the viruses to a different position. Instead, the flow appears to provide a shear force that works on all surface-bound viruses regardless of their position and opposes their interaction with the surface. Additional measurements between 1 μL/min and 5 μL/min indicate a nonlinear trend (Figure 7d).

Curk and Tito described a theoretical model for multivalent particles that bind superselectively to a surface under a force that opposes binding.19 If a pulling force works on a bound particle that is not strong enough to break all interactions between the particle and the surface at the threshold receptor density, the threshold receptor density is shifted and superselectivity is enhanced. The shift depends on the strength of the force by

graphic file with name nn1c00166_m011.jpg 7

where c°R,eff = σR,thresholdNA is the shifted intrinsic transition point under the applied force, c°R the intrinsic transition point without applied force, k the spring constant, R the ideal gas constant, T the absolute temperature, Fpull the pulling force, and NL the number of participating ligands. Fpull acts perpendicularly to the surface, so this theory may not be accurate for the shear force directly.

We used a finite element simulation in COMSOL to estimate Fpull. We simulated a laminar flow of water at 1 μL/min and 5 μL/min through a 2000 μm × 500 μm × 50 μm channel with a 112 nm sphere at the bottom surface in the middle of the channel at 0.8× the channel length and computed the flow velocity in the channel and the drag force on the sphere (Figure 7c). At a flow rate of 5 μL/min, the drag force was 42.5 fN, which is 10-fold higher than the product of the virus cross section and the shear force that was reported previously for a simulation of a microchannel of the same cross section.33 The simulated drag force is much lower than the rupture force of a single HA–sialic acid interaction in AFM.8 We fitted k to obtain the relationship shown in Figure 7d, which fits the data qualitatively, but found k/RT = 2.21 × 10–15 nm–2, which is extremely low.

It is probable that the actual drag force near the wall is higher due to local interaction with the no-slip wall. Nir et al. described an analytical model that considers the interaction of a nanoparticle tethered to a wall by a DNA strand:

graphic file with name nn1c00166_m012.jpg 8

where F is the hydrodynamic force, kB the Boltzmann constant, D0 the diffusion constant of the particle, f the Faxén correction factor which is a function of the particle radius and its distance from the wall, ẏ the shear rate, and δz the length of the transverse fluctuations of the particle.48 From the molecular dynamics simulations described in ref (15), the minimum and maximum length of 2,6-S(LN)3 are 2.9 and 4.5 nm. We estimate therefore that 2.9 nm is the minimum distance of the virus from the wall and δz = 1.6 nm. This would give a Faxén correction factor of f = 0.33, a hydrodynamic force of F = 130 fN at a flow rate of 5 μL/min, and a spring constant of k/RT = 2.07 × 10–14 nm–2.

Contrary to the enhanced superselectivity that was predicted by Curk and Tito in the case of a perpendicular pulling force,19 the experimental binding profiles as a function of receptor density under shear force show a less steep transition around the threshold density at higher flow rate (Figure 7e). Together with the extremely low spring constant that is fitted with eq 7, this suggests that the model does not fully apply for forces parallel to the surface in its current form, even though the experimental data shows the predicted increase in threshold receptor density with applied force. A deeper theoretical effort would need to be invested to examine how the theory changes when particles are under shear flow as opposed to surface-normal force. Similarly, the length and flexibility of receptors and ligands are expected to influence the theory. The present model also ignores the kinetics of forming multiple interactions under a shear force. Although the kinetics of forming multiple interactions have been reported to be relatively fast,20 it is possible that fewer simultaneous interactions are possible than eq 7 assumes. Molecular dynamics simulations may form a valuable tool in adjusting the model for the case of influenza virus under shear flow.

The flow rates of 1–5 μL/min that were addressed in this study correspond to wall shear stresses of 0.9–4.3 dyn/cm2,33 which are within the range of those a virus may encounter in vivo, although the medium viscosity and the spring constant of receptors in the glycocalyx that covers the surface of cells may be very different from the values in the flow cell. In healthy blood vessels, the wall shear stress ranges from 0.8 to 60 dyn/cm2.49 In the airways and nasal cavity, the wall shear stress ranges from 0.5 to 3 dyn/cm2 during regular breathing and up to 1700 dyn/cm2 during coughing.50,51 In the periciliary layer, in which beating cilia propel the mucus above it, wall shear stresses around 0.08 dyn/cm2 are estimated.52 The strong effect of variations in shear force on the threshold receptor density of IAV may play an important role in virus tropism. The decreased avidity of the virus under high shear force may facilitate airborne transmission via sneezing and coughing.

Conclusions

Visualization of virus adsorption (or of other multivalent entities) on receptor density gradients in a single image is an efficient way to perform receptor density titrations. In addition to requiring fewer measurements, performing a titration in one image provides the internal standards that are necessary for normalizing a virus binding profile. The two-dimensional character of an image offers a high number of data points as compared to a series of spots or a linear gradient.

Receptor gradients over 100 μm corrals covered a range of receptor densities that was sufficient to visualize superselective binding of the influenza virus PR8. The multiplicity in the chip has been exploited for accurate determination of the threshold receptor density. A layout of different corral lengths may be useful for efficient optimization but offers fewer data points around the threshold receptor density. For larger particles, such as bacteria, the larger corrals may be favorable.33 Lowering the potential during gradient formation may increase the number of data points around the threshold as long as sufficient data points in the lower and higher plateau can be taken for normalization.

During adsorption of virus particles, the observed threshold receptor density stabilizes over time: while long incubation times up to 16 h were used, the threshold receptor density did not change significantly after 6 h, and even after 2 h relatively little change was observed. When the gradient formation leads to biotin densities at the high end beyond what is necessary to saturate the surface with SAv, the average receptor density is overestimated and thereby the threshold receptor density as well. The effect of virus concentration on the threshold receptor density is very small. When a shear force is exerted on bound viruses, the threshold receptor density is increased.

The MAP chip allows direct visualization of superselective binding, which not only gives a clearer insight in superselectivity but also makes it a more efficient platform for the quantitative assessment of multivalent interactions than platforms that probe one receptor density at a time, such as BLI. This flow cell can also be a powerful experimental tool in further elucidating the relationship between superselectivity and hydrodynamic forces, which may offer insights into the airborne transmission of pathogens as well as tools to optimize the targeted delivery of drugs that are distributed via the blood circulation.

Methods

Materials

Biotinylated glycans 2,6-S(LN)3 and (LN)2 were provided by Zeshi Li and Geert-Jan Boons and synthesized as described previously.15 All other starting materials and chemicals were purchased from commercial suppliers and used as received, unless otherwise stated.

Virus Stock Preparation

Influenza A/Puerto Rico/8/34 virus (Mt. Sinai strain) stocks were prepared by propagating the virus in 10-day-old embryonated chicken eggs (GD Animal health, Deventer, The Netherlands) at 33 °C. Allantoic fluids were harvested after 48–72 h and cleared from debris by centrifugation at 3000 rpm for 10 min at 4 °C. Subsequently, the viruses were pelleted by centrifugation at 7000 rpm for 18 h at 4 °C and resuspended in PBS (pH 7.4) (Lonza). Viruses were then purified further by loading of the virus sample on a discontinuous sucrose gradient (10–50% w/v) and centrifugation for 45 min at 25,000 rpm using a SW41 swing-out rotor. The virus-containing sucrose layer was finally harvested and dialyzed (Slide-A-Lyzer, Thermo Scientific) for 48 h at 4 °C to remove the remaining sucrose. Finally, the virus particle count and size distribution were determined using a NS300 nanoparticle tracking analyzer (Malvern, Nanosight), and diluted to a final stock concentration of 1 × 1011 particles/mL, UV-inactivated (50 mJ/cm2, at a wavelength of 365 nm), and aliquots were frozen at −80 °C. Inactivation was confirmed by growing these viruses on Madin-Darby canine kidney (MDCK) cells. The receptor binding capacity of the viruses was confirmed with a hemagglutination assay that was performed as described elsewhere53 to obtain a titer of 2048.

Virus Labeling

Influenza viruses were fluorescently labeled using the lipophilic dye octadecyl rhodamine B (R18; Thermo Scientific), which binds the virus membrane with the fluorophore at the aqueous interface. R18 dye was mixed with inactivated virus stocks to a final concentration of 80 nM and incubated in the dark for 2 h on ice. Free dye was subsequently separated from the R18-labeled viruses by adding 25 μL Capto core 700 virus purification beads (GE Healthcare) per 1 mL of virus and incubating by rotating the mixture for 30 min at 4 °C. Finally, the beads were cleared from the virus-containing supernatant by pelleting of the beads by centrifugation at 1200 rpm for 10 min in a table centrifuge at 4 °C.

Chip Fabrication

Flow cells were fabricated according to the procedure described earlier.40 A bilayer lift-off recipe was used for fabricating Au electrodes on Mempax glass wafers (Schott). First, LOR 5A (MicroChem) was spin-coated, after which normal lithography was performed on top with Olin OiR 907–17 photoresist (FujiFilm) to create a bilayer resist stack. Electrode patterns were made by exposing the photoresist through a patterned photomask and developing in Olin OPD 4262 (FujiFilm). The develop step washed away the exposed photoresist, and etching through the LOR 5A layer created an undercut. Then, 5 nm Ti and 95 nm Au were deposited via e-beam evaporation (BAK 600, Balzers). The bilayer resist was then removed by sonication in acetone (20 min) and isopropanol (10 min) followed by 5 min immersion in OPD 4262, serving as a sacrificial layer to leave patterned Au electrodes on Mempax glass. To fabricate the Cr corrals (10 nm thick) in between the Au electrodes, the same procedure was performed a second time, but in this case following alignment with respect to the Au electrodes.

PDMS Flow Channel

Silicon flow channel masters were produced by standard photolithography steps and deep reactive ion etching. The polydimethylsiloxane (PDMS) flow channels were prepared from a degassed mixture of 10:1 Sylgard 184 elastomer and curing agent (Dow Corning Corp), which was cast onto the silicon master and cured at 60 °C overnight. The flow channels were cut to size, and inlets and outlets were punched using a 1 mm Ø punch (Harris Unicore, Sigma-Aldrich). After bonding to the chip, a flow channel of 6000 × 500 × 50 μm3 was prepared with a second channel entering from the side.

PDMS Bonding

Chips were rinsed and sonicated extensively with acetone, ethanol, and Milli-Q water, and dried prior to UV–ozone exposure (UV/Ozone Procleaner plus, Bioforce Nanosciences) for at least 20 min. After UV exposure, the chips were rinsed with ethanol and water, and dried under a stream of nitrogen. Both cut-out PDMS flow channels and cleaned chips were treated with oxygen plasma for 30 s at 40 W (Plasma prep II, SPI supplies) after which they were bonded immediately. The chips were placed on a hotplate for 10 min at 70 °C to increase the binding strength. Tygon Microbore tubing S-54-HL (VWR, 0.25 mm inner Ø and 0.75 mm outer Ø) of 80 cm for the inlets and 40 cm for the outlets was inserted into the PDMS. The assembled flow cell was placed in an oven at 60 °C for 1 h. Leak-free operation was shown for flow rates up to 200 μL/min.

Lipid Vesicle Preparation

MPPC (1-myristoyl-2-palmitoyl-sn-glycero-3-phosphocholine, Avanti Polar Lipids) and DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine, Avanti) were stored as a 10 mg/mL stock solution in chloroform at −20 °C. Biotin-cap-DOPE (1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(cap biotinyl), Avanti) was stored as 0.2 mg/mL solution. Desired molar ratios were mixed in a glass vial, dried under a flow of nitrogen, and kept under vacuum for at least 1 h. The resulting film was resuspended by vortexing in Milli-Q water at room temperature for DOPC and 50 °C for MPPC to form multilamellar vesicles (MLVs) at 1 mg/mL. The MLV solution was extruded 11 times through a 100 nm polycarbonate membrane (Avanti) at room temperature for DOPC and 50 °C for MPPC. The resulting large unilamellar vesicles (LUVs) were kept at room temperature and used within 1 week.

SLB Formation and Functionalization

Before SLB formation, the flow cells were washed with 2% SDS (Sigma-Aldrich), then rinsed with Milli-Q and washed overnight with 2% Hellmanex to activate the glass surface. Flow cells were mounted onto a heating plate using Scotch tape and rinsed with Milli-Q and PBS, while heating to 50 °C. Shortly before LUV incubation, the LUV solution was diluted to 0.5 mg/mL with PBS. The diluted LUV solution was passed through the flow cells through the secondary inlet for 30 min (10 μL/min; primary inlet 1 μL/min PBS) to allow adsorption and rupture of the vesicles on the chips. The chips were then washed with Milli-Q (100 μL/min secondary inlet, 10 μL/min primary inlet), after which freshly prepared 0.5 mM hydroxymethylferrocene (FcMeOH, Acros Organics) was passed through the device (50 μL/min, both inlets). A potential difference of 2.0 V was applied over the device for 30 min to induce electrophoresis in the SLBs. Subsequently, the chips were cooled rapidly on a heat exchanger to fix the surface gradient. The flow cells were then rinsed with Milli-Q. Bovine serum albumin (SigmaAldrich) 50 mg/mL (0.5 mL, 10 μL/min) was passed through the flow cells to form an antifouling layer on the tubing. The flow cells were rinsed with PBS. SAv with Alexa Fluor 488 label (Thermo Fischer) 20 μg/mL was passed through the secondary inlet (10 μL/min, primary inlet 1 μL/min). The flow cells were rinsed with PBS. The SAv-modified SLBs were inspected with fluorescence microscopy on an Olympus inverted IX71 epi-fluorescence research microscope with X-cite 120PC mercury vapor lamp as light source and a digital Olympus DR70 camera for image acquisition. For Alexa Fluor 488, blue excitation (460 ≤ λex ≤ 490 nm) and green emission (505 ≤ λem ≤ 545 nm) was filtered using the U-MWG2 Olympus filter cube. Glycan 2,6-S(LN)3-biotin 500 nM solutions were passed through the primary inlet (10 μL/min, secondary inlet 1 μL/min), after which the flow cells were rinsed with PBS. During all steps, care was taken to ensure that no air bubbles entered the flow cell.

Binding Studies

Solutions of IAV Puerto Rico/8/1934 mt. Sinai with R18 label were prepared in PBS with 200 μM Zanamivir (GlaxoSmithKline). The virus solution in the desired concentration was passed through the primary inlet of the flow cells at the desired flow rate with the secondary inlet PBS at 10% of the flow rate through the primary inlet. The bound virus was imaged with fluorescence microscopy. For R18, green excitation (510 ≤ λex ≤ 550 nm) and red emission (λem > 590 nm) was filtered.

Image Analysis

8-bit RGB fluorescence micrographs were aligned and cropped into corrals using a custom-written MATLAB program. The fluorescence intensities of receptor and virus labels in matching pixels were listed. The receptor density and virus coverage in each pixel were calculated using eqs 1 and 2. Binding profiles were obtained by fitting eq 4 with Ki/NAVexplore as fitting parameter, using a gradient descend fitting method.

Statistical Comparisons

To determine the confidence interval of threshold receptor densities, point clouds from each corral were fitted individually. Corrals where no gradient had formed or where minimum and maximum virus binding could not be determined were omitted from analysis. Mean and standard deviation 95% confidence intervals for each group were determined for the fitted threshold receptor densities of all corrals in the group. To determine the value of the threshold receptor density in a group, point clouds from multiple corrals, from multiple positions in the microchannel and multiple experiments were combined into a single larger point cloud to which the fitting was performed after exclusion of outliers. This afforded a better fit than the average of each corral. The 95% confidence interval of the fit was without exception smaller than the 95% confidence interval over the threshold densities from all corrals in the group. Unless otherwise specified, the threshold receptor densities shown have been obtained from the combined point cloud with the 95% confidence interval over all corrals in the group. The significance of the differences in threshold receptor densities was determined with an analysis of variance followed by a multiple comparison test using the MATLAB functions anovan and multcompare.

Hazards

No unexpected or unusually high safety hazards were encountered.

Acknowledgments

This study was supported by the Volkswagen Foundation (FlapChips project) and The Netherlands Organization for Scientific Research (NWO, TOP 715.015.001). Nicholas Tito is thanked for his help with the theoretical models. Zeshi Li and Geert-Jan Boons are thanked for the synthesis of the glycans. Wouter Vijselaar is thanked for the cleanroom fabrication of the gradient chips. Annemarie Huijser and Willem Vos are thanked for discussions with regards to the fluorescence quantification. Nicole Zeijen and Bea Overeem-Quist are thanked for their help with statistics.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.1c00166.

  • MATLAB scripts and test set (ZIP), containing: Avidity.m calculates the multivalent equilibrium constant using eq 3; Avidity_defaults.m contains the default values for parameters such as virus size, virus concentration, and contact area; contourPlot.m is called upon in pointCloudToFit.m for the visualization of binding profiles; folderToPointCloud.m extracts the fluorescence intensity from corrals that are saved by tiffStackToFolder.m, normalizes the intensity using eqs 1 and 2, and saves point clouds for visualization and fitting; ginputc.m is a script by Jiro Doke used in tiffStackToFolder.m; param.m is used in pointCloudToFit.m to generate a table; pointCloud_YNormalization.m is used in folderToPointCloud.m to determine the minimum and maximum fluorescence intensity in a virus micrograph; pointCloudToFit.m visualizes a point cloud as binding profile using a rolling window average and fits eq 4 to the point cloud; runThisFile.m prompts to select a TIF file with a virus and receptor micrograph as two layers and executes the image analysis, data visualization, and fitting; Theta.m calculates the virus coverage using eq 4; tiffStackToFolder.m aligns fluorescence micrographs and allows the user to select corrals and background that are cropped and saved for analysis; tricontour.m is a script by DC.Hanselman used in pointCloud_YNormalization.m; Test set is a folder containing four TIF files which are two-image stacks of a virus and receptor micrograph that can be used as test files for runThisFile.m, tiffStackToFolder.m, and any derived scripts. COMSOL model to simulate the hydrodynamic forces on a bound virus in the microchannel (ZIP)

The authors declare no competing financial interest.

Supplementary Material

nn1c00166_si_001.zip (9.4MB, zip)

References

  1. Petrova V. N.; Russell C. A. The Evolution of Seasonal Influenza Viruses. Nat. Rev. Microbiol. 2018, 16, 47–60. 10.1038/nrmicro.2017.118. [DOI] [PubMed] [Google Scholar]
  2. Krammer F.; Smith G. J. D.; Fouchier R. A. M.; Peiris M.; Kedzierska K.; Doherty P. C.; Palese P.; Shaw M. L.; Treanor J.; Webster R. G.; García-Sastre A. Influenza. Nat. Rev. Dis. Prim. 2018, 4, 3. 10.1038/s41572-018-0002-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Benton D. J.; Martin S. R.; Wharton S. A.; McCauley J. W. Biophysical Measurement of the Balance of Influenza A Hemagglutinin and Neuraminidase Activities. J. Biol. Chem. 2015, 290, 6516–6521. 10.1074/jbc.M114.622308. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Paulson J. C.; de Vries R. P. H5N1 Receptor Specificity as a Factor in Pandemic Risk. Virus Res. 2013, 178, 99–113. 10.1016/j.virusres.2013.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Zhang W.; Shi Y.; Lu X.; Shu Y.; Qi J.; Gao G. F. An Airborne Transmissible Avian Influenza H5 Hemagglutinin Seen at the Atomic Level. Science 2013, 340, 1463–1467. 10.1126/science.1236787. [DOI] [PubMed] [Google Scholar]
  6. Di Iorio D.; Verheijden M. L.; van der Vries E.; Jonkheijm P.; Huskens J. Weak Multivalent Binding of Influenza Hemagglutinin Nanoparticles at a Sialoglycan-Functionalized Supported Lipid Bilayer. ACS Nano 2019, 13, 3413–3423. 10.1021/acsnano.8b09410. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Xiong X.; Coombs P. J.; Martin S. R.; Liu J.; Xiao H.; McCauley J. W.; Locher K.; Walker P. A.; Collins P. J.; Kawaoka Y.; Skehel J. J.; Gamblin S. J. Receptor Binding by a Ferret-Transmissible H5 Avian Influenza Virus. Nature 2013, 497, 392–396. 10.1038/nature12144. [DOI] [PubMed] [Google Scholar]
  8. Cuellar-Camacho J. L.; Bhatia S.; Reiter-Scherer V.; Lauster D.; Liese S.; Rabe J. P.; Herrmann A.; Haag R. Quantification of Multivalent Interactions between Sialic Acid and Influenza A Virus Spike Proteins by Single-Molecule Force Spectroscopy. J. Am. Chem. Soc. 2020, 142, 12181–12192. 10.1021/jacs.0c02852. [DOI] [PubMed] [Google Scholar]
  9. Reiter-Scherer V.; Cuellar-Camacho J. L.; Bhatia S.; Haag R.; Herrmann A.; Lauster D.; Rabe J. P. Force Spectroscopy Shows Dynamic Binding of Influenza Hemagglutinin and Neuraminidase to Sialic Acid. Biophys. J. 2019, 116, 1037–1048. 10.1016/j.bpj.2019.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hamming P. H.; Overeem N. J.; Huskens J. Influenza as a Molecular Walker. Chem. Sci. 2020, 11, 27–36. 10.1039/C9SC05149J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Vahey M. D.; Fletcher D. A. Influenza A Virus Surface Proteins are Organized to Help Penetrate Host Mucus. eLife 2019, 8, e43764. 10.7554/eLife.43764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Guo H.; Rabouw H.; Slomp A.; Dai M.; van der Vegt F.; van Lent J. W. M.; McBride R.; Paulson J. C.; de Groot R. J.; van Kuppeveld F. J. M.; de Vries E.; de Haan C. A. M. Kinetic Analysis of the Influenza A Virus HA/NA Balance Reveals Contribution of NA to Virus-Receptor Binding and NA-Dependent Rolling on Receptor-Containing Surfaces. PLoS Pathog. 2018, 14, e1007233. 10.1371/journal.ppat.1007233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. de Graaf M.; Fouchier R. A. M. Role of Receptor Binding Specificity in Influenza A Virus Transmission and Pathogenesis. EMBO J. 2014, 33, 823–841. 10.1002/embj.201387442. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Yamada S.; Suzuki Y.; Suzuki T.; Le M. Q.; Nidom C. A.; Sakai-Tagawa Y.; Muramoto Y.; Ito M.; Kiso M.; Horimoto T.; Shinya K.; Sawada T.; Kiso M.; Usui T.; Murata T.; Lin Y.; Hay A.; Haire L. F.; Stevens D. J.; Russell R. J.; Gamblin S. J.; Skehel J. J.; Kawaoka Y. Haemagglutinin Mutations Responsible for the Binding of H5N1 Influenza A Viruses to Human-Type Receptors. Nature 2006, 444, 378–382. 10.1038/nature05264. [DOI] [PubMed] [Google Scholar]
  15. Overeem N. J.; Hamming P. H. E.; Grant O. C.; Di Iorio D.; Tieke M.; Bertolino M. C.; Li Z.; Vos G.; de Vries R. P.; Woods R. J.; Tito N. B.; Boons G.-J. P. H.; van der Vries E.; Huskens J. Hierarchical Multivalent Effects Control Influenza Host Specificity. ACS Cent. Sci. 2020, 6, 2311–2318. 10.1021/acscentsci.0c01175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Müller M.; Lauster D.; Wildenauer H. H. K.; Herrmann A.; Block S. Mobility-Based Quantification of Multivalent Virus-Receptor Interactions: New Insights into Influenza A Virus Binding Mode. Nano Lett. 2019, 19, 1875–1882. 10.1021/acs.nanolett.8b04969. [DOI] [PubMed] [Google Scholar]
  17. Martinez-Veracoechea F. J.; Frenkel D. Designing Super Selectivity in Multivalent Nano-Particle Binding. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 10963–10968. 10.1073/pnas.1105351108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Dubacheva G. V.; Curk T.; Mognetti B. M.; Auzély-Velty R.; Frenkel D.; Richter R. P. Superselective Targeting Using Multivalent Polymers. J. Am. Chem. Soc. 2014, 136, 1722–1725. 10.1021/ja411138s. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Curk T.; Tito N. B. First-Order ‘Hyper-Selective’ Binding Transition of Multivalent Particles under Force. J. Phys.: Condens. Matter 2020, 32, 214002. 10.1088/1361-648X/ab6d12. [DOI] [PubMed] [Google Scholar]
  20. Scheepers M. R. W.; van IJzendoorn L. J.; Prins M. W. J. Multivalent Weak Interactions Enhance Selectivity of Interparticle Binding. Proc. Natl. Acad. Sci. U. S. A. 2020, 117, 22690–22697. 10.1073/pnas.2003968117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Dam T. K.; Brewer C. F. Lectins as Pattern Recognition Molecules: The Effects of Epitope Density in Innate Immunity. Glycobiology 2010, 20, 270–279. 10.1093/glycob/cwp186. [DOI] [PubMed] [Google Scholar]
  22. Vachieri S. G.; Xiong X.; Collins P. J.; Walker P. a; Martin S. R.; Haire L. F.; Zhang Y.; McCauley J. W.; Gamblin S. J.; Skehel J. J. Receptor Binding by H10 Influenza Viruses. Nature 2014, 511, 475–477. 10.1038/nature13443. [DOI] [PubMed] [Google Scholar]
  23. Smith D. F.; Cummings R. D. Investigating Virus-Glycan Interactions Using Glycan Microarrays. Curr. Opin. Virol. 2014, 7, 79–87. 10.1016/j.coviro.2014.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. McQuillan A. M.; Byrd-Leotis L.; Heimburg-Molinaro J.; Cummings R. D. Natural and Synthetic Sialylated Glycan Microarrays and Their Applications. Front. Mol. Biosci. 2019, 6, 88. 10.3389/fmolb.2019.00088. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Stevens J.; Blixt O.; Tumpey T. M.; Taubenberger J. K.; Paulson J. C.; Wilson I. A. Structure and Receptor Specificity of the Hemagglutinin from an H5N1 Influenza Virus. Science 2006, 312, 404–410. 10.1126/science.1124513. [DOI] [PubMed] [Google Scholar]
  26. Stevens J.; Blixt O.; Glaser L.; Taubenberger J. K.; Palese P.; Paulson J. C.; Wilson I. A. Glycan Microarray Analysis of the Hemagglutinins from Modern and Pandemic Influenza Viruses Reveals Different Receptor Specificities. J. Mol. Biol. 2006, 355, 1143–1155. 10.1016/j.jmb.2005.11.002. [DOI] [PubMed] [Google Scholar]
  27. Blixt O.; Head S.; Mondala T.; Scanlan C.; Huflejt M. E.; Alvarez R.; Bryan M. C.; Fazio F.; Calarese D.; Stevens J.; Razi N.; Stevens D. J.; Skehel J. J.; van Die I.; Burton D. R.; Wilson I. a; Cummings R.; Bovin N.; Wong C.-H.; Paulson J. C. Printed Covalent Glycan Array for Ligand Profiling of Diverse Glycan Binding Proteins. Proc. Natl. Acad. Sci. U. S. A. 2004, 101, 17033–17038. 10.1073/pnas.0407902101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Yen H.-L.; Liang C.-H.; Wu C.-Y.; Forrest H. L.; Ferguson A.; Choy K.-T.; Jones J.; Wong D. D.-Y.; Cheung P. P.-H.; Hsu C.-H.; Li O. T.; Yuen K. M.; Chan R. W. Y.; Poon L. L. M. M.; Chan M. C. W. W.; Nicholls J. M.; Krauss S.; Wong C.-H.; Guan Y.; Webster R. G.; Webby R. J.; Peiris M. Hemagglutinin-Neuraminidase Balance Confers Respiratory-Droplet Transmissibility of the Pandemic H1N1 Influenza Virus in Ferrets. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 14264–14269. 10.1073/pnas.1111000108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Van Dover R. B.; Schneemeyer L. F.; Fleming R. M. Discovery of a Useful Thin-Film Dielectric Using a Composition-Spread Approach. Nature 1998, 392, 162–164. 10.1038/32381. [DOI] [Google Scholar]
  30. Suresh S. Graded Materials for Resistance to Contact Deformation and Damage. Science 2001, 292, 2447–2451. 10.1126/science.1059716. [DOI] [PubMed] [Google Scholar]
  31. Fisher S. A.; Tam R. Y.; Fokina A.; Mahmoodi M. M.; Distefano M. D.; Shoichet M. S. Photo-Immobilized EGF Chemical Gradients Differentially Impact Breast Cancer Cell Invasion and Drug Response in Defined 3D Hydrogels. Biomaterials 2018, 178, 751–766. 10.1016/j.biomaterials.2018.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Tanes M. L.; Xue J.; Xia Y. A General Strategy for Generating Gradients of Bioactive Proteins on Electrospun Nanofiber Mats by Masking with Bovine Serum Albumin. J. Mater. Chem. B 2017, 5, 5580–5587. 10.1039/C7TB00974G. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Van Weerd J.; Sankaran S.; Roling O.; Sukas S.; Krabbenborg S.; Huskens J.; le Gac S.; Ravoo B. J.; Karperien M.; Jonkheijm P. A Microfluidic Device with Continuous Ligand Gradients in Supported Lipid Bilayers to Probe Effects of Ligand Surface Density and Solution Shear Stress on Pathogen Adhesion. Adv. Mater. Interfaces 2016, 3, 1600055. 10.1002/admi.201600055. [DOI] [Google Scholar]
  34. Tong W.; Yao X.; Duan S.; Yu B.; Ding X.; Ding X.; Xu F.-J. Gradient Functionalization of Various Quaternized Polyethylenimines on Microfluidic Chips for the Rapid Appraisal of Antibacterial Potencies. Langmuir 2020, 36, 354–361. 10.1021/acs.langmuir.9b02747. [DOI] [PubMed] [Google Scholar]
  35. Huang M. L.; Cohen M.; Fisher C. J.; Schooley R. T.; Gagneux P.; Godula K. Determination of Receptor Specificities for Whole Influenza Viruses Using Multivalent Glycan Arrays. Chem. Commun. 2015, 51, 5326–5329. 10.1039/C4CC08613A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Nicosia C.; Krabbenborg S. O.; Chen P.; Huskens J. Shape-Controlled Fabrication of Micron-Scale Surface Chemical Gradients via Electrochemically Activated Copper(I) ‘Click’ Chemistry. J. Mater. Chem. B 2013, 1, 5417–5428. 10.1039/c3tb20902d. [DOI] [PubMed] [Google Scholar]
  37. Krabbenborg S. O.; Nicosia C.; Chen P.; Huskens J. Reactivity Mapping with Electrochemical Gradients for Monitoring Reactivity at Surfaces in Space and Time. Nat. Commun. 2013, 4, 1667. 10.1038/ncomms2688. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Van Weerd J.; Krabbenborg S. O.; Eijkel J.; Karperien M.; Huskens J.; Jonkheijm P. On-Chip Electrophoresis in Supported Lipid Bilayer Membranes Achieved Using Low Potentials. J. Am. Chem. Soc. 2014, 136, 100–103. 10.1021/ja411287u. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Krabbenborg S. O.; van Weerd J.; Karperien M.; Jonkheijm P.; Huskens J. Locked-In Biomimetic Surface Gradients that Are Tunable in Size, Density and Functionalization. ChemPhysChem 2014, 15, 3460–3465. 10.1002/cphc.201402509. [DOI] [PubMed] [Google Scholar]
  40. Overeem N. J.; Hamming P. H.; Huskens J. Time-Dependent Binding of Molecules and Nanoparticles at Receptor-Modified Supported Lipid Bilayer Gradients in a Microfluidic Device. ChemistrySelect 2020, 5, 9799–9805. 10.1002/slct.202002593. [DOI] [Google Scholar]
  41. Jansen A. J. G.; Spaan T.; Low H. Z.; Di Iorio D.; van den Brand J.; Tieke M.; Barendrecht A.; Rohn K.; van Amerongen G.; Stittelaar K.; Baumgärtner W.; Osterhaus A.; Kuiken T.; Boons G.-J.; Huskens J.; Boes M.; Maas C.; van der Vries E. Influenza-Induced Thrombocytopenia is Dependent on the Subtype and Sialoglycan Receptor and Increases with Virus Pathogenicity. Blood Adv. 2020, 4, 2967–2978. 10.1182/bloodadvances.2020001640. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Hinrichsen E. L.; Feder J.; Jøssang T. Random Packing of Disks in Two Dimensions. Phys. Rev. A: At., Mol., Opt. Phys. 1990, 41, 4199–4209. 10.1103/PhysRevA.41.4199. [DOI] [Google Scholar]
  43. Dubacheva G. V.; Araya-Callis C.; Geert Volbeda A.; Fairhead M.; Codée J.; Howarth M.; Richter R. P. Controlling Multivalent Binding through Surface Chemistry: Model Study on Streptavidin. J. Am. Chem. Soc. 2017, 139, 4157–4167. 10.1021/jacs.7b00540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Nagle J. F.; Tristram-Nagle S. Structure of Lipid Bilayers. Biochim. Biophys. Acta, Rev. Biomembr. 2000, 1469, 159–195. 10.1016/S0304-4157(00)00016-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Harris A.; Cardone G.; Winkler D. C.; Heymann J. B.; Brecher M.; White J. M.; Steven A. C. Influenza Virus Pleiomorphy Characterized by Cryoelectron Tomography. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 19123–19127. 10.1073/pnas.0607614103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Benton D. J.; Wharton S. A.; Martin S. R.; McCauley J. W. Role of Neuraminidase in Influenza A(H7N9) Virus Receptor Binding. J. Virol. 2017, 91, e02293–16. 10.1128/JVI.02293-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Di Iorio D.Designer Surfaces for the Quantification of Multivalent Biological Interactions; Ph.D. Dissertation; University of Twente, Enschede, The Netherlands, 2019. 10.3990/1.9789036548199. [DOI] [Google Scholar]
  48. Nir G.; Chetrit E.; Vivante A.; Garini Y.; Berkovich R. The Role of Near-Wall Drag Effects in the Dynamics of Tethered DNA under Shear Flow. Soft Matter 2018, 14, 2219–2226. 10.1039/C7SM01328K. [DOI] [PubMed] [Google Scholar]
  49. Brown D. L.Cardiovascular Plaque Rupture; CRC Press: Boca Raton, 2002. [Google Scholar]
  50. Button B.; Boucher R. C. Role of Mechanical Stress in Regulating Airway Surface Hydration and Mucus Clearance Rates. Respir. Physiol. Neurobiol. 2008, 163, 189–201. 10.1016/j.resp.2008.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Button B. M.; Button B. Structure and Function of the Mucus Clearance System of the Lung. Cold Spring Harbor Perspect. Med. 2013, 3, a009720. 10.1101/cshperspect.a009720. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Vanaki S. M.; Holmes D.; Jayathilake P. G.; Brown R. Three-Dimensional Numerical Analysis of Periciliary Liquid Layer: Ciliary Abnormalities in Respiratory Diseases. Appl. Sci. 2019, 9, 4033. 10.3390/app9194033. [DOI] [Google Scholar]
  53. Rimmelzwaan G. F.; Baars M.; Claas E. C. J.; Osterhaus A. D. M. E. Comparison of RNA Hybridization, Hemagglutination Assay, Titration of Infectious Virus and Immunofluorescence as Methods for Monitoring Influenza Virus Replication in Vitro. J. Virol. Methods 1998, 74, 57–66. 10.1016/S0166-0934(98)00071-8. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn1c00166_si_001.zip (9.4MB, zip)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES