Fenchel duality of Cox partial likelihood with an application in survival kernel learning

Abstract

The Cox proportional hazard model is one of the most widely used methods in modeling time-to-event data in the health sciences. Due to the simplicity of the Cox partial likelihood function, many machine learning algorithms use it for survival data. However, due to the nature of censored data, the optimization problem becomes intractable when more complicated regularization is employed, which is necessary when dealing with high dimensional omic data. In this paper, we show that a convex conjugate function of the Cox loss function based on Fenchel duality exists, and provide an alternative framework to optimization based on the primal form. Furthermore, the dual form suggests an efficient algorithm for solving the kernel learning problem with censored survival outcomes. We illustrate performance and properties of the derived duality form of Cox partial likelihood loss in multiple kernel learning problems with simulated and the Skin Cutaneous Melanoma TCGA datasets.

1. Introduction

Time to an event analysis has become one of the most important topics in many fields of medicine, especially cancer studies. Cancer treatments are developed with extend patients lives as their primary focus outcomes of interest can include time to recurrence, progression, or overall survival time[1, 2, 3, 4]. Some of other examples might be related to the progression of a disease such as mild cognitive impairment to Alzheimer’s disease[5, 6] or diabetes[7, 8], or A main challenge in time to event analyses is that patients are not diagnosed, or do not start the treatment at the same time but the patients are studied until a fixed time point. At the end of the study, it is unknown how long it takes for the event of interest to occur in each patient, but they provide useful information, namely that the time until the event is greater than some length of time. There have been studies that have simply dichotomized the sample based on whether the event occurred after certain length of time or if the event did occur before the specified time, and remove patients that were not studied for that length of time. This analysis can lead to biased results, does not utilize the fact all patients were studied for some length of time, and eliminates the magnitude/ordering of the times. Additionally, the cut point used dichotimize patients is arbitrary and often times there may not be a clinical or biological justification for a particular cutoff. Due to these challenges, many statistical models and machine learning algorithms have been developed to address these issues [9, 10]. There are several models and a variety of techniques to deal with censored data and in this paper we present an alternative approach using multiple kernel learning. Implementation of our MKL approach will be publicly available in RMKL package on CRAN, and on github https://github.com/cwilso6/RMKL.

The two most widely utilized models for censored survival data are the Cox proportional hazard (PH) model [11] and accelerated failure time (AFT), due to their flexibility and efficiency [12]. Cox PH models are the most widely used model in health and clinical sciences, while the AFT model is more popular in engineering. The Cox model is a semi-parametric regression method where no assumptions are imposed on the baseline hazard function and it assumes the effect of a feature is proportional to the baseline, λ(t|X_i) = λ₀(t)exp(X_iβ) where λ(t|X_i) is the hazard function for subject i with feature vector X_i at time t and λ₀ is the baseline hazard. This allows us to conduct hypothesis tests on the coefficients, as well as, interpretation of the effects. The parametric regression coefficients quantify the effect size of each covariate and the exponential of the coefficient is interpreted as the unit increase of the hazard ratio. The Cox model works well in practice because it can tolerate a modest deviation from the PH assumption. The partial likelihood in the Cox model is defined as the probability that one individual will experience the event at a time t among those who have survived longer than t. It was shown that maximizing the partial likelihood provides an asymptotically efficient estimation of regression coefficients [13]. The Cox model has been successfully extended to various high-dimensional settings, where the number of features is more than the number of samples. Additionally, the log partial likelihood (LPL) is differentiable and convex. Thus the Cox LPL coupled with ℓ1 (lasso), ℓ2 (ridge), or elastic net penalties can be directly solved by standard Newton-Rapshon method. These forms can generically be written as

$$\min \{L(\mathbf{X},\beta )+R(\beta )\},$$ (1.1)

where L is the Cox partial likelihood function, R is a regularization function, and β is the vector of coefficients. Furthermore, the convex combined loss function often guarantees the convergence of efficient optimization algorithms including coordinate descent [14], which is the core algorithm implemented in glmnet R package. The Cox LPL has also been adopted in many machine learning approaches as a loss function to the survival setting. For example, Ridgeway [15] adapted the gradient boosting method for the Cox model. Li and Luan [16] also considered a boosting procedure using smoothing splines to estimate the proportional hazards models. Despite this flexibility, it is difficult to use Cox models in an integrative way such that multiple data sources are used independently to estimate the hazard ratios.

Kernel methods, specifically support vector regression, have been utilized in regression settings and can transform a high dimensional problem to a problem 40 that relies only a similarity of each subject. In other words, convert a problem where n << p to the optimization based on a n × n matrix, where n and p are the number of samples and feature, respectively. Li and Luan [17] developed a SVR based kernel Cox regression framework for survival data. There have been many recent developments in kernel regression, specifically the development of multiple kernel learning (MKL) which can estimate a regression function with a convex combination of several kernels. By learning an convex combination of kernels, MKL can eliminate cross validation for finding the best kernel shape and hyperparamaters, and can allow for the integration of multiple high thoughput data source or allow for grouping of biologically related features. Additionally, MKL has the flexibility to utilize ℓ1, ℓ2, and elastic net regularization on the kernel weight in an analogous way as penalized regression.

In this paper, we follow the framework used to develop SpicyMKL[18] in order to extend MKL to a survival setting. To that end, we derive the Fenchel dual form of Cox partial likelihood, which is a key step in the implementation of machine learning approaches for survival outcomes that can incorporate multiple high throughput data sources. Optimizing the dual problem is a common strategy in machine learning and is commonly used in nonlinear programming and convex optimization to provide an approximation for the optimal value of the primal problem. It is often easier to optimize the dual problem and it has fewer variables in the high dimensional setting. The resulting function, called Fenchel conjugate, is always convex regardless of the convexity of the original function. Note that the Lagrangian and Fenchel dual are defined under different contexts, even though many Lagrangian duals can be derived from Fenchel conjugate functions. In many cases, both of them are referred to as a “dual problem”. The Lagrangian duality form is defined within the context of the optimization problem (often with constraints), while the Fenchel form is more general and is defined for any function. Our work is motivated by the need to bridge the gap between modern machine learning techniques and survival models. To apply methods like SVM, survival data are often dichotomized with a cutoff time point. Such a method will yield biased results because censored data points are excluded from the analysis, additionally, the results will be affected by different cutoff values.

The remainder of the paper is organized as follows. In Section 2, we review the Cox proportional hazard model and Fenchel duality. In Section 3, we derive a conjugate function for the Cox model. We perform simulations in Section 4 to demonstrate the usage of the derived form in the multiple kernel learning. We analyze both Skin Cutaneous Melanoma (SKCM) gene and miRNA expression data from The Cancer Genome Atlas (TCGA). Finally we conclude with a discussion in Section 6.

2. Methods

2.1. Cox proportional hazard model and partial likelihood

The Cox PH model relates the covariates to the hazard function of the outcome at time t using the following equation,

$$h_i(t)=h_0(t)\exp \left\{\langle {\mathbf{x}}_i,\mathit{\beta }\rangle \right\},$$ (2.1)

where h₀(t) is the baseline hazard function at time t and x_i is the vector of predictor variables for the i^th subject [11] The partial likelihood is expressed as

$$PL=\prod _{i\in D}\frac{\exp \left(\langle {\mathbf{x}}_i,\mathit{\beta }\rangle \right)}{{\sum }_{l\in R}\exp \left(\langle {\mathbf{x}}_l,\mathit{\beta }\rangle \right)}=\prod _{i\in D}\frac{\exp \left(\langle {\mathbf{x}}_i,\mathit{\beta }\rangle \right)}{{\sum }_{l\in R}I\left(t_l\ge t_j\right)\exp \left(\langle {\mathbf{x}}_l,\mathit{\beta }\rangle \right)},$$ (2.2)

where D is the set of uncensored subjects and R is the set of the observations at risk at time t. An appealing property of the PL is that the regression coefficients estimates are obtained without parametric assumptions about the baseline hazard function. The PL can be understood as constructing the conditional probability that the event occurs to a particular subject at time t. Typically, we optimize the negative log of Cox PL 2.2,

$$\mathcal{L}=-\log (PL)=-\sum _{i=1}^n{\delta }_i\left(\langle {\mathbf{x}}_i,\mathit{\beta }\rangle -\log \sum _{l\in R}\exp \left(\langle {\mathbf{x}}_l,\mathit{\beta }\rangle \right)\right),$$

where δ is the event indicator. It can be shown that $\mathcal{L}$ is convex and thus obtaining the regression coefficients that minimize $\mathcal{L}$ can be conducted by using gradient based methods. This framework can be extended to penalized regression by adding a regularization term to $\mathcal{L}$. For example, the lasso solution of regression coefficients corresponds to $\widehat{\beta }={\mathrm{argmin}}_{\beta }(\mathcal{L}(\beta )+R(\beta ))$, where R(β) denotes the regularization terms applied to constrain coefficients, such as the ℓ1/ℓ2 or group lasso penalty terms [19].

2.2. Multiple Kernel Learning

The traditional Cox regression framework assumes a linear relationship between predictors and the survival time. However, in reality, the relationship is far more complex. Meanwhile, nonlinear models are often hard to analyze and interpret. Kernel methods are non-parametric methods that utilize reproducing kernel Hilbert space (RKHS) [20, 21], and provide a useful alternative to linear or nonlinear models. Kernel functions map a predictor matrix from n × p to n × n. Thus the complexity of the feature space can be avoided and we can focus on a linear relationship between a similarity measure. For instance, using polynomial kernel (K(x, y) = (〈x, y〉+c)^d), we can map a circle boundary problem to a linear boundary problem, which dramatically reduces our computation cost. Some common kernels that are used for continuous variables, especially high throughput genomic data, are:

• Linear $K(x,y)=\langle x,y\rangle$

• Polynomial $K(x,y)={(\langle x,y\rangle +c)}^d$

• Radial Basis functions $K(x,y)=\exp \left\{-\sigma \Vert x-y{\Vert }^2\right\},$

where x and y are two samples, c is an offset parameter, and σ controls the radius of the kernel[22, 23]. These will be the types of kernels that will be considered in Section 4. There has also been substantial work to develop kernels for a network structure utilizing the Laplacian matrix L = D − A, where A is the adjacency matrix and D is the degree matrix. An advantage of this kernel is that known biology, such regulatory pathway membership, can be exploited[24]. The Laplacian will be studied when we consider high dimensional data in Section 5.

The exact relationships between predictions and outcomes are unknown, hence selecting an optimal kernel function presents a challenge. There are no clear rules for selecting a single optimal kernel, but cross-validation is usually implemented[25, 26, 27]. An interesting property of kernels is that a linear combination of two kernel functions results in another kernel function [20]. Many methods utilize this fact and have shown that convex combinations of multiple kernels can provide more accurate classifiers than single kernels[25, 28, 18]. Learning the optimal kernel weights is referred to as multiple kernel learning (MKL).

Under the MKL framework, we can denote our target problem as

$$\underset{\alpha }{\mathrm{argmin}}\left(L(\overline{K}\alpha +b)+{\varphi }_C(\alpha )\right),$$ (2.3)

where L(·) is the loss function of Cox proportional hazards model, $\overline{K}=\left(K_1,\cdots ,K_M\right)$ are a set of kernels, α is the coefficient matrix for each kernels, b is an offset parameter, and ϕ_C (·) is the regularized term for coefficients matrix. In this paper we use elastic net (EN) penalty which can be written as

$${\varphi }_C(\alpha )=\sum _{m=1}^M{\varphi }_C^{(m)}\left({\alpha }_m\right)=C\sum _{m=1}^M\left[(1-\lambda ){\Vert {\alpha }_m\Vert }_{K_m}+\frac{\lambda }{2}{\Vert {\alpha }_m\Vert }_{K_m}^2\right].$$ (2.4)

where λ ∈ [0,1] defines the amount of weight is assigned to the ℓ2 and ℓ1 regularizer, α_m corresponds to the value of α at the m^th iteration of the algorithm and C is a multiplier that changes the impact prediction error on the objective function in 2.3. The EN penalty allows us to strike a balance between the ℓ1 and ℓ2 regularization. In other words, it allows for sparse selection that the coefficients for non-informative kernels will be shrunk to zeros referred to as group property, and the coefficients for similar kernels tend to be close, which would return a consistent result [18, 29]. For instance, genes that are members of the same pathway can be forced to have the same coefficients in the final model by making a kernel for each pathway we intend to study. The elastic net penalty is non-smooth, we can use the theory of Moreau’s envelope function obtain the approach to solve this problem.

2.3. Moreau Envelope and Elastic Net

A challenge of regularized regression is that many of the penalties imposed are not smooth which can lead to issues for gradient descent. The Moreau envelope function allows us to approximate a non-smooth function with a smooth function leading to simpler optimization task. Let $g:{ℝ}^n\to ℝ$ be a function, for every γ > 0 we define the Moreau envelope as

$$e_{\gamma }g(x)=\underset{y}{\inf }\left\{g(y)+\frac{1}{2\gamma }\Vert x-y{\Vert }^2\right\}.$$ (2.5)

The Moreau envelope strikes a balance between function approximation accuracy and smoothness through the parameter γ. Additionally, if $e_{\gamma }g(x)$ is differentiable and the smooth derivative is given by

$$\nabla e_{\gamma }g(x)={\gamma }^{-1}(Id-prox(y\mid g)),$$ (2.6)

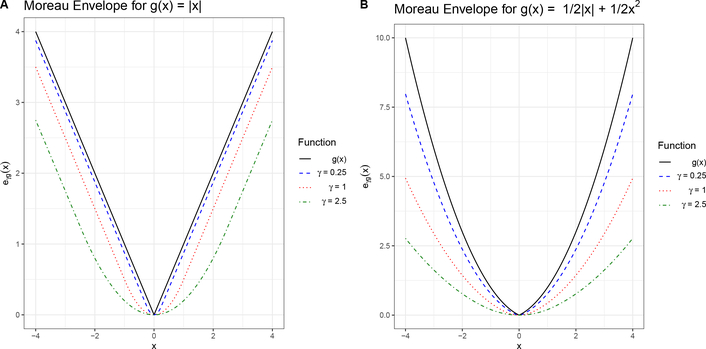
where Id is the identity function[30]. An example of the Moreau envelope, for the lasso regularization, is shown in Figure 1A. As γ increases the approximation of the function becomes worse and the shape of the function around x = 0 is increasingly rounded.

Figure 1:

Moreau envelope for (A lasso regularizer g(x) = |x| for several values of smoothing parameter γ, and (B) elastic net regularizer g(x) = 1/2|x| + 1/2ײ. Notice that as the value for γ increases we obtain a function that is more smooth, but a worse approximation of g(x).

Now we apply the concept of the Moreau envelope to the EN. We set x = α_m and $y={\alpha }_m^{\prime }$ from 2.6 resulting in

$$prox\left({\alpha }_m\mid {\varphi }_C^{(m)}\right)=\underset{{\alpha }_m^{\prime }\in R^N}{\mathrm{argmin}}\left(Cg\left({\Vert {\alpha }_m^{\prime }\Vert }_{K_m}^2\right)+\frac{1}{2\gamma }{\Vert {\alpha }_m^{\prime }-{\alpha }_m\Vert }_{K_m}^2\right),$$ (2.7)

where $g(x)=(1-\lambda )\sqrt{x}+\frac{\lambda }{2}x$.

Using Cauchy-Schwarz inequality we have

$${\tilde{g}}_C\left({\Vert {\alpha }_m^{\prime }\Vert }_{K_m}\right)+\frac{1}{2\gamma }{\Vert {\alpha }_m^{\prime }-{\alpha }_m\Vert }_{K_m}^2\ge {\tilde{g}}_C\left({\Vert {\alpha }_m^{\prime }\Vert }_{K_m}\right)+\frac{1}{2\gamma }{\left({\Vert {\alpha }_m^{\prime }\Vert }_{K_m}-{\Vert {\alpha }_m\Vert }_{K_m}\right)}^2.$$

Therefore, we can obtain the minimum solution that

$$\begin{gathered} {\Vert {\alpha }_m^{\prime }\Vert }_{K_m}=\underset{x\ge 0}{\mathrm{argmin}}\left({\tilde{g}}_C(x)+\frac{1}{2\gamma }{\left(x-{\Vert {\alpha }_m\Vert }_{K_m}\right)}^2\right) \\ =prox\left({\Vert {\alpha }_m\Vert }_{K_m}\mid {\tilde{g}}_C\right)=\{\begin{array}{ll}0\hfill & {\Vert {\alpha }_m\Vert }_{K_m}\le C(1-\lambda )\hfill \\ \frac{{\gamma }^{-1}{\Vert {\alpha }_m\Vert }_{K_m}-C(1-\lambda )}{\left(C\lambda +{\gamma }^{-1}\right){\Vert {\alpha }_m\Vert }_{K_m}}{\alpha }_m\hfill & \text{else,}\hfill \end{array} \end{gathered}$$

where prox (·) is known as the soft operator, see 1B. The Moreau envelope approximation of a function allows us obtain a smooth estimate for the elastic net loss function, allowing us to conduct minimization using gradient descent.

2.4. Fenchel duality

The fenchel duality is a freamework that transforms that optimization of (2.3) into a more tractable problem. The fenchel dual is differentiable and thus coordinatewise optimization is efficient. Suppose we have a function f (x) on Rⁿ, then the Fenchel convex conjugate of f (x) is defined as

$$f^{*}(\rho )=\underset{x\in R^n}{\sup }\left({\rho }^{*}x-f(x)\right).$$

The mapping from f(.) to f^∗(.) defined above is also known as the Legendre-Fenchel transform. The convex conjugate function measures the maximum gap between line function ρ^Tx and original function f (x), where each pair of (ρ, f^∗ (ρ)) corresponds to a tangent line of the original function f (x). The resulting function f^∗ has the nice property to be always convex, because it is the supremum of affine functions. Figure 2 illustrates how the conjugate dual for f(x) = |x| is derived. Note in Figure 1A, when |ρ| > 1 that as x → ∞ then |ρ|x → ∞, thus sup_x{ρx − |x|} = ∞. Alternatively, when |ρ| ≤ 1 that |ρ|x ≤ x for all x, hence the largest value for sup_x{ρx − |x|} = 0, when x = 0. The complex conjugate is illustrated in Figure 1B, which is a convex function. The conjugate function offers one important option for the dual problem that might be more tractable or computationally efficient than the primal problem.

Figure 2:

“Visvil derivation” of the complex conjugate function is computed. (A)-(C) Shows the proerties of ρx – f(x), where f(x) = |x| for particular values for ρ = 2, 1, 0.5. Notice that he diffrence between ρx and f(x) remains less than infinity only when |ρ| ≤ 1, while when ρ > 0, ρx increases faster than f(x). The final form of the convex conjugate is displayed in (D).

By Fenchel-Moreau theorem, f = f^∗∗ if only and only if f is a convex and and lower-semi continuous function which holds for Cox proportional hazards model 2.1. and f (·) and g (·) are convex, we have

$$\underset{x}{\inf }(f(x)+g(x))=\underset{y}{\text{sup}}\left(-f^{*}(y\right)-g^{*}(-y)).$$

Optimal solutions minimizing h(x) = f(x)+g(x) occur when ∇h = ∇f+∇g = 0 or when ∇f = −∇g. Hence, Fenchel duality theorem shows us that minimizing the summation of two convex function can be reduced to the problem of maximizing the gap between their parallel tangent lines since it is the lower bound of primary problem. In our case, both the Cox loss function and regularizer, elastic net (EN), are both convex. Then we can apply this theorem that our target problem 1.1 which reduces to the following problem

$$\max \left(-L^{*}(-\rho )-{\varphi }_C\left(\Vert \rho {\Vert }_{K_m}\right)\right)$$

where L^∗ and ϕ are the conjugate function of L and R, K_m Hilbert space that is generated by the reproducing kernel K_m, and ϕ.

3. SpicyMKL algorithm for Cox Proportional Hazard

In section 2, we introduced Frenchel’s dual which provides us with a way to estimate Cox proportional hazards model with an smooth approximated of a penalty function. SpicyMKL was introduced as an efficient implementation of MKL that could learn the best convex combination of potentially 1000 candidate kernels. In order to accomplish this the MKL problem was reformulated using the Moreau envelope and the convex conjugate to ensure that the sum of the loss and regularization penalties is a smooth and convex function [18]. SpicyMKL was introduced for multiple loss function and regularization function, but was not extended to the survival setting.

In our problem, we denote L^* (·) as the conjugate fumtion of the Cox loss function

$$\begin{gathered} L^{*}(-\rho )=\underset{z\in R^n}{\sup }\left({(-\rho )}^{T}z-L(z)\right) \\ =\{\begin{array}{ll}\hfill & {\rho }_i<{\delta }_i,i=1,\dots ,n,\text{and}\hfill \\ h(\rho )\hfill & {\sum }_{j=i}^n{\rho }_j<0,i=2,\dots ,n,\text{and}\hfill \\ \hfill & {\sum }_{j=1}^i{\rho }_j=0\hfill \\ +\infty \hfill & \text{else,}\hfill \end{array} \end{gathered}$$

where

$$\begin{gathered} h(\rho )=\sum _{i=1}^n\left({\delta }_i-{\rho }_i\right)\log \left({\delta }_i-{\rho }_i\right)-\sum _{i=1}^{n-1}{\rho }_i\log \left(\frac{{\prod }_{j=i+1}^n\left({\delta }_j-{\sum }_{k=j}^n{\rho }_k\right)}{{\prod }_{j=i+1}^n\left(-{\sum }_{k=j}^n{\rho }_k\right)}\right) \\ -\sum _{i=1}^n{\delta }_i\log \left({\delta }_i-\sum _{j=i}^n{\rho }_j\right), \end{gathered}$$

and $g_C={\sum }_{m=1}^M{g}_C^{(m)}$ is the conjugate function of the soft operator of the regularizer,

$$g_C^{(m)}\left(\Vert \rho {\Vert }_{K_m}\right)=\{\begin{array}{ll}0\hfill & \Vert \rho {\Vert }_{K_m}\le C(1-\lambda )\hfill \\ \frac{{\left[\Vert \rho {\Vert }_{K_m}-C(1-\lambda )\right]}^2}{2C\lambda }\hfill & \text{else.}\hfill \end{array}$$

A detailed derivation can be found in the supplemental materials. We can see that both L^∗ and g_C are twice differentiable, we can use Newton method to solve above questions.

The conjugate function of L is twice differentiable where the first derivative is given by

$$L_i^{{*}^{\prime }}=\{\begin{array}{ll}\log \left(\frac{{\prod }_{j=i+1}^n\left(-{\sum }_{k=j}^n{\rho }_k\right)}{\left({\delta }_i-{\rho }_i\right){\prod }_{j=i+1}^n\left({\delta }_j-\left({\sum }_{k=j}^n{\rho }_k\right)\right)}\right)\hfill & i<n\hfill \\ -\log \left({\delta }_n-{\rho }_n\right)\hfill & i=n\hfill \end{array}.$$ (3.1)

We can see that if j < i, the derivative with respect to the i^th component does not contain j, so the $L_{ij}^{{*}^{\prime }}=0$. If j > i, $L_{ij}^{{*}^{\prime }}=L_{ji}^{{*}^{\prime }}=0$. Hence the Hessian matrix of the conjugate function is diagonal matrix, then we can obtain by taking the second derivative,

$$L_{ij}^{*\prime \prime }=\{\begin{array}{ll}\frac{1}{{\delta }_i-{\rho }_i}\hfill & j=i\hfill \\ 0\hfill & j\ne i.\hfill \end{array}$$ (3.2)

We can calculate gradient and Hessian matrix of $g_C^{(m)}$ using (3.1) and (3.2) which are given by

$$\begin{gathered} g_C^{{(m)}^{\prime }}\left(\Vert \rho {\Vert }_{K_m}\right)=\{\begin{array}{ll}0\hfill & \Vert \rho {\Vert }_{K_m}\le C(1-\lambda )\hfill \\ \frac{\Vert \rho {\Vert }_{K_m}-C(1-\lambda )}{C\lambda }\hfill & \text{else.}\hfill \end{array} \\ {g}_C^{{(m)}^{\prime \prime }}\left(\Vert \rho {\Vert }_{K_m}\right)=\{\begin{array}{ll}0\hfill & \Vert \rho {\Vert }_{K_m}\le C(1-\lambda )\hfill \\ \frac{1}{C\lambda }\hfill & \text{else.}\hfill \end{array} \end{gathered}$$

We can see that the conjugate function is feasible if λ > 0, which means we can only use the smooth dual form for elastic net but not block one norm penalt The block one norm penalty is a kernelized version of group lasso [31, 32].

From derivation of the SpicyMKL algorithm, we have

$$\begin{gathered} {\nabla }_{\rho }{\varphi }^{*}\left(\Vert \rho {\Vert }_{K_m}\right)=\frac{K_m\rho }{\Vert \rho {\Vert }_{K_m}}{g}_C^{{(m)}^{\prime }}\left(\Vert \rho {\Vert }_{K_m}\right) \\ \nabla {\nabla }_{\rho }^{\prime }{\varphi }^{*}\left(\Vert \rho {\Vert }_{K_m}\right)=\left(\frac{K_m}{\Vert \rho {\Vert }_{K_m}}-\frac{K_m\rho {\rho }^{\prime }{K}_m}{\Vert \rho {\Vert }_{K_m}^3}\right)g_C^{{(m)}^{\prime }}\left(\Vert \rho {\Vert }_{K_m}\right) \\ +\frac{K_m\rho {\rho }^{\prime }{K}_m}{\Vert \rho {\Vert }_{K_m}^2}{g}_C^{{(m)}^{\prime \prime }}\left(\Vert \rho {\Vert }_{K_m}\right). \end{gathered}$$

Using Newton algorithm we can obtain the optimal $\widehat{\rho }$. As shown in the supplemental material, the step size of Newton update is given by the size that will not make the update of ρ goes beyond the domain of L*. To satisfy the ${\sum }_{i=1}^n{\rho }_i=0$ constraint for L^*, we added a penalty function $\frac{{10}^5}{2}{\left({\mathbf{1}}^{\prime }\rho \right)}^2$. Using Rockafellar[33] (Theorem 31.3), we have

$$\overline{K}\widehat{\alpha }=-{\nabla }_{\rho }{L}^{*}(-\widehat{\rho }).$$ (3.3)

Under Karush–Kuhn-Tucker (KKT) condition.

$$\begin{gathered} \nabla L^{*}(-\rho )=-\sum _{m=1}^M{\nabla }_{\rho }{g}_C^{(m)}\left(\Vert \widehat{\rho }{\Vert }_{K_m}\right) \\ =-\sum _{m=1}^M\frac{K_m\widehat{\rho }}{\Vert \widehat{\rho }{\Vert }_{K_m}}{g}_C^{{(m)}^{\prime }}\left(\Vert \widehat{\rho }{\Vert }_{K_m}\right), \end{gathered}$$

and the solution to (3.3) is

$$\Rightarrow {\widehat{\alpha }}_m=\frac{\widehat{\rho }}{\Vert \widehat{\rho }{\Vert }_{K_m}}{g}_C^{{(m)}^{\prime }}\left(\Vert \widehat{\rho }{\Vert }_{K_m}\right)$$

Next, we will illustrate theperformance of using multiple kernel learning in the cox proportional hazards setting. For the remainder of the paper, when we refer to regularization we will be discussing regularization of the kernel weight, as opposed to the individual features.

4. Simulation Data

4.1. Study of Overall Performance

To evaluate the performance of Multiple Kernel Cox regression (MKCox), we simulate data that are generated with different relationships between the features and the hazard function. Our simulations were inspired by Katzman [34]. We simplify these simulations to benchmark and explore the properties of MKCox. We simulate the features from a bivariate normal distribution, X = [X₁, X₂], with μ = 0, σ_X1 = σ_X2 = 1 and ρ = 0.5, an the following hazard function:

$$h(X)=X_1+2\ast X_2,\text{and}$$ (4.1)

$$h(X)=\log (\lambda )\exp \left(-\frac{\left(X_1^2+X_2^2\right)}{2\ast r^2}\right)$$ (4.2)

where λ = 5, and r = 1/2. Then the survival times are generated by:

$$T=-\frac{\log (u)}{\exp (h(X))},\text{where}u\sim U(0,1)$$

a censoring time is established, so that approximately 50% of patients have observed an event. Two kernels will be used in our illustration K₁ is the radial basis function with hyperparameter σ = 2, and K₂ is a linear kernel C = 0.05 and λ = 0.5. MKCox will be compared to the following methods random survival forest[35] (RF) implemented in randomForestSRC (2.9.0), stochastic gradient boosted[36] Cox regression (GBM) conducted in gbm (2.1.5), survival extreme learning machine[37] carried out using SurvELM (0.9.0). All our analyses were performed in R (3.6.0).

We aim to obtain a good estimate of the hazard function, as well as, maintain a good prediction of survival time. In Figures 3 and 4, we see that all methods can capture the structure of the hazard function when the underlying relationship is linear. Additionally, MKCox can recover the underlying patterns in the hazard function better than Cox regression and GBM, while both RSF and MKCox both capture the nonlinear pattern for accurately. To evaluate the performance of MKCox will compute popular metrics for survival models such as the concordance index. These results are shown in Table 1. Notice in the linear case that all methods provide similar concordance indices, while in the nonlinear case Cox performs substantially worse and MKCox slightly better than other machine learning methods. These simulations illustrate that MKCox can produce similar or better results under different underlying relationships between the hazard ratio and the features.

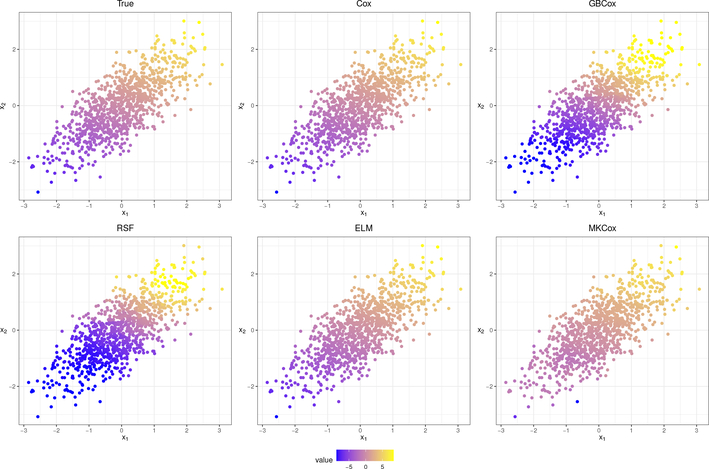
Figure 3:

True (top left) and estimated hazard function values for a realization from the model in (4.1), h(x) = x₁ + 2×₂. All five models capture the general trend of the hazard function, but Cox PH (Cox), extreme learning (ELM), and MKCox are the closer to the correct value than random survival forest (RSF) and gradiest boosting (GBCox).

Figure 4:

True (top left) and estimated hazard function values for a realization from the model in (4.2), h(x) = log(5)exp(−(x₁ + x₂/(2 * (1/2) * 2))). The gradient boosting (GBCox) and MKCox models are to capture some of the radial structure of the hazard function. Cox PH (Cox) estimate follows a gradient, extreme learning (ELM) appears to estimate similar values or ea ‘ observation, and the estimates from random survival forest (RSF) do not seem to follow a pattern.

Table 1:

Mean (standard deviation * 100) concordance index for each model for 100 simulations. GBM is bold because the standard error is lower than MKCox.

Dataset	Cox	MKCox	RF	GBM	SurvELM
Linear Simulation	0.869 (0.517)	0.873 (0.521)	0.863 (0.537)	0.873 (0.513)	0.871 (0.530)
Non-linear Simulation	0.513 (0.90)	0.659 (1.12)	0.598 (1.61)	0.625 (1.24)	0.587 (1.29)

To further the assess the performance MKCox, we conduct experiments in a high dimensional setting. One hundred datasets were simulated with 1000 observations and 500 features, where 25 features had a nonzero regression coefficient. Each feature was centered at 0 with unit variance and the covariance of the i and j feature is given by ${\mathrm{\Sigma }}_{ij}={0.5}^{|i-j|}$. This study was conducted considering two relationships between the hazard function and the features, (1) h(X) = Xβ, and (2) h(X) = log(5)exp(−Xβ/(2 ∗ (1/2)²)) where the nonzero elements of β were set to 1. Two kernels were used in MKCox where the first was a linear kernel and the second kernel was a radial kernel with σ = 2, and the MKCox parameters were set to C = 0.05 and λ = 0.5 for both sets of experiments. The SurvELM was implememnted using the ELMBoost function with a linear kernel was used for relationship (1) and radial kernel with a hyperparameter value of 2 was used for relationship (2). Table 2 and Figure 5 show the mean and boxplots of the concordance from SurvELM, GBM, RF, and MKCox. For the linear example (1), ELM has the lowest concordance, while GBM. RF, and MKCox have similar performance where GBM has a slightly higher average concordance than MKCox. On the other hand, MKCox has dramatically larger concordance than the other methods in the non-linear datasets (2). These experiments display the that MKCox can be used in high dimensional data setting and outperform existing machine learning techniques.

Table 2:

Mean concordance index for each model for 100 simulations with each dataset having 1000 observations and 500 features. The bolded values correspond the the largest concordance in the respective high dimensional setting.

Dataset	MKCox	RSF	GBM	SurvELM
Linear	0.885	0.891	0.897	0.850
Non-linear	0.755	0.495	0.572	0.541

Figure 5:

Box plots of the concordance resulting from the high dimensional experiments outlined in 4.1. The relationship between the hazard function and the features is linear (left) and nonlinear (right).

4.2. Properties of MKCox

In this section, we will illustrate the dual advantages of MKL. First it can be used as a variable selection technique, and second it can greatly reduce amount of cross validation, by learning the convex combination of kernels there is no need to do grid search over possible kernel parameters or shapes. Though cross validation is still needed to find an appropriate value for C. Here features are generated from a multivariate normal distribution, X = [X₁, X₂, X₃], with μ = 0, σ_X1 = σ_X2 = σ_X3 = 1 and X₁, X₂ and X₃ are independent. The following linear relationship between features and hazard function are assumed:

$$h(\mathbf{X})=X_1+2*X_2+0*X_3.$$

In this study, each kernel will be comprised of a single feature, where L₁, L₂, and L₃ will be linear kernels, and R₁, R₂, and R₃ are radial basis functions. Here L_i and R_i correspond the the linear and radial basis function kernels for the i^th feature. We will be studying three combinations of kernels: (1) all six kernels, (2) only the three linear kernels, and (3) only the three radial basis functions, where we vary the λ in the EN regularizer 2.4.

In scenario 1 and 3, we see that L₃ has the least weight, for λ < 1, which is to be expected since this variable had no impact on the hazard function. Note that L₁ tends to be assigned less weight than L₂ because L₁ has smaller impact on the hazard function than L₂. On the other hand, in scenarios 1 and 2, the kernel weights are uniform for R₁, R₂, and R₃ regardless of their regression coefficient and only using radial kernels leads to the worst performing models. We see that including both linear and radial kernels for each feature does lead to improved concordance. One might expect that only using linear kernels would be optimal but since survival times are censored radial kernels should be included. Across all of the scenarios, using uniform weights, λ = 1, appears to provide reasonable results but there can be modest improvements by reallocating the weights. This has also been observed in the using MKL in a classification setting [38].

5. Case Study

The Cancer Genome Atlas (TCGA) project is a large initiative to study the multiomics effect of gene expression RNAseq and stem loop expression on patients’ survival time[39, 40]. We downloaded the data from Genomic Data Commons (GDC) Data Portal. The latest survival data were downloaded using the TCGAbiolinks ([41]) package in R. The gene expression and miRNA expression data were downloaded from University of California at Santa Cruz (UCSC) Xena ([42]) (https://xena.ucsc.edu/) database. For gene expression, we used the fragments per kilobase of transcript per million mapped reads upper quartile FPKM-UQ) with log₂ (x + 1) transformation on mRNA via high-throughput sequencing (HTseq) ([43]) technique with gencode v22, while for stem loop expression, we used the per million mapped reads (RPM) with log₂ (x + 1) transformation via miRNA expression quantification technique aligned to GRCh38. In total, we have 235 dead and 215 alive (450 in total) patients. The code for data collection will be presented in supplemental materials Section 3.

Since we have two features sources (gene expression and stem loop expression), we kernelized the two feature sources separately using kernels with $K_i=X_i{L}_i^{-1}{X}_i$ where K_i, X_i and L_i are the kernel matrix, feature matrix and standardized Laplacian matrix for each feature source, respectively. So our model can be written as

$$l\left(\text{survival}\text{time,}\sum _{i=1}^2{K}_i{\alpha }_i\right)+C\left((1-\lambda )\sum _{i=1}^2{\Vert {\alpha }_i\Vert }_{K_i}+\frac{\lambda }{2}\sum _{i=1}^2{\Vert {\alpha }_i\Vert }_{K_i}^2\right)$$

which is equivalent to a linear grouped network regularized model

$$l\left(\text{survival}\text{time,}\sum _{i=1}^2{X}_i{\beta }_i\right)+C^{\prime }\left(\left(1-{\lambda }^{\prime }\right)\sum _{i=1}^2{\Vert {\beta }_i\Vert }_{L_i}+\frac{{\lambda }^{\prime }}{2}\sum _{i=1}^2{\Vert {\beta }_i\Vert }_{L_i}^2\right)$$

where ${\beta }_i=L_i^{-1}{\alpha }_i$ so that we can obtain the coefficient of feature i using this transformation. The Laplacian matrices were estimated empirically by neighbor network and coexpression network method proposed by [44].

To evaluate the performance we split that data into 301 training and 149 test samples, stratified by survival status (dead versus alive). The models we compared were all trained on training data and the results were obtained on test data. The parameters for our MKL model and GBM models were tuned by 5 fold cross-validation. From Table 4 we can see that our proposed multiple kernel learning using network kernels worked the best. Though it was a linear model, it achieved a higher concordance index than nonlinear tree-based models like the random forest, stochastic gradient boosting machine, and extreme learning methods. Due to the flexibility and efficiency of MKCox can incorporate many different kernel representations for multiple data types.

Table 4:

Concordance index results from SKCM data. Note that the traditional Cox model is included in this section to due to the high dimensionality of the data.

Dataset	MKCox	RF	GBM	SurvELM
SKCM	0.640	0.606	0.536	0.595

6. Conclusion

In this paper, we derived an efficient multiple kernel learning algorithm for survival prediction models and the convex conjugate function for Cox proportional hazards loss function. A challenge for deriving efficient algorithms for proportional hazard models is that the Hessian is not a diagonal matrix. However, through the convex conjugate function we can utilize the diagonal property to achieve a time competitive algorithm. Therefore, the Cox proportional hazards loss function can be more easily implemented than other machine learning methods.

Results from both the simulations and case study showed a robust performance of our proposed method in likelihood function estimation and how kernel weights can be interpreted. Simulations also show that MKCox can be used for feature selection, in sense that it can assign more importance to features that contribute more to the hazard function. It also illustrated that including radial kernels for each feature can increase the accuracy of the model even if the features have a linear relationship with hazard function. MKCox method showed superior in cancer genomic studies[45]. MKCox allows users to input and interpret several different high throughput data or gene sets to prioritize the importance of each source allowing for the opportunity for deeper biological impact. Future studies include extending the model to other more complex survival problems including competing risks.

Table 3:

Summary of scenarios 1–3, where the concordance from a standard Cox regression model was 0.845.

Scenario	λ	MKCox	R1	R2	R3	L1	L2	L3
1	1.00	0.877	0.167	0.167	0.167	0.167	0.167	0.167
	0.75	0.877	0.215	0.211	0.217	0.158	0.2	0
	0.50	0.879	0.239	0.226	0.243	0.098	0.194	0
	0.25	0.885	0.285	0.247	0.292	0.01	0.165	0
	0.00	0.835	0.201	0.203	0.198	0.186	0.212	0
2	1.00	0.836	0.333	0.333	0.333	-	-	-
	0.75	0.779	0.332	0.334	0.333	-	-	-
	0.50	0.723	0.331	0.333	0.335	-	-	-
	0.25	0.633	0.332	0.326	0.342	-	-	-
	0.00	0.719	0.334	0.337	0.329	-	-	-
3	1.00	0.847	-	-	-	0.333	0.333	0.333
	0.75	0.845	-	-	-	0.398	0.426	0.176
	0.50	0.844	-	-	-	0.407	0.475	0.118
	0.25	0.842	-	-	-	0.431	0.569	0
	0.00	0.843	-	-	-	0.393	0.607	0