Random effects models for complex designs

Abstract

Plaid designs are characterised by having one set of treatments applied to rows and another set of treatments applied to columns. In a 2003 publication, Farewell and Herzberg presented an analysis of variance structure for such designs. They presented an example of a study in which medical practitioners, trained in different ways, evaluated a series of videos of patients obtained under a variety of conditions. However, their analysis did not take full account of all error terms. In this paper, a more comprehensive analysis of this study is presented, informed by the recognition that the study can also be regarded as a two-phase design. The development of random effects models is outlined and the potential importance of block-treatment interactions is highlighted. The use of a variety of techniques is shown to lead to a better understanding of the study. Examination of the variance components involved in the expected mean squares is demonstrated to have particular value in identifying appropriate error terms for F-tests derived from an analysis of variance table. A package such as ASReml can also be used provided an appropriate error structure is specified. The methods presented can be applied to the design and analysis of other complex studies in which participants supply multiple measurements under a variety of conditions.

1 Introduction

At the simplest level, many studies involve randomly allocating people to treatment groups, making measurements and then undertaking an analysis to examine the size and significance of treatment effects. Solomon et al.¹ describe such a study in which medical practitioners, trained in different ways, evaluate a series of videos of patients obtained under a variety of conditions. The key questions in the study centre around the impact of training and how that impact might relate to the variety of conditions under which the videos are produced.

Examples similar to the Solomon et al.¹ study occur, for example, in agriculture, where a field experiment involving a number of crop varieties may be evaluated through a taste-testing experiment involving a large number of tasters each evaluating a relatively small number of varieties. Such studies, referred to as two-phase studies when introduced by McIntyre,² occur when material from a primary experiment is evaluated within a second experiment. These studies present significant challenges both at the design and the analysis stages and, particularly, in the determination of appropriate error terms for specific treatment effects. A recent informative description and review of such studies is provided by Brien³ who also notes that many studies involving human subjects, such as that reported in Solomon et al.,¹ have been multi-phase experiments but have not been recognised as such.

Plaid designs, originally introduced by Yates,⁴ typically have one set of treatments applied to rows and another set of treatments applied to columns. Farewell and Herzberg⁵ characterised the Solomon et al.¹ study as having a plaid design, and presented an analysis of variance (ANOVA) structure to examine treatment effects and error terms for such designs. However, with the aim of highlighting the basic structure of these designs, the significance tests from the ANOVA given in Farewell and Herzberg⁵ did not take full account of all error terms. The further level of nesting below the primary plaid design introduced additional complexity, similar to a split-plot structure for this component of the design, but this was not fully addressed by Farewell and Herzberg.⁵

This paper aims to further develop the analysis presented by Farewell and Herzberg⁵ and to examine how the logic and techniques of two-phase studies may help to elucidate appropriate error terms for each of the factors involved at the various stages of that study. In particular, it will identify that block-treatment interactions between the two phases, if they occur, can lead to more complex error structures that need to be taken into account. Examination of variance component terms in expected mean squares (EMSs) aids both in identifying these interactions and determining appropriate error terms to examine treatment effects. The hope is that this will lead to better understanding of, and potentially improvements in, both the design and analysis of similar studies.

2 The example

The experiment reported by Solomon et al.¹ consisted of medical practitioners using the Facial Action Coding System to rate the expression of pain when viewing videos of individuals, for convenience denoted as patients here, undergoing two types of painful movements. For the purposes of this paper, the data used by Farewell and Herzberg⁵ will be assumed to comprise the study. In this scenario, 74 medical practitioners were randomly assigned, 37 to each of two groups. The first group of medical practitioners received training in facial pain recognition and the other no training. If each of these practitioners provided a single reading, the analysis of such an experiment would be straightforward. However, each practitioner rated each of 16 videos, which were obtained as follows. Eight patients were selected from a previous study of a more detailed coding system, with four of those patients judged to express high levels of pain facially and by self-report (Expressive) and four to express low levels of pain (Not Expressive). Each patient was recorded in two videos, one of which involved the patient undertaking active movements without assistance (Active) and the other involving passive movements with the assistance of a therapist (Passive). Patients provided their own assessment of the pain level, and the scores used in the analysis were the absolute value of the difference between the patient’s score and the rater’s score. Table 1 is a reproduction from Farewell and Herzberg,⁵ with rows representing the 74 raters and columns representing the 16 videos.

Table 1.

Study design used in Farewell and Herzberg.⁵

		Patients
		Expressive								Unexpressive
		P 1		P 2		….		P 4		P 5		….		P 8
Raters		a	p	a	p			a	p	a	p			a	p
Trained	R 1
	R 2
	↓
	R 37
No training	R 38
	R 39
	↓
	R 74

a: active movement; p: passive movement.

As outlined in Farewell and Herzberg,⁵ the primary interest is in the factor T, which represents whether the practitioners are trained or not. However, there is also interest in whether the effect due to the factor T depends on the levels of the factor E, namely whether patients are in the expressive or non-expressive group, or the levels of the factor M, namely whether the patients are undergoing active or passive movement while the videos are being recorded. Thus, the interactions between the three factors are also of interest.

There are in fact seven “treatment” terms here that might be considered: the three main effects for the factors T, E and M; the three two-factor interactions TE, TM and EM; and the three-factor interaction TEM. Each of these terms can be calculated quite readily from the table of eight means corresponding to the two levels of each of the three factors. However, determining an appropriate error term for each of the main effects and interactions (and hence appropriate test statistics and confidence intervals) is not so straightforward. The purpose of this paper is to highlight that this experiment has the structure of a two-phase design and to model and understand the sources of variability and then to demonstrate how suitable error terms might be determined in this and other similar studies. Given the large number of raters, this study could have additionally examined other characteristics of the raters in addition to treatment, e.g. gender, and the analyses outlined subsequently could be extended to deal with this.

In particular, one motivation for the current paper is that the analysis in Farewell and Herzberg⁵ tests the TE interaction against a single error term. As noted in their paper (p.963), this may not be appropriate if there is significant interaction between (Raters within T) and E or between T and (Patients within E). If either of these terms is shown to be significant, this paper shows that the testing of the TE interaction needs to be adjusted. In fact, adjustments need to be made for the testing of all fixed effects in this case. In addition, the paper provides an appropriate approach for terms involving M which are linked to the additional level of nesting in this plaid design.

3 Two-phase designs

The structure of many two-phase designs,² of which this design is an example, is that an initial experiment (phase 1) is laid out in a field, but the material from that experiment is taken to a laboratory where that material is laid out according to a second and independent design (phase 2). In the context of Table 1, the column headings represent the experimental units associated with phase 1, while the row headings represent the experimental units associated with phase 2. What is typical of all two-phase designs is that each of the phases could be analysed as a relatively simple experimental design if there were only a single measurement for each experimental unit in that phase. The complexity arises from the fact that measurements are only obtained by undertaking both phases.

Other examples of two-phase designs occur in plant breeding experiments,⁶ microarray experiments,⁷ and taste-testing trials. Brien and Bailey⁸ give a large number of examples and Brien et al.⁹ deal with a specific example involving human subjects which is also discussed in the review by Brien.³ In the context of Table 1, the traditional two-phase experiment would focus on the treatment factors related to the phase 1 study, in this case the Patients and the associated factors E for expressiveness and M for movement. The phase 2 study would represent the experimental program necessary to get the measurements required to answer these questions. The difference in the current example is that primary interest is on the factor T related to the training (or not) of the raters, while the factors E and M, related to the Patients, and the various interactions are of secondary importance. Note, however, that there is, formally, complete symmetry between T and E in the data structure given in Table 1 and that any analysis will have a comparable symmetry in the analysis of factors related to T and E, although they are linked to different phases of the experiment.

4 A simplified example

In order to understand the two-phase aspect of this design better and to explain its complexities, consider a modification to the example above in which (i) the number of Raters in each Training group is reduced from 37 to 6 and (ii) the design is simplified by averaging over the two levels of movement. This averaging means that Table 1 becomes symmetrical and smaller, with the rows linked to 12 Raters, divided into two groups of 6, and columns linked to 8 Patients divided into two groups of 4.

An initial model for this design can be represented as

$$y_{i(l)j(m)}=\mu +{\alpha }_i+{\beta }_j+{\delta }_{ij}+e_{i(l)}+e_{j(m)}+e_{i(l)j(m)}$$ (1)

where the factors T and E are linked to fixed effects α and β, with subscripts i and j, and with numbers of levels a and b, respectively. It is expected that the results of this experiment will be applied to future raters and patients and that, therefore, rater and patient effects should therefore be regarded as random in the sense that the experimental sample is a small part of the population of interest.¹⁰ A rater random effect, subscript i(l), represents the lth rater within the ith level of T and a patient random effect, subscript j(m), represents the mth patient within the jth level of E. The effect TE is represented by the term δ_ij. The parameter constraints are

$${\displaystyle \sum _i{\alpha }_i}={\displaystyle \sum _j{\beta }_j}={\displaystyle \sum _i{\delta }_{ij}}={\displaystyle \sum _j{\delta }_{ij}}=0$$

while the variance terms in this initial model are, respectively

$$e_{i(l)}\sim N(0,{\sigma }_R^2),e_{j(m)}\sim N(0,{\sigma }_P^2)\hspace{0.17em}\hspace{0.17em}\mathit{and}{e}_{i(l)j(m)}\sim N(0,{\sigma }_{RP}^2)$$

This model provides an analysis of variance in which the residual term in the Rater:Patient stratum has 76 degrees of freedom. Testing of the treatment effects also follows naturally, with T being tested against Raters within T (R), E being tested against Patients within E (P) and the TE interaction being tested against the other 76 degrees of freedom in the Rater:Patient interaction (RP). Table 2 shows this analysis of variance table for a particular choice of 12 Raters, using the average over the two levels of movement. The decision to split the residual in the Rater:Patient stratum into three components will be explained subsequently.

Table 2.

ANOVA table for simplified example.

Source	Df	Mean square	F	p
T	1	33.18	4.78	0.054
R	10	6.94	5.93 a	<0.001	(d)
E	1	1263.30	6.59	0.043
P	6	191.70	163.85	<0.001	(e)
TE	1	24.36	12.73	<0.001
RE	10	5.29	4.52	<0.001	(a)
TP	6	3.75	3.21	0.009	(b)
RP	60	1.17			(c)
Total	95

^aF-tests for variance components in italics.

P: patient; E: expressiveness; R: rater; T: training.

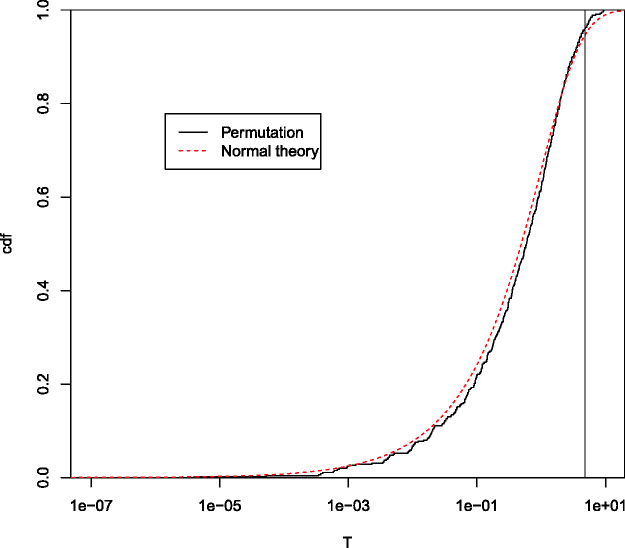
The tests shown in Table 2 mimic the permutation tests that would be considered appropriate here. For example, the permutation test for T would consist of obtaining the rank of the observed T among the 924 possible values of T obtained by all choices of two groups of 6 from the 12 Raters, while the test for E would consist of obtaining the rank of the observed E among the 70 possible values of E obtained by all choices of two groups of 4 from the 8 Patients. Because the sum of squares for Raters is constant for all these permutations, the ordering of the values for the sum of squares for T is the same as the ordering of the F-statistics. Figure 1 shows the cumulative distribution function of the F-statistics for T for both the permutation distribution and the corresponding normal-theory F-distribution applicable in this case. The p-value for this permutation test is 0.041. Finally, the test for the TE interaction would consist of finding the rank of the observed TE among the 924 × 70 = 64680 possible permutations of both Raters and Patients. The ranking of these TE interactions is the same as the ranking of the F-test for TE, where TE is tested against the other 76 degrees of freedom in this bottom stratum.

Figure 1.

Permutation distribution for T.

While the overall effect of T is certainly measured by averaging over the Patients, there is the possibility that the effect of T differs between Patients. If the T effect does differ between Patients, as would be demonstrated by a large value for the term TP, then the variability in those alternative estimates of T would be expected to have some impact on the test for T, particularly as conclusions about the impact of T will be applied to future populations of Patients. Yet the test in Table 2 is unaffected by this value. And, in view of the symmetry in this design, it may also be that the effect of E may differ among Raters. Table 2 shows that these two random effects are present in this case – it is in fact even more obvious if these tests are done with the full data set.

The presence of these random effects requires an extension to the model in equation (1), namely

$$\begin{array}{c}{y}_{i(l)j(m)}=\mu +{\alpha }_i+{\beta }_j+{\delta }_{ij}+e_{i(l)}+e_{j(m)}+e_{i(l)j}+e_{ij(m)}+e_{i(l)j(m)}\end{array}$$

where the additional terms

$$e_{i(l)j}\sim N(0,{\sigma }_{RE}^2)\mathrm{\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}}{e}_{ij(m)}\sim N(0,{\sigma }_{TP}^2)$$

capture the way in which the E effect varies between Raters and the T effect varies between Patients, respectively.

The terms required are most easily identified by considering all terms in the expansion of

$$\left(\text{I}+\text{T}+\text{R}\right)\times \left(\text{I}+\text{E}+\text{P}\right)=\text{I}+\text{T}+\text{R}+\text{E}+\text{TE}+\mathrm{RE}+\text{P}+\text{TP}+\mathrm{RP}$$

with degrees of freedom respectively given by the equivalent expansion

$$\left(\text{1}+\text{1}+\text{1}0\right)\times \left(\text{1}+\text{1}+\text{6}\right)=\text{1}+\text{1}+\text{1}0+\text{1}+\text{1}+\text{1}0+\text{6}+\text{6}+\text{6}0$$

where I represents the grand mean, R represents “Raters within T” and P represents “Patients within E”.

In this representation, T, E and TE are considered to be fixed effects, while terms involving R and P are, for the reasons given earlier, random effects. Following Snedecor and Cochran,¹¹ each EMS contains ${\sigma }^2$ plus terms according to the following rules

• each fixed effect term has a term for itself plus variance components for each random effect nested within it and for its interactions with any other random effects,

• each random effect term has its own variance component, with a separate variance component for each term nested within it,

• the coefficient of each variance component is the number of observations divided by the number of distinct levels for the corresponding term in the model.

The properties of this model can be formally derived by expressing the model in matrix notation. If the data are ordered sequentially by column, so that the results for the 12 raters are given for each of the 8 patients in turn, the model can be written as

$$\mathbf{y}=\mu \mathbf{1}+\mathit{A}\mathit{\alpha }+\mathit{B}\mathit{\beta }+\mathit{D}\mathit{\delta }+\mathit{R}\mathit{\rho }+\mathit{C}\mathit{\gamma }+\mathit{F}\varphi +\mathit{N}\mathit{\eta }+\in$$

where A, B and D are the matrices for the three treatment parameters, and R, C, F and N represent, respectively, the random effects for Raters, Patients, the RE interaction and the TP interaction. These matrices can be written in Kronecker product form and it then follows that

$$\begin{array}{l}Var(\mathbf{y})={\sigma }^2\mathit{I}+{\sigma }_R^2\mathit{R}{\mathit{R}}^{\prime }+{\sigma }_P^2\mathit{C}{\mathit{C}}^{\prime }+{\sigma }_{RE}^2\mathit{F}{\mathit{F}}^{\prime }+{\sigma }_{TP}^2\mathit{N}\mathit{N}\prime \\ ={\sigma }^2\mathit{I}+8{\sigma }_R^2({\mathit{J}}_8\otimes {\mathit{I}}_{12})+12{\sigma }_p^2({\mathit{I}}_8\otimes {\mathit{J}}_{12})\\ +4{\sigma }_{RE}^2({\mathit{I}}_2\otimes {\mathit{J}}_4\otimes {\mathit{I}}_{12})+6{\sigma }_{TP}^2({\mathit{I}}_8\otimes {\mathit{I}}_2\otimes {\mathit{J}}_6)\end{array}$$

where I is the identity matrix, J is the rank 1 idempotent matrix with all elements equal $({\mathit{J}}_n=11^{\prime }/n)$ and the subscripts indicate the size of each matrix. The ordering of the matrices in the Kronecker products is determined by the order in the data vector, moving from the subscript that changes most slowly (factor E) to the one that changes most quickly (Raters within T). The idempotent matrices in the last expression can be reformulated into orthogonal idempotents which constitute the terms in Table 3, where $\mathit{K}\mathit{=}\mathit{I}-\mathit{J}$. The EMS for a given term with sum of squares of the form ${\mathbf{y}}^{\mathbf{\prime }}\mathit{P}\mathbf{y}$ can then be determined as

$$E({\mathbf{y}}^{\mathbf{\prime }}P\mathbf{y})\text{=tr}\{\text{E}(P\mathbf{y}{\mathbf{y}}^{\mathbf{\prime }})\}\text{=}{\mathit{\nu }}^{\mathit{\prime }}P\mathit{\nu }\text{+tr}(P\mathit{V})$$

where $\mathbf{\text{v}}=\text{E}\left(\mathbf{\text{y}}\right)=\mu 1+\mathit{A}\mathit{\alpha }+\mathit{B}\mathit{\beta }+\mathit{D}\mathit{\delta }$ and V = Var(y). Here, the treatment effects are taken as $\pm \alpha$ for the two levels of T, $\pm \beta$ for the two levels of E and $\pm \delta$ for the two levels of TE. The coefficients for variance components in the EMS obtained from this agree with the rules of Snedecor and Cochran¹¹ cited earlier. For example, in this case, there are 12 raters, so the coefficient of ${\sigma }_R^2$ is 96/12 = 8.

Table 3.

ANOVA table showing mean squares and EMS.

Source	Df	Mean square	EMS
T	1	$\mathbf{y}\prime \{{\mathit{J}}_8\otimes {\mathit{K}}_2\otimes {\mathit{J}}_6\}\mathbf{y}$	${\sigma }^2$+8${\sigma }_R^2$+6${\sigma }_{TP}^2$+4${\sigma }_{RE}^2$+96${\alpha }^2$
R	10	$\mathbf{y}\prime {\mathit{J}}_8\otimes ({\mathit{I}}_2\otimes {\mathit{K}}_6)\mathbf{y}$	${\sigma }^2$+ 8${\sigma }_R^2$+4${\sigma }_{RE}^2$
E	1	$\mathbf{y}\prime \{{\mathit{K}}_2\otimes {\mathit{J}}_4\otimes {\mathit{J}}_{12}\}\mathbf{y}$	${\sigma }^2$+12${\sigma }_P^2$+6${\sigma }_{TP}^2$+4${\sigma }_{RE}^2$+96${\beta }^2$
P	6	$\mathbf{y}\prime ({\mathit{I}}_2\otimes {\mathit{K}}_4)\otimes {\mathit{J}}_{12}\mathbf{y}$	${\sigma }^2$+12${\sigma }_P^2$+6${\sigma }_{TP}^2$
TE	1	$\mathbf{y}\prime \{{\mathit{K}}_2\otimes {\mathit{J}}_4\}\otimes \{{\mathit{K}}_2\otimes {\mathit{J}}_6\}\mathbf{y}$	${\sigma }^2$+4${\sigma }_{RE}^2$+6${\sigma }_{TP}^2$+96${\delta }^2$
RE	10	$\mathbf{y}\prime \{{\mathit{K}}_2\otimes {\mathit{J}}_4\}\otimes ({\mathit{I}}_2\otimes {\mathit{K}}_6)\mathbf{y}$	${\sigma }^2$+4${\sigma }_{RE}^2$
TP	6	$\mathbf{y}\prime ({\mathit{I}}_2\otimes {\mathit{K}}_4)\otimes \{{\mathit{K}}_2\otimes {\mathit{J}}_6\}\mathbf{y}$	${\sigma }^2$+6${\sigma }_{TP}^2$
RP	60	$\mathbf{y}\prime ({\mathit{I}}_2\otimes {\mathit{K}}_4)\otimes ({\mathit{I}}_2\otimes {\mathit{K}}_6)\mathbf{y}$	${\sigma }^2$
Total	95

In general, for ANOVA tables from complex designed experiments, expected mean squares should be used to guide the construction of appropriate F-ratios and hypothesis tests. Green and Tukey¹⁰ discussed this and other issues arising in the analysis of complex experiments. The first thing to note from Table 3 is that the term T has an additional variance component compared with the term R and that, consequently, the test performed earlier for T is no longer unbiased. The additional error term in the EMS for T involves the variance component ${\sigma }_{TP}^2$. This random effect captures how the T effect varies randomly between “blocks” (patients). It is often assumed that such block by treatment interaction does not exist or that it is included in the “residual” error. However, the evidence from the mean squares in Table 2 suggests otherwise, as can be seen by comparing the third and fourth observed MS values [(b) and (c)] in the third section of Table 2. This generates an F test on 6 and 60 degrees of freedom with a test statistic value of 3.21, generating a significance level of 0.009.

Two different techniques, closely related, are available for obtaining unbiased tests in these circumstances. In the first of these, the raw treatment estimates are used and Satterthwaite approximations¹² provide unbiased estimates of the variances for each of the treatment terms.

For the second method, if T is defined as the matrix $\mathit{T}=\left[\mathit{A}\left|\mathit{B}\right|\mathit{D}\right]$ and $\mathit{\theta }$ as the vector $\mathit{\theta }=[\mathit{\alpha }\mathit{\beta }\mathit{\delta }{]}^{\prime }$, then the weighted least squares estimates of $\theta$ are given by

$$\widehat{\mathit{\theta }}={({\mathit{T}}^{\hspace{0.17em}\prime }{\mathit{V}}^{-1}\mathit{T})}^{-1}\mathit{T}\hspace{0.17em}\prime {\mathit{V}}^{-1}\mathbf{y}$$

with variance $\mathit{Var}(\widehat{\mathit{\theta }})={({\mathit{T}}^{\prime }{\mathit{V}}^{-1}\mathit{T})}^{-1}.$ This latter is the method adopted by ASReml,¹³ with estimates of the variance components obtained using REML.

In this particular case, both methods provide the same estimate and the same variance formula. In the case of the second method, the matrix V splits into the nine orthogonal idempotents shown in Table 3, with coefficients given by the variance terms in the EMS of Table 3, and each of the three terms in T aligns with exactly one of the idempotents. As a result, the weighted least squares estimates of the three 1 degree of freedom treatment terms, T, E and TE, are their raw means, with the variances ascribed to them as in Table 3. To generate an appropriate error for testing the main effect of T, mean squares from Table 2 can be combined, guided by the expected mean squares in Table 3. An unbiased estimate of the error variance for T is given by

$$d+b-c=6.94+3.75-1.17=9.52$$

which provides a mean square against which T can be tested. Satterthwaite approximations¹² can then provide an approximate degrees of freedom. Assuming that each of these is a Chi-square with the appropriate degrees of freedom, then, with an obvious notation

$$E(d+b-c)=\delta +\beta -\gamma$$

and

$$\mathit{Var}(d+b-c)=2({\delta }^2/10+{\beta }^2/6+{\gamma }^2/60)$$

and this will behave approximately like a Chi-square divided by its degrees of freedom (DF). In such a case $E^2/\mathit{Var}=(DF)/2$, implying that the estimate of DF is

$$2(E^2/\mathit{Var})={(\delta +\beta -\gamma )}^2/({\delta }^2/10+{\beta }^2/6+{\gamma }^2/60)$$

where the Greek letters are replaced by their estimates. The resulting estimated error variance is 9.52 on 12.62 degrees of freedom. The F-test on (1,12.62) degrees of freedom takes the value 33.18/9.52 = 3.48 (p = 0.085), compared to the value of p = 0.054 given in Table 2. Similar tests can be determined for E and the TE interaction.

As advocated by Nelder and Lane,¹⁴ marginality should be invoked so that a significant result for TE implies that both T and E should be included in any model regardless of whether they are significant or not.

This raises the question of whether there are any appropriate permutation tests that might replace those described earlier. Anderson and Ter Braak¹⁵ provide a methodology for obtaining exact or approximate permutation tests where an error mean square with the correct variance can be identified but this is not the case in the current situation. One possibility for T, as an example, is to form the 924 permutations as described earlier, calculate the ratio $\text{MS(T)}/(d+b-c)$ for each and then determine the rank of the observed ratio within the ordered list. In this case, the value 3.48 ranks 28 out of 924, implying a p-value of 28/924 = 0.030. Similar permutation tests can be conducted for the other effects, with all 64,680 permutations of T and E needed for tests other than those for T and E. A simulation study, using variance components similar to those obtained here, establishes that this test has good Type I error properties, whereas T/R does not.

5 Potential strategies

A number of different strategies can be used to help in developing models and appropriate analyses for studies such as these. The following strategies have been used in examining the plaid design in Table 1 and together have proved useful in providing greater understanding of the design and its analysis.

1. Subsetting: Analyse subsets of the data and use this to build the analysis into a coherent whole. For a factor at two levels, analyse averages and differences to add insight and help establish a final analysis. The previous section is an example of this technique as it deals only with averages.

2. Permutation tests: Develop tests based on permutation theory to provide useful insight into appropriate models and tests. However, as the previous section shows, the usual permutation tests may not be appropriate in the presence of interactions of fixed-effects with random-effects terms.

3. One phase at a time: For each of the phases in turn, consider what the analysis would be if a number of repeated, but unstructured, measurements were made for each experimental unit in that phase. These repeated measurements represent a form of pseudo-replication which suggests limitations on the degrees of freedom available for testing the effects at each phase.

4. Formal modelling: Formulate a comprehensive linear model with various fixed and random effects to describe all the various aspects of the study. The previous section illustrates the way in which the analysis of variance can be used to assess the appropriateness of a proposed model.

6 Analysis of the complete study

This section will provide an analysis of the complete study, informed by the analysis of the earlier sections. The rater/patient pairs generate two measurements, one for each level of M. Thus, M is essentially a split-plot treatment within the rater/patient pairs. For analyses not involving M, both measurements should contribute similarly and it is therefore appropriate to focus on the average of the two measurements, as in the previous sections. This produces an ANOVA as in Farewell and Herzberg.⁵ To make the results of this comparable with the approach adopted subsequently based on formal modelling, it is necessary to multiply all sums of squares in this ANOVA by 2 since if a measurement error is ${\sigma }^2$ then an average of two values will have variance ${\sigma }^2/2$. The resulting ANOVA table corresponds to the upper part of Table 4.

Table 4.

ANOVA table, following Farewell and Herzberg.⁵

Source	Df	Mean square	F	p
(i) Averages
T	1	99.28	11.39	0.001
Error 1: R	72	8.72	2.74 a	<0.001	(d)
E	1	16606.21	7.35	0.035
Error 2: P	6	2257.96	710.05	<0.001	(e)
TE	1	20.39	6.41	0.012
RE	72	8.23	2.58	<0.001	(a)
TP	6	9.93	3.12	0.005	(b)
Error 3: RP	432	3.18			(c)
(ii) Differences
M	1	7565.23
TM	1	43.68	5.29	0.024
Error 4: RM	72	8.26	2.47	<0.001	(d1)
EM	1	4328.11	37.77	0.001
Error 5: PM	6	114.58	34.20	<0.001	(e1)
TM	1	36.09	10.77	0.001
REM	72	7.48	2.23	<0.001	(a1)
TPM	6	9.89	2.95	0.008	(b1)
Error 6: RPM	432	3.35			(c1)
Total	1183

^aF-tests for variance components in italics.

P: patient; E: expressiveness; R: rater; T: training; M: movement.

For analyses involving M, it is the difference between the two observations from each rater/patient pair that will be informative. These 592 differences, like the averages, can be viewed as arising from a single plaid design involving raters and patients with factors T and E. The overall average of the differences, by analogy with the grand mean term in a linear model, represents the main effect of M, while the T ‘effect’ for the differences corresponds to the TM interaction. Similarly, the E ‘effect’ for the differences represents the EM interaction and the TE ‘effect’ represents the TEM interaction. Unlike the analysis of the averages, an error term for testing the hypothesis that M is zero is required. The lower half of Table 4 presents the relevant rows for an ANOVA for the differences but, again, to be consistent with the formal modelling approach, the sums of squares are divided by 2 since a difference will have a variance $2{\sigma }^2$ if the measurement error is ${\sigma }^2$.

The formal tests provided in Table 4 would be appropriate if the only random effects were associated with the six terms identified as “Error” terms in the table.

7 Formal modelling

The model in the earlier section can now be extended to cover the additional layer relating to the levels of M

$$\begin{array}{l}{y}_{i(l)j(m)k}=\mu +{\alpha }_i+{\beta }_j+{\gamma }_k+{(\alpha \beta )}_{ij}+{(\alpha \gamma )}_{ik}+{(\beta \gamma )}_{jk}+{(\alpha \beta \gamma )}_{\mathit{ijk}}\\ +e_{i(l)}+e_{j(m)}+e_{i(l)j}+e_{ij(m)}+e_{i(l)j(m)}\\ +e_{i(l)k}+e_{j(m)k}+e_{i(l)jk}+e_{ij(m)k}+e_{i(l)j(m)k}\end{array}$$

In this model, the additional subscript k refers to the levels of M. The parameter constraints seen earlier are extended to include

$$\begin{array}{l}{\displaystyle \sum _k{\gamma }_k}={\displaystyle \sum _i{(\alpha \gamma )}_{ik}}={\displaystyle \sum _k{(\alpha \gamma )}_{ik}}={\displaystyle \sum _j{(\beta \gamma )}_{jk}}={\displaystyle \sum _k{(\beta \gamma )}_{jk}}=0\\ {\displaystyle \sum _i{(\alpha \beta \gamma )}_{\mathit{ijk}}}={\displaystyle \sum _j{(\alpha \beta \gamma )}_{\mathit{ijk}}}={\displaystyle \sum _k{(\alpha \beta \gamma )}_{\mathit{ijk}}}=0\end{array}$$

By analogy with the earlier model, there are now an additional five variance terms:

$$\begin{array}{l}{e}_{i(l)k}\sim N(0,{\sigma }_{RM}^2),e_{j(m)k}\sim N(0,{\sigma }_{PM}^2),e_{i(l)j(m)k}\sim N(0,{\sigma }_{\mathit{RPM}}^2)\\ e_{i(l)jk}\sim N(0,{\sigma }_{\mathit{REM}}^2)\hspace{0.17em}\mathit{and}\hspace{0.17em}{e}_{ij(m)k}\sim N(0,{\sigma }_{\mathit{TPM}}^2)\end{array}$$

Table 5 presents expressions for expected means squares, together with the appropriate degrees of freedom when the number of levels for T, E and M is a, b and c, respectively, the number of raters at each level of T is n and the number of patients at each level of E is p. The expressions of the form $\Phi ()$ correspond to the sum of squared fixed effects. Comparison of the mean squares in Table 4 with the EMSs given in Table 5 suggests that the variance components ${\sigma }_R^2,{\sigma }_{RE}^2,{\sigma }_{TP}^2$ and ${\sigma }_{RP}^2$ are all zero, and only ${\sigma }_P^2$ from this set of five has a nonzero value.

Table 5.

Degrees of freedom and expected mean squares for the formal model.

		EMS
Source	Df	${\sigma }_{\mathit{RPM}}^2$	${\sigma }_{\mathit{TPM}}^2$	${\sigma }_{\mathit{REM}}^2$	${\sigma }_{PM}^2$	${\sigma }_{RM}^2$	${\sigma }_{RP}^2$	${\sigma }_{TP}^2$	${\sigma }_{RE}^2$	${\sigma }_P^2$	${\sigma }_R^2$
Grand mean	1	1	n	p	an	bp	c	nc	pc	anc	bpc
T	a – 1	1	n	p		bp	c	nc	pc		bpc	$+\mathit{bnpc}\Phi (\alpha )$
R	$a(n-1)$	1		p		bp	c		pc		bpc		(d)
E	b – 1	1	n	p	an		c	nc	pc	anc		$+\mathit{anpc}\Phi (\beta )$
P	$b(p-1)$	1	n		an		c	nc		anc			(e)
TE	$(a-1)(b-1$	1	n	p			c	nc	pc			$+\mathit{npc}\Phi (\alpha \beta )$
RE	$a(n-1)(b-1)$	1		p			c		pc				(a)
TP	$(a-1)b(p-1)$	1	n				c	nc					(b)
RP	$a(n-1)b(p-1)$	1					c						(c)
M	$(c-1)$	1	n	p	an	bp						$+\mathit{abnp}\Phi (\gamma )$
TM	$(a-1)(c-1)$	1	n	p		bp						$+\mathit{bnp}\Phi (\alpha \gamma )$
RM	$a(n-1)(c-1)$	1		p		bp							$(\mathrm{d}1)$
EM	$(b-1)(c-1)$	1	n	p	an							$+\mathit{anp}\Phi (\beta \gamma )$
PM	$b(p-1)(c-1)$	1	n		an								(e1)
TEM	$(a-1)(b-1)(c-1)$	1	n	p								$+np\Phi (\alpha \beta \gamma )$
REM	$a(n-1)(b-1)(c-1)$	1		p									(a1)
TPM	$(a-1)b(p-1)(c-1)$	1	n										(b1)
RPM	$a(n-1)b(p-1)(c-1)$	1											(c1)
Total	anbpc

The EMS expressions in Table 5 mimic very closely what was obtained earlier in Table 3. Each of the seven treatment terms has a variance which can only be estimated by a linear combination of three of the error variances, leading to quite different tests from those indicated in Table 4.

To generate an appropriate test for the main effect of T, mean squares from Table 4 are combined, guided by the expected mean squares in Table 5. An unbiased estimate of the error variance for T is given by

$$d+b-c=8.72+8.23-3.18=15.47$$

and this provides a mean square against which T can be tested. The Satterthwaite approximation,¹² as described earlier, provides an approximate degrees of freedom of 13.66. The F-test on (1,13.66) degrees of freedom takes the value 99.28/15.47 = 6.42 (p = 0.025), compared to the value of p = 0.001 given by Farewell and Herzberg.⁵

Each of the factorial terms is tested against a different combination of the error terms, as shown in Table 6. In each of these calculations, three mean squares are used in the Satterthwaite approximation. As mentioned earlier, the marginality ideas of Nelder and Lane¹⁴ should be applied so that, where higher order interactions are present, terms marginal to those should be included in the model whether significant or not. It is notable that the degrees of freedom for testing only vary from 6 to about 14 in this case. In broad terms, this arises from the fact that there are only eight patients involved in the study, limiting the estimation of some variance components to only 6 degrees of freedom. The implication is that a more appropriate design would have an increased number of patients, but possibly fewer raters would be needed.

Table 6.

Formal tests for each effect.

Term	Effect	Mean Sq	Variance formula	Variance	F	Df	p
G	6.011
T	0.579	99.28	R+TP−RP	15.47	6.42	13.66	0.025
E	−7.490	16606.21	RE+ P−RP	2263.01	7.34	6.03	0.035
TE	−0.263	20.39	RE+TP−RP	14.98	1.36	12.90	0.266
M	5.056	7565.23	RM + PM−RPM	119.49	63.31	6.52	<0.001
TM	0.384	43.68	RM +TPM−RPM	14.80	2.95	12.68	0.112
EM	−3.824	4328.11	REM+ PM−RPM	118.71	36.46	6.44	0.001
TEM	−0.349	36.09	REM+TPM−RPM	14.02	2.57	11.49	0.137

The model developed here was also fitted using ASReml¹³ and the R platform,¹⁶ with very similar results. Choosing to allow variance components to be negative leads to the same variance component estimates as are obtained here. The formal Wald tests, using the Kenward–Rogers¹⁷ approximation, give F-values and denominator degrees of freedom almost identical to those shown in Table 6.

8 Estimation

While the role of formal testing through the ANOVA table remains important, estimation of effects and their standard errors is vital in assessing outcomes. From Table 6, the square root of an F-value provides a t-statistic. The ratio of the effect to its t-statistic provides a standard error of each effect. In the three-way table of means, each mean is the overall mean plus half the sum of the seven effects, with appropriate signs. The effects can be shown to be uncorrelated, and hence the variance matrix of the means can be determined. The means so obtained are shown in Table 7. The standard error of differences (SED) can be summarised as follows:

• 0.45, for comparisons in the same row.

• 0.95, for other comparisons within the same square.

• 2.85, for comparisons between means in different squares.

Table 7.

Treatment means.

		Trained	Untrained
Expressive	Active	5.26	5.37
	Passive	13.41	14.98
Unexpressive	Active	1.51	1.79
	Passive	2.71	3.06

Under the ASReml approach, treatment means and standard errors of differences agree closely with the results here.

9 Discussion

ANOVA tables can be of great value in understanding the structure of an experimental design and confirming potential sources of variation. This can be linked to the choice of a formal model for inference purposes and inclusion of appropriate error terms. However, it may be the case that when EMS terms in an ANOVA are not carefully examined, the ‘natural’ choice of error terms from an ANOVA may be based on assumptions that are unwarranted.

For the plaid designs discussed in this paper, the ANOVA table illustrates clearly that treatments T and E applied to the rows and columns, respectively, are, separately and symmetrically, linked to an upper level component of the ANOVA table associated with row and column means, respectively, but that their interaction TE is associated with the interaction of rows and columns. However, the interaction between rows and columns may include additional variance components, identified here as the interactions of the row treatments with columns and the column treatments with rows. If the variance components corresponding to these block-treatment interactions are nonzero, they affect the testing not only of the TE interaction but also, perhaps less obviously, the main effects T and E as well.

Careful investigation of the ANOVA structure is facilitated by examining the structure of the study from different perspectives. For the Solomon et al.¹ study, the recognition that this study falls into the category of two-phase experiments provides fresh insight into the structure and potential analysis of the study. The two-phase structure of this experiment also helps to provide heuristic arguments for the number of degrees of freedom available for testing various effects.

Permutation theory can also provide insight into study design and analysis, although for plaid designs it does not address the problem of block-treatment interactions. An adjustment to these permutation tests is proposed here and warrants further investigation. For the Solomon et al.¹study, there was an additional level of nesting below the plaid design. The identification of the appropriate model and analysis for effects linked to this additional level of nesting is facilitated by subsetting of the data. For this study, this corresponded to looking at averages and differences of the two measurements taken for each rater–patient pair.

The role of ANOVA here has been to identify the various terms that are needed for an appropriate error structure. While techniques such as Satterthwaite approximations¹² can be used to provide non-standard inferences from the ANOVA table, the availability of modern computing packages such as ASReml¹³ provides an alternative and preferred approach to the analysis and testing for treatment effects. However, the use of ASReml relies critically on the identification of an appropriate set of variance components and, in this case at least, that is facilitated by a careful examination of the ANOVA table, as also suggested by Brien et al.⁹ As well, there is an advantage to considering multiple approaches to inference to add certainty to any inference strategy.

In general, the use of a variety of techniques is proposed and encouraged in order to better understand the important features of any study. This approach, applied to the Solomon et al.¹ study, allowed the elucidation of appropriate formal tests for each of the factors and interactions in the study. Some of these results differ from the suggestions given in Farewell and Herzberg.⁵ In particular, the methods outlined here can be applied to the design and analysis of other studies in which the participants in a study supply multiple measurements under a variety of conditions.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The financial support from Grains Research and Development Corporation to Richard Jarrett through the Statistics for Australian Grains Industry in Southern Region project (SAGI-STH) and from the Natural Sciences and Engineering Research Council of Canada to Agnes M. Herzberg is gratefully acknowledged.

ORCID iD

VT Farewell https://orcid.org/0000-0001-6704-5295

Supplemental Material

Data files and selected computer code can be found at https://doi.org/10.17863/CAM.54494.