Continuous Prediction of Mortality in the PICU: A Recurrent Neural Network Model in a Single-Center Dataset*

Supplemental Digital Content is available in the text.

OBJECTIVES:

Develop, as a proof of concept, a recurrent neural network model using electronic medical records data capable of continuously assessing an individual child’s risk of mortality throughout their ICU stay as a proxy measure of severity of illness.

DESIGN:

Retrospective cohort study.

SETTING:

PICU in a tertiary care academic children’s hospital.

PATIENTS/SUBJECTS:

Twelve thousand five hundred sixteen episodes (9,070 children) admitted to the PICU between January 2010 and February 2019, partitioned into training (50%), validation (25%), and test (25%) sets.

INTERVENTIONS:

None.

MEASUREMENTS AND MAIN RESULTS:

On 2,475 test set episodes lasting greater than or equal to 24 hours in the PICU, the area under the receiver operating characteristic curve of the recurrent neural network’s 12th hour predictions was 0.94 (CI, 0.93–0.95), higher than those of Pediatric Index of Mortality 2 (0.88; CI, [0.85–0.91]; p < 0.02), Pediatric Risk of Mortality III (12th hr) (0.89; CI, [0.86–0.92]; p < 0.05), and Pediatric Logistic Organ Dysfunction day 1 (0.85; [0.81–0.89]; p < 0.002). The recurrent neural network’s discrimination increased with more acquired data and smaller lead time, achieving a 0.99 area under the receiver operating characteristic curve 24 hours prior to discharge. Despite not having diagnostic information, the recurrent neural network performed well across different primary diagnostic categories, generally achieving higher area under the receiver operating characteristic curve for these groups than the other three scores. On 692 test set episodes lasting greater than or equal to 5 days in the PICU, the recurrent neural network area under the receiver operating characteristic curves significantly outperformed their daily Pediatric Logistic Organ Dysfunction counterparts (p < 0.005).

CONCLUSIONS:

The recurrent neural network model can process hundreds of input variables contained in a patient’s electronic medical record and integrate them dynamically as measurements become available. Its high discrimination suggests the recurrent neural network’s potential to provide an accurate, continuous, and real-time assessment of a child in the ICU.

An automated, continuous assessment of a patient’s severity of illness (SOI) could provide decision support and alert clinicians to a patient’s changing status during intensive care. Electronic medical records (EMRs), with continuous data capture, provide the possibility of dynamically analyzing these data to assess an individual child’s risk of mortality (ROM). Numerous static scoring systems, including 1) Pediatric Risk of Mortality (PRISM) III, 2) Pediatric Index of Mortality (PIM) 2, and 3) Pediatric Index of Cardiac Surgical Intensive Care Mortality analyze measurements from a fixed time window to make single predictions. These evaluate SOI using a limited number of physiologic, laboratory, and organ dysfunction variables and correlate well with ROM. Previous reports of continuous application of static scoring systems (4–9) demonstrate a long-standing desire to have a continuously updating patient assessment.

This study aims to develop, as a proof of concept, a previously described (10–13) deep learning methodology, namely a long short-term memory (LSTM) recurrent neural network (RNN) to continuously assess an individual child’s ROM throughout their ICU stay as a proxy measure of SOI. Deep learning methods combine variables in many more different ways than logistic regression, giving rise to many more coefficients or weights than the number of input variables, enabling them to capture more complex interactions among inputs than those captured by simpler algorithms such as a logistic regression. Improvements in regularization techniques, including L1 and L2 constraints, dropout techniques, initial learning rate, and learning rate decay, enable deep learning models to manage hundreds of inputs while improving their accuracy (14–18).

RNNs are specifically designed to process sequential data. The “recurrent” architecture allows integration of information from previous timesteps with newly acquired data to update its risk assessment, making the model dynamic instead of static. RNNs analyze all available data with neither preconception about which measures may be important in determining a patient’s clinical status nor the need to engineer features specific to a given clinical condition (19). Previous work has demonstrated RNNs are robust when using high dimensional inputs that may include extraneous features for predicting a range of clinical outcomes (12). The flexibility and accuracy of RNNs have made them increasingly popular for predictive modeling of many time-based clinical tasks (11–13, 20–23).

MATERIALS AND METHODS

Data Sources

Data were extracted from deidentified EMR (Cerner, Kansa, MO) of patients admitted to the PICU of Children’s Hospital Los Angeles (CHLA) between January 2010 and February 2019. Data previously collected for Virtual Pediatric Services, LLC (24) participation, including patient disposition, were linked with the EMR data before deidentification. The Institutional Review Board (IRB) at CHLA waived the need for consent and IRB approval. Data included charted measurements of physiologic observations, laboratory results, therapies administered, patient demographic data, and episode disposition (survived or died). Diagnoses were available but not used as ROM predictors. The 12,516 PICU episodes (9,070 children) were randomly split on the patient level into three sets: a training set for deriving model weights (50%), a validation set for optimizing hypervariables (25%), and a holdout test set for measuring performance (25%). No other stratifications were applied.

Preprocessing of EMR data has been previously described (10; see Supplement A, Supplemental Digital Content 1, http://links.lww.com/PCC/B671, for details). Data preprocessing required data aggregation, imputation of missing data, and normalization of observed values. Aggregation included combining like values from all sources and resulted in 430 distinct physiologic, demographic, laboratory, and therapeutic variables. Imputation of missing values was done in a prospective, disciplined fashion (Supplement A, Supplemental Digital Content 1, http://links.lww.com/PCC/B671). Data were z normalized and (0, 1) scaled for computational stability. Binary indicators of continuous therapies (1—present, 0—absent) were maintained from the time an intervention began until discontinuation. Diagnoses were used for descriptive analyses but not as RNN inputs. Discharge time for survivors and time of death (or declaration of brain death) for nonsurvivors were noted. See Table S-1 (http://links.lww.com/PCC/B672), Table S-2 (http://links.lww.com/PCC/B673), Table S-3 (http://links.lww.com/PCC/B674), Table S-4 (http://links.lww.com/PCC/B675), and Table S-5 (http://links.lww.com/PCC/B676) for a list of input variables and acronyms.

RNN Model

Figure 1 illustrates the flow of inputs and outputs of the many-to-many LSTM RNN model trained to provide ROM of individual patients at any time (t_i) during their ICU episode a recorded measurement becomes available. The model input (denoted by x[t_i]) consists of all preprocessed measurements (recorded or imputed) at that time, whereas the output (denoted by y[t_i]) is trained to match the binary indicator of ICU mortality. Two LSTM (25) layers followed by a logistic regression layer comprised this RNN model similar to previous work (10–13). Table S-6 (Supplemental Digital Content 7, http://links.lww.com/PCC/B677) provides details of the model architecture, variables, and training, including regularizers. The Python library Keras 2.0.7 with Theano 1.0.2 backend was used to implement and train the model. The “recurrent” architecture, depicted by horizontal arrows in Figure 1, allows retention of information from previous times and integration with newly acquired data to make a new prediction. The LSTM’s internal states hold the information, and a horizontal arrow in Figure 1 represents these internal states propagating information between timesteps. This is a key difference between the RNN model and “continuously updating scores” such as the daily Pediatric Logistic Organ Dysfunction (PELOD) (4, 5) and the Rothman Index (7, 8).

Figure 1.

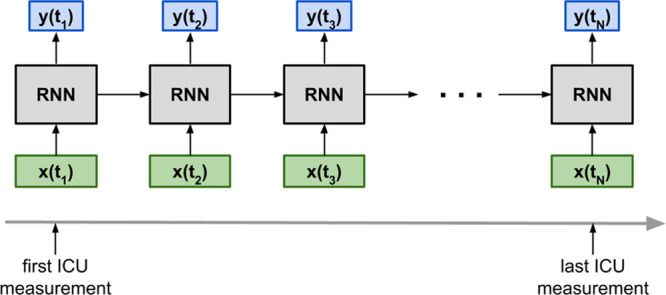
Overview of the recurrent neural network (RNN) model with its inputs (denoted by x) and outputs (denoted by y). Note that the RNN model is a many-to-many model that generates an output at every timestep where there is an input. t = time.

Model Evaluation

Performance was evaluated using the area under the receiver operating characteristic curve (AUROC). In accordance with the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis Initiative (26) standards, performance metrics were computed only on the test set. All computations for these analyses were implemented in Python 3 and used the Python library Scikit-learn 0.22.1. AUROCs were computed for predictions generated by the RNN at various time points: 0, 1, 3, 6, 12, and 24 hours after ICU admission, as well as 1, 3, 12, and 24 hours prior to discharge (the RNN’s N-hour AUROCs). For context, the AUROCs of PELOD day 1, PIM2, and the 12-hour PRISM III scores are shown. To quantify the effect of lead time (27), the RNN’s N-hour AUROCs were computed for two subcohorts of the test set with different PICU length of stay (LOS): 4–8 and greater than or equal to 10 days.

The receiver operating characteristic (ROC) and precision-recall curves for the RNN’s 12th hour predictions were compared with those of the other models. To ensure a constant cohort for the RNN’s N-hour AUROCs and fair comparison across models, the AUROCs were computed for episodes lasting greater than or equal to 24 hours and had PELOD day 1, PIM 2, and PRISM III scores. Bootstrap sampling (1,000 iterations) was used to generate 95% CIs for the RNN (12th hr predictions), PIM 2, PRISM III, and PELOD day 1 AUROCs on this cohort. Performance in subcohorts partitioned according to primary diagnosis, age, and LOS was also computed. AUROCs of the daily PELOD and RNN scores were computed for a subset of test set episodes with LOS greater than or equal to 5 days. The associated p values comparing any two AUROCs were computed using Hanley and McNeil’s estimation method (28).

Calibration metrics were computed for RNN predictions at all timesteps of the test set. These included the Hosmer-Lemeshow C* statistic, the Brier score, and Cox calibration regression with the logit transformation (29, 30). CIs for regression line variables (slope and intercept) were computed using the Python library statsmodels v0.10.1.

Finally, to assess the feasibility of clinical deployment, the computation times of patient predictions from clinically relevant scenarios was calculated. Developing the model and making predictions were done using a computer equipped with an Intel i9-7929X CPU, 128 Gb of RAM, and a Titan V GPU (NVIDIA, Santa Clara, CA). To estimate the time to generate a single prediction during deployment, the total time taken to generate all predictions (all time points of all test set episodes) was divided by the total number of predictions.

RESULTS

Table 1 displays demographic information. The distributions of gender, age, ICU LOS, PIM 2, PRISM III (12th hr), and PELOD day 1 scores were similar across the three datasets. In the combined training and validation sets, the top six primary diagnoses were respiratory (31%), neurologic (14%), oncologic (10%), injury/poisoning/adverse effects (9%), orthopedic (7%), and infectious (7%). The test set had similar proportions: respiratory (31%), neurologic (15%), oncologic (11%), injury/poisoning/adverse effects (10%), infectious (7%), and orthopedic (5%).

TABLE 1.

Demographics of the Training, Validation, and Test Sets

Characteristics and Demographics	Training Set	Validation Set	Test Set (All)	Test Set (Subcohorta)
Episodes, n	6,172	3,214	3,130	2,475
Number of timesteps	1,541,739	783,056	721,024	659,835
Patients, n	4,534	2,268	2,268	1,820
Mortality rate, %	3.8	3.9	3.6	4.0
Gender (% female)	43.7	43.9	44.6	45.0
Age groups (yr), %
0–1	17	17	17	18
1–5	26	25	25	24
5–10	18	19	18	18
10–18	32	32	32	33
18+	7	7	8	8
Age, median (IQR) (yr)	6.7 (1.3–13.8)	7.0 (1.8–13.7)	7.2 (1.8–13.8)	7.2 (1.7–13.8)
ICU length of stay, median (IQR) (d)	2.3 (1.2–4.9)	2.3 (1.2–4.9)	2.3 (1.2–4.9)	2.9 (1.8–5.6)
Pediatric Index of Mortality 2, median (IQR)	–4.8 (–6.2 to –3.7)	–4.8 (–6.2 to –3.5)	–4.8 (–6.2 to –3.8)	–4.7 (–6.2 to –3.5)
Pediatric Risk of Mortality III, median (IQR)	2.0 (0.0–6.0)	3.0 (0.0–6.0)	2.0 (0.0–6.0)	3.0 (0.0–6.0)
Pediatric Logistic Organ Dysfunction day 1, median (IQR)	10 (1–11)	10 (1–11)	10 (0–11)	10 (1–11)

IQR = interquartile range.

^aSubcohort: episodes lasting at least 24 hr in the ICU and had available Pediatric Index of Mortality 2, Pediatric Risk of Mortality III, and daily Pediatric Logistic Organ Dysfunction scores.

Figure 2 displays the RNN’s N-hour AUROCs for 2,475 test set episodes with greater than or equal to 24 hours ICU LOS. At admission, when the RNN had only a single time point of data, its 0.74 (CI, 0.71–0.78) AUROC compared poorly with the three clinical models (PELOD day 1 = 0.85; CI, 0.81–0.89; p < 0.002 and PIM 2 = 0.88; CI, 0.85–0.91; p < 0.001 and PRISM III = 0.89; CI, 0.86–0.92; p < 0.001). The RNN’s AUROC rapidly increased with time; by the sixth hour after ICU admission, its AUROC started to surpass those of the other three models. At 12 hours, the RNN achieved an AUROC of 0.94 (CI, 0.93–0.95), greater than the other models’ AUROCs (p < 0.002 vs PELOD; p < 0.02 vs PIM2; and p < 0.05 vs PRISM III). Twenty-four hours prior to discharge or death, the RNN achieved an AUROC of 0.99 (p < 0.03 relative to RNN 12th hr). Figure S-1 (Supplemental Digital Content 9, http://links.lww.com/PCC/B679; legend, Supplemental Digital Content 1, http://links.lww.com/PCC/B671) shows the N-hour AUROCs of the RNN predictions for the two subcohorts whose ICU LOS were 4–8 days (median = 5.3 d; interquartile range [IQR], [2.6–6.3 d]) and ≥ 10 d (median = 14.3 d; IQR, [12.0–20.7 d]). The AUROC difference between the two groups was 0.2 in the first 24 hours; this difference disappeared in the last 48 hours. In both groups, the RNN AUROCs increased by 0.15 between admission and 24 hours later.

Figure 2.

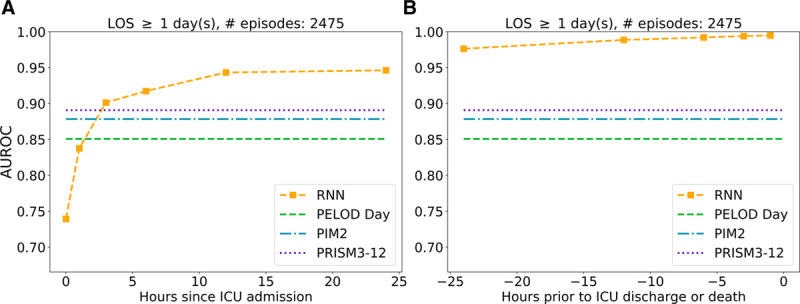
Recurrent neural network (RNN) area under the receiver operating characteristic curve (AUROC), as a function of time relative to ICU admission (A) or ICU discharge (B), on test set episodes whose length of stay (LOS) was at least 24 hr and had Pediatric Logistic Organ Dysfunction (PELOD) day 1, Pediatric Index of Mortality (PIM) 2, and Pediatric Risk of Mortality (PRISM) III scores.

Figure 3 shows AUROCs computed from 692 test set episodes with LOS greater than or equal to 5 days (7.2% mortality). RNN AUROCs steadily increased from day 1 to day 5 and were higher than their PELOD counterparts on days 4 and 5 (p < 0.006).

Figure 3.

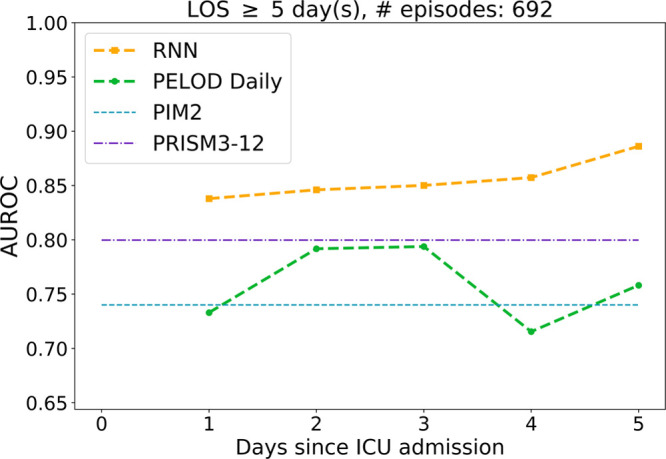
Area under the receiver operating characteristic curve (AUROC), as a function of days since ICU admission, of recurrent neural network (RNN) predictions and Pediatric Logistic Organ Dysfunction (PELOD) daily scores on test set episodes whose length of stay (LOS) was at least 5 d and had Pediatric Index of Mortality (PIM) 2 and Pediatric Risk of Mortality (PRISM) III scores.

Table 2 compares the AUROC of the RNN predictions at the 12th hour after PICU admission with those of PELOD day 1, PIM 2, and PRISM III scores. The AUROCs were computed over the 2,475 test set episodes with greater than or equal to 24 hours ICU LOS and had the three clinical scores available. Figure S-2 (Supplemental Digital Content 10, http://links.lww.com/PCC/B680; legend, Supplemental Digital Content 1, http://links.lww.com/PCC/B671) shows the corresponding ROC and precision-recall curves. At any fixed level of sensitivity or recall, the RNN 12th hour predictions had a higher specificity or precision than the other three scoring systems. Table 2 parses the AUROCs according to primary diagnostic category, age, and ICU LOS. When parsing by primary diagnosis, all four models generally showed the best discrimination in neurologic patients and least in respiratory patients. Among the age groups, the RNN’s lowest AUROC (0.89) was in the youngest group (< 1 yr) and highest (0.97) in the 10–18 years group. The youngest group had the highest incidence of respiratory patients (48%), whereas the 10–18 years group the lowest (17%). In terms of LOS, all four models performed worse on longer episodes. Even so, for the greater than or equal to 10 days cohort, the RNN AUROC increased from 0.74 (12 hr after admission) to 0.97 at 24 hours prior to discharge (p < 10^–4).

TABLE 2.

Comparison of Area Under The Receiver Operating Characteristic Curves of Different Scores Evaluated Across Different Subgroups of the Test Set

Primary Diagnosis Category	No. of Episodes	Median ICU LOS (d)	No. of Died	Mortality Rate, %	Recurrent Neural Network (12th hr)	Pediatric Index of Mortality 2	Pediatric Risk of Mortality III (12th hr Variant)	Pediatric Logistic Organ Dysfunction Day 1 Score
All	2,475	2.9	99	4.0	0.94	0.88b	0.89a	0.85c
Respiratory	781	3.3	25	3.2	0.87	0.79	0.82	0.68b
Neurologic	370	2.6	21	5.7	0.98	0.96	0.98	0.97
Oncologic	281	2.9	7	2.5	0.99	0.93	0.89	0.88
Infectious	197	3.2	14	7.1	0.90	0.81	0.85	0.79
Gastrointestinal	111	4.9	8	7.2	0.92	0.85	0.88	0.85
Age group (yr)
0–1	437	3.6	24	5.5	0.88	0.88	0.86	0.82
1–5	600	3.0	23	3.8	0.95	0.88	0.86	0.88
5–10	437	2.8	17	3.9	0.94	0.88	0.96	0.84
10–18	813	2.8	29	3.6	0.98	0.87a	0.90	0.86a
18+	188	3.0	6	3.2	0.90	0.88	0.92	0.85
LOS, d
1–3	1,270	1.8	28	2.2	0.99	0.95	0.94	0.94
3–5	513	3.9	21	4.1	0.97	0.92	0.90	0.88
5–10	389	6.8	17	4.4	0.94	0.87	0.89	0.86
10+	303	14.2	33	10.9	0.74	0.64	0.72	0.66

LOS = length of stay.

p values of comparisons between the recurrent neural network and one of the three other models are denoted by subscripts (^ap < 0.05; ^bp < 0.01; ^cp < 0.001).

The RNN predictions at all test set time points (N = 721,024) were partitioned into 50 quantiles, compared with quantile actual outcomes, and showed good calibration (chi-square = 0.16; p = 1.00) (Fig. 4). Table S-7 (Supplemental Digital Content 8, http://links.lww.com/PCC/B678) displays the Brier score, the Hosmer-Lemeshow C* statistic (50 DoF), and Cox calibration regression metrics computed from the 721,024 RNN predictions. The Cox calibration regression line’s slope was 0.73 with a chi-square of 15.66 (p = 0).

Figure 4.

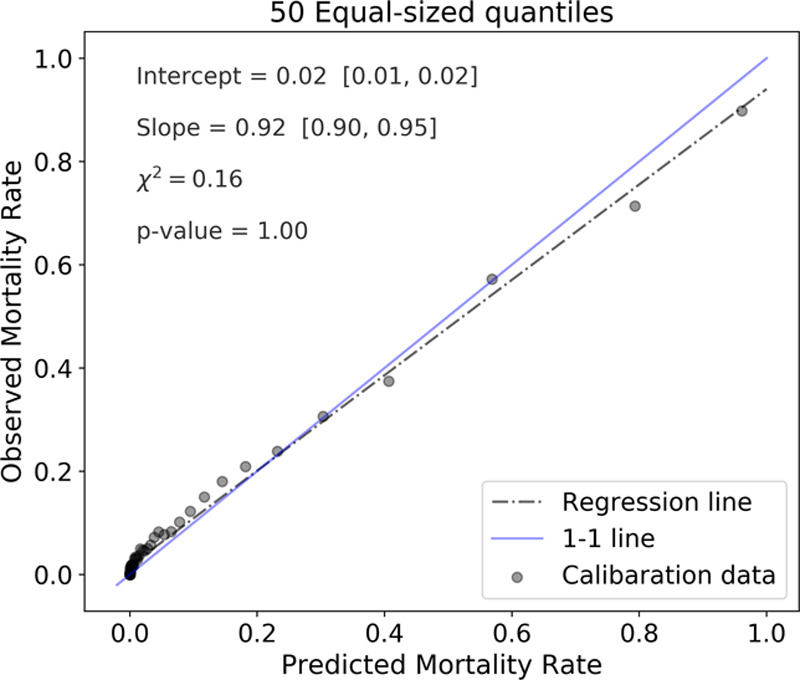
Calibration of recurrent neural network predictions at all 721,024 time points of all test set episodes. Each of the 50 quantiles contains either 13,865 or 13,866 predictions.

Although the preceding results reflect the RNN’s population-level behavior and performance, Figure 5 illustrates trajectories of RNN predictions in four patient episodes, showing the dynamic nature of individual predictions. The four episodes show the following: a survivor whose ROM started high but fell toward zero (dashed green), a survivor whose ROM stayed low throughout (dash-dot cyan), a nonsurvivor whose ROM stayed high for the entire episode (solid purple), and a nonsurvivor whose ROM started low but increased over time (dotted orange).

Figure 5.

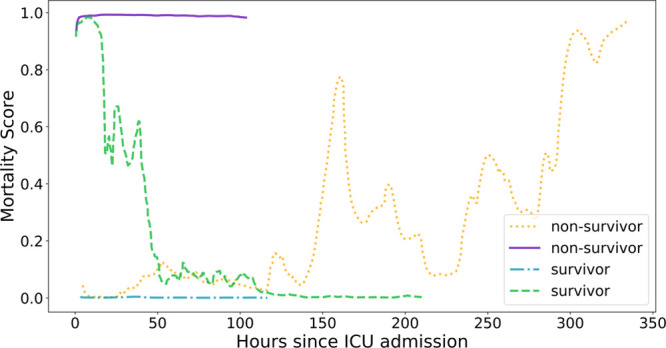
Recurrent neural network–generated mortality risks, as functions of time, for two surviving episodes (cyan and green) and two nonsurviving ones (purple and orange).

Training the model took approximately 9 hours. Generating a single prediction took approximately 30 ms.

DISCUSSION

Recently, it has become increasingly clear that artificial intelligence and deep learning hold the promise of assessing a great number of inputs in a timely, automated fashion at the bedside, providing continuous assessment of a child’s condition (11–14, 19–22). There has been appropriate and long-standing concern about applying population-based ROM assessments to individual patients. Scores developed for quality assessment and benchmarking are intended for different purposes than those meant to assess changes in an individual patient’s condition. An RNN model is presented here as a proof of concept for a deep learning methodology that provides the latter type of score, which could be useful to guide patient care especially when patient condition changes rapidly. This method improves on previous systems that periodically or continuously update, such as the daily PELOD scores and the Rothman Index, by sequentially processing large amounts of streaming clinical data (containing hundreds of variables) as they become available and explicitly integrating new measurements in the context of previous data.

The RNN’s patient SOI assessment is based on predicting ICU mortality. As the Rothman Index developers argued, “there is no generally accepted definition of patient condition” even though this is an important concept to those providing care, and a patient considered “far from death” (i.e., has low mortality risk) at any given time is also considered in “good condition” (7). The point of critical care is to decrease a patient’s ROM or at least prevent it from increasing. This intuitively and necessarily must alter an individual’s risk assessment over time, and this should be reflected in a changing ROM. The AUROC was chosen to measure discrimination performance of this dichotomous predictive task because it reflects how well a model can extract information about the relative well-being of an individual. The AUROC measures the probability that a model correctly discriminates between a randomly chosen survivor and a randomly chosen nonsurvivor, that is, it measures how often a model correctly ranks their mortality risks relative to each other (28). Therefore, a model with a high AUROC would predict a higher ROM for patient A than for patient B if patient A is in “worse condition” or more severely ill, than patient B, with the premise that “close to death” is equivalent to “in bad condition.” Similarly, the model’s predicted ROM for an individual patient would increase when the patient’s condition worsens. Although PIM 2 and PRISM III were developed for different purposes, the AUROCs of these scores for this study’s cohort were shown to provide some context for the RNN, serving as comparators.

The RNN model’s discrimination performance improved over time (Figs. 2 and 3) as a result of both increased observation time and reduced lead time. Performance improved the closer the prediction was to discharge, with its AUROC reaching 0.99 a full day before discharge (for survivors) or death. Figure S-1 (Supplemental Digital Content 9, http://links.lww.com/PCC/B679; legend, Supplemental Digital Content 1, http://links.lww.com/PCC/B671) illustrates the effect of lead time. In the first 24 hours after admission, there was a 0.2 absolute difference in AUROCs between the two groups; in this period, the observation time is the same for both groups, but the lead time differs by a median ICU LOS 9 days. In the last 48 hours prior to discharge, when the lead time is the same for both groups, there is no longer a significant AUROC difference. Hence, the 0.2 AUROC difference between the two groups in the first 24 hours is an estimate of the impact of a 9-day lead time. Note that the increase in observation time from admission to 24 hours later is a small fraction of the prediction lead time, and in that short time window, the RNN AUROCs for both groups increased by 0.15.

The discrimination of the RNN’s predictions at 12 hours after admission was better than that of PELOD’s day 1 score, PIM 2, and PRISM III (Table 2, first row) despite PELOD being derived from a 24-hour window and PIM 2 and PRISM III incorporating data from pre-ICU admission not available to the RNN. Most likely, the RNN performs better because it uses more variables and integrates their measurements dynamically, in context, as it acquires them. Further, the RNN uses many more coefficients or weights than the number of its input variables, allowing the model to capture more complex interactions than a logistic regression applied to those same variables. These points are further illustrated by the AUROC comparisons between the RNN and daily PELOD scores (Fig. 3). Comparing the performance of the daily PELOD and RNN scores with the pediatric Rothman Index (pRI) in our cohort would make this study more comprehensive; however, the proprietary nature of the pRI did not make this possible.

The RNN training cohort contained episodes including all diagnoses, although, unlike PIM and PRISM, the RNN did not use diagnostic information as an input. The RNN (12th hr predictions) performed well on different primary diagnoses, generally achieving higher AUROC than the other three scores (Table 2). All four models displayed similar discrimination in neurologic patients, and each discriminated better in neurologic and oncologic patients than in respiratory patients. The respiratory group classification includes all patients with respiratory failure, whether due to primary lung disease or some other cause, making this diagnosis somewhat of a farrago of other diagnoses. The respiratory patients also have longer LOS than the neurologic and oncologic patients. These two factors may contribute to greater heterogeneity of ROM predictions for respiratory patients, decreasing discrimination between survivors and nonsurvivors especially in the first 24 hours. Across age groups, the only significant difference in the RNN AUROCs was between the 10–18 years (0.98) and less than 1 year (0.88) groups (p < 0.03). Interestingly, the difference in the incidence of respiratory patients in the two groups (48% in the youngest group vs 17% in the 10–18 yr group) is likely the reason for the AUROC difference between the two groups. It is also worth noting that the 10–18 group comprised about 32% in the development (training and validation) set, making it the largest age group in the cohort, whereas the less than 1 year group was one of the smaller age groups (Table 1).

Not surprisingly, the AUROC of all four models (12th hr predictions for RNN) consistently decreased for longer stays. For episodes in the shortest-stay group, the RNN predictions are made no more than 3 days prior to discharge, whereas in the last group, the predictions can be more than 30 days prior to discharge. The changes in the RNN AUROC across these groups are consistent with the lead time effects previously discussed. For the complex, long-stay patients, continuous assessment by the RNN provides a continuous indication of patient status which may change over time. The RNN assessment performs particularly well 24 hours prior to the end of these lengthy episodes. Indeed, two of the example trajectories in Figure 5 keenly illustrate this: the predicted ROM for a survivor who was in the PICU for almost 10 days was above 80% for most of the first 24 hours then fell below 0.5% for the last 100 hours, consistent with the successful resuscitation of the child. In contrast, the predicted ROM for a nonsurvivor who was in the PICU for almost 15 days started below 0.5% but increased to over 80% at different intervals, indicating deterioration. The changing patient scores over time may at first suggest inconsistent calibration over time, but Figure 4 shows consistent calibration behavior over all time points. This implies that even though a prediction may change over time, it remains reasonably calibrated at each time point. The high Hosmer-Lemeshow C* statistic and Cox line regression metrics (Table S-7, Supplemental Digital Content 8, http://links.lww.com/PCC/B678) are a direct result of the large number of predictions (n = 721,024) that went into its computation; therefore, these metrics can be misleading (29, 30).

The generally high AUROCs of the RNN model at different prediction times and in different subpopulations combined with the premise that mortality risk is a proxy for SOI support the notion that the RNN predictions potentially could serve as a real-time acuity score. The fact that the scores change over time for some patients is hardly surprising. One would hope that a child with a high SOI could receive effective therapy that would decrease their expected mortality as shown in Figure 5. Conversely, a child who presents with a low ROM may undergo a life-threatening event or acute deterioration unexpectedly which would be reflected in a ROM increase. The former of these observations would be consistent with a positive response to clinical interventions, whereas the latter could serve as a warning of a patient’s deleterious change in status and indication for a change in management. Further, the magnitude and speed of these changes could indicate the need for the urgency and amount of an intervention.

If appreciable changes of the RNN ROM within an individual patient episode are to be helpful for clinicians to guide therapy, it would be helpful to understand which measurements led to such changes. The physiologic and other variables analyzed by the established models are clinically understandable; one readily understands that a low pH or hypoxia or the presence of a ventilator is associated with a greater ROM. The weights of these logistic regression models indicate which variables are contributing to the scores, and in the case of PELOD, also how they are changing. This is perhaps less clear in a complex deep learning model with hundreds of inputs. Nevertheless, a parallel feature contribution analysis can also be provided for the RNN predictions. Previous research quantified the contribution of different classes of features for clinical tasks (10), and further analysis of relative feature contribution in deep learning models is the subject of another investigation (31).

Finally, although PELOD scores are updated daily, their temporal granularity may not be sufficient to track rapidly changing patient conditions in the critical care setting. The frequency of the RNN updates is limited only by availability of new measurements. As the computation timings showed, the execution time for a single prediction is negligible.

We emphasize the “proof of principle” nature of this study’s methodology. Unlike published PIM and PRISM models, the RNN model (its exact inputs and weights) is not meant for deployment at other institutions. Rather, this article shows the feasibility of an accurate, EMR-based, dynamically and continuously updating SOI assessment using an advanced deep learning technique and to motivate further research. Because of the single-center nature of the cohort used in this study, the EMR data aggregation, curation, imputation strategy, and other preprocessing steps that created the input variables used to develop this particular RNN model may not be appropriate for other institutions with their own protocols and implementations of disparate EMR systems. Additionally, the associations captured by this RNN model reflect the practices of one institution but not necessarily those of others. We hope that this proof of concept demonstration of the RNN’s potential will encourage practitioners and vendors to improve their data capture and data science capabilities and harness them for the care of critically ill children. Because the principles used in the development are easily generalizable to other populations, the framework established here can be used by other institutions to train and analyze models using variables that are available to them. Developing a model requires many steps and decisions; what data to include, how to impute, and which algorithm (a single logistic regression or a deep RNN) to use for fitting the assembled data are just a few of those steps. Several reasonable choices can be made at each step. It is important to have an appropriate and robust performance assessment schema that can measure the impact of any of those choices.

This is a study on previously collected data. Although these data are presented in a clinically relevant fashion to the RNN as they occur, these findings await a more realistic concurrent clinical demonstration of their potential value. Such demonstrations or deployment will require careful understanding of many different areas well outside the scope of this study (32, 33).

CONCLUSIONS

An RNN was trained to continuously generate individual SOI scores from EMR data by predicting risk of ICU mortality. It has the capability to process hundreds of variables from the EMR and integrate them dynamically as the measurements become available. The results show the potential to provide an accurate, continuous, and real-time assessment of a child’s condition in the ICU.

ACKNOWLEDGMENTS

We are grateful to the L.K. Whittier Foundation for funding this work and to Alysia Flynn, PhD, for her assistance in data management.