A single-embryo, single-cell time-resolved model for mouse gastrulation

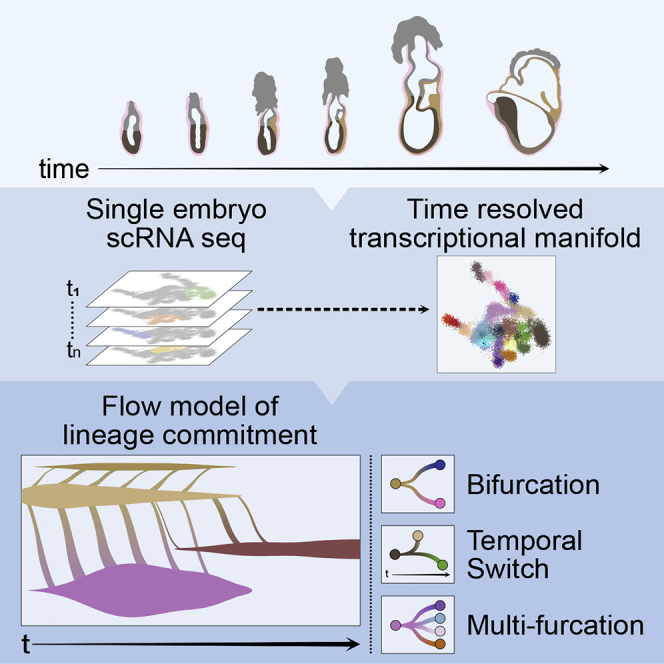
Summary

Mouse embryonic development is a canonical model system for studying mammalian cell fate acquisition. Recently, single-cell atlases comprehensively charted embryonic transcriptional landscapes, yet inference of the coordinated dynamics of cells over such atlases remains challenging. Here, we introduce a temporal model for mouse gastrulation, consisting of data from 153 individually sampled embryos spanning 36 h of molecular diversification. Using algorithms and precise timing, we infer differentiation flows and lineage specification dynamics over the embryonic transcriptional manifold. Rapid transcriptional bifurcations characterize the commitment of early specialized node and blood cells. However, for most lineages, we observe combinatorial multi-furcation dynamics rather than hierarchical transcriptional transitions. In the mesoderm, dozens of transcription factors combinatorially regulate multifurcations, as we exemplify using time-matched chimeric embryos of Foxc1/Foxc2 mutants. Our study rejects the notion of differentiation being governed by a series of binary choices, providing an alternative quantitative model for cell fate acquisition.

Graphical abstract

Highlights

• •Single-embryo scRNA-seq synthesis of morphology and transcriptional staging
• •A network flow model infers differentiation of embryonic cell ensembles
• •Gastrulation is dominated by progenitor states that continuously multi-furcate
• •Single-embryo chimeras control functional studies of TFs over time and lineage

A time-resolved, high-resolution model charts differentiation dynamics during mouse gastrulation and reveals that for most lineages, cell fates arise from multi-furcation events rather than classical tree-like bifurcation.

Introduction

Early embryonic development in mammals proceeds through robust acquisition of specialized cellular properties by individual cells that specify the basic embryonic lineages, which, in turn, form the first organs. Decades of research using model organisms have provided tremendous insight into the activity of genes and pathways driving this process and ensuring its robustness (Arnold and Robertson, 2009; Bedzhov et al., 2014; Ebisuya and Briscoe, 2018; Tam and Ho, 2020). This had far-reaching implications for other fields such as cancer and regenerative medicine (Ben-Porath et al., 2008; Spagnoli and Hemmati-Brivanlou, 2006). Advances in single-cell technologies recently enabled high-resolution charting of mouse embryonic development, mapping comprehensively the transcriptional states of developing embryos during gastrulation (Argelaguet et al., 2019; Chan et al., 2019; Cheng et al., 2019; Grosswendt et al., 2020; Ibarra-Soria et al., 2018; Lescroart et al., 2018; Mohammed et al., 2017; Nowotschin et al., 2019; Pijuan-Sala et al., 2019; Scialdone et al., 2016) and organogenesis (Cao et al., 2019; Chan et al., 2019; de Soysa et al., 2019; Han et al., 2018; Nowotschin et al., 2019; Tam and Ho, 2020). Yet, moving from atlases toward the inference of quantitative dynamics during cell state transitions represents a major open challenge in the field. Pseudotemporal ordering defines the progression of cell trajectories based on computational inference of transcriptional similarities (Tanay and Regev, 2017). However, the rapid nature of development, characterized by a continuous flux of intracellular molecular changes within a short time frame, poses unique challenges for this approach (Tritschler et al., 2019) (e.g., when bifurcation points are fuzzy or when distinct differentiating populations converge by activating common gene modules in a non-hierarchical manner). Similarly, pseudo-temporal ordering is difficult when differentiation to a specific cell type occurs over a wide range of time during development. Alternative approaches that aim at merging single-cell analysis with lineage relationships are rapidly evolving, using the estimation of transcriptional derivatives (RNA velocity) (La Manno et al., 2018), time series experiments (Fischer et al., 2019; Schiebinger et al., 2019), or by simultaneous direct recording of cell histories, with promising but still partial coverage (Bowling et al., 2020; Chan et al., 2019; Kalhor et al., 2018; Raj et al., 2018; Spanjaard et al., 2018). In principle, atlases can be constructed from samples that are staged using traditional methods (Cao et al., 2019; Pijuan-Sala et al., 2019), thus facilitating coarse-grained temporal modeling of inferred transcriptional states. However, refining such classical staging and augmenting it with quantitative kinetic modeling of transcriptional regulation remains to be addressed.

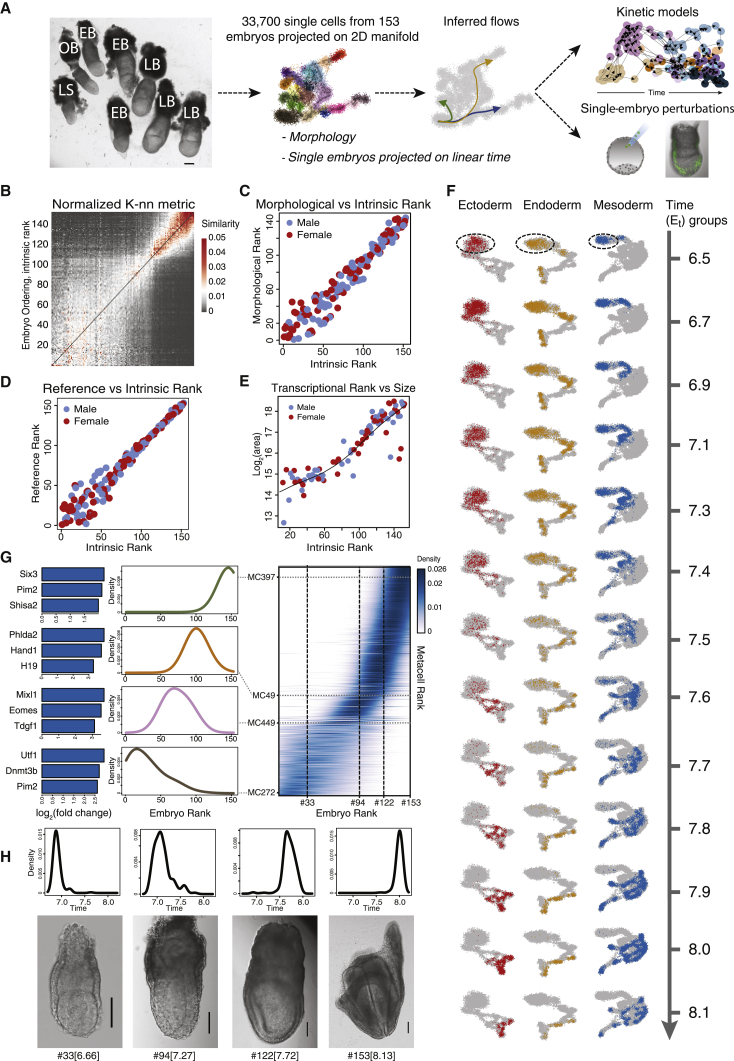
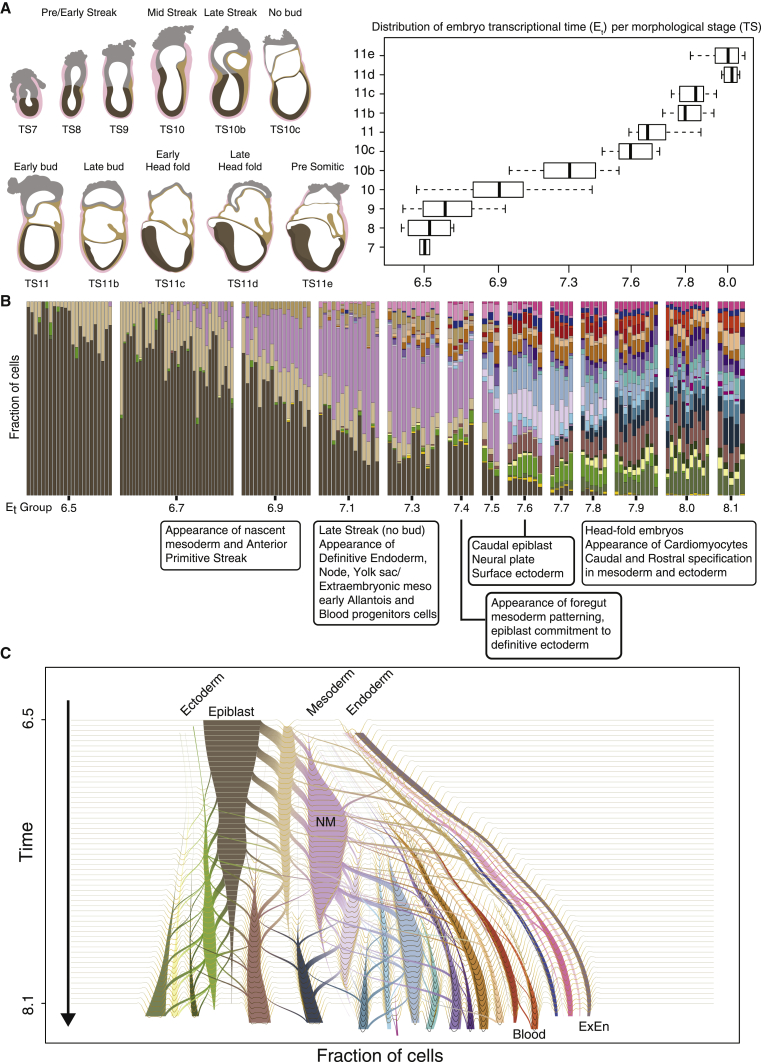
Precise staging of developmental progression is critical in order to describe sequences of developmental events in a consistent and comparable fashion, in particular when studying multiple strains, genetic perturbations, and other interventions. In the mouse, timing of development using “days postcoitum” (dpc) provides only a nominal estimate of progression for each embryo. This is because litters are often highly heterogeneous, frequently constituting embryos from several morphologically distinct embryonic stages (Figure 1A) (Downs and Davies, 1993). Another unique challenge of studying viviparous development is that up to the point of extraction, the embryo is largely concealed. To address this, methods for staging embryos using morphological features, such as those proposed by Theiler (1989) and later elaborated on by Downs and Davies (1993), are still considered the gold-standard in the field. However, morphology-based approaches are limited by the resolution provided by the number of such distinguishable stages and the qualitative nature of such classification.

Figure 1.

Resolving time and gene expression in single cells and single embryos

(A) Natural variation among litters and littermates (left panel) is harnessed to generate a temporal transcriptional model of embryonic development. Shown is a schematic representation of the workflow. Image of a single litter isolated at 7.75 dpc. Scale bar, 200 μm. LS, late streak; OB, no bud; EB, early bud; LB, late bud.

(B) Embryo-embryo similarity matrix ranking the embryos according to their intrinsic transcriptional makeup.

(C) Comparison between intrinsic transcriptional rank and ranking based on morphological feature analysis.

(D) Comparison of intrinsic versus external ordering using projection on a reference atlas (Pijuan-Sala et al., 2019).

(E) Comparison between transcriptional rank and size estimate of embryo cross-section (log2, μm², fitted line using smooth spline interpolation with λ = 7.1 × 10⁻³).

(F) Projection of cells following binning of embryos into 13 time groups, over 2D MC projections, separately for each of the three embryonic germ layers (epiblast is marked by dashed ovals).

(G) Metacells (MCs) represent a transcriptional state shared by cells from numerous embryos, spanning a time range. Right panel: distribution of embryo rank (columns) for cells included in each MC (each represented by a single row). Rows are normalized to reflect the temporal heterogeneity of each MC. Left panel: highlighted rank distributions of individual MCs from different lineages, and the expression of selected marker genes from each MC (bar plots; log2, relative to mean expression over all MCs).

(H) Four representative embryos are shown alongside the time distribution of their comprising cells (calculated from the MCs mean age). Scale bar, 100 μm. #Embryo rank; in brackets, calculated time (E_t).

See also Figure S1 and Table S1.

In the current study, we wished to move further toward an ideal representation of mammalian embryonic development as a continuous process. We reasoned that single-cell RNA sequencing (scRNA-seq) of individual embryos, in correlation with morphological measures obtained from microscopy, will allow placing the embryos on a continuum of transcriptional transformation. Assigning a singular developmental time to cells originating from the same embryo provided a timestamp to each cell in our dataset. This enabled the construction of a flow model (Ahuja et al., 1993) for the transition of cells on the transcriptional manifold. Flow analysis distinguished early specialization of few embryonic cell types, identified their stepwise acquisition of transcriptional identity and linked it with the hierarchical activity of fate-specific transcription factors (TFs). However, for most of the cells in the embryo, the data suggest complex transcriptional dynamics in multipotent progenitor states and complex combinatorial activity of TFs that drive multi-furcation rather than the classical tree-like bifurcation. The temporal atlas and associated flow model form the foundations for elucidating intrinsic and extrinsic effects shaping cell fate decisions in vivo. This is illustrated by studying mesoderm gene regulation by Foxc1 and Foxc2, using single-cell chimera knockout experiments with tight single-embryo time control.

Results

Quantification of morphology and scRNA-seq data from 153 E6.5–E8.25 embryos

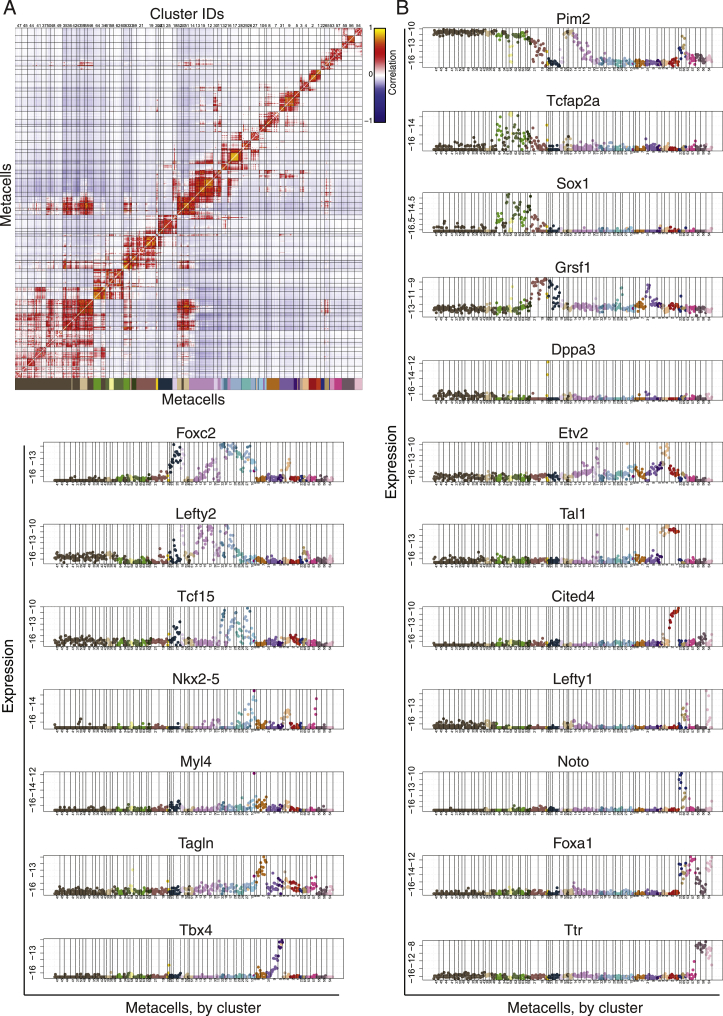
To generate a continuous fate map of mouse gastrulation up to somitogenesis, we performed scRNA-seq on dissociated cells from individual embryos representing early post-implantation up to pre-somitic stages, corresponding to embryonic day (E) ∼E6.5–E8.25 (Figure 1A; Table S1). Each embryo was handled and imaged separately for subsequent assessment of morphological features and size measurements. To focus on tissues that contribute to the embryo proper, the ectoplacental cone, parietal endoderm, and much of the extraembryonic ectoderm, were removed prior to dissociation. To allow sequencing of single cells separately from each embryo, we used MARS-seq (Jaitin et al., 2014), where single cells are index-sorted directly into multi-well plates using a flow cytometer, in which they are barcoded prior to pooling. In this manner, 33,700 cells from 153 embryos were sequenced at a median coverage of 4,100 unique molecular identifiers (UMIs) per cell (Figure S1A). A sufficient representation of the various developmental stages was ensured by morphological assessment. Due to the inherent sparsity of scRNA-seq data, metacell analysis (Baran et al., 2019) was employed on the entire dataset, by which transcriptionally similar single cells are aggregated to form more cohesive and distinct transcriptional states termed metacells (MCs). In this manner, we robustly mapped all transcriptional states and generated their similarity graph.

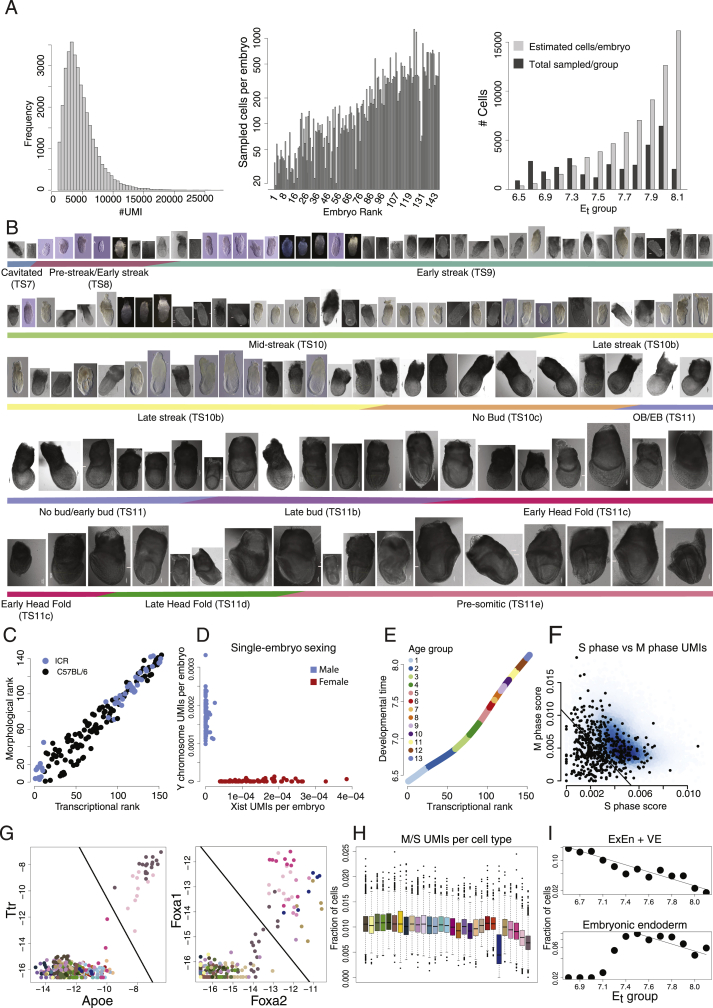
Figure S1.

Sampling single embryos, related to Figures 1 and 2

(A) Distribution of unique reads (UMI) per cell in the manifold. Cells with less than 1000 UMIs were filtered out of the analysis (left panel), Number of cells from each embryo represented in the manifold, sorted according to intrinsic rank (middle panel), and sampled number of cells per age group relative to the estimated number of cells (Figure 2B) (right panel).

(B) Pictures of embryos sampled in the study, ranked and sorted according to morphology. Images are uniformly scaled, scale bar = 100um.

(C) Classification of embryos according to parental strain used in this study (ICR and C57BL/6), demonstrating coordinated correlation between morphology and transcriptional ranks between strains.

(D) Sexing of individual embryos according to the expression of Xist and Y- chromosome genes. Number of UMIs are normalized by total number of UMIs per embryo.

(E) Age group allocation of embryos: Embryos are partitioned into 13 age groups. Intrinsic ranks are translated into a developmental timescale using transcription and size measurements of embryos (Figure 1E).

(F) Density plot of single-cell calculated cell-cycle scores according to combined M- and S- phase UMI counts. Cutoff line represents cells having a low cell-cycle score. These cells are highlighted in the 2D projection in Figure 2C. Black dots represent endoderm cell types (definitive endoderm, foregut, node/notochord, VE, ExEn), that are enriched for low score cells.

(G) Classification of embryonic and extraembryonic endoderm (ExEn) in the flow model: All MCs above the cutoff line in the left panel (Ttr versus Apoe expression) were classified as ExEn. All MCs not classified as ExEn that exhibit high Foxa2 and Foxa1 expression, were assigned to the group of embryonic endoderm. For both groups, growth loss constants ${\text{λ}}^t>0$ were used in the flow model (see I).

(H) Boxplot distribution of single-cell cell-cycle score according to cell type.

(I) Estimation of growth loss constants ${\text{λ}}^t$ for embryonic endoderm and ExEn/VE. Shown is the fraction of these cells over time (log scale). Lines correspond to growth loss constants ${\text{λ}}^t=0.17$ for ExEn/VE, and ${\text{λ}}^t=0.12$ for embryonic endoderm, as used in the network flow model.

Projection of single embryos over an absolute developmental timescale

To place the embryos on a sequential time axis, we first ranked them using morphology alone (Figure S1B). We then developed a strategy for ranking embryos by K-nn similarities among single-cell profiles (Figure 1B). This resulted in remarkably high comparability between the two independent ranking schemes (ρ = 0.97) (Figures 1C and S1C). For external validation, we projected cells from each embryo onto a recently published mouse single-cell gastrulation atlas (Pijuan-Sala et al., 2019) and re-timed our single cells using this reference atlas consisting of pooled embryos from 6-h time intervals. We averaged the external cell timing for each embryo, deriving again a high degree of concordance with our internal ranking strategy (ρ = 0.98) (Figure 1D). Finally, comparison of embryo ranking to the estimation of embryos’ physical growth rate (approximated by the physical area under the microscope) provided alignment of our ranks to an absolute size scale (ρ = 0.91) (Figure 1E). Single-embryo sampling also facilitated controlled analysis of male and female embryos (genotyped based on Y chromosome RNA) (Figure S1D), demonstrating comparable size and transcriptional distributions between the sexes at these stages (Figures 1C–1E, red versus blue dots). For older embryos, we observed more precise ordering, consistent with the less accurate assignment of morphology and size at early stages, and with acceleration in transcriptional diversification from mid/late streak stage onward. To synthesize all observations, each embryo was assigned a calculated timestamp based on size and transcription (hereinafter designated as E_t). To reduce possible sampling noise and facilitate downstream statistical analysis, we formed thirteen temporal groups labeled E_t6.5–E_t8.1 corresponding to the mean approximated developmental time of embryos within them (3–36 embryos and 884–6,442 cells for each group) (Figures S1A and S1E).

Embryo time and transcriptional states cannot be approximated by one pseudotime

For initial visualization of differentiation dynamics, we separated the dataset using canonical markers into three transcriptional manifolds describing development from the epiblast toward the three germ layers (ectoderm, mesoderm, and endoderm) (Figure 1F). Projection of the thirteen groups of timed embryos on these manifolds showed clear directional transition from the epiblast ground state and subsequent differentiation and diversification, supporting the notion that pseudotime can approximate embryonic development over the manifold. Because each MC is made up of cells from different embryos corresponding to the same transcriptional state, we could estimate a pseudotime for each MC using the calculated ages of the embryos contributing to them (Figure 1G). In a pseudotime representation of a highly synchronous process, MCs are expected to consist of cells from a narrow range of embryonic times. However, the variation in embryonic times for each MC was generally high (SD 1.1–12 h) (Figure 1G, left panel). Conversely, individual embryos consisted of cells belonging to MCs with varied pseudotimes (SD 1.4–6.5 h) (Figure 1H). This demonstrates that dynamics of transcriptional states are far from coherent and synchronous and accentuates the need for models that represent embryonic development as concurrent and unsynchronized collections of single cells that transition through the transcriptional manifold.

The embryo transcriptional manifold and its growth dynamics

To infer developmental dynamics from the series of acquired single-embryo maps, we made two assumptions: (1) embryos that are similarly timed will include cells that are similarly distributed over the transcriptional manifold, such that progression in time will involve a gradual change in states over manifold links; and (2) progression in time involves rapid cell proliferation, with rates that may change depending on cell type or position on the manifold. To derive quantitative models supporting the first assumption, we represented the transcriptional space of embryonic development using 461 MC states. These states are linked using a logistic metric function to form a manifold structure (Figure 2A). In this manner, the likelihood of cells to exhibit transcriptional changes between any two states over time is estimated by a probabilistic (i.e., Markovian) manifold distance over the MC graph (STAR Methods). Because MC linkage is not (in practice, cannot be) fully captured by the 2D model representation, we explicitly visualize neighboring MCs using edges on top of the standard 2D embedding of the model (i.e., links on Figure 2A), even if these edges are not well accommodated by the 2D embedding.

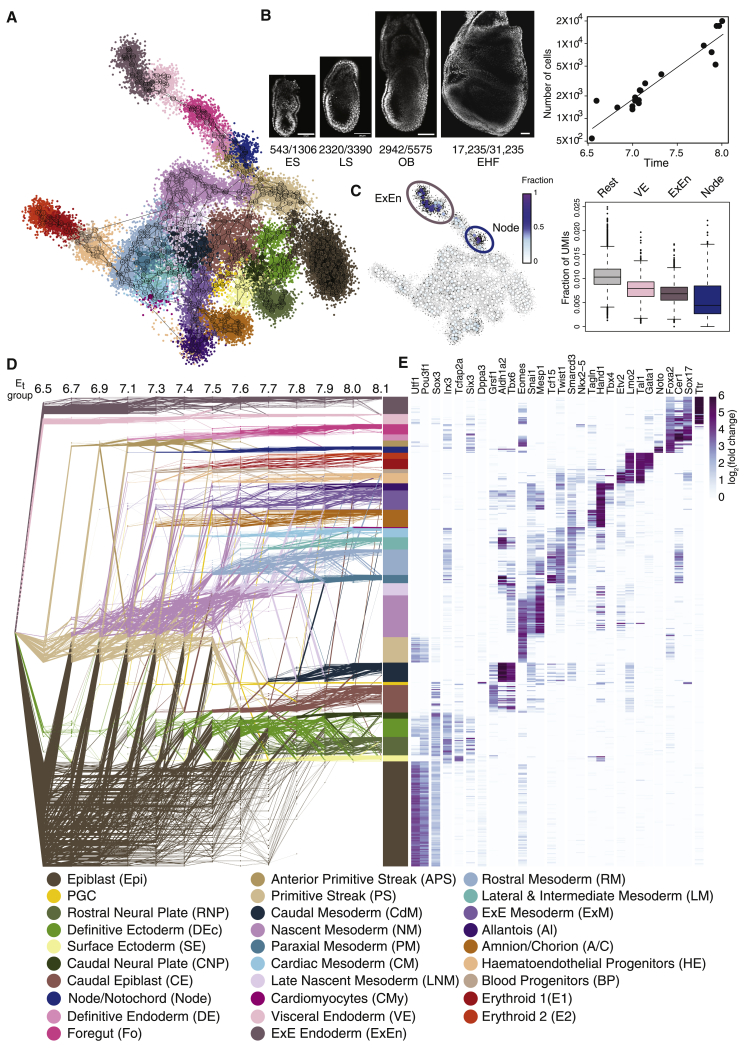
Figure 2.

A network flow model for gastrulation

(A) Color coded 2-D projection of the metacell (MC) graph (numbered nodes connected by edges depicting the most similar neighbors for each MC), representing the entire transcriptional manifold. Single cells indicated by small dots are colored according to the MC they comprise. See color annotation legend below.

(B) Growth rate during gastrulation was estimated by counting DAPI stained nuclei. Left: cell counts of the embryonic compartment out of the total counted cells per embryo are shown for four representative examples. ES, early streak; LS, late streak; OB, no bud; EHF, early head-fold. Scale bar, 100 μm. Right: comparison of embryos’ (n = 19) cell count and estimated embryonic time. For each embryo, time was assigned based on morphological similarity to sequenced embryos.

(C) Single cells with low S-phase and M-phase gene expression (black dots) are highlighted on the 2D projection (left, see Figure S1F and STAR Methods). MCs are colored according to the fraction of such cells they contain. Boxplots (right) depicting the distribution of S-phase/M-phase expression for the identified slower cycling cell types (legend below) and all other cells (Rest). Boxes show interquartile range (IQR) with median of the data. Length of whiskers corresponds to 1.5 IQR, or distance to the extremal value if within 1.5 IQR.

(D) The gastrulation network flow model consists of MCs (nodes in rows) distributed in time (x axis), and flows (edges) that link MCs between adjacent time points. The first time point represents a common source for all MCs. Annotation (color-coded) relies on both marker expression and flow-based fate mapping.

(E) Heatmap showing relative expression (log fold change) of key lineage-specific genes.

See also Figures S2 and S3 and Table S2.

To provide quantitative support to the second assumption regarding proliferation rates, we first estimated the average embryonic growth rate, using image analysis to count nuclei in DAPI-stained embryos that were timed by morphology (Figure 2B). This analysis confirmed the remarkably rapid exponential growth from 900–1,300 cells at E7.0 to 10,000–13,000 cells at E8.0 (average calculated doubling time ∼7 h), consistent with previously reported histology and dissociated cell-based counting (Palis et al., 1999; Snow, 1977). This is also in alignment with studies demonstrating that apoptosis levels in early post-implantation embryos are low and randomly distributed among the embryonic germ layers (Tam and Behringer, 1997). To estimate proliferation rate biases over the manifold, we noted that a distinct and small 10% sub-population of the single cells showed low expression of both M- and S-phase-related genes (Figure S1F), whereas the remaining 90% of the single-cell population showed a distinctive smooth transition between M- and S-stereotypic expression. Initial annotation of MCs using known markers showed that states linked with the embryonic endoderm, node/notochord, visceral endoderm (VE), and extraembryonic endoderm (ExEn) transcriptional programs were enriched for the low proliferation population, in agreement with previous reports (Bellomo et al., 1996; Snow, 1977) (Figures 2C, S1G, and S1H). Tracking of cell-type frequencies over inferred embryonic time allowed estimation of the relative (lower) growth for these populations compared with the rest of the embryo (r = 0.88, 0.83 for embryonic endoderm, VE/ExEn, respectively) (Figure S1I). In summary, the inferred manifold model and estimated cell-type-specific growth rates together set the stage for a model accommodating the two forces that shape embryo cell-state composition over time: the transition between transcriptional states (i.e., differentiation) and the massive growth and proliferation enabling it.

A network flows model infers embryonic differentiation dynamics

To progress toward a fully resolved model of embryonic differentiation dynamics, we developed a network flow model connecting the manifold distributions of the 13 groups of timed embryos, based on our model for differentiation and growth dynamics (Figure 2D). In this representation, MCs are depicted as nodes distributed horizontally over time, and edges denote their predicted transition to the next time point. The flow model uses an approximated mass-conservation strategy (or optimal transport) (Schiebinger et al., 2019) to track cellular differentiation along the manifold links in time. This is implemented via a mincost-maxflow algorithm with convex costs that accommodates uncertainty in sampling cell types at each time point, while considering the variation in cell-type growth rates over time (Figures S2A and S2B; see also STAR Methods, sensitivity and bootstrap analysis). We next used the flow model to refine marker-based cell-type annotation over the transcriptional manifold using the computationally inferred cell fate of MCs representing early differentiating states (Figures 2E and S3; Table S2). This resulted in the annotation of embryonic MCs into 29 cell types (extending annotations in Pijuan-Sala et al. [2019]). We note that annotation assisted by the flow model effectively refines and resolves weakly differentiated and transcriptionally ambiguous groups. For example, we distinguish between two phases of noncommitted nascent mesoderm (early and late) that display differences in differentiation potential and define the first ectodermal cells arising from the epiblast as definitive ectoderm due to their potential to contribute to both surface ectoderm and neural plate fates (Figure 2D) (Harvey et al., 2010).

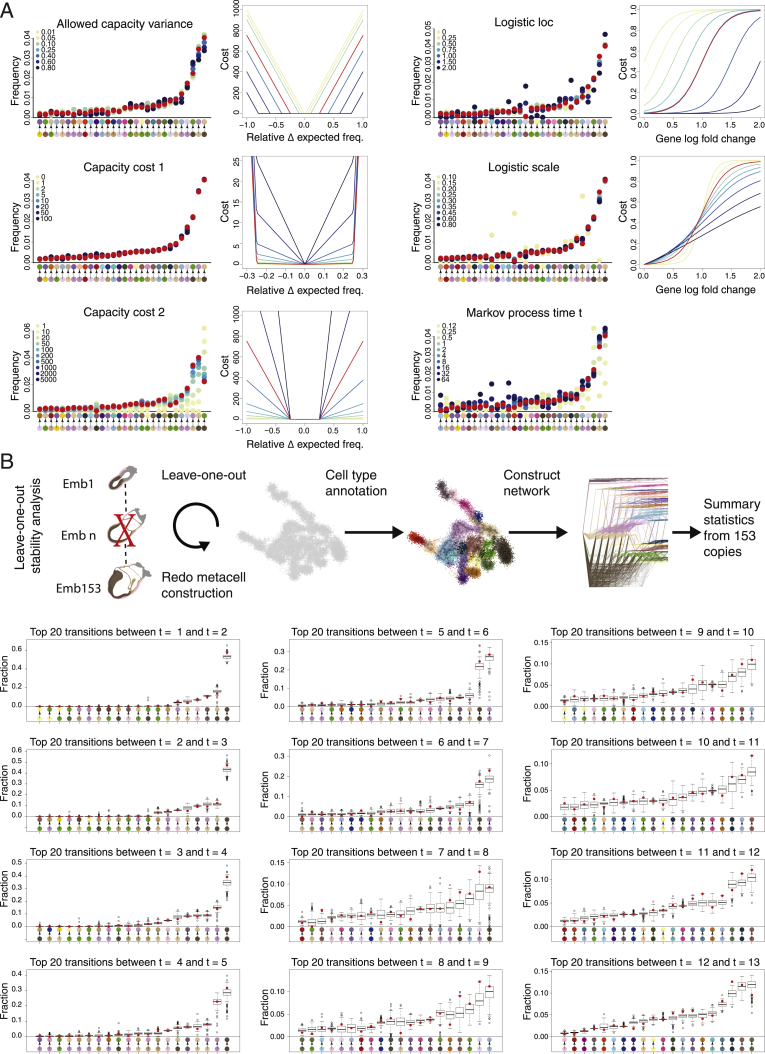
Figure S2.

Robustness and parameter sensitivity analysis of the mincost flow model, related to Figure 2

(A) Parameter sensitivity of cell type transitions. For each parameter examined, flows were re-computed and the mean transition frequency over all time points between pairs of cell types was reported (left panel for each shown parameter). Capacity variance and capacity costs 1 and 2 are the three parameters defining the convex capacity cost (cost functions are depicted in the right panel of each parameter). Logistic loc and scale as well as Markov process time t are parameters used to define manifold distances between MCs. For the parameters logistic loc and logistic scale, the different shapes of the resulting logistic distance are plotted on the right (see STAR Methods for complete description of the mincost flow model). The values used to derive the flow model in Figure 2 are marked in red in all panels.

(B) Robustness analysis of the mincost flow model: For each replica MC model (one embryo left out per iteration), manifold distances and flows are recomputed. Boxplots show for each transition $t\to t+1$ the 20 most frequent flow transitions between two cell types. Boxes represent values of the 153 replica flows, and the transition frequencies of the original flow model are marked as red dots.

Figure S3.

Expression of marker genes and fate map correlation matrix, related to Figure 2

(A) Annotation of MCs using flows. Shown is the second-order correlation matrix of time-averaged incoming and outgoing flows per MC. Correlation matrix was hierarchically clustered into 65 groups. See STAR Methods for additional information.

(B) Canonical marker genes expression supporting the clusters annotation. MCs are sorted and separated according to the hierarchical cluster tree from A (log2 of UMI frequency, y axis).

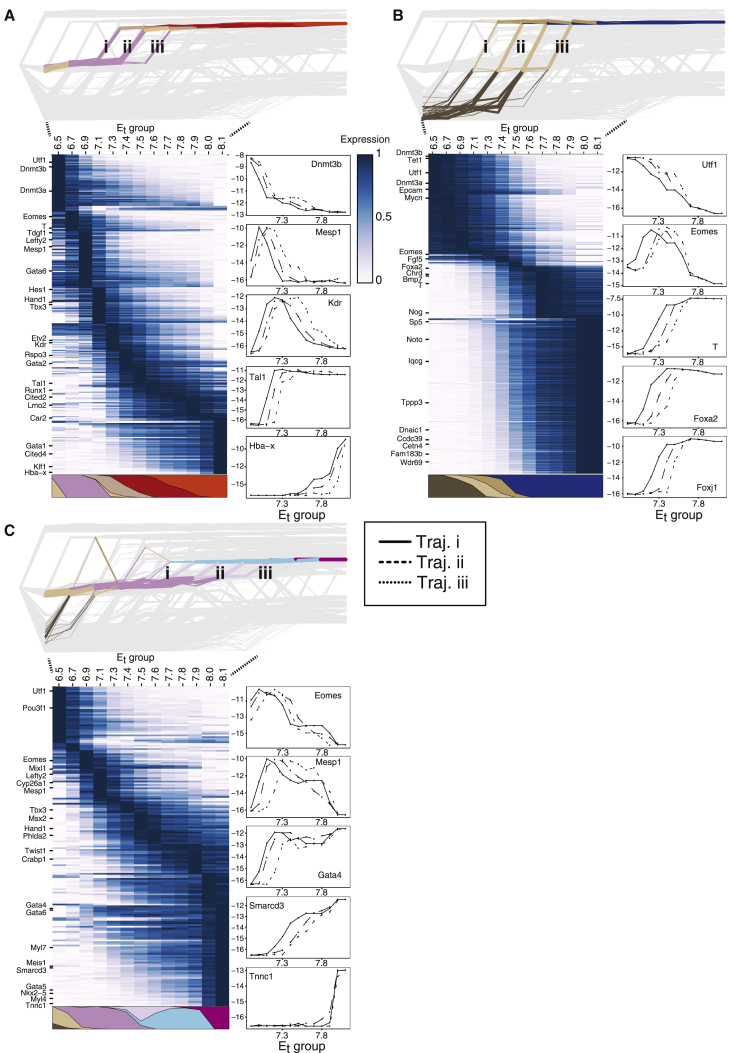
Tracing back the kinetics of committed developmental trajectories

Network flows provide a framework for understanding how strongly committed cell states emerge over time. The flow model defines different possible timed trajectories leading to any strongly specified transcriptional state, which can be depicted as paths over the network diagram (Figure 3, top panels). The kinetics of genes participating in a differentiation program can be estimated as the mean expression per absolute time (Figure 3, heatmaps) and can also be decomposed into the main temporal regimes composing it (Figure 3, line graphs). These tools provide a quantitative view into the differentiation of blood, node, and cardiomyocyte cells, the first highly specialized cell types in the early embryo. Early blood progenitors are among the first functional cells to be specified. Consistent with previous studies that identified the origins of the extra-embryonic mesoderm, including primitive hematopoiesis, to the proximal primitive streak (Huber et al., 2004; Lawson and Pedersen, 1992), our model predicts that primitive erythroid cells originate from primitive streak (PS) cells at the earliest time point (Figure 3A). In fact, according to our model, PS cells from E_t6.7 onward are unlikely to contribute to the blood lineage (Figure 3A). These cells, passing through a transient nascent mesoderm (NM) state (characterized by genes such as T, Mixl1, and Mesp1), rapidly lose the epiblast gene signature and begin expressing sequential waves of key regulatory genes. Notably, Tal1, Kdr, and Etv2 are observed to be expressed at appreciable levels by E_t6.9, closely followed by a combination of factors restricting the cells to the hematopoietic fate, such as Runx1 and Lmo2 (Figure 3A).

Figure 3.

Traceback of differentiation fates and their expression kinetics

(A–C) Flow tracebacks were performed from (A) erythroid 2 (MC#1), (B) node/notochord (MC#367), and (C) cardiomyocyte (MC#57) states. Network plots depict traced-back flows color-coded by annotated cell types and labeled (roman numerals) according to key temporal trajectories. Heatmaps show average expression kinetics for genes with the highest variance over the trajectories. Colored polygons represent the cell type composition of the traceback at each time point (combining the trajectories). Line graphs show the absolute expression level (log2 of UMI frequency, y axis) for select marker genes, along each of the trajectories shown in the respective network plot.

The node is a distinct structure that arises from the anterior PS at the distal tip of the late streak embryo (Figure 3B). The node constitutes a major signaling center and is critical for correct patterning of the embryo and determination of the left-right axis. This is achieved by directional flow of extracellular fluid driven by clockwise rotation of specialized cilia (Hirokawa et al., 2006). The ciliated node cells observed in our manifold are identified as cells expressing high levels of Foxj1, a TF known to be critical for ciliary development (Chen et al., 1998), and numerous genes directly relating to cilia structure and function such as Tppp3, Fam183b, and Nek1 (Figure 3B). A small number of Foxj1⁺ cells can be identified as early as E_t6.9 and begin expressing cilia genes closely thereafter. These cells are predicted to arise from anterior PS progenitors, consistent with previous reports (Balmer et al., 2016; Tam and Beddington, 1987). Foxj1 expression correlates to the expression of additional TFs critical for node morphogenesis such as Noto (Beckers et al., 2007), Rfx3, and T. These are preceded by the expression of TFs characteristic of the anterior PS, Gsc, Mixl1, Eomes, and Foxa2 and anti-correlated with the canonical epiblast gene signature (Figure 3B). Similar analysis illustrates transcriptional kinetics in early progenitors of the embryonic heart (Figure 3C). In summary, the model allows reconstituting the rapid and precise establishment of specialized transcriptional programs toward the blood, node, and heart. Such specialized cells, however, comprise only a small fraction (∼10%) of the embryo by E_t8.1, whereas for the majority of embryonic cell states, differentiation appears more complex, involving more gradual commitment and specialization.

Prototypical dynamics of cell fate transitions in the epiblast, primitive streak, and nascent mesoderm

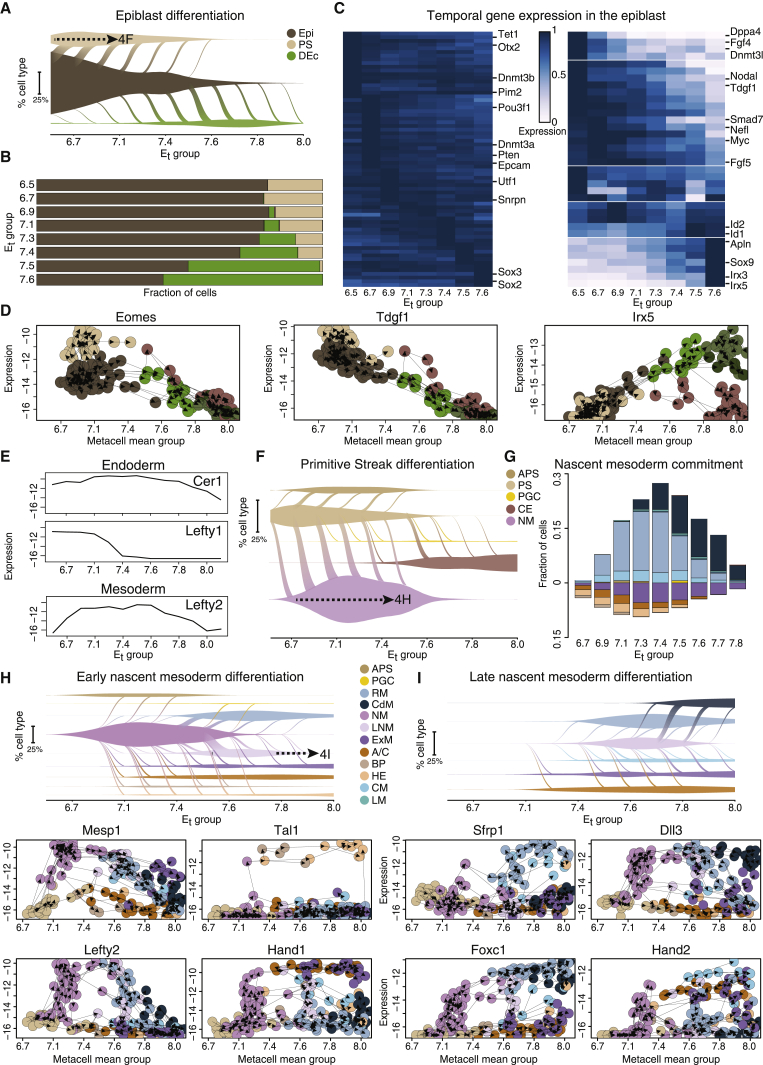
After validating the flow model via analysis of differentiation toward highly specialized fates, we focused our analysis on complex fate decision dynamics, which may involve selection between two fates or more (bifurcation and multi-furcation, respectively). One early example of such process is the segregation of the epiblast to the mesoderm and endoderm lineages through the PS and the restriction of this potential by the formation of definitive ectoderm. This process is shown in our model to span a prolonged period of time between E_t6.5–E_t7.6. To represent the continuous dynamics of transitions, we introduce the “vein plot” (Figure 4A). This plot displays the relative abundance of transcriptional states over time and the differentiation flux between them, as indicated by the relative width of the diagonal connections that span the time points. In this manner, it is clear that epiblast differentiation is dynamic and largely biphasic: 88% of the flow toward the PS fate occurs by E_t7.1, whereas 89% of the ectoderm restriction takes place at E_t7.3 or later (Figures 4A and 4B). Throughout this extended period, epiblast cells maintain robust expression of the core pluripotency factors Utf1, Pou3f1, Dnmt3b, and Pim2 (Figures 4C, left, and S4A). Interestingly, we discovered major expression changes occur over time even within the seemingly homogeneous epiblast because it continuously supplies cells to the PS and definitive ectoderm (Figure 4C, right). Most notably, downregulation of Nodal signaling genes (Nodal and Tdgf1) happens in parallel to PS differentiation and precedes the induction of definitive ectoderm markers Sox9, Irx3, and Irx5 (Figures 4D and S4A). Interestingly, distinct rostral and caudal signatures are evident in the definitive ectoderm already in E_t7.5 (Figure S4B). Activation of the definitive ectoderm program is largely considered to be achieved by secreted antagonists emanating from the distal and anterior VE, protecting the overlying epiblast from differentiation to PS, and further patterned by signals from the endoderm and axial mesoderm (Arkell and Tam, 2012; Balmer et al., 2016; Hemmati-Brivanlou and Melton, 1997), such as bone morphogenetic protein (BMP) and Nodal agonist-antagonist gradients (Li et al., 2013; Liu et al., 2018; McMahon et al., 1998). Using the flow model absolute timescale, we show that, concomitant with nodal signaling repression in the anterior epiblast, transforming growth factor β (TGF-β) superfamily modulators Cer1 and Lefty1 are expressed in the VE, while interestingly, Lefty2 is transiently induced in the nascent and early rostral mesoderm (Figure 4E).

Figure 4.

Temporal dynamics during epiblast, primitive streak, and nascent mesoderm commitment

(A) Vein plots describe the continuous transition of cell types to their direct descendants (represented by diagonal flows spanning time points), and the dynamic relative frequencies of these cell types in the embryo over time (vein width on the y axis). This panel shows transitions emanating from the epiblast to the primitive streak (PS) and definitive ectoderm (DEc). Vein connection width represents flow flux at each time point. Dashed arrow represents a link to a subsequent panel (here, F).

(B) Bars represent the composition of direct differentiation targets of epiblast cells at each time group.

(C) Row-normalized heatmaps of expression in the epiblast per time. Genes with homogeneous expression are shown on the left, clusters of variable expression, on right.

(D) Gene-flow plots in which nodes represent MCs, and edges link each MC to the source MC with the highest contributing flow in the network. MC level expression versus MC mean time is depicted for Eomes, Tdgf1, and Irx5 genes. Only MCs from Epiblast and related cell types are shown.

(E) Expression of members of TGF-β superfamily signaling modulators over time. Line graphs represent total transcript levels for the entire endoderm or mesoderm for each age group.

(F) Vein plot (as in A) describing the flow model emanating from PS to its predicted direct descendants.

(G) Predicted fate composition of early/late NM cells at each age group. Columns represent fraction of cells committing to each of the mesoderm fates, separated into hematoendothelial and extraembryonic lineages (negative values), and embryonic mesoderm (positive values).

(H and I) Vein plots illustrating the flow emanating from early and late NM (respectively) and gene-flow plots for key NM markers.

See also Figure S4.

Figure S4.

Dynamics of cell fate transitions, related to Figure 4

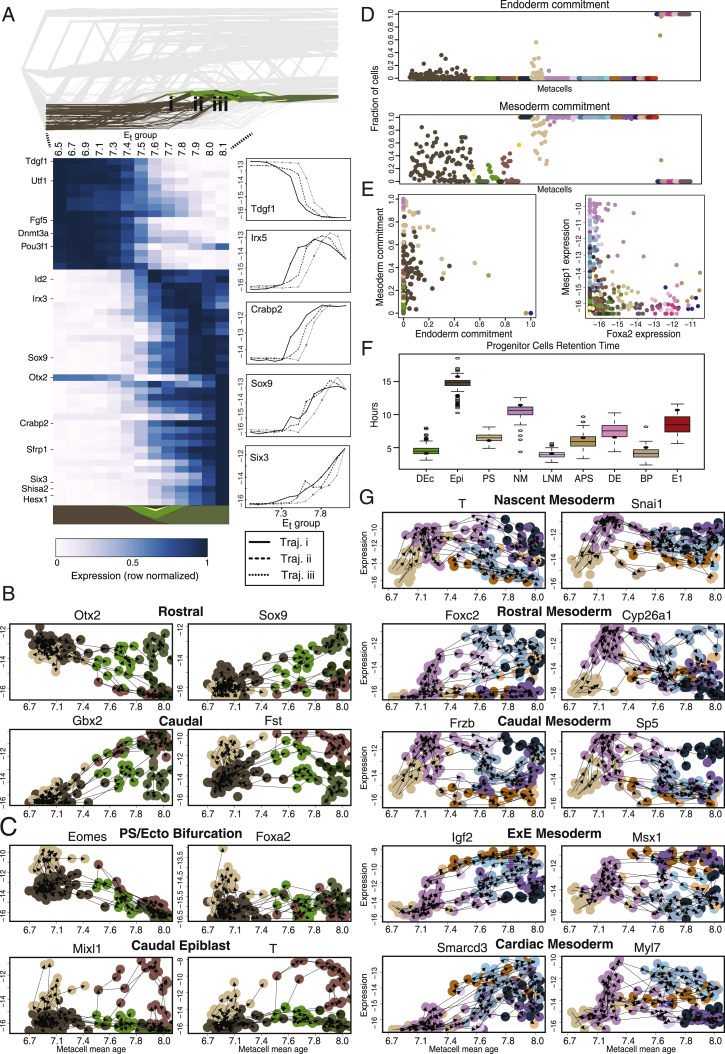
(A) Similar to Figure 3, for flows traced back from MC#397 (rostral neural plate).

(B) Gene-flow plots in which nodes represent MCs, and edges link each MC to the source MC with the highest contributing flow in the network. MC level expression versus MC mean time is depicted for key genes correlated with rostral and caudal neural ectoderm.

(C) Gene-flow plots of key genes associated with PS and caudal epiblast.

(D) Mesoderm and endoderm commitment per MC. Panels show the fraction of the flow passing through each MC that contributes to mesoderm or endoderm at the final time point. The remaining fraction contributes to ectoderm (not shown).

(E) The PS is predicted to be the only bi-potential cell type which significantly contributes to both mesoderm and endoderm (other than the pluripotent epiblast, and a single APS MC) (left). MC expression of key endoderm (Foxa2) and mesoderm (Mesp1) TFs (right).

(F) Retention time of progenitor cell types: Shown is the median length of time a cell spends in each cell type according to the flows. Boxes represent distribution of retention times computed for the 153 iterated MC models (see Figure S2B).

(G) Gene-flow plots of genes characteristic for specific mesodermal fates.

Biphasic differentiation over a prolonged period of massive proliferation as shown for the epiblast is in marked contrast to the developmental dynamics of the PS (Figures 4F). Flows demonstrate the continuous replenishment of the PS by the epiblast to compensate for the massive egress toward the NM and anterior PS. This process is accompanied by the activation of early endoderm and mesoderm markers such as Eomes, Foxa2, Mixl1, and T (Figure S4C), representing the potential of the PS to differentiate to both lineages (Figure S4D). However, calculating a commitment score for each MC identified only a few MCs with such potential (Figure S4E). Furthermore, unlike epiblast and NM, cells quickly transition through the PS without stabilizing their state thus forming a sharp bifurcation (Figures 4F and S4F). This lack of PS stability implies that the mesoderm/endoderm bifurcation occurs very rapidly on exit from the pluripotent state, such that no stable self-renewing mesendodermal progenitor cell state can be defined.

Differentiation from the NM defines a third type of prototypic developmental dynamics that differs from both the epiblast and the PS. NM differentiation occurs gradually and continuously through E_t6.7–E_t8.0, during which the intrinsic uncommitted state is continuously produced (Figure S4F). Using the flow model, we depict NM multi-furcation into 10 mesodermal programs by computing the relative NM fraction contributing to each of these fates over time (Figure 4G). Up to E_t6.9, NM cells are heavily biased toward the hematoendothelial and extraembryonic mesoderm lineages. Cardiac progenitors and rostral mesoderm then emerge, trailed by an increased dominance for caudal mesoderm fates, starting at E_t7.4. During this period (E_t6.7–E_t7.8), NM cells are continuously marked by high levels of Mesp1, T, Mixl1, Lefty2, and Snai1 (Figures 4H and S4G). Concomitantly, temporal activation of key mesodermal factors such as Tal1, Etv2 (hematoendothelial fate), Hand1/2 (extraembryonic mesoderm and cardiac fates), and Foxc1 and Dll3 (rostral and caudal mesoderm, respectively) marks initial commitment toward more specified mesodermal programs (Figures 4H, 4I, and S4G). In conclusion, these data support an extended notion of developmental fate acquisition that can go through phased fate determination (as in the epiblast), rapid transitional bifurcation (as in the PS), or complex and time-dependent multi-furcation (as observed for the NM).

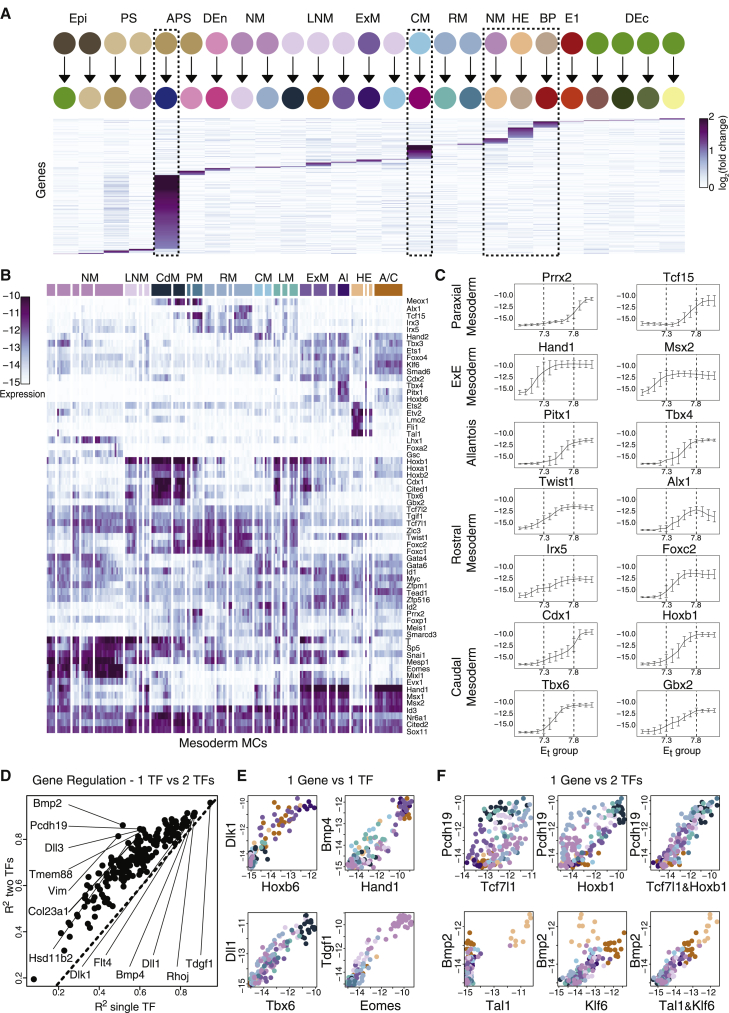
Evidence for combinatorial regulation of mesodermal multifurcation

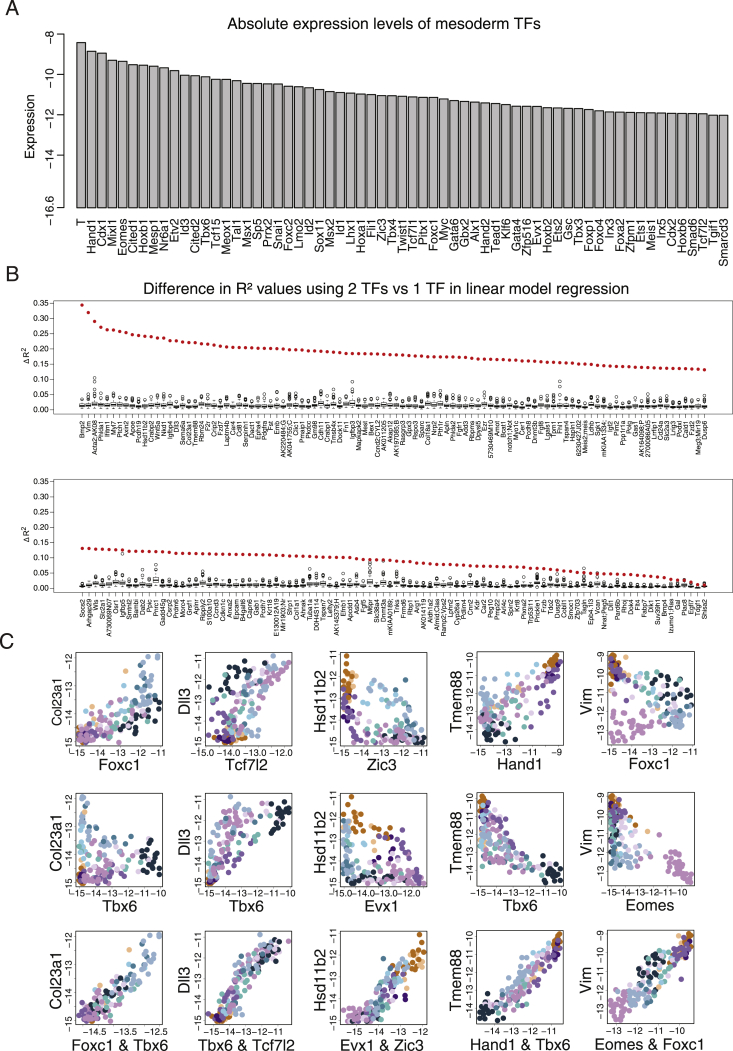
The classical stepwise differentiation model for development describes a series of specific gene expression signatures, each defining a direct transition between a progenitor state and a more specialized progeny state. We searched for such specific steps by identifying genes whose activation was unique to only one of the major fate transitions predicted by the flow model (Figure 5A). Interestingly, this analysis demonstrated that transitions toward the node, cardiomyocytes, and the hematoendothelial lineages are characterized by highly specific gene programs, in line with their early specification and specialized molecular functions. However, most transitions involved gene expression dominated by combinatorial signatures and lacking unique regulator genes or other specific makers. This was most evident in the complex repertoire of mesodermal fates, which, as shown above, represent temporally dynamic multi-furcation from the NM toward extraembryonic, rostral, and caudal programs. To model the regulation of this complex process, we focused on the combinatorial expression of 63 TFs with variable expression within the mesoderm (Figure 5B). TFs dominate the mesodermal transcriptional programs (59 out of the 256 most variable genes in the mesoderm are TFs), however, only some are likely to drive initial NM differentiation. Distinguishing between driver TFs and “responder” TFs can be achieved by analysis of their temporal kinetics (Figure 5C) and absolute expression level (Figure S5A).

Figure 5.

Combinatorial rather than hierarchical TF expression and regulation in the mesoderm

(A) Identification of genes specifically associated with one of the major cell type transitions during gastrulation. Shown are relative expression levels of genes, comparing between the source cell population and its progeny (columns). Dashed boxes mark the enriched, early-specialized lineages. Selection criteria for genes: (1) minimal gap of 0.5 between largest and second-largest log fold-change along a transition, and (2) second-largest fold-change smaller than 1.

(B) Absolute expression of highly variable TFs in the mesoderm. Columns represent individual MCs following hierarchical clustering.

(C) Temporal expression of key TFs within the mesoderm. For each TF, we identified the MCs with maximum expression in the mesoderm (see STAR Methods). The inferred TF expression kinetics along trajectories leading to such MCs are shown. Error bars reflect SD of expression for traced-back MCs at each time point. y axis, absolute expression.

(D) R² values for the best regression model using a pair of mesodermal TFs versus the best model using only one TF, trained on non-TFs with the highest variance in the mesoderm, and validated using permutation tests (see Figure S5).

(E and F) Prominent examples of target genes that can be accurately fitted in the mesoderm (R² > 0.8) using a single TF (E) or a linear combination of two TFs (F). Each dot represents a MC, axes represent absolute expression of TFs and predicted gene (x and y, respectively).

Figure S5.

Supporting information, related to Figure 5

(A) Maximal log2 base expression within the mesoderm for most variable TFs

(B) Permutation test to control for overfitting in linear regression analysis. Shown in red is the maximal gain in $R^2$ when using two TFs instead of one TF to predict target gene expression. Boxes represent the maximal gain in $R^2$ after fixing for each target the best-fitting single TF and using randomly shuffled TF vectors for the second variable. Random shuffling was repeated 100 times.

(C) Examples of highly variable mesodermal genes with poor predictability based on linear regression with one TF, but strongly improved $R^2$ values when using two TFs as explanatory variables. Shown is gene expression of target versus either one of the two TFs, or the combination of both.

TFs expression reflected the overall high-level organization of the mesoderm into 4 main regimes: progenitor states (marked by Eomes, Mixl1, and Mesp1), extraembryonic fates (Msx1/2, Hand1), and a spectrum of rostral (Foxc1/2, Twist1) and caudal (Cdx1, Hoxb1, Hoxa1) programs (Figure 5C). However, none of these TFs define a precise bifurcation pattern. For example, characteristic high expression of Hand1 in extraembryonic mesoderm is also observed in some rostral mesoderm MCs. Similarly, although Foxc1/2 are not expressed in most of the extraembryonic mesoderm lineages, they otherwise show only quantitative preferences to some (e.g., rostral, paraxial) mesodermal fates. The complex combinatorics of the mesoderm TFs is likely to have a major regulatory impact on target genes. To start and quantify this effect, for each mesoderm gene we compared the attainable fit by a regression model using one or two input TFs (Figures 5D and S5B). For a few genes, we observe very tight linkage with the expression of a single TF (e.g., Tdgf1 and Eomes). However, for most genes, we gain significant (compared to shuffled controls) predictive power when using two TFs as regulatory inputs (e.g., Pdch19, Bmp2, Dll3, and Vim) (Figures 5E, 5F, and S5C). The data suggest that although a cascade of master regulators expression can drive bifurcation and differentiation of specialized cell types, multifurcation in the mesoderm depends on complex combinations of many TFs rather than hierarchical TF expression. The correlation-based analysis presented here can use temporally resolved data to derive an initial understanding of such combinatorial schemes. Yet, such analysis is limited in its specificity as models become more complex and must therefore be combined with perturbations of candidate TFs.

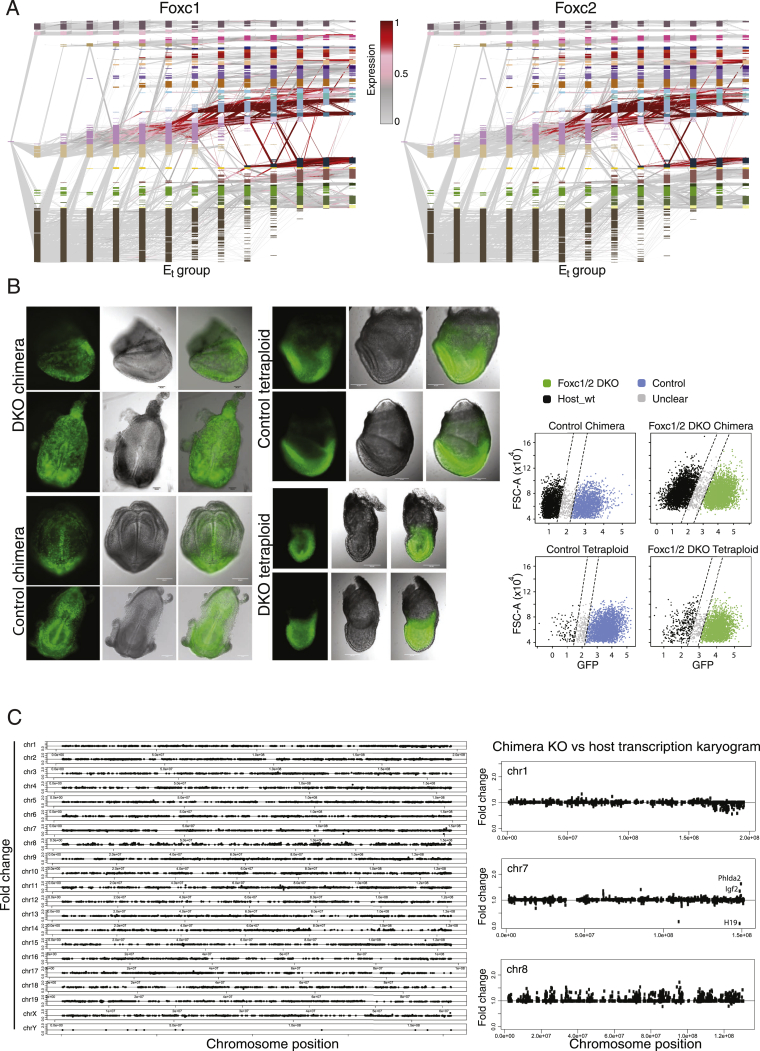
Studying the temporal effects of Foxc1 and Foxc2 on mesoderm specification

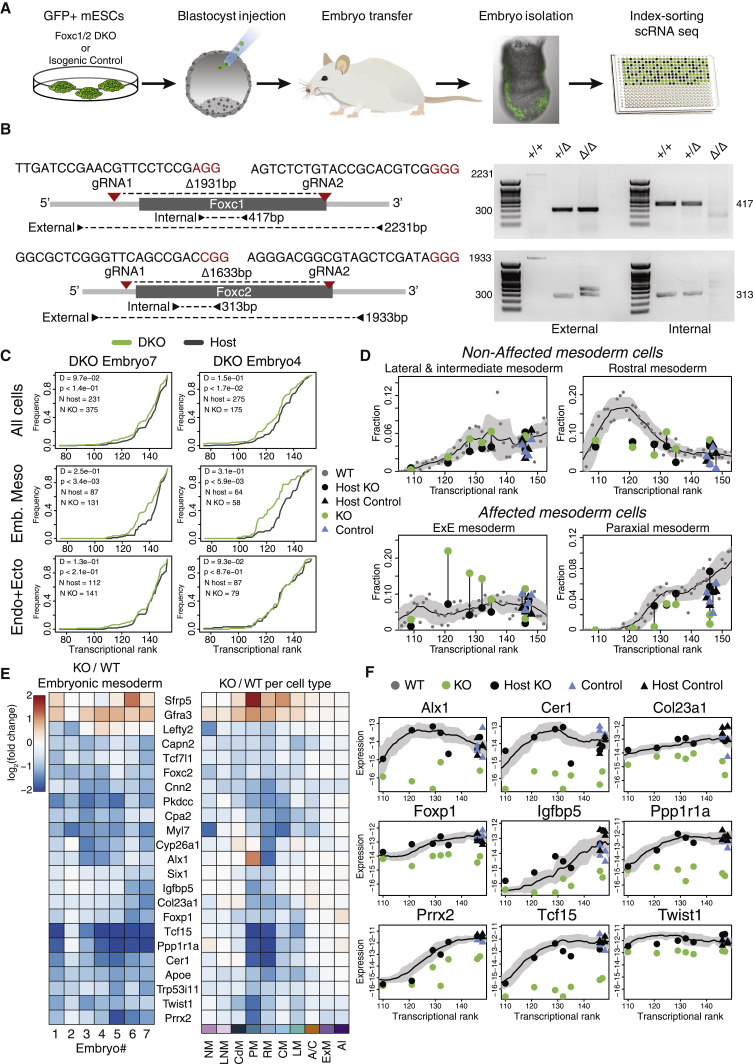
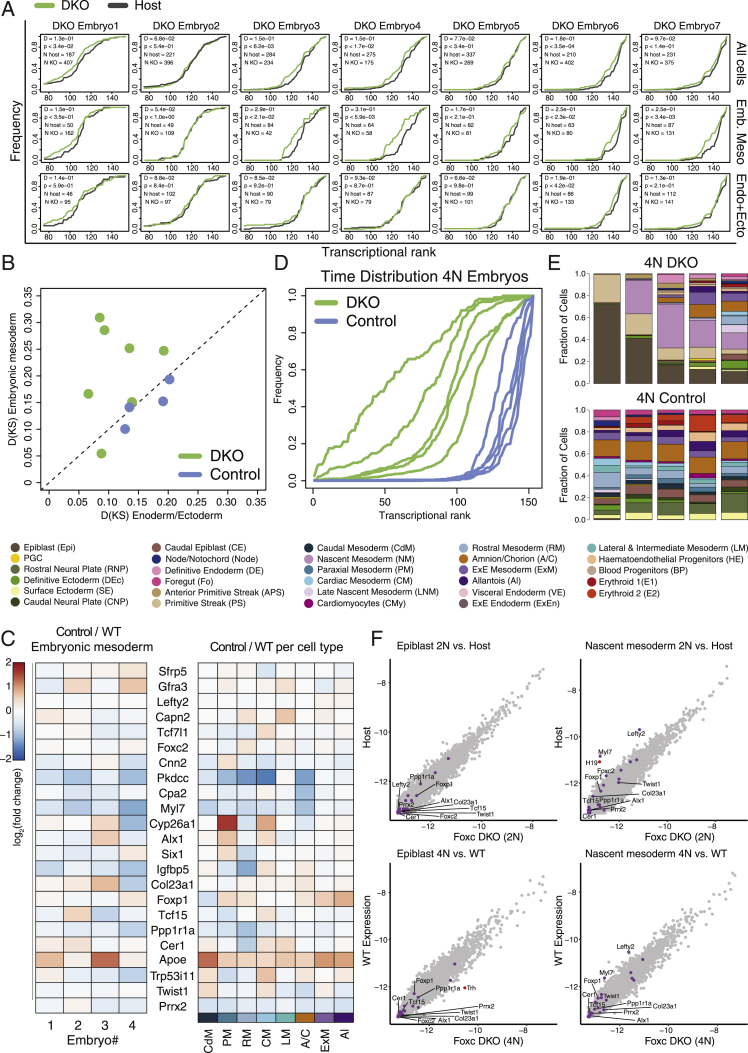
Forkhead box C1 and C2 genes (Foxc1 and Foxc2) exhibit broad and largely overlapping expression patterns in non-axial mesoderm. Mice harboring deletions of both genes die at mid-gestation with notable phenotypes in somites, intermediate mesoderm derivatives, blood vessels, heart, and neural crest (Fatima et al., 2016; Kume, 2009; Winnier et al., 1997). In our data, Foxc1/Foxc2 are expressed in rostral and caudal mesoderm, as well as weakly in subpopulations of hematoendothelial progenitors and the foregut (Figures 5B and S6A). Furthermore, Foxc1 expression peaks in early paraxial mesoderm, suggesting that it may play an instructive role in its specification. To this end, we adapted the chimeric embryo approach for use with precise single-embryo quantification (Figure 6A). We generated isogenic pairs of fluorescently tagged Foxc1/2 double knockout (DKO) and control mouse embryonic stem cells (mESCs), which were subsequently injected into host blastocysts followed by index sorting of single-embryo cells and MARS-seq (Figures 6B and S6B). In this manner, we could separately project injected and host cells from the same embryo onto the wild-type model. Generating seven such paired single-cell profiles, together with four isogenic control injected chimeras, provided a robust internally controlled platform to assess cell-autonomous effects of Foxc1/2 DKO over time. We then tested the impact of Foxc1/2 loss on the temporal dynamics within the embryo. We further performed in silico analysis to control for loss of imprinting and chromosomal abnormalities that are frequently associated with mESC cultures (Figure S6C). Overall, host and DKO cells consistently match in terms of embryonic time (as quantified by analysis of K-nn similarities between knockout or host cells and the reference temporal model) (Figures 6C and S7A). However, in 4 of 7 chimeras, DKO cells matched embryonic mesoderm of significantly younger reference embryos relative to the host cells. This phenotype, indicating retarded differentiation, is specific to the embryonic mesoderm, as timing based on ectoderm/endoderm cells was similar to the host (D = 0.21, p = 3.8e−11; D = 0.06, p = 0.17, Kolmogorov-Smirnov D statistic and p value for the mesoderm and combined endoderm/ectoderm, respectively) (Figures 6C and S7A). Specificity was further substantiated by directly comparing DKO cells to their isogenic controls (Figure S7B).

Figure S6.

Supporting information, related to Figure 6

(A) Color coded expression for Foxc1 and Foxc2 per time and MC, plotted along inferred flows.

(B) Images of representative chimera and tetraploid embryos (GFP, phase contrast and overlay). Scale bar = 200um (except DKO chimera, where 100um). On the right, flow cytometry side-scatter width (SSC-W) plotted against GFP fluorescence intensity for each cell (after applying logical transformation from R flowcore package) (Ellis et al., 2020). Cells above the upper GFP threshold were classified as mESC derived, and cells below the lower threshold as host cells. Cells in between the thresholds (classified as unclear) were excluded from further analysis.

(C) Chimera DKO versus host differential expression karyogram. Shown is fold-change between all DKO and host cells organized by chromosome position $\left(\left({10}^{-5}+e_g\left(KO\right)\right)/\left({10}^{-5}+e_g\left(host\right)\right)\right)$. On the right, chromosomes 1, 7 and 8 are highlighted. Injected embryonic stem cells display (i) loss of imprinting of the Igf2/H19 locus (chromosome 7), (ii) a trisomy chromosome 8 and (iii) possible monosomy of the distal part of chromosome 1.

Figure 6.

Foxc1/Foxc2 loss delays embryonic mesoderm and inhibits paraxial program

(A) Experimental scheme for the generation and analysis of Foxc1/2 double knockout (DKO) chimera embryos.

(B) Gene targeting design and validation for Foxc1/2 DKO, both are single-exon genes and the entire coding sequence was deleted in a biallelic manner.

(C) DKO mesoderm (meso) cells are developmentally retarded as compared to their matched host cells. The cumulative distribution of nearest neighbor wild-type intrinsic ranks was calculated separately for DKO and host cells (green and black lines, respectively) in each chimeric embryo. Similar analysis shows no significant delay in the ectoderm (ecto) and endoderm (endo) cells. Shown are two representative embryos, with Kolmogorov-Smirnov D statistics and p value highlighted for each (see also Figure S7).

(D) Fractions of cell types per embryo. Black, blue, and green symbols, represent host, isogenic control, and DKO cells (respectively), connected by a vertical line for each chimera embryo. Embryos were assigned a transcriptional rank according to the most similar wild-type embryo based on host cells only. Grey dots represent individual embryos of the wild-type model, and shaded area represents the moving average for wild-type embryos and moving SD (window size = 9).

(E) Relative expression of the most significant differentially expressed genes in the embryonic mesoderm between DKO and matched wild-type embryo cells, shown either per embryo (numbered 1–7 according to transcriptional rank from “youngest” to “oldest”), or across cells per cell type (see STAR Methods for selection criteria).

(F) Absolute expression of key genes per embryo, for injected mESC-derived versus host embryonic mesoderm cells, relative to smoothed wild-type expression (black line, moving average length = 11). Shaded area corresponds to moving SD across neighboring embryos (window length = 11). Units represent UMIs per million UMIs.

See also Figure S6.

Figure S7.

Analysis of tetraploid complemented embryos and supporting information, related to Figure 6

(A) Cumulative distribution of nearest neighbor wild-type intrinsic ranks calculated separately for DKO and host cells (green and black lines, respectively) for each chimeric embryo, with Kolmogorov-Smirnov D statistic and p value.

(B) Scatterplot of Kolmogorov-Smirnov D statistics for DKO and control isogenic chimeras demonstrating mesoderm specific temporal retardation in the Foxc1/2 chimeras.

(C) Relative expression between control isogenic mESC and host in chimeric embryos of genes associated with the DKO phenotype (as in Figure 6E), shown either per embryo (numbered 1-4 according to transcriptional rank, from ‘youngest’ to ‘oldest’), or across cells per cell type.

(D) Cumulative distribution of nearest neighbor wild-type intrinsic ranks calculated for the embryonic compartment of DKO and isogenic control tetraploid embryos (4N; green and blue, respectively).

(E) Relative cell type distributions for each embryo calculated for the tetraploid (4N) complemented embryos (arranged from left to right according to intrinsic rank).

(F) Comparison of gene expression of bulk epiblast and early NM between Foxc1/2 DKO cells and host cells (or wild-type embryo cells in the case of tetraploid embryos) demonstrating only minor changes in the DKO derived cells in these populations. Highlighted are genes with high differential expression between DKO cells and host/wt cells (log₂ fold change > 1.5, red) as well as differentially expressed genes in the embryonic mesoderm as shown in Figure 6E (purple).

We next asked whether the observed delay in mesoderm differentiation is driven by specific cell types as a function of time. Time-matched comparison of cell type frequencies indeed showed a reduction in paraxial mesoderm cells in the DKO, together with increased abundance of extraembryonic mesoderm cells (Figure 6D). To search for the most promising direct regulatory targets of Foxc1/2 in the embryonic mesoderm, we performed differential expression analysis comparing pooled expression on timed single cells classified as host or knockout embryonic mesoderm. This showed consistently that the expression of key paraxial and rostral mesoderm TFs (e.g., Tcf15, Prrx2, and Twist1) and regulators (e.g., Ppp1r1a and Cer1), was markedly reduced in knockout cells (Figures 6E and 6F). Differential expression between isogenic unmanipulated cells and their corresponding host cells provided strong validation for the specificity of these genes as potential targets of Foxc1/2 (Figure S7C). Yet, this analysis also stressed the necessity of including isogenic control cells because a noticeable reduction in Pkdcc in the control cells suggested that, for this gene, perturbations may originate already in the parental mESCs (Figure S7C).

To further control for non-cell-autonomous effects, we utilized a tetraploid complementation assay. We injected Foxc1/2 DKO, or isogenic control cells into 4N host blastocysts and dissected the resulting embryos at E8 (dpc). In this manner, the embryonic compartment was solely contributed by the injected cells, allowing evaluating the non-cell-autonomous effects on gastrulation (Figure S6B). Interestingly, knockout embryos generated by 4N complementation assay were significantly younger compared to their isogenic control counterparts, dissected at the same time (Figure S6, Figure S7B and S7D). Yet, unlike in the case of the 2N chimeric embryos, both mesoderm and non-mesoderm lineages were significantly delayed in these embryos (Figure S7E). Surprisingly, however, directly comparing 4N individual knockout or control embryos to time-matched embryos identified only minor changes in gene expression (Figure S7F). Together, these results suggest that the global delay in 4N knockout embryos is due to a failure to correctly execute mesoderm differentiation programs in the absence of Foxc1/2. This may affect key signaling required for the synchronous maturation of mesoderm and non-mesoderm lineages (e.g., Lefty2) (Figure S7F). This effect is compensated in 2N chimeric embryos, most likely due to the ability of host cells to correctly activate mesoderm programs. Taken together, the data highlight Foxc1 and Foxc2 as key early mesodermal regulators and strongly implicates them in the regulation of multiple secondary TFs that lead toward the paraxial mesoderm fate.

Discussion

Fertilization triggers the course of development, whereby individual embryos progress in time toward maturation. To achieve rapid diversification after implantation, gastrulating embryos undergo massive cell proliferation that involves a continuous flux of parallel intracellular molecular changes that break transcriptional and structural symmetry (Bedzhov et al., 2014; Rossant and Tam, 2009). The complexity of modeling this process is best manifested when aiming to assign time to embryos and cells. Unlike individual embryos that can be assigned with absolute time, cells comprising an embryo may represent transcriptional states that exist at multiple time points in development. Therefore, faithfully charting cell state transitions during embryonic development requires unified models that synthesize quantitative transcriptional kinetics of individual cells and embryos.

To address this challenge, we conducted a phenomenological characterization of mouse gastrulation at the resolution of single embryos and the single cells comprising them. Ordering embryos on a transcriptional continuum allowed us to assign a unique time-stamp to each embryo that is based on the transcriptional profile of its comprising cells (denoted E_t). Comparing transcription time with classical morphology-based staging showed an overall high correlation between the two approaches. However, morphology was able to capture only part of the variation in the transcriptional landscape between embryos (Figure 7A). In part, this is due to the limited number of distinguishable morphological changes and the qualitative nature of such classification. In many cases, molecular specification precedes the appearance of an appreciated morphological structure as evident, for example, in the cases of the allantois, cardiomyocytes, and early blood specification (Figure 7B). Our data provide a synthesis between transcription and morphology, thus significantly refining classical embryo staging approaches.

Figure 7.

Acquisition of morphological and transcriptional traits during gastrulation

(A) Staged traces of representative embryos highlighting the major phenotypical alterations during gastrulation and up to somitogenesis. Boxplot indicating the distribution of calculated developmental time (E_t) per embryo according to morphological classification (see Figure S1B for complete embryo compendium). Boxes show interquartile range (IQR) with median. Whisker length corresponds to 1.5 IQR or the distance to the extremal value of the distribution if within 1.5 IQR.

(B) Cell type distribution per embryo, arranged according to intrinsic rank and separated into the 13 age groups.

(C) Complete flow model showing all cell types and major predicted transitions. Map “altitude” represents the degree of specification of each cell type, from shallow “basins” (e.g., epiblast and NM) to deep “canyons” (e.g., ExEn and blood).

To infer differentiation flows and lineage specification dynamics over the embryonic transcriptional manifold, we developed algorithms that integrate single-embryo time, transcriptional identity of single cells, and estimation of the growth rates for key embryonic lineages. The ability to chart simultaneous programs in the embryo at high temporal resolution provides a holistic view across cell types, thus allowing suggesting co-dependence between them. A notable example of such an interaction is the significant reduction in Nodal signaling genes in the otherwise largely homogeneous epiblast, situated juxtaposed to the source of high levels of the Nodal inhibitors Lefty1 and Cer1 from the VE (Costello et al., 2015; Perea-Gomez et al., 2002) and temporally correlated with the onset of Lefty2 expression by the emerging mesoderm. This transcriptional switch coincides with a shift in the differentiation potential of the epiblast: from early predominant contribution to mesoderm and endoderm fates through the PS, to en masse commitment to definitive ectoderm commencing E_t7.0. Interestingly, the watershed-like switch in epiblast commitment correlates with the previously described sharp reduction in the efficiency to isolate epiblast stem cells from late streak embryos (Brons et al., 2007; Kojima et al., 2014; Tesar et al., 2007).

Consistent with previous findings in Xenopus (Hemmati-Brivanlou and Melton, 1997), our model predicts that epiblast commitment to ectoderm initiates through a common progenitor cell population termed definitive ectoderm. These cells are predicted by the flows to differentiate to either neural plate or surface ectoderm (epidermis) fates. Indeed, such cells have been previously identified in the mouse (Cajal et al., 2012) and further isolated in vitro (Harvey et al., 2010; Li et al., 2013; Liu et al., 2018). Yet, the transient nature of definitive ectoderm (retention time 4.8 ± 0.8 h) (Figure S4F), the lack of distinctive markers, and difficulty in tracing their fate in vivo make elucidating the potential of these cells a challenging task. Our data suggest that early distinct spatial expression within this population may predict anterior/posterior patterning (Figure S4B). This potentially extends recent findings demonstrating regionalization of the spinal cord prior to neural differentiation (Metzis et al., 2018), in contrast to the long-standing initiation transformation model (for review, see Stern et al., 2006).

The flow model clearly uncovered prototypic rapidly bifurcating cell state transitions associated with the first specialized cells of the embryo: blood, node/notochord, and cardiomyocytes. Nevertheless, gastrulation appeared to be dominated by enduring progenitor populations that gradually multifurcate to give rise to distinct cell fates. Regulation of such regimes seems combinatorial and nuanced with no single major TF or clear hierarchical stepwise program driving transitions. We propose an approach that focuses on the multi-faceted regulation within such states, combining temporal and kinetic modeling with experimental systems that integrate reporters, perturbations, and single-cell readout for in-depth analysis in vivo. We show that single chimeric embryos, harboring gene-specific mutations, allow separation of the effect of key regulators on developmental timing from their effect on direct target genes. Specifically, in the case of Foxc1/Foxc2 mutants, we could reproduce the previously described loss of paraxial mesoderm, but in the same experiment also trace back this phenotype to gene expression changes in its progenitors. Our data show that knockout cells that were destined toward rostral and paraxial fates are developmentally delayed and may later compensate by elevating alternative programs (e.g., those involving extra-embryonic mesoderm fates). Multi-furcation in the mesoderm, therefore, emerges as a process involving a delicate balance between differentiation programs within a multipotent mesodermal progenitor state.

Continuous commitment over time represents a key limitation of pseudotime methods that inherently forces a rigid tree-like structure on inferred cell state transitions. Similarly, convergence of distinct states into the same program is not easily modeled using pseudotemporal ordering. One such example is the contribution of the VE to the embryonic endoderm recently demonstrated during early mouse gastrulation (Kwon et al., 2008; Nowotschin et al., 2019; Peng et al., 2019). Our work provides a unified model of mouse gastrulation that considers continuous, parallel, and converged differentiation toward multiple lineages (Figure 7C). In such a “basin-like” representation of development, rapid bifurcations into highly functional cells are depicted as “canyons,” whereas progenitor states that gradually multifurcate over several time points are depicted as basins (Figure 7C). Collectively, our work introduces a quantitative temporal model of embryonic development, holding great promise for elucidating the roles of multiple regulatory layers in shaping and memorizing functional programs. Nevertheless, moving forward toward a complete realization of these processes will require integrating spatial information into the model, creating spatiotemporal models that represent development as a concurrent, and interacting collection of intra-cellular processes with progressively specialized and robust transcriptional and spatial identities.

Limitations of study

Limitations of our study are related first to our model resolution and accuracy. Model accuracy is defined by the number of embryos sampled and the uniformity of their absolute (a priori unknown) temporal distribution. Resolution in our model is directly affected by cellular diversity. Indeed, current sampling depth allows more precise tracking for embryonic times showing extensive cellular diversity (at E_t6.9 and thereafter) but provides lower resolution for the earlier, inherently less-diverse, time bins. In addition, dissection of extra-embryonic tissues may have variable efficiency and can affect inference of flows for these lineages. These issues can be improved on by sequencing additional embryos up to the noise limits of sampling and scRNA-seq. More fundamental limitations relate to the use and interpretation of the model. The flow model makes assumptions on proliferation rates of different cell types over time, which were extrapolated from bulk measurements and cell-cycle-related gene expression. Measurements involving specific cell type isolation or monitoring lineage dynamics using time-lapse microscopy will allow a more precise evaluation of cell proliferation rates. Finally, the precision of the estimated breakdown of embryonic cells into types per time point is based on thresholding a continuous space of differentiation, and when visualizing the flow model, we must use it as is (e.g., for color-coding).

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
scRNA-seq embryonic profiles	This paper	GEO: GSE169210
Gastrulation scRNA-seq atlas	Pijuan-Sala et al., 2019	PMID: 30787436
Experimental models: Cell lines
Mouse: V6.5 mouse embryonic stem cells	Jaenisch lab, MIT	RRID:CVCL_C865
Mouse: Foxc1/2 dKO mESCs	This paper	N/A
Mouse: isogenic control mESCs	This paper	N/A
Experimental models: Organisms/strains
Mouse: C57BL/6JRccHsd	Envigo	RRID: MGI:6151402
Mouse: Hsd:ICR(CD-1)	Envigo	RRID: MGI:5649797
Mouse: B6D2F1	Envigo	RRID: MGI:5651959
Oligonucleotides
FoxC1 5′ gRNA: gTTGATCCGAACGTTCCTCCG	This paper	N/A
FoxC1 3′ gRNA: gAGTCTCTGTACCGCACGTCG	This paper	N/A
FoxC2 5′ gRNA: GGCGCTCGGGTTCAGCCGAC	This paper	N/A
FoxC2 3′ gRNA: gAGGGACGGCGTAGCTCGATA	This paper	N/A
Recombinant DNA
Cas9 targeting plasmid: px330	Wu et al., 2013	Addgene plasmid: #98750
HTNC expression plasmid: pTriEx-HTNC	Peitz et al., 2002	Addgene plasmid: #13763
Software and algorithms
Metacell	Baran et al., 2019	PMID: 31604482
Network flow inference algorithm	This paper	https://github.com/tanaylab/embflow https://doi.org/10.5281/zenodo.4646177
MARS-seq pipe mapping/UMI pipeline	Keren-Shaul et al., 2019	PMID: 31101904

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Yonatan Stelzer (Yonatan.stelzer@weizmann.ac.il).

Materials availability

Plasmids and cell lines generated in this study will be made available by the Lead Contact upon request.

Data and code availability

The accession number for the raw and processed data reported in this paper is GEO: GSE169210.

Code has been deposited at https://github.com/tanaylab/embflow, https://doi.org/10.5281/zenodo.4646177.

Interactive independent analysis can be performed at https://tanaylab.weizmann.ac.il/embflow.

Experimental model and subject details

Cell culture and genetic manipulation

Mouse embryonic stem cells (mESCs, v6.5) were cultured under standard conditions on a feeder layer of X-ray irradiated mouse embryonic fibroblasts (MEF, DR4). Standard mESC medium: DMEM (High glucose, GIBCO), 20% FBS (US certified, Biological Industries), 20mg/lit recombinant leukemia inhibitory factor (LIF), 0.1mM 2-mercaptoethanol (GIBCO), Penicillin/streptomycin (Biological Industries), 1mM L-glutamine (Biological Industries), 1% non-essential amino acids (Biological Industries). For chimera assays medium was supplemented with 1mM PD0325901 (Sigma, 1 mM), and 3mM CHIR99021 (Sigma), 48hrs prior to blastocyst injection.

Embryo Collection and Documentation

All animal procedures were approved by the Institutional Animal Care and Use Committee and were performed in strict adherence to Weizmann Institute guidelines. Mice were monitored for health and activity and were given ad libitum access to water and standard mouse chow with 12-hr light/dark cycles. Embryos were collected from timed pregnant immune competent C57BL/6JRccHsd or Hsd:ICR(CD-1) females (obtained from Envigo and mated in house with males of the same strain), between E6.5-8.25 (see Figure S1F). Pregnant mice were not involved in previous studies. Embryos were removed from their implantation sites using fine forceps, in PBS, and Reichert’s membrane and ectoplacental cone removed. Embryos were then washed in fresh PBS and transferred to chilled DMEM (Phenol-red free, GIBCO) supplemented with 10% FBS (Biological Industries) for imaging prior to dissociation. Phase contrast images were taken with an Eclipse Ti2 inverted microscope (Nikon) and Zyla sCMOS camera (Andor). Size measurement of the embryonic component of each embryo was performed as previously described (Downs and Davies, 1993). Embryo staging was performed according to (Downs and Davies, 1993) and EMAP (eMouse Atlas Project; http://www.emouseatlas.org/emap/home.html) (Richardson et al., 2014).

The same single investigator performed both staging and measurements for consistency.

Generation of Foxc1/Foxc2 double knock out cells

mESCs expressing constitutive GFP were generated by integration of a Lox-DsRed-Lox-GFP cassette (based on Addgene plasmid #32702) into acceptor attP sites integrated in the H11 locus (using Addgene plasmid #52544), followed by Cre recombination using recombinant His-TAT-NLS-Cre (HTNC) protein (Addgene plasmid #13763), as previously described (Peitz et al., 2002). Cells were then co-transfected using TransIT-X2 (Mirus, according to manufacturers protocol) with four SpCas9 vectors (px330, Addgene plasmid #98750) (Wu et al., 2013), each expressing a single gRNA designed to remove the entire protein coding sequence of either Foxc1 or Foxc2. gRNAs were selected for minimal off targets using CCTop - CRISPR/Cas9 target online predictor (https://cctop.cos.uni-heidelberg.de:8043/) (Stemmer et al., 2015). For genotyping, individual clones were grown for two passages on gelatin-coated plates to eliminate residual MEF, and genomic DNA extracted with PCR compatible lysis buffer (10mM Tris, PH = 8, 0.45% Triton X-100, 0.45% tween-20, 0.2mg/ml Proteinase-K). Validation by genomic PCR used a set of primers flanking the expected deletions, and internal primers, as well as by Sanger sequencing.

Method details

Flow cytometry

Prior to dissociation, to focus on tissues that contribute to the embryo proper, the ectoplacental cone, parietal endoderm, and much of the extraembryonic ectoderm, were removed using fine forceps. For isolation of single cells for scRNA-seq, embryos were dissociated with 0.25% Trypsin-A, 0.02% EDTA (Biological Industries) solution for 5′ at 37°C, and resuspended in DMEM w/o phenol red (GIBCO) supplemented with 10% FBS (Biological Industries). Samples were run on a FACSAria-III flow cytometer (BD Biosciences) using the ‘index sort’ option to retain the spectral properties of each individual sorted cell.

Single-cell RNA-sequencing

Single-cell cDNA libraries were prepared using the MARS-Seq method, as described (Jaitin et al., 2014; Keren-Shaul et al., 2019), with the following modifications: The final concentration of the RT1 primers was 2nM, and pooling was done via centrifugation to VBLOCK200 reservoir (Clickbio). Klenow reaction was not followed by heat inactivation. The volume of the first RT and Exonuclease I reactions mix were scaled down to 1 and 0.5 ul, respectively, and dispensed by MANTIS liquid handler (FORMULATRIX). In brief, single cells were sorted using flow cytometer directly lysis solution containing well identifying poly-T barcodes. mRNA from cell capture plates was then converted into cDNA and pooled. Pooled samples were amplified by T7 in vitro transcription, and the resulting RNA was fragmented and converted into a sequencing-ready library by tagging the samples with pool barcodes and Illumina sequences during ligation, reverse transcription, and PCR.

Estimation of total nuclei counts in E6.25 – E8.0 embryos

To estimate total cell counts in embryos of different developmental stages, we harvested 19 embryos from E6.25 to E8.0 and fixed them overnight using 4% PFA. The embryos were subsequently washed with PBS-0.1% tween (PBST), nuclear-stained using DAPI (Sigma-Aldrich D9564) diluted to 1.0 μg/mL in PBS and incubated overnight in 70% glycerol-PBS on a tilting platform to clarify the tissue. The embryos were mounted on a Cellvis 35mm glass-bottom dish and imaged using a Zeiss LSM-880 confocal with automatically optimized Z-interval. The raw images were next processed using Bitplane Imaris software. E6.25-E7.0 embryos were processed along the entire span of the confocal stack, while embryos from later stages were cropped to half of the span along the lateral-to-medial extent, discarding dimmer Z sections distal to the lens. We used the Imaris “surface” feature to manually segment the image stack into embryonic and extra-embryonic domains. We next used the “spots” feature with optimized parameters to assess the distribution of cell nuclei in each domain separately. For embryos older than E7.0, the nuclei counts were multiplied by a factor of two to account for the entire left-right axis of each embryo.

Blastocyst injections

Blastocyst injections were performed using (C57BL/6xDBA) B6D2F1 (Envigo) host embryos. In brief, 3-4-week old B6D2F1 females were hormone primed by an intraperitoneal (i.p.) injection of pregnant mare serum gonadotropin (PMSG, Vetmarket) followed 46 hr later by an injection of human chorionic gonadotropin (hCG, Sigma). Embryos were harvested at the zygote stage, and cultured in a CO2 incubator until blastocyst stage. On the day of the injection, groups of embryos were placed in drops of M2 medium using a 16-um diameter injection pipet (Biomedical Instruments). Approximately ten cells were injected into the blastocoel of each embryo using a Piezo micromanipulator (Prime Tech). For tetraploid complementation, 2-cell embryos were fused to one cell using a CF150/F instrument (BLS), by 2 DC square pulses of 30V 40ms and 1-2V AC, in 0.3M Manitol solution with BSA. An average of 15 cells were injected to the blastocoel of such embryos. Approximately 20 blastocysts were transferred to each recipient female (CD1 female mice, Envigo); the day of injection was considered as 2.5dpc. Mice were handled in accordance with institutional guidelines and approved by the Institutional Animal Care and Use Committee (IACUC).

MARS-seq and other scRNA-seq processing

MARS-seq reads were processed using the MARS-seq2.0 pipeline (Keren-Shaul et al., 2019). In Brief, After removing plate barcodes (4 base pairs) from Read 1, reads were mapped to the mm9 genome using bowtie2. Demultiplexing of the reads and construction of the single-cell UMI matrix was based on the well barcodes (7 base pairs) and UMI barcodes (8 base pairs) from Read 2.To demultiplex single-cell datasets into individual embryos, we recorded embryo identity per well during sorting and mapped well barcodes to embryo IDs as part of the MARS-seq post-processing stage. We removed mitochondrial transcripts from all cells in the UMI matrix. Overall we processed 40868 wells, out of which we retained 33,900 well-covered cells for further analysis. In particular, cells with the less than 1000 UMIs were filtered out. To analyze chimeric embryos, we used FACS index sorting to record GFP fluorescence per cell in addition to embryo identity per well. We then distinguished knockout and host single cells using thresholding of the green channel bimodal distribution. To allow comparison of our temporal atlas to the published gastrulation atlas we used 116,312 QC positive cells and mapped 10x gene names to MARS-seq gene names using naive matching of gene symbols.

Quantification and statistical analysis

Experimental design

Replication in this study is based on collecting individual embryos. All analyses were validated to be robust to subsets of the embryos acquired. Data collection involved sampling embryos at different estimated times, in several iterations given temporal analysis to insure complete coverage (See Table S1). For scaling embryos in time bins we corroborated scRNA-seq data with estimation of embryo size, thereby preventing bias or skewing of the timescale. We used blinding for staging embryos using two independent methods (scRNA-seq and morphology-based). The study did not involve a-priori determination of required sample size since the robustness of single-embryo sampling was not known in advance. However we did determine temporal bin size (based on the total number of cells from embryos in the bin, aiming at a minimum of 1000). There were no formal inclusion/exclusion criteria in this study.

Metacell analysis

To select feature genes for MC analysis we followed standard practice and identified 804 high variance genes in the UMI matrix downloaded to 1,653 UMIs (Baran et al., 2019). We then filtered cell-cycle and stress-related genes using manual annotation of 80 gene clusters. This resulted in a set of 665 feature genes. MCs were derived as described (Baran et al., 2019) using K = 100 and standard bootstrapping, MC splitting and outlier filtering. To avoid potential bias due to sometimes incomplete removal of extraembryonic tissues, residual MCs corresponding to extraembryonic ectoderm and parietal endoderm were removed prior to further analysis. The derived reference model included 461 MCs on 33,700 cells, leaving 200 outlier cells.

For a representation of temporal trends in Figure 1, we split the MC partition into separate endoderm, mesoderm and ectoderm graphs using known germ layer marker. This classification was not used in subsequent modeling and annotation, which are all based on flows described in Figure 2.

Embryo timing algorithms - K-nn ordering

Intrinsic temporal ordering of embryos is inferred using analysis of the cell-cell similarities and optimization of the linear ordering of embryos minimizing the temporal distance between similar cells. This analysis is done after excluding cells from the extraembryonic endoderm (defined by marker expression of Ttr and Apoe, Figure S1G) and the hematopoietic lineage (defined by expression of Cited4, Figure S3), since sampling of these tissues is variable between embryos. Given the filtered UMI matrix, we construct the adjacency matrix $E_{uv}$ encoding the balanced K-nn graph as defined by the MC pipeline for $K=50$. We marginalize over embryos to compute raw embryo similarity: $N_{ij}=\sum _{u\in C_i,v\in C_j}{E}_{uv}$, where $C_i$ represent the cells of embryo i. We then normalize raw similarities in two steps. First, we normalize columns given the number of cells in each embryo $S_{ij}^{pre}={\left(\left|C_j\right|\right)}^{-1}{N}_{ij}.$ We next normalize rows while also considering embryo sampling batch effect. To do this, assume the sampling batch of each embryo is $b\left(i\right)$ and assume some initial embryo ordering $ord\left(i\right)$ (e.g., based on morphology alone). We compute the embryo batch effect by estimating the increase in similarity only among embryos that are within the same approximated time range (to avoid computing large batch effects due to differences in scheduled embryo harvesting)

$${\beta }_i=\sum _{|ord\left(i\right)-ord\left(j\right)]\le 10,b\left(i\right)=b\left(j\right)}{S}_{ij}^{pre}/\sum _{|ord\left(i\right)-ord\left(j\right)]\le 10,b\left(i\right)\ne b\left(j\right)}{S}_{ij}^{pre}.$$

We correct similarities between embryos within the same batch and $\left|ord\left(i\right)-ord\left(j\right)\right|\le 10$ by setting $S_{ij}^{pre,b}={\left({\beta }_i\right)}^{-1}{S}_{ij}^{pre}$ (keeping all other $S^{pre}$ values unchanged), and then define:

$$S_{ij}=S_{ij}^{pre,b}/\sum _k{S}_{ik}^{pre,b}$$

We can now define the ordering optimization problem

$$\tau =argmi{n}_{\text{τ}(\cdot )}\sum _{ij}{S}_{ij}\left|\text{τ}\left(i\right)-\text{τ}\left(j\right)\right|$$

among all possible orderings $\text{τ}(\cdot )$ of the embryos. We solve the problem using a sorting heuristic. We initialize embryo ordering by their annotated Theiler stage (randomly ordering within each stage). Embryos for which Theiler staging was not possible (9 embryos), were assigned to the most abundant Theiler stage of their litter. We then run a bubble-sort-like algorithm by iteratively switching the position of neighboring embryos if this lowers the goal function until a local minimum is reached. We found that this simple heuristic is sufficiently powerful given that the initial Theiler ordering already defines the correct coarse-grained solution.

Defining absolute developmental time using size measurements

To transform embryo ordering into physical developmental times (in units of hours) we had to consider non-uniform embryo sampling and correct it using some independent physical measurement. We used area measurement $A_i$ for a subset of the embryos (using only C57BL/6 data to minimize strain-effects). Given the embryos exponential growth dynamics, we fit $log\left(A_i\right)$ as a function of the intrinsic rank of each embryo $i$ using a smoothing spline interpolation (R function smooth.spline with parameter $spar=0.9$, Figure 1E). To extend the boundaries, the interpolation function was linearly extrapolated. To derive absolute time, the log area scale $log\left(A\right)$ was transformed into a developmental timescale $E_t$ by assuming a linear relationship $t\sim log\left(A\right)$ and setting the median time of the first age group to 6.5 and the median time of the last age group to 8.1.

Comparison of inferred time to reference gastrulation atlas

We constructed a reference MC object for the mouse gastrulation atlas published in Pijuan-Sala et al. (2019). Most atlas cells are labeled by collection time $t_c$ into 6h intervals between e6.5 and e8.5. Using these labels, we computed the mean atlas age for each reference MC. We then computed for each of our embryos a projected mean age as follow:

• i)we matched MARS-seq and 10X gene symbols and used only feature genes as defined by the MC pipeline
• ii)for each embryo cell, we identified the atlas MC with maximal correlation (using log scaled single-cell UMI counts correlation to log scale gene frequency in MCs).
• iii)we computed the mean reference MC time matching all cells within each embryo. This is then defined as the projected atlas time of the embryo. Comparisons of these times to the intrinsic embryo ordering is shown in Figure 1.

Manifold construction and distance metrics

Given a MC solution over all embryos’ cells, we define first the gene expression distribution within each MC using the fraction of UMI’s per gene g in MC i, denoted $e_{gi}$ (computed by the MC package). Each MC consists of cells from different time groups, represented by vectors $n_i^t$ specifying the number of cells from time group t and MC i. We assume analysis is done using a set of feature genes $F$ including genes that involve significant transcriptional variance and are filtered so as not to include batch-affected genes or genes linked with the cell cycle.

To compute manifold distances between MCs we perform the following steps:

• i)define parametric pairwise distances: we use a logistic function on the regularized $e_{gi}$ values over the set of features genes $F$:

$$d_{ij}=\sum _{g\in F}plogis(log2(\epsilon +e_{gi})-log2\left(\epsilon +e_{gj}\right);loc,scale)$$

where loc (default 1) and scale (default 0.2) are parameters for a standard logistic function and $\epsilon$ (default 5e-4) is a regularization parameter.

• ii)defined manifold neighborhoods. We only trust the above parametric pairwise distances over highly related transcriptional states (e.g., for $e_{gi}$ vectors that are generally similar). We therefore identify pairs of MCs $E^{pre}$ such that $\left(i,j\right)\in E^{pre}if{d}_{ij}<\text{α∗min}\left(T_i,T_j\right)$, where $T_i$ is the distance between MC I and its second most similar neighbor, and $\alpha$ is a tolerance parameter (default 3). We further filter $E^{pre}$ such that each MC include at most 5 neighbors (those with the smallest distances), and construct a manifold graph M = (I, E) over MCs, with edge weights that equal the original $d_{ij}$ values for the retained edges. This graph is visualized in Figure 2A.
• iii)We next define a rate matrix $Q=\left(r_{ij}\right)$ where $r_{ij}=\left(D/d_{ij}\right)$ for $\left(i,j\right)\in E$ and 0 otherwise, setting the diagonal as $r_{ii}=-\sum _{\left\{i\ne j\right\}}{r}_{ij}$ and using $D=media{n}_i\left(\underset{\text{j}}{\max }{d}_{ij}\right)$ for scaling distances. The manifold transition probabilities are now computed as:

$p_{ij}=e^{-tQ}$, i.e., assuming a Markov process over the manifold with the rate matrix Q and timescale t (we use t = 1 to derive the flow models as discussed below). The manifold costs are derived from the probabilities by scaling each row and taking the inverse:

$$c_{ij}=\underset{j}{\max }\left(p_{ij}\right)/p_{ij}$$

Cell cycle modules and growth loss constant estimation

For each cell, we computed a mitosis and synthesis phase score by counting the number of UMIs from mitosis (M) and replication (S) genes and normalizing this count by the total number of UMIs per cell. The group of M-phase genes includes Mki67, Cenpf, Top2a, Smc4;SMC4, Ube2c, Ccnb1, Cdk1, Arl6ip1, Ankrd11, Hmmr;IHABP, Cenpa;Cenp-a, Tpx2, Aurka, Kif4, Kif2c, Bub1b, Ccna2, Kif23, Kif20a, Sgol2, Smc2, Kif11, Cdca2, Incenp, Cenpe. The group of S-phase genes includes Pcna, Rrm2, Mcm5, Mcm6, Mcm4, Ung, Mcm7, Mcm2, Uhrf1, Orc6, Tipin. We detected reduced S phase and M phase scores for cells from extraembryonic and embryonic endoderm (Figure 2C). We also observed exponential decay of the fraction of cells per embryo as a function of inferred embryo time, fitting in log space a global trend of decrease in their relative frequency with coefficients of 0.83 and 0.88 for extraembryonic and embryonic endoderm respectively (Figure S1I). We did not observe significant evidence for differential growth rates in other cell types. We therefore assume a growth loss constant of ${\lambda }_{exeendo}^t=1-0.83$ = 0.17 for extraembryonic endoderm at all time groups, and of ${\lambda }_{embendo}^t=1-0.88=0.12$. for all embryonic endoderm types. We set the loss constant to 0 for all other cell types. We note that these estimations are only approximating a much more complex and dynamically changing process, but within the time window studied here, these estimations provide sufficient compensation with minimal additional parameter fitting.

Network flow inference and modeling

Recall each MC consists of cells from different time groups, represented by vectors $n_i^t$. We normalize these count vectors and generate a probability distribution per time point $p_{it}=n_i^t/\sum _i{n}_i^t$. We define a flow model over this time resolved MC model using a flow matrix $f_{ij}^t$ for every time point t < T (T being the last time point), describing the fraction of cells from time t at MC i transitioning to MC j at time t+1.

The ideal “mass conservation” constraint in the model ensures the total flow in and out of each MC at each time point equals the observed frequency of single cells within it – specifically:

$$\sum _j{f}_{ij}^t=p_i^t\left(forward\right),\sum _j{f}_{ji}^{t-1}=p_i^t\left(backward\right)$$

where the boundary constraints (forward at the t = T, backward at t = 1), are ignored.

In practice however, we must relax these constraints given two considerations – First, we must consider differential growth rates between MCs. Second, uncertainty on our estimations of $p_i^t$ (which are a result of a single cell sampling process with considerable variance) must be considered.

To account for differential growth rates we use the growth loss constants ${\lambda }_i^t$ (as described in the previous section). We assume that at each time step, MCs with ${\lambda }_i^t>0$ emit “dilution” flow proportionally to their frequency - ${\lambda }_i^t{p}_i^t$. The total lost flow at time t, ${\lambda }^t=\sum _i{\lambda }_i^t{p}_i^t$ is being redistributed proportionally among all MCs toward time t+1, adding ${\gamma }_i^t=p_i^{t+1}{\lambda }^t$ to the flows going into each MC at time t+1. To define the resulted generalized conservation of mass, we introduce the flow constraints for each MC and time point:

$$CNST{R}_{flow}\equiv \sum _j{f}_{ij}^t+p_i^t{\lambda }_i^t=\sum _j{f}_{ji}^{t-1}+p_i^t{\lambda }^{t-1}=f_i^t$$

We can now consider the uncertainty on the estimation of $p_i^t$ by computing relative total flow error per MC and time point $d_i^t=\left(f_i^t-p_i^t\right)/p_i^t$ and using a cost function to penalize flows with large d magnitude –

$$cos{t}_{cap}=\sum _{i,t}flow\_error\left(d_i^t\right)$$

where the flow error is a piecewise linear convex function with a minimum at 0 (shown in the right panels in Figure S2A).

Given the relaxed formulation of the mass conservation and growth constraints, we can next write down a general optimization goal function for flows, which consider also the transcriptional manifold and the MC-MC distances defined by it – in simple terms:

$$cos{t}_{manif}=\sum _{i,j,t}{c}_{ij}{f}_{ij}^t$$

The resulted combined optimization problem:

$$\text{min}\left(cos{t}_{manif}\left(F\right)+cos{t}_{cap}\left(F\right)\right)$$

Subject to the constraint $CNST{R}_{flow}$ and the global flow constraints $\sum _i{f}_i^1=1$. In fact, these constraints and cost function define a classical network min-cost max-flow problem with convex costs. This problem is polynomial, and we derive an optimal solution the highly efficient simplex algorithm (Ahuja et al., 1993).

Annotation of metacells using flows

To annotate MCs, we added to the analysis of marker gene expression in each MC an examination of the inferred flow from (and to) them. MCs. In some cases, these supported identification of progenitor states that are already primed toward specific fates despite having only mild marker expression specificity. Let $F_{ij}=\sum _{t=1}^{12}{f}_{ij}^t$ be the average MC MC flow, $F^3=F\cdot F\cdot F$ (matrix multiplication) and let $G$ be the concatenation of $F^3$ and the transpose ${\left(F^3\right)}^T$ containing the third-order ingoing and outgoing MC flows for each MC (rows). For $G$ we compute the first-order correlation matrix

$$C_{ij}^1=co{r}_k\left(G_{ik},G_{jk}\right)$$

with the diagonal set to zero and the second-order correlation matrix $C_{ij}^2=co{r}_k\left(C_{ik}^1,C_{jk}^1\right)$. The diagonal of $C_{ij}^2$ is again set to zero. MCs are then clustered into 65 groups using hierarchical clustering (Ward.D method) of Euclidean distances between columns of $C_{ij}^2$. The second-order correlation matrix is shown in Figure S3A. Clusters were manually annotated based on selected markers shown in Figure S3B. In cases where intra-cluster gene expression was not sufficiently homogeneous, single MCs were reannotated accordingly.

Flow robustness and sensitivity analysis

For the analysis in Figure S2A, we used a fixed MC solution and recomputed flows while changing only one parameter at a time. To generate Figure S2B, 153 replica single-cell UMI matrices where generated leaving out the cells of one of the 153 embryos each time. MC partitions, manifold distances and flows were recomputed for each replica using the same parameters as in the original analysis. MCs were annotated with cell types by projecting each replica MC to the best correlated original MC using log transformed mean gene UMI fractions on feature genes. Intrinsic ranks of embryos as well as the age group partitioning was kept unchanged.

Flow propagation

Using the flow matrices $f_{ij}^t$ that are the solutions of the mincost flow problem, we define forward and backward probability transition matrices between MCs via

$$P_{ij}^{t,fw}=\frac{f_{ij}^t}{{\sum }_k{f}_{ik}^t}{P}_{ij}^{t,bw}=\frac{f_{ij}^t}{{\sum }_k{f}_{kj}^t}.$$

Given a distribution $p_i^t$ over MCs at time $t$, we can iteratively forward and backward propagate it through

$$p^{t+1}={\left(P^{t,fw}\right)}^T{p}^t{p}^{t-1}=P^{t-1,bw}{p}^t.$$

Vein plots

To summarize flows as shown in the “vein plots” of Figures 4 and 7, we group cells based on their annotated cell type and time-bin. We then summarize flows between cell types at each time point (where total flows between subsequent time points is 1). We are smoothing total frequency of each cell type per time using local polynomial regression and create “veins” with changing width that is proportional to cell type frequency. Flows between cell types are simplified by eliminating low magnitude flows between cell types (using a threshold of 0.005), and we visualize each edge with a width that is proportional to flow magnitude.

Unique genes specific to only one cell type transition

To generate Figure 5A, we selected for each cell type the ancestral cell type mostly contributing to it according to the flows. For each pair of cell type transitions $T_1\to T_2$ we calculated gene expression profiles

$$e_g^1=\frac{{\sum }_{i\in T_1,j\in T_2}{e}_{gi}{F}_{ij}}{{\sum }_{i\in T_1,j\in T_2}{F}_{ij}},e_g^2=\frac{{\sum }_{i\in T_1,j\in T_2}{e}_{gj}{F}_{ij}}{{\sum }_{i\in T_1,j\in T_2}{F}_{ij}}$$

corresponding to bulk expression of cells before and after the transition $T_1\to T_2$. Denote by $lf\left(g;T_1\to T_2\right)={\log }_2\left(\epsilon +e_g^2\right)-{\log }_2\left(\epsilon +e_g^1\right)$ the fold change corresponding to that transition $\left(\text{ε}={10}^{-5}\right)$. We then selected genes that are differentially expressed along a transition, i.e., that satisfy

$$\left|{\log }_2\left(\epsilon +e_g^2\right)-{\log }_2\left(\epsilon +e_g^1\right)\right|>1,{\log }_2\left({10}^{-5}+\max \left(e_g^1,e_g^2\right)\right)\succ -15$$

for at least one transition $T_1\to T_2$. Among these genes, we filtered genes, that are uniquely differentially expressed along one transition, i.e., that (i) have a gap

$$ma{x}_{\left(T_1\to T_2\right)}lf\left(g;T_1\to T_2\right)>0.5+lf\left(g;T_1\to T_2\right)$$

for all transition pairs $\left(T_1\to T_2\right)$ not equal to the maximizing pair and (ii) for which the second largest fold change along a transition $\left(T_1\to T_2\right)$ is smaller than 1. Figure 5A shows $lf\left(g;T_1\to T_2\right)$ for all included genes and included pairs $T_1,T_2$.

Mesoderm combinatorial TF expression and kinetic analysis

We filtered 63 mesodermal transcription factors that display high absolute expression as well as high variance within the mesoderm, i.e., ($\text{ε}=3\cdot {10}^{-5}$)

$$lo{g}_2\left(\text{ε}+\underset{i\in meso}{max}{e}_{gi}\right)\succ 12,{\text{Δ}}_{max}\left(g\right)>2.$$

with ${\text{Δ}}_{max}\left(g\right)=lo{g}_2\left(\text{ε}+\underset{i\in meso}{max}{e}_{gi}\right)-lo{g}_2\left(\text{ε}+\underset{i\in meso}{min}{e}_{gi}\right).$ These factors were visualized on a heatmap over all mesoderm MCs.

To estimate the kinetics of a TF g over time, we selected the mesodermal MCs, where it is highly expressed,

$$\left(lo{g}_2\left(\text{ε}+e_{gi}\right)-lo{g}_2\left(\text{ε}+\underset{i\in meso}{min}{e}_{gi}\right)\right)>0.8\cdot {\text{Δ}}_{max}\left(g\right).$$

Flows were then propagated through these MCs. The kinetics of selected transcription factors along their propagated flows is shown in Figure 5C.

TF linear regression models

We identified genes that have at least an 8-fold difference between minimal and maximal gene expression within the mesoderm. Gene expression levels of highly variable genes (that are not transcription factors) were predicted in terms of transcription factor levels using standard linear regression. For each variable gene, the most predictive single transcription factor and the most predictive pair of transcription factors was reported (Figure 5D). Because $Rˆ2$ values of linear regressions always increase when increasing the number of explanatory variables, we performed a permutation test for comparing gene expression predictions from two transcription factors with predictions from one transcription factor. To this end, we first shuffled the TF expression matrix. We then used the best fitting single TF in the original data as a fixed anchor and estimated the improvement in Rˆ2 derived when adding to this anchor the best fitting shuffled TF vector. A comparison of the gain in Rˆ2 in the unshuffled matrix and shuffled matrix provided control for the over-fitting we perform when extending the model.

Cell type annotation of chimera cells

We constructed a common balanced K-nn graph consisting of 33.889 cells from the wild-type atlas and 4284 cells from seven Foxc1/2 KO chimera embryos. Using the common K-nn graph, we associate to each cell $i$ a probability vector $p^i$ counting the fraction of cells from each cell type among its 50 nearest neighbor cells, i.e.

$$p_i\left(celltypeA\right)=\frac{\#wildtypeneighborcellsfromcelltypeA}{\#wildtypeneighborcells}.$$

Note that we can calculate $p_i$ for both wild-type and chimera cells, while only wild-type cells come with a cell type tag. Using $p_i$, we then assigned each chimera cell to a cell type by projecting it on that wild-type cell $j$, whose $p_j$ is most correlated with $p_i$. A MC 2d projection of the combined single-cell graph is shown in Figure S6C. Chimera cells are colored according to their inferred cell type, wild-type cells are plotted in gray.

Timing of KO and host cells within chimera embryos

We used the balanced K-nn graph of the combined chimera and wildetype embryo dataset to time host and KO cells from each chimera embryo separately. More precisely, for each cell $i$ let $NN\left(i\right)$ be the nearest neighbor wild-type cell that is not from the same embryo as cell $i$. We then attach to each cell $i$ the intrinsic rank (between 1 and 153) of the embryo of its nearest neighbor cell $NN\left(i\right)$,

$$t_i=R_{NN\left(i\right)}.$$

We noted that simply computing the mean embryo time of NN cells as the representation of chimera cell population timing would introduce biases at the boundaries of the analyzed time interval (e.g., very early embryos cannot have neighbors in embryos even more early). We therefore refined the analysis of NN times per knockout and host cells as follows. For a selection $S$ of cell types, for instance, embryonic mesoderm or ectoderm, we define for each chimera embryo $E$ the cumulative distributions $q_E^{S,KO}\left(t\right)$ and $q_E^{S,host}\left(t\right)$ of nearest neighbor time stamps $t_i$ for all KO/host cells $i$ from the chimera embryo $E$ and selected cell types $S$. For each wild-type embryo $E$ we can compute an analogous nearest neighbor cumulative distribution $p_E^S\left(t\right)$. By finding for each $q_E^{S,KO}\left(t\right)$ or $q_E^{S,host}\left(t\right)$ the best correlated wild-type $p_E^{S,}\left(t\right)$, we can match each chimera embryo $E$ with a wild-type embryo $E^{\prime }$, separately for KO and host cells. This procedure is used to independently time KO and host cells from ecto-/endoderm, embryonic mesoderm and extraembryonic mesoderm. The group of ecto-/endoderm contains foregut, definitive endoderm, primitive node, definitive ectoderm, surface ectoderm, rostral neural plate, caudal neural plate and caudal epiblast. Embryonic mesoderm contains early nascent, late nascent, caudal, lateral & intermediate, paraxial, and rostral mesoderm as well as cardiac crescent and cardiomyocyte cells. Extraembryonic mesoderm consists of allantois, amnion/chorion, and extraembryonic mesoderm cells.

Differential expression analysis

We calculated bulk expression profiles $e_{g,+}^{KO}$ and $e_{g,+}^{WT}$ for all KO chimera and WT cells from cell types with high Foxc1/2 expression (rostral, paraxial and caudal mesoderm) and defined the log fold change ${\text{δ}}_g^{+}={\log }_2\left(e_{g,+}^{KO}+\text{ε}\right)-{\log }_2\left(e_{g,+}^{WT}+\text{ε}\right)$ for $\text{ε}=5\cdot {10}^{-5}$. As a negative control, we averaged bulk expression profiles $e_{g,i}^{KO}$ and $e_{g,i}^{WT}$ per cell type $i$ and gene $g$ over all cell types not expressing Foxc1/2 (Amnion/Chorion, Allantois, Caudal epiblast, Caudal neural plate, Definitive ectoderm, Definitive endoderm, Epiblast, ExE mesoderm, Node/Notochord, PS, Rostral neural plate and Surface ectoderm) and calculated the log fold change ${\text{δ}}_{-}$ between the two:

$${\text{δ}}_g^{-}={\log }_2\left(mea{n}_i\left(e_{g,i}^{KO}\right)+\text{ε}\right)-{\log }_2\left(mea{n}_i\left(e_{g,i}^{WT}\right)+\text{ε}\right).$$

To identify candidate differentially expressed gene, we filtered genes satisfying

$$\left|{\text{δ}}_g^{+}\right|>0.7\left|{\text{δ}}_g^{+}-{\text{δ}}_g^{-}\right|>0.5,$$

i.e., genes with sufficiently high differential expression among Foxc1/2 expressing cell types that was absent among the non-Foxc1/2 expressing cells. From the remaining list of 27 genes we further removed Igf2 and H19 whose opposite differential expression was attributed to loss of parental imprinting.

Additional resources

To make the data accessible to all users, we have developed an online interactive data exploration interface (https://tanaylab.weizmann.ac.il/embflow).

Published: April 30, 2021