Abstract
Significant losses can occur for various smart grid stake holders due to the Power Quality Disturbances (PQDs). Therefore, it is necessary to correctly recognize and timely mitigate the PQDs. In this context, an emerging trend is the development of machine learning assisted PQDs management. Based on the conventional processing theory, the existing PQDs identification is time-invariant. It can result in a huge amount of unnecessary information being collected, processed, and transmitted. Consequently, needless processing activities, power consumption and latency can occur. In this paper, a novel combination of signal-piloted acquisition, adaptive-rate segmentation and time-domain features extraction with machine learning tools is suggested. The signal-piloted acquisition and processing brings real-time compression. Therefore, a remarkable reduction can be secured in the data storage, processing and transmission requirement towards the post classifier. Additionally, a reduced computational cost and latency of classifier is promised. The classification is accomplished by using robust machine learning algorithms. A comparison is made among the k-Nearest Neighbor, Naïve Bayes, Artificial Neural Network and Support Vector Machine. Multiple metrics are used to test the success of classification. It permits to avoid any biasness of findings. The applicability of the suggested approach is studied for automated recognition of the power signal’s major voltage and transient disturbances. Results show that the system attains a 6.75-fold reduction in the collected information and the processing load and secures the 98.05% accuracy of classification.
1. Introduction
1.1. Background and problem statement
Several problems are raised in the conventional and smart grids due to the PQDs [1]. Such irregular events can significantly affect the output of power networks. The PQ events mainly influence one or more attributes of the supply such as frequency and voltage [2]. They can appear after an accidental fuse of circuit breaker, problems with capacitor switching, use of nonlinear loads, electrical equipment abnormal functioning and overheating of transformers [3, 4].
The power consumption is globally increasing and an increased power generation by using conventional approaches could harm the environment. Therefore, in the aim of attaining the green supply, the trend is to integrate renewable energy sources in smart grids. However, integration of various energy sources is challenging and also originate the PQDs [5, 6].
The economy of any society can suffer from failures which occur due to the PQDs. It is particularly unbearable for sensitive facilities such as hospitals, data centres and nuclear reactors. Therefore, such customers are inclined to install the automated on-site PQDs recognition and mitigation equipment [5]. Such systems use the smart sensors, controllers and actuators for PQDs automated management. The recent advancements in the domain of machine learning have evolved a variety of automated solutions [7–14]. The same trend is followed by the automated PQDs mitigation techniques [15–17]. The PQDs identification should be carried out with precision and minimum possible latency. A timely assessment of PQDs permits to protect the critical and expensive power generation and distribution equipments and loads connected to the network. This could prevent the massive economical losses [4, 18].
PQDs are of non-stationary and sporadic nature. The monitoring mechanism characterizes these PQDs, their corresponding instance of occurrence and location. The findings can be used to pilot the appropriate actuators in order to mitigate the recognized PQDs in a quasi-real-time manner. To effectively mitigate PQDs, an uninterrupted monitoring of the power signals must be performed. It is a tiresome job and cannot be performed manually. Moreover, due to fatigue and lack of concentration mistakes can be made by the onsite power engineers. In this context, for the recognition and mitigation of PQDs, automatic approaches have been suggested [15, 16, 19–23].
1.2. Related works
In any automatic PQDs identification scheme, the power signals mainly goes through three steps namely conditioning, features extraction and classification [24, 25]. In [19] Borges et al. have used the time-domain and frequency-domain methods for the statistical features extraction. Onward, these extracted features are processed by the Artificial Neural Network (ANN) classifier for the PQDs identification. In [15] Hussain et al. have used the singular spectrum analysis and Curvelet transform methods for the features extraction. Onward, these extracted features are processed by the deep Convolutional Neural Network (CNN) classifier for the PQDs identification. In [20] Agüera-Pérez et al. have used the higher-order statistical analysis method for the features extraction. The categorization is achieved by using a higher-order statistical estimator. In [16] Manikandan et al. have used the sparse signal decomposition with hybrid dictionary for the features extraction. The categorization is achieved by using the hierarchical decision tree algorithm. In [21] Decanini et al. have used the discrete wavelet transform and entropy norm for the features extraction. The categorization is achieved by using the ANN. In [22] Singh et al. have used the non-dominated sorting genetic algorithm based on S-transform and time-time transform for the features extraction. Decision Tree (DT) is used for the classification purpose. In [23] Ferreira et al. have used the Independent Component Analysis (ICA) for the features extraction. Onward, the categorization is achieved by using the Multi Layer Perceptron (MLP).
1.3. Research gap and contribution
In the aim of achieving a precise identification and mitigation of the power quality issues, a fine grained power signal recording and processing is necessary [26]. Almost all existing automatic power signal processing systems operate at fixed-rate regardless of the rate of information in the incoming signal. It can cause a useless processing, storage and transmission of information [26]. In this framework, compressed sensing and analog–to–information conversion solutions have been devised [27].
In continuation of works presented in [24, 28, 29], this research enhances the existing fix-rate automated PQ events identifiers. Shortfalls of the classical fixed-rate power signal processing systems are compensated by using the signal-piloted power signals recording and analysis. It records the necessary details of the intended power signal while noticeably diminishing the amount of collected information. It brings a remarkable real-time compression along a computational load diminishing of the suggested adaptive-rate PQ events identifiers in comparison with the fix-rate counterparts [15, 16, 19–23]. The following are the key contributions of this paper.
Suggesting an efficient and precise solution for major power voltage and transient disturbances recognition. It processes the power signal in an efficient adaptive-rate manner and extracts the classifiable features directly in time-domain without using any computationally complex transformation based approach.
- Intelligently combining the signal-piloted Analog to Digital Converters (SPADCs), Activity Selection Algorithm (ASA), time-domain features extraction and machine learning algorithms for an efficient classification of PQ events:
- Power signals are acquired at adaptive-rates by using the SPADCs.
- The segmentation is achieved by using the MASA
- A novel features extractor directly analyzes each segment in time-domain to determine its discriminating attributes.
- The PQDs categorization is realized by using the forehand time-domain extracted features by using robust machine learning algorithms.
1.4. Paper organization
The proposed signal-piloted and adaptive-rate power signal processing scheme is described in Section 2. The power quality disturbances model, novel time-domain features extraction and robust machine learning based classification algorithms are also described in Section 2. Moreover, Section 2 also presents the system performance evaluation measures. Section 3 presents an experimental evaluation of the devised method. Section 4 discusses the main findings and features of the suggested approach. It also presents a performance comparison with contemporary PQDs classification methods. Finally the conclusion is made in Section 5.
2. Materials and methods
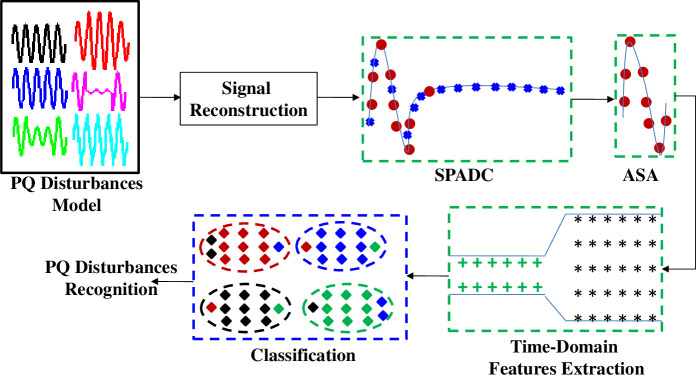
The different stages of proposed system are displayed in Fig 1. Modules enclosed by the solid black colour line ‘______’ are modelling scenarios for testing the suggested solution. Modules enclosed by the dashed green colour line ‘- - -’represent stages, proposed to be embedded in the frontend processing chain. The dashed blue colour line ‘- - -’encloses the classification stage, which could be realized via a cloud or server based application. Implementing the optimized processing modules in frontend processor and keeping the classification operation on the cloud allows realizing an effective and configurable solution [30].
Fig 1. The suggested system block diagram.
2.1. Power Quality Disturbances (PQDs) model
The collection of PQDs is not straightforward. Therefore, a common tendency is to generate the real-like signals by utilizing the mathematical models [2, 31]. The synthetic PQDs have been used in previous studies for the evaluation of proposed features extraction and recognition approaches [15–17, 20–22]. In this study four major categories of power signals namely pure signal, sag, interruption and swell are generated by using MATLAB R2019b [32]. The employed PQDs generation model is based on the IEEE recommended standard for PQDs and it generates PQDs waveforms in a random fashion [33, 34]. Concretely, the voltages and occurrence timings, of intended PQDs, are randomly changed. It is performed within the limits of their corresponding bounds, presented in [34]. In order to approach the realistic case, random noise is added in these signals in order to attain a Signal to Noise Ratio (SNR) of 40 dB [19].
A description of these power signals is provided in the following. For equal representation, 200 instances are considered from each category. It results in 800 instances in total. Each instance is produced for a half-second period, equal to the 25 cycles of pure power signal of frequency 50Hz. By following the process, presented in [19], it is sampled at a rate of 6.4 kHz. Each instance is composed of 3200 samples. It results in the dataset dimensionality of 800x3200.
2.1.1. The Pure Signal (PUS)
It is the faultless power signal which represents a desired supply. Eq (1) introduces this phenomenon mathematically [33, 34]. Where, A and f are respectively the power signal amplitude and frequency. The f = 50 Hz is selected [33, 34]. tn and φ are the instants of sampling and phase.
| (1) |
2.1.2. The sag
It causes the Root Mean Square (RMS) voltage to decrease briefly between 0.1–0.9 per unit (pu). It is a PQD that might last between half cycle to 1-minute [33, 34]. Sags can occur due to momentary short circuits or by turning on heavy loads such as big motors. It can also be caused by overloading transformers or due to the deployment of undersized conductors. Eq (2) introduces this phenomenon mathematically. tn and φ are the instants of sampling and phase.
| (2) |
In Eq (2), 0.1 ≤ α ≤0.9, T ≤ t2 –t1 ≤ 49T and Sec.
2.1.3. The Interruption (Intr.)
It takes place due to defects in the power grid, equipment malfunction and controller shortfalls [31]. This causes loss of supply voltage for a limited period, usually less than a minute. It temporarily reduces the RMS voltage supply below 0.1 pu [33, 34]. Eq (3) introduces this phenomenon mathematically. Where, tn and φ are the instants of sampling and phase.
| (3) |
In Eq (3), 0.9 ≤ ρ ≤ 1, T ≤ t2 –t1 ≤ 49T and Sec.
2.1.4. The swell
It can be originated by turning off a heavy load or by energizing a large network of condensers [31]. It causes a momentarily rise in the power line voltage. When renewable energy sources such as solar panels are linked to the network, they can also originate swells. It causes the RMS voltage to increase briefly between 1.1–1.8 pu. It is a PQD that might last between half cycle to 1-minute. Eq (4) introduces this phenomenon mathematically [33, 34]. Where, tn and φ are the instants of sampling and phase.
| (4) |
In Eq (4), 0.1 ≤ β ≤ 0.8, T ≤ t2 –t1 ≤ 9T and Sec.
2.2. Reconstruction and signal-piloted acquisition
The considered instances of power signals are reconstructed. It allows evaluating the SPADC [35]. Up-sampling is realized by using a combination four cascaded cubic-spline interpolators [36]. It transforms the incoming signal y(tn) in its quasi analog version . The relationship between and y(tn) is given by Eq (5). Onward, the noise is added in to obtain the noisy signal, given by Eq (6). The probability density function of is given by Eq (7). Where, μ is mean and σ is the standard deviation.
| (5) |
| (6) |
| (7) |
The contemporary automated PQDs identifiers are frequently using the ADCs. The acquisition of signals is typically founded on the time-invariant and fix-rate concept [36]. The implementation of these systems is thus realized for the extreme scenarios [36]. However, such solutions are not efficient in the case of unpredictable PQDs [37]. To compensate these limitations, the SPADCs are used. Based on the Level-Crossing Sensing (LCS), a real-time self-organization capability is available in SPADCs [37]. It permits to change their rate of acquisition as per changes in the incoming signal, [37]. The process of sampling is triggered by the predefined thresholds crossings, made by . Consequently, samples are non-uniformly arranged in time. The process is given by Eq (8). Where dtn is the time elapse among the current instant of sampling, tn, and the prior one, tn-1.
| (8) |
For SPADC, the amplitude of a sample is equivalent to one of the preconfigured thresholds and the instant of that sample is recorded with the help of an appropriate timer circuit [35]. A 4-Bit resolution uniform quantization based SPADC is used for acquiring the power signals. The choice of resolution is made while achieving a favourable compromise among the system implementation and computational complexities and precision in the detection of PQDs.
In contrast to conventional ADCs, the signal-to-noise-ratio (SNR) of SPADCs is independent of the quantizer resolution. It solely depends on the operating frequency, FTimer, of the timer circuit and is given by Eq (9). Where, Ttimer is the timer step and is equal to [35]. fsig = 50Hz is the desired frequency of power supply. In this study, FTimer = 1MHz is selected. It renders an ideal SPADC SNR of more than 12-Bit, which is a suitable resolution for the automated PQDs recognition methods [15, 16, 19–23].
| (9) |
2.3. Adaptive-rate segmentation
To efficiently segment the SPADC outcome, a modified version of the Activity Selection Algorithm is used [35, 37]. It is named as MASA and is realized by the use of implicit information, available in the employed sampling process non-uniformity. It permits to segment the SPADC output in a real-time and self organised manner. The functioning of MASA is depicted with the help of a flow chart, shown in Fig 2.
Fig 2. Flow chart of the MASA.
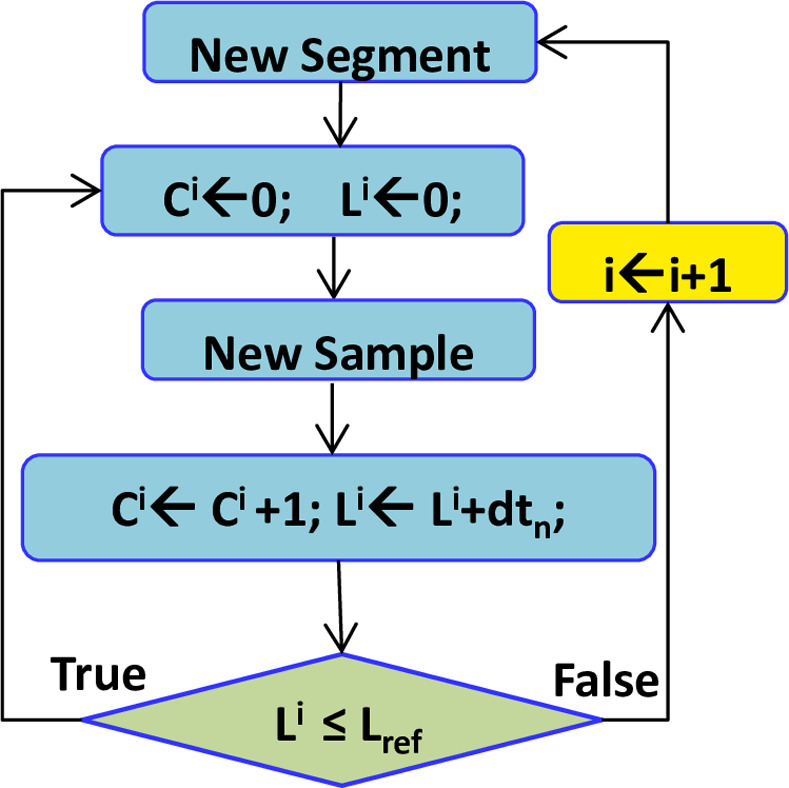
In Fig 2, Ci is the count of samples and Li is the length in seconds of the ith selected segment Wi. In the beginning, Ci and Li are reset to zero. Onward, keep adding samples in Wi. For each added sample, xn, the Ci and Li are updated and are respectively given by Eqs (10) and (11). The process continues unless Li ≤ Lref. Once, the condition Li ≤ Lref violates, i is incremented and the processing of new segment begins. In this case, Lref = 100-mSec is the selected upper bound on the length of segments [35]. This choice of Lref is made in an incremental manner while taking in account the statistical characteristics of the intended PQ events [33, 34]. This decision is made as a function of attaining the best compromise among the system performance and processing complexity. Consequently, for this choice of Lref, for each instance of 0.5-Second duration, the MASA delivers 5 selected segments. Due to the adaptive-rate and signal-piloted acquisition approach, the samples count for each selected segment could vary. It adapts in accordance with the variations.
| (10) |
| (11) |
2.4. Features extraction
The Thanks to the SPADC and the ASA processes, the time domain data possesses significant information about the signal frequency content [35]. Thus, compared to alternative methods which are based on frequency or time-frequency representation, the designed method does not require any computationally complex transformation [15–17, 21–24, 26]. In the time-domain, the signal-piloted acquisition based data is immediately used to mine the relevant classifiable features.
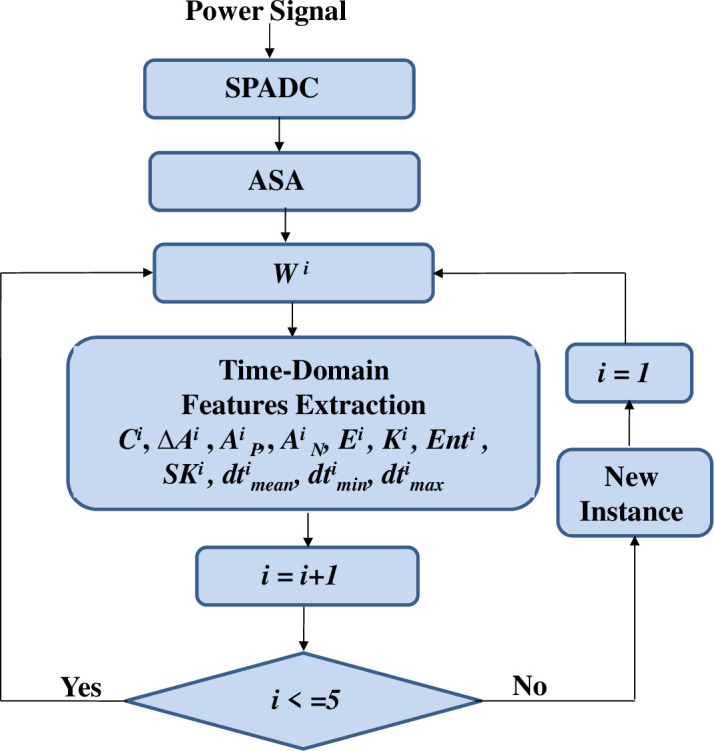
The ASA delivers 5 selected segments per instance. Eleven different features, in time-domain, are mined for each segment. In this way 55 features are used to present each instance. The mechanism is also shown in Fig 3. It presents that for Wi the mined attributes are: the count of samples, Ci, the positive peak, , the energy, Ei, the negative peak, , the peak-to-peak amplitude, ΔAi, the skewness SKi, the average sampling step, , the entropy, Enti, the minimum sampling step, , the kurtosis, Ki and the maximum sampling step, .
Fig 3. The features extraction principle.
2.5. Classification methods
After features extraction each intended instance is represented by 55 features. The employed dataset has four power signals classes. 800 instances are considered for all classes, resulting in a selected features dataset, P, with a dimension of 800x55. The well-known robust methods, k-Nearest Neighbor (KNN), Support Vector Machine (SVM), ANN and Naïve Bias (NB), are used for classification. Because of the small data collection, the classification’s accuracy could be biased. The cross-validation scheme is frequently used to compensate this impact of biasness and to avoid over fitting [38]. Accordingly, this analysis uses 10-fold cross-validation. The MATLAB program is used to carry out the classification [32].
2.5.1. k-Nearest Neighbor (KNN)
The KNN is regarded as computationally effective but powerful classifier [38]. It employs features’ distance to label the test samples. A sample, z, is classified by majority voting of its K neighbours, determine the maximum probability [38]. The process is given by Eq (12). Where, C is the features set of total number of classes and y is the output label.
| (12) |
The Euclidian distance measure is used. The choice of K should be appropriately made. In a step-by-step fashion, various K values are evaluated and the value with the least classification error is chosen. The best results are obtained for K = 5 in this study.
2.5.2. Naïve Bayes (NB)
One of the most common machine-learning techniques is the Naïve Bayes classifier. Its "naive" presumption sets the conditions for all characteristics to be independent. Parameters are separately studied with each attribute and this greatly simplifies the learning. Consequently, because of its independence presumption that simplifies the algorithm [39], the Naïve Bayes algorithm is often used for classification of a high-dimensionality features vector. It predicts its own probability for each class when classifying a sample [38]. The process is given by Eq (13). Where z represent a sample under test and y is the predicted label. C is the features set of total number of classes. p is the probability and argmax outcomes the maximum value for the targeted function.
| (13) |
In this study, the Gaussian Naïve Bayes classifier is used with a batch size of 100.
2.5.3. Support Vector Machine (SVM)
The support vector machine locates a hyperplane in an N- spacer that classifies the test samples distinctly [40]. The aim is to find a plane with the greatest range. Maximizing the gap from the margins gives sufficient clarification. Therefore, potential test samples can be identified with better assurance [40]. Eq (14), mathematically described the process of separating hyperplane. Where, X is the sample vector X = [x1, x2…xq] having q attributes, W = [w1,w2…wq] is the weights vector, and b is a scalar bias. SVM is particularly good for solving two class problems. Various methods can be employed while dealing with multiple classes. In this case, the One-vs-All strategy is used with Sequential Minimal Optimization (SMO) to train the classifier. In a step-by-step manner, the best suitable value of the regularisation parameter is found to be 100 while using the polynomial kernel.
| (14) |
2.5.4. Artificial Neural Network (ANN)
The ANN follows the principle of biological neural networks [41]. The fundamental building block of an ANN is an artificial neuron. Multiplication, summation, and activation are the three fundamental stages of an ANN. It is a network of the input and output units, interlinked via hidden layers. The weight of each interlinking node is tuned during the training process. It permits the development of non-linear and complicated input-output relations. Onward, this knowledge is used for labelling the test data. The major drawback of an ANN is the unknown behaviour of neural networks that may result in unexplainable classification output. Furthermore, as the number of hidden layers grows, ANN necessitates a significant volume of data for proper training. The principle of labelling a sample z as y is given by Eq (15). Where f is a nonlinear activation function. X is the features vector X = [x1, x2…xq] having q attributes and W = [w1,w2…wq] is the weights vector. b is a scalar bias.
| (15) |
The multilayer perceptron (MLP) technique is used in this study. The best precision is secured while using three hidden layers, each containing 50 nodes for the reduced setting and 90 nodes for the full setting.
2.6. Performance measures
2.6.1. The samples ratio (SR)
It presents the ratio between the counts of power signal samples, collected in the traditional case and the proposed case for a given time length. Let SRi be the samples ratio for Wi then it is given by Eq (16). Where, Nr and Ci are respectively the number of samples exist in Wi for the classical and the devised approaches.
| (16) |
2.6.2. The compression ratio (RCOMP)
This tests the success of suggested method in reducing the amount of information to be transmitted to the classifier. The comparison is made with traditional methods which, without any reduction in the dimension, conveys the captured power signals to the classifier [2]. In the conventional and proposed cases, let Nr and P present datasets that must be transmitted and classified, respectively. In this case, each element of Nr and P is presented with 12-Bit resolution [2, 33, 34]. Therefore, the compression ratio in bits, RCOMP, can be computed by using Eq (17).
| (17) |
2.6.3. The classification accuracy (Acc)
The proposed solution is beneficial because of its signal-piloted nature. It can bring real-time reduction in the count of samples, compression and processing effectiveness [37]. However, its classification performance can be compromised compared to the traditional fixed-rate equals.
The accuracy score tests the success of suggested method in categorizing the PQDs. It is the percentage of correctly identified labels. The process is given by Eq (18). Where, true positive, true negative, false positive and false negative are respectively denoted by TP, TN, FP and FN. In the studied case it provides an appropriate evaluation of the classification performance because all the considered class sizes are equal.
| (18) |
2.6.4. The F-measure (F1)
The F1seeks to find a balance between values of recall and precision. In the analyzed scenario, all groups have the same data size, so we simply use the F-measure macro given by Eq (19), where precision = and recall = .
| (19) |
2.6.5. The area under the ROC curve (AUC)
The ROC curves, on the horizontal axis, map the TN rate against the TP rate on the vertical axis. The ROC curve is closely based on the specifics of the particular test data set. This dependency can be reduced by using the cross-validation technique. It supposes that the probability estimates of the predictors which are constructed from the various training sets are all built on random data samples of the same size. The larger the area underneath the ROC curves, the better is the classifier, and vice versa [42].
2.6.6. The kappa index
It statistically measures the agreement between two clustering. The Cohen’s kappa measure is used. It is popularly employed for evaluating clustering results and is expressed by using Eq (20). Where, the likelihood of agreement between the expected and target labels is denoted by po, while pe is the probability of such an agreement happening by chance.
| (20) |
3. Results
The In this study four major categories of power signals are considered namely PUS, sag, swell and intr. Fig 4 displays examples of the normalized waveforms of the intended power signals.
Fig 4. The instances for pure signal, sag, swell and intr.

In order to show the impact of noise, the zoom of waveforms for the case of typical sag and intr. Instances are respectively shown in Fig 5A and 5B.
Fig 5. Zooms of instances of sag and intr.
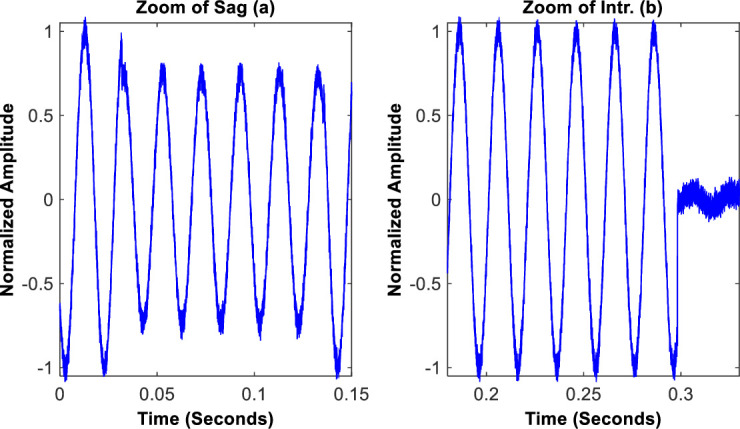
The considered power signal instances are generated at a sampling rate of 6.4 kHz. Each instance subsequently undergoes through the up-sampling by a factor of 100. Examples of zooms of typical instances, digitized with a 4-bit resolution SPADC, of sag and intr. are shown in Fig 6.
Fig 6. The instances acquired with a 4–bit resolution SPADC for sag (left) and intr. (right).

Fig 6 indicates gains of using SPADC. It supports that it updates its sampling frequency, for a given resolution, based on variations in the incoming signal [35].
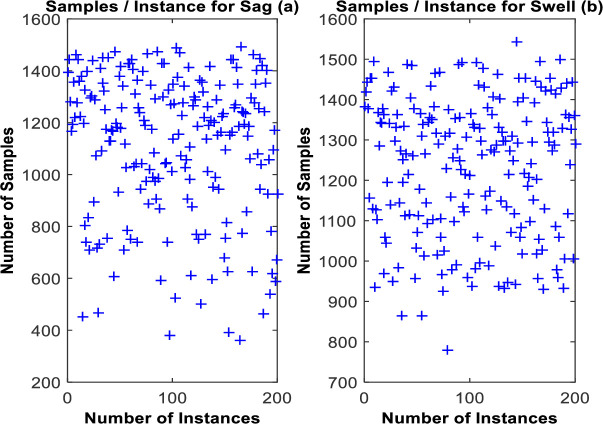
In this study, the ASA is used to segment the output of SPADC [35]. For each incoming power instance, 5 selected segments are delivered by the ASA. However, the count of thresholds, Ci, changes according to the time variations in the pattern of incoming instance. The phenomenon is clear from Fig 7, which shows the total number of samples, collected for each considered instance of sag and swell. It also confirms the random nature of studied dataset.
Fig 7. Number of samples per instance for sag (left) and swell (right).
Conventionally, is continuously acquired at 6.4 kHz regardless of its variations. Therefore, an augmented collection and processing of redundant samples happen. 640 samples per segment are collected for Lref = 100mSec. Consequently, the post-processing modules analyse redundant data which results in an increased processing load, transmission and power consumption overhead.
The overall sample ratios, for 200 instances of each class, are calculated by using Eq (7). Findings are outlined in Table 1. This reveals that the designed approach reaches an overall average samples count reduction, obtained for all intended classes, of 6.75-fold.
Table 1. Summary of the samples ratios.
| Power Signal | Maximum | Minimum | Mean | Median |
|---|---|---|---|---|
| Sag | 17.68 | 4.28 | 6.29 | 5.41 |
| Swell | 8.22 | 4.15 | 5.30 | 5.03 |
| PUS | 4.27 | 4.26 | 4.26 | 4.26 |
| Intr. | 71.11 | 4.31 | 11.14 | 7.97 |
Each intended power instance is presented by 55 features, after application of the proposed features extraction technique. On the other hand, each power instance is originally composed of 3200 samples. It results in a RCOMP = 58.18. This promises the same reduction factor in data transmission operation, bandwidth usage, and power consumption plus classifier’s computational efficiency.
In total 800 instances are studied, for the considered categories of power signals, in this study. To account for the size limit of the dataset, the 10-fold cross-validation approach is used [42]. As mentioned in Section 2.5, the parameters of each classifier are configured during the training process. The evaluation measures namely Acc, F1, AUC and Kappa are measured while classifying the considered dataset.
The obtained percentage accuracies of identification are listed in Table 2 respectively for the KNN, NB, SVM and ANN classifiers.
Table 2. Accuracy scores for power signals recognition, obtained by different classifiers.
| Power Signal | Acc (%age) | |||
|---|---|---|---|---|
| KNN | NB | SVM | ANN | |
| Sag | 91.55 | 92.46 | 96.25 | 94.62 |
| Swell | 99.05 | 98.13 | 99.87 | 100 |
| PUS | 97.71 | 100 | 99.48 | 99.34 |
| Intr. | 92.72 | 93.16 | 96.61 | 94.97 |
Table 2 outlines that for KNN classifier the accuracy score of the classification of PQ signals received is 91.55% for the sag, 99.05% for the swell, 97.71% for the pure signal and 97.72% for the interruption. The overall average classification accuracy score of KNN is 95.26%.
The accuracy score for NB classifier is 92.46% for the sag, 98.13% for the swell, 100% for the pure signal and 93.16% for the interruption. For all categories, the overall classification accuracy score of NB is 95.94%.
The accuracy score of SVM classifier is 96.25% for the sag, 99.87% for the swell, 99.48% for the pure signal and 96.61% for the interruption. For all categories, the overall classification accuracy score of SVM is 98.05%.
The accuracy score of ANN classifier is 94.62% for the sag, 100% for the swell, 99.34% for the pure signal and 94.97% for the interruption. For all categories, the overall classification accuracy score is ANN is 97.23%.
The obtained average F1, AUC and Kappa values for each considered classifier are listed in Table 3. It reveals that, as compared to KNN and NB, the suggested signal-piloted processing chain in combination with SVM and ANN identifies better the intended PQDs. It is because the SVM and ANN are less likely to be biased. However, KNN and NB can be easily distracted particularly if the data contains outliers. This statement is further enforced by the findings, average scores across F1, AUC and Kappa, which are summarized in Table 3.
Table 3. Performance of considered classifiers using F1, AUC and Kappa metrics on the test dataset.
| Classifier | F1 | AUC | Kappa |
|---|---|---|---|
| KNN | 0.910 | 0.970 | 0.880 |
| NB | 0.920 | 0.978 | 0.893 |
| SVM | 0.961 | 0.981 | 0.948 |
| ANN | 0.945 | 0.991 | 0.927 |
We considered the detailed classification outcomes for each expected class for further study, as shown in Tables 4 and 5. Relative to KNN, NB and ANN, the total FP and FN counts using SVM are the lowest, thus confirms the better performance of the SVM compared to other algorithms under consideration.
Table 4. Confusion matrices for the KNN and the NB classifiers.
| KNN& NB | Predicted (KNN) | Predicted (NB) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Sag | Swell | PUS | Intr. | Sag | Swell | PUS | Intr. | ||
| Actual | Sag | 168 | 0 | 10 | 22 | 185 | 4 | 0 | 11 |
| Swell | 2 | 193 | 5 | 0 | 6 | 193 | 0 | 1 | |
| PUS | 0 | 0 | 200 | 0 | 0 | 0 | 200 | 0 | |
| Intr. | 33 | 0 | 2 | 165 | 39 | 3 | 0 | 158 | |
Table 5. Confusion matrices for the SVM and the ANN classifiers.
| SVM & ANN | Predicted (SVM) | Predicted (ANN) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Sag | Swell | PUS | Intr. | Sag | Swell | PUS | Intr. | ||
| Actual | Sag | 184 | 0 | 3 | 13 | 179 | 0 | 4 | 17 |
| Swell | 1 | 199 | 0 | 0 | 0 | 200 | 0 | 0 | |
| PUS | 0 | 0 | 200 | 0 | 0 | 0 | 200 | 0 | |
| Intr. | 13 | 0 | 1 | 186 | 22 | 0 | 1 | 177 | |
4. Discussion
The designed PQDs recognition mechanism is evaluated by using the real-like model-based power signal instances. The PQ events are randomly generated as per the IEEE-1159 standards [2, 33, 34]. The obtained results are appealing and are outlined in Section 3. The technique yields an overall 16.87-fold reduction in count of collected samples over traditional equals. This assures a major decrease in arithmetic complexity and the overhead capacity consumption of the proposed solution. In addition, SPADC embedding and features selection functionality in PQDs elucidators greatly decreases data storage and communication operation between frontend sensors and cloud-based classifier relative to traditional methods. The compression ratio achieved is 58.18-fold for the studied case. Moreover, features are extracted in time-domain without the application of any computationally complex transformation. This confirms the superiority of the suggested solution over the existing ones [9, 16, 23, 43]. The used SPADC is of much inferior, 4-Bit, resolution. Nonetheless, a 12-Bit ADC is used in the fix-rate equals to acquire the power signals [15, 16, 19–23]. This guarantees a significant decrease in the processing cost and complexity of the system’s hardware relative to conventional equivalents.
In the fix-rate solutions, a lower sampling rate and a bigger quantization step can also be used. However, it decreases the ADC SNR [35] and can lower the precision of automated PQDs classification. The SNR of SPADC, does not depend on the quantum value and is based on the timer circuit frequency which is used to measure the sampling instants [35]. Furthermore, the uniform sampling-based approach would lack in extracting the necessary information of the PQD instances in solely time-domain. Therefore, these techniques use analysis methods in both time and frequency domains for mining the classifiable attributes. It can increase the complexity of computing and latency relative to the suggested method.
The accuracy score of 98.05% is secured with the SVM classifier for the studied scenario. The ANN follows with 97.23% accuracy. The NB attains the accuracy of 95.94% and the KNN achieves the lowest average accuracy of 95.26%. For the studied case, the SVM performs better as compared to the ANN, NB and KNN. It is also confirmed by other evaluation scores such as F1, AUC and Kappa statistics. It is because of the SVM ability to successfully prune the most unnecessary possibilities when classifying an instant under test. This states that the suggested framework, based on the SPADC, ASA, time-domain features mining and the SVM offers the best interpretation of the intended power signals.
The idea of integrating the signal-piloted acquisition and adaptive-rate time-domain features mining in the PQDs elucidators is new. Comparing the suggested method with the state-of-the-art approaches is not obvious, as they are based on standard fixed-rate sampling and processing [9, 15, 16, 20–23]. In addition, each research uses various categories of the PQDs, processing and analysis tools and classification algorithms. However, a comparison is made between the key preceding studies, carried out on synthetic PQDs. For all considered studies, the best classification accuracies are outlined in Table 6. It reveals that the accuracy of PQDs categorisation, attained by the suggested method, is similar or superior than the fix-rate equivalents.
Table 6. Comparison with state-of-the-art methods.
| Study | Features Extraction | Classification | Accuracy (%) |
|---|---|---|---|
| [19] | Tim-domain and frequency-domain statistical features. | Artificial Neural Network (ANN) | 96.03 |
| [15] | singular spectrum analysis and Curvelet transform | Deep convolutional neural networks | 100 |
| [20] | Higher-order Statistical features | Higher-Order Statistical Estimator | 83.00 |
| [16] | Sparse signal decomposition with hybrid dictionary | Hierarchical Decision Tree Algorithm | 97.3 |
| [21] | discrete wavelet transform and entropy norm | ANN | 99.66 |
| [22] | Non-dominated sorting Genetic algorithm based on S-transform and time–time transform | Decision tree | 99.93 |
| [23] | Independent component analysis | Multi Layer Perceptron (MLP) | 97.00 |
| This Study | SPADC with ASA and time-domain statistical features | SVM | 98.05 |
5. Conclusion
A novel approach of automatically identifying the primary voltage and transient-based power quality events is proposed. It is developed by intelligently combining the signal-piloted acquisition, adaptive-rate segmentation, time-domain features extraction, and machine learning tools. In contrast to the counterparts, this method does not employ arithmetically complex transformations for feature extraction. It is demonstrated that signal-piloted sampling has resulted in a 16.87-fold decrease in the amount of recorded information compared to the fix-rate counterparts. It aptitudes an enhanced performance in terms of processing and power consumption diminishing. Additionally, a similar reduction is promised in the information management activity and post-classification complexity. The developed framework also offers a simplified hardware complexity while achieving an equivalent or superior PQDs recognition accuracy score with respect to the contemporary equals. The designed solution attains the best average classification accuracy score of 98.05%. It confirms the benefit of incorporating the suggested method in modern PQDs management solutions.
In this study a uniform quantization based SPADC is investigated while considering four major classes of the power quality disturbances. Investigating the application of non-uniform quantization-based SPADC with broader categories of power quality disturbances is future work. Another prospect is to evaluate the possible integration of other robust classifiers such as Rotation Forest, Random Forest, ensemble algorithms, and deep learning methods in the suggested solution.
Supporting information
(ZIP)
(DOCX)
Acknowledgments
The author is thankful to Engineer R. Aljefri for her assistance during the simulation process. Author is also thankful to editor and reviewers for their valuable feedback.
Data Availability
All relevant data are within the manuscript and its Supporting Information files.
Funding Statement
S.M.Q secures funding for this project. The project is funded by the Effat University, Jeddah, KSA under the grant No. UC#9/29 April.2020/7.1-22(2)3. https://www.effatuniversity.edu.sa/English/Pages/default.aspx The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Van den Broeck G., Stuyts J., and Driesen J., “A critical review of power quality standards and definitions applied to DC microgrids,” Appl. Energy, vol. 229, pp. 281–288, 2018. [Google Scholar]
- 2.R. Igual, C. Medrano, F. J. Arcega, and G. Mantescu, “Integral mathematical model of power quality disturbances,” in 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), 2018, pp. 1–6.
- 3.V. Kumar, A. S. Pandey, and S. K. Sinha, “Grid integration and power quality issues of wind and solar energy system: A review,” in 2016 International Conference on Emerging Trends in Electrical Electronics & Sustainable Energy Systems (ICETEESES), 2016, pp. 71–80.
- 4.Rönnberg S. and Bollen M., “Power quality issues in the electric power system of the future,” Electr. J., vol. 29, no. 10, pp. 49–61, 2016. [Google Scholar]
- 5.R. A. Flores, “State of the art in the classification of power quality events, an overview,” in 10th International Conference on Harmonics and Quality of Power. Proceedings (Cat. No. 02EX630), 2002, vol. 1, pp. 17–20.
- 6.Kow K. W., Wong Y. W., Rajkumar R. K., and Rajkumar R. K., “A review on performance of artificial intelligence and conventional method in mitigating PV grid-tied related power quality events,” Renew. Sustain. Energy Rev., vol. 56, pp. 334–346, 2016. [Google Scholar]
- 7.Abbasi R. et al., “Author classification using transfer learning and predicting stars in co-author networks,” Softw. Pract. Exp., vol. 51, no. 3, pp. 645–669, 2021. [Google Scholar]
- 8.Panigrahi R. et al., “A Consolidated Decision Tree-Based Intrusion Detection System for Binary and Multiclass Imbalanced Datasets,” Mathematics, vol. 9, no. 7, p. 751, 2021. [Google Scholar]
- 9.Alazab M., Khan S., Krishnan S. S. R., Pham Q.-V., Reddy M. P. K., and Gadekallu T. R., “A multidirectional LSTM model for predicting the stability of a smart grid,” IEEE Access, vol. 8, pp. 85454–85463, 2020. [Google Scholar]
- 10.Pham Q.-V. et al., “Deep Learning for Intelligent Demand Response and Smart Grids: A Comprehensive Survey,” ArXiv Prepr. ArXiv210108013, 2021. [Google Scholar]
- 11.Ebenuwa S. H., Sharif M. S., Alazab M., and Al-Nemrat A., “Variance ranking attributes selection techniques for binary classification problem in imbalance data,” IEEE Access, vol. 7, pp. 24649–24666, 2019. [Google Scholar]
- 12.Qaisar S. M. and Hussain S. F., “Effective epileptic seizure detection by using level-crossing EEG sampling sub-bands statistical features selection and machine learning for mobile healthcare,” Comput. Methods Programs Biomed., vol. 203, p. 106034, 2021. 10.1016/j.cmpb.2021.106034 [DOI] [PubMed] [Google Scholar]
- 13.Qaisar S. M., Mihoub A., Krichen M., and Nisar H., “Multirate Processing with Selective Subbands and Machine Learning for Efficient Arrhythmia Classification,” Sensors, vol. 21, no. 4, p. 1511, 2021. 10.3390/s21041511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Qaisar S. M. and Subasi A., “Cloud-based ECG monitoring using event-driven ECG acquisition and machine learning techniques,” Phys. Eng. Sci. Med., vol. 43, no. 2, pp. 623–634, 2020. 10.1007/s13246-020-00863-6 [DOI] [PubMed] [Google Scholar]
- 15.Liu H., Hussain F., Shen Y., Arif S., Nazir A., and Abubakar M., “Complex power quality disturbances classification via curvelet transform and deep learning,” Electr. Power Syst. Res., vol. 163, pp. 1–9, 2018. [Google Scholar]
- 16.Manikandan M. S., Samantaray S., and Kamwa I., “Detection and classification of power quality disturbances using sparse signal decomposition on hybrid dictionaries,” IEEE Trans. Instrum. Meas., vol. 64, no. 1, pp. 27–38, 2014. [Google Scholar]
- 17.Ucar F., Alcin O. F., Dandil B., and Ata F., “Power quality event detection using a fast extreme learning machine,” Energies, vol. 11, no. 1, p. 145, 2018. [Google Scholar]
- 18.Latran M. B., Teke A., and Yoldaş Y., “Mitigation of power quality problems using distribution static synchronous compensator: a comprehensive review,” IET Power Electron., vol. 8, no. 7, pp. 1312–1328, 2015. [Google Scholar]
- 19.Borges F. A., Fernandes R. A., Silva I. N., and Silva C. B., “Feature extraction and power quality disturbances classification using smart meters signals,” IEEE Trans. Ind. Inform., vol. 12, no. 2, pp. 824–833, 2015. [Google Scholar]
- 20.Agüera-Pérez A., Palomares-Salas J. C., De la Rosa J. J. G., Sierra-Fernández J. M., Ayora-Sedeño D., and Moreno-Muñoz A., “Characterization of electrical sags and swells using higher-order statistical estimators,” Measurement, vol. 44, no. 8, pp. 1453–1460, 2011. [Google Scholar]
- 21.Decanini J. G., Tonelli-Neto M. S., Malange F. C., and Minussi C. R., “Detection and classification of voltage disturbances using a fuzzy-ARTMAP-wavelet network,” Electr. Power Syst. Res., vol. 81, no. 12, pp. 2057–2065, 2011. [Google Scholar]
- 22.Singh U. and Singh S. N., “Optimal feature selection via NSGA-II for power quality disturbances classification,” IEEE Trans. Ind. Inform., vol. 14, no. 7, pp. 2994–3002, 2017. [Google Scholar]
- 23.Ferreira D. D., de Seixas J. M., and Cerqueira A. S., “A method based on independent component analysis for single and multiple power quality disturbance classification,” Electr. Power Syst. Res., vol. 119, pp. 425–431, 2015. [Google Scholar]
- 24.Qaisar S. M. and Aljefri R., “Event-Driven Time-Domain Elucidation of the Power Quality Disturbances,” Procedia Comput. Sci., vol. 168, pp. 217–223, 2020. [Google Scholar]
- 25.Khokhar S., Zin A. A. B. M., Mokhtar A. S. B., and Pesaran M., “A comprehensive overview on signal processing and artificial intelligence techniques applications in classification of power quality disturbances,” Renew. Sustain. Energy Rev., vol. 51, pp. 1650–1663, 2015. [Google Scholar]
- 26.Qaisar S. M. and Alsharif F., “Signal Piloted Processing of the Smart Meter Data for Effective Appliances Recognition,” J Electr Eng Technol, 2020. [Google Scholar]
- 27.Wang Q., Meng C., and Wang C., “Analog-to-Information Conversion for Nonstationary Signals,” IEEE Access, vol. 8, pp. 134067–134083, 2020. [Google Scholar]
- 28.Qaisar S. M. and Aljefri R., “Effective Power Quality Disturbances Identification Based on Event-Driven Processing and Machine Learning,” Green Energy Sol. Energy Photovolt. Smart Cities, pp. 191–219, 2020. [Google Scholar]
- 29.Qaisar S. M. and Aljefri R., “Time-Domain Identification of the Power Quality Disturbances Based on the Event-Driven Processing,” 2019, pp. 1–5. [Google Scholar]
- 30.Mian Qaisar S. and Fawad Hussain S., “Arrhythmia Diagnosis by Using Level-Crossing ECG Sampling and Sub-Bands Features Extraction for Mobile Healthcare,” Sensors, vol. 20, no. 8, p. 2252, 2020. 10.3390/s20082252 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rodriguez-Guerrero M. A., Carranza-Lopez-Padilla R., Osornio-Rios R. A., and de J R. Romero-Troncoso, “A novel methodology for modeling waveforms for power quality disturbance analysis,” Electr. Power Syst. Res., vol. 143, pp. 14–24, 2017. [Google Scholar]
- 32.P. MatLab, “9.7. 0.1190202 (R2019b),” MathWorks Inc Natick MA USA, 2018.
- 33.Naderian S. and Salemnia A., “Method for classification of PQ events based on discrete Gabor transform with FIR window and T2FK-based SVM and its experimental verification,” IET Gener. Transm. Distrib., vol. 11, no. 1, pp. 133–141, 2017. [Google Scholar]
- 34.“IEEE Recommended Practice for Monitoring Electric Power Quality,” IEEE Std 1159–2019 Revis. IEEE Std 1159–2009, pp. 1–98, August. 2019, 10.1109/IEEESTD.2019.8796486 [DOI] [Google Scholar]
- 35.Qaisar S. M., “Efficient mobile systems based on adaptive rate signal processing,” Comput. Electr. Eng., vol. 79, p. 106462, 2019. [Google Scholar]
- 36.Ingle V. K. and Proakis J. G., Digital signal processing using matlab: a problem solving companion. Cengage Learning, 2016. [Google Scholar]
- 37.Qaisar S. M., Fesquet L., and Renaudin M., “Adaptive rate filtering a computationally efficient signal processing approach,” Signal Process., vol. 94, pp. 620–630, 2014. [Google Scholar]
- 38.Bonaccorso G., Machine learning algorithms. Packt Publishing Ltd, 2017. [Google Scholar]
- 39.Taniguchi H., Shirakawa T., and Takahashi T., “Implementation of human cognitive bias on naive Bayes,” 2016, pp. 483–489. [Google Scholar]
- 40.Gandhi R., “Support Vector Machine—Introduction to Machine Learning Algorithms,” Medium, July. 05, 2018. https://towardsdatascience.com/support-vector-machine-introduction-to-machine-learning-algorithms-934a444fca47 (accessed Apr. 08, 2020). [Google Scholar]
- 41.Van Gerven M. and Bohte S., “Artificial neural networks as models of neural information processing,” Front. Comput. Neurosci., vol. 11, p. 114, 2017. 10.3389/fncom.2017.00114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hall M., Witten I., and Frank E., “Data mining: Practical machine learning tools and techniques,” Kaufmann Burlingt., 2011. [Google Scholar]
- 43.Rodrigues Junior W. L., Borges F. A., Rabelo R. de A., Rodrigues J. J., Fernandes R. A., and da Silva I. N., “A methodology for detection and classification of power quality disturbances using a real-time operating system in the context of home energy management systems,” Int. J. Energy Res., 2020. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(ZIP)
(DOCX)
Data Availability Statement
All relevant data are within the manuscript and its Supporting Information files.