1. Introduction
Nervous systems evolved in highly dynamic environments. Adaptive behavior in the natural world requires not just learning which actions improve survival, but also changing behavior as the environment changes. This describes an active feedback process in which organisms interact with the environment through actions, learn from feedback, and adjust future actions adaptively. The ability to behave flexibly is a ubiquitous feature of life, ranging from flies (Ofstad et al., 2011) to humans1 Despite the ubiquity of flexible decision making, it is a historically understudied problem in systems neuroscience. Progress in reinforcement learning over the past two decades has provided a biologically-plausible and mathematically-sophisticated framework for studying these problems (Bertsekas and Tsitsiklis, 1996; Sutton and Barto, 1998). Parallel progress in tool development in mice has enabled the dissection of neural circuits needed for detailed biological insight (Luo et al., 2018). The intersection of these two fields — reinforcement learning and neural circuit dissection — holds promise to further our algorithmic- and implementation-level understanding of cognition.
This chapter reviews behavioral assays for investigating value-guided behavior, explores biologically-plausible algorithms of value-based decision making, and ends with an overview of the neural systems thought to instantiate these functions. We highlight recent evidence demonstrating value computations in the medial prefrontal cortex (mPFC) and cortico-basal-ganglia loops. Given the myriad decision making dysfunctions seen in patients with mental illnesses, understanding its neural basis on multiple levels is crucial for developing targeted therapies (Cáceda et al., 2014).
2. Value-based decision making
Decision making is at the heart of many fields, including economics, political science, psychology, engineering, medicine, and neuroscience. A decision is defined as a deliberative process that results in commitment to a categorical proposition (Gold and Shadlen, 2007). Decisions are the result of integrating both external (e.g., sensory) as well as internal evidence (e.g., predictions). These two domains have largely been studied in the context of perceptual (i.e., external evidence) and value-based (i.e., internally-generated evidence) decision-making tasks (Gold and Shadlen, 2007; Yu, 2015). Within each domain, quantitative mathematical frameworks have provided semantically-meaningful interpretations of neural activity in key brain structures. A key concept is the decision variable, which “represents the accrual of all sources of priors, evidence, and value into a quantity that is interpreted by the decision rule to produce a choice” (Gold and Shadlen, 2007). The decision variable represents the common currency used by the brain to generate a single categorical action among all possibilities.
Value-based decision making tasks require subjects to choose on the basis of expected utility or subjective value (Sugrue et al., 2005; Sanfey et al., 2006; Glimcher et al., 2005). Typically, sensory stimuli are salient, which minimizes perceptual uncertainty. Decisions are made on the basis of values learned over long time periods (Morris et al., 2006) or values learned over short timescales (Sugrue et al., 2004; Lau and Glimcher, 2005; Tsutsui et al., 2016). Importantly, these values are not sensory properties of stimuli (like brightness or contrast) but are internal variables that must be learned through experience. Compared to perceptual tasks, the subjective nature of value-based tasks makes them much more difficult to control. However, rigorous formalisms from the fields of economics (Rangel et al., 2008) and reinforcement learning (Sutton and Barto, 1998) have greatly benefited the study of value-based decisions. As such, these tasks are well-poised to address questions about representations of cognitive information.
2.1. Pavlovian systems
Pavlovian behavior describes innate, reflexive behavioral responses to stimuli that have been assigned value (Rescorla, 1988). The phenomenon was discovered by Ivan Pavlov while conducting studies of the digestive system in dogs (Pavlov and Anrep, 1928)2. In the case of reward, the Pavlovian response is preparatory (e.g., approach) and consummatory. In the case of punishment, the Pavlovian response is avoidance (Rangel et al., 2008). These responses can be innate (e.g., avoidance of predator odors) or learned through experience. Owing to their simplicity, Pavlovian behavioral tasks have been invaluable in studying the neural basis of reward learning. One of the most celebrated examples at the intersection of reinforcement learning and neuroscience — that midbrain dopamine neurons encode reward prediction errors — was discovered in monkeys performing Pavlovian behaviors (Schultz et al., 1997). The simplicity of Pavlovian tasks is also limiting, particularly if there is a mismatch between the innate Pavlovian behavior and the response needed to obtain reward (e.g., withhold an action to obtain reward; Dayan et al., 2006).
2.2. Habitual systems
Habitual behavior describes the mapping of a large range of arbitrary motor responses to stimuli, through repeated reinforcement. Habit systems in the brain learn through trial-and-error over relatively long timescales (Balleine and O’Doherty, 2010). Once learned, values are thought to be cached and behavior can be carried out ‘automatically’. As such, habits are thought to be computationally cheap but inflexible (Daw et al., 2005). It can also be difficult to unlearn habitual behavior. This particular feature is the rationale for outcome devaluation, a gold-standard test of habitual behavior. In outcome devaluation experiments, animals are first trained to associate a stimulus with a response (e.g., pressing a lever in response to a tone) to receive a reward. Following training, the outcome is devalued either by pairing with sickness or making the outcome freely available before the task. Animals are then tested to see if they respond to the stimulus. Continued behavioral responses are consistent with habitual behavior (Balleine and O’Doherty, 2010).
2.3. Goal-directed systems
Goal-directed systems are responsible for flexible decision making. They are thought to compute the outcomes associated with particular actions on fast timescales. As such, they are sensitive to changes in environmental contingencies. Outcome devaluation is also used to test the contribution of goal-directed systems to behavior (Balleine and O’Doherty, 2010). A reduction in responding is taken as evidence that behavior was driven largely by goal-directed systems. This chapter focuses on delineating the contributions of goal-directed systems to flexible decision making. We will focus largely on behaviors, primarily because, in contrast to studies of sensory decision making, it is paramount to have a controlled behavior, in which the experimenter can quantify hidden variables, such as value.
3. Matching behavior
Several behavioral tasks have been used to study flexible decision making: outcome devaluation, reversal learning, set shifting, foraging, ‘mixed-strategy’ games, and matching behavior. Matching behavior (or the matching law) is a type of behavior that we will argue provides excellent conditions to study continual value-based learning. In matching tasks, animals freely choose among two or more options to harvest reward (Herrnstein and Heyman, 1979). Matching describes the tendency of animals to ‘match’ the fraction of choices to a particular option with the fraction of rewards received from that option. Mathematically, matching describes the following relationship:
| (1) |
where ci is the number of choices allocated to option i and ri is the number of rewards obtained from option i, given N possible options. Matching behavior was first observed in pigeons (Herrnstein, 1961) and has since been observed in mice (Fonseca et al., 2015; Bari et al., 2019), rats (Gallistel et al., 2001; Graft et al., 1977), monkeys (Sugrue et al., 2004; Lau and Glimcher, 2005; Tsutsui et al., 2016), and humans (Pierce and Epling, 1983). Matching behavior is typically highly dynamic, with animals switching between options on fast timescales. In trial-based tasks, animals typically switch from one option to another with a mode of 1 trial. However, animals remain reward sensitive, and repeat recently-rewarded choices. As such, it can be considered a form of goal-directed behavior.
3.1. Task conditions
Experimental psychologists use tasks in which reward delivery is contingent on schedules of reinforcement (Ferster and Skinner, 1957). Two commonly-used schedules are called ‘variable ratio’ and ‘variable interval.’ Matching behavior is classically observed in tasks with variable interval schedules.
Variable ratio schedules are intuitive — reward is simply delivered with a fixed probability, much like flipping a (biased) coin. If given the choice between two variable ratio schedules, the optimal policy is to choose the higher probability option exclusively. Note that exclusively choosing one option is trivially consistent with matching behavior since all choices are allocated to one option, and all rewards are received from that option. Variableratio-schedule tasks are typically called ‘two-armed bandit’ tasks and tasks with changing probabilities are called ‘dynamic two-armed bandit’ tasks or, if the probabilities reverse, ‘probabilistic reversal learning’ tasks. In variable interval schedules, reward is delivered after a fixed time has elapsed. Once the time has elapsed, that option is ‘baited,’ guaranteeing reward delivery once chosen. This feature is thought to make these tasks ethologically relevant to study foraging. Although this seems like a trivial change, it changes the optimal policy significantly, which will be expanded on below. Intuitively, if given the choice between two variable interval schedules, it does not make sense to choose one option exclusively. Instead, one should occasionally probe the lower-probability option, to not miss out on a baited reward. In these circumstances, matching behavior emerges. In modern, trial-based tasks, discrete versions of variable interval schedules are used, to allow for independent control over inter-trial intervals.
Variable ratio and variable interval schedules are not necessarily different categories but may be thought of as two extremes of a competitive foraging environment (Sakai and Fukai, 2008a). Under this interpretation, ‘baited’ rewards are withdrawn with a particular probability. Variable interval schedules describe environments where the withdrawal probability is 0, imitating herbivore foraging environments without competitors. Intermediate withdrawal probabilities between 0 and 1 imitate competitive foraging environments where food may be intercepted by competitors. Variable ratio schedules are ones where the withdrawal probability is 1, which may resemble the foraging of carnivores.
3.2. Matching behavior is generally a suboptimal probabilistic policy
Given the task conditions that engender matching behavior, a natural question to ask is whether animals are matching because they are aware of baiting (i.e., accounting for environmental statistics) or are they agnostic to it? A key insight into this problem was developed by Sakai and Fukai (2008b), which we expand on below.
For simplicity, we will assume two choices (options a and b). Matching (equation 1) then reduces to the following form
| (2) |
Matching occurs when the relative fraction of choices to option i, ci, ‘matches’ the relative fraction of rewards, ri, from option i. Rearranging either equation gives . In other words, matching occurs when the mean reward from all options is equated. Written compactly,
| (3) |
The average reward from both options can be written as
| (4) |
where πi is the probability of choosing option i. Because we have two options, πb = 1 − πa. We assume that the policy is controlled by a parameter x, yielding3
| (5) |
The parameter x explicitly influences the policy and implicitly influences the reward probabilities. Under variable-interval schedules, the longer one has stayed away from an option, the higher the probability of reward when that option is eventually selected4.
To maximize reward, we take the derivative of with respect to x and set it equal to 0.
| (8) |
This equation defines the optimal probabilistic policy. The first set of terms in parentheses is the explicit change in behavior when x is changed. The second set of terms is the implicit change in the environment brought about by the animal’s policy. One may hypothesize that this first computation (explicit change in behavior) is easy for the brain to perform while the second computation (implicit change in environment) is much more difficult. Sakai and Fukai’s critical insight was to recognize that the brain might ignore this second computation, which yields the reduced form
| (9) |
It can be shown that solving equation (9) yields matching behavior. In other words, the solution is when . Under what conditions is matching optimal?
Figure 1 provides a geometric intuition for how the policy influences reward in standard matching paradigms. Both options follow variable interval schedules (pa = 0.4; pb = 0.1). Light and dark blue illustrate and , respectively, as a function of the policy. The consequences of baiting are clear. The less often option a is chosen, the greater the probability of reward when it is chosen. The orange trace illustrates which, from equation (4), is the reward rate from both options, weighted by the probability of choosing each option. The optimal reward is at the maximum of this function, which occurs at P(choice to option a) ≈ 0.86. Matching behavior, when (equation (3)), occurs when the two blue traces intersect one another. In standard matching paradigms, matching is the optimal probabilistic policy. However, in this circumstance matching can occur either if animals are aware of environmental statistics (equation (8)) or if they ignore it (equation (9)).
Figure 1:
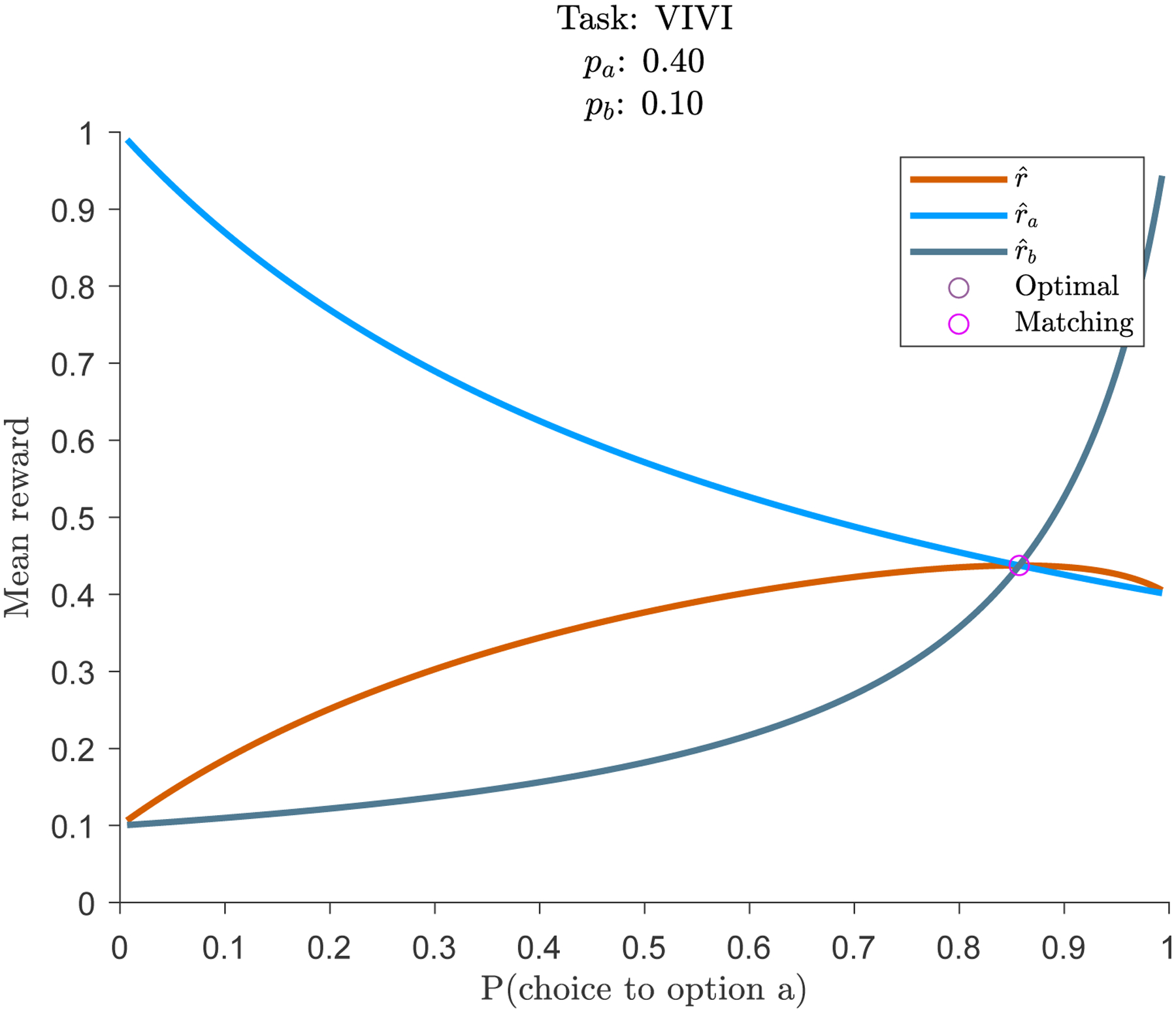
Matching is the optimal probabilistic policy in variable-interval / variable-interval tasks.
There is a strong-inference experiment that can test whether animals will continue to exhibit matching behavior, even when it is suboptimal. If they continue to show matching behavior, this is evidence that they likely do not take into account environmental statistics to make decisions. If they show optimal behavior, then they likely are. The key experiment is to only let one option follow a variable-interval schedule. The second option should deliver reward with a fixed reward probability (variable-ratio schedule). This example is illustrated in Figure 2 (pa = 0.3, variable-ratio option; pb = 0.24, variable-interval option). It is clear that option a, the variable ratio option, does not benefit from baiting. No matter how often it is chosen, the probability of reward is fixed. In this task, matching is not the optimal solution. When these types of tasks have been tested, matching behavior has been observed (Williams, 1985; Herrnstein and Heyman, 1979; Vyse and Belke, 1992), including in humans (Savastano and Fantino, 1994). Under the theory proposed by Sakai and Fukai, these findings indicate that animals behave as if they are not aware of environmental statistics. This should not be taken as evidence that animals are unable to calculate these environmental statistics — simply that under these task conditions, they behave as if they do not. Manipulations designed to encourage optimal behavioral can be successful — for example, rewards that differ in magnitude rather than probability, and allowing practice without reinforcement (Tunney and Shanks, 2002).
Figure 2:
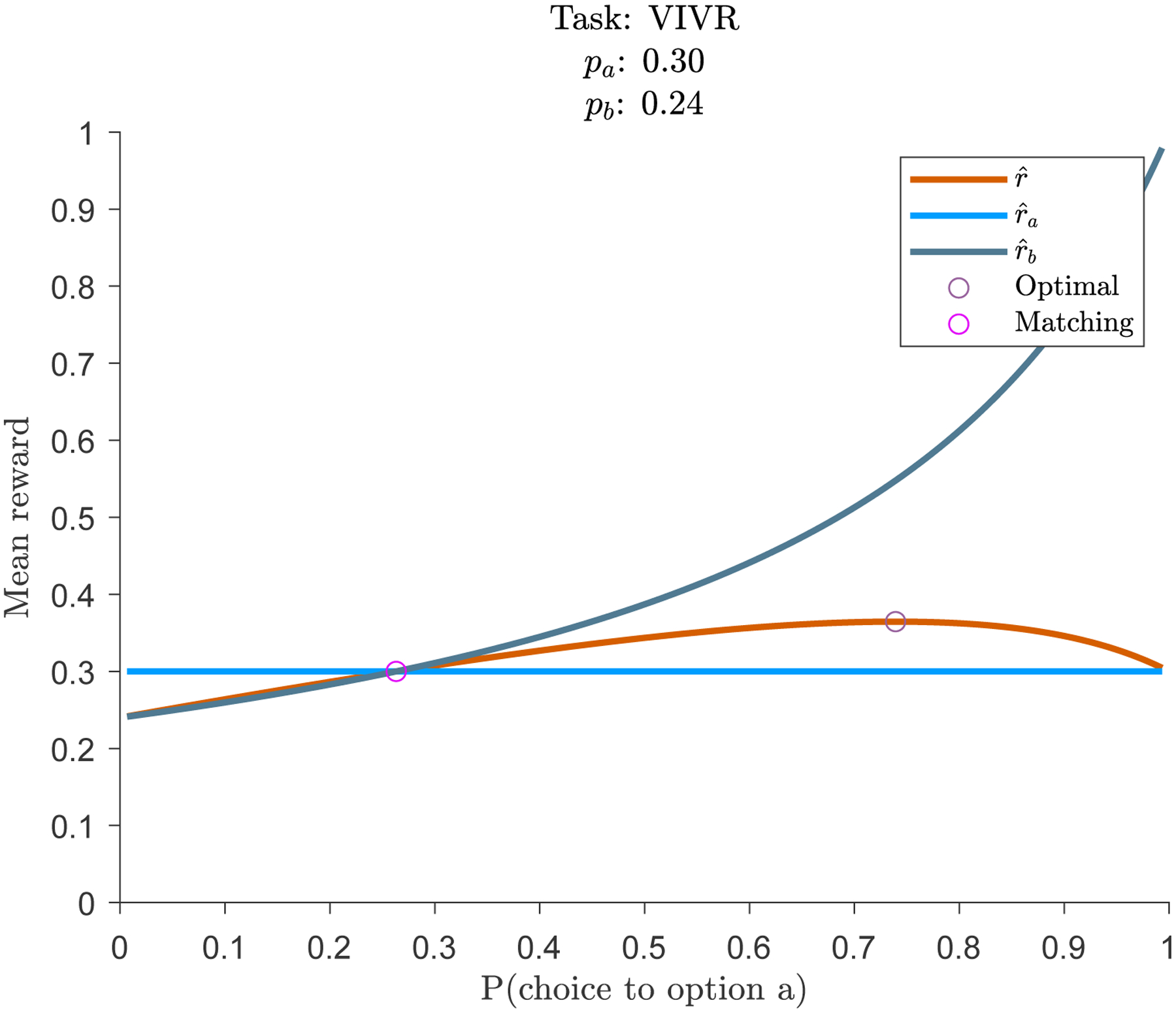
Matching is not optimal in variable-interval / variable-ratio tasks.
Animals do not adopt deterministic switching policies
One limitation of the argument above is that it is limited to probabilistic policies. Deterministic switching policies (i.e., sample the other arm every n choices) are the true optimal policies. For example, if given two variable-interval options in which the base probabilities are pa = 0.4 and pb = 0.1, the optimal policy is to choose option a four times and choose option b once. This is because, according to equation (6), after not being selected for four consecutive trials, the probability of reward from option b has climbed from 0.1 to 0.4095, at which point the probability of reward is greater than option a, and it should be chosen. After option b has been chosen, the probability of reward drops again to 0.1, the probability of reward on option a is now 0.64 (since it has not been chosen for one trial), and option a should be chosen.
These policies are easy to diagnose, since stay duration histograms will not display a characteristic exponential shape. Under the hypothesis that animals are adopting a deterministic switching policy, stay durations should instead display a bimodal shape. We are not aware of any human or animal studies demonstrating such behavior, although a computational study trained artificial neural networks which exhibited these switching policies in certain conditions (Wang et al., 2018).
Matching behavior vs. probability matching
Matching behavior should not be confused with probability matching. Matching behavior and probability matching are observed in very different task conditions. Probability matching refers to the tendency of subjects to match the relative fraction of choices to the probability of reward in two-armed bandit tasks (Mongillo et al., 2014). In two-armed bandit tasks, unlike matching behavior tasks, reward probability does not depend on past choices - the options follow variable-ratio schedules. For example, if pa = 0.75 and pb = 0.25, probability matching occurs when subjects choose option a 75% of the time and option b 25% of the time. This is clearly a suboptimal policy, since the subject should choose option a 100% of the time.
Mathematically, probability matching can be written as
| (10) |
where pi is the probability of reward associated with option i. Unlike matching behavior, there is no circumstance in which probability matching is optimal. Intuitively, in a two-armed bandit task, the optimal policy is to exclusively choose the high-probability option. To see more rigorously how matching behavior and probability matching are incompatible, note that the actual reward received from option i is ri = pi · ci. Matching behavior is therefore
| (11) |
With fixed reward probabilities, matching behavior is obtained when ca = 0 or cb = 0, which is incompatible with probability matching. In two-armed bandit tasks, matching behavior is (trivially) to exclusively choose one option - the optimal policy.
Interestingly, probability matching and undermatching, the tendency to behave more randomly than perfect matching behavior, may share the same underlying mechanism. If subjects believe the world is more unstable or prone to change than it truly is, both of these phenomena can emerge (Shanks et al., 2002; Yu and Cohen, 2009; Yu and Huang, 2014).
3.3. Dynamic foraging tasks
In addition to the ethological relevance of matching behavior, a useful feature is the tendency of animals to exhibit highly flexible behavior, switching from one option to another on short timescales. However, one limitation of classic matching paradigms is reward contingencies are typically fixed within sessions and varied across sessions. Practically, both trial-by-trial algorithmic studies of behavior and neurophysiologic studies of flexible behavior benefit from task designs that better capture the full dynamic range of matching within session. Take the example in Figure 3. Matching behavior is typically illustrated in these types of plots, with the relative reward ratio on the x-axis and choice ratio on the y-axis. Imagine a single session with fixed reward contingencies that yield a reward ratio of ~ 0.8 and a choice ratio of ~ 0.6. This single data point would be consistent with both undermatching (the blue curve; tendency to behave more randomly than perfect matching) and biased matching (the orange curve; tendency to prefer one choice more than another). Since these two hypotheses have very different algorithmic and neural underpinnings, it is useful to use a task design that allows one to measure along multiple choice/reward ratios. Dynamic foraging tasks are variable-interval/variable-interval tasks with multiple reward contingency changes in one session (Sugrue et al., 2004; Lau and Glimcher, 2005; Tsutsui et al., 2016; Gallistel et al., 2001). This task variant elegantly solves this problem.
Figure 3:
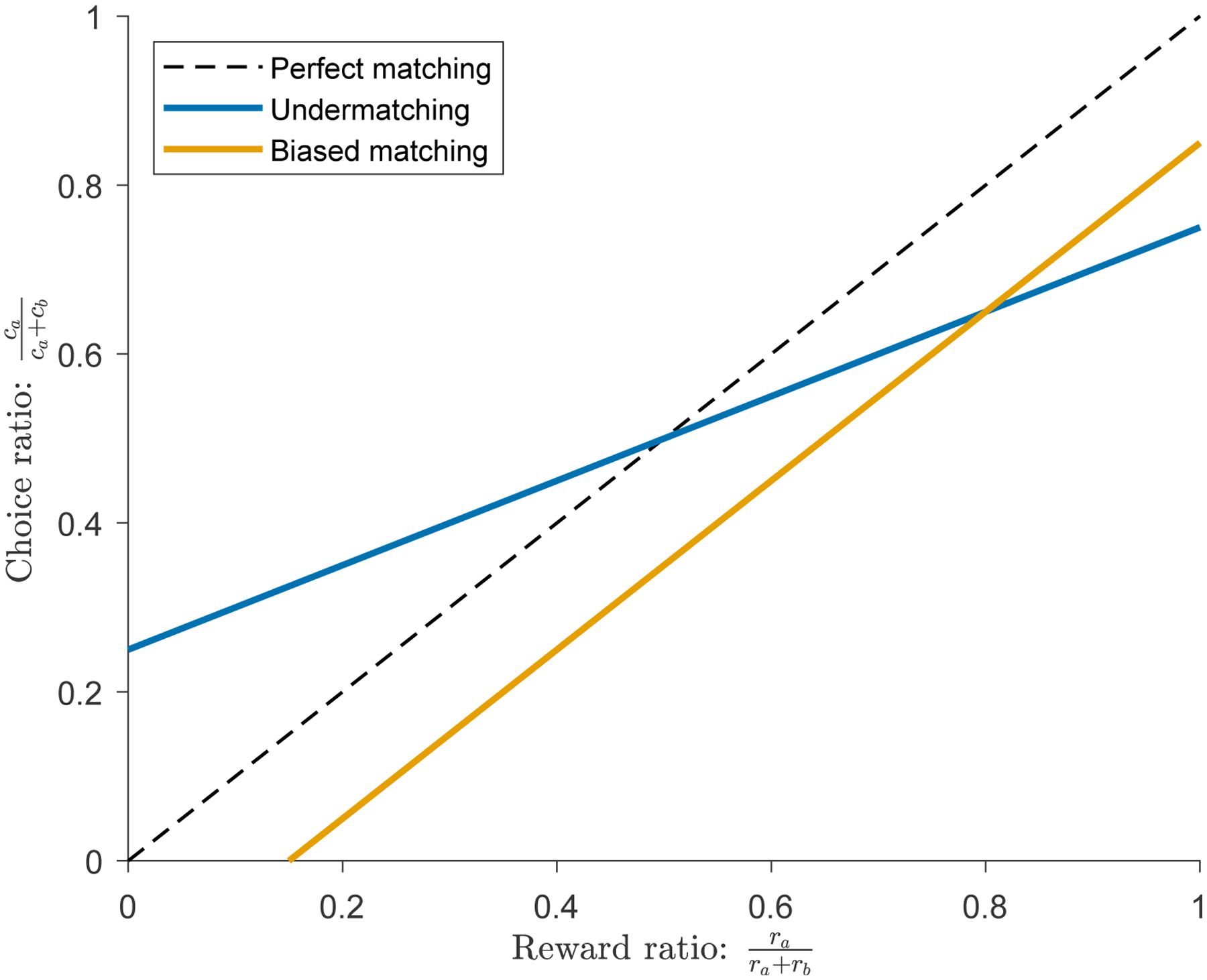
Dynamic foraging tasks allow for better characterization of behavior
4. Algorithms underlying matching behavior
Matching is a description of macroscopic, averaged behavior. An important question therefore is how does matching behavior emerge from trial-by-trial behavior?
4.1. Melioration
Melioration is among the earliest trial-by-trial algorithms developed to solve this problem (Herrnstein and Vaughan, 1980). This algorithm states that behavior should tend towards the option with the highest local rate of reinforcement (the highest ratio), which yields matching behavior in the limit. This algorithm was studied extensively by Herrnstein and others, largely to contrast with theories of optimal decision making (Herrnstein, 2000).
4.2. Local matching
Local matching is another algorithm designed to yield matching behavior (Sugrue et al., 2004). Under local matching, the agent exponentially integrates reward from each option and maps the local reward ratio to a probability of choice.
| (12) |
where is the local estimate of reward. For example, can be updated as
| (13) |
each time option i is chosen (where R is reward). Although melioration and local matching both do a reasonable job describing behavior, deep insight is limited since both of these algorithms were designed to exhibit matching behavior.
4.3. Covariance-based update rules
A general insight into this problem was developed by Loewenstein and Seung (2006). Assume a change in synaptic weights ΔW is given by the following form
| (14) |
where α is a plasticity rate, R is reward, and N is neural activity. It can be shown that synaptic plasticity update rules of this form converge to matching behavior. Examples of these update rules include
| (15) |
| (16) |
| (17) |
where E(X) is the expected value. These particular update rules are equivalent to the learning rules in the direct actor and actor-critic reinforcement learning algorithms (Dayan and Abbott, 2001; Sakai and Fukai, 2008a,b). These results demonstrate that matching behavior can be the outcome of very simple learning rules, a remarkably deep insight and one that makes it possible to more confidently interpret neural correlates of value-based decision making in these behaviors.
4.4. Logistic regressions
One of the most common means of analyzing behavior in dynamic foraging tasks is to calculate logistic regressions to predict choice as a function of reward history and choice history (Lau and Glimcher, 2005; Fonseca et al., 2015; Sul et al., 2011; Tsutsui et al., 2016). These models take the following form
| (18) |
where
| (19) |
| (20) |
and vice versa for Rb(t) and cb(t).
These particular models are powerful since they can capture arbitrary linear combinations of reward and choice history (up to N trials into the past) to predict upcoming choices. A frequent observation is that choices have a positive dependence on reward history ( coefficients), often multiple trials into the past. The interpretation is that previous rewarded choices reinforce future choices to that option. Previous choices (generally 1–2 trials) tend to have negative coefficients ( coefficients), meaning animals tend to switch their choices over short timescales, regardless of reward history. Interestingly, negative coefficients are generally not seen in tasks without baiting (Parker et al., 2016). Given the arguments above suggesting that animals behave as if they are not aware of the baiting rule, one potential explanation is that animals are implementing a simple ‘switch’ heuristic to increase reward rate.
A major limitation of the logistic regression formulation is that only linear combinations of the input can be used. An immediate consequence of this can be seen by observing that when Ra(t) − Rb(t) = 0, the model cannot discriminate whether it was option a that was not rewarded or option b. A solution to this problem may exist, since it has been shown that the logistic regression model is identical to an action-value reinforcement learning model with identical learning and forgetting rates (Katahira, 2015). This suggests that the action-value reinforcement learning model may be a suitable template to build interpretable algorithms that capture the essence of matching behavior.
4.5. Action-value reinforcement learning algorithm (Q-learning)
The action-value reinforcement learning (or Q-learning) algorithm is a general-purpose learning algorithm that keeps track of the values (i.e., expected future reward) of available actions and makes decisions based on the difference between action values (Watkins and Dayan, 1992). It has been widely applied both in neuroscience (Samejima et al., 2005; Sul et al., 2010; Li and Daw, 2011; Akam et al., 2017) and machine learning (Mnih et al., 2015). If we assume a task with two actions, a common implementation is to assume a single state and update the Q-values as follows. If action on trial t = a
| (21) |
| (22) |
The difference between Q-values is used as an input into a softmax function to produce the probability of a choice.
| (23) |
| (24) |
Forgetting can be introduced as (where action on trial t = a)
| (25) |
| (26) |
Forgetting can be applied to just the unchosen action or both actions (Katahira, 2015; Farashahi et al., 2018; Bari et al., 2019; Hattori et al., 2019).
4.6. Bayesian inference
Bayesian inference algorithms use Bayes rule to iteratively update estimates of reward probability. They are powerful since they estimate full probability distributions, allowing them to make decisions that take into account uncertainty in their estimates, as well as higher-order moments. For example, if the algorithm estimates both options to have a mean reward probability pa = pb = 0.5, but the uncertainty of pa > pb, then it is adaptive to choose pa since the true mean reward rate might be higher, increasing reward in the long term (Sutton and Barto, 1998). These algorithms have been used to argue that matching might occur due to uncertainty about changing reward dynamics (Yu and Huang, 2014). In general, they have seen limited use for quantifying matching behavior, since simpler models often do well enough.
5. Movement vigor during flexible decision making
Decisions are much more complex than just discrete choices. Behavior occurs in real-time and the nervous system must finely calibrate the vigor of movements. Vigor, often defined as reaction time plus speed of movements, has long been studied in the context of motor control (Choi et al., 2014; Rigas et al., 2016; Reppert et al., 2018). Recently, vigor has been appreciated as a reflection of value (Shadmehr et al., 2019). Vigor is increased by increasing reward (Summerside et al., 2018), decreased by increasing effort (Stelmach and Worringham, 1988), and modulated on short, individual-decision timescales (Reppert et al., 2015).
From a normative perspective, modulating vigor in relation to value/effort is an appropriate computation (Niv et al., 2007; Yoon et al., 2018). Because increased vigor requires greater energy (Selinger et al., 2015; Hoyt and Taylor, 1981; Ralston, 1958), it is not always appropriate to move with high vigor. However, in the context of a highly rewarding environment, it can be worth increasing vigor to increase reward rate, since slow movements necessitate a longer time between movement initiation and receipt of reward. It is clear that the brain modulates movement vigor to maximize reward rates (Haith et al., 2012).
In the context of flexible decision making, moment-to-moment vigor has been shown to be as flexible as choice-based behavior. One study employed a dynamic two-armed bandit task in rats and found that latency of task initiation was highly correlated with instantaneous probability of reward (Hamid et al., 2016). Movement vigor was most strongly modulated by the reward rate of the environment (how much reward can be expected regardless of action), and much less so by relative reward rates (how much better one option is relative to another). A number of studies have demonstrated that recent reward history modulates movement vigor (Del Arco et al., 2017; Simon et al., 2015; Bari et al., 2019; Ottenheimer et al., 2020).
6. Brain structures underlying flexible behavior
Extensive work, most of it in humans, has correlated changes in activity in multiple brain regions with variables from reinforcement-learning models (e.g., Daw et al., 2006; Doya, 2008). The vast majority of these studies have focused on brief changes in activity of neurons or fMRI signal (seconds or less) and model variables that change on similar timescales.
One key variable, common to many algorithms, is the reward prediction error, the difference between actual and predicted reward. We know much about these signals, especially in the context of foraging (Morris et al., 2006; Parker et al., 2016). However, we know much less about the representations of the decision variables updated by these reward prediction errors. In particular, all algorithms of flexible behavior require memory: a summary of previous interactions with the environment that allows for adaptive behavior in the future. Whereas this memory signal — typically in the form of action values or their arithmetic combinations — has been observed in several brain structures, most notably the dorsal striatum (e.g., Samejima et al., 2005), it is largely transient and occurs around the time of cues and actions. It is less clear where these memory signals reside in between bouts of interaction with the environment.
6.1. Cortico-basal-ganglia loops: medial prefrontal cortex and dorsomedial striatum
The medial prefrontal cortex (mPFC) and its downstream target, the dorsomedial striatum, have long been studied as critical components for generating flexible behavior5. One view of this circuit is that cortex provides signals to bias action selection (Murakami et al., 2017) and the striatum is responsible for action selection itself. Cortical circuitry is predominantly recurrent, which is hypothesized to allow for integration of information which can be routed to striatum to bias action selection. Striatal circuitry, in contrast, is predominantly inhibitory and weak, with lateral inhibition motifs, facilitating a winner-take-all operation (Morita et al., 2016). The classic view of the striatum considers two parallel cortico-striato-cortical loops, operating to initiate and inhibit actions (Figure 4). The ‘Direct’ or ‘Go’ pathway, consists of cortical inputs to D1-expressing medium spiny neurons in the striatum, which synapse onto globus pallidus pars interna (entopeduncular nucleus in the rodent (Grillner and Robertson, 2016; Wallace et al., 2017)) and the substantia nigra pars reticulata. These in turn synapse onto the thalamus, and back to the cortex, completing the loop. The ‘Indirect’ or ‘No-Go’ pathway consists of cortical inputs synapsing onto D2-expressing medium spiny neurons, which in turn synapse onto the globus pallidus pars externa → subthalamis nucleus → globus pallidus pars interna and substantia nigra pars reticulata → thalamus, and finally back to cortex (Shipp, 2017).
Figure 4:
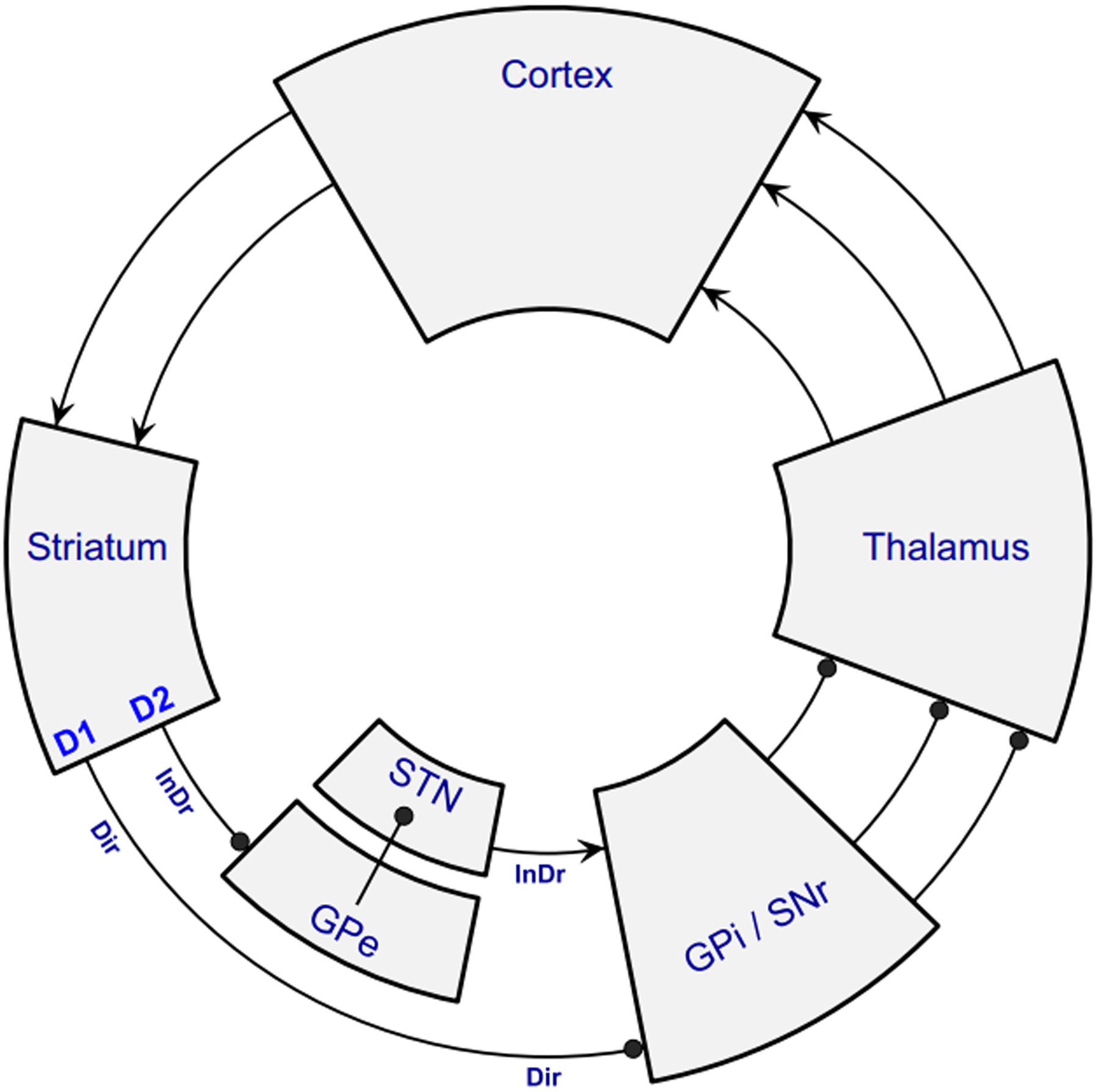
Classic view of the ‘Direct’ and ‘Indirect’ striatal pathways. Figure adapted from Shipp (2017).
Lesions of either the medial prefrontal cortex or the dorsomedial striatum are known to abolish goal-directed behavior and render behavior under the control of sensorimotor associations (Balleine et al., 2007; Kennerley et al., 2006). Neurons in rat dorsal mPFC predict upcoming outcomes, before they have been presented (Del Arco et al., 2017), and monitor action/outcome contingencies (Simon et al., 2015; Hyman et al., 2013; Sul et al., 2010). Neurons in primate medial frontal cortex signal prediction errors of action values (Matsumoto et al., 2007) and those in anterior cingulate cortex encode reward history as well as reward prediction errors6 (Seo and Lee, 2007). In humans, fMRI studies have revealed a role for medial frontal regions in encoding reward magnitude and value of chosen actions (Daw et al., 2006). Higher network coordination between cortex and striatum predicts changes in learning and decision making (Gerraty et al., 2018).
Recordings in the primate caudate, a homolog of the rodent dorsomedial striatum, have demonstrated encoding of action values and chosen values, key signals in reinforcement learning models of behavior (Samejima et al., 2005; Lau and Glimcher, 2008). Later studies discovered preferential encoding of the difference of temporally-discounted values, and encoding of future actions (Cai et al., 2011). Recordings in the dorsomedial striatum of the rat have confirmed these findings (Ito and Doya, 2009, 2015; Kim et al., 2013; Seo et al., 2012), and extended them by demonstrating encoding of total value, necessary for modulating vigor (Wang et al., 2013). Manipulation of striatal subpopulations modulates choice-based behavior in a manner consistent with changes in action values (Tai et al., 2012). Unilateral activation of D1-expressing medium spiny neurons in the dorsomedial striatum bias animals to make more contralateral actions. Conversely, unilateral activation of D2-expressing neurons in the dorsomedial striatum bias animals to make more ipsilateral actions. Similar results were obtained with pharmacological manipulation of D1/D2 receptors in the primate putamen (Ueda et al., 2017). These findings align with the classic view that D1-expressing neurons are organized into the ‘Go’ pathway to initiate behavior, and D2-expressing neurons are organized into a ‘No-Go’ pathway to inhibit behavior.
Recent work has focused on mouse mPFC, a structure known to have persistent working-memory-like neural correlates (Liu et al., 2014), as the potential site where decision variables are maintained in between bouts of interaction with the environment. Persistent activity is a viable network mechanism for maintaining representations of decision variables in the times between choices. Persistent activity, defined here as activity that lasts longer than the time constants of synaptic inputs, was first described in the prefrontal cortex and mediodorsal thalamus of primates and is thought to be a critical component of working memory (Fuster and Alexander, 1971).
We recently recorded from mPFC neurons, including those that projected to dorsomedial striatum, in mice performing a matching task (Bari et al., 2019). Individual mPFC neurons showed persistent representations of two key decision variables for matching behavior: relative value — used to bias choices — and total value — used to bias response time (or “vigor”). Remarkably, these two forms of persistent activity showed different rates of decay, that matched the behavior they supported. Relative-value activity did not appear to decay during long inter-choice intervals (tens of seconds); neither did the mouse’s memory of its choice policy (Figure 5). In contrast, total-value activity decayed slowly over long inter-choice intervals; likewise, mice made slower choices after long waiting times. These variables did not appear to be robustly encoded by tongue premotor neurons. These data suggest that cortico-basal-ganglia-thalamo-cortical loops maintain value-based decision variables, and that information flow in the circuit is not a simple linear flow of computations.
Figure 5:
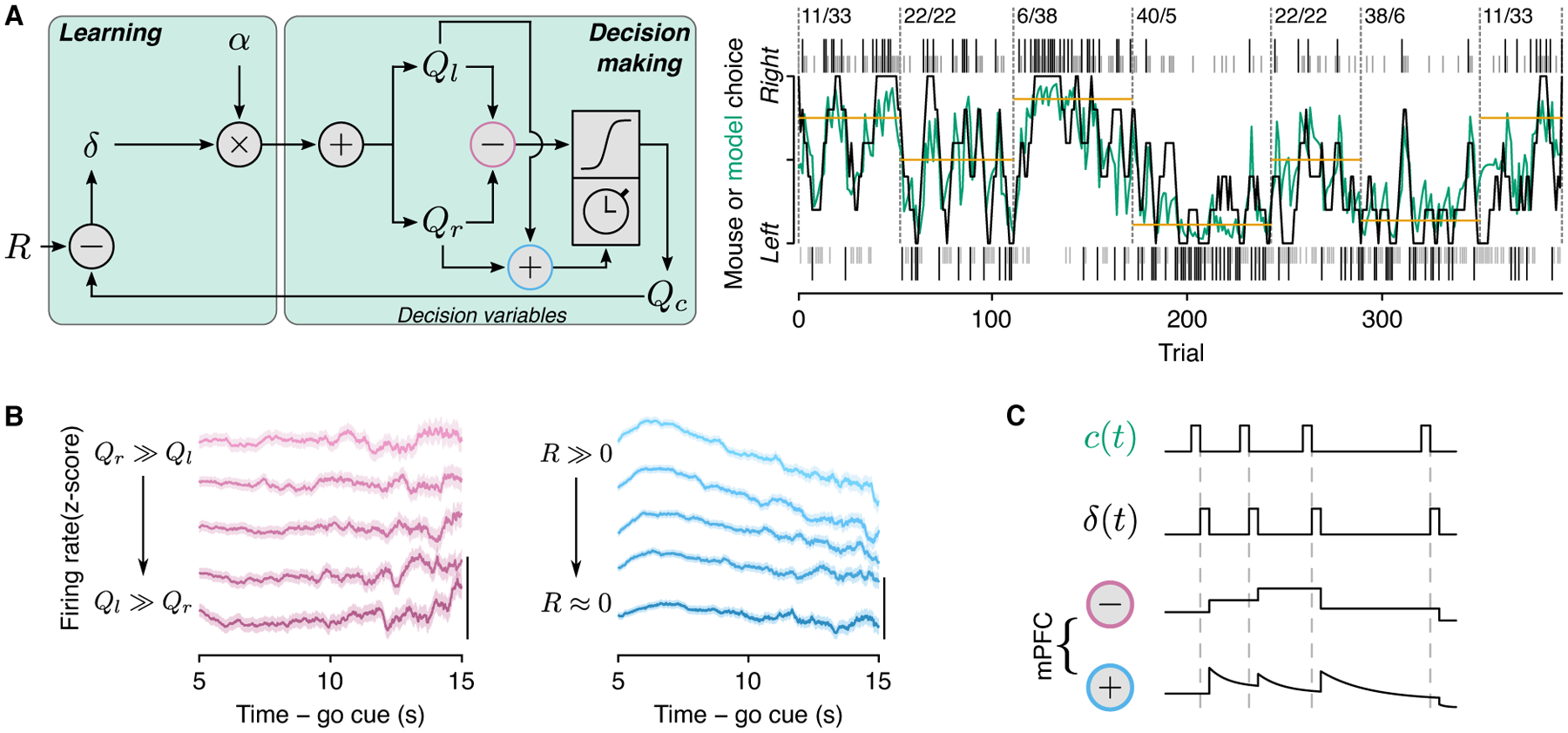
(A) Reinforcement-learning model (left) and fit to example mouse behavior (right). (B) Persistent activity representing relative (left panel) and total (right panel) value. (C) Schematic of variables from the model represented in mPFC. Figure adapted from Bari et al. (2019).
Tool development has allowed for precise pathway-specific modulation. In our recent study, we found that inactivation of the mPFC → dorsomedial striatal pathway disrupted choice behavior and slowed vigor, consistent with a disruption of cognitive variables necessary for value-based decision making (Bari et al., 2019). This is similar to a recent study which demonstrated that the mPFC → striatum and mPFC → thalamus pathways were necessary for choice behavior, but not the mPFC → mPFC pathway (Nakayama et al., 2018). Another group demonstrated that the mediodorsal → mPFC pathway, but not the mPFC → mediodorsal thalamus, is necessary for updating understanding about the causal structure of actions, although both were necessary for goal-directed behavior (Alcaraz et al., 2018). This is consistent with the notion that the cortico-basal ganglia system is critical for flexible behavior, since the former, but not the latter, pathway is part of this system.
Taken together, these results highlight the key concept that the brain has dedicated circuitry for different behavioral strategies, and that the rodent dorsal medial prefrontal cortex and downstream dorsomedial striatum are important structures for driving flexible behavior.
6.2. Neuromodulatory systems
Neuromodulatory systems are remarkably unique. These systems are each composed of very small numbers of cells, yet have outputs that arborize to span large volumes of tissue. This feature makes them poised to exert global control over neural states and computations.
Midbrain dopamine is a particularly well-studied neuromodulator. Dopamine neurons in the midbrain encode reward prediction errors, a critical variable in reinforcement learning models of flexible behavior (Schultz et al., 1997; Bayer and Glimcher, 2005; Morris et al., 2006; Roesch et al., 2007; Cohen et al., 2012). Manipulation of the dopamine system profoundly affects learning, for both Pavlovian associations (Steinberg et al., 2013) and for flexible decisions (Parker et al., 2016; Hamid et al., 2016). Dopamine densely innervates the striatum, where it bidi-rectionally modulates the plasticity of corticostriatal synapses, depending on the downstream receptor (Reynolds and Wickens, 2002). This feature makes dopamine an integral component that enables the cortico-basal ganglia system to modulate flexible behavior.
Serotonin is comparatively less-well understood, in large part to substantial heterogeneity in this system relative to midbrain dopamine. In large thanks to tool development (Lima et al., 2009), extracellular recording of single cell-type-identified serotonin neurons has allowed for inroads to be made. Recent work has shown that a subset of serotonin neurons in the dorsal raphe nucleus encodes value over very long timescales (Cohen et al., 2015), which may relate to the encoding of background reward rate, a key variable in models of optimal foraging behavior (Charnov et al., 1976). Activation of dorsal raphe serotonin neurons in mice performing a dynamic foraging task leads to increases in learning rates (Iigaya et al., 2018) and promotes persistence in mice performing a patch foraging task (Lottem et al., 2018). These findings must be interpreted with caution, however, since serotonin manipulation can have opposite effects on behavior, depending on the outputs of distinct subpopulations of neurons (Ren et al., 2018).
Norepinephrine produced by neurons in the locus coeruleus is thought to be critical for behavioral flexibility. These neurons respond to salient events, which has led to the hypothesis that norepinephrine is critical for arousal and attention (Kety, 1970; Carter et al., 2010; Aston-Jones et al., 2000; Harley, 1987). Classic work demonstrated that activation of locus coeruleus norepinephrine can alleviate forgetting in a complex maze task (Devauges and Sara, 1991) and facilitate attentional shifts (Devauges and Sara, 1990). Formal theories of norepinephrine suggest that the system encodes unexpected uncertainty (Dayan and Yu, 2006; Yu and Dayan, 2003, 2005) and facilitate exploitation/exploration of task contingencies (Aston-Jones and Cohen, 2005).
6.3. Other structures
Although we have focused heavily on cortico-basal ganglia systems and neuromodulatory systems, flexible behavior relies on a much larger network of structures. The orbitofrontal cortex, and its upstream/downstream structures, are critical for flexible behavior. Examples include the orbitofrontal cortex → submedius nucleus pathway (Fresno et al., 2019) and the amygdala → orbitofrontal cortex pathway (Fiuzat et al., 2017). The orbitofrontal cortex encodes reward magnitude (Simon et al., 2015) and codes for chosen value and reward prediction errors more strongly than mPFC (Sul et al., 2010). Other important structures include the posterior parietal cortex and posteromedial cortex (Funamizu et al., 2016) and the ventral hippocampus (Yoshida et al., 2019). This list is by no means exhaustive and serves simply to indicate that large portions of the brain are critical for flexible decision making.
7. Future directions
Despite sophisticated theoretical and modeling insight about flexible decision making, there remains a gap in our knowledge of how the entire loop — sensory signal to discrete action — is instantiated in neural circuitry. One direction that we believe is due for further study is expanding action space to more than two discrete actions, especially using continuous action space. This is likely to enhance our theories of value representation in the mPFC, extending beyond the relatively impoverished regime of binary choices.
Footnotes
It has even been observed in organisms without nervous systems (pea plants; Dener et al. (2016)).
Although it is commonly stated that Ivan Pavlov used a bell as a stimulus, this story appears to be apocryphal (Cambiaghi and Sacchetti, 2015).
For example, assume πa (x) is a softmax function: .
| (6) |
| (7) |
In rodents, mPFC typically refers to (from dorsal to ventral) the anterior cingulate cortex, the prelimbic cortex, the infralimbic cortex, and the medial orbital cortex. Dorsal mPFC usually means anterior cingulate cortex and prelimbic cortex, and ventral mPFC usually means infralimbic cortex and medial orbital cortex. In general, since the study of mPFC is still nascent, especially in mice, stereotactic coordinates are useful for comparing studies.
Comparisons between rodent and primate frontal structures should be taken with a grain of salt, as anatomical homologies between these orders is weak (Uylings et al., 2003).
References
- Akam T, Rodrigues-Vaz I, Zhang X, Pereira M, Oliveira R, Dayan P, Costa RM. Single-Trial Inhibition of Anterior Cingulate Disrupts Model-based Reinforcement Learning in a Two-step Decision Task. bioRxiv p. 126292, 2017. [Google Scholar]
- Alcaraz F, Fresno V, Marchand AR, Kremer EJ, Coutureau E, Wolff M. Thalamocortical and corticothalamic pathways differentially contribute to goal-directed behaviors in the rat. Elife 7: e32517, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aston-Jones G, Cohen JD. An integrative theory of locus coeruleus-norepinephrine function: adaptive gain and optimal performance. Annu Rev Neurosci 28: 403–450, 2005. [DOI] [PubMed] [Google Scholar]
- Aston-Jones G, Rajkowski J, Cohen JD. Locus coeruleus and regulation of behavioral flexibility and attention. Progress in brain research 126: 165–182, 2000. [DOI] [PubMed] [Google Scholar]
- Balleine BW, Delgado MR, Hikosaka O. The role of the dorsal striatum in reward and decision-making. J Neurosci 27: 8161–8165, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balleine BW, O’Doherty JP. Human and rodent homologies in action control: corticostriatal determinants of goal-directed and habitual action. Neuropsychopharmacology 35: 48–69, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bari BA, Grossman CD, Lubin EE, Rajagopalan AE, Cressy JI, Cohen JY. Stable representations of decision variables for flexible behavior. Neuron 103: 922–933, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayer HM, Glimcher PW. Midbrain dopamine neurons encode a quantitative reward prediction error signal. Neuron 47: 129–141, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertsekas DP, Tsitsiklis JN. Neuro-Dynamic Programming. Athena Scientific Belmont, 1996. [Google Scholar]
- Cáceda R, Nemeroff CB, Harvey PD. Toward an Understanding of Decision Making in Severe Mental Illness. The Journal of Neuropsychiatry and Clinical Neurosciences 26: 196–213, 2014. [DOI] [PubMed] [Google Scholar]
- Cai X, Kim S, Lee D. Heterogeneous coding of temporally discounted values in the dorsal and ventral striatum during intertemporal choice. Neuron 69: 170–182, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cambiaghi M, Sacchetti B. Ivan Petrovich Pavlov (1849–1936). Journal of Neurology 262: 1599–1600, 2015. [DOI] [PubMed] [Google Scholar]
- Carter ME, Yizhar O, Chikahisa S, Nguyen H, Adamantidis A, Nishino S, Deisseroth K, de Lecea L. Tuning arousal with optogenetic modulation of locus coeruleus neurons. Nature neuroscience 13: 1526–1533, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charnov EL, et al. Optimal foraging, the marginal value theorem. Theoretical Population Biology, 1976. [DOI] [PubMed] [Google Scholar]
- Choi JE, Vaswani PA, Shadmehr R. Vigor of movements and the cost of time in decision making. Journal of neuroscience 34: 1212–1223, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JY, Amoroso MW, Uchida N. Serotonergic neurons signal reward and punishment on multiple timescales. eLife 4, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JY, Haesler S, Vong L, Lowell BB, Uchida N. Neuron-type-specific signals for reward and punishment in the ventral tegmental area. Nature 482: 85–88, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw ND, Niv Y, Dayan P. Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nature neuroscience 8: 1704–1711, 2005. [DOI] [PubMed] [Google Scholar]
- Daw ND, O’Doherty JP, Dayan P, Seymour B, Dolan RJ. Cortical substrates for exploratory decisions in humans. Nature 441: 876–879, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P, Abbott LF. Theoretical neuroscience: computational and mathematical modeling of neural systems. MIT press, 2001. [Google Scholar]
- Dayan P, Niv Y, Seymour B, Daw ND. The misbehavior of value and the discipline of the will. Neural networks : the official journal of the International Neural Network Society 19: 1153–1160, 2006. [DOI] [PubMed] [Google Scholar]
- Dayan P, Yu AJ. Phasic norepinephrine: a neural interrupt signal for unexpected events. Network 17: 335–350, 2006. [DOI] [PubMed] [Google Scholar]
- Del Arco A, Park J, Wood J, Kim Y, Moghaddam B. Adaptive encoding of outcome prediction by prefrontal cortex ensembles supports behavioral flexibility. J Neurosci 37: 8363–8373, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dener E, Kacelnik A, Shemesh H. Pea Plants Show Risk Sensitivity. Current Biology 26: 1763–1767, 2016. [DOI] [PubMed] [Google Scholar]
- Devauges V, Sara SJ. Activation of the noradrenergic system facilitates an attentional shift in the rat. Behavioural Brain Research 39: 19–28, 1990. [DOI] [PubMed] [Google Scholar]
- Devauges V, Sara SJ. Memory retrieval enhancement by locus coeruleus stimulation: evidence for mediation by beta-receptors. Behavioural brain research 43: 93–97, 1991. [DOI] [PubMed] [Google Scholar]
- Doya K Modulators of decision making. Nat Neurosci 11: 410–416, 2008. [DOI] [PubMed] [Google Scholar]
- Farashahi S, Rowe K, Aslami Z, Gobbini MI, Soltani A. Influence of learning strategy on response time during complex value-based learning and choice. PloS one 13: e0197263, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferster CB, Skinner BF. Schedules of reinforcement. East Norwalk: Appleton-Century-Crofts, 1957. [Google Scholar]
- Fiuzat EC, Rhodes SEV, Murray EA. The role of orbitofrontal-amygdala interactions in updating action-outcome valuations in macaques. J Neurosci 37: 2463–2470, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fonseca MS, Murakami M, Mainen ZF. Activation of dorsal raphe serotonergic neurons promotes waiting but is not reinforcing. Curr Biol 25: 306–315, 2015. [DOI] [PubMed] [Google Scholar]
- Fresno V, Parkes SL, Faugère A, Coutureau E, Wolff M. A thalamocortical circuit for updating action-outcome associations. eLife 8: 1–13, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funamizu A, Kuhn B, Doya K. Neural substrate of dynamic Bayesian inference in the cerebral cortex. Nature Neuroscience 19: 1682–1689, 2016. [DOI] [PubMed] [Google Scholar]
- Fuster JM, Alexander GE. Neuron activity related to short-term memory. Science 173: 652–654, 1971. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Mark TA, King AP, Latham PE. The rat approximates an ideal detector of changes in rates of reward: implications for the law of effect. J Exp Psychology Anim Behav Proc 27: 354–372, 2001. [DOI] [PubMed] [Google Scholar]
- Gerraty RT, Davidow JY, Foerde K, Galvan A, Bassett DS, Shohamy D. Dynamic flexibility in striatal-cortical circuits supports reinforcement learning. J Neurosci, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glimcher PW, Dorris MC, Bayer HM. Physiological utility theory and the neuroeconomics of choice. Games and Economic Behavior 52: 213–256, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci 30: 535–574, 2007. [DOI] [PubMed] [Google Scholar]
- Graft DA, Lea SEG, Whitworth TL. The matching law in and within groups of rats. Journal of the Experimental Analysis of Behavior 27: 1333563, 1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grillner S, Robertson B. The basal ganglia over 500 million years. Current Biology 26: R1088–R1100, 2016. [DOI] [PubMed] [Google Scholar]
- Haith AM, Reppert TR, Shadmehr R. Evidence for hyperbolic temporal discounting of reward in control of movements. J Neurosci 32: 11727–11736, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamid AA, Pettibone JR, Mabrouk OS, Hetrick VL, Schmidt R, Vander Weele CM, Kennedy RT, Aragona BJ, Berke JD. Mesolimbic dopamine signals the value of work. Nat Neurosci 19: 117–126, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harley CW. A role for norepinephrine in arousal, emotion and learning?: limbic modulation by norepinephrine and the Kety hypothesis. Progress in neuro-psychopharmacology & biological psychiatry 11: 419–458, 1987. [DOI] [PubMed] [Google Scholar]
- Hattori R, Danskin B, Babic Z, Mlynaryk N, Komiyama T. Area-Specificity and plasticity of History-Dependent value coding during learning. Cell 177: 1858–1872, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein RJ. Relative and absolute strength of response as a function of frequency of reinforcement. J Exp Anal Behav 4: 267–272, 1961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein RJ. The matching law: Papers in psychology and economics. Harvard University Press, 2000. [Google Scholar]
- Herrnstein RJ, Heyman GM. Is matching compatible with reinforcement maximization on concurrent variable interval variable ratio? Journal of the Experimental Analysis of Behavior 31: 209–223, 1979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein RJ, Vaughan W. Melioration and behavioral allocation. Limits to action: The allocation of individual behavior pp. 143–176, 1980. [Google Scholar]
- Hoyt DF, Taylor CR. Gait and the energetics of locomotion in horses. Nature 292: 239, 1981. [Google Scholar]
- Hyman JM, Whitman J, Emberly E, Woodward TS, Seamans JK. Action and outcome activity state patterns in the anterior cingulate cortex. Cereb Cortex 23: 1257–1268, 2013. [DOI] [PubMed] [Google Scholar]
- Iigaya K, Fonseca MS, Murakami M, Mainen ZF, Dayan P. An effect of serotonergic stimulation on learning rates for rewards apparent after long intertrial intervals. Nat Commun 9: 2477, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito M, Doya K. Validation of decision-making models and analysis of decision variables in the rat basal ganglia. J Neurosci 29: 9861–9874, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito M, Doya K. Distinct neural representation in the dorsolateral, dorsomedial, and ventral parts of the striatum during fixed- and free-choice tasks. J Neurosci 35: 3499–3514, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katahira K The relation between reinforcement learning parameters and the influence of reinforcement history on choice behavior. Journal of Mathematical Psychology 66: 59–69, 2015. [Google Scholar]
- Kennerley SW, Walton ME, Behrens TEJ, Buckley MJ, Rushworth MFS. Optimal decision making and the anterior cingulate cortex. Nat Neurosci 9: 940–947, 2006. [DOI] [PubMed] [Google Scholar]
- Kety SS. The Biogenic Amines in the Central Nervous System: Their Possible Roles in Arousal, Emotion, and Learning. In Schmitt FO (ed.) The Neurosciences: Second Study Program, pp. 324–336. New York: Rockefeller University Press, 1970. [Google Scholar]
- Kim H, Lee D, Jung MW. Signals for previous goal choice persist in the dorsomedial, but not dorsolateral striatum of rats. J Neurosci 33: 52–63, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau B, Glimcher PW. Dynamic response-by-response models of matching behavior in rhesus monkeys. J Exp Anal Behav 84: 555–579, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau B, Glimcher PW. Value representations in the primate striatum during matching behavior. Neuron 58: 451–463, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Daw ND. Signals in human striatum are appropriate for policy update rather than value prediction. J Neurosci 31: 5504–5511, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lima SQ, Hromádka T, Znamenskiy P, Zador AM. PINP: a new method of tagging neuronal populations for identification during in vivo electrophysiological recording. PLoS One 4: e6099, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu D, Gu X, Zhu J, Zhang X, Han Z, Yan W, Cheng Q, Hao J, Fan H, Hou R, Chen Z, Chen Y, Li CT. Medial prefrontal activity during delay period contributes to learning of a working memory task. Science 346: 458–463, 2014. [DOI] [PubMed] [Google Scholar]
- Loewenstein Y, Seung HS. Operant matching is a generic outcome of synaptic plasticity based on the covariance between reward and neural activity. Proc Natl Acad Sci U S A 103: 15224–15229, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lottem E, Banerjee D, Vertechi P, Sarra D, Lohuis MO, Mainen ZF. Activation of serotonin neurons promotes active persistence in a probabilistic foraging task. Nat Commun 9: 1000, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo L, Callaway EM, Svoboda K. Genetic Dissection of Neural Circuits: A Decade of Progress. Neuron 98: 256–281, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsumoto M, Matsumoto K, Abe H, Tanaka K. Medial prefrontal cell activity signaling prediction errors of action values. Nat Neurosci 10: 647–656, 2007. [DOI] [PubMed] [Google Scholar]
- Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, Graves A, Riedmiller M, Fidjeland AK, Ostrovski G, et al. Human-level control through deep reinforcement learning. Nature 518: 529, 2015. [DOI] [PubMed] [Google Scholar]
- Mongillo G, Shteingart H, Loewenstein Y. The misbehavior of reinforcement learning. Proceedings of the IEEE 102: 528–541, 2014. [Google Scholar]
- Morita K, Jitsev J, Morrison A. Corticostriatal circuit mechanisms of value-based action selection: Implementation of reinforcement learning algorithms and beyond. Behav Brain Res 311: 110–121, 2016. [DOI] [PubMed] [Google Scholar]
- Morris G, Nevet A, Arkadir D, Vaadia E, Bergman H. Midbrain dopamine neurons encode decisions for future action. Nat Neurosci 9: 1057–1063, 2006. [DOI] [PubMed] [Google Scholar]
- Murakami M, Shteingart H, Loewenstein Y, Mainen ZF. Distinct Sources of Deterministic and Stochastic Components of Action Timing Decisions in Rodent Frontal Cortex. Neuron 94: 908–919.e7, 2017. [DOI] [PubMed] [Google Scholar]
- Nakayama H, Ibañez Tallon I, Heintz N. Cell-type-specific contributions of medial prefrontal neurons to flexible behaviors. J Neurosci 38: 4490–4504, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niv Y, Daw ND, Joel D, Dayan P. Tonic dopamine: opportunity costs and the control of response vigor. Psychopharmacology 191: 507–520, 2007. [DOI] [PubMed] [Google Scholar]
- Ofstad TA, Zuker CS, Reiser MB. Visual place learning in Drosophila melanogaster. Nature 474: 204–209, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ottenheimer DJ, Bari BA, Sutlief E, Fraser KM, Kim TH, Richard JM, Cohen JY, Janak PH. A quantitative reward prediction error signal in the ventral pallidum. Nature Neuroscience pp. 1–10, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker NF, Cameron CM, Taliaferro JP, Lee J, Choi JY, Davidson TJ, Daw ND, Witten IB. Reward and choice encoding in terminals of midbrain dopamine neurons depends on striatal target. Nat Neurosci 19: 845–854, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlov IP, Anrep GV. Conditioned Reflexes. Journal of Philosophical Studies 3: 380–383, 1928. [Google Scholar]
- Pierce WD, Epling WF. Choice, Matching, and Human Behavior: A Review of the Literature. The Behavior Analyst 6: 57–76, 1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ralston HJ. Energy-speed relation and optimal speed during level walking. Internationale Zeitschrift für Angewandte Physiologie Einschliesslich Arbeitsphysiologie 17: 277–283, 1958. [DOI] [PubMed] [Google Scholar]
- Rangel A, Camerer C, Montague PR. A framework for studying the neurobiology of value-based decision making. Nature Reviews Neuroscience 9: 545–556, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren J, Friedmann D, Xiong J, Liu CD, Ferguson BR, Weerakkody T, DeLoach KE, Ran C, Pun A, Sun Y, et al. Anatomically defined and functionally distinct dorsal raphe serotonin sub-systems. Cell 175: 472–487, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reppert TR, Lempert KM, Glimcher PW, Shadmehr R. Modulation of Saccade Vigor during Value-Based Decision Making. J Neurosci 35: 15369–15378, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reppert TR, Rigas I, Herzfeld DJ, Sedaghat-Nejad E, Komogortsev O, Shadmehr R. Movement vigor as a traitlike attribute of individuality. Journal of neurophysiology 120: 741–757, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rescorla RA. Behavioral Studies Of Pavlovian Conditioning. Annual Review of Neuroscience 11: 329–352, 1988. [DOI] [PubMed] [Google Scholar]
- Reynolds JN, Wickens JR. Dopamine-dependent plasticity of corticostriatal synapses. Neural networks 15: 507–521, 2002. [DOI] [PubMed] [Google Scholar]
- Rigas I, Komogortsev O, Shadmehr R. Biometric recognition via eye movements: Saccadic vigor and acceleration cues. ACM Transactions on Applied Perception (TAP) 13: 6, 2016. [Google Scholar]
- Roesch MR, Stalnaker TA, Schoenbaum G. Associative encoding in anterior piriform cortex versus orbitofrontal cortex during odor discrimination and reversal learning. Cerebral cortex (New York, NY : 1991) 17: 643–652, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakai Y, Fukai T. The Actor-Critic Learning Is Behind the Matching Law: Matching Versus Optimal Behaviors. Neural Computation 20: 227–251, 2008a. [DOI] [PubMed] [Google Scholar]
- Sakai Y, Fukai T. When does reward maximization lead to matching law? PloS ONE 3: e3795, 2008b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samejima K, Ueda Y, Doya K, Kimura M. Representation of action-specific reward values in the striatum. Science 310: 1337–1340, 2005. [DOI] [PubMed] [Google Scholar]
- Sanfey AG, Loewenstein G, McClure SM, Cohen JD. Neuroeconomics: cross-currents in research on decision-making. Trends in Cognitive Sciences 10: 108–116, 2006. [DOI] [PubMed] [Google Scholar]
- Savastano HI, Fantino E. Human choice in concurrent ratio-interval schedules of reinforcement. Journal of the Experimental Analysis of Behavior 61: 453–463, 1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz W, Dayan P, Montague P. A neural substrate of prediction and reward. Science 275: 1593–1599, 1997. [DOI] [PubMed] [Google Scholar]
- Selinger JC, O’Connor SM, Wong JD, Donelan JM. Humans can continuously optimize energetic cost during walking. Current Biology 25: 2452–2456, 2015. [DOI] [PubMed] [Google Scholar]
- Seo H, Lee D. Temporal filtering of reward signals in the dorsal anterior cingulate cortex during a mixed-strategy game. J Neurosci 27: 8366–8377, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seo M, Lee E, Averbeck BB. Action selection and action value in frontal-striatal circuits. Neuron 74: 947–960, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Reppert TR, Summerside EM, Yoon T, Ahmed AA. Movement Vigor as a Reflection of Subjective Economic Utility. Trends in neurosciences, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shanks DR, Tunney RJ, McCarthy JD. A re-examination of probability matching and rational choice. Journal of Behavioral Decision Making 15: 233–250, 2002. [Google Scholar]
- Shipp S The functional logic of corticostriatal connections. Brain Struct Funct 222: 669–706, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon NW, Wood J, Moghaddam B. Action-outcome relationships are represented differently by medial prefrontal and orbitofrontal cortex neurons during action execution. J Neurophysiol 114: 3374–3385, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinberg EE, Keiflin R, Boivin JR, Witten IB, Deisseroth K, Janak PH. A causal link between prediction errors, dopamine neurons and learning. Nature neuroscience 16: 966, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stelmach GE, Worringham CJ. The preparation and production of isometric force in Parkinson’s disease. Neuropsychologia 26: 93–103, 1988. [DOI] [PubMed] [Google Scholar]
- Sugrue LP, Corrado GS, Newsome WT. Matching behavior and the representation of value in the parietal cortex. Science 304: 1782–1787, 2004. [DOI] [PubMed] [Google Scholar]
- Sugrue LP, Corrado GS, Newsome WT. Choosing the greater of two goods: neural currencies for valuation and decision making. Nat Rev Neurosci 6: 363–375, 2005. [DOI] [PubMed] [Google Scholar]
- Sul JH, Jo S, Lee D, Jung MW. Role of rodent secondary motor cortex in value-based action selection. Nat Neurosci 14: 1202–1208, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sul JH, Kim H, Huh N, Lee D, Jung MW. Distinct roles of rodent orbitofrontal and medial prefrontal cortex in decision making. Neuron 66: 449–460, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Summerside EM, Shadmehr R, Ahmed AA. Vigor of reaching movements: reward discounts the cost of effort. Journal of neurophysiology 119: 2347–2357, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Reinforcement Learning: An Introduction. MIT Press; Cambridge, 1998. [Google Scholar]
- Tai LH, Lee AM, Benavidez N, Bonci A, Wilbrecht L. Transient stimulation of distinct subpopulations of striatal neurons mimics changes in action value. Nat Neurosci 15: 1281–1289, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsutsui KI, Grabenhorst F, Kobayashi S, Schultz W. A dynamic code for economic object valuation in prefrontal cortex neurons. Nat Commun 7: 12554, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tunney RJ, Shanks DR. A re-examination of melioration and rational choice. Journal of Behavioral Decision Making 15: 291–311, 2002. [Google Scholar]
- Ueda Y, Yamanaka K, Noritake A, Enomoto K, Matsumoto N, Yamada H, Samejima K, Inokawa H, Hori Y, Nakamura K, Kimura M. Distinct functions of the primate putamen direct and indirect pathways in adaptive outcome-based action selection. Front Neuroanat 11: 66, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uylings HB, Groenewegen HJ, Kolb B. Do rats have a prefrontal cortex? Behavioural brain research 146: 3–17, 2003. [DOI] [PubMed] [Google Scholar]
- Vyse SA, Belke TW. Maximizing versus matching on concurrent variable-interval schedules. Journal of the Experimental Analysis of Behavior 58: 325–334, 1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace ML, Saunders A, Huang KW, Philson AC, Goldman M, Macosko EZ, McCarroll SA, Sabatini BL. Genetically distinct parallel pathways in the entopeduncular nucleus for limbic and sensorimotor output of the basal ganglia. Neuron 94: 138–152, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang AY, Miura K, Uchida N. The dorsomedial striatum encodes net expected return, critical for energizing performance vigor. Nat Neurosci 16: 639–647, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang JX, Kurth-Nelson Z, Kumaran D, Tirumala D, Soyer H, Leibo JZ, Hassabis D, Botvinick M. Prefrontal cortex as a meta-reinforcement learning system. Nat Neurosci 21: 860–868, 2018. [DOI] [PubMed] [Google Scholar]
- Watkins CJ, Dayan P. Q-learning. Machine learning 8: 279–292, 1992. [Google Scholar]
- Williams BA. Choice behavior in a discrete-trial concurrent VI-VR: A test of maximizing theories of matching. Learning and Motivation 16: 423–443, 1985. [Google Scholar]
- Yoon T, Geary RB, Ahmed AA, Shadmehr R. Control of movement vigor and decision making during foraging. Proc Natl Acad Sci U S A 115: E10476–E10485, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida K, Drew MR, Mimura M, Tanaka KF. Serotonin-mediated inhibition of ventral hippocampus is required for sustained goal-directed behavior. Nature neuroscience p. 1, 2019. [DOI] [PubMed] [Google Scholar]
- Yu AJ. Decision-making tasks. Encyclopedia of computational neuroscience pp. 931–937, 2015. [Google Scholar]
- Yu AJ, Cohen JD. Sequential effects: Superstition or rational behavior? Advances in neural information processing systems 21: 1873–1880, 2009. [PMC free article] [PubMed] [Google Scholar]
- Yu AJ, Dayan P. Expected and unexpected uncertainty: ACh and NE in the neocortex. In Advances in Neural Information Processing Systems 15: Proceedings of the 2002 Conference, pp. 157–164. 2003. [Google Scholar]
- Yu AJ, Dayan P. Uncertainty, neuromodulation, and attention. Neuron 46: 681–692, 2005. [DOI] [PubMed] [Google Scholar]
- Yu AJ, Huang H. Maximizing masquerading as matching in human visual search choice behavior. Decision 1: 275–287, 2014. [Google Scholar]


