Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Apr 8;125(15):8244–8252. doi: 10.1021/acs.jpcc.1c01505

Oxygen Recombination Probability Data for Plasma-Assisted Atomic Layer Deposition of SiO2 and TiO2

Karsten Arts †, Sanne Deijkers †, Riikka L Puurunen ‡, Wilhelmus M M Kessels †,*, Harm C M Knoops †,§,*
PMCID: PMC8162759  PMID: 34084261

Abstract

graphic file with name jp1c01505_0008.jpg

Atomic layer deposition (ALD) can provide nanometer-thin films with excellent conformality on demanding three-dimensional (3D) substrates. This also holds for plasma-assisted ALD, provided that the loss of reactive radicals through surface recombination is sufficiently low. In this work, we determine the surface recombination probability r of oxygen radicals during plasma ALD of SiO2 and TiO2 for substrate temperatures from 100 to ∼240 °C and plasma pressures from 12 to 130 mTorr (for SiO2). For both processes, the determined values of r are very low, i.e., ∼10–4 or lower, and decrease with temperature and pressure down to ∼10–5 within the studied ranges. Accordingly, deposition on trench structures with aspect ratios (ARs) of <200 is typically not significantly limited by recombination and obtaining excellent film conformality is relatively facile. For higher AR values, e.g., approaching 1000, the plasma time needed to reach saturation increases exponentially and becomes increasingly dependent on the process conditions and the corresponding value of r. Similar dependence on process conditions can be present for plasma ALD of other materials as well, where, in certain cases, film growth is already recombination-limited for AR values of ∼10. Radical recombination data and trends as provided by this work are valuable for optimizing plasma ALD throughput and feasibility for high-AR applications and can also serve as input for modeling of radical recombination mechanisms.

Introduction

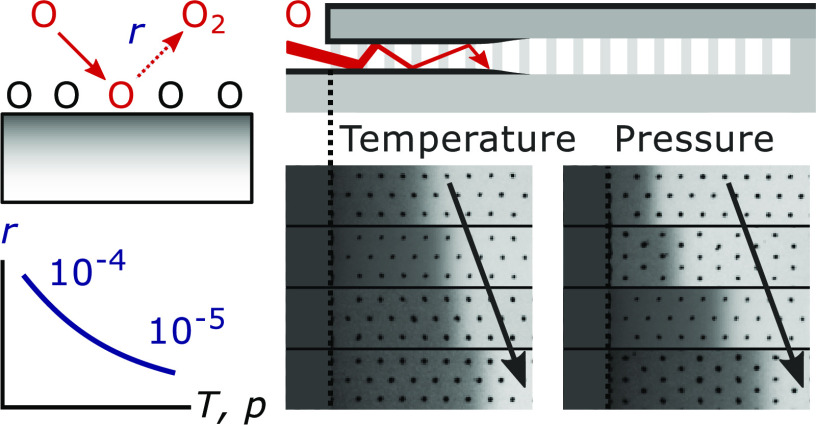
Plasma-assisted atomic layer deposition (plasma ALD),1,2 a technique used to synthesize nanometer-thin films with atomic-level thickness control, has become an established tool in the semiconductor industry. Especially, plasma ALD of SiO2 is widely applied and plays a vital role in device fabrication, for example, in self-aligned multiple patterning.3 An important benefit of plasma ALD, in general, is that it often allows for lower process temperatures and higher material qualities than purely thermally driven ALD.2 On the other hand, for many materials, thermal ALD is better at providing a high level of film conformality. This is because the reactive plasma radicals, which enable film growth during plasma ALD, can be lost through surface recombination when diffusing into a high aspect ratio structure. As a result, the surface recombination probability r of these radicals generally limits the aspect ratio (AR) up to which the conformal film growth by plasma ALD is feasible.4,5

Since values of r are often not available, this maximum achievable AR is an important unknown for many plasma ALD processes. As reported by Knoops et al.,4 it was estimated that plasma ALD of a conformal film is achievable on trenches with an AR of ∼30 or lower.6 Yet more recent work has revealed that much higher ARs are attainable for certain plasma ALD processes, depending on the value of r.5 In particular, it has been demonstrated that for plasma ALD of SiO2 and TiO2 the value of r is low enough (i.e., <10–4) to reach ARs as high as ∼900.5 This low value could also explain why plasma ALD of SiO2 and TiO2 are successfully used in the industry for demanding applications. In the fabrication of three-dimensional (3D) NAND devices, for example, plasma ALD of SiO2 is used to deposit conformal dielectric liners on slits with an AR of 40–60.7 Furthermore, plasma ALD of SiO2 and TiO2 are reported to be used for gap-filling of electrical isolation regions.7−9 The challenging nature of gap-filling is demonstrated in Figure 1, which shows a SiO2 film grown by plasma ALD on vertical trenches with different ARs (see the Supporting Information for the experimental details). Even though the channels can become extremely narrow during deposition (e.g., up to AR ∼ 100), a seamless gap-fill is still observed.

Figure 1.

Figure 1

Open in a new tab

Cross-sectional transmission electron microscopic image of a SiO2 film grown by plasma ALD on vertical trenches with different aspect ratios. A seamless gap-fill is obtained, demonstrating good film conformality even when using short plasma exposures of 5 s (see the Supporting information for further details).

To predict whether a process can be used for demanding applications or under what conditions it can be used, it is essential to gain quantitative information on r for different processes and process conditions. Such quantitative data on r is currently only available for a very limited number of plasma ALD processes,4,5,10 where the influence of process conditions such as temperature and pressure is completely unexplored. In this work, we reveal how the surface recombination probability of oxygen radicals during plasma ALD of SiO2 and TiO2 is influenced by the substrate temperature and plasma pressure. The values of r are determined using the (recombination-limited) penetration depths of the deposited films into extremely high-AR trench structures, as described in our previous work.5 Moreover, we discuss the impact of r on the minimum plasma time needed to reach saturation on a high-AR structure. We focus on acquiring values of r to build a database that is valuable for practical applications in industry and to provide input for fundamental insight into the underlying radical–surface interaction.

Modeling

In our previous work,5 we derived a direct relation between r and the AR up to which film growth is achieved by plasma ALD. This relation (eq 6) is used here to determine values of r under different process conditions. Furthermore, in this work, we also derive which factors other than r influence the minimum plasma time needed to reach saturation on a high-AR structure. This serves to physically interpret the saturation times determined for different substrate temperatures and plasma pressures. Finally, we discuss that the validity of the method is not significantly influenced by the changes in the temperature and pressure within our studied regimes. Note that the adopted model does strongly simplify the complex surface chemistry by capturing the effect of all physical processes in terms of one effective surface recombination probability. By this approach, the model and the determined values of r can be used to describe plasma ALD on high-AR structures in a generic and practical way. This approach can also be applied to other energy-enhanced ALD methods, where the reactive species can recombine at surfaces, such as ozone-based ALD.11

Film Penetration into High-AR Structures: Direct Relation with r

For clarity, we first briefly repeat the derivation of the relation used to determine r. On the basis of the reaction–diffusion model reported by Yanguas-Gil and Elam,12 plasma ALD on a one-dimensional high-AR structure such as a semi-infinite trench is described by the following coupled equations

graphic file with name jp1c01505_m001.jpg 1
graphic file with name jp1c01505_m002.jpg 2

Here, z (m) is the distance into the high-AR structure, t (s) is the dosing time, D (m2/s) is the diffusion coefficient, and S/V is the surface to volume ratio of the structure (m–1). In the description of a plasma half-cycle, n(z, t) (m–3) represents the number density of the gas-phase radicals having an initial sticking probability s0, a surface recombination probability r, and a thermal velocity vth (m/s). The self-limiting nature of ALD is described by the factor (1 – θ), where the surface coverage θ(z, t) is defined as the reacted fraction of the available adsorption sites. 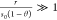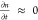Finally, each adsorption site occupies an effective surface area A0 (m2), which can be determined from the growth per cycle (GPC) and mass density of the film.12,13 As described in more detail in our previous work,5 surface recombination becomes dominant (i.e., Inline graphic) when approaching saturation (i.e., θ → 1) in the region that needs to be passed by the radicals to reach the growth front. This results in a situation where the incoming flux of gas-phase radicals is balanced by the loss through surface recombination, such that Inline graphic and eq 1 can be simplified to

graphic file with name jp1c01505_m005.jpg 3

Using the boundary conditions n(z = 0) = n0 and 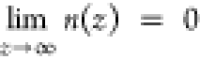Inline graphic, eq 3 is solved as

graphic file with name jp1c01505_m007.jpg 4

which shows that an exponential decay in the gas-phase radical density is obtained during recombination-limited growth. This exponential decay ultimately limits the AR up to which film growth can practically be achieved. To relate this relation with our experimental results, eq 4 is specified for the extremely high-AR microscopic trench structures used in this work (see the Experimental Details section). These structures have a nominal gap height of h = 500 nm, which is much smaller than the typical mean free path of the radicals (λmfp∼0.1 mm)10 under the plasma pressures used (12–130 mTorr). Therefore, the Knudsen approximation for molecular flow in a trench can be adopted, with a diffusion coefficient D = 2/3 vthh.13 Furthermore, the surface-to-volume ratio of the used trench structures is accurately approximated by S/V = 2/h. Using these expressions for D and S/V, eq 4 is specified as

graphic file with name jp1c01505_m008.jpg 5

where the decay in the gas-phase radical density is thus only determined by the surface recombination probability r and the scaled distance z/h into the trench. Note that eqs 5 and 6 also hold for a circular pore with diameter d, when replacing h by d/2 (see the Supporting Information). This is related to the equivalent aspect ratio (EAR) of the particular structure,10,14 where 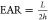Inline graphic for a trench and EAR = L/d for a circular pore.10

As a result of the steady-state exponential decay in radical density, it takes exponentially more time to reach a certain coverage at a further distance z into the trench. Correspondingly, as described in more detail in our previous work,5 the penetration depth of the deposited film increases logarithmically with the plasma exposure time according to

graphic file with name jp1c01505_m010.jpg 6

Here, the half-thickness-penetration-depth PD50% is defined as the depth at which the film thickness has decreased to 50% of its value at the entrance of the high-AR structure,10 which in our model corresponds to the depth at which 50% coverage (i.e., θ = 1/2) has been reached. Equation 6 indicates that the slope of PD50%/h versus ln(t) is only dependent on r. This is used in this work to experimentally determine r for a range of process conditions (see Figures 2−4). The time constant t50%, which is also fitted from the experimental data on PD50%/h versus ln(t), is in first approximation equal to the time it takes to reach 50% coverage on a planar substrate. The values of r and t50% combined are used in the Results and Discussion section to predict the saturation times for different high-AR structures (see Figure 6).

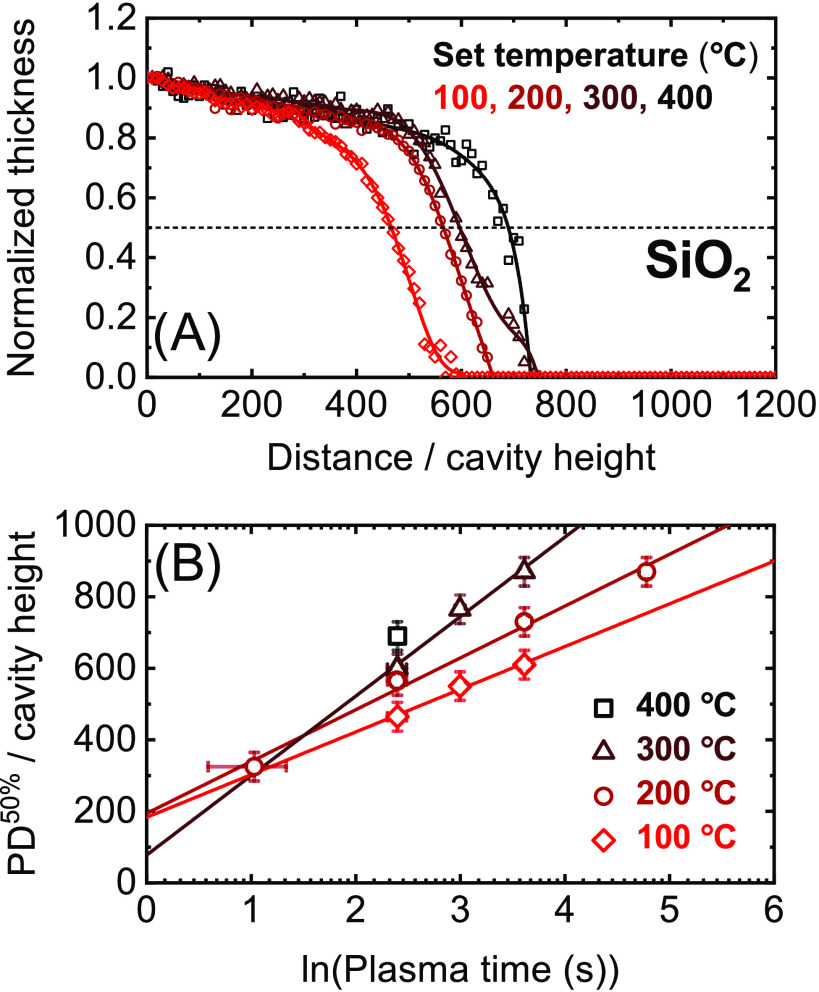
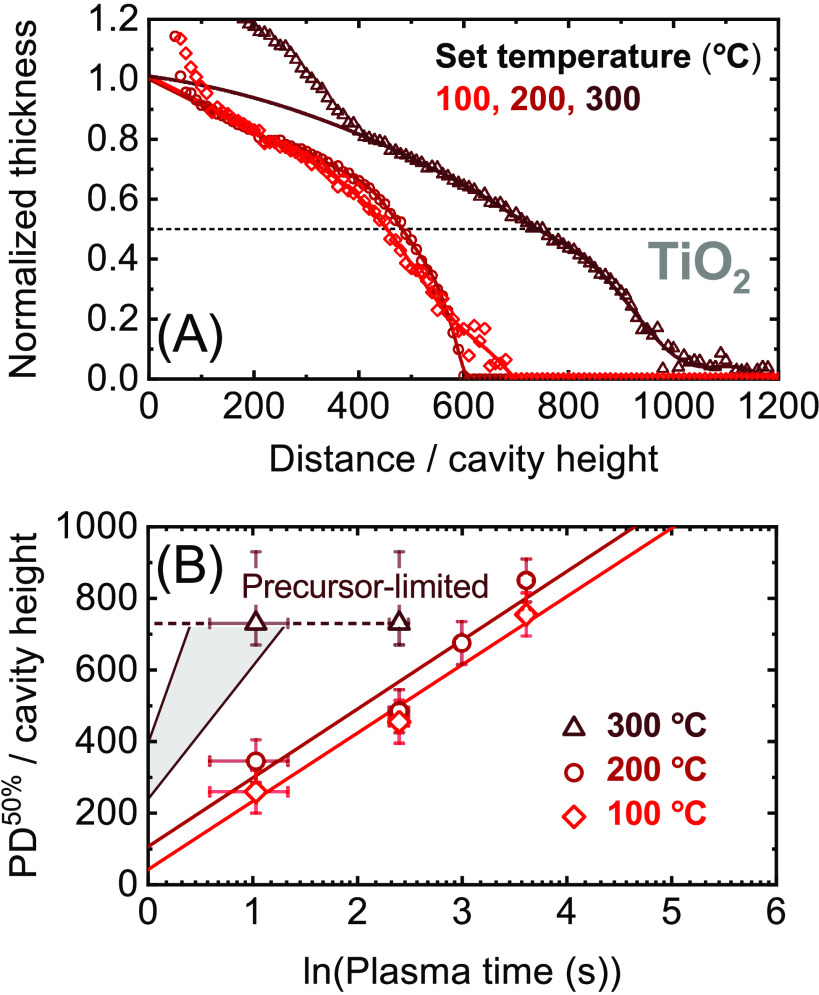
Figure 2.

Figure 2

Open in a new tab

Panel (A): Normalized thickness profiles of SiO2 films grown by plasma ALD on lateral-high-aspect-ratio (LHAR) cavity structures at different temperature setpoints and a fixed plasma exposure time of 12 s per ALD cycle. Similar thickness profiles have been determined for plasma exposure times other than 12 s (at 100, 200, and 300 °C, see the Supporting Information), of which the scaled half-thickness penetration depths are plotted in panel (B).

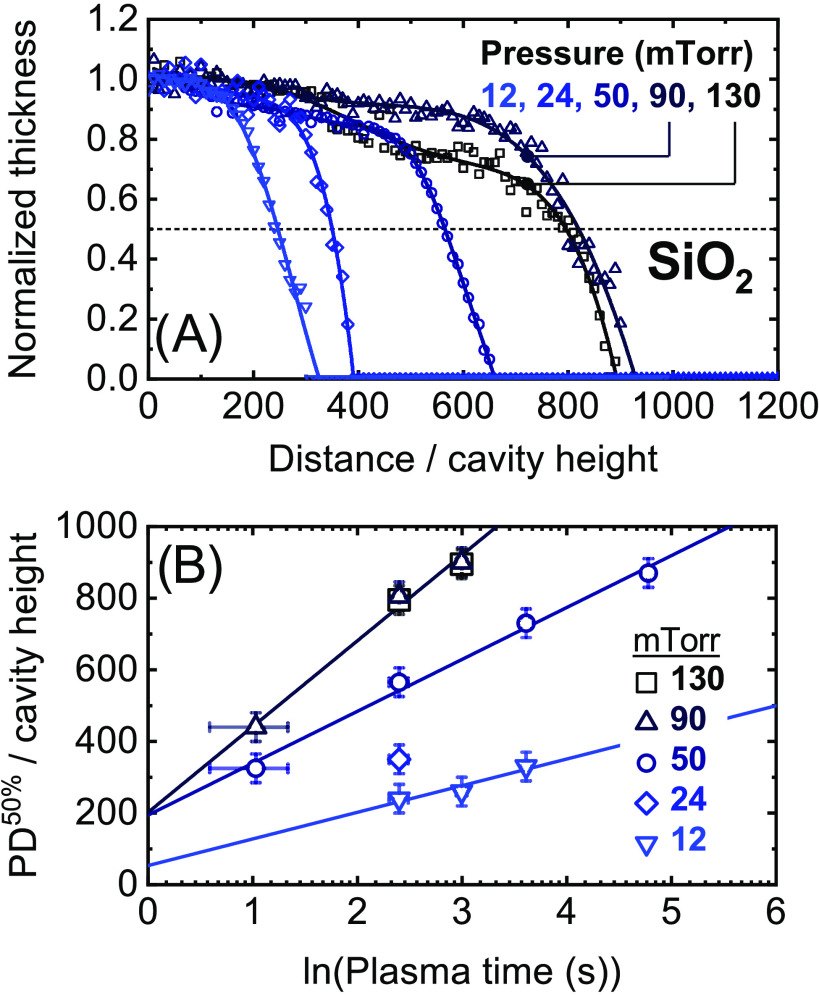
Figure 4.

Figure 4

Open in a new tab

Panel (A): Normalized thickness profiles of SiO2 films grown by plasma ALD on LHAR cavity structures at different plasma pressures and a fixed plasma exposure time of 12 s per ALD cycle. Similar thickness profiles have been determined for plasma exposure times other than 12 s (see the Supporting Information), of which the scaled half-thickness penetration depths are plotted in panel (B).

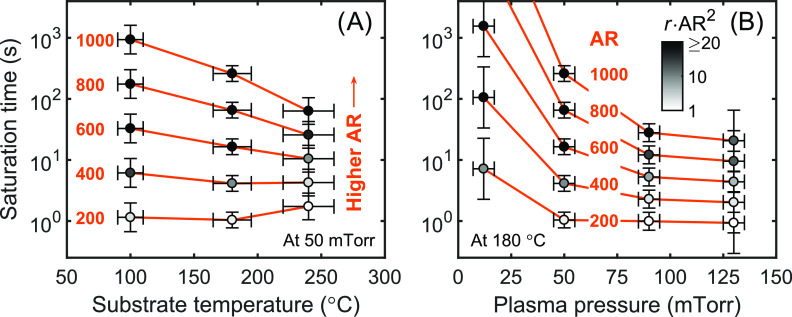
Figure 6.

Figure 6

Open in a new tab

Plasma exposure times needed to reach saturation for trenches with AR values of 200–1000, calculated using eq 10 and the values of r and t50% determined for plasma ALD of SiO2 at different substrate temperatures (A) and plasma pressures (B). The plasma pressure in (A) was kept at 50 mTorr and the substrate temperature in (B) at ∼180 °C. For each datapoint, the value of rAR2 is specified by the grayscale bar. For ARs below ∼200, film growth is no longer recombination-limited (rAR2 < 1), such that the saturation time is similar to that for a planar substrate and not significantly influenced by r.

Film Penetration into High-AR Structures: Required Plasma Exposure Time

To understand which parameters influence t50%, eq 2 is solved and evaluated for θ = 1/2, giving

graphic file with name jp1c01505_m011.jpg 7

as the 50% saturation time on a planar substrate, where n = n0. Fast saturation on a planar substrate is thus obtained in case of a high radical flux 1/4 n0vth, a low adsorption site density 1/A0, and a high initial sticking probability s0. To relate the time constant t50% in eq 6 to t50%,planar for a planar surface, t50%,planar has to be corrected by a factor that accounts for the time it takes for recombination to become dominant during plasma ALD on a high-AR structure (see the Supporting Information). This correction factor is numerically determined as 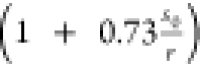Inline graphic, such that

graphic file with name jp1c01505_m013.jpg 8

Combined, eqs 6 and 8 give a complete expression for the film penetration into a high-AR trench during recombination-limited growth. From these equations, it is clear that, in the used model, parameters such as the radical density, reactivity, adsorption site density, and the recombination probability all influence the film penetration depth but r has the largest impact.

Validity of the Model under Different Process Conditions

Since the value of r is determined under different temperatures and pressures, it is important that the temperature and pressure have no significant influence on the accuracy of the method, for instance on the value of the diffusion coefficient. To illustrate why this is indeed the case, we note that the surface recombination probability r is defined according to the number of collisions of the radicals with the surface and the corresponding reduction in the gas-phase radical density. In that context, the factor 3/4(z/h)2 used in eq 5 can be interpreted as the average number of surface collisions that a radical undergoes during diffusion up to a distance z into the trench. This factor is determined assuming molecular diffusion with a diffusion time of 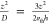Inline graphic and a collision rate of 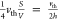Inline graphic, where the thermal velocity cancels out in the product. Under these assumptions, the actual number of collisions with the surface is expected to be independent of temperature and pressure within the studied regimes. Temperature and pressure could influence the average residence time of the radicals on the surface, but the residence time has no influence on the gas-phase diffusion and a corresponding number of sidewall collisions (provided that the type of re-emission remains the same). Moreover, surface diffusion can be neglected, since the predicted surface diffusion length is much smaller (≪1 nm)15 than the gas-phase distance in between two wall collisions (∼h = 500 nm). Finally, the Knudsen approximation λmfp ≪ h is expected to be valid for all investigated pressures.

Experimental Details

To study the film conformality, plasma ALD of SiO2 and TiO2 was carried out on all-silicon microscopic lateral-high-aspect-ratio (LHAR) trench structures (PillarHall LHAR generation 3 and 4), which are described in detail in previous publications (see, for instance, Gao et al.16 and Yim et al.17). The main advantage of these structures is that the horizontally oriented trenches have extremely high aspect ratios of up to 10 000, such that film growth in practice never reaches the end of the trench. This allows for determining the factors limiting film penetration and conformality, such as the value of r in this work. Detailed information on the film conformality is obtained by measuring the thickness profile of the film deposited into the LHAR structure. This is relatively straightforward because the horizontal trenches are formed by a removable membrane, which is suspended above the substrate (with a nominal gap height of 500 nm) and supported by narrow pillars (with a pillar-to-pillar spacing of 28, 49, 50, or 98 μm, depending on the PillarHall version). After deposition and removal of the membrane using adhesive tape, top-view diagnostics can thus be used to measure the thickness profile of the deposited film, for which we used reflectometry (Filmetrics F40-UV with a StageBase-XY10-Auto-100 mm mapping stage). An additional advantage for this study is that the anisotropic flux of ions does not penetrate into the horizontal trench.18 Therefore, film growth is obtained by nondirectional radicals, while the surface conditions and chemistry are not influenced by ions. This is especially useful for comparing different plasma pressures since any influence of ions would have been dependent on the plasma pressure and the resulting ion energy and flux.

The depositions were carried out in a FlexAL ALD reactor of Oxford Instruments, which was equipped with a remote inductively coupled plasma (ICP) source operated at 13.56 MHz.19 For all depositions, O2/Ar plasma was generated using an ICP power of 600 W, an O2 flow of 100 sccm, and an Ar flow of 50 sccm. The pressure was controlled using an automated butterfly valve limiting the flow to the pump. The precursors SiH2(NEt2)2 (bis(diethylamino)silane, BDEAS) and Ti(NMe2)4 (tetrakis(dimethylamino)titanium, TDMAT) were used for the growth of SiO2 and TiO2, respectively. All SiO2 films were grown using 250 ALD cycles, except for the depositions done at a table temperature of 200 °C and plasma pressure of 50 mTorr, where 400 cycles were used. All TiO2 films were also grown using 400 cycles. For both processes, high precursor doses were used (e.g., ∼830 mTorr·s/cycle) such that film penetration was generally limited by the plasma half-cycles.

For the temperature series, table temperature setpoint values of 100, 200, 300, and 400 °C were used, while using a plasma pressure of 50 mTorr. Due to limited thermal contact and a chamber wall temperature of 145 °C (or 100 °C at the setpoint temperature of 100 °C), these setpoint temperatures corresponded to substrate temperatures of approximately 100, 180, 240, and 310 °C, respectively. For the pressure series, plasma pressure values of 12, 24, 50, 90, and 130 mTorr were used, while the table temperature was set at 200 °C. The corresponding substrate temperature of ∼180 °C may have been altered by a maximum of 20 °C under the influence of different pressures, since the thermal contact somewhat improves with plasma pressure. This was observed to have no significant influence on r compared to the larger impact of the plasma pressure. Finally, at each condition, depositions were done using different plasma exposure times in the range of 3.8–120 s/cycle, where the shorter plasma exposure times have a relatively higher uncertainty due to the striking time of the plasma and other startup effects.

Results and Discussion

The data obtained under the aforementioned conditions are summarized in Figure 2 (temperature series SiO2), Figure 3 (temperature series TiO2), and Figure 4 (pressure series SiO2). In each of these figures, as an example, panel (A) displays the normalized thickness profiles obtained using plasma steps of 12 s. The profiles are normalized by the thickness obtained just inside the cavity, corresponding to a local GPC of approximately 1.45 Å/cycle for all SiO2 films.18 For TiO2, GPC-values of approximately 0.49, 0.63, and 0.85 Å/cycle are used for normalizing the data obtained at set table temperature values of 100, 200, and 300 °C, respectively. The values of the 50% thickness penetration depth corresponding to these thickness profiles and to those obtained using different plasma exposure times are plotted in panel (B). A complete overview of all measured thickness profiles is provided in the Supporting Information.

Figure 3.

Figure 3

Open in a new tab

Panel (A): Normalized thickness profiles of TiO2 films grown by plasma ALD on LHAR cavity structures at different temperature setpoints and a fixed plasma exposure time of 12 s per ALD cycle (solid lines serve as a guide to the eye). Similar thickness profiles have been determined for plasma exposure times other than 12 s (see the Supporting Information), of which the scaled half-thickness penetration depths are plotted in panel (B). At 300 °C, the penetration depth is limited by the precursor half-cycle rather than the plasma half-cycle and, when using shorter plasma steps, is expected to follow a trend as indicated by the shaded area (i.e., increase with ln(t)).

For each series, we first discuss the overall influence of the varied conditions on the obtained film conformality. Subsequently, in Figure 5, we provide the determined values of the surface recombination probability. The correspondingly determined values of t50% are reported in the Supporting Information. Finally, in Figure 6, we discuss the impact of the observed changes in r on the minimum plasma time needed to reach saturation on an extremely high-AR structure, which is relevant information for optimizing process throughput and feasibility.

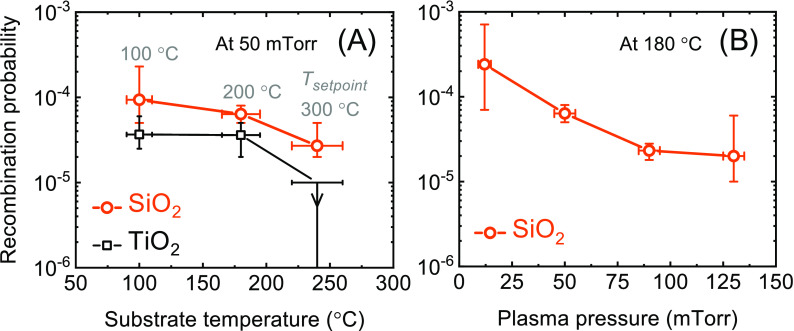
Figure 5.

Figure 5

Open in a new tab

Determined surface recombination probabilities of oxygen radicals during plasma ALD of SiO2 (orange circles) and TiO2 (black squares) at different substrate temperatures (A) and plasma pressures (B). A plasma pressure of 50 mTorr was used in (A), while the substrate temperature in (B) was held at ∼180 °C (corresponding to a table temperature setpoint of 200 °C). For TiO2, the value of r at a substrate temperature of ∼240 °C is estimated to be lower than 10–5.

Effect on Film Conformality

The temperature series for plasma ALD of SiO2 is presented in Figure 2, showing that film growth is achieved up to extremely high-AR values of >400. Clearly, the reached 50% thickness penetration depth tends to be higher for higher deposition temperatures. As given by eq 6, the slope of the PD50% data fitted in panel (B) is directly related to the value of the surface recombination probability r, where a higher slope corresponds to a lower value of r. Panel (B) thus indicates that r reduces with increasing temperature in the investigated range, resulting in a higher penetration depth of the deposited film. Note that the logarithmic increase of PD50% with plasma time, which is observed for all temperatures, confirms that the penetration depth was limited by the plasma half-cycles and that eq 6 is valid for determining r.

In addition to information on r (to be addressed in the following section), the thickness profiles presented in panel (A) also give insight into other aspects limiting film conformality. In particular, for all temperatures, a moderate but consistent decrease in thickness with distance is observed in the initial region up to a scaled distance (i.e., distance/cavity height) of ∼400, where afterward the thickness rapidly decreases at the profile front. In the initial region, a fully saturated and therefore constant thickness is predicted by the Langmuir model, where the sticking probability s0(1 – θ) goes to zero. Since the slight decrease in thickness is not influenced by the plasma exposure time (see the Supporting Information), it is probably related to soft saturation during the SiH2(NEt2)2 half-cycle, which should not affect the r values determined.

For plasma ALD of TiO2, of which the temperature series is presented in Figure 3, comparably high penetration depths as for SiO2 are obtained. Here, it is noted that at all temperatures there is a jump in TiO2 thickness in the beginning of the trench. This jump in thickness can be related to the presence of crystalline material grown in the ion-exposed region18,20 near the entrance of the trench (unpublished results). For the normalization of the thickness profiles, these jumps are not included, as indicated by the solid lines in panel (A), which serve as a guide to the eye. Similar to SiO2, the film penetration depth seems to increase with temperature, although for TiO2, the results obtained at set table temperatures of 100 and 200 °C are quite comparable. The penetration depths obtained at 200 °C are slightly higher than at 100 °C, but the slopes of PD50%/h versus ln(t) indicate an approximately equal value of r. Much higher penetration depths are obtained at 300 °C, where the film growth reaches an AR of ∼700 even when using relatively short plasma steps of 3.8 s. This indicates that the value of r at 300 °C is even lower than at 100 and 200 °C.

Here, it should be noted that the penetration depth at 300 °C does not increase with the plasma exposure time employed, revealing that film penetration was actually limited by the precursor half-cycle rather than by the plasma half-cycle. Only for plasma times lower than 3.8 s, film penetration is expected to become plasma-limited and follow a trend as illustrated by the shaded area in panel (B). When film penetration is precursor-limited, the slope of PD50%/h as a function of ln(t) does not reflect the value of r. An upper value of r can still be estimated using eq 6 and an estimated value of t50%, which in this work typically lies in the range of 0.2–1 s (see the Supporting Information). Still, the determination of r is most reliable when three or more thickness profiles are measured, where PD50% should steadily increase with ln(t) as observed, for instance, at 100 and 200 °C. Moreover, such a logarithmic trend indicates that film growth was recombination-limited and thus provided by recombining species such as atomic oxygen. Growth by molecular O2, as reported, for instance, by Provine et al.,21 is not expected to play a significant role.

Regarding the shape of the TiO2 thickness profiles, the film thickness again gradually decreases with distance into the trench. In contrast to the results for SiO2, the gradual decrease in TiO2 thickness seems to be related to the plasma half-cycle (i.e., soft saturation or other effects), since the profile tends to become flatter in the initial region of the trench when using longer plasma steps (see the Supporting Information). Furthermore, additional effects such as surface poisoning3,22 and precursor decomposition could contribute to the development of a sloping thickness profile. However, the influence of decomposition seems to be limited since the gradual decrease in thickness is also observed at 100 °C, where Ti(NMe2)4 should not decompose.23 More importantly, these effects do not significantly influence the determination of r.

Finally, the pressure series carried out for plasma ALD of SiO2 is presented in Figure 4. Here, the thickness profiles indicate that the plasma pressure has a strong influence on the film penetration depth. Using plasma steps of 12 s, growth up to an AR of ∼800 is achieved at a plasma pressure of 90 and 130 mTorr, while film penetration at 12 mTorr is limited to an AR of ∼200. Based on the increasing slope of the PD50% data fitted in panel (B), the increase in the penetration depth with pressure is mostly related to a reduction in r. The fitted values of t50% are relatively constant around 0.4 s (see the Supporting Information), which suggests that the plasma pressure has only a limited effect on the supplied flux of reactive radicals for this specific plasma setup and operating regime. The strong impact of pressure observed in Figure 4 indicates that the plasma pressure is an important knob for optimizing film conformality during plasma ALD of SiO2, especially in the case of temperature-sensitive applications where a high temperature cannot be used.

Extracted Recombination Probabilities

As explained in the Modeling section, the film penetration depths plotted in panels (B) of Figures 2–4 are used to determine the surface recombination probability of oxygen radicals at different temperatures and plasma pressures. The determined values are provided in Figure 5. From this figure, it is observed that r indeed significantly reduces with temperature and pressure within the ranges investigated, from around ∼10–4 down to ∼10–5 or even lower. For SiO2, the determined r-values are in good correspondence with our previous publication5 and with the wide range of values reported in the literature for SiO2 or SiO2-based surfaces (i.e., Pyrex or Vycor glass).24−34 In addition to the effect of temperature and pressure, the large spread in literature values can possibly be related to differences in surface treatment,28,29 roughness,24 radical flux,31,32 and the influence of ions.30−32 Here, it is noted that the conditions used in this work are most relevant for plasma ALD on high-AR structures. The r-values determined for TiO2 are slightly lower than the value reported in our previous publication,5 in which only two data points of PD50% were available to calculate r, but the values agree within their uncertainty. The given uncertainties of r are based on the number of PD50% values and on their measurement uncertainty (see the Supporting Information).

In several studies, an increase in r with temperature is reported for O atoms on SiO2-based surfaces.26,27,33,34 This is often attributed to the thermal energy available for activating a recombination reaction.15,24,26,33,34 The decrease in r with temperature observed in this work, and, for instance, by Kim and Boudart in the range of approximately 70–400 °C,24 could be caused by an increased desorption rate of O atoms.15,24,26,33,34 In this work, the density of adsorbed O atoms may be the limiting factor for surface recombination as the flux of O atoms inside the LHAR structures is much lower than in studies using directly exposed planar surfaces.

The observed impact of substrate temperature and plasma pressure illustrates the importance of measuring r for several process conditions. The determined values of r are directly relevant for plasma ALD of thin films on high-AR structures, but can also serve as input for simulations and for obtaining a deeper understanding of the radical–surface interaction involved. Regarding the impact of r on film conformality, it should be noted that the values of r are very low under all conditions investigated. Correspondingly, even for the condition with the highest value of r, film growth is achieved up to an AR higher than 200. This suggests that the influence of radical recombination can be neglected in most present-day applications of plasma ALD of SiO2 and TiO2.

Whether or not film growth is limited by radical recombination can be predicted using the value of r. This is done by calculating the reduction in gas-phase radical density at the end of the high-AR structure. For a trench with length L and AR = L/h, for example, eq 5 states that the gas-phase radical density at the end of the trench, so at a distance z = L, is in steady state given by

graphic file with name jp1c01505_m016.jpg 9

The reduction in gas-phase radical density is thus determined by the product rAR2. When rAR2 < 1, the gas-phase radical density at the end of the high-AR trench is similar to that at the entrance, such that the plasma time needed to reach saturation is similar to that for a planar substrate (assuming that t50% ≈ t50%,planar). In contrast, when rAR2 ≫ 1, the gas-phase radical density is strongly reduced by surface recombination, which is referred to as recombination-limited growth. For plasma ALD of SiO2 and TiO2, r < 10–4 under almost all investigated conditions, such that film growth is only recombination-limited for AR values of at least ∼100 or higher. In comparison, r is on the order of 10–3 up to 10–1 for plasma ALD of Al2O3 and HfO2,5 where film growth is therefore recombination-limited for AR values around ∼10. Note that a high film conformality can still be achieved when the growth is in a recombination-limited regime. However, the plasma time needed to reach saturation on a high-AR structure is highly dependent on r when rAR2 ≫ 1. This is further discussed in the following section (Figure 6).

Impact on Saturation Time and Process Feasibility

In the recombination-limited growth regime, when rAR2 ≫ 1, the plasma time needed for saturation on a high-AR structure can be adequately estimated by the time it takes for the penetration depth PD50% to reach the end of the structure. Formally, this saturation time tsat corresponds to the time needed to reach a coverage of 0.5 at z = L. Using PD50%(tsat) = L, AR = L/h, and eq 6 for PD50% then gives the following expression for the estimated saturation time:

graphic file with name jp1c01505_m017.jpg 10

As an illustrative example of the practical impact of r, Figure 6 gives the saturation times calculated for plasma ALD of SiO2 under the various process conditions investigated, for trenches with an AR of 200–1000. The values of r and t50% used in this calculation are given in Figure 5 and in the Supporting Information, respectively. Figure 6 shows that, when going to higher AR values, the saturation time increases exponentially and becomes more and more susceptible to the process conditions and the corresponding value of r. For example, at AR = 200, the saturation time is still only ∼1 s and relatively independent of r (and hence the substrate temperature and plasma pressure). Specifically, at AR = 200, the relatively small variation in saturation time with substrate temperature is mainly related to the value of t50%, which was higher at a substrate temperature of ∼240 °C. For higher AR values, the growth becomes more recombination-limited, as indicated by the darker data points (see grayscale bar for the values of rAR2), and differences in r have a larger impact. At AR = 1000, for instance, tsat decreases from ∼103 to <102 s with increasing substrate temperature and decreases even more strongly with plasma pressure, which are both directly caused by the decrease in r given in Figure 5.

Based on the aforementioned results, film growth is not recombination-limited for most state-of-the-art applications of plasma ALD of SiO2 and TiO2 in the semiconductor industry, where the ARs involved are typically well below 200 and rAR2 ≪ 1. In these applications, the value of r only has a limited influence and the saturation time is similar to that of a planar substrate. Other aspects such as the influence of directional ions18,35,36 can govern film conformality in cases where rAR2 ≪ 1. Figure 6 therefore illustrates that minimizing the value of r is especially important for extremely demanding applications such as the coating of powders or porous materials. Such applications are expected to become more important in the future. Moreover, similar effects of temperature and pressure will likely be present for other plasma ALD processes as well. We expect that this holds not only for oxides but also for plasma ALD of metal nitrides, sulfides, and metals, where in certain cases, film growth can already be recombination-limited for ARs of ∼10 or even lower.4,5,10 Especially in those cases, finding the process conditions that can be used to minimize r is essential.

Conclusions

In this work, we have studied film penetration into extremely high-AR structures during plasma ALD of SiO2 and TiO2 for various substrate temperatures (100–240 °C) and plasma pressures (12–130 mTorr, for SiO2). For each condition, the value of the surface recombination probability r of oxygen radicals was determined directly from the recombination-limited penetration depths of the deposited films. Such data on the influence of temperature and pressure on r were not yet available for ALD-relevant conditions. Very low r-values of <10–4 were determined under all conditions for both processes, where r was observed to decrease with temperature and pressure down to ∼10–5 within the studied ranges. These low r-values enable conformal film growth on trench structures with a high AR of <200 using similar plasma exposure times (e.g., ∼1 s) as needed for saturation on a planar substrate. For even higher ARs, specifically when rAR2 ≈ 1 or higher, the saturation time increases exponentially and becomes highly dependent on the value of r (e.g., ∼50 s or >1000 s for a trench with AR = 1000, depending on the value of r). In those cases, process conditions where r is minimized may be required for obtaining acceptable cycle times. In conclusion, this work can serve as a framework for building a database of r-values for several materials and process conditions, which we have demonstrated to be valuable for optimizing plasma ALD throughput and feasibility in demanding high-AR applications.

Acknowledgments

This work is part of the research program HTSM with Project No. 15352, which is (partly) financed by the Netherlands Organization for Scientific Research (NWO). R.L.P. acknowledges funding from Academy of Finland, ALDI project, decision no. 331082. VTT Technical Research Centre of Finland Ltd. and Dr. M. Utriainen are acknowledged for supplying the PillarHall LHAR3 and LHAR4 conformality test structures. Lam Research Corp. is acknowledged for providing vertical trench nanostructures. Solliance and the Dutch province of Noord Brabant are acknowledged for funding the TEM facility. Finally, the authors thank Dr. M.A. Verheijen for the TEM imaging, Dr. B. Barcones Campo for the FIB preparation of the TEM sample, and C. van Helvoirt for the technical support.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.1c01505.

  • Further details on the analytical model employed; an overview of the measured thickness profiles and determined values of r and t50%; the calculation of the uncertainties in r and t50%; and the experimental details regarding the TEM image provided in the introduction (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp1c01505_si_001.pdf (1.1MB, pdf)

References

  1. George S. M. Atomic Layer Deposition: An Overview. Chem. Rev. 2010, 110, 111–131. 10.1021/cr900056b. [DOI] [PubMed] [Google Scholar]
  2. Profijt H. B.; Potts S. E.; van de Sanden M. C. M.; Kessels W. M. M. Plasma-Assisted Atomic Layer Deposition: Basics, Opportunities, and Challenges. J. Vac. Sci. Technol., A 2011, 29, 050801 10.1116/1.3609974. [DOI] [Google Scholar]
  3. Knoops H. C. M.; Faraz T.; Arts K.; Kessels W. M. M. Status and Prospects of Plasma-Assisted Atomic Layer Deposition. J. Vac. Sci. Technol., A 2019, 37, 030902 10.1116/1.5088582. [DOI] [Google Scholar]
  4. Knoops H. C. M.; Langereis E.; van de Sanden M. C. M.; Kessels W. M. M. Conformality of Plasma-Assisted ALD: Physical Processes and Modeling. J. Electrochem. Soc. 2010, 157, G241–G249. 10.1149/1.3491381. [DOI] [Google Scholar]
  5. Arts K.; Utriainen M.; Puurunen R. L.; Kessels W. M. M.; Knoops H. C. M. Film Conformality and Extracted Recombination Probabilities of O Atoms during Plasma-Assisted Atomic Layer Deposition of SiO2, TiO2, Al2O3, and HfO2. J. Phys. Chem. C 2019, 123, 27030–27035. 10.1021/acs.jpcc.9b08176. [DOI] [Google Scholar]
  6. Dingemans G.; van Helvoirt C. A. A.; Pierreux D.; Keuning W.; Kessels W. M. M. Plasma-Assisted ALD for the Conformal Deposition of SiO2: Process, Material and Electronic Properties. J. Electrochem. Soc. 2012, 159, H277–H285. 10.1149/2.067203jes. [DOI] [Google Scholar]
  7. ASM International Analyst and Investor Technology Seminar, presented at Semicon West. https://www.asm.com/Downloads/ASMI%20Analyst%20and%20Investor%20Technology%20Seminar%20July%209%202019%20revREL.PDF (accessed July 9, 2019).
  8. Tang W.; Park J. D.; Schravendijk B.; Van Ashtiani K.. Systems and Methods for Eliminating Seams in Atomic Layer Deposition of Silicon Dioxide Film in Gap Fill Applications. U.S. Patent US9.406,544B12016.
  9. Swaminathan S.; Pasquale F. L.; LaVoie A.. Plasma Assisted Atomic Layer Deposition Titanium Oxide for Conformal Encapsulation and Gapfill Applications. U.S. Patent US9,373,500B22016.
  10. Cremers V.; Puurunen R. L.; Dendooven J. Conformality in Atomic Layer Deposition: Current Status Overview of Analysis and Modelling. Appl. Phys. Rev. 2019, 6, 021302 10.1063/1.5060967. [DOI] [Google Scholar]
  11. Knoops H. C. M.; Elam J. W.; Libera J. A.; Kessels W. M. M. Surface Loss in Ozone-Based Atomic Layer Deposition Processes. Chem. Mater. 2011, 23, 2381–2387. 10.1021/cm2001144. [DOI] [Google Scholar]
  12. Yanguas-Gil A.; Elam J. W. Self-Limited Reaction-Diffusion in Nanostructured Substrates: Surface Coverage Dynamics and Analytic Approximations to ALD Saturation Times. Chem. Vap. Deposition 2012, 18, 46–52. 10.1002/cvde.201106938. [DOI] [Google Scholar]
  13. Ylilammi M.; Ylivaara O. M. E.; Puurunen R. L. Modeling Growth Kinetics of Thin Films Made by Atomic Layer Deposition in Lateral High-Aspect-Ratio Structures. J. Appl. Phys. 2018, 123, 205301 10.1063/1.5028178. [DOI] [Google Scholar]
  14. Gordon R. G.; Hausmann D.; Kim E.; Shepard J. A Kinetic Model for Step Coverage by Atomic Layer Deposition in Narrow Holes or Trenches. Chem. Vap. Deposition 2003, 9, 73–78. 10.1002/cvde.200390005. [DOI] [Google Scholar]
  15. Lopaev D. V.; Malykhin E. M.; Zyryanov S. M. Surface Recombination of Oxygen Atoms in O2 Plasma at Increased Pressure: I. the Recombination Probability and Phenomenological Model of Surface Processes. J. Phys. D: Appl. Phys. 2011, 44, 015201 10.1088/0022-3727/44/1/015201. [DOI] [Google Scholar]
  16. Gao F.; Arpiainen S.; Puurunen R. L. Microscopic Silicon-Based Lateral High-Aspect-Ratio Structures for Thin Film Conformality Analysis. J. Vac. Sci. Technol., A 2015, 33, 010601 10.1116/1.4903941. [DOI] [Google Scholar]
  17. Yim J.; Ylivaara O. M. E.; Ylilammi M.; Korpelainen V.; Haimi E.; Verkama E.; Utriainen M.; Puurunen R. L. Saturation Profile Based Conformality Analysis for Atomic Layer Deposition: Aluminum Oxide in Lateral High-Aspect-Ratio Channels. Phys. Chem. Chem. Phys. 2020, 22, 23107–23120. 10.1039/d0cp03358h. [DOI] [PubMed] [Google Scholar]
  18. Arts K.; Deijkers J. H.; Faraz T.; Puurunen R. L.; Kessels W. M. M.; Knoops H. C. M. Evidence for Low-Energy Ions Influencing Plasma-Assisted Atomic Layer Deposition of SiO2: Impact on the Growth per Cycle and Wet Etch Rate. Appl. Phys. Lett. 2020, 117, 031602 10.1063/5.0015379. [DOI] [Google Scholar]
  19. Heil S. B. S.; van Hemmen J. L.; Hodson C. J.; Singh N.; Klootwijk J. H.; Roozeboom F.; van de Sanden M. C. M.; Kessels W. M. M. Deposition of TiN and HfO2 in a Commercial 200 Mm Remote Plasma Atomic Layer Deposition Reactor. J. Vac. Sci. Technol., A 2007, 25, 1357–1366. 10.1116/1.2753846. [DOI] [Google Scholar]
  20. Arts K.; Deijkers J. H.; Utriainen M.; Puurunen R. L.; Kessels W. M. M.; Knoops H. C. M.. Role of Ions in Film Conformality and Quality during Plasma-Assisted ALD of SiO2 and TiO2, AVS 20th International Conference on Atomic Layer Deposition, June 28–July 1, 2020.
  21. Provine J.; Schindler P.; Torgersen J.; Kim H. J.; Karnthaler H.-P.; Prinz F. B. Atomic Layer Deposition by Reaction of Molecular Oxygen with Tetrakisdimethylamido-Metal Precursors. J. Vac. Sci. Technol., A 2016, 34, 01A138 10.1116/1.4937991. [DOI] [Google Scholar]
  22. Knoops H. C. M.; Potts S. E.; Bol A. A.; Kessels W. M. M.. Atomic Layer Deposition. In Handbook of Crystal Growth: Thin Films and Epitaxy; Elsevier B.V., 2014; Vol. 3, pp 1101–1134. [Google Scholar]
  23. Yun J.; Park M.; Rhee S. Comparison of Tetrakis(Dimethylamido)Titanium and Tetrakis(Diethylamido)Titanium as Precursors for Metallorganic Chemical Vapor Deposition of Titanium Nitride. J. Electrochem. Soc. 1999, 146, 1804–1808. 10.1149/1.1391847. [DOI] [Google Scholar]
  24. Kim Y. C.; Boudart M. Recombination of O, N, and H Atoms on Silica: Kinetics and Mechanism. Langmuir 1991, 7, 2999–3005. 10.1021/la00060a016. [DOI] [Google Scholar]
  25. Berkowitz-Mattuck J. B.The Structure and Chemistry of Solid Surfaces; Somorjai G. A., Ed.; John Wiley & Sons: New York, 1969. [Google Scholar]
  26. Seward W. A.; Jumper E. J. Model for Oxygen Recombination on Silicon-Dioxide Surfaces. J. Thermophys. Heat Transfer 1991, 5, 284–291. 10.2514/3.262. [DOI] [Google Scholar]
  27. Greaves J. C.; Linnett J. W. Recombination of Atoms at Surfaces. Part 6 - Recombination of Oxygen Atoms on Silica From 20°C to 600°C. Trans. Faraday Soc. 1959, 55, 1355–1361. 10.1039/TF9595501355. [DOI] [Google Scholar]
  28. Cartry G.; Magne L.; Cernogora G. Atomic Oxygen Recombination on Fused Silica: Experimental Evidence of the Surface State Influence. J. Phys. D: Appl. Phys. 1999, 32, L53–L56. 10.1088/0022-3727/32/15/101. [DOI] [Google Scholar]
  29. Greaves J. C.; Linnett J. W. Recombination of Atoms at Surfaces. Part 5 - Oxygen Atoms at Oxide Surfaces. Trans. Faraday Soc. 1959, 55, 1346–1354. 10.1039/TF9595501346. [DOI] [Google Scholar]
  30. Cartry G.; Duten X.; Rousseau A. Atomic Oxygen Surface Loss Probability on Silica in Microwave Plasmas Studied by a Pulsed Induced Fluorescence Technique. Plasma Sources Sci. Technol. 2006, 15, 479–488. 10.1088/0963-0252/15/3/025. [DOI] [Google Scholar]
  31. Gomez S.; Steen P. G.; Graham W. G. Atomic Oxygen Surface Loss Coefficient Measurements in a Capacitive/Inductive Radio-Frequency Plasma. Appl. Phys. Lett. 2002, 81, 19–21. 10.1063/1.1490630. [DOI] [Google Scholar]
  32. Booth J. P.; Guaitella O.; Chatterjee A.; Drag C.; Guerra V.; Lopaev D.; Zyryanov S.; Rakhimova T.; Voloshin D.; Mankelevich Y. Oxygen (3P) Atom Recombination on a Pyrex Surface in an O2 Plasma. Plasma Sources Sci. Technol. 2019, 28, 055005 10.1088/1361-6595/ab13e8. [DOI] [Google Scholar]
  33. Macko P.; Veis P.; Cernogora G. Study of Oxygen Atom Recombination on a Pyrex Surface at Different Wall Temperatures by Means of Time-Resolved Actinometry in a Double Pulse Discharge Technique. Plasma Sources Sci. Technol. 2004, 13, 251–262. 10.1088/0963-0252/13/2/009. [DOI] [Google Scholar]
  34. Bedra L.; Balat-Pichelin M. J. H. Comparative Modeling Study and Experimental Results of Atomic Oxygen Recombination on Silica-Based Surfaces at High Temperature. Aerosp. Sci. Technol. 2005, 9, 318–328. 10.1016/j.ast.2005.01.011. [DOI] [Google Scholar]
  35. Faraz T.; Knoops H. C. M.; Verheijen M. A.; van Helvoirt C. A. A.; Karwal S.; Sharma A.; Beladiya V.; Szeghalmi A.; Hausmann D. M.; Henri J.; et al. Tuning Material Properties of Oxides and Nitrides by Substrate Biasing during Plasma-Enhanced Atomic Layer Deposition on Planar and 3D Substrate Topographies. ACS Appl. Mater. Interfaces 2018, 10, 13158–13180. 10.1021/acsami.8b00183. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Vallée C.; Bonvalot M.; Belahcen S.; Yeghoyan T.; Jaffal M.; Vallat R.; Chaker A.; Lefèvre G.; David S.; Bsiesy A.; et al. Plasma Deposition—Impact of Ions in Plasma Enhanced Chemical Vapor Deposition, Plasma Enhanced Atomic Layer Deposition, and Applications to Area Selective Deposition. J. Vac. Sci. Technol., A 2020, 38, 033007 10.1116/1.5140841. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp1c01505_si_001.pdf (1.1MB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES