Illuminating elite patches of chemical space

Abstract

In the past few years, there has been considerable activity in both academic and industrial research to develop innovative machine learning approaches to locate novel, high-performing molecules in chemical space. Here we describe a new and fundamentally different type of approach that provides a holistic overview of how high-performing molecules are distributed throughout a search space. Based on an open-source, graph-based implementation [J. H. Jensen, Chem. Sci., 2019, 10, 3567–3572] of a traditional genetic algorithm for molecular optimisation, and influenced by state-of-the-art concepts from soft robot design [J. B. Mouret and J. Clune, Proceedings of the Artificial Life Conference, 2012, pp. 593–594], we provide an algorithm that (i) produces a large diversity of high-performing, yet qualitatively different molecules, (ii) illuminates the distribution of optimal solutions, and (iii) improves search efficiency compared to both machine learning and traditional genetic algorithm approaches.

We report a novel algorithm that produces a large diversity of high-performing molecules, illuminates the distribution of optimal solutions, and improves search efficiency compared to both machine learning and genetic algorithm approaches.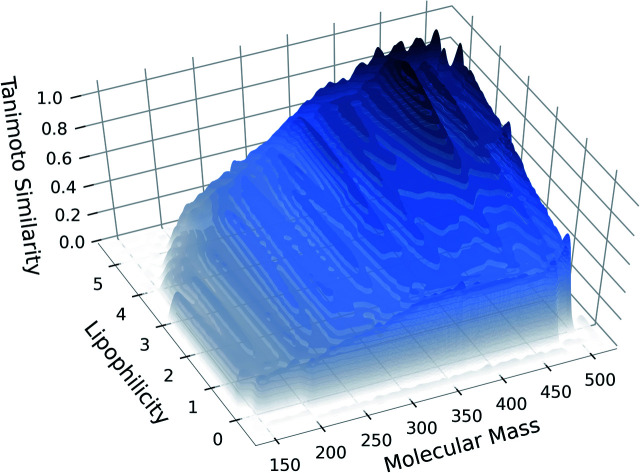

1. Introduction

Recent years have seen a surge^1–10 of machine learning (ML) papers focused on generating de novo molecules optimised for performance with regard to a chosen objective function, e.g. melting point¹¹ or binding affinity to a target protein.¹² These ML models aim to generate chemical compounds which exhibit desired behaviour, without reverting to explicit chemical rules, patterns or transformations. Instead, ML models learn from experimental data, and attempt to extrapolate the relevant aspects of the underlying chemistry. In terms of performance, however, ML models for molecular optimisation are rivalled by more traditional and often simpler, rule-based approaches^13,14 such as genetic algorithms (GA).

In this paper, we introduce a novel rule-based algorithm which we call graph-based elite patch illumination (GB-EPI). This algorithm enforces diversity among a set of high-performing molecules and leverages^15–18 them to obtain efficient optimisation. In addition, GB-EPI provides the user with a map relating the performance of generated molecules to chosen physicochemical properties. The algorithmic methodology of GB-EPI is discussed in the next section, followed by results of standard benchmarks and an in-depth comparative efficiency analysis between a graph-based genetic algorithm (GB-GA) and GB-EPI.

2. Algorithmic methodology

The goal of a classical optimisation algorithm is to obtain the highest performing solution in a search space. If the exact mathematical form of the evaluation function is inaccessible, as is typically the case in molecular optimisation, heuristic search methods¹⁹ become a necessity. Many of these heuristic methods are inspired by biological phenomena. Genetic algorithms^20,21 are based on the theory of evolution and aim to optimise with regard to an evaluation function, incrementally improving on existing solutions. Specifically, novel solutions are generated by randomly changing or stochastically combining solutions from the existing population. In the genetic algorithm community, these two operations are respectively known as mutations and crossovers. Solutions found by genetic algorithms are called phenotypes and each solution is described by an underlying genome. The performance of a solution with respect to the chosen evaluation function is known as the fitness of a phenotype.

Genetic algorithms can be highly effective in straightforward optimisation problems, but are known to struggle^22,23 when trying to cross low-performing valleys or to break out of local optima, and both of these occurrences can lead to evolutionary stagnation. We have based GB-EPI on an existing genetic algorithm for molecular optimisation, but evade evolutionary stagnation by enforcing molecular diversity. Moreover, GB-EPI speeds up the optimisation process by decoupling mutations from crossovers, and introduces the concept of positional analogue scanning to genetic algorithms. These and other technical aspects‡ of GB-EPI are discussed in the upcoming paragraphs.

2.1. Graph-based genetic algorithm

The current leading rule-based model for molecular optimisation is the graph-based genetic algorithm¹⁴ (GB-GA). In GB-GA, genomes of molecules are encoded by their molecular graphs. Novel molecules are generated by mutating or combining the graphs of molecules in the existing population. The initial population of candidate molecules is typically obtained from freely accessible molecular data-sets like ZINC²⁴ or ChEMBL.²⁵ Every generation, as a form of selection pressure, only the most fit molecules (with respect to the evaluation function) present in the population are retained.

This paper, and hence our algorithm, builds on the conceptual developments made in GB-GA by continuing to work with molecular graphs as genomes. We maintain the graph-based aspect of the crossover and mutation operators, but apply crossovers and mutations in parallel instead of sequentially. Our motivation for decoupling these two operators lies in the fact that crossovers customarily only support efficient exploration of chemical space in the early generations of a genetic algorithm. Later on, the nearly-converged solutions are typically only improved by the comparatively smaller effects of mutations.

2.2. Multi-dimensional archive of phenotypic elites

The multi-dimensional archive of phenotypic elites algorithm¹⁶ (MAP-Elites) is a simple, efficacious and surprisingly powerful tool developed in the context of soft robot design, and serves as the core architecture of our GB-EPI algorithm. MAP-Elites mimics diversity in biological evolution and explores the search space by introducing the concept of niches^26–28 to genetic algorithms. In MAP-Elites, candidate solutions are generated by a genetic algorithm but are assigned to different niches depending on their characterising features. Each generation, the best performing solution in each of the individual niches – with respect to a global evaluation function – is retained.

Dividing the search space into feature-based niches and explicitly enforcing population diversity stands in stark contrast with classical genetic algorithms which typically only retain the top high-scoring solutions regardless of their diversity, or lack thereof. The enforced variation between niches makes crossovers more diverse, and by mutating existing solutions, potent scaffolds can spread into other niches. Most importantly, because at every generation MAP-Elites contains solutions spread out over feature space, diverse solutions in far-away niches can be used a resource to escape stagnation. In Fig. 1 we provide pseudocode of the MAP-Elites algorithm for de novo molecule design as applied in GB-EPI.

Fig. 1. Pseudocode description of the MAP-Elites algorithm adapted to the setting of molecular optimisation.

In practical terms, users of GB-EPI can choose their own features of interest, and define relevant ranges of variation to construct a feature space. If, for instance, a user wants to find medicinally relevant molecules in chemical space, they could construct a feature space based on physicochemical properties like lipophilicity and molecular mass, and practical concerns like synthetic accessibility. The chosen ranges in which to explore these features can be used to specify a desired subset of chemical space in which to generate new molecules.

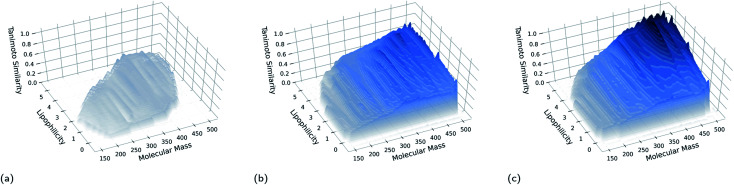
The fitness score obtained by the molecule occupying a niche at the end of a GB-EPI run represents the capability of the corresponding part of feature space to contain high-performance molecules. In this way, GB-EPI illuminates the relationship between the chosen features of interest and how varying them affects performance, either positively or, equally relevant, negatively. As can be seen in Fig. 2, the molecules at the end of a GB-EPI run form a patchwork of locally elite solutions (with respect to the chosen evaluation function) in a part of chemical space.

Fig. 2. Illumination of a patch of elite solutions for the rediscovery of troglitazone after (a) 1 generation, (b) 200 generations, and (c) 400 generations. For this visualisation, the feature space of GB-EPI was spanned by molecular mass and lipophilicity, and divided into 200 niches. The starting population consisted of 100 random compounds from a standardised subset of the ChEMBL database, further described in Section 3. The surface was obtained by interpolating, refining and triangulating the results. Darker shading indicates higher Tanimoto similarities with respect to troglitazone.

2.3. Centroidal Voronoi tesselations

In a regular grid partition, the number of niches grows exponentially with the dimensionality of feature space. To effectively partition high-dimensional feature spaces into niches, we can rely on a technique from computational geometry called the centroidal Voronoi tessellation^29–31 (CVT). The CVT can be used to create a pre-defined number of niches, irrespective of the dimensionality of the feature space. Because the number of niches is fixed, the use of a CVT partition in MAP-Elites maintains selection pressure for performance, even in higher-dimensional feature spaces.³²

A CVT is constructed by forming the lattice reciprocal to the cluster centroids of a uniform distribution over feature space. Each of the lattice cells outlines the space contained in a single niche. Computationally, the centroidal Voronoi tessellation can be constructed by Lloyd's clustering algorithm.³³ Efficient look-up of the nearest centroid to a given point in feature space is necessary to determine the niche to which a new solution belongs. Fortunately, this is made possible through fast multi-dimensional tree algorithms.³⁴

2.4. Positional analogue scanning and memoisation

Changes in molecular interactions and physicochemical properties resulting from small molecular structure modifications are used in in vitro medicinal chemistry to optimise lead compounds.³⁵ To minimise the number of experimental design cycles in lead optimisation, medicinal chemists apply small structure modifications in systematic batches, in a procedure known as positional analogue scanning.³⁶ During this procedure, series of molecular analogues of a lead compound are generated by the systematic exchange of heteroatoms or functional groups, and rapidly evaluated.

Similar to the small structure modifications used in the lab, GB-GA uses molecular mutations to work towards compounds with desired properties. Inspired by the success of positional analogue scanning, we repurpose the mutation operator in GB-EPI to systematically return not just a single mutated molecule, but all of its positional analogues. This approach accelerates convergence by allowing a potent design to spread out to several niches in a single generation. To speed up convergence even further, we extend the mutation operator to allow for the addition and removal of user-specified functional groups.

Memoisation³⁷ is a computational technique that ensures that a program does not unnecessarily repeat calculations, by keeping an on-the-fly record of obtained results. To balance memory and efficiency, the set of remembered results is typically limited to a fixed size and controlled by a first-in-first-out replacement algorithm. In this paper, memoisation was applied to fitness calculation, as this often carries the prohibitive computational cost, but memoisation can be readily extended to the other calculations in the algorithm. We note that memoisation can be used to reduce or even fully resolve the computational overhead introduced by positional analogue scanning.

2.5. Filters and parallelism

To rule out unwanted and potentially toxic molecules, we use functional group knowledge from the ChEMBL database²⁵ and a combination of ADME property calculations.^38–40 We remove undesirable compounds before they enter the evaluation step of the algorithm. Removing these compounds at an early stage makes the algorithm more efficient, increases the predictive value of the final outcome, and significantly decreases overall processing time.

To reduce clock time, we implemented a concurrent version of GB-EPI. The program distributes function evaluations, mutations and crossovers over a CPU/GPU architecture and receives performance scores, new molecules and behavioural descriptors from the individual nodes. Concurrency has no effect on the overall results obtained by the algorithm. All of the experiments in this paper can be reproduced either with or without concurrency.

3. Results and benchmarks

To standardise the assessment of models for de novo molecular design, the bioinformatics company BenevolentAI released a benchmarking suite named GuacaMol.¹³ The suite is open source and is meant to provide researchers with a variety of molecular optimisation tasks, related to the basic needs of computational and medicinal chemists. In this paper, we use GuacaMol as a starting point to quantify the performance of GB-EPI. We present and compare the results on the selected benchmarks for a deep-learning algorithm (SMILES LSTM), a rule-based algorithm (GB-GA), and the illumination algorithm GB-EPI presented in this paper.

SMILES LSTM⁴¹ is a deep learning model for de novo molecule generation, based on natural language processing and reinforcement learning. SMILES LSTM uses a simple text representation of molecules known as Simplified Molecular-Input Line-Entry System⁴² (SMILES) strings and trains a recurrent neural network (RNN) as a statistical language model for these textual descriptors of molecular structures. To obtain numerical stability in training through back-propagation, the RNN is enhanced with long shortterm memory⁴³ (LSTM) cells, making it capable of learning dependencies from larger collections of information.

After the SMILES LSTM model is sufficiently trained to produce chemically feasible SMILES strings, reinforcement learning⁴⁴ is applied to bias the generation of new chemical structures towards molecules with the desired chemical properties. Reinforcement learning is powerful, yet brittle; initialisation of the underlying LSTM network and the hyperparameters of the reinforcement learning algorithm must be done carefully. If successful, however, SMILES LSTM is able to cover and explore a large portion of chemical space.⁴⁵

In this paper, we run both SMILES LSTM and GB-GA in their standard GuacaMol baseline implementations.¹³ In particular, for each rediscovery target, the GB-GA algorithm was run with a mating pool of 200 molecules for a total of 1000 generations, unless there was no improvement for 5 consecutive generations. The SMILES LSTM baseline is a pre-trained recurrent neural network model, further optimised for each specific benchmark over 20 epochs by means of a hill-climbing algorithm. Each epoch the model generates 8192 molecules, of which the best 1024 are used to steer the reinforcement learning algorithm for further tuning.

3.1. Rediscovery of small molecule drugs

Rediscovery benchmarks, which require the explicit rediscovery of a target molecule on top of scoring for similarity, are a common potency test for de novo molecule generating models. By requiring explicit rediscovery, these benchmarks are more robust against exploitation⁴⁶ of metric deficiencies by generative models than – for instance – similarity metrics with a thresholded linear score modifier.¹³ The similarity between a generated molecule and the target compound is determined by the Tanimoto similarity of their extended-connectivity fingerprints⁴⁷ (ECFPs).

ECFPs are circular topological fingerprints, meaning that they encode molecular structures in terms of concentric atomic neighbourhoods. These fingerprints were originally⁴⁸ designed for similarity searching in high-throughput screening, but have also found applications in chemical clustering and compound library analysis. The main advantage of ECFPs, compared to more involved similarity measures, is that they can be rapidly calculated and inherently represent the presence or absence of molecular substructures.

In GuacaMol, three marketed and FDA-approved drugs are proposed as targets for rediscovery: celecoxib (an anti-inflammatory), troglitazone (an antidiabetic), and thiothixene (an antipsychotic). Together, these three ligands cover a wide range of physicochemical properties and pharmacological applications. To increase the effectiveness of the benchmarks, molecules highly similar to the targets (bit-vector Tanimoto similarity above 0.323) were removed by GuacaMol from the database of initial molecules. That initial database is derived from ChEMBL, which exclusively consists of molecules that have both been synthesised in a lab and tested against biological targets.

To set up GB-EPI for the rediscovery benchmarks, we chose the feature space to be spanned by molecular mass, 140 u to 520 u, and lipophilicity, log P = −0.4 to log P = 5.6. The ranges were chosen to roughly correspond to properties of orally active drugs, and the space was feature subdivided into 150 niches. More complex, higher-dimensional feature spaces are possible and often advisable, but here we limit the algorithm to its simplest form. The number of generations for GB-EPI was limited to a maximum of 400.

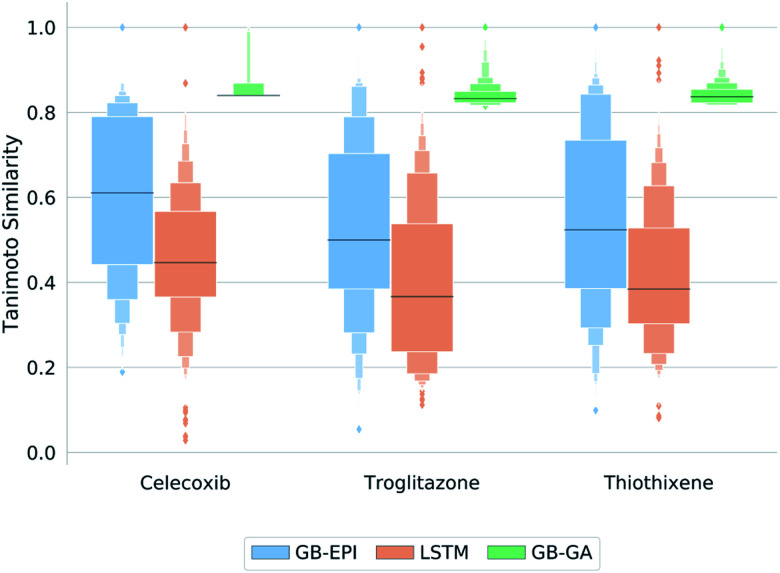
GB-EPI is successful in rediscovering these three drug-like molecules, just as SMILES LSTM and GB-GA. Whereas the power to differentiate between models through these GuacaMol rediscovery tasks can hence be debated, these simple tasks do give insight in the properties of the algorithms. The letter-value plots⁴⁹ in Fig. 3 show that the three distributions obtained by the algorithms at the end of each of the GuacaMol rediscovery benchmarks are highly distinct from each other. Whereas the GB-GA population provides a concentrated group of high-scoring molecules, SMILES LSTM generates a broad distribution of molecules with a few high-scoring outliers.

Fig. 3. Letter-value plots⁴⁹ of the final molecule distributions obtained by GB-EPI, SMILES LSTM, and GB-GA for the GuacaMol rediscovery benchmarks in terms of Tanimoto similarity to the target. The length of the innermost box represents the interquartile range, whereas the protruding boxes represent subsequent interquantiles (i.e. interoctiles, intersedecimiles, …). The horizontal line marks the median, while outliers (conventionally assumed to be the outer 0.7% of the population) are shown as individual diamonds beyond the largest interquantile displayed.

GB-EPI combines diversity with local selection pressure, and the obtained population distributions reflect this by having median scores above those of SMILES LSTM, and a more balanced spread than the distributions of GB-GA. While GB-GA only retains the highest-scoring molecules in its population, GB-EPI deliberately keeps lower-scoring molecules that are the best in their niche. In fact, the GB-GA median lies near the bottom of the narrow interquartile range because most of the molecules proposed by GB-GA have high internal similarity²² and hence nearly identical scores.

3.2. Simultaneous similarity for conflicting compounds

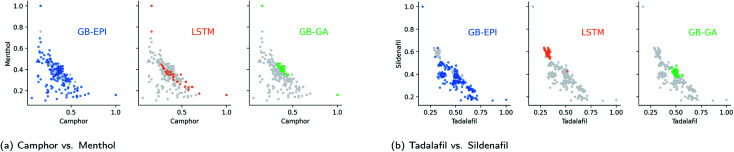
In a median molecules benchmark, the goal is to maximise similarity to several small-drug molecules simultaneously. The standard GuacaMol benchmark starts from the highest scoring molecules in the ChEMBL subset described in Section 3.1. These benchmarks are explicitly designed to be conflicting and can be regarded as challenging tasks. The GuacaMol benchmarking suite provides two of these tasks: camphor vs. menthol (two topical antitussives) and tadalafil vs. sildenafil (two drugs used to treat erectile dysfunction and pulmonary hypertension).

To increase the real-world relevance of these benchmarks, we filter out molecules that contain macrocycles, fail at Veber's rule,⁴⁰ or raise structural alerts from ChEMBL. The feature space of GB-EPI was again chosen to be spanned by lipophilicity and molecular mass. For both benchmarks, the feature space of GB-EPI was divided into 200 niches and the algorithm ran for 600 iterations. Furthermore, the GB-GA algorithm was only halted after 50 consecutive iterations without progress.

As shown in Table 1 and Fig. 4, these median molecules benchmarks are far more strenuous than the rediscovery benchmarks and can differentiate between the different models more accurately. Here, SMILES LSTM scores lower than the rule-based algorithms GB-GA and GB-EPI. To ensure an accurate comparison between the three generative models, two of which are pure optimisation algorithms (SMILES LSTM, GB-GA) and one of which (GB-EPI) balances quality and diversity, we only recorded the single highest score obtained by each algorithm.

Results for the maximum median molecule.

Benchmark	GB-EPI	SMILES LSTM	GB-GA
Standard
Camphor vs. menthol	0.419	0.415	0.419
Tadalafil vs. sildenafil	0.453	0.422	0.453
Randomised
Camphor vs. menthol	0.419	0.400	0.345
Tadalafil vs. sildenafil	0.370	0.368	0.313

Fig. 4. Distribution of proposed median molecules – coloured and highlighted by algorithm type – for the conflicting targets in the GuacaMol benchmarks, after filtering out structurally problematic molecules from the 100 highest-scoring ones. For camphor vs. menthol, the ranges of feature space for GB-EPI were chosen to be log P = −0.4 to 5.6, and 100 u to 350 u For tadalafil vs. sildenafil, the ranges were log P = −0.4 to 5.6, and 350 u to 600 u GB-EPI's inherent strategy to explore broader swaths of chemical space in an optimisation problem is clear in both figures. In contrast, the molecules proposed by GB-GA are focused around small regions of high-scoring median molecules.

To make the benchmark more informative, we also recorded the results for all algorithms on both benchmarks for a completely random subset of the standardised dataset. In the randomised subset benchmarks, GB-GA and GB-EPI begin with 100 arbitrary compounds, whereas the SMILES-LSTM model is pre-trained on a larger set of molecules from the same collection but not hyper-tuned by top scoring molecules from the dataset. Both SMILES LSTM and GB-GA have trouble crossing the larger distance in chemical space to the median molecules and score significantly lower than GB-EPI.

3.3. Comparing efficiency of GB-EPI and GB-GA

To study the difference in efficiency of GB-EPI and GB-GA, we make a statistical analysis of a representative rediscovery task (troglitazone). In line with earlier work^14,50 on the efficiency of GB-GA, we calculate the average number of fitness function evaluations and CPU time needed for rediscovery, and the rediscovery success rate of both algorithms. As we learned from the median molecule task, starting from a randomised set of molecules elucidates the exploratory power of the algorithms more.

Therefore, we start this rediscovery task with the 100 top-scoring molecules from 10 000 molecules randomly chosen from a 1.6 million ChEMBL subset, as constructed by Henault et al.⁵⁰ In this subset all molecules with a bit-vector Tanimoto similarity to the target above 0.323 are removed.¹³Table 2 shows the results for 100 runs of GB-EPI and GB-GA (with settings taken from Henault et al.⁵⁰), both with a maximum of 1000 generations per run.

Efficiency of GB-EPI and GB-GA in the rediscovery of troglitazone, in terms of the average number of required score evaluations and CPU time in the case of a successful run, and the overall success ratio over 100 independent, randomly seeded runs of both algorithms.

Algorithm	Evaluations	CPU time	Success ratio
GB-EPI	14 258	3 min 5 s	100%
GB-GA	24 216	11 min 37 s	81%

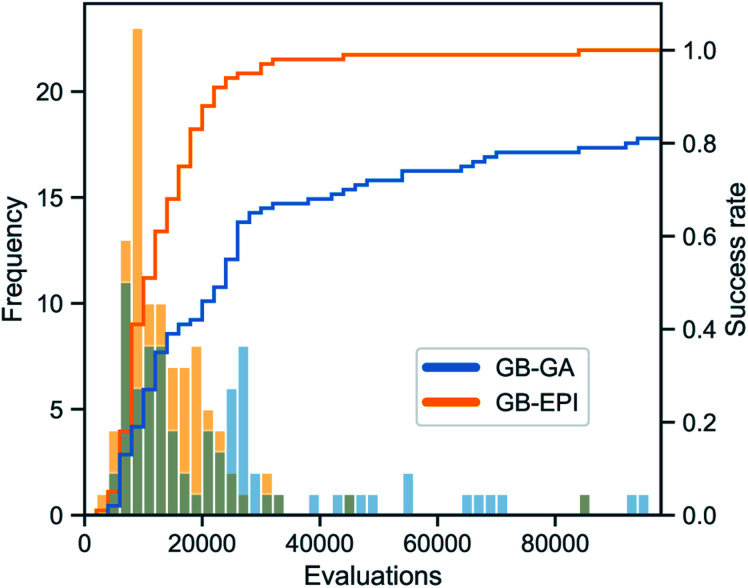
While chemical space consists of an estimated 10⁶⁰ molecules, it has been argued⁵⁰ that the perfect, omnipotent search algorithm would be able to find small drug-like molecules (i.e. excluding peptides, antibodies, …) in a few hundred transformation operations (crossovers and mutations) and corresponding fitness evaluations. With this idealised benchmark in mind, it can be observed from Table 2 and Fig. 5 that GB-EPI makes a sizeable improvement (approx. 41%) to the average number of function evaluations needed for rediscovery. Similarly, we note that the average CPU time needed for rediscovery decreased starkly (approx. 73%) in GB-EPI compared to GB-GA.

Fig. 5. Distribution of the number of score function evaluations necessary for the rediscovery of troglitazone and corresponding cumulative success rate, for 100 independent runs of GB-GA (blue) and GB-EPI (orange). Both distributions are shown on the same scale.

In addition, the success ratios affirm that GB-GA suffers from stagnation issues, whereas GB-EPI can leverage molecular diversity to escape local optima of the scoring metric. The success rate of GB-GA for this rediscovery is 81%, meaning that at least 3 GB-GA searches are needed for the rediscovery to succeed with at least 99% certainty. Taking this into account would further increase the number of score evaluations to about 70 000 before an expected successful rediscovery. Similarly the expected CPU time before rediscovery by GB-GA will be of the order of 35 minutes.

4. Conclusion and outlook

This paper introduces the concept of illumination to de novo molecule generating algorithms through an algorithm called GB-EPI. Previous molecular optimisation algorithms, like SMILES LSTM and GB-GA, aim to obtain the highest performing solution in chemical space. In contrast, our novel algorithm constructs a whole patch of high-performing solutions spread out over niches covering a selected part of chemical space. By exploring what is chemically possible, in addition to leveraging diversity to efficiently discover what is purely optimal, GB-EPI illuminates design trade-offs and encourages synergy between design algorithms and human chemists.

For instance, researchers wishing to understand how the binding affinity with a target protein changes with physicochemical properties of an inhibitor could use GB-EPI to scan a feature space spanned by the lipophilicity, molar refractivity, and mass of the candidate molecules. In contrast, an industrial chemist could find more use in a feature space spanned by estimated production costs and synthetic accessibility. In both cases, molecules that are predicted to have a desired combination of properties can easily be selected for further examination.

Future extensions of GB-EPI could include adaptive meshing of the centroidal Voronoi tessellations⁵¹ to increase the number of niches in the most suitable regions of feature space, surrogate modelling techniques^52,53 to reduce the number of necessary fitness function evaluations, or crossovers based on intermolecular correlations.⁵⁴ In addition, deep learning models could be trained to predict which mutations are most beneficially applied to which molecules. Combined, these extensions have the potential to significantly speed up the current GB-EPI algorithm.

Some attention should also be drawn to the exciting prospect of steering GB-EPI by direct experimental feedback. Through active learning⁵⁵ – a small-data alternative to deep learning – and graph-based retrosynthesis,^56,57 molecules proposed by GB-EPI could be selected for in vitro synthesis and analysis.§ The experimental results could then be used to update the fitness model. The practical aspects of this iterative loop could perhaps even be executed autonomously by a robotics platform, creating a self-driving laboratory⁵⁹ for molecular design.

Conflicts of interest

There are no conflicts to declare.