Investigation of Phosphorylation-Induced Folding of an Intrinsically Disordered Protein by Coarse-Grained Molecular Dynamics

Abstract

Apart from being the most common mechanism of regulating protein function and transmitting signals throughout the cell, phosphorylation has an ability to induce disorder-to-order transition in an intrinsically disordered protein. In particular, it was shown that folding of the intrinsically disordered protein, eIF4E-binding protein isoform 2 (4E-BP2), can be induced by multisite phosphorylation. Here, the principles that govern the folding of phosphorylated 4E-BP2 (pT37pT46 4E-BP2_18–62) are investigated by analyzing canonical and replica exchange molecular dynamics trajectories, generated with the coarse-grained united-residue force field, in terms of local and global motions and the time dependence of formation of contacts between C^αs of selected pairs of residues. The key residues involved in the folding of the pT37pT46 4E-BP2_18–62 are elucidated by this analysis. The correlations between local and global motions are identified. Moreover, for a better understanding of the physics of the formation of the folded state the experimental structure of the pT37pT46 4E-BP2_18–62 is analyzed in terms of a kink (heteroclinic standing wave solution) of a generalized discrete nonlinear Schrödinger equation. It is shown that without molecular dynamics simulations the kinks are able to identify not only the phosphorylated sites of protein, the key players in folding, but also the reasons of the weak stability of the pT37pT46 4E-BP2_18–62.

Graphical Abstract

1. Introduction

Post-translational modifications (PTMs) may have a dramatic effect on protein secondary structure and susceptibility to conformational changes.¹ Among more than 400 different post-translational protein modifications² protein phosphorylation is the most common and possibly the most significant post-translational protein modification. Phosphorylation plays important role in regulating protein synthesis, cell cycle, growth, apoptosis, cell division, and signal transduction.^3–5 Phosphorylation can cause striking effects in the regulation of intrinsically disordered proteins (IDPs) and intrinsically disordered regions (IDRs), the characteristic feature of which is a lack of a well-defined three-dimensional structure in solution when they exist alone, but upon binding to their partner molecules they fold into particular structures in many cases. For example, α-synuclein expression studies in cell cultures have demonstrated that phosphorylation, along with some other PTMs (oxidation and sumoylation), is primarily involved in α-synuclein aggregation and toxicity.⁶ Moreover, it may serve as a conformational switch from the native to disordered state.^7,8

Recently, Bah et al.⁹ demonstrated that phosphorylation can induce disorder-to-order transition, as well. In particular, they studied the phospho-regulation of interaction between eukaryotic translation initiation factor 4E (eIF4E) and IDP 4E-BP2, the major neural isoform of the family of three mammalian proteins, and found that the phosphorylation of T37 and T46 residues in 4E-BP2 can cause the folding of the P18-R62 fragment of 4E-BP2 (pT37pT46 4E-BP2_18–62) into a four β-stranded and a short 3₁₀ helix folded domain. Wild type (WT) 4E-BP2 exhibits a high binding affinity toward eIF4E and competes with eukaryotic translation initiation factor 4G (eIF4G) for binding to eIF4E through a conserved⁵⁴YDRKFLL⁶⁰ binding motif that undergoes a disorder-to-helix transition upon binding.^10–12 The protein structure folded upon T37 and T46 phosphorylation is weakly stable, and the binding affinity of 4E-BP2 with eIF4E reduces by ~ 100-fold; however, Bah et al.⁹ and later Dawson et al.¹³ demonstrated that the fully-phosphorylated (pT37/pT46/pS65/pT70/pS83) 4E-BP2 is more stable and the binding affinity with eIF4E decreases by ~ 4000-fold, which enables eIF4G to outcompete 4E-BP2 and proceed translation initiation.¹⁴

Although many studies show that phosphorylation can regulate the functions of IDPs,^15,16 the detailed regulation mechanism of phosphorylation on the structures and the interactions of IDPs remains elusive, which hinders understanding of IDP function. To this end, molecular dynamics (MD) simulations can serve as a good means of studying the details of the regulation mechanism, in this case the folding mechanism of phosphorylated 4E-BP2. Recently, several computational studies were carried out to understand the folding mechanism induced by phosphorylation,^17–21 in which the mechanism of how two phosphorylated residues can fold the protein along with key residues playing important role in stabilization were identified. Both canonical and replica-exchange molecular dynamics (REMD) simulations have been employed in these investigations. In particular, the canonical MD simulations were performed at different temperatures and started from the NMR structure with PDB ID 2MX4,⁹ which enabled the authors to study the unfolding process of 4E-BP2. In order to examine the folding of 4E-BP2, the REMD simulations were carried out, in which the temperature-unfolded structures were used as initial structures.^18–21 Unfortunately, in some cases REMD simulations failed to find the experimentally determined folded state.¹⁸

In the present work, we addressed the folding of the phosphorylated 4E-BP2 by carrying out (i) 80 canonical MD trajectories, generated with the coarse-grained united residue (UNRES) force field,^22–26 for both pT37pT46 and WT 4E-BP2_18–62 at two different temperatures (40 MD trajectories at each temperature), which were below (280K) and at the experimentally determined melting point (293K); and (ii) 40 multiplexed replica exchange molecular dynamics (MREMD)²⁷ simulations with the UNRES force field for both phosphorylated and WT 4E-BP2_18–62. All trajectories in both canonical and MREMD simulations start with the same initial fully-extended structure but with different velocities.

Among 40 canonical MD trajectories at 280K, pT37pT46 4E-BP2_18–62 folds in 11 trajectories (27.5%), whereas at 293K it finds the experimentally determined folded state only in 6 trajectories (15%). The time that pT37pT46 4E-BP2_18–62 remains in the folded state is quite short. In particular, in different trajectories at 280K it varies between ~0.2% and ~10.8% of the entire trajectory length, and between ~0.1% and ~0.5% at 293K. These results indicate a weak stability of the system, and are in agreement with an earlier experimental study.⁹ A difference between the average energies of the folded and unfolded conformations is only ~1.0 kcal/mol, which is not surprising because of the weak stability of the protein.

Two folding trajectories of pT37pT46 4E-BP2_18–62 and one nonfolding trajectory of WT 4E-BP2_18–62 at 280K were selected and analyzed in terms of principal component analysis (PCA)^23,28–30 (see Principal Component Analysis in the Supporting Information) describing the global motions of the protein, local motions of each residue [free-energy profiles (FEPs) along the amino acid sequence^23,30,31], and distances between the C^αs of selected pairs of residues (including phosphorylated) forming hairpins over time.

Although MD simulations have proven to be a very powerful tool for examining the dynamics of protein folding, the correctness of such simulations depends on the force field employed to describe physical interactions within and between peptide units. It should be noted that, the present force fields, both all-atom and coarse-grained, are far from being accurate. Even small errors in the description of protein energy surfaces can accumulate over a polypeptide chain to distort the correct fold. The inaccuracy problem becomes more significant when the folding of weakly stable proteins is studied, in which barriers between folded and unfolded states are very low. Hence, in the present work, we also studied the experimental structures of the pT37pT46 4E-BP2_18–62⁹ from another, complementary point of view. In particular, rather than analyzing individual interactions that contribute to the formation of the folded structure, model-independent principles which are based on symmetry are explored. We advocate that all the physical forces, both strong and weak, combine together to give boost to a specific type of protein dynamics, expressed by a generalized version of the discrete nonlinear Schrödinger (DNLS) equation, and propose that various parametrizations of a kink, or heteroclinic standing wave solution, of a generalized version of the DNLS equation to be employed as the basic modular building blocks of folded proteins.^32–45 It should be noted that, unlike the most recent studies,^{32–39, 41–44} in which the epithet topological (dark) soliton was used, here we prefer to use kink. This choice highlights that the potential in the DNLS equation displays spontaneous breakdown of a discrete symmetry, and the kink describes the ensuing domain wall;^46–50 in the case of a folded protein an individual kink corresponds to a supersecondary structure such as a strand-loop-strand or helix-loop-helix motif. Moreover, the kink considered here is not related with the concept of Davydov’s soliton.⁵¹ The kink in a protein is a purely topological (geometric) structure, whereas the Davydov’s soliton is associated with collective excitations traveling along a chain (perturbations of electron density).

2. Methods

2.1. UNRES Force Field.

Detailed descriptions of the UNRES force field and its parametrization are available in references^52,53 and at http://www.unres.pl; hence, only a brief outline of the force field is presented here. UNRES is a highly coarse-grained model of polypeptide chain(s), in which the main chain is defined by a sequence of α-carbon (C^α) atoms, which are not interaction sites but geometric points, and each amino acid residue has two interaction sites, namely the united peptide group (p) located in the middle between the two consecutive C^αs and the united side chain (SC), attached to the respective C^α (Figure 1). The solvent is implicit in the model. The force field was derived as the potential of mean force (PMF) (or the restricted free energy (RFE) function) of a system of polypeptide chain(s) in solvent, in which all degrees of freedom except the coordinates of the C^α atoms and SC centers were averaged out. The effective energy function consists of multibody terms, as well as local and site-site interactions, which were obtained by decomposing the PMF into factors corresponding to clusters of interactions within and between coarse-grained sites.²² The contribution from solvation is implicitly included in the SC-SC interaction potentials.^22,23,54 The force field has been optimized to reproduce the structure and thermodynamics of small proteins.

Figure 1.

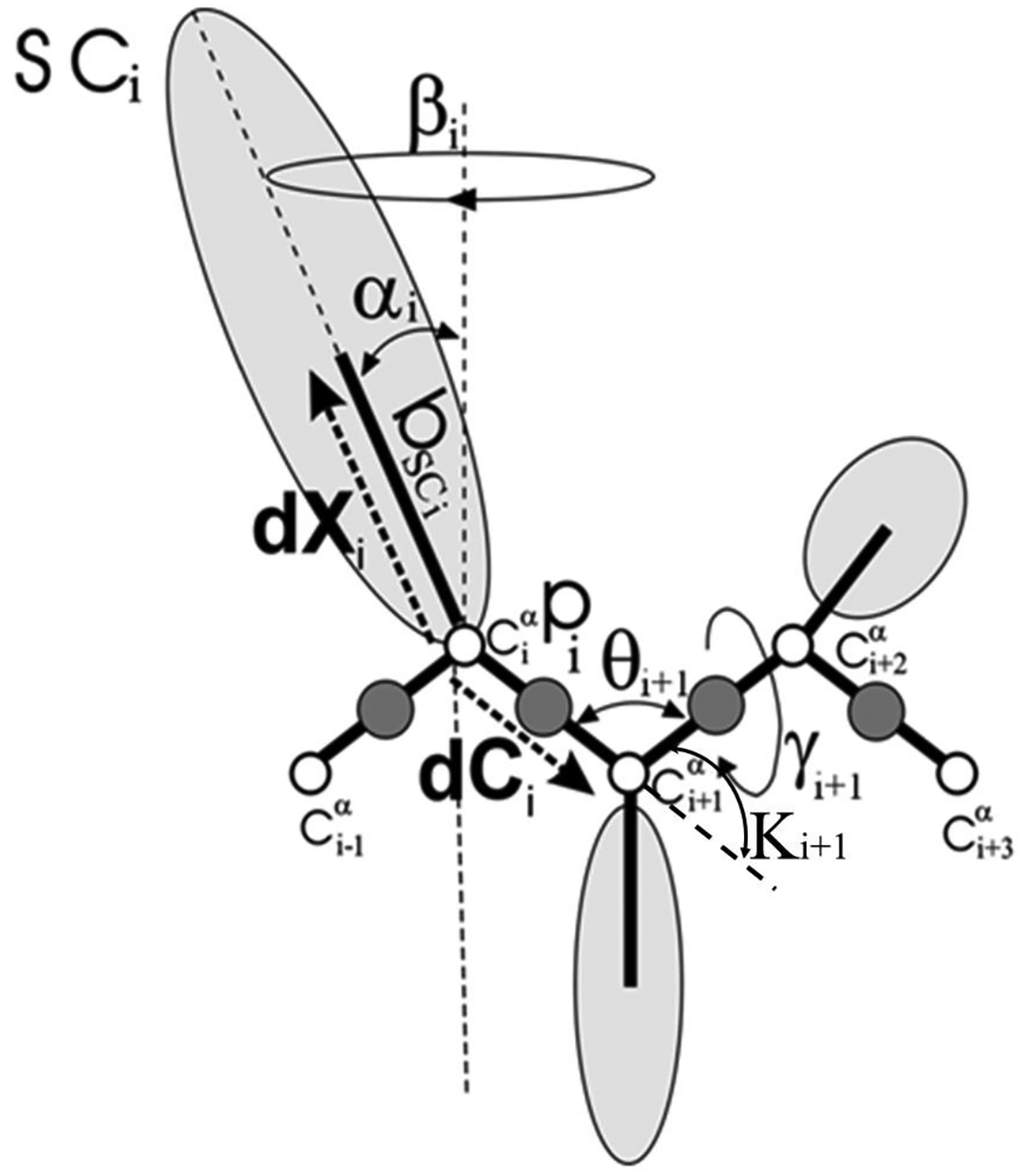
The UNRES model of polypeptide chains. The interaction sites are peptide-bond centers (p), and side-chain ellipsoids of different sizes (SC) attached to the corresponding α-carbons with different “bond lengths”, b_SC. The α-carbon atoms are represented by small open circles. The equilibrium distance of the C^α…C^α virtual bonds is taken as 3.8 Å, which corresponds to planar trans peptide groups. The geometry of the chain can be described either by the virtual-bond vectors dC_i (C^α_i…C^α_i+1), i = 1, 2,…, N − 1 and dX_i (C^α_i…SC_i), i = 2, 3,…, N − 1 (represented by thick dashed arrows), where N is the number of residues, or in terms of virtual-bond lengths, backbone virtual-bond angles θ_i, i = 2, 3,…, N − 1, backbone virtual-bond-dihedral angles γ_i, i = 2, 3,…, N − 2, and the angles α_i and β_i, i = 2, 3,…, N − 1 that describe the location of a side chain with respect to the coordinate frame defined by C^α_i-1, C^α_i and C^α_i+1. The angles κ_i used here are complements of the θ_i angles, i.e., π − θ_i.

2.2. Kinks.

Detailed descriptions of kinks of the DNLS equation are available in our previous papers;^32–45 therefore, we will only outline the main aspects of the approach here and provide some details in the Supporting Information. The methodology is very general and applicable to most globular proteins. It is based on the Landau-Ginsburg-Wilson paradigm, which states that the energy function must be built so it respects the symmetries of the physical system. By following the Landau-Ginsburg-Wilson paradigm we develop a complementary approach to model proteins and their dynamics. We introduce a free energy description that is designed to model folded proteins and their properties at the level of the tertiary structures [see Eq. (S11) in the SI]. It is a deformation of the energy function of the integrable DNLS.^46–48 The conventional DNLS equation is known to support kinks, therefore, the free energy, defined in Eq. (S11), can support kink solutions as well. Although we do not know an analytical expression of the kink solution to Eq. (S13), an excellent approximative solution can be obtained by discretizing the heteroclinic standing wave solution to the continuum nonlinear Schrödinger equation^32–45 [see Eq. (S15) in the SI].

2.3. Molecular Dynamics Simulations.

For each system (pT37pT46 and WT 4E-BP2_18–62), a total of 80 canonical and 40 MREMD simulations were carried out with the UNRES force field. The lengths of each canonical MD trajectory for pT37pT46 and WT 4E-BP2_18–62 were 8 × 10⁷ and 4 × 10⁷ steps, respectively, which are equivalent to ~0.4 μs and ~0.2 μs UNRES time and ~0.4 ms and ~0.2 ms actual time (the time step in MD simulations is dt = 0.1 mtu; and 1 mtu = 48.9 fs is the “natural” time unit of molecular dynamics,²⁵ which should be multiplied by ~1000 when it is compared to the actual experimental time because the fast degrees of freedom are averaged²⁶ in UNRES). The simulations were performed with the Berendsen thermostat with coupling time 49.8 fs. The lengths of MREMD trajectory for both pT37pT46 and WT 4E-BP2_18–62 were 5.37 × 10⁷ steps (~0.26 μs UNRES time and ~0.26 ms actual time per replica). The MREMD temperature set was: 250, 270, 280, 290, 295, 300, 310, 330, 350 and 370 K with four trajectories in each temperature. Replica in MREMD simulations exchanged every 10000 steps. It should be noted that the time used in the Results and Discussion section is the UNRES time. Also, PULCHRA software⁵⁵ has been used for all-atom reconstruction of coarse-grained conformations obtained from UNRES simulations.

3. Results and Discussion

3.1. Weighted Histogram Analysis with Clustering of MREMD Trajectories.

The MREMD simulations revealed that pT37pT46 4E-BP2_18–62 folds into experimentally determined folded structure, while the WT 4E-BP2_18–62 does not fold (Figure 2). In particular, the root-mean-square-deviation (RMSD) of the structure, that is the most similar to the folded structure and obtained after clustering of the WT 4E-BP2_18–62, was 9.93Å, whereas the RMSD of the cluster of the phosphorylated protein pT37pT46 4E-BP2_18–62 was 5.21Å. As can be seen in Figure 2, the pT37pT46 4E-BP2_18–62 obtains the proper fold, the probability of this cluster is 14%. The largest differences between the simulated and experimental structures can be observed in the N-terminal loop and in the C-terminal fragment of the protein. The structure of the nonfolded unphosphorylated protein (WT 4E-BP2_18–62) with the lowest RMSD is also the one with the highest probability of the cluster (55%).

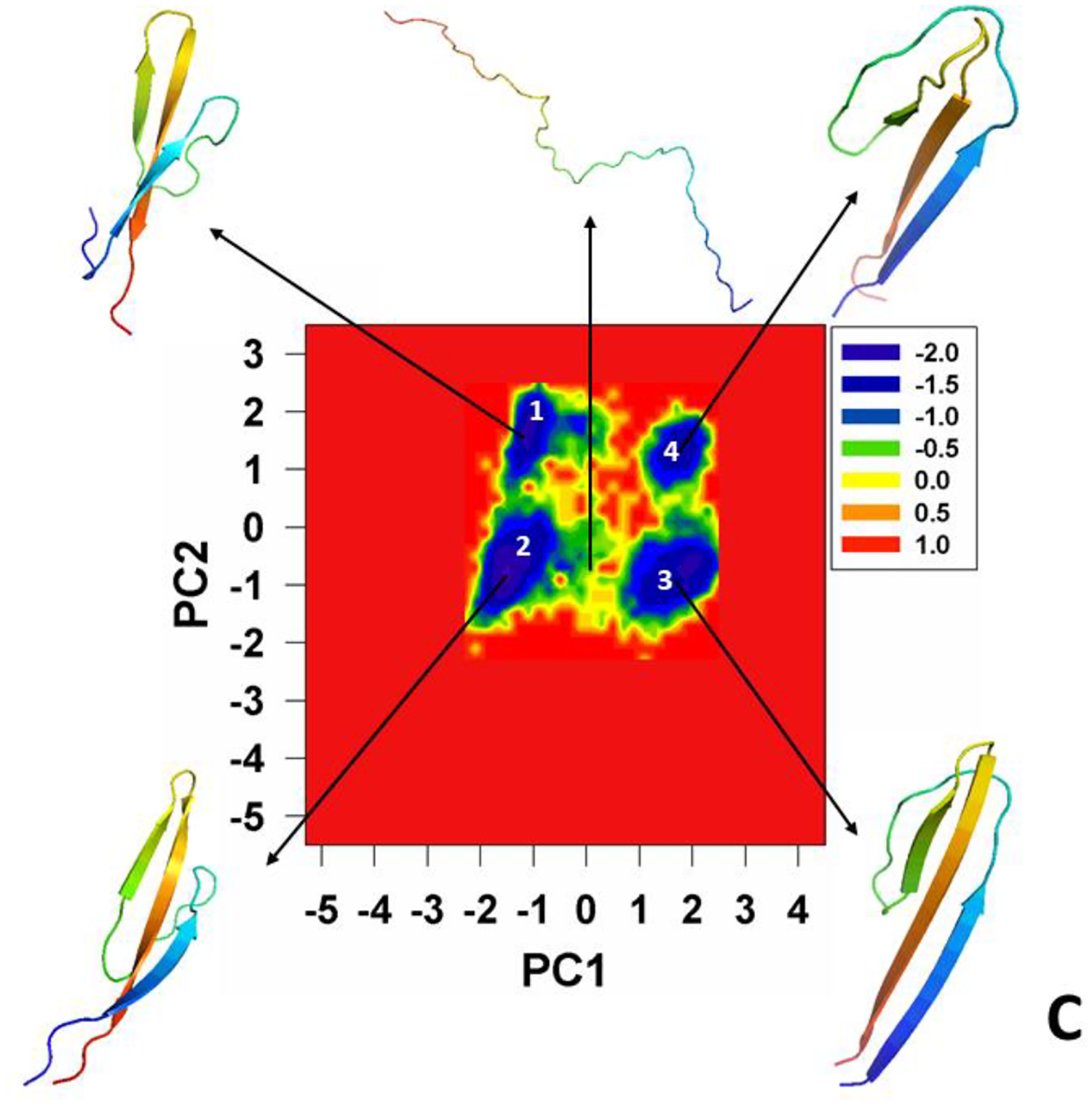
Figure 2.

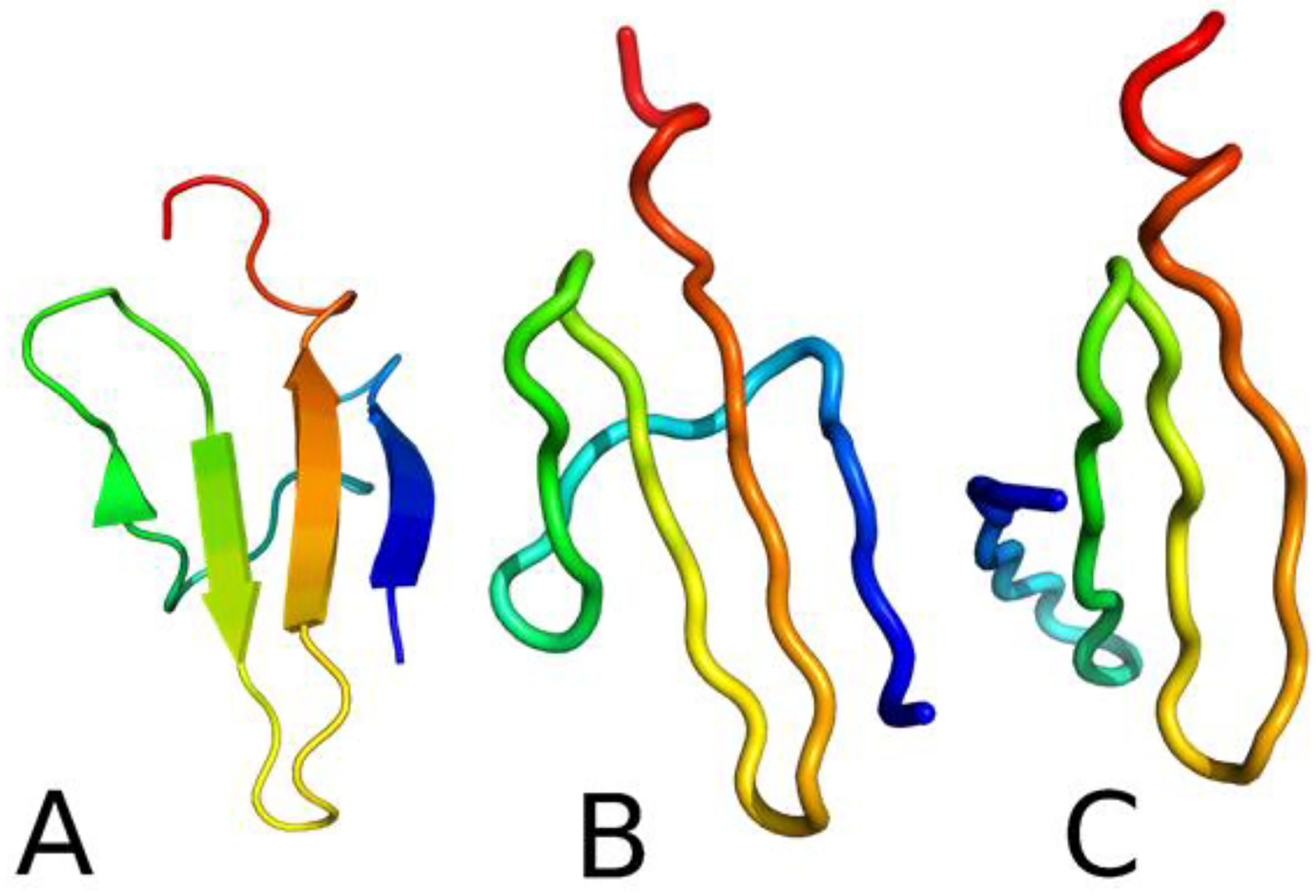
The experimental structure of pT37pT46 4E-BP2_18–62 (A) compared with the most similar structures obtained after simulations and clustering of pT37pT46 4E-BP2_18–62 (B) and WT 4E-BP2_18–62 (C).

3.2. Free-energy Landscape and Folding/Nonfolding Pathways of pT37pT46 and WT 4E-BP2_18–62.

It is well-known, from theoretical and conceptual points of view, that a study of free-energy landscapes (FELs) provides an understanding of how proteins fold and function.^56–58 It is practically impossible to present a FEL as a function of all degrees of freedom of a protein. Therefore, we should rely on the coordinates along which the intrinsic folding pathways can be viewed. To this end, PCA, which has proven to be an effective tool for the analysis of protein folding trajectories capturing most of the total displacements from the average protein structure with the first few PCs during simulations,^29,30 is a good alternative.

Among 11 canonical folding trajectories of pT37pT46 4E-BP2_18–62 at 280K, we selected two trajectories, in which the system folds differently based on the RMSD vs time (Figure 3A,B). In particular, in the first trajectory (Figure 3A), the protein jumps to the folded state at the beginning of the trajectory (~17.7 ns), remains there for a short time (~32.6 ns), and then starts jumping back and forth between the folded and unfolded states during ~189.2 ns until it unfolds completely. In the second trajectory (Figure 3B), the system looks more loose and folds only after ~129.2 ns, it remains in the folded state for ~23.3 ns and then jumps to the unfolded state. In addition, for comparison and better understanding of folding mechanisms, we picked and examined one of the nonfolding trajectories of WT 4E-BP2_18–62 at 280K (Figure 3C).

Figure 3.

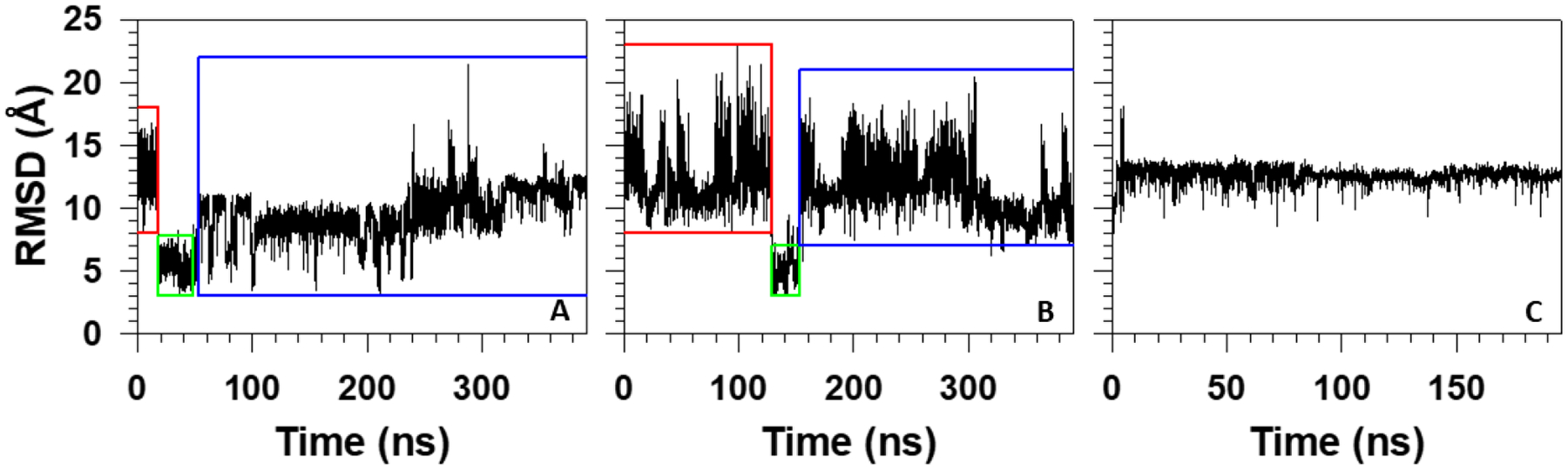
RMSD with respect to the folded structure as a function of time for folding trajectories of pT37pT46 4E-BP2_18–62 at 280K (panels A and B) and for nonfolding trajectory of WT 4E-BP2_18–62 (panel C). The red and blue rectangles correspond to the unfolded state, and the green rectangles correspond the folded state.

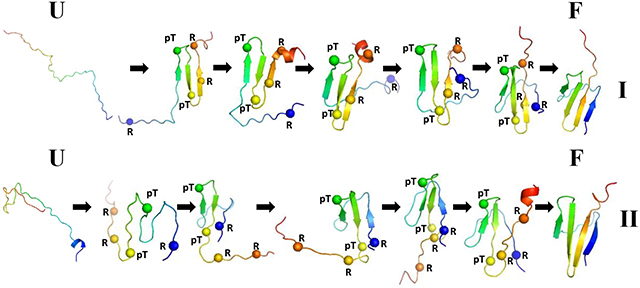
The free-energy landscapes along the first two PCs [μ(PC₁, PC₂) = −k_BTlnP(PC₁, PC₂), where P, T and k_B are the probability distribution function (pdf), the absolute temperature, and the Boltzmann constant, respectively] for these three trajectories with representative structures are illustrated in Figure 4. Since the transitions from the unfolded to folded state and vice versa are the most interesting parts of the MD trajectories, we plotted, in addition, the structures of transition states illustrating the folding and unfolding pathways of the system. The spheres in the structures correspond to phosphorylated Threonine (pT) and Arginine (R) residues, which according to previous studies^17–21 can form salt bridges and play a crucial role in the stabilization of tertiary structure.

Figure 4.

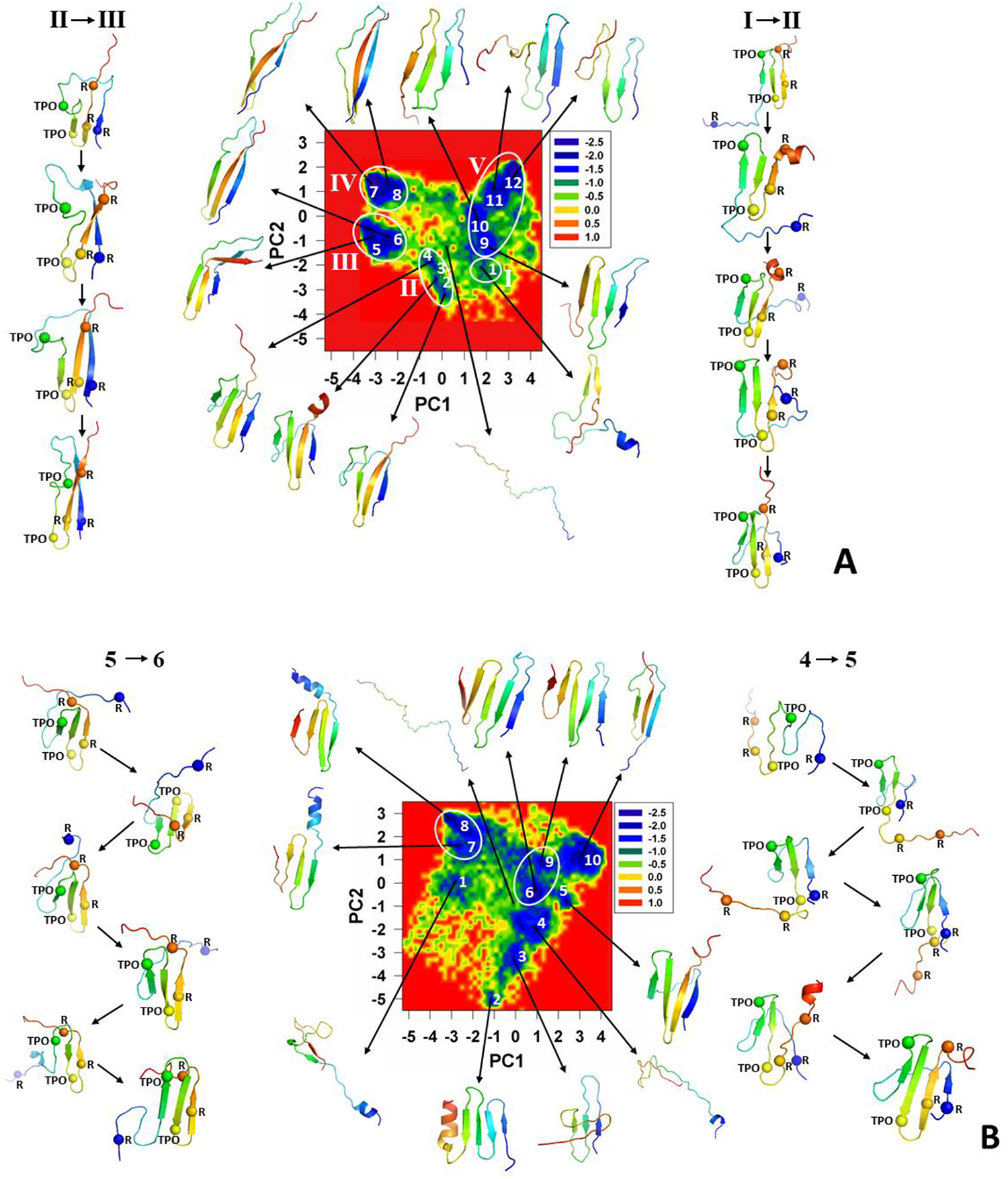
FELs (in kcal/mol) along the first two PCs with representative structures at the minima for folding trajectories of the pT37pT46 4E-BP2_18–62 at 280K (panels A and B) and for nonfolding trajectory of the WT 4E-BP2_18–62 (panel C).

We observe five major basins in the FEL of the first folding trajectory of pT37pT46 4E-BP2_18–62 (Figure 4A). Each basin contains either few minima or only a single minimum. The representative structures of the basins and transition states indicate that the folding of pT37pT46 4E-BP2_18–62 starts with formation of a β-hairpin around pT46 in the early stage of simulation (representative structure of the basin I), followed by formation of a β-hairpin around pT37 (representative structures of transition states between the basins I and II) and the first β-strand (representative structures of basin II). After spending ~32.6 ns in the folded state (minimum 4), the system starts unfolding, losing the secondary and tertiary structures of the second β-strand and β-hairpin around pT37, respectively (representative structures of transition states between the basins II and III), followed by the conversion of 3₁₀ helix and part of the loop connecting the first and second β-strands into β-strand (representative structures of the basin III), and final complete misfolding (representative structures of the basins IV and V).

The FEL of the second folding trajectory is more “entropic” (Figure 4B) and the basins are not as distinct as those in the FEL of the first trajectory. Therefore, we observed only two basins with two minima in each. At the beginning of the trajectory the protein misfolds (representative structures of the minima 2 and 3) and spends a considerable amount of time in minima 2 and 3. In order to find the correct folding pathway, the system unfolds completely (representative structure of the minimum 4) and starts folding with formation of a β-hairpin around pT37, followed by formation of the first β-strand and β-hairpin around pT46 (representative structures of transition states between the minima 4 and 5). After spending ~23.3 ns in the folded state (minimum 5), the system starts unfolding with losing the secondary structure of the first β-strand and drastically changing the position of the loop connecting the first and second β-strands (representative structures of transition states between the minima 5 and 6), followed by formation of two extra β-hairpins and final complete misfolding (representative structures of the minima 6–10).

The FEL of the nonfolding trajectory of WT 4E-BP2_18–62 (Figure 4C) exhibits four distinct minima which, based on their representative structures, can be considered as parts of one misfolded basin. The point is that the protein misfolds in the early stage of simulation (representative structure of the minimum 1) and remains in the misfolded state during the entire trajectory without showing any signs of significant conformational changes (representative structures of the minima 2–4). Consequently, the conformational space explored by the system is smaller compare to previous trajectories.

Besides the FELs, we have calculated the contributions of two main principal modes [solid lines with filled (principal mode 1) and empty (principal mode 2) circles in Figure 5] to the MSFs along the θ (Figure 5A, C, E) and γ angles (Figure 5B, D, F) and the percentages of the total fluctuations captured by the PCs (Figure 5G) for these three trajectories.^30,59,60

Figure 5.

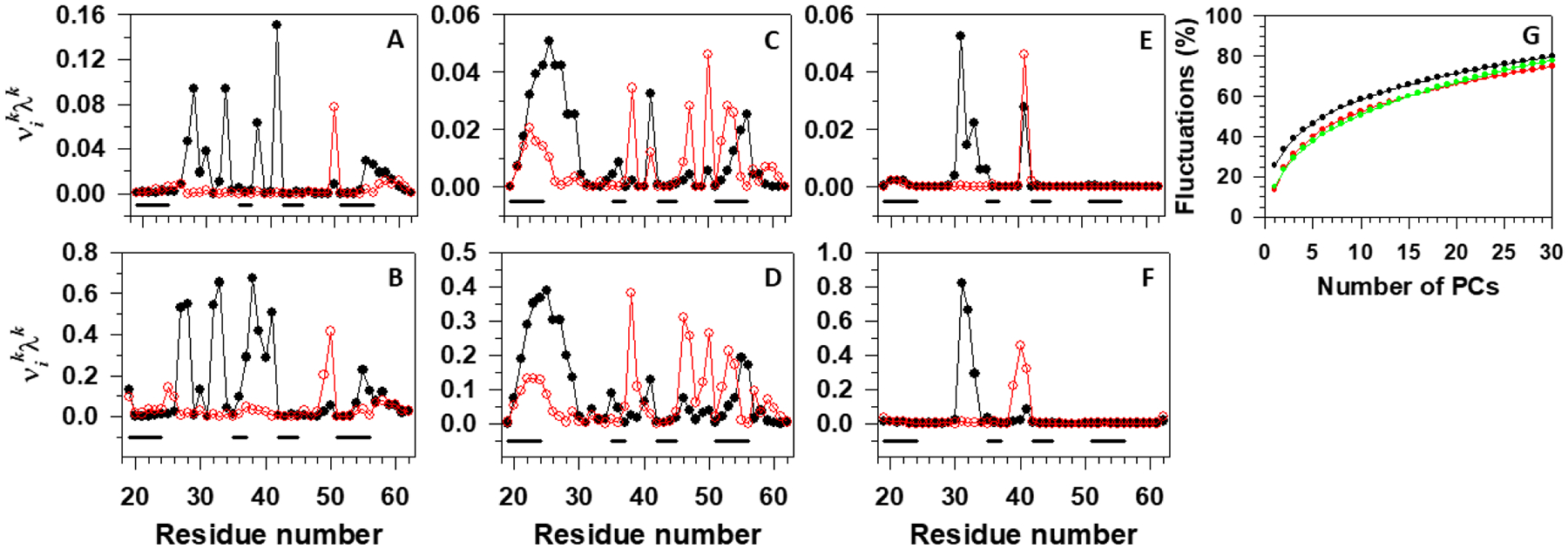
Contributions of the principal modes [${\nu }_i^k{\lambda }^k$; black lines with filled circles (principal mode 1) and red lines with empty circles (principal mode 2)] to the MSFs along the θ and γ angles for the first folding (A,B), second folding (C,D) trajectories of the pT37pT46 4E-BP2_18–62, and nonfolding (E,F) trajectory of the WT 4E-BP2_18–62. The black lines on the bottoms of panels A-F correspond to the β-strand regions. Panel G represents percentages of the total fluctuations captured by the PCs for two folding trajectories (black and red lines) of the pT37pT46 4E-BP2_18–62, and nonfolding trajectory (green line) of the WT 4E-BP2_18–62.

As was expected, the main contributions to the fluctuations in the first folding trajectory come from the first and second loops (Figure 5A, B), while almost the entire sequence contributes to the fluctuations in the second folding trajectory (Figure 5C, D). The largest portion of the protein does not fluctuate in the nonfolding trajectory, only small parts of the first and second loops contribute to the fluctuations (Figure 5E, F).

The percentage of total fluctuations captured by the first two PCs in the first folding trajectory (Figure 5G, black line) is ~35%, whereas the first two PCs in the second folding and nonfolding trajectories capture only ~25% (Figure 5G, red and green lines) of total fluctuations. We have shown previously that the FEL constructed along PCs can describe the folding dynamics correctly if these PCs can capture at least 40% of the total fluctuations.⁶¹ Therefore, here, we examined two folding trajectories in 3D and 5D PC spaces, respectively (one of them, 3D FEL of the first folding trajectory, is illustrated in Figure S1); however, we could not find any new major basins. Hence, 2D FELs are sufficient in these trajectories.

3.3. Mechanisms of Hairpin Folding and Protein Stabilization.

The representative structures of the minima and transition states in FELs (Figure 4) indicate that the interactions of phosphorylated residues with Arginine residues are crucial for folding. However, there might be other interactions, which can also play an important role in protein folding and stabilization.

In order to elucidate the mechanisms for hairpin formation and stabilization, we examined the behavior of the distances between the C^αs of selected residues, pertaining to the first and fourth, the second and third, the third and fourth β-strands, and the second and third loops (Figure 6). As we can see, ~42% of the sequence is hydrophobic, therefore, it is of interest to know what role hydrophobic interactions play in the folding and stability of the tertiary structure of pT37pT46 4E-BP2_18–62. The selected pairs of residues, shown in Figure 6, contain both hydrophobic and phosphorylated residues.

Figure 6.

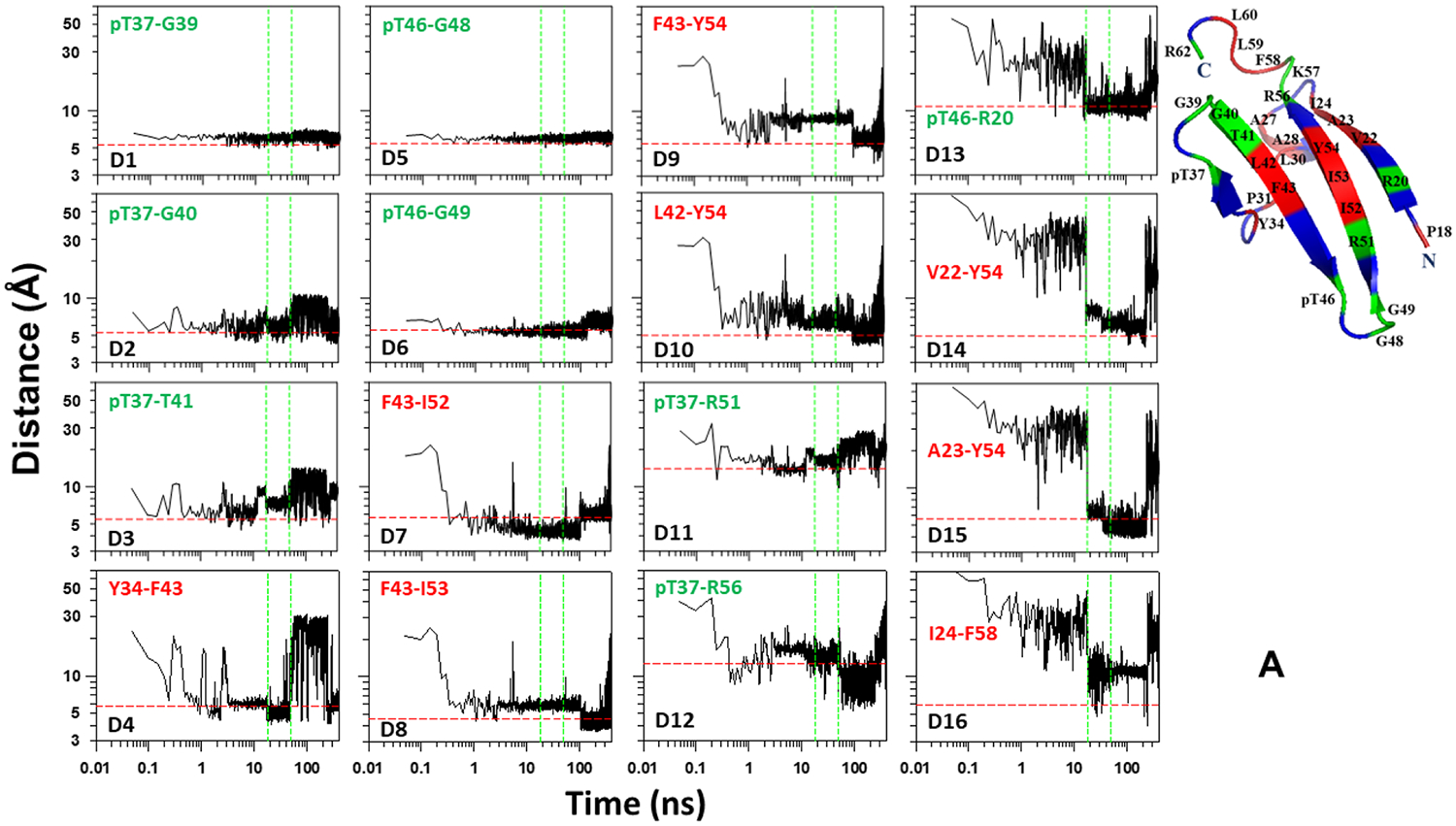
Distances between C^αs of selected pairs of residues, pertaining to the first and fourth, the second and third, the third and fourth β-strands, and the second and third loops, as functions of time for the pT37pT46 4E-BP2_18–62 (A, B) and WT 4E-BP2_18–62 (C).

The results plotted in Figure 6A correspond to the first folding trajectory. The panels D1, D2, D3, D5, and D6 of this Figure show that the distances between the phosphorylated residues, pT37 and pT46, and G39/G40/T41 and G48/G49, respectively, reach (or are very close to) the experimental distances in the early stage of simulation and remain stable (in most cases) until the last stage of the trajectory when the protein unfolds. The distances between hydrophobic pairs pertaining to the β-hairpins around pT37 (panel D4) and pT46 (panels D7, D8, D9, and D10) reach the experimental distances a bit later, however, some of them still continue to fluctuate and need some time to become stable until unfolding. The distances between the phosphorylated residues, pT37 and pT46, and Arginine residues (panels D11, D12, and D13) reach the experimental distances and keep stability either much earlier than the protein folds (panels D11 and D12) or the moment when the protein folds (panel D13). The distances between hydrophobic pairs pertaining to the first and fourth β-strands (panels D14, D15, and D16) reach the experimental distances and become stable when the protein jumps to the folded state. These results indicate that in the beginning of the trajectory the phosphorylated residues, pT37 and pT46, initiate the formation of the second and third loops and stabilize them by forming hydrogen bonds with neighboring residues G39, G40, T41 and G48, G49, respectively. Once these loops are formed the hydrophobic residues pertaining to the second, third and fourth β-strands start interacting, forming hydrophobic contacts and enforcing the formation of the β-hairpins around pT37 and pT46. Once these two β-hairpins are formed, the phosphorylated residue pT37 interacts with R51 and R56 and forms salt bridges, which give extra stability to the already-formed β-hairpins. The final step of the folding is initiated by the interaction and then formation of a salt bridge between the phosphorylated residue pT46 and R20, followed by interactions between hydrophobic residues pertaining to the first and fourth β-strands. It should be noted that, the results presented in Figure 6A also indicate that the β-hairpins around pT37 and pT46 fold through the mechanism proposed by Matheson and Scheraga,⁶² which is based on transient hydrophobic interactions and considers the nucleation process as an initial aspect of folding, converting an extended chain to a collapsed hydrophobic pocket. This model is known in the literature as a zipper model.⁶³

Unlike the first folding trajectory, only the third loop exhibits signs of formation and stabilization in the early stage of simulation in the second folding trajectory (Figure 6B). It takes some time (~2 ns) for the second loop to show some signs of formation and stabilization, however, the rest of the parts of the β-hairpins around pT37 and pT46 remain unstable until the protein jumps to the folded state. Interestingly, quite strong interactions between pT46 and R20 can be seen before the folding, followed by interactions between hydrophobic residues pertaining to the first and fourth β-strands, which result in the transient folding events of this part of the protein until the entire system jumps into the folded state.

In the nonfolding trajectory, the results of which is illustrated in Figure 6C, both the second and third loops form and stabilize in the beginning of the trajectory. The β-hairpin around T46 forms and stabilizes right after formation of loops and remains stable during almost the entire trajectory. The β-hairpin around T37 forms only transiently in the beginning of the trajectory, and T46 does not form a hydrogen bond with R20, which appears to be crucial for the first and fourth β-strands and, hence, for the entire system to misfold.

By analyzing van der Waals and average-electrostatic interactions between peptide groups, we determined the electrostatic contacts between peptide groups. Figure 7 illustrates electrostatic contacts (in percentages) formed by phosphorylated (pT37 and pT46) and non-phosphorylated (T37 and T46) residues (panels A-C), and by hydrophobic residues (panel D). As was expected, in both folding trajectories, the main electrostatic contacts formed by pT37 and pT46 are with G39 and G48, respectively. The same trend is observed in the nonfolding trajectory only for T37 and T46. The percentages of electrostatic contacts with other residues vary with trajectory. Both pT37 and pT46, in the second folding trajectory, form more electrostatic contacts with different residues than in the first folding trajectory, which can be explained by the lower stability of the system in the second folding trajectory. It should be noted that, some electrostatic contacts in both folding trajectories, such as pT37 with R56 and K57, and pT46 with R20, are not as frequent as foregoing contacts, however, they play a crucial role in the folding and stabilization of the protein by forming salt bridges. Hence, it is not surprising that the third nonfolding trajectory does not exhibit these contacts. The results illustrated in panel D indicate that all hydrophobic pairs, discussed in Figure 6, form electrostatic contacts, although the number of contacts in each pair vary with trajectories. Therefore, we can clearly see which hydrophobic pair is more responsible for the formation and stability of each β-hairpin. For example, it is clear that the F43-I52 pair is the main player in the formation and stability of the β-hairpin around pT46 in all three trajectories; while the Y34-F43 and A23-Y54 pairs are responsible for the formation and stability of the β-hairpin around pT37 and the first and fourth β-strands, respectively, in both folding trajectories. It should be noted that, there are no electrostatic contacts between A23-Y54 and V22-Y54 pairs in the nonfolding trajectory, which indicates that the first and fourth β-strands fold incorrectly.

Figure 7.

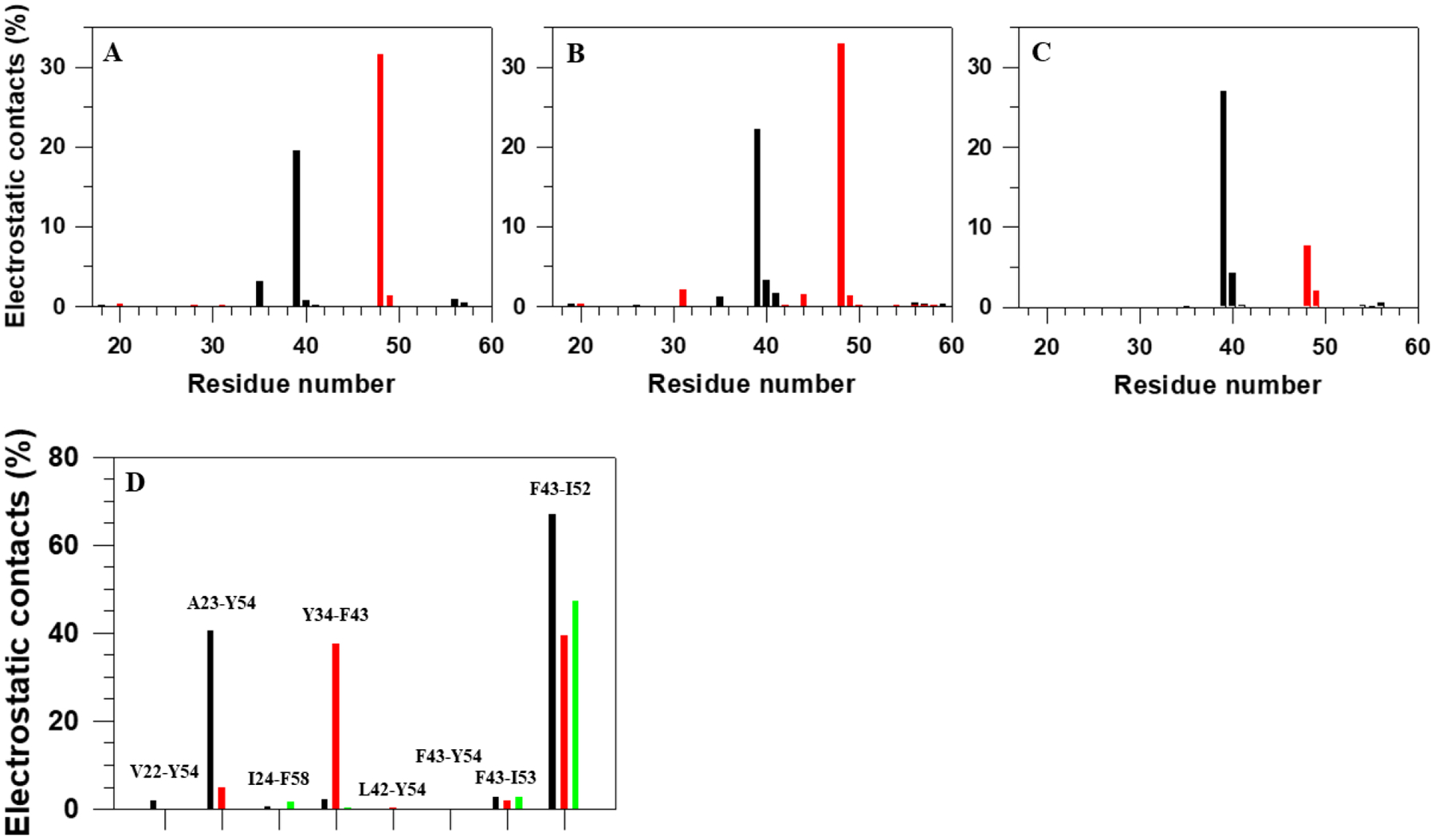
Electrostatic contacts (in percentages) formed by phosphorylated residues pT37 (black bars) and pT46 (red bars) in the first two folding trajectories of the pT37pT46 4E-BP2_18–62 (A, B), by non-phosphorylated residues T37 (black bars) and T46 (red bars) in the nonfolding trajectory of the WT 4E-BP2_18–62 (C), and by hydrophobic residues (D) in the first two folding trajectories of the pT37pT46 4E-BP2₁₈ (black and red bars, respectively) and in the nonfolding trajectory of WT 4E-BP2_18–62 (green bars).

3.4. FEPs Along θ_i and γ_i Angles of Folding/Nonfolding Trajectories.

In order to explain the origins of two different folding scenarios and nonfolding (Figure 4), we studied the local motions of each residue along the sequence. In particular, we examined the FEPs along the backbone virtual bond angle θ and backbone virtual bond dihedral angle γ of each residue (Figure 1). The quantity θ_i for residue i is the angle formed by the vectors (virtual bonds) joining three successive C^α atoms (i − 1, i, i + 1) along the primary sequence. The first angle along the sequence is θ₂ and the last is θ_N−1 in which N is the total number of residues. The quantity γ_i for residue i is the dihedral angle formed by the vectors (virtual bonds) joining four successive C^α atoms (i − 1, i, i + 1 and i + 2) along the primary sequence. The first dihedral angle along the sequence is γ₂ and the last is γ_N−2.

The FEPs along the θ_i and γ_i angles of the entire trajectory [μ(θ)=−k_BTlnP(θ), μ(γ)=−k_BTlnP(γ)] are very helpful to identify the key residues in the folding process,^23,30 the analysis of the FEPs of the entire trajectory does not provide information about the way in which each residue explores its own FEP in the course of time nor to what extent the motion of each residue is coupled to the global motion of the protein as it (i) proceeds towards its folded state, (ii) remains in the folded state, and (iii) jumps from its folded state. To answer these questions, for both selected folding trajectories, we have calculated FEPs along the θ_i and γ_i angles for certain periods of time in each trajectory: (i) before the system reaches its folded state; (ii) the system remains in the folded state; and (iii) after the system starts unfolding (see Figure 3A, B). In order to find out which residues play a crucial role in folding, we compared the FEPs of the full folding trajectories to those computed for one full nonfolding trajectory (Figure 3C).

We should mention that the FEPs introduced here are effective FEPs, which differ from the actual FEPs. Unlike the actual FEP, which is an equilibrium thermodynamic property and has to be calculated from the entire series of folding and nonfolding trajectories, the effective FEP is calculated from a non-equilibrium probability density and depends on the time period of the trajectory and on the initial conditions. Because of this, the effective FEP has proven to be an effective tool for the detailed analysis of the MD trajectories and for extraction of the reasons of protein (non)folding in a single MD trajectory.

Figure 8 illustrates the FEPs along the θ_i (panels A and C) and γ_i angles (panels B and D) computed from the above-discussed two folding trajectories. The red, green, blue and black curves correspond to the FEPs calculated over time intervals indicated in Figure 3, i.e., time from the beginning of the trajectory until the system reaches the folded state (red), time that the system spends in the folded state (green), time after jumping from the folded state until the end of the trajectory (blue), and over the entire duration of the trajectory (black). Small blue circles at the bottom of each panel in Figure 8 are the NMR-derived structural data of 2MX4.⁹

Figure 8.

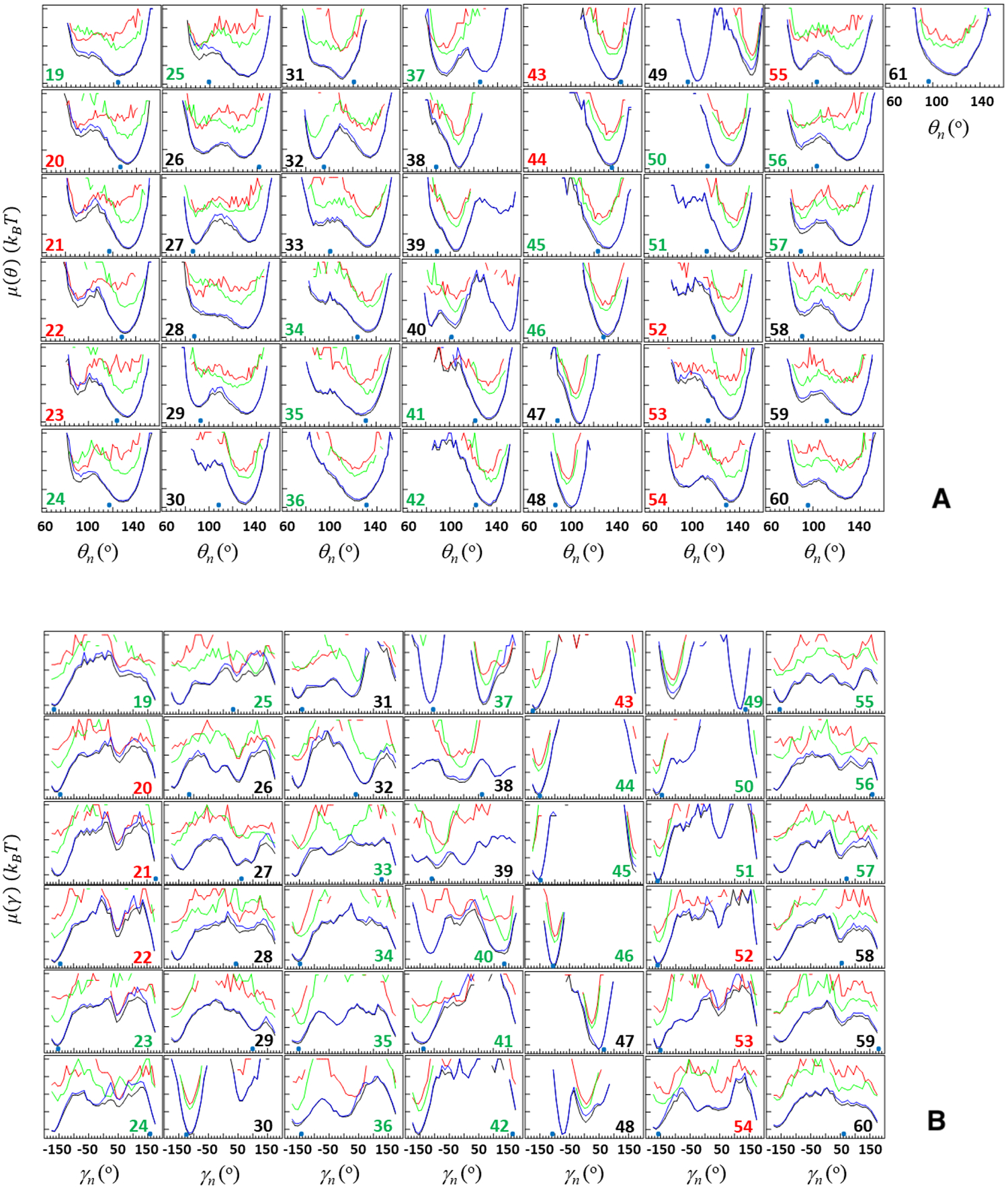
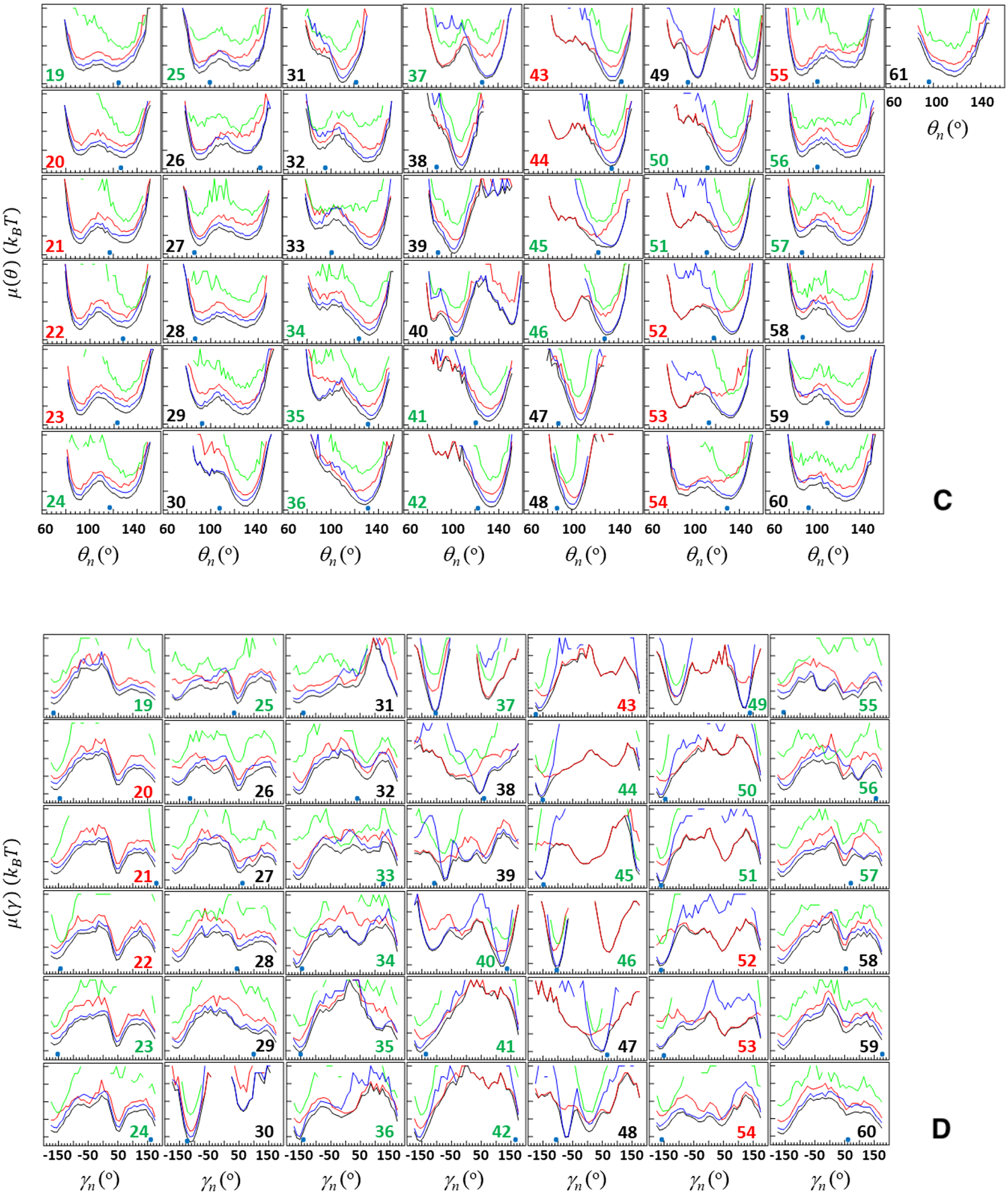
Free-energy profiles (FEPs), μ(θ) and μ(γ), along the θ and γ angles for the first folding (panels A and B, respectively) and second folding (panels C and D, respectively) MD trajectories of the pT37pT46 4E-BP2_18–62. Red, green, blue and black curves correspond to FEPs computed over the following time intervals: time from the beginning of the trajectory until the system reaches the folded state (red), time that the system spends in the folded state (green), time after jumping from the folded state until the end of the trajectory (blue), and over the entire MD trajectories (black). The black numbers pertain to FEPs along the θ and γ angles which include only residues of the loops and ends; the red numbers pertain to FEPs along the θ and γ angles which include only residues of β-strands; the green numbers pertain to FEPs along θ and γ angles which include the residues from both loop and β-strands (and 3₁₀ helix) or from both ends and β-strands. The NMR-derived structural data (small blue circles at the bottom of each panel) are computed from the first model of the PDB ID code 2MX4.⁹

By comparing the FEPs along all of the θ and γ angles of these trajectories at the first stage (red curves in Figure 8), we found the causes of the protein’s fast (panels A and B) and slow folding (panels C and D). As was expected, most of the angles in the slow-folding trajectory explore much larger regions of angle space than ones in the fast-folding trajectory. In particular, in the slow-folding trajectory the θ and γ angles not only explore the local minimum but also spend some time (less than in the local minimum for θ_i and γ_i, i = 26, 28, 29, 32, 33, 37, 49, 52 – 54, 57, 58, 60; almost equal to the local minimum for θ_i and γ_i, i = 19 – 25, 46, 51, 56; and more than in the local minimum for θ_i and γ_i, i = 27, 30, 31, 34 – 36, 39 – 45, 50, 55, 59) in the global minimum. In the fast-folding trajectory, both θ_i and γ_i angles also explore both local and global minima, however, in most cases these minima are very shallow and for some angles one of the minima just disappears (θ_i and γ_i, i = 32 – 34, 37, 42 – 46, 49 – 52). These results indicate that key players in the slowing down of the folding process are residues pertaining to the first loop (i = 32 – 34), third β-strand (i = 42 – 45), fourth β-strand (i = 49 – 52), and phosphorylated residues (i = 37, 46).

Once the protein jumps into the folded state, in both folding trajectories, as was expected, a majority of the angles pertaining to β-strands starts exploring the global minimum and staying there until the protein jumps out from the folded state; however, some angles pertaining to the loops and edges either partially or barely explore the global minimum (see green curves in Figure 8). Based on these results, we can conclude that the protein may not be fully stable in its folded state, therefore, it is not surprising that it jumps out from the folded state after some time and starts unfolding. This finding is supported by earlier experiments,^9,13 in which the weak stability of the folded state of the pT37pT46 4E-BP2_18–62 was observed.

After jumping out from the folded state, almost all angles either continue to explore the global minimum and then start exploration of new (or old) local minima or vice versa. (see blue curves in Figure 8).

Figure 9 illustrates the FEPs of two full folding trajectories (black and red curves) and one full nonfolding trajectory (green curves). Based on these results, the main differences between the FEPs of folding and nonfolding trajectories, which may cause nonfolding, are observed along the angles pertaining to the first loop (θ_i and γ_i, i = 27 – 29) and the edge of fourth β-strand (θ_i and γ_i, i = 57). It should be noted that, the FEPs of the nonfolding trajectory differ from the FEPs of the folding trajectories along other angles, as well, pertaining to the third loop, fourth β-strand, and the edge of fourth β-strand (θ_i and γ_i, i = 49, 51 – 56). However, these angles in the nonfolding trajectory remain in the global minimum during the entire trajectory and do not explore local minima, and consequently cannot participate in the nonfolding of the protein.

Figure 9.

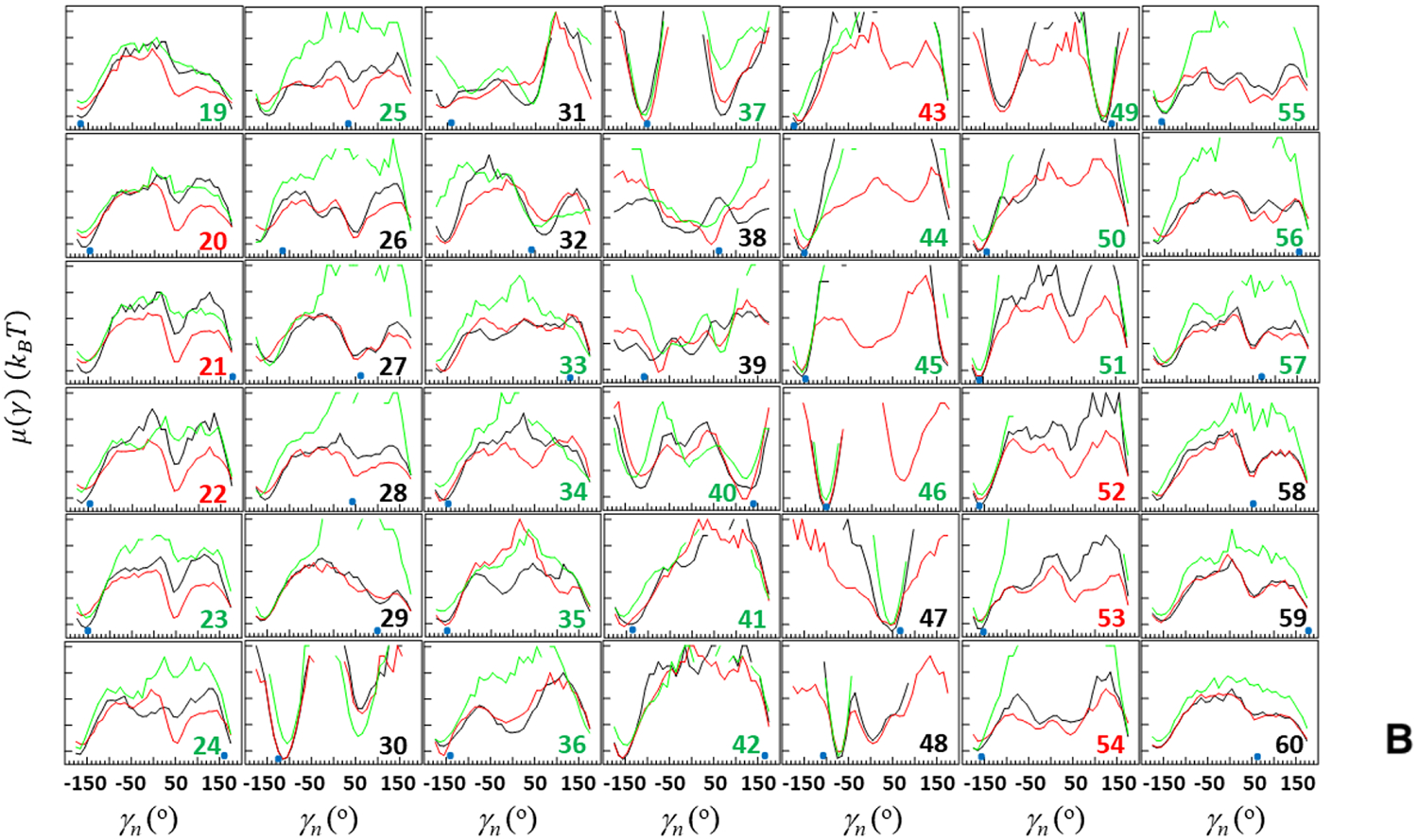
FEPs, μ(θ) and μ(γ), along the θ (A) and γ (B) angles for two folding trajectories of the pT37pT46 4E-BP2_18–62 (black and red curves, respectively) and one nonfolding trajectory of the WT 4E-BP2_18–62 (green curves). The black numbers pertain to FEPs along the θ and γ angles which include only residues of the loops and ends; the red numbers pertain to FEPs along the θ and γ angles which include only residues of β-strands; the green numbers pertain to FEPs along θ and γ angles which include the residues from both loop and β-strands (and 3₁₀ helix) or from both ends and β-strands. The NMR-derived structural data (small blue circles at the bottom of each panel) are computed from the first model of the PDB ID code 2MX4.⁹

The results presented in Figures 5 and 9 illustrate a clear correlation between the FEPs along the θ and γ angles and the contributions of the principal modes to the MSF. In particular, the θ and γ, along which the FEPs exhibit one or more local minima (Figure 9), have peaks in the plots of the principal modes, which is unsurprising, because an existence of local minima on an FEP is a manifestation of jumps that the angles make, back and forth, between the global and local minima; consequently, these angles contribute to the MSF. Contributions to the MSF increase with the deepness of local minima. Therefore, the principal modes of the nonfolding trajectory, which misfolds very fast and stays in the misfolded state until the end of the trajectory, have the least number of peaks (it should be noted that, the nonfolding protein is WT 4E-BP2_18–62, which is an IDP, however, here in order to find out which residues play a crucial role in folding, we compare the FEPs of the folding trajectories of the pT37pT46 4E-BP2_18–62 and the nonfolding trajectory of the WT 4E-BP2_18–62, and consider the NMR structure with PDB ID 2MX4⁹ as the folded structure for both systems). Because the FEPs and principal modes are correlated, we can conclude that the FEPs (Figure 9) and FELs (Figure 4) are correlated, as well. In other words, the local minima on the FEPs and FELs are correlated to each other.

3.5. Investigation of the experimental structure of the pT37pT46 4E-BP2_18–62 in terms of kinks.

The investigation of kinks is more straightforwardly understood from a differential representation of the protein backbone. Indeed, the angle θ_i is directly related to the local curvature κ_i (κ = π − θ) of the protein backbone whereas the angle γ_i is the local torsion of the backbone (see Figure 1 and Kink and Protein Backbone Geometry in the SI). Assuming constant virtual bond distances between the C^α atoms, the free-energy of the polymer can be written in terms of (κ,γ) internal coordinates using a Landau-Ginzburg-Wilson free-energy model^32–45 [Eq. (S11) in the SI]. Minimizing this free-energy relative to κ and γ lead to a nonlinear equation of motion for the curvature similar to a generalized DNLS which admits kinks as particular solutions [Eqs. (S13) and (S14) in the SI].

In earlier studies,^32–45 the modular building blocks of folded proteins, i.e. super-secondary structure such as a helix-loop-helix or strand-loop-strand motif, were described in terms of the kink of a generalized version of the DNLS equation. It has been found that the formation of a kink is initiated by an abrupt change in the orientation of a pair of consecutive side chains in the loop region.⁴⁰ It was demonstrated that in order to obtain a clear picture of kink formation it is necessary to start MD simulations from the full α-helical or β-strand structure and study the dynamics of the formation of loops, otherwise it would be blurred by α-helix or β-strand formation.⁴⁰ Moreover, kink analysis allowed us to realize the importance of local interactions, specifically the bimodal character of the potential of mean force in virtual-bond angles κ, as the driving force of folding.⁴⁰ It should be noted that the only long-range interaction present in the Landau-Ginzburg-Wilson Hamiltonian^32–45 is a step-wise Pauli exclusion that introduces self-avoidance and prevents chain crossing. The effects of the long-range Coulomb and Van der Waals interactions are accounted for by the global multi-kink profile resulting from the minimization of free energy.⁴² The multi-kink structure describes both local and collective motions. Previously, it was illustrated that by using kink parameters that are derived from the experimental folded protein structure, its folding can be simulated,^{37,38,39,41,43,44} as well as without MD simulations the kinks are able to capture the sites of the protein that govern the system to change the folding scenario.⁴⁵ Moreover, phase diagram of the protein with temperature (T) and acidity (pH) as the thermodynamic variables can be constructed.⁴⁴ Therefore, it is of interest to investigate whether a kink analysis of the experimental structure⁹ can uncover the mechanisms, which govern the pT37pT46 4E-BP2_18–62 to fold.

In this study, we carried out a detailed analysis of the experimental structures of the pT37pT46 4E-BP2_18–62 in terms of kinks. Using experimental values of the κ and γ angles, we started resolving the kink structures of the pT37pT46 4E-BP2_18–62. The multi-kink is a configuration that minimizes free energy [Eq. (S11) in the SI], with an acceptable³⁶ small deviation, RMSD, from the three-dimensional experimental structure. Minimum energy, as well as RMSD fitting, is achieved using a combination of simulated annealing and gradient descent methods. Multi-kink structures that are combinations of 7 individual kinks, differing in the arrangement along the protein chain, were obtained for the system. With RMSD < 1.0 Å, a total of 117 structures were initially obtained for the pT37pT46 4E-BP2_18–62. Three representative structures (with RMSD = 0.78; 0.82; 0.81 Å) were then selected for a detailed analysis. Figure 10 illustrates comparison of the κ and γ angles, experimental and calculated, along the chains of three selected structures of the pT37pT46 4E-BP2_18–62. In addition, Figures 11 shows experimental values of the κ and γ angles in the first panel, and most representative kink structures in the three remaining panels. Data on this figure enable us to examine the correlations between the location of kinks and folding paths. [The experimental and three computed representative structures for the pT37pT46 4E-BP2_18–62 are shown in Figure S2].

Figure 10.

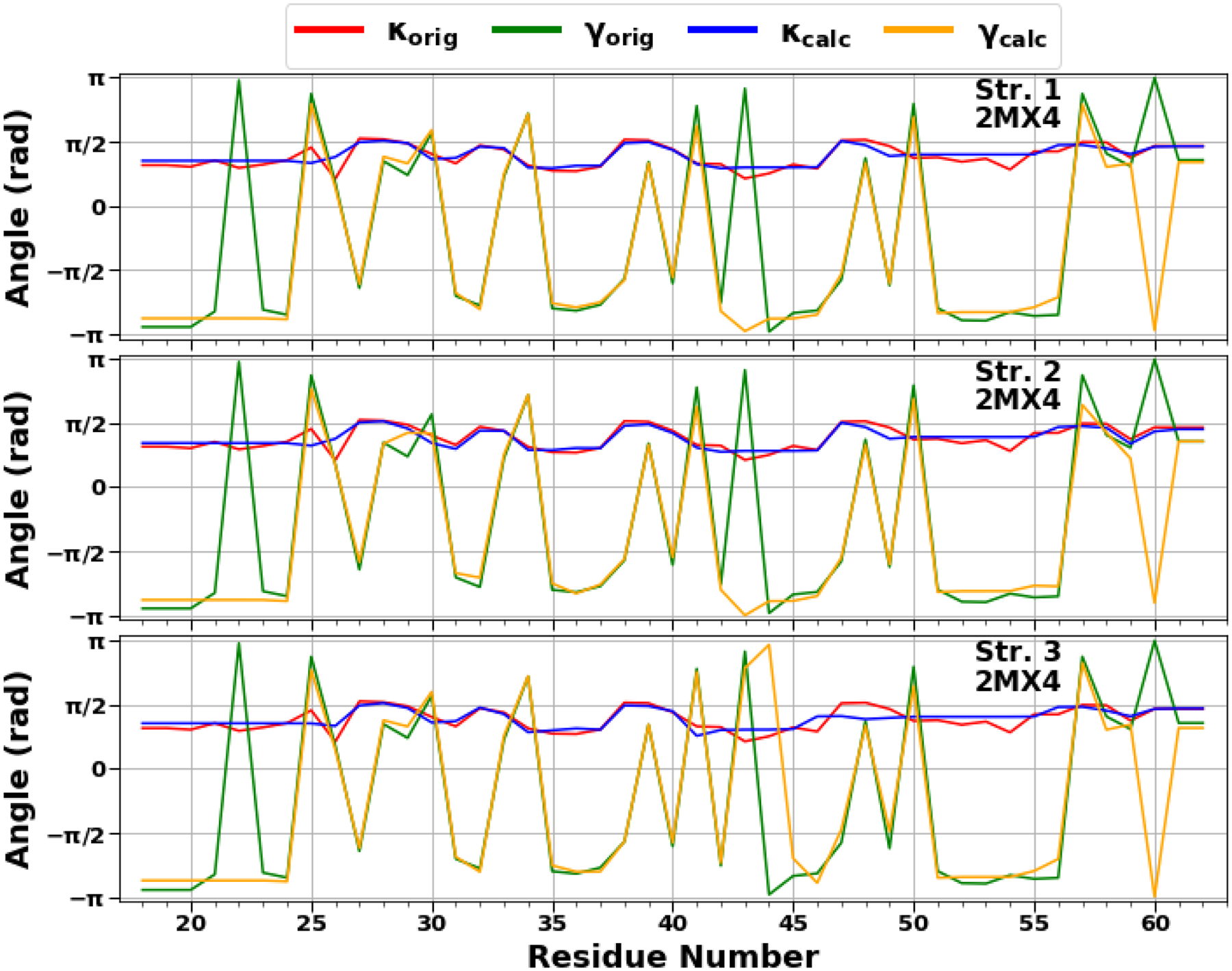
The comparison of experimental and calculated angle spectra of three selected structures for the pT37pT46 4E-BP2_18–62 in terms of virtual-bond κ_i (experimental-red, calculated-blue) and torsion γ_i (experimental-green, calculated-yellow) values.

Figure 11.

Top panel represents experimental values of the virtual-bond κ_i (red) and torsion γ_i (blue) angle spectra of the pT37pT46 4E-BP2_18–62. Remaining three panels illustrate kink structures, i.e., the virtual-bond κ (red) and torsion γ_i (green) angle spectra for three selected structures of the pT37pT46 4E-BP2_18–62, after ℤ₂ gauge transformation (eq. S8 in the SI) was made. Blue circles represent centers of kinks, purple rhombuses represent the right edges of left kinks.

The kink locations along almost the entire sequence of the pT37pT46 4E-BP2_18–62 in all three structures are changing, only the centers of the 4^th (at 37^th residue) and 6^th (at 48^th residue) kinks are the same (Figure 11), which indicates a weak stability of the system except for the parts where phosphorylated residues are located. These findings are in harmony with the experiment.⁹ It should be noted that the 6^th kink has a center at the 48^th residue in all 88 structures with RMSD < 0.9 Å. Only 6 structures out of 117 have a center of the 6^th kink at 50^th residue.

We scrutinized the stability of the pT37pT46 4E-BP2_18–62 by simulating heating and cooling (unfolding and folding) trajectories using the Glauber algorithm.⁴⁴ The heating/cooling maps for three calculated structures of protein, plotted in Figure 12 (A–C), show the system’s (dis)ordering during a heating and cooling simulation cycle as a function of temperature in terms of the average value of torsion angles γ. The first part of the maps (from the beginning up to log₁₀T_G ≈ −8) corresponds to the thermal unfolding, the middle part of the maps (from log₁₀T_G ≈ −8 to log₁₀T_G ≈ −8) is the random walk phase, and the last part of the maps (from log₁₀T_G ≈ −8 to the end) corresponds to folding due to protein cooling. The radius of gyrations (R_G) of three calculated structures as functions of Glauber temperature are plotted in panel D of Figure 12. Based on these maps, the behavior of the first two calculated structures is quite similar. All four β-strands along with phosphorylated sites of these two structures correctly react to heating/cooling process, i.e., γ angles pertaining to β-strands and phosphorylated sites change during thermal unfolding, remain stable in the random walk phase, and return to initial values with cooling. Among four β-strands the third one is the most sensitive to the heating process by starting to unfold at log₁₀T_G ≈ −14, while others start unfolding at log₁₀T_G ≈ −10. Half of the γ angles pertaining to the loops have the same reaction to the heating/cooling process as β-strands, and the other half of the γ angles remain unchanged during the entire heating/cooling process. The behavior of the third calculated structure is quite different (panel C), which can be considered thermally unstable. Only the first and fourth β-strands react correctly to the heating/cooling process and, surprisingly, the γ₃₈ angle jumps to a local minimum in the beginning of the trajectory and never goes back to the global minimum. The R_G vs Glauber temperature plots (panel D) reflect the differences found in the heating/cooling maps. The R_G plots corresponding the first two calculated structures are very similar to each other showing an apparent folding intermediate at log₁₀T_G ≈ −12, which is a result of the fast disorder of the third β-strand at log₁₀T_G ≈ −14. Because of the instability of the third structure, the R_G of this structure is higher than ones for the first two calculated structures by ~ 2Å from the beginning of the trajectory up to log₁₀T_G ≈ −14 and from log₁₀T_G ≈ −14 to the end of the trajectory. The differences in these regions of the temperature can be explained as follows: the γ₃₈ angle in the third structure unfolds in the beginning of the trajectory and remains unfolded during the entire trajectory, whereas the first two structures start unfolding only at log₁₀T_G ≈ −14 (the third β-strand) and remain unfolded until log₁₀T_G ≈ −14 (panels A, B), consequently they are folded in the log₁₀T_G ≈ −18 − log₁₀T_G ≈ −14 and log₁₀T_G ≈ −14 − log₁₀T_G ≈ −18 temperature regions.

Figure 12.

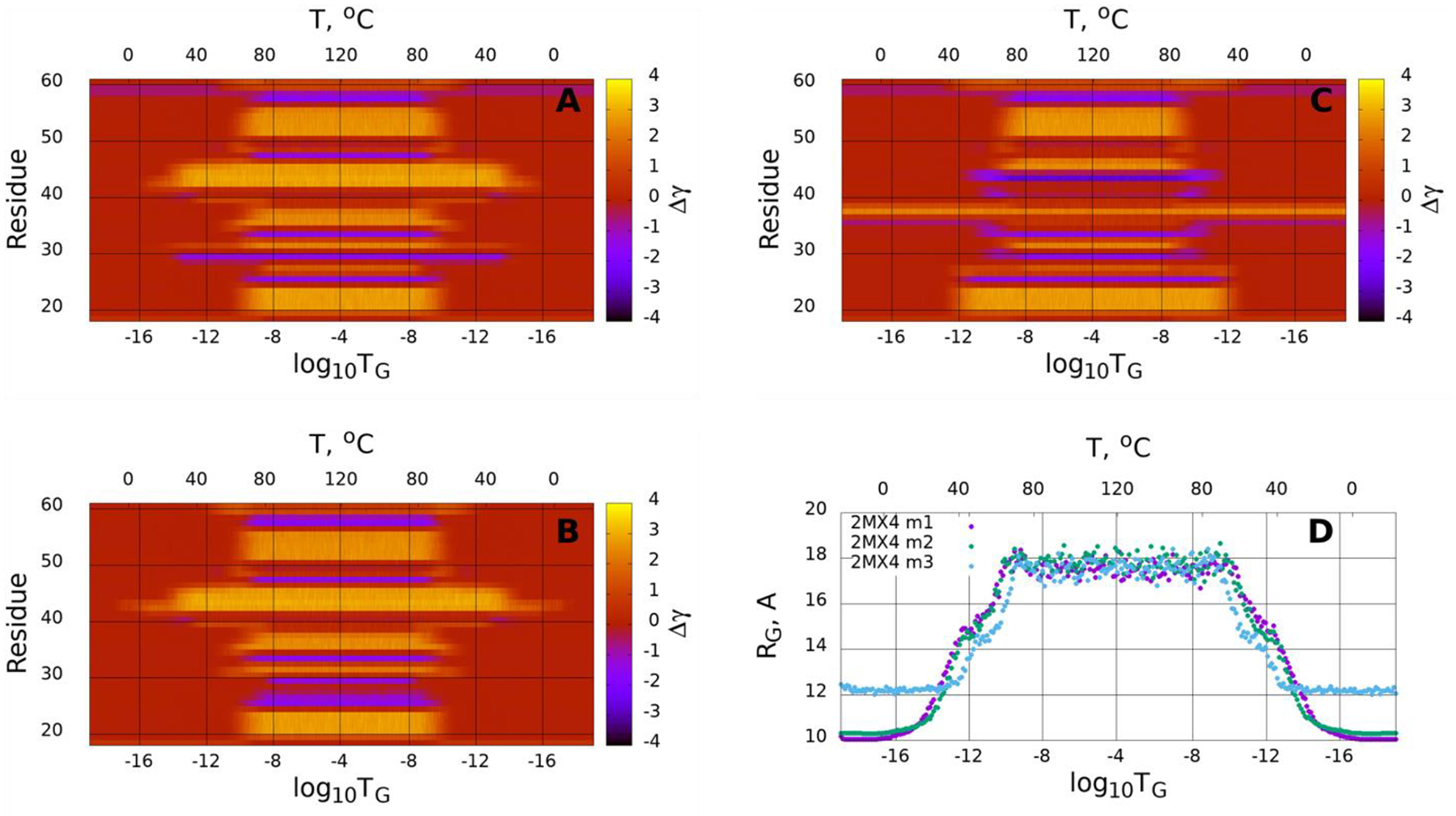
(Dis)ordering during a heating and cooling simulation cycle as a function of Glauber temperature in terms of the average value of torsion angles γ for three selected structures of the pT37pT46 4E-BP2_18–62 (A-C), and the radius of gyrations of three selected structures as functions of Glauber temperature (D).

In order to find out the reason for the unusual behavior of the third calculated structure, we examined carefully the structural differences between the calculated and experimental structures by superimposing calculated and experimental structures (Figure S2) and by computing the differences between the κ and γ angles of the calculated and experimental structures (Figure S3). Although all three structures have very small RMSD values, the 2^nd and 3^rd β-strands, in the third calculated structure, are shifted from experimental ones (row C in Figure S2), while they are nicely superimposed in the first two calculated structures (rows A and B in Figure S2). Also, the loop connecting the second and third β-strands is slightly distorted in the third structure. The differences between the κ and γ angles of calculated and experimental structures (Figure S3) reveals that the main discrepancies between the third calculated and experimental structures are in the vicinity of the second phosphorylated site, while the same region in the first two calculated structures does not exhibit a big difference. It should be noted that, the foregoing differences may not be very influential on the stability of the regular folded proteins, however, it might be critical for the weakly stable protein pT37pT46 4E-BP2_18–62, especially when the differences occur in the vicinities of the phosphorylated sites.

Figure 13 displays the accumulation of the folding index⁴⁰ [Eqs. (S18, S19) in the SI] along the trajectory for the pT37pT46 4E-BP2_18–62 (A), together with the folding index dependence on length of proteins (B). We can see that the folding index captures successfully not only the phosphorylated sites of the system (two main peaks on the graph) but also the locations of kink centers (minima and maxima on the graph) within an accuracy of one residue. The existence of the peaks in the vicinity of phosphorylated residues indicates the stability of those sites.

Figure 13.

The folding index trajectories for the pT37pT46 4E-BP2_18–62 (A), and the folding index for the pT37pT46 4E-BP2_18–62 (B).

4. Conclusions

By analyzing the MD trajectories of the pT37pT46 4E-BP2_18–62 and WT 4E-BP2, generated with the coarse-grained UNRES force field, in terms of the local and global motions, the electrostatic contacts between peptide groups, and the distances between C^αs of selected pairs of residues over time, we studied the folding mechanisms of the intrinsically disordered protein and made the following findings:

1. The pT37pT46 4E-BP2_18–62 can fold through two different folding pathways with a different order of formation of the hairpins.

2. Four major steps are identified in the folding pathway: the first, the phosphorylated residues, pT37 and pT46, initiate the formation of the second and third loops and stabilize them by forming hydrogen bonds with neighboring residues; the second, after formation of the loops, the hydrophobic residues pertaining to the second, third and fourth β-strands start interacting, forming hydrophobic contacts and enforcing the formation of the β-hairpins around pT37 and pT46; the third, once these two β-hairpins are formed, the phosphorylated residue pT37 interacts with R51 and R56 and forms salt bridges, which give extra stability to the already-formed β-hairpins; and the final fourth step of the folding is initiated by the interaction and then formation of a salt bridge between the phosphorylated residue pT46 and R20, followed by interactions between hydrophobic residues pertaining to the first and fourth β-strands.

3. The local and global motions are correlated in protein folding trajectories.

Finally, the experimental structure of the pT37pT46 4E-BP2_18–62 was analyzed in terms of kinks. It was found that without MD simulations the kinks are able to capture the sites of the protein that govern the folding and cause a weak stability of the pT37pT46 4E-BP2_18–62, which further confirms the essential role of the phosphorylated residues.