Transfer Learning in Medical Image Segmentation: New Insights from Analysis of the Dynamics of Model Parameters and Learned Representations

Abstract

We present a critical assessment of the role of transfer learning in training fully convolutional networks (FCNs) for medical image segmentation. We first show that although transfer learning reduces the training time on the target task, improvements in segmentation accuracy are highly task/data-dependent. Large improvements are observed only when the segmentation task is more challenging and the target training data is smaller. We shed light on these observations by investigating the impact of transfer learning on the evolution of model parameters and learned representations. We observe that convolutional filters change little during training and still look random at convergence. We further show that quite accurate FCNs can be built by freezing the encoder section of the network at random values and only training the decoder section. At least for medical image segmentation, this finding challenges the common belief that the encoder section needs to learn data/task-specific representations. We examine the evolution of FCN representations to gain a deeper insight into the effects of transfer learning on the training dynamics. Our analysis shows that although FCNs trained via transfer learning learn different representations than FCNs trained with random initialization, the variability among FCNs trained via transfer learning can be as high as that among FCNs trained with random initialization. Moreover, feature reuse is not restricted to the early encoder layers; rather, it can be more significant in deeper layers. These findings offer new insights and suggest alternative ways of training FCNs for medical image segmentation.

1. Introduction

1.1. Background and motivation

Deep learning has made a significant impact in the field of medical image analysis. For semantic segmentation, fully convolutional neural networks (FCNs) have shown to be powerful models. Many studies have shown that deep learning methods achieve more accurate segmentations than alternative segmentation methods [3] [5] [27] [32] [61]. Commonly, FCNs are trained in a supervised manner, i.e., by minimizing some loss function that penalizes the disagreement between the ground truth and predicted segmentations on a set of labeled training images. In medical applications, obtaining ground truth labels is challenging because it requires detailed annotation of large 3D images by domain experts. To address this challenge, a wide range of techniques have been proposed. Some of the main categories of these methods include semi-supervised learning, transfer learning, learning from noisy labels, and learning from computer-generated labels. Recent reviews of these methods for medical image analysis can be found in [28, 11, 51]. The focus of this study is on transfer learning.

Transfer learning refers to any learning strategy that uses the knowledge gained in solving one problem, Problem S, in subsequently solving a separate problem, Problem T. Transfer learning is related to other training strategies such as multi-task learning. In order to distinguish transfer learning from related training strategies such as multi-task learning, it is assumed that Problem T is addressed separately after Problem S [47, 41]. A formal definition can be found in [41]. According to this formal definition, transfer learning involves the concepts of domain and task. A domain $\mathcal{D}$ is defined by a feature space $\mathcal{X}$ and a probability distribution P(X) defined over $\mathcal{X}$. A task $\mathcal{T}$, on the other hand, is defined by a label space $\mathcal{Y}$ and a prediction function f(x) = P(y|x) for x ∈ X and y ∈ Y. Now, consider a source domain and task $\left({\mathcal{D}}_S,{\mathcal{T}}_S\right)$ and a target domain and task $\left({\mathcal{D}}_T,{\mathcal{T}}_T\right)$, where either $D_S\ne {\mathcal{D}}_T$ and/or ${\mathcal{T}}_S\ne {\mathcal{T}}_T$. Transfer learning aims at learning f_S, and subsequently learning f_T by utilizing the knowledge gained in learning f_S. Whereas the above is a formal description of transfer learning, its implementation in practical applications can take many different forms, depending on what kind of information is transferred and how it is utilized in learning f_T [16, 41].

Transfer learning, in its various manifestations, has been widely employed in training deep learning models. Some of the notable examples include studies that aim at learning deep representations that can be re-purposed for other tasks [60, 14], Deep Adaptation Networks for domain adaptation [36], and few/zero-shot learning [62, 59]. However, for vision applications, the most widely used approach is to pre-train a model on a source domain/task and then fine-tune that same model on the target domain/task [18]. In this approach, the knowledge that is transferred from the source to the target problem is in the form of the values of the network parameters.

Transfer learning has also been used in training deep learning models for various medical image analysis applications [11, 51]. However, for segmentation, which is the focus of this work, most of the previous studies have only reported segmentation accuracy measures, without investigating how transfer learning takes place and in what ways the models learned with and without transfer learning differ. This paper aims at filling this gap by presenting a more comprehensive and more in-depth assessment of the effect of transfer learning for FCN-based medical image segmentation.

1.2. Related works

Many studies in recent years have used transfer learning for medical image segmentation. Recent reviews of these studies can be found in [11, 51]. Here we briefly review some typical examples. In fact, the way the segmentation problem is formulated and the approach used for transfer learning vary greatly between these studies, making some of them less relevant to our work. As an example, one study used transfer learning for segmentation of carotid intima-media boundary and found that transfer learning with a model pre-trained on natural images was useful [52]. However, they formulated the segmentation problem as a pixel-wise classification task and used a (non-FCN) classification network architecture. Such studies are not directly relevant to our work, which focuses on FCN segmentation models.

One study found that a model trained for liver and kidney segmentation on a dataset of 35 MR images performed very poorly when applied on a second dataset of 45 images, even though the main difference between the two datasets were image size and resolution [54]. The authors found that fine-tuning the model trained on the first dataset for the segmentation on the second dataset performed equally with training a model from scratch. They proposed using Reverse Classification Accuracy, [53], to select the most useful images for annotation in the target domain and showed that with this strategy, using as few as five images in the target domain was sufficient to match the accuracy obtained with all 45 images, both with fine-tuning and with training from scratch.

For brain white matter hyperintensity segmentation in MRI, one study evaluated the effect of transfer learning when source and target domains differed in terms of acquisition protocol [17]. Compared with training from scratch, transfer learning achieved better results. As the number of training images in the target domain decreased, achieving good performance with transfer learning required limiting the fine-tuning to the top two layers. Similar observations were reported for multiple sclerosis lesion segmentation in multisite datasets in [55].

A transfer learning method for cross-modality domain adaptation was proposed in [15] and successfully applied for segmentation of cardiac CT images using models pre-trained on MR images. The method included a domain adaptation module, based on adversarial training, to map the target data to the source data in feature space. A GAN-based method for mapping the target images to the appearance of source images was proposed in [8]. This method also showed promising results on the segmentation of cross-site chest X-ray datasets.

Even though the studies reviewed above present useful knowledge regarding the effectiveness of transfer learning for medical image segmentation, they are all limited to a single dataset or application. Furthermore, they all lack any analysis of the role of transfer learning beyond the gross segmentation accuracy values. One recent paper reported an in-depth study of transfer learning for medical image analysis [46]. However, that study was limited to 2D images and examined transfer learning with models pre-trained on natural images, which is not relevant for 3D medical images. Moreover, that study was dedicated to classification tasks, whereas the work presented in this paper focuses on voxel-wise semantic segmentation.

1.3. Contributions of this work

The main contributions of this work include:

• We experimentally assess the impact of transfer learning in training FCNs for medical image segmentation. The difference between source and target domains in our experiments spans a wide range of important factors including image modality, organ of interest, image quality, and subject age. We show that although transfer learning reduces the training time on the target task, the improvement in segmentation accuracy is highly task/data-dependent and often very marginal.

• To shed light on our experimental observations, we carry out a detailed analysis of the dynamics of model parameters and learned representations during training. We show that the representations learned by the encoder section of the model do not change significantly from their randomly- initialized or pre-trained values during training/fine-tuning. Furthermore, we show that the filters of the encoder section of the converged models look random. We explain this behavior by arguing that the responses of such random filters are similar to useful operations such as edge detectors.

• We further show that it is possible to freeze the filters of the encoder section of the model at their initial random state and train only the decoder section. We show that this training strategy leads to very small or no loss of test accuracy, and may speed up the convergence too.

• We analyze FCN representations to gain a deeper understanding of the effects of transfer learning on these models. Our analysis shows that there is substantial variability among the converged models in terms of learned representations throughout the network. In this regard, models trained with transfer learning can be as diverse as models trained from scratch. Moreover, we show that feature reuse is not restricted to the early layers; rather, it can be even more significant in deeper layers, suggesting viable alternative approaches to model fine-tuning on the target task.

2. Materials and Methods

2.1. Data

Table 1 summarizes the information about the datasets used in this work. For all experiments with any of these datasets, we used 70% of the images for training and validation and the remaining 30% for test. Our data pre-processing included: 1) resampling images and segmentations for each dataset to an isotropic voxel size; depending on the original voxel spacing of the images in a dataset, the re-sampled voxel size ranged from 0.8 mm to 2.0 mm, 2) intensity normalization: Computed Tomography (CT) images were normalized by linearly mapping the Hounsfield Unit values in the range [−1000, 1000] to intensity range [0, 1], whereas Magnetic Resonance (MR) images were normalized by dividing each image by the standard deviation of its voxel intensities.

Table 1.

Summary of the information on the datasets used in this study. The first column shows the names that we use to refer to each dataset throughout the paper. CP stands for brain cortical plate.

name	modality	organ	data size	source
CP- younger fetus	T2 MRI	brain cortical plate	27	In-house (Boston Children’s Hospital)
CP- older fetus	T2 MRI	brain cortical plate	15	In-house (Boston Children’s Hospital)
CP- newborn	T2 MRI	brain cortical plate	558	[4]
KiTS	CT	kidney	300	[22]
LiTS	CT	liver	130	[6]
Liver-CT	CT	liver	19	[21]
Spleen	CT	spleen	41	https://decathlon-10.grand-challenge.org/
Pancreas	CT	pancreas	281	https://decathlon-10.grand-challenge.org/
Prostate	MRI	prostate	32	https://decathlon-10.grand-challenge.org/
Hippocampus	MRI	hippocampus	260	https://decathlon-10.grand-challenge.org/
BRATS	MRI	brain tumor	484	https://decathlon-10.grand-challenge.org/
TSC	MRI	Tuberous sclerosis complex lesions	165	In-house (Boston Children’s Hospital)
Liver-MRI-SPIR	MRI	liver	20	[33]
Liver-MRI-DUAL-in	MRI	liver	20	[33]
Liver-MRI-DUAL-out	MRI	liver	20	[33]
Whole-Brain-MRI	MRI	brain	2500	In-house (Boston Children’s Hospital)

2.2. Network architecture and training details

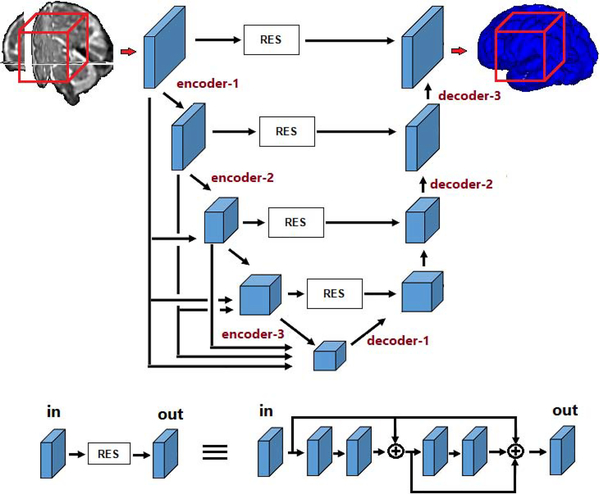
Figure 1 shows the main network architecture used in this study. The overall architecture is similar to the 3D U-Net and V-Net [12, 38], with additional connections between different feature maps in the encoder section of the network. Such connections have been recently shown to improve the segmentation accuracy in natural image segmentation. The model accepts 96³-voxel image blocks as input, which are sampled from random image locations during training. The number of feature maps in the first stage of the network was set to 14, which was the largest number of feature maps possible on the memory of our GPU. In the encoder section, the number of these feature maps increase in each stage by factors of 2; i.e., the number of feature maps in the subsequent encoder layers are 28, 56, 112, and 224. At the same time, the size of the feature maps decrease by factors of 2; that is the size of feature maps in the subsequent encoder layer are 48³, 24³, 12³, and 6³. The reverse takes place in the decoder section, where the feature maps increase in size while the number of feature maps decrease, again by factors of 2. The feature maps computed in each stage of the encoder go through a residual block with short and long skip connections (as shown in the lower part of Figure 1) and are concatenated to the decoder feature maps of the same size. All convolutional kernels are of size 3 and all convolutional operations are followed by ReLU activations. In Figure 1, we have marked three layers in the encoder section and three layers in the decoder section. These are six layers that we will focus on below when we investigate the training dynamics and the effects of transfer learning.

Figure 1:

Schematic representation of the our FCN architecture. The lower part of the figure shows details of the residual block.

Many differeent network architectures have been proposed for medical image segmentation. Recent review of these architectures can be found in [50, 9]. Based on these reviews, we chose four additional network architectures in this study. These are briefly explained below. We refer the reader to the original papers for detailed description of each architecture.

• HRNet [58]. The novelty of this architecture is that it allows the network to maintain high-resolution features through the network. The network starts with a high-resolution stream of representations and gradually adds high-resolution to low-resolution paths. As a result, the i^th stage of the network will have i streams of representations, each with a different resolution.

• UNet++ [63]. As the name implies, this is an extension of the UNet [12, 48]. It includes deep supervision. Moreover, it connects encoder and decoder subnetworks using a series of nested, dense skip connections.

• Method of [25], which we refer to as Tiramisu. This architecture is an extension of DenseNet [23] for semantic segmentation. Densely-connected networks are among the most common architectures used in vision applications, including segmentation.

• Autofocus [43]. This network is based on autofocus convolutional layer, which aims to improve multi-scale processing of the image in segmentation. It includes multiple parallel convolutional paths, each with a different dilation rate. Other specific aspects of the network include weight sharing between parallel paths as well as an attention mechanism.

In addition to our own network (Figure 1) and the above four architectures, in some experiments we also use the original V-Net architecture [38]. Please note that our aim is not to compare the segmentation accuracy of different network architectures. By experimenting with different architectures, we aim at showing that our findings in terms of the impact of transfer learning are not limited to a certain architecture.

At test time, a sliding window approach with a 24-voxel overlap between adjacent blocks was used to process an image. In addition to random shifts, other data augmentations used during training included flip, rotation by integer multiples of π/2, and addition of random Gaussian noise to voxel intensity values. When training from scratch, we use the initialization method proposed in [20]. This method initializes convolutional filters with zero-mean Gaussian random variables with a standard deviation of $\sqrt{2/n}$, where n is the number of connections to the convolutional filter from the previous layer. The network was trained by minimizing the negative of the Dice Similarity Coefficient (DSC) between the predicted and target segmentation maps using Adam [34]. We used an initial learning rate of 10⁻⁴, which was reduced by 0.90 after every 2000 training iterations if the loss did not decrease.

For our transfer learning experiments, we reduced the initial learning rate by half and fine-tuned all model layers. This has been referred to as deep fine-tuning [52]. Some studies, e.g., [17], have reported that fine-tuning only certain network layers could be preferable in some applications. However, in our experiments we found that fine-tuning the entire network invariably led to models that were better than or as good as models fine-tuned partially. We use the terms “training with random initialization” and “training from scratch”, interchangeably, to refer to model training without transfer learning. To quantify segmentation performance, we mainly use DSC, Average Symmetric Surface Distance (ASSD), and the 95 percentile of the Hausdorff Distance (HD95). In experiments with brain lesion segmentation, we also report the lesion-count F1-score for completeness.

2.3. Analysis of model training

Due to their deep hierarchical structure and large number of parameters, deep learning models are considered to be more difficult to interpret and understand than many other machine learning models. Nonetheless, there exist methods for probing the inner workings of these models. In this study, we use some of the recent methods that have been developed for investigating how neural network representations evolve over time and for comparing the representations learned by different networks [45, 39, 46].

These methods are based on canonical correlation analysis (CCA) [1]. Given two vectors of random variables, $x\in {ℝ}^n$ and $y\in {ℝ}^m$, CCA seeks projection vectors $u_1\in {ℝ}^n$ and $v_1\in {ℝ}^m$ such that the correlation between the projected random variables, ${\rho }_1=\mathrm{corr}\left(u_1^{T}x,v_1^{T}y\right)$, is maximized. This process can be carried out min(m, n) times, with the condition that the next pair of projection vectors, u_i and v_i, are pairwise-orthogonal to the previously-computed ones. It has been shown that CCA can be used to compare the representations learned by different neural networks [45, 39]. In this setting, elements of vectors x and y correspond to individual neurons of a fully-connected layer or (as in this work) different channels of a convolutional feature map. These random vectors can be sampled by passing data through the network and recording the neuron activation values. In our experiments, we sampled blocks from random locations in the test images and recorded the values of the convolutional layer neurons.

The output of CCA is a set of projection directions, {u_i, v_i}, and a measure of how strongly the two representations are correlated along those directions, {ρ_i}. In [45], it was suggested to use the average of ρ_is as a measure of similarity of two convolutional layers. It was later shown in [39] that the computed directions can vary greatly in terms of the amount of variability in the original data that they explain. Therefore, a weighted average of ρ_is was proposed for estimating the similarity between two convolutional layers:

$$\mathrm{RSIM}\left(L_1,L_2\right)=\sum {\alpha }_i{\rho }_i,$$ (1)

where L₁ and L₂ denote the convolutional layers being compared and α_i are the normalized weights that are proportional to the amount of variability explained by each direction [39]. In this study, we use this method to compute the similarity of convolutional representations within and across networks to understand the effect of transfer learning.

3. Results and Discussion

In this section, we first present the results of a series of experiments to assess the impact of transfer learning in medical image segmentation with FCNs. Each experiment displays a distinct difference between source and target domains or tasks.

3.1. Transfer across acquisition protocols

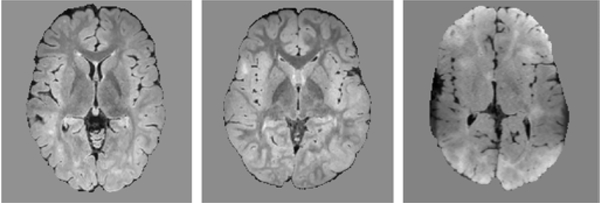
A recurring theme in medical image data involves varying image quality, such as when different scanners or acquisition protocols are used. As an example of this scenario, we consider the TSC dataset. The TSC dataset included 165 scans from five different centers, with 18–47 scans per center. The MRI scans were acquired using 3T scanners. The imaging protocol for each patient included the following: (1) a T1-weighted high-resolution magnetization-prepared rapid-acquisition gradient echo (MPRAGE) image. The voxel size was 1.0 × 1.0 × 1.0 mm³, echo time (TE): 1.66âĂŞ3.39 ms, repetition time (TR): 1,130âĂŞ2,530 ms, field of view (FOV): 19.2âĂŞ25.6 cm, and flip angle: 7 – 9°; (2) a T2-weighted turbo spin echo (TSE) image with 0.4 mm² in-plane resolution with 2mm slice thickness; and (3) sagittal 3D isotropic T2 fluid-attenuated inversion recovery (FLAIR) with voxel size of 0.90 × 0.90 × 1.0 mm, number of excitations of 1, TR=5,000 ms, TE= 390âĂŞ400 ms, echo train length 141, flip angle= 20°, FOV: 19âĂŞ26 cm, acquisition matrix 256× 256. Imaging protocols were harmonized to the extent permitted by each platform. All scans had been manually annotated in detail. Nonetheless, two or three scans from each center (for a total of 12 scans) were selected for more accurate and detailed annotation by two annotators; these scans were used as test data and the remaining 16–44 scans per center were used for training. For one of these centers, which we refer to as Center 5, the images had reduced gray matter - white matter contrast and resolution compared to the other centers due to the capabilities of the acquisition device in that center. Sample FLAIR images from centers 1, 3, and 5 are shown in Figure 2. When we trained and tested models separately on data from each center, the segmentation accuracy on Center 5 was much lower than the other four centers, confirming that the reduced image contrast and resolution resulted in poor model accuracy.

Figure 2:

Example FLAIR images in the TSC data from Center 1 (left), Center 3 (middle) and Center 5 (right). Compared to other centers, the FLAIR images from Center 5 had lower tissue contrast and lower effective spatial resolution.

In order to investigate the potential of transfer learning to improve the segmentation accuracy on data from Center 5, we trained models using three strategies: 1) training from scratch on data from Center 5, 2) fine-tuning models pre-trained on each of the other four centers, 3) fine-tuning a model pre-trained on the pool of all data from the other four centers. With respect to the formalism of transfer learning that we presented in Section 1.1, clearly in this experiment the source and target tasks are the same $\left({\mathcal{T}}_S\equiv {\mathcal{T}}_T\right)$ because they both involve TSC lesion segmentation. On the other hand, the source and target domains are different $\left({\mathcal{D}}_S\ne {\mathcal{D}}_T\right)$ because of the change in image quality and hence the change in the distribution P(X). Table 2 shows the results of these experiments, where for the second training strategy we show the average of four trials. The results show a remarkable improvement in the segmentation accuracy of this challenging dataset with transfer learning. Fine-tuning the model trained on the pool of data from all four centers led to better results than fine-tuning the model trained on data from one center. Interestingly, as can be seen in the table, we observed similar improvements in DSC and F1 score due to transfer learning with the other four architectures as well.

Table 2.

Test segmentation accuracy on data form Center 5 in the TSC dataset for models trained with R.I. and with T.L. via fine-tuning models pre-trained on data from other centers.

Network architecture		DSC	F1
Figure 1	R.I.	0.421	0.393
	T.L. (train on one center)	0.577	0.514
	T.L. (train on four centers)	0.582	0.525
HRNet	R.I.	0.410	0.385
	T.L. (train on one center)	0.545	0.485
	T.L. (train on four centers)	0.558	0.487
UNet++	R.I.	0.418	0.382
	T.L. (train on one center)	0.569	0.508
	T.L. (train on four centers)	0.595	0.532
Tiramisu	R.I.	0.410	0.385
	T.L. (train on one center)	0.565	0.502
	T.L. (train on four centers)	0.585	0.520
Autofocus	R.I.	0.390	0.373
	T.L. (train on one center)	0.525	0.495
	T.L. (train on four centers)	0.542	0.504

3.2. Transfer across imaging modalities

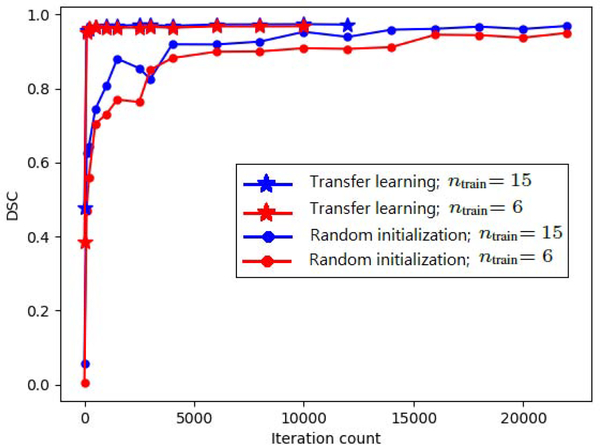
Here, the source and target organs of interest are the same, but the imaging modalities are different. Hence, with respect to the framework presented in Section 1.1, in this case the source and target domains are different, but the tasks are the same $\left({\mathcal{D}}_S\ne {\mathcal{D}}_T,{\mathcal{T}}_S\equiv {\mathcal{T}}_T\right)$. The example considered here is liver segmentation. We train a model for segmentation of liver in the pool of the three liver MRI datasets (Table 1). We then fine-tune that model for segmentation of the Liver-CT dataset. The comparison with training from scratch is shown in Table 3 for two sets of experiments with 15 and 6 target training images for all five network architectures. In this table, and henceforth in the paper, we use T.L. and R.I. as short for transfer learning and random initialization (i.e., training from scratch), respectively. Figure 3 shows the test DSC as a function of training iteration count. We see that transfer learning improves the convergence speed. However, in terms of segmentation accuracy, the difference between models trained with transfer learning and learned from scratch is marginal. Paired t-tests did not reveal any significant differences at p = 0.05 between T.L. and R.I. for experiments with 15 and 6 target training images. This observation was the same with all five network architectures. In terms of segmentation accuracy, there were slight differences between different network architectures. However, in terms of the impact of transfer learning, there were no differences between the five networks.

Table 3.

Test segmentation accuracy on the Liver-CT dataset for models learned from scratch with random initialization (R.I.) and for transfer learning (T.L.) via fine-tuning a model pre-trained on liver MRI datasets.

network			DSC	HD95 (mm)	ASSD (mm)
Figure 1	ntrain = 15	R.I.	0.97 ± 0.01	5.07 ± 1.94	1.47 ± 0.33
		T.L.	0.97 ± 0.01	4.75 ± 1.81	1.43 ± 0.33
	ntrain = 6	R.I.	0.95 ± 0.01	5.47 ± 2.00	1.61 ± 0.36
		T.L.	0.96 ± 0.01	5.25 ± 2.09	1.56 ± 0.34
HRNet	ntrain = 15	R.I.	0.94 ± 0.03	5.23 ± 1.88	1.50 ± 0.36
		T.L.	0.95 ± 0.03	5.12 ± 1.90	1.48 ± 0.38
	ntrain = 6	R.I.	0.94 ± 0.03	5.50 ± 2.09	1.62 ± 0.39
		T.L.	0.94 ± 0.02	5.42 ± 2.22	1.56 ± 0.37
UNet++	ntrain = 15	R.I.	0.95 ± 0.02	5.12 ± 1.94	1.40 ± 0.28
		T.L.	0.97 ± 0.03	5.08 ± 1.87	1.41 ± 0.27
	ntrain = 6	R.I.	0.94 ± 0.02	5.44 ± 2.11	1.55 ± 0.30
		T.L.	0.97 ± 0.04	5.35 ± 2.04	1.52 ± 0.31
Tiramisu	ntrain = 15	R.I.	0.95 ± 0.02	5.28 ± 1.87	1.40 ± 0.27
		T.L.	0.97 ± 0.03	5.17 ± 1.70	1.30 ± 0.25
	ntrain = 6	R.I.	0.94 ± 0.04	5.87 ± 2.21	1.64 ± 0.42
		T.L.	0.94 ± 0.03	5.63 ± 2.19	1.53 ± 0.40
Autofocus	ntrain = 15	R.I.	0.93 ± 0.03	6.01 ± 2.24	1.70 ± 0.39
		T.L.	0.95 ± 0.01	5.80 ± 2.02	1.54 ± 0.28
	ntrain = 6	R.I.	0.92 ± 0.03	6.52 ± 2.39	1.92 ± 0.44
		T.L.	0.94 ± 0.02	5.83 ± 2.22	1.68 ± 0.30

Figure 3:

Test DSC as a function of training iteration count for segmentation of the Liver-CT dataset with models trained from scratch and transfer learning.

3.3. Transfer across subject age

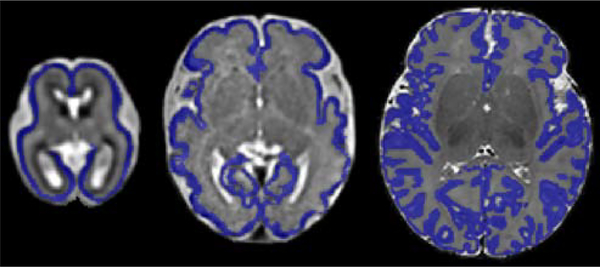
Often the source and target tasks can be different due to a shift in factors such as subject age or body size. An example of such a shift is represented by the three cortical plate segmentation datasets used in this work. As shown in Figure 4, the shape of the cortical plate undergoes significant changes during early brain development. Therefore, in this case, with respect to the formalism presented in Section 1.1, the source and target domains are the same $\left({\mathcal{D}}_S\equiv {\mathcal{D}}_T\right)$ but the tasks are different because of the substantial change in the shape of the cortical plate to be segmented $\left({\mathcal{T}}_S\ne {\mathcal{T}}_T\right)$.

Figure 4:

From left to right, example images and segmentations (in blue) from CP- younger fetus, CP- older fetus, and CP- newborn datasets.

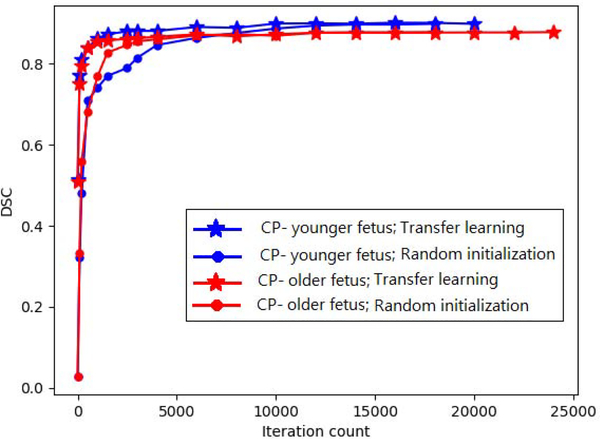
The numbers of images in CP-younger fetus, CP-older fetus, and CP-newborn datasets were, respectively, 27, 15, and 558. We trained a model on CP-newborn, achieving a DSC of 0.93. We then fine-tuned this model on CP-younger fetus and CP-older fetus datasets, both with their entire training set as well as with subsets of 5 images from each dataset. The results obtained with two different network architectures are presented in Table 4.. Figure 5 shows the convergence for the network architecture shown in Figure 1. They show faster convergence with transfer learning. However, improvements in model performance are generally small. Statistically significant improvements were only observed for segmentation of CP-older fetus when 5 images were used from the target domain. In Table 4 and the rest of the tables in this paper, we use an asterisk (*) to denote statistical significance at p = 0.05 due to transfer learning. These results suggest that transfer learning may be more effective when source and target domains are more similar and the target training data is smaller. The results with the other three network architectures (i.e., HRNet, Tiramisu, and Autofocus) were very similar to those of our network and UNet++, and therefore they were not included in this table. In particular, with these three networks, too, the only statically significant differences were observed for segmentation of CP-older fetus when 5 images were used from the target domain.

Table 4.

Test accuracy on CP-younger fetus and CP-older fetus datasets for models learned with R.I. and with T.L. via fine-tuning a model pre-trained on CP-newborn.

				DSC	HD95 (mm)
Figure 1	CP- younger fetus	n train=16	R.I.	0.90 ± 0.03	0.80 ± 0.02
			T.L.	0.90 ± 0.03	0.80 ± 0.01
		n train=5	R.I.	0.88 ± 0.03	0.86 ± 0.12
			T.L.	0.89 ± 0.03	0.83 ± 0.06
	CP- older fetus	n train=10	R.I.	0.82 ± 0.05	1.02 ± 0.19
			T.L.	0.82 ± 0.05	0.96 ± 0.19
		n train=5	R.I.	0.79 ± 0.05	1.20 ± 0.26
			T.L.	0.82 ± 0.04*	0.97 ± 0.20*
UNet++	CP- younger fetus	n train=16	R.I.	0.90 ± 0.04	0.92 ± 0.06
			T.L.	0.91 ± 0.05	0.87 ± 0.04
		n train=5	R.I.	0.90 ± 0.04	0.99 ± 0.10
			T.L.	0.91 ± 0.03	0.84 ± 0.06*
	CP- older fetus	n train=10	R.I.	0.83 ± 0.03	1.15 ± 0.16
			T.L.	0.84 ± 0.04	1.10 ± 0.17
		n train=5	R.I.	0.80 ± 0.05	1.41 ± 0.28
			T.L.	0.84 ± 0.02*	1.05 ± 0.18*

Asterisk (*) denote statistical significance due to T.L.

Figure 5:

Test DSC as a function of iteration count for segmentation of CP-younger fetus and CP-older fetus datasets with models trained from scratch and transfer learning.

3.4. Transfer across segmentation tasks

A common scenario arises when a source dataset from the same modality is available but the organ of interest is different between source and target domains. We present two sets of experiments representing this scenario.

The first set of experiments is on segmentation of the Pancreas-CT dataset. We trained models from scratch using 150 and 15 training images. We also pre-trained a model on the Liver-CT dataset and fine-tuned it on the same number of target (Pancreas-CT) images. With respect to the definition of transfer learning in Section 1.1, clearly in this setting the source and target tasks are different $\left({\mathcal{T}}_S\ne {\mathcal{T}}_T\right)$. In addition, the source and target domains are not the same because the distribution of representations in the feature space, P(X), between the source and target are different, especially at the deeper network layers. Comparison of test accuracy for this experiment is shown in Table 5. The improvement in segmentation accuracy was small when 150 target training images were used in the target domain. With only 15 training images in the target domain, statistically significant improvements were observed for DSC, HD95, and ASSD. As shown in Table 5, we made the same observation with all five network architectures.

Table 5.

Test segmentation accuracy on the Pancreas- CT dataset for models learned with R.I. and with T.L. via fine-tuning a model pre-trained on the the other four CT datasets from Table 1.

network			DSC	HD95 (mm)	ASSD (mm)
Figure 1	ntrain = 150	R.I.	0.80 ± 0.07	7.68 ± 2.45	2.04 ± 0.50
		T.L.	0.81 ± 0.07	7.55 ± 2.24	2.01 ± 0.43
	ntrain = 15	R.I.	0.70 ± 0.13	9.12 ± 2.63	2.55 ± 0.60
		T.L.	0.74 ± 0.10*	8.11 ± 2.21*	2.23 ± 0.54*
HRNet	ntrain = 150	R.I.	0.78 ± 0.11	7.44 ± 2.57	2.11 ± 0.51
		T.L.	0.78 ± 0.10	7.32 ± 2.51	2.08 ± 0.47
	ntrain = 15	R.I.	0.68 ± 0.12	9.14 ± 2.88	2.50 ± 0.57
		T.L.	0.74 ± 0.09*	8.02 ± 2.39*	2.22 ± 0.46*
UNet++	ntrain = 150	R.I.	0.80 ± 0.08	7.66 ± 2.57	2.11 ± 0.52
		T.L.	0.81 ± 0.07	7.57 ± 2.40	2.12 ± 0.50
	ntrain = 15	R.I.	0.72 ± 0.13	8.99 ± 2.41	2.48 ± 0.56
		T.L.	0.76 ± 0.07*	8.11 ± 2.13*	2.15 ± 0.50*
Tiramisu	ntrain = 150	R.I.	0.82 ± 0.10	7.55 ± 2.66	2.01 ± 0.44
		T.L.	0.82 ± 0.08	7.34 ± 2.43	2.00 ± 0.43
	ntrain = 15	R.I.	0.70 ± 0.12	9.11 ± 2.60	2.57 ± 0.56
		T.L.	0.77 ± 0.10*	8.97 ± 2.31*	2.23 ± 0.48*
Autofocus	ntrain = 150	R.I.	0.79 ± 0.08	7.87 ± 2.80	2.14 ± 0.51
		T.L.	0.79 ± 0.09	7.64 ± 2.44	2.08 ± 0.45
	ntrain = 15	R.I.	0.70 ± 0.13	9.90 ± 2.57	2.48 ± 0.59
		T.L.	0.76 ± 0.11*	7.85 ± 2.55*	2.20 ± 0.50*

The second set of experiments was on segmentation of brain lesions in the TSC dataset. This dataset was briefly described above in Section 3.1. As we mentioned there, the images in this dataset came from five different centers. We ran two experiments on data from each center: 1) training from scratch, 2) transfer learning by fine-tuning a model pre-trained on the BRATS dataset. With regard to the formalism of transfer learning presented in Section 1.1, in this experiment the source and target are different in terms of the task $\left({\mathcal{T}}_S\ne {\mathcal{T}}_T\right)$ because the source and target tasks involve segmentation of two different types of lesions. Specifically, the BRATS dataset involves segmentation of brain tumors (glioma) [37], whereas the TSC dataset involves segmentation of Tuberous Sclerosis Complex lesions [13].

Therefore, in this experiment the BRATS dataset is the source dataset and the TSC dataset is the target dataset. We compared transfer learning and training from scratch in two different scenarios: 1) using all training images in the target (TSC) dataset, and 2) using only 3 scans from each center in the target (TSC) dataset. Table 6 shows the accuracy on the 12 test scans. Results show only a marginal improvement when 16–44 training scans were available in the target domain. With only 3 training scans in the target domain, the improvements gained with transfer learning were statistically significant. As shown in this table, we made very similar observations with UNet++ and Tiramisu in terms of the impact of transfer learning in this experiment. The results with HRNet and Autofocus were also very similar and therefore were not shown.

Table 6.

Comparison of test segmentation accuracy on the TSC dataset for models trained with R.I. and with T.L. via fine-tuning a model pre-trained on the BRATS dataset.

network architecture			DSC	F1
Figure 1	ntrain = 16 – 44	R.I.	0.63 ± 0.14	0.67 ± 0.18
		T.L.	0.64 ± 0.14	0.69 ± 0.18
	ntrain = 3	R.I.	0.48 ± 0.20	0.50 ± 0.17
		T.L.	0.60 ± 0.15*	0.64 ± 0.16*
UNet++	ntrain = 16 – 44	R.I.	0.62 ± 0.12	0.66 ± 0.17
		T.L.	0.62 ± 0.11	0.67 ± 0.14
	ntrain = 3	R.I.	0.47 ± 0.18	0.50 ± 0.16
		T.L.	0.59 ± 0.13*	0.62 ± 0.13*
Tiramisu	ntrain = 16 – 44	R.I.	0.65 ± 0.14	0.67 ± 0.15
		T.L.	0.65 ± 0.11	0.70 ± 0.14
	ntrain = 3	R.I.	0.51 ± 0.15	0.52 ± 0.14
		T.L.	0.63 ± 0.13*	0.63 ± 0.11*

3.5. Scalability

In this section, we present the results of a set of experiments to investigate the impact of the number of training images in the source and target domains on the effectiveness of transfer learning. Please note that our experiments presented in Sections 3.2, 3.3, and 3.4 also investigated this factor. For example, in Section 3.2 we presented the results of transfer learning with both 6 and 15 target training images. However, in the experiments presented in this section we consider two larger datasets in the source and target domains. In this experiment, we first trained a model for brain segmentation in the Whole-Brain-MRI dataset and then transferred the model for brain cortical plate segmentation in CP- newborn dataset. Whole-Brain-MRI dataset is the source dataset and contains 2500 images. CP- newborn dataset is the target dataset and contains 558 images. We used 108 images in the CP- newborn dataset as test set in the target domain. We used 50, 250, or 2500 images from the Whole-Brain-MRI dataset for pre-training the model. Then we used 50, 150, or 450 images from the CP- newborn dataset for fine-tuning the transferred model. For each of 50, 150, or 450 images from the CP- newborn dataset we also trained models with random initialization. Table 7 shows the detailed results of this experiment. Note that in this table using zero images in the source domain corresponds to training from scratch (R.I.). The results show that the number of training images in the target domain has a slightly larger impact than the number of images in the source domain. When the number of training images in the target domain was 150 or 450, there was very little difference between training from scratch (R.I.) and transfer learning models trained with 50, 250, or even 2500 images in the source domain. Even with 50 target training images, the impact of transfer learning was minimal and not statistically significant in terms of DSC and HD95. We ran the same experiment with HRNet and UNet++, and we made the same observation. This agrees with our experiments reported in the above subsections; i.e., it seems that the impact of transfer learning is not significant when there are more than a few tens of target training images.

Table 7.

Results of the experiment to investigate the impact of dataset size in the source and target domains on the effect of transfer learning. In this experiment, the source task is whole brain segmentation in the Whole-Brain-MRI dataset, and the target task is brain cortical plate segmentation in the CP-newborn dataset. For each setting of the number of images in the target domain, there were no statistically significant differences in the results obtained with different numbers of images in the source domain (p = 0.05).

number of images in the target domain	number of images in the source domain	DSC	HD95 (mm)
50	0 (R.I.)	0.888 ± 0.036	0.841 ± 0.092
	50	0.906 ± 0.039	0.837 ± 0.087
	250	0.906 ± 0.035	0.837 ± 0.082
	2500	0.908 ± 0.034	0.833 ± 0.084
150	0 (R.I.)	0.901 ± 0.035	0.837 ± 0.080
	50	0.904 ± 0.036	0.840 ± 0.081
	250	0.908 ± 0.038	0.836 ± 0.077
	2500	0.910 ± 0.034	0.830 ± 0.066
450	0 (R.I.)	0.926 ± 0.029	0.810 ± 0.068
	50	0.926 ± 0.033	0.820 ± 0.071
	250	0.926 ± 0.030	0.813 ± 0.072
	2500	0.930 ± 0.031	0.805 ± 0.061

3.6. Investigation of the dynamics of learned representations

We used the tools described in Section 2.3 to investigate the dynamics of learned representations to gain a deeper understanding of the effects of transfer learning. Results reported in this section are mainly based on the network shown in Figure 1. Our observations with the other architectures were very similar, as we occasionally discuss.

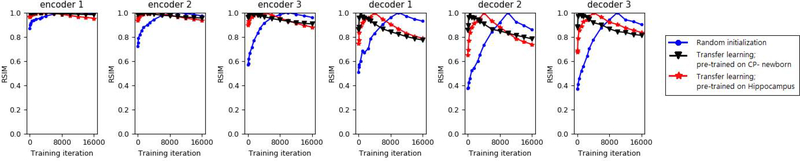
Figure 6 shows the evolution of learned representations for segmentation of CP-younger fetus dataset for two transfer learning trials as well as training from random initialization. As we explained in Section 2.3, RSIM(L₁, L₂) quantifies the similarity between the two representations L₁ and L₂. In order to investigate the evolution of learned representations with RSIM, we need a reference point during training. As suggested in [46], we chose the “convergence epoch”, which we defined as the epoch when the DSC on the validation set reached within 0.5% of its maximum. We then computed the similarity of the learned representations between each training epoch and the convergence epoch using Eq. (1). Given the large number of convolutional layers in our network, we present this evaluation for the six layers shown in Figure 1.

Figure 6:

Evolution of learned representations with training for segmentation of CP-younger fetus dataset. Plots show values of RSIM between the representations at each time point with the convergence epoch. Convergence epoch can be identified as the point where RSIM=1.

Several interesting observations can be made from Figure 6. First, as expected, the model converged much faster with transfer learning, compared with training from scratch. The convergence epoch can be identified as the point where RSIM=1 since, as we mentioned above, we are comparing the representations in each epoch with those at the convergence epoch. The second observation is that the representations in all layers continue to change significantly well after the model’s segmentation accuracy has converged. Since we are comparing each representation at a certain epoch with the representation at a fixed reference (i.e., the convergence epoch), this indicates that the representations continue to change after network’s performance has converged. Please note that RSIM is not a measure of segmentation performance; rather, it is a measure of change in the learned representations with respect to the reference (here, the convergence epoch). It is worth noting that after the convergence epoch, the training and test accuracies changed very little. This indicates that the model weight values that can result in a specific test accuracy are far from being unique. This is evidenced by the fact that after the convergence epoch the network’s segmentation accuracy remains almost constant while the network weights continue to change as shown in Figure 6. The third observation is the effect of the dataset used in pre-training. In this experiment we used two different pre-trained models for transfer learning: one trained on CP-newborn dataset and the other trained on Hippocampus dataset. Figure 6 shows that the model pre-trained on CP-newborn led to faster convergence and smaller changes in the representations compared with the model pre-trained on Hippocampus. We should point out that for all three training trials in this experiment, the test accuracy of the final models were very close. Therefore, the difference is mainly in terms of the convergence speed. Nonetheless, this experiment suggests that the more similar the source domain is to the target domain, the faster will be the convergence of the model on the target task and less significant will be the changes in the representations during fine-tuning.

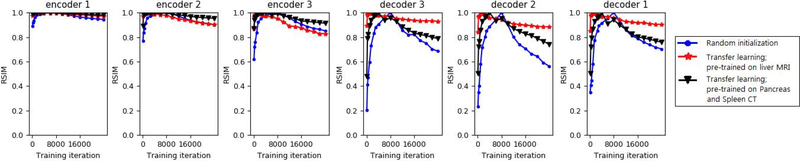
We show another example of the evolution of representations for segmentation of Liver-CT dataset in Figure 7. This figure displays some of the observations explained above for cortical plate segmentation. In one of the transfer learning trials in this experiment, we pre-trained the model on Pancreas CT and Spleen CT datasets, which share the imaging modality (CT) with the target task. In the other transfer learning experiment, we pre-trained on the three liver MRI datasets (see Table 1). An interesting observation is that, compared with the model pre-trained on Pancreas and Spleen CT datasets, the model pre-trained on liver MRI went through less changes in the decoder section during fine-tuning. This makes intuitive sense because the network pre-trained on liver MRI had to learn many high-level shape representations that were relevant for liver CT segmentation as well. On the other hand, in terms of the encoder representations, networks pre-trained on MRI and CT images were not very different. This may seem counter-intuitive because one may expect that for segmentation of liver in CT a model pre-trained on CT images should go through less changes in the encoder section during fine-tuning. We will further explain this observation later in this section.

Figure 7:

Evolution of learned representations for segmentation of the Liver-CT dataset. The plots show RSIM values computed between the representations at each time point with the convergence epoch. Convergence epoch can be identified as the point where RSIM=1.

Another interesting observation from both Figures 6 and 7 is that, both with transfer learning and with training from scratch, the encoder representations changed much less than the decoder representations. The early encoder layer representations, in particular, changed very little even when trained from random initializations. To further confirm this observation, in Figure 8 we show randomly-selected convolutional filters from the encoder and decoder sections of the network at the beginning and end of training, both for training from scratch and for transfer learning. The most striking observation is that the filters change very little during training, and the shape of the filters remain almost unchanged. This example is for brain lesion segmentation on the TSC dataset, and the transfer learning was performed on the BRATS dataset. When training from scratch, the network weights at convergence look random and still very close to the weights at initialization. Some of the filters of the network pre-trained on BRATS look more “organized” as edge detectors, but still there are random-looking filters, and during fine-tuning on the TSC dataset weights changed very little. We made similar observations in experiments with other datasets as well as with other architectures. In our experiments, the average relative change in the norm of the filters at convergence was typically below 25% of the filter norm at the start of training. We also found that, in most cases, the filters in the intermediate layers of the network changed more than the early and late layer filters. This may be related to the observation in previous studies that optimization of the middle layers is more difficult [60]. The reason why decoder representations change much more than encoder representations (as shown in Figures 6 and 7) is because the change in each representation is the “cumulative” effect of the changes in all its preceding convolutional layers.

Figure 8:

Selected filters from different sections of the network at the start of training and convergence, and their differences. In this experiment, the network was trained on the TSC dataset and for transfer learning the model was pre-trained on the BRATS dataset. From top to bottom, filters belong to encoder-1, encoder-3, decoder-1, and decoder-3 layers (see Figure 1).

Figure 9 shows randomly-selected filters from encoder and decoder sections of V-Net at random initialization and at convergence for segmentation of the Liver-CT dataset. V-Net has larger convolutional filters of size 5. Nonetheless, similar to Figure 8, filters at convergence have changed little compared with those at initialization and still look random. We further investigate this observation in the following subsection.

Figure 9:

Selected filters from encoder and decoder sections of V-Net trained on Liver-CT dataset at the start of training, convergence, and their difference.

3.7. Segmentation networks with random encoders

The observation that convolutional filters of fully-trained models look random and only slightly change from their initial random values may seem surprising at first. One may speculate that this is due to limited training data. However, we conducted a multi-task segmentation experiment in which we trained a single model to segment 10 of the datasets listed in Table 1, consisting of more than 1200 images. We observed similar patterns as those shown in Figure 8. We should point out that, even on small datasets, if we continue training the network well beyond the convergence, the weights will continue to change and become more different from the weights at initialization. However, we are only interested in the “necessary” change that occurs from the start of training until convergence.

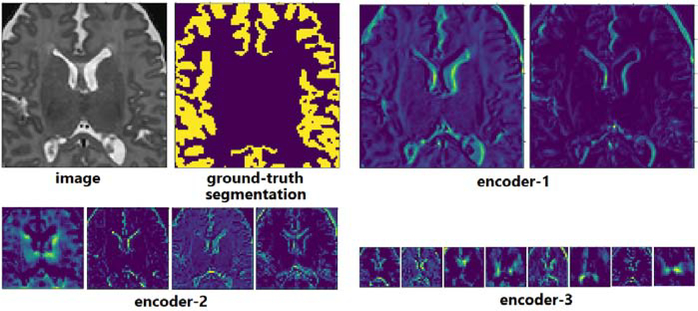
The above observation may seem to contradict the expectation that “useful” filters such as edge detectors and Gabor-type filters should emerge in the encoder section of the network. However, this observation can be explained by prior studies on neural networks with random weights [49, 7]. Well before the recent surge of deep learning, studies had shown that neural networks with completely random weights could perform well on various vision tasks [24, 42]. Saxe et al. explained these observations by showing a remarkable response similarity between sinusoidal and random convolutional filters [49]. Specifically, they showed that for both sinusoidal and random filters, the maximum-response input was in the form of a sinusoid with a frequency equal to the maximum frequency of the filter. We can visually confirm this by looking at the feature maps of the encoder section of our network at convergence. Figure 10 shows example feature maps of a network trained on the CP-newborn dataset. Although the filters of this network looked random (similar to those shown in Figure 8), the extracted features do not look random; rather, they embody meaningful low-level and high-level features.

Figure 10:

Example feature maps computed with random-looking convolutional filters of a model trained on CP-newborn dataset on an example image patch.

Given the above observations, two questions are worth further investigation. First, how would an FCN with completely random filters (i.e., not undergone any training) in the encoder section perform on medical image segmentation tasks? Second, if a network with random filters is a viable model, can we say anything about the space of the models that can successfully perform a segmentation task, and does transfer learning constrain this space? Below, we report experiments that aim at shedding some light on these questions.

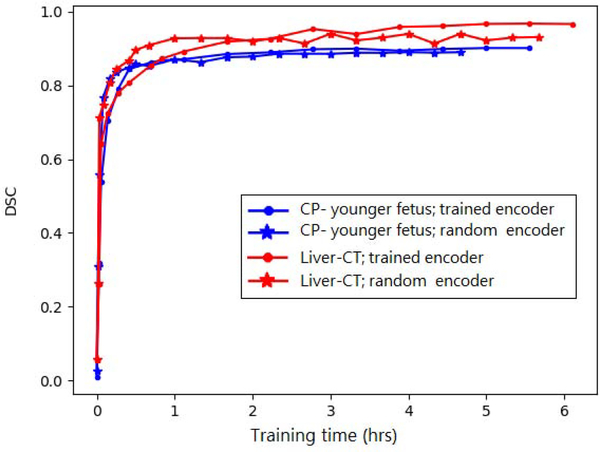
In a set of experiments, we initialized the network shown in Figure 1 at random, and then froze the encoder section of the model, only training the decoder section. This network includes 33 convolutional layers in the encoder section and 18 convolutional layers in the decoder section. Figure 11 shows a comparison of this training strategy with the standard approach of training the entire network on two datasets, i.e., CP-younger fetus and Liver-CT. The time to run one optimization operation on our GPU was 1.08 and 0.63 seconds, respectively, for optimizing the entire network and optimizing the decoder alone. Therefore, the horizontal axis is shown in hours, rather than iteration count. For Liver-CT dataset, the test DSC at convergence was 0.967 and 0.940, respectively, for the experiments with the trained encoder and with the random frozen encoder. For CP-younger fetus dataset, the DSC at convergence was 0.896 and 0.884, respectively, for experiment with trained encoder and with random frozen encoder. This indicates a small drop in performance when the encoder section was frozen at its initial random state. On the other hand, the network with frozen encoder converged in shorter time compared to the network with trained encoder.

Figure 11:

Comparison of a training strategy whereby the encoder section of the network is frozen at its initial random values, only training the decoder section, with the standard strategy of training the entire network.

The above experimental results suggests that the encoder section does not have to be trained. We cannot claim that this would be the case for every medical image segmentation task. Nonetheless, we made the same observation on many experiments with various datasets in Table 1 as well as with other network architectures. As a concrete example with a very different dataset than the two datasets used above, in an experiment with the TSC dataset from one of the five centers, we obtained DSC and F1 score, respectively, of 0.678 and 0.758 when the entire network was trained and 0.670 and 0.758 when the encoder section was frozen at its random initialization. These observations clearly challenge the common belief that the encoder filters have to learn data/task-specific features.

Based on our observations with FCNs with random encoders and the response of random convolutional filters discussed above, one can describe a possible operation mode of these networks as follows. The encoder filters extract a set of useful representations from the image. Although the filters might be random-looking, the representations embody relevant features such as edges in early layers and high-level features in deeper layers. Given that filters are initialized independently at random, these feature maps will constitute a diverse and rich set of representations. The decoder section learns to compute the segmentation label based on these representations.

In order to further understand the effect of transfer learning on the learned representations, we conducted other experiments. The goal of these experiments was to assess the similarity of FCNs trained from scratch compared with similarity of FCNs trained via transfer learning. In these experiments, too, we used RSIM for comparing the representations. Note that RISM can be used to quantify the similarity between pairs of learned representations. These representations can come from the same network, as for example in the experiments reported above in Section 3.6 where we used RSIM to compare the representations of the same layer across training epochs. However, RSIM can also be used to quantify the similarity of the learned representations across networks, which is what we perform in this section. Prior studies have also used similar metrics to compare the representations of networks trained with different strategies [39]. Table 8 shows the results of such an experiment with CP-younger fetus dataset. For this experiment, we trained 1) 10 networks with different random initializations, and 2) 10 networks trained with transfer learning, each initialized from a different model pre-trained on CP-newborn. We then computed the similarity between pairs of networks trained from scratch (RSIM(R.I., R.I.)), pairs of networks trained with transfer learning (RSIM (T.L., T.L.)), as well as similarity between pairs of networks trained using the two different strategies (RSIM(R.I., T.L.)). Table 8 shows these similarities for the six layers shown in Figure 1.

Table 8.

Similarity of representations between different layers of pairs of networks trained from random initialization (R.I.) and via transfer learning (T.L.).

	encoder-1	encoder-2	encoder-3	decoder-1	decoder-2	decoder-3
RSIM(R.I., R.I.)	0.247 ± 0.045	0.358 ± 0.034	0.405 ± 0.018	0.463 ± 0.046	0.540 ± 0.064	0.398 ± 0.041
RSIM(T.L., T.L.)	0.243 ± 0.010	0.370 ± 0.009	0.433 ± 0.005	0.510 ± 0.018	0.492 ± 0.047	0.333 ± 0.050
RSIM(R.I., T.L.)	0.287 ± 0.019	0.386 ± 0.014	0.460 ± 0.021	0.597 ± 0.024	0.636 ± 0.046	0.534 ± 0.057

The results presented in Table 8 show that models trained via transfer learning are as different from each other as models learned from scratch. This is evidenced by the fact that RSIM (T.L., T.L.) values are very close to RSIM(R.I., R.I.) values for all six layers. We conducted statistical t-tests to compare RSIM(R.I., R.I.) with RSIM (T.L., T.L.). The results of these tests showed that only encoder-3 and decoder-1 layers (i.e., the most intermediate of the six layers) were different at p = 0.05. On the other hand, statistical t-tests showed that RSIM(R.I., T.L.) was significantly larger than RSIM(R.I., R.I.) at p = 0.05 on all six layers. Similarly, RSIM (R.I., T.L.) was also statistically significantly larger than RSIM(T.L., T.L.) on all six layers at p = 0.05. Therefore, pairs of networks that have been trained from scratch are more similar to each other than they are to networks that have been trained with transfer learning (because RSIM(R.I., R.I.) < RSIM (R.I., T.L.)). Similarly, pairs of networks that have been trained with transfer learning are more similar to each other than they are to networks that have been trained from scratch (because RSIM(T.L., T.L.) < RSIM (R.I., T.L.)). Therefore, these results indicate that the diversity of networks trained using transfer learning is as high as that of networks trained from scratch (because RSIM(R.I., R.I.) and RSIM (T.L., T.L.) were not statistically different). However, it also shows that networks trained from scratch form a different “cluster” than networks trained via transfer learning. This is because RSIM(R.I., R.I.) and RSIM(T.L., T.L.) are smaller than RSIM(R.I., T.L.).

Finally, we performed a set of experiments to quantify the feature reuse with transfer learning in different layers of the network. For this purpose, we trained 10 networks from scratch with random initialization and 10 networks with transfer learning. We then computed the similarity between the network layers at the start of training and at convergence, using RSIM. From these, we computed the difference between the average of these similarities for the networks trained from scratch and networks trained with transfer learning. We use this difference as a measure of feature reuse in each layer. This approach to estimating feature reuse is the same as the approach proposed in [46].

Table 9 shows the computed feature reuse for four such experiments. Our results are different from the results reported in [46] in several aspects. Note that the application in [46] was 2D medical image classification with transfer learning from ImageNet. Authors of that study found that feature reuse was highest in the first network layers. They also found that the maximum feature reuse was around 0.20. Moreover, their results showed that feature reuse decreased monotonically from the bottom layers of the network to the top layers. Our results disagree with those of [46]. Specifically, as shown in Table 9, in our experiments feature reuse can increase from the first encoder layers to the deeper decoder layers. Moreover, as shown in this table, much higher feature reuse of up to 0.690 can occur in FCN-based medical image segmentation. These observations regarding the degree of feature reuse in different parts of the network can guide us in devising transfer learning strategies. As an example, consider the scenario where a network trained on liver MRI is fine-tuned for Liver-CT segmentation. As shown in Table 9, in this case feature reuse in the decoder section of the network is very high. This may indicate that fine-tuning of decoder layers of the network may be unnecessary. To test this hypothesis, we performed an experiment where we pre-trained a network on liver MRI and then fine-tuned only the encoder layers and the last layer of the decoder on Liver CT. This network achieved a mean test DSC of above 0.95 on Liver-CT dataset. We were also able to train equally-accurate models by keeping the decoder and output layers fixed and only training the encoder section of the network. These training strategies achieved DSC and HD95 values that were statistically not different than when the entire network was fine-tuned. On the other hand, training only the encoder section reduced the training time to convergence by 40%. In another experiment, we considered transferring a network trained on the CP-newborn for segmentation of the CP-younger fetus dataset. As shown in Table 9, this scenario also represents high feature reuse in the decoder layers. During fine-tuning, we kept all decoder layers at their values pre-trained on CP-newborn and only fine-tuned the encoder layers and the output layer of the network. We achieved a DSC of 0.887 with this transfer learning strategy, while reducing the training time to convergence by 30% compared to the case when the entire network was fine-tuned. We repeated this experiment with UNet++, Tiramisu, and Autofocus networks as well, and achieved DSC of 0.891, 0.878, and 0.880, respectively, on the target (CP-younger fetus) dataset with these networks. On the other hand, when fine-tuning the model pre-trained on the Hippocampus dataset, we could not achieve the same high segmentation accuracy without fine-tuning all decoder layers. This is an observation that could have been predicted from the feature reuse values presented in Table 9 because in this case feature reuse in the decoder layers is much lower.

Table 9.

Feature reuse in different network layers in four transfer learning experiments.

	encoder-1	encoder-2	encoder-3	decoder-1	decoder-2	decoder-3
Liver-CT, transfer learning from liver MRI	0.123	0.210	0.339	0.690	0.611	0.530
Liver-CT, transfer learning from Pancreas and Spleen CT	0.156	0.162	0.242	0.214	0.203	0.107
CP- younger fetus; transfer learning from CP- newborn	0.164	0.267	0.394	0.392	0.484	0.611
CP- younger fetus; transfer learning from Hippocampus	0.120	0.212	0.305	0.239	0.203	0.224

To the best of our knowledge, this is the first study to investigate the dynamics of learned representations and model weights in FCN-based medical image segmentation. However, there have been many prior works that have used transfer learning for medical image segmentation. Recent reviews of these works can be found in [11, 51]. We mentioned some of these works in the Introduction section. Here, we briefly describe the results of some of these prior studies. For segmentation of traumatic brain injuries in multi-center data, one study proposed a transfer learning method [26]. The authors showed that transfer learning substantially improved the segmentation accuracy (in terms of DSC, precision, and recall) compared to the baseline where the network trained in the source domain was applied directly on the target domain without fine-tuning. For white matter hyper-intensity segmentation, one study investigated transferring a CNN trained on legacy MRI scanners to images acquired on newer scanners, with different image quality and contrast [17]. They found that, without fine-tuning, the model trained on legacy scanners completely failed on the images from the new scanners. On the other hand, when only two labeled training images were available in the target domain, fine-tuning the CNN pre-trained on legacy data was more successful than training from scratch. Another study reported an improvement of 15% in DSC in segmentation of white matter hyperintensities due to transfer learning with a UNet architecture [44]. These results are close to the improvements we observed in our experiments (e.g., Table 2). A smaller improvement (from a DSC of 0.70–0.71 without transfer learning to a DSC of 0.72 with transfer learning) was reported in [35] but the authors found that this small improvement was still statistically significant. Transfer learning with a basic UNet between ultrasound datasets with different image quality improved the DSC by approximately 0.20 [19]. Cardiac segmentation accuracy has also benefited from transfer learning across acquisition protocols, with a DSC increase of up to 0.16 [10]. Transfer learning with UNet architectures pre-trained on large amounts of CT images improved the segmentation of lung nodules (by approximately 3.5%), liver segmentation (by approximately 5%) and brain tumor segmentation (by approximately 0.5%) in [64]. The authors reported that the improvements in all of their experiments were statistically significant. However, the authors did not clarify the number of training images in the target domain. In a different study on left ventricle segmentation, a CNN was pre-trained on balanced-Steady State Free Precession (bSSFP)-MR images and then fine-tuned for the same segmentation task on Late Gadolinium Enhanced (LGE) MR images [56]. With only four training images in the target domain, the authors observed an improvement of approximately 10% in DSC. Direct comparison of our results with prior works is not easy because of the differences in datasets and details of the experiments. However, an overall comparison of our results, presented in Sections 3.1 to 3.5, with those reported in prior studies suggest that prior studies have reported more positive results. In the majority of prior works on this topics, transfer learning has shown to lead to statistically significant improvements in segmentation accuracy. This may be due to a tendency, on the side of the authors as well as the reviewers, to favor studies with positive results. Therefore, we think our experimental results in Sections 3.1 to 3.5 and analysis of the dynamics of learned representations and model weights in Sections 3.6 and 3.7 add valuable new insights into the potential of transfer learning for medical image segmentation.

Future studies may expand our work in several directions. In this work, we focused on supervised training scenario. Future works may carry out similar analyses for other training methods such as semi-supervised training and zero/few-shot training [11, 57]. Furthermore, in this work we focused on the most common implementation of FCNs for medical image segmentation, which is based solely on predicting a dense voxel-wise segmentation map. However, there are variations to this approach. For example, some studies have suggested combining statistical shape models of the organ of interest into the deep learning framework for improved segmentation accuracy and robustness [40, 29, 31]. Analysis of the role of transfer learning for such models could be highly informative as well. Finally, although FCNs are the most common deep neural network architectures for medical image segmentation, there exist important alternative networks architectures such as those based on recurrent neural networks and attention [2, 30], which can be studied in future works. Finally, in this work we only used a scalar measure of similarity to compare networks trained from scratch with networks trained via transfer learning. One may gain additional insights by also comparing these networks in terms of the projection directions mentioned in Section 2.3.

4. Conclusion

Our experimental results show that for segmenting organs such as liver or brain cortical plate, transfer learning has a small effect on the segmentation accuracy. One may argue that the segmentation accuracy achieved by FCNs is close to optimal and the remaining gap in performance (DSC gap of 0.03 for liver and 0.10 for cortical plate) may be, in part, due to error in the training/test labels. Our experiments with pancreas and brain lesion segmentation seem to give some credence to this hypothesis. In those experiments, the segmentation accuracy (e.g., in terms of DSC) was much lower and we observed larger gains with transfer learning. We observed large gains in segmentation accuracy when images in the target domain were of a different/lower quality and small in number (Table 2). This is important since medical image datasets of varying quality are common in clinical and research applications. We also observed that transfer learning and learning with a frozen encoder reduced the convergence time. This could be useful when training time is critical or in hyperparameter/architecture search, where one would like to compare a large number of models or hyperparameter settings. We showed that random filters extracted a rich set of useful features, and that quite accurate models could be built by training only the decoder section of the model. We further demonstrated that, depending on the source and target domains, feature reuse in transfer learning can be more significant in deeper layers and in the decoder section of the network. We showed examples of how these observations could be used in devising transfer learning strategies.

• We critically study and analyze transfer learning in medical image segmentation

• We show that model weights change little from random initialization during training

• We show viability of models with random encoders, challenging the established beliefs

• We study evolution of learned representations, offering alternative training methods