Abstract
Airborne transmission is considered as an important route for the spread of infectious diseases, such as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), and is primarily determined by the droplet sedimentation time, that is, the time droplets spend in air before reaching the ground. Evaporation increases the sedimentation time by reducing the droplet mass. In fact, small droplets can, depending on their solute content, almost completely evaporate during their descent to the ground and remain airborne as so-called droplet nuclei for a long time. Considering that viruses possibly remain infectious in aerosols for hours, droplet nuclei formation can substantially increase the infectious viral air load. Accordingly, the physical-chemical factors that control droplet evaporation and sedimentation times and play important roles in determining the infection risk from airborne respiratory droplets are reviewed in this article.
Keywords: Airborne virus transmission, Droplet evaporation, Droplet sedimentation, Droplet nuclei, Wells model
Graphical abstract
Introduction
Airborne transmission of virus-containing saliva droplets produced by speaking, coughing, or sneezing is one of the well-known [1,2] mechanisms that play a crucial role in the spread of numerous infectious diseases, such as influenza [3,4] and severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) [5, 6, 7, 8]. When a saliva droplet evaporates to a so-called droplet nucleus, which is a small particle with much reduced water content [9], it can remain suspended in air for a long time. According to current WHO guidelines, the term droplet nucleus refers to droplets with radii smaller than [10]. However, such a sharp cutoff lineation does not account for the continuous crossover between droplet and droplet nucleus behavior [11]. The term aerosol in fact encompasses all kinds of droplets and particles over a wide radius range from a few nanometers to hundreds of micrometers. Considering recent experiments reporting that viruses can remain infectious in aerosols for hours [12, 13∗∗, 14], it follows that formation of droplet nuclei can significantly increase the infectious viral air load [15,16]. Accordingly, a fundamental question regarding the infection risk from airborne virus-containing droplets is whether they dry out to a droplet nucleus before falling to the ground. A seminal answer to this question was provided by the classical Wells model [1], which suggested that the fate of an evaporating droplet is mainly dependent on its initial size. The results provided by this model, which were partly confirmed in later studies [16∗∗, 17, 18], indicated that droplets with radii smaller than completely evaporate before falling to the ground, whereas larger droplets settle faster than they evaporate. Recent measurements [17] revealed that droplets with radii smaller than evaporate in the region of cough airflow and, thus, stay longer at the initial height at which they were expelled, which leads to a higher probability of infection. The Wells model assumes that the environmental air is well-mixed [19] or, in other words, that droplets are isolated and have no interaction with inhomogeneous velocity, temperature, and humidity fields caused by other droplets [20]. Recent investigations [20∗∗, 21, 22, 23, 24], however, revealed that turbulent eddies in the exhailed humid puff can trap small clusters of respiratory droplets and thereby decrease their evaporation rate substantially because of the locally moist and warm atmosphere within the gas cloud. This causes a slowdown of evaporation as compared to the classical Wells model and decreases the probability of droplet nuclei formation. On the other hand, wind currents and airflows around a falling droplet are found to decrease the droplet evaporation time [25] and thereby increase its sedimentation time and travel distance [26,27].
Although the Wells model neglects some important physical-chemical aspects of evaporation and sedimentation, the importance of the initial size for the time droplets stay suspended in air is generally agreed upon by scientists. So far, many experimental studies have been carried out to measure the size distribution of droplets produced by various respiration-based activities, such as sneezing, coughing, speaking, and breathing, all showing that such droplets vary widely in size. However, the size distribution of the expelled droplets is found almost independent of how violent the respiratory activity is [28]. In a seminal work, Duguid [29] measured the size of respiratory droplets using microscopy measurement of droplet stain-marks found on slides. Although the droplet radii calculated in that work were reported to widely range from to , of the droplets were found to have radii between and , which is the range where droplets are prone to form droplet nuclei. Later studies [11,30, 31, 32, 33, 34] revealed the existence of a noticeable number of much smaller droplets with radii in the submicron range among the droplets produced by coughing and speaking. Also, multimodal droplet size distributions have been reported in a few studies [35,36]. Despite all these studies, major uncertainties on the respiratory droplet-size distribution persist, partly due to the complexities of the physical mechanisms at play during droplet formation and complexities of the measurement process. It has been experimentally shown that breakup of the fluid into droplets continues to occur outside of the respiratory tract and involves complex fluid-fragmentation processes [23]. The rate of droplet emission during human speaking has been found to be significantly dependent on the violence of the respiratory activity [37,38] and the voice loudness [39]. For example, experiments reveal higher emission rates of aerosol droplets for singing than for speaking [40], although children and adolescents emit fewer aerosols during singing than what has been estimated for adults [41]. Recent observations from highly sensitive laser light scattering [42,43] have revealed that loud speaking can emit thousands of oral droplets per second, which is orders of magnitude larger than reports in earlier works [22,39]. This clearly demonstrates that the measured droplet-radius distribution significantly depends on the experimental conditions, the size-sensitivity of the measurement technique used, and the time droplets spend in air before measurement.
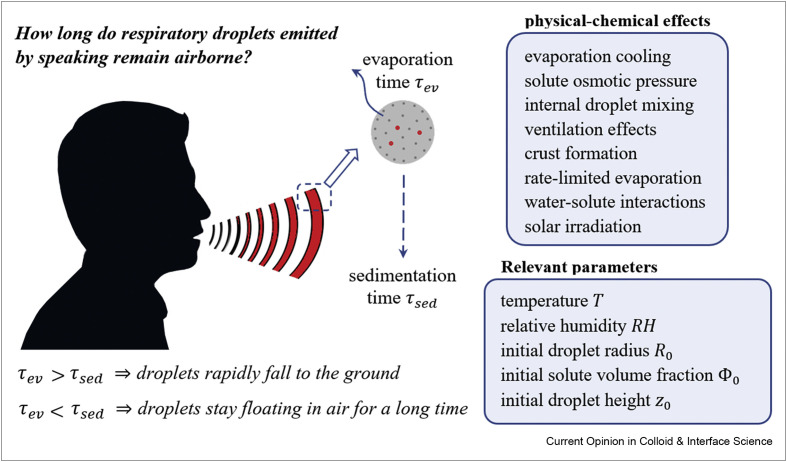
In addition to the uncertainties associated with the droplet-size distribution, the sedimentation and evaporation processes of saliva droplets expelled from the mouth or nose are affected by a variety of different physical and chemical effects, which make modeling of airborne virus transmission even more complex. These effects include the evaporation-induced cooling of the droplet [28,44, 45, 46], airflows and ventilation effects for large droplets [21,25,47], finite evaporation rate effects for small droplets [48,49], solar irradiation effect [50,51], and solute-induced effects, including water vapor-pressure lowering [52,53], local solute-concentration gradients [54, 55, 56], crust formation due to solute crystallization [54,57,58], liquid-liquid phase separation [59, 60, 61], and a possible solute-concentration dependence of the viscosity [62,63] and the water-diffusion coefficient [63,64] inside the droplet. These effects are themselves dominated by various parameters, such as the initial size of the droplet, the type and the initial volume fraction of solutes, the ambient temperature [47,50,65,66], the relative humidity [47,65,67, 68, 69, 70, 71], nonideal effects due to interparticle interactions inside the droplet [72,73], the internal morphology of droplets [59,74,75], and the initial height at which droplets are released into the air, as schematically shown in Figure 1 . Among these parameters, the relative humidity and the initial solute-volume fraction play key roles in determining the size of the droplet nuclei produced at the end of the evaporation process. Also, the morphology of the droplet nuclei is mainly controlled by the Péclet number [76,77], defined as the ratio of the particle-diffusion time inside the droplet to the droplet evaporation time [78], and the degree of saturation of the liquid solution [76]. The experimental results suggest that morphological and physical-chemical changes occurring during droplet evaporation may affect the viability of viruses and pathogens contained within the droplet [60] and, thus, influence the efficiency of airborne transmission of infectious diseases.
Figure 1.
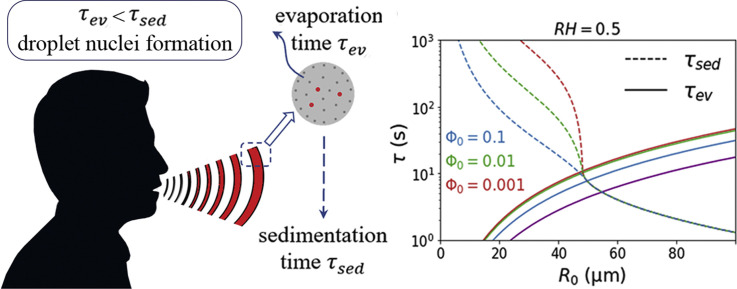
A main question regarding the airborne transmission of infection is how long human respiratory droplets stay floating in air. To answer this question, the evaporation and sedimentation processes of saliva droplets have to be characterized. If droplets are small enough to completely evaporate to so-called droplet nuclei before they hit the ground, they will remain airborne for hours. Larger droplets, however, fall to the ground in a few seconds. Sedimentation and evaporation times of droplets are controlled by various physical-chemical effects and relevant parameters, which are listed in the diagram.
All the aforementioned findings, contradictions, and complexities regarding the airborne transmission of infections highlight the need for coherent investigations of the physical-chemical fundamentals of aerosol droplet properties to help policy-makers develop more effective pandemic management models. Among the hygiene measures recently suggested to deal with SARS-CoV-2, social distancing and wearing a mouth cover [2,42,79] have been regarded as most effective means of reducing the person-to-person transmission of viruses, especially in indoor environments. Using the recent estimates of the average viral load in sputum [80] and the average droplet emission rate while speaking [42,43], the airborne viral air load caused by the constant speaking of a single infected person without a mouth cover is more than 104 virions at a given time, which results in a high virion inhalation frequency by an unmasked bystander of at least 2.5 per minute in a midsize indoor environment. For initial droplet radii larger than 20 μm, this amount is only moderately reduced by air-exchange rates in the typical range of up to about 20 per hour. Wearing mouth covers by both the infected person and passive bystanders not only significantly decreases this virion inhalation rate [81] but also decreases the travel distance of the droplets by half [82]. However, the use of a mask is inadequate alone because many droplets still spread around and away from the cover during cough cycles [82], and aerosol droplets can both penetrate and circumnavigate masks [5,83]. In particular, using a face mask that loosely fits the face [84] or covering a tight-fitting mask by cloth or medical masks [82] can increase the possibility of leakage around the mask's edge. In addition, nonmedical face masks have very low filter efficiency (2–38%) [85,86], and the mask efficiency is found to decrease during time (more than 8% after ten cough cycles [82]) and after washing [87]. On the other hand, social distancing alone does not provide complete protection from aerosols that remain suspended in the air or are carried by air currents [5]. The best recommendation so far is to both wear a medical mask and keep a sufficient social distance in indoor environments while keeping the relative humidity between 40% and 60%, which is the optimal relative humidity for human health in indoor places [28,67]. In outdoor environments, the airborne infection risk presumably is orders of magnitude less than the indoor risk [88] and, thus, fewer protective measures are needed.
Despite the vast research conducted in several directions after the SARS-CoV-2 pandemic, part of which was reviewed previously, there are many uncertainties and open questions regarding airborne virus transmission and its contribution to the spreading of infectious diseases, which require future research along different lines. This review summarizes various aspects of the physical chemistry behind this problem and presents simple equations that model the process of evaporation and sedimentation of respiratory aerosol droplets suspended in air. The equations provided in this review are derived using the diffusion-limited stagnant-flow approximation for a single droplet. This approximation is valid for droplets with initial radii between and , which includes the droplet size range that produces the largest viral air load [48]. The presence of a turbulent flow field around the droplet, which can be locally warm and moist and tends to slow down the droplet evaporation [20], is neglected here. The results are, therefore, relevant for respiratory aerosol droplets that remain airborne after leaving the moist and warm puff of exhaled air, that is, a few seconds after their release into the air. Also, the possibility of droplet coagulation due to interdroplet collisions [89] is neglected. This factor, which tends to decrease the mean sedimentation time by increasing the average droplet size [90], seems more relevant for droplets produced during violent respiratory activities such as coughing and sneezing, where the flow field is turbulent and the droplet concentration is sufficiently high. In the first few seconds after the droplets have been released into the air, they disperse over a wide volume, which results in a sharp decrease in the aerosol concentration [91] and considerably decreases the possibility of droplet coagulation. Thus, the stagnant-flow approximation and the single-droplet analysis used here are valid for aerosol droplets that remain suspended in air for more than a few seconds, which is much less than the typical sedimentation time of droplets that form droplet nuclei, which play the main role in airborne transmission of viruses and are the main subject of this review. Derivations of all equations are presented in the articles by Netz and Rezaei [48,92].
Results and discussion
Droplet sedimentation without evaporation
We briefly discuss the basic equations that describe the sedimentation process of a droplet without considering its size variation due to evaporation. A spherical droplet that is falling in a viscous medium (such as air) is mainly under the influence of gravitational and Stokesian-viscous forces that act in opposite directions. By balancing these two forces on a falling droplet with radius and mass density , the mean sedimentation time, that is, the time it takes for the droplet to reach the ground from an initial height of , follows as
| (1) |
where is the viscosity of air and is the gravitational acceleration. Considering the values for the viscosity of air and water density at 25 °C (Table 1 ), the numerical prefactor in Eq. (1) turns out to be . Therefore, a droplet with a radius of (the threshold radius given by the Wells model below which evaporation becomes important), which is initially placed at a height of (the average height above ground for the mouth of a standing human adult), needs to fall to the ground. It is worth noting that Eq. (1) neglects the time it takes for the droplet to reach its terminal velocity, which is a justifiable assumption according to Netz [48]. The dotted line in Figure 2 shows the sedimentation time calculated from Eq. (1) as a function of the droplet radius.
Table 1.
List of numerical constants at 25 °C [96].
| Viscosity of air | ||
| Liquid water density | ||
| Water diffusion constant in air | ||
| Water diffusion constant in water | ||
| Saturated water vapor concentration | ||
| Liquid water molecular volume | ||
| Condensation reaction rate constant |
Figure 2.
Evaporation and sedimentation times of pure water droplets as a function of the initial droplet radius for an initial height of . Results are shown for different relative humidities. Solid and broken lines indicate the evaporation times (Eq. (2)) and the sedimentation times (Eq. (4)), respectively. In the limit of , no evaporation takes place, and Eq. (4) yields a sedimentation time that equals Eq. (1) (shown by a dotted line), which neglects the evaporation-induced variation of the droplet size. Droplets with initial radii below the critical radius given by Eq. (5) (which is the initial radius at which the evaporation and sedimentation times are equal) completely evaporate before they hit the ground, and thus, their sedimentation time is infinity.
Droplet sedimentation and evaporation in the absence of nonvolatile solutes
Water evaporation decreases the radius of a falling droplet and, according to Eq. (1), increases the droplet sedimentation time. Therefore, it is important to account for evaporation effects in modeling the droplet sedimentation process. The evaporation process can be described by solving the coupled diffusion and heat flux equations outside the droplet, the latter of which accounts for the temperature reduction at the droplet surface due to the evaporation-induced cooling effect. The droplet size plays a key role in the derivation of the relevant equations. Another important parameter is the ratio of the water diffusion coefficient in air to the condensation reaction rate constant , which controls the characteristic droplet radius below which the droplet evaporation is reaction-rate-limited [48]. Considering the values of and at 25 °C (Table 1), this characteristic droplet radius is around . Therefore, water evaporation from droplets with radii smaller than is limited by the rate at which water molecules evaporate from the droplet surface, while for droplet radii larger than , the limiting factor is the speed at which water molecules diffuse away from the droplet [48]. For droplets larger than , the flow field around the sedimenting droplet accelerates the evaporation process and, at the same time, becomes non-Stokesian because of nonlinear hydrodynamics effects, which can be accounted for by using double-boundary-layer theory including concentration and flow boundary layers [48,93]. However, evaporation effects are negligible for droplets with radii larger than because they fall rapidly to the ground [1]. On the other hand, according to Eq. (1), it takes an extremely long time (more than 3 days) for droplets with radii smaller than to reach the ground, even if we neglect evaporation effects. Therefore, evaporation effects are most relevant in the radius range , where the diffusion-limited stagnant-flow approximation is valid. In this range, the evaporation time, which is defined as the time needed to shrink the droplet radius to zero, is given by Netz [48]
| (2) |
where is the initial droplet radius, is the relative air humidity, and is a numerical prefactor given by
| (3) |
, , and in Eq. (3) are the water diffusion constant in air, the saturated water-vapor concentration, and the water molecular volume in the liquid phase, respectively. The factor in Eq. (3) accounts for the evaporation-induced droplet cooling, where is a coefficient that describes the reduction of the water vapor concentration at the droplet surface due to the temperature depression and , with being the molecular evaporation enthalpy of water and the heat conductivity of air, controls the dependence of the temperature depression at the droplet surface on the relative humidity [48,92]. At a room temperature of 25 °C, the evaporation cooling factor equals , demonstrating that cooling considerably slows down the evaporation process. The values of , , and at 25 °C are listed in Table 1. Considering these values, the numerical prefactor defined in Eq. (3) turns out to be at 25 °C. It is worth mentioning that Eq. (2) is derived for a droplet in stagnant air, that is, the presence of a finite flow field around the droplet is neglected. A locally warm and moist environment will tend to delay evaporation [20] and thereby decrease the sedimentation time. As the moist and warm puff of exhaled air will expand and cool off over a few seconds while the typical sedimentation times we are concerned with are in the range of tens of seconds to a few minutes, the effects of an initially warm and moist environment can be neglected. The calculation leading to Eq. (2) uses the adiabatic approximation, that is, the water vapor concentration outside the droplet is taken as the stationary solution of the diffusion equation, which is justified because the droplet radius changes rather slowly. For a droplet with an initial radius of at a relative humidity of , a common value for indoor environments, Eq. (2) yields , which is longer than the sedimentation time estimated from Eq. (1) for the same parameters, leading to . As stated before, Eq. (1) neglects the effect of water evaporation on the droplet size. Considering evaporation, the droplet sedimentation time at a finite relative humidity can be written in terms of the evaporation time as [48]
| (4) |
According to Eq. (4), the sedimentation time of an evaporating water droplet with an initial radius of and an initial height of at a relative humidity of is , which is significantly larger than the value given by Eq. (1) in the absence of evaporation .
The critical droplet radius below which the droplet completely evaporates before falling to ground, that is, the droplet radius at which , can be calculated according to Eq. (4) as
| (5) |
For and , one obtains , which is very close to the threshold radius given by the classical Wells model (which however neglected evaporation cooling effects). In Figure 2, the sedimentation and evaporation times obtained from Eqs. (2), (4) are shown for an initial height of and different relative humidities. According to this figure, an increase in the relative humidity increases the evaporation time (due to the decreased evaporation rate in humid environments), which causes a slight decrease in sedimentation time of small droplets. This figure also shows that the critical droplet radius below which evaporation effects become important decreases with relative humidity, as follows from Eq. (5).
Droplet sedimentation and evaporation in the presence of nonvolatile solutes
Saliva comprises a volume percentage of about 99.5% water but also contains a variety of organic and inorganic substances such as salt, proteins, peptides, mucins, enzymes, and so on [94]. SARS-CoV-2 patient sputum is reported [80] to additionally include viral RNAs per milliliter on average, with a maximum of copies per milliliter. Accordingly, a saliva droplet with a radius of is expected to carry exactly one virion on average and up to virions considering the upper bound of the virion concentration in sputum. Of course, the viral load in sputum is crucially dependent on the time elapsed since the onset of symptoms. To provide more precise estimates, further experiments are required to directly measure the viral load in aerosol droplets. According to previous reports for diverse viruses, the vast majority of infectious aerosols presumably include only one to a few virions [95].
The presence of nonvolatile components (including virions) within an evaporating saliva droplet causes a reduction in the water vapor concentration at the droplet surface [52,53], which decreases the water evaporation rate and produces a lower limit for the water concentration and, consequently, the droplet radius that can be reached by evaporation. Neglecting the possibility of crust formation due to phase separation at the droplet surface when the solute solubility limit is reached [92], the droplet radius at the end of the evaporation process can be expressed as [48,92]
| (6) |
where is the initial volume fraction of solutes, and is the water activity coefficient that accounts for nonideal effects caused by water-solute and solute-solute interactions. According to Eq. (6), the evaporation-equilibrium radius of a droplet for ideal solution conditions with an initial solute volume fraction of at is , while the same droplet in completely dry air with dries out to the minimal possible radius of .
Assuming that water diffusion inside the droplet is sufficiently rapid, so that the water concentration remains homogeneous during the evaporation process, the time it takes for the droplet radius to shrink from its initial value to can be approximated as [48]
| (7) |
Again, effects of the initially moist and warm gas cloud that surrounds the droplets released during respiratory activities will extend the droplet evaporation time and are neglected here. Also, the solute-concentration dependence of evaporation cooling is neglected in the derivation of Eq. (7). As detailed in the study by Rezaei and Netz [92], solute effects on the evaporation cooling can be accounted for by replacing , which describes evaporation cooling of a pure water droplet (Eq. (3)), by , where is the momentary volume fraction of solutes that increases over time. Replacing by in the calculations leading to Eq. (7), however, gives rise to a differential equation that is not analytically solvable and thus has to be solved numerically, as will be discussed later in this article.
The logarithmic term in Eq. (7) reflects the osmotic slowing down of evaporation due to the solute-induced water vapor-pressure reduction. According to Figure 3 , this term only becomes relevant for droplet radii close to the final equilibrium radius , where the droplet has lost most of its water content and enters the solute-dominated evaporation regime. Independent of its initial size, a droplet is found to enter the solute-dominated regime when its radius becomes smaller than [48]. In this regime, solute effects cause a diverging evaporation time, as demonstrated in Figure 3. These effects are, however, negligible in the case of droplets with low initial solute volume fraction (see Figure 3 and inset). In such case, nonideal effects due to solute-water and solute-solute interactions are small, and thus, the liquid solution can be considered ideal. Accordingly, one can neglect the logarithmic term and after that set and in Eq. (7) to obtain an approximate expression for the evaporation time in the presence of solutes in terms of the evaporation time of a pure water droplet
| (8) |
Figure 3.
Variation of the droplet radius with time in the presence of nonvolatile solutes according to Eq. (7). The liquid solution is assumed ideal , and data are shown for initial droplet radius , relative humidity , and two different initial solute volume fractions of (main figure) and (inset). The y-axis is rescaled by , the equilibrium radius of the droplet at the end of the evaporation process (Eq. (6)). Solid and dashed lines indicate the results considering and neglecting the effect of the solute-induced water vapor-pressure reduction (which is reflected by the logarithmic term in Eq. (7)), respectively.
Eq. (8) accounts for the decreased droplet evaporation time due to the solute-induced increased size of the droplet nucleus produced at the end of the evaporation process. This factor affects the sedimentation time of droplets that are small enough to reach their equilibrium size before falling to the ground. In such case, the sedimentation time can be split into two stages: In the first stage, the droplet radius shrinks to its equilibrium value because of water evaporation, and in the second stage, the droplet stays sedimenting in air for an extended time while its radius remains constant. For larger droplets that hit the ground before they reach their final equilibrium size, Eq. (4) describes the sedimentation time very accurately. Accordingly, the total sedimentation time of a solute-containing droplet follows from Eqs. (1), (4), (8) as
| (9) |
with being the distance by which the droplet falls during its evaporation time.
Figure 4a shows the evaporation and sedimentation times obtained from Eqs. (8), (9) as a function of the initial droplet radius . This figure is plotted for an initial solute volume fraction , initial height , and different relative humidities. The main difference between this figure and Figure 2 (for pure water droplets) is that here, droplets do not disappear at the end of the evaporation process but reach a minimal size, as discussed previously. Therefore, even droplets with initial radii smaller than sediment to the ground in a finite time, as demonstrated in Figure 4. For and , the droplet already initially has its equilibrium size, as follows from Eq. (6), meaning that no evaporation takes place and the droplet size remains constant during the sedimentation process. In such case, Eq. (9) recovers the result of Eq. (1) (the black dotted line in Figure 4a), which neglects the evaporation-induced variation of the droplet size. Figure 4b shows the results for fixed relative humidity and different initial solute volume fractions. This figure indicates that for , which covers the range of solute volume fractions reported for saliva droplets [94], the critical radius is almost independent of . For higher values of , however, slightly decreases with increasing . For and , the droplet is initially in the evaporation-equilibrium state (Eq. (6)), and thus, Eq. (9) recovers the result of Eq. (1). Figure 4 also indicates that the typical sedimentation time of small droplets that dry quickly enough to form droplet nuclei (i.e. those for which ) is in the range of tens of seconds to a few minutes, which is much longer than the time it typically takes for the warm and moist exhaled vapor puff around the droplets to disappear. The approximation of a single droplet in stagnant air is, therefore, valid for such droplets, as discussed in Section 1.
Figure 4.
Evaporation and sedimentation times as a function of the initial radius in the presence of nonvolatile solutes, for an initial height of . Panel (a) shows results for a fixed initial solute volume fraction and different relative humidities. Panel (b) shows results for a fixed relative humidity and different initial solute volume fractions. Solid and broken lines indicate the evaporation and sedimentation times, which are obtained from Eqs. (8), (9), respectively. For and , and and , no evaporation takes place, and Eq. (9) recovers the result of Eq. (1) (shown by dotted lines).
Solute-induced osmotic effects
As stated previously, the effect of the solute-induced water vapor-pressure reduction is neglected in the derivation of Eq. (8). To account for such effect, one can define the evaporation time as the time at which the radius has almost reached its equilibrium value, , because according to Eq. (7), the time it takes for the droplet radius to reach its equilibrium value is infinity. Using this definition, the evaporation time of a solute-containing droplet can be estimated from Eq. (7) as
| (10) |
Broken and dotted lines in Figure 5 a show the evaporation times calculated with (Eq. (10)) and without (Eq. (8)) considering the solute-induced water vapor-pressure reduction, respectively. This figure clearly shows that solute effects significantly increase the droplet evaporation time, especially in the case of droplets with high initial solute volume fraction. Such an increase in the evaporation time tends to decrease the critical radius below which a droplet completely evaporates before reaching the ground, compared with what is shown in Figure 4. Figure 5a also indicates that an increase in the initial solute volume fraction causes a nonmonotonic variation of the evaporation time, which cannot be captured when the water vapor-pressure reduction effect is neglected.
Figure 5.
Evaporation time as a function of the initial solute volume fraction . The liquid solution is assumed ideal , and the initial droplet radius is . Panel (a) shows results for different relative humidities. Solid lines indicate results from Eq. (11), which accounts for the solute-induced water vapor-pressure reduction, the presence of internal concentration and diffusivity profiles, and the solute-concentration dependence of evaporation cooling. Dashed lines show the results from Eq. (10), which neglects the presence of internal concentration and diffusivity profiles and the solute-concentration dependence of evaporation cooling, but accounts for the solute-induced water vapor-pressure reduction. Dotted lines indicate the results from Eq. (8), in which the water vapor-pressure reduction is also neglected. Panel (b) shows the evaporation times estimated from Eq. (11) (solid line) along with those obtained from numerical solutions of the heat-conduction and water-diffusion equations for fixed relative humidity . Open squares indicate results that account for the solute-induced water vapor-pressure reduction, the presence of internal concentration and diffusivity profiles, the solute-concentration dependence of evaporation cooling, and the dependence of the water diffusivity on the local solute concentration profile. Downward triangles are obtained for infinitely rapid water diffusion in the droplet (i.e. neglecting internal water concentration gradients), filled circles are obtained for a constant but finite water diffusivity inside the droplet, and upward triangles are obtained for a constant finite water diffusivity inside the droplet and additionally neglecting the solute-concentration dependence of the evaporation cooling effect by setting (Eq. (3)) in numerical calculations.
Effect of internal concentration and diffusivity profiles and the solute-concentration dependence of evaporation cooling
Although Eq. (7) provides a rather accurate approximation for the evaporation time in the presence of nonvolatile solutes, this equation neglects a few important details of the evaporation process, such as the reduced evaporation cooling in the presence of solutes and the solute-concentration dependence of the water diffusivity within the liquid droplet. Most importantly, Eq. (7) is derived using the assumption of a homogeneous solute concentration inside the droplet, while fast water evaporation will increase the solute concentration at the droplet surface and thus create a water concentration gradient in the droplet. To account for these effects, one needs to solve the diffusion and heat-conduction equations both inside and outside the droplet with the boundary condition set by water and solute mass conservation. Although the resulting equations are not analytically solvable, the evaporation time can be accurately approximated using numerical methods described in the study by Rezaei and Netz [92] as
| (11) |
where is a numerical prefactor that has units of a diffusion constant. It is worth noting that Eq. (11) is obtained by fitting a heuristic function to the numerical data. Solid lines in Figure 5a show the evaporation times obtained from Eq. (11), considering the internal concentration and diffusivity profiles and the solute-concentration dependence of the evaporation cooling effect. This figure clearly shows that the cumulative effect of these mechanisms is not significant, especially at low to medium relative humidity conditions, and thus Eq. (10) estimates the evaporation time rather accurately.
Figure 5b shows the evaporation time obtained from numerical solutions of the complete water and heat transport equations inside and outside the droplet for fixed relative humidity and different initial solute volume fractions using the adiabatic approximation, with and without considering effects that arise from an inhomogeneous water-concentration profile within the droplet. To account for the solute-concentration dependence of the water diffusivity, the internal water diffusivity is assumed to follow the heuristic expression , with and being the water diffusion coefficients in the presence and in the absence of solutes, respectively, being the time-dependent solute-concentration profile, and being a solute-specific coefficient. This linear equation with describes the water diffusivity in NaCl salt solutions rather accurately [63]. The results obtained with and without considering the concentration dependence of the water diffusivity are shown in Figure 5b by open squares and solid circles, respectively, indicating that this effect is rather negligible. This figure also shows that neglecting water concentration gradients inside the droplet, corresponding to an infinitely fast water diffusivity within the droplet , slightly underestimates the evaporation time (downward triangles), while neglecting the solute-concentration dependence of the evaporation cooling effect, which corresponds to using in numerical calculations, leads to a slight overestimate of the evaporation time (upward triangles).
Conclusion
The contribution of airborne aerosols to the spread of infectious diseases, such as influenza and SARS-CoV-2, is a controversial issue that has been the subject of numerous articles, reports, and guidelines. Recent experiments reported that viruses can remain infectious in aerosols for a long time [10, 11, 12] and thus stress the importance of this issue in the context of effective hygiene measures. The basic question is “how long do respiratory droplets remain airborne?”. According to experiments [1], the answer to this question is mainly dependent on the droplet size: Small droplets completely evaporate before they hit the ground and remain airborne as so-called droplet nuclei for a long time, whereas larger droplets rapidly fall to the ground. Accordingly, the physical-chemical effects that control the droplet evaporation process, such as evaporation cooling and solute-induced effects, play key roles in determining the droplet sedimentation time. Analytical investigations [48] show that evaporation-induced cooling of droplets considerably slows down the evaporation process and, thus, decreases the probability of droplet nuclei formation. Neglecting this factor in numerical and theoretical models, therefore, causes an overestimate of the viral air load. Comparing the results for pure water droplets with those for solute-containing droplets, it transpires that the presence of solutes reduces the evaporation speed and thereby also the evaporation-cooling of the droplet [84]. In fact, the analysis shows that the solute-induced slowdown of the evaporation process is not only due to the solute-induced water vapor-pressure reduction but also due to local water concentration gradients inside the droplet that result from the drying process of solute-containing droplets [92]. On the other hand, the presence of solutes tends to decrease the droplet evaporation time by producing a lower limit for the water concentration inside the droplet that can be reached by evaporation, although this effect is rather small. In addition, the presence of solutes also affects the water diffusivity in the liquid droplet. The numerical analysis [92], however, reveals that this does not significantly affect the droplet evaporation time.
The factors that affect droplet evaporation are controlled by various parameters, such as the initial droplet size, the type and the initial volume fraction of solutes, the ambient temperature, the relative humidity, nonideal effects due to solute interactions inside the droplet, and the internal morphology of the droplet. Among these parameters, the relative humidity and the initial solute volume fraction are found to play key roles in determining the size of the droplet nuclei that form at the end of the evaporation process. According to analytical investigations [48], an increase in either the initial solute volume fraction or the relative humidity increases the final equilibrium radius of droplets, which causes a reduction of the mean time droplet nuclei can remain airborne. The morphology of droplet nuclei, which is expected to affect the viability of contained viruses [60], is mainly dominated by the solubility limit of solutes and the ratio of the particle-diffusion time inside the droplet to the droplet evaporation time. Also, the critical droplet radius below which droplets are expected to completely evaporate to droplet nuclei is found to decrease with an increasing relative humidity while this parameter is almost independent of the initial solute volume fraction.
To complement our current comprehension of airborne virus transmission, more accurate experiments are needed to measure the precise size distribution of droplets produced by different respiratory activities, the virus content of saliva droplets at different infection stages, and the mean time that viruses remain infectious in droplet nuclei in different environmental conditions. Also, a few open questions regarding the evaporation process of aerosol droplets should be answered: (I) How do nonideality effects due to solute-water interactions affect the drying process? (II) What is the exact mechanism of water evaporation in the presence of dry crusts formed due to crystallization of salts and organic solutes? (III) What happens after the formation of gel-like skins that are expected to form on the surface of biopolymer-containing droplets?
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors gratefully acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG) via grant NE810/11 and the SFB 1114 (project C02) and by the European Research Council (ERC) Advanced Grant NoMaMemo No. 835117.
This review comes from a themed issue on Hot Topic: COVID-19
Edited by Reinhard Miller and Libero Liggieri
References
- 1.Wells W.F. ON air-borne infection∗: study II. Droplets and droplet nuclei. Am J Epidemiol. 1934;20:611–618. [Google Scholar]
- 2.Leung Nancy H.L., Chu Daniel K.W., Shiu Eunice Y.C., Chan Kwok-Hung, McDevitt James J., Hau Benien J.P., Yen Hui-Ling, Li Yuguo, Ip Dennis K.M., Malik Peiris JS, Seto Wing-Hong, Leung Gabriel M., Milton Donald K., Cowling Benjamin J. Respiratory virus shedding in exhaled breath and efficacy of face masks. Nat Med. 2020;26:676–680. doi: 10.1038/s41591-020-0843-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schulman J.L., Kilbourne E.D. Experimental transmission OF influenza virus infection IN mice. II. Some factors affecting the incidence OF transmitted infection. J Exp Med. 1963;118:267–275. doi: 10.1084/jem.118.2.267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bridges C., Kuehnert M., Hall C. Transmission of influenza: implications for control in health care settings. Clin Infect Dis. 2003;37:1094–1101. doi: 10.1086/378292. [DOI] [PubMed] [Google Scholar]
- 5.Klompas M., Baker M., Rhee C. Airborne transmission of SARS-CoV-2: theoretical considerations and available evidence. J Am Med Assoc. 2020;324 doi: 10.1001/jama.2020.12458. [DOI] [PubMed] [Google Scholar]
- 6.E. National Academies of Sciences . The National Academies Press; Washington, DC: 2020. Medicine, airborne transmission of SARS-CoV-2: proceedings of a workshop—in brief. [PubMed] [Google Scholar]
- 7.Prather K.A., Marr L.C., Schooley R.T., McDiarmid M.A., Wilson M.E., Milton D.K. Airborne transmission of SARS-CoV-2. Science. 2020;370:303. doi: 10.1126/science.abf0521. [DOI] [PubMed] [Google Scholar]
- 8.Samet J.M., Prather K., Benjamin G., Lakdawala S., Lowe J.-M., Reingold A., Volckens J., Marr L.C. Airborne transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2): what we know. Clin Infect Dis. 2021 doi: 10.1093/cid/ciab039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Basu S., Kabi P., Chaudhuri S., Saha A. Insights on drying and precipitation dynamics of respiratory droplets from the perspective of COVID-19. Phys Fluids. 2020;32:123317. doi: 10.1063/5.0037360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.O. World Health . World Health Organization; Geneva: 2007. Infection prevention and control of epidemic- and pandemic-prone acute respiratory diseases in health care : WHO interim guidelines. World Health Organization, Geneva. [PubMed] [Google Scholar]
- 11.Gralton J., Tovey E., McLaws M.-L., Rawlinson W.D. The role of particle size in aerosolised pathogen transmission: a review. J Infect. 2011;62:1–13. doi: 10.1016/j.jinf.2010.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kulmala M., Vesala T., Wagner P.E. An analytical expression for the rate of binary condensational particle growth: comparison with numerical results. J Aerosol Sci. 1992;23:133–136. [Google Scholar]
- van Doremalen N., Bushmaker T., Morris D.H., Holbrook M.G., Gamble A., Williamson B.N., Tamin A., Harcourt J.L., Thornburg N.J., Gerber S.I., Lloyd-Smith J.O., de Wit E., Munster V.J. Aerosol and surface stability of HCoV-19 (SARS-CoV-2) compared to SARS-CoV-1. N Engl J Med. 2020;382:1564–1567. doi: 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]; The aerosol and surface stabilities of SARS-CoV-2 and SARS-CoV-1 are analysed to estimate the decay rate of viruses using a Bayesian regression model and to show that viruses can remain infectious in aerosols for hours and on surfaces up to days.
- 14.Asadi S., Bouvier N., Wexler A.S., Ristenpart W.D. The coronavirus pandemic and aerosols: does COVID-19 transmit via expiratory particles? Aerosol Sci Technol. 2020;54:635–638. doi: 10.1080/02786826.2020.1749229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieber C., Melekidis S., Koch R., Bauer H.-J. Insights into the evaporation characteristics of saliva droplets and aerosols: levitation experiments and numerical modeling. J Aerosol Sci. 2021;154:105760. doi: 10.1016/j.jaerosci.2021.105760. [DOI] [PMC free article] [PubMed] [Google Scholar]; The equilibrium radius of saliva droplets is measured using acoustic levitator and microscopic imaging and the results are used to establish the Wells evaporation-falling curve.
- Biswas P., Dhawan S. 2020. Evaporation of emitted droplets are an important factor Affecting the lifetime of the airborne coronavirus. [Google Scholar]; A methodology for the coupling of aerosol phenomena, such as evaporation and particle transport, is proposed to accurately establish the lifetimes of droplets.
- 17.Wang H., Li Z., Zhang X., Zhu L., Liu Y., Wang S. The motion of respiratory droplets produced by coughing. Phys Fluids. 2020;32:125102. doi: 10.1063/5.0033849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vuorinen V., Aarnio M., Alava M., Alopaeus V., Atanasova N., Auvinen M., Balasubramanian N., Bordbar H., Erästö P., Grande R., Hayward N., Hellsten A., Hostikka S., Hokkanen J., Kaario O., Karvinen A., Kivistö I., Korhonen M., Kosonen R., Kuusela J., Lestinen S., Laurila E., Nieminen H.J., Peltonen P., Pokki J., Puisto A., Råback P., Salmenjoki H., Sironen T., Österberg M. Modelling aerosol transport and virus exposure with numerical simulations in relation to SARS-CoV-2 transmission by inhalation indoors. Saf Sci. 2020;130:104866. doi: 10.1016/j.ssci.2020.104866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhang S., Lin Z. Dilution-based evaluation of airborne infection risk - thorough expansion of wells-riley model. medRxiv. 2020;194:107674. doi: 10.1016/j.buildenv.2021.107674. 2020.10.03.20206391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chong K.L., Ng C.S., Hori N., Yang R., Verzicco R., Lohse D. Extended lifetime of respiratory droplets in a turbulent vapor puff and its implications on airborne disease transmission. Phys Rev Lett. 2021;126 doi: 10.1103/PhysRevLett.126.034502. [DOI] [PubMed] [Google Scholar]; Numerical simulations are used to show that the evaporation time of small droplets in the expelled humid puff is considerably longer than what is suggested by the classical Wells model.
- 21.Wei J., Li Y. Airborne spread of infectious agents in the indoor environment. Am J Infect Contr. 2016;44:S102–S108. doi: 10.1016/j.ajic.2016.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ai Z.T., Melikov A.K. Airborne spread of expiratory droplet nuclei between the occupants of indoor environments: a review. Indoor Air. 2018;28:500–524. doi: 10.1111/ina.12465. [DOI] [PubMed] [Google Scholar]
- 23.Scharfman B.E., Techet A.H., Bush J.W.M., Bourouiba L. Visualization of sneeze ejecta: steps of fluid fragmentation leading to respiratory droplets. Exp Fluid. 2016;57:24. doi: 10.1007/s00348-015-2078-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bourouiba L., Dehandschoewercker E., Bush John W.M. Violent expiratory events: on coughing and sneezing. J Fluid Mech. 2014;745:537–563. [Google Scholar]
- 25.Kukkonen J., Vesala T., Kulmala M. The interdependence of evaporation and settling for airborne freely falling droplets. J Aerosol Sci. 1989;20:749–763. [Google Scholar]
- 26.Dbouk T., Drikakis D. On coughing and airborne droplet transmission to humans. Phys Fluids. 2020;32 doi: 10.1063/5.0011960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Li H., Leong F.Y., Xu G., Ge Z., Kang C.W., Lim K.H. Dispersion of evaporating cough droplets in tropical outdoor environment. Phys Fluids. 2020;32:113301. doi: 10.1063/5.0026360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Božič A., Kanduc M. Relative humidity in droplet and airborne transmission of disease. J Biol Phys. 2021;47:1–29. doi: 10.1007/s10867-020-09562-5. [DOI] [PMC free article] [PubMed] [Google Scholar]; This paper reviews the physical principles that govern the fate of virus-containing respiratory droplets, with a focus on the role of relative humidity.
- 29.Duguid J.P. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. Epidemiol Infect. 1946;44:471–479. doi: 10.1017/s0022172400019288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Papineni R.S., Rosenthal F.S. The size distribution of droplets in the exhaled breath of healthy human subjects. J Aerosol Med. 1997;10:105–116. doi: 10.1089/jam.1997.10.105. [DOI] [PubMed] [Google Scholar]
- 31.Yang S., Lee G.W.M., Chen C.-M., Wu C.-C., Yu K.-P. The size and concentration of droplets generated by coughing in human subjects. J Aerosol Med. 2007;20:484–494. doi: 10.1089/jam.2007.0610. [DOI] [PubMed] [Google Scholar]
- 32.Xie X., Li Y., Sun H., Liu L. Exhaled droplets due to talking and coughing. J R Soc Interface. 2009;6(suppl_6):S703–S714. doi: 10.1098/rsif.2009.0388.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhang H., Li D., Xie L., Xiao Y. Documentary research of human respiratory droplet characteristics. Procedia Eng. 2015;121:1365–1374. doi: 10.1016/j.proeng.2015.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chao C.Y.H., Wan M.P., Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M., Mengersen K., Corbett S., Li Y., Xie X., Katoshevski D. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. J Aerosol Sci. 2009;40:122–133. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Johnson G.R., Morawska L., Ristovski Z.D., Hargreaves M., Mengersen K., Chao C.Y.H., Wan M.P., Li Y., Xie X., Katoshevski D., Corbett S. Modality of human expired aerosol size distributions. J Aerosol Sci. 2011;42:839–851. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Somsen G.A., van Rijn C., Kooij S., Bem R.A., Bonn D. Small droplet aerosols in poorly ventilated spaces and SARS-CoV-2 transmission. Lancet Respir Med. 2020;8:658–659. doi: 10.1016/S2213-2600(20)30245-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fernstrom A., Goldblatt M. Aerobiology and its role in the transmission of infectious diseases. J Pathog. 2013;2013:493960. doi: 10.1155/2013/493960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Fiegel J., Clarke R., Edwards D.A. Airborne infectious disease and the suppression of pulmonary bioaerosols. Drug Discov Today. 2006;11:51–57. doi: 10.1016/S1359-6446(05)03687-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asadi S., Wexler A.S., Cappa C.D., Barreda S., Bouvier N.M., Ristenpart W.D. Aerosol emission and superemission during human speech increase with voice loudness. Sci Rep. 2019;9:2348. doi: 10.1038/s41598-019-38808-z. [DOI] [PMC free article] [PubMed] [Google Scholar]; Experimental data is used to show that the rate of particle emission during normal human speech is positively correlated with the loudness of vocalization.
- 40.Mürbe D., Kriegel M., Lange J., Rotheudt H., Fleischer M. Aerosol emission is increased in professional singing. OSF Preprints. 2020 doi: 10.31219/osf.io/znjeh. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mürbe D., Kriegel M., Lange J., Schumann L., Hartmann A., Fleischer M. Aerosol emission of adolescents voices during speaking, singing and shouting. PloS One. 2021;16 doi: 10.1371/journal.pone.0246819. [DOI] [PMC free article] [PubMed] [Google Scholar]; A laser particle counter in cleanroom conditions is used to show that adolescents emit fewer aerosol particles during singing than suggested by previous estimates for adults.
- Anfinrud P., Stadnytskyi V., Bax C.E., Bax A. Visualizing speech-generated oral fluid droplets with laser light scattering. N Engl J Med. 2020;382:2061–2063. doi: 10.1056/NEJMc2007800. [DOI] [PMC free article] [PubMed] [Google Scholar]; A laser light-scattering experiment is used to accurately measure and visualize speech-generated droplets and their trajectories.
- Stadnytskyi V., Bax C.E., Bax A., Anfinrud P. The airborne lifetime of small speech droplets and their potential importance in SARS-CoV-2 transmission. Proc Natl Acad Sci Unit States Am. 2020;117:11875. doi: 10.1073/pnas.2006874117. [DOI] [PMC free article] [PubMed] [Google Scholar]; Highly sensitive laser light scattering methods are used to show that loud speech can emit thousands of oral fluid droplets per second, which is far more than what could be detected previously.
- 44.Sazhin S.S., Rybdylova O., Pannala A.S., Somavarapu S., Zaripov S.K. A new model for a drying droplet. Int J Heat Mass Tran. 2018;122:451–458. [Google Scholar]
- 45.Xu X., Ma L. Analysis of the effects of evaporative cooling on the evaporation of liquid droplets using a combined field approach. Sci Rep. 2015;5:8614. doi: 10.1038/srep08614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Su Y.-y., Miles R.E.H., Li Z.-m., Reid J.P., Xu J. The evaporation kinetics of pure water droplets at varying drying rates and the use of evaporation rates to infer the gas phase relative humidity. Phys Chem Chem Phys. 2018;20:23453–23466. doi: 10.1039/c8cp05250f. [DOI] [PubMed] [Google Scholar]
- 47.Wang B., Wu H., Wan X.-F. Transport and fate of human expiratory droplets—a modeling approach. Phys Fluids. 2020;32 doi: 10.1063/5.0021280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Netz R.R. Mechanisms of airborne infection via evaporating and sedimenting droplets produced by speaking. J Phys Chem B. 2020;124:7093–7101. doi: 10.1021/acs.jpcb.0c05229. [DOI] [PMC free article] [PubMed] [Google Scholar]; Analytical equations are presented for the droplet evaporation and sedimentation times, including evaporation cooling and solute osmotic-pressure effects.
- 49.Netz R.R., Eaton W.A. Physics of virus transmission by speaking droplets. Proc Natl Acad Sci Unit States Am. 2020;117:25209. doi: 10.1073/pnas.2011889117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Dombrovsky L.A., Fedorets A.A., Levashov V.Y., Kryukov A.P., Bormashenko E., Nosonovsky M. Modeling evaporation of water droplets as applied to survival of airborne viruses. Atmosphere. 2020;11 [Google Scholar]
- 51.Heck K., Coltman E., Schneider J., Helmig R. Influence of radiation on evaporation rates: a numerical analysis. Water Resour Res. 2020;56 [Google Scholar]
- 52.Donati E.R., Andrade–Gamboa J. Kinetic approach for the vapor pressure lowering by non volatile solutes. Educ Quím. 2010;21:274–277. [Google Scholar]
- 53.Yang Y., Cao Q., Song B., Wang Y., Fan J.-N., Liu F., Zhang Y., Zhang Y. Applicability of vapor pressure models on the prediction of evaporation and motion of sulfuric and hydrochloric droplets in free-falling process. Build Environ. 2021;189:107533. [Google Scholar]
- 54.Otero Fernandez M., Thomas R.J., Oswin H., Haddrell A.E., Reid J.P. Transformative approach to investigate the microphysical factors influencing airborne transmission of pathogens. Appl Environ Microbiol. 2020;86 doi: 10.1128/AEM.01543-20. e01543-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bandyopadhyay A., Pawar A., Venkataraman C., Mehra A. Modelling size and structure of nanoparticles formed from drying of submicron solution aerosols. J Nanopart Res. 2015;17:1–14. [Google Scholar]
- 56.Gregson F.K.A., Robinson J.F., Miles R.E.H., Royall C.P., Reid J.P. Drying kinetics of salt solution droplets: water evaporation rates and crystallization. J Phys Chem B. 2019;123:266–276. doi: 10.1021/acs.jpcb.8b09584. [DOI] [PubMed] [Google Scholar]
- 57.Misyura S.Y. The crystallization behavior of the aqueous solution of CaCl2 salt in a drop and a layer. Sci Rep. 2020;10:256. doi: 10.1038/s41598-019-57169-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Dai S., Shin H., Santamarina J. Formation and development of salt crusts on soil surfaces. Acta Geotech. 2016;11 [Google Scholar]
- 59.Freedman M.A. Liquid–liquid phase separation in supermicrometer and submicrometer aerosol particles. Acc Chem Res. 2020;53:1102–1110. doi: 10.1021/acs.accounts.0c00093. [DOI] [PubMed] [Google Scholar]
- 60.Vejerano E.P., Marr L.C. Physico-chemical characteristics of evaporating respiratory fluid droplets. J R Soc Interface. 2018;15:20170939. doi: 10.1098/rsif.2017.0939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.O'Brien R.E., Wang B., Kelly S.T., Lundt N., You Y., Bertram A.K., Leone S.R., Laskin A., Gilles M.K. Liquid–liquid phase separation in aerosol particles: imaging at the nanometer scale. Environ Sci Technol. 2015;49:4995–5002. doi: 10.1021/acs.est.5b00062. [DOI] [PubMed] [Google Scholar]
- 62.Simha R. Effect of concentration on the viscosity of dilute solutions. J Res Natl Bur Stand. 1949;42:409–418. doi: 10.6028/jres.042.036. [DOI] [PubMed] [Google Scholar]
- 63.Kim J.S., Wu Z., Morrow A.R., Yethiraj A., Yethiraj A. Self-diffusion and viscosity in electrolyte solutions. J Phys Chem B. 2012;116:12007–12013. doi: 10.1021/jp306847t. [DOI] [PubMed] [Google Scholar]
- 64.Teng X., Huang Q., Dharmawardhana C.C., Ichiye T. Diffusion of aqueous solutions of ionic, zwitterionic, and polar solutes. J Chem Phys. 2018;148 doi: 10.1063/1.5023004. 222827-222827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Zhao L., Qi Y., Luzzatto-Fegiz P., Cui Y., Zhu Y. COVID-19: effects of environmental conditions on the propagation of respiratory droplets. Nano Lett. 2020;20:7744–7750. doi: 10.1021/acs.nanolett.0c03331. [DOI] [PubMed] [Google Scholar]
- 66.Shadloo-Jahromi A., Bavi O., Hossein Heydari M., Kharati-Koopaee M., Avazzadeh Z. Dynamics of respiratory droplets carrying SARS-CoV-2 virus in closed atmosphere. Results Phys. 2020;19:103482. doi: 10.1016/j.rinp.2020.103482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ahlawat A., Wiedensohler A., Mishra S.K. An overview on the role of relative humidity in airborne transmission of SARS-CoV-2 in indoor environments. Aerosol Air Qual Res. 2020;20:1856–1861. [Google Scholar]
- 68.Marr L., Tang J., Van Mullekom J., Lakdawala S. Mechanistic insights into the effect of humidity on airborne influenza virus survival, transmission and incidence. J R Soc Interface. 2019;16:20180298. doi: 10.1098/rsif.2018.0298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Yang W., Marr L.C. Dynamics of airborne influenza A viruses indoors and dependence on humidity. PloS One. 2011;6 doi: 10.1371/journal.pone.0021481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Walker J.S., Archer J., Gregson F.K.A., Michel S.E.S., Bzdek B.R., Reid J.P. Accurate representations of the microphysical processes occurring during the transport of exhaled aerosols and droplets. ACS Cent Sci. 2021;7:200–209. doi: 10.1021/acscentsci.0c01522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Chaudhuri S., Basu S., Kabi P., Unni V.R., Saha A. Modeling the role of respiratory droplets in Covid-19 type pandemics. Phys Fluids. 2020;32 doi: 10.1063/5.0015984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Xue H., Moyle A.M., Magee N., Harrington J.Y., Lamb D. Experimental studies of droplet evaporation kinetics: validation of models for binary and ternary aqueous solutions. J Atmos Sci. 2005;62:4310–4326. [Google Scholar]
- 73.Fang B., Chen L., Li G., Wang L. Multi-component droplet evaporation model incorporating the effects of non-ideality and thermal radiation. Int J Heat Mass Tran. 2019;136:962–971. [Google Scholar]
- 74.Maurice U., Mezhericher M., Levy A., Borde I. Drying of droplets containing insoluble nanoscale particles: second drying stage. Dry Technol. 2015;33:1837–1848. [Google Scholar]
- 75.Boel E., Koekoekx R., Dedroog S., Babkin I., Vetrano M.R., Clasen C., Van den Mooter G. Unraveling particle formation: from single droplet drying to spray drying and electrospraying. Pharmaceutics. 2020;12 doi: 10.3390/pharmaceutics12070625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Ordoubadi M., Gregson F.K.A., Melhem O., Barona D., Miles R.E.H., D’Sa D., Gracin S., Lechuga-Ballesteros D., Reid J.P., Finlay W.H., Vehring R. Multi-solvent microdroplet evaporation: modeling and measurement of spray-drying kinetics with inhalable pharmaceutics. Pharmaceut Res. 2019;36:100. doi: 10.1007/s11095-019-2630-7. [DOI] [PubMed] [Google Scholar]
- 77.Wei Y., Deng W., Chen R.-H. Effects of insoluble nano-particles on nanofluid droplet evaporation. Int J Heat Mass Tran. 2016;97:725–734. [Google Scholar]
- 78.Vehring R. Pharmaceutical particle engineering via spray drying. Pharmaceut Res. 2008;25:999–1022. doi: 10.1007/s11095-007-9475-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Stutt R.O.J.H., Retkute R., Bradley M., Gilligan C.A., Colvin J. A modelling framework to assess the likely effectiveness of facemasks in combination with ‘lock-down’ in managing the COVID-19 pandemic. Proc Math Phys Eng Sci. 2020;476:20200376. doi: 10.1098/rspa.2020.0376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Wölfel R., Corman V.M., Guggemos W., Seilmaier M., Zange S., Müller M.A., Niemeyer D., Jones T.C., Vollmar P., Rothe C., Hoelscher M., Bleicker T., Brünink S., Schneider J., Ehmann R., Zwirglmaier K., Drosten C., Wendtner C. Virological assessment of hospitalized patients with COVID-2019. Nature. 2020;581:465–469. doi: 10.1038/s41586-020-2196-x. [DOI] [PubMed] [Google Scholar]
- 81.Kähler C., Hain R. Fundamental protective mechanisms of face masks against droplet infections. J Aerosol Sci. 2020;148 doi: 10.1016/j.jaerosci.2020.105617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Dbouk T., Drikakis D. On respiratory droplets and face masks. Phys Fluids. 2020;32 doi: 10.1063/5.0015044. (Woodbury, N.Y. : 1994). 063303-063303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Kumar S., Lee H.P. The perspective of fluid flow behavior of respiratory droplets and aerosols through the facemasks in context of SARS-CoV-2. Phys Fluids. 2020;32:111301. doi: 10.1063/5.0029767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Perić R., Perić M. 2020. Analytical and numerical investigation of the airflow in face masks used for protection against COVID-19 virus--implications for mask design and usage. arXiv preprint arXiv:2005. [Google Scholar]
- 85.Rengasamy S., Eimer B., Shaffer R.E. Simple respiratory protection--evaluation of the filtration performance of cloth masks and common fabric materials against 20-1000 nm size particles. Ann Occup Hyg. 2010;54:789–798. doi: 10.1093/annhyg/meq044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Bowen L.E. Does that face mask really protect you? Appl Biosaf. 2010;15:67–71. [Google Scholar]
- 87.Neupane B.B., Mainali S., Sharma A., Giri B. Optical microscopic study of surface morphology and filtering efficiency of face masks. PeerJ. 2019:e7142. doi: 10.7717/peerj.7142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Rowe B.R., Canosa A., Drouffe J.M., Mitchell J.B.A. Simple quantitative assessment of the outdoor versus indoor airborne transmission of viruses and covid-19. medRxiv. 2021;198:111189. doi: 10.1016/j.envres.2021.111189. 2020.12.30.20249058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Varaksin A.Y. Collision of particles and droplets in turbulent two-phase flows. High Temp. 2019;57:555–572. [Google Scholar]
- 90.Buajarern J., Mitchem L., Ward A.D., Nahler N.H., McGloin D., Reid J.P. Controlling and characterizing the coagulation of liquid aerosol droplets. J Chem Phys. 2006;125:114506. doi: 10.1063/1.2336772. [DOI] [PubMed] [Google Scholar]
- 91.Verma S., Dhanak M., Frankenfield J. Visualizing droplet dispersal for face shields and masks with exhalation valves. Phys Fluids. 2020;32 doi: 10.1063/5.0022968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rezaei M., Netz R.R. arXiv e-prints; 2021. Water evaporation from solute-containing aerosol droplets: effects of internal concentration and diffusivity profiles and onset of crust formation. arXiv:2104.03865. [DOI] [PMC free article] [PubMed] [Google Scholar]; The evaporation process of solute-containing droplets is modeled considering effects of internal concentration and diffusivity profiles and onset of crust formation.
- 93.Batchelor C.K., Batchelor G.K. Cambridge University Press; 1967. An introduction to fluid dynamics. [Google Scholar]
- 94.Humphrey S.P., Williamson R.T. A review of saliva: normal composition, flow, and function. J Prosthet Dent. 2001;85:162–169. doi: 10.1067/mpr.2001.113778. [DOI] [PubMed] [Google Scholar]
- 95.Zuo Y.Y., Uspal W.E., Wei T. Airborne transmission of COVID-19: aerosol dispersion, lung deposition, and virus-receptor interactions. ACS Nano. 2020;14:16502–16524. doi: 10.1021/acsnano.0c08484. [DOI] [PubMed] [Google Scholar]
- 96.Lide D.R. 89 ed. CRC Press; Cleveland, OH: 2008. CRC handbook of chemistry and physics. [Google Scholar]