Feature Selection Methods for Protein Biomarker Discovery from Proteomics or Multiomics Data

Abstract

Untargeted mass spectrometry (MS)-based proteomics provides a powerful platform for protein biomarker discovery, but clinical translation depends on the selection of a small number of proteins for downstream verification and validation. Due to the small sample size of typical discovery studies, protein markers identified from discovery data may not be generalizable to independent datasets. In addition, a good protein marker identified using a discovery platform may be difficult to implement in verification and validation platforms. Moreover, although multiomics characterization is being increasingly used in discovery cohort studies, there is no existing method for multiomics-facilitated protein biomarker selection. Here, we present ProMS, a computational algorithm for protein marker selection. The algorithm is based on the hypothesis that a phenotype is characterized by a few underlying biological functions, each manifested by a group of coexpressed proteins. A weighted k-medoids clustering algorithm is applied to all univariately informative proteins to identify both coexpressed protein clusters and a representative protein for each cluster as markers. In two clinically important classification problems, ProMS shows superior performance compared with existing feature selection methods. ProMS can be extended to the multiomics setting (ProMS_mo) through a constrained weighted k-medoids clustering algorithm, and the protein panels selected by ProMS_mo show improved performance on independent test data compared with ProMS. In addition to superior performance, ProMS and ProMS_mo also have two unique strengths. First, the feature clusters enable functional interpretation of the selected protein markers. Second, the feature clusters provide an opportunity to select replacement protein markers, facilitating a robust transition to the verification and validation platforms. In summary, this study provides a unified and effective computational framework for selecting protein biomarkers using proteomics or multiomics data. The software implementation is publicly available at https://github.com/bzhanglab/proms.

Graphical Abstract

Highlights

• •New algorithms enable protein biomarker discovery from proteomics or multiomics data.
• •Superior performance is demonstrated in two clinically important classification problems.
• •Feature clusters facilitate functional interpretation of the identified protein biomarkers.
• •Alternative choices are provided for each identified protein biomarker.

In Brief

Untargeted mass spectrometry–based proteomics provides a powerful platform for protein biomarker discovery, but clinical translation depends on the selection of a small number of proteins for verification and validation. We present feature selection methods for protein biomarker selection from proteomics or multiomics data. The algorithms show good performance, enable functional interpretation of the identified markers, and provide alternative choices for each identified marker to facilitate a robust transition to the verification and validation platforms.

According to the definition from the Food and Drug Administration–National Institutes of Health (FDA-NIH) Biomarker Working Group, a biomarker is “a defined characteristic that is measured as an indicator of normal biological processes, pathogenic processes or responses to an exposure or intervention” (1). Being the functional molecules of the cell, proteins have long been recognized as an important source of putative biomarkers for disease diagnosis, prognosis, and response to therapeutic intervention. Since the approval of human hemoglobin as a fecal test for the detection of colorectal cancer in 1976, more than 20 tumor protein markers have been approved by the FDA and are currently used in clinical practice (2). Protein biomarker development typically includes three phases: discovery, verification, and validation (3, 4). The discovery phase is now powered by the mass spectrometry (MS)-based untargeted proteomics technology, which enables the identification and quantification of more than 10,000 proteins in clinical specimens (5). This provides an excellent opportunity to identify new protein biomarker candidates in an unbiased manner. Moreover, it is well recognized that a combination of biomarkers, rather than an individual protein, is needed to distinguish biological states. By quantifying all proteins simultaneously, MS proteomics provides an ideal platform for identifying biomarker combinations. Despite the immense promise of MS proteomics in protein biomarker discovery, few new biomarkers have been introduced into clinical practice during the past decade.

One of the rate-limiting steps in protein biomarker development is the identification of a small number of promising candidates from thousands of proteins quantified by untargeted MS proteomics for downstream verification and validation using targeted assays. Although MS-based discovery platforms provide measurements for a large number of proteins (i.e., features), they are often carried out using a limited number of samples, leading to the “large p, small n” problem (6). This challenge is typical in all omics-based association studies and is commonly addressed by dimension reduction techniques such as principal component analysis (PCA) and its supervised alternatives (7). The goal of PCA is to rotate the data into a new axis system where the greatest amount of variance is captured in a few dimensions. Transformed data are represented by a set of principal components (PCs) ordered by the amount of variance they capture. Usually, a small number of PCs capture most of the variance of a dataset, leading to dimension reduction. However, because each PC is a linear combination of all original features, predictive models constructed based on the PCs require genome-wide measurements as inputs and cannot be implemented as targeted clinical assays.

Feature selection algorithms can be used to select biomarker combinations from high-dimensional data for predictive model construction. Throughout the paper, we use the terms “feature” and “marker” interchangeably. Feature selection algorithms can be categorized into filter methods, wrapper methods, and embedded methods. Filter methods evaluate the importance of features according to some univariate or multivariate evaluation criteria (8, 9). A naïve filter method ranks proteins according to their univariate association with the phenotype label of samples and then picks the top-ranking proteins. Due to the functional connection and coregulation relationships among proteins, top ranking proteins are usually highly redundant, leading to poor performance of this method. The Minimum Redundancy and Maximum Relevance (MRMR) algorithm addresses this issue by selecting features that have the highest relevance with the phenotype label and are also minimally redundant, i.e., they are dissimilar to each other as much as possible (10). Wrapper methods assess the quality of feature subsets based on the performance of a learning algorithm (11, 12, 13). The feature subset with the highest performance is returned as the selected features. Due to the exponential number of subset combinations, these methods are rarely used in biomarker selection where the number of original features typically are in the thousands. Embedded methods employ an integrated process to select features during the model construction (14, 15). One commonly used strategy is through the mechanism of regularization. For example, the least absolute shrinkage and selection operator (LASSO) method regularizes parameters of a linear regression model by reducing some coefficients to zero, allowing the selection of features with nonzero coefficients (16).

All feature selection algorithms are prone to overfitting to small training data, albeit at different degrees. Thus, protein markers selected based on a discovery cohort may not be generalizable to new test cohorts. This represents a major computational challenge in the protein biomarker development pipeline. In addition, because different platforms are used in the discovery and validation phases, a good protein marker identified in the discovery platform may be difficult to implement in the validation platform. In particular, although MS-based targeted proteomics has been increasingly used in biomarker verification and validation (17), antibody-based assays remain the most common assays used in the clinics. Many proteins do not have high-quality antibodies, limiting their utility in antibody-based clinical assays.

In this paper, we present a new protein marker selection algorithm to address these challenges. Similar to MRMR, our algorithm also seeks to identify a predefined number of k features with the highest relevance with the phenotype label and is also minimally redundant. However, our algorithm is based on the reasoning that there are typically a number of informative features for a given phenotype, that these features are often associated with a much smaller number of biological functions underlying the phenotype, and that coexpressed proteins tend to share similar biological functions (18). Accordingly, our algorithm first identifies all informative features through univariate association analysis, then groups them into k clusters based on their coexpression patterns, and finally selects one most representative feature from each cluster to create a set of k markers. We hypothesize that anchoring protein markers on biological functions defined by coexpressed proteins could improve generalizability of the markers. Moreover, when there is difficulty implementing a selected protein marker on the verification and validation platform, our algorithm provides alternative solutions by replacing the selected marker with another highly coexpressed protein in the same cluster. In addition, unlike the methods mentioned above, our algorithm is extendable to the multiomics setting, providing a unique potential to leverage multiomics data to enhance protein marker selection. We name our algorithm and its multiomics extension as PROtein Marker Selection (ProMS) and ProMS_Multi-Omics (ProMS_mo), respectively. We demonstrate these algorithms using published proteomics and multiomics data from two colon and rectal cancer (CRC) studies (19, 20) and two hepatocellular carcinoma (HCC) studies (21, 22). For CRC, we select protein markers to predict the tumor's microsatellite instability (MSI) status, which has both prognostic and therapeutic implications (23, 24). For HCC, we select protein markers to predict patient prognosis.

Experimental Procedures

Datasets

For MSI status prediction in CRC, label-free proteomic data and RNA-seq data were obtained from a published study (19) for protein marker selection and model training. Label-free proteomic data obtained from another study (20) was used for independent testing (supplemental Table S1). Protein quantification for both cohorts was based on spectral counting (20). mRNA quantification was based on Fragments Per Kilobase of transcript per Million mapped reads (FPKM). For both proteomic and RNA-seq data, genes with missing values were removed. Data were then subjected to log2-transformation followed by feature-wise standardization within each cohort. Samples with MSI-Low or microsatellite stable (MSS) status were labeled as class 0 and those with MSI-High as class 1. The training data had 70 class 0 and 15 class 1 samples, whereas the test data had 75 class 0 and 21 class 1 samples.

For patient prognosis prediction in HCC, tandem mass tag (TMT)-based proteomic and phosphoproteomic data and RNA-seq data were obtained from a published study (22) for marker selection and model training. Proteomic and phosphoproteomic data were normalized using the median centering method so that log2 TMT ratio values are centered at zero. Proteins and phosphorylation sites having more than 50% missing data were excluded before k-nearest neighbor (kNN) imputation was applied to the remaining data. mRNA quantification was computed using RNA-Seq by Expectation Maximization (RSEM) followed by upper quartile normalization and log2 transformation. Label-free proteomic data obtained from another study (21) was used for independent testing. Protein quantification was computed using the intensity-based absolute quantification (iBAQ) method implemented in MaxQuant (25). The MaxQuant quantification data was downloaded from PRIDE (26) with accession number PXD006512. The expression matrix was quantile normalized and then log2 transformed. Features with missing values were removed and all remaining features were standardized. To formulate prognosis prediction as a binary classification problem, samples were dichotomized into two groups according to their overall survival time. Patients with overall survival longer than 24 months were labeled as good prognosis (class 0) and those survived less than 24 months were labeled as poor prognosis (class 1). The training data had 117 class 0 and 42 class 1 samples, whereas the test data had 75 class 0 and 9 class 1 samples.

Protein Marker Selection With Proteomics Data Alone

Data matrix D of size n × p is employed to depict the protein expression where rows correspond to samples (s₁,…,s_n) and columns correspond to proteins (f₁,…,f_p) (Fig. 1A.1). We aim to identify k protein markers that can be used collectively to predict the binary phenotype label accurately. The algorithm ProMS works as follows. As a first step to remove uninformative features, ProMS examines each feature individually to determine the strength of the relationship between the feature and the phenotype label (Fig. 1A.2). A symmetric area under the receiver operating characteristic curve (AUROC) score AUC_sym is defined to evaluate such strength: $AU{C}_{sym}=2\times |AUC-0.5|$. The rationale is that AUCs higher or lower than 0.5 typically indicate some predictive power of the feature although in the latter case the feature tends to predict the labels of the opposite class. This should not be a problem in our case since a final classifier can readily detect that trend and assign the weight of that feature accordingly. Since the feature is evaluated one at a time, we can simply use the expression data and phenotype label to compute the AUC. Of note, the range of AUC_sym is the same as that of the original AUC. ProMS only keeps the features with the top α% highest AUC_sym scores. Here ɑ is a hyperparameter that needs to be tuned jointly with other hyperparameters of the final classifier. After the filtering step, data matrix D is reduced to D′ of size n × p′ where $p^{\prime }<<p$.

Fig. 1.

Overview of protein biomarker selection framework. A, ProMS. Uninformative features in a proteomics data matrix are first filtered out based on univariate analysis. A weighted k-medoids clustering step is performed in sample space. The identified medoids are output as the selected markers. B, ProMS_mo. Data matrices from each omics platform are filtered separately through univariate analysis. Resulting matrices are then combined. Features are partitioned into groups with constrained weighted k-medoids clustering, in which only protein markers can be selected as medoids.

To reduce the redundancy among the remaining features, ProMS groups p′ features into k clusters with k-medoids clustering (27) in sample space. Here we consider the dataset D′ containing p′ data points denoted by f₁,…,f_p in an n-dimensional sample space. The goal is to determine a partition {C₁…C_k} and k representatives g₁,…,g_k so that the following objective function:

$$J=\sum _{i=1}^k\sum _{f\in C_i}Dist\left(f,g_i\right)$$ (1)

is minimized. In other words, the sum of the distances of the different data points to their closest representatives needs to be minimized. k-medoids clustering is related to k-means clustering for partitioning a dataset into k clusters. The main difference is that the representatives, called medoids, are always selected from the actual data points (i.e., features in this case). Each medoid corresponds to the most centrally located data point in the containing cluster because the total distance between the medoid and all other members of the cluster is minimized. These medoids provide a natural solution to the biomarker selection problem, a unique strength that does not come with k-means clustering, where the center of a cluster is the average between the data points in the cluster instead of an actual data point. The distance between two data points f_i and f_j is calculated as: $Dist(f_i,f_j)=1-{\rho }_{ij}$, where ρ_ij represents the Pearson correlation coefficient between f_i and f_j. ProMS employs a weighted version of k-medoids algorithm where each feature is assigned a weight, $w_f=AU{C}_{sym,f}$, obtained in the filtering step. Therefore the new objective function is given as:

$$J=\sum _{i=1}^k\sum _{f\in C_i}{w}_{f}Dist\left(f,g_i\right)$$ (2)

This is based on the argument that features with larger univariate predictive power should be given higher preference of being selected as a medoid. The k medoids are selected as the markers for building a final classifier (Fig. 1A.3)

Protein Marker Selection With Multiomics Data

We have H data sources, D₁,…,D_H, representing H different types of omics measurements that jointly depict the same set of samples s₁,…,s_n. D_i (i = 1,…,H) is a matrix of size n × p_i where rows correspond to samples and columns correspond to features in ith data source. Without the loss of generality, we use D₁ to represent the proteomic data from which we seek to select a set of informative markers that can be used to predict the target labels. Our hypothesis is that by integrating information from other omics, a set of more informative protein markers can be identified. To test this hypothesis, we adapted ProMS to ProMS_mo as follows. Similar to ProMS, the first step of ProMS_mo involves filtering out uninformative features from each data source separately (Fig. 1B.1). Again, we use AUC_sym as the scoring metric. ProMS_mo first applies the univariate filtering to target data source D₁ and keeps only the top α% features with the highest scores. We denote the minimal score among these remaining features as θ. For other data source, ProMS_mo only keeps those features with score larger than θ. Filtered data matrices are combined into a new matrix D′ of size n × p′ where. $p^{\prime }=\sum _{i=1}^H{p}_i^{\prime }$ and $p_i^{\prime }$ is the number of features in the filtered data source i (Fig. 1B.2). Finally, weighted k-medoids clustering is performed to partition the p′ features into k clusters in sample spaces (Fig. 1B.3). To guarantee that only protein markers are selected as medoids, ProMS_mo first initializes the k medoids to protein markers. During the iterative steps of optimization, a medoid can only be replaced by another protein marker if such exchange improves the objective function. This can be formulated as a constrained optimization problem. After the iterative process converges, k medoids are selected as the final protein markers for constructing a classifier.

Other Marker Selection Methods

We compared ProMS with other popular feature selection or dimension reduction methods, including a filter method MRMR (10), a model based method LASSO, and a supervised PCA (SPCA) method (7). MRMR is implemented as a part of an open-source package called scikit-feature (28). As described in the original work, we used mutual information as the metric to measure the degree of relevance and redundancy. LASSO is implemented in scikit-learn (29), and we required that there should be exactly k features with nonzero coefficients in the final model. The amount of penalty added to the model was therefore adjusted accordingly to meet this requirement. The SPCA implementation started with a prefiltering step as described in ProMS. It was followed by applying the standard PCA method on the remaining data matrix. We then selected the first k components as the new features. This is indeed not a feature selection method because each PC is a linear combination of many original features.

Model Training and Testing

We evaluated ProMS and ProMS_mo with the CRC and HCC datasets. Each cancer type included a training set (D_train) and an independent test set (D_test). We aimed to select a few different numbers of markers with k={5,10,15,20}. For each k, we repeated the following Monte Carlo cross-validation process 100 times: D_train is first randomly split into two sets: one for feature selection and classifier building (70%, T), one for validation (30%, V). Five feature selection methods were considered: ProMS, ProMS_mo, MRMR, LASSO, and SPCA. We trained four classifiers using the selected features: logistic regression (LR), support vector machine (SVM), random forest (RF), and gradient boosting machine (GBM). A number of hyperparameters were tuned using grid search with 3-fold cross-validation within the training set T. These include one from univariate filtering step (α) and several others specific to the individual classifier. The trained classifiers were then evaluated with the validation set V (different for each of the 100 repeats) as well as the independent test set D_test (same for all 100 repeats). Finally, we used all data in D_train to repeat the feature selection and classifier building process and fit a full model to be evaluated with the independent test set D_test.

Gene Ontology and Pathway Analysis

Gene Ontology (GO) analysis was performed using WebGestalt (30, 31) through overrepresentation analysis. All genes were used as the reference set. Default parameters were used for the analysis.

Software Implementation

ProMS and ProMS_mo were implemented in the python package proms (https://pypi.org/project/proms). The source code, example data, and user guide are available at https://github.com/bzhanglab/proms.

Results

Marker Selection Using Proteomics Data

We trained and evaluated four classifiers (LR, SVM, RF, and GBM) using different numbers of features (k={5,10,15,20}) selected by ProMS, MRMR, LASSO, and SPCA, respectively. Of note, SPCA uses PCs to construct predictive models where each PC is a linear combination of all original features. Therefore, it cannot be used for marker selection. We included SPCA only as a reference for “optimal” performance. Evaluations were performed on both set-aside cross-validation data from the same cohort and test data from an independent cohort. Probably due to the small numbers of selected features, LR achieved similar or better performance compared with other more complicated modeling algorithms in almost all scenarios. For simplicity, we only present results from LR. For MSI status prediction in CRC, SPCA performed the best on both set-aside validation data (Fig. 2A) and independent test data (Fig. 2B) for all feature numbers. This was expected because the PC features capture much more information than the small number of protein features selected by other methods. MRMR showed consistently lower performance in all cases. Although both ProMS and MRMR are filter methods, ProMS substantially outperformed MRMR and achieved similar or even better performance compared with the model-based method LASSO (Fig. 2, A and B). MRMR gained increased performance with increased feature numbers, but the other three methods showed relatively consistent performance across all ks, suggesting that there inherently exists a small set of protein markers that can predict MSI status effectively. Comparing performance on the cross-validation and independent test data, PCA best maintained the performance on the test data, while MRMR showed the largest performance drop on the test data compared with other methods, indicating a significant degree of overfitting. Performance drop for LASSO was slightly higher than that for ProMS, but both showed relatively stable performance between the validation and test data.

Fig. 2.

Comparison of ProMS with MRMR, LASSO, and SPCA. The performance of each feature selection method was evaluated by the ability of trained logistic regression models to classify the problem specific labels (as indicated by the area under ROC curve; AUROC). A and B, performance for predicting MSI status in CRC. C and D, performance for predicting patient prognosis in HCC. k: number of features selected. A and C, performance in the set-aside cross-validation data from the same cohort. B and D, performance in the independent data. All results are based on 100 times of Monte Carlo cross-validations. ns: p  >  0.05; ∗p  ≤  0.05; ∗∗p  ≤  0.01; ∗∗∗p ≤  0.001; ∗∗∗∗p ≤ 0.0001 (Wilcoxon rank sum test).

For patient prognosis prediction in HCC, the AUROCs were much lower in general compared with MSI status prediction in CRC (Fig. 2, C and D). However, most of the patterns described in the CRC analysis were reproducible in the HCC analysis. One new observation is that ProMS not only outperformed MRMR but also outperformed LASSO in this more challenging clinical prediction problem. LASSO gained increased performance with increased feature numbers, and it also suffered notable performance drop in the independent test data. Thus, the performance difference between ProMS and LASSO was more obvious in the test data and when a smaller number of features were selected. The performance of ProMS matched or approached that of the SPCA in all cases although the latter uses combinations of many features in the original dataset. Moreover, both ProMS and SPCA showed consistent performance between the validation and test data, suggesting no observable overfitting during training. Together, these results demonstrate strong performance of the ProMS algorithm in selecting markers from proteomics data.

Marker Selection Using Multiomics Data

A key aspect of ProMS_mo is the ability to mine multiomics data but only select protein features. Feature selection with MRMR, LASSO, and SPCA cannot be readily adapted to incorporating multiomics data to facilitate protein marker selection. Here we focused on comparing the performance of models using features selected by ProMS_mo with those using features selected by ProMS. Again, SPCA was included only as a reference for comparison. Figure 3 depicts the results from LR models on MSI status prediction in CRC (A-B) and patient prognosis prediction in HCC (C-D) across different feature numbers. In cross-validation, we did not observe significant performance difference between models built upon features selected by ProMS_mo and ProMS. However, when the cross-validation models were tested on the independent test data, ProMS_mo outperformed ProMS in all eight cases, with significant difference observed for six cases. For patient prognosis prediction in HCC, the performance of ProMS_mo showed similar or occasionally better performance compared with SPCA. These results suggest that using information from multiomics data may enhance the robustness of protein marker selection, leading to improved performance on independent test data.

Fig. 3.

Comparison of ProMS, ProMS_mo, and SPCA. The performance of each feature selection method was evaluated by the ability of trained logistic regression models to classify the problem specific labels (as indicated by the area under ROC curve; AUROC). A and B, performance for MSI status prediction in CRC. C and D, performance prognosis prediction in HCC. k: number of features selected. A and C, performance in the set-aside cross-validation data from the same cohort. B and D, performance in the independent data. All results are based on 100 repeats of Monte Carlo cross-validations. ns: p > 0.05; ∗p ≤ 0.05; ∗∗p ≤ 0.01; ∗∗∗p ≤ 0.001; ∗∗∗∗p ≤ 0.0001 (Wilcoxon rank sum test).

Performance of the ProMS_mo Full Models and Selected Markers

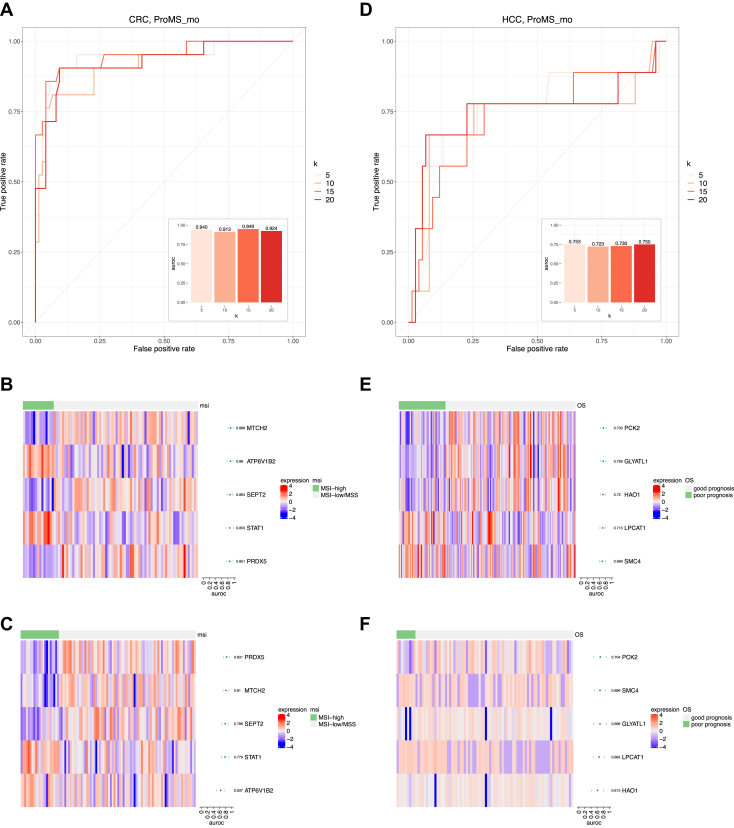
After demonstrating performance of the ProMS_mo approach using cross-validation models, we applied the approach to the whole training data to identify the final marker panels for full model development. For MSI status prediction in CRC, all models with protein marker numbers ranging from 5 to 20 achieved excellent performance on the independent test data (Fig. 4A). In particular, the model with only five protein markers achieved an AUROC of 0.94. The five markers selected by ProMS_mo included two proteins with increased abundance in MSI-H tumors (ATP6V1B2 and STAT1) and three proteins with decreased abundance (MTCH2, SEPT2, and PRDX5). All proteins showed distinct expression patterns between MSI-high and MSI-low/MSS tumors in the training data (Fig. 4B). The differences were reduced but still obvious in the test data (Fig. 4C).

Fig. 4.

Analysis of full models and markers selected by ProMS_mo. A–C, MSI status prediction in CRC. D and E, patient prognosis prediction in HCC. A and D, performance of the final full model evaluated on the independent test cohort. k: number of selected features. B and E, protein expression patterns of selected markers (k = 5) in the training dataset. C and F, protein expression patterns of selected markers in the test dataset. Markers are ordered by the univariate analysis metric (AUROC).

Patient prognosis prediction in HCC was more challenging. The model with five protein markers achieved an AUROC of 0.75, and increasing the number of protein markers did not lead to increased prediction performance (Fig. 4D). The five markers selected by ProMS_mo included two proteins with increased abundance in tumors with poor prognosis (SMC4 and LPCAT1) and three proteins with decreased abundance (PCK2, GLYATL1, and HAO1). All five proteins showed distinct expression patterns between tumors with poor and good prognosis in the training data (Fig. 4E). Although the discrimination power of individual markers in the test data was reduced (Fig. 4F), the five-marker panel still achieved good prediction performance (Fig. 4D).

Some of the selected markers have previously reported roles in the phenotype of interest. For example, signal transducer and activator of transcription 1 (STAT1) is a key immune response modulating factor, and MSI-H CRCs are associated with high immune infiltration (20). Alteration of phospholipid composition regulated by lysophosphatidylcholine acyltransferase 1 (LPCAT1) is related to HCC progression, and it has been reported as a potent target molecule to inhibit HCC progression (32). In addition, elevated LPCAT1 expression in patients with clear cell renal cell carcinoma (33) and lung adenocarcinoma (34) is reportedly associated with poor clinical outcome. Structural maintenance of chromosome subunit 4 (SMC4) is a core subunit of condensin complexes and is widely reported to contribute to chromosome condensation and segregation. Earlier studies show that SMC4 can effectively promote tumor cell growth rate expression in HCC (35), and it is useful for the early detection and prediction of primary HCC progression (36). The identification of these previously reported markers further supports the validity of our biomarker selection approach.

Functional and Clinical Utilities of the Feature Clusters

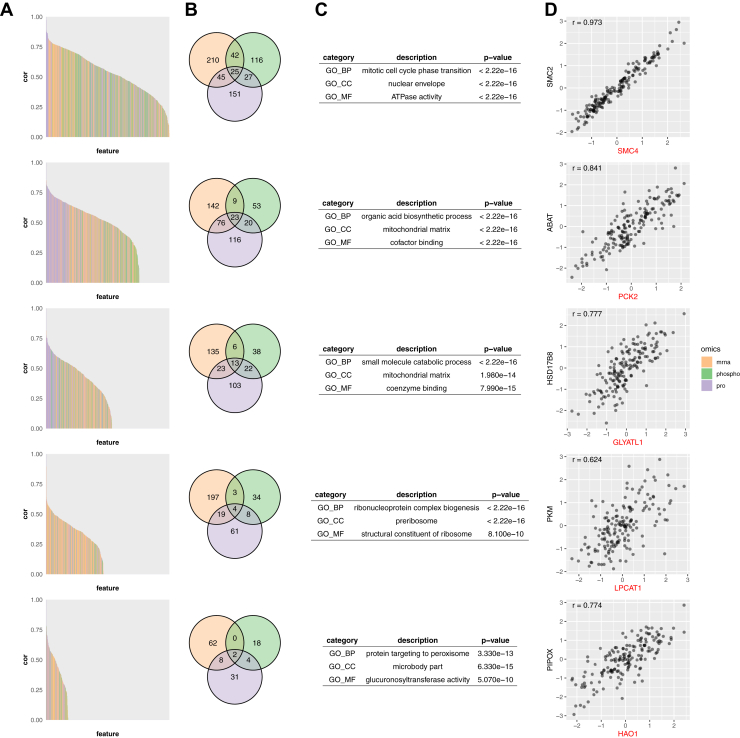
A unique advantage of our framework for protein biomarker selection is that each selected marker is associated with a cluster of other molecular features, providing biological context for functional interpretation of the selected markers. Using patient prognosis prediction in HCC (k = 5) as an example, the five clusters included 616, 439, 340, 326, and 125 features, respectively, and 247, 234, 160, 91, 44 features in these clusters were protein features. We retrieved a subnetwork with all protein features in the five clusters from the STRING network (37). The modularity of the subnetwork with respect to the given cluster membership was 0.281, much higher (Z-score: 16.37) than the modularity scores derived from random clusterings with five clusters of same sizes, which had a mean modularity of 0.015 and standard deviation of 0.016. This result suggests that proteins in the five clusters are more likely to be connected to other proteins in the same cluster as compared with proteins in the other clusters, supporting functional coherence of the clusters.

A wide range of variability was observed for Pearson's correlation coefficients between features in each cluster and their corresponding selected protein markers, SMC4, PCK2, GLYATL1, LPCAT1, and HAO1 (Fig. 5A). Each cluster included a mixture of features from all three omics platforms. Although a small fraction of genes were supported by all three platforms, most genes were uniquely contributed by one omics platform (Fig. 5B). Thus, features from all omics platforms collectively inform the underlying biological themes of the clusters, which could be revealed through GO enrichment analysis. For each cluster, the top enriched GO terms in biological process (BP), cellular component (CC), and molecular function (MF), respectively, are listed in Figure 5C. Some proteins, such as SMC4, have well-defined biological functions. Identifying these known functions in our analysis not only reinforces existing knowledge but also strengthens our rationale for using feature clusters to enable functional interpretation of other selected biomarkers with limited preexisting functional information.

Fig. 5.

Analysis of the feature clusters for prognosis prediction in HCC (k = 5). A, bar plot showing the Pearson's correlation coefficients between each member of the cluster and its medoid. B, Venn diagrams show overlapping features among omics data sources. C, top enriched biological process (GO_BP), cellular component (GO_CC), and molecular function (GO_MF) terms for each feature cluster. D, scatter plot comparing relative abundance of selected marker (red) and the most correlated protein in its respective cluster (r: Pearson's correlation coefficient).

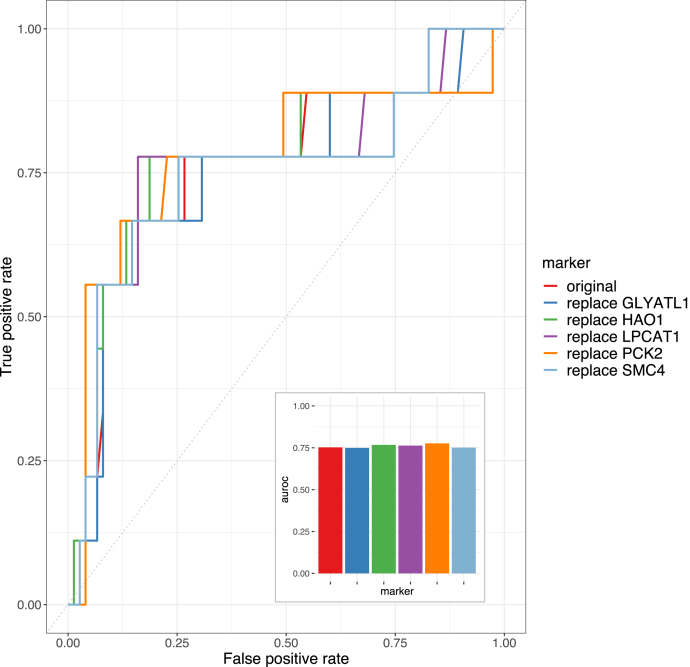
Another advantage of our framework is that it provides options for alternative markers in the event that there are difficulties in implementing the originally selected proteins in a clinical setting, e.g., unable to find high-quality antibodies for the development of immunohistochemistry assays. Because our cluster analysis tends to place proteins with similar expression patterns and biological functions in the same cluster, we reasoned that the predictive power remains even if the originally selected proteins are replaced with other highly correlated proteins in the same cluster (Fig. 5D). To test this hypothesis, we used the HCC training data to train five additional prognosis prediction models where one of the markers was replaced by the most-correlated protein in its cluster. Consistent with our expectation, the overall performance of these models on the independent test data was comparable to the models trained with the original set of markers (Fig. 6). Thus, our framework provides a robust approach to facilitate clinical implementation.

Fig. 6.

Performance comparison when the selected marker is replaced by the most correlated marker in its containing cluster. For prognosis prediction in HCC, five additional models were constructed using the protein markers identified by ProMS_mo except one of them was replaced with the most correlated protein marker in each cluster.

Discussion

Untargeted MS proteomics provides a powerful platform for protein biomarker discovery, but an effective transition from discovery to verification and validation relies on the selection of a small panel of protein biomarkers from discovery proteomics data. We presented ProMS, a new computational algorithm to facilitate protein biomarker selection. ProMS showed superior performance over MRMR and marginal improvements over LASSO for feature selection in the case of MSI status prediction in CRC, and performance improvements were more evident with the more challenging prognosis prediction in HCC. In addition to good performance, ProMS also has a few unique characteristics that are missing in other feature selection algorithms. First, the feature clusters enable functional interpretation of the selected protein markers. Second, the feature clusters provide an opportunity to select replacement protein markers, facilitating a smooth transition to the verification and validation platforms. Finally, the algorithm is easily extendable to the multiomics setting, and ProMS_mo leverages multiomics data to improve protein biomarker selection.

ProMS is conceptually similar to the widely used MRMR algorithm. Both algorithms aim to select features that have high association with the class label, but low association with each other. MRMR achieves this by maximizing an objective function that simultaneously maximizes the relevance and minimizes the redundancy. Guided by the objective function, the algorithm identifies features one at a time in an iterative fashion. In contrast to the inductive approach taken by MRMR, ProMS takes a deductive approach, which is based on the hypothesis that a phenotype is characterized by a few underlying biological functions, each manifested by a group of coregulated and coexpressed proteins. A weighted k-medoids clustering algorithm is used to identify both protein groups and a representative protein for each group as markers. MRMR showed inferior performance in our evaluations, likely due to its greedy, inductive nature. Aiming to achieve the same goal, ProMS is driven by biological reasoning rather than simple mathematical optimization. As a result, it not only significantly outperformed MRMR but also achieved better performance than the model-based feature selection method LASSO, which typically shows better performance than filter methods. For patient prognosis prediction in HCC, ProMS even approached the performance of the SPCA method, which utilizes information from a lot more proteins. Selection of the number of k may be guided by clinical feasibility. In addition, in both the ProMS and ProMS_mo implementations, users can simultaneously provide multiple k's as input and the one with the best performance in cross-validation will be selected for the construction of the final full model. In order to help users decide whether the selected k is close to optimal, the software also includes as an option the SPCA method, which is not an actual feature selection method but can serve as a reference for “optimal” performance as shown in our analyses.

Recent works have shown that multiomics characterization enables a more complete understanding of biological systems (38, 39, 40). However, feature selection from multiomics datasets poses even bigger challenges due to higher data dimensionality and increased data heterogeneity. An important branch of machine learning, called multiview learning, offers new perspectives and approaches to exploit complementary information presented in different data sources in order to construct models with high predictive power (41). For example, MRMR has been adapted to the multiview case where the importance of each view is taken into consideration to guide feature selection (42). A method has also been proposed to perform feature selection with LASSO and low-rank matrix approximation jointly in the context of multiview learning (43). However, these methods select features globally, and features from any view can be included in the final feature set. While conceptually interesting, clinical translation of heterogeneous markers is challenging due to the requirement of multiple assay platforms. ProMS_mo is conceptually different from these methods because it only selects proteins although all multiomics data are used to facilitate protein marker selection. Theoretically, features with cis- (i.e., mRNA, phosphosites, and proteins from the same gene) or trans- (phosphosites phosphorylated by a kinase or mRNAs regulated by a transcription factor) relationships are more likely to have similar abundance patterns; therefore, these functional relationships could reinforce true protein–phenotype associations to enhance protein biomarker selection.

While ProMS achieved better performance than the other feature selection methods in both the CRC and the HCC studies, the AUROCs were much lower in the HCC study. This suggests that prognosis prediction is much more difficult than MSI status prediction. Although the MSI phenotype is driven by a more homogeneous mechanism, the survival phenotype may be driven by much more heterogeneous mechanisms. Thus, a larger sample size is required when the phenotype of interest is expected to be associated with heterogeneous mechanisms. Moreover, for simplicity, survival in the HCC study was dichotomized as a binary phenotype in our analysis. One future development is to enable the analysis of nonbinary phenotype data, such as continuous, ordinal, or censored data, in ProMS.

ProMS_mo significantly outperformed ProMS when evaluated on the independent data; however, the improvements are marginal in many cases. Moreover, the two algorithms performed similarly in cross-validation. One possible explanation is that the omics data used in this study, including transcriptomics and phosphoproteomics, are closely related to proteomics data, which may limit the amount of improvement. Notably, ProMS_mo is not limited by gene-based data, and other types of measurements, such as metabolomics data or imaging data, can also be incorporated in the analysis. Therefore, a clear future direction is to test ProMS_mo with other types of non-gene-based data, which may better complement proteomics data than transcriptomics and phosphoproteomics.

Data availability

The source code and documentation of the ProMS package are available at https://github.com/bzhanglab/proms.

Supplemental Data

This article contains supplemental data.

Conflict of interest

The authors declare no competing interests.