NetMix: A Network-Structured Mixture Model for Reduced-Bias Estimation of Altered Subnetworks

Abstract

A classic problem in computational biology is the identification of altered subnetworks: subnetworks of an interaction network that contain genes/proteins that are differentially expressed, highly mutated, or otherwise aberrant compared with other genes/proteins. Numerous methods have been developed to solve this problem under various assumptions, but the statistical properties of these methods are often unknown. For example, some widely used methods are reported to output very large subnetworks that are difficult to interpret biologically. In this work, we formulate the identification of altered subnetworks as the problem of estimating the parameters of a class of probability distributions that we call the Altered Subset Distribution (ASD). We derive a connection between a popular method, jActiveModules, and the maximum likelihood estimator (MLE) of the ASD. We show that the MLE is statistically biased, explaining the large subnetworks output by jActiveModules. Based on these insights, we introduce NetMix, an algorithm that uses Gaussian mixture models to obtain less biased estimates of the parameters of the ASD. We demonstrate that NetMix outperforms existing methods in identifying altered subnetworks on both simulated and real data, including the identification of differentially expressed genes from both microarray and RNA-seq experiments and the identification of cancer driver genes in somatic mutation data.

1. Introduction

A standard paradigm in computational biology is to use interaction networks as prior knowledge in the analysis of high-throughput omics data, with numerous applications, including: protein function prediction (Deng et al., 2003; Nabieva et al., 2005; Chua et al., 2006; Sharan et al., 2007; Radivojac et al., 2013), gene expression analysis (Ideker et al., 2002; Dittrich et al., 2008; de la Fuente, 2010; Cho et al., 2012; Xia et al., 2015), germline variants (Lee et al., 2011; Califano et al., 2012; Leiserson et al., 2013; Hormozdiari et al., 2015; Huang et al., 2018), somatic variants in cancer (Nibbe et al., 2010; Vandin et al., 2011; Hofree et al., 2013; Creixell et al., 2015; Leiserson et al., 2015; Shrestha et al., 2017), and other analysis of other data (modENCODE Consortium et al., 2010; Wang et al., 2011; Berger et al., 2013; Halldórsson and Sharan, 2013; Gligorijević and Pržulj, 2015; Chasman et al., 2016; Cowen et al., 2017; Luo et al., 2017).

One classic approach is to identify active, or altered, subnetworks of an interaction network that contain unusually high or low measurements. The altered subnetwork problem takes as input: (1) an interaction network whose vertices are biological entities (e.g., genes or proteins) and whose edges represent biological interactions (e.g., physical or genetic interactions, co-expression, etc.); and (2) a measurement or score for each vertex. The goal is to find high-scoring subnetworks that correspond to groups of similarly altered vertices. This problem was introduced in Ideker et al. (2002) for gene expression analysis, where gene scores were derived from p-values of differential expression. Ideker et al. (2002) developed the jActiveModules algorithm to solve this problem and identify altered subnetworks of differentially expressed genes. Subsequently, Dittrich et al. (2008) introduced heinz as “the first approach that really tackles and solves the original problem raised by Ideker et al. (2002) to optimality.” jActiveModules and heinz have since become widely used tools with diverse applications; a few recent examples include mass-spectrometry proteomics (Kim and Hwang, 2016; Liu et al., 2018), damaging de novo mutations in schizophrenia and other neurological disorders (Gulsuner et al., 2013; Choi et al., 2016), and single-cell RNA-seq (Soul et al., 2015; Guo et al., 2016; Klimm et al., 2019).

In the past two decades, many algorithms have been developed to identify altered subnetworks in biological data (reviewed in Mitra et al., 2013; Creixell et al., 2015; Dimitrakopoulos and Beerenwinkel, 2017; Cowen et al., 2017). Each publication describing a new algorithm demonstrates the performance of their algorithm on specific biological datasets, and many of these publications also benchmark their algorithm against existing algorithms on real and/or simulated data. However, few of these publications prove theoretical guarantees for their algorithm’s performance on a well-defined generative model of the data. Thus, the true performance of these algorithms is often unknown. Indeed, recent benchmarking studies (Batra et al., 2017; He et al., 2017) of several widely used network algorithms—including jActiveModules and heinz—show considerate disagreement between subnetworks identified by different methods on the same biological datasets. Moreover, these benchmarking studies (and many others) do not compare network algorithms against single-gene tests that do not use the network; thus, the tacit assumption that interaction networks necessarily improve gene prioritization is often not tested.

Separately, many publications in the statistics and machine-learning literature investigate the problem of detecting whether or not a network contains an anomalous subnetwork, or a network anomaly (Arias-Castro et al., 2006, 2008, 2018; Addario-Berry et al., 2010; Arias-Castro et al., 2011; Sharpnack and Singh, 2013; Sharpnack et al., 2013a, 2016). These papers describe specific generative models of network anomalies and use a rigorous hypothesis-testing framework to prove asymptotic results regarding the conditions under which it is possible to detect a network anomaly. Importantly, these papers also provide theoretical guarantees about conditions under which a network contributes to anomaly detection. However, the network anomaly literature does not address the specific altered subnetwork problem studied in computational biology, with three key differences. First, the detection problem of deciding whether or not an altered subnetwork exists is not the same as the estimation problem of identifying the vertices in an altered subnetwork. Second, biological networks have a finite size, and it is unclear what guarantees the asymptotic results provide for finite-size networks. Finally, the topological constraints on network anomalies are often different from those considered in computational biology.

In this article, we aim at bridging the gap between the theoretical guarantees in the network anomaly literature and the practical problem of identifying altered subnetworks in biological data. We provide a rigorous formulation of the Altered Subnetwork Problem, the problem that jActiveModules (Ideker et al., 2002), heinz (Dittrich et al., 2008), and other methods aim at solving. Our formulation of the Altered Subnetwork Problem is inspired by the generative model used in the network anomaly literature, but it requires that the altered subnetwork is a connected subnetwork, a constraint motivated by the topology of signaling pathways (Bhalla and Iyengar, 1999); Kelley et al., 2004) and by the seminal works of Ideker et al. (2002) and Dittrich et al. (2008).

We show that the Altered Subnetwork Problem is equivalent to estimating the parameters of a distribution, which we define as the Altered Subset Distribution (ASD). We prove that the jActiveModules problem (Ideker et al., 2002) is equivalent to finding a maximum likelihood estimator (MLE) of the parameters of the ASD for connected subgraphs. At the same time, we demonstrate that if (1) the size of the altered subnetwork is moderately small and (2) the scores of vertices inside and outside of the altered subnetwork are not well separated, then the MLE is a biased estimator of the size of the altered subnetwork. This statistical bias provides a rigorous explanation for the large subnetworks produced by jActiveModules (Nikolayeva et al., 2018). We also show that the size of the altered subnetworks identified by heinz (Dittrich et al., 2008) is biased for most choices of its user-defined parameters.

We introduce a new algorithm, NetMix, that combines a Gaussian mixture model (GMM) and a combinatorial optimization algorithm to identify altered subnetworks. We show that NetMix is a reduced-bias estimator of the size of the altered subnetwork. We demonstrate that NetMix outperforms other methods for identifying altered subnetworks on simulated data, gene expression data, and somatic mutation data.

2. Altered Subnetworks, Altered Subsets, and Maximum Likelihood Estimation

2.1. Altered subnetwork problem

Let $G=\left(V,E\right)$ be a biological interaction network with a measurement, or score, $X_v$ for each vertex $v\in V$. We assume that there is a connected subnetwork $A$ in $G$, the altered subnetwork, whose scores are derived from a different distribution than the scores of the vertices not in $A$ (Fig. 1). The goal of the Altered Subnetwork Problem is to find $A$. The problem is defined formally as follows.

FIG. 1.

Altered Subnetwork Problem. Measurements, or scores, $X$ from a high-throughput experiment are drawn from one of two distributions: genes/proteins in an altered subnetwork $A$ of an interaction network $G=\left(V,E\right)$ have scores drawn from an altered distribution $N\left(\mu ,1\right)$ with $\mu >0$, whereas genes/proteins not in $A$ have scores drawn from a background distribution $N\left(0,1\right)$. The goal is to identify $A$ from $X$ and $G$; the difficulty of this problem depends on the separation $\mu$ between the distributions and the size $\left|A\right|$ of the altered subnetwork. ASD, Altered Subset Distribution.

Altered Subnetwork Problem (ASP)

Let $G=\left(V,E\right)$ be a graph with vertex scores and let $A\subseteq V$ be a connected subgraph of $G$. Suppose that

where $D_A$ is the altered distribution and $D_B$ is the background distribution. Given $G$ and $X$, find $A$.

Note that the Altered Subnetwork Problem (ASP) assumes that the interaction network $G$ has a single altered subnetwork $A$. This is a reasonable assumption in some cases, for example, when the altered subnetwork $A$ is large or the interaction network $G$ has small diameter or high connectivity. More generally, when the network contains multiple altered subnetworks, one can recursively solve the ASP to identify more than one altered subnetwork.

The seminal algorithm for solving the ASP is jActiveModules (Ideker et al., 2002). jActiveModules takes as input a $p$-value $p_v$ for each vertex $v$; for example, a $p$-value of differential gene expression. jActiveModules transforms the $p$-values into scores $X_v={\Phi }^{-1}\left(1-p_v\right)$, where $\Phi$ is the cumulative distribution function (CDF) of a standard normal distribution. Under the null hypothesis, the $p$-values $p_v$ across genes are distributed according to the uniform distribution $U\left(0,1\right)$, and thus by transforming $p$-values, jActiveModules solves the ASP with background distribution $D_B=N\left(0,1\right)$. jActiveModules aims to find a connected subgraph $Â$ that maximizes^* $\Gamma \left(S\right)=\frac{1}{\sqrt{\left|S\right|}}{\sum }_{v\in S}{X}_v$, that is,

The presentation of jActiveModules in Ideker et al. (2002) does not specify the altered distribution $D_A$. However, in Section 2.2, we argue that the choice of the objective function in Equation (2) implicitly assumes that $D_A=N\left(\mu ,1\right)$ for some parameter $\mu >0$. Thus, we define the normally distributed ASP as follows.

Normally Distributed Altered Subnetwork Problem

Let $G=\left(V,E\right)$ be a graph with vertex scores and let $A\subseteq V$ be a connected subgraph of $G$. Suppose that for some $\mu >0$,

Given $G$ and $X$, find $A$.

The Normally Distributed ASP has a sound statistical interpretation: if the $p$-values $p_v$ of the genes are derived from an asymptotically normal test statistic, as is often the case, then the transformed $p$-values $X_v={\Phi }^{-1}\left(1-p_v\right)$ are distributed as $N\left(0,1\right)$ for genes satisfying the null hypothesis and $N\left(\mu ,1\right)$ for genes satisfying the alternative hypothesis (Hung et al., 1997). Normal distributions have previously been used to model transformed $p$-values from differential gene expression experiments (Pan et al., 2003; McLachlan et al., 2006; Wang et al., 2009).

More generally, the Normally Distributed Altered Subnetwork Problem is related to a larger class of network anomaly problems, which have been studied extensively in the machine-learning and statistics literature (Arias-Castro et al., 2006, 2008, 2011, 2018; Addario-Berry et al., 2010; Sharpnack and Singh, 2013; Sharpnack et al., 2013a, b; Sharpnack et al., 2016). To better understand the relationships between these problems and the algorithms developed to solve them, we will describe a generalization of the Altered Subnetwork Problem. We start by defining the following distribution, which generalizes the connected subnetworks in the Normally Distributed Altered Subnetwork Problem to any family of altered subsets.

Normally Distributed ASD

Let $n>0$ be a positive integer, let S be a family of subsets of $\left\{1,\dots ,n\right\}$, and letbe distributed according to the Normally Distributed $AS{D}_S\left(A,\mu \right)$ provided

Here, $\mu >0$ is the mean of the ASD and $A$ is the altered subset of the ASD.

More generally, the ASD can be defined for any background distribution $D_B$ and altered distribution $D_A$. We will restrict ourselves to normal distributions in accordance with the Normally Distributed Altered Subnetwork Problem, and we will subsequently assume normal distributions in both the Altered Subset Distribution (ASD) and the Altered Subnetwork Problem.

The distribution in the Altered Subnetwork Problem is the $AS{D}_S\left(A,\mu \right)$, where the family $\mu$ of subsets are connected subgraphs of the network $G$. In this terminology, the Altered Subnetwork Problem is the problem of estimating the parameters $A$ and $\mu$ of the ASD given data $X\sim AS{D}_S\left(A,\mu \right)$ and knowledge of the parameter space S of altered subnetworks $A$. Thus, we generalize the Altered Subnetwork Problem to the Altered Subset Distribution Estimation Problem, defined as follows.

ASD Estimation Problem

The ASD Estimation Problem is a general problem of estimating the parameters of a structured alternative distribution, sometimes known as a “structured normal means” problem in statistics (Sharpnack et al., 2013a). Different choices of S for the ASD Estimation Problem yield a number of interesting problems, some of which have been previously studied in the altered subnetwork literature.

• $S=P_n$, the power set of all subsets of $\left\{1,\dots ,n\right\}$. We call the distribution $AS{D}_{P_n}\left(A,\mu \right)$ the unstructured ASD.

• $S=C_G$, the set of all connected subgraphs of a graph $G=\left(V,E\right)$. We call $AS{D}_{C_G}\left(A,\mu \right)$ the connected ASD. The connected ASD Estimation Problem is equivalent to the Altered Subnetwork Problem described earlier.

• $S=D_G\left(\rho \right)$, the set of all subgraphs of a graph $G=\left(V,E\right)$ with edge density $\ge \rho$. Guo et al. (2007), Vanunu et al. (2010), and Ayati et al. (2015) identify altered subnetworks with high edge density, and Amgalan and Lee (2014) identifies altered subnetworks with edge density $\rho =1$, that is, cliques.

• $S=N_G=\left\{N\left(v\right):v\in V\right\}$, the set of all first-order network neighborhoods of a graph $G=\left(V,E\right)$. Cho et al. (2016) and Horn et al. (2018) use first-order network neighborhoods to prioritize cancer genes.

• $S\subseteq P_n$, a family of subsets. Typically, $\left|S\right|\ll \left|P_n\right|$ and $S$ is not defined in terms of a graph. A classic example is gene set analysis [see Hung et al. (2011) for a review].

2.2. Bias in maximum likelihood estimation of the ASD

One reasonable approach for solving the ASD Estimation Problem is to compute an MLE for the parameters of the ASD. We derive the MLE next and show that it has undesirable statistical properties. All proofs are in the Supplementary Data.

Theorem 1. Let $X\sim AS{D}_S\left(A,\mu \right)$. The MLEs ${Â}_{ASD}$ and ${\widehat{\mu }}_{ASD}$ of $A$ and $\mu$, respectively, are

$${Â}_{ASD}={argmax}_{S\in \mu }\Gamma \left(S\right)={argmax}_{{}_{S\in \mu }}\frac{1}{\sqrt{\left|S\right|}}{\sum }_{v\in S}{X}_{v}and{\widehat{\mu }}_{ASD}=\frac{1}{\left|{Â}_{ASD}\right|}{\sum }_{v\in {Â}_{ASD}}{X}_v.$$ (5)

The maximization of $\Gamma$ over $S$ in Equation (5) is a version of the scan statistic, a commonly used statistic to study point processes on lines and rectangles under various distributions (Kulldorff, 1997; Glaz et al., 2001). Comparing Equations (5) and (2), we see that jActiveModules (Ideker et al., 2002) computes the scan statistic over the family $S=C_G$ of connected subgraphs of the graph $G$. Thus, although jActiveModules (Ideker et al., 2002) neither specifies the anomalous distribution $D_A$ nor provides a statistical justification for their subnetwork scoring function, Theorem 1 above shows that jActiveModules implicitly assumes that $D_A$ is a normal distribution, and that jActiveModules aims to solve the Altered Subnetwork Problem by finding the MLE ${Â}_{ASD.}$.

Despite this insight that jActiveModules computes the MLE, it has been observed that jActiveModules often identifies large subnetworks. Nikolayeva et al. (2018) note that the subnetworks identified by jActiveModules are large and “hard to interpret biologically.” They attribute the tendency of jActiveModules to identify large subnetworks to the fact that a graph typically has more large subnetworks than small ones. Although this observation about the relative numbers of subnetworks of different sizes is correct, we argue that this tendency of jActiveModules to identify large subnetworks is due to a more fundamental reason: The MLE ${Â}_{ASD}$ is a biased estimator of $A$.

First, we recall the definitions of bias and consistency for an estimator $\widehat{\theta }$ of a parameter $\theta$.

Definition 1. Let $\widehat{\theta }=\widehat{\theta }\left(X\right)$ be an estimator of a parameter $\theta$ given observed data $X=\left(X_1,\dots ,X_n\right)$. (a) The bias in the estimator $\widehat{\theta }$ of $\theta$ is $Bia{s}_{\theta }\left(\widehat{\theta }\right)=E\left[\widehat{\theta }\right]-\theta$. We say that $\widehat{\theta }$ is a biased estimator of $\theta$ if $Bia{s}_{\theta }\left(\widehat{\theta }\right)\ne 0$, and it is an unbiased estimator of $\theta$ otherwise. (b) We say that $\widehat{\theta }$ is a consistent estimator of $\theta$ if $\widehat{\theta }{\to }^p\theta$, where ${\to }^p$ denotes convergence in probability as $n\to \infty$, and it is an inconsistent estimator of $\theta$ otherwise.

When it is clear from context, we omit the subscript $\theta$ and write $Bias\left(\widehat{\theta }\right)$ for the bias of estimator $\widehat{\theta }$.

Let $X\sim AS{D}_{P_n}\left(A,\mu \right)$ be distributed according to the unstructured ASD. We observe that the estimators $\left|{Â}_{ASD}\right|∕n$ and ${\widehat{\mu }}_{ASD}$ are both biased and inconsistent when both $\left|A\right|∕n$ and $\mu$ are moderately small (Fig. 2). We summarize these observations in the following conjecture:

FIG. 2.

Scores $X\sim AS{D}_{P_n}\left(A,\mu \right)$ are distributed according to the unstructured ASD. (A) $Bias\left(\left|{Â}_{ASD}\right|∕n\right)$ in the maximum likelihood estimate of $\left|A\right|∕n$ as a function of the mean $\mu$ and altered subset size $\left|A\right|∕n$ for $n=10^4$. (B) $Bias\left(\left|{Â}_{ASD}\right|∕n\right)$ for $n=10^4$ and several values of $\left|A\right|∕n$. Dotted lines indicate first and third quartiles in the estimate of the bias. (C) $Bias\left(\left|{Â}_{ASD}\right|∕n\right)$ as a function of $n$ for $\mu =3$ and for several values of $\left|A\right|∕n$.

Conjecture. Let $X=\left(X_1,\dots ,X_n\right)\sim AS{D}_{P_n}\left(A,\mu \right)$. Then, there exist ${\mu }_0>0$ and $\beta >0$ such that, if $\mu <{\mu }_0$ and $\left|A\right|∕n<\beta$, then $\left|{Â}_{ASD}\right|∕n$ and ${\widehat{\mu }}_{ASD}$ are biased and inconsistent estimators of $\left|A\right|∕n$ and $\mu$, respectively.

Note that there are many examples in the literature of biased MLEs; for example, the MLE for the variance of a (univariate) normal distribution or the MLE for the inverse of the mean of a Poisson distribution (Firth, 1993). However, examples of inconsistent MLEs are somewhat rare (Ferguson, 1982).

Although we do not have a proof of the earlier conjecture, we prove the following results that partially explain the bias and inconsistency of the estimators $\left|A_{ASD}\right|$ and ${\mu }_{ASD}$. For the bias, we prove the following.

Theorem 2. Let $X=\left(X_1,\dots ,X_n\right)\sim AS{D}_{P_n}\left(A,\mu \right)$ with $A=\varnothing$. Then $\left|{Â}_{ASD}\right|=cn$ for sufficiently large $n$ and with high probability, where $0<c<0.35$ is independent of $n$.

Empirically, we observe $c\approx 0.27$, that is, ${Â}_{ASD}$ contains more than a quarter of the scores (Fig. 2). This closely aligns with the observation in Nikolayeva et al. (2018) that jActiveModules reports subnetworks that contain ∼$29\%$ of all vertices in the graph. Based on Theorem 2, one may suspect that $\left|{Â}_{ASD}\right|\approx cn$ when $\mu$ or $\left|A\right|∕n$ is sufficiently small, providing some intuition for why $\left|{Â}_{ASD}\right|∕n$ is biased. For inconsistency, we prove that the bias is independent of $n$.

Theorem 3. Let $X=\left(X_1,\dots ,X_n\right)\sim AS{D}_{P_n}\left(A,\mu \right)$, where $\left|A\right|=\theta \left(n\right)$. For sufficiently large $n$, $Bias\left(\left|{Â}_{ASD}\right|∕n\right)$ and $Bias\left({\widehat{\mu }}_{ASD}\right)$ are independent of $n$.

3. The Netmix Algorithm

Following the observation that the MLEs of the distribution $AS{D}_{P_n}\left(A,\mu \right)$ are biased, we aim at finding a less biased estimator by explicitly modeling the distribution of the scores $X$. In this section, we derive a new algorithm, NetMix, that solves the Altered Subnetwork Problem by fitting a GMM to $X$.

3.1. Gaussian mixture model

We start by recalling the definition of a GMM.

Gaussian Mixture Model

Let $\mu >0$ and $\alpha \in \left(0,1\right)$. $X$ is distributed according to the GMM $\left(\alpha ,\mu \right)$ with parameters $\alpha$ and $\mu$ provided

$$X\sim \alpha N\left(\mu ,1\right)+\left(1-\alpha \right)N\left(0,1\right).$$ (6)

An alternate interpretation of the GMM is to draw a latent variable $Z\sim Bernoulli\left(\alpha \right)$ and select $X\sim N\left(\mu ,1\right)$ if $Z=1$, and $X\sim N\left(0,1\right)$ if $Z=0$.

Given data $X=\left(X_1,\dots ,X_n\right)$, we define ${\widehat{\mu }}_{GMM}$ and ${\widehat{\alpha }}_{GMM}$ to be the MLEs for $\mu$ and $\alpha ,$ respectively, obtained by fitting a GMM to $X$. In practice, ${\widehat{\mu }}_{GMM}$ and ${\widehat{\alpha }}_{GMM}$ are obtained by the expectation-maximization (EM) algorithm (Dempster et al., 1977), which is known to converge to the MLEs as the number of samples goes to infinity (Xu et al., 2016; Daskalakis et al., 2017). Further, if ${X_i}_{\sim }^{i.i.d.}GMM\left(\mu ,\alpha \right)$ are distributed according to the GMM with $\alpha \ne 0$, then ${\widehat{\mu }}_{GMM}$ and ${\widehat{\alpha }}_{GMM}$ are consistent (and therefore asymptotically unbiased) estimators of $\mu$ and $\alpha ,$ respectively (Chen, 2017).

Analogously, by fitting a GMM to data $X\sim AS{D}_{P_n}\left(A,\mu \right)$ from the unstructured ASD, we observe that ${\widehat{\alpha }}_{GMM}$ is a less biased estimator of $\left|A\right|∕n$ than $\left|{Â}_{ASD}\right|∕n$ (Fig. 3A, B). We also observe that ${\widehat{\alpha }}_{GMM}$ is a consistent estimator of $\left|A\right|∕n$ (Fig. 3C). We summarize our findings in the following conjecture:

FIG. 3.

Scores $X\sim AS{D}_{P_n}\left(A,\mu \right)$ are distributed according to the unstructured ASD, and parameters ${\widehat{\alpha }}_{GMM}$ and ${\widehat{\mu }}_{GMM}$ are obtained by the EM algorithm. (A) $Bias\left({\widehat{\alpha }}_{GMM}\right)$ as a function of the mean $\mu$ and altered subnetwork size $\left|A\right|∕n$ for $n=10^4$. Compare with Figure 2A. (B) $Bias\left({\widehat{\alpha }}_{GMM}\right)$ and $Bias\left(\left|{Â}_{ASD}\right|∕n\right)$ as functions of the mean $\mu$ for $\left|A\right|∕n=0.05$ and $n=10^4$. (C) $Bias\left({\widehat{\alpha }}_{GMM}\right)$ as a function of $n$ for mean $\mu =3$ and several values of $\left|A\right|∕n$. Compare with Figure 2C. EM, expectation maximization.

3.1.2. Conjecture

Let $X\sim AS{D}_{P_n}\left(A,\mu \right)$ with $\left|A\right|>0$, and let ${Â}_{ASD}$ be the MLE of $A$ as defined in Equation (5). Let ${\widehat{\alpha }}_{GMM}$ and ${\widehat{\mu }}_{GMM}$ be the MLEs of $\alpha$ and $\mu$ obtained by fitting a GMM to $X$. Then, $Bia{s}_{\left|A\right|∕n}\left({\widehat{\alpha }}_{GMM}\right)<Bia{s}_{\left|A\right|∕n}\left(\left|{Â}_{ASD}\right|∕n\right)$. Moreover, ${\widehat{\alpha }}_{GMM}$ and ${\widehat{\mu }}_{GMM}$ are consistent estimators of $\left|A\right|∕n$ and $\mu$, respectively.

Although we do not have a proof of the earlier conjecture, a partial justification is the following relationship between the unstructured ASD and the GMM distribution. Let $X=\left(X_1,\dots ,X_n\right)$ be drawn from a mixture of unstructured ASDs over all possible anomalous sets $A$ of size $k$; in other words, $X\sim B\cdot {\sum }_{\left|A\right|=k}AS{D}_{P_n}\left(A,\mu \right)$, where $B=1{/}\left(\begin{array}{c}n\\ k\\ \end{array}\right)$ is a normalizing constant. Let $Y_1,\dots ,{Y_n}_{\sim }^{i.i.d.}GMM\left(\alpha ,\mu \right)$ be independent samples from the GMM for $\mu >0$ and $\alpha =\frac{k}{n}$ with corresponding latent variables $Z_1,\dots ,Z_n$. Then, the joint distribution of the GMM samples $Y=\left(Y_1,\dots ,Y_n\right)$ conditioned on ${\sum }_{i=1}^n{Z}_i=k$ is equal to the distribution of $X$:

$$X{=}^d\left(Y\left|{\sum }_{i=1}^n{Z}_i=k\right.\right).$$ (7)

3.2. NetMix algorithm

We derive an algorithm, NetMix, that uses the MLEs ${\widehat{\mu }}_{GMM}$ and ${\widehat{\alpha }}_{GMM}$ from the GMM to solve the Altered Subnetwork Problem. Note that the GMM is not identical to the $ASD$, the distribution that generated the data. Despite this difference in distributions, the earlier conjecture provides justification that the GMM yields less biased estimators of $A$ and $\mu$ than the MLEs of the $ASD$ distribution.

Given a graph $G=\left(V,E\right)$ and scores $X=(Xv)v\in V$, NetMix first computes the responsibility $r_v=Pr\left(v\in A|X_v\right)$, or the probability that $v\in A$, for each vertex $v\in V$. The responsibilities $r_v$ are computed from the GMM MLEs ${\widehat{\mu }}_{GMM}$ and ${\widehat{\alpha }}_{GMM}$ (which are estimated by the EM algorithm) according to the formula

$${\widehat{r}}_v=\frac{{\widehat{\alpha }}_{GMM}\cdot P\left(N\left({\widehat{\mu }}_{GMM},1\right)=X_v\right)}{{\widehat{\alpha }}_{GMM}\cdot P\left(N\left({\widehat{\mu }}_{GMM},1\right)=X_v\right)+\left(1-{\widehat{\alpha }}_{GMM}\right)\cdot P\left(N\left(0,1\right)=X_v\right)}$$ (8)

where $P\left(N\left(\mu ,1\right)=X_v\right)$ is the probability density function (PDF) of the normal distribution $N\left(\mu ,1\right)$ evaluated at $X_v$.

Next, NetMix aims at finding a connected subgraph $C$ of size $\left|C\right|\approx n\alpha$ that maximizes ${\sum }_{v\in C}{r}_v$. To find such a subgraph, NetMix assigns a weight $w\left(v\right)={\widehat{r}}_v-\tau$ to each vertex $v,$ where $\tau$ is chosen so that approximately $n{\widehat{\alpha }}_{GMM}$ vertices have non-negative weights. NetMix then computes the maximum weight connected subgraph (MWCS) ${Â}_{NetMix}$ in $G$ by adapting the integer linear program in Dittrich et al. (2008). The use of $\tau$ is motivated by the observation that, if ${\widehat{\alpha }}_{GMM}\approx \alpha$, then we expect $\left|{Â}_{NetMix}\right|\approx n{\widehat{\alpha }}_{GMM}\approx n\alpha =\left|A\right|$.

We formally describe the NetMix algorithm for solving the Altered Subnetwork Problem later.

NetMix algorithm. Given a network $G=\left(V,E\right)$ and vertex scores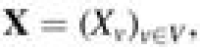

1. Compute ${\widehat{\alpha }}_{GMM}$ and ${\widehat{\mu }}_{GMM}$, the MLEs of $\alpha$ and $\mu$, by fitting a GMM to $X$ using EM.

2. Compute the estimated responsibilities ${\widehat{r}}_v$ for each vertex $v$ by using Equation (8).

3. Compute $\tau$ such that $\left|\left\{v\in V:{\widehat{r}}_v>\tau \right\}\right|=\lceil n{\widehat{\alpha }}_{GMM}\rceil$, where $\lceil \cdot \rceil$ is the ceiling function.

4. Find the connected subgraph ${Â}_{NetMix}$ defined by

$${Â}_{NetMix}={argmax}_{{}_{connectedC\subseteq V}}{\sum }_{v\in C}\left({\widehat{r}}_v-\tau \right)$$ (9)

using integer linear programming.

NetMix bears some similarities to heinz (Dittrich et al., 2008), another algorithm to identify altered subnetworks. However, there are two important differences. First, heinz does not solve the Altered Subnetwork Problem defined in the previous section. Instead, heinz models the vertex scores (assumed to be $p$-values) with a beta-uniform mixture (BUM) distribution. The motivation for the BUM is based on an empirical goodness-of-fit in Pounds and Morris (2003); however, later work by the same author (Pounds and Cheng, 2004) observes that the BUM tends to underestimate the number of $p$-values drawn from the altered distribution.

Second, heinz requires that the user specify a false discovery rate (FDR) and shifts the $p$-values according to this FDR. We show later that nearly all choices of the FDR lead to a biased estimate of $\left|A\right|$. Moreover, the manually selected FDR allows users to selectively tune the value of this parameter to influence which genes are in the inferred altered subnetwork, analogous to “$p$-hacking” (Ioannidis, 2005; Head et al., 2015; Nuzzo, 2015). Indeed, recently published analyses using heinz use a wide range of FDR values, ranging anywhere from $10^{-25}$ to $0.05$ (Liang et al., 2012; Choi et al., 2016; He et al., 2017; Klimm et al., 2019). See the Supplementary Data for more details on the differences between heinz and NetMix.

Despite these limitations, the ILP given in heinz to solve the MWCS problem is very useful for implementing NetMix and for computing the scan statistic [Eq. (2)] used in jActiveModules (Section 4).

4. Results

We compared NetMix with jActiveModules (Ideker et al., 2002) and heinz (Dittrich et al., 2008) on simulated instances of the Altered Subnetwork Problem and on real datasets, including differential gene expression experiments from the Expression Atlas (Petryszak et al., 2015) and somatic mutations in cancer. jActiveModules is accessible only through Cytoscape (Shannon et al., 2003; Cline et al., 2007) and not a command-line interface, making it difficult to run on a large number of datasets. Thus, we implemented jActiveModules^*, which computes the scan statistic [Eq. (5)] by adapting the integer linear program in heinz.^† jActiveModules^* output relies on the global optimum of the scan statistic, whereas jActiveModules relies on heuristics (simulated annealing and greedy search) to find a local optimum.

4.1. Simulated data

We compared NetMix, jActiveModules^*, and heinz on simulated instances of the Altered Subnetwork Problem by using the HINT+HI interaction network (Leiserson et al., 2015), a combination of binary and co-complex interactions in High-quality INTeractones (HINT) (Das and Yu, 2012) with high-throughput derived interactions from the Human Interactone (HI) network (Rolland et al., 2014) as the graph $G$. For each instance, we randomly selected a connected subgraph $A\subseteq V$ with size $\left|A\right|=0.05n$ by using the random walk method of Lu and Bressan (2012), and we drew a sample $X\sim AS{D}_{C_G}\left(A,\mu \right)$. We ran each method on $X$ and $G$ to obtain an estimate $Â$ of the altered subnetwork $A$. We ran heinz with three different choices of the FDR parameter ($FDR=0.001$, $FDR=0.1$, and $FDR=0.5$) to reflect the variety of FDRs used in practice.

We found that NetMix output subnetworks whose size $\left|{Â}_{NetMix}\right|$ was very close to the true size of the altered subnetwork across all values of $\mu$ in the simulations (Fig. 4A). In contrast, jActiveModules^* output subnetworks that were much larger than the altered subnetwork for $\mu <5$. This behavior is consistent with our earlier conjectures about the large bias in the MLE ${Â}_{ASD}$ for the unstructured ASD. Note that $\mu >5$ corresponds to a large separation between the background and alternative distributions, and the network is not needed to separate these two distributions.

FIG. 4.

Comparison of altered subnetwork identification methods on simulated instances of the Altered Subnetwork Problem using the HINT+HI interaction network with $n=15,074$ vertices, and where the altered subnetwork $A$ has size $\left|A\right|=0.05n$. [Dashed vertical line ($\mu =1$) represents the smallest $\mu$ such that one can detect whether $G$ contains an altered subnetwork]. (A) Size $\left|Â\right|∕n$ of identified altered subnetwork $Â$ as a function of mean $\mu$. (B) $F$-measure for $Â$ as a function of $\mu$. (C) $F$-measure for $Â$ at $\mu =1$, comparing performance with the network (left series for each method) and without the network (right series for each method). HI, Human Interactone; HINT, High-quality INTeractone.

We also quantified the overlap between the true altered subnetwork $A$ and the subnetwork $Â$ output by each method using the $F$-measure, finding that NetMix outperforms other methods across the full range of $\mu$ (Fig. 4B). heinz requires the user to select an FDR value, and we find that the size of the output subnetwork and the $F$-measure varies considerably for different FDR (Fig. 4A, B). When $\mu$ was small, a high FDR value ($FDR=0.5$) yielded the best performance in terms of $F$-measure. However, when $\mu$ was large, a low FDR value ($FDR=0.001$) gave better performance. Although there are FDR values where the performance of heinz is similar to NetMix, the user does not know what FDR value to select for any given input, as the values of $\mu$ and the size $\left|A\right|$ of the altered subnetwork are unknown.

The bias in $\left|Â\right|∕n$ observed using jActiveModules^* with the interaction network (Fig. 4A) is similar to the bias for the unstructured ASD (Fig. 2A). Thus, we also evaluated how much benefit the network provided for each method. For small $\mu$, we found that NetMix had a small but noticeable gain in performance when using the network; in contrast, other methods had nearly the same performance with or without the network (Fig. 4C with further details in the Supplementary Data). These results emphasize the importance of evaluating network methods on simulated data and demonstrating that a network method outperforms a single-gene test; neither of these was done in the jActiveModules (Ideker et al., 2002) and heinz (Dittrich et al., 2008) papers, nor are they common in many other papers on biological network analysis.

4.2. Differential gene expression subnetworks

We compared NetMix, jActiveModules^*, and heinz on gene expression data from the Expression Atlas (Petryszak et al., 2015). We analyzed $945$ differential expression experiments, including $292$ RNA-seq experiments and $653$ microarray experiments. For $84\%$ of these experiments, the GMM used by NetMix provided a better fit to the $p$-value distributions than the BUM (Pounds and Morris, 2003) used by heinz (see the Supplementary Data for more details). In addition, the GMM provided a better fit in $83∕85$ experiments, where the null proportion (fraction of genes not differentially expressed) estimated by the GMM and BUM differed by $\ge 0.25$. In all $85$ of these experiments, the BUM estimated a higher null proportion, consistent with the report in Pounds and Cheng (2004) that the BUM tends to overestimate the null proportion.

As many experiments had a small null proportion (i.e., most genes in the experiment were differentially expressed), we restricted our analysis to the $157$ experiments from the Expression Atlas with a null proportion $\ge 0.8$ as estimated by the GMM. We ran NetMix, jActiveModules^*, and heinz on these $157$ experiments with the HINT+HI network. For heinz, we used three FDR values: $FDR=0.1$, $FDR=0.001$, and the FDR value such that $\left|{Â}_{NetMix}\right|$ genes have a positive weight in the heinz scoring. These choices demonstrate how users might “$p$-hack” the FDR value to achieve desirable results. We also compared these with a method that ignores network topology, selecting the $\left|{Â}_{NetMix}\right|$ genes with the lowest $p$-values; we call this method “top $p$-values.” See the Supplementary Data for specific details on these methods.

Both NetMix and heinz identified subnetworks that were significantly smaller than jActiveModules^* (Fig. 5A), which is consistent with previous observations (Nikolayeva et al., 2018) that jActiveModules estimates overly large subnetworks. At the same time, NetMix identified subnetworks with significant overlap ($FDR\le 0.01$) with more biological process gene ontology (GO) terms than heinz ($p=3.3\times 10^{-12}$, $t$-test; Fig. 5B) or top $p$-values ($p<2.2\times 10^{-16}$, $t$-test; Fig. 5B). We also found that subnetworks identified by NetMix had greater overlap (as quantified by $F$-measure) with genes in the top $k$ GO terms (Fig. 5C). These results suggest that NetMix identifies subnetworks that are more relevant to differential expression experiments than other methods.

FIG. 5.

(A) Fraction of genes in the HINT+HI interaction network that are in the subnetwork identified by each method. ${}^{\ast \ast \ast }p\le 10^{-4}$ indicate significant $p$-values in paired $t$-test between and other methods. (B) Number of enriched GO biological process terms for altered subsets identified by each method. (C) $F$-measure of the $k$ most enriched GO terms. GO, gene ontology.

We examined the experiment E-GEOD-11199 in more detail. This experiment compared Mtb-stimulated and unstimulated macrophages (Thuong et al., 2008). NetMix identified a subnetwork containing $706$ genes, half the size of the jActiveModules^* subnetwork containing $1450$ genes. Both of these subnetworks contained $37$ of the $42$ genes whose differential expression was experimentally validated by reverse-transcription polymerase chain reaction (RT-PCR) (Thuong et al., 2008). Although the NetMix subnetwork was less than half the size of the jActiveModules^* subnetwork, the NetMix subnetwork overlapped more GO terms ($445$ vs. $179$). In contrast, heinz (using $FDR=0.27$) identified a subnetwork of $382$ genes containing only $25$ RT-PCR validated genes. Finally, the $692$ genes with the smallest $p$-values include only $7$ validated genes. These results show that the NetMix subnetwork contains many biologically relevant genes, including most of the RT-PCR validated genes, without being overly large.

4.3. Somatic mutations in cancer

We compared the performance of NetMix, jActiveModules^* (Arias-Castro et al., 2008; Addario-Berry et al., 2010), jActiveModules (Ideker et al., 2002), heinz (Dittrich et al., 2008), and Hierarchical HotNet (Reyna et al., 2018) in identifying cancer driver genes, using the MutSig2CV driver $p$-values (Lawrence et al., 2014) from the TCGA PanCanAtlas project (Bailey et al., 2018). We ran all methods on the HINT+HI interaction network described earlier, as well as the iRefIndex 15.0 (Razick et al., 2008) and ReactomeFI 2016 (Croft et al., 2014; Fabregat et al., 2016) interaction networks. See the Supplementary Data for more details on the datasets.

We evaluated the quality of the subnetwork $Â$ reported by each method by computing the overlap with the curated list of cancer genes from the COSMIC Cancer Gene Census (CGC) (Futreal et al., 2004; Forbes et al., 2016) (Table 1). We found that NetMix outperforms all other methods in $F$-measure across all interaction networks. For example, using the HINT+HI network, NetMix achieved an $F$-measure of $0.277$, compared with $F$-measures of $0.191$ for jActiveModules^*, $0.216$ for heinz ($FDR=0.001$), $0.264$ for heinz ($FDR=0.1$), and 0.214 for Hierarchical HotNet.^‡ Both the NetMix and Hierarchical HotNet results were statistically significant ($p<0.01$) on all three interaction networks according to permutation tests from Reyna et al. (2018). The modest $F$-measures for all methods are not surprising; the genes in CGC have diverse alterations across cancer types and, thus, high recall is not expected by this restricted analysis of single-nucleotide mutations in a subset of cancer types. Nevertheless, the higher performance of NetMix across all networks is encouraging.

Table 1.

Results of Network Methods on Cancer Driver Gene Prediction Using MutSig2CV Driver $p$-Values from the TCGA PanCanAtlas Project and Multiple Interaction Networks

Method	Network
	None	HINT+HI	iRefIndex	ReactomeFI
jActiveModules*	2,136/0.155	1,575/0.191	1,815/0.174	557/0.261
jActiveModules (greedy search)	NA/NA	NA/NA	NA/NA	NA/NA
jActiveModules (simulated annealing)	NA/NA	12,284/0.086	15,046/0.074	8,329/0.118
heinz ($FDR=0.001$)	115/0.205	119/0.216	109/0.217	114/0.215
heinz ($FDR=0.1$)	259/0.244	249/0.264	259/0.255	253/0.215
Hierarchical HotNet	NA/NA	228/0.214	297/0.215	228/0.214
NetMix	307/0.254	263/0.277	296/0.270	264/0.270

Bold values indicate the highest score.

Each entry reports the size/$F$-measure of the altered subnetwork identified by each method.

FDR, false discovery rate; HI, Human Interactone; HINT, High-quality INTeractone.

5. Discussion

In this article, we revisit the classic problem of identifying altered subnetworks in high-throughput biological data. We formalize the Altered Subnetwork Problem as the estimation of the parameters of the ASD. We show that the seminal algorithm for this problem, jActiveModules (Ideker et al., 2002), is equivalent to an MLE of the ASD. At the same time, we show that the MLE is a biased estimator of the altered subnetwork, with especially a large positive bias for small altered subnetworks. This bias explains previous reports that jActiveModules tends to output large subnetworks (Nikolayeva et al., 2018).

We leverage these observations to design NetMix, a new algorithm for the Altered Subnetwork Problem. We show that NetMix outperforms existing methods on simulated and real data. NetMix fits a GMM to observed vertex scores and then finds a maximum-weighted connected subgraph by using vertex weights derived from the GMM. heinz (Dittrich et al., 2008), another widely used method for altered subnetwork identification that also derives vertex weights from a mixture model (a BUM of $p$-values) and finds a maximum weighted connected subgraph. However, heinz does not solve the Altered Subnetwork Problem in a strict sense; rather, heinz requires users to choose a parameter (an FDR estimate for the mixture fit) that implicitly constrains the size of the identified subnetwork. This user-defined parameter may encourage $p$-hacking (Ioannidis, 2005; Head et al., 2015; Nuzzo, 2015), and we find that nearly all values of this parameter lead to biased estimates of the size of the altered subnetwork.

We note a number of directions for future work. The first is to generalize our theoretical contributions to the identification of multiple altered subnetworks, a situation that is common in biological applications where multiple biological processes may be perturbed (Menche et al., 2015). Although it is straightforward to run NetMix iteratively to identify multiple subnetworks—as jActiveModules does—a rigorous assessment of the identification of multiple altered subnetworks would be of interest.

Second, our results on simulated data (Section 4.1) show that altered subnetwork methods have only marginal gains over simpler methods that rank vertices without information from network interactions. We hypothesize that this is because connectivity is not a strong constraint for biological networks; indeed, the biological interaction networks that we use have both small diameter and small average shortest path between vertices (see the Supplementary Data for specific statistics). Specifically, we suspect that most subsets of vertices are “close” to a connected subnetwork in such biological networks, and thus the MLE of the connected ASD has similar bias as the MLE of the unstructured ASD. In contrast, for other network topologies such as the line graph, connectivity is a much stronger topological constraint (see the Supplementary Data for a brief comparison of different topologies). It would be useful to investigate this hypothesis and characterize the conditions when networks provide benefit for finding altered subnetworks. In particular, other topological constraints such as dense subgraphs (Guo et al., 2007; Ayati et al., 2015), cliques (Amgalan and Lee, 2014), and subgraphs resulting from heat diffusion and network propagation processes (Vanunu et al., 2010; Vandin et al., 2011; Leiserson et al., 2015; Cowen et al., 2017) have been used to model altered subnetworks in biological data. Generalizing the theoretical results in this article to these other topological constraints may be helpful for understanding the parameter regimes where these topological constraints provide a signal for the identification of altered subnetworks. In general, which topological constraints best model altered subnetworks remains an open question.

Finally, we note that biological networks often have substantial ascertainment bias: More interactions are annotated for well-studied genes (Rolland et al., 2014; Horn et al., 2018), and so these well-studied genes, in turn, may also be more likely to have outlier measurements/scores. Thus, any network method should carefully quantify the regime where it outperforms straightforward approaches—for example, methods based on ranking vertices by gene scores or degree—both on well-calibrated simulations and on real data.

Data Availability

NetMix is available online at https://github.com/raphael-group/netmix

Author Disclosure Statement

B.J.R. is a cofounder of, and consultant to, Medley Genomics.

Funding Information

M.A.R. was supported in part by the National Cancer Institute of the NIH (Cancer Target Discovery and Development Network grant U01CA217875). B.J.R. was supported by US National Institutes of Health (NIH) grants R01HG007069 and U24CA211000.

Supplementary Material

Supplementary Data