Significance
Accurate simulation of fluids is important for many science and engineering problems but is very computationally demanding. In contrast, machine-learning models can approximate physics very quickly but at the cost of accuracy. Here we show that using machine learning inside traditional fluid simulations can improve both accuracy and speed, even on examples very different from the training data. Our approach opens the door to applying machine learning to large-scale physical modeling tasks like airplane design and climate prediction.
Keywords: machine learning, turbulence, computational physics, nonlinear partial differential equations
Abstract
Numerical simulation of fluids plays an essential role in modeling many physical phenomena, such as weather, climate, aerodynamics, and plasma physics. Fluids are well described by the Navier–Stokes equations, but solving these equations at scale remains daunting, limited by the computational cost of resolving the smallest spatiotemporal features. This leads to unfavorable trade-offs between accuracy and tractability. Here we use end-to-end deep learning to improve approximations inside computational fluid dynamics for modeling two-dimensional turbulent flows. For both direct numerical simulation of turbulence and large-eddy simulation, our results are as accurate as baseline solvers with 8 to 10× finer resolution in each spatial dimension, resulting in 40- to 80-fold computational speedups. Our method remains stable during long simulations and generalizes to forcing functions and Reynolds numbers outside of the flows where it is trained, in contrast to black-box machine-learning approaches. Our approach exemplifies how scientific computing can leverage machine learning and hardware accelerators to improve simulations without sacrificing accuracy or generalization.
Simulation of complex physical systems described by nonlinear partial differential equations (PDEs) is central to engineering and physical science, with applications ranging from weather (1, 2) and climate (3, 4) and engineering design of vehicles or engines (5) to wildfires (6) and plasma physics (7). Despite a direct link between the equations of motion and the basic laws of physics, it is impossible to carry out direct numerical simulations at the scale required for these important problems. This fundamental issue has stymied progress in scientific computation for decades and arises from the fact that an accurate simulation must resolve the smallest spatiotemporal scales.
A paradigmatic example is turbulent fluid flow (8), underlying simulations of weather, climate, and aerodynamics. The size of the smallest eddy is tiny: For an airplane with chord length of 2 m, the smallest length scale (the Kolomogorov scale) (9) is m. Classical methods for computational fluid dynamics (CFD), such as finite differences, finite volumes, finite elements, and pseudo-spectral methods, are only accurate if fields vary smoothly on the mesh, and hence meshes must resolve the smallest features to guarantee convergence. For a turbulent fluid flow, the requirement to resolve the smallest flow features implies a computational cost scaling like , where , with and the typical velocity and length scales and the kinematic viscosity. A 10-fold increase in leads to a thousandfold increase in the computational cost. Consequently, direct numerical simulation (DNS) for, e.g., climate and weather, is impossible. Instead, it is traditional to use smoothed versions of the Navier–Stokes equations (10, 11) that allow coarser grids while sacrificing accuracy, such as Reynolds averaged Navier–Stokes (12, 13) and large-eddy simulation (LES) (14, 15). For example, current state-of-the-art LES with mesh sizes of to million has been used in the design of internal combustion engines (16), gas turbine engines (17, 18), and turbomachinery (19). Despite promising progress in LES over the last two decades, there are severe limits to what can be accurately simulated. This is mainly due to the first-order dependence of LES on the subgrid-scale (SGS) model, especially for flows whose rate controlling scale is unresolved (20).
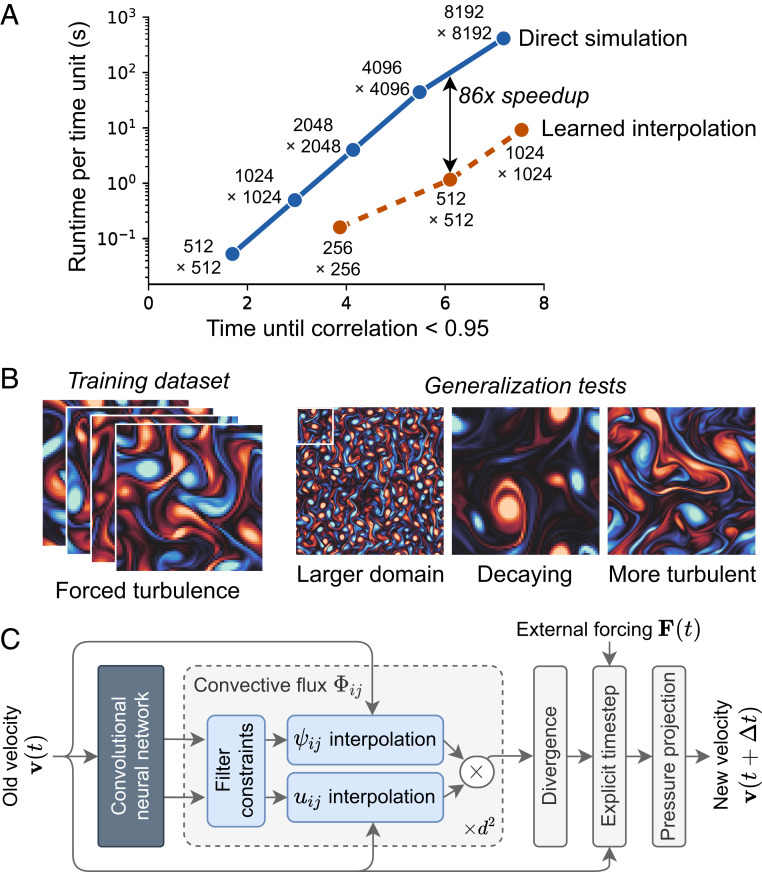
Here, we introduce a method for calculating the accurate time evolution of solutions to nonlinear PDEs, while using an order-of-magnitude coarser grid than is traditionally required for the same accuracy. This is a type of numerical solver that does not average unresolved degrees of freedom but instead uses discrete equations that give pointwise accurate solutions on an unresolved grid. We discover these algorithms using machine learning (ML), by replacing the components of traditional solvers most affected by the loss of resolution with learned alternatives. As shown in Fig. 1A, for a two-dimensional DNS of a turbulent flow our algorithm maintains accuracy while using coarser resolution in each dimension, resulting in a -fold improvement in computational time with respect to an advanced numerical method of similar accuracy. The model learns how to interpolate local features of solutions and hence can accurately generalize to different flow conditions such as different forcings and even different Reynolds numbers (Fig. 1B). We also apply the method to a high-resolution LES simulation of a turbulent flow and show similar performance enhancements, maintaining pointwise accuracy on LES simulations using coarser grids with -fold computational speedup.
Fig. 1.
Overview of our approach and results. (A) Accuracy versus computational cost with our baseline (direct simulation) and ML-accelerated [learned interpolation (LI)] solvers. The axis corresponds to pointwise accuracy, showing how long the simulation is highly correlated with the ground truth, whereas the axis shows the computational time needed to carry out one simulation time unit on a single Tensor Processing Unit (TPU) core. Each point is annotated by the size of the corresponding spatial grid; for details see SI Appendix. (B) Illustrative training and validation examples, showing the strong generalization capabilities of our model. (C) Structure of a single time step for our LI model, with a convolutional neural net controlling learned approximations inside the convection calculation of a standard numerical solver. and refer to advected and advecting velocity components. For spatial dimensions there are replicates of the convective flux module, corresponding to the flux of each velocity component in each spatial direction.
There has been a flurry of recent work using ML to improve turbulence modeling. One major family of approaches uses ML to fit closures to classical turbulence models based on agreement with high-resolution DNSs (21–24). While potentially more accurate than traditional turbulence models, these new models have not achieved reduced computational expense. Another major thrust uses “pure” ML, aiming to replace the entire Navier–Stokes simulation with approximations based on deep neural networks (25–30). A pure ML approach can be extremely efficient, avoiding the severe time-step constraints required for stability with traditional approaches. Because these models do not include the underlying physics, they often cannot enforce hard constraints, such as conservation of momentum and incompressibility. While these models often perform well on data from the training distribution, they often struggle with generalization. For example, they perform worse when exposed to novel forcing terms. We believe “hybrid” approaches that combine the best of ML and traditional numerical methods are more promising. For example, ML can replace (31) or accelerate (32) iterative solves used inside some simulation methods without reducing accuracy. Here we focus on hybrid models that use ML to correct errors in cheap, underresolved simulations (33–35). These models borrow strength from the coarse-grained simulations and are potentially much faster than pure numerical simulations due to the reduced grid size.
In this work we design algorithms that accurately solve the equations on coarser grids by replacing the components most affected by the resolution loss with better-performing learned alternatives. We use data-driven discretizations (36, 37) to interpolate differential operators onto a coarse mesh with high accuracy (Fig. 1C). We train the model inside a standard numerical method for solving the underlying PDEs as a differentiable program, with the neural networks and the numerical method written in a framework [JAX (38)] supporting reverse-mode automatic differentiation. This allows for end-to-end gradient-based optimization of the entire algorithm, similar to prior work on density functional theory (39), molecular dynamics (40), and fluids (33, 34). The methods we derive are equation-specific and require high-resolution ground-truth simulations for training data. Since the dynamics of a PDE are local, the high-resolution simulations can be carried out on a small domain. The models remain stable during long simulations and have robust and predictable generalization properties, with models trained on small domains producing accurate simulations on larger domains, with different forcing functions and even with different Reynolds number. Comparison to pure ML baselines shows that generalization arises from the physical constraints inherent in the formulation of the method.
Background
Navier–Stokes.
Incompressible fluids are modeled by the Navier–Stokes equations:
| [1a] |
| [1b] |
where is the velocity field, the external forcing, and denotes a tensor product. The density is a constant, and the pressure is a Lagrange multiplier used to enforce Eq. 1b. The Reynolds number dictates the balance between the convection (first) and diffusion (second) terms on the right hand side of Eq. 1a. Higher Reynolds number flows dominated by convection are more complex and thus generally harder to model; flows are considered “turbulent” if .
DNS solves Eq. 1 directly, whereas LES solves a spatially filtered version. In the equations of LES, is replaced by a filtered velocity and a subgrid term arising from convection is added to the right side of Eq. 1a, with the subgrid stress defined as . Because is unmodeled, solving LES also requires a choice of closure model for as a function of . Numerical simulation of both DNS and LES further requires a discretization step to approximate the continuous equations on a grid. Traditional discretization methods (e.g., finite differences) converge to an exact solution as the grid spacing becomes small, with LES converging faster because it models a smoother quantity. Together, discretization and closure models are the two principal sources of error when simulating fluids on coarse grids (33, 41).
Methods
Learned Solvers.
Our principal aim is to accelerate DNS without compromising accuracy or generalization. To that end, we consider ML modeling approaches that enhance a standard CFD solver when run on inexpensive-to-simulate coarse grids. We expect that ML models can improve the accuracy of the numerical solver via effective superresolution of missing details. Unlike traditional numerical methods, our learned solvers are optimized to fit the observed manifold of solutions to the equations they solve, rather than arbitrary polynomials. Empirically, this can significantly improve accuracy over high-order numerical methods (36), although we currently lack a theoretical explanation. Because we want to train neural networks for approximation inside our solver, we wrote a new CFD code in JAX (38), which allows us to efficiently calculate gradients via automatic differentiation. Our base CFD code is a standard implementation of a finite volume method on a regular staggered mesh, with first-order explicit time stepping for convection, diffusion, and forcing and implicit treatment of pressure; for details see SI Appendix.
The algorithm works as follows. In each time step, the neural network generates a latent vector at each grid location based on the current velocity field, which is then used by the subcomponents of the solver to account for local solution structure. Our neural networks are convolutional, which enforces translation invariance and allows them to be local in space. We then use components from standard numerical methods to enforce inductive biases corresponding to the physics of the Navier–Stokes equations, as illustrated by the light gray boxes in Fig. 1C; the convective flux model improves the approximation of the discretized convection operator, the divergence operator enforces local conservation of momentum according to a finite volume method, and the pressure projection enforces incompressibility and the explicit time-step operator forces the dynamics to be continuous in time, allowing for the incorporation of additional time-varying forces. “DNS on a coarse grid” blurs the boundaries of traditional DNS and LES modeling and thus invites a variety of data-driven approaches. In this work we focus on two types of ML components: learned interpolation and learned correction. Both center on convection, the key term in Eq. 1 for turbulent flows.
Learned Interpolation.
In a finite volume method, denotes a vector field of volume averages over unit cells, and the cell-averaged divergence can be calculated via Gauss’ theorem by summing the surface flux over each face. This suggests that our only required approximation is calculating the convective flux on each face, which requires interpolating from where it is defined. Rather than using typical polynomial interpolation, which is suitable for interpolation without prior knowledge, here we use an approach that we call learned interpolation based on data-driven discretizations (36). We use the outputs of the neural network to generate interpolation coefficients based on local features of the flow, similar to the fixed coefficients of polynomial interpolation. This allows us to incorporate two important priors: 1) The equation maintains the same symmetries and scaling properties (e.g., rescaling coordinates ) as the original equations and 2) the interpolation is always at least first-order accurate with respect to the grid spacing, by constraining the filters to sum to unity. It is also possible to visualize interpolation weights to interpret predictions from our model; see SI Appendix, Fig. S2 and our prior work (36, 37) for examples.
Learned Correction.
An alternative approach, closer in spirit to LES modeling, is to simply model a residual correction to the discretized Navier–Stokes equations (Eq. 1) on a coarse grid (33, 34). Such an approach generalizes traditional closure models for LES but in principle can also account for discretization error. We consider learned correction models of the form , where LC (learned correction) is a neural network and is the uncorrected velocity field from the numerical solver on a coarse grid. Modeling the residual is appropriate both from the perspective of a temporally discretized closure model and pragmatically because the relative error between and in a single time step is small. Learned correction models have fewer inductive biases and are less interpretable than learned interpolation models, but they are simpler to implement and potentially more flexible. We also explored learned correction models restricted to take the form of classical closure models (e.g., flow-dependent effective tensor viscosity models), but the restrictions hurt model performance and stability.
Training.
The training procedure tunes the ML components of the solver to minimize the discrepancy between an expensive high-resolution simulation and a simulation produced by the model on a coarse grid. We accomplish this via supervised training where we use a cumulative pointwise error between the predicted and ground truth velocities as the loss function:
| [2] |
where MSE denotes the mean-squared error. The ground truth trajectories are obtained by using a high-resolution simulation that is then coarsened to the simulation grid. Including the numerical solver in the training loss ensures fully “model-consistent” training where the model sees its own outputs as inputs (23, 34, 41), unlike typical “a priori” training where simulation is only performed offline. As an example, for the Kolmogorov flow simulations below with Reynolds number 1,000, our ground-truth simulation had a resolution of 2,048 cells along each spatial dimension. We coarsen these ground-truth trajectories along each dimension and time by a factor of 32. For training we use 32 trajectories of 4,800 sequential time steps each, starting from different random initial conditions. To evaluate the model, we generate much longer trajectories (tens of thousands of time steps) to verify that models remain stable and produce plausible outputs. Unrolling over multiple time steps in training improves inference performance over long trajectories (both accuracy and stability) but makes training less stable (34); as a compromise, we unroll for steps. To avoid the prohibitive memory requirements of saving neural network activations inside each unrolled time step in the forward pass we use gradient checkpointing at the start of each time step (42).
Results
We take a utilitarian perspective on model evaluation: Simulation methods are good insofar as they demonstrate accuracy, computational efficiency, and generalization. DNS excels at accuracy and generalization but is not efficient. Useful ML methods for fluids should be faster than standard baselines (e.g., DNS) with the same accuracy. Although trained on specific flows, they must readily generalize to new simulation settings, such as different domains, forcings, and Reynolds numbers. In what follows, we first compare the accuracy and generalization of our method to both DNS and several existing ML-based approaches for simulations of two-dimensional turbulence flow. In particular, we first consider Kolmogorov flow (43), a parametric family of forced two-dimensional turbulent flows obeying the Navier–Stokes equation (Eq. 1), with periodic boundary conditions and forcing , where the second term is a velocity-dependent drag preventing accumulation of energy at large scales (44). Kolmogorov flow produces a statistically stationary turbulent flow, with flow complexity controlled by a single parameter, the Reynolds number .
Accelerating DNS.
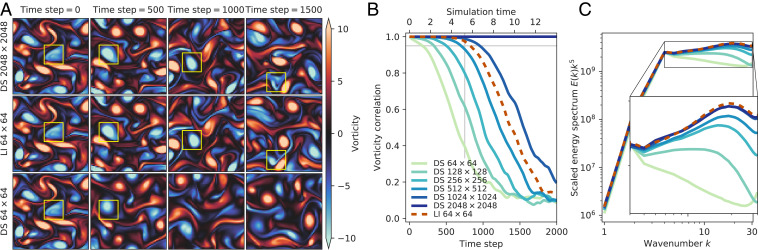
The accuracy of a DNS quickly degrades once the grid resolution cannot capture the smallest details of the solution. In contrast, our ML-based approach strongly mitigates this effect. Fig. 2 shows the results of training and evaluating our model on Kolmogorov flows at Reynolds number . All datasets were generated using high-resolution DNS, followed by a coarsening step.
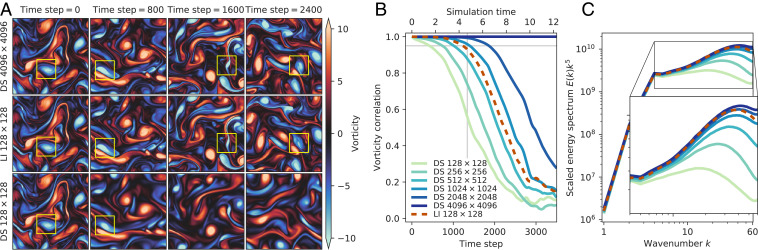
Fig. 2.
Learned interpolation (LI) achieves accuracy of direct simulation at higher resolution. (A) Evolution of predicted vorticity fields for reference (DS 2,048 × 2,048), learned (LI ), and baseline (DS ) solvers, starting from the same initial velocities. The yellow box traces the evolution of a single vortex. (B) Comparison of the vorticity correlation between predicted flows and the reference solution for our model and DNS solvers. (C) Energy spectrum scaled by averaged between time steps 10,000 and 20,000, when all solutions have decorrelated with the reference solution.
Accuracy.
The scalar vorticity field is a convenient way to describe two-dimensional incompressible flows (44). Accuracy can be quantified by correlating vorticity fields,* between the ground-truth solution and the predicted state . Fig. 2 compares the learned interpolation model () to fully resolved DNS of Kolmogorov flow (2,048 × 2,048) using an initial condition that was not included in the training set. Strikingly, the learned discretization model matches the pointwise accuracy of DNS with a × finer grid. The eventual loss of correlation with the reference solution is expected due to the chaotic nature of turbulent flows; this is marked by a vertical gray line in Fig. 2B, indicating the first three Lyapunov times. Fig. 2A shows the time evolution of the vorticity field for three different models: the learned interpolation matches the ground truth (2,048 × 2,048) more accurately than the baseline, whereas it greatly outperforms a baseline solver at the same resolution as the model ().
The learned interpolation model also produces an energy spectrum similar to DNS. With decreasing resolution, DNS cannot capture high-frequency features, resulting in an energy spectrum that “tails off” for higher values of . Fig. 2C compares the energy spectrum for learned interpolation and direct simulation at different resolutions after time steps. The learned interpolation model accurately captures the energy distribution across the spectrum.
Computational efficiency.
The ability to match DNS with a × coarser grid makes the learned interpolation solver much faster. We benchmark our solver on a single core of Google’s Cloud TPU v4, a hardware accelerator designed for accelerating ML models that is also suitable for many scientific computing use cases (45–47). The TPU is designed for high-throughput vectorized operations, with extremely high throughput matrix–matrix multiplication in low precision (bfloat16). On sufficiently large grid sizes ( and larger), our neural net makes good use of matrix-multiplication unit, achieving 12.5× higher throughput in floating-point operations per second than our baseline CFD solver. Thus, despite using 150 more arithmetic operations, the ML solver is only about 12 slower than the traditional solver at the same resolution. The gain in effective resolution in three dimensions (two space dimensions and time, due to the Courant condition) thus corresponds to a speedup of .
Generalization.
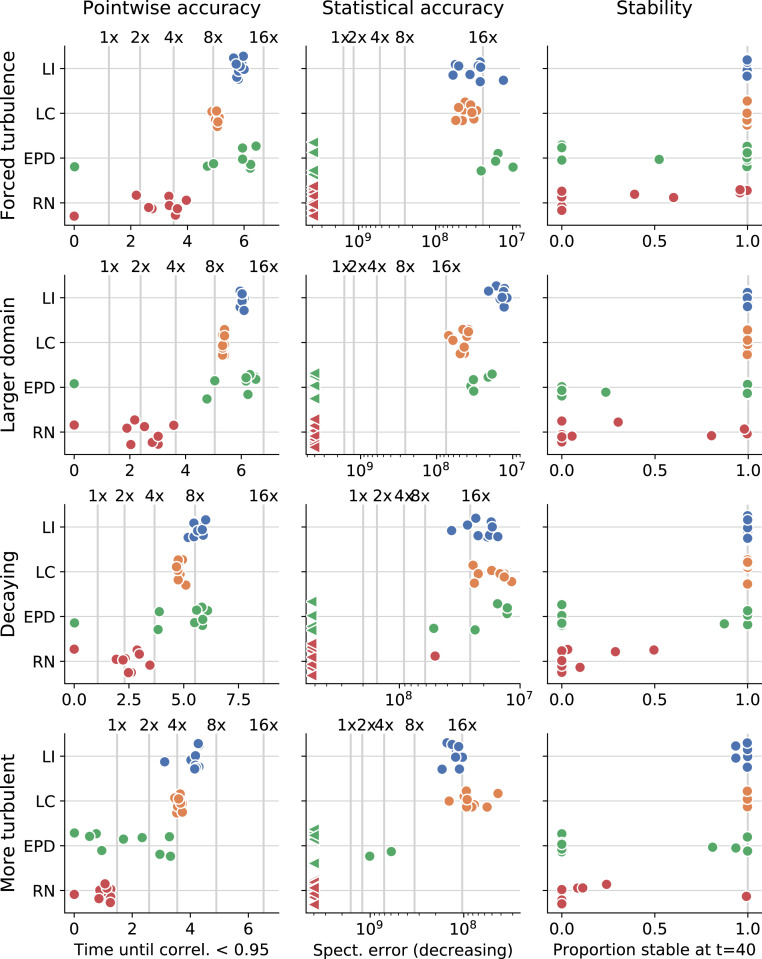
In order to be useful, a learned model must accurately simulate flows outside of the training distribution. We expect our models to generalize well because they learn local operators: Interpolated values and corrections at a given point depend only on the flow within a small neighborhood around it. As a result, these operators can be applied to any flow that features similar local structures to those seen during training. We consider three different types of generalization tests: 1) larger domain size, 2) unforced decaying turbulent flow, and 3) Kolmogorov flow at a larger Reynolds number.
First, we test generalization to larger domain sizes with the same forcing. Our ML models have essentially the exact same performance as on the training domain, because they only rely upon local features of the flows (SI Appendix, Fig. S5 and see Fig. 5).
Fig. 5.
Learned discretizations outperform a wide range of baseline methods in terms of accuracy, stability, and generalization. Each row within a subplot shows performance metrics for nine model replicates with the same architecture but different randomly initialized weights. The models are trained on forced turbulence, with larger domain, decaying, and more turbulent flows as generalization tests. Vertical lines indicate performance of nonlearned baseline models at different resolutions (all baseline models are perfectly stable). The pointwise accuracy test measures error at the start of time integration, whereas the statistical accuracy and stability tests are both performed on simulations at much later time. For all cases except for the decaying turbulence we used time 40 after about 5,600 time integration steps (twice the number of steps for more turbulent flow). For the decaying turbulence generalization test we measured statistical accuracy at time 14 after 2,000 time integration steps and stability at time 40. The points indicated by a left-pointing triangle in the statistical accuracy tests are clipped at a maximum error.
Second, we apply our model trained on Kolmogorov flow to decaying turbulence, by starting with a random initial condition with high wavenumber components and letting the turbulence evolve in time without forcing. Over time, the small scales coalesce to form large-scale structures, so that both the scale of the eddies and the Reynolds number vary. Fig. 3 shows that a learned discretization model trained on Kolmogorov flows with can match the accuracy of DNS running at × finer resolution. The standard numerical method at the same resolution as the learned discretization model is corrupted by numerical diffusion, degrading the energy spectrum as well as pointwise accuracy. The learned model slightly overestimates the energy at the smallest spatial scales, an indication of overfitting to the statistics of forced turbulence from the training dataset.
Fig. 3.
Learned interpolation (LI) generalizes well to decaying turbulence. (A) Evolution of predicted vorticity fields as a function of time. (B) Vorticity correlation between predicted flows and the reference solution. (C) Energy spectrum scaled by averaged between time steps 2,000 and 2,500, when all solutions have decorrelated with the reference solution.
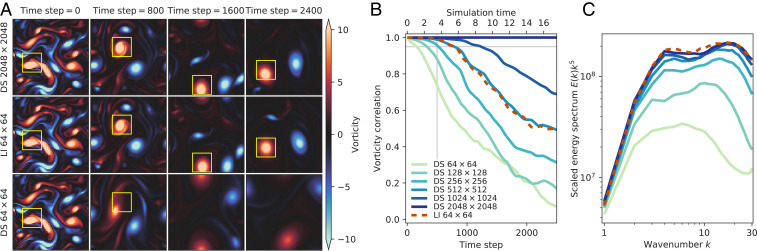
Our final generalization test is harder: Can the models generalize to higher Reynolds number where the flows are more complex? The universality of the turbulent cascade (1, 48, 49) implies that at the size of the smallest eddies (the Kolmogorov length scale), flows “look the same” regardless of Reynolds number when suitably rescaled. This suggests that we can apply the model trained at one Reynolds number to a flow at another Reynolds number by simply rescaling the model to match the new smallest length scale. To test this we construct a new validation dataset for Kolmogorov flow with . The theory of two-dimensional turbulence (50) implies that the smallest eddy size decreases as , implying that the smallest eddies in this flow are half the size of those for original flow with . We therefore can use a trained model at by simply halving the grid spacing. Fig. 4A shows that with this scaling our model achieves the accuracy of DNS running at 6× finer resolution. This degree of generalization is remarkable, given that we are now testing the model with a flow of substantially greater complexity. Fig. 4B visualizes the vorticity, showing that higher complexity is captured correctly, as is further verified by the energy spectrum shown in Fig. 4C.
Fig. 4.
LIs can be scaled to simulate higher Reynolds numbers without retraining. (A) Evolution of predicted vorticity fields as a function of time for Kolmogorov flow at . (B) Vorticity correlation between predicted flows and the reference solution. (C) Energy spectrum scaled by averaged between time steps 6,000 and 12,000, when all solutions have decorrelated with the reference solution.
Comparison to Other ML Models.
Finally, we compare the performance of learned interpolation to alternative ML-based methods. We consider three popular ML methods: ResNet (51), encoder–processor–decoder (52, 53) architectures, and the learned correction model introduced earlier. These models all perform explicit time stepping without any additional latent state beyond the velocity field, which allows them to be evaluated with arbitrary forcings and boundary conditions and to use the time step based on the Courant–Friedrichs–Lewy condition. By construction, these models are invariant to translation in space and time and have similar runtime for inference (varying within a factor of 2). To evaluate training consistency, each model is trained nine times with different random initializations on the same Kolmogorov dataset described previously. Hyperparameters for each model were chosen as detailed in SI Appendix, and the models are evaluated on the same generalization tasks. We compare their performance using several metrics: time until vorticity correlation falls below 0.95 to measure pointwise accuracy for the flow over short time windows, the absolute error of the energy spectrum scaled by to measure statistical accuracy for the flow over long time windows, and the fraction of simulated velocity values that does not exceed the range of the training data to measure stability.
Fig. 5 compares results across all considered configurations. Overall, we find that learned interpolation performs best, although learned correction is not far behind. We were impressed by the performance of the learned correction model, despite its weaker inductive biases. The difference in effective resolution for pointwise accuracy ( vs upscaling) corresponds to about a factor of 2 in run time. There are a few isolated exceptions where pure black-box methods outperform the others, but not consistently. A particular strength of the learned interpolation and correction models is their consistent performance and generalization to other flows, as seen from the narrow spread of model performance for different random initialization and their consistent dominance over other models in the generalization tests. Note that even a modest effective coarse graining in resolution still corresponds to a computational speed-up. In contrast, the black box ML methods exhibit high sensitivity to random initialization and do not generalize well, with much less consistent statistical accuracy and stability.
Accelerating LES.
Finally, up until now we have illustrated our method for DNS of the Navier–Stokes equations. Our approach is quite general and could be applied to any nonlinear PDE. To demonstrate this, we apply the method to accelerate LES, the industry standard method for large-scale simulations where DNS is not feasible.
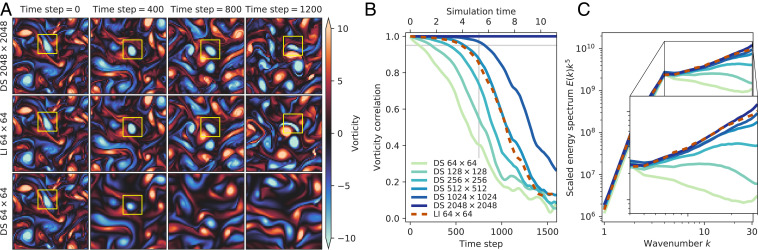
Here we treat the LES at high resolution as the ground-truth simulation and train an interpolation model on a coarser grid for Kolmogorov flows with Reynolds number according to the Smagorinsky–Lilly SGS model (8). Our training procedure follows the exact same approach we used for modeling DNS. Note in particular that we do not attempt to model the parameterized viscosity in the learned LES model but rather let learned interpolation model this implicitly. Fig. 6 shows that learned interpolation for LES still achieves an effective upscaling, corresponding to roughly speed-up.
Fig. 6.
Learned discretizations achieve accuracy of LES simulation running on finer resolution. (A) Evolution of predicted vorticity fields as a function of time. (B) Vorticity correlation between predicted flows and the reference solution. (C) Energy spectrum scaled by averaged between time steps 3,800 and 4,800, when all solutions have decorrelated with the reference solution.
Discussion
In this work we present a data-driven numerical method that achieves the same accuracy as traditional finite difference/finite volume methods but with much coarser resolution. The method learns accurate local operators for convective fluxes and residual terms and matches the accuracy of an advanced numerical solver running at 8 to finer resolution, while performing the computation 40 to faster. The method uses ML to interpolate better at a coarse scale, within the framework of the traditional numerical discretizations. As such, the method inherently contains the scaling and symmetry properties of the original governing Navier–Stokes equations. For that reason, the methods generalize much better than pure black-box machine-learned methods, not only to different forcing functions but also to different parameter regimes (Reynolds numbers).
What outlook do our results suggest for speeding up three-dimensional turbulence? In general, the runtime for efficient ML augmented simulation of time-dependent PDEs should scale like
| [3] |
where is the cost of ML inference per grid point, is the cost of baseline numerical method, is the number of grid points along each dimension of the resolved grid, is the number of spatial dimensions, and is the effective coarse graining factor. Currently, , but we expect that much more efficient ML models are possible, e.g. by sharing work between time steps with recurrent neural nets with physical motivated architectures (54, 55). We expect the decrease in effective resolution discovered here to generalize to three-dimensional and more complex problems. This suggests that speed-ups in the range of to may be possible for three-dimensional simulations. Further speed-ups, as required to capture the full range of turbulent flows, will require either more efficient representations (e.g., based on solution manifolds rather than a grid) or being satisfied with statistical rather than pointwise accuracy (e.g., as done in LES modeling).
In summary, our approach expands the Pareto frontier of efficient simulation in CFD, as illustrated in Fig. 1A. With ML-accelerated CFD, users may either solve expensive simulations much faster or increase accuracy without additional costs. To put these results in context, if applied to numerical weather prediction, increasing the duration of accurate predictions from 4 to 7 time units would correspond to approximately 30 y of progress (56). These improvements are possible due to the combined effect of two technologies still undergoing rapid improvements: modern deep learning models, which allow for accurate simulation with much more compact representations, and modern accelerator hardware, which allows for evaluating said models with a remarkably small increase in computational cost. We expect both trends to continue for the foreseeable future and to eventually impact all areas of computationally limited science.
Supplementary Material
Acknowledgments
We thank John Platt and Rif A. Saurous for encouraging and supporting this work and for important conversations and Yohai bar Sinai, Anton Geraschenko, Yi-fan Chen, and Jiawei Zhuang for important conversations.
Footnotes
Competing interest statement: The authors are employees of Google, which sells hardware and software for machine learning. A patent filing has been submitted based on this work.
This article is a PNAS Direct Submission.
*In our case the Pearson correlation reduces to a cosine distance because the flows considered here have mean velocity of 0.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2101784118/-/DCSupplemental.
Data Availability
Source code for our models, including learned components, and training and evaluation datasets are available at GitHub (https://github.com/google/jax-cfd).
References
- 1.Richardson L. F., Weather Prediction by Numerical Process (Cambridge University Press, 2007). [Google Scholar]
- 2.Bauer P., Thorpe A., Brunet G., The quiet revolution of numerical weather prediction. Nature 525, 47–55 (2015). [DOI] [PubMed] [Google Scholar]
- 3.Schneider T., et al. , Climate goals and computing the future of clouds. Nat. Clim. Change 7, 3–5 (2017). [Google Scholar]
- 4.Neumann P., et al. , Assessing the scales in numerical weather and climate predictions: Will exascale be the rescue? Philos. Trans. R. Soc. A 377, 20180148 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Anderson J. D., “Basic philosophy of CFD” in Computational Fluid Dynamics, J. F. Wendt, Ed. (Springer, 2009), pp. 3–14. [Google Scholar]
- 6.Bakhshaii A., Johnson E. A., A review of a new generation of wildfire–atmosphere modeling. Can. J. For. Res. 49, 565–574 (2019). [Google Scholar]
- 7.Tang W. M., Chan V. S., Advances and challenges in computational plasma science. Plasma Phys. Contr. Fusion 47, R1 (2005). [Google Scholar]
- 8.Pope S. B., Turbulent Flows (Cambridge University Press, 2000). [Google Scholar]
- 9.Frisch U., Turbulence: The Legacy of A. N. Kolmogorov (Cambridge University Press, 1995). [Google Scholar]
- 10.Moser R. D., Haering S. W., Gopal R. Y., Statistical properties of subgrid-scale turbulence models. Annu. Rev. Fluid Mech. 53 (2020). [Google Scholar]
- 11.Meneveau C., Katz J., Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32, 1–32 (2000). [Google Scholar]
- 12.Boussinesq J., Theorie de l’ecoulement tourbillant. Mémoires de l’Acad. des Sci. 23, 46–50 (1877). [Google Scholar]
- 13.Alfonsi G., Reynolds-averaged Navier–Stokes equations for turbulence modeling. Appl. Mech. Rev. 62, 040802 (2009). [Google Scholar]
- 14.Smagorinsky J., General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 91, 99–164 (1963). [Google Scholar]
- 15.Lesieur M., Metais O., New trends in Large-Eddy simulations of turbulence. Annu. Rev. Fluid Mech. 28, 45–82 (1996). [Google Scholar]
- 16.Malé Q., et al. , Large eddy simulation of pre-chamber ignition in an internal combustion engine. Flow Turbul. Combust. 103, 465–483 (2019). [Google Scholar]
- 17.Wolf P., Staffelbach G., Gicquel L. Y. M., Müller J.-D., Poinsot T., Acoustic and large eddy simulation studies of azimuthal modes in annular combustion chambers. Combust. Flame 159, 3398–3413 (2012). [Google Scholar]
- 18.Esclapez L., et al. , Fuel effects on lean blow-out in a realistic gas turbine combustor. Combust. Flame 181, 82–99 (2017). [Google Scholar]
- 19.Arroyo C. P., Kholodov P., Sanjosé M., Moreau S., “CFD modeling of a realistic turbofan blade for noise prediction. Part 1: Aerodynamics” in Proceedings of the Global Power and Propulsion Society (GPPS, 2019).
- 20.Pope S. B., Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 6, 35 (2004). [Google Scholar]
- 21.Ling J., Kurzawski A., Templeton J., Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 807, 155–166 (2016). [Google Scholar]
- 22.Duraisamy K., Iaccarino G., Xiao H., Turbulence modeling in the age of data. Annu. Rev. Fluid Mech. 51, 357–377 (2019). [Google Scholar]
- 23.Maulik R., San O., Adil R., Prakash V., Subgrid modelling for two-dimensional turbulence using neural networks. J. Fluid Mech. 858, 122–144 (2019). [Google Scholar]
- 24.Beck A., Flad D., Munz C.-D., Deep neural networks for data-driven les closure models. J. Comput. Phys. 398, 108910 (2019). [Google Scholar]
- 25.Kim B., et al. , Deep fluids: A generative network for parameterized fluid simulations. Comput. Graph. Forum 38, 59–70 (2019). [Google Scholar]
- 26.Li Z., et al. , Neural operator: Graph kernel network for partial differential equations. arXiv [Preprint] (2020). https://arxiv.org/abs/2003.03485 (Accessed 16 March 2021). [Google Scholar]
- 27.Bhattacharya K., Hosseini B., Kovachki N. B., Stuart A. M., Model reduction and neural networks for parametric PDEs. arXiv [Preprint] (2020). https://arxiv.org/abs/2005.03180 (Accessed 10 December 2020).
- 28.Wang R., Kashinath K., Mustafa M., Albert A., Yu R., “Towards physics-informed deep learning for turbulent flow prediction” in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (ACM, 2020), pp. 1457–1466.
- 29.Lusch B., Kutz J. N., Brunton S. L., Deep learning for universal linear embeddings of nonlinear dynamics. Nat. Commun. 9, 1–10 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Erichson N. B., Muehlebach M., Mahoney M. W., Physics-informed autoencoders for lyapunov-stable fluid flow prediction. arXiv [Preprint] (2019). https://arxiv.org/abs/1905.10866 (Accessed 10 December 2020).
- 31.Tompson J., Schlachter K., Sprechmann P., Perlin K., “Accelerating Eulerian fluid simulation with convolutional networks” in 34th International Conference on Machine Learning (2017). http://proceedings.mlr.press/v70/tompson17a/tompson17a.pdf. Accessed 10 December 2020.
- 32.Obiols-Sales O., Vishnu A., Malaya N., Chandramowlishwaran A., “CFDNet: A deep learning-based accelerator for fluid simulations” in 34th ACM International Conference on Supercomputing (ACM, 2020).
- 33.Sirignano J., MacArt J. F., Freund J. B., DPM: A deep learning PDE augmentation method with application to large-eddy simulation. J. Comput. Phys., 423:109811, 2020. [Google Scholar]
- 34.Um K., Brand R., Fei Y. R., Holl P., Thuerey N., “Solver-in-the-loop: Learning from differentiable physics to interact with iterative PDE-solvers” inAdvances in Neural Information Processing Systems, Larochelle H., Ranzato M., Hadsell R., Balcan M. F., and Lin H., Eds. (Curran Associates, Inc, 2020), vol. 33, pp. 6111–6122. [Google Scholar]
- 35.Pathak J., et al. , Using machine learning to augment coarse-grid computational fluid dynamics simulations. arXiv [Preprint] (2020). https://arxiv.org/abs/2010.00072 (Accessed 10 December 2020).
- 36.Bar-Sinai Y., Hoyer S., Hickey J., Brenner M. P., Learning data-driven discretizations for partial differential equations. Proc. Natl. Acad. Sci. U.S.A. 116, 15344–15349 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhuang J., et al. , Learned discretizations for passive scalar advection in a two-dimensional turbulent flow. Phys. Rev. Fluid., in press.
- 38.Bradbury J., et al. , JAX: Composable transformations of Python+NumPy programs. http://github.com/google/jax. Deposited 15 December 2020.
- 39.Li L., et al. , Kohn-Sham equations as regularizer: Building prior knowledge into machine-learned physics. Phys. Rev. Lett. 126, 036401 (2021). [DOI] [PubMed] [Google Scholar]
- 40.Schoenholz S. S., Cubuk E. D., “JAX, M.D.: A framework for differentiable physics” in Advances in Neural Information Processing Systems, Larochelle H., Ranzato M., Hadsell R., Balcan M. F., and Lin H., Eds. (Curran Associates, Inc., 2020), vol. 33, pp. 11428–11441. [Google Scholar]
- 41.Duraisamy K., Perspectives on machine learning-augmented Reynolds-averaged and large eddy simulation models of turbulence. arXiv [Preprint] (2020). https://arxiv.org/abs/2009.10675 (Accessed 16 March 2021).
- 42.Griewank A., Achieving logarithmic growth of temporal and spatial complexity in reverse automatic differentiation. Optim. Methods Software 1, 35–54 (1994). [Google Scholar]
- 43.Chandler G. J., Kerswell R. R., Invariant recurrent solutions embedded in a turbulent two-dimensional Kolmogorov flow. J. Fluid Mech. 722, 554–595 (2013). [Google Scholar]
- 44.Boffetta G., Ecke R. E., Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451 (2012). [Google Scholar]
- 45.Ben-Haim Z., et al. , Inundation modeling in data scarce regions. arXiv [Preprint] (2019). https://arxiv.org/abs/1910.05006 (Accessed 10 December 2020).
- 46.Yang K., Chen Y.-F., Roumpos G., Colby C., Anderson J., “High performance Monte Carlo simulation of ising model on TPU clusters” in Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (Association for Computing Machinery, New York, 2019), pp. 1–15. [Google Scholar]
- 47.Lu T., Chen Y.-F., Hechtman B., Wang T., Anderson J.. Large-scale discrete fourier transform on TPUs. arXiv [Preprint] (2020). https://arxiv.org/abs/2002.03260 (Accessed 10 December 2020).
- 48.Kolmogorov A. N., The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Cr. Acad. Sci. URSS 30, 301–305 (1941). [Google Scholar]
- 49.Kraichnan R. H., Montgomery D., Two-dimensional turbulence. Rep. Prog. Phys. 43, 547 (1980). [Google Scholar]
- 50.Boffetta G., Ecke R. E., Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451 (2012). [Google Scholar]
- 51.He K., Zhang X., Ren S., Sun J., “Deep residual learning for image recognition” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2016), pp. 770–778.
- 52.Battaglia P. W., et al. , Relational inductive biases, deep learning, and graph networks. arXiv [Preprint] (2018). https://arxiv.org/abs/1806.01261 (Accessed 10 December 2020).
- 53.Sanchez-Gonzalez A., et al. , “Learning to simulate complex physics with graph networks” in 37th International Conference on Machine Learning (2020). http://proceedings.mlr.press/v119/sanchez-gonzalez20a/sanchez-gonzalez20a.pdf. Accessed 12 May 2021. [Google Scholar]
- 54.Nguyen T., Baraniuk R., Bertozzi A., Osher S., Wang B., “Momentumrnn: Integrating momentum into recurrent neural networks” in Advances in Neural Information Processing Systems, Larochelle H., Ranzato M., Hadsell R., Balcan M. F., and Lin H., Eds. (Curran Associates, Inc., 2020), vol. 33, pp. 1924–1936. [Google Scholar]
- 55.Hoedt P.-J., et al. , MC-LSTM: Mass-Conserving LSTM. arXiv [Preprint] (2021). https://arxiv.org/abs/2101.05186 (Accessed 16 March 2021).
- 56.Bauer P., Thorpe A., Brunet G., The quiet revolution of numerical weather prediction. Nature 525, 47–55 (2015). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Source code for our models, including learned components, and training and evaluation datasets are available at GitHub (https://github.com/google/jax-cfd).