Study of SEIR epidemic model and scenario analysis of COVID-19 pandemic

Abstract

In recent times, the Coronavirus disease (caused by COVID-19) is evidently observed to be the extremely contagious one with high fatality rate worldwide. In March 2020, the disease was declared a “global pandemic” by the World Health Organization (WHO). So far, there is no known/effective vaccine or medicine. In this paper, we propose and analyze an SEIR compartment model. We also compare and analyze the case study of India and Brazil. The model system is discussed by using MATLAB (2018a) software and the numerical results are verified graphically.

1. Introduction

Coronavirus disease 2019 (COVID-19), that has generated a pandemic, is primarily a respiratory illness, caused by a novel coronavirus that spreads from person to person, poses a serious public health risk with its high contagion rate. In most cases, the infected people perceive mild respiratory symptoms that usually disappear on their own, but some people develop severe illness, like pneumonia [1]. The virus is transmitted through contact with an infected person or via respiratory droplets when an infected person coughs or sneezes.

Since December 2019, an outbreak of a new coronavirus named SARS-COV-2 has been reported in many countries and has infected thousands of people all over the world with a high mortality rate. The World Health Organization has declared COVID-19 to be a pandemic. First it was identified in Wuhan city, Hubei Province of China on December 31, 2019 [2]. The symptoms of COVID-19 appearing within 2–14 days after infection include fever, cough, a running nose and difficulty in breathing. There is a higher risk of infection if one has been in a contaminated area or if one has been in close contact with a person infected with the new coronavirus. There is also a higher risk if one suffers from co-morbidities. In recent times, most of the countries are in the clutches of COVID-19 and a large number of people are infected. COVID-19, has seriously affected the lives of people in multiple ways and incurred huge losses to the economy.

Coronavirus is common among animals. However, animal to human transmission is reportedly rare. It causes damage to the respiratory tract ranging from the common cold to severe conditions like SARS [3]. The outbreak of Coronavirus (officially known as Covid-19), which started in China, has so far killed 567,657 people and infected 12,844,410 people across the globe (as on July 12, 2020) [4]. In India, 849,553 confirmed cases and 22,674 deaths have been reported so far according to official figures released by the Union Ministry of Health and Family Welfare (MoHFW) [5].

Mathematical models can be viable tools in analyzing the spread and control of infectious disease; for instance, the epidemic model developed by Kermack and Mckendrick in 1927 [6]. In epidemiology there are different models to predict and explain the dynamics of an epidemic. The data of the Covid-19 outbreak can also be studied through various mathematical models such as SIR, SEIR (Susceptible, Exposed, Infected and Recovery), SIQR (Susceptible, Infectious, Quarantined and Recovered) and so on [[7], [8], [9], [10], [11], [12]]. Tang, Wang, Li and Bragazzi [13] presented a compartmental deterministic model that would integrate the clinical development of the disease, the epidemiological status of the patient and the measures for intervention. In this situation, several studies have been conducted using real time data of the affected countries and distinct characteristics of the outbreak [14,15] have been examined. Kamrujjaman, Ghosh and Islam [16] developed the Susceptible Exposed Infectious Recovered model (SEIR) to clarify the dynamics of COVID-19 case. The SEIR model divides the population into four parts, namely the susceptible S(t), the exposed E(t), the infected I(t) and the recovered R(t) at time t. Several researchers have worked on mathematical modeling of the novel coronavirus. It exposes that those SIS, SIR and SEIR models can reflect the dynamics of various epidemics well. Concurrently, different models have been used to model the COVID-19 [[17], [18], [19], [20], [21], [22], [23], [24]]. Its one variant, SEIR [25] is considered to be the most appropriate modeling technique for COVID-19. It may be observed that the specifications of this virus require more complex models in the days to come.

Some of the frequently asked questions that need to be answered are as follows. How many people exactly recover from COVID-19 over a certain period of time? How many people are infected from the disease? How many people died from it? Recently, several mathematical models suitable for the study of the dynamics and evolution of this pandemic have been published as an attempt to answer the above questions.

In the present work we introduce and analyze the most basic transmission model for a directly transmitted infectious disease caused by bacteria, viruses or fungi. Direct transmission occurs through individual-to-individual contact, through a sneeze or cough or through skin-skin contact.

The purpose of the present work is:

• 1.Study of the dynamical behavior of the model and its stability.
• 2.Confirmation of the results by numerical simulation to control the spread of COVID-19.
• 3.Comparison and analysis of the scenarios of two countries, namely India and Brazil.
• 4.Validation and discussion of the model in COVID-19 cases of a state named West Bengal in India.

Brazil is the fifth largest country in the world with India at the seventh position. It has a much lower population density than India. However, Brazil shows higher number of confirmed cases and a higher mortality rate than India. The above observations motivate us to conduct a comparative study of COVID -19 cases between India and Brazil.

The article is organized as follows:

In Section 2 we describe the SEIR Model and study the equilibrium points. Section 3 is devoted to the discussion of stability analysis and stability criterion of the model. The case studies of India and Brazil are presented in Section 4. In Section 5 we perform numerical simulation using MATLAB. We discuss the comparison between India and Brazil in Section 6. In Section 7, we exhibit the validation of the model. Finally, Section 8 includes conclusion of the paper.

2. Model formulation

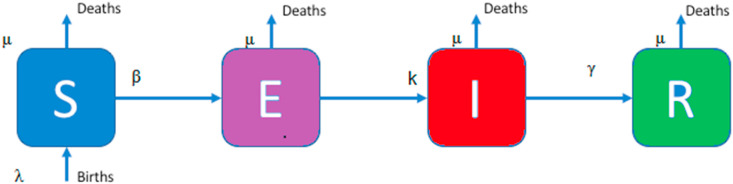
Consider a Susceptible –Exposed –Infected – Recovered (SEIR) model for the present epidemic. The SEIR disease transmission model is based on several strong assumptions [26]. The population (N) is divided into four classes: the susceptible individuals (S), the exposed individuals (E), the infected individuals (I) and the recovered individuals (R) at any time t $\ge$ 0 (see Fig. 1 ). Therefore, we have

$$N\left(t\right)=S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)$$

$$\begin{array}{l}\frac{dS}{dt}=\lambda -\beta SI-\mu S,\\ \frac{dE}{dt}=\beta SI-(\mu +k)E,\\ \frac{dI}{dt}=kE-\left(\mu +\gamma \right)I,\\ \frac{dR}{dt}=\gamma I-\mu R,\end{array}\}$$ (i)

with initial condition S(0) = S₀ > 0, E(0) = E₀ $\ge 0$,I(0) = I₀ > 0 and R(0) = R₀ $\ge 0$.

Fig. 1.

The Diagram of the SEIR model.

2.1. Positivity and boundedness of solutions

Theorem

All the variables are non-negative for all t$\ge$0.

The closed region$\Omega =\{(S,E,I,R)\in {\mathbb{R}}^4:0<N\le \frac{\lambda }{\mu }\}$is positive invariant for the system (i).

• Proof. From the equation (i), we get

$$\frac{dS}{dt}=\lambda -\beta SI-\mu S\ge -(\beta I+\mu )S$$

We have,$S\left(t\right)\ge S\left(0\right)exp(-\underset{0}{\overset{t}{\int }}(\beta I+\mu )dp)>0.$

Now $\frac{dE}{dt}=\beta SI-\left(\mu +k\right)E\ge -\left(\mu +k\right)E.$

We have, $E\left(t\right)\ge E\left(0\right)\text{ exp}(-\underset{0}{\overset{t}{\int }}(\mu +k)dp)>0.$

Also$\frac{dI}{dt}=kE-(\mu +\gamma )I\ge -(\mu +\gamma )I$.

We have, $I\left(t\right)\ge I\left(0\right)exp(-\underset{0}{\overset{t}{\int }}(\gamma +\mu )dp)>0.$

Now $\frac{dR}{dt}=\gamma I-\mu R\ge -\mu R.$

We have, $R\left(t\right)\ge R\left(0\right)\exp (-\underset{0}{\overset{t}{\int }}\left(\mu \right)dp)>0$.

Again $\frac{d(S+E+I+T)}{dt}=\lambda -\mu (S+E+I+T)$ .

Therefore,

$$\frac{dN}{dt}=\lambda -\mu N\dots$$ (ii)

If$\mathrm{\lambda }-\mathrm{\mu }\text{N}$< 0 then $\frac{dN}{dt}<0$.

Therefore, the equation (ii) is bounded by $\frac{\lambda }{\mu }$.

Then we get S, E ,I and $\text{R}$ as positive function.

2.2. Basic reproduction number, disease-free equilibrium state and epidemic equilibrium state

The basic reproduction number $R_0$, is the number ofsecondary infections that one infected person would produce in a fully susceptible population through the entire duration of the infectious period. $R_0$ provides a threshold condition for the stability of the disease-free equilibrium point (for most models).

The disease-free equilibrium point is locally asymptotically stable when $R_0$< 1 i.e., the disease dies out. The disease-free equilibrium point is unstable when $R_0$> 1 i.e., the disease establishes itself in the population or an epidemic occurs. Since, the considered model has disease-free equilibrium at ($\frac{\lambda }{\mu },0,0,0$), the basic reproduction number can be found analytically.

The basic reproduction number ($R_0$) for the COVID-19 model can be obtained from the leading eigen value of the matrix FV⁻¹ [27] where,

F = $\left[\begin{array}{ll}\frac{\beta \lambda }{\mu }\hfill & 0\hfill \\ 0\hfill & 0\hfill \end{array}\right]$ and V = $\left[\begin{array}{ll}0\hfill & k+\mu \hfill \\ \gamma +\mu \hfill & -k\hfill \end{array}\right]$.

Therefore, the reproduction number

$$\left(R_0\right)=\frac{k\beta \lambda }{\mu \left(k+\mu \right)(\gamma +\mu )}\dots$$ (iii)

3. Stability analysis

The equilibrium points are obtained by equating the right hand side of the equations in system (i) to zero.

$\frac{dS}{dt}=\frac{dE}{dt}=\frac{dI}{dt}=\frac{dR}{dt}=$ 0.

The two equilibrium points are given by $E_0$ = ( $\frac{\lambda }{\mu },0,0,0$ ) which is the disease-free equilibrium point and $E_1=(S^{\ast },E^{\ast },I^{\ast },R^{\ast })$ which is the unique epidemic point of the system (i), where.

$S^{\ast }$ = $\frac{\lambda -\left(\mu +k\right)E}{\mu }$,

$E^{\ast }$ = $\frac{\left\{\mu \left(\mu +k\right)\left(\mu +\gamma \right)\right\}(R_0-1)}{\beta k(\mu +k)}$,

$I^{\ast }$ = $\frac{kE}{\mu +\gamma }$,

$R^{\ast }$ = $\frac{\lambda kE}{\mu (\mu +\gamma )}$ .

With $R_0$ given by equation (iii). In case of an epidemic, $E^{*}$will exist only when $R_0$>1.

3.1. Theorem

The disease-free equilibrium of the system is locally stable if $R_0$< 1 and unstable if $R_0$> 1.

Proof: From equation (i) we consider

$$\lambda -\beta SI-\mu S=F_1,$$

$$\beta SI-\left(\mu +k\right)E=F_2,$$

$$kE-\left(\mu +\gamma \right)I=F_3,$$

$$\gamma I-\mu R=F_4.$$

The Jacobian matrix is,

$$J=\left[\begin{array}{lll}-\beta I-\mu \hfill & 0\hfill & \begin{array}{ll}-\beta S\hfill & 0\hfill \end{array}\hfill \\ \beta I\hfill & -(\mu +k)\hfill & \begin{array}{ll}\beta S\hfill & 0\hfill \end{array}\hfill \\ \begin{array}{l}0\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{l}k\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{ll}-(\mu +\gamma )\gamma \hfill & 0-\mu \hfill \end{array}\hfill \end{array}\right]$$

At the equilibrium point $E_0$ = ( $\frac{\lambda }{\mu },0,0,0$ ), the Jacobian matrix becomes,

$$J\left(E_0\right)=\left[\begin{array}{lll}-\mu \hfill & 0\hfill & -\begin{array}{ll}\frac{\beta \lambda }{\mu }\hfill & 0\hfill \end{array}\hfill \\ 0\hfill & -(\mu +k)\hfill & \begin{array}{ll}\frac{\beta \lambda }{\mu }\hfill & 0\hfill \end{array}\hfill \\ \begin{array}{l}0\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{l}k\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{ll}-(\mu +\gamma )\gamma \hfill & 0-\mu \hfill \end{array}\hfill \end{array}\right]$$

Therefore, its characteristic equation is

$$\left|\begin{array}{lll}-\mu -x\hfill & 0\hfill & -\begin{array}{ll}\frac{\beta \lambda }{\mu }\hfill & 0\hfill \end{array}\hfill \\ 0\hfill & -\left(\mu +k\right)-x\hfill & \begin{array}{ll}\frac{\beta \lambda }{\mu }\hfill & 0\hfill \end{array}\hfill \\ \begin{array}{l}0\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{l}k\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{ll}-\left(\mu +\gamma \right)-x\gamma \hfill & 0-\mu -x\hfill \end{array}\hfill \end{array}\right|=0$$

The characteristic roots are $–\mu$, $–\mu$, $–(\mu +\lambda )$ and ( $\mu +$ k) ($R_0-1$).

The first three roots are negative and the last one is will be negative if $R_0$<1 and positive if $R_0$>1.

Hence the equilibrium point $E_0$ is locally asymptotically stable if $R_0$<1 and unstable if $R_0$>1.

3.2. Theorem

If $R_0$>1, the epidemic equilibrium $E_1$ is locally asymptotically stable.

• Proof: We consider the equations

$$F_1=\lambda -\beta SI-\mu S,$$

$$F_2=\beta SI-(\mu +k)E,$$

$$F_3=kE-(\mu +\gamma )I,$$

$$F_4=\gamma I-\mu R.$$

The Jacobian matrix.

J = $\left[\begin{array}{lll}-\beta I-\mu \hfill & 0\hfill & \begin{array}{ll}-\beta S\hfill & 0\hfill \end{array}\hfill \\ \beta I\hfill & -(\mu +k)\hfill & \begin{array}{ll}\beta S\hfill & 0\hfill \end{array}\hfill \\ \begin{array}{l}0\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{l}k\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{ll}-(\mu +\gamma )\gamma \hfill & 0-\mu \hfill \end{array}\hfill \end{array}\right]$.

At the equilibrium point$E_1=(S^{\ast },E^{\ast },I^{\ast },R^{\ast })$, the Jacobian matrix becomes,

J($E_1$) = $\left[\begin{array}{lll}-\beta I^{\ast }-\mu \hfill & 0\hfill & \begin{array}{ll}-\beta S^{\ast }\hfill & 0\hfill \end{array}\hfill \\ \beta I^{\ast }\hfill & -(\mu +k)\hfill & \begin{array}{ll}\beta S^{\ast }\hfill & 0\hfill \end{array}\hfill \\ \begin{array}{l}0\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{l}k\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{ll}-(\mu +\gamma )\gamma \hfill & 0-\mu \hfill \end{array}\hfill \end{array}\right]$.

Therefore, its characteristic equation is $\left|\begin{array}{lll}-\beta I^{\ast }-\mu -x\hfill & 0\hfill & \begin{array}{ll}-\beta S^{\ast }\hfill & 0\hfill \end{array}\hfill \\ \beta I^{\ast }\hfill & -\left(\mu +k\right)-x\hfill & \begin{array}{ll}\beta S^{\ast }\hfill & 0\hfill \end{array}\hfill \\ \begin{array}{l}0\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{l}k\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{ll}-\left(\mu +\gamma \right)-x\gamma \hfill & 0-\mu -x\hfill \end{array}\hfill \end{array}\right|$ = 0.

Or, ($-\mu -x$) ($x^3+a{x}^2+bx+c)$ = 0, where

$$a=\beta I^{\ast }+3\mu +k+\gamma$$

$$b=(\beta I^{\ast }+\mu )(2\mu +k+\gamma )+(\mu +k)(\mu +\gamma )$$

$$c=(\beta I^{\ast }+\mu )(\mu +k)(\mu +\gamma )–\mu \beta k{S}^{\ast }$$

By Routh-Hurwitz Criterion, the system (i) is locally asymptotically stable if. $a>0,b>0,ab>c.$

Thus,$E_1$ is a locally asymptotically stable equilibrium point.

3.3. Theorem

The disease-free equilibrium of the system (i) is globally asymptotically stable if $R_0$< 1.

• Proof: Considering the following linear Lyapunov function

$$\text{L}={\text{B}}_1\text{E}+{\text{B}}_2\text{I}$$

With Lyapunov derivative (where a dot represents differentiation with respect to time)

$$\dot{\text{L}}={\text{B}}_1\dot{\text{E}}+{\text{ B}}_2\dot{\text{I}}$$

Substituting the expression for $\dot{E}and\dot{I}$ from (i), we have

$$\frac{dL}{dt}={\text{B}}_1\left[\beta SI-\left(\mu +k\right)E\right]+{\text{ B}}_2[kE-\left(\mu +\gamma \right)I]\dots$$ (iv)

Little perturbation from equation (iv) with the reproduction number (iii) gives:

$${\text{B}}_1=\lambda k,\cdot {\text{B}}_2=\mathrm{\mu }(\mathrm{\mu }+\text{k})\dots$$ (v)

Substituting the expression of ${\text{B}}_1,{\text{ B}}_2$ obtained from equation (v) we have:

$$\begin{array}{l}\frac{dL}{dt}=\beta SI\lambda k-\left(\mu +\gamma \right)\mathrm{\mu }(\mathrm{\mu }+\text{k})I\\ =I[\beta S\lambda k-\left(\mu +\gamma \right)\mathrm{\mu }\left(\mathrm{\mu }+\text{k}\right)]\\ =I\left[\left(\mu +\gamma \right)\mathrm{\mu }\left(\mathrm{\mu }+\text{k}\right)\right][\frac{\beta S\lambda k}{\left(\mu +\gamma \right)\mathrm{\mu }\left(\mathrm{\mu }+\text{k}\right)}-1]\end{array}$$

Since,$S=\frac{\lambda }{\mu }\le N$, it follows that

$$\frac{dL}{dt}\le I\left[\left(\mu +\gamma \right)\mathrm{\mu }\left(\mathrm{\mu }+\text{k}\right)\right][\frac{\beta \lambda k}{\left(\mu +\gamma \right)\mathrm{\mu }\left(\mathrm{\mu }+\text{k}\right)}-1]$$

$$=>\frac{dL}{dt}\le I\left[\left(\mu +\gamma \right)\mathrm{\mu }\left(\mathrm{\mu }+\text{k}\right)\right][R_0-1]$$

Hence if $R_0<1$, then $\frac{dL}{dt}<0$. Hence, by LaSalle''s extension to Lyapunov's principle [28,29], the disease free equilibrium points is globally asymptotically stable.

3.4. Theorem

If $R_0$>1, the epidemic equilibrium $E_1$ is globally asymptotically stable.

• Proof: Consider the model (i) and $R_0$>1, so that the epidemic equilibrium $E_1$ of model exists.

We consider the following non-linear Lyapunov function of Goh-Volterra type:

$$V=\left(S-S^{\ast }-log\frac{S}{S^{\ast }}\right)+\left(E-E^{\ast }-log\frac{E}{E^{\ast }}\right)+Q(I-I^{\ast }-log\frac{I}{I^{\ast }})$$

With Lyapunov derivative (where a dot represents differentiation with respect to time)

$$\dot{V}=\left(\dot{S}-\frac{S^{\ast }\dot{S}}{S}\right)+\left(\dot{E}-\frac{E^{\ast }\dot{E}}{E}\right)+Q(\dot{I}-\frac{I^{\ast }\dot{I}}{I})\dots$$ (vi)

Substituting the value $\dot{S},\dot{E},\dot{I}$ from (i) into (vi), we have

$$\begin{array}{l}\dot{V}=\left(\lambda -\beta SI-\mu S-\frac{S^{\ast }(\lambda -\beta SI-\mu S)}{S}\right)+\left((\beta SI-(\mu +k\left)E\right)-\frac{E^{\ast }(\beta SI-(\mu +k\left)E\right)}{E}\right)+Q\left(\right(kE-\\ (\mu +\gamma )I)-\frac{I^{\ast }(kE-(\mu +\gamma \left)I\right)}{I})\dots \end{array}$$ (vii)

At steady state from equation (i) we have:

$$\lambda =\beta S^{\ast }{I}^{\ast }+\mu S^{\ast }\dots$$ (viii)

Substituting equation (viii) into (vii) gives:

$$\begin{array}{l}\dot{V}=\left(\beta S^{\ast }{I}^{\ast }+\mu S^{\ast }-\beta SI-\mu S-\frac{S^{\ast }(\beta S^{\ast }{I}^{\ast }+\mu S^{\ast }-\beta SI-\mu S)}{S}\right)+((\beta SI-(\mu +k\left)E\right)-\\ \frac{E^{\ast }(\beta SI-(\mu +k\left)E\right)}{E})+Q\left(\right(kE-(\mu +\gamma )I)-\frac{I^{\ast }(kE-(\mu +\gamma \left)I\right)}{I})\dots \end{array}$$ (ix)

Further simplification gives:

$$\begin{array}{l}\dot{V}=\left(\beta S^{\ast }{I}^{\ast }+\mu S^{\ast }-\mu S-\frac{S^{\ast }(\beta S^{\ast }{I}^{\ast }+\mu S^{\ast }-\beta SI-\mu S)}{S}\right)+\left((-(\mu +k\left)E\right)-\frac{E^{\ast }(\beta SI-(\mu +k\left)E\right)}{E}\right)+\\ Q\left(\right(kE-(\mu +\gamma )I)-\frac{I^{\ast }(kE-(\mu +\gamma \left)I\right)}{I})\dots \end{array}$$ (x)

Collecting all infected class without single star (*) from (x) and equating to zero:

$$S^{\ast }\beta I-\left(\mu +k\right)E+Q\left(kE-\left(\mu +\gamma \right)I\right)=0\dots$$ (xi)

A little perturbation of steady state from (i) and (xi) resulted into:

$$Q=\frac{S^{\ast }\beta }{\left(\mu +\gamma \right)},\cdot \left(\mu +k\right)=\frac{I^{\ast }{S}^{\ast }\beta }{E^{\ast }},\cdot k=\frac{(\mu +\gamma )I^{\ast }}{E^{\ast }}\dots$$ (xii)

Substituting the expression from (xii) into (x) gives:

$$\dot{V}=\left(\beta S^{\ast }{I}^{\ast }+\mu S^{\ast }-\mu S-\frac{S^{\ast }(\beta S^{\ast }{I}^{\ast }+\mu S^{\ast }-\mu S)}{S}\right)+\left(-\frac{E^{\ast }\beta SI}{E}+I^{\ast }{S}^{\ast }\beta \right)+(-\frac{I^{\ast }{S}^{\ast }E\beta I^{\ast }}{I{E}^{\ast }}+\beta S^{\ast }{I}^{\ast })\dots$$ (xiii)

Finally, since the arithmetic mean exceeds the geometric mean, we have

$$(2-\frac{s}{S^{\ast }}-\frac{S^{\ast }}{S})\le 0,\cdot (3-\frac{S^{\ast }}{S}-\frac{I^{\ast }E}{I{E}^{\ast }}-\frac{S{E}^{\ast }I}{E})\le 0$$

Thus, $\dot{V}\le 0$ for $R_0$>1.

Hence,$V$ is a Lyapunov function, by LaSalle's Invariance Principle [29], the epidemic equilibrium $E_1$ is globally asymptotically stable.

4. Case study

In this section we observe the scenario of COVID-19 pandemic in India and Brazil.

4.1. India

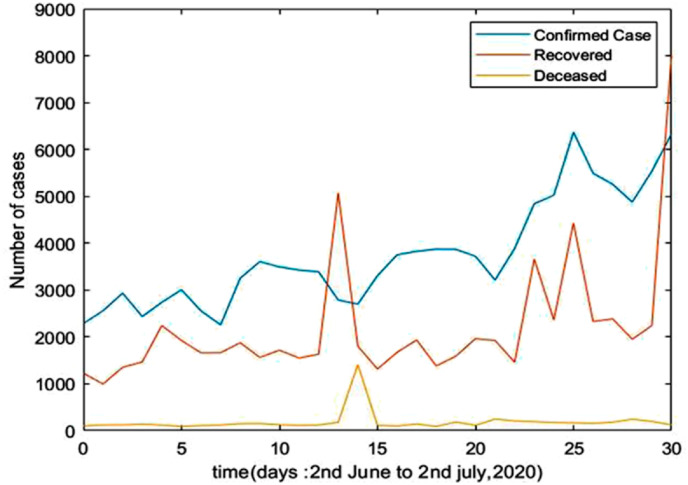
We have considered the number of confirmed cases, death cases and recovered cases of India as given in Ref. [4]. The first case of COVID-19 was reported on January 30, 2020. During the month of February, the number of cases reported was only 3 and remained the same during the whole month. In March it was noted that the number of cases started increasing. However, an explosion in the number happened ultimately in May 2020. To describe the spread of COVID-19 using SEIR model, few considerations and assumptions were made due to limited availability of data [4,13,30,31]. We have considered the number of infected, recovered and deceased cases from 2nd June to July 2, 2020 [32] which is depicted in Fig. 2 . The estimated values of the parameters given in Table 1 are as follows: effective contact rate $\mathrm{\beta }\approx$0.476, birth rate of susceptible $\mathrm{\lambda }\approx$0.0182 and mortality rate $\mathrm{\mu }\approx$ 0.0073. We obtain the recovery rate $\mathrm{\gamma }\approx$ 0.286.

Fig. 2.

Confirmed cases, Recovered cases and Deceased cases with respect to time (Days).

Table 1.

Model parameters and their descriptions.

Notation	Interpretations
$\beta$	Effective contact rate
$\lambda$	Birth rate of susceptible
$\mu$	Mortality rate
$k$	Progression rate exposed to infected
$\gamma$	Recovery rate

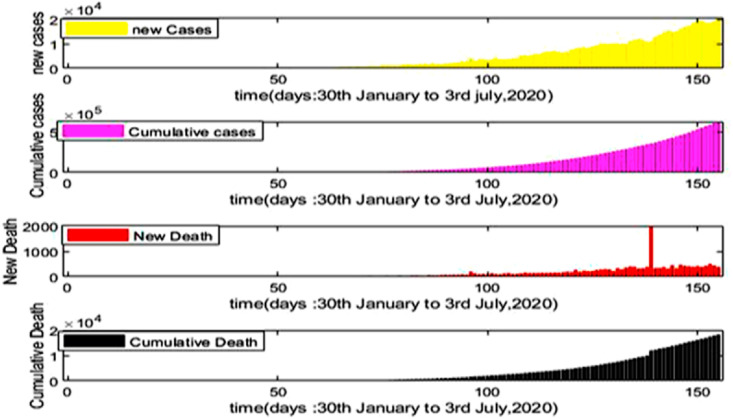
In Fig. 3 , the bar diagram shows the number of new cases as well as cumulative new cases and new death along with cumulative death from 30th January to 3rd July 2020 in India due to COVID-19 [32]. Therefore, we obtain an estimation of the value of $R_0$ from the equation (iii) as 3.67.

Fig. 3.

New cases, Cumulative cases and New death, Cumulative death with respect to time (Days).

In this study, we have only predicted the number of confirmed cases. We have used only time series data for confirmed cases and death cases. An increase in active cases is an alarming situation because as discussed earlier, India is one of the largest populations in the whole world.

4.2. Brazil

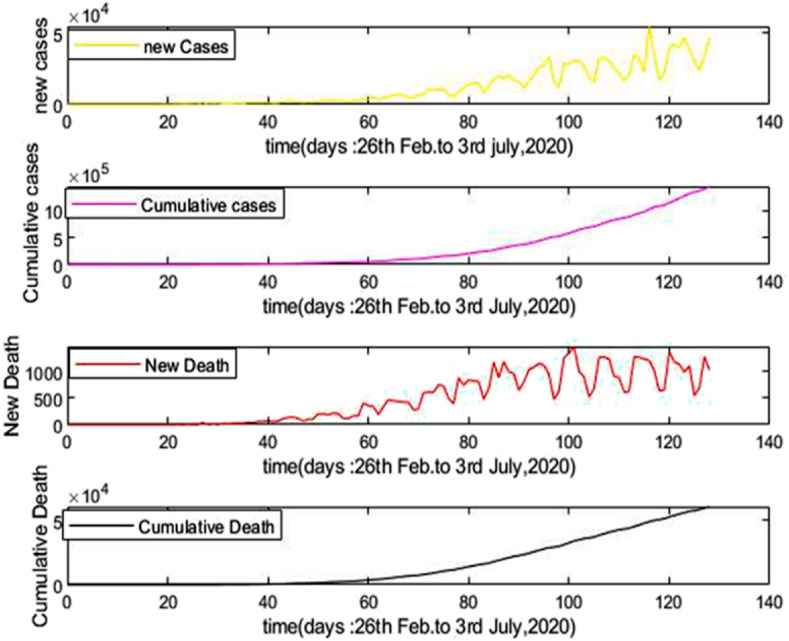
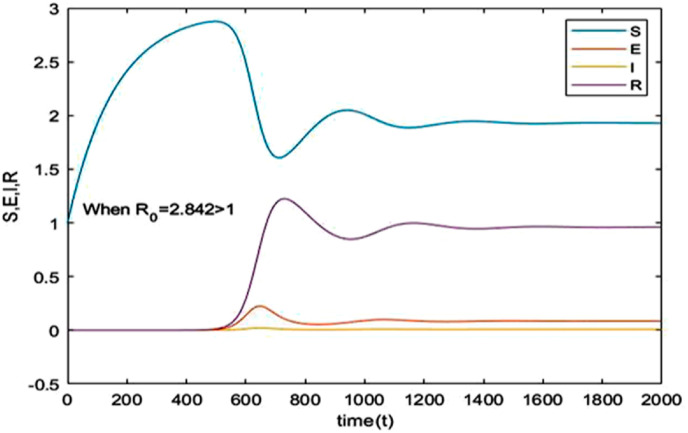
The first case in Brazil was a 61-year-old man who had returned from Lombardy (Italy) and tested positive for the virus. The study of evolution of COVID 19 and its prediction in Brazil is based on the data provided by Ref. [5] during the period of 26th February to July 3, 2020. The estimated values of the parameters given in Table 1 are as follows: effective contact rate $\mathrm{\beta }\approx$0.4417, birth rate of susceptible $\mathrm{\lambda }\approx$0.01867 and mortality rate $\mathrm{\mu }\approx$ 0.00626. We obtain the recovery rate $\mathrm{\gamma }\approx$ 0.07143. Therefore, we obtain an estimation of the value of ${\text{R}}_0$ from the equation (iii) as 2.8421.

Fig. 4 shows the number of new cases as well as cumulative cases and new death as well as cumulative death from 26th February to July 3, 2020 of Brazil due to COVID-19.

Fig. 4.

New cases, Cumulative cases and New death, Cumulative death with respect to time (Days).

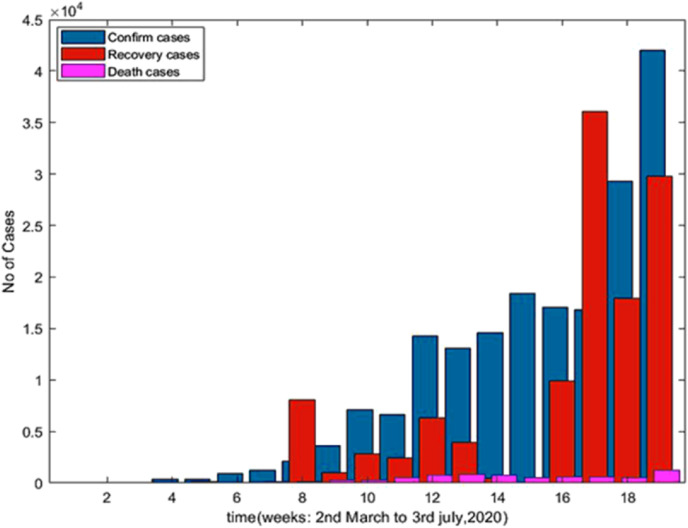
Fig. 5 is a diagrammatic representation of confirmed cases, death cases and recovered cases during the period of 2nd March to July 3, 2020 in Brazil. It is observed that the confirmed cases are gradually increasing with respect to death cases from 2nd March to July 3, 2020.

Fig. 5.

Confirmed cases, Recovered cases and Death cases with respect to time (Days).

5. Numerical simulation

In this section, we implement meticulous numerical validation of the results obtained analytically. We have used mathematical software MATLAB (2018a) to numerically approximate the solution of our model system (i) [14,16].

The estimated values of the parameters in the case of COVID-19 in India and Brazil are as follows:

6. Comparison between India and Brazil

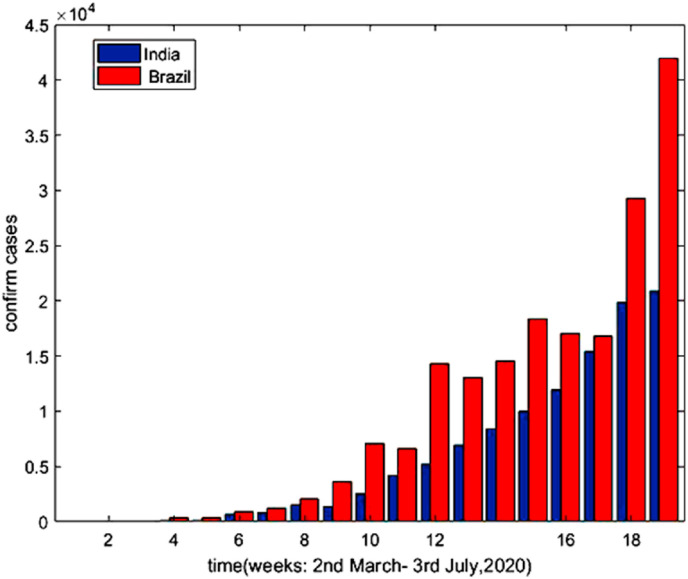
Fig. 9 is the graphical representation of comparison of confirmed cases during 2nd march to 3rd July 2020 between India and Brazil, according to the data provided in Ref. [5] and Ref. [32]. Although the number of infected cases gradually increases during this period, Brazil shows a much higher rate of increase than India.

Fig. 9.

Confirm Cases with respect to time (Days).

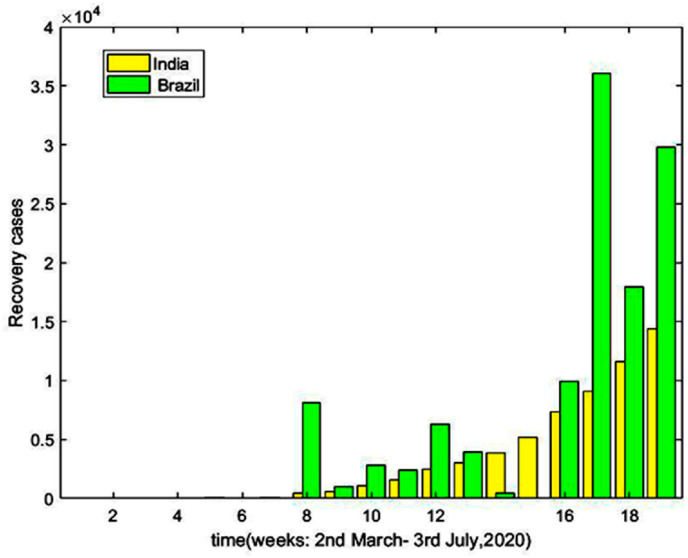
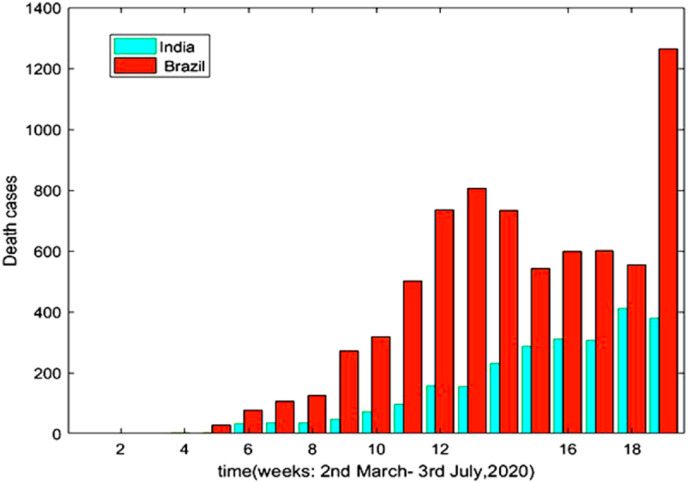
Fig. 10 and Fig. 11 are the graphical representation of comparison of recovered cases and death cases respectively during 2nd march to 3rd July 2020 between India and Brazil, according to the data provided in Ref. [5] and Ref. [32]. There is a gradual increase in the recovery rate as well as death rate for both the countries during this period. The representation also indicates a greater recovery rate and death rate for Brazil.

Fig. 10.

Recovery Cases with respect to time (Days).

Fig. 11.

Death Cases with respect to time (Days).

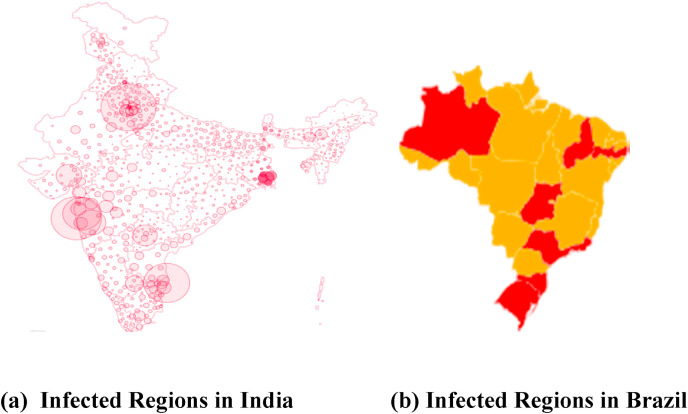
Fig. 12 shows that the geographical distribution of infected cases on 3rd July 2020 of India and Brazil. It should be noted that the average testing rate (per million) in both the countries are way behind the testing rate in some of the developed countries of the world. It is expected that with an increase in the testing rate there will be an increase in the infected regions in both the countries.

Fig. 12.

Infected region.

7. Model validation and discussion

In this section, the infection rate is taken into consideration for validation of the solution obtained from Equation (i) with real time data. For $k,\mu and\gamma$ as given in Table 2 and if the population does not follow lockdown (i.e., E$\approx$ I), we have from the equation (i),

$$\frac{dI}{dt}=kE-(\mu +\gamma )I.$$

Table 2.

Parameter values of proposed model of system (i).

Parameter	Value for India	Value for Brazil	Reference
$\beta$	0.476	0.4417	Estimated
$\lambda$	0.0182	0.01867	Estimated
$\mu$	0.0073	0.00626	Estimated
$k$	0.071	0.77751938	[5]
$\gamma$	0.286	0.07143	[5]
$R_0$	3.67	2.8421	Estimated

Then, $\frac{dI}{dt}=[k-(\mu +\gamma )]I$.

Therefore,

$$I\left(t\right)=I_{0}exp\left[k-\left(\mu +\gamma \right)\right]t\dots$$ (xiv)

$I_0$ being the initial number of infected cases.

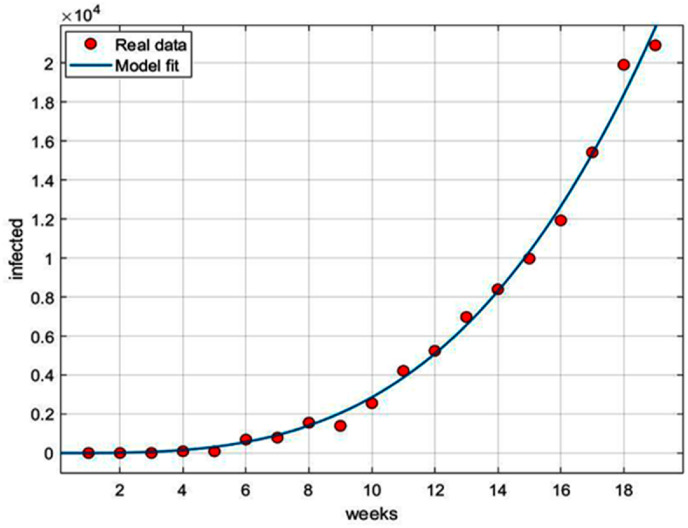
Fig. 13 shows the goodness of fit of Eq. (xiv) with the real time data of total infected cases in India as reported from 2nd March to July 3, 2020. Fitted parameters are $\left\{k-\left(\mu +\gamma \right)\right\}=0.2171$ with 95% confidence interval as (0.1952, 0.239) and $I_0=368.5$with 95% confidence interval as (228.8, 508.2).

Fig. 13.

Infected cases.

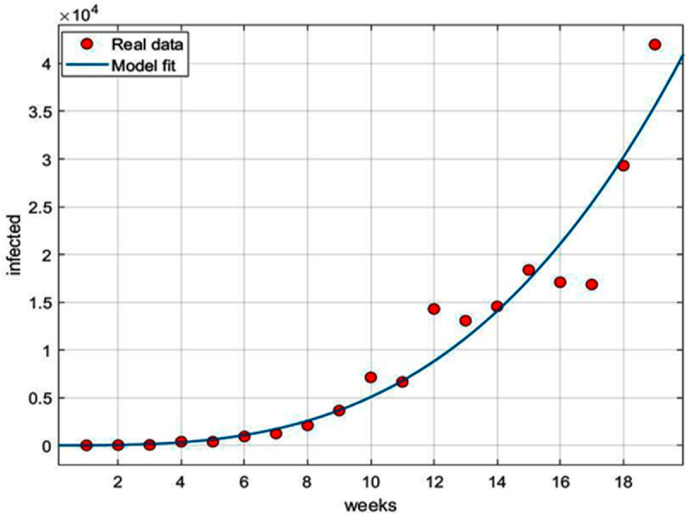
Fig. 14 shows the goodness of fit of Eq. (xiv) with the real time data of total infected cases in Brazil as reported from 2nd March to July 3, 2020. Fitted parameters are$\left\{k-\left(\mu +\gamma \right)\right\}=0.2166$, with 95% confidence interval as (0.173, 0.2603) and $I_0=618.3$with 95% confidence interval as (151.3, 1085).

Fig. 14.

Infected cases.

8. Conclusion

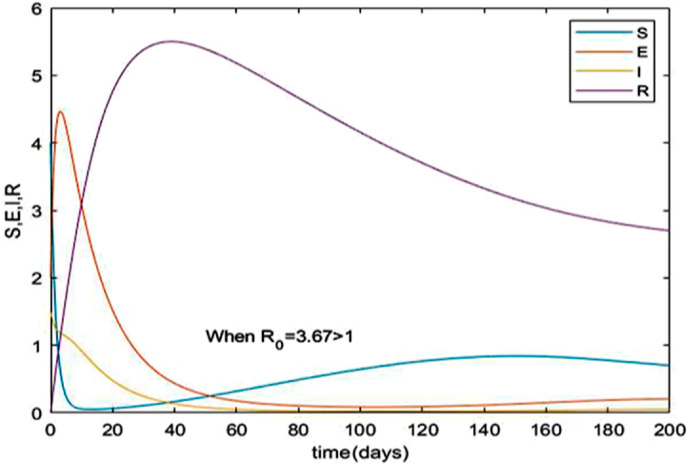
The Susceptible-Exposed-Infection-Recovered (SEIR) model is used in this paper to study the dynamical behavior and stability of the model characterizing the spread of COVID-19. Graphical representations of comparison of the spread of the disease and its mortality rates are extensively discussed for India and Brazil. The essential parameters namely effective contact rate $\left(\beta \right)$, birth rate of susceptible$\left(\lambda \right),$ mortality rate $\left(\mu \right)$ and recovery rate $\left(\gamma \right)$ are estimated for both countries using the current data [5,32] and are shown in Table 2. The reproduction number ($R_0$) given by equation (iii) is 3.67 for India and 2.8421 for Brazil which gives a clear indication that India will be encountering an increased number of infected cases in near future. Fig. 6 and Fig. 7 indicates a time series plot of the SIER model for given $R_0$ in case of India and Brazil respectively. It may be observed that the COVID-19 scenario will prevail for a much longer period of time than expected. Fig. 8 shows that the infected cases exhibit a rapid ascent and reaches its peak for different increasing values of contact rate $\left(\beta \right)$.

Fig. 6.

Time series plot of equation (i) with parameter values for India given in Table 2.

Fig. 7.

Time series plot of equation (i) with parameter values for Brazil given in Table 2.

Fig. 8.

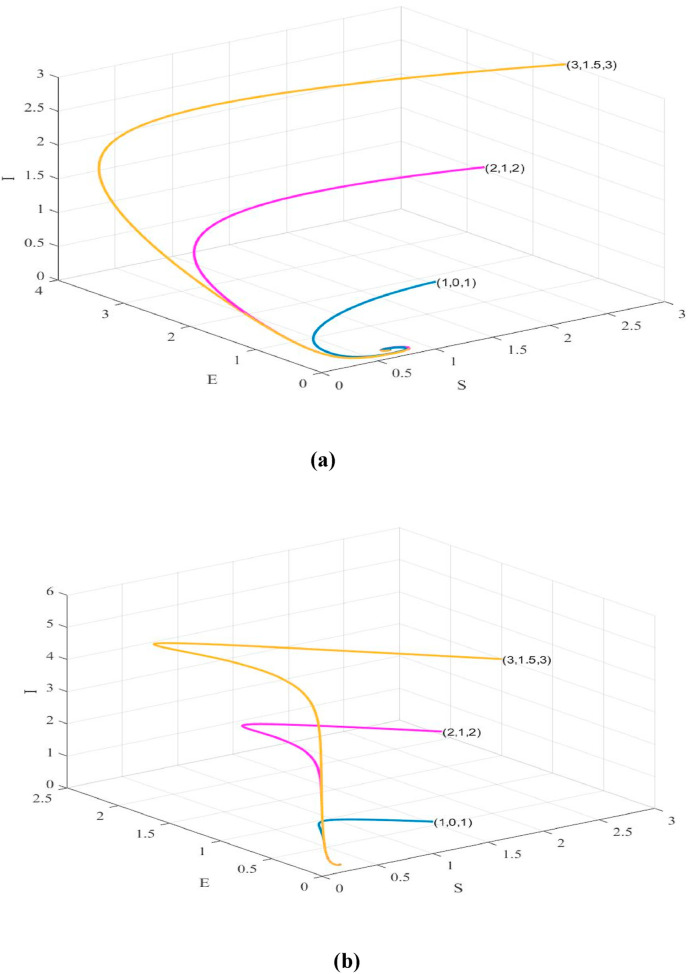
Shows that global stability of $E_1$in S-E-I plane using different initial values ((1,0,1),(2,1,2) and (3,1.5,3)) and the values of parameters for (a) India (b) Brazil.

We have compared the analytical results of infected cases obtained in equation (iv) with the numerical data in Figs. 13 and 14. The graphs are in good agreement with the numerical simulations performed with the help of MATLAB.

From our study of the present situation it is recommended that the rate of disease transmission needs to be controlled, otherwise a huge proportion of population will be affected within an extremely short period of time. Among the popular preventive measures are enforcement of lockdown, curfews and specification of containment zones. Mainly, the government's strategy must be to restrict the contamination by reducing unnecessary mobilization and restricting unwanted social interactions.

We wish to extend our study towards a modified SEIR compartmental model accounting for infection from undiagnosed individuals and for different levels of population isolation in order to evaluate effects of contact reduction in the epidemic temporal dynamics.

CRediT authorship contribution statement

Subrata Paul: Conceptualization, Methodology. Animesh Mahata: Data curation, Software, Investigation. Uttam Ghosh: Software, Validation. Banamali Roy: Supervision, Writing – review & editing.