Thermal resistance effect on anomalous diffusion of molecules under confinement

Significance

Diffusion is the primary process in practical multidisciplinary areas such as separation and catalysis. Transportation is usually positively correlated with temperature due to thermal motion. We show here an anomalous phenomenon wherein a higher temperature effectively slows diffusion for linear-chain hydrocarbon molecules under confinement. Such an obstruction in diffusion results from the novel mechanism of “thermal resistance effect,” in which the configuration of a guest molecule is significantly deformed with temperature effect and then strongly restrains the process of transportation in nanoscale channels at high temperature. This work will enrich our understanding of an anomalous mechanism of the diffusion phenomenon and could shed light on a fundamental understanding of the diffusion process.

Abstract

Diffusion is generally faster at higher temperatures. Here, a counterintuitive behavior is observed in that the movement of long-chain molecules slows as the temperature increases under confinement. This report confirms that this anomalous diffusion is caused by the “thermal resistance effect,” in which the diffusion resistance of linear-chain molecules is equivalent to that with branched-chain configurations at high temperature. It then restrains the molecular transportation in the nanoscale channels, as further confirmed by zero length column experiments. This work enriches our understanding of the anomalous diffusion family and provides fundamental insights into the mechanism inside confined systems.

Molecules or atoms are subject to permanent random movement as a consequence of their thermal energy in the condensed phase (i.e., Brownian motion). The diffusion process is a universal phenomenon that occurs on different time scales in all states of matter (1). It is critically important in the separation and catalytic processes involving the application of nanoporous materials (2–5).

Besides the condensed phase, diffusion in the confined space of channels at nanoscale (i.e., less than 1 nm) has spurred significant interest recently (5). Of the various nanoporous materials, zeolites with regular crystalline shapes and a wide variety of topologies are well known due to their widespread use in industrial applications but also their widespread study on the microscale (3). An intriguing case of molecular movement inside a zeolite is called “single-file diffusion”; this only occurs in one-dimensional (1-D) channels where the molecules cannot pass each other, and a dramatic increase in mobility of the molecules could be observed (6). Single-file diffusion has been found in many materials with 1-D channels; this has been detected by NMR experiments (7–9). Derouane and coworkers found the “levitation effect” for the maximum self-diffusivity of a molecule whose diameter is close to the pore size of zeolite (10). Nag et al. illustrated the efficacy of the levitation effect for separating mixtures of both linear n-pentane and its branched isomer (11). Other interesting effects include incommensurate diffusion (12, 13), molecular traffic control (14), resonance diffusion (15, 16), window effect (17), and molecular path control (18). Anomalous diffusion is still being discovered and continues to be an exciting field of research with many surprises.

For all the diffusion behavior (i.e., normal and anomalous described above), the transport of sorbate is influenced by temperature. Generally, the diffusivity and temperature follow the Arrhenius equation (Eq. 1). Thus, a higher temperature leads to faster diffusion behavior (19, 20):

$$D_s=D_0{e}^{\frac{-Ea}{RT}}.$$ [1]

Here, D_s represents the self-diffusion coefficient, D₀ is a pre-exponential factor, E_a stands for the diffusion activation energy, and R and T are the molar gas constant and temperature, respectively. For instance, Ghysels et al. showed that the diffusion coefficients (D_s) of ethene in several zeolites have a monotonic increase with temperature (21). Gao et al. measured the diffusion coefficients of different alkane species at different temperatures in various zeolites by pulsed field gradient NMR (PFG-NMR) and found that they follow Eq. 1 as well. In this work, an anomalous effect for long-chain molecules (i.e., alkane and alkene [SI Appendix, Table S2]) inside MFI zeolite (silicalite-1) was observed, where the diffusion coefficient slowed with increasing temperature for n-dodecane (C12) molecules (Fig. 1B). Although the diffusion of C12 has been investigated in zeolites, this phenomenon had not been reported yet (16, 22–26). The connection between the structure and anomalous diffusion has been established based on molecular dynamics (MD) simulations and zero length column (ZLC) experiments, which provide fundamental insights into the diffusion properties inside confined channels.

Fig. 1.

(A) Three-dimensional channels of MFI zeolite. The blue and orange cylinders represent the straight and zigzag channels, respectively. (B) Self-diffusion coefficients of methane (C1), n-butane (C4), n-octane (C8), and n-dodecane (C12) in MFI zeolite at different temperatures. (C) Distributions of interaction energy between molecules and MFI zeolite, and (D) distributions of strain energy for alkane molecules (n-butane [C4] and n-dodecane [C12]) at 298, 473, and 773 K.

Results

The diffusion behaviors of molecules inside the confined channel are strongly correlated with the framework of the zeolite. Fig. 1A shows the three-dimensional (3-D) channels of MFI, which possess 10-ring zigzag channels with a window size of 5.1 Å × 5.5 Å along the X and Z direction, as well as 10-ring straight channel (5.3 Å × 5.6 Å) distributed in the Y direction (SI Appendix, Fig. S1A). It is well known that the self-diffusion coefficient (D_s) could quantitatively describe the movement of guest molecules inside confined channels (22). In this work, the D_s of linear alkane molecules (i.e., methane [C1], n-butane [C4], n-octane [C8], and n-dodecane [C12]) were studied because they are the main components of natural gas, gasoline, and diesel and are widely investigated in the petrochemical industry (23). The results show that D_s of alkane inside MFI agrees with Jobic’s work on the order from 10⁻⁹ to 10⁻⁸ m²/s (24, 25). SI Appendix, Table S1 shows that the simulated D_s of methane at 473 K is ∼2.21 × 10⁻⁸ m²/s, which is almost the same as experimental result (2.05 × 10⁻⁸ m²/s) detected by quasi-elastic neutron scattering (QENS) at the same temperature (24). As for C4 at ambient temperature, our result (0.35 × 10⁻⁸ m²/s) is also on the same order of Leroy and coworkers (0.41 × 10⁻⁸ m²/s) (26). In addition, Runnebaum and coworkers reported D_s of C12 in zeolite MFI at 400 K (∼0.40 × 10⁻⁸ m²/s) (16). Thus, further confirming the validity of our calculations (0.39× 10⁻⁸ m²/s).

According to Eq. 1, the D_s of linear alkane molecules is strongly dependent on the temperature. Fig. 1B shows that for the short-chain alkane molecules (i.e., C1 and C4), the diffusion is positively correlated with temperature, because the higher temperature increased the thermal movement. However, in contrast to short-chain alkanes, there is no monotonic increase of D_s as temperature increases for long-chain paraffin (e.g., C8 and C12). In particular for C12, a counterintuitive diffusion behavior was determined whereby the movement of molecules slowed down as the temperature increases. D_s is 0.76 ×10⁻⁸ m²/s at 298 K, but it inversely decreases to 0.29 ×10⁻⁸ and 0.15 ×10⁻⁸ m²/s at 473 K and 773 K, respectively (SI Appendix, Table S1). Apparently, an anomalous diffusion as a function of temperature variations inside zeolite was observed.

Diffusion behaviors are closely related to the interaction between adsorbate and zeolite framework (20). Thus, the interaction energy and strain energy (configuration energy) of C4 and C12 were investigated to understand the anomalous diffusion. Fig. 1C shows that the interaction energy within zeolite for C12 is approximately threefold stronger than that for C4 due to its longer chain. However, there was no notable variance on this quantity for both C4 and C12 at different temperatures, which indicates that the interaction energy may not be the main factor that induces the anomalous diffusion. However, the strain energy is within 5 kcal/mol with the variation of temperature for C4. The strain energy is significantly increased from 6 kcal/mol (298 K) to 17 kcal/mol (773 K) for C12 (Fig. 1D). The larger strain energy clearly indicated the severe structural distortion for C12 at a relatively high temperature.

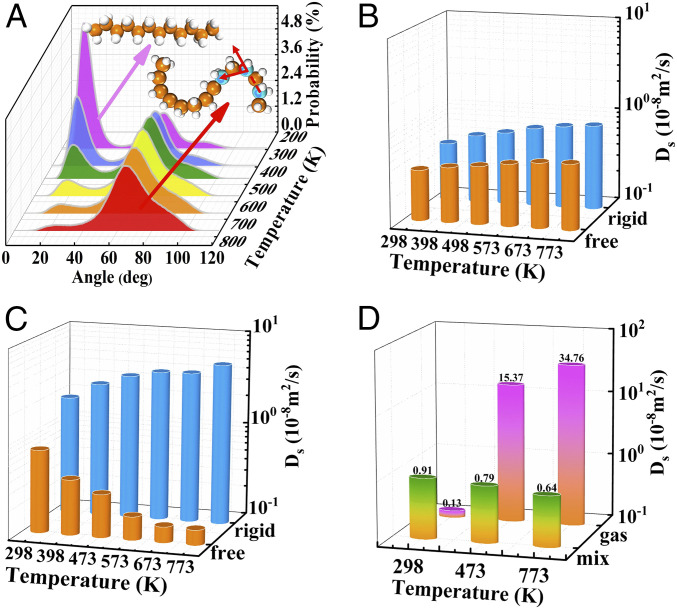
The structural distortion was also quantitatively confirmed by the intramolecular bending angle of the molecule. Fig. 2A and SI Appendix, Figs. S2 and S3A show that the number (ratio) of bending molecules increases with increasing temperature: 40% of C12 with the intramolecular C-C-C angle are distorted by more than 45° at 298 K (Fig. 2A), while almost 90% are larger than 45° under 773 K, which confirmed its pronounced deformation. Thus, the anomalous diffusion may be caused by the structural deformation of the long-chain paraffin.

Fig. 2.

(A) Distributions of distorted angle for n-dodecane at various temperatures. (B) D_s of rigid C4 (linear-C4, blue histogram), and free C4 (flexible C4, orange histogram). (C) D_s of rigid C12 (linear-C12, blue histogram) and free C12 (flexible C12, orange histogram). (D) D_s of mixture for rigid linear-C12/branched-C12 (green orange gradient histogram) inside MFI and at gas phase (pink orange gradient histogram) at 298, 473, and 773 K.

To further determine the effect of the molecular deformation with the increasing temperature on the anomalous diffusion in MFI zeolite, we performed a theoretical simulation on the basis of a model, which only contains fixed structure without any structural deformation (as rigid molecule) for C4 and C12. As shown in Fig. 2B, structural distortion contributes to diffusion deceleration for short chain alkanes like C4. For instance, the D_s of C4 are 0.43 × 10⁻⁸, 0.61 × 10⁻⁸, and 0.81 × 10⁻⁸ m²/s at 298, 473, and 773 K, respectively, which are slightly larger than the according flexible model (i.e., 0.35 × 10⁻⁸ [298 K], 0.42 × 10⁻⁸ [473 K], and 0.51 × 10⁻⁸ [773 K] m²/s). The molecular bending inside the zeolite confined space could hinder the mass transfer even for the short chain C4 but still maintain a positive correlation for the significant contribution of the kinetic energy for high temperature. In contrast to C4, the D_s of C12 with rigid and flexible construction possessed an antipodal temperature dependence. Fig. 2C clearly indicates that the anomalous diffusion disappeared and presented a positive relationship between D_s and the temperature when the rigid C12 is applied. For example, the self-diffusion coefficients of rigid C12 molecules are 1.83 ×10⁻⁸ (298 K), 3.45 × 10⁻⁸ (473 K), and 5.18 × 10⁻⁸ m²/s (773 K). In addition, a controllable simulation of a mixture of rigid linear C12 and rigid branched C12 both without deformation was applied to check the effect of concentration of branched-chain component (i.e., M_n-C12/M_branched-C12) on the diffusion properties. According to MD simulation, the relative ratios of M_linear-C12/M_branched-C12 were varied with temperature (e.g., 8:4, 4:8, 2:10 at 298 K, 473 K, and 773 K). Interestingly, the diffusion coefficients are indeed reduced as the temperature increased (Fig. 2D), which agrees with the trend of realistic simulation for flexible n-dodecane (C12) in MFI zeolite (Fig. 1B), suggesting that the significant diffusion resistance of linear-chain molecules is due to the presence of branched-chain–like configurations at high temperatures.

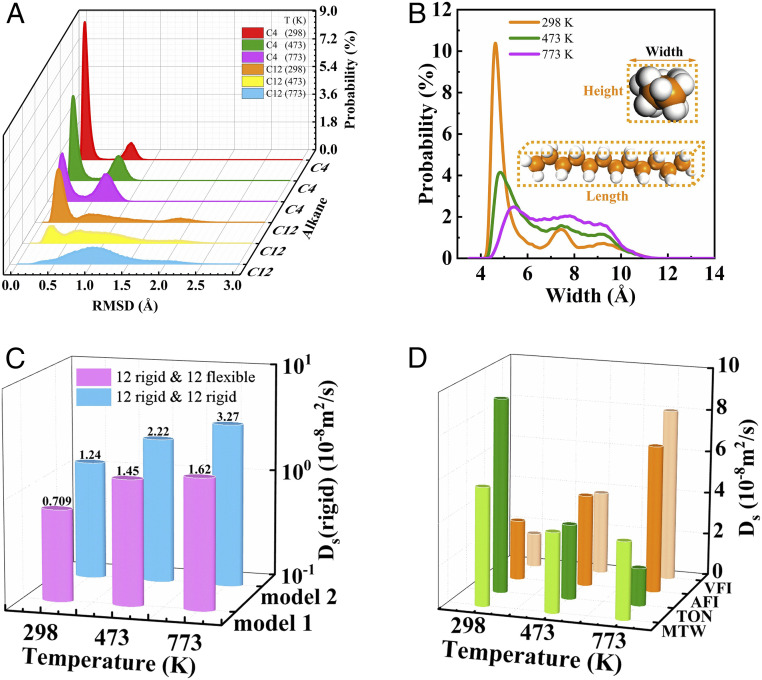
Quantitative comparison of molecular deformation at different temperatures will further illustrate the anomalous effect. The root-mean-square deviation (RMSD) of Cartesian positions is a standard parameter to evaluate the molecular deformation in the confined zeolite (SI Appendix, Table S3) (27). The value of RMSD is calculated by comparing the minimum position changes of the reference configuration and the transient one. The RMSD of C4 is less than 1.0 Å even at 773 K (Fig. 3A), and the two peaks at 0.5 and 1 Å are the smaller and the larger distortion of the adsorbates consistent with the results mentioned above; the molecular deformation increases gradually as the temperature increases. The peak at 1 Å enhances while the peak at 0.5 Å reduces. This is why the strain energy increases as the temperature goes up. In C12, a peak at 2.0 Å was observed at 773 K (Fig. 3A), which means that the long chain molecule is dramatically distorted at higher temperatures. Furthermore, a wide distribution of RMSD of C12 with high temperatures is apparently illustrated such that the linear structure of C12 at low temperatures was gradually undermined, and a more notable deformation was present at higher temperatures. This consequently led to the anomalous diffusion.

Fig. 3.

(A) The RMSD of C4 and C12 molecule inside MFI zeolite. (B) The distribution of width for C12 molecule inside MFI zeolite at various temperatures. (C) Self-diffusion coefficient at different temperatures of 12 rigid C12 molecules in a system of 12 rigid and 12 flexible (blue), and 12 rigid and 12 rigid (pink). (D) Self-diffusion coefficients of C12 inside MTW, TON, AFI, and VFI zeolites.

The width (the second largest size) of the molecule inside the confined space has a great impact on the diffusion process (refer to SI Appendix for the specific calculation method). Fig. 3B illustrates that a higher temperature leads to a larger value of C12’s molecule width as well as slows the diffusion. For example, the width is distributed in 4.6 Å at 298 K, but it increased to 4.8 Å and 5.4 Å at 473 K and 773 K, respectively. One is more likely to find a larger molecule with slow movement under higher temperatures. As mentioned above, molecules get shorter (length) (SI Appendix, Fig. S4) and broader (width and height) (Fig. 3B and SI Appendix, Fig. S5) in shape because the higher temperature causes molecular bending. Therefore, the diffusion was strongly hindered at high temperatures for a larger C12. There was also negative correlation between diffusion coefficient and temperature (The length and height of C12 are plotted in SI Appendix, Fig. S5).

A thermistor is a temperature sensitive component, and the thermistor with a positive temperature coefficient has a larger resistance under the higher temperature (28). Interestingly, this anomalous behavior shows a similar property to thermistors and thus can be named as the “thermal resistance effect” (TRE) in the diffusion process. The temperature could lead to a decreased diffusion coefficient of C12 due to the structural distortion of long-chain alkanes (Figs. 2A and 4). Furthermore, bending molecules not only blocks the diffusion of the induced-bulky configuration themselves but also strongly obstruct the movement of the other linear component during the diffusion process (as shown in Fig. 3C). Two models were simulated to verify this viewpoint. Model 1 is a system with 12 rigid coexisted with 12 flexible molecule C12. Model 2 is another comparative system with 24 rigid C12. The D_s of the 12 rigid molecules of both systems are calculated for the determination of how the flexible and rigid molecules affect the diffusion of other structures. The former system with flexible skeleton owns a smaller D_s (for model 1, D_s is 0.71 × 10⁻⁸ [298 K], 1.45 × 10⁻⁸ [473 K], 1.62 × 10⁻⁸ [773 K] m²/s) than the latter one (model 2, 1.24 × 10⁻⁸ [298 K], 2.22 × 10⁻⁸ [473 K], 3.27 × 10⁻⁸ [773 K] m²/s) which only has a rigid configuration. Furthermore, a marginal difference of D_s between the two systems at low temperatures is exhibited (0.53 × 10⁻⁸ m²/s at 298 K); however, the difference becomes significantly more obvious as the temperature increases (1.65 × 10⁻⁸ m²/s at 773 K). More linear-chain molecules are present in the branched-like configuration at higher temperatures and consequently slow down the diffusion. In general, two kinds of resistance are seen for the deformed molecule in MFI zeolite during the diffusion process: hinder the diffusion of the molecules themselves (Fig. 2 B and C) and also restrain the diffusion of other molecules coadsorbed in the zeolite channels (Fig. 3C).

Fig. 4.

The scheme of TRE for C12 molecule diffused inside zeolite channels at low and high temperatures. The diffusion resistance of linear-chain molecules at high temperatures is equivalent to that of the branched-chain configuration, which induces slow diffusion under confinement. There is no TRE for C12 in a large-size channel.

The temperature-induced deformation of the molecule shows a general trend for the gas molecule. However, there is no TRE to be observed in the gas phase even for the distorted (SI Appendix, Fig. S3D) molecules at high temperatures (SI Appendix, Table S2 and Fig. 2D). TRE is strongly correlated to the zeolite framework and its pore size. Therefore, we discussed the existence conditions of TRE of the diffusion in the zeolite systems. MTW, TON, AFI, and VFI are 1-D channel zeolite with a pore size of 5.6 Å × 6.0 Å, 4.6 Å × 5.7 Å, 7.3 Å × 7.3 Å, and 12.7 Å ×12.7 Å, respectively (SI Appendix, Fig. S1 B–E). TRE diffusion is only present in MTW and TON zeolite (Fig. 3D and SI Appendix, Table S2) whose pore size is similar to that of MFI. A normal behavior was obtained in the larger channel of AFI and VFI zeolite due to the weaker host–guest interactions between the distorted C12 and framework at high temperatures (SI Appendix, Fig. S3 and Fig. 4). Furthermore, the confinement effect in the zeolite can be qualitatively assessed by the scatter plot of the reduced density gradient (RDG) in real space (28). This is an effective and widely used tool to visualize noncovalent interactions between adsorbates and zeolite.

The RDG scatters are one kind of method to qualitatively describe the interaction in the host–guest system (29). As illustrated by RDG scatters of the n-C12 in MFI, MTW, and VFI at 298 K and 773 K in Fig. 5, the difference on RDG scatters at different temperature was reflected in the range from −0.03 to 0.01 atomic unit (orange squares). Normally, the density of points at this range indicates the strength of the van der Waals (vdW) interaction, but the density of points out of this range indicates the strong intramolecular interaction (blue region) and intramolecular repulsive interaction (red region) under the premise of excluding these interactions between n-C12 and zeolites. Obviously, vdW interactions reveal different tendencies. For example, dodecane inside MFI and MTW at higher temperatures (Fig. 5 B and D) has a region with the higher density than that at lower temperatures (Fig. 5 A and C), which indicates a stronger interaction between C12 and MFI (or MTW) at high temperatures. The density of C12 in VFI is almost the same at both the low (Fig. 5E) and high temperatures Fig. 5F, which clearly illustrated that the variations of the temperature will lead to subtle changes in the interactions. Moreover, a less concentrated distribution of the RDG versus those of MFI and MTW show the lesser confinement effects of C12 inside VFI zeolite channel with large pore size, regardless of the degree of dodecane deformation with the temperature.

Fig. 5.

The RDG scatter of dodecane in MFI (A and B), MTW (C and D), and VPI (E and F) zeolties at 298 K and 773 K, respectively..

We also consider the effect of concentration (SI Appendix, Supplemental Material and Fig. S6) as well as other long chain molecules such as cetane and dodecatylene (SI Appendix, Table S2). This shows that this anomalous diffusion was also presented, which clearly illustrated the robustness of the TRE in the diffusion. In addition, the deformation of adsorbate was also confirmed by the ab initio MD (AIMD) simulation (SI Appendix, Fig. S7), which was able to capture the dynamic behavior of molecules more accurately (30). Moreover, the results of our ZLC experiments (SI Appendix, Fig. S8) also proved the existence of thermal resistance effect. Overall, the confinement effect of zeolite channels as well as high temperatures induced the distortion of long-chain molecules and will lead to a TRE.

Discussion

In summary, an anomalous effect for molecules diffusion dependent on temperature was observed whereby a higher temperature would induce a smaller diffusion coefficient of long-chain molecules (e.g., C12 and other longer chains hydrocarbon molecules) inside the confined channel of zeolite. This counterintuitive effect originates from the deformation of adsorbate as well as the increased confinement (i.e., host–guest interaction) results via the relatively bulky size under the higher temperature in the zeolite channels. Similar to the thermistor, this is a TRE in the diffusion behavior inside zeolite confined channels. This work will enrich our understanding of an anomalous mechanism of the diffusion phenomenon and could shed light on a fundamental understanding of the diffusion process.

Materials and Methods

MD Simulation.

In our simulations, the initial structures of MFI, MTW, TON, AFI, and VFI were taken from the International Zeolite Associations (IZA) database (SI Appendix, Fig. S1) (31) and optimized by GULP (32) with SLC core-shell force field (33, 34). A 2 × 2 × 3 supercell with the loading of 12 molecules (C4, C8, C12) was used for MFI, while larger 3 × 3 × 4 supercell of MFI was performed for CH₄ (36 molecules) to avoid larger fluctuations in temperature. The 2 × 10 × 4, 2 × 2 × 6, 3 × 3 × 5, and 3 × 3 × 6 supercells with a loading of 16, 8, 9, and 9 C₁₂H₂₆ (n-dodecane) molecules were used for MTW, TON, AFI, and VFI, respectively. MD simulations were performed in the canonical ensemble (NVT), where the number of particles (N), volume (V), and temperature (T) were kept constant. The simulated temperature ranged from 298 K to 773 K (i.e., 298, 398, 473, 573, 673, and 773 K) as controlled by a Nosé-Hoover thermostat with a coupling time constant of 0.1 ps. For the molecules in condensed phase, the NPT ensemble (constant number of particles N, pressure P, and temperature T) was used for equilibration so that the volumes were stable at a pressure of 1 atm and various temperatures. The NVT ensemble was conducted to study the diffusion behaviors. The leapfrog Verlet algorithm was used to integrate Newton’s equations of motion with a time step of 0.5 fs. The TraPPE-zeo (35) and TraPPE-UA (36) force field were used for zeolite and hydrocarbon, respectively. All the Lennard–Jones cross-interaction parameters were determined by the Lorentz–Berthelot mixing rules, and the cutoff radius was 14 Å. Each MD simulation was equilibrated for 2 × 10⁶ steps, and then 4 × 10⁷ steps of production were recorded for the research on the diffusion behaviors of adsorbate molecules. The trajectories were recorded every 1,000 steps, and three independent MD simulations were conducted for better statistics. All MD simulations were performed in the DL_POLY 2.0 code (37). The details of the AIMD calculations are presented in section 1.6 of the SI Appendix.

Diffusion Coefficient.

In this work, the mean square displacement (MSD) of adsorbates is defined via the following equation:

$$MSD\left(\tau \right)=\frac{1}{N_{\text{m}}}{\displaystyle \sum _i^{N_m}\frac{1}{N_{\tau }}}{\displaystyle \sum _{t_0}^{N_{\tau }}}{\left[r_i\left(t_0+\tau \right)-r_i\left(t_0\right)\right]}^2.$$ [2]

Here, N_m is the number of gas molecules, N_τ is the number of time origins used in calculating the average, and r_i is the coordinate of the ith molecule. In addition, the slope of the MSD as a function of time determines the self-diffusion coefficient (D_s) defined according to the so-called Einstein relationship (38):

$$MSD\left(\tau \right)=2\text{n}{D}_s\tau +b,$$ [3]

where n is the dimension of frameworks (n = 1 for 1-D diffusion, i.e., along the X, Y, and Z in MFI, as well as in 1-D MTW, TON, AFI, and VFI zeolites; n = 3 for MFI and in gas phase). The diffusion coefficients were obtained by fitting the linear region of MSD using a least-square fit. The D_s values were calculated as the average of three dependent MD trajectories.

ZLC Measurements.

The ZLC setup was similar to the apparatus reported by Shiran et al. (39). The ZLC and switching value were placed in Bruker 450 GC oven to ensure that the system had a constant temperature. The effluent gas stream was continuously monitored with the flame ionization detector detector of the same gas chromatography. Here, 5.0 mg silicalite-zeolite was pretreated at 300 °C for 5 h to remove moisture and residual impurities. It was then cooled to the desired temperature. The partial pressures of n-dodecane and n-butane are 0.31 and 0.27 kPa, respectively. The desorption measurements were performed by purging with pure nitrogen at the same flow rate. Further details are provided in the SI Appendix.

Data Availability

All study data are included in the article and/or SI Appendix.