Significance
Which crystal structures are possible if the restrictions of the quantum realm are lifted? Our knowledge of ordered particle geometries was previously restricted to the kinds of structures observable in hard condensed matter—on the atomic scale. Here, we use freely tunable computational models to represent particles with variable properties, and we determine the crystal structures into which they self-assemble. The resulting arrangements often correspond to structures known from atomic-scale materials; however, we discover a comparable number of previously unknown crystal structures with different local coordination motifs, incompatible with the limitations of the chemical bond. Our results can be used to engineer soft condensed matter with unprecedented, ordered geometries, paving the way toward materials with potentially novel properties.
Keywords: self-assembly, crystal structures, isotropic pair potentials
Abstract
The rigid constraints of chemistry—dictated by quantum mechanics and the discrete nature of the atom—limit the set of observable atomic crystal structures. What structures are possible in the absence of these constraints? Here, we systematically crystallize one-component systems of particles interacting with isotropic multiwell pair potentials. We investigate two tunable families of pairwise interaction potentials. Our simulations self-assemble a multitude of crystal structures ranging from basic lattices to complex networks. Sixteen of the structures have natural analogs spanning all coordination numbers found in inorganic chemistry. Fifteen more are hitherto unknown and occupy the space between covalent and metallic coordination environments. The discovered crystal structures constitute targets for self-assembly and expand our understanding of what a crystal structure can look like.
Do we know all conceivable crystal structures? This question appears naïve at first, because crystallography is a mature field, but the list of reported inorganic crystal structures is not necessarily representative of all kinds of order that are possible on other scales. Atomic crystal structures are affected by the discreteness of the periodic table and the resulting constraints on chemical bonding (1). Molecular crystals (2), metal organic frameworks (3), nanoparticle superlattices (4), and other soft-matter assemblies (5) are free from these chemical constraints and can exhibit entirely new types of crystallographic order distinct from those found with atoms. A universal list of all plausible crystal structures in systems of particles ranging from the angstrom to the micrometer scale would benefit the search for—and design of—new materials.
Crystal structures observed on the atomic scale are subject to the laws of quantum mechanics and to the discrete nature of the atom. The constraints of the chemical bond limit the ways in which atoms can be arranged; in particular, inorganic compounds display geometries that are specific to different kinds of bonding, for example, tetrahedral coordinations in the case of covalent bonding with -hybridized orbitals, or high coordination numbers (CNs) in the case of metallic bonding. For example, in the case of water, angular information is usually directly encoded into the computational model (6, 7); however, structures with similar local arrangements have recently been observed in simulations with isotropic multiwell potentials (8, 9). In addition to known crystal structures, these tunable pair potentials can also be parametrized to model particles “in between” the discontinuous types of behaviors that are possible on the atomic scale, due to the quantized nature of the realm of electronic interactions. As a result, these interaction potentials can model systems on the mesoscopic soft-matter length scale, where particle properties and shapes are highly variable. How do these crystal structures differ from those observed on the atomic scale?
Here we show that molecular dynamics simulations of single-component systems interacting via simple isotropic oscillating pair potentials (OPPs) can produce—via crystallization from disordered initial conditions—the majority of reported one-component as well as several multicomponent inorganic crystal structures (10). Our findings are obtained with pair potentials that encode coordination geometry solely via the shape of the radial function of the interaction, and contain no angular terms. We characterize simulation outcomes semiautomatically with the help of computational crystal structure identification techniques. Among the crystal structures we observe are many previously unknown structures, some resembling known ones and some surprisingly complex. The previously unknown crystal structures cluster near each other in parameter space in islands of complexity, demonstrating that certain pair potential features promote specific coordination environments, and that certain coordination environments are inherently prone to crystallographic diversity. Because the functional form of the potential is generic, chemical constraints do not play a role in our simulations, and the particles explore feasible geometries more freely. Such geometries should be accessible, if not to atomic crystals, then to colloidal crystals of nanoparticles where valence is easily tunable.
Materials and Methods
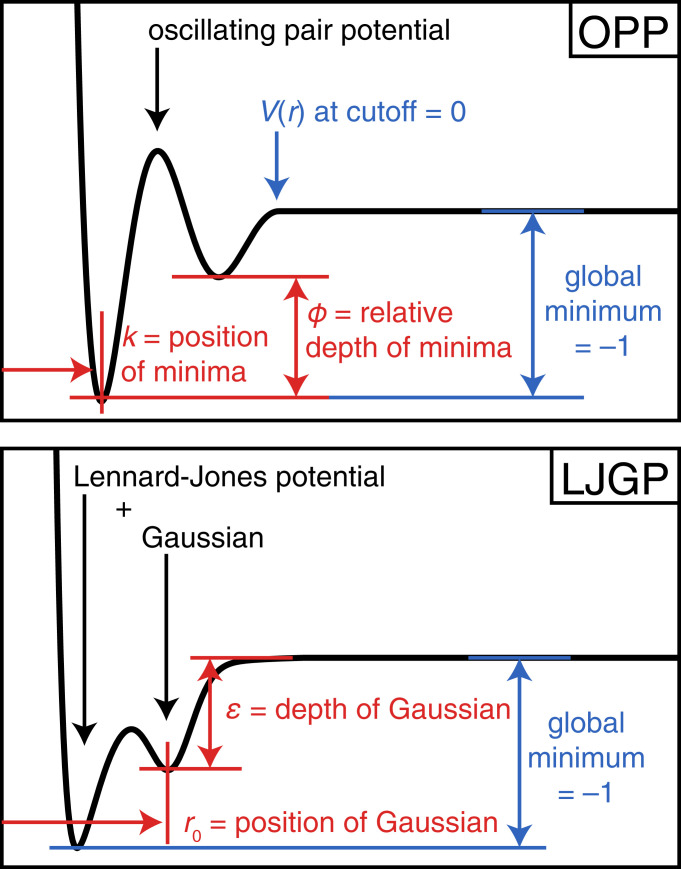
We chose interaction potentials that are as simple as possible (i.e., have the fewest and simplest features) while at the same time flexible enough to allow all possible coordination environments. The OPP and the Lennard-Jones Gauss potential (LJGP), illustrated schematically in Fig. 1, fulfill these conditions. Both potentials are short ranged, with up to two attractive wells located at relative depths and positions tunable by two independent parameters. In the following, we identify and categorize all three-dimensional crystals that self-assemble with these potentials within their two-dimensional parameter spaces.
Fig. 1.
Schematic illustration of the OPP (Top) and the LJGP (Bottom). The OPP is characterized by a wavenumber and a phase shift defining the relative well positions and their relative depths. The LJGP is the sum of a Lennard–Jones potential and a negative Gaussian potential. Parameters and determine the position and depth of the Gaussian.
The OPP and LJGP model different classes of materials. The OPP is representative of functional forms that mimic the behavior of intermetallic systems based on electronic interactions (11). Whereas many pair potential shapes for the study of intermetallics are empirically adapted to specific compositions, the present study varies the potential shapes continuously and systematically. A first glimpse of the structures accessible within this family of potentials revealed a variety of structures, including a few simple ones, a Frank–Kasper phase, clathrates, and a series of icosahedral quasicrystals (9), and more recently, the phase diagram of the OPP has been explored via inverse materials design (12). The LJGP, on the other hand, has been used to model particle interactions in soft-matter systems (13, 14).
The functional form of the OPP that we use is based on the Mihalkovič–Henley interaction potential (11). Its shape is closely related to the potential form used for the self-assembly of complex structures in monatomic systems (15). The OPP is given by
| [1] |
Parameters and describe the wavenumber and phase shift of a damped oscillation, respectively. The oscillation is truncated and shifted to zero at the local maximum following the second attractive well.
The LJGP is constructed by adding a negative Gaussian to the Lennard-Jones pair potential (13),
| [2] |
where we fixed the width of the Gaussian to (and in the Lennard-Jones potential is set to and ). The two remaining parameters are the position and depth of the Gaussian. Because the potential converges rapidly, we truncated it at . The parameters and for the OPP and the parameters and for the LJGP define the two parameter spaces to be explored.
We performed all molecular dynamics simulations with the open-source simulation package HOOMD-blue (16, 17). Independent simulations were run at state points with , and , for the OPP (3,050 simulations in total) and at state points with , and , for the LJGP (5,500 simulations). Systems of (OPP) and (LJGP) particles were initialized in random arrangements at low density, effectively corresponding to zero pressure. Simulations were started at high temperature and gradually cooled in the isochoric-isothermal () ensemble over at least time steps (with ) to promote the formation of single-crystalline assemblies. Additional, slower simulations were carried out in parameter regions where no ordering had been observed with faster cooling, as detailed in SI Appendix. Because all potentials are attractive and the systems were initialized at low densities, our simulations generally resulted in a compact cluster of particles that does not span the simulation box across periodic boundaries. Thus, mechanical stresses and structural defects often present in bulk simulations relax in our setup.
We analyzed the final frames of all simulation trajectories to identify self-assembled structures in crystallographic detail. Phase diagrams were obtained, first, automatically with global bond-orientational order parameters and, later, manually via analysis of bond-orientational order diagrams (BODs) and visual inspection of the three-dimensional structures. To extract unit cells, we isolated a single-crystalline grain from the final frame and then—via the real-space particle positions as well as the BOD—aligned the crystal with the relevant high-symmetry directions, depending on the crystal system. Periodicity along these directions was analyzed via a cylindrical BOD that identifies the most frequent interparticle distances along specified directions. The determined unit cell vectors were then used to project all particle positions onto one unit cell, which, if correct, clearly shows that the projected particle positions cluster. The list of averaged cluster positions constitutes the extracted crystal structure. Space groups were determined manually or using Spglib (18). To check whether the identified structures are already known, we consulted the Inorganic Crystal Structure Database (ICSD) (19).
The diverse structures observed in this study are characterized by CNs. The CN of a particle is its number of nearest neighbors. Particles are considered to be nearest neighbors if their spacing falls within the first peak of the radial distribution function (RDF). The average CN, , is the average of CN over all particles, since a given structure can have multiple distinct particle environments. CN and can be determined irrespective of periodicity and the degree of order; however, in this study, we specify the CN values according to the different Wyckoff positions in the determined unit cells and based on the overall RDF of the assembly. The is then determined by weighing the different CN values with the multiplicity associated with each Wyckoff position in the unit cell of the respective crystal.
Results
Phase Diagrams from Simulation Data.
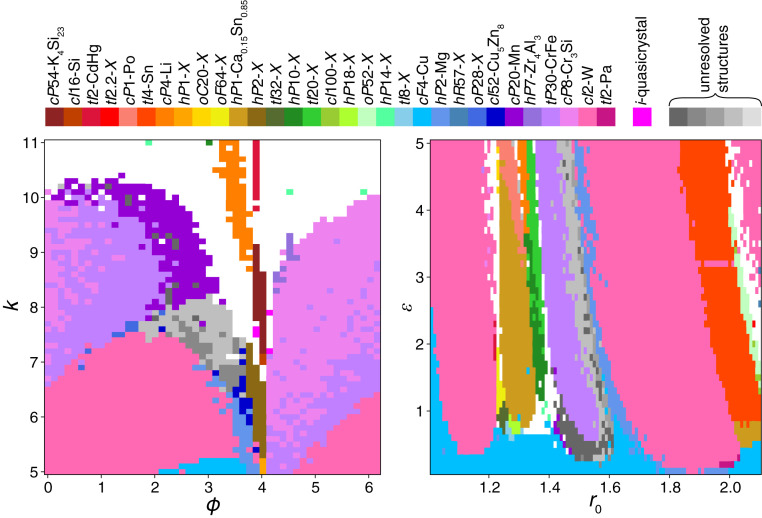
Simulation outcomes as a function of the two potential parameters are summarized in phase diagrams. The phase diagram of the OPP (Fig. 2, Left) is periodic in the parameter and consists of a few large domains of crystal structures separated by a narrow stripe of high structural diversity in the range . In this range, an icosahedral quasicrystal was discovered (9, 20). At large , the OPP oscillates rapidly, and simulations do not exhibit clear long-range order. The phase diagram of the LJGP (Fig. 2, Right) consists of several large domains that extend in the parameter direction. High structural diversity appears in the range . With few exceptions, the LJGP always leads to crystalline order. In both phase diagrams, regions of unusually complex order are marked by shades of gray. The following discussion focuses on the 31 crystal structures indicated by colors in Fig. 2.
Fig. 2.
Phase diagrams of OPPs (Left) and LJGPs (Right) indicating self-assembled crystal structures. Each colored rectangle corresponds to one simulation. Colors denote different crystal structures consistently across both diagrams as specified in the color bar (top), together with Pearson symbols and representative compounds. White regions indicate simulations that assemble structures with no discernible long-range order.
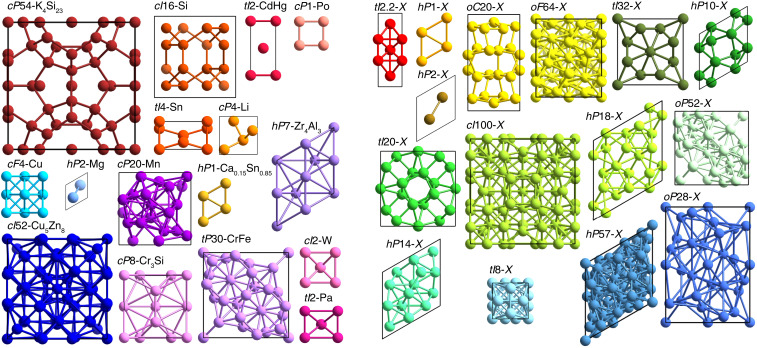
All 31 crystal structures are illustrated in Fig. 3 and listed in Table 1. Crystal structures are identified by their Pearson symbol, which consists of a lowercase letter representing the crystal system (, cubic; , tetragonal; , orthorhombic; , hexagonal/trigonal; , monoclinic; and , triclinic), an uppercase letter representing the lattice centering (, primitive; , body centered; , face centered; ///, base centered; and , rhombohedrally centered), and the number of atoms per unit cell, as well as the representative compound, usually the first one that was found to exhibit the crystal structure. While 16 of the crystal structures observed in these datasets correspond to known compounds, some of which have been reported in simulation before (9, 15, 21), we also discovered 15 previously unknown crystal structures. We indicate these structures without atomic equivalents by replacing the representative compound with an .
Fig. 3.
Unit cells of the crystal structures reported in this study. Unit cells of all 16 known crystal structures (Left) and all 15 previously unknown crystal structures (Right) are shown. The particles are colored according to the color bar in Fig. 2; unit cell outlines are shown in black.
Table 1.
List of crystal structures divided into known crystal structures and previously unknown crystal structures
| Pearson symbol | Space group | CN | OPP | LJGP | Colloquial name or comments | |||
| Known crystal structures | ||||||||
| - |  |
0/4 | 3.4 | “clathrate-I” | ||||
| -Si |  |
4 | 4 | high-pressure silicon | ||||
| -CdHg |  |
4 | 4 | — | ||||
| -Po |  |
6 | 6 | “sc” | ||||
| -Sn |  |
6 | 6 | “-tin” | ||||
| -Li |  |
6 | 6 | structure prediction only | ||||
| - |  |
8 | 8 | — | ||||
| -Cu |  |
12 | 12 | ccp/“fcc” | ||||
| -Mg |  |
12 | 12 | hcp | ||||
| - |  |
12/13 | 12.7 | “-brass” | ||||
| -Mn |  |
12/14 | 12.8 | “-manganese” | ||||
| - |  |
12/14/15 | 13.4 | Frank-Kasper (FK) phase | ||||
| -CrFe |  |
12/14/15 | 13.5 | “-phase”/FK phase | ||||
| -Si |  |
12/14 | 13.5 | “A15”/FK phase | ||||
| -W |  |
14 | 14 | “bcc” | ||||
| -Pa |  |
14 | 14 | distorted “bcc” | ||||
| – |  |
icosahedral quasicrystal | ||||||
| Previously unknown crystal structures | ||||||||
| - |  |
4 to 5 | 4.8 | — | ||||
| - |  |
6 | 6 | stretched - | ||||
| - |  |
6 | 6 | — | ||||
| - |  |
6 to 8 | 7.0 | — | ||||
| - |  |
8 | 8 | compressed hcp/-Mg | ||||
| - |  |
8 to 11 | 8.8 | modulated/disordered | ||||
| - |  |
8/10 | 9.2 | stacked octahedra + columns | ||||
| - |  |
9/10 | 9.2 | related to incommensurate -Rb | ||||
| - |  |
8 to 12 | 9.3 | — | ||||
| - |  |
10 | 10 | stacked octahedra | ||||
| - |  |
9 to 12 | 10.3 | — | ||||
| - |  |
11/12 | 11.1 | octahedra + tetrahedra | ||||
| - |  |
11/12 | 11.3 | modulated/disordered | ||||
| - |  |
12 | 12 | — | ||||
| - |  |
12 to 16 | 12.6 | FK phase | ||||
| – |  |
unresolved crystal structures | ||||||
Given are the Pearson symbol, space group, CN of the first-shell environments, , occurrence in the OPP and LJGP phase diagrams (“+“ = yes), and colloquial name or comments. All particles are equivalent in the simplest observed structures (e.g., cF4-Cu, hP2-Mg, cI2-W), but several structures have multiple different—albeit similar—CNs.
Analysis of Coordination Numbers for Known Structures.
An atom’s CN reflects the nature of its chemical bonding. We analyzed our dataset of self-assembled crystal structures by determining CN of individual particles as well as of all structures in Table 1. The CN values present in the known crystal structures among our data cover almost the full range of CNs represented by one-component structures in the ICSD—ranging from 4 to 15. (We do not observe the molecular-type structures with to 3.) CN values are concentrated at the low end with , representative of covalent bonding, and at the high end with , representative of metallic bonding. We now discuss the known structures in order of increasing CN.
Atoms with correspond to -hybridized, covalently bonded silicon- and carbon-based frameworks. A representative structure that we observe is clathrate-I -. Most particles in clathrate-I build up a tetrahedral framework of fullerene-like cages with 20 or 24 vertices. The remaining particles occupy cage centers and do not have nearest neighbors at the shortest interparticle distance. Another structure on the low end of the CN range is the high-pressure silicon structure -Si. The structure -CdHg is crystallographically equivalent to -Pa, but, due to its different unit cell dimensions ( vs. ; with ), their topologies and thus their structures differ. The -CdHg consists of flat square lattice layers, where each neighboring layer is offset by .
Atoms with include covalent environments in chemistry, for example, for aluminum atoms, but also occur in salts like NaCl. Known one-component crystal structures with are the simple cubic packing -Po, the -tin phase -Sn, and a chiral, high-pressure lithium phase -Li. Ionic compounds can have higher values, such as in the case of CsCl. An example of a one-component structure with is the stacking of the two-dimensional triangle tiling in -.
Crystal structures with to 11 are rare in the ICSD. Among the elements, these CNs are known in high-pressure phases only. No one-component atomic structures exist with CN values of exclusively 5 or 7. The only atomic crystal structures that have local instances of or 7 are complex phases of boron. (In our data, but also in the ICSD, odd-numbered CN values are less common than even-numbered ones.)
At the high end of the CN spectrum with lie metallically bonded compounds, a group that is most prominently represented by sphere packings such as the cubic close-packed (ccp, often also termed fcc after its face-centered cubic Bravais lattice; here -Cu) and hexagonal close-packed (hcp; here -Mg) structures. Another common structure with high CN is the body-centered cubic structure (often termed bcc; here -W) with . The -Pa represents a distorted version of -W. The more complex -manganese structure -Mn has two Wyckoff positions with and that correspond to distorted Frank–Kasper polyhedra. Other prominent examples of complex high-CN structures that we observe are -brass - and three Frank–Kasper phases: -, the “A15”-phase -Si, and the -phase -CrFe. All of these phases represent multicomponent sphere packings having local environments with to 16.
Analysis of Coordination Numbers for Previously Unknown Crystal Structures.
Two previously unknown structures we observe in our data have the same Pearson symbol, space group, and Wyckoff position as known structures—but different ratios. The - is a stretched variant of -. Both structures are periodic stackings of triangular lattice layers directly on top of one another, corresponding to an AA stacking (distinct from the common ABCABC and ABAB stackings found in -Cu and -Mg, respectively, which correspond to dense packings due to the alternating layer positions). Particles in have a hexagonal bipyramid for a coordination polyhedron () in contrast to the flat hexagon coordination () in -. The distance between hexagonal layers in - is so large that the layers become partially decorrelated, and stacks of two to three A layers followed by a stacking fault are common. The other structure with a familiar-looking Pearson symbol—-—also differs from -Mg in its larger ratio. The - has a bicapped triangular prism () as coordination polyhedron, while -Mg has an anticuboctahedron ().
Four of the previously unknown structures are best understood as columnar arrangements. The stackings in the direction of the columns can be periodic or exhibit nontrivial order. In -, particles form columns of face-sharing octahedra. In -, columns of face-sharing octahedra coexist with columns of individual particles. The - is related to the high-pressure phase -Rb (22). Both have columns of face-sharing square antiprisms and intermediate columns of individual particles, but, while - is periodic, the column periodicities are incommensurate in -Rb, requiring a four-dimensional superspace description (23, 24). Finally, - consists of columns of edge-sharing tetrahedra on a square grid together with columns of individual particles. While the columns of tetrahedra are fully ordered, the individual particles occur in three sites along the column direction corresponding to three equivalent local environments. Averaged over the simulation volume, the three sites occur with equal probability. Whether the decoration of the sites is decorrelated or locally correlated without global order (25, 26) cannot be decided based on our data. Longer and larger simulations are necessary to fully characterize the presence of incommensurate modulations and correlated disorder.
We also observe partial disorder in two other previously unknown structures. The - consists of alternating buckled and flat layers. The buckled square lattice layers are fully ordered. The flat triangle–square tiling layers (corresponding to the semiregular snub square tiling, ) adopt one of two orientations. Relative positions of the two orientations are at least partially decorrelated across the buckled layer. The - consists of a -CdHg–like underlying structure: flat square lattice layers alternating in their positions with an offset of . Additional interstitial particles are positioned just above or below the flat layers and are offset with respect to the in-layer squares, effectively forming a flat square pyramid. The high global symmetry of this particle position combined with its low occupancy leads to for 80% of the particles in this structure, resulting in .
The seven remaining structures cannot be understood as stackings of layers or packings of columns. They combine some of the geometric building blocks described above in a fully three-dimensional fashion. The - is a network of face-sharing octahedra as well as vertex- and face-sharing tetrahedra. The - is a framework of square antiprisms, octahedra, and tetrahedra, among other polyhedra. The - exclusively exhibits environments with , only approximately a third of which are icosahedral in shape. The remaining coordination environments are too distorted to be assigned regular polyhedral shapes. The - is a Frank–Kasper phase previously postulated (27) but not yet reported. It consists of all four, partially distorted, topologically close-packed Frank–Kasper polyhedra with . Particles in - have , with 40% of them surrounded by slightly distorted, and another 40% by strongly distorted, octahedral environments, and the remaining 20% surrounded by triangular prismatic environments. The - features particle environments with to 8. Particles with have irregularly shaped environments, and 25% of particles with are surrounded by distorted octahedra. The even more broadly distributed coordination environments in - comprise cuboctahedra with but also more irregular shapes for to 10.
Besides these 15 previously unknown structures described here, we observed a few additional unusually complex structures. Their location is indicated by shades of gray in the phase diagrams in Fig. 2. Preliminary analysis indicates that these crystal structures are so complicated that they cannot be resolved with the methods of this study. They will be discussed in a separate publication with more advanced structure analysis tools. Crystallographic details for all described structures, as well as visualizations, are given in SI Appendix.
Discussion and Conclusion
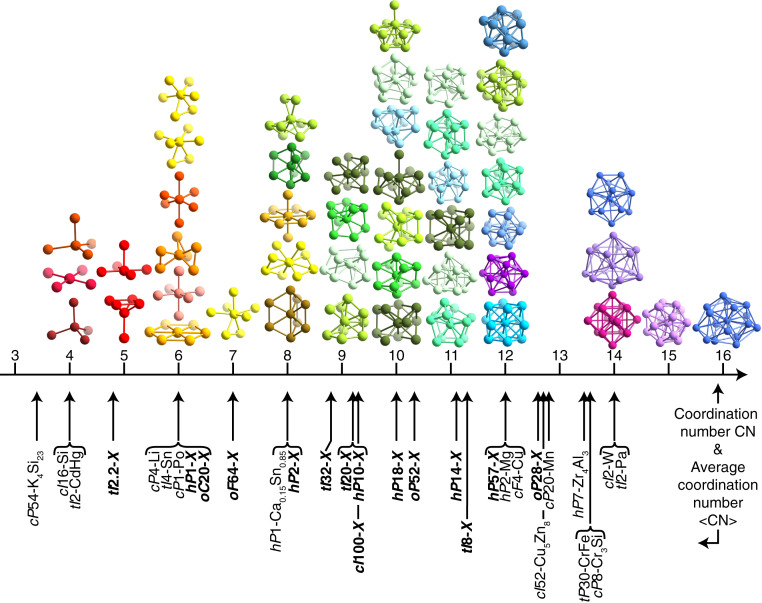
Altogether, we documented the self-assembly of 16 known crystal structures and 15 previously unknown crystal structures without atomic equivalents using multiwell isotropic pair potentials in a one-component system using molecular dynamics simulations. The structures reported have unit cell sizes containing up to 100 particles and also include aperiodic and partially disordered structures. Particles in these structures have CNs between 4 and 16. The structures with atomic equivalents exhibit s of 4, 6, 8, and 12 to 14. While the low and medium values occur mostly discretely—that is, with all particles in these structures having the same CN—high s seem to be more tunable. The presence of a variety of slightly differing noninteger values is correlated with the higher structural complexity in this group, which is a prerequisite for multiple symmetrically inequivalent particle positions and environments with different CNs = 12 to 16 to coexist in the same crystal structure.
We find that the previously unknown crystal structures are predominantly clustered in the intermediate range with to 11 (Table 1). This range is characterized by a particularly high number of distinct coordination polyhedra (shown in Fig. 4). At the same time, one-component atomic structures almost never have these CN values: The restrictions dictated by the periodic table of elements and the nature of chemical bonds select for the crystal structures currently known and available to materials scientists. Apparently, the list of all geometrically possible crystal structures that can be stable is much larger and extends beyond the constraints of chemistry. The previously unknown crystal structures we report are candidates for soft-matter and nanoscale materials.
Fig. 4.
Coordination polyhedra in the 31 crystal structures self-assembled with OPPs and LJGPs (displayed in colors representing their structures in Figs. 2 and 3). Coordination polyhedra are grouped by CN in the range CN = 4 to 16. Reported structures are listed by Pearson symbols below the CN axis and indicated by arrows pointing to their (the largest average CN observed is ). Pearson symbols of previously unknown structures are labeled in bold font.
Our results complement inverse methods for materials design (8, 28–30) that target specific geometries and fuel both experimental and computer-driven materials searches across the scales where coarse-grained interactions can be used to explore particle assembly. Particles in our simulations readily assemble many simple structures with only a few particles in the unit cell, but also highly complex ones with up to 100 particles in the unit cell. The simplicity of the models (isotropic interactions with few features in the pair potential) and our focus on one-component systems does not preclude structural complexity. While the here-discussed simulations are conducted at effectively zero pressure, additional structural variety can likely be accessed by observing the self-assembly behavior of these systems as a function of pressure (e.g., ref. 29). The kinetic pathways permitting this complexity, and whether similar behavior is also present in binary mixtures or compounds with even more components, will be subjects of future work.
Supplementary Material
Acknowledgments
We thank Matthew Spellings and Andrew L. Goodwin for helpful discussions. This research was supported, in part, by the Department of Defense/Assistant Secretary of Defense for Research and Engineering under Award N00244-09-1-0062. J.D. acknowledges support through the Early Postdoc.Mobility Fellowship from the Swiss National Science Foundation, Grant P2EZP2_152128. P.F.D. was supported by the University of Michigan Center of Excellence in Materials Research and Innovation for Photonics and Multiscale Nanomaterials funded by the NSF Materials Research Science and Engineering Center Program DMR 1120923. C.L.P. was funded by the Office of the Director through the Aneesur Rahman Postdoctoral Fellowship, Argonne National Laboratory. M.E. acknowledges support from the Deutsche Forschungsgemeinschaft through Project EXC 315/2. Computational resources and services were supported by Advanced Research Computing at the University of Michigan, Ann Arbor, and by the Argonne Leadership Computing Facility at Argonne National Laboratory, which is supported by the Office of Science of the US Department of Energy under Contract DE-AC02-06CH11357.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
See online for related content such as Commentaries.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2024034118/-/DCSupplemental.
Data Availability
All study data are included in the article and SI Appendix.
References
- 1.Pauling L., The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry (Cornell University Press, 1960). [Google Scholar]
- 2.Desiraju G. R., Crystal engineering: From molecule to crystal. J. Am. Chem. Soc. 135, 9952–9967 (2013). [DOI] [PubMed] [Google Scholar]
- 3.Furukawa H., Cordova K. E., O’Keeffe M., Yaghi O. M., The chemistry and applications of metal-organic frameworks. Science 341, 1230444 (2013). [DOI] [PubMed] [Google Scholar]
- 4.Boles M. A., Engel M., Talapin D. V., Self-assembly of colloidal nanocrystals: From intricate structures to functional materials. Chem. Rev. 116, 11220–11289 (2016). [DOI] [PubMed] [Google Scholar]
- 5.Glotzer S. C., Solomon M. J., Anisotropy of building blocks and their assembly into complex structures. Nat. Mater. 6, 557–562 (2007). [DOI] [PubMed] [Google Scholar]
- 6.Molinero V., Moore E. B., Water modeled as an intermediate element between carbon and silicon. J. Phys. Chem. B 113, 4008–4016 (2009). [DOI] [PubMed] [Google Scholar]
- 7.Cisneros G. A., et al. , Modeling molecular interactions in water: From pairwise to many-body potential energy functions. Chem. Rev. 116, 7501–7528 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jain A., Errington J. R., Truskett T. M., Dimensionality and design of isotropic interactions that stabilize honeycomb, square, simple cubic, and diamond lattices. Phys. Rev. X 4, 031049 (2014). [Google Scholar]
- 9.Engel M., Damasceno P. F., Phillips C. L., Glotzer S. C., Computational self-assembly of a one-component icosahedral quasicrystal. Nat. Mater. 14, 109–116 (2015). [DOI] [PubMed] [Google Scholar]
- 10.Steurer W., Dshemuchadse J., Intermetallics – Structures, Properties, and Statistics (Oxford University Press, 2016). [Google Scholar]
- 11.Mihalkovič M., Henley C. L., Empirical oscillating potentials for alloys from ab initio fits and the prediction of quasicrystal-related structures in the Al-Cu-Sc system. Phys. Rev. B 85, 092102 (2012). [Google Scholar]
- 12.Zhou P., Proctor J. C., Van Anders G., Glotzer S. C., Alchemical molecular dynamics for inverse design. Mol. Phys. 17, 3968–3980 (2019). [Google Scholar]
- 13.Engel M., Trebin H.-R., Self-assembly of monatomic complex crystals and quasicrystals with a double-well interaction potential. Phys. Rev. Lett. 98, 225505 (2007). [DOI] [PubMed] [Google Scholar]
- 14.Engel M., Trebin H.-R., Structural complexity in monodisperse systems of isotropic particles. Z. Kristallogr. 223, 721–725 (2008). [Google Scholar]
- 15.Elenius M., Zetterling F. H. M., Dzugutov M., Fredrickson D. C., Lidin S.. Structural model for octagonal quasicrystals derived from octagonal symmetry elements arising in -Mn crystallization of a simple monatomic liquid. Phys. Rev. B 79, 144201 (2009). [Google Scholar]
- 16.Anderson J. A., Lorenz C. D., Travesset A., General purpose molecular dynamics simulations fully implemented on graphics processing units. J. Comput. Phys. 227, 5342–5359 (2008). [Google Scholar]
- 17.Glaser J., et al. , Strong scaling of general-purpose molecular dynamics simulations on GPUs. Comput. Phys. Commun. 192, 97–107 (2015). [Google Scholar]
- 18.Togo A., Tanaka I., Spglib: A software library for crystal symmetry search. arXiv [Preprint](2018). https://arxiv.org/abs/1808.01590 (Accessed 3 December 2018).
- 19.Karlsruhe F. I. Z., Inorganic crystal structure Database – ICSD. https://icsd.fiz-karlsruhe.de. Accessed 5 November 2018.
- 20.Spellings M., Glotzer S. C., Machine learning for crystal identification and discovery. AIChE J. 64, 2198–2206 (2018). [Google Scholar]
- 21.Zetterling F. H. M., Dzugutov M., Lidin S., .-Brass crystallization in a simple monotomic liquid. MRS Proc. 643, K9.5 (2000). [Google Scholar]
- 22.McMahon M. I., Rekhi S., Nelmes R. J., Pressure dependent incommensuration in Rb-IV. Phys. Rev. Lett. 87, 55501 (2001). [DOI] [PubMed] [Google Scholar]
- 23.Janssen T., Chapuis G., De Boissieu M., Aperiodic Crystals – Fom Modulated Phases to Quasicrystals(IUCr Monographs on Crystallography, Oxford University Press, 2007), vol. 20. [Google Scholar]
- 24.Van Smaalen S., Incommensurate Crystallography(IUCr Monographs on Crystallography, Oxford University Press, 2007), vol. 21. [Google Scholar]
- 25.Keen D. A., Goodwin A. L., The crystallography of correlated disorder. Nature 521, 303–309 (2015). [DOI] [PubMed] [Google Scholar]
- 26.Welberry T. R., Diffuse X-ray Scattering and Models of Disorder(IUCr Monographs on Crystallography, Oxford University Press, 2010), vol. 16. [Google Scholar]
- 27.Sikirić M. D., Delgado-Friedrichs O., Deza M., Space fullerenes: A computer search for new Frank–Kasper structures. Acta Crystallogr. A 66, 602–615 (2010). [DOI] [PubMed] [Google Scholar]
- 28.Lindquist B. A., Jadrich R. B., Truskett T. M., Communication: Inverse design for self-assembly via on-the-fly optimization. J. Chem. Phys. 145, 111101 (2016). [Google Scholar]
- 29.Damasceno P. F., Glotzer S. C., Engel M., Non-close-packed three-dimensional quasicrystals. J. Phys. Condens. Matter 29, 234005 (2017). [DOI] [PubMed] [Google Scholar]
- 30.Adorf C. S., Antonaglia J., Dshemuchadse J., Glotzer S. C., Inverse design of simple pair potentials for the self-assembly of complex structures. J. Chem. Phys. 149, 204102 (2018). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and SI Appendix.