Continuous learning of emergent behavior in robotic matter

Significance

In the last century, robots have been revolutionizing our lives, augmenting human actions with greater precision and repeatability. Unfortunately, most robotic systems can only operate in controlled environments. While increasing the complexity of the centralized controller is an instinctive direction to enable robots that are capable of autonomously adapting to their environment, there are ample examples in nature where adaptivity emerges from simpler decentralized processes. Here we perform experiments and simulations on a modular and scalable robotic platform in which each unit is stochastically updating its own behavior to explore requirements needed for a decentralized learning strategy capable of achieving locomotion in a continuously changing environment or when undergoing damage.

Abstract

One of the main challenges in robotics is the development of systems that can adapt to their environment and achieve autonomous behavior. Current approaches typically aim to achieve this by increasing the complexity of the centralized controller by, e.g., direct modeling of their behavior, or implementing machine learning. In contrast, we simplify the controller using a decentralized and modular approach, with the aim of finding specific requirements needed for a robust and scalable learning strategy in robots. To achieve this, we conducted experiments and simulations on a specific robotic platform assembled from identical autonomous units that continuously sense their environment and react to it. By letting each unit adapt its behavior independently using a basic Monte Carlo scheme, the assembled system is able to learn and maintain optimal behavior in a dynamic environment as long as its memory is representative of the current environment, even when incurring damage. We show that the physical connection between the units is enough to achieve learning, and no additional communication or centralized information is required. As a result, such a distributed learning approach can be easily scaled to larger assemblies, blurring the boundaries between materials and robots, paving the way for a new class of modular “robotic matter” that can autonomously learn to thrive in dynamic or unfamiliar situations, for example, encountered by soft robots or self-assembled (micro)robots in various environments spanning from the medical realm to space explorations.

Traditional robots typically exhibit well-defined motions and are often controlled by a centralized controller that uses sensor data to provide feedback to its actuators (1, 2). While these systems are capable of operating in well-known and controlled environments, adapting their behavior to various unforeseen circumstances remains one of the main challenges in robotics (3). Toward this goal, reinforced learning strategies can be used to deal with more complex tasks that cannot directly be programmed in the behavior of the robot. By sensing their environment, robots can build models of themselves (4) or optimize human-made models with machine learning strategies to improve their behavior (1, 2, 4–8). Apart from a clear division between training and task execution, these systems rely on a centralized architecture that—with an increasing number of active components—demands advanced models and higher computational power.

A recent key idea to simplify the computational task, while allowing for adaptability to the environment, is to make soft robots. These are robots fabricated with materials with stiffness resembling human tissue (3, 9–12), that exhibit so-called embodied intelligence (13–15) and adjust their shape when subjected to forces resulting from interactions with their environment. While this physical adaptability enhances the robustness of the robot’s behavior, allowing it to, e.g., operate in more complex environments, it is not guaranteed that they operate optimally, or even operate at all. For example, a soft robot that is able to walk on various surfaces still requires a different actuation sequence to crawl through a narrow opening (16). At the moment, and because of the unpredictable nature of the robot’s behavior in varying environments, this sequence is externally (and manually) adjusted. A natural question to ask is if such higher levels of decision-making and learning can also be embodied in robots, similar to, e.g., the decentralized neural networks of squids (17, 18).

In fact, decentralized approaches are already applied in swarm robotics, where an increasing number of active components can cooperatively achieve complex behavior when sensing or communication capabilities are incorporated into the individual units (19–22). In such a robotic system, behavior emerges from local interactions, rather than being centrally controlled. Inspired by social animals such as ants, bees, or birds, researchers have been able to achieve emerging properties out of simple unit-to-unit interactions, such as adaptation to mechanical stimuli (23), self-assembly (22, 24), construction (25), and locomotion (20, 26). Interestingly, such behavior does not have to be programmed and could also be learned using the same decentralized architecture (27, 28).

In this work, we develop and perform experiments on modular robots that are connected to form a single body, in order to explore similar decentralized strategies. Using this platform, our aim is to simplify the learning strategy, while focusing on the fundamental challenge to ensure robust and optimal behavior under varying external conditions and damage. We do so by having each element continuously learn and adapt to changing circumstances. To that end, we develop a fully decentralized and universal reinforced learning strategy that can be easily implemented, is scalable, and allows the robotic system to autonomously achieve and maintain specific emergent behavior.

Individual Unit Behavior

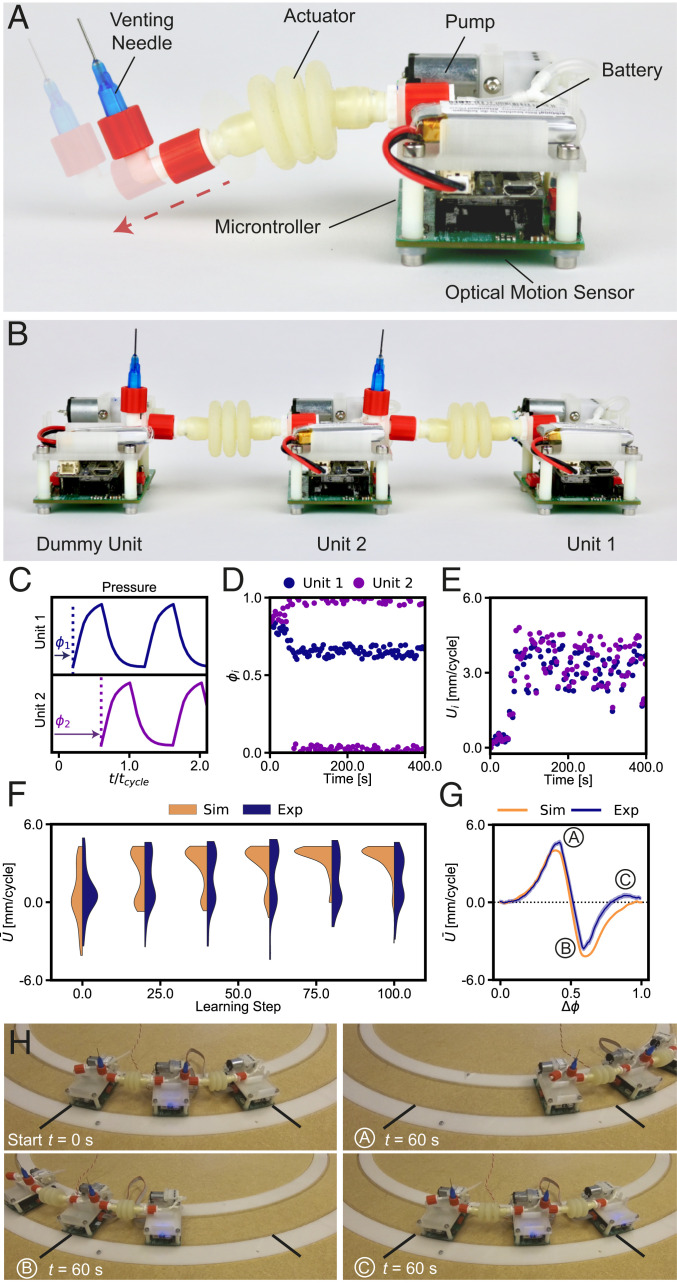
Such an approach holds potential for a wide variety of robotic systems, and we illustrate this here with a robot made of several identical units connected by soft actuators that periodically extend and contract along one direction. Each robotic unit operates independently and consists of a microcontroller, optical motion sensor, pump, pneumatic actuator, and battery (Fig. 1A and SI Appendix). The actuator is activated by cyclically turning the pump on and off at a ratio of $\alpha =t_{on}/t_{\text{cycle}}=0.4$ with a total cycle duration of $t_{\text{cycle}}=2\hspace{0.17em}s$. By continuously venting the air in the actuator through a needle, the actuator extends and contracts (Fig. 1A). Note that the units are not capable of locomotion by themselves and require being physically attached to other units to move, which we refer to as the emergent behavior that our assembled robot exhibits.

Fig. 1.

Robotic unit design and initial learning experiments for an assembled robot consisting of two active units. (A) Design of a single robotic unit in its relaxed and extended state. (B) Robot assembled from two active units and one dummy unit. (C) Each active unit can vary its phase ${\varphi }_i{t}_{\text{cycle}}$, which affects the actuation timing as shown by the cyclic pressure in the soft actuators. (D and E) Evolution of phases ${\varphi }_i$ and measured velocity $U_i$ in the active units as a function of time for a single learning experiment. (F) Distribution of average robot velocity $Ū$ as a function of the learning step for 112 learning simulations and 56 learning experiments. (G) Simulated and experimental velocity as function of phase difference $\mathrm{\Delta }\varphi ={\varphi }_2-{\varphi }_1$, exemplified by three experiments (H).

Importantly, each unit aims to move as quickly as possible in the same predefined direction. To achieve this, it can adapt its behavior by varying the phase of actuation ${\varphi }_i{t}_{\text{cycle}}$. As a first trial for a potential learning algorithm that is capable of learning emergent behavior, we implement a Monte Carlo scheme (29) in each unit. At the beginning of every learning step, the unit perturbs its phase according to ${\varphi }_i^{\prime }={\varphi }_i+ϵ\mathrm{\Delta }s$, in which $ϵ$ is a random number drawn from a uniform distribution on the interval $\left[-\mathrm{1,1}\right]$ and $\mathrm{\Delta }s=0.1$ is the step size indicating the maximum change in phase allowed per learning step. Then, after performing $n_{\text{act}}=2$ cycles the unit determines its average velocity $U_i^{\prime }$ via the motion sensor and compares it with the velocity $U_i$ stored in memory. The unit will update the phases and velocities in its memory with probability $e^{\left(U_i^{\prime }-U_i\right)/T}$, in which $T$ is a “temperature” that can be used to tune the acceptance probability when $U_i^{\prime }-U_i<0$. We refer to this algorithm as the “Thermal algorithm” (see pseudocode in SI Appendix, Fig. S1).

Results of Two Units

In order to test if the system can optimize its movement in a predefined direction, we first focus on the most basic assembly of two active units (Fig. 1B). Note that we also need one dummy unit without an actuator at the end of the assembly to make sure all of the other actuators are connected on both sides. We place the units on a circular track and initialize the active units with a random actuation phase ${\varphi }_i$ (Fig. 1C) and let the system run for $n_{\text{learn}}=100$ learning iterations. At the beginning of each learning step the units update their phases independently, without exchanging any information. The pushing and pulling forces applied by the pneumatic actuators are the only interactions between the units (Movie S1). The results in Fig. 1 D and E show that the assembled robot learns to move forward and reaches its fastest speed after just $80\hspace{0.17em}\text{s}$ (i.e., 20 learning iterations). This grants each unit a forward motion of $\approx 4.5\hspace{0.17em}\text{mm/cycle}$ (see SI Appendix for specifics on the velocity calculation).

For the remaining $320\hspace{0.17em}\text{s}$ the units try to continuously increase their speed, resulting in random perturbations around the optimal behavior. We then repeat this learning experiment 56 times with the same settings, but with different random initial phases. We additionally model the robot behavior with a simple mass-spring system that includes static friction (SI Appendix) and perform 112 learning experiments. The distribution of the average robot velocities $Ū={\sum }_i{U}_i$ during learning is shown in Fig. 1F. We find that, while the average speed after learning is distributed around $Ū\approx 4.5\hspace{0.17em}\text{mm/cycle}$ for both simulations and experiments, in the latter case we also find an additional optimum for $Ū\approx 1\hspace{0.17em}\text{mm/cycle}$. The distribution stabilizes at these two values after $\approx 20$ learning steps.

To determine the underlying cause for this bimodal velocity profile shown in experiments we map the behavior that this assembled robot can exhibit. Although each unit updates its phase individually, the overall motion of the assembled robot depends only on the phase difference $\mathrm{\Delta }\varphi ={\varphi }_2-{\varphi }_1$ between the two units. Fig. 1G shows a scan of the potential velocities $Ū$ the robot can exhibit, obtained in experiments by setting ${\varphi }_1=0$ and varying ${\varphi }_2$ between 0 and 1. From these results we find that the optimal speed is achieved at a phase difference of $\mathrm{\Delta }\varphi \approx 0.4$, at which the robot reaches a velocity of $\approx 4.5\hspace{0.17em}\text{mm/cycle}$. At the optimal behavior, the system seems to undergo peristaltic behavior, where the phase difference is approximately equal to the actuation period $\mathrm{\Delta }\varphi \approx \alpha$ (SI Appendix, Fig. S2). The same phase difference of $\mathrm{\Delta }\varphi \approx 0.4$ is observed in our first learning experiment (Fig. 1D). Similarly, for $\mathrm{\Delta }\varphi =0.6$ the robot moves in the opposite direction with a reversed actuation pattern with a velocity of $\approx -3\hspace{0.17em}\text{mm/cycle}$, while at $\mathrm{\Delta }\varphi \approx 0.9$ we find a local maximum in experiments with lower speed of $\approx 1\hspace{0.17em}\text{mm/cycle}$. These three cases are demonstrated in Fig. 1H, where we show both the starting and the end position after $60\hspace{0.17em}\text{s}$. It is important to note that while we expected symmetric behavior between forward and backward motion, as also demonstrated by the mass-spring model (Fig. 1G), in experiments we observe asymmetric motion. We believe that this asymmetry arises from a reduction of the friction due to the vibration of the pumps, which only occurs in the active units. The placement of the dummy unit therefore influences the behavior the robot can achieve. Also note that when applying the learning strategy in the simulations (Fig. 1 F and G) we find that the system only stabilizes around the maximum at $\mathrm{\Delta }\varphi \approx 0.4$, since no significant local optima are observed.

Results of Three Units

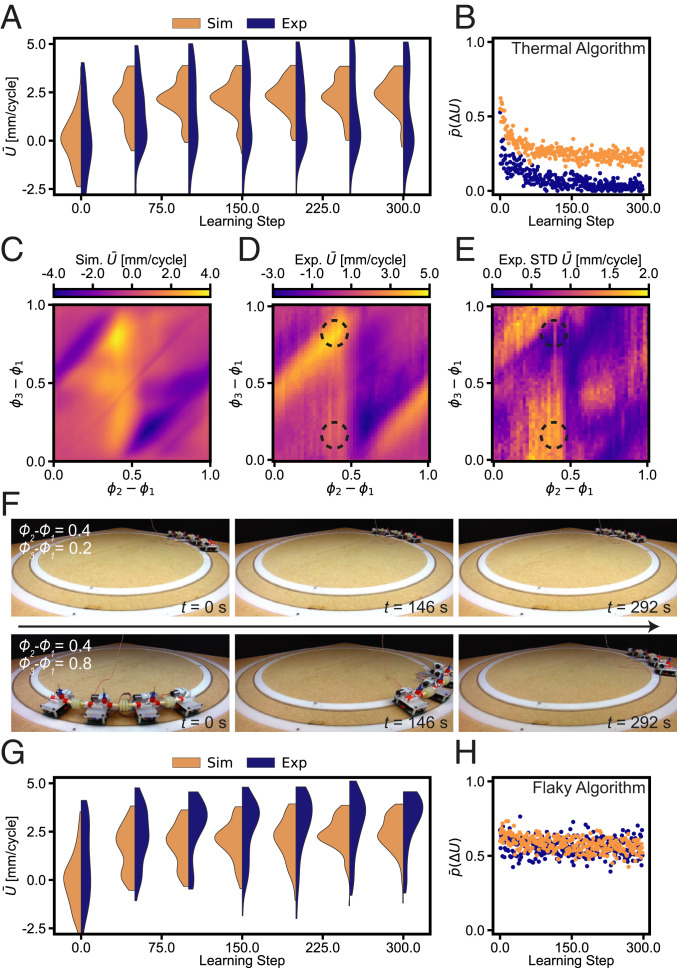
While the results for a robot assembled from two active units seem promising, the system’s average score function $Ū$ is relatively simple (Fig. 1G). Therefore, we next increase the complexity by performing experiments on a robot assembled from three active units and one dummy unit (Movie S1). In Fig. 2A we show the distribution of the average velocities $Ū$ during learning, of 112 simulations and 56 experiments. We observe both in experiments and simulations an initial improvement of $Ū$ during the first few $\approx 50$ learning iterations, similar to the assembled robot containing two active units. Interestingly, while the simulations stabilize at a $Ū$ with a mean positive value and an acceptance rate of $\approx 0.25$ (Fig. 2B), for experiments we observe a decrease of the mean $Ū$ after $\approx 200$ learning steps. This is accompanied by a decrease in the average acceptance rate of new phases, which approaches zero soon after the learning starts.

Fig. 2.

Adaptability to variations in the environment of an assembled robot consisting of three active units. (A and B) Distribution of average velocities $Ū$ and average acceptance rate $\overline{p}$ for the Thermal algorithm, as a function of the learning step, for 112 simulations and 56 experiments. (C and D) Average velocity $Ū$ obtained in simulations and experiments as a function of all of the possible combinations of phases ${\varphi }_3-{\varphi }_1$ and ${\varphi }_2-{\varphi }_1$ (with ${\varphi }_1=0$). (E) Standard deviation of the average velocity $Ū$ observed over 20 experimental runs. (F) Two different experiments with fixed phases, to highlight the effect of the track on the robot’s behavior. (G and H) Distribution of average velocities $Ū$ and average acceptance rate $\overline{p}$ for the Flaky algorithm as a function of the learning step, for 112 simulations and 56 experiments.

To understand the qualitative difference between simulations and experiments, and specifically the decrease in $Ū$ in experiments, we measure $Ū$ for all potential phase combinations in both simulations (Fig. 2C) and experiments (Fig. 2D). As expected, the results show a diverse range of possibilities, with multiple maxima. While our relatively simple model seems to capture the behavior of the assembled robot, there are two main differences in experiments. First, in experiments we observe significant noise, which could, e.g., be the result of how the measurements are taken (SI Appendix). Second, in experiments the performance of the robot seems to depend on where it is located on the circular track, which could be a result of variations in track width and the resulting friction (SI Appendix and SI Appendix, Fig. S3). This is supported when considering the standard deviation of the observed $Ū$ measured over 20 experiments, which exhibits nonnegligible variations (Fig. 2E and SI Appendix, Fig. S4A). For example, when running an experiment with ${\varphi }_2-{\varphi }_1=0.4$ and ${\varphi }_3-{\varphi }_1=0.2$ (bottom circle in Fig. 2 D and E), we find that for some parts of the track this assembled robot is capable of achieving $Ū\approx 2\hspace{0.17em}\text{mm/cycle}$, while the robot comes to a complete stop when reaching different parts of the track (Fig. 2F and Movie S2). In contrast, other regions in the phase space appear to be robust against track variations; see, e.g., the phase combination ${\varphi }_2-{\varphi }_1\approx 0.4$ and ${\varphi }_3-{\varphi }_1\approx 0.8$ (top circle in Fig. 2 D and E), for which the robot displacement $Ū\approx 4.5\hspace{0.17em}\text{mm/cycle}$ is at a maximum (Fig. 2F and Movie S2).

A More Robust Learning Strategy

To understand the effect that noise and changes in environment can have on our proposed decentralized learning algorithm and the reason that the algorithm stops accepting new phases, we need to consider how the memory is updated. At the moment, each unit only updates its $U_i$ that is stored in memory when achieving a higher $U_i^{\prime }$, with the exception of a probability to accept lower $U_i^{\prime }$ depending on the specified temperature $T$. If in the previous step the noise caused an overestimation of the $U_i$ that was stored in memory, the probability to accept realistic $U_i^{\prime }$ becomes smaller. Similarly, if changes in the environment cause a decrease in $U_i^{\prime }$, it will become less likely that the value of $U_i$ that is stored in memory is updated. This will influence the overall acceptance probability (Fig. 2B) and reduce the ability to adapt to variations and noise as also demonstrated by including noise in the simulations (SI Appendix, Fig. S5 A and B).

Therefore, while the Thermal algorithm performs well in a noiseless and static environment, in order to improve the adaptability of our system in real dynamic experimental conditions we need to change how memory is stored in each active unit. So far, we stored the last accepted phase ${\varphi }_i$ and corresponding displacement $U_i$ in memory. Instead, we propose an improved algorithm in which we update the memory according to the newly obtained velocity $U_i^{\prime }$, while still only updating the phase to ${\varphi }_i^{\prime }$ in case of acceptance. We refer to the this new strategy as the “Flaky algorithm” (see pseudocode in SI Appendix, Fig. S1). As such, with this new formulation each unit is constantly aware of the landscape and does not rely on past information that may not be reliable anymore (Movie S1).

To determine the performance of this updated algorithm, we repeated the learning study and gathered data from 112 simulations and 56 experiments. The results in Fig. 2G show that with the Flaky algorithm the active units are now capable of adapting to variations in their environment, achieving velocities of $Ū\approx 4\hspace{0.17em}\text{mm/cycle}$. Interestingly, the units now accept $\approx 60\%$ of all new candidates, independent of the learning step (Fig. 2H). As a result, the robot is able to adapt its behavior to noise and variations in the environment, which significantly improves its overall robustness. The difference in adaptivity between the Thermal and Flaky algorithms can also be illustrated by simulations in which we implement a sudden reduction in friction during learning (SI Appendix, Fig. S6). Moreover, simulations indicate that the acceptance rate of the Flaky algorithm is not affected by the noise level, in contrast to the Thermal algorithm (SI Appendix, Fig. S5C).

While the Flaky algorithm seems more suitable for dynamic environments than the Thermal algorithm, we can still observe certain conditions for which the Flaky algorithm is starting to have problems. For example, when increasing the friction in this system as shown in SI Appendix, Fig. S3 E and F we observe potential behavior that changes more abruptly with a change in actuation phase. As such, the derivative of the score with respect to the phases is close to zero everywhere, except for a few boundaries between domains. In this case the memory in the Flaky algorithm can be reset almost instantaneously, after which it will accept any other phase combination. As such, the Flaky algorithm requires some notion of smoothness, with variations occurring over domains that are larger than the step size.

Adaptivity to Damage

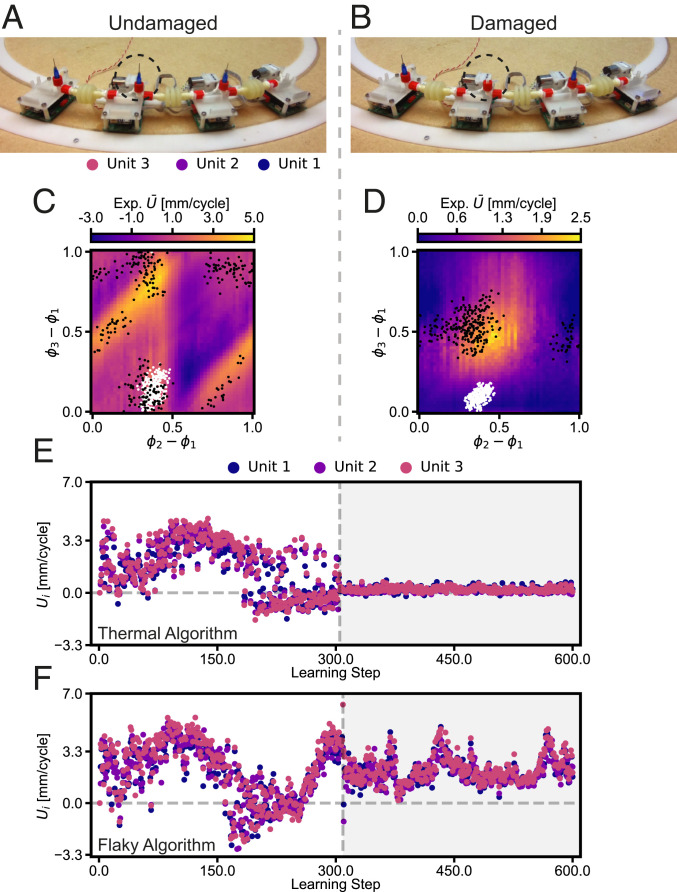
With the adoption of the Flaky algorithm, we next explore if and how the assembled robot adapts to suddenly applied damage. In order to show this, we consider a learning experiment with three active units and one dummy unit, in which we intentionally damage the robot after $\approx 300$ learning steps by removing the venting needle in the second unit (Fig. 3 A and B and Movie S3). This dramatically alters the possible behaviors the robot can exhibit, as indicated by the contour plots of the score before and after damage (Fig. 3 C and D and SI Appendix, Fig. S4). Once damaged, the robot must find a new locomotion pattern. It should be noted that although the second actuator cannot inflate after damage we still observe the presence of a global optimum at ${\varphi }_2-{\varphi }_1\approx {\varphi }_3-{\varphi }_1$, for which unit two and three are actuating simultaneously. While one would expect no influence of the damaged unit’s phase on the overall score (SI Appendix, Fig. S7), we find that by turning the pump on and off unit two seems to control its friction properties and as a result still plays a role in the optimal behavior. Importantly, when directly comparing the experiment and simulation results of the Thermal and the Flaky algorithms as shown in Movie S3, Fig. 3 E and F, and SI Appendix, Fig. S7, we find that the Thermal algorithm is not able to adapt to the damage and gets stuck at a certain phase, while the Flaky algorithm is able to overcome damage by completely adapting its behavior.

Fig. 3.

Adaptability of the assembled robot to damage using the Thermal and Flaky algorithms. (A and B) An assembled robot consisting of three active units is damaged by removing one of the needles. (C and D) Average velocity $Ū$ obtained in experiments for an intact and damaged robot, as a function of the possible range of combinations of phases ${\varphi }_3-{\varphi }_1$ and ${\varphi }_2-{\varphi }_1$ (with ${\varphi }_1=0$). The white and black dots represent the tried phases in two learning experiments in which the robot is damaged after 300 learning steps, using the (E) Thermal and (F) Flaky algorithms, respectively.

Scalability of the Learning Behavior

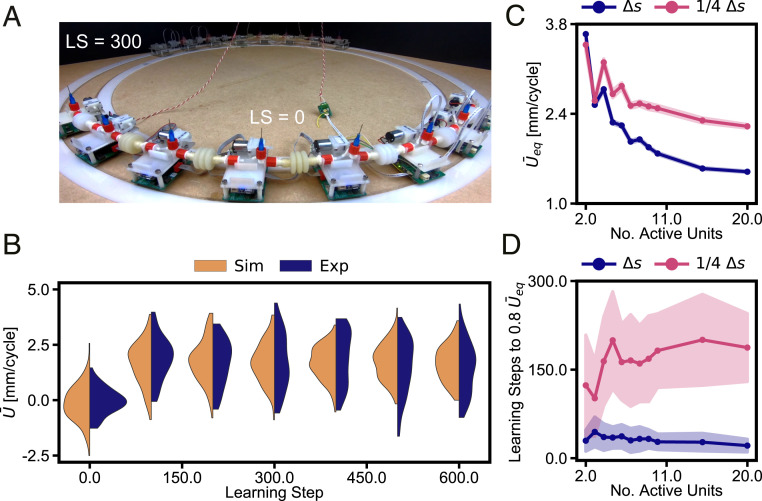
Finally, to verify if our learning strategy is scalable and can be applied to assembled robots consisting of more than three active units, we performed 112 simulations and 56 experiments on a robot consisting of seven active units and one dummy unit (Fig. 4A and Movie S4). In Fig. 4B we show the distribution of average velocity $Ū$ as a function of the learning step. While the average displacement $Ū\approx 2.5\hspace{0.17em}\text{mm/cycle}$ is lower than before, the initial learning occurs within a comparable number of learning steps. Note that during learning the assembled robot occasionally does reach higher speeds up to $Ū\approx 4\hspace{0.17em}\text{mm/cycle}$, however it is not able to maintain these speeds, likely due to the random guesses made by each unit during normal operation. To better understand how the system’s behavior is affected by its size, we performed 112 simulations for sizes up to 20 active units. To determine the equilibrium velocity ${Ū}_{\text{eq}}$ as shown in Fig. 4C, we fitted an exponential function to the average learning behavior (SI Appendix, Fig. S8A). We find that the equilibrium velocity decreases for larger number of units but appears to asymptotically reach a value close to $Ū\approx 1.7\hspace{0.17em}\text{mm/cycle}$.

Fig. 4.

Scalability of the learning behavior for an assembled robot ranging from 2 to 20 active units. (A) Initial and final position after 300 learning steps (1,200 s) of an assembled robot consisting of seven active units. (B) Distribution of average velocities $Ū$ as a function of the learning step, for 112 simulations and 56 experiments. (C) Relation between the number of active units and the equilibrium velocity ${Ū}_{\text{eq}}$, obtained using simulations, for $\mathrm{\Delta }s=0.1$ and $\mathrm{\Delta }s=0.1/4$. (D) Average number of learning steps, and standard deviation, needed to reach equilibrium (i.e., $0.8\hspace{0.17em}{Ū}_{\text{eq}}$) as a function of the number of active units. Here we only consider the simulation which reach the $0.8\hspace{0.17em}{Ū}_{\text{eq}}$ threshold within the assigned number of learning steps. While for $\mathrm{\Delta }s=0.1$ all of the simulations reach the threshold, for $\mathrm{\Delta }s=0.1/4$ we find that a percentage of simulations do not reach $0.8\hspace{0.17em}{Ū}_{\text{eq}}$ (SI Appendix, Fig. S8B).

Here, it should be noted that scalability could refer to two things, which are the behavior that the robotic platform can exhibit and the ability to learn “good” behavior. In the results shown in Fig. 4C we are investigating both factors for scalability simultaneously. One could argue that the velocity at the typical optimal peristaltic behavior that our system is aiming to achieve should not depend on the number of units, such that the system is apparently not able to find the optimal behavior for larger system size. This might be explained by the fact that our learning algorithm is exploring the behavior in a probabilistic way, such that equilibrium relates to some extent to the standard deviation of the system’s potential behavior (SI Appendix, Fig. S9). However, further studies should be performed to support this statement.

Interestingly, we do find that an increase in the number of units does not affect the rate of learning, as indicated by Fig. 4D, and that on average the units only need 35 learning steps to reach speeds within 80% of the equilibrium velocity ${Ū}_{\text{eq}}$. Furthermore, we can increase the equilibrium velocity ${Ū}_{\text{eq}}$ at the cost of learning rate by decreasing the steps size used to update the phases (Fig. 4 C and D), which underpins the assumption that better behavior is attainable but depends on the stochastic nature of the algorithm.

Conclusion

In this work, we implemented a basic decentralized reinforced learning algorithm in a modular robot to improve and adapt its emergent global behavior. We demonstrated that such a decentralized learning approach is an effective way to adapt the robot’s behavior to a changing environment or damage. One of the most important findings of this work is the requirement on how previous scores (measured by the sensors) should be stored in each unit, where we find that the memory should be representative of the current environment in order for the algorithm to be adaptive. We implemented this in the Flaky algorithm by always keeping the last measured displacement, in contrast to the more classic Thermal algorithm that keeps the last accepted displacement, and therefore can only overcome sudden changes in conditions according to a specific temperature parameter.

Interestingly, our proposed system was able to learn peristaltic locomotion gaits (20, 30, 31) without any prior knowledge, making this decentralized learning strategy suitable for the exploration of environments whose governing physical conditions are unknown. Given that each unit in the robot is identical, no electrical connections are needed, and there is no centralized controller; the robot can be reconfigured into any shape and maintain its capability to learn, for example after shuffling the units (Movie S5). As a result, each module represents a unit cell capable of learning, such that the learning capability becomes essentially a material property, e.g., when cutting the robot in two, both parts would maintain the ability to learn. We therefore refer to this kind of system as “robotic matter” (32–34).

Although we performed one-dimensional experiments to simplify the potential behaviors, the robot does not need to be confined to a track (Movie S5). Importantly, we believe that our approach is applicable to a large range of robotic systems with different architectures, actuators, and sensors, including (soft) robots with many degrees of freedom that are assembled in two-dimensional patterns (20), or that fully deform in three dimensions (16). Furthermore, the simplicity of our learning strategy and the fact that it can be coded using only a few lines makes it suitable for (microsized) robots that have limited computational power and dedicated electronic circuits (35–37) and could potentially even be realized through other means than an electronic circuit such as microfluidics (9, 38), and even material behavior (39). The simplicity and robustness of our proposed robotic matter is an important step toward robotic systems that can autonomously learn to thrive in a broad range of applications at different length scales, spanning from in vivo healthcare to disaster relief and space exploration.

Materials and Methods

Details on the materials and methods are provided in SI Appendix.

Data Availability

The experimental and numerical data that support the findings of this study and all computer algorithms necessary to run the models have been deposited at Figshare (10.6084/m9.figshare.13626110).