Background-free dual-mode optical and ¹³C magnetic resonance imaging in diamond particles

Significance

We report on progress toward combining magnetic resonance imaging (MRI) and optical imaging in diamond microparticles. Our approach relies on the nitrogen vacancy (NV) center-driven optical nuclear hyperpolarizability in diamond particles, that renders them “bright” in MRI while simultaneously fluorescing optically. Both imaging modes allow suppression of background signals. We elucidate how such “dual-mode” imaging can perform better than either modes taken separately, leveraging relative strengths of optics and MRI with respect to resolution and imaging in scattering media. Finally, we propose a protocol for accelerated imaging that exploits the Fourier conjugacy in images obtained via optics and MRI. Our work suggests methods to combine optical and RF imaging in classes of deployable nanoparticles.

Abstract

Multimodal imaging—the ability to acquire images of an object through more than one imaging mode simultaneously—has opened additional perspectives in areas ranging from astronomy to medicine. In this paper, we report progress toward combining optical and magnetic resonance (MR) imaging in such a “dual” imaging mode. They are attractive in combination because they offer complementary advantages of resolution and speed, especially in the context of imaging in scattering environments. Our approach relies on a specific material platform, microdiamond particles hosting nitrogen vacancy (NV) defect centers that fluoresce brightly under optical excitation and simultaneously “hyperpolarize” lattice ${}^{13}\mathrm{\text{C}}$ nuclei, making them bright under MR imaging. We highlight advantages of dual-mode optical and MR imaging in allowing background-free particle imaging and describe regimes in which either mode can enhance the other. Leveraging the fact that the two imaging modes proceed in Fourier-reciprocal domains (real and k-space), we propose a sampling protocol that accelerates image reconstruction in sparse-imaging scenarios. Our work suggests interesting possibilities for the simultaneous optical and low-field MR imaging of targeted diamond nanoparticles.

In the quest toward high signal-to-noise (SN) imaging, significant power can be brought to bear by multimodal or multimessenger techniques (1, 2). They entail capturing an object through more than one imaging mode simultaneously, often at widely disparate wavelengths. Exploiting correlations between the different modes portends approaches such as Kalman filtering (3) that can deliver noise or background suppression. Furthermore, under appropriate conditions these correlations can engender additional image sampling and reconstruction strategies to accelerate image acquisition.

In this paper, we consider whether such methods could be applied to combine together MRI and optical imaging (4, 5). These two modes offer diametrically complementary advantages. Visible-wavelength optics are fast and cheap and can image at high resolution, yet often suffer from scattering, attenuation, and aberration distortions while imaging through real media. MRI, on the other hand, is noninvasive and scattering-free, is fully three dimensional, and can be chemically functional; yet it is slow, suffers from weak signals, and offers poor spatial resolution (millimeter level). Notably, optical and magnetic resonance (MR) imaging are carried out in Fourier-reciprocal spaces (x- and k-space). This redundancy makes a combined modality attractive—not only are there complementary advantages in sensitivity and resolution to be gained, but also it opens possibilities to access hybrid acquisition strategies that sample both real space and k-space simultaneously to yield image acceleration.

Here we illustrate proof-of-concept demonstrations of dual-mode optical and ${}^{13}\mathrm{\text{C}}$ MR imaging in diamond microparticles. We demonstrate high-fidelity imaging in either mode and show they can be rendered background-free. We propose three imaging regimes wherein such dual-mode imaging provides benefits over either mode considered individually. In particular, in either scattering or scattering-free media, optics and MRI can complement each other with respect to resolution, signal-to-noise ratio (SNR), and depth of imaging. We propose a hybrid sampling strategy, wherein conjugate imaging is carried out simultaneously in real space and k-space to enable image acceleration and power reduction in wide field-of-view settings.

Combined optical-MR imaging is made possible by special features of the diamond material medium. The diamond particles are incorporated with $\gtrsim$1 ppm of nitrogen vacancy (NV) defect centers (6). Under subbandgap illumination $<$575 nm, the particles fluoresce brightly in the red with high luminosity ($\sim$90 cd/${\mathrm{m}}^2$) and optical stability. Fluorescence occurs concurrently with the optical polarization (>10%) of the electronic spins. This can be transferred to ${}^{13}\mathrm{\text{C}}$ nuclei in the surrounding lattice, hyperpolarizing them and making them amenable to direct MR imaging (7). We exploit a recent mediated hyperpolarization technique (8) that allows large ($\sim$1%) ${}^{13}\mathrm{\text{C}}$ polarization levels in diamond particles at room temperature and low magnetic fields.

Results

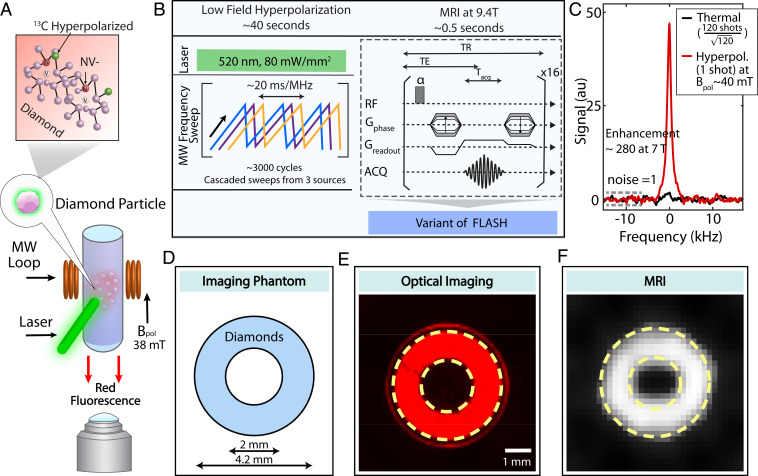
Fig. 1A is a schematic of the experiment. Diamond particles (200 $\mathrm{\mu }$m size, $\sim$40 mg) arranged in a ring-shaped phantom (Fig. 1D) are imaged optically under continuous 520-nm illumination and 630-nm long-pass filtering (Fig. 1E). The particles fluoresce brightly ($\sim 12\times 10^{11}$ cps) (SI Appendix). The same optical excitation polarizes (initializes to $m_s$ = 0) the electron spins, and microwave (MW) sweeps across the electron spin resonance (ESR) spectrum drive Landau–Zener (LZ) dynamics that transfer polarization to the ${}^{13}\mathrm{\text{C}}$ nuclei in an orientation-independent manner (Fig. 1B) (8, 9). We obtain $\sim$0.3% ${}^{13}\mathrm{\text{C}}$ spin polarization in 40 s under 1 W total optical illumination, enabling hyperpolarized MR imaging (Fig. 1B). This level corresponds to a signal enhancement of 280 times over thermal ${}^{13}\mathrm{\text{C}}$ polarization at 7 T (Fig. 1C) or 206 times over 9.4 T ($\sim 5\times {\mathrm{10}}^4$ over 38 mT) and $\sim {\mathrm{10}}^5$ acceleration in MR imaging time.

Fig. 1.

Dual-mode optical and ${}^{13}\mathrm{\text{C}}$ MR imaging. (A) Experiment schematic. Diamond particles with centers are imaged with fluorescence under green (520 nm) excitation by a complementary metal oxide semiconductor (CMOS) detector, as well as under ${}^{13}\mathrm{\text{C}}$ MRI through polarization transferred to lattice ${}^{13}\mathrm{\text{C}}$ nuclei from optically polarized electrons. (B) Hyperpolarization and detection protocol. The ${}^{13}\mathrm{\text{C}}$ DNP occurs at low field $\sim$38 mT under MW sweeps across the ESR spectrum. FLASH MR imaging is performed after sample shuttling to 9.4 T. Here echo time TE = 0.5 ms, repetition time TR = 6 ms, acquisition time ${\mathrm{T}}_{\mathrm{\text{acq}}}$ = 0.36 ms. (C) Typical hyperpolarization signal enhancement, showing signal gain $\approx 280\hspace{0.17em}\pm$ 5 against thermal signal at 7 T, corresponding to $\sim$5 orders of magnitude acceleration in MR imaging time. For a fair comparison, the noise in both datasets is normalized to 1 (dashed lines). (D) Ring-shaped phantom filled with 40 mg of 200-$\mathrm{\mu }$m diamond particles employed for dual-mode imaging. (E) Fluorescence image captured through a 630-nm long-pass filter. (F) A ${}^{13}\mathrm{\text{C}}$ MR FLASH image with 16 averages ($\approx$8 s total imaging time) and a square pixel length of 160 $\mathrm{\mu }$m and square FOV with a 6.4-mm edge.

Compared to conventional dynamic nuclear polarization (DNP) techniques, our method requires relatively low laser ($\sim$2 mW/mg) and MW power ($\sim$0.05 mW/mg) (10). The MRI demonstration in Fig. 1F employed a laser power density of $\sim$80 mW/${\mathrm{m}\mathrm{m}}^2$ to polarize $\sim$40 mg of diamonds. While this work is focused on diamond particle imaging, we note possible extension for in vivo studies assuming that specific absorption rate (SAR) can be controlled to safe limits, and the diamond particles can be eliminated from the body. In the context of potential in vivo applicability, we estimate a MW SAR of 1.1$\times {\mathrm{10}}^4$ W/${\mathrm{k}\mathrm{g}\left[\mathrm{G}\right]}^2$. Hyperpolarization efficiency scales approximately logarithmically with MW power beyond a particular threshold (8), indicating that the SAR can potentially be curtailed without severely degrading the DNP enhancement factors (SI Appendix).

We use a variant of fast low angle shot (FLASH) (11) to produce the MRI images at 9.4 T (Fig. 1 B and F), with short echo times (0.5 ms) to accommodate short $T_2\approx$1 ms of ${}^{13}\mathrm{\text{C}}$ in diamond. To eliminate pulse interference during the $\sim 200\mathrm{\mu }$s gradient switching periods, imaging was performed without a slice selection gradient (Fig. 1B). The SNR of the MR image (Fig. 1F) is $\sim$4 in 16 scans (each scan preceded by hyperpolarization), limited by rapid ${}^{13}\mathrm{\text{C}}\hspace{0.17em}{T}_2$ decay, low sample filling factor ($\approx$0.007), and laser-limited hyperpolarization. The use of dynamic decoupling sequences, such as quadratic echos (12), spin locking (13), or a recently developed approach to enhance free induction decay (FID) time exceeding 2 s (14), can improve the imaging SNR by at least an order of magnitude. If the application at hand permits higher optical powers close to saturation intensity, similar gains can be concurrently obtained. In particular, materials advances would boost MR image SNR by an order of magnitude through ${}^{13}\mathrm{\text{C}}$ enrichment and through the use of high-temperature annealing (15). Further improvements may be realized by optimizing the detection coil geometry and filling factor, for instance through the use of small-volume inductively coupled receiver coils (16). These concerted gains in MR signal could also permit similar high-contrast images in nanosized particles ($<$100 nm), although these smaller particles display lower ($\approx 10^{-2}$) hyperpolarizability than the microparticles employed in this work (15). The MRI spatial resolution here is 640 $\mathrm{\mu }$m $\propto 1/\left(\gamma G_{\mathrm{\text{max}}}\tau \right)$, where $G_{\mathrm{\text{max}}}$ = 950 mT/m.

The DNP method here presents advantages over traditional hyperpolarization methods for solids imaging, employed for instance in ²⁹Si microparticles (17). We work at room temperature and low field ($\sim$40 mT) and polarize samples in under 1 min of laser pumping. Conventional methods, in contrast, require high magnetic field ($\gtrsim$3 T) and low temperature ($<$4 K) and polarization buildup can take several hours (18). While the absolute polarization is lower in our method, we circumvent the high polarization loss (as large as 99%) (19) accrued upon thawing and sample transfer out of the cryostat. Technologically, our technique aids end-user operation—MW amplifiers and sweep sources are low cost and readily available, and hyperpolarized particles can be delivered by a portable device (10). Since the DNP process is detection-field agnostic, the technique is especially interesting in the context of low-field MRI where hyperpolarization can be replenished continuously.

Background-Free Imaging

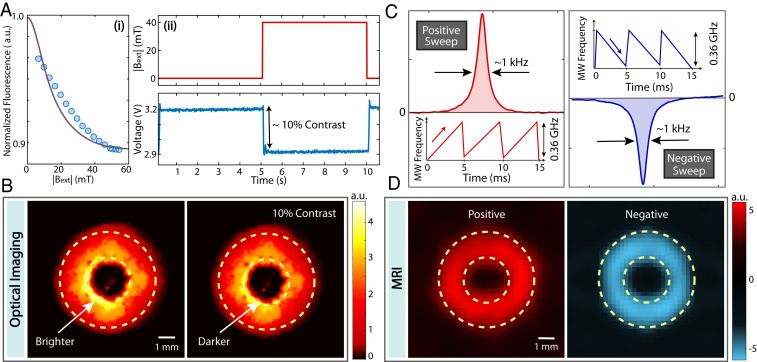
Both optics and MR modalities allow on-demand image amplitude modulation, enabling common-mode suppression of background signals. The NV fluorescence is conditioned strongly on the misalignment angle $\theta$ of the N-to-V axis to the applied field (20, 21), especially at low fields approaching 50 mT. This arises from mixing of the $m_s=\pm$1 spin levels in the excited state. Since the randomly oriented particles sample all possible $\theta$ angles, this enables a simple method to modulate the optical images by applying a pulsed field ${\mathbf{B}}_{ext}$ (22). In Fig. 2 A, i, we simulate fluorescence dependence under ${\mathbf{B}}_{ext}$ using a seven-level model of the NV center (20): $\frac{\mathrm{d}{n}_i}{\mathrm{d}t}={\sum }_{j=1}^7\left(k_{ji}{n}_j-k_{ij}{n}_i\right)$, where $n_i$ is the population of the $\left|i\right.⟩$ state, and $k_{ij}$ denotes the kinetic transition rate between states $\left|i\right.⟩$ and $\left|j\right.⟩$ (measured in ref. 20). In steady state, photoluminescence (purple line in Fig. 2 A, i, obtained evaluating $\int n_i\left({\mathbf{B}}_{ext},\theta \right)\sin \theta d\theta$) decreases with ${\mathbf{B}}_{ext}$, in reasonable agreement with (normalized) measurements (blue dots). In our experiments (Fig. 2B), ${\mathbf{B}}_{ext}=$40 $\pm$ 2 mT takes the value identical to that used for hyperpolarization, and we obtain an $\sim$10% optical modulation contrast (Fig. 2 A, ii).

Fig. 2.

On-demand dual-mode image modulation. (A, i) Normalized fluorescence signal for a randomly oriented diamond particle ensemble under an applied magnetic field (points, experiment; purple line, simulation). We ascribe the discrepancy to scattering effects. (A, ii) Optical modulation under 40 $\pm$ 2 mT pulsed magnetic field showing a signal contrast $\sim$10%. (B) Optical images under 0 and $\sim$40 mT applied field showing weak $\sim$10% optical contrast. (C) The ${}^{13}\mathrm{\text{C}}$ hyperpolarization sign control. MW frequency sweeps in low-to-high (high-to-low) fashion across the ESR spectrum lead to positive (negative) hyperpolarization. Shown are 7 T ${}^{13}\mathrm{\text{C}}$ NMR spectra under opposite sweep conditions. (D) The ${}^{13}\mathrm{\text{C}}$ MR images under opposite MW sweep conditions, showing full sign reversal and $\sim$194% modulation contrast. Here FLASH images were taken with TE = 0.6 ms and TR = 6 ms.

MRI mode allows for similar signal modulation. Such modulation refers to controlling the ${}^{13}\mathrm{\text{C}}$ hyperpolarization sign based on the direction of MW sweeps between alternate scans (as opposed to continuously modulated signal in optics). This effect originates from LZ dynamics excited by the chirped microwaves (Fig. 2C) (8, 9). The ${}^{13}\mathrm{\text{C}}$ nuclei are aligned (antialigned) with the polarization field under low-to-high (high-to-low) frequency sweeps. This allows complete sign reversal of the MRI images at full contrast. As a figure of merit, we characterize modulation contrast as the difference ratio of the MR images $\mathcal{I}$ and $\overline{\mathcal{I}}$ under opposite MW sweeps (Fig. 2D) as $\mathrm{\Delta }=\frac{1}{N^2}\left(\frac{\mathcal{I}-\overline{\mathcal{I}}}{\mathcal{I}+\overline{\mathcal{I}}}\right)$, where $N^2$ is the total number of pixels. From the data in Fig. 2 E and F, we obtain $\mathrm{\Delta }$=(194 $\pm$ 0.3)%. Similar modulation contrasts are challenging to achieve in conventional cryogenic DNP due to technical limitations of MW cavity switching (19, 23).

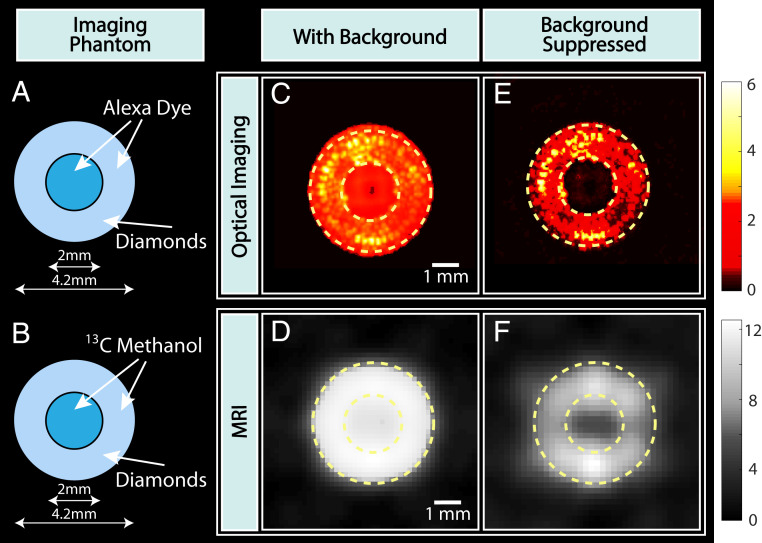
Signal modulation allows background-free imaging of the diamond particles. We refer to “background” in this context as media with fluorescence or ${}^{13}\mathrm{\text{C}}$ NMR signals that overlap in wavelength (or NMR frequency) with the diamond particles. As a proof of concept (Fig. 3), we consider particles being coincluded with a high concentration of Alexa 647, a fluorescent dye with emission in the 650- to 670-nm range (SI Appendix), as well as [¹³C]-methanol, which has a chemical shift nearly overlapping that of diamond. These solution media fill both the inner and outer spaces of the capillary tube that compose the diamond phantom in Fig. 3 A and B. The backgrounds result in images that are circle shaped since the diamond phantom is completely indiscernible within it (Fig. 3 C and D). To recover the diamond signals in the optical mode, we perform lock-in detection under a 40-mT 0.1-Hz square-modulated field. We record a 2,000-frame movie at 0.1 fps and computationally apply lock-in suppression on each pixel. The resulting image (Fig. 3E) shows recovery of the diamond signal, in this case, from the 2 times stronger background. Optical background suppression is ultimately limited by the modulation contrast, and up to an order of magnitude is experimentally feasible (22). Concurrent MRI background suppression is realized by subtracting the images under opposite sweep-ramp hyperpolarization conditions in alternative scans. The [¹³C]-methanol signal was 5 times larger than the diamond signal and is efficiently canceled (Fig. 3F).

Fig. 3.

Dual-mode background suppression. (A and B) Schematic of imaging phantoms. Diamonds are arranged in a ring-shaped phantom, cosituated with Alexa 647 dye and [¹³C]-methanol that present an artificial background for optical and MR imaging, respectively. (C and D) Optical and MR images with the background. Dashed lines serve as a guide to the eye for the imaging phantom. Diamond particles are indistinguishable from the background in both imaging dimensions. (E and F) Background suppressed optical and MR images employing signal modulation (reversal) allow complete recovery of the original diamond phantom in both imaging modes.

Regimes for Combined Dual-Mode Imaging

While Fig. 3 shows the optical and MR imaging separately, what may one accomplish by combining them together in a dual-imaging modality? Consider that MRI is natively immune to optical scattering, while optics provide superior resolution in scattering-free media. This can make a combined mode persuasive in specific imaging regimes.

Consider first the fluorescent imaging of nanodiamond particles embedded in a scattering medium (e.g., in tissue). One has to contend with round-trip attenuation and scattering losses (scaling $\sim {\lambda }^{-4}$) that restrict the proportion of collected photons. In tissue, for instance, attenuation and scattering at 650 nm lead to exponential losses with coefficients 0.1 and 1.1 ${\mathrm{m}\mathrm{m}}^{-1}$, respectively (24, 25). We estimate a round-trip attenuation loss of 0.2 and scattering loss of $10^{-4}$ at 3 mm depth. There are further photon losses stemming from green–red conversion ($\sim 10^{-5}$) and the unusually high refractive index differential between diamond and its environment ($\sim 10^{-2}$), as well as the finite numerical aperture limited by geometric solid-angle constraints of the detector at high fields of view (FOVs) ($\sim 10^{-3}$) (SI Appendix). Scattering also leads to a simultaneous loss in imaging resolution. Random scattering of the beam blurs the optical image, spreading it as much as 800 $\mathrm{\mu }$m at 1 cm depth (see SI Appendix for simulations).

In contrast, hyperpolarized MR imaging SNR can be competitively efficient, especially at increasing imaging depth $d$. One partakes of losses only in the one-way illumination of the particles with 520 nm light. Hyperpolarization efficiency is $\sim 2\times {\mathrm{10}}^{-4}$ per ${}^{13}\mathrm{\text{C}}$ nucleus per incident photon (8). The high detection losses and geometric solid-angle collection constraints are replaced by more benign factors related to sample-coil filling, detector Q, and the overall MR detection frequency (26). Surface coils matched to the sample and the use of high-Q ferrite resonators can lead to substantially more efficient detection (27). In this regime MR imaging could have a higher overall SNR than its optical counterpart. This cross-over point in efficiency occurs at depths $d\approx \frac{1}{1.2}\log \left({\eta }_d\right)$ at 650 nm, where ${\eta }_d$ is the ratio of optical and MR imaging SNR for surface diamond particles. Immunity to scattering also means that MR imaging resolution is independent of imaging depth (SI Appendix).

To now elucidate advantages of dual-mode optical MR imaging, we consider the effect of one mode enhancing the other. We focus on two imaging regimes, conditioned on imaging in media with and without optical scattering, respectively. In each regime we consider a “primary” imaging mode (either optics or MRI) and wherein a “secondary” (complementary) mode is added to enhance it (Table 1).

Table 1.

Dual-mode imaging regimes from a combination of optics and MRI

Regimes I and II consider optics and MRI being primary imaging modes in scattering and scattering-free media, respectively. Regime III considers sampling in both imaging dimensions as elucidated in the algorithm of dual-mode imaging. Red color indicates parameters where image enhancements can be gained via dual-mode combination, while blue indicates less improvement. For clarity, the variables here refer to ${\gamma }_0$, ratio between optical SNR and MR SNR at $d=0;$ $P_i$, incident power density; $\mathrm{\Delta }x$, pixel size; ${\alpha }_i$, ${\alpha }_{ϵ}$, incident and emission light loss coefficients, including scattering and attenuation; $d$, object depth; $T$, imaging time; $\mathrm{\Delta }{x}_{\mathrm{o}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s}}$, $\mathrm{\Delta }{x}_{\mathrm{m}\mathrm{r}\mathrm{i}}$, pixel size for optical and MRI; FOV, field of view; and $s$, sparsity, the proportion of dark pixels.

*Extrapolated from SI Appendix, Fig. S2, and taking a depth of 15 mm.

^†The SNR gain in the third mode is defined as the ratio between dual-mode SNR and optical SNR.

^$‡$Extrapolated from experimental number to $d=$ 3 mm, using loss coefficient 13.5 ${\mathrm{c}\mathrm{m}}^{-1}$ for 532-nm laser and 12.1 ${\mathrm{c}\mathrm{m}}^{-1}$ for 650-nm fluorescence in scattering media (see SI Appendix, section 1A, diamond mass $\sim$40 mg). The coefficients are calculated based on fatty tissue data in ref. 32.

^§Taken from the dual-mode experiment demonstrated in Fig. 1 (SI Appendix, section 1A).

^¶Extrapolated from the experiment demonstrated in Fig. 1, assuming $\mathrm{F}\mathrm{O}\mathrm{V}=$ (6.4 mm)² (details in SI Appendix, section 1B).

^#Based on gyromagnetic ratio of ${}^{13}\mathrm{\text{C}}$, $G_{max}$ can be up to 60 T/m in ref. 33, and $\tau \sim T_2\approx$ 1 ms.

^$\parallel$Power reduction is defined as the ratio between the power required by the single primary mode and the dual-mode approach to achieve certain SNR.

^**Obtained from Fig. 4 when assuming $\left(1-s\right)=0.9\times 10^{-3}$.

^††See Fig. 3.

Regime I.

Consider first optical imaging (primary mode) in scattering media. Scattering deteriorates image SNR by a factor of $e^{-{\alpha }_{i}d}{e}^{-{\alpha }_{ϵ}d}$, where ${\alpha }_i$, ${\alpha }_{ϵ}$ are incident and fluorescent loss coefficients, respectively. Instead, the ability to image via the secondary MRI mode can improve SNR compared to the primary mode by a factor $e^{-{\alpha }_{ϵ}d}$ and imaging resolution ($\propto d$). Table 1 shows these factors, with estimated numerical gains possible in the scenario with imaging depth $d=$ 3 mm (see footnotes in Table 1). In fact, the depth penetrability of MRI and its relative immunity to scattering can also provide imaging capability in three dimensions.

Regime II.

Alternately, consider when MRI is chosen as the primary mode and is applied in a scattering-free imaging regime. Here the resolution can be augmented from $\delta x_{\mathrm{m}\mathrm{r}\mathrm{i}}$ (640 $\mathrm{\mu }$m in Fig. 1) to $\delta x_{\mathrm{o}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s}}$ (40 $\mathrm{\mu }$m in Fig. 1, ultimately limited by diffraction) by rastering a laser beam across the field of view to selectively hyperpolarize one single pixel at a time. Assuming the available total power is fixed, focusing the beam increases power density by a factor of $\frac{\mathrm{F}\mathrm{O}\mathrm{V}}{\mathrm{\Delta }{x}_{\mathrm{o}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s}}^2}$. Despite pixel size change and imaging time extension, these factors can provide an SNR enhancement of $\frac{\sqrt{FOV}\mathrm{\Delta }{x}_{\mathrm{o}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s}}}{\mathrm{\Delta }{x}_{\mathrm{m}\mathrm{r}\mathrm{i}}^2}$ simultaneously with resolution gain.

Accelerated Conjugate-Space Imaging

While the discussion above considers dual-mode imaging in terms of relative merits of optics and MRI with respect to scattering and resolution, here we propose an additional regime (regime III) exploiting the native ability of the two imaging methods to sample in Fourier reciprocal spaces. This allows feed-forwarding information from one space to guide the sampling in the other space. Every sampled point in one space carries information from all of the points in the other space; this is exploited to provide speedup in sparse imaging settings. This approach shares similarities with compressed sensing (28, 29) (see SI Appendix for a detailed comparison), but is different in the sense that image sampling here physically occurs in two conjugate spaces.

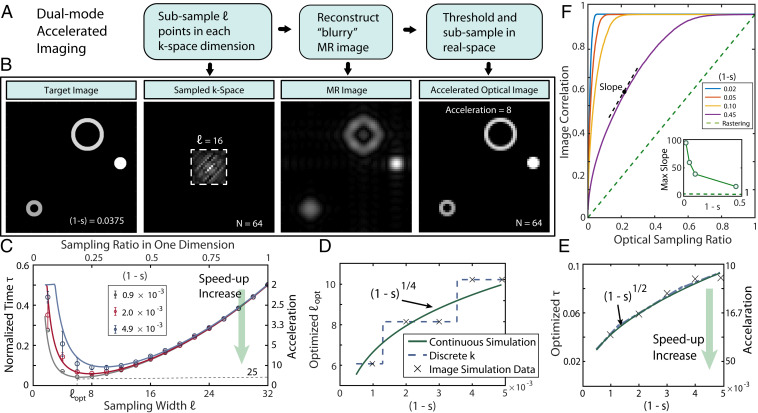
As a specific example, consider a wide FOV imaging scenario where optical imaging is performed by rastering a low-power beam across a sample of nanodiamonds distributed in a volume. We assume the objects are sparse in FOV and, for simplicity, that the per-pixel imaging time cost is identical for both optics and MRI. Fig. 4 describes the imaging protocol. Given the sparse original image to be acquired, a subset of $\ell$ points in each dimension is first sampled in k-space via MRI. The resulting blurry low-k image is thresholded and fed forward to confine real-space points to be sampled through optics. At high sparsity $s$, defined herein as the fraction of zero pixels in the FOV, this k-space reduces the number of points in real space to be rastered over and accelerates image acquisition. Fig. 4B simulates the method applied to an image with high sparsity, $\left(1-s\right)=$ 0.0375. Employing $\ell$ = 16 k-space samples in each dimension, and thresholding at 10% of the mean, we estimate image acceleration of 16-fold by eliminating sampling from large parts of the (real-space) image.

Fig. 4.

Accelerated x-k conjugate-space imaging. (A) Protocol for accelerated imaging. $\ell$ samples of the image are first acquired in k-space, and the resulting image upon thresholding is fed forward to constrain the real-space points to be scanned over. (B) Exemplary scenario where the target image FOV consists of sparsely distributed objects. By sampling over $\ell$ = 16 k-space points in each dimension, a blurry yet faithful image is formed of the target (Center two panels) and can serve to restrict real-space sampling (Right panel), leading to $\sim$14 times acceleration. (C) Normalized imaging time $\tau$ with different values of $\ell$ for images in a ${\mathrm{32}}^2$-pixel square FOV of different sparsity factors. Right axis indicates corresponding imaging acceleration. Here images consisted of unit-pixel objects, and we averaged over 30 random image configurations with identical sparsity; error bars denote standard deviations. The presence of an optimal k-space sample threshold ${\ell }_{\mathrm{\text{opt}}}$ is evident, stemming from a compromise between better confinement in real-space imaging and associated time cost for k-space imaging. (D) Scaling of ${\ell }_{\mathrm{\text{opt}}}$ with image sparsity, showing that more k-space values are required to account for increasing imaging complexity. Points: Given discrete possible values of $k$, ${\ell }_{\mathrm{\text{opt}}}$ has a staircase-like behavior. Solid line: scaling of ${\ell }_{\mathrm{\text{opt}}}$ assuming continuous $k$ values. (E) Optimized imaging acceleration through sampling ${\ell }_{\mathrm{\text{opt}}}$ points, showing orders of magnitude time savings at high sparsity. (F) Trajectory of image convergence quantified by image correlation $\mathcal{C}$ with protocol advancement. Green dashed line shows linear convergence under conventional optical rastering. In contrast, hybrid sampling in conjugate spaces can lead to rapid image convergence. (Inset) Slope of image approach to target rapidly increases with sparsity.

Let us now analyze the regime of applicability and inherent trade-offs involved. For simplicity, we assume as before that the time cost to be accrued per sample (pixel) is identical for both optical and MR imaging dimensions, although it is straightforward to scale the results by the cost ratio $\eta$ as appropriate. There is an optimal k-space sample ${\ell }_{\mathrm{\text{opt}}}$, arising as a compromise between better constraining real-space sampling and taking longer to image. Fig. 4C demonstrates this for a 32 $\times$ 32-pixel FOV, where we consider normalized imaging time savings over either modality for target images with varying sparsity to identify ${\ell }_{\mathrm{\text{opt}}}$. We estimate that hybrid sampling can deliver more than an order of magnitude in time savings (right axis in Fig. 4C), while requiring only the scanning of ${\ell }_{\mathrm{\text{opt}}}\approx$ 10% of total k-space (upper axis). As expected, ${\ell }_{\mathrm{\text{opt}}}$ decreases with sparsity, a reflection that larger k-samples are required with increasing image complexity (Fig. 4D). Given the small FOV and discrete values of k-samples, this manifests in the staircase-like pattern in Fig. 4D, but scales ${\ell }_{\mathrm{\text{opt}}}\propto {\left(1-s\right)}^{1/4}$ (solid line) as we shall derive below. Finally, in Fig. 4E we consider the combined imaging time $\tau$ under optimized conditions as a function of image sparsity, assuming that time for optical imaging is 1. Indeed, the imaging acceleration can be quite substantial, scaling as ${\tau }^{-1}\propto {\left(1-s\right)}^{-1/2}$.

We now elucidate origins of the imaging acceleration by studying the convergence trajectory of the reconstructed image as it approaches the target with each step of the protocol (Fig. 4F). Considering several image configurations with a fixed sparsity, we analyze in Fig. 4F the overlap of the reconstructed image $\prime$ to the target image through the correlation $\mathcal{C}=\sum \left(-⟨⟩\right)\left(\prime -⟨\prime ⟩\right)$, where $⟨\cdot ⟩$ indicates the mean value. Indeed, under usual rastered optical image acquisition (dashed green line in Fig. 4F), the reconstructed image linearly approaches the target as more samples are acquired. In contrast, employing the hybrid acquisition of a few k-space points, and by constraining the space over which the final image is to be acquired, one obtains a rapid convergence with the target. Numerically, the slope of convergence scales approximately $\propto {\left(1-s\right)}^{-1/2}$ (Fig. 4 F, Inset), indicating rapid gains can be amassed at high image sparsity. To analytically elucidate image acceleration at high sparsity (solid lines in Fig. 4 D and E), let us consider the real-space target image $f\left(x,y\right)$, which in k-space is $\mathcal{F}\left[f\right]=\widehat{f}\left(k_x,k_y\right)$, where $\mathcal{F}$ denotes a spatial Fourier transform. As k-space sampling now occurs just to $\ell$th order, one obtains the reconstructed image, ${\widehat{f}}_{\ell }\left(k_x,k_y\right)=\widehat{f}\left(k_x,k_y\right)\cdot \mathrm{\Pi }\left(\frac{k_x}{W_{kx}}\right)\cdot \mathrm{\Pi }\left(\frac{k_y}{W_{ky}}\right)$, where $\mathrm{\Pi }$ is a rectangular function representing a sampling window with a side length of, for instance, $W_{kx}=\delta k_x\ell$, where $\delta k_x=1/N_x$ is the k-space pixel size. Transformation back to real space gives the convolution, ${\mathcal{F}}^{-1}\left[\widehat{f_{\ell }}\right]=f{\left(x,y\right)}^{*}\left(W_{kx}\mathrm{\text{sinc}}\left(W_{kx}x\right)\cdot W_{ky}\mathrm{\text{sinc}}\left(W_{ky}y\right)\right)$. An object of pixel radius $r$ is effectively blurred, $r\to r_0\left(\frac{N}{\ell }\right)$, where the factor $r_0$ is set by the thresholding level employed (SI Appendix), and $\ell /N$ is the effective k-space sampling ratio. Increasing $\ell$ makes a more faithful representation and improves regional constraints, but it is associated with a time cost. To analytically evaluate the time savings let us as an example consider the FOV consists of $n_d$ objects of radius $r$, giving $\left(1-s\right)=n_d\pi r^2/N^2$. The normalized imaging time is then $\tau =\left(1-s\right)+\frac{2r_0}{r}\frac{1}{\ell }\left[\left(1-s\right)N\right]+\frac{r_0^2}{r^2}\frac{1}{{\ell }^2}\left[\left(1-s\right)N^2\right]+\frac{{\ell }^2}{N^2}$ (SI Appendix). In the limit of high sparsity, $\left(1-s\right)\to 0$, $\left(1-s\right)N\to 0$, and $\left(1-s\right)N^2\to \mathcal{O}\left(1\right)$, giving $\tau \approx C_0\frac{\left(1-s\right)}{{\ell }^2}+\frac{1}{N}{\ell }^2$, where $C_0=\frac{r_0^2{N}^2}{r^2}$ is a constant. Determining the optimal $\ell$ to minimize $\tau$ gives ${\ell }_{\mathrm{\text{opt}}}\propto {\left(1-s\right)}^{1/4}$, and the optimal (normalized) time $\tau \propto {\left(1-s\right)}^{1/2}$. The scaling from this simple model is shown as the solid lines in Fig. 4 D and E and closely matches numerical results in the limit of high sparsity.

Finally, we comment that imaging acceleration results in a lower total optical power delivered to the sample by the same factor as the acceleration gain. This protocol might have real-world applications given that most imaging of targeted nanodiamond operates in the high-sparsity limit $s>$ 95% (30, 31).

Conclusions

We have demonstrated a method for dual-mode optical and MR imaging in diamond microparticles. Our approach relied on optically fluorescent centers that simultaneously spin polarize ${}^{13}\mathrm{\text{C}}$ nuclei, making the particles “bright” under MR imaging. We discussed means by which the two modalities can be combined, exploiting complementary advantages for scattering-free and high-resolution imaging. We finally proposed methods for image acceleration exploiting the Fourier conjugacy inherent to optics and MRI.

Data Availability

All study data are included in this article and/or SI Appendix.