Critical slowing down suggests that the western Greenland Ice Sheet is close to a tipping point

Significance

It has been suggested that, in response to anthropogenic global warming, the Greenland Ice Sheet may reach a tipping point beyond which its current configuration would become unstable. A crucial nonlinear mechanism for the existence of this tipping point is the positive melt-elevation feedback: Melting reduces ice sheet height, exposing the ice sheet surface to warmer temperatures, which further accelerates melting. We reveal early-warning signals for a forthcoming critical transition from ice-core-derived height reconstructions and infer that the western Greenland Ice Sheet has been losing stability in response to rising temperatures. We show that the melt-elevation feedback is likely to be responsible for the observed destabilization. Our results suggest substantially enhanced melting in the near future.

Abstract

The Greenland Ice Sheet (GrIS) is a potentially unstable component of the Earth system and may exhibit a critical transition under ongoing global warming. Mass reductions of the GrIS have substantial impacts on global sea level and the speed of the Atlantic Meridional Overturning Circulation, due to the additional freshwater caused by increased meltwater runoff into the northern Atlantic. The stability of the GrIS depends crucially on the positive melt-elevation feedback (MEF), by which melt rates increase as the overall ice sheet height decreases under rising temperatures. Melting rates across Greenland have accelerated nonlinearly in recent decades, and models predict a critical temperature threshold beyond which the current ice sheet state is not maintainable. Here, we investigate long-term melt rate and ice sheet height reconstructions from the central-western GrIS in combination with model simulations to quantify the stability of this part of the GrIS. We reveal significant early-warning signals (EWS) indicating that the central-western GrIS is close to a critical transition. By relating the statistical EWS to underlying physical processes, our results suggest that the MEF plays a dominant role in the observed, ongoing destabilization of the central-western GrIS. Our results suggest substantial further GrIS mass loss in the near future and call for urgent, observation-constrained stability assessments of other parts of the GrIS.

During the last century, the Greenland Ice Sheet (GrIS) has lost mass at an accelerating rate (1, 2). The mass loss is caused by solid ice discharge into the North Atlantic and surface melting due to increasing temperatures. The relative contribution of the latter has increased from $42\%$ before 2005 to $68\%$ between 2009 and 2012, and surface runoff caused $84\%$ of the increase in mass reduction since 2009 (3). The complete melting of the GrIS would cause a global sea level rise of more than 7 m (4, 5). Continued melting of the GrIS has been suggested to potentially lead to a collapse of the Atlantic Meridional Overturning Circulation via increased freshwater flux into the North Atlantic (6, 7), which may, in turn, trigger a cascade of transitions in additional tipping elements such as the Amazon rainforest and the tropical monsoon systems (6, 8–10).

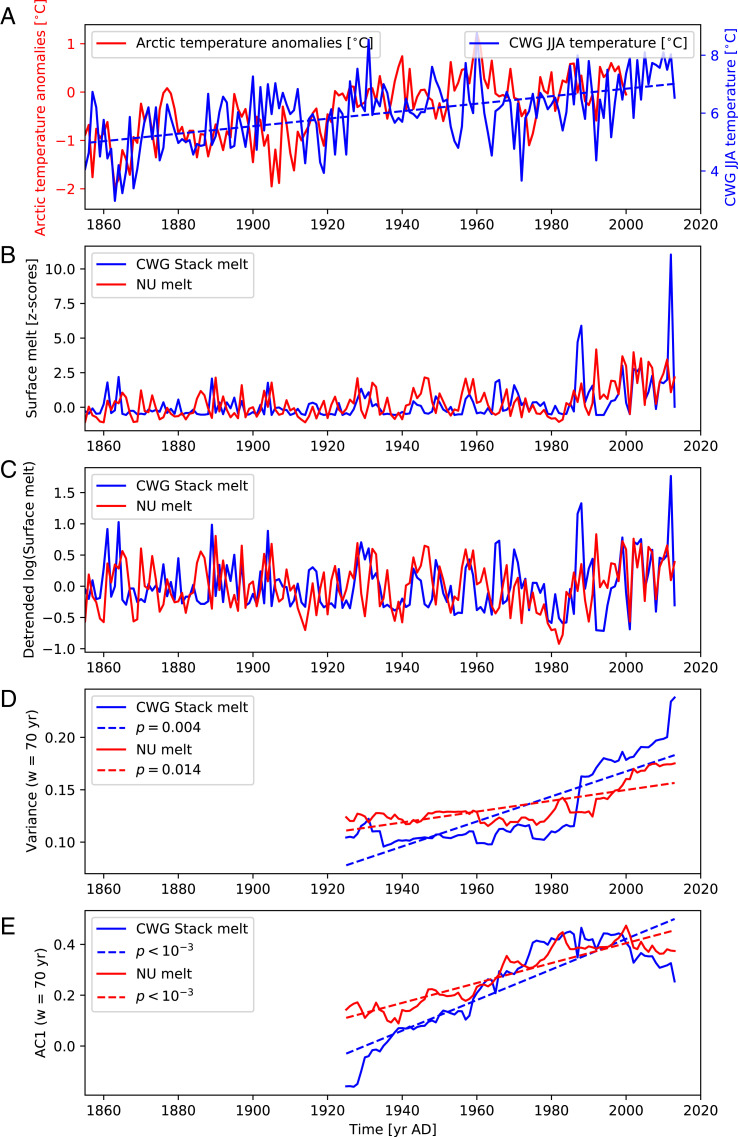
In addition to the centennial-scale variability associated with the increasing trend in mean temperatures related to anthropogenic climate change, the pace of mass loss has decadal-scale fluctuations caused by natural variations in external oceanic and atmospheric forcing. The imprints of these natural, decadal-scale fluctuations are spatially heterogeneous across the GrIS. Since the early 2000s, periods of persistently negative phases of the North Atlantic Oscillation (NAO) and a positive phase of the East Atlantic Pattern (11) have led to a weakening and southward shift of the jet stream, and more persistent blocking (12) over Greenland during summer, resulting in overall increased mass reduction rates (2, 13). On the other hand, a slowing down of mass loss since 2013—which inverted again in 2019—was caused by more periods with a persistent positive NAO (14). Moreover, recent observations show that the Jakobshavn glacier has been advancing again since 2016 due to anomalous wintertime heat loss in the boundary current around southern Greenland (15). However, these natural fluctuations do not have a sustained impact on melt rates comparable to the longer-term trend toward overall increasing melt rates caused by anthropogenic global warming (Fig. 1A).

Fig. 1.

(A) Summer sea level temperatures from the Ilulissat station in CWG (25) (blue curves) and Arctic temperature anomalies (26) (red curves). The linear trend of the station data (dashed blue curve) corresponds to $1.3\hspace{0.17em}°$C warming per century. Arctic temperature anomalies are shown only for comparison; only the station data (blue curves) are used for our analysis. (B) Melt rates from the CWG ice core stack (blue curve) and the NU peninsula core (red curve), given as z scores with respect to a normal distribution (18). (C) Detrended logarithmic CWG (blue curve) and NU (red curve) melt rates. A Gaussian filter with bandwidth $\sigma =30$ y was used for detrending. The runoff and melt time series are preprocessed in this way before computing the EWS indicators to exclude potential biases by underlying trends; in particular, we take the logarithm of the melt rates in order to account for skewed data distributions. (D) The variance of the CWG (blue curves) and NU (red curves) melt rates. (E) The AC1 of the CWG (blue curves) and NU (red curves) melt rates. Note that the AC1, despite a significantly positive trend, appears to have at least temporarily stabilized in the last few decades. It should be noted, however, that the AC1 is generally influenced by (multi)decadal variability (27). The window size for computing the variance and the AC1 is $w=70$ y, and values are plotted at the windows’ endpoints. Data for the first $w=70$ y are omitted to ensure that all windows contain the same number of data points. The dashed lines in D and E indicate linear trends of the variance and AC1, and P values for positive slopes as determined from a phase surrogate test are indicated in the legend (see Materials and Methods). The statistical significance of the positive trends is robust across wide ranges of the bandwidth $\sigma$ and the sliding window size (SI Appendix, Fig. S1).

Early model simulations suggest that melting of the GrIS is inevitable beyond a critical global mean temperature threshold of $0.8\hspace{0.17em}°$C to $3.2\hspace{0.17em}°$C above preindustrial levels, with a best estimate of $1.6\hspace{0.17em}°$C (16). More recent comprehensive modeling results show that, for the representative concentration pathway 8.5 (RCP8.5), the GrIS melts entirely until AD 3000 (5). Arctic temperatures have increased more than the global average (17) (Fig. 1A), and the nonlinear increase in GrIS melt rates and runoff that have recently been detected (18) (Fig. 1B) suggests that the critical temperature threshold may be closer than previously thought. We emphasize that the surface mass balance turning negative is not a necessary condition for stability loss, and the temperature may reach a critical threshold years before a turning point in the mass balance (16).

Idealized models of critical transitions in natural systems suggest that the loss of stability of an equilibrium (fixed point) is observable before the abrupt transition (19). In dynamical systems with random forcing, one can show that, if a system approaches a bifurcation where an equilibrium point loses its stability, the variance of the fluctuations around the equilibrium will increase, as will the characteristic decay time of the autocorrelation function of these fluctuations. The change in dynamics that occurs as stability is lost is often called critical slowing down, and the associated statistical precursor signs in terms of rising variance and lag-one autocorrelation (AC1) are called early-warning signals (EWS) (19). Such statistical EWS associated with critical slowing down are, for example, detectable in the temperature proxy from the North Greenland Ice Core Project before several of the Dansgaard–Oeschger events of the last glacial interval (20, 21), as well as before other abrupt transitions in past climates (22). In the context of anthropogenic global warming, EWS are expected to precede potential abrupt transitions in the Earth system’s major tipping elements, such as the polar ice sheets, the Atlantic Meridional Overturning Circulation, or the tropical monsoon systems (23). We investigate here a possible tipping point for the GrIS based on the theory of critical slowing down.

In the following, we will first show that central-western Greenland (CWG) melt rates exhibit robust and significant EWS. We then reconstruct the corresponding CWG ice sheet height changes and show that they can be captured well by a simple model focusing on the melt elevation feedback (MEF). We then demonstrate that pronounced EWS can also be found in the fluctuations of the reconstructed ice sheet height around the equilibrium of the model and show that these EWS are consistent with the theoretical expectations provided by the MEF model.

Results

For detrended melt rates measured in a stack of ice cores (18) located in CWG at elevations between 2,200 and 2,500 m above sea level, but also for the detrended melt rates from an ice core from the Nuusuaq (NU) peninsula (18) that we show for comparison (Fig. 1B), we find EWS for a critical transition in terms of highly significantly ($P=0.005$ for the CWG stack and $P<0.015$ for the NU core) increasing variance and highly significantly ($P<10^{-3}$ for both records) increasing AC1 (Fig. 1 D and E). The statistical significance of the trends is determined using a phase surrogates method that accounts for serial correlations in the underlying data (as in refs. 20–22 and 24, for example; see Materials and Methods for further details). The EWS are robust to varying the bandwidth used for detrending the time series and the window size used to estimate the variance and AC1 (SI Appendix, Fig. S1) and are not caused by corresponding fluctuations that could be mistaken for EWS in the driving temperatures (SI Appendix, Fig. S2).

To provide further evidence that the central-western part of the GrIS is close to a critical transition, we connect the observed EWS to the underlying physical processes and derive results that demonstrate the consistency of our hypothesis. In addition to ice discharge at the ice sheet margins and the melt–albedo feedback (28, 29), the MEF is the crucial mechanism determining the stability of the GrIS (5, 30, 31). A nonlinear equation of motion for the change of GrIS height $\mathrm{\Delta }h$ has been previously derived to describe the feedback, based on the idealized one-dimensional Vialov profile for ice sheets (32) and the assumption of linear dependence of the ice sheet surface melt rate and the elevation (33),

$$C\frac{d\mathrm{\Delta }h}{dt}=-p_0\left(\mathrm{\Delta }{h}^m-p_1\right)+p_2\left(\mathrm{\Delta }h-p_1\right)-\left(T-p_3\right)+\eta \left(t\right).$$ [1]

The equation includes sea-level temperature $T$, a noise term $\eta$, a sensitivity constant $C$, and positive parameters $\left(p_0,p_1,p_2,p_3\right)$ that are associated with the atmospheric lapse rate, the melting sensitivity of the ice sheet surface, and a temperature offset (33, 34) (see Materials and Methods). This model’s form has been derived, in detail, from the underlying physical equations of motion of glacier dynamics (33, 35). In particular, an exponent value of $m=8$ follows from $m=2\left(n+1\right)$ with Glen’s flow law exponent $n=3$ (33). For sufficiently low values of $T$, this simple dynamical system has a stable fixed point $h^{*}$ and an unstable fixed point, while, for $T$ larger than a critical value $T_{\text{c}}$, the stability of the current ice sheet state is lost (Fig. 2 and SI Appendix, Fig. S3). Physically, this nonlinear model and its instability beyond the critical temperature threshold arise because of the positive MEF, by which effective temperatures at the ice sheet surface increase with decreasing ice sheet elevation due to the atmospheric lapse rate, leading to further melting and elevation reductions.

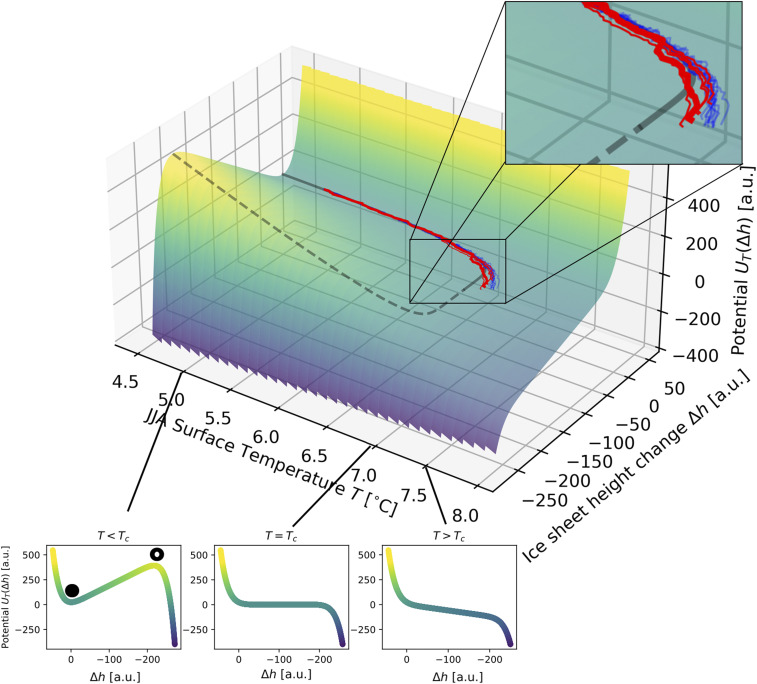
Fig. 2.

Potential landscape $U_T\left(\mathrm{\Delta }h\right)$ corresponding to Eq. 1. CWG ice sheet height changes $\mathrm{\Delta }h$ derived from the measured melt rates (18) (see Materials and Methods) are shown in bold red curves, corresponding process-based simulations using regional climate models (18) are shown in thin red curves, and simulations according to the model described by Eq. 1 are shown in thin blue curves (see the upper inset for a zoomed-in version). Note the high similarity between the reconstructions, process-based simulations, and the conceptual model simulations. The solid (dashed) gray curve indicates the system’s theoretical stable (unstable) equilibrium points; note that the simulations closely follow the stable equilibrium and that the blue and red curves accordingly overprint the solid gray curve. The three lower insets show the potential for different values of the control parameter $T$. Only for $T<T_{\text{c}}$, there exists a stable (closed black circle) and an unstable (open black circle) fixed point, given by the potential’s minimum and maximum, respectively. See SI Appendix, Fig. S3 for a two-dimensional version of this figure.

Using the recently reported measurements of GrIS melt rates $M$ and summer air temperatures at sea level $T$ (18), we derive the reconstructed temporal evolution of height anomalies $\mathrm{\Delta }h\left(t\right)$ in CWG (Figs. 2 and 3A and Materials and Methods). Given that $\mathrm{\Delta }h\left(t\right)$ fluctuates around the stable solution of Eq. 1 (i.e., the system’s equilibrium), the reconstructed $\mathrm{\Delta }h\left(t\right)$ can be used to determine optimal values for the model parameters $\left(p_0,p_1,p_2,p_3\right)$ (see Materials and Methods). Note that, since the transient dynamics are likely to overshoot the equilibrium to some degree, the method produces a conservative estimate of the critical temperature threshold. The potential landscape $U_T$ with control parameter $T$, corresponding to Eq. 1 via the relation $d\mathrm{\Delta }h/dt=-U_T^{\prime }\left(\mathrm{\Delta }h\right)$, shows that the reconstructed GrIS height has followed the potential’s minimum (i.e., the stable fixed point) in the past. According to our results, this minimum has recently ceased to exist. The reconstructed observations (bold red curve in Fig. 2), process-based simulations using regional climate models (18) (thin red curve in Fig. 2), as well as simulations of the model given by Eq. 1 (thin blue curve in Fig. 2), driven by the observed summer sea-level temperatures (25), are currently converging toward much higher height reduction rates.

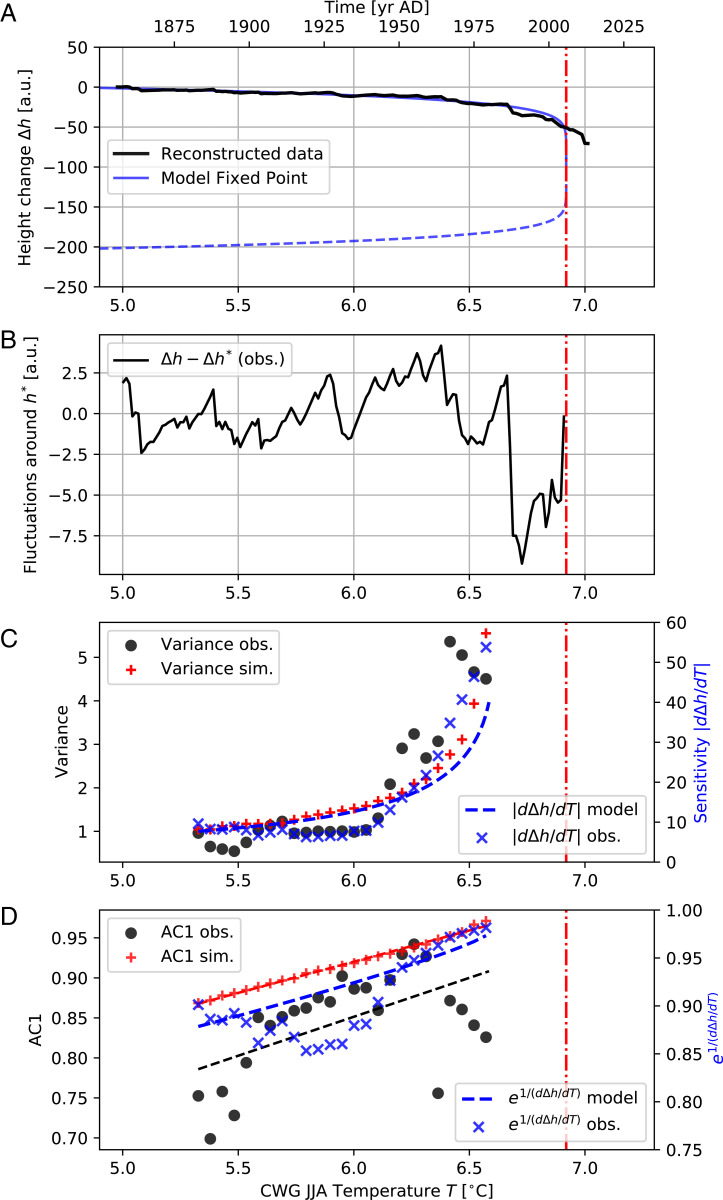
Fig. 3.

(A) Reconstructed CWG ice sheet height change (solid black curve) and corresponding bifurcation diagram of the optimized model given in Eq. 1 (blue curves). The coefficient of determination for fitting the model of Eq. 1 to the height reconstructions is $R^2=0.94$. Stable (unstable) model fixed points are shown in solid (dashed) blue curve. (B) Fluctuations of the reconstructed height change around the stable model fixed point. (C) Variance of the observed fluctuations around the fixed point (black circles), of corresponding simulations of the model given by Eq. 1 with optimized parameters (red plus sign), as well as the sensitivity $|d\mathrm{\Delta }h/dT|$ for the reconstructed observations (blue crosses, estimated by numerical differentiation) and the expected sensitivity of the model (dashed blue curve). (D) Same as C, but for the AC1, compared to the theoretically expected expression $\exp \left(1/\left(d\mathrm{\Delta }h*/dT\right)\right)$ (see Materials and Methods). Both variance and AC1 are estimated for sliding window sizes $w=50$ data points, and the initial and final 25 data points are accordingly omitted. These results are robust for different choices of the sliding window size (SI Appendix, Fig. S5) and the parameter used for reconstructing the ice sheet height change (Materials and Methods and SI Appendix, Fig. S6). The critical temperature value $T_{\text{c}}$ is indicated in A–D by the vertical dash-dotted line.

The excellent fit of Eq. 1 to the reconstructed $\mathrm{\Delta }h\left(t\right)$ (the coefficient of determination of the fit is $R^2=0.94$) is only a partial result. Our main finding is that the fluctuations around this curve behave consistently with critical slowing down as the critical temperature threshold induced by the MEF is approached. Given the particular structure of Eq. 1, a theoretical expression can be derived for how the variance of fluctuations around the stable equilibrium increases as the temperature approaches the critical threshold (see Materials and Methods). We find that the variance of the fluctuations should increase proportionally to the sensitivity of the equilibrium ice sheet height to temperature changes, that is, $⟨\mathrm{\Delta }{h}^2⟩\propto |d\mathrm{\Delta }{h}^{*}/dT|$. This prediction is verified by the reconstructed temporal evolution of height change $\mathrm{\Delta }h$ derived from measured melt rates in CWG: In the estimated bifurcation diagram (Fig. 3A), we observe that the fluctuations of the reconstructed height change $\mathrm{\Delta }h$ around the stable equilibrium point are growing as summer sea-level temperatures $T$ rise (Fig. 3B). Indeed, the variance of these fluctuations (black circles in Fig. 3C) increases significantly as the temperature approaches the critical value $T_{\text{c}}$. This increase is consistent with corresponding results for time series obtained from simulations of Eq. 1 (red plus signs in Fig. 3C). Moreover, the height’s sensitivity to temperature ($d\mathrm{\Delta }h/dT$), computed for the reconstructed height change $\mathrm{\Delta }h$ by numerical differentiation, shows very similar behavior (blue crosses in Fig. 3C) and closely follows the theoretical expectation from the MEF model (blue dashed curve in Fig. 3C). Likewise, we find increasing AC1 for the observations, closely following the AC1 of the model simulations. Theoretically, the AC1 is expected to increase proportionally to the expression $\exp \left(a/\left(d\mathrm{\Delta }h*/dT\right)\right)$ (see Materials and Methods), which is confirmed by our results (Fig. 3D). Note that the reconstructed and simulated height anomalies $\mathrm{\Delta }h$ (Fig. 3) exhibit substantially higher AC1 values than the melt rates (Fig. 1). This difference can be explained by the fact that the state variable relevant for the MEF is the height anomaly, for which also the model is formulated. The EWS in the melt rates are, according to our results, caused by the critical slowing down of the height anomaly, from where the signals propagate to the melt rates.

The increasing variance and AC1, together with the high correlations between the variance of the observed fluctuations and the sensitivity $d\mathrm{\Delta }h*/dT$ (the Pearson correlation coefficient between the variance and the absolute value of the sensitivity is equal to 0.9), as well as between the AC1 and the corresponding expression of the sensitivity, provide strong evidence of critical slowing down and a resulting destabilization of the central-western GrIS: Without a collapse of the stable fixed point, or more generally for linear dynamics, one would not expect the variance and AC1 to increase rapidly, and one would not find a proportionality (see Materials and Methods). Therefore, our results rule out that the ice sheet dynamics in CWG can be characterized by a linear response to the driving temperatures, since the consistency between observed and simulated variance, AC1, and sensitivity estimates is broken in that case (SI Appendix, Fig. S4). Note that the high resemblance between the modeled $d\mathrm{\Delta }h*/dT$ and the corresponding expression obtained for the reconstructed heights by numerical differentiation, as well as the corresponding similarity for the expression $\exp \left(a/\left(d\mathrm{\Delta }h*/dT\right)\right)$, adds further evidence that the nonlinear model given in Eq. 1 describes the observed ice sheet height dynamics. These results are robust against the size of the sliding windows used to estimate the variance and AC1 (SI Appendix, Fig. S5) and the parameter used to reconstruct the height changes (SI Appendix, Fig. S6).

The critical temperature value $T_{\text{c}}$ (Fig. 3) is below the values of $T$ reported for the last few years (Fig. 1A), suggesting that temperatures in CWG may indeed have crossed the critical threshold recently. Although our model fits the reconstructed height anomalies accurately, the value of the critical temperature threshold is uncertain and will be affected by other, possibly competing, feedbacks as outlined above. Therefore, the critical temperature threshold should be investigated further with comprehensive process-based models, ideally constrained by observations and with extensive sensitivity analyses to quantify the uncertainties. Due to the lack of observational melt rate records for other parts of the GrIS, it remains unclear to what extent our results generalize to the entire GrIS. Recent satellite measurements show that the central-western parts of the GrIS have experienced the most substantial decreases in ice sheet height, but, in the course of the last three decades, height reductions have also accelerated in most other parts of the GrIS closer to the coasts (36).

Discussion

We have explained the statistical EWS that we revealed in melt rate time series from CWG ice cores (Fig. 1) in terms of a simplified model of the MEF that follows from the equations of glacier dynamics (Fig. 2) and have shown that the fluctuations of reconstructed CWG height changes $\mathrm{\Delta }h$ around the model fixed point exhibit clear signs of critical slowing down in terms of rising variance and AC1 (Fig. 3). Comparing the variance and AC1 of the reconstructed height changes to corresponding expressions of the sensitivity of the ice sheet height to temperature ($d\mathrm{\Delta }{h}^{*}/dT$; see Materials and Methods) allowed us to quantitatively relate the statistical EWS to the underlying physical mechanisms. In the case at hand, the EWS observed in the different melt rates from CWG ice cores, and in the GrIS height time series inferred from them, behave exactly as theoretically expected from the MEF. This provides strong evidence that the MEF is indeed the mechanism responsible for the detected destabilization of the central-western GrIS. Given these findings, the critical temperature threshold should be reassessed with comprehensive, process-based ice sheet models coupled to high-resolution general circulation models.

In addition to the MEF, further positive feedbacks related to changing albedo (29) and outlet glacier thinning (5) are likely relevant for the future evolution of the GrIS. On the other hand, negative feedbacks related to increasing GrIS accumulation due to the higher water-holding capacity of a warmer atmosphere and changing atmospheric circulation patterns caused by reduced GrIS height (37) could at least partly compensate for the effects of the positive feedbacks. The competing effects of the positive and negative feedbacks could lead to the existence of alternative stable ice sheet states at intermediate levels, as has been found in model simulations of the buildup of the GrIS from lower elevations and under cooler conditions than today (38, 39). However, based on different coupled model simulations, it has been argued that the positive feedbacks, and, in particular, the MEF, will dominate and that the existence of intermediate stable GrIS states at current and warmer temperatures is unlikely (5, 16, 37, 38). In turn, rapid and substantial reductions of anthropogenic greenhouse gas emissions could potentially restabilize the GrIS at such intermediate (lower-elevation) stable states if the melting time scales are sufficiently slow for global mean temperatures to reach a turning point in due time. The time scales of melting once the temperature surpasses the critical value $T_{\text{c}}$ depend strongly on future ${\mathrm{C}\mathrm{O}}_2$ emissions and how much temperatures will rise beyond $T_{\text{c}}$ in the future (5, 16, 38). For the RCP8.5 scenario with constant temperatures from AD 2500 onward, the GrIS is projected to melt completely until AD 3000 (5). Moreover, the melt time scales depend strongly on the exact contributions by the different feedbacks mentioned above, and there is an urgent need to investigate the future development of the GrIS further.

Materials and Methods

Data and Code Availability.

We used summer sea-level temperatures from stations and melt intensities from ice cores in CWG and corresponding model simulations (18); the different time series can be retrieved from https://www.nature.com/articles/s41586-018-0752-4#Sec14. All Python code used for the analysis is available on GitHub (https://github.com/niklasboers/GrIS-EWS) (40).

Significance of Trends.

The significance of the linear trends of the evolution of the variance and AC1 shown in Fig. 1 D and E are estimated using a method based on phase surrogates to account for serial correlations in the underlying data. For this purpose, we compute Fourier transforms of the respective time series and compute 1 million surrogates by randomizing the phases $\varphi \in \left[\mathrm{0,2}\pi \right]$ uniformly in Fourier space. The resulting surrogate test statistic thus preserves both variance and power spectrum, and hence the autocorrelation structure. We derive $P$ values for the slopes measured in the observations by computing the fraction of surrogates with a slope greater or equal to the observed slope. We note that using the Mann–Kendall test, which is widely employed to test the significance of trends, does not account for serial correlations and would lead to an overestimation of statistical significance (20–22, 24, 41). According to the more conservative phase surrogate test, we obtain highly significant positive trends for the variance and AC1 of the runoff and the CWG and NU stack melt time series (see P values given in the legends of Fig. 1 D and E for precise values).

Ice Sheet Height Reconstruction.

From the CWG stack melt rates (18), we derive the temporal evolution of the height change $\mathrm{\Delta }h$ in CWG (in arbitrary units, since the values for the CWG stack melt rates $M\left(t\right)$ are given as z scores) via

$$\mathrm{\Delta }h\left(t\right)=-{\int }_0^t\left(M\left(s\right)-A\left(s\right)\right)ds.$$

Here $A\left(s\right)$ denotes ice accumulation due to precipitation, as a function of time $s$. In accordance with the precipitation–temperature feedback (42), we model the accumulation to be proportional to the linear increase in sea-level temperatures $T$, that is, $A\left(s\right)=cT\left(s\right)$. This approach is in agreement with the reconstructed, approximately linear increase of accumulation to temperature as reported in ref. 43). The proportionality constant $c$ is adjusted such that the height remains constant until around AD 1900, consistent with different reconstructions of GrIS height evolution (1, 18, 44). Our results are insensitive to the value of $c$ within bounds that lead to height reconstructions consistent with previously reported estimates of the GrIS height evolution (see sensitivity tests below and SI Appendix, Fig. S6). In particular, relative fluctuations around the fixed point of ice sheet height, which are used to estimate the variance and AC1 increases as a measure for critical slowing down, are not affected by this constant choice.

Model Calibration.

By representing the time evolution of CWG summer (June through August) temperatures (18) (blue curve in Fig. 1A) as a linear function of time in addition to a fluctuating part, that is, $T_{\text{total}}\left(t\right)=T\left(t\right)+T_{\text{fluct}}\left(t\right)$, we obtain a one-to-one relationship between time $t$ and the linear approximation of the temperature evolution $T$ (dashed blue line in Fig. 1A), which can be used to represent the reconstructed height change $\mathrm{\Delta }h$ as a function of $T$. The stable fixed point $\mathrm{\Delta }h*$ of the conceptual model, for which the right-hand side of Eq. 1 is equal to zero, can also be regarded as a function of $T$, and, by fitting the resulting $\mathrm{\Delta }h*\left(T\right)$ to the reconstructed $\mathrm{\Delta }h$, optimal values for the model parameters $\left(p_0,p_1,p_2,p_3\right)$ are obtained by fitting the fixed point curve (i.e., the sequence for fixed points for different values of temperature $T$) to the reconstructed height $\mathrm{\Delta }h$ using a standard Levenberg–Marquardt algorithm. For the choices $c=0.06\hspace{0.17em}{\text{K}}^{-1}$, $C=0.01$ K, and $\sigma =5$ for the standard deviation of the noise forcing $\eta$, we obtain $\left(p_0,p_1,p_2,p_3\right)=\left(1.927\times 10^{-16},1.015\times 10^{-2},9.558\times 10^{-8},6.919\right)$ and a coefficient of determination $R^2=0.94$.

EWS and Model Sensitivity.

For the model in Eq. 1, and, more generally, for models of the form

$$\frac{d\mathrm{\Delta }h}{dt}=F\left(\mathrm{\Delta }h\right)-aT+\eta \left(t\right),$$ [2]

there is a proportionality between the variance of the random fluctuations around a fixed point $\mathrm{\Delta }h*$ (according to the linear approximation) and the sensitivity of the fixed point $\mathrm{\Delta }h*$ to the control parameter $T$. The latter can be defined as the derivative of $\mathrm{\Delta }h*$ with respect to $T$. By definition of a fixed point, it holds that $\mathrm{\Delta }h*$ is a root of $F\left(\mathrm{\Delta }h\right)=aT$. Computing the derivative of both sides of this equation with respect to the control parameter $T$, and evaluating at the fixed point $\mathrm{\Delta }h*$, yields

$$F^{\prime }\left(\mathrm{\Delta }h*\right)\frac{d\mathrm{\Delta }h*}{dT}=a,$$

where $F^{\prime }$ denotes the derivative of the function $F$. We thus obtain, for the sensitivity,

$$\frac{d\mathrm{\Delta }h*}{dT}=\frac{a}{F^{\prime }\left(\mathrm{\Delta }h*\right)}.$$

The linear approximation of Eq. 2 around $\mathrm{\Delta }h*$ is

$$\frac{d\left(\mathrm{\Delta }h-\mathrm{\Delta }h*\right)}{dt}=-\theta \left(\mathrm{\Delta }h-\mathrm{\Delta }h*\right)+\eta \left(t\right),$$

and defines an Ornstein–Uhlenbeck (OU) process [the continuous-time version of an AR(1) process] with damping rate $\theta =-F^{\prime }\left(\mathrm{\Delta }h*\right)$. The variance of a discretized OU process with damping rate $\theta$ can be estimated as (45)

$$\text{var}\left(\mathrm{\Delta }h-\mathrm{\Delta }h*\right)=\frac{{\sigma }^2}{2\theta \mathrm{\Delta }t},$$

where ${\sigma }^2$ is the variance of the white-noise term $\eta \left(t\right)$ and $\mathrm{\Delta }t=1$ in our case. Since $\theta =-F^{\prime }\left(\mathrm{\Delta }h*\right)$, it follows that

$$\text{var}\left(\mathrm{\Delta }h-\mathrm{\Delta }h*\right)=-\frac{{\sigma }^2}{2a}\frac{d\mathrm{\Delta }h*}{dT}.$$

The dashed blue curve in Fig. 3C is obtained by computing the derivative $d\mathrm{\Delta }h*/dT$ from Eq. 1 with the fitted parameter values. By definition of stability of a fixed point, the damping rate $\theta$ changes sign at the critical temperature $T_{\text{c}}$, and, consequently, the sensitivity $d\mathrm{\Delta }h*/dT$ and the variance of the fluctuations in the linear approximation have a vertical asymptote at $T_{\text{c}}$.

Correspondingly, the AC1 of a time-discrete sample of an OU process is given by $\alpha \left(1\right)=\exp \left(-\theta \mathrm{\Delta }t\right)$ (45), leading, along the lines of the above, to the expression

$$\alpha \left(1\right)=\exp \left(\frac{a}{\frac{d\mathrm{\Delta }h*}{dT}}\right),$$

which is confirmed by our results shown in Fig. 3D.

Sensitivity of Results.

The results shown in Fig. 1 remain very similar when varying the bandwidth used for detrending and varying the size of the sliding windows used to estimate the variance and AC1 (SI Appendix, Fig. S1). For the results shown in Figs. 2 and 3, we used, for the proportionality constant between temperature and accumulation, a value of $c=0.06$, which assures that the GrIS height reduction initiates around AD 1900. Varying the parameter $c$ between bounds so that the height decrease still initiates close to AD 1900, in accordance with independent reconstructions of the GrIS height evolution, does not affect our results (SI Appendix, Fig. S6). Changing our choice for the proportionality constant $c$ between broader bounds would lead to the height reduction initiating substantially too early or too late, compared to the observations (1, 18, 34, 44). Note that the changes in the position of the unstable fixed point (blue dashed curve in SI Appendix, Fig. S6) are not relevant for the dynamics studied here.