Encapsulation of ribozymes inside model protocells leads to faster evolutionary adaptation

Significance

Organization into cells is believed to have been crucial for the emergence of life, as the cell membrane would prevent loss of biochemical contents and define an evolutionary entity. RNA is a candidate primordial biomolecule, as it can encode and transmit information and also fold into catalytically active structures. Biomolecules are known to behave differently inside cells compared to bulk solution due to differences in the biophysical environment. However, the consequences of encapsulation on early evolution are unknown. We found that, in a lipid-rich environment, ribozyme encapsulation would promote greater activity and faster adaptation. Better RNA catalysts experience greater gains in a “rich-get-richer” phenomenon. Rather than acting as passive containers, protocells would provide functional and evolutionary benefits to encapsulated contents.

Abstract

Functional biomolecules, such as RNA, encapsulated inside a protocellular membrane are believed to have comprised a very early, critical stage in the evolution of life, since membrane vesicles allow selective permeability and create a unit of selection enabling cooperative phenotypes. The biophysical environment inside a protocell would differ fundamentally from bulk solution due to the microscopic confinement. However, the effect of the encapsulated environment on ribozyme evolution has not been previously studied experimentally. Here, we examine the effect of encapsulation inside model protocells on the self-aminoacylation activity of tens of thousands of RNA sequences using a high-throughput sequencing assay. We find that encapsulation of these ribozymes generally increases their activity, giving encapsulated sequences an advantage over nonencapsulated sequences in an amphiphile-rich environment. In addition, highly active ribozymes benefit disproportionately more from encapsulation. The asymmetry in fitness gain broadens the distribution of fitness in the system. Consistent with Fisher’s fundamental theorem of natural selection, encapsulation therefore leads to faster adaptation when the RNAs are encapsulated inside a protocell during in vitro selection. Thus, protocells would not only provide a compartmentalization function but also promote activity and evolutionary adaptation during the origin of life.

RNA is believed to have been a central constituent of early life (1–3). In the “RNA world” theory, functional RNAs (e.g., ribozymes) would both perform catalytic functions and store and transfer genetic information in a simple living system (4–6). Encapsulation of ribozymes in cell-like compartments, such as protocells, is thought to be an essential feature for the emergence of early life (7–11). In particular, compartmentalization would retain useful metabolites in the vicinity (12) and prevent a cooperative, self-replicating ribozyme system from collapsing under parasitization by selfish RNAs (13, 14). A major model of protocells is lipid vesicles, which consist of an aqueous interior surrounded by a semipermeable membrane (15, 16). However, while the ultimate advantages of compartmentalization may be clear, how encapsulation and confinement inside protocell vesicles would affect the activity and early evolution of ribozymes is not understood well.

Confinement by lipid membranes presents a biophysical environment similar to macromolecular crowding (17). The effect of macromolecular crowding on the activity, function, and specificity of biomolecules (i.e., proteins and nucleic acids) has been examined extensively (18–23) using crowding agents such as dextran, polyethylene glycol, and Ficoll in vitro (24–29). In general, macromolecular crowding agents decrease the accessible volume for biomolecules, leading to the excluded-volume effect, in which the relative stability of compacted and folded structures is increased (30, 31). At the same time, chemical interactions between the crowding agents and the biomolecule can also stabilize or destabilize the folded structure, influencing catalytic activity (24, 32). While chemical interactions depend on the properties of the specific molecules under study, the excluded-volume effect resulting from spatial confinement inside vesicles is expected to be general. The effect of confinement can be studied while controlling for chemical interactions by comparing the encapsulated condition to the nonencapsulated but membrane-exposed condition. This comparison represents the prebiotic scenario in which RNAs would be present in the same milieu as lipids (33) and may become encapsulated or not. In this way, confinement inside vesicles was shown to increase the binding affinity of the malachite green RNA aptamer (34). Interestingly, spatial confinement inside a tetrahedral DNA framework has also been shown to increase thermodynamic stability and binding affinity of aptamers by facilitating folding (35).

While these and other case studies (17, 25, 36–43) illustrate mechanisms by which RNA activity might be perturbed inside vesicles, understanding how encapsulation would affect evolution requires a broader scale of information. In particular, detailed knowledge of how encapsulation affects the sequence-activity relationship is required. This information is captured in the “fitness landscape,” or the function of fitness over sequence space, which embodies many important evolutionary features [e.g., fitness maxima, epistasis, and the viability of evolutionary trajectories (44–47)]. In practice, the fitness of a ribozyme can be considered to be its chemical activity for a particular function in the given environment (48–53).

In the present work, we investigated how encapsulation inside model protocells would affect the catalytic activity and evolution of self-aminoacylating ribozymes. We studied tens of thousands of RNA sequences derived from five previously selected self-aminoacylating ribozyme families (53). These sequences were encapsulated in a mixed fatty acid/phospholipid vesicle system. Fatty acids mixed with phospholipids (1:1 molar ratio) have been used as model protocell membranes, as the vesicles tolerate Mg²⁺ concentrations needed for ribozyme activity and the membrane allows small, charged molecules to permeate while preserving large polynucleotides in the vesicle interior (54, 55). To study the biophysical effect of confinement rather than chemical interactions with the membrane, RNA activity inside vesicles was compared with RNA activity when exposed to the same vesicles without encapsulation. We show that ribozymes generally exhibit higher catalytic activity inside the vesicles and that more active sequences experience greater benefit. Using in vitro selection, we demonstrate that one of the evolutionary consequences of this trend is that encapsulation inside vesicles causes a greater rate of genotypic change due to natural selection.

Results

Encapsulation of Self-Aminoacylating Ribozymes in Model Protocells.

We examined whether the model protocells would be compatible with the self-aminoacylating ribozyme reaction in terms of substrate permeability and vesicle stability. Ribozyme S-1A.1-a, previously identified from in vitro selection (53), was synthesized and used as a model ribozyme for the following tests. To test the ability of the substrate, biotinyl-Tyr(Me)-oxazolone (BYO), to permeate the membrane, S-1A.1-a was encapsulated in vesicles composed of oleic acid (OA)/1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) in a 1:1 mixture and then incubated with different concentrations of BYO added externally. Formation of the encapsulated product, aminoacyl-RNA (i.e., aa-RNA), was monitored by a gel shift assay in the presence of streptavidin, which binds to the biotinylated product (Fig. 1A and SI Appendix, Fig. S1A). The yield of aa-RNA increased with increasing BYO concentration, suggesting that the model protocells exhibit the required permeability to allow entry of BYO while retaining RNAs inside the vesicle. The stability of the vesicles in the reaction was examined by monitoring the size distribution. Dynamic light scattering (SI Appendix, Fig. S1B) showed that the vesicles were stable under the tested conditions. The size distribution of vesicles was consistently centered at ∼100 nm in various conditions, and the distribution was significantly left shifted when the vesicles were disrupted by the addition of excess Triton X-100 detergent (SI Appendix, Fig. S1B). Vesicles with encapsulated RNA presented a more-polydisperse population, likely resulting from the centrifugation used to concentrate the vesicles after purification. To check for leakage of RNA from the vesicles after centrifugation, the RNA concentration of the buffer was measured using a Qubit 3.0 fluorometer. The RNA concentration was lower than the detection limit (i.e., <250 pg/μL), indicating no significant leakage of RNA. Overall, the results verified that the blended OA/POPC (1:1) vesicle system could provide the required stability and permeability for ribozyme activity under encapsulation.

Fig. 1.

Experimental scheme and verification of activity for self-aminoacylating ribozymes in the OA/POPC (1:1) vesicle system. (A) Experimental design of the RNA libraries. The synthetic DNA templates are composed of the T7 transcription promoter sequence, 5′-TAA​TAC​GAC​TCA​CTA​TA-3′ (red) and a 21-nt variable region (blue) flanked by constant regions (black). For the doped pool DNA library of each ribozyme family, partial randomness is introduced at the 21-nt variable region during DNA synthesis. Self-aminoacylation of RNA was carried out by incubating the RNA pool with BYO. The aa-RNA carries a biotin tag for downstream purification and assays. (B) The activity of wild-type ribozyme S2a was determined in the InV (blue) and OutV (red) conditions using RT-qPCR. The fraction of aa-RNA increases as [BYO] increases, consistent with permeability of the vesicles to the BYO substrate and retention of RNA in the vesicles. Ribozyme rates were obtained by fitting to a pseudo-first-order rate equation. (C) Schematic workflow of the k-Seq assay, inside vesicles (InV) and outside vesicles (OutV). The reacted ribozymes are represented by stars (f = fraction reacted). For the InV condition, ribozymes were encapsulated in OA/POPC vesicles and reacted with BYO substrate, which permeated the membrane to react with the encapsulated ribozyme. For the OutV condition, ribozymes were incubated with BYO substrate in a solution containing empty OA/POPC vesicles (85 mM; SI Appendix, Fig. S1C).

Kinetic Sequencing Activity Assay of Ribozyme Libraries: Encapsulated versus Nonencapsulated.

DNA libraries based on five ribozyme sequences (“doped” libraries), which comprise three previously identified catalytic motifs (53), were synthesized (Fig. 1A). In this study, two Motif 1 sequences (S-1A.1-a and S-1B.1-a), two Motif 2 sequences (S-2.1-a and S-2.2-a), and one Motif 3 sequence (S-3.1-a) were used as the bases of the libraries (sequences abbreviated here as S1a, S1b, S2a, S2b, and S3, respectively; sequences given in Materials and Methods). Each synthesized DNA sequence contained a T7 promoter sequence as well as a central variable region of 21 nt flanked by two constant regions. The doped DNA libraries contained random variation at a level of 9% at each site in the central region (i.e., 91% frequency of the wild-type nucleotide and 3% frequency of each of the other three nucleotides); thus, the DNA pool was composed of five families of sequences, with each family centered on one of five known ribozyme sequences (“wild types”). Notably, the Hamming distance between any two wild-type ribozymes was >12, so there was no practical ambiguity in the assignment of a sequence to its ribozyme family. The libraries were transcribed and purified to produce RNA and either encapsulated inside OA/POPC vesicles (i.e., InV condition) or merely exposed to vesicles without encapsulation (i.e., OutV condition) (Fig. 1C).

To measure the activity of the ribozymes, we performed kinetic sequencing (k-Seq), a massively parallel assay for measuring the activity of many different ribozyme sequences in a mixed pool (Fig. 1C). For all analyzable sequences s, the reaction rate constant (k_s) and the maximum reaction amplitude (A_s) were estimated from fitting to a pseudo-first-order kinetic equation (53). For low-activity sequences (k_s < ∼0.5 min⁻¹ ⋅ M⁻¹), k_s and A_s could not be accurately estimated individually with the substrate concentration range used because the activity curve did not plateau at high substrate concentrations, but the product k_sA_s could be robustly estimated due to the inverse correlation between k_s and A_s during curve fitting (56). Therefore, the product k_sA_s, corresponding to a possible prebiotic scenario of relatively low substrate concentration, was used to represent the activity of each ribozyme for all analyzable sequences.

The high-throughput sequencing (HTS) results yielded 1,399,829 and 1,073,520 sequence reads for the encapsulated and nonencapsulated conditions, respectively. Sequences in both conditions having very low count (i.e., an average of <10 reads per sample) were removed from the analysis due to the large measurement noise associated with small numbers (56). Hence, 81,065 (i.e., 81,060 mutants plus 5 wild-type sequences) and 59,665 (i.e., 59,660 mutants plus 5 wild-type sequences) unique sequences in the encapsulated and nonencapsulated conditions, respectively, were considered to be analyzable by the aforementioned fitting process. The set of analyzable sequences included all single, all double, and some triple mutants of the five ribozyme family centers (SI Appendix, Table S1). For the following analysis, we focus on the 50,205 (i.e., 50,200 mutants plus 5 wild-type sequences) sequences that were analyzed in both encapsulated and nonencapsulated conditions.

Ribozymes Generally Exhibit Higher Activity when Encapsulated Compared to Nonencapsulated.

A comparison of the activity distributions of the 50,205 sequences showed a rightward shift for the encapsulated RNAs compared to the nonencapsulated RNAs, indicating generally greater activity inside vesicles (Fig. 2A, Inset). This shift was more pronounced when examining the subset of sequences having average counts >100 in the HTS sample (6,711 ribozymes; Fig. 2A), which represents ribozymes with greater activity and less measurement noise. The change in distribution shape, namely a rightward skew, suggested that encapsulation was particularly favorable for ribozymes having higher activity. The activity of ribozyme S2a was measured in the encapsulated condition (InV) and nonencapsulated condition (OutV) using RT-qPCR to quantify the reaction products (Fig. 1B). Higher activity was observed in the InV condition (kA = 43 ± 12 min⁻¹ ⋅ M⁻¹) than in the OutV condition (kA = 16 ± 4 min⁻¹ ⋅ M⁻¹), supporting the general trend.

Fig. 2.

Catalytic activities of five self-aminoacylating ribozyme families when encapsulated (InV) versus nonencapsulated (OutV), measured by the k-Seq assay. (A) A rightward shift in the distribution of catalytic activity, log₁₀(k_sA_s), is observed when RNAs are InV (red) compared to OutV (black). The data are shown for sequences have >100 counts per HTS sample on average, as well as for all analyzable sequences (Inset). (B) Comparison of the encapsulation effect among different ribozyme families. The activity values [log₁₀(k_sA_s)] of each RNA sequence when InV versus OutV indicate that all families exhibit higher activity when encapsulated, as seen by the predominance of points above the line of identity (dotted black line). S2a (blue), S2b (cyan), and S3 (green) families show a greater effect than S1a (red) and S1b (yellow). The correlation coefficients for linear regression (using all analyzable sequences) are as follows: r² = 0.9546, 0.9401, 0.7558, 0.5705, and 0.8593) for families S1a, S1b, S2a, S2b, and S3, respectively. The sequences with >100 average counts are shown, with all analyzable sequences shown in the inset. The ribozyme families are plotted separately in SI Appendix, Fig. S2.

To determine whether the trend of greater activity inside vesicles was similar across different ribozyme families, the sequences were classified into the five different families if the sequences were within a Hamming distance of ≤3 from the family wild types (S1a, S1b, S2a, S2b, and S3). The trend toward higher activity inside vesicles can be seen for all families (Fig. 2B and SI Appendix, Fig. S2), although ribozymes of the S1a and S1b families showed a less-pronounced effect compared to the S2a, S2b, and S3 families (SI Appendix, Fig. S2 and Text S1). Thus, Motif 1 ribozymes appeared to be less sensitive to the encapsulation effect compared to Motifs 2 and 3.

One may ask whether the general enhancement of activity could be due to a change in the reaction mechanism when encapsulated. If this were the case, one would expect that the pattern of mutational effects (i.e., how deleterious or beneficial each mutation is) would differ between the encapsulated versus nonencapsulated environments. We compared how each possible single mutant of the five ribozyme families (i.e., 63 mutants per family) affected k_sA_s for the encapsulated (Fig. 3A) versus nonencapsulated (Fig. 3B) conditions. All single mutations, regardless of the ribozyme family or the studied condition, were either neutral or deleterious to catalytic activity compared to the wild-type sequence of the family. For all families, mutations near the middle of the sequence tended to severely reduce activity. The patterns of mutational effects were qualitatively similar between the two conditions for all ribozyme families. These results, combined with the high correlation observed between activities when encapsulated versus nonencapsulated (Fig. 2B), suggested that no major change to the reaction mechanism was caused by encapsulation.

Fig. 3.

The pattern of mutational effects on ribozyme activity (k_sA_s) for single mutants is similar for the encapsulated (A) and nonencapsulated (B) conditions. The sequence of the central 21-nt region for the wild-type family center is displayed on the x-axis. The ratio of average activity of three single mutants ($k{A}_{mutants}^{avg}$) and wild-type ribozyme (kA_WT) is indicated by the heat map along the RNA sequence, with cyan and magenta representing deleterious and neutral substitutions, respectively. Each dot shows the activity of a single-point mutant at the given position in the variable region, with dot color illustrating the nucleotide identity at the position (A: red, U: blue, C: green, and G: orange). The activity of the wild type is shown by the black dashed line. The error bars correspond to the 95% CI of the activity measurement from bootstrap analysis of k-Seq data. The activity ratio between the encapsulated and nonencapsulated conditions for each single mutant is shown in SI Appendix, Fig. S3. (C) k-Seqlogo representation illustrating the importance of each nucleotide in the central 21-nt region for the catalytic activity of five ribozyme families. The information content at each position is shown for the InV (open circles) and the OutV (solid line). The stacked letters in the figure are given for the encapsulated condition. It can be seen that higher information content corresponds to greater mutational effects (A and B), and greater information is seen with encapsulation for some families (S2a, S2b, and S3).

Mutations Generally Have Stronger Effects when Ribozymes Are Encapsulated.

To quantify the mutational effects and how encapsulation affected them, we assessed each mutation within the central 21-nt region of five ribozyme families in both encapsulated and nonencapsulated conditions. A multilinear regression model was fit to the activities of ribozymes in the same family, incorporating k-Seq data of single and double mutants (SI Appendix, Fig. S4). This model makes the simplifying assumption that the activity of a given sequence is a linear combination of the wild-type activity and the effect of each mutation that is present (63 possible substitutions for a 21-nt region, disregarding genetic background). The coefficient ${\beta }_{i,j}$ represents the mutational effect of nucleotide i (i = A, T, C, and G) at locus j. Hence, for each ribozyme family, 63 ${\beta }_{i,j}$ parameters are obtained from fitting to this model for each condition (encapsulated and nonencapsulated). All fitted ${\beta }_{i,j}$ values were negative or indistinguishable from zero in both conditions (Fig. 4), indicating deleterious or neutral effects from the mutations, consistent with the observations of single mutants (Fig. 3 A and B). The ${\beta }_{i,j}$ values of S1a and S1b families aligned well to the identity line, supporting the suggestion above that Motif 1 is relatively insensitive to encapsulation (Fig. 4A). However, for S2a, S2b, and S3 families, the ${\beta }_{i,j}$ values are more negative in the encapsulated condition, indicating that mutations are more deleterious to catalytic activity when the RNAs are encapsulated compared to nonencapsulated (Fig. 4 B and C and SI Appendix, Fig. S5). For these families, encapsulation inside vesicles would present a more-stringent selection environment among mutants despite the generally higher level of activity compared to the nonencapsulated environment.

Fig. 4.

The mutational effect coefficients in the encapsulated (${\beta }_{InV}$, y-axis) and nonencapsulated (${\beta }_{OutV}$, x-axis) conditions, obtained from fitting k-Seq data to the multilinear regression model, shown for (A) Motif 1 families (S1a [red] and S1b [yellow]), (B) Motif 2 families (S2a [blue] and S2b [cyan]), and (C) the Motif 3 family (S3 [green]). The dotted black line indicates the identity line. The error bars show the 95% CI for the coefficient.

To visualize the information content of the ribozyme sequences with respect to activity, we constructed a modified “sequence logo” representation of each ribozyme family based on the mutational effects β. We term this a “k-Seqlogo” representation, in analogy to Seqlogo, which is calculated based on a position weight matrix. Like Seqlogo, a k-Seqlogo shows the relative frequency of each nucleotide at each position and an information content (measured in bits) of each position, which is summed from the information content of the four nucleotides at each position. However, in k-Seqlogo, information content corresponds to the importance of the nucleotide for activity (rather than conservation) in the given ribozyme family. Greater information content indicates less tolerance to mutations with respect to activity. As shown in Fig. 3C, the tallest letter at each position corresponded to the nucleotide of the wild type at the position, as expected since the wild type is the highest-activity sequence of the family.

Encapsulation increased the information content of the ribozymes of Motifs 2 and 3, as seen by comparison of the k-Seqlogos for encapsulated versus nonencapsulated conditions (Fig. 3C). However, for families of Motif 1, encapsulation did not appear to affect information content, consistent with the observation that encapsulation had little effect on mutational effects β for Motif 1. Combined with the overall effect of encapsulation increasing the magnitude of β-values (Fig. 4), this analysis confirms that for Motifs 2 and 3, encapsulation would create greater activity differences among sequences. These observations lead to the prediction, according to Fisher's fundamental theorem of natural selection (57–59), that encapsulation should increase the rate of natural selection.

The Encapsulated Environment Leads to Greater Evolutionary Rate among Ribozyme Sequences.

During in vitro selection, sequence diversity is initially very high due to the large number of sequences present in a complex pool, and selective pressures decrease the diversity as functional sequences emerge. A similar situation can be presumed to hold under prebiotic conditions, in which the chemical repertoire might initially contain a large diversity of sequences. The greater mutational effects seen in the encapsulated environment should correspond to greater fitness differences, which should accelerate evolution (i.e., faster change in relative genotype frequencies). During an in vitro selection experiment, this should be observable as a faster reduction of sequence diversity.

To test this prediction, we conducted in vitro selection of RNA from random sequence pools for both conditions (selection of RNA inside vesicles versus selection of RNA exposed to vesicles but nonencapsulated). For both conditions, the selection experiments were performed by incubating the RNA pools with the same concentration of BYO (i.e., 50 μM) for the same reaction time (90 min) throughout the entire selection process (four and five rounds of selection for the encapsulated and the nonencapsulated conditions, respectively). To assess diversity, sequences within a Hamming distance of three from the wild-type family centers were categorized into each of the five ribozyme families. S1b and S2b families were excluded from the diversity analysis since only the wild types from these families were observed after selection. Intrafamily diversity was roughly assessed by the fraction of mutant sequences (i.e., f_m =1 − f_wt, where f_wt is the fraction of wild type in the family). The mutant fractions of all families from the encapsulated selection were lower than those in the nonencapsulated selection, suggesting that the encapsulated environment resulted in reduced diversity (SI Appendix, Table S2). The reductions in mutant fraction in encapsulated compared to nonencapsulated conditions were larger for S2a and S3 than S1a, consistent with the overall finding that ribozymes of Motifs 2 and 3 were more sensitive to the encapsulation environment compared to Motif 1.

The rate of evolution broadly corresponds to the rate at which advantageous traits become fixed in the population. This rate can be measured either by phenotypic change or genotypic change. For in vitro evolution, the phenotypic activity of the entire pool as it progresses through the selection can be estimated by the extent of product formation, measured from the number of PCR cycles needed to amplify the recovered RNA (60–62) (SI Appendix, Fig. S6). These measurements showed that pool activity increased more quickly in the encapsulated selection. In addition, the rate of genotypic change could be assessed by the rate at which the pool converged to a small number of ribozymes, as determined from the HTS data. In both selections, the pool largely converged to S1a and S2a. These ribozymes became dominant (comprising >50% of the pool) earlier when encapsulated (Round 3) than in the nonencapsulated selection (Round 4), confirming that the rate of genotypic change was faster when the RNAs were encapsulated (SI Appendix, Fig. S7).

We further quantified the overall rate of evolutionary convergence for the encapsulated and nonencapsulated conditions by monitoring the Gini-Simpson index of diversity (D_s) at different rounds of selection (Fig. 5). The D_s value is equal to the probability that two randomly selected sequences are different. The Gini–Simpson index (D_s), which varies from 0 to 1, is calculated as $D_s=1-{\displaystyle \sum }_i{p}_i^2$, where $p_i$ represents the proportional abundance of sequence i in the sequencing results. This index is relatively robust to sample size and sequencing depth as it gives more weight to dominant sequences; hence, it is less affected by sequences with very low reads in the HTS results. In both conditions, D_s dropped substantially at the later selection rounds, as expected due to in vitro selection. Notably, D_s began to drop precipitously after Round 2 during the encapsulated selection, but a similar drop was observed later, at Round 4, for the nonencapsulated selection. The earlier drop in diversity index in the encapsulated condition indicated faster convergence and thus higher evolutionary rate in the encapsulated environment.

Fig. 5.

Sequence diversity over selection rounds, quantified by the Gini–Simpson index (D_s) during two different selections: encapsulated RNA (open circles) and nonencapsulated RNA (crosses).

Encapsulation Leads to Increased Epistatic Interactions and Greater Ruggedness of the Local Fitness Landscape.

While the linear regression model described above neglected interactions between mutations, or epistasis, these are important characteristics of the fitness landscape. Greater epistasis reflects greater ruggedness on the fitness landscape and thus a greater possibility of a ribozyme being “trapped” in a local, rather than global, fitness optimum during natural selection. To understand how encapsulation impacts the local evolutionary landscape of each ribozyme family, we measured epistasis as the difference between the observed fitness of a combination of mutations and the fitness expected from simple addition of the effects of the individual mutations. Pairwise epistasis (ε) was calculated for the studied ribozyme families in the encapsulated and nonencapsulated conditions. Overall, about 70% of combinations were characterized by the double mutant exhibiting a different magnitude of effect compared to the additive expectation but in the same direction (i.e., magnitude epistasis, in which the combination of two deleterious mutations still produces a deleterious double-mutant phenotype) (SI Appendix, Figs. S8 and S9). In the remaining 30% of combinations, the double mutant exhibited a fitness effect in the opposite direction from one single mutant (sign epistasis, 25%) or both single mutants (reciprocal sign epistasis, 5%). Sign epistasis essentially blocks an evolutionary pathway through one mutant by creating a low-fitness intermediate, and reciprocal sign epistasis blocks both pathways for evolution, preventing evolutionary access of the wild type from the double mutant through single mutations. Comparison of epistasis categorization in the encapsulated and nonencapsulated conditions showed no substantial difference in the distribution of epistasis among the three categories of interactions (SI Appendix, Figs. S8 and S9).

Considering epistasis quantitatively, the majority of combinations show positive epistasis (ε > 0) in both encapsulated and nonencapsulated conditions, indicating that the activity of the double mutant is higher than expected from adding effects of the two single mutations. These interactions often result from combinations of single mutations that substantially reduce catalytic activity, so an additional deleterious mutation seems to have relatively little effect on the already substantially reduced activity (i.e., a saturation effect) (51, 63). To understand the quantitative effect of encapsulation, we compared epistasis values for the encapsulated (${\epsilon }_{InV}$) and the nonencapsulated (${\epsilon }_{OutV}$) conditions (Fig. 6A). In general, ${\epsilon }_{InV}$ and ${\epsilon }_{OutV}$ are well correlated. However, deviations from the identity line become clear at the higher end, with greater epistasis in the encapsulated condition compared to the nonencapsulated condition (Fig. 6B and SI Appendix, Table S3).

Fig. 6.

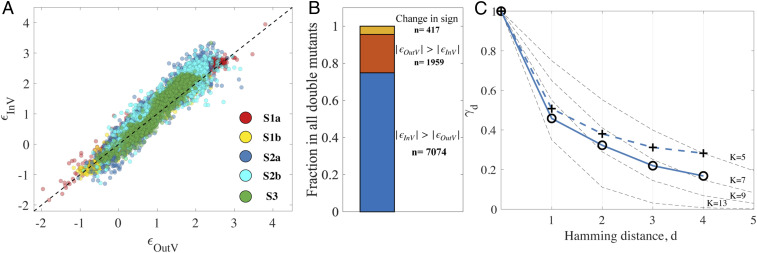
Effect of encapsulation on epistasis and ruggedness of the fitness landscape. (A) ε in the encapsulated (y-axis, ε_InV) versus the nonencapsulated (x-axis, ε_OutV) condition for all double mutants in the central 21-nt region (i.e., 1,890 double mutants), for each of the five ribozyme families as indicated by color. The families are plotted separately in SI Appendix, Fig. S11. The dotted black line indicates the identity line. High correlations are observed, but ε_InV magnitudes tend to be higher than ε_OutV magnitudes (SI Appendix, Table S3). (B) Bar chart showing the total fraction of double mutants exhibiting |ε_InV| > |ε_OutV| (blue) or |ε_OutV| > |ε_InV| (red) when ε_OutV and ε_InV have the same sign, and the fraction for which ε_OutV and ε_InV have opposite sign (yellow). The total number of sequences (n) within each group is indicated. The predominance of |ε_InV| > |ε_OutV| indicates greater epistasis when encapsulated. (C) Ruggedness (epistatic correlation γ_d) of the fitness landscape as a function of hamming distance d for family S2a, illustrating lower correlation in the encapsulated (open circles) versus nonencapsulated (crosses) condition. The gray dashed lines depict the theoretical γ_d dependence for the NK model landscape with N = 21 and K as labeled in the plot.

To understand the landscape beyond double mutants of the central sequence, we also quantified landscape ruggedness by calculating the so-called epistatic correlation, the average correlation of activity effects of single mutations between sequences at Hamming distance d of each other (γ_d, Materials and Methods). Higher γ_d indicates a smoother fitness landscape, while low γ_d indicates a less-correlated, more-rugged landscape. As expected, γ_d gradually decreased as d increased, illustrating that the activities of more-distant sequences are less correlated for all studied ribozyme families in both conditions (Fig. 6C and SI Appendix, Fig. S10). For all ribozyme families, the γ_d values are smaller in the encapsulated condition than the nonencapsulated condition, indicating a less-correlated, more-rugged landscape for the ribozyme fitness peak when encapsulated (Fig. 6C and SI Appendix, Fig. S10).

The decay curves can be matched to a model fitness landscape in order to gain an intuitive appreciation for the degree of ruggedness. The observed pattern of γ_d resembles that seen in the NK model, a well-known theoretical model for a fitness landscape with tunable ruggedness (47, 64, 65). In this model, K is the number of sites that interact with one another and N is the total number of sites. A visual match of decay curves with varying K (N = 21) suggests that the effect of encapsulation is analogous to the increase in ruggedness caused by increasing K by ∼1 to 2 (Fig. 6C and SI Appendix, Fig. S10).

Discussion

The encapsulation of ribozymes inside vesicles is an important scenario in prebiotic evolution (10–12, 66, 67). Prior studies on isolated RNA sequences have pointed toward the possibility that encapsulation and related biophysical effects could increase ribozyme and aptamer activity (34, 35, 68), but the generality of these findings has been unclear. In addition, while compartmentalization is known to be important for the evolution of cooperative phenotypes (69–71), the evolutionary consequences of RNA encapsulation on noncooperative phenotypes have been largely unstudied, despite being the subject of speculations (13, 72–74). Here, we present a systematic study of the effect of encapsulation for five different ribozyme families, previously derived from an exhaustive search of sequence space for self-aminoacylating RNAs, representing three distinct ribozyme motifs and including tens of thousands of different mutant sequences. This chemical activity, which links amino acids to RNAs, could be critical precursor to the development of a genetic code in an RNA world. Evolutionary consequences of encapsulation for these ribozymes were further probed experimentally by in vitro selection in a side-by-side comparison of encapsulated and nonencapsulated ribozymes reacted in an amphiphile-rich environment.

The model protocells consisted of fatty acids, which are prebiotically plausible (66, 75, 76), and phospholipids, which are not usually considered to be prebiotic molecules. However, this composition has been used as a model system due to its tolerance of Mg²⁺ conditions necessary for ribozyme activity, and the experimental comparison between encapsulated and nonencapsulated (but vesicle-exposed) RNA allowed a control for potential chemical interactions with the membrane. In addition, prior work on an RNA aptamer found that encapsulation in fatty acid vesicles and POPC vesicles gave similar effects on RNA activity (34). Exploration of different vesicle compositions mimicking protocells, such as cyclic phospholipids (77), might be an avenue of future interest.

Encapsulation was found to be generally beneficial to ribozyme activity. Ribozyme activity is governed by inherent structural dynamics as well as the interchange among active and inactive conformers (78–82). Studies of biophysical confinement effects on RNA structure indicate that the conformational equilibrium shifts toward relatively compacted structures in a confined environment (e.g., crowded by macromolecules or encapsulated) due to a greater reduction in configurational entropy for the unfolded state relative to the folded state (the excluded-volume effect) (36, 37, 39). Assuming that the actively folded conformers are relatively compact, the excluded-volume effect would increase activity (39). At the same time, other mechanisms may affect the enthalpy of reaction, such as the chemical interaction between the membrane surface or crowding agent and the RNA (32, 83–89). For instance, the activity of template-directed RNA polymerization in coacervates was affected by the identity of polycations in the system, likely due to extensive electrostatic interactions with the RNAs (90). A hammerhead ribozyme exhibits a modestly reduced self-cleavage rate when encapsulated in fatty acid vesicles compared to bulk solution environment (91), and the effect of crowding agents on the malachite green aptamer depends greatly on the identity of the agent (34). These examples illustrate the potential importance of chemical interactions between the RNA and other structures. Indeed, the activities of the self-aminoacylating RNAs in this study, whether encapsulated or merely exposed to vesicles, were generally lower than the activities measured in solution lacking vesicles entirely (53). Such effects were controlled in the present study, since ribozymes were exposed to the membrane surface under both conditions, with the difference being only whether the RNA was inside or outside of the vesicles (SI Appendix, Text S2). This comparison mimics the prebiotic scenario of a lipid-containing milieu, with some RNAs being encapsulated (e.g., by chance) and others not. The experiments here probed an amphiphile-rich environment, being above the critical aggregation concentration and in a plateau regime in which the activity drop experienced by nonencapsulated ribozymes appears to be saturated (SI Appendix, Fig. S1C). Although not specifically tested at other amphiphile concentrations, the conclusions can be expected to hold quantitatively in this plateau regime (e.g., >10 mM OA/POPC) and may hold qualitatively for lower concentrations. In particular, as discussed below, the encapsulated selection exhibited faster adaptation both when compared to an environment lacking amphiphiles (53) as well as when compared to an environment rich in amphiphiles (as determined in the present work).

While encapsulation resulted in generally increased activities, higher-activity ribozymes benefitted more from encapsulation compared to less-active ribozymes. This asymmetry has interesting evolutionary consequences. First, the variance of fitness among genotypes would be greater for encapsulated ribozymes compared to nonencapsulated ribozymes. According to Fisher's fundamental theorem of natural selection, the rate at which the average fitness of the population increases during selection is proportional to the variance of fitness (57–59, 92). This implies that encapsulation, by conferring greater variance of fitness to the RNA population, would lead to more-rapid evolutionary adaptation. Indeed, we verified that evolutionary convergence to the most-active sequences occurred more quickly when the RNAs were encapsulated during in vitro selection compared to the nonencapsulated environment (Fig. 5). In particular, the encapsulated selection proceeded one to two rounds faster than the nonencapsulated selection. The encapsulated selection also proceeded two to three rounds faster than an otherwise identical selection performed in bulk solution without amphiphiles (53). Since this ribozyme selection requires a total of only three to six rounds to reach a high level of convergence, the differences indicate a substantial acceleration of adaptation.

Second, the amplification of fitness differences also effectively decreases the correlation of fitness among related genotypes. For all ribozyme families, most single mutants exhibited low activity (Fig. 3 A and B), suggesting that the selected ribozymes are generally fragile to mutations. Indeed, the mutational robustness of naturally occurring RNAs appears to be higher than that of artificially selected functional RNAs, probably due to the relatively controlled environment of in vitro selections (93–95). Since encapsulation did not affect these low-activity mutants very much, the enhancement of high-activity mutants effectively reduced the fitness correlation and increased epistasis values. These effects may be understood as quantitatively increasing the ruggedness of the local fitness landscape. However, encapsulation did not substantially alter the amount of reciprocal sign epistasis. Thus, while fitness clines might be steeper, encapsulation would not change the number of local fitness maxima that serve as evolutionary “traps” during natural selection.

Taken together, these results indicate that encapsulation sharpens the divide among sequences, resulting in greater selection pressure inside the vesicle and accelerated evolution. Although our experiments did not directly probe the mutation–selection balance, stronger selection would presumably lead to reduced diversity at steady state under the encapsulated condition. By raising the stringency of selection, confinement inside vesicles could hasten the selection of active ribozymes inside protocells. In concert with biophysical mechanisms causing positive feedback between vesicles and encapsulated replicators (96–99), such a phenomenon may contribute to a Matthew effect (100), accelerating evolution of an active RNA world.

Materials and Methods

Materials.

Unless otherwise specified, all chemicals used in this study were from Sigma-Aldrich. POPC was obtained from Avanti Polar Lipids. OA (C18:1 cis-9) was obtained from Nu-Chek Prep. All DNA libraries were chemically synthesized and polyacrylamide gel electrophoresis (PAGE)-purified by Integrated DNA Technologies. BYO was synthesized as previously described (53).

OA/POPC Vesicle Preparation.

OA/POPC vesicles (1:1 molar ratio) were prepared by mixing the amphiphiles in chloroform and drying in a glass tube under vacuum for 12 h. The dried lipid films were first equilibrated with one equivalent of KOH to OA. Then, the resuspension buffer was added (100 mM HEPES, 100 mM NaCl, 100 mM KCl, pH = 7) to a final concentration of 85-mM total amphiphiles and incubated overnight. Vesicles were extruded through polycarbonate 100-nm pore size membranes (Whatman) with the aid of a lipid extruder (Avanti Polar Lipids, #61000).

Preparation of Vesicle-Encapsulated RNA and RNA Exposed to Empty Vesicles.

To prepare vesicles encapsulating RNA, RNAs were added into the resuspension buffer and incubated overnight with the dried lipid films, followed by extrusion as above. The RNA amounts before the encapsulation were 125, 200, and 100 µg for the initial doped RNA pool, RNA pool for the first round of selection, and RNA pools for the subsequent rounds of selection, respectively. After extrusion, 5 mM MgCl₂ and 5 mM CaCl₂ were added into the liposome solution and incubated for 30 min. The RNA-containing vesicles were purified by a Sepharose 4B size exclusion column (Sigma-Aldrich), with the aminoacylation buffer (100 mM HEPES [pH = 7], 100 mM NaCl, 100 mM KCl, 5 mM MgCl₂, and 5 mM CaCl₂) as the mobile phase to remove unencapsulated RNAs. The purified RNA-containing vesicles were concentrated by a 50-kDa molecular weight cutoff Amicon Ultra-4 centrifugal filter unit (MilliporeSigma). The final RNA concentration of samples before BYO incubation was 0.5 µM.

To prepare nonencapsulated RNA exposed to empty vesicles, 5 mM MgCl₂ and 5 mM CaCl₂ were added to the extruded liposome solution and then equilibrated for 30 min, followed by the addition of RNA solution. The RNA amounts added into the solution were 12.5, 200, and 20 µg for the initial doped RNA pool, RNA pool for the first round of selection, and RNA pools for the subsequent rounds of selection, respectively. The final RNA concentration of samples before the BYO incubation was 0.5 µM. The final concentration of the OA/POPC mixture was 85-mM amphiphiles. When OutV conditions were varied with different amphiphile concentrations, the amphiphile concentration of the stock solution was 112.5 mM before dilutions.

RT-qPCR Assay and Gel Shift Assay.

For the RT-qPCR assay, InV and OutV samples were incubated for 90 min with various BYO substrate concentrations (10, 50, 100, 250, 500, and 1,000 µM) in the aminoacylation buffer. The reactions were stopped by removing unreacted substrate using Bio-Spin P-30 Tris desalting columns (Bio-Rad). Lipids were removed by chloroform extraction using 5PRIME Phase Lock Gel light tubes (Quanta bio) followed by ethanol precipitation. RNA pellets were dissolved in phosphate-buffered saline (PBS) buffer (pH = 7.5). The RNA concentration of each sample was quantified by Qubit 3.0 Fluorometer (Thermo Fisher Scientific). To isolate the reacted RNA, streptavidin MagneSphere paramagnetic beads (Promega) were added to all reacted RNA samples (20-ng RNA for each sample from the dissolved reacted RNA stock solutions) with a volume ratio of 1:1. Samples were incubated for 10 min at room temperature with end-over-end tumbling, followed by three washing steps. The aminoacylated RNAs were eluted with UltraPure diethyl pyrocarbonate–treated water (Invitrogen) incubation at 70 °C for 2 min as previously described (101). The amounts of aminoacylated RNAs were quantified using iTaq SYBR green mix (#1725150, Bio-Rad) using Bio-Rad CFX96 Touch system. The samples were prepared following the manufacturer's protocol. Samples of 2 μL were mixed in the total 10-μL RT-qPCR reaction volume with 500 nM of both forward and reverse primers. The forward and reverse primers sequence were 5′-GAT​AAT​ACG​ACT​CAC​TAT​AGG​GAA​TGG​ATC​CAC​ATC​TAC​GA-3′ and 5′-CAG​CTT​CGT​CAA​GTC​TGC​AGT​GAA-3′, respectively. A calibration standard curve was measured for each RT-qPCR measurement batch to reduce measurement error. The standard RNA sequence was 5′-GGG​AAU​GGA​UCC​ACA​UCU​ACG​AAU​UCA​AAA​ACA​AAA​ACA​AAA​ACA​AAN​UUC​ACU​GCA​GAC​UUG​ACG​AAG​CUG-3′ which has the same length (i.e., 71 base pairs) and primer-complementary regions as the ribozymes used in this study. The standard curve was determined by adding 2 μL standard RNA samples with the concentrations of 1,000, 100, 10, 1, and 0.1 pg/μL (SI Appendix, Fig. S12). Triplicates were performed for each sample.

For the gel shift assay, samples were incubated with the BYO substrate for 90 min at various concentrations of BYO (0, 10, 50, 100, 250, 500, and 1,000 µM) in the aminoacylation buffer. After desalting, samples were incubated with 2 µM streptavidin for 15 min in 10 mM Tris (pH = 7.0) and then analyzed by native PAGE. Gels were stained by SYBR Gold (Invitrogen) and imaged on an Amersham Typhoon 5 Biomolecular Imager (GE Healthcare Life Sciences).

Dynamic Light Scattering of Vesicles.

Vesicle stability was examined by incubating the extruded vesicle solution under different experimental conditions. Samples were placed at room temperature for 120 min before measurements. Dynamic light scattering measurements were performed using the Zetasizer Nano ZSP (Malvern Instruments) at room temperature. Photons were collected at 173° scattering angle, and the scattering intensity data were processed using the instrumental software to determine the hydrodynamic size of the vesicles of different samples. Triplicate measurements were performed.

Preparation of RNA Libraries.

Chemical synthesis was used to obtain a library of DNA molecules having the sequence 5′-GAT​AAT​ACG​ACT​CAC​TAT​AGGG​AAT​GGA​TCC​ACA​TCT​ACG​AAT​TC-N21-TTC​ACT​GCA​GAC​TTG​ACG​AAG​CTG-3′, where the nucleotides upstream of the transcription start site for T7 RNA polymerase are underlined and N21 denotes 21 consecutive nucleotides, which are varied for different ribozyme families in preparing the 'doped pool' RNA. The sequences of the N21 region for five different ribozyme families are: CTA​CTT​CAA​ACA​ATC​GGT​CTG (S1a), CCA​CAC​TTC​AAG​CAA​TCG​GTC (S1b), ATT​ACC​CTG​GTC​ATC​GAG​TGA (S2a), ATT​CAC​CTA​GGT​CAT​CGG​GTG (S2b), and AAG​TTT​GCT​AAT​AGT​CGC​AAG (S3). Randomness of 9% (i.e., 91% for the peak center nucleotide and 3% for each other nucleotide) in the N21 region was introduced during the DNA library synthesis. The theoretical fraction for the peak center, single mutants, double mutants, triple mutants, and other mutants for each of the synthesized DNA libraries is ∼14, 29, 28, 18, and 10%, respectively. Due to the limitation of sequencing depth, the sequencing results presented in this study covered the peak centers, all single and double mutants, and a fraction of the triple mutants. The doped pool RNA was prepared by mixing equal amounts of the five transcribed and purified RNA libraries.

For the DNA library of the selection pool, the N21 region was entirely random (i.e., 25% of each nucleotide). RNAs were transcribed using HiScribe T7 polymerase (New England Biolabs) and purified by denaturing PAGE (National Diagnostics). For the selection pool, 6 µg of double-stranded DNA (∼323 pmol) was used for the RNA transcription reaction to ensure high (∼45-fold) coverage of sequence space for N21.

k-Seq of the RNA Libraries.

The previously used k-Seq assay (53) was carried out for the doped pool RNA library in the InV) and OutV conditions, with modifications described below required due to sample properties in the presence of vesicles. k-Seq is a massively parallel assay for measuring ribozyme kinetics using HTS, similar to HTS-Kin and related methods (46, 56, 102–105). InV and OutV samples were incubated for 90 min with various BYO substrate concentrations (10, 50, 100, 250, 500, and 1,000 µM) in the aminoacylation buffer. Samples were then treated as described in the RT-qPCR assay. Notably, a sample with no BYO was prepared and served as an input control in the following analysis. The input control was separately prepared without the beads incubation to characterize the initial population of each sequence in the doped RNA pool. The cycle quantification value (i.e., C_q) of each k-Seq sample was determined by the CFX Manager Software (Bio-Rad) using the built-in regression method. The aminoacylated RNAs were reverse transcribed and then amplified by PCR with the cycle number determined by the RT-qPCR measurements. In general, C_q + 1 cycle was used for the PCR. The DNA library of each sample was then barcoded and pooled for sequencing by the Illumina NextSEq 500 (Biological Nanostructures Laboratory, California NanoSystems Institute at University of California, Santa Barbara).

The raw, paired-end, demultiplexed Illumina read files (i.e., FASTQ files) of all k-Seq samples were processed with the EasyDIVER pipeline to create count files containing dereplicated lists of the central variable region sequences and their count reads (106). Every unique sequence detected in the count file of the input sample was tracked across all k-Seq samples. The concentration of sequence s of the k-Seq sample (samples denoted as BYO_i, where i specifies the BYO concentration) was calculated as $\left(n_s^{BY{O}_i}/n_{total}^{BY{O}_i}\right)\ast {\left[total\right]}^{BY{O}_i}$, where the superscript denotes the sample, $n_s^{BY{O}_i}$ and $n_{total}^{BY{O}_i}$ are the number of reads of sequence s and the total number of reads, respectively, in sample BYO_i, and ${\left[total\right]}^{BY{O}_i}$ is the total RNA concentration of sample BYO_i, determined by the RT-qPCR results. Results were fit to the pseudo-first-order rate equation $F_s\left(\left[BYO\right]\right)=A_s\left(1-e^{-k_s\left[BYO\right]t}\right)$, where

$$F_s=\frac{\left(n_s^{BY{O}_i}/n_{total}^{BY{O}_i}\right)\ast {\left[total\right]}^{BY{O}_i}}{\left(n_s^{input}/n_{total}^{input}\right)\ast {\left[total\right]}^{input}},$$

where A_s is the maximum reacted fraction, t is the incubation time of 90 min, and k_s is the effective rate constant of the aminoacylation reaction catalyzed by sequence s. The two fitting parameters A_s and k_s are poorly estimated individually for low-activity sequences (c.a., k_s < 0.5 min⁻¹ ⋅ M⁻¹), but due to the inverse correlation between estimated A_s and k_s during curve fitting, the product of the estimated k_s and estimated A_s is more accurate (56). Therefore, the product of the two estimated parameters, k_sA_s, from the pseudo-first-order curve fitting was used to represent the catalytic activity of all ribozymes in the present study. To minimize the contribution of sequencing error, an empirical threshold was applied such that only sequences having >10 reads on average across k-Seq samples were included in the analysis. To estimate the experimental error, bootstrapping analysis was conducted using the k-Seq data (56). The bootstrap analysis was conducted by iterating the fitting process 2,000 times, with each resample generated by randomly picking 21 data points from the original data set (i.e., triplicates for seven different [BYO]). Hence, 2,000 sets of best-fit parameters from the bootstrap analysis of each analyzable sequence were obtained. The 95% CI of the bootstrap results was defined by the range between the 97.5 percentile and the 2.5 percentile. In this study, the estimated k_sA_s value is the median (i.e., 50 percentile) among bootstrap samples. The source code for the k-Seq data analysis were written in MATLAB (MathWorks Inc.) The raw HTS data and source code are available at Dryad (https://doi.org/10.5068/D1PX0K).

In Vitro Ribozyme Selection in the Encapsulated and Nonencapsulated Conditions.

For both InV and OutV selections, 200-μg RNAs (coverage of N21 sequence space ∼500-fold) were applied in the first round. For the InV selection, the RNA-containing vesicles were purified as described above. For the OutV selection, RNAs were externally added to the vesicle solution without encapsulation. The RNA-containing solutions were incubated with 50-µM BYO substrate in the aminoacylation buffer for 90 min. After the reaction, samples were desalted, chloroform extracted, ethanol precipitated, and then resuspended in PBS buffer. The aminoacylated RNAs were selected by adding streptavidin beads at a volume ratio of 1:4 (RNA solution: bead-containing slurry) and then were eluted after 10 min incubation time. Sequences were prepared for the next round of selection by RT-PCR. The amount of aminoacylated RNAs recovered from the streptavidin beads increased after each round of selection; hence the number of PCR cycles was reduced accordingly to prevent PCR artifacts. The selection process was ended when the number of PCR cycles necessary was reduced to four. Four and five rounds of the selection process were performed in the InV and OutV conditions, respectively. The selected DNA libraries were barcoded and pooled for sequencing by Illumina NextSEq 500 (Biological Nanostructures Laboratory, California NanoSystems Institute at UCSB).

First, we examined whether any novel ribozyme families arose in either selection condition. The HTS result of each selection pool was analyzed by EasyDIVER pipeline (106) to create dereplicated lists of the central variable region sequences and their count reads. The sequences on the list were clustered into a peak if the sequences were within a Hamming distance of ≤3 from the known family wild types (S1a, S1b, S2a, S2b, and S3). Both selected RNA pools were found to be >85% populated by the three known active Motifs, and no new Motifs could be identified in either pool after clustering similar sequences (SI Appendix, Fig. S13).

Estimating Mutational Effects on Ribozymes.

A multilinear regression model was introduced to assess the mutational effect of a particular mutation i at locus j in the central 21-nt region of a peak center sequence (p). The log-scale activities of mutants were defined as a vector $\mathit{Y}=\left[y_{i,j}\right]=\left[ln\left(k_{i,j}{A}_{i,j}\right)\right]$. The sequence of each modeled mutant ($p_{i,j}$) was represented by ${\overline{{\rm X}}}_{i,j}$, which is a binary vector encoding all possible mutations of p. The multilinear model was constructed for predicting the activity of mutant as ${\widehat{\text{y}}}_{i,j}=y_0+{\overline{\beta }}_{i,j}\cdot {\overline{{\rm X}}}_{i,j}$, where ${\widehat{\text{y}}}_{i,j}$ is the modeled activity of mutants, $y$₀ is the activity of the wild-type family center ($y$₀$=ln\left(k_0{A}_0\right)$), ${\overline{\beta }}_{i,j}$ is a vector which represents the modeled mutational effects of all possible mutations, [${\beta }_{i,j}$] (63 elements in this study). Then, we can obtain the simulated activity of all mutants $\widehat{\mathit{Y}}=\left[{\widehat{\text{y}}}_{i,j}\right]$. The regression analysis was performed by minimizing the least-squares error between Y and $\widehat{\mathit{Y}}$. Note that only single and double mutants were included in the modeling, and the model does not account for the contribution of epistasis.

k-Seqlogo Analysis.

The Seqlogo illustration is a graphical representation for depicting the information content of a sequence, representing the consensus sequence region and the diversity of a collection of aligned sequencing results (107). By adapting the k-Seq results and the multilinear regression analysis into the Seqlogo representation, we illustrated the information content relevant to activity measurements obtained from the k-Seq assay (which we termed a “k-Seqlogo” representation). The basis of this illustration is the supposition that each sequence in a family should be represented at a level that is related to its activity. From the above multilinear regression model, we approximate the Arrhenius activation energy change caused by a particular mutation i at locus j as

$$\mathrm{\Delta }{E}_{i,j}=-k_B{T}_0\left({\widehat{\text{y}}}_{i,j}-y_0\right)=-k_B{T}_0\left({\beta }_{i,j}\right),$$

where ${\beta }_{i,j}$ is the modeled mutational effect on the activity of mutation i at locus j, $k_B$ is the Boltzmann constant, and $T_0$ is the reaction temperature. If i is the peak center nucleotide, ${\beta }_{i,j}=0$. Note the approximation that rate constant k_s = Ck_sA_s for constant C. A partition function of locus j ($Z^j$) can be computed as

$$Z^j={\displaystyle \sum }_{i=A,U,C,G}{e}^{\left({\beta }_{i,j}\right)}.$$

This theoretically constructed ensemble would include each sequence at a relative frequency that depends exponentially on the activation energy, in analogy to an ensemble of conformations having different energy levels. The Shannon entropy of locus j ($H^j$) within this theoretical ensemble can be calculated as

$$H^j=-{\displaystyle \sum }_{i=A,U,C,G}{f}_{i,j}\ast {\log }_2\left(f_{i,j}\right),$$

where $f_{i,j}=e^{\left({\beta }_{i,j}\right)}/Z_j$. Therefore, the information content (R), measured in bits, of each locus can be derived as $R_j={\log }_2\left(4\right)-H_j$. The height of each nucleotide letter in the logo is calculated as $R_j\ast f_{i,j}$. Therefore, k-Seqlogo illustrates the importance of the different nucleotides at each position by considering its effect on changing the activation energy of the ribozyme reaction.

Pairwise Epistasis Calculation.

Pairwise epistasis (ε) was calculated as ${\epsilon }_{a,b}=\text{ln}\left(k{A}_{a,b}\ast k{A}_0/\left(k{A}_a\ast k{A}_b\right)\right)$, where $k{A}_a$ and $k{A}_b$ are the activity of RNA variants with a single mutation, $k{A}_{a,b}$ is the activity of the RNA variant with both a and b mutations, and $k{A}_0$ is the activity of the wild-type family center. Positive values of ${\epsilon }_{a,b}$ indicate synergistic interactions (i.e., the double mutant is more fit than expected), while negative values indicate antagonistic interactions (i.e., the double mutant is less fit than expected). Each epistatic interaction was further categorized into one of three categories: magnitude epistasis, sign epistasis, and reciprocal sign epistasis (SI Appendix, Table S4 and Fig. S14). Magnitude epistasis is defined as a double-mutant activity aligned in direction with the expected linear combination of single mutants but differing in magnitude. Sign epistasis occurs when one mutation has the opposite effect on fitness in the presence of another mutation. Reciprocal sign epistasis is an extreme case of sign epistasis in which separately advantageous mutations became unfavorable when both are present.

Calculation of Ruggedness of the Chemical Activity Landscape.

The ruggedness (γ_d) of the chemical activity landscape was quantitatively estimated as previously described (53). γ_d is defined as the correlation of the effect of a certain mutation at locus j in sequence s, ${\mathrm{\Delta }}_j\left(s\right)$, and the effect of the same mutation in a d mutant background, ${\mathrm{\Delta }}_j\left(s_{\left[i_1,i_2\dots i_d\right]}\right)$, averaged over all possible sequences s, variants i, and loci j (108, 109). The parameter d is the Hamming distance (i.e., the minimum number of substitutions) between two related sequences.

$${\gamma }_d=\frac{{{\displaystyle \sum }}_s{{\displaystyle \sum }}_{i_1}{{\displaystyle \sum }}_{i_2>i_1}\dots {{\displaystyle \sum }}_{i_d>i_{d-1}}{{\displaystyle \sum }}_{j\ne i_{1,}{i}_2\dots i_d}{\mathrm{\Delta }}_j\left(s\right)\cdot {\mathrm{\Delta }}_j\left(s_{\left[i_1,i_2\dots i_d\right]}\right)}{{{\displaystyle \sum }}_s{{\displaystyle \sum }}_{i_1}{{\displaystyle \sum }}_{i_2>i_1}\dots {{\displaystyle \sum }}_{i_d>i_{d-1}}{{\displaystyle \sum }}_{j\ne i_{1,}{i}_2\dots i_d}{\left({\mathrm{\Delta }}_j\left(s\right)\right)}^2}.$$

The effect of a mutation at locus j is measured as the change in (log scale) activity of sequence s, as ${\mathrm{\Delta }}_j\left(s\right)=\text{ln}\left(k_{s_{\left[j\right]}}{A}_{s_{\left[j\right]}}\right)-\text{ln}\left(k_s{A}_s\right)$. For each pair of sequences having a certain mutation at locus j, we identify all possible d mutant backgrounds by finding every other pair of sequences in the pool with the same mutation. ${\gamma }_d$ is defined as a correlation and is bounded by $-1\le {\gamma }_d\le 1$. ${\gamma }_d=1$ corresponds to a perfectly smooth peak. ${\gamma }_d=0$ corresponds to a highly rugged, completely uncorrelated peak. ${\gamma }_d=-1$ corresponds to a maximally rugged, anticorrelated peak.

The average ${\gamma }_d$ for the rugged NK model (47, 64, 65) can be calculated as ${\gamma }_d^{NK}=\frac{\left(\begin{array}{c}N-d-1\\ K\end{array}\right)}{\left(\begin{array}{c}N-1\\ K\end{array}\right)}$, where N is the number of total loci and K is the number of interacting loci. Larger K indicates a more-rugged fitness landscape. $K=0$ corresponds to an additive model with independent contributions from each gene, while $K=N-1$ corresponds to the fully random, uncorrelated fitness landscape (i.e., house-of-cards model).

Data Availability

Sequencing data and source code data have been deposited in Dryad Digital Repository (https://doi.org/10.5068/D1PX0K) (110).