Three-Dimensional (3D) Nanometrology Based on Scanning Electron Microscope (SEM) Stereophotogrammetry

Abstract

Three-dimensional (3D) reconstruction of a sample surface from scanning electron microscope (SEM) images taken at two perspectives has been known for decades. Nowadays, there exist several commercially available stereophotogrammetry software packages. For testing these software packages, in this study we used Monte Carlo simulated SEM images of virtual samples. A virtual sample is a model in a computer, and its true dimensions are known exactly, which is impossible for real SEM samples due to measurement uncertainty. The simulated SEM images can be used for algorithm testing, development, and validation. We tested two stereophotogrammetry software packages and compared their reconstructed 3D models with the known geometry of the virtual samples used to create the simulated SEM images. Both packages performed relatively well with simulated SEM images of a sample with a rough surface. However, in a sample containing nearly uniform and therefore low-contrast zones, the height reconstruction error was ≈46%. The present stereophotogrammetry software packages need further improvement before they can be used reliably with SEM images with uniform zones.

Introduction

Over the past decade, semiconductor device and integrated circuit technology has evolved enormously from conventional scaling-driven planar devices to complex three-dimensional (3D) transistor architectures, giving rise to new measurement requirements (Bunday et al., 2013). Fin-shaped field-effect transistors have now become the dominant microprocessor device architecture (International Technology Roadmap for Semiconductors, 2013) for the fastest devices. Critical performance characteristics of these semiconductor devices are governed by 3D shape and size. Evaluation of structural parameters of 3D shapes of such devices requires measurement of many parameters which are beyond traditional critical dimensions (CD), including sidewall angle, top corner rounding and footing, roughness, recesses, and undercuts. The challenges associated with the 3D nature of all dimensional measurements on such non-planar devices are also daunting because the features on integrated circuits are already small and the allowable uncertainty in their measurements is smaller yet. A true 3D nanometer scale high-throughput integrated circuit metrology solution is urgently required (Vládar et al., 2012, 2014).

Imaging and accurate 3D high-throughput measurements of these nanoscale devices present great metrological challenges as no single metrological tool or method is sufficient (Bunday et al., 2014). For example, the CD atomic force microscope (CD-AFM) has limitations for sub 20 nm node production due to tip size constraints in the very narrow spaces present in the devices. Scatterometry/optical CD techniques are time-consuming to optimize, are sensitive to process changes, and have lower spatial resolution (limited by wavelength or illumination spot size). Scanning electron microscopy has been used in the semiconductor industry for imaging and measuring objects with various dimensions ranging from millimeters to nanometers. Scanning electron microscopes (SEMs) offer high depth of field, excellent spatial resolution, and quick on-the-spot measurements. However, secondary electron images produced by SEMs have only two spatial dimensions. They do contain some information related to the third dimension which cannot be extracted in a simple way. Fortunately, a few nondestructive approaches for recovering the third dimension (depth or height) have already been developed, including a model-based library (MBL) SEM method (Villarrubia et al., 2005), a shape-from-shading method (Drzazga et al., 2006), tilt-beam CD-SEM (Su et al., 2000; Zhang et al., 2014) and several variants of SEM 3D reconstruction from two or more viewpoints generated by tilting the sample or the beam (Xie, 2011; Eulitz & Reiss, 2015; Tafti et al., 2015; Gontard et al., 2016, 2017). This article concerns hurdles and opportunities in SEM-based 3D nanometrology using as examples methods from the last group, in which the inputs are two or three images obtained by altering the sample tilt.

SEMs are capable of acquiring images from several points of view by tilting the sample. These images, in the form of stereo-pairs or stereo-triplets, can be merged digitally to produce a 3D image with depth representation and perception. Theoretical understanding of SEM stereophotogrammetry has been well established for several decades (Piazzesi, 1973). Fully reconstructing a 3D surface involves calculating the height of every point in the stereo image pair. The tilt angle generates parallax values for the surface features of different heights in the stereo-pair images. The parallax values combined with the relative tilt angle can be used for calculating the third dimension (Xie, 2011). Several SEM stereophotogrammetry software packages have been developed, some of them sold commercially, for 3D shape, size and surface reconstruction (e.g., 3D_TOPx, EZEImage, MeX, Mountains Map, Scandium height, Sem3D, STERECON, and STIMAN-3D).^a

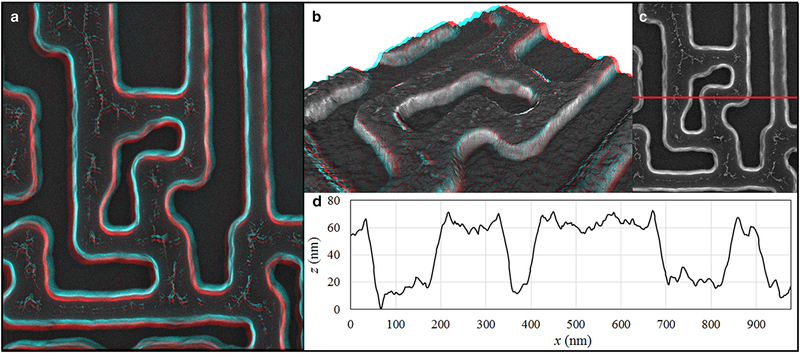
Figure 1 shows an example of a 3D reconstruction of a semiconductor circuit by one of the commercial SEM stereoscopy software packages. The 3D reconstruction was created using stereo images with 18° relative tilt. Figure 1a shows an anaglyph with a horizontal field of view (HFV) of ~1.1 μm. The three-dimensionality is clearly visible. Features as small as 10 nm are visible as they were in the original SEM images. Figure 1b shows a close-up view of a reconstructed 3D model where the surface seems rougher than in the anaglyph. Here, the features around 10 nm cannot be well distinguished. Figure 1c shows a height profile path and Figure 1d shows the corresponding height profile. It is tempting to compare such height profiles with AFM generated height profiles (Vanderlinde, 2008), but this is not always possible or practical in the semiconductor industry (Zhang et al., 2014).

Figure 1.

a: A red-cyan anaglyph of a semiconductor structure (horizontal field of view ~1.1 μm): (b) close-up, tilted view of the three-dimensional (3D) model anaglyph, (c) cross-sectional profile path, and (d) the corresponding height of the profile. You will need red-cyan glasses to see the anaglyphs in 3D.

The questions then arise: Can one trust these results? That is, how accurate is current state-of-the art 3D reconstruction? Do different commercial software packages differ significantly in accuracy of reconstruction given the same data? How do we test existing or newly developed software packages built with different algorithms? A vital prerequisite for a test problem is that the right answer be known. For this purpose, it is useful to have simulated SEM images of a virtual sample where one can predefine geometrical parameters such as the shape, size, and roughness, and SEM image quality parameters such as contrast, noise, beam spot size, etc. In this case, the sample geometry is known exactly.

The only uncertainty associated with the input is the fidelity with which the simulation imitates nature. In a recent study, Villarrubia et al. (2015) measured and Java Monte Carlo Simulator for Secondary Electrons (JMONSEL) modeled images were in good agreement, with 88% of the difference between them attributable to the observed measurement noise. SEM measurement results based on the model were compared with transmission electron microscopy and CD small-angle X-ray scattering (CD-SAXS) of the same sample. Differences in measured mean feature widths were <1 nm. In contrast, 3D photogrammetric reconstruction relies on correlation of image features with no accounting for the physics that relates the image and the geometry. Thus, between the absent (or implicit) model in the photogrammetry software and the explicit and partially tested model in the simulator, it is reasonable to believe the latter provides a reasonable standard by which to judge the former.

In our previous study (Villarrubia et al., 2016), simulated SEM images of an isolated 3D linewidth semiconductor structure with a rough surface were used for testing the software packages, but no attempt was made to use simulated SEM images of a virtual sample having large areas where there is an almost homogeneous image content or uniform zones. Semiconductor integrated circuits can have such areas. A 3D SEM software package will be useful in the semiconductor industry only if it successfully processes rough as well as homogeneous image content.

In the present study, we use mainly two types of simulated SEM images: (i) images of a linewidth structure with a rough surface as in the earlier report (Villarrubia et al., 2016) but with a different set of tilt angles and a different analysis approach, and (ii) images of a linewidth array with a smooth surface (homogenous image content or uniform zones). We purchased three commercial software packages to perform stereo reconstruction. We wanted to find out how closely these software packages reconstruct overall 3D shape and size. In our pilot study, we had found that one of these three packages employed a windowing function that reconstructed a subset of the image smaller than the part visible in all images of the set (Villarrubia et al., 2016). Therefore, in the present study, 3D reconstruction was restricted to using the two remaining software packages. We refer to these as Packages A and B. Finally, we argue that simulated SEM images can be very useful for algorithm testing and validation of any stereophotogrammetry package and, if required, for developing a completely new module useful for the semiconductor industry.

Materials and Methods

Virtual Sample and Its Images

A Monte Carlo SEM simulator (JMONSEL) (Villarrubia et al., 2005) was used to produce simulated SEM images. The virtual samples were comprised entirely of silicon. The simulator tracks each incident beam electron and each electron in the secondary electron cascade. Elastic scattering was modeled using relativistic Mott cross-sections. Secondary electron generation was modeled with dielectric function theory. Refraction or reflection at the sample/vacuum interface was treated in the wide (classical) barrier limit. Inside the sample, uncharged silicon was assumed. Electrons were propagated in trajectory steps each of which was terminated by a scattering, boundary crossing, or trajectory termination event. Electrons with energy up to 50 eV that escaped to a hemispherical collector above the sample were counted and converted to a proportional intensity level to produce images. Details of the implementation of these models, as well as its legitimacy and success, are available elsewhere (Villarrubia et al., 2015). SEM images from several viewing angles were computed. In some respects the simulated images provide an easier test of the photogrammetry software than will an actual reconstruction. The simulated images have a nondiverging beam so remain in focus. They have a small amount of noise from Monte Carlo statistics, but none from other sources.

Linewidth Structure with Rough Surface

A linewidth structure with a rough surface was simulated for study. Figure 2a shows the central cross-section or middle height profile of the 3D structure at 0° tilt. The detailed procedure for creating the high magnification simulated SEM images using this height profile has been reported earlier (Villarrubia et al., 2016). This structure was created by wrapping a rough surface (0 nm mean, 1 nm rms roughness, 15 nm correlation length) onto an underlying smooth sample shape 80 nm high and 50 nm wide at half-height. Unlike a real object, the entire surface is known in detail. It was wider on the bottom than the top with sidewalls 3° from the vertical, and has 10 nm top corner radii. For each simulated image, 10,000 beam electrons incident at 500 eV plus all secondary electrons in the resulting cascade were simulated at each landing position. The targeted landing positions were raster-scanned horizontally with y (along the line) ranging from − 25 to 25 nm and x (perpendicular to y in the horizontal plane) ranging from − 50 to 50 nm, both in 0.5 nm increments. Actual landing positions were normally distributed about the target positions with SD 0.5 nm. Simulated SEM images with − 5°, 0°, and 5° tilt angles were used in this study. These images are shown in Figures 2b to 2d.

Figure 2.

a: The central cross-section or middle height profile of the three-dimensional (3D) isolated line structure at 0° tilt. b–d: Simulated scanning electron microscope images of the 3D linewidth structure with rough surface (b) −5°, (c) 0°, and (d) 5° tilt angles. The horizontal field of view for each image in (b–d) is 90.4 nm. The horizontal line drawn on (c) shows the location of the cross-section shown in (a).

Linewidth Array with a Smooth Surface

A linewidth array with a smooth surface was simulated for study. As with the previous case, the sample’s geometry was predefined. As shown in Figure 3a, the basic shape (central cross-section or middle height profile) consists of lines with 3° sidewalls, 60 nm height, 60 nm linewidth at half-height, 100 nm center-to-center spacing, with 10 nm radius top corners. JMONSEL was used to import a constructive solid geometry representation of the virtual sample and produce images of the same location at sample tilts of − 5°, 0°, and 5°. For each simulated image, 4,000 beam electrons incident at 500 eV plus all secondary electrons in the resulting cascade were simulated at each landing position. The targeted landing positions were raster-scanned horizontally with y (along the line) ranging from − 25 to 25 nm and x (perpendicular to y in the horizontal plane) ranging from − 50 to 50 nm, both in 1 nm increments. Actual landing positions were normally distributed about the target positions with SD 0.5 nm. The HFV for each image shown in Figures 3b to 3d is 997 nm. The parallel projection approximation (that the beam angle is the same at all points in the image) is valid for high magnification SEM images such as those shown in Figures 2b to 2d and 3b to 3d.

Figure 3.

a: The central cross-section or middle height profile of the structure used in Java Monte Carlo Simulator for Secondary Electrons simulation at 0° tilt. Only three lines of the sample are shown here. b–d: Simulated scanning electron microscope images of the linewidth array structure with smooth surface (b) − 5°, (c) 0°, and (d) 5° tilt angles. The horizontal field of view for each image in (b–d) is 997 nm (pixel size is 1 nm). The horizontal line drawn on (c) shows the location for the central cross-section or middle height profile. a: The central cross-section or middle height profile of any three lines of (c).

Results

3D Reconstruction from Simulated SEM Images

3D reconstruction from simulated SEM images was performed using Packages A and B. Package A accepts three images as input. We used the ones at tilts of −5°, 0°, and 5°. Package B accepts only two images. We used the ones at −5° and 5°. Both packages need the pixel size and relative tilt between the images as input parameters. Package A additionally needs the distance from the SEM raster’s pivot point to the top surface of the sample (we used 13.9 mm, but this distance with a scan size <1 μm produces negligible variation in the angle of incidence, so the results were not sensitive to this choice). For 3D reconstruction, Package A took typically up to 1 min or more whereas Package B took typically 10 s or less.

Linewidth Structure with Rough Surface

In our previous study (Villarrubia et al., 2016), in order to have enough information to determine the width of a linewidth structure with a rough surface, we reconstructed both the left and right sides of the linewidth structure. This required two sets of stereo images, one set all at negative tilts to make the left side visible in all its images, and another set all at positive tilts to make the right side visible. The negative set consisted of the three images of − 25°, − 20°, and − 15° tilt angles and the positive set were the three at 15°, 20°, and 25° tilt angles. We performed separate reconstructions and stitched the results ourselves. However, in semiconductor devices and integrated circuits, the choice of the maximum tilt angles will be limited by the aspect ratio and the density of the structure to be measured (Zhang et al., 2014). In the present study, we used only − 5°, 0°, and 5° tilt angle images to reconstruct the 3D structure. Choosing a tilt angle difference is a compromise between competing factors. The range of angles can be larger if permitted by the aspect ratio and the density of the structure to be measured. A larger tilt angle difference increases the disparity between images and may, for this reason, yield a higher vertical resolution, but if an angle difference is too large it may lead to pattern recognition errors, leading to mismatches and resulting reconstruction errors. The reconstructed pattern might become distorted or unrecognizable and more features are hidden by other areas of the sample.

The best choice of tilt angles and magnification depends on the morphology of the sample as well as the information desired. For instance, in the present study the aim was to reconstruct the height and the overall shape of the object and not to determine sidewall roughness, and therefore the choice of the tilt angle image set was − 5°, 0°, and 5°. A larger tilt angle image set will be necessary to determine sidewall roughness (Villarrubia et al., 2016).

Figures 4a and 4b show anaglyphs created by Packages A and B, respectively. This stereoscopic 3D effect was achieved by combining ±5° tilt angle images with different colors, here red and cyan. When viewed through red-cyan glasses it gives the perception of a 3D scene or structure.

Figure 4.

Anaglyphs generated by (a) Package A and (b) Package B. The relative tilt angle difference was 10°. You will need red-cyan glasses to see the anaglyphs in 3D.

Figures 5a and 5b show the 3D surface reconstruction of the sample by Packages A and B, respectively. We will compare the middle profile (i.e., in a plane at constant y, at mid-line) with the corresponding true middle profile shown in Figure 2a. Identifying the middle profiles of the height map with the reconstruction is immune to certain errors that might arise if the reconstruction omits a symmetrical border around the image or reverses an image top to bottom, since the middle is invariant under these operations. We know that the input sample has within-profile (along x) and profile-to-profile (along y) variation governed by the same height roughness probability distribution. Visually, we can see that this is also the case for the reconstructed surfaces in Figure 5. That is, there are no sudden jumps or misbehaviors in the reconstructed surfaces. Variation is consistent with the expected roughness, and the roughness within the chosen profile gives us a good estimate of its representativeness. Figures 2c and 6a show the profile path and the corresponding height profile generated by Package A and Figures 2b and 6b show the profile path and the corresponding height profile generated by Package B. These profiles are drawn through the middle of their 3D models.

Figure 5.

Three-dimensional (3D) model anaglyphs generated by Packages (a) A and (b) B. You will need red-cyan glasses to see the anaglyphs in 3D.

Figure 6.

Reconstructed height profiles generated by (a) Package A and (b) Package B.

We noticed two main differences: (1) Package A, using three images (0° and ±5°) produced a symmetrical looking 3D reconstruction. This is because it produced a 3D model with reference to the central 0° tilt image (Fig. 2c). This is evident from Figures 2c and 6a. Package B, using only two images (±5°), produced a 3D model with reference to the −5° tilt image (Fig. 2b) and therefore looks tilted. This is evident from Figures 2b and 6b. (2) Another difference that we noticed was the 3D model produced by Package A with its default setting appeared to be a smoothed version of the actual reconstructed 3D shape. We suspect that Package A used an unknown internal filtering step. The 3D model produced by Package B with its default setting was noisier and had many outliers. We specified increased filtering in order to achieve a smooth 3D model comparable to that produced by Package A. Therefore, the profile shown in Figure 6a is the default profile produced by Package A, whereas Figure 6b is a profile of comparable waviness produced by Package B.

Because Package B referenced its result to −5°, in order to do comparisons with our true profile (referenced to 0°) we applied a +5° rotation correction to the Package B profile. We compared profiles Figures 6a and 6b (corrected) to the actual known values of the middle profile (Fig. 2a) of the virtual rough sample. The results and the corresponding errors (result—true values) are shown in Table 1.

Table 1.

Comparison of Reconstructed Results With True Values.

Parameters	True (nm)	Package A (nm)	Errors, Package A (Result—True) (nm)	Package B (nm)	Errors, Package B (Result—True) (nm)
Height (Hrough)	79.5	78.1	−1.4	75.9	−3.6
Linewidth (LWrough)
LWrough at z = 70 nm	42.4	39.2	−3.1	40.7	−1.7
LWrough at z = 60 nm	46.6	43.9	−2.7	44.0	−2.6
LWrough at z = 50 nm	46.2	47.1	0.9	46.0	−0.2
LWrough at z = 40 nm	47.3	49.9	2.6	48.5	1.2
LWrough at z = 30 nm	53.3	52.8	−0.5	50.5	−2.8
LWrough at z = 20 nm	51.8	55.8	3.9	56.0	4.2
LWrough at z = 10 nm	55.5	58.9	3.4	58.2	2.7
Mean LWrough values	49.3	49.8	0.5	49.1	−0.2

In order to find the height (H_rough) of profiles, each profile was partitioned into regions defining the top (or upper plateau) of the line, the left baseline or substrate, the right baseline or substrate, and the edges (transition between baseline regions and upper plateau) as shown in Figures 2a and 6. Heights were determined for each profile by subtracting the average z value of the left and right baseline regions from the average z value of the top region (these values are indicated by dashed horizontal lines in the figures). The true mean H_rough value was 79.5 nm as indicated in Table 1. Package A had an error of −1.4 nm and Package B had an error of −3.6 nm. To get an understanding of the overall width, the linewidth (LW_rough) was calculated at z values at 1 nm intervals from 10 to 70 nm above the substrate. A representative sampling is shown in Table 1. The LW_rough calculated at these different z values by Packages A and B had mean errors 0.5 and −0.2 nm, respectively.

Errors on the order of a nanometer or two are consistent with those from the previous study (Villarrubia et al., 2016). Errors of this size are not necessarily due to reconstruction errors by the software. The x and z coordinates of the reconstructed profiles are shifted from those of the input shape. This required us to assign corrective x and z shifts in order to make the above comparison (we did so to produce the best match). As we do not have access to the inner workings of the software, our shifts are probably close but not exact. Mismatch could produce errors on the order of 1 nm, mostly arising from the baseline subtraction. The packages did not reconstruct the entire baseline. The smaller sampling of baseline points coupled with the sample roughness can produce errors at the 1 nm scale. If we pessimistically attributed all of the difference between SEM model-based measurements and those of CD-SAXS or TEM (Villarrubia et al., 2015) to the SEM model, we would have errors in a similar range. For our present purpose (comparison of performance on this sample with performance on the samples we will describe next), we will consider the mean values of height and width (first and last rows in Table 1) to be in acceptable agreement with the true values. Disagreements in width at individual z values appear to be associated with the smoothing evident in the reconstructed profiles. That is, the reconstruction did not accurately capture the surface roughness, but it did a reasonable job with the mean shape.

Linewidth Array with Smooth Surface

As mentioned earlier, our previous study (Villarrubia et al., 2016) did not include virtual SEM images having homogenous image content or uniform zones as shown in Figure 3c. Figures 7a and 7b show 3D models created by Packages A and B, respectively, using images shown in Figures 3b to 3d.

Figure 7.

Three-dimensional (3D) model anaglyphs generated by (a) Package A and (b) Package B. The maximum relative tilt angle difference was 10°. You will need red-cyan glasses to see the anaglyphs in 3D.

Here again Package A used three images at tilt angles 0° and ±5° and Package B used two images at tilt angles ±5°. On inspection of Figure 7, one observes that Package B produced unrealistic triangular narrow linewidth and triangular wide trenchwidth shapes. Package A did a better job but still could not reconstruct the actual flat surface on the line top and substrate surface inside the trenches.

Figures 8a and 8b show the height profiles generated by Package A and by Package B. This time there was no need to specify increased filtering with Package B (as there had been for Fig. 6b). Therefore, the profile Figures 8a and 8b are both default profiles produced by Packages A and B. These profiles are cross-sections through the middle of their 3D models. We compared these profiles to the known values of the virtual smooth sample. From Figures 3a, 8a and 8b, it is clear that both packages failed to calculate the height accurately. The actual profile consisted of identical periodic repetitions of the same structure, so the varying shape and height of lines in the reconstructed profiles is not correct. The actual shape had the valley floor at z = 0 nm and line tops at z = 60 nm. The z coordinate took on one of these two values almost everywhere, since the shape was nearly rectangular and the steeply sloped edges and rounded top corners produced intermediate heights at only a small fraction of each period. In the reconstructions, however, the transitions between the upper and lower levels occupy a considerably larger fraction of the period, so much so that it becomes unclear how one should define the height of the reconstructed patterns. We decided to calculate the height (H_smooth) of the reconstructed profile by calculating the difference between the mean peak z coordinate (the upper broken line in profile) and mean valley z coordinate (the lower broken line in profile). The variability of the individual peak coordinates contributes an uncertainty of $\sigma /\sqrt{N}$ to the associated mean value, with σ the standard deviation of the individual peak z values and N the number of those values (10 in this case). The variability of the individual valley depth z values likewise contributes an uncertainty to the lower mean value, calculated in a like manner. The root sum of squares of the standard deviations of the peak and valley mean z values is their combined contribution to the uncertainty of H_smooth. Clearly, among reasonable possible ways to assign the height, this one produces a larger estimate. Nevertheless, even this nearly largest possible estimate was considerably smaller than the true height. The H_smooth calculated by Packages A and B had errors −27.6 ± 1.2 nm and − 27.8 ± 0.5 nm, respectively. At half of the mean value (the middle broken line in profile) of H_smooth (0.5 H_{smooth_mean}), we have reported the results of linewidth (LW_smooth), trenchwidth (TW_smooth), and pitch (P_smooth) measurements by calculating the mean value and its standard deviation. These results and the corresponding errors (result—true values) are shown in Table 2. Although both packages calculate P_smooth reasonably well (i.e., scale disagreement is not an issue), Package B showed large errors in calculating LW_smooth and TW_smooth. Package B returned a −22.6 ± 0.7 nm error in the calculation of LW_smooth and a 22.7 ± 0.7 nm error in the calculation of TW_smooth. In brief, both packages failed to reconstruct overall shape and size adequately.

Figure 8.

Reconstructed height profiles of the smooth line/space array, as generated by (a) Package A and (b) Package B.

Table 2.

Comparison of Reconstructed Results With True Results for Linewidth Array With Smooth Surface.

Parameters	True (nm)	Package A (nm)	Errors, Package A (Result—True) (nm)	Package B (nm)	Errors, Package B (Result—True) (nm)
Height (Hsmooth)	60	32.4 ± 1.2	− 27.6 ± 1.2	32.2 ± 0.5	− 27.8 ± 0.5
Linewidth (LWsmooth) at 0.5 Hsmooth_mean	60	60.3 ± 1.0	0.3 ± 1.0	37.4 ± 0.7	− 22.6 ± 0.7
Trenchwidth (TWsmooth) at 0.5 Hsmooth_mean	40	39.5 ± 0.7	− 0.5 ± 0.7	62.7 ± 0.7	22.7 ± 0.7
Pitch (Psmooth) at 0.5 Hsmooth_mean	100	99.8 ± 0.3	− 0.2 ± 0.3	100.1 ± 0.3	0.1 ± 0.3

Linewidth Array with Hemispherical Bumps

As shown in Tables 1 and 2, both Packages A and B did relatively well reconstructing a linewidth structure with a rough surface, but failed on a linewidth array with homogenous image content. In the latter case, these packages probably faced difficulties in finding the homologous points in both images due to the homogeneous image content. Package A did a better job (see, Table 2) in calculating LW_smooth and TW_smooth whereas the Package B failed to calculate all three parameters H_smooth, LW_smooth, and TW_smooth correctly. Therefore, in our next attempt, new simulated images were made using JMONSEL and these images were used only to test Package A. The sample’s base geometry remained as shown in Figure 3a. To aid Package A for surface point matching in the stereo images, the basic structure (shown in Fig. 3a) was then “decorated” with hemispheres of varying radius (2.5, 5, 10 nm) on top (centered) or on the sides at heights of 15, 30, 45 nm.

Figures 9a to 9c show simulated SEM images at − 5°, 0°, and 5° tilt angles. The HFV for each image is 997 nm. The pixel size is 1 nm. Figure 9d shows the 3D model generated by Package A. Here, we visually noticed that (1) the hemispherical bumps are not well resolved, and (2) Package A still could not reconstruct the flat surface on the line top between the hemispherical bumps or the flat surface inside the trenches. The Figure 9e shows (upper) a path that avoids bumps and (lower) the height profile of the corresponding cross-section. Avoiding the hemispherical bumps in this way allows Figure 9e to be compared directly with Figure 8a.

Figure 9.

a–c: Simulated scanning electron microscope image of linewidth array with hemispherical bumps. a: − 5°, (b) 0°, and (c) 5° tilt angles. The horizontal field of view for each image is 997 nm (pixel size is 1 nm). d: Three-dimensional (3D) model anaglyph generated by Package A. You will need red-cyan glasses to see the anaglyph in 3D. e: Cross-sectional path of the profile on (b) avoiding bumps and, the corresponding height of the profile.

Again the profile (Fig. 9e) shows considerable incorrect variation of line shape and size. We calculated the height (H_bumpy), linewidth (LW_bumpy), trenchwidth (TW_bumpy), and pitch (P_bumpy) using the same methods we used in Table 2 for the sample without bumps. The results and the corresponding errors (result—true values) are shown in Table 3. The calculated H_bumpy had error − 23.4 ± 2.0 nm. Although, the package could calculate P_bumpy reasonably well, this time as compared with the previous results of Package A (see Table 2), the errors in calculation of LW_bumpy and TW_bumpy have increased. It is −5 ± 0.4 nm in calculation of LW_bumpy and 5 ± 0.2 nm error in calculation of TW_bumpy. It seems that the addition of hemispherical bumps did not improve homologous point matching enough to noticeably improve the reconstruction. The package still failed to reconstruct the overall shape and size adequately.

Table 3.

Comparison of Reconstructed Results With True Results for Linewidth Array With Hemispherical Bumps.

Parameters	True (nm)	Package A (nm)	Errors, Package A (Result—True) (nm)
Height (Hbumpy)	60	36.6 ± 2.0	− 23.4 ± 2.0
Linewidth (LWbumpy) at 0.5 Hbumpy_mean	60	55 ± 0.4	− 5 ± 0.4
Trenchwidth (TWbumpy) at 0.5 Hbumpy_mean	40	45 ± 0.2	5 ± 0.2
Pitch (Pbumpy) at 0.5 Hbumpy_mean	100	100 ± 0.4	0 ± 0.4

Discussion

The reconstructed results are compared with the true values and summarized in Table 4. The letter “a” designates results in agreement with the true result to within the stated uncertainty. Otherwise, a discrepancy is calculated. As seen in the Table 4, both Packages A and B, performed well with simulated SEM images of 3D linewidth structure with rough surface (i.e., Figs. 2b–2d). The results from Package A and B were in agreement with true values within uncertainty. In the case of simulated SEM images of linewidth array with smooth surface (i.e., Figs. 3b–3d) both packages failed to reconstruct H_smooth. Package A showed the results of LW_smooth and TW_smooth agreement to within the uncertainty with the true values, whereas Package B showed discrepancy in the calculation of LW_smooth and TW_smooth, respectively. Adding hemispherical bumps on linewidth array (i.e., Figs. 9a–9c) did not meaningfully improve the results.

Table 4.

Summary of Comparison of Reconstructed Values With the True Ones.

Figures	Parameters	Package A	Package B
Figures 2b–2d	Hrough	“a”	“a”
Linewidth structure with rough surface	LWrough	“a”	“a”
Figures 3b–3d	Hsmooth	− 46%	− 46.3%
Linewidth array with smooth surface	LWsmooth	“a”	− 37.6%
	TWsmooth	“a”	56.8%
	Psmooth	“a”	“a”
Figures 9a–9c	Hbumpy	− 39%
Linewidth array with hemispherical bumps	LWbumpy	− 8.3%
	TWbumpy	12.5%
	Pbumpy	“a”

The letter “a” designates values in agreement with the true value to within the stated uncertainty. Otherwise, the discrepancy is calculated.

Generally, the 3D reconstruction time of Package B was found to be nearly 10 times faster than the 3D reconstruction time of Package A. In the case of simulated SEM images of lines with rough surfaces (i.e., Figs. 2b–2d), the reconstruction results by Package B were relatively noisier. The reconstruction results by Package A were too smooth, probably an indication of internal filtering. Therefore, in the present study, it was not possible to compare surface roughness calculated by these different packages meaningfully. We consider it preferable to allow users to choose nondefault filter settings. Evaluating the accuracy of reconstruction of features on the sides is also important, because one of the semiconductor industry applications would be measurement of sidewall roughness. However, meaningful sidewall reconstruction is not to be expected with our chosen set of angles, since each sidewall is visible in only one of the images of the set.

SEM images of semiconductor linewidth samples will usually have some homogeneous image content. Neither package performed well in such a case (i.e., Figs. 3b–3d). However, the fact that Package A performed better than Package B in calculating LW_smooth and TW_smooth, but that Package A failed to calculate the sample height H_smooth correctly suggests that there is a path to improve these stereophotogrammetry packages further.

Another such suggestion comes from the fact that we can ourselves reconstruct heights from these images with fairly simple analysis. There are usually at least two identifiable features in an edge: the base, where it intersects the substrate, and the top, where in the SEM there is generally a characteristic peak. Heights of features are often very important in semiconductor electronics (and probably other) applications, and these two features, one at the top, one at the bottom, and very close to one another in the x–y direction are inviting targets from which to ascertain a height. In Figure 10, we show that one can do a by-hand calculation matching intensity profiles (of secondary electrons) at different sample tilts and produce results close to the real values. Figure 10a shows that the tilt angle θ generates lateral movement causing disparity in a eucentric tilt setting where point “p” on the surface remains stationary. Using simple trigonometry one can write $h=\frac{\Delta x_1-\Delta x_0\cos \theta }{\sin \theta }$.

Figure 10.

a: Tilt angle θ generates lateral movement in a eucentric tilt setting, where the surface is rotated about point “p”. b: The 4th line from the right in Figures 9b and 9c was used. The path of the profile shown goes through a small hemisphere of height 2.5nm. c: The corresponding intensity profiles at 0° (blue/darker) and 5° (orange/lighter) tilt angles are compared.

In Figure 10 the 4th line from the right in Figures 9b and 9c (shown again in Fig. 10b) was used. The path of the chosen profile goes through a small hemisphere of height 2.5 nm, as shown. Figure 10c shows the corresponding intensity profiles at 0° (blue/darker) and 5° (orange/lighter) tilts.

Here, Δx₀ = 31.4nm at 0° tilt and Δx₁ = 36.4nm at 5° tilt.

Therefore, the above equation gives h = 58.7 nm. This is much closer to the true value of 62.5 nm (60 nm line height + 2.5 nm hemisphere height) than the reconstruction result produced from Package A as shown in Tables 3 and 4.

SEM stereophotogrammetry is subject to errors from many sources (Marinello et al., 2008). Because of mechanical errors, sample tilts will not be exactly at the indicated orientations. The instrument’s scale calibration may have errors, and its scan may not be perfectly linear nor the x, y, and z axes exactly orthogonal. The sample may vibrate, drift, or charge during imaging. SEM stereophotogrammetry algorithms look for offsets in x and y that maximize the correlation between regions in both images. However, correlation will not be perfect, partly because features look different when viewed from different angles. At the nanometer scale this is in part due to differences in secondary electron generation when the electrons impinge on a feature from different angles. In that case, to get good inter-correlation, algorithms will have to employ different strategies, approximations, amounts of filtering for noise reduction, etc. These errors will propagate to produce errors in the reconstruction. It also suggests that there is a need to develop reliable measurement protocols for acquiring SEM images with as little error as possible.

SEM stereophotogrammetry software developers could use virtual SEM images as shown in this study internally to optimize their algorithms’ accuracies. Virtual SEM images can be extremely helpful for algorithm testing, development, and validation because a virtual sample is a model in a computer and its true dimensions are known exactly. This is impossible in the case of real SEM samples due to repeatability problems and to generally high measurement uncertainty. The virtual images can be also made with different image quality parameters including instrument errors such as defocus, tilt angle error, nonlinearity of a scan, etc. with complete repeatability.

We think that it would not be necessary to simulate images for every measurement. A relatively small number of test images to validate and establish trust in the whole process may be all that is required. If the errors on typical but known test samples are small enough, semiconductor electronics manufacturers might decide that they can trust the 3D reconstruction software for their use for process control or other industrial measurements.

Conclusions

Virtual samples and their corresponding simulated SEM images offer an opportunity to test 3D reconstruction on test problems where the right answer is known. On our test problem, both Packages A and B performed relatively well with virtual images of a 3D linewidth structure with a rough surface. Both packages failed with virtual images of a 3D linewidth array with uniform zones. The height reconstruction error in the latter case was found to be ≈− 46% whereas a simple “by-hand calculation” approach using the same input data had only −6% error. SEM images of semiconductor linewidth samples will have some homogeneous content or uniform zones. 3D SEM software packages will be useful in the semiconductor industry only if they successfully process images with smooth as well as rough surfaces. The fact that Package A did better than Package B in calculating the linewidth and trenchwidth in the case of simulated images with uniform zones, and that neither Package A nor Package B determined height as accurately as the “by-hand” calculation suggests that there is unused information in the images—and therefore we hope that these stereophotogrammetry algorithms could be improved further.