Twins and Causal Inference: Leveraging Nature's Experiment

Abstract

In this review, we discuss how samples comprising monozygotic and dizygotic twin pairs can be used for the purpose of strengthening causal inference by controlling for shared influences on exposure and outcome. We begin by briefly introducing how twin data can be used to inform the biometric decomposition of population variance into genetic, shared environmental, and nonshared environmental influences. We then discuss how extensions to this model can be used to explore whether associations between exposure and outcome survive correction for shared etiology (common causes). We review several analytical approaches that can be applied to twin data for this purpose. These include multivariate structural equation models, cotwin control methods, direction of causation models (cross-sectional and longitudinal), and extended family designs used to assess intergenerational associations. We conclude by highlighting some of the limitations and considerations that researchers should be aware of when using twin data for the purposes of interrogating causal hypotheses.

Twin studies are most often associated with the estimation of heritability and understanding the extent to which correlated traits share common genetic causes. This focus on genetics often means that the role of twin studies in understanding nongenetic influences on human behavior is overlooked. However, twin studies have demonstrated that around half of the variance in human traits is attributable to nongenetic influences (Polderman et al. 2015). Furthermore, as well as partitioning variance into genetic and environmental influences, it is possible to use twin studies to ask whether associations between exposure and outcome remain after accounting for the confounding effects of shared etiology (common causes). In this manner, twin studies can be thought of as quasi-experimental. By controlling for common causes, twin studies can test what have been referred to as “quasi-causal hypotheses” (Turkheimer and Harden 2014). The use of phrases like “quasi-causality” and “causal inference” (as opposed to straightforward “causality”) highlights that twin studies (like other epidemiological approaches) cannot typically demonstrate causality between two variables—they cannot prove that X (the exposure) causes Y (the outcome). They can, however, show that X does (or does not) continue to predict Y after controlling for shared etiology, thereby strengthening the ability of researchers to make causal inferences. This is the primary focus of our review.

THE TWIN MODEL

Before discussing the use of twin studies in causal inference, it is necessary first to briefly introduce the logic underlying twin studies. The classical twin design typically decomposes phenotypic variance (Vp) into three components: additive genetic (A), shared environment (C), and nonshared environment (E) influences. Additive genetic influences (A) refer to effects of alleles or loci which act in an additive manner (two copies of a risk allele at the same locus confer twice the risk of one copy).⁵ Shared environment (C) refers to environmental effects that make members of the same family similar to one another. In twin studies, the shared environment is typically defined as environmental effects that make twins similar to one another regardless of zygosity.⁶ Because twins share fewer environmental experiences as they age, the effect of the shared environment diminishes with age for most traits (e.g., Haworth et al. 2010). In extended family studies, it is possible to vary the definition of shared environmental effects to include, for example, siblings or entire nuclear families. The nonshared environment (E) refers to effects that make members of the same family different from one another. While typically referred to as the nonshared environment, the E component in a twin model comprises the residual variance in a trait remaining after genetic and shared environmental effects are considered. As such, E will comprise error variance and the effects of random nonshared biological events (Smith 2011; Tikhodeyev and Shcherbakova 2019) as well as true nonshared environmental influences.

In Figure 1, we show the classical univariate twin model used to decompose variance in a trait into A, C, and E components. The method involves comparing the degree of resemblance between pairs of monozygotic (MZ) twins and dizygotic (DZ) twins. Resemblance within MZ twin pairs (r_MZ) is attributable to twins sharing all of their genes and a shared environment (r_MZ = A + C). Resemblance within DZ pairs (r_DZ) is expressed as r_DZ = ½(A) + C; as DZ twins share only half their segregating genes on average, but they are assumed to share the shared environment to the same extent as MZ pairs (100%).

Figure 1.

Path diagram of the univariate twin model. All of our path diagrams follow standard structural equation modeling conventions, whereby measured variables are represented with squares and latent variables are represented with circles. Although not included in the path diagram, the variances of all latent variables are fixed to unity. (a₁₁) Additive genetic effects on phenotype, (c₁₁) shared environmental effects on phenotype, (e₁₁) nonshared environmental effects on phenotype, (A₁) additive genetic variance component, (C₁) shared environmental variance component, (E₁) nonshared environmental variance component. In the classical twin design, the predicted variances of each trait (a₁₁² + c₁₁² + e₁₁²) and the predictions for the covariances (a₁₁² + c₁₁² for MZ and 0.5a₁₁² + c₁₁² for DZ pairs) are fitted to the observed variances and covariances to obtain the most likely estimates for the A, C, and E effects.

In the twin design, heritability is calculated as twice the difference between MZ and DZ correlations: A = 2(r_MZ – r_DZ). Shared environments can be estimated as the difference between the MZ correlation and the heritability: C = r_MZ – A. As nonshared environment is the only influence that acts to make MZ twins different from one another, it can be calculated as the total Vp (often standardized to 1 for ease of interpretation) minus the MZ correlation: E = Vp – r_MZ.

UNDERSTANDING CONFOUNDING USING TWIN MODELS

In their “Top 10 replicated findings from behavioral genetics,” two of the most replicated findings highlighted by Plomin et al. (2016) are of crucial importance to researchers interested in drawing causal inference from associations among variables in nonexperimental studies:

Phenotypic Correlations among Traits Often Show Substantial Genetic Influence

In other words, when two traits correlate, it is often because they share common genetic causes. This can be attributed to the joint influences of pleiotropy (whereby genetic variants associate with multiple traits) and polygenicity (whereby traits are associated with many genetic variants). The possibility of shared genetic influences highlights a major reason why associations among traits should not be interpreted as indicative of causal influences of one trait on another. Importantly, this applies to prospective as well as cross-sectional associations. That is, we cannot assume that genetic factors that influence trait X (exposure) at time point 1 will not influence trait Y (outcome) at time point 2, thus explaining some or all of their covariance. For example, anxiety in childhood is predictive of later depression, and while this may be because anxiety leads to depression, it is also possible that genetic influences underlying childhood anxiety may manifest as depression later in life (Rice et al. 2004).

It is worth considering here that the above discussion assumes horizontal pleiotropy, whereby genetic variants influence both X and Y and induce or inflate covariance between them. However, genetic covariance between X and Y can also come about through vertical pleiotropy, whereby X causally influences Y, resulting in genetic variants associated with X becoming associated with Y. Horizontal pleiotropy constitutes a source of confounding on the association between X and Y, whereas vertical pleiotropy does not. In practice, it is difficult to distinguish these two possibilities, and most twin studies aimed at testing quasi-causal hypotheses do not attempt to do so, instead accounting for genetic covariance among traits and evaluating whether associations persist. Where genetic covariance is attributable to vertical pleiotropy, associations may therefore be overcorrected. However, provided that genetic factors do not explain all of the variance in X, then controlling for vertical pleiotropy as though it were horizontal pleiotropy will not reduce the association between X and Y to zero, because the residual variance in X will still predict Y. Given that no phenotypes are 100% heritable (or indeed 100% familial [Polderman et al. 2015; Plomin et al. 2016]), then where a significant causal effect of X on Y exists, their association should not reduce to zero when controlling for potential familial confounds using twin methods. Implicit here is the expectation that the residual covariance will be large enough to be detected. A caveat to this is that where heritability of X is very high, then power to detect a residual association after accounting for genetic correlation may be limited.

Most Measures of Putative “Environmental Exposures” Show Genetic Influence

Measures that index experiences and environments such as life events, social support, and exposure to toxins (i.e., variables commonly conceptualized as environmental exposures that may influence human traits) correlate with (and may be under the influence of) genetic factors (Jaffee and Price 2007; Kendler and Baker 2007). This is referred to as gene–environment correlation (rGE) and has important consequences for researchers interested in drawing causal inferences from associations between putative environmental exposures and outcomes. That is, if an environmental exposure is predictive of a particular outcome, but both outcome and exposure are heritable, then it is possible that the association is partially or entirely accounted for by shared genetic influences. Again, the joint influences of pleiotropy and polygenicity mean that genetic correlations between putative environmental exposures and outcomes should be considered likely.

Three forms of rGE are typically distinguished from one another and give some insight into why putative environmental variables may be heritable: (1) Passive rGE occurs when people are born into an environment that correlates with their genotype. For example, most children are reared by their biological relatives, so many elements of their environment will be correlated with their genotype. Recently, this concept has been reintroduced into the literature in discussions surrounding “genetic nurture” and “dynastic effects”—the environmentally mediated genetic effects of biological relatives (Fletcher 2011; Fletcher and Lehrer 2011; Eaves et al. 2014; Kong et al. 2018; Young et al. 2019; Ystrom and Eilertsen 2019). See Cheesman et al. (2020) and Hwang et al. (2020) for more discussion on this. (2) Evocative rGE occurs when an individual's genetically influenced traits evoke a particular response from the environment, leading to a correlation between genotype and environment. For example, a child may be genetically predisposed toward characteristics that evoke negative responses from other people. In this manner, evocative rGE can lead to measures of parental negativity correlating with the child's genotype, and thus being heritable (e.g., Neiderhiser et al. 2004, 2007b). (3) Active rGE occurs when an individual seeks out an environment that matches their genotype. For example, an adolescent may actively seek a peer group composed of adolescents similar to them. In this manner, active rGE could lead to a measure of peer group deviancy being heritable (Kendler et al. 2007).

Crucially, any of these forms of rGE can lead to an association between a putative environmental exposure and an outcome without the environmental exposure causally influencing the outcome. Similarly, when an environmental exposure does have an effect, rGE may inflate the magnitude of the association between environment and outcome. To extend the three examples above: (1) Passive rGE can inflate associations between parent and child traits. For example, exposure to maternal depression during childhood is predictive of child emotional and behavioral problems, but this association is inflated by genetic overlap between parent and child traits (Gjerde et al. 2019). (2) Evocative rGE can lead to associations between adolescent behavioral problems and parental negativity, even if parental negativity does not necessarily cause adolescent behavioral problems (McAdams et al. 2013). (3) Active rGE may inflate the association between peer group deviancy and adolescent delinquency (Kendler et al. 2008).

Clearly then, accounting for rGE is important where researchers want to know the extent to which a putative environmental risk factor may have a direct effect on an outcome of interest. That said, it is worth noting that while rGE is often conceptualized and treated as a cause of confounding between exposure and outcome, there are situations in which rGE can provide a tool through which the effects of environmental exposures can be assessed. For example, where variants are causally predictive of exposure, they can be used as instrumental variables to assess links between exposure and outcome (Gage et al. 2016; Millwood et al. 2019; Richmond 2020).

MULTIVARIATE TWIN MODELS AND CAUSAL INFERENCE

A major challenge when testing associations between exposures and outcome in nonexperimental research settings is the effective identification and measurement of confounding variables. Confounders may be unknown and when not accounted for they will have the effect of biasing estimates of associations. Furthermore, it is likely that most associations could be confounded by many shared influences. For example, the consumption of alcohol has been shown to correlate with a range of health outcomes in positive and negative directions. Most of these associations could potentially be confounded by a wide range of socioeconomic, cultural, dietary, and health-behavior-related influences. Identifying and controlling for all of these confounders would be a huge (and essentially impossible) challenge, and including them all in a regression analysis would reduce the power of that analysis to identify any remaining effects. Even if all relevant confounders could be included, errors in the measurement of these confounders could still vitiate the ability to statistically control for them, and thus lead to biased effect estimates. Twin data can be used to circumvent many of these issues by controlling for genetic and shared environmental influences common to exposure and outcome. In this manner, multivariate twin models can control for common causes without the need to identify and measure specific confounders.

It is beyond the scope of this paper to review all multivariate models to date applied to twin data but, suffice it to say that such data can be used to explore etiological overlap among traits, and between exposures and outcomes, in many ways. For the purpose of this review, we focus on models that are (or can be) used in attempts to draw causal inference. We do not claim to cover all such models, but the underlying logic that we discuss will typically extend to twin models we do not cover.

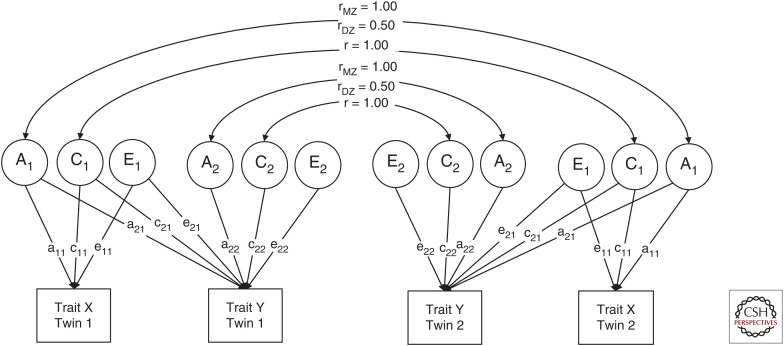
Where univariate twin models are used to decompose the variance of a trait into genetic and environmental influences, multivariate models are concerned with decomposing covariance among traits in a similar manner. Figure 2 shows how to specify a twin model such that the covariance between two variables, X and Y, is decomposed into A, C, and E components in the manner of a Cholesky decomposition.

Figure 2.

Cholesky decomposition twin model.

The Cholesky decomposition disaggregates the variance in trait X into genetic (A₁), shared environmental (C₁), and nonshared environmental (E₁) factors, which have their effects on X via paths a₁₁, c₁₁, and e₁₁. These factors are also able to account for variance in trait Y via paths a₂₁, c₂₁, and e₂₁. It is these paths that account for the covariance between trait X and Y. By comparing MZ and DZ cross-twin, cross-trait correlations (e.g., correlations between trait X in twin 1 and trait Y in twin 2), it is possible to decompose the covariance among traits. The residual variance in trait Y (that is not accounted for by A₁, C₁, and E₁) is decomposed into A₂, C₂, and E₂ factors. In Table 1, we show this with a variance–covariance matrix that details how the Cholesky decomposition is specified.

Table 1.

Variance–covariance specification for a bivariate Cholesky decomposition

	Trait X Twin 1	Trait Y Twin 1	Trait X Twin 2	Trait Y Twin 2
Trait X Twin 1	a112 + c112 + e112	a11*a21 + c11*c21 + e11*e22	.5*a112 + c112	a11*.5*a21 + c11*c21
Trait Y Twin 1	a11*a21 + c11*c21 + e11*e22	a212 + c212 + e212 + a222 + c222 + e222	a11*.5*a21 + c11*c21	.5*a212 + c212 + .5*a222 + c222
Trait X Twin 2	a112 + c112	a11*a21 + c11*c21	a112 + c112 + e112	a11*a21 + c11*c21 + e11*e22
Trait Y Twin 2	a11*a21 + c11*c21	a212 + c212 + a222 + c222	a11*a21 + c11*c21 + e11*e22	a212 + c212 + e212 + a222 + c222 + e222

Variances are highlighted in pale blue with black outlines on the diagonal. MZ twin covariances are given below the diagonal and DZ twin covariances are given above the diagonal. Within-twin, cross-trait covariances are highlighted in dark blue. Cross-twin, within-trait covariances are highlighted in pale green. These can be used to decompose variances in X and Y. Cross-twin, cross-trait covariances are highlighted in darker green. These are used to decompose covariance between X and Y. Note that e paths are never involved in covariance between twins, only within.

In Figure 3, we demonstrate how the decomposition of covariance among traits can be used to assess whether an association remains and/or is attenuated after accounting for the effects of genetic and shared environmental influences common to both traits. Figure 3i shows a standard linear regression of Y (the outcome or dependent variable) on X (the exposure or independent variable). This model assumes a causal relationship running from X to Y via B_yx. However, this relationship may be confounded by a common causal variable. In Figure 3ii, we show how such a potential confounding variable may operate, and how to model this possibility wherein both X and Y are regressed on a potential confounding variable, Z. In this model B_yx, is the effect of X on Y after controlling for the confounding effects of Z.⁷ In Figure 3iii, we show the partial path diagram for the previously introduced bivariate Cholesky decomposition (for a single individual; in Fig. 2, we show how the same model is specified for twin pairs). We have rearranged the model slightly to highlight similarities to the model in Figure 3ii and to demonstrate how it can be used to control for latent genetic and environmental confounders without the need to identify and measure them. Here, the covariance structure of the data combined with the logic of the twin model enables the decomposition of covariance into A, C, and E components. In this model, A₁ correlates between members of a twin pair (1.00 for MZ twins and 0.50 for DZs) and indexes genetic influences on X and on correlations between X and Y (within and between twins, as specified in Fig. 2 and Table 1). In this manner, A₁ accounts for the confounding effects of common genetic influences affecting both X (the exposure) and Y (the outcome). C₁ is perfectly correlated between twins of both zygosities and indexes shared environmental influences on X and on correlations between X and Y (within and between twins). As such, C₁ accounts for familial environmental influences that may confound the association between X and Y. E₁ does not correlate between twins so only indexes the within-person correlation between X and Y after accounting for the genetic and environmental influences that make members of a twin pair similar to one another. In this manner, A₁ and C₁ account for latent genetic and shared environmental confounders in the same way that Z accounts for measured confounders. The advantage in using twin data is that researchers do not have to identify all of the potential confounders that might account for or inflate the association between X and Y. By using twin data, all potential confounders shared by members of a twin pair (genetic and shared environmental influences) can be accounted for.

Figure 3.

Modeling causality. In the above models, B_yx is the causal effect of X on Y. In model i, V_x denotes the variance of X, and R_y denotes the residual variance of Y (the variance of Y remaining after regressing out the effects of X). In model ii, V_z denotes the variance of Z, and R_x and R_y denote the residual variances of X and Y (variance remaining after regressing out the effect of Z (on X) and Z and X (on Y)). Twin models shown are partial path diagrams for a single individual. All latent factors have a variance of 1 (not shown).

In Figure 3iv, we show how twin data can be used to create a model very close to that of 3ii. Arguably, given that B_yx is not recovered from a Cholesky decomposition, the model in Figure 3iv provides the “cleanest” test when using twin data to assess whether the association between X and Y survives correction for common confounders, although Cholesky decompositions are more often applied in the literature. Importantly though, the models shown in Figure 3iii and 3iv will result in the same conclusions being drawn if fitted to the same data. That is, if B_yx explains covariance between X and Y in model 3iv, then the path running e₁₁*e₁₂ in model 3iii will also do so. Either of these paths can be used to evaluate whether the association between X and Y persists after accounting for common genetic and shared environmental influences (Turkheimer and Harden 2014). It should be noted, however, that such a residual association does not on its own constitute evidence of causality for at least two reasons. First, nonshared environmental confounders are unaccounted for and could still explain some or all of the associations between X and Y. It is of course possible to further control for additional observed nonshared environmental confounders (e.g., differences in birth weight or baseline levels of the outcome). However, challenges encountered in identifying and measuring specific nonshared environmental influences may make this a challenging task (Neiderhiser et al. 2007a). Second, reverse causation can bias estimates resulting from these models, that is, the estimate of the effect of X on Y can (partially) reflect the effect of Y on X. Longitudinal models with clear temporality (e.g., birth weight to attention-deficit/hyperactivity disorder [ADHD] symptoms) or repeated measures of the exposure and the outcome can mitigate but not always fully account for reverse causation.

THE COTWIN CONTROL DESIGN

The application of structural equation models to decompose covariance among variables is one technique through which researchers can use multivariate twin data to ask the question “does the association between X and Y persist after accounting for genetic and shared environmental confounds?” Another method involves strengthening causal inference by using one twin in a pair as a direct matched control for the other. This approach is known as the “cotwin control design” in the field of behavioral genetics and as one implementation of the “fixed effects” approach in econometrics. Whereas the biometrical decomposition of variance discussed above is most often used to dissect the etiological architecture of phenotypes, the main purpose of the cotwin design is causal inference.

The cotwin control design is best understood within the counterfactual framework for causal inference (Lynch 2020). In the (theoretical) counterfactual situation, a given individual receives a treatment (or is exposed to a risk factor value) and, at the same time, the same individual does not receive the treatment. In this ideal situation, the treated individual is literally the same as the control individual, the only difference being the treatment. It thus becomes possible to estimate the causal effect of that treatment, even at the individual level. Naturally, in real life, the same individual cannot at the same time receive and not receive a treatment, so strict causal inference is impossible. However, all causal inference designs can be conceived as aiming to approximate this ideal counterfactual situation (Pingault et al. 2018). One way to approximate this situation is to find the best match possible. This is when twins, and in particular MZ twins, come into play. Indeed, an exposed twin shares all of their genetic material and, by definition, their shared environment with the nonexposed cotwin. At a basic level, the cotwin design involves comparing outcomes between the exposed and nonexposed twin, and thus controlling for genetic and shared environmental influences. If the risk factor (e.g., smoking) causes the outcome (e.g., lung cancer), we should expect that on average smoking twins will have a higher incidence of lung cancer than their nonsmoking cotwins. If there was no difference in the incidence of lung cancer in the smoking versus nonsmoking twin, then this would suggest the relationship between the risk factor and the outcome is noncausal and due to genetic or shared environmental confounding.

The cotwin control design is often referred to as the “discordant twin design” when the exposure is binary, and the “twin differences design” when the exposure is continuous. A comprehensive review of regression models used to fit the cotwin design can be found in Carlin et al. (2005). For continuous exposure and outcome, twin differences in the exposure and the outcome are first computed. The causal effect is estimated by a simple regression without intercept of the twin differences in the outcome on the twin differences in the exposure. A more complex multilevel model can be fitted, modeling both the within-family estimates and the between-family estimates. The within-family estimates will give exactly the same estimates of the causal effect as the aforementioned simpler approach. This type of model must allow for both an intraclass correlation (the within-twins correlation), which affects the estimate, and robust standard errors. The phenotypic relationship between the exposure and the outcome is a weighted mean of the within- and between-family estimates. They can be fitted in a variety of statistical frameworks that provide very similar estimates and confidence intervals, including mixed models, generalized estimating equations, and structural equation modeling.

The cotwin control design has been widely used for causal inference, confirming for example the causal link between smoking and lung cancer (Hjelmborg et al. 2017), demonstrating the impact of bullying victimization on childhood mental health (Silberg et al. 2016), and suggesting that birth weight impacts the development of ADHD symptoms (Lim et al. 2018). Findings from the cotwin design can shed new light on the role of risk factors. For example, simple associations suggest that bullying victimization is a risk factor for most mental health outcomes over the long term, whereas twin differences designs point toward more specific effects (e.g., prominently on anxiety, depressive symptoms, and self-harm) and shorter-term effects (Singham et al. 2017). More elaborate longitudinal models can also be built based on twin differences. For example, a latent growth model has been implemented to show that differences in birth weight predict ADHD symptoms from childhood to adolescence, but that the size of the effect decreases with age, consistent with a partial “catch-up” effect (Lim et al. 2018). Cross-lag models can be implemented with twin differences to look at reciprocal influences between two phenotypes over time, while controlling for genetic and shared environmental confounding (Cecil et al. 2012).

Comparing the Cotwin Control Design with the Classical Twin Decomposition

The cotwin control design and the classical twin decomposition can be conceived as two approaches to decomposing a relationship: The former decomposes covariance among variables into within- and between-family effects, the latter into genetic, shared environmental and nonshared environmental components. In the majority of instances, when using twin samples for causal inference, these two methods are equivalent and should lead to the same conclusions. That is, when using the cotwin control design to focus on differences between MZ twins (within-family effects), researchers are in fact focusing on nonshared environmental variance (the E component in biometric twin models). When asking whether differences in X predict differences in Y, they are asking whether nonshared environmental variance in X predicts nonshared environmental variance in Y. Such statistical equivalence does not mean that one or the other method should be considered redundant. Twin decompositions will be of use to researchers interested in quantifying the relative effects of genetic, shared environmental and nonshared environmental correlations on covariance among variables. Conversely, cotwin control studies are not appropriate to examine the genetic architecture of traits; they have been used and are most useful for causal inference research as a particular implementation of fixed-effect models.

In the context of causal inference, both biometric decomposition and twin differences approaches suffer from the same two major limitations of unobserved, nonshared environmental confounders and the possibility of reverse causation. However, while twin differences and biometric decompositions are usually equivalent, there may be circumstances in which one design is appropriate and the other is not. For example, a version of the twin difference design has been applied to a sample of genotyped DZ twins to explore the extent to which differences in polygenic scores predicted differences in several early-life outcomes (Selzam et al. 2018, 2019). The intention was to control for the potential confounding effects of those influences shared within DZ twin pairs including population stratification, assortative mating, and indirect genetic effects from parents (genetic nurture). Genetic nurture occurs for example when genetic variants for education in the parents affect parental education, which in turn environmentally impacts child education. Such effects, although originating in the parental genotypes, are environmentally mediated and do not reflect direct genetic effects of the child genotype on the child phenotype (Eaves et al. 2014; Kong et al. 2018; Young et al. 2018; Hwang et al. 2020). Selzam et al. (2019) showed that twin differences in polygenic scores predicted differences in height, body mass index (BMI), intelligence, educational achievement, and ADHD symptoms. However, the within-family prediction was attenuated for intelligence and educational attainment, indicating a degree of confounding. This finding required the use of a twin differences approach. A biometric decomposition would not be appropriate here as it would be inappropriate to treat polygenic scores as phenotypes (as any polygenic score would correlate 1 within MZ twins and 0.50 on average in DZ twins, resulting in A = 100%, which would not capture and adjust for the genetic nurture effects).

DIRECTION OF CAUSATION IN TWIN MODELS

Longitudinal Data

In the models we have discussed thus far, the assumption has been that the direction of causation (DoC) runs from X to Y and not vice versa. However, often it is not possible to know with certainty whether this is the case. For example, in cross-sectional data, it may well be that Y causes X but it would not be possible using the models we have discussed to identify the true DoC. An often-used technique to identify the direction of effects is to use longitudinal data in which variables have a temporal order to them. For example, in a bivariate Cholesky decomposition, if X was measured before Y, one could argue that the data should be modeled such that X predicts Y and not vice versa. That said, temporal ordering of measurement is often not justification enough to assume that a variable at time 1 should be modeled as a cause of a variable at time 2. For example, if school performance were measured at time 1 and IQ at time 2, the temporal ordering of measurement would not justify modeling the data based on the assumption that school performance causes IQ. Ideally, IQ and school performance would each be measured at time 1 and time 2, so that we can ask whether school performance prospectively predicts IQ after accounting for the correlation between IQ and school performance at time 1 and stability in IQ between time 1 and time 2.

Autoregressive cross-lagged models are frequently used so that prospective associations among variables can control for the combined effects of contemporaneous associations among traits and across time stability within traits. For example, in Figure 4i, the prediction from X1 to Y2 controls for the effects of Y1 on Y2 and the covariance between X1 and Y1 (although see Hamaker et al. [2015] for a critique of some misperceptions regarding autoregressive cross-lagged models and alternative specifications). A bivariate Cholesky decomposition of X1 predicting Y2 would potentially capture the confounding effects of Y1 through the genetic and shared environmental influences common to all but would not capture potential nonshared environmental confounders indexed by Y1.

Figure 4.

A phenotypic autoregressive cross-lagged model and partial path diagrams of a twin autoregressive cross-lagged model.

Malanchini et al. (2017) present a biometric genetic version of the autoregressive cross-lagged model in which four variables are decomposed into genetic, shared environmental and nonshared environmental components, and each of these components allowed to predict one another in the manner of an autoregressive cross-lagged simplex model (see Fig. 4ii–iv). In this model, the cross-lagged E predictions tell us whether, for example, X1 predicts Y2 after accounting for genetic and shared environmental influences common to these two variables and those influences—including nonshared environmental influences—shared with Y1.⁸ Malanchini et al. (2017) demonstrated the utility of this model by showing that although the phenotypic cross-lags between reading motivation and reading achievement in children were of equal magnitude, only the prediction from motivation to achievement survived correction for shared etiologies.

An alternative biometric autoregressive cross-lagged model to that presented here comprises a combination of the Cholesky decomposition and the correlated factors model (where, e.g., in Fig. 4ii, causal effects would run from A_x1 and A_y1 directly to X2 and Y2 rather than via A_x2 and A_y2; see Torvik et al. 2017, 2019). This model has been used to show that social anxiety disorder prospectively predicts alcohol use disorder—and not vice versa—after accounting for shared etiology (Torvik et al. 2019).

Cross-Sectional Data and Direction of Causation Twin Models

While longitudinal data is typically considered ideal for identifying the direction of effects, it is not always available. In such cases, cross-sectional twin data can, to some degree, help strengthen causal inference between two traits X and Y. The DoC twin model (Heath et al. 1993; Duffy and Martin 1994) is distinct from most of the models described here in that the focus is not on controlling for the confounding effects of common etiologies. Rather it is on determining the likely direction of effects between two variables where temporal ordering is not present or is unknown (see Fig. 5i). That is, the extent to which an association between X and Y is driven by X predicting Y versus Y predicting X. The power of this design is derived from the differential predictions that come about regarding the cross-twin, cross-trait correlations for MZ and DZ twin pairs when comparing the two potential causal models (X causes Y vs. Y causes X). Differences in the covariance structure are predicted where the etiological structure (i.e., the relative importance of A, C, and E) is distinct for trait X versus trait Y. For example, where A affects trait Y but not X, and C affects trait X but not Y.

Figure 5.

The direction of causation (DoC) twin model.

Figure 5 contains examples in which trait X is under the influence of C and E, and trait Y is under the influence of A and E. In 5ii, trait X causes Y, and in 5iii, Y causes X. If X causes Y, the expected cross-twin, cross-trait correlation (i.e., correlation between X in twin 1 and Y in twin 2, or Y in twin 1 and X in twin 2) can only be explained via the variance of variable X. Because variable X is influenced by C and E only, the cross-twin, cross-trait correlations will be driven by C. If C is the only thing that explains correlations between, for example, X in twin 1 and Y in twin 2, then these correlations will be the same for MZs and DZs (because C, the shared environment, by definition influences MZ and DZ twins equally). However, if Y causes X, then the cross-twin, cross-trait correlations will be driven by variance in variable Y. Given that Y in our example is under the influence of A, the cross-twin, cross-trait correlations will be larger for MZs than DZs (Gillespie and Martin 2005). Whereas our example involves traits of very different etiologies, it is also possible to distinguish the direction of causation when the two traits have a similar but distinct etiology, for example, where trait X is under greater genetic influence than trait Y. In this manner, it has been shown that for the relationship between autism spectrum disorder and other mental health problems, best-fitting models suggest a unidirectional phenotypic influence of hyperactivity on identification of ASD. Relationships between ASD and emotional symptoms and conduct problems were best explained by correlated genetic and environmental factors, respectively (Tick et al. 2016).

A major assumption of the DoC model is that the association between X and Y is causal, that is, that it is not attributable to common causes unmodeled. In theory, it is possible to allow for correlations between etiological components of X and Y (i.e., between A₁ and A₂ or C₁ and C₂); however, doing so will reduce the ability of the model to distinguish the direction of effects. In practice, it is more usual for researchers to compare, for example, a Cholesky decomposition of Y on X with a DoC model and then select the model that provides the best fit to the data (e.g., Gillespie et al. 2012).

One way of thinking about the DoC model is that the variance components of one trait are being treated as instrumental variables in their prediction of the other trait. That is, their effects only operate through the causal effect of the intermediate trait. For example, A₂ can only predict trait X through trait Y. This is an assumption of the model and is analogous to the use of genetic variants and polygenic scores as instrumental variables in those methods collectively referred to under the umbrella term Mendelian randomization (Davey Smith and Ebrahim 2003; Smith and Ebrahim 2005; Davey Smith and Hemani 2014). Hwang et al. (2020) discuss extensions to the DoC model that incorporate Mendelian genetic tools to further strengthen the ability to draw causal inferences using this model. An alternative version of the DoC has also been suggested, in which the DoC between latent C and E factors (as opposed to among phenotypes) can be detected using datasets with non-normally distributed variables (Ozaki and Ando 2009).

EXTENDED FAMILY DESIGNS

Twin models make use of the fact that MZ and DZ twins differ in how genetically related they are to one another, and this information is used to infer how important genetic and environmental factors are in explaining variance in a trait and covariance among traits. However, the logic of the twin design is not confined to use in twin samples only. Indeed, it is possible to apply biometric ACE models to any datasets comprising differentially related relatives. For example, it is possible to use samples comprising siblings and half-siblings or cousins and half-cousins to estimate heritability and to explore the nature of covariance among phenotypes.⁹ Various extended family models have been proposed that make use of multigenerational data to examine the etiology of traits measured in two or more generations (Truett et al. 1994; Keller et al. 2009; Maes et al. 2009). Such models allow for the modeling of assortative mating, gene–environment covariance, and other possibilities not feasible in a single-generation dataset. Extended family data also provides the opportunity for researchers to examine associations between family members. That is, they have the opportunity to ask questions about whether family members have an effect on one another, after accounting for their relatedness. For example, using data comprising twins and their children, it is possible to assess whether associations between parents and children persist after accounting for genetic relatedness (D'Onofrio et al. 2003; Silberg and Eaves 2004; McAdams et al. 2014).

Children-of-Twins-and-Siblings Models

Often, researchers are interested in the potential for parents to influence the development of their children. For example, associations between parenting behaviors and child behavioral and emotional traits are often interpreted in ways that imply that parenting causes child behavior (and/or vice versa). And intergenerational similarities in personality, psychopathology, and behavior are often interpreted as though exposure to a parent trait causes the development of the child trait. However, in most instances, parents and children are genetically related to one another and share an environment. As such, parent–child associations are likely to be at least partially attributable to the confounding effects of shared genetic and environmental influences.

Using samples comprising twins and their children, it is possible to decompose intergenerational associations into genetic and environmental components in much the same way that samples of twins can be used to decompose within-person associations. Where twin studies use differences in MZ and DZ cross-twin, cross-trait correlations, children-of-twin studies use differences in avuncular correlations (that between a twin and their cotwin's child/ren). As with twin data, children-of-twin data can be analyzed using a variety of models (Heath et al. 1985) and can be extended to include siblings (as well as twins) with children (Kuja-Halkola et al. 2014; Hannigan et al. 2018), multiple offspring per parent (McAdams et al. 2018), and spouses (Silberg et al. 2010). In Figure 6, we show a simple version of a children-of-twins model comprising MZ and DZ twin pairs with one child per twin. In this model, both parent and child phenotypes are decomposed into genetic and environmental influences. In the child generation, this is possible by comparing cousins whose parents are MZ twins to those whose parents are DZ twins (rG = .25 and .125, respectively). If multiple children per twin are included, then siblings can be included in these estimations (rG = .50). Because cousins do not share a nuclear family environment, C (as typically defined) cannot be estimated in the offspring generation without the use of siblings. The intergenerational association between parent and child is decomposed into a genetic component (A₁′), an extended family component (C₁′),¹⁰ and the remaining residual phenotypic association (p). If this “p” path predicts the child trait, then this indicates the association between parent and child phenotypes remains after accounting for shared genetic and environmental influences.

Figure 6.

Children of twins structural equation model. (a₁) Additive genetic effects on parental phenotype, (c₁) shared environmental effects on parental phenotype, (e₁) nonshared environmental effects on parental phenotype, (a₁′) genetic effects common to parental phenotype and offspring phenotype, (c₁′) extended family environment effects on offspring phenotype, (a₂) genetic effects specific to offspring phenotype, (c₂) shared environmental effects on offspring phenotype (not estimable using cousin data), (e₂) nonshared environmental effects on offspring phenotype, (p) phenotypic effect of parent on offspring, (NB) the pathway between A₁ and A₁′ is fixed to 0.50 because parents and children share 50% of their genome. To avoid overcomplicating path diagrams, variance paths have been omitted but for all latent factors, variance = 1. For A₁′ this means that residual variance (after accounting for the path between A₁ and A₁′) is 0.75.

Models similar to that shown in Figure 6 have been used to examine a range of associations between parent and child traits, demonstrating, for example, that maternal depression during pregnancy does not predict later childhood emotional and behavioral problems after accounting for genetic confounding (Hannigan et al. 2018), and that maternal smoking during pregnancy predicts birth weight and preterm birth but not cognitive abilities or externalizing behaviors in offspring after accounting for genetic confounds (Kuja-Halkola et al. 2014). Whereas most of these analyses are bivariate, these models are just as flexible as other twin models, so where appropriate data is available it will be possible, for example, to ask questions about the DoC between parent and child (Narusyte et al. 2008), longitudinal associations between parent and child, and gene–environment interplay.

TWIN DATA AND EXPERIMENTAL DESIGN

Thus far, we have discussed quasi-experimental research designs using samples of twin pairs. However, another (rarely employed) approach involves designing experiments using twin samples. Typically, experiments involve the random assignment of individuals to treatment and control conditions, with this random assignment intended to account for any confounders that might exist in a nonexperimental situation. Matched-pair designs go one step further and match pairs of subjects in the control and experimental conditions on any potentially important factors that might make pairs different from one another. Using twin data such that twin 1 receives a treatment and twin 2 does not provides an extreme example of this matched-pair design. Whereas twin 1 and 2 are members of an MZ pair, they will be matched on all genetic and shared environmental influences. Examples of this method include studies demonstrating how supplementation with vitamin C has no effect on self-reported incidences of the common cold (Carr et al. 1981; Martin et al. 1982).

An alternative take on the use of twins in experiments comes from a study by Haworth et al. (2016), in which they estimated changes in etiological influences on well-being and mental health in response to an online intervention delivered to all twins in a sample. They found that mean levels of well-being and mental health improved across the study, and that changes in well-being were accounted for by changes in nonshared environmental influences. However, while means changed and new nonshared environmental influences were evident postintervention, estimates of the relative importance of A, C, and E in explaining variance did not vary in magnitude pre- versus postintervention. These findings highlight a fundamental characteristic of biometric (ACE) twin models; such models focus on population variance in traits, not population means. Means can change without necessarily affecting the relative importance of genetic, shared environmental and nonshared environmental components.

DISCUSSION

In the preceding review, we have covered several ways in which twin data can be used by researchers interested in testing quasi-causal and causal hypotheses. As with all statistical models, those we have presented require careful and considered interpretation. In the following section, we explore some issues that we believe are important when attempting causal inference with twin data.

Nonshared Environmental Confounds Are Not Accounted For

Most of the models presented in this chapter are focused on controlling for genetic and shared environmental sources of confounding, and do not do anything to control for potential nonshared confounders. As such, the potential for nonshared environmental influences to confound associations should always be considered. For example, in an analysis in which smoking is the predictor, twins who smoke more than their cotwins may also drink more alcohol, such that alcohol rather than the putative risk factor—smoking—may be responsible for adverse outcomes. It is possible to statistically control for twin differences in covariates (e.g., alcohol consumption), but the models presented will still assume that there are no additional (unobserved) nonshared environmental confounders. To the extent that there are nonshared environmental confounders that are not accounted for, any residual association between predictor and outcome will be inflated.

Some Environments of Interest Do Not Differ between Twins

It is worth noting that some environmental variables, such as childhood socioeconomic status (SES), or neighborhood characteristics during childhood, will not typically vary between twins. That is, where twins are reared by the same parents, in the same household, go to the same school, and live in the same neighborhood, they will not differ in terms of environmental measures related to parents, households, schools, and neighborhoods. This precludes the estimation of heritability of such variables using the twin design (i.e., MZ and DZ correlations will both be 1 in these cases). It also precludes the calculation of difference scores in the cotwin control design. Importantly, this does not necessarily mean that such variables are not under the influence of genetic factors, it is simply a limitation of the twin design that heritability cannot be estimated for variables that do not differ within twin pairs. As such, it is not possible to correct for etiological overlap involving such variables.

One solution to this problem lies in the use of intergenerational multiple-children-of-twins-and-siblings models. If a dataset comprises twins and siblings in the parent generation as well as the offspring generation (which would also then include cousins), it becomes possible to model the etiology of traits that can differ among siblings in the parent generation, such as, for example, parental SES. By modeling genetic and environmental relatedness between parents and children, it then becomes possible to account for genetic overlap between parent trait and child outcome. For example, this method has been used to demonstrate that parental educational attainment is predictive of child ADHD symptoms and academic problems at school, but not child depression symptoms, after accounting for genetic relatedness (Torvik et al. 2020).

Statistical Power

Much has been written about statistical power and twin studies (e.g., Visscher 2004; Verhulst 2017; Ahmadzadeh et al. 2020). In univariate studies, power to detect A (defined as twice the difference between MZ and DZ correlations) is contingent upon MZ and DZ correlations being significantly different from one another. Power to detect C is typically lower than that to detect A, and relies on twins being more similar to one another than heritability accounts for. E will always be nonzero because it contains error variance.

When using bivariate and multivariate models as discussed in this article, the focus is on whether residual associations remain after accounting for potential genetic and shared environmental confounds. Whereas E (residual variance after accounting for A and C) will always be nonzero in univariate models that explain variance in a single trait, this is not the case for covariance among traits, where residual covariance attributable to E can equal zero. As such, when decomposing covariance among traits for the purposes of causal inference, there should be two primary concerns relating to power:

1. How much power is there to detect genetic and shared environmental influences on the covariance?

2. If power to detect genetic and shared environmental influences on covariance is adequate, how large would the residual covariance need to be to be detected?

Where covariance among traits is low, or sample sizes are small, power to detect A or C influences on covariance will be low, and this may lead to incorrect conclusions being drawn regarding the significance and/or magnitude of residual covariance terms. Researchers should therefore be careful when interpreting residual covariance and consider how much power they have to detect confounding. Power calculations can be performed by simulating a dataset in which the sample composition, covariance, and proportions of covariance attributable to A, C, and the residual/E are known. By varying these proportions, researchers can evaluate the power they have in their own data (e.g., see Verhulst 2017 and associated website).

Measurement Error

Measurement error is aggravated when computing difference scores, to the extent that traits are correlated within pairs. As a result, estimates from MZ differences may be attenuated compared to estimates in DZ differences, which themselves are attenuated compared to phenotypic estimates, even in the absence of confounding. This may lead to an underestimation of causal effects. Causal estimates can also be biased when the magnitude of measurement error is different for the risk factor and the outcome. This can be dealt with by directly modeling measurement error when possible, or by conducting a sensitivity analysis to estimate how much measurement error would be needed to substantially change the conclusions.

The Importance of Context

When using twin data to account for genetic or environmental overlap between two traits, one can think of the estimate of shared genetic influences as a “bivariate heritability” estimate—an estimate of genetic influence on covariance (rather than variance). Like heritability estimates, these bivariate heritability estimates are population-specific and should not be assumed to necessarily generalize to other populations. Estimates of genetic and environmental influences on variance are known to vary with age (Haworth et al. 2010), across socioeconomic gradients (Tuvblad et al. 2006), and between countries (Hur 2008; Ball et al. 2009; Xu et al. 2015). In other words, contextual conditions have an effect on how much variance in a trait is explained by genetic and environmental variance in a population. This is also likely to be true for bivariate estimates and thus has implications for the use of twin data for the purposes of causal inference. If we find that the association between X and Y is entirely attributable to genetic overlap in our sample, this does not necessarily mean that the same will be true in other samples. Indeed, it may even be possible that the nature of the association varies within a sample. When this is deemed plausible, it is worth considering the inclusion of moderators in models where feasible. For example, it is conceivable that parental SES could moderate the nature of the association between maternal depression and child internalizing such that at high levels of SES (where social and economic resources are abundant), the association may be entirely genetic, but at low levels of SES (where support may be less available), there could be a causal effect of maternal depression on child internalizing. Where moderation is taking place but is not modeled, estimates regarding the association between X and Y will be biased.

SUMMARY

In this review, we have described some of the ways in which twin data can be used to interrogate causal hypotheses, particularly where experimental manipulation is not possible. The advantage of using twin and family data lies in the ability to control for latent genetic and shared environmental sources of potential confounding. This provides researchers with a powerful alternative to the often prohibitively challenging task of explicitly identifying and collecting data on potential confounds. We would argue that where an association of interest survives correction for the potential confounding effects of common genetic and shared environmental effects, then this should strengthen the argument for drawing causal inferences from the data (always bearing in mind the quasi-experimental nature of the design used). For example, if X predicts Y after controlling for latent genetic and shared environmental effects that influence both variables, then it is possible that X causes Y and less likely that the association is attributable to common causes. If so, then interventions aimed at increasing or reducing X may have an effect on Y. However, if the association between X and Y does not persist after controlling for latent genetic and shared environmental confounds, then it is unlikely that X causes Y. It should therefore be considered less likely that intervening to alter X will also alter Y.

In discussing the potential inherent in using twin and family data to interrogate causal hypotheses, we have highlighted some of the limitations, assumptions, and nuances that researchers should consider when doing so. It is worth noting, however, that many of these limitations are shared with other research methods and broadly relate to the generalizability of findings, and the importance of being cognizant of assumptions when interpreting results. Providing these issues are borne in mind, twin studies provide an extremely powerful tool for researchers interested in teasing apart potential causality from the effects of unknown confounders—a fundamental and central goal of all scientists concerned with the study of human beings.

For readers interested in using twin data for causal inference, a list detailing twin registries around the world, with links to detailed overviews of each, is published periodically in the journal Twin Research and Human Genetics (see Hur et al. 2020 for the most recent version).