Abstract
This paper aims to develop an automatic method to segment pulmonary parenchyma in chest CT images and analyze texture features from the segmented pulmonary parenchyma regions to assist radiologists in COVID-19 diagnosis. A new segmentation method, which integrates a three-dimensional (3D) V-Net with a shape deformation module implemented using a spatial transform network (STN), was proposed to segment pulmonary parenchyma in chest CT images. The 3D V-Net was adopted to perform an end-to-end lung extraction while the deformation module was utilized to refine the V-Net output according to the prior shape knowledge. The proposed segmentation method was validated against the manual annotation generated by experienced operators. The radiomic features measured from our segmentation results were further analyzed by sophisticated statistical models with high interpretability to discover significant independent features and detect COVID-19 infection. Experimental results demonstrated that compared with the manual annotation, the proposed segmentation method achieved a Dice similarity coefficient of 0.9796, a sensitivity of 0.9840, a specificity of 0.9954, and a mean surface distance error of 0.0318 mm. Furthermore, our COVID-19 classification model achieved an area under curve (AUC) of 0.9470, a sensitivity of 0.9670, and a specificity of 0.9270 when discriminating lung infection with COVID-19 from community-acquired pneumonia and healthy controls using statistically significant radiomic features. The significant features measured from our segmentation results agreed well with those from the manual annotation. Our approach has great promise for clinical use in facilitating automatic diagnosis of COVID-19 infection on chest CT images.
Keywords: COVID-19, Chest CT, Pulmonary parenchyma segmentation, Deep learning, 3D V-Net
1. Introduction
The coronavirus disease 2019 (COVID-19) is spreading rapidly and widely since the end of 2019. By December 24th, 2020, more than 78.7 million COVID-19 cases have been confirmed worldwide, and what is even worse, 1.73 million of the patients lost their lives [1]. Early detection is essential because infected subjects with or without symptoms who were not successfully detected spread the virus to healthy people [2]. Real-time reverse transcriptase polymerase chain reaction (rRT-PCR) is recognized as the gold standard for detecting COVID-19 [3]. However, it is time-consuming and suffers from a high false negative response. Moreover, many countries are not ready for PCR tests in the early stage of the coronavirus pandemic while imaging devices are widely available; thus a diagnosis system based on imaging is practical and vital for early prevention and diagnosis of COVID-19 infection [4].
Imaging techniques, such as chest X-Ray (CXR) and chest computed tomography (CT), have been widely used to assess pulmonary lesions. Although X-Ray scanners demonstrate higher accessibility, most COVID-19 subjects show bilateral pulmonary parenchymal ground-class opacities and lung consolidation with a rounded morphology [5], making it difficult to distinguish COVID-19 infection from CXR scans. In contrast, 3D chest CT is effective in discriminating soft tissue and visualizing the morphological patterns of pulmonary parenchyma, which has been widely used for the diagnosis of COVID-19 and regarded as an important complement to rRT-PCR tests [3,6]. Automatic extraction and computer-aided interpretation of lung regions of interest (ROIs) play a key role in assisting radiologists to detect the infection and assess the progression, and thus benefit the precise diagnosis and treatment.
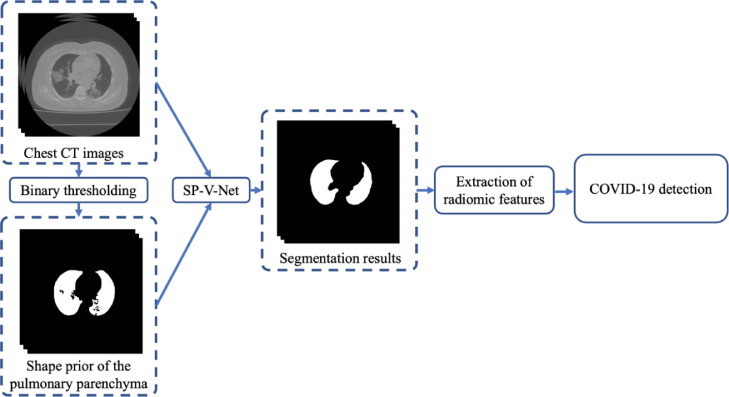
Medical image processing using deep learning plays a vital role due to its accurate and robust performance [7]. Some researchers have dedicated their studies to computer vision using deep learning for COVID-19 diagnosis with chest CT. Unlike most existing AI approaches in the diagnosis of COVID-19, which are focused on the end-to-end classification, our goal is to extract and understand the image features and discover clinically interpretable knowledge. In this paper, we proposed a new method integrating three-dimensional (3-D) V-Net with shape priors (SP-V-Net) for pulmonary parenchyma segmentation and then performing COVID-19 detection with the interpretable radiomic features measured from the segmentation results. The proposed segmentation method included a V-Net for lung segmentation using a two-channel image containing the original chest CT scans and pulmonary shape prior, and a shape deformation module based on a spatial transform network (STN) to restrict the V-Net output to optimize the weights of the V-Net. Significant texture features on the extracted pulmonary parenchyma were selected for COVID-19 detection. Instead of building an end-to-end model, our proposed approach contains two separate models, including image segmentation and statistical feature analysis, and has high interpretability to support clinical use. The flowchart of our proposed approach is shown in Fig. 1. Our code is available now at https://github.com/MIILab-MTU/KD4COVID19.
Fig. 1.
The workflow of the proposed approach for lung segmentation and COVID-19 detection. A thresholding method was applied to generate the shape prior of the pulmonary parenchyma; the combination of the original image and shape prior was input to the proposed shape prior V-Net segmentation model (SP-V-Net). Statistical analyses were applied to the radiomic features extracted from the segmentation results to discover the statistically significant features and build the prediction model for COVID-19 detection.
The innovations and main contributions of our approach are:
-
(1)
A new deep-learning-based method that integrates a 3D V-Net with shape priors was proposed for medical image segmentation. The shape prior was used to optimize the model weights in both V-Net input and output, which significantly improved the model performance.
-
(2)
Instead of building an end-to-end model, our approach employed models with high interpretability in analyzing features and generating detection results. It has a great promise to support the computer-aided diagnosis of COVID-19 infection.
2. Related work
2.1. COVID-19 detection using deep learning
Due to the powerful performance of feature representation, deep-learning-based approaches have demonstrated impressive capability for COVID-19 detection. Both transfer learning-based networks [8] and customized deep networks [9] have been developed for classification and segmentation related to COVID-19 infection.
It requires a great number of data and high computational power to train a deep neural network. Transferring pre-trained weights into a deep network facilitates the convergence while keeping the feature representation. Weights trained using ImageNet for natural image classification were widely applied to COVID-19 detection tasks. Li et al. used 2D U-Net to segment lung ROIs on CT slices, and then developed a COVNet which incorporated ResNet-50 as the backbone to perform COVID-19 detection [10]. The features were locally extracted from each slice and a max-pooling layer was used to capture the global features from the set of local features. Javaheri et al. proposed a CovidCTNet, which contained a BCDU-Net for lung segmentation and a convolution neural network (CNN) to distinguish COVID-19, community-acquired pneumonia (CAP), and healthy control subjects [11]. The BCDU-Net was pre-trained using the data from a Kaggle lung segmentation competition [12]. Chen et al. [13] employed a U-Net++ with ResNet-50 pretrained weights for COVID-19 infection detection. Ardakani et al. tested ten state-of-the-art CNNs for COVID-19 diagnosis using the labeled infected regions [14]. Most of the existing transfer learning-based CNNs focused on importing weights from the 2D image classification network to predict COVID-19 infection. However, 2D networks cannot fully use the information from 3D CT scans, and thus influence the accuracy of infection detection.
Compared with transfer learning-based networks, the CNN architectures from scratch are not limited by existing weights. Hasan et al. presented a combined deep learning model that contained a Q-deformed entropy feature extraction module and a CNN for discriminating COVID-19 infection from CAP and healthy controls using CT scans [15]. In this study, a long short-term memory (LSTM) layer was employed to process the feature sequences extracted from the CT slices and the designed network achieved an accuracy of 99.68% for classifying COVID-19, pneumonia and healthy cases. A multi-task deep learning model, which contained COVID-19 lesion segmentation and COVID-19 classification was proposed by Amyar et al [16]. The designed model achieved a Dice score of 0.78 for lung segmentation and an area under the receiver operating characteristic (ROC) curve of 93% for COVID-19 detection. Singh et al. proposed a CNN that was fine-tuned by multi-objective differential evolution for feature extraction and severity assessment of COVID-19 [17]. The model achieved the best accuracy of 93% for distinguishing COVID-19 subjects from healthy controls. Using customized CNN, the function of the CNN is not limited to classification and segmentation, which provides the ability to design flexible architectures for the specific applications and improves the consistency and accuracy [9].
Redundant and non-related regions of interest limit the performance of infection detection and degrade the effectiveness of feature extraction and further analysis [18]. The pulmonary parenchyma segmentation remains a challenge even though existing models achieved impressive performance for COVID-19 detection.
2.2. Shape priors in image segmentation
Image segmentation has been widely investigated using traditional image processing techniques, such as a clustering-based method [19], and a filter-based method [20]. Recently, medical image segmentation using deep learning models has achieved excellent performance. Nevertheless, it is beneficial and important to incorporate shape priors of the segmentation object with the segmentation models for improved performance and accelerated convergence. A strong reason is that shape is one of the most important geometric attributes of anatomical objects [21], and the shape priors can reduce the searching space of the potential segmentation outputs for deep learning models [22]. In addition, the shape mesh provides sufficient information for the identification of 3D objects [23]. However, it is challenging to develop an effective and pervasive approach by integrating shape priors to improve model generalizations.
Zheng et al. embedded the conditional random fields (CRFs) into CNN as a post-processing module to perform image segmentation and trained an end-to-end neural network [24] to refine segmentation results. Ravishankar et al [25] demonstrated that autoencoders, such as deep belief networks and convolutional autoencoders, could capture a low dimension of shape representation for image segmentation. In [26], CNN was first employed to perform object detection, and a stacked autoencoder was used to infer the shape of the object. Then, the shape deformation module was used to incorporate the predicted shape to improve the segmentation accuracy. In addition, non-machine learning-based methods, such as level set and active contour models, were combined with deep learning models to refine the segmentation results [27,28]. However, most of the existing methods only incorporated shape priors into model inputs, and there are only a limited number of studies that incorporate shape priors into model outputs. It is difficult to generate shape priors automatically. Even if possible, the generated shape priors are inaccurate, making it less effective to guide model training.
3. Methodology
3.1. Image acquisition and pre-processing
In total, 112 CT scans were enrolled into this retrospective study from Shanghai Public Health Clinical Center, including 58 subjects with confirmed COVID-19 infection, 24 subjects with CAP and 30 healthy controls. Within the COVID-19 subjects, 30 cases were infected with severe COVID-19 and 7 of them died eventually. The study was approved by the ethics committee of the Shanghai Public Health Clinical Center.
Rescaling and resampling strategies were applied to CT images to overcome the GPU memory limit and accelerate the training/test process. For all CT scans, the slice thickness was resampled into 5 mm. The in-plane pixel size ranged from 0.579 mm to 0.935 mm. For each CT slice, we cropped the central part with a fixed size of 384×384 for further analysis. As a result, the number of CT slices ranged from 52 to 90 for each subject. Then, experienced operators manually delineated the contours of the bilateral lungs for all the 112 subjects. Because the number of subjects was relatively limited in terms of the segmentation task, data augmentation, including random flipping, random cropping and random rotation, was applied. In the following COVID-19 diagnosis task, all subjects were categorized into the COVID-19 and non-COVID-19 groups for a binary classification based on statistical analyses.
3.2. Pulmonary parenchyma segmentation
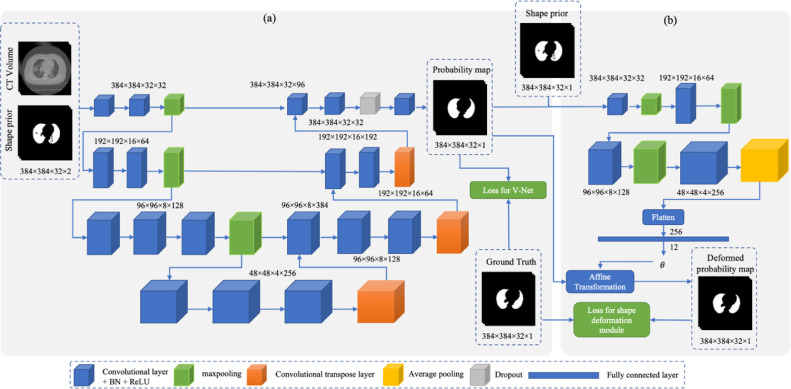
The architecture of the proposed segmentation is a unified network containing two modules, as illustrated in Fig. 2. Basically, our SP-V-Net has a 3D V-Net and a shape deformation module. The 3D V-Net was used to perform an end-to-end lung extraction and the shape deformation module was utilized to refine the V-Net output using prior shape knowledge.
Fig. 2.
The architecture of the proposed SP-V-Net for pulmonary parenchyma segmentation. (a) An end-to-end 3D V-Net for lung segmentation. (b) The shape prior deformation module is based on a spatial transformation network (STN) to refine the V-Net output.
3.2.1. Shape prior generation
A thresholding method was applied to generate the shape priors of the pulmonary parenchyma. In CT slices in our dataset, the Hounsfield unit (HU) values of voxels ranged from -2048 to +4000. -2048 represented the area without the CT scan. Air has the value of -1000 HU, and water has the value of 0 HU. The air-filled structure, such as the lung, ranges from -830 HU to -200 HU. A binary thresholding method was applied with the threshold of -320 to extract pulmonary parenchyma. Because the HU scale is typically regarded as a calibrated scale [29], the thresholding method's generalizability is guaranteed.
In practice, the binary thresholding method often generates discrete regions due to the variation of the brightness and contrast of the lung CT. To remove the discrete regions, we calculated the volume of the extracted regions. If the volume of a region was greater than 1% percent of the whole CT volume, the region was kept; otherwise, the region was removed. After that, a morphological closing operation, which contained a morphological dilation followed by erosion, was performed to smoothen the boundaries of the extracted regions.
3.2.2. The proposed 3D V-Net
The 3D V-Net designed in this study was a volume-based deep learning neural network. The input of the V-Net was two-channel 3D images with a size of 384×384×32×2 containing a cropped CT volume and a binary mask of the lung from the shape prior. The V-Net output was the probability map of the pulmonary parenchyma with the size of 384×384×32, where 1 indicates the lung region and 0 represents the background. The V-Net contained an encoder to extract hierarchical features and a decoder to restore the extracted features and generate the final segmentation probability map. The architecture of the designed V-Net is shown in Fig. 2(a).
The encoder contained three max-pooling layers and several convolutional layers. Each convolutional layer was followed by a batch normalization layer and a ReLU activation function. The kernel size of the convolutional layers was fixed as 3×3×3. The stride of the max-pooling layers was set as 2 through each axis, and thus the size of the feature maps shrunk by half after applying each pooling operation. By extracting features from the feature maps with different sizes, the hieratical features were obtained and the receptive fields of the deep neural network were enhanced. The deconvolutional layers in the decoder were responsible for restoring the down-sized feature maps. The stride of the deconvolution layer was 2 so that the size of the feature maps was enlarged twice after applying each deconvolution layer. Moreover, a dropout technique [30] was adopted to prevent overfitting. One dropout layer was inserted before the last convolutional layer in the V-Net, as shown in Fig. 2(a). During the training period, the dropout probability was set as 0.5.
3.2.3. Incorporating shape priors by spatial transformer network
Since the size of pre-defined shape priors is not the same as that of the manually delineated pulmonary parenchyma, direct incorporation of shape priors into the V-Net input limits the model performance. To further utilize the shape prior of the pulmonary parenchyma, improve the accuracy of the V-Net output and restrict the V-Net output, an image deformation module was applied to align the V-Net output according to the shape prior. In our SP-V-Net, the shape deformation module performed a non-rigid affine transformation.
In detail, a non-rigid shape deformation module which was implemented by a spatial transformer network (STN) [31], was embedded in the SP-V-Net. The STN inputs were the pre-defined shape prior to the pulmonary parenchyma and the V-Net generated probability map of the pulmonary parenchyma mask. The sizes of the two inputs were the same and they were concatenated as a two-channel image. The output of the STN was the 12 parameters of the affine transformation matrix . The parameters of the optimal affine transformation were trained by the difference between the probability map generated by the V-Net and the pre-defined shape prior.
Denote the input CT volume with the size of , and the pre-defined shape prior as , where is a binary image and it has the same size as . The ground truth of the pulmonary parenchyma is defined as . The V-Net output is defined as with the same size as , where is a probability map of the pulmonary mask. The affine transformed output is denoted by . The shape deformation module takes both the V-Net output and the binary template as a two-channel input image to calculate the parameters of the affine transformation matrix . The basic affine transform containing translation, scaling and shearing matrices is constituted by:
Because the numbers at the last row of the above three matrices are fixed constants, the calculated affine transformation matrix is a matrix as follows:
where represent the scaling parameters, are the translation parameters, and indicate the shearing parameters.
Suppose that the coordination of a voxel in is and the coordination of a voxel in is . The affine transformation performed by the STN is shown in Eq. (1).
| (1) |
where represents the transformation function, and is the index of the voxels. Note that the coordinate mapping is from the target volume to the source volume . The shape deformation module tends to find the mapping that fills all the voxels in the target according to the source; thus, the module is required to iterate each voxel in the target volume rather than in the source volume. Typically, to limit the model output space and prevent the model from collapsing, the coordinates of the voxels in the source and target volumes are scaled into [0, 1], respectively.
The coordinates obtained by the affine transformation were float numbers that could not be used as the positions of the voxels. Thus, a trilinear interpolation module was applied to sample the coordinates and prevent the transformed voxel from extrapolating the outside of the 3D volume, as defined in Eq. (2):
| (2) |
The architecture of the designed shape deformation network is shown in Fig. 2(b). Three convolutional layers and max-pooling layers were employed to extract hierarchical features from the concatenated two-channel input image. An average pooling layer converted the extracted feature maps into a flattened feature vector, and the fully connected layer generated the transformation matrix.
3.2.4. Loss function and optimization
The proposed SP-V-Net contained a V-Net for pulmonary parenchyma segmentation and a shape deformation module implemented by STN for refinement of the segmentation. The discrepancy between the V-Net output and the corresponding ground truth was calculated by pixel-wise loss. To train the V-Net, a sigmoid cross entropy was employed to minimize the discrepancy between the V-Net output and the ground truth as follows:
| (3) |
where represents all weights in the V-Net and is a L2 regularizer.
However, the STN is an unsupervised network since the gold standard of the calculated affine transformation parameters is unknown. Instead of directly optimizing the weights of the shape deformation module using the gold standard of the transformation parameters, the affine transformation was applied to the V-Net output to generate , and then the discrepancy between the transformed output and the ground truth was utilized to fine-tune the weights of the shape deformation module. To train the shape deformation module, another sigmoid cross entropy was utilized to penalize the discrepancy between and , as illustrated in Eq. (4).
| (4) |
where , and represents the weights of the shape deformation module.
During the model training, the shape deformation module and the designed V-Net were trained jointly with the loss function defined in Eq. (5).
| (5) |
The entire architecture of the proposed SP-V-Net contained two parts: a V-Net and an STN. At first, the two different parts were trained separately, and then the two parts were trained jointly. To train the SP-V-Net, a multi-step training strategy was used. The strategy is shown in Algorithm 1.
Algorithm 1.
Multi-step strategy for training the SP-V-Net.
| Inputs: : a cropped CT volume; : the pre-defined shape prior; |
| : ground truth of pulmonary parenchyma; e: the number of the training epochs. |
| Output: trained SP-V-Net. |
| In epoch 1 to epoch 0.2e: |
| Step 1: Training V-Net while fixing the weights of the STN using the loss function defined in Eq. (3). |
| In epoch 0.2e to epoch 0.4e: |
| Step 2: Training STN while fixing the weights of the V-Net using the loss function defined in Eq. (4). |
| In epoch 0.4e to epoch e. |
| Step 3: Training SP-V-Net jointly using the loss function defined in Eq. (5). |
In the beginning, the weights in the V-Net and shape deformation module were randomly initialized. Thus, the affine transformation matrix was randomly generated, and the calculated deformation loss in Eq. (4) was extremely high. In addition, the V-Net generated mask, , was not close to the ground truth of the lungs. Randomly transforming the V-Net segmentation result biases the V-Net weights and could cause the model to collapse. Thus, in step 1, the weights in the shape deformation module were fixed at the initial training epochs, and the training was only performed on the V-Net. In step 2, the V-Net was well-trained; however, the shape deformation module was still randomly initialized. Because the loss calculated by Eq. (4) is substantial compared with the loss calculated by Eq. (3) at this point, fine-tuning the weights in the shape deformation module and the V-Net jointly causes a great bias to the weights of V-Net. Thus, the V-Net weights were fixed, and the training process was only performed on the shape deformation module. In step 3, we adopted Eq. (5) as the loss function to fine-tune the SP-V-Net jointly for the rest epochs.
Our SP-V-Net model was implemented in Python using TensorFlow, and the model was trained on a workstation with an NVIDIA Titan V GPU. The Adam Optimizer was used to fine-tune the weights of the SP-V-Net. The model was trained for 1000 epochs with a batch size of 1. A 5-fold stratified cross-validation was performed to validate the model, and the subjects were randomly selected according to the proportion of subjects in each category, i.e. CAPs, healthy controls and COVID-19 patients. In the 5-fold cross-validation, 80% of the subjects were used as the training set, and the rest 20% were used in the testing set. Data augmentation techniques, such as rotation, flipping, brightness transform, and Gaussian noise transform were randomly applied to the cropped CT volumes. The corresponding rotation and flipping were applied to the generated shape priors as well.
3.3. Feature extraction and analysis for COVID-19 detection
After segmentation, the lung regions were cropped for feature extraction and analysis. Among the 85 radiomic features measured from the lung regions [32], in order to overcome the high-dimensional curse, only a small number of features were selected using feature selection algorithms for statistical analyses to detect COVID-19 infection. These selected features were investigated to evaluate their classification performance by the univariate and multivariate regression, and ROC curves. Furthermore, the multivariate analysis was tested to build the COVID-19 diagnosis model. The correlation between the features measured from our segmentation results and manual annotation was analyzed as well.
3.3.1. Feature extraction
Eighty-five texture features, as presented in [32], were measured. They can be divided into seven types of features, including first-order histogram-based features, gray level co-occurrence matrix (GLCM) features, gray level size zone matrix (GLSZM) features, gray level run length matrix (GLRLM) features, neighboring gray-tone difference matrix (NGTDM) features and gray level dependence matrix (GLDM) features. All these CT texture features are associated with histopathology, such as pulmonary fibrosis [33], which have been shown in more than one-third of COVID-19 patients after recovery [34].
3.3.2. Feature selection and COVID-19 detection
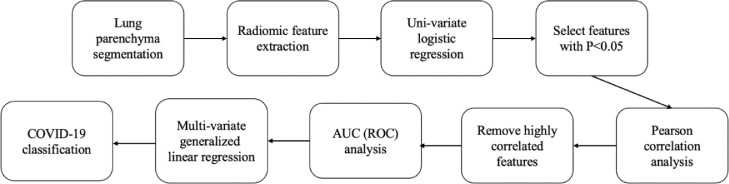
The feature selection and COVID-19 detection were implemented by statistical analysis, as shown in Fig. 3. After feature extraction, a univariate binary logistic regression analysis was applied to evaluate the potential features for COVID-19 classification. In the univariate binary logistic regression analysis, each feature was used as the independent variable, and the label (0 or 1) of a subject was used as the dependent variable. '1′ means that the subject has COVID-19 and '0′ means that the subject does not have COVID-19. The output of the univariate binary logistic regression analysis is the probability of the subject having COVID-19 given the value of the feature. The p-value for the univariate binary logistic regression analysis was calculated using a likelihood-ratio test [35].
Fig. 3.
Workflow of the feature extraction and analysis for COVID-19 detection. ROC,receiver operating characteristic (ROC) curves; AUC, area under the curve.
Using the univariate binary logistic regression analysis, all the features with p<0.05 (which are statistically significant) were selected to construct a feature set for further analysis. After that, for each feature in the selected feature set, we computed the Pearson's correlation coefficient between this feature and each other feature in the feature set. If the Pearson's correlation coefficient was more than a threshold (0.83 in this paper), then the feature with a lower AUC value was removed from the feature set.
The features selected from the aforementioned step were used for COVID-19 classification. For simplicity and interpretability, we estimated a multivariate generalized linear model [36] for classification. During the experiments, a 5-fold cross-validation was performed to validate the model performance, in which 80% of the subjects were used as the training set and the rest 20% as the testing set.
Instead of using the features automatically extracted in the deep CNN, the COVID-19 classification task of our approach is based on statistical analysis with the handcraft radiomic features. The proposed classification method focuses on the interpretability of the features and the relationship with clinical decision making, which has important advantages to support clinical uses. Since the radiomic features were high dimensional and the number of subjects in our dataset was limited, the univariate, multivariate, Pearson, and ROC analyses were applied to select statistically significant features, remove the redundant features, and build prediction models.
3.4. Evaluation metrics
Metrics for segmentation. We evaluated the performance of the proposed SP-V-Net segmentation model using Dice similarity coefficient (DSC), sensitivity (SN) and specificity (SP). DSC measures the proportion of the intersection between the voxels extracted by our segmentation model and the voxels in the ground truth. The definition of DSC is defined as
| (6) |
where indicates the OTSU binarization method [37], represents the ground truth of the lung mask, represents the predicted probability map, and indicates the number of foreground (pulmonary) voxels within a specific CT volume.
The SN measures the proportion of the true positive (TP) voxels that are correctly detected, while the SP measures the proportion of the true negative (TN) voxels that are correctly predicted. The definitions of SN and SP are shown in Eq. (7) and Eq. (8), respectively.
| (7) |
| (8) |
where FN and FP indicate the false negative voxels and the false positive voxels, respectively.
Because the DSC cannot reflect the accuracy of the extracted surface of the lung parenchyma, the surface Dice similarity coefficient (SDSC) was used to measure the surfaces' overlap instead of the volumes in our study. The definition of SDSC is shown in Eq. (9).
| (9) |
where is the function used to extract the surface of the corresponding volume. SDSC calculation was implemented by searching the neighbor voxels for each voxel in the volume.
A DSC, SN, SP, or SDSC of 1 implies a perfect agreement between the segmentation results and the ground truth.
In addition, the Hausdorff distance (HD) was adopted to measure the maximum voxel distance between the predicted lung masks and the ground truth. The mean surface distance (MSD) [38] was used to evaluate the average surface distance. An HD or MSD of 0 indicates a perfect agreement.
Metrics for classification. The COVID-19 detection task is a binary classification task. The AUC, SN and SP were employed to evaluate the model performance.
4. Experimental results and discussion
4.1. Segmentation of pulmonary parenchyma
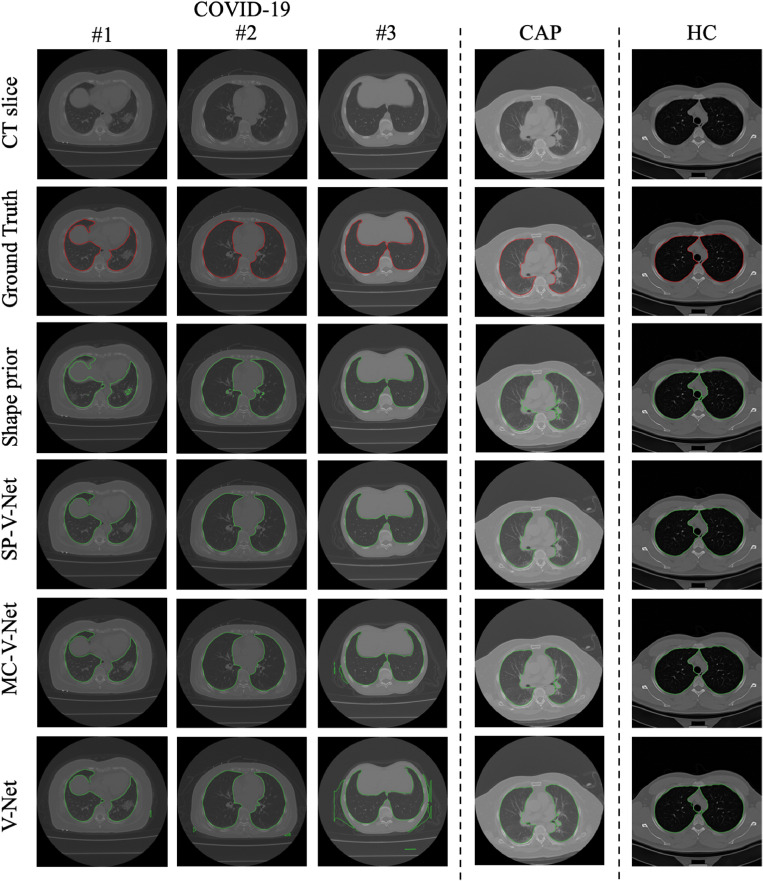
To demonstrate the effectiveness of the proposed SP-V-Net, two baseline models were implemented by removing the shape prior and the shape deformation module, respectively. Therefore, a plain V-Net with one-channel input (the CT volume) and a multi-channel V-Net (MC-V-Net) with two-channel input (containing the CT volume and the shape prior of the CT volume) were obtained as the baseline models. In these two baselines, the shape deformation module was removed. And in the experiments, the plain V-Net and MC-V-Net were trained by the loss function defined in Eq. (3). However, the architectures of the V-Nets in the three models were the same. The segmentation results of five subjects are shown in Fig. 4.
Fig. 4.
Examples of segmentation results. From left to right are three COVID-19 subjects, one CAP subject, and one healthy control. Row 2, ground truth; Row 3, contours from shape prior by binary thresholding; Rows 4-6, contours by SP-V-Net, MC-V-Net, and the plain V-Net, respectively. CAP, community-acquired pneumonia. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
In our dataset, three different types of subjects were enrolled, where the morphological shapes of the pulmonary ROIs differed significantly. According to Fig. 4, the contours generated by the SP-V-Net were smoother than those generated by the MC-V-Net and the plain V-Net among all the three types of subjects. By visual comparison, it can be noted that irregularities were removed by applying SP-V-Net, because the connected small regions away from the pulmonary parenchyma vanished. In addition, the adopted thresholding method was not able to generate a precise contour due to the variation of the HU values among the COVID-19 subjects, CAP subjects, and healthy controls.
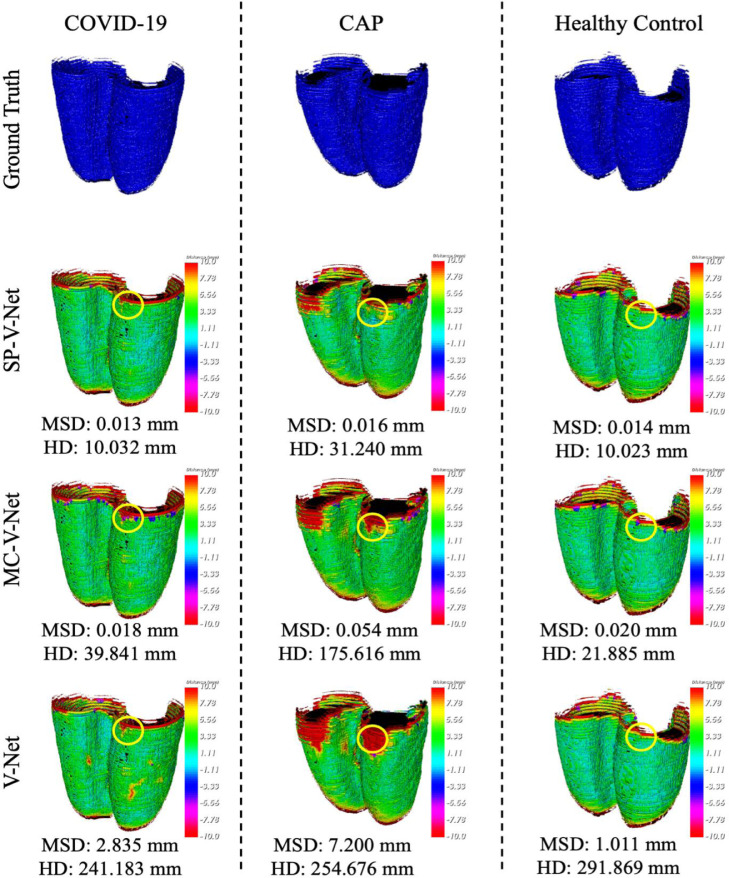
To better visualize the results generated by the plain V-Net, MC-V-Net and SP-V-Net, the surface distances were visualized from three different view angles, as shown in Fig. 5. The corresponding HD and MSD are depicted in Fig. 5 as well.
Fig. 5.
Visualization of surface distances for a COVID-19 subject, a CAP subject, and a healthy control subject. All the volumes were resampled with a fixed voxel spacing of 1mm and a slice thickness of 1mm. The color bar indicates the surface distances. The areas highlighted by circles represent the areas with a smaller surface distance acquired by SP-V-Net (Row 2) than those by MC-V-Net (Row 3) and by plain V-Net (Row 4). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
According to Fig. 5, even though the shape priors generated by the thresholding method were not precise, incorporating shape priors into the V-Net was still beneficial to the segmentation model. As a result, the MSDs within the selected three subjects were significantly reduced in MC-V-Net and SP-V-Net compared with the results generated by the plain V-Net. Due to the large slice thickness (5mm) in our dataset, errors occurred in the first several slices of the lung where the contrast was low due to the low density of the tissue. The areas highlighted by circles demonstrate that the proposed SP-V-Net effectively reduced the surface distances in the initial slices of the pulmonary parenchyma. The quantitative comparison among the segmentation models is listed in Table 1 .
Table 1.
Quantitative evaluation for the thresholding method, the plain V-Net, MC-V-Net, and the proposed SP-V-Net for different cohorts. ALL means all enrolled subjects in the test set; CAP means community-acquired pneumonia; HC means healthy controls. DSC, Dice similarity coefficient; SDSC, surface Dice similarity coefficient; HD, Hausdorff distance; MSD, mean surface distance.
| Method | Cohort | SN | SP | DSC | SDSC | HD (mm) | MSD (mm) |
|---|---|---|---|---|---|---|---|
| Threshold method | ALL | 0.9548 | 0.9741 | 0.9042 | 0.4228 | 33.9402 | 0.4107 |
| COVID-19 | 0.9506 | 0.9766 | 0.9017 | 0.4128 | 31.8981 | 0.2618 | |
| CAP | 0.9603 | 0.9761 | 0.9027 | 0.4365 | 34.9263 | 0.2231 | |
| HC | 0.9581 | 0.9656 | 0.9121 | 0.4304 | 37.6577 | 0.9933 | |
| V-Net | ALL | 0.9781 | 0.9785 | 0.9404 | 0.7365 | 360.9046 | 1.5006 |
| COVID-19 | 0.9790 | 0.9765 | 0.9366 | 0.7204 | 364.6403 | 1.0620 | |
| CAP | 0.9643 | 0.9773 | 0.9257 | 0.7161 | 371.5045 | 4.0511 | |
| HC | 0.9888 | 0.9868 | 0.9683 | 0.8133 | 337.2297 | 0.4853 | |
| MC-V-Net | ALL | 0.9744 | 0.9954 | 0.9732 | 0.9005 | 41.0517 | 0.0434 |
| COVID-19 | 0.9736 | 0.9955 | 0.9705 | 0.8984 | 36.5794 | 0.0524 | |
| CAP | 0.9617 | 0.9976 | 0.9749 | 0.8885 | 71.2026 | 0.0387 | |
| HC | 0.9899 | 0.9930 | 0.9819 | 0.9196 | 26.5537 | 0.0167 | |
| SP-V-Net | ALL | 0.9840 | 0.9943 | 0.9796 | 0.9134 | 20.2249 | 0.0318 |
| COVID-19 | 0.9822 | 0.9940 | 0.9775 | 0.9068 | 21.1892 | 0.0398 | |
| CAP | 0.9826 | 0.9964 | 0.9830 | 0.9225 | 25.6124 | 0.0211 | |
| HC | 0.9918 | 0.9931 | 0.9833 | 0.9277 | 11.4624 | 0.0146 |
In Table 1, the comparisons based on SDSC, HD and MSD illustrate that the proposed SP-V-Net significantly improved the segmentation accuracy in the cohorts of ALL (all enrolled subjects in the test set), COVID-19, CAP, and healthy control. The SDSC was improved by 1% in the proposed SP-V-Net than that in the MC-V-Net among all subjects. Compared with MC-V-Net, the average HD of the SP-V-Net was reduced by half, and the MSD was reduced by 26% (from 0.0434 mm to 0.0318 mm) among all subjects. For the COVID-19 cohort, the MSD was reduced from 0.0524 mm in MC-V-Net to 0.0398 mm in SP-V-Net; and for the CAP cohort, the MSD was reduced from 0.0387 mm in MC-V-Net to 0.0211 mm in SP-V-Net. Accordingly, Table 1 demonstrates that the proposed SP-V-Net achieved the best segmentation performance for all cohorts.
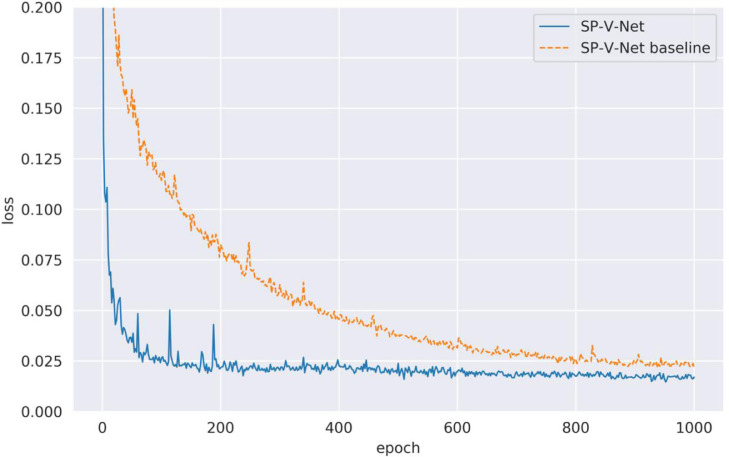
To verify the effectiveness of the proposed multi-step training strategy for optimizing SP-V-Net, the loss values for the V-Net module in the SP-V-Net, which are calculated by Eq. (3), are depicted in Fig. 6. For comparison, we trained the SP-V-Net using the loss function defined in Eq. (5) during the entire training period, called as 'SP-V-Net baseline'. Fig. 6 shows that the proposed SP-V-Net with the multi-step training strategy achieved a lower loss at the epoch 1000. In contrast, the loss of the SP-V-Net baseline dropped slowly at the initial training epochs. Thus, the proposed multi-step training was effective. The loss values in SP-V-Net were successfully backpropagated, and the weights of the SP-V-Net were well fine-tuned.
Fig. 6.
Loss values calculated by Eq. (3) for SP-V-Net with multi-step training and without multi-step training. To better reflect the training loss, we only visualized the loss between 0 and 0.2.
4.2. COVID-19 detection and feature interpretation
4.2.1. COVID-19 detection
Using the methods listed in Section 3.3.1, 85 features were extracted for statistical analysis. All the subjects were included in the COVID-19 classification task. In our dataset, a total of 112 CT scans were enrolled, and there were 58 subjects with confirmed COVID-19 infection, 24 subjects with CAP, and 30 healthy controls. In the COVID-19 detection task, all the COVID-19 subjects were positive samples while the rest were negative samples. As a result, the dataset used for COVID-19 detection was relatively balanced.
Eighty-five features were measured from the lung regions for the univariate analysis. Features with a p<0.05 in the univariate analysis were selected as the statistically significant features [39]. The Pearson analysis was further applied to investigate the correlations among these selected features and if the correlation was above a cut-off of 0.83, only the features with the higher AUC score were kept. After this step, only 10 features were kept and used for COVID-19 detection. In the experiments, the COVID-19 detection was a binary classification task. There are many classification algorithms available to this task. In this paper, we used a simple generalized multivariate linear regression model because it is simple and has a high interpretability. It achieved the best performance compared with other machine learning algorithms. For comparison, for the lung regions generated by plain V-Net, MC-V-Net and SP-V-Net, we extracted the same 10 features and used them to train the multivariate generalized linear regression model, respectively, and then the trained models were used to detect COVID-19 infection. A 5-fold stratified cross validation was used to train and validate the model performance. Before the training and test, the data was normalized by a z-score method. The detection performance is illustrated in Table 2 . According to Table 2, using the contours generated by SP-V-Net, the generalized linear model achieved the highest AUC score of 0.9470.
Table 2.
Quantitative evaluation of COVID-19 detection using radiomic features measured from lung regions by different segmentation models.
| Method | ACC | SN | SP | AUC |
|---|---|---|---|---|
| V-Net | 0.9090 | 0.9167 | 0.9000 | 0.9083 |
| MC-V-Net | 0.9445 | 0.9167 | 1.0000 | 0.9383 |
| SP-V-Net | 0.9460 | 0.9670 | 0.9270 | 0.9470 |
To further demonstrate the effectiveness of the proposed feature selection method, data normalization, and generalized linear regression model, more experiments were performed. Besides the proposed linear regression model, we performed experiments using other classification algorithms. These algorithms included logistic regression model (LR), support vector machine (SVM), random forest (RF) and k-nearest neighbors (KNN). The results are listed in Table 3 .
Table 3.
Performance comparison for COVID-19 detection using different models. LR means logistic regression; KNN means k-nearest neighbors; RF means random forest; SVM means support vector machine; GLM means generalized linear model, which is demonstrated in Section 3.3.2. ACC, accuracy; SN, sensitivity; SP, specificity; AUC, area under the receiver operating characteristic curve. Feature selection YES means that the features were obtained using the feature selection method proposed in Section 3.3.2 (only 10 features were used). Feature selection NO means that 85 radiomic features were used. The normalization YES means that the features were normalized before classification.
| Feature selection | Normalization | Methods | ACC | SN | SP | AUC | |
|---|---|---|---|---|---|---|---|
| 1 | YES | YES | LR | 0.9240 | 0.9230 | 0.9250 | 0.9260 |
| 2 | YES | YES | KNN | 0.8210 | 0.8970 | 0.7050 | 0.9150 |
| 3 | YES | YES | RF | 0.8570 | 0.8610 | 0.8550 | 0.9390 |
| 4 | YES | YES | SVM | 0.9450 | 0.9850 | 0.9091 | 0.9870 |
| 5 | YES | YES | GLM | 0.9460 | 0.9670 | 0.9270 | 0.9470 |
| 6 | YES | NO | LR | 0.7937 | 0.8773 | 0.7055 | 0.9235 |
| 7 | YES | NO | KNN | 0.7502 | 0.6924 | 0.7800 | 0.7673 |
| 8 | YES | NO | RF | 0.8660 | 0.8606 | 0.8727 | 0.9400 |
| 9 | YES | NO | SVM | 0.4735 | 0.5500 | 0.4182 | 0.5087 |
| 10 | YES | NO | GLM | 0.9280 | 0.9318 | 0.9272 | 0.9295 |
| 11 | NO | YES | LR | 0.9379 | 0.9251 | 0.9091 | 0.9356 |
| 12 | NO | YES | KNN | 0.8213 | 0.8439 | 0.6872 | 0.9056 |
| 13 | NO | YES | RF | 0.8217 | 0.8924 | 0.7454 | 0.9012 |
| 14 | NO | YES | SVM | 0.9458 | 0.9233 | 0.9191 | 0.9440 |
| 15 | NO | NO | LR | 0.4822 | 0.0000 | 1.0000 | 0.6484 |
| 16 | NO | NO | KNN | 0.6426 | 0.8136 | 0.4618 | 0.6683 |
| 17 | NO | NO | RF | 0.8217 | 0.8924 | 0.7454 | 0.9012 |
| 18 | NO | NO | SVM | 0.4545 | 0.6333 | 0.2600 | 0.5541 |
The grid search was performed to find the parameters for the best performance for each classifier. The best logistic regression was obtained by using an L2 regularizer. The number of the neighbors in the best KNN classifier was 3. The best random forest classifier was trained by using Gini impurity with the max depth of 4 and an estimator number of 15. The best support vector machine was trained with a radial basis function kernel. According to Table 3, the generalized linear regression used in this study outperformed other classification methods in terms of ACC and SP for the COVID-19 classification.
Table 3 also demonstrates that the generalized linear regression model with the proposed feature selection achieved nearly the same performance when using the normalized or un-normalized features (Row 5 and Row 10). Using the normalized features, the generalized linear model with the proposed feature selection achieved the highest accuracy and specificity than other experimental settings. However, using the normalized selected features, the SVM with the proposed feature selection achieved a higher SN and AUC.
One important finding was that with the normalization, the performance of the machine learning methods was enhanced significantly, while the generalized linear regression model achieved a relatively high performance even if without normalization. Another finding was that the feature selection processed by the univariate and Pearson correlation analyses (Row 1 to Row 10 in Table 3) was effective for improving the model performance and reducing the computational complexity. The performance of machine learning methods using all features and unnormalized data was influenced significantly by the small training sample size, especially for LR (Row 6 and Row 15 in Table 3) and KNN (Row 7 and Row 16 in Table 3). In summary, the proposed feature selection was effective, and the generalized linear model was robust for COVID-19 classification.
Table 4 compares the performance of our proposed classification method (generalized linear model with the proposed feature selection and data normalization) with those by the state-of-the-arts. Because different subjects were enrolled, Table 4 only provides a limited comparison. In Table 4, our proposed COVID-19 detection method achieved a higher accuracy and specificity compared with the method proposed by Zhang et al. [40] and Panwer et al. [41]. One reason is that they only used CT slices instead of the entire CT volumes. In both of their approaches, the features were extracted using deep neural networks. However, our method focuses on radiomic features, which has a high interpretability. Our method also achieved a higher AUC score compared with Harmon et al. [42]. In [42], the CT volume was used to perform lung segmentation and COVID-19 detection. However, their approach achieved a DSC of 0.95 for lung segmentation, while our SP-V-Net achieved a DSC of 0.9796. Finally, the method in [42] achieved an AUC of 0.9410 for COVID-19 detection, which is inferior to ours. All of these indicate that accurate lung segmentation is important for COVID-19 detection, and it is beneficial to use the entire CT volume for an overall classification.
Table 4.
Performance comparison of our proposed COVID-19 detection approach with state-of-the-arts. ACC, accuracy; SN, sensitivity; SP, specificity; AUC, area under the receiver operating characteristic curve.
4.2.2. Feature analysis and interpretation
The 10 features selected after applying the univariate and Pearson analysis based on the lung regions extracted by our proposed SP-V-Net are shown in Table 5 . As a comparison, the results of the multivariate analysis using the lung regions from the ground truth are depicted in Table 6 .
Table 5.
Multivariate generalized linear analysis of COVID-19 classification using lung regions extracted by the SP-V-Net segmentation. P-value < 0.05 indicates that it is a statistically significant feature. The odds ratio (OR) is listed correspondingly. An asterisk indicates that the feature was selected in both experiments using lung regions from our SP-V-Net segmentation and the ground truth.
| Variable Type | Variables | p-value | OR |
|---|---|---|---|
| GLCM | Cluster Shade | 0.001 | 0.999 |
| Informational Measure of Correlation | 0.220 | 0.006 | |
| GLSZM | Size Zone Non Uniformity* | 0.688 | 0.999 |
| Large Area High Gray Level Emphasis* | 0.061 | 1.000 | |
| Small Area Emphasis | 0.000 | 5.464e+10 | |
| First order | Median* | 0.185 | 1.000 |
| Range* | 0.534 | 0.999 | |
| 90Percentile* | 0.054 | 1.001 | |
| GLDM | Small Dependence Low Gray Level Emphasis* | 0.488 | 1.905e+07 |
| Large Dependence High Gray Level Emphasis* | 0.004 | 1.000 |
Table 6.
Multivariate generalized linear analysis of COVID-19 classification using lung regions from the manually annotated ground truth. An asterisk indicates that the feature was selected in both experiments using lung regions from our SP-V-Net segmentation and the ground truth. OR, odds ratio.
| Variable Type | Variables | p-value | OR |
|---|---|---|---|
| GLSZM | Size Zone Non Uniformity Normalized | 0.000 | 2.245e+06 |
| Size Zone Non Uniformity* | 0.487 | 1.000 | |
| Small Area High Gray Level Emphasis | 0.005 | 0.999 | |
| Large Area High Gray Level Emphasis* | 0.000 | 1.000 | |
| First order | Median* | 0.000 | 1.003 |
| Range* | 0.734 | 0.999 | |
| 90Percentile* | 0.227 | 1.000 | |
| GLDM | Small Dependence Low Gray Level Emphasis* | 0.658 | 0.000 |
| Large Dependence High Gray Level Emphasis* | 0.001 | 1.000 |
According to Tables 5 and 6, 10 and 9 features were included in the multivariate analysis using the lung regions from our SP-V-Net segmentation and manual annotation, respectively. Furthermore, 3 features from lung regions generated by SP-V-Net were statistically significant, while 5 features from manual annotation were statistically significant. More importantly, 7 shared features were included in the two multivariate analysis experiments, which suggested that there was a high agreement between the features measured from the SP-V-Net segmentation and those from the manual annotation. More details about these features are explained as follows:
GLSZM features: A GLSZM feature quantifies gray level zones in an image. A gray-level zone is denoted as the number of the connected voxels that share the same gray level intensity, i.e. the same HU value in CT slices. In our experiments, the infinity norm was implemented by 26-connected regions. The small area emphasis measures the distribution of small size zones.
First order features: three features, including median, range, and 90 percentile were selected in both experiments. The first order features were calculated by the voxel intensities within the lung region. Since the infection area and the abnormal region of interest for the COVID-19 subjects occupy limited voxels, the intensity-based features are not important for differentiating COVID-19 from healthy controls using CT images.
GLDM features: two features were kept in the multi-variable analysis for both experiments. A GLDM quantifies gray level dependency in the CT images. A gray level dependency is denoted as the number of connected voxels within the center voxel dependent on the center voxel. The element located at (i, j) in the GLDM indicates the number of times that a voxel with gray level i with j dependent voxels in its neighborhood appears in the 3D volume. The large dependence high gray level emphasis (LDHGLE) measures the distribution of large dependence with higher gray-level values. A higher gray value in the lung region indicates the voxel near lung nodule, ground-class opacities and lung consolidation with a rounded morphology [5]; thus LDHGLE is important for COVID-19 classification. In addition, by comparing Tables 5 and 6, only one feature, LDHGLE, was commonly selected in both experiments and was statistically significant for COVID-19 classification.
Table 7 shows the mean values, ranges, and standard derivations (STD) of the statistically significant variables (with p<0.05) from different cohorts in Table 5. It can be observed that the mean value and range of the LDHGLE are significantly different between the COVID-19 cohort and other cohorts, which indicates that this interpretable feature is important.
Table 7.
Information about the statistically significant features for COVID-19 detection from different cohorts. CAP, community-acquired pneumonia; HC, healthy controls; STD, standard derivations.
| Variable Type | Variables | Cohort | Mean | Range | STD |
|---|---|---|---|---|---|
| GLCM | Cluster Shade | COVID-19 | 6051.7986 | [2595.0043, 12735.9115] | 2231.6201 |
| CAP | 7475.7171 | [3058.1410, 13854.4794] | 3071.6227 | ||
| HC | 6619.6907 | [3749.2333, 14663.6807] | 2388.6481 | ||
| GLSZM | Small Area Emphasis | COVID-19 | 0.7424 | [0.7092, 0.7730] | 0.0163 |
| CAP | 0.7205 | [0.6909, 0.7521] | 0.0136 | ||
| HC | 0.7270 | [0.6883, 0.7420] | 0.0107 | ||
| GLDM | Large Dependence High | COVID-19 | 15900.5727 | [6445.3997, 47463.3938] | 8079.9679 |
| Gray Level Emphasis (LDHGLE) | CAP | 8116.1659 | [5195.6416, 13651.4083] | 2110.4785 | |
| HC | 2893.1982 | [1385.6956, 12329.7105] | 2944.3454 |
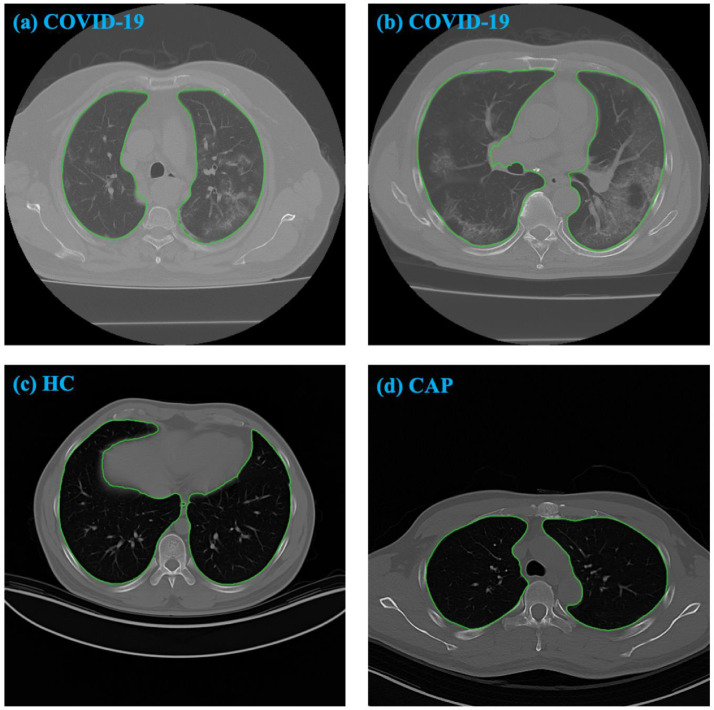
In Fig. 7, CT slices from different cohorts are illustrated. The "ground glass" areas can be seen in the two COVID-19 subjects. The difference in the corresponding LDHGLEs between the COVID-19 subjects and other cohorts is extremely large, indicating that this interpretable feature is also important.
Fig. 7.
CT slices from different cohorts. The contours are generated by SP-V-Net. The corresponding LDHGLE values are 7144.72457 in (a), 17754.2829 in (b), 1671.4857 in (c), and 1385.6956 in (d). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The Pearson correlations between the features from the lung regions by the SP-V-Net segmentation and those by manual annotation are illustrated in Table 8 . A higher Pearson correlation indicates that the features are significantly correlated, and the SP-V-Net model has a high accuracy. According to Table 8, the Pearson correlation analysis indicates the features measured from lung regions extracted by the SP-V-Net highly correlated with the features measured from manual annotation for the 10 selected features, except two features, including the range feature, which belongs to the first order features, and cluster shade, which belongs to the GLCM features.
Table 8.
Pearson correlations between the features measured from lung regions extracted by the SP-V-Net segmentation and those by manual annotation. All the features in Table 5 are included.
| Variable Type | Variables | Pearson Correlation |
|---|---|---|
| GLCM | Cluster Shade | 0.7217 |
| Informational Measure of Correlation | 0.9726 | |
| GLSZM | Size Zone Non Uniformity* | 0.9653 |
| Large Area High Gray Level Emphasis* | 0.9989 | |
| Small Area Emphasis | 0.9441 | |
| First order | Median* | 0.9962 |
| Range* | 0.5902 | |
| 90 Percentile* | 0.9571 | |
| GLDM | Small Dependence Low Gray Level Emphasis* | 0.9998 |
| Large Dependence High Gray Level Emphasis* | 0.9992 |
5. Conclusion and future work
In this paper, a new automatic approach for COVID-19 detection in chest CT images is presented. An image deformation-based segmentation model, named as SP-V-Net, was proposed to extract pulmonary parenchyma first. The designed SP-V-Net contained a 3D V-Net for CT image segmentation and an STN for output restriction and refinement. The features measured from the segmented lung regions were used for statistical analysis with a high interpretability to detect COVID-19 infection. The proposed segmentation model achieved a DSC of 0.9796, an HD of 20.2249 mm, an SDSC of 0.9134, and an MSD of 0.0318 mm. Furthermore, our COVID-19 classification model using statistically significant radiomic features achieved an AUC of 0.9470, a sensitivity of 0.9670, and a specificity of 0.9270.
Our approach has a great promise for clinical use. First, it has excellent interpretability in the radiology lab since our detection method is based on sophisticated statistical models. Second, segmentation is essential for radiologists' daily image interpretation. Our SP-V-Net produced the state-of-the-art segmentation performance. Its application in large cohorts of subjects would provide additional insights into assessing COVID-19 infection severity, the effectiveness of medication and other factors. The architecture of our proposed SP-V-Net model can also be applied to other medical image segmentation tasks, where the shape estimation as prior and important knowledge is easy to obtain. In our future studies, we will investigate other methods to generate the shape priors, such as active contours [43], to further improve our approach.
Declaration of Competing Interest
The authors declare no conflicts of interest.
Funding
This research was supported by a new faculty startup grant from Michigan Technological University Institute of Computing and Cybersystems (PI: Weihua Zhou) and a COVID-19 research seed grant from Michigan Technological University College of Computing (PI: Weihua Zhou). It was also supported in part by a research seed fund from Michigan Technological University Health Research Institute (PI: Weihua Zhou). Dr. Tang was supported by a research seed grant from Michigan Technological University College of Engineering.
Biographies
Chen Zhao received the B.S. and M.S. degrees in computer science form Xi'an University of Posts and Telecommunications, Xi'an, China in 2016 and 2019. He is currently pursuing the Ph.D. degree in computer science and engineering in the Department of Applied Computing at Michigan Technological University, USA. His research interests include medical image processing and deep learning, especially for medical image segmentation, classification and feature representation.
Yan Xu received a master's degree in medicine from Shandong University and works in the Department of Radiology at Shanghai Public Health Clinical Center. Her main research direction is imaging diagnosis of infectious diseases.
Zhuo He received the B.S. degree in Central South University in 2015. She is now a Ph.D. candidate in the Department of Applied Computing at Michigan Technological University. Her research interests are medical imaging and informatics.
Dr. Jinshan Tang is Full professor of medical informatics program and data science program in the Department of Applied Computing at Michigan Technological University. He received his Ph.D in 1998 from Beijing University of Posts and Telecommunications, and got post-doctoral training in Harvard Medical School and National Institute of Health. Dr. Tang's research interests include biomedical image processing, biomedical imaging, deep learning, and computer aided detection and diagnosis. He has obtained more than two million dollars grants in the past years as a PI or Co-PI. He published more than 110 refereed journal and conference papers. He published two edited books on medical image analysis. One is Computer Aided Cancer Detection: Recent Advance and the other is Electronic Imaging Applications in Mobile Healthcare. Dr. Tang is a editor and leading guest editor of several journals on medical image processing and computer aided detection and diagnosis (e.g. IEEE System Journal, IEEE Transactions on SMC: Part C, Pattern Recognition, IEEE Trans. Selected Topics in Signal Processing ). He is a senior member of IEEE and TC Co-chair of the Technical Committee on Information Assurance and Intelligent Multimedia-Mobile Communications, IEEE SMC society. His research has been supported by USDA, DoD, NIH, Air force, DoT, and DHS.
Yijun Zhang graduated from the program of medical imaging equipment at Shanghai University of Technology in 2006. At present, he is the chief technician in the Department of Radiology at Shanghai Public Health Clinical Center. His main research direction includes the research and optimization of CT and MR imaging technology.
Jungang Han is a professor at Xi'an University of Posts and Telecommunications. He is the author of two books, and more than100 articles in the field of computer science. His current research interests include artificial intelligence and deep learning for medical image processing.
Yuxin Shi received a doctorate degree in medicine from Fudan University and served as a doctoral supervisor and professor in imaging studies at Fudan University. He also works in Shanghai Public Health Clinical Center. His main research direction is imaging diagnosis of infectious diseases.
Weihua Zhou is an Assistant Professor in the Department of Applied Computing at Michigan Technological University. He received his PhD of Computer Science from Wuhan University in 2008 and his PhD of Computer Engineering from Southern Illinois University Carbondale in 2012. His research interests include medical image analysis, computer vision and machine learning.
References
- 1.Huang C., Wang Y., Li X., Ren L., Zhao J., Hu Y., Zhang L., Fan G., Xu J., Gu X. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet. 2020;395(10223):497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nogrady B. What the data say about asymptomatic COVID infections. Nature. 2020;587(7835):534–535. doi: 10.1038/d41586-020-03141-3. [DOI] [PubMed] [Google Scholar]
- 3.Wang W., Xu Y., Gao R., Lu R., Han K., Wu G., Tan W. Detection of SARS-CoV-2 in different types of clinical specimens. JAMA. 2020;323(18):1843–1844. doi: 10.1001/jama.2020.3786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gostic K., Gomez A.C., Mummah R.O., Kucharski A.J., Lloyd-Smith J.O. Estimated effectiveness of symptom and risk screening to prevent the spread of COVID-19. eLife. 2020;9:e55570. doi: 10.7554/eLife.55570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chung M., Bernheim A., Mei X., Zhang N., Huang M., Zeng X., Cui J., Xu W., Yang Y., Fayad Z.A. CT imaging features of 2019 novel coronavirus (2019-nCoV) Radiology. 2020;295(1):202–207. doi: 10.1148/radiol.2020200230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kroft L.J.M., van der Velden L., Girón I.H., Roelofs J.J.H., de Roos A., Geleijns J. Added value of ultra–low-dose computed tomography, dose Equivalent to chest x-ray radiography, for diagnosing chest pathology. J. Thorac. Imaging. 2019;34(3):179–186. doi: 10.1097/RTI.0000000000000404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hu Z., Tang J., Wang Z., Zhang K., Zhang L., Sun Q. Deep learning for image-based cancer detection and diagnosis-a survey. Pattern Recognit. 2018;83:134–149. [Google Scholar]
- 8.Loey M., Manogaran G., Taha M.H.N., Khalifa N.E.M. A hybrid deep transfer learning model with machine learning methods for face mask detection in the era of the COVID-19 pandemic. Measurement. 2021;167 doi: 10.1016/j.measurement.2020.108288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Islam M.M., Karray F., Alhajj R., Zeng J., A review on deep learning techniques for the diagnosis of novel coronavirus (covid-19), IEEE Access, 9 (2021) 30551-30572. [DOI] [PMC free article] [PubMed]
- 10.Li L., Qin L., Xu Z., Yin Y., Wang X., Kong B., Bai J., Lu Y., Fang Z., Song Q. Artificial intelligence distinguishes COVID-19 from community acquired pneumonia on chest CT. Radiology. 2020;296(2):65–71. doi: 10.1148/radiol.2020200905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Javaheri T., Homayounfar M., Amoozgar Z., Reiazi R., Homayounieh F., Abbas E., Laali A., Radmard A.R., Gharib M.H., Mousavi S.A.J., CovidCTNet: an open-source deep learning approach to diagnose covid-19 using small cohort of CT images, NPJ digital medicine, 4 (2021) 1-10. [DOI] [PMC free article] [PubMed]
- 12.Scott Mader K., Finding and Measuring Lungs in CT Data: A collection of CT images, manually segmented lungs and measurements in 2/3D [Internet]. Available from: https://www.kaggle.com/kmader/finding-lungs-in-ct-data.
- 13.Chen J., Wu L., Zhang J., Zhang L., Gong D., Zhao Y., Chen Q., Huang S., Yang M., Yang X. Deep learning-based model for detecting 2019 novel coronavirus pneumonia on high-resolution computed tomography. Sci. Rep. 2020;10(1):1–11. doi: 10.1038/s41598-020-76282-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ardakani A.A., Kanafi A.R., Acharya U.R., Khadem N., Mohammadi A. Application of deep learning technique to manage COVID-19 in routine clinical practice using CT images: Results of 10 convolutional neural networks. Comput. Biol. Med. 2020;121 doi: 10.1016/j.compbiomed.2020.103795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hasan A.M., Al-Jawad M.M., Jalab H.A., Shaiba H., Ibrahim R.W., Al-Shamasneh A.R. Classification of Covid-19 coronavirus, pneumonia and healthy lungs in CT Scans using Q-deformed entropy and deep learning features. Entropy. 2020;22(5):517. doi: 10.3390/e22050517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Amyar A., Modzelewski R., Li H., Ruan S. Multi-task deep learning based CT imaging analysis for COVID-19 pneumonia: Classification and segmentation. Comput. Biol. Med. 2020;126 doi: 10.1016/j.compbiomed.2020.104037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Singh D., Kumar V., Kaur M. Classification of COVID-19 patients from chest CT images using multi-objective differential evolution–based convolutional neural networks. Eur. J. Clin. Microbiol. Infect. Dis. 2020;39:1379–1389. doi: 10.1007/s10096-020-03901-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Teixeira L.O., Pereira R.M., Bertolini D., Oliveira L.S., Nanni L., Costa Y.M.G., Impact of lung segmentation on the diagnosis and explanation of COVID-19 in chest X-ray images, arXiv preprint arXiv:2009.09780, (2020). [DOI] [PMC free article] [PubMed]
- 19.Avula S.R., Tang J., Acton S.T. An object-based image retrieval system for digital libraries. Multimed. Syst. 2006;11(3):260–270. [Google Scholar]
- 20.Tang J., Guo S., Sun Q., Deng Y., Zhou D. Speckle reducing bilateral filter for cattle follicle segmentation. BMC Genom. 2010;11(2):1–9. doi: 10.1186/1471-2164-11-S2-S9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ravishankar H., Venkataramani R., Thiruvenkadam S., Sudhakar P., Vaidya V. Proceedings of the International Conference on Medical Image Computing and Computer-assisted Intervention. Springer; 2017. Learning and incorporating shape models for semantic segmentation; pp. 203–211. [Google Scholar]
- 22.Lee M.C.H., Petersen K., Pawlowski N., Glocker B., Schaap M. Proceedings of the International Conference on Medical Imaging with Deep Learning Extended Abstract Track. 2019. Template transformer networks for image segmentation. [DOI] [PubMed] [Google Scholar]
- 23.Hu Z., Tang J., Zhang P., Jiang J. Deep learning for the identification of bruised apples by fusing 3D deep features for apple grading systems. Mech. Syst. Signal Process. 2020;145 [Google Scholar]
- 24.Zheng S., Jayasumana S., Romera-Paredes B., Vineet V., Su Z., Du D., Huang C., Torr P.H.S. Proceedings of the IEEE International Conference on Computer Vision (ICCV) 2015. Conditional random fields as recurrent neural networks; pp. 1529–1537. [Google Scholar]
- 25.Ravishankar H., Venkataramani R., Thiruvenkadam S., Sudhakar P., Vaidya V. Proceedings of the International Conference on Medical Image Computing and Computer-assisted Intervention (MICCAI. Springer; 2017. Learning and incorporating shape models for semantic segmentation; pp. 203–211. [Google Scholar]
- 26.Avendi M., Kheradvar A., Jafarkhani H. A combined deep-learning and deformable-model approach to fully automatic segmentation of the left ventricle in cardiac MRI. Med. Image Anal. 2016;30:108–119. doi: 10.1016/j.media.2016.01.005. [DOI] [PubMed] [Google Scholar]
- 27.Ngo T.A., Lu Z., Carneiro G. Combining deep learning and level set for the automated segmentation of the left ventricle of the heart from cardiac cine magnetic resonance. Med. Image Anal. 2017;35:159–171. doi: 10.1016/j.media.2016.05.009. [DOI] [PubMed] [Google Scholar]
- 28.Rupprecht C., Huaroc E., Baust M., Navab N., Deep active contours, arXiv preprint arXiv:1607.05074, (2016).
- 29.Chung H., Mossahebi S., Gopal A., Lasio G., Xu H., Polf J. Evaluation of computed tomography scanners for feasibility of using averaged hounsfield unit–to–stopping power ratio calibration curve. Int. J. Part. Ther. 2018;5(2):28–37. doi: 10.14338/IJPT-17-0035.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Srivastava N., Hinton G., Krizhevsky A., Sutskever I., Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014;15(1):1929–1958. [Google Scholar]
- 31.Jaderberg M., Simonyan K., Zisserman A., Kavukcuoglu K. Spatial transformer networks. Preceed. Adv. Neural Inf. Process. Syst. 2015;28:2017–2025. [Google Scholar]
- 32.Zwanenburg A., Vallières M., Abdalah M.A., Aerts H., Andrearczyk V., Apte A., et al. The Image Biomarker Standardization Initiative: Standardized Quantitative Radiomics for High-Throughput Image-based Phenotyping. Radiology, 295 (2), 328-338. [DOI] [PMC free article] [PubMed]
- 33.Lubner M.G., Smith A.D., Sandrasegaran K., Sahani D.V., Pickhardt P.J. CT texture analysis: definitions, applications, biologic correlates, and challenges. Radiographics. 2017;37(5):1483–1503. doi: 10.1148/rg.2017170056. [DOI] [PubMed] [Google Scholar]
- 34.Kamal M., Abo Omirah M., Hussein A., Saeed H. Assessment and characterisation of post-COVID-19 manifestations. Int. J. Clin. Pract. 2020;75(3):e13746. doi: 10.1111/ijcp.13746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Glover S., Dixon P. Likelihood ratios: a simple and flexible statistic for empirical psychologists. Psychon. Bull. Rev. 2004;11(5):791–806. doi: 10.3758/bf03196706. [DOI] [PubMed] [Google Scholar]
- 36.Gill J., Gill J.M., Torres M., Pacheco S.M.T. Sage Publications; 2019. Generalized Linear Models: A Unified Approach. [Google Scholar]
- 37.Otsu N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979;9:62–66. [Google Scholar]
- 38.Dice L.R. Measures of the amount of ecologic association between species. Ecology. 1945;26(3):297–302. [Google Scholar]
- 39.Bursac Z., Gauss C.H., Williams D.K., Hosmer D.W. Purposeful selection of variables in logistic regression. Source Code Biol. Med. 2008;3(17):1–8. doi: 10.1186/1751-0473-3-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhang K., Liu X., Shen J., Li Z., Sang Y., Wu X., Zha Y., Liang W., Wang C., Wang K. Clinically applicable AI system for accurate diagnosis, quantitative measurements, and prognosis of COVID-19 pneumonia using computed tomography. Cell. 2020;181(6):1423–1433. doi: 10.1016/j.cell.2020.04.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Panwar H., Gupta P.K., Siddiqui M.K., Morales-Menendez R., Singh V. Application of deep learning for fast detection of COVID-19 in X-Rays using nCOVnet. Chaos Solitons Fractals. 2020;138 doi: 10.1016/j.chaos.2020.109944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Harmon S.A., Sanford T.H., Xu S., Turkbey E.B., Roth H., Xu Z., Yang D., Myronenko A., Anderson V., Amalou A. Artificial intelligence for the detection of COVID-19 pneumonia on chest CT using multinational datasets. Nat. Commun. 2020;11(4080):1–7. doi: 10.1038/s41467-020-17971-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tang J., Millington S., Acton S.T., Crandall J., Hurwitz S. Proceeding of the International Conference on Image Processing (ICIP) 2004. Ankle cartilage surface segmentation using directional gradient vector flow snakes; pp. 2745–2748. [Google Scholar]