Abstract
Purpose:
Multimodal deformable image registration is essential for many image-guided therapies. Recently, deep learning approaches have gained substantial popularity and success in deformable image registration. Most deep learning approaches use the so-called mono-stream “high-to-low, low-to-high” network structure, and can achieve satisfactory overall registration results. However, accurate alignments for some severely deformed local regions, which are crucial for pinpointing surgical targets, are often overlooked, especially for multimodal inputs with vast intensity differences. Consequently, these approaches are not sensitive to some hard-to-align regions, e.g., intra-patient registration of deformed liver lobes.
Methods:
We propose a novel unsupervised registration network, namely Full-Resolution Residual Registration Network (F3RNet), for multimodal registration of severely deformed organs. The proposed method combines two parallel processing streams in a residual learning fashion. One stream takes advantage of the full-resolution information that facilitates accurate voxel-level registration. The other stream learns the deep multi-scale residual representations to obtain robust recognition. We also factorize the 3D convolution to reduce the training parameters and enhance network efficiency.
Results:
We validate the proposed method on 50 sets of clinically acquired intra-patient abdominal CT-MRI data. Experiments on both CT-to-MRI and MRI-to-CT registration demonstrate promising results compared to state-of-the-art approaches.
Conclusion:
By combining the high-resolution information and multi-scale representations in a highly interactive residual learning fashion, the proposed F3RNet can achieve accurate overall and local registration. The run time for registering a pair of CT-MRI images is less than 3 seconds using a GPU. In future works, we will investigate how to cost-effectively process high-resolution information and fuse multi-scale representations.
Keywords: Multimodal image registration, Residual learning, Image-guided therapy, Deep learning
1. Introduction
In image-guided therapies (IGT), e.g., pre-operative planning, intervention and diagnosis, multimodal deformable image registration is the key to integrate complementary information contained in different image modalities. For instance, Computed Tomography (CT) is important for dose planning as it can provide the tissue density information, while the corresponding Magnetic Resonance Imaging (MRI) with high soft-tissue contrast can be used for delineating the tumors and organs at risk. Therefore, developing fast and accurate multimodal image registration methods is beneficial for the performance of IGT.
Recently, due to the substantial improvement in computational efficiency over the traditional iterative registration, learning-based image registration approaches are becoming more prominent in time-intensive applications [8]. Most learning-based registration approaches use fully supervised [5,19,3] or semi-supervised learning strategy [14,6], and heavily rely on ground-truth voxel correspondences and/or organ segmentation labels. Although these approaches struggle with imperfect ground-truth labels, they have made a significant impact on the field of deformable image registration. With the development of Spatial Transformer Network (STN) [15], registration approaches that are based on unsupervised learning have also been introduced. For example, VoxelMorph [2] is a monumental unsupervised registration framework that focuses on registering brain images of the same modality (unimodal registration). By modifying VoxelMorph, researchers have further proposed more unsupervised unimodal registration approaches [13,25,17,21,7].
The multimodal image registration, e.g., CT-to-MRI registration, is much more challenging than unimodal image registration because it is difficult for the network to learn a shared appearance representation due to the significant difference in their intensity distributions. Most existing learning-based registration approaches use the so-called mono-stream “high-to-low, low-to-high” network structure with augmented modules, e.g., skip-connection [2,9], multi-resolution fusion [13] and intermediate supervision [18]. This structure can significantly increase the size of the receptive field which is highly desirable for recognizing object information in images, but needs to recover the high-resolution information from the low-resolution representations. With increased receptive field sizes, these approaches prioritize overall registration accuracy, which is governed by the majority of easy-to-align regions, and overlook some severely deformed local regions. For example, livers with tumors usually have large local deformation due to progressed disease, and the deformations of the surrounding kidney and spleen are less significant. In a CT-to-MRI abdominal image registration, the aforementioned approaches are likely to estimate a deformation field that accurately registers kidney and spleen, yet perform poorly at local liver lobes alignment.
Besides, most of the image registration networks utilize 3D Convolutional Neural Networks (3D CNN) to exploit the semantic information in each CT/MRI slice and the spatial relationships across consecutive slices. It is understood that the training of 3D CNN is computationally expensive, and may lead to insufficient training due to the small number of clinical datasets.
To address the above problems, we propose a novel unsupervised Full-Resolution Residual Registration Network (F3RNet), which is shown in 1(a). Distinct from the conventional mono-stream network structure, F3RNet consists of two parallel streams, namely “Full-resolution stream” and “Multi-scale residual stream”. Inspired by the success of using a high-resolution stream in human pose estimation and image inpainting tasks [22,10,26], “Full-resolution stream” takes advantage of the detailed image information and facilitates accurate voxel-level registration. While the “Multi-scale residual stream” learns the deep multi-scale residual representations to robustly recognize corresponding organs in both images and guarantee a high overall registration accuracy. Using the Multi-scale Residual Block (MRB) modules, the network can progressively fuse information from the two parallel streams in a residual learning fashion [11] to further boost the performance. In addition, we factorize the 3D convolution into two correlated 2D and 1D convolutions, thus effectively avoid over-parameterization [23].
To the best of our knowledge, we are the first to incorporate full-resolution representations with multi-scale high-level representations in a residual learning fashion to boost multimodal image registration performance. The main contributions of our work can be summarized as follows:
– Our approach can unite the strong capability of capturing deep multi-scale representations with precise full-resolution spatial localization of the anatomical structures by interactively combining two parallel streams via the proposed MRB module and the residual learning mechanism. By taking into account such full-resolution information, the registration network is more sensitive to the hard-to-align regions, and can provide better alignments for severely deformed local regions.
– The factorization of 3D convolution can markedly reduce the training parameters and enhance the network efficiency.
– We validate the proposed F3RNet on a clinically acquired CT-MRI dataset consisting of 50 pairs of CT and MRI. The experimental results on CT-to-MRI and MRI-to-CT registration show that our method achieves superior performance over existing state-of-the-art traditional and learning-based methods.
The outline of the paper is as follows: Section 2 describes the details of our F3RNet, Section 3 presents the experimental details and registration results on CT-MRI abdominal data and Section 4 will draw conclusions of the paper.
2. Methods
Representing the moving image as Im and the fixed image as If, medical image registration aims to estimate an optimal deformation field ϕ with three channels (x, y, z displacements) that can align Im to If. In this section, we present our Full-resolution Residual Registration Network (shown in Figure 1) firstly. Then, we describe the detailed structure of the designed Residual Block (RB) and Multi-scale Residual Block (MRB) respectively. The factorization of 3D convolution is presented in Section 2.4, and the loss function of our network is described in Section 2.5.
Fig. 1.
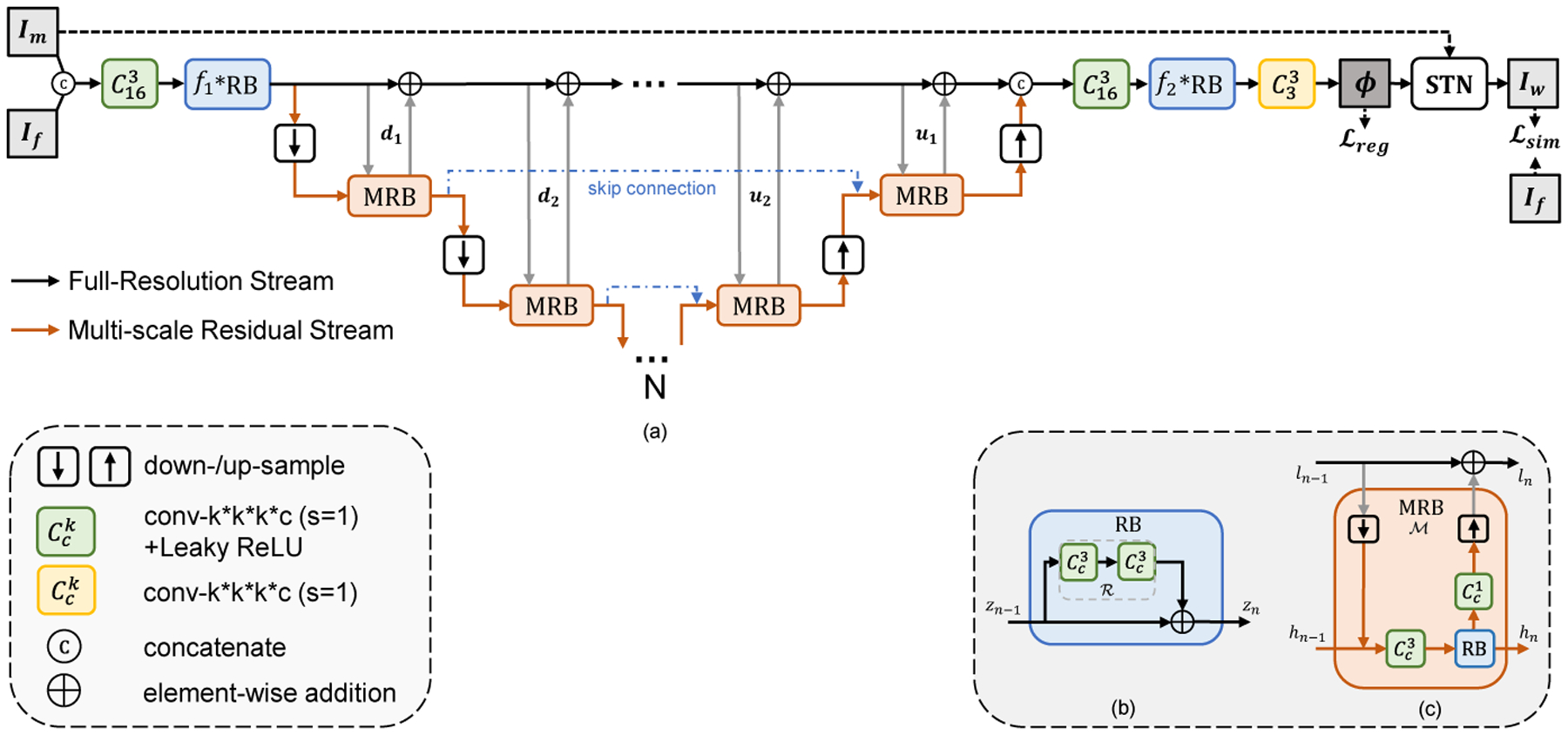
Illustration of Full-Resolution Residual Stream Network (F3RNet). (a) shows the overview of our F3RNet; (b) shows the residual block (RB); (c) shows the multi-resolution residual block (MRB). The network learns parameters for a dense deformation field ϕ that aligns the moving image Im to the fixed image If. N denotes the minimum volume is (1/2N) the size of the input images.
2.1. Overview of the Network
Distinct from the regular high-to-low, low-to-high one-pass network architecture, Full-Resolution Residual Registration Network (F3RNet) unifies two parallel streams:
– Full-resolution Stream. Maintaining high-resolution features has demonstrated its superior performance for dense prediction [22,20,26,10]. The black line in Figure 1(a) indicates the data flow of the full-resolution stream. This stream first concatenates Im and If, followed by a 3D convolution and a series of Residual Blocks (RB, described in Section 2.2). Then, the low-level features on this stream are successively computed by adding the residual from the other parallel stream. After that, the full-resolution stream reduces the number of channels via consecutive RBs and 3D convolutions step-by-step, and estimates the 3-channel deformation field ϕ. Spatial Transformation Network (STN) [15] is applied to warp the moving image Im with ϕ, so that the similarity between the warped image Iw and fixed image If can be evaluated. This stream does not employ any downsampling operation, resulting in good boundary localization but poor performance in deep semantic recognition. As such, the hard-to-align regions are propagated throughout the stream. Specifically, the convolutions in the full-resolution stream are all with 16 channels in our experiments except for the final 3-channel convolution used to generate the deformation field.
– Multi-scale Residual Stream. The data flow of Multi-scale Residual Stream is depicted as the orange line in Figure 1(a). In contrast to the full-resolution stream, this stream is good at capturing high-level features that can improve the organ recognition performance. Specifically, successive pooling and convolution operations are leveraged to increase the receptive fields and enhance the robustness against small noises in the images. We also inherit the skip-connection design in regular high-to-low, low-to-high architecture that the feature spaces with same resolution are skip-connected by addition operation. Besides, with the help of our proposed Multi-scale Residual Blocks (MRB) that can simultaneously operate on both streams, the high-level features can directly interact with low-level features. The interior architecture of MRB is shown in Figure 1(c) with elaboration in Section 2.3. In our experiments, each convolution within the multi-scale residual stream is with 32 channels, and we set N to 4, which is the same as VoxelMorph [2], denoting that the lowest resolution is 1/16 of the original image.
The information of the two distinct streams are automatically fused via residual learning [11]. By repeatedly fusing the features between two streams via computing successive multi-scale residuals, the full-resolution representations become rich for the dense deformation field prediction. At the same time, richer low-level full-resolution information can in turn enhance the high-level multi-scale information.
2.2. Residual Block (RB)
ResNets, proposed in [11], has demonstrated that residual learning can improve the training characteristics over traditional one-pass feed-forward learning. The interior architecture of the Residual Block (RB) is depicted in Figure 1(b). The output zn of the RB can be formulated as:
| (1) |
where represents the residual branch consisting of two 3D convolutions with a kernel size of 3 × 3 × 3 followed by LeakyReLU activations. Instead of computing zn directly as in the traditional feed-forward network, the convolutional branch only needs to compute the residual in this architecture.
2.3. Multi-scale Residual Block (MRB)
The Multi-scale Residual Block (MRB) follows the basic idea of Residual Block (RB) but elegantly achieves interaction between the full-resolution stream and multi-scale residual stream. An MRB consists of a series of pooling, 3D convolution and upsampling layers, as shown in Figure 1(c). Each MRB has two inputs, ln−1 as full-resolution low-level features and hn−1 as multi-resolution high-level features, and two corresponding outputs ln and hn. Intuitively, denoting the entire MRB operation as , the output ln can be computed as:
| (2) |
Specifically, first, the resolution of ln−1 is reduced to that of hn−1 by a pooling operation, followed by a feature map concatenation. Then, the concatenated feature map undergoes a 3D convolution with a kernel size of 3×3×3, followed by a Residual Block (RB) with the same number of channels, and the output hn is connected to the next process of the multi-scale residual stream. Meanwhile, the output of the 3×3×3 convolutional module adjusts the number of channels and the resolution to be consistent with ln−1 through a 1×1×1 convolutional bottleneck layer and an upsampling layer at the other end. By such a process, we can readily use addition operations to integrate the residuals learned in the MRB in the full-resolution stream, thus forming a dual-stream highly interactive residual module.
2.4. Factorized 3D Convolution (F3D)
Most medical images, as shown in Figure 2(a), consist of 3D image stacks with the size of W ×H ×D, where W, H, D represents the width, height, and the number of sequential slices. Inspired by the Inception [24] where large 2D convolution is factorized into two smaller ones, we factorize 3D convolution block for learning the volumetric representation. Specifically, suppose that we have a 3D convolution with kernel size of 3 × 3 × 3 (Fig. 2(b)), it can be factorized into a 3×3×1 convolution and a 1×1×3 convolution in a cascaded fashion (Fig. 2(c)) to continuously capture dense 2D features in W × H slices with 1D attention weights that build sparse sequential relationships across adjacent slices. As such, the number of trainable parameters is reduced from O(33 = 27) to O(3×3+3 = 12), where we can reduce the parameters by half and improve the learning efficiency.
Fig. 2.
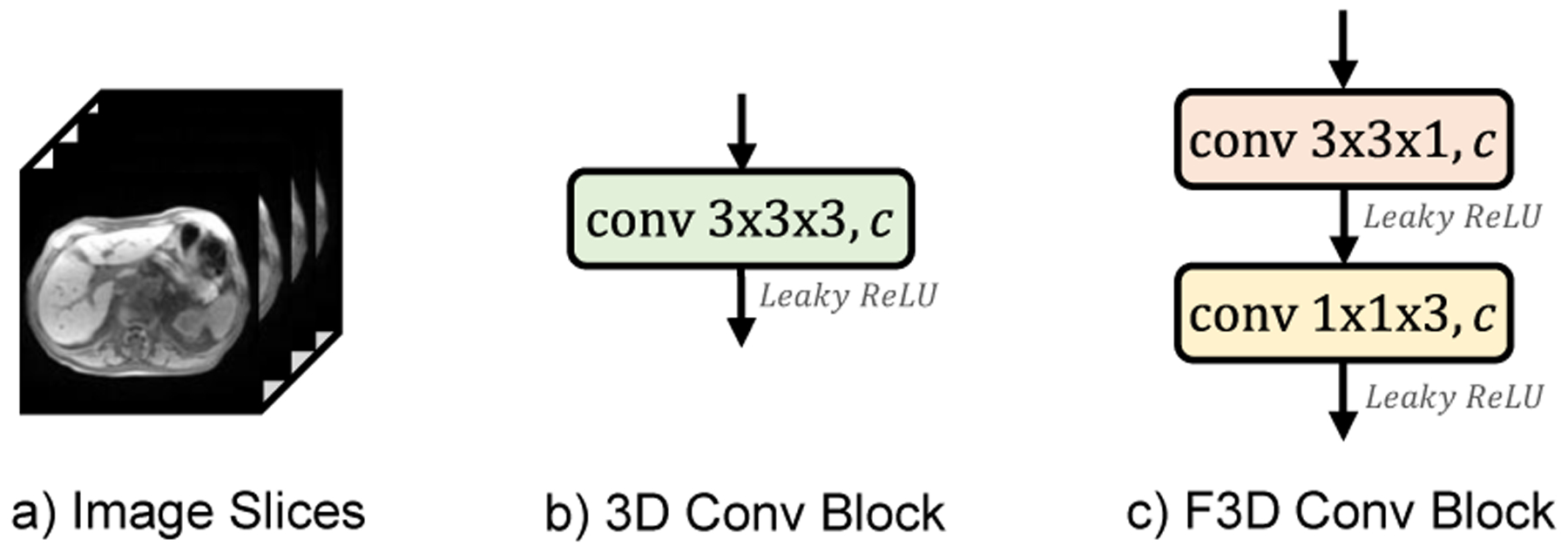
Illustration of a) 3D medical image scans, b) regular 3D convolution with kernel size of 3 × 3 × 3, c) F3D convolution block.
However, it is noteworthy that the factorization is not totally equivalent to regular 3D convolution, and a further ablation study over factorized 3D convolution is presented in Section 3.2.1.
2.5. Loss Function
The loss function of our network consists of two components as shown in Eq.(3). The similarity loss penalizes the dissimilarity between the fixed image If and the warped image Iw(Im ◦ ϕ). The deformation regularization adopts an L2-norm of the gradients of the final deformation field ϕ with a trade-off weight λ. We write the total loss as:
| (3) |
Specifically, Modality Independent Neighborhood Descriptor (MIND) [12] is used to measure the similarity of multimodal images. MIND is a modality-invariant structural representation, and we can minimize the difference in the MIND features between the warped image Iw(Im ◦ ϕ) and the fixed image If to effectively train multimodal registration network. We define:
| (4) |
where N denotes the number of voxels in input images Iw(Im ◦ ϕ) and If, R is a non-local region around voxel x.
3. Experiments
3.1. Dataset and Implementation
In this work, although we specifically focus on the application of abdominal CT-MRI subject-to-subject registration, the full-resolution residual learning strategy can be easily extended to other registration tasks.
Under the IRB approved study, we obtained an intra-patient CT-MRI dataset containing paired CT and MR images from 50 patients. The liver, kidney and spleen in both CT and MRI were manually segmented for quantitative evaluation. Standard preprocessing steps, including affine spatial normalization, resampling and intensity normalization, were performed. The images were cropped into 144 × 144 × 128 subvolume with 1mm isotropic voxels and randomly divided into two groups for training (40 cases) and testing (10 cases).
The proposed method is implemented using Keras [4] with the Tensorflow backend. We train the network on a NVIDIA Titan X (Pascal) GPU using Adam optimizer [16] with a learning rate of 1e-5. The batch size is set to 1.
3.2. Experimental Results
3.2.1. Ablation Study of F3D Convolution
As mentioned in Section 2.4, although convolution factorization can dramatically reduce the training parameters, it may not be totally equivalent to the regular 3D convolution in practice. Therefore, we investigate the different combinations of F3D convolution in our F3RNet. In our experiments, except for the final 3-channel 3D convolution used to generate the deformation field, other 3×3×3 convolutions can be replaced. The variants of F3RNet are presented in Table 1. “More MRBs” indicates that two extra MRBs are added at the lowest resolution path.
Table 1.
Different combinations of F3D convolution (✓) in proposed F3RNet.
| Network | FR stream | MS stream | More MRBs | |
|---|---|---|---|---|
| Encoder | Decoder | |||
| F3RNet-w/o F3D | ||||
| F3RNet-w/ F3D | ✓ | ✓ | ✓ | |
| F3RNet-Enc | ✓ | |||
| F3RNet-Dec | ✓ | |||
| F3RNet-FR | ✓ | |||
| F3ENet-MS | ✓ | ✓ | ||
| F3RNet-MRB | ✓ | ✓ | ✓ | ✓ |
Figure 3 presents the average Dice scores of ROIs on the hold-out test set for varying values of the smoothing trade-off weight λ. The best Dice scores occur when λ = 1.5 for F3RNet-w/o F3D, F3RNet-w/ F3D, F3RNet-Dec, F3RNet-FR and F3RNet-MRB, and λ = 2 for F3RNet-Enc and F3RNet-MS. In particular, F3RNet-w/o F3D and F3RNet-MRB achieve better Dice scores than all other variants. Moreover, after achieving the best Dice scores at λ = 1.5, the results vary slowly over larger λ for F3RNet-w/o F3D and F3RNet-MRB, showing that the two models are more robust to the choice of λ.
Fig. 3.
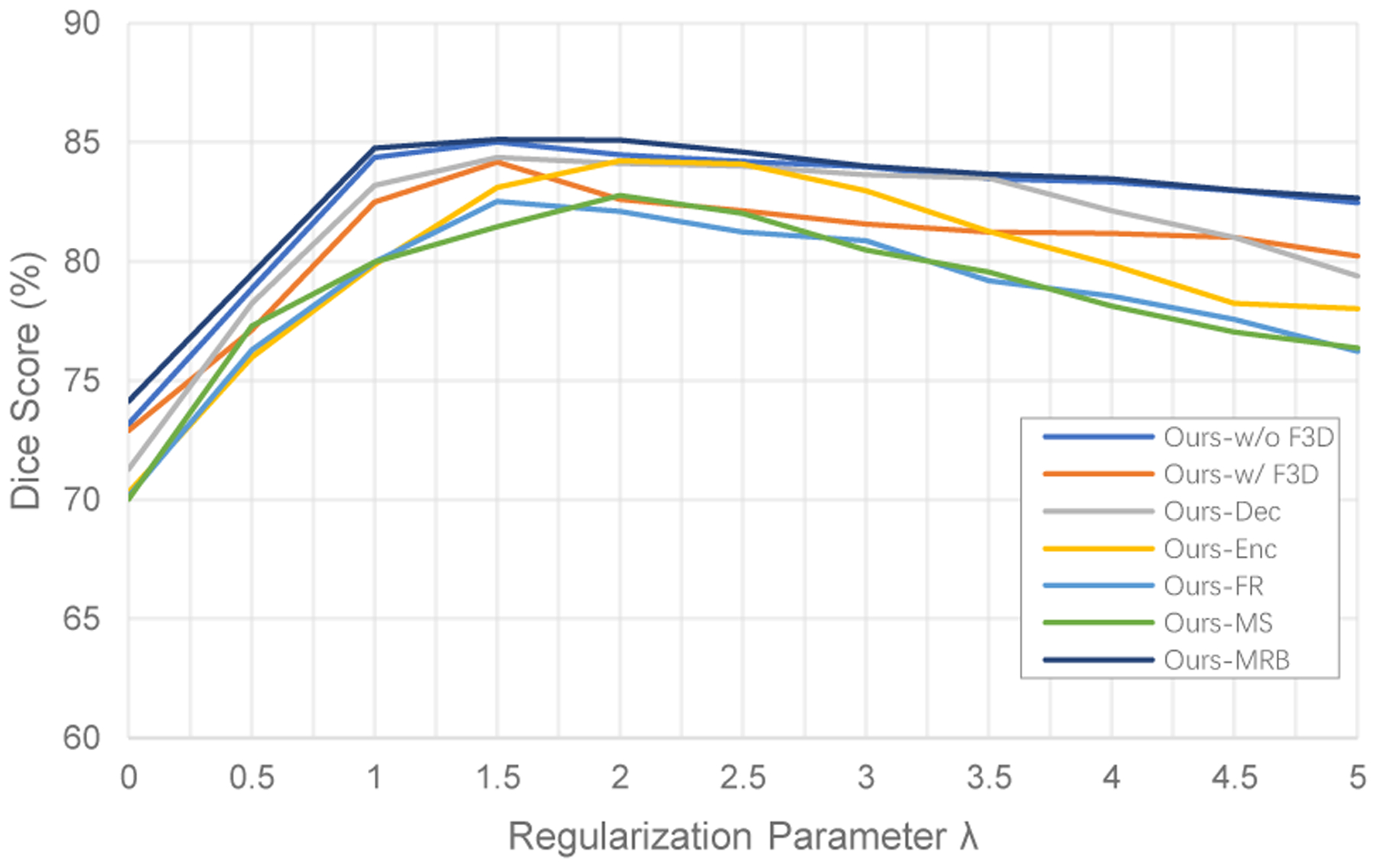
Results of varying the trade-off weight λ on average Dice score of ROIs.
Figure 4 shows visual results of warped images for the ablation analysis. We can firstly see that the original F3RNet (F3RNet-w/o F3D) can effectively register the multimodal images. If we replace all 3D convolutions with F3D (F3RNet-w/ F3D) or only replace the convolution in encoder and decoder (F3RNet-Enc and F3RNet-Dec), our methods can still effectively register the CT image but have slight performance degradation. Interestingly, if we replace the regular convolution on the entire multi-scale residual stream or full-resolution stream alone, this will cause the information of the two streams to not effectively interact and introduce noise, resulting in unstable performance and significant registration degradation. Therefore, if we use F3D to reduce the model parameters, the 3D convolution on both streams must be replaced at the same time. Further, we can use the reduced parameters to add more MRBs (F3RNet-MRB). From the visual results, it can be seen that the registration performance is either maintained or slightly improved.
Fig. 4.
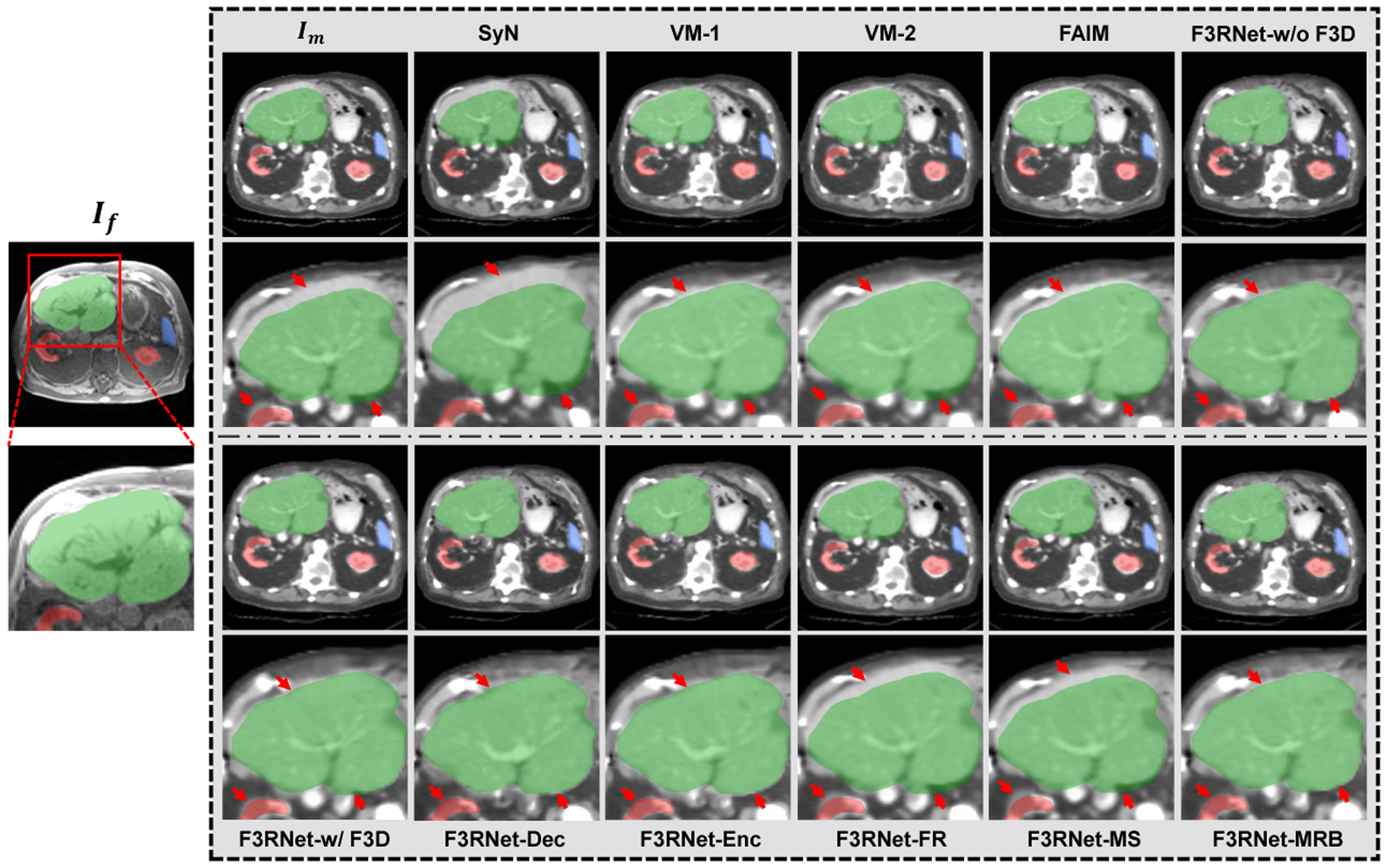
Visual results of an example for CT-to-MRI registration. Outside the grey box shows an example fixed MR image and a zoom-in region with the segmentation masks of the liver (green), kidney (red), and spleen (blue). The corresponding warped CT images and zoom-in regions for baselines and ablation study are presented in the grey box. A good registration will cause structures in warped images to close to the corresponding fixed segmentation masks. The red arrows indicate the registration of interest at the boundary of the organ.
Table 2 also provides the quantitative results in terms of the Average Surface Distance (ASD) and Dice score for all baseline methods and the variants of our F3RNet with different combinations of F3D. As for the results for ablation analysis, we can see that F3RNet-w/o F3D and F3RNet-MRB achieve the best performance. Specifically, with only 39.7% parameters of F3RNet-w/o F3D, F3RNet-MRB achieves better ASD results in the liver and kidney registration than F3RNet-w/o F3D, while it also achieves better Dice score in liver and spleen registration. Meanwhile, consistent with the visual assessment, we can also see that F3RNet-FR and F3RNet-MS both yield significant performance degradation over ASD and Dice score as they cause the features of the two streams to be disjointed.
Table 2.
The quantitative evaluation (mean±std.) for CT-to-MRI registration of all baseline methods and F3RNet with different combinations of F3D. Best results are shown in bold.
| Methods | ASD(mm) | Dice(%) | Params(M) | Times(s) GPU/CPU | ||||
|---|---|---|---|---|---|---|---|---|
| Liver | Spleen | Kidney | Liver | Spleen | Kidney | |||
| Moving | 4.95±0.82 | 1.97±0.52 | 2.01±0.36 | 77.18 ± 4.13 | 78.24 ± 3.21 | 80.14 ± 3.17 | - | - |
| SyN | 4.81±0.79 | 1.54±0.63 | 1.92±0.41 | 79.18 ± 4.37 | 80.21 ± 3.41 | 82.91 ± 3.08 | - | -/97 |
| VM-1 | 3.98±0.74 | 1.42±0.54 | 1.75±0.52 | 82.39 ± 4.11 | 82.83 ± 2.68 | 82.34 ± 2.97 | 0.260 | 1.32/21 |
| VM-2 | 3.92±0.53 | 1.47±0.37 | 1.72±0.49 | 84.17 ± 3.57 | 82.76 ± 2.98 | 83.51 ± 3.36 | 0.300 | 1.33/23 |
| FAIM | 3.88±0.73 | 1.51±0.63 | 1.66±0.41 | 84.51 ± 3.76 | 81.99 ± 2.84 | 83.12 ± 3.24 | 0.217 | 1.29/20 |
| F3RNet-w/o F3D | 2.19 ±0.37 | 1.28±0.39 | 1.37±0.38 | 86.65 ± 3.42 | 85.39 ± 2.75 | 83.58 ± 3.18 | 0.746 | 2.31/26 |
| F3RNet-w/ F3D | 2.63 ±0.52 | 1.36±0.86 | 1.41±0.72 | 85.16 ± 4.19 | 84.39 ± 2.23 | 82.98 ± 3.43 | 0.236 | 1.22/25 |
| F3RNet-Dec | 2.77 ±0.69 | 1.33±0.69 | 1.43±0.48 | 85.87 ± 4.23 | 84.18 ± 2.77 | 83.06 ± 3.92 | 0.544 | 1.93/25 |
| F3RNet-Enc | 2.73 ±0.47 | 1.39±0.52 | 1.38±0.36 | 85.32 ± 4.35 | 84.27 ± 3.35 | 83.11 ± 3.28 | 0.488 | 1.79/23 |
| F3RNet-FR | 3.82 ±0.59 | 1.53±0.39 | 1.56±0.43 | 81.43 ± 4.27 | 82.97 ± 3.18 | 83.13 ± 3.52 | 0.697 | 2.13/25 |
| F3RNet-MS | 3.94±0.75 | 1.51±0.44 | 1.52±0.67 | 82.31 ± 3.84 | 83.06 ± 3.33 | 82.99 ± 3.28 | 0.286 | 1.41/24 |
| F3RNet-MRB | 2.17±0.46 | 1.29±0.48 | 1.34±0.26 | 86.79 ± 3.18 | 85.42 ± 2.98 | 83.16 ± 3.43 | 0.296 | 1.42/25 |
3.2.2. Comparison with Baseline Methods on CT-to-MRI registration
To evaluate our proposed method, four open-source state-of-the-art baseline approaches are also compared, including one traditional method SyN [1] with Mutual Information (MI) metric [27], and three unsupervised learning-based methods, marked as VoxelMorph-1 (VM-1) [2], VoxelMorph-2 (VM-2) [2], and FAIM [17]. The three methods are initially proposed for unimodal registration, and we extend them to multimodal registration by using MIND-based similarity metric.
Figure 4 also illustrates the warped CT images produced by other baseline methods. As we have mentioned above, liver registration is much more challenging in the abdominal image registration task. From the results, we can see that the traditional method SyN fails to align the liver with large local deformation. As for other deep learning methods, VM-1, VM-2, and FAIM achieve better results than SyN but still have considerable disagreements. Except for F3RNet-FR and F3RNet-MS, our methods have the most visually appealing boundary alignment, which demonstrates that our F3RNet can better register the hard-to-align regions.
The quantitative results for the baseline methods are also presented in Table 2. Consistent with the visual results, the evaluations over ASD and Dice scores of our proposed methods are better than the traditional method and other state-of-the-art unsupervised registration methods, except for F3RNet-FR and F3RNet-MS. Furthermore, the traditional method takes more than one minute to register an image pair, while all deep learning methods can complete a registration task in 3 seconds with a GPU, which makes it appealing for image-guided therapies with intense time demand.
3.2.3. Experiments on MRI-to-CT registration
Among all the proposed networks for CT-to-MRI registration, F3RNet-w/o F3D and F3RNet-MRB provide superior results. To further validate the effectiveness of the two proposed methods, we also perform the MRI-to-CT registration in turn. The division of the dataset and the other training settings of the networks, e.g., regularization trade-off weights, etc, are consistent with the CT-to-MRI registration task.
The visualization of the registration results in Figure 5 shows that our methods, F3RNet-w/o F3D and F3RNet-MRB, achieve more accurate organ alignment than other traditional and deep learning approaches, especially for the liver.
Fig. 5.
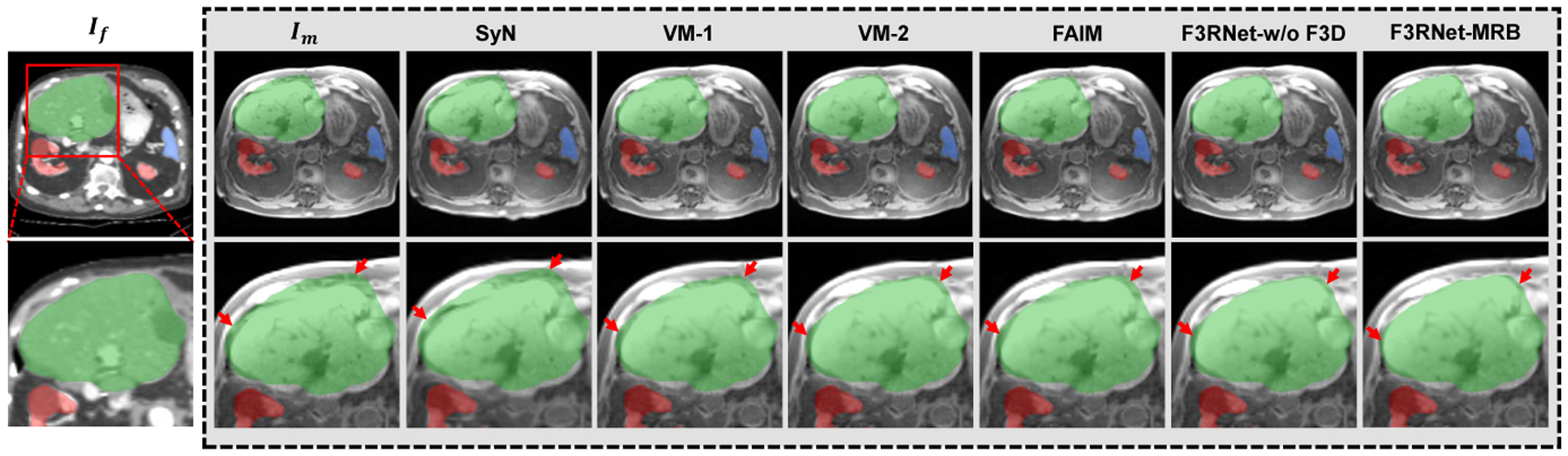
Visual results of an example for MRI-to-CT registration. Outside the grey box shows an example fixed CT image and a zoom-in region with the segmentation masks of the liver (green), kidney (red), and spleen (blue). The corresponding warped MR images and zoom-in regions for all methods are presented in the grey box. The red arrows indicate the registration of interest at the boundary of the organ.
The quantitative evaluation of MRI-to-CT registration is summarized in Table 3. Our proposed methods achieve better results in terms of ASD and Dice scores than that of the traditional method and other state-of-the-art unsupervised learning registration methods. In particular, F3RNet-MRB achieves the best performance among all the methods.
Table 3.
The quantitative evaluation (mean ± std.) for MRI-to-CT registration. Best results are shown in bold.
| Methods | ASD(mm) | Dice(%) | ||||
|---|---|---|---|---|---|---|
| Liver | Spleen | Kidney | Liver | Spleen | Kidney | |
| Moving | 4.95±0.82 | 1.97±0.52 | 2.01±0.36 | 77.18± 4.13 | 78.24±3.21 | 80.14± 3.17 |
| SyN | 4.73±0.68 | 1.63±0.57 | 1.99±0.33 | 78.36± 4.67 | 78.53±3.39 | 81.38± 2.98 |
| VM-1 | 4.02±0.73 | 1.61±0.64 | 1.95±0.28 | 81.34±4.06 | 80.72±3.02 | 82.46± 3.07 |
| VM-2 | 3.59±0.67 | 1.53±0.52 | 1.87±0.36 | 83.28±4.03 | 82.81± 3.14 | 83.37± 2.83 |
| FAIM | 3.71±0.87 | 1.51±0.63 | 1.89±0.31 | 84.33±3.64 | 81.06±3.48 | 83.44± 2.92 |
| F3RNet-w/o F3D | 3.12 ±0.59 | 1.43±0.59 | 1.68±0.42 | 85.75± 4.11 | 83.02± 3.26 | 84.07± 3.04 |
| F3RNet-MRB | 3.04±0.65 | 1.38±0.51 | 1.67±0.35 | 85.93±3.52 | 83.47± 3.51 | 84.39±2.77 |
3.3. Insight into the Parallel Streams
Figure 6 gives an insight into how the network better tackles the registration for hard-to-align regions by visualizing the intermediate feature maps on the two parallel streams. We can see that the representations in Full-resolution Stream (Figure 6 (a)) become rich for accurate dense deformation field estimate by repeatedly fusing the features from Multi-scale Residual Stream. At the same time, as the receptive field increases in the Multi-scale Residual Stream, the multi-scale branch is more capable of recognition but the localization of features is significantly deteriorated (Figure 6 (b)). Previous mono-stream structures are difficult to decode accurate voxel-wise information from low-resolution features for final dense prediction. With the interactive MRB modules, the information obtained by the Multi-scale Residual Stream includes not only the information of the previous process of this stream, but also the full-resolution information, yielding better low-resolution information decoding. Further, the residual stream focuses on computing the residual, which makes the network more sensitive to hard-to-align regions with large deformations, i.e., the liver in this case (shown in the last row of Figure 6 (b) with red arrows). We believe that this highly interactive design through residual learning is the key to boosting registration performance.
Fig. 6.
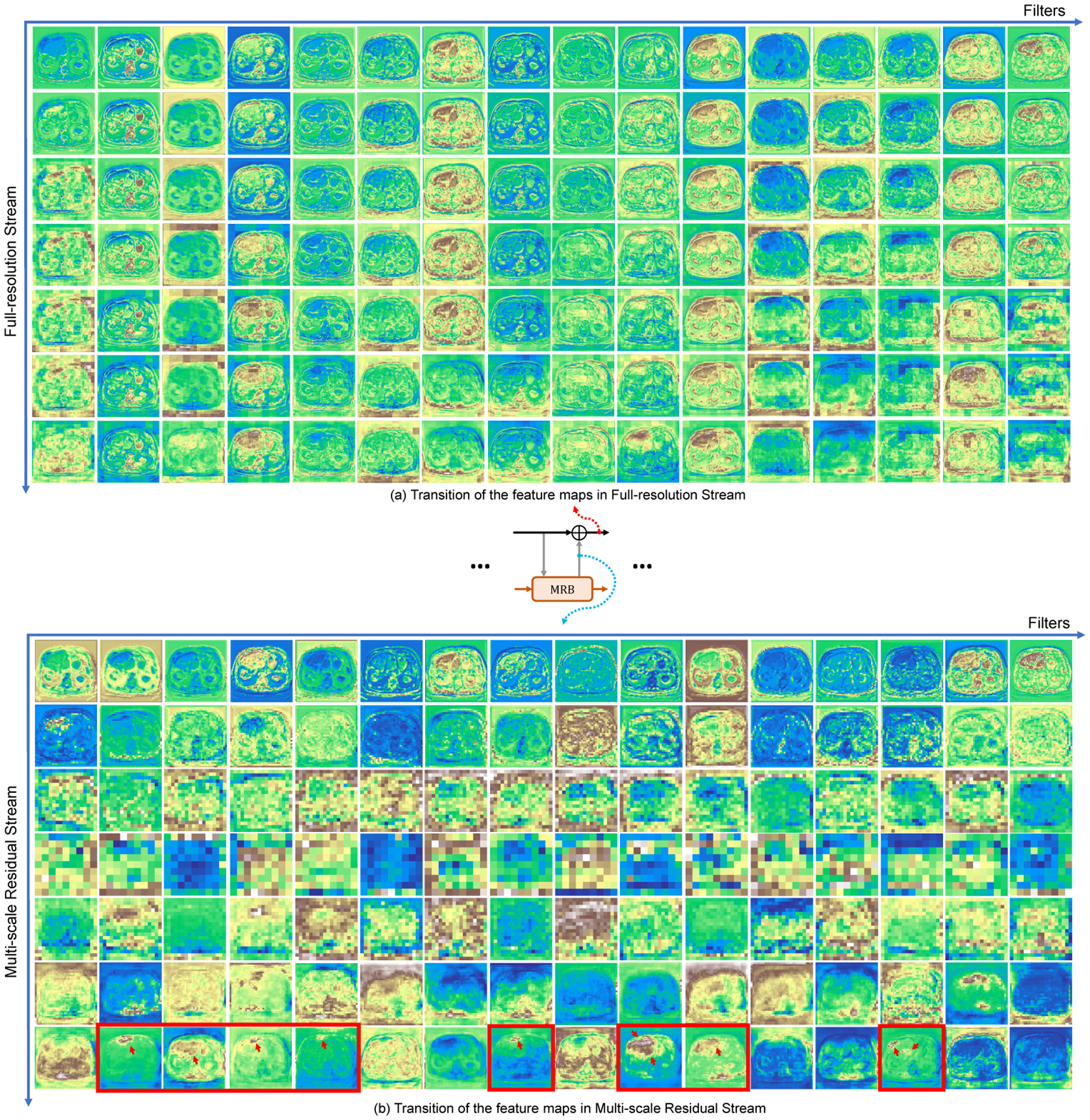
Example of transition of the intermediate feature maps in (a) Full-resolution Stream and (b) Multi-scale Residual Stream. Each feature map has 16 channels (horizontal axis) and their transition in both streams are presented (vertical axis). Some hard-to-align regions are more accurately detected in residual stream (red arrows at the last row of (b)).
4. Conclusions
In this work, we propose a novel unsupervised registration network, namely Full-Resolution Residual Registration Network (F3RNet), which takes advantage of full-resolution information, multi-scale fusion, deep residual learning framework and 3D convolution factorization, to improve multimodal registration. The experimental results indicate that our network can better register the hard-to-align region, yielding superior accuracy of registration. In our experiments, we found the current input size to be a good compromise between image resolution and GPU memory limitation. Future works will focus on the lighter and more adaptive ways to leverage high-resolution information and multi-scale fusion.
Acknowledgements
This project was supported in part by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health (Grant No. R01EB025964, R01DK119269, and P41EB015898) and in part by the Overseas Cooperation Research Fund of Tsinghua Shenzhen International Graduate School (Grant No. HW2018008).
Footnotes
Conflict of interest
Jayender Jagadeesan owns equity in Navigation Sciences, Inc. He is a co-inventor of a navigation device to assist surgeons in tumor excision that is licensed to Navigation Sciences. Dr.Jagadeesan’s interests were reviewed and are managed by BWH and Partners HealthCare in accordance with their conflict of interest policies.
Ethical approval
All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Contributor Information
Zhe Xu, Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, China; Brigham and Women’s Hospital, Harvard Medical School, Boston 02115, USA.
Jie Luo, Brigham and Women’s Hospital, Harvard Medical School, Boston 02115, USA; Graduate School of Frontier Sciences, The University of Tokyo, Tokyo 158-8557, Japan.
Jiangpeng Yan, Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, China.
Xiu Li, Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, China.
Jagadeesan Jayender, Brigham and Women’s Hospital, Harvard Medical School, Boston 02115, USA.
References
- 1.Avants BB, Epstein CL, Grossman M, Gee JC: Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical image analysis 12 1, 26–41 (2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Balakrishnan G, Zhao A, Sabuncu MR, Guttag J, Dalca AV: An unsupervised learning model for deformable medical image registration. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 9252–9260 (2018) [Google Scholar]
- 3.Chee E, Wu Z: Airnet: Self-supervised affine registration for 3d medical images using neural networks. arXiv preprint arXiv:1810.02583 (2018) [Google Scholar]
- 4.Chollet F: Keras (2015). URL https://github.com/fchollet/keras
- 5.Fan J, Cao X, Yap PT, Shen D: Birnet: Brain image registration using dual-supervised fully convolutional networks. Medical image analysis 54, 193–206 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ferrante E, Dokania PK, Silva RM, Paragios N: Weakly supervised learning of metric aggregations for deformable image registration. IEEE journal of biomedical and health informatics 23(4), 1374–1384 (2018) [DOI] [PubMed] [Google Scholar]
- 7.Ferrante E, Oktay O, Glocker B, Milone DH: On the adaptability of unsupervised cnn-based deformable image registration to unseen image domains. In: International Workshop on Machine Learning in Medical Imaging, pp. 294–302. Springer; (2018) [Google Scholar]
- 8.Fu Y, Lei Y, Wang T, Curran WJ, Liu T, Yang X: Deep learning in medical image registration: a review. Physics in Medicine & Biology (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ghosal S, Ray N: Deep deformable registration: Enhancing accuracy by fully convolutional neural net. Pattern Recognition Letters 94, 81–86 (2017) [Google Scholar]
- 10.Guo Z, Chen Z, Yu T, Chen J, Liu S: Progressive image inpainting with full-resolution residual network. In: Proceedings of the 27th ACM International Conference on Multimedia, pp. 2496–2504 (2019) [Google Scholar]
- 11.He K, Zhang X, Ren S, Sun J: Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 770–778 (2016) [Google Scholar]
- 12.Heinrich MP, Jenkinson M, Bhushan M, Matin T, Gleeson FV, Brady M, Schnabel JA: Mind: Modality independent neighbourhood descriptor for multi-modal deformable registration. Medical image analysis 16(7), 1423–1435 (2012) [DOI] [PubMed] [Google Scholar]
- 13.Hu X, Kang M, Huang W, Scott MR, Wiest R, Reyes M: Dual-stream pyramid registration network. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, pp. 382–390. Springer; (2019) [Google Scholar]
- 14.Hu Y, Modat M, Gibson E, Li W, Ghavami N, Bonmati E, Wang G, Bandula S, Moore CM, Emberton M, Ourselin S, Noble JA, Barratt DC, Vercauteren T: Weakly-supervised convolutional neural networks for multimodal image registration. Medical image analysis 49, 1–13 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jaderberg M, Simonyan K, Zisserman A: Spatial transformer networks. In: Advances in neural information processing systems, pp. 2017–2025 (2015) [Google Scholar]
- 16.Kingma DP, Ba J: Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014) [Google Scholar]
- 17.Kuang D, Schmah T: Faim–a convnet method for unsupervised 3d medical image registration. In: International Workshop on Machine Learning in Medical Imaging, pp. 646–654. Springer; (2019) [Google Scholar]
- 18.Li H, Fan Y: Non-rigid image registration using self-supervised fully convolutional networks without training data. In: 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), pp. 1075–1078. IEEE; (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lv J, Yang M, Zhang J, Wang X: Respiratory motion correction for free-breathing 3d abdominal mri using cnn-based image registration: a feasibility study. The British journal of radiology 91, 20170788 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pohlen T, Hermans A, Mathias M, Leibe B: Full-resolution residual networks for semantic segmentation in street scenes. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 4151–4160 (2017) [Google Scholar]
- 21.Sheikhjafari A, Noga M, Punithakumar K, Ray N: Unsupervised deformable image registration with fully connected generative neural network (2018)
- 22.Sun K, Xiao B, Liu D, Wang J: Deep high-resolution representation learning for human pose estimation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 5693–5703 (2019) [Google Scholar]
- 23.Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z: Rethinking the inception architecture for computer vision. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) pp. 2818–2826 (2016) [Google Scholar]
- 24.Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z: Rethinking the inception architecture for computer vision. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 2818–2826 (2016) [Google Scholar]
- 25.de Vos BD, Berendsen FF, Viergever MA, Sokooti H, Staring M, Išgum I: A deep learning framework for unsupervised affine and deformable image registration. Medical image analysis 52, 128–143 (2019) [DOI] [PubMed] [Google Scholar]
- 26.Wang J, Sun K, Cheng T, Jiang B, Deng C, Zhao Y, Liu D, Mu Y, Tan M, Wang X, Liu W, Xiao B: Deep high-resolution representation learning for visual recognition. IEEE transactions on pattern analysis and machine intelligence (2020) [DOI] [PubMed] [Google Scholar]
- 27.Wells III WM, Viola P, Atsumi H, Nakajima S, Kikinis R: Multi-modal volume registration by maximization of mutual information. Medical image analysis 1(1), 35–51 (1996) [DOI] [PubMed] [Google Scholar]


