Measurement of cellular-interstitial water exchange time in tumors based on diffusion-time-dependent diffusional kurtosis imaging

Abstract

Purpose:

To assess the feasibility of using diffusion-time-dependent diffusional kurtosis imaging (tDKI) to measure cellular-interstitial water exchange time (τ_ex) in tumors, both in animals and in humans.

Methods:

Preclinical tDKI studies at 7 T were performed with the GL261 glioma model and the 4T1 mammary tumor model injected into the mouse brain. Clinical studies were performed at 3 T with women who had biopsy-proven invasive ductal carcinoma. tDKI measurement was conducted using a diffusion-weighted STEAM pulse sequence with multiple diffusion times (20–800 ms) at a fixed echo time, while keeping the b-values the same (0–3000 s/mm²) by adjusting the diffusion gradient strength. The tDKI data at each diffusion time t were used for a weighted linear least-squares fit method to estimate the diffusion-time-dependent diffusivity, D(t), and diffusional kurtosis, K(t).

Results:

Both preclinical and clinical studies showed that, when diffusion time t ≥ 200 ms, D(t) did not have a noticeable change while K(t) decreased monotonically with increasing diffusion time in tumors and t ≥ 100 ms for the cortical ribbon of the mouse brain. The estimated τ_ex averaged median and interquartile range (IQR) of GL261 and 4T1 tumors were 93 (IQR = 89) ms and 68 (78) ms, respectively. For the cortical ribbon, the estimated τ_ex averaged median and IQR were 41 (34) ms for C57BL/6 and 30 (17) ms for BALB/c. For invasive ductal carcinoma, the estimated τ_ex median and IQR of the two breast cancers were 70 (94) and 106 (92) ms.

Conclusion:

The results of this proof-of-concept study substantiate the feasibility of using tDKI to measure cellular-interstitial water exchange time without using an exogenous contrast agent.

1 |. INTRODUCTION

Cellular-interstitial water exchange time has been a parameter of interest in cancer studies, as it reflects a number of important cellular properties, such as membrane permeability and size of the cells, that are relevant to tumor aggressiveness^1,2 and treatment response.^3–5 Water molecules can cross the plasma membrane through specialized water-selective channels, known as aquaporins, as well as by simple diffusion through the plasma membrane, although substantially slower.⁶ In addition, it has been shown that water exchange depends on cell membrane ion-pump activity, a measure of mitochondrial metabolism, suggesting that cellular-interstitial, ie transcytolemmal, water exchange rate may be a sensitive indicator of cellular energy turnover.^5,7,8 Earlier studies have shown that cancer cells have increased metabolic activity associated with higher water exchange rates compared with normal tissues.^9–11 It was also reported that intracellular water lifetime, the reciprocal of water exchange rate from the intracellular to interstitial space, appeared to correlate with tumor aggressiveness¹ and the overall survival of head and neck cancer patients after chemoradiation therapy.⁴ However, the underlying mechanism and role of transcytolemmal water exchange are not fully understood yet. Furthermore, in vivo measurement of transcytolemmal water exchange remains non-trivial to date, as most previous studies have been based on the difference in compartmental relaxation rates induced by gadolinium-based contrast agent injection.^12,13

In this study, we consider diffusion MRI (dMRI) methods to measure transcytolemmal water exchange without using a contrast agent. dMRI is a unique in vivo imaging technique sensitive to cellular microstructure at the scale of the water diffusion length, of the order of a few micrometers.^14,15 The feasibility of using dMRI to assess cancer treatment response has been demonstrated by a number of studies.^16–18 The diffusion coefficient (or the diffusivity) D, as well as higher-order dMRI metrics, typically measured at a fixed diffusion time, remain non-specific to multiple tissue microstructural factors, such as cell size, cell density, compartmental diffusivities and water exchange between compartments.^19–23 Quantifying the sizes of spheres and cylinders by varying the diffusion time with NMR (before MRI) dates back to the 1968 work of Murday and Cotts²⁴ and other works in later years.^25,26 With the advent of MRI, diffusion-time dependence of diffusion tensor eigenvalues was observed in muscle,^23,27 cancer,²⁸ and brain.^29,30 The characteristic time for restrictive effects is $t_c~L_c^2/D$, where L_c is a typical distance that water molecules travel to encounter the barriers (the correlation length of cell packing), and D is the diffusivity of the bulk fluid. For cancer cells, with radius ~4 μm and D~1.5 μm²/ms, the effects of restriction are expected to be observed most clearly when diffusion time t is about 10 ms (ie, it matches the characteristic time). This means that diffusion times ranging from substantially shorter than 10 ms to substantially longer than 10 ms are required to estimate biophysical parameters of cancer cells, such as cell size, extracellular volume fraction and free diffusivity in intra- and extracellular spaces.^15,19

The time dependence of the dMRI signal due to restriction effects noticeably decreases beyond the characteristic time and the decay pattern is affected by water exchange between the intra- and extracellular compartments.^31–33 Investigation of the exchange effect well beyond the characteristic time in tumors requires long diffusion times in the range of hundreds of milliseconds, which are challenging with conventional spin-echo sequences due to T₂ decay and require alternatives such as the stimulated-echo acquisition mode (STEAM) technique. One of the promising dMRI methods to measure transcytolemmal water exchange is to use diffusion-time-dependent diffusional kurtosis imaging (tDKI). The diffusional kurtosis K is a next-order cumulant of the dMRI signal, beyond the diffusion coefficient.³⁴ As K = 0 in a homogeneous medium, a non-zero kurtosis can serve as a measure of diffusional heterogeneity within a voxel of interest. Such heterogeneity in diffusion can be affected by the exchange of water molecules between compartments; water exchange “homogenizes” the magnetization between the exchanging compartments, thereby decreasing K when diffusion time is sufficiently longer than the exchange time.³⁴ A Monte Carlo simulation study of a two-compartment exchange model of diffusion³⁵ showed that, when the residence time in a cell is much longer than the time it takes to diffuse across it and across the correlation length of cell packing, τ_ex ≫ t_c, ie, the exchange is “barrier limited”, the exchange time τ_ex can be measured from the decreasing part of the K(t) curve.

Time-dependent kurtosis K(t) was observed in rat cortex,³⁶ mouse brains³⁷ and ex vivo cuprizone-treated mouse brains³⁸ using both conventional pulsed and oscillating gradient spin echo techniques. Recently, time-dependent kurtosis was observed in normal human cortical gray matter, where the specific ~t^−1/2 decrease of K(t) was ascribed to the structural disorder along the neurites.³⁹ However, the feasibility of measuring the water exchange time τ_ex from K(t) has not yet been clearly demonstrated in vivo. Furthermore, K(t) in tumors has not been reported.

In this work, we use the time-dependent K(t) to quantify water exchange in tumor cells with in vivo data of tumor lesions. In particular, we investigate the dependence of K on diffusion time, and assess the feasibility of measuring transcytolemmal water exchange time τ_ex using K(t) in mouse tumor models and breast cancer patient data.

2 |. METHODS

2.1 |. Diffusional kurtosis and exchange time

In the case of simple Gaussian diffusion (eg in free water), a dMRI measurement can be characterized by a single parameter, the b-value b = q²t, with q the diffusion wave vector set by the gradient pulse, and t the diffusion time, such that the dMRI signal decays as S = S₀ exp(−bD). However, in biological tissues, it has been shown that non-Gaussian diffusion effects cannot be ignored when the b-value is sufficiently large, b ≥ 1000 s/mm².^40–43 The signal can be characterized by including higher-order terms in its cumulant expansion³⁴:

$$\text{ln}\left(S/S_0\right)=-bD+(K/6){(bD)}^2+O\left(b^3\right)$$ (1)

with O(b³) denoting the error term in the approximation. When a voxel of interest has multiple non-exchanging Gaussian compartments, the diffusional kurtosis is given by the relative variance of compartmental diffusivities, $K_0=3\frac{\text{var}(D)}{D^2}$, and is time independent.

The time dependence of all the cumulants in Equation (1), including D(t) and K(t), can be explored by varying the diffusion time t.^23,39,44,45 For short diffusion times, t ≪ t_c, the kurtosis increases.^35,36 As shown by Fieremans et al (2010),³⁵ in the barrier-limited exchange case τ_ex ≫ t_c, K(t) peaks around t ~ t_c, beyond which point both intra- and extracellular spaces become effectively homogenized separately, while their mixing is not yet relevant (this is the physical meaning of exchange being barrier limited). Hence, the maximal K(t) is approximately given by the unmixed expression for K₀ above (after Equation (1)), where the variance var(D) should be taken over the coarse-grained diffusivities (ie taken in the tortuosity limit, and neglecting the exchange).

When the diffusion time becomes sufficiently long, t ≫ t_c, and begins to match τ_ex, the barrier-limited exchange between intra- and extracellular compartments can be considered independent of the position of water molecules within each compartment, and the physics of diffusion asymptotically maps³⁵ onto that of the Kärger model,⁴⁶ which assumes a two-component system where Gaussian diffusion in each component is modified by the exchange between them occurring at every point in space. Clearly, this simplified description only applies asymptotically, in the limit where each of the tissue compartments is coarse-grained by the diffusion, while the exchange is slow on the coarse-graining time scale t_c. For a biological tissue in the Kärger model regime, the overall D(t) = (1 − v_e)D_i+v_eD_e = const, where D_i and D_e are the time-independent (fully coarse-grained) effective intra- and extracellular diffusivities, respectively, and v_e is the extracellular volume fraction. The overall time-dependent K(t)decreases with time^34,47:

$$K(t)=K_0\frac{2{\tau }_{ex}}{t}\left[1-\frac{{\tau }_{ex}}{t}\left(1-e^{-t/{\tau }_{ex}}\right)\right];+K_{\infty }$$ (2)

with the exchange time τ_ex = v_eτ_i = (1 − v_e)τ_e, ie an equilibrium condition that the amount of water crossing into the cell is equal to the amount of water crossing out to maintain constant water fraction. In Equation (2), we employed $K_0=3\frac{\text{var}(D)}{D^2}$, where var(D) = v_e(1 − v_e) (D_i − D_e)², and added the term K_∞ (nominally zero in the Kärger model), which in our case accounts for other tissue heterogeneity effects within the voxel, unrelated to or not involved in the water exchange measured by the tDKI method in this study. This is because addition of the signal from the water molecules not participating in the water exchange leads to addition of the cumulant generating functions.

We note that the kurtosis in Equation (2) decreases monotonically with increasing diffusion time, whereas the kurtosis from actual tissues first increases, and then decreases, as described above. Hence, the relationship (Equation (2)) between K(t) and τ_ex in the Kärger model regime can be applied only for the data at long enough diffusion times, in which D(t) has already reached its constant tortuosity asymptote (ie, diffusion in each compartment has become Gaussian), while K(t) decreases solely because of the exchange, with a rate 1/τ_ex, as shown in Equation (2). The parameters used in this framework are summarized in Table 1.

TABLE 1.

Parameters used in the two-compartment exchange model of tDKI

Parameter	Definition
ve	Extracellular water fraction
tc	Characteristic diffusion time that water molecules travel to encounter the barriers
τex	Water exchange/mixing time of two compartments; τex = τive = τe(1 − ve)
τi	Intracellular water lifetime; τi = τex/ve
τe	Extracellular water lifetime; τe = τex/(1 − ve)
Di	Long-time effective intracellular diffusivity
De	Long-time effective extracellular diffusivity
K0	Diffusional kurtosis from water molecules participating in water exchange
K∞	Diffusional kurtosis from water molecules not participating in water exchange

2.2 |. Mouse tumor models

Six- to eight-week-old C57BL/6 mice (n = 8) were given 10⁵ GL261 mouse glioma cells suspended in 4 μL of PBS using a Hamilton syringe for stereotactic intracranial injection. The same technique was also used to inject 10⁵ 4T1 mouse mammary tumor cells in BALB/c mice (n = 5) of the same age. All mice were scanned between post-injection days 7 and 21 when the longest diameter of the tumor was approximately 5 mm or larger. For MRI scans, general anesthesia was induced by 1.5% isoflurane in air. The animal body temperature was maintained at 34 ± 2 °C during the scan. All mice were treated in strict accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals, and this study was approved by the Institutional Animal Care and Use Committee.

2.3 |. Data acquisition of mouse tumor models

MRI experiments were performed on a Bruker 7 T micro-MRI system, consisting of a BioSpec Avance III-HD console (Bruker BioSpin MRI, Ettlingen, Germany) with an actively shielded gradient coil (Bruker, BGA-12; gradient strength 600 mT/m) and a four-channel phased array cryogenically cooled receive-only coil with a volume transmit coil (Bruker). In each imaging session, T₂-weighted images were acquired using a rapid acquisition with relaxation enhancement (RARE) pulse sequence with TR/TE = 3.4 s/20 ms, image matrix = 128 × 128 × 8, voxel size = 0.16 × 0.16 mm² and slice thickness = 0.8 mm with a gap of 0.2 mm. Time-dependent dMRI data were acquired using a diffusion-weighted STEAM pulse sequence for tumor (eight slices with 1 mm thickness) in the sagittal direction with an echo-planar imaging (EPI) readout (TR = 8 s, TE = 30 ms, FOV = 20 × 20 mm², image matrix = 80 × 80, resolution = 0.25 × 0.25 mm² with two averages). dMRI measurement was conducted with multiple diffusion times between 20 and 800 ms while keeping the same b-values (b = 200, 500, 1000, 1500, 2000, 3000 s/mm²) by adjusting the diffusion gradient strength. The diffusion gradient duration (δ) was kept constant at 7 ms. The diffusion weighting gradient was applied in only one direction (x-axis) assuming isotropic diffusion in the tumor. The acquisition time was 3 min 12 s for each diffusion time (20 ms to 800 ms), with total acquisition time about 35 min.

2.4 |. Breast cancer patients

This Health Insurance Portability and Accountability Act-compliant prospective study was performed with approval from our institutional review board and waived informed consent. tDKI measurement was conducted with two women (35 and 56 years) as part of their clinical breast MRI examinations. Both patients had biopsy proven invasive ductal carcinoma. All scans were performed using a whole-body Siemens MAGNETOM Trio 3 T scanner (Erlangen, Germany) with a 16-element breast coil array (Invivo, Gainesville, Florida). We measured diffusion using a STEAM-DTI sequence with an EPI readout and Spectral Attenuated Inversion Recovery (SPAIR) fat suppression (T_R/T_E = 3000/52 ms, matrix = 56 × 128 × 4, resolution = 2.8 × 2.8 × 5 mm³) with three b-values (200, 1000 and 2000 s/mm²). The diffusion weighting gradient was applied to only one direction (x-axis), assuming that the diffusional displacement is isotropic in tumor. The acquisition was repeated using five different diffusion times (t = 120, 200, 300, 450 and 650 ms) by varying the mixing time. The diffusion gradient duration (δ) was kept constant at 15 ms. Compared with the preclinical scans with the mouse models, smaller numbers of diffusion times and b-values were used, in order to keep the total scan time for tDKI to approximately 5 min. Tumors were identified from post-contrast T₁-weighted images.

2.5 |. Data analysis

The contribution of the imaging gradients at each diffusion time was included in the b-value calculation so that the same b-values were used for all diffusion times by adjusting the diffusion weighting gradient accordingly. dMRI data at each diffusion time t was used to estimate D(t) and K(t) using a weighted linear least-squares fit method.⁴⁸ Tumors were identified using both T₂-weighted RARE images and diffusion-weighted images. Regions of interest (ROIs) for tumors were manually drawn in dMRI images with b = 1000 s/mm² and t = 20 ms, and then propagated to other diffusion times. τ_ex was estimated, along with K₀ and K_∞, by fitting Equation (2) to the K(t) estimated from data with sufficiently long diffusion times (t = 200–800 ms) where D(t) ≈ const. The assumption of D(t) ≈ const was evaluated using a linear model, D(t) = At+D₀, with A for the slope and D₀ for the y-intercept. The ROI data analysis was performed using a bootstrapping approach to obtain the mean and standard deviation of the estimated parameters, in which multiple averaged data (n = 1000) were generated by randomly selecting 50% of voxels within the ROI.

For comparison, the cortical ribbon of the mouse brain was included in the analysis using the same approach except including shorter diffusion times (t = 100–800 ms) where D(t) ≈ const with a clear decreasing pattern of K(t). The cortical ribbon of the mouse brain has low diffusion anisotropy, close to zero near the cortical surface. Hence, we assumed that the diffusion in the cortical ribbon ROI is near isotropic such that our tDKI data with diffusion weighting in only one direction is still adequate to assess the diffusion time dependence of the diffusivity and kurtosis without a significant effect of the tissue structural directionality. The breast cancer patient data were analyzed in the same way as described for the mouse tumor ROIs using data with diffusion times of 200 ms or longer and the same bootstrapping approach. The parameter estimation was conducted using the simplex algorithm⁴⁹ provided as the function fminsearch in MATLAB (MathWorks, Natick, Massachusetts).

The same tDKI data were also used to assess whether the T₁-weighted decays of the signal intensities of the tumor and cortical ribbon ROIs remain mono-exponential over the diffusion time ranges used for measurement of τ_ex. A mono-exponential decay pattern would indicate that there is a negligible variation in the T₁-weightings of the intra- and extracellular compartments of the STEAM data over the selected diffusion times. Since the tDKI data did not include b = 0 s/mm², the S₀ values estimated from the DKI analysis using Equation (1) were used for estimation of T₁.

3 |. RESULTS

3.1 |. GL261 mouse glioma model

Figure 1 shows representative diffusion-weighted images from one of the mice with the GL261 murine glioma model. The signal-to-noise ratio (SNR) was measured as the mean signal intensity of the tumor ROI divided by the standard deviation of background noise in the air. The SNR ranged from 29 (for t = 800 ms and b = 3000 s/mm²) to 133 (for t = 700 ms and b = 200 s/mm²). The lower panel of Figure 1 shows the D(t) and K(t) parameter maps estimated for individual diffusion times. It can be observed that the D(t) maps did not show any remarkable change with diffusion time, whereas the K(t) maps show noticeable decreases in most voxels.

FIGURE 1.

Representative diffusion-weighted images of one of the mice with the GL261 murine glioma model. The top panel shows one slice in the middle of the tumor with the lowest and highest b-values (ie 200 and 3000 s/mm²) at all the diffusion times used in this study between 20 and 800 ms. A red box marks the area with the tumor. The area in the red box is shown in the lower panel with the estimated D(t) and K(t) maps for individual diffusion times, which demonstrate substantial decreases of K(t) in most voxels

Figure 2 shows the plots of D(t) and K(t) measured from the same mouse tumor as shown in Figure 1. For diffusion time t > 150 ms, D(t) did not change noticeably, while K(t) decreased with diffusion time. This is where the Kärger model is considered valid to describe tissue microstructure, such that the water exchange model of diffusional kurtosis in Equation (2) can be used to estimate τ_ex. D(t) and K(t) plots measured from the cortical ribbon are also shown in Figure 2 for comparison.

FIGURE 2.

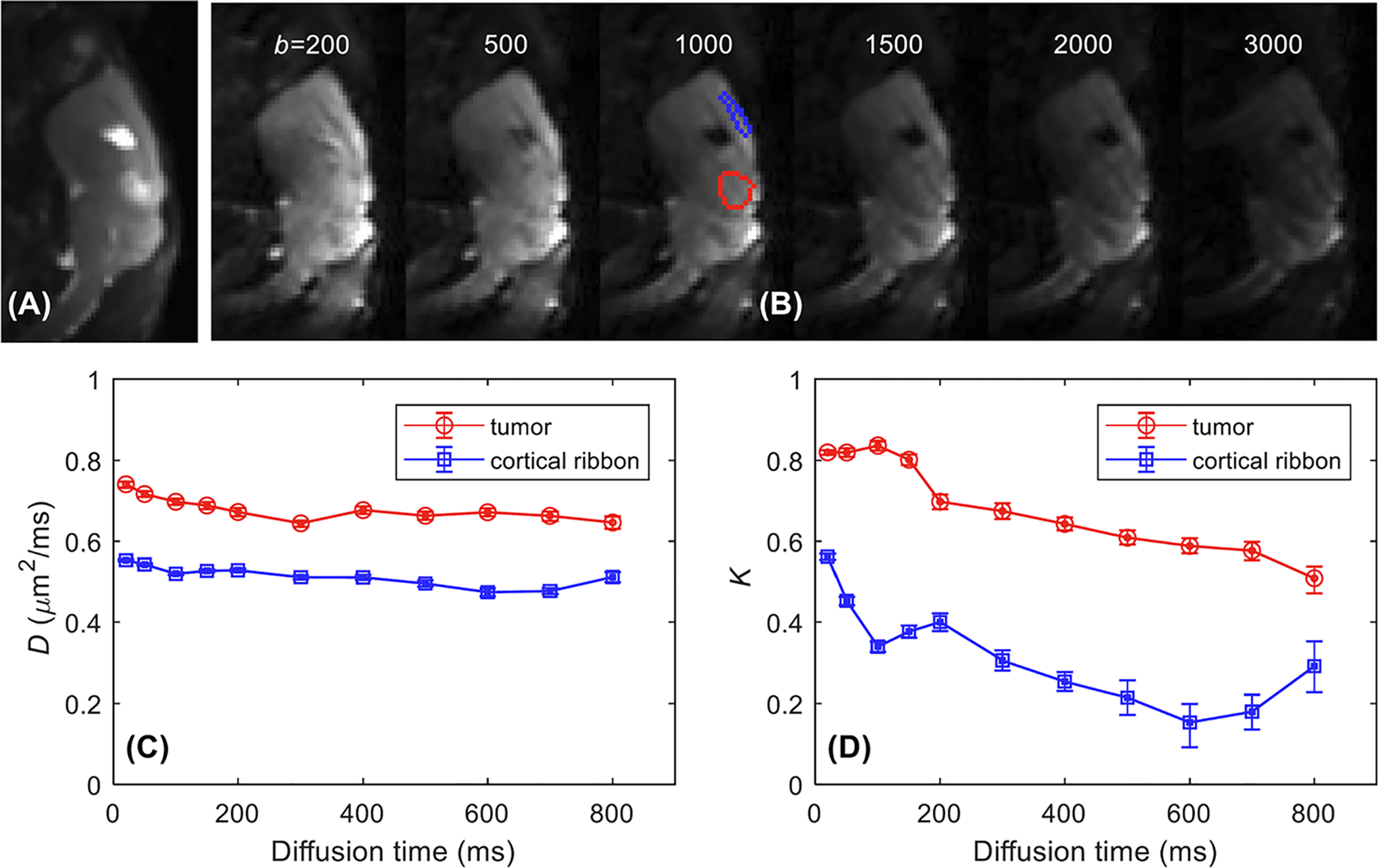
A representative example of tDKI data acquired from a GL261 tumor (the same one as shown in Figure 1). A, T₂-weighted RARE sagittal image that was used to identify the tumor. B, Diffusion-weighted images for diffusion time t = 200 ms with different b-values (s/mm²) with tumor (red ROI) and cortex ribbon (blue ROI) delineated on the T₂-weighted RARE image. C, D, Median D(t) (C) and K(t) curves (D) show the diffusion time dependence of diffusivity and kurtosis for the tumor and the cortical ribbon from the bootstrapping analysis

Similar patterns of D(t) and K(t) were observed with all GL261 tumors, as shown in Figure 3. Decrease of D(t) was consistently observed in all tumors for t < 200 ms. The average data of all tumors shown in Figure 3B showed almost no noticeable change for t ≥ 200 ms, as supported by the slope (A) near zero. K(t) also showed a consistent pattern of decrease when D(t) const, supporting the use of the Kärger model to estimate the water exchange rate. The estimated parameters of individual tumor data are presented in Table 2. The ROI analysis of all the GL261 tumors (Table 2) shows that the averaged median value and interquartile range (IQR) are A = −0.46 (IQR = 0.35) × 10⁻⁴ μm²/ms², D₀ = 0.69 (0.02) μm²/ms, K₀ = 0.87 (0.44), τ_ex = 93 (89) ms and K_∞ = 0.33 (0.12).

FIGURE 3.

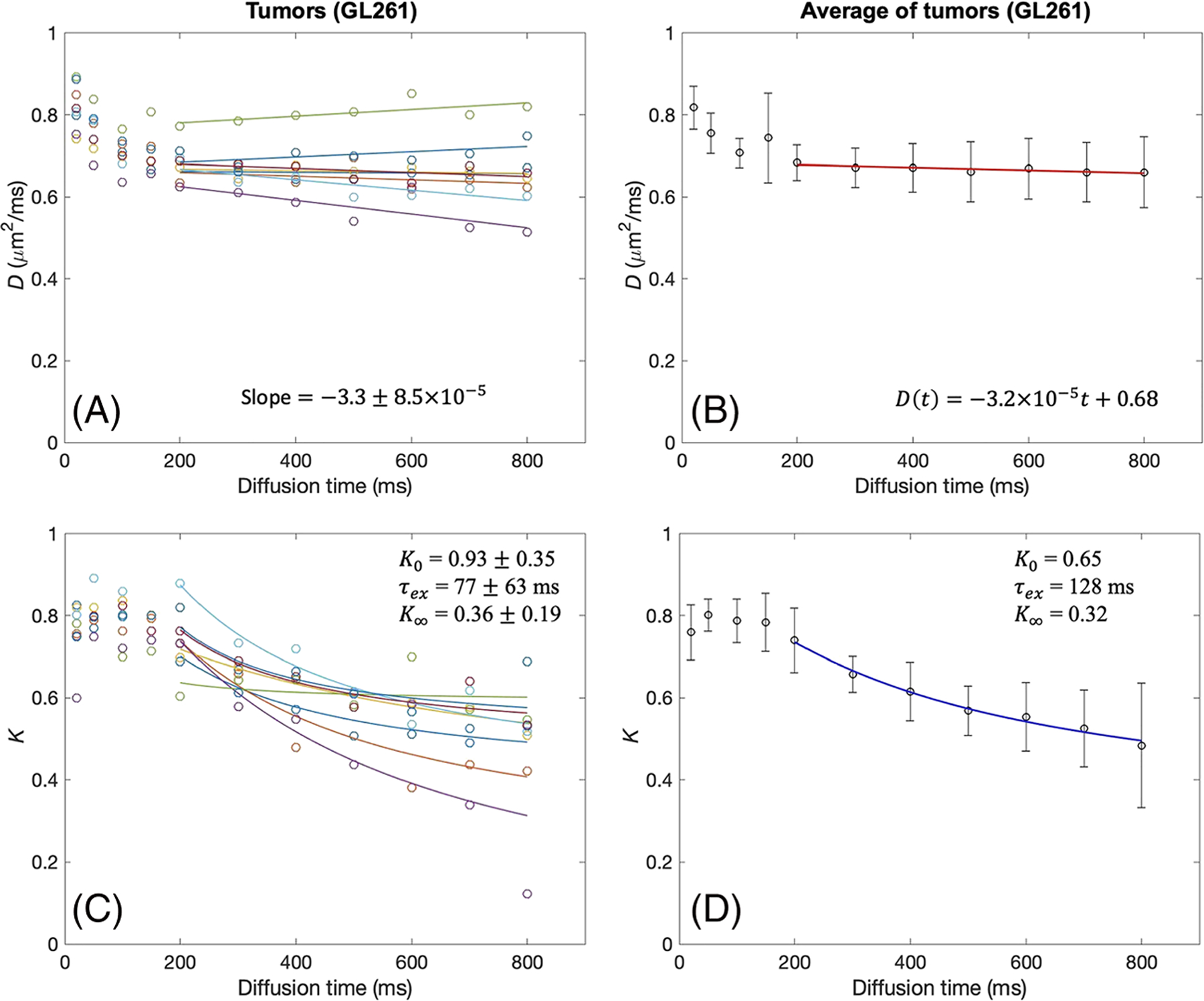
tDKI metrics in GL261 tumors. A, B, Diffusivity shows a weak time dependence for t = 200–800 ms, with the slopes of linear model fits (solid lines) close to zero, in each tumor (A) and the data averaged over all tumors (B). C, D, For the same diffusion times, kurtosis shows a distinct time dependence that can be well described by the Kärger model (solid lines) in each tumor (C) and the data averaged over all tumors (D)

TABLE 2.

Summary of tDKI data measured in GL261 and 4T1 tumors using a linear fit to D(t) and the Kärger model to K(t) for t = 200–800 ms. A linear model of D(t) is defined as D(t) = At+D₀ with diffusion time t in milliseconds for consistency with the unit of D. The reported values are medians with interquartile ranges in parentheses

Mouse		A (10−4 μm2/ms2)	D0 (μm2/ms2)	K0	τex (ms)	K∞
GL261	1	−0.33 (0.35)	0.67 (0.01)	0.71 (0.16)	117 (94)	0.29 (0.15)
	2	−0.17 (0.34)	0.66 (0.02)	0.98 (0.14)	106 (71)	0.18 (0.14)
	3	0.04 (0.28)	0.66 (0.02)	0.43 (0.09)	139 (97)	0.45 (0.08)
	4	−1.50 (0.31)	0.65 (0.02)	1.10 (0.35)	67 (55)	0.23 (0.12)
	5	0.48 (0.40)	0.77 (0.03)	0.55 (0.32)	96 (105)	0.44 (0.07)
	6	−1.52 (0.36)	0.70 (0.02)	1.11 (0.31)	70 (57)	0.36 (0.12)
	7	−0.60 (0.26)	0.69 (0.02)	0.82 (0.62)	82 (99)	0.38 (0.12)
	8	−0.05 (0.45)	0.70 (0.03)	1.25 (0.87)	68 (114)	0.30 (0.14)
	Average	−0.46 (0.35)	0.69 (0.02)	0.87 (0.44)	93 (89)	0.33 (0.12)
4T1	9	−0.99 (0.33)	0.50 (0.02)	1.88 (1.38)	64 (63)	0.29 (0.22)
	10	−0.27 (0.25)	0.46 (0.02)	1.55 (0.90)	74 (85)	0.50 (0.16)
	11	0.48 (0.23)	0.74 (0.02)	0.30 (0.09)	69 (75)	0.48 (0.06)
	12	0.02 (0.53)	0.69 (0.02)	0.96 (0.68)	43 (49)	0.43 (0.08)
	13	−0.48 (0.47)	0.40 (0.02)	1.19 (0.72)	87 (96)	0.41 (0.29)
	Average	−0.25 (0.37)	0.56 (0.02)	1.20 (0.85)	68 (78)	0.42 (0.19)

3.2 |. 4T1 mouse mammary tumor model

The D(t) and K(t) of the 4T1 tumors showed trends similar to those observed in the GL261 tumors (Figure 4). The 4T1 tumors appear to have a larger difference in D(t) and K(t) values among the tumors than the GL261 tumors, as the D(t) and K(t) curves are not closely overlapping with each other (Figure 4A and 4C). However, individual tumors have the same typical patterns of D(t) and K(t) as observed in GL261 tumors: no remarkable change of D(t) and substantial decrease of K(t) for t ≥ 200 ms. The estimated parameters of individual 4T1 tumor data are presented in Table 2. The ROI analysis of all the 4T1 tumors (Table 2) shows that the averaged median value and IQR are A = −0.25 (IQR = 0.37) × 10⁻⁴ μm²/ms², D₀ = 0.56 (0.02) μm²/ms, K₀ = 1.20 (0.85), τ_ex = 68 (78) ms and K_∞ = 0.42 (0.19).

FIGURE 4.

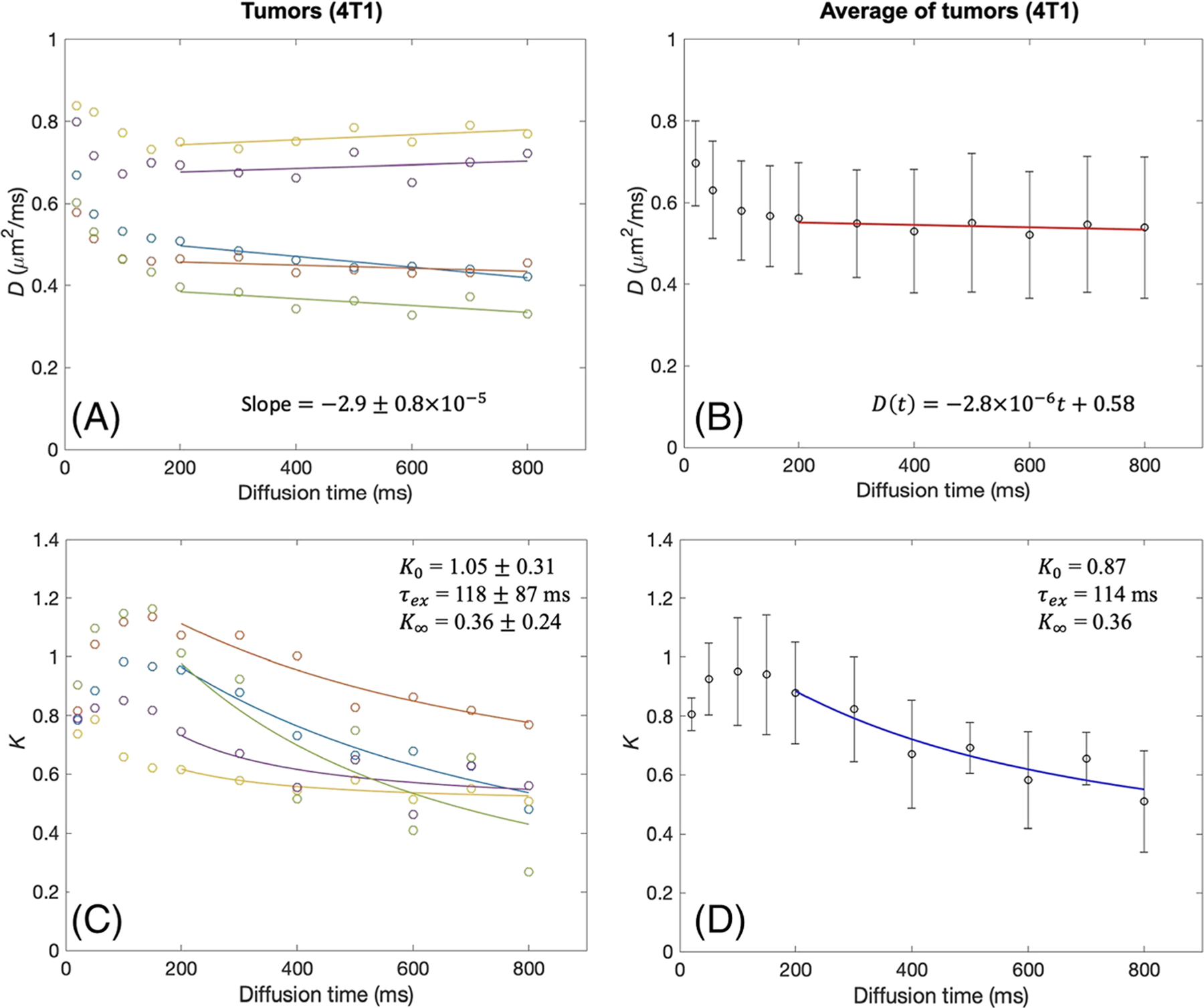
tDKI metrics in 4T1 tumors. A, B, Diffusivity shows a weak time dependence for t = 200–800 ms, with the slopes of linear model fits (solid lines) close to zero, in each tumor (A) and the data averaged over all tumors (B). C, D, For the same diffusion times, kurtosis shows a distinct time dependence that can be well described by the Kärger model (solid lines) in each tumor (C) and the data averaged over all tumors (D)

3.3 |. Cortical ribbons of mouse brain

The D(t) and K(t) of the cortical ribbons of the C57BL/6 mice and BALB/c mice were analyzed in the same way as the tumor data and are shown in Figures 5 and 6. The cortical ribbons showed much smaller changes of D(t), compared with that of tumors, over the range of diffusion times used in this study, potentially due to smaller cell sizes in the gray matter. K(t) also shows a decrease from the shortest diffusion time (20 ms) used in this study. The linear fit to D(t) for t ≥ 50 ms showed a similar magnitude of negative slope as shown in Figures 5B and 6B, although larger than those of tumor. The Kärger model was found to be an adequate representation of K(t) for t ≥ 50 ms, as shown in Figures 5D and 6D. Analysis of all the cortical ribbon ROIs in C57BL/6 mice (Table 3) shows that the averaged median value and IQR are A = −1.01 (IQR = 0.36) × 10⁻⁴ μm²/ms², D₀ = 0.55 (0.01) μm²/ms, K₀ = 0.64 (0.38), τ_ex = 41 (34) ms and K_∞ = 0.11 (0.10). Analysis of all the cortical ribbon ROIs in BALB/c mice (Table 3) shows that the averaged median value and IQR are A = −1.47 (0.32) × 10⁻⁴ μm²/ms², D₀ = 0.54 (0.02) μm²/ms, K₀ = 0.74 (0.18), τ_ex = 30 (17) ms and K_∞ = 0.21 (0.09).

FIGURE 5.

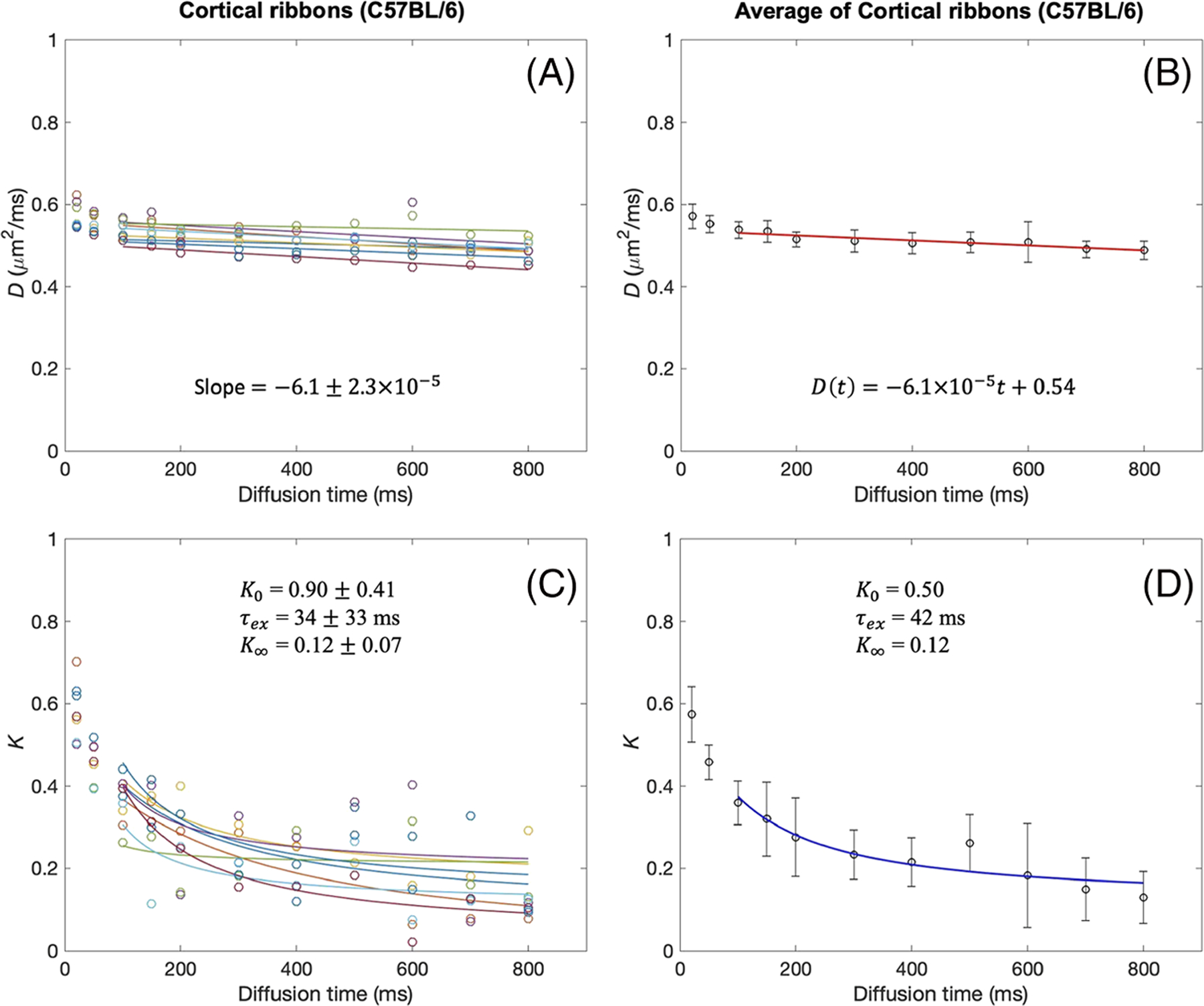
tDKI metrics in the cortical ribbon of C57BL/6 mouse brains. A, B, Diffusivity shows a weak time dependence for t = 100–800 ms, with the slopes of linear model fits (solid lines) close to zero, in each tumor (A) and the data averaged over all tumors (B). C, D, For the same diffusion times, kurtosis shows a distinct time dependence that can be well described by the Kärger model (solid lines) in each tumor (C) and the data averaged over all tumors (D)

FIGURE 6.

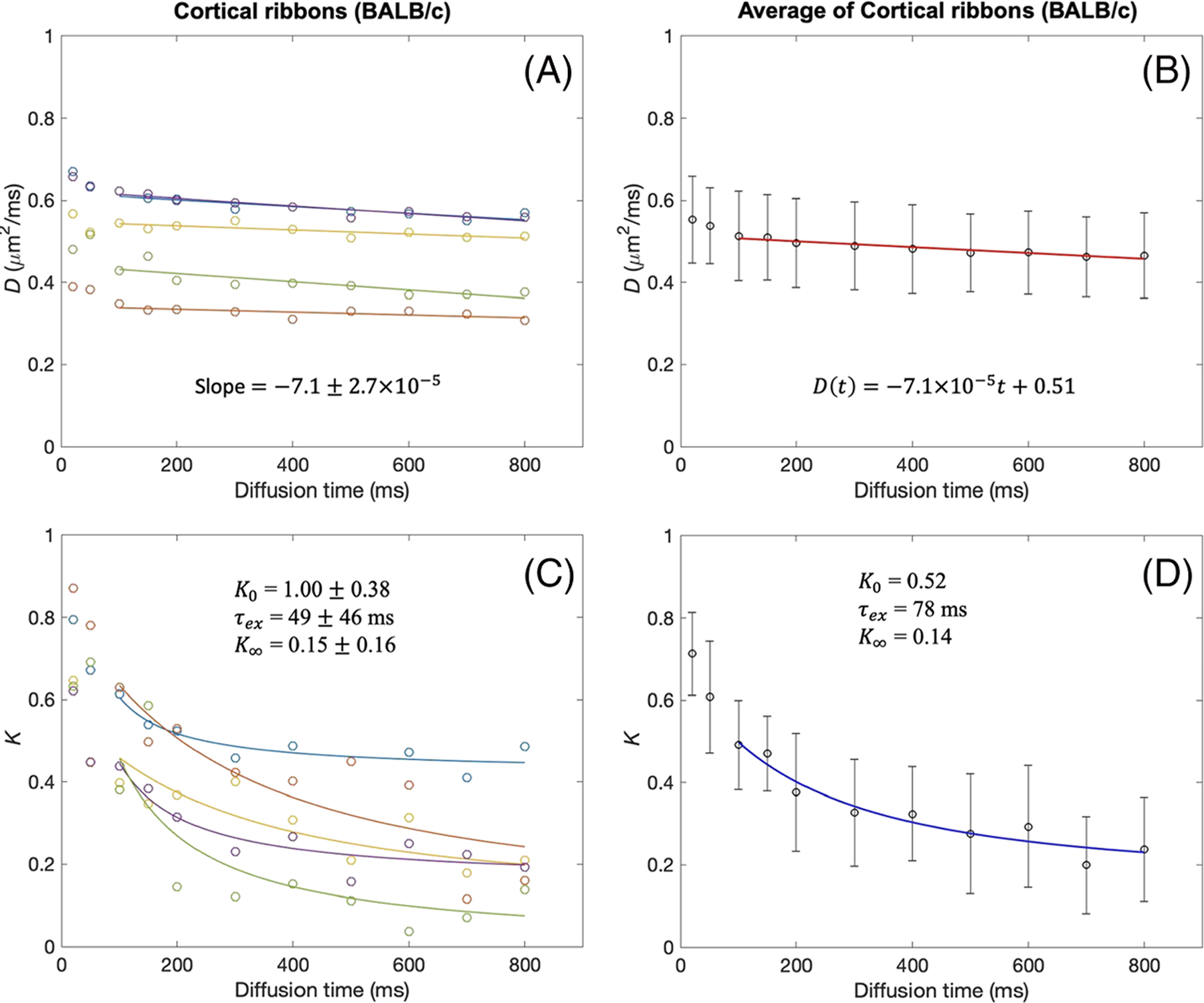
tDKI metrics in the cortical ribbon of BALB/c mouse brains. A, B, Diffusivity shows a weak time dependence for t = 100–800 ms, with the slopes of linear model fits (solid lines) close to zero, in each tumor (A) and the data averaged over all tumors (B). C, D, For the same diffusion times, kurtosis shows a distinct time dependence that can be well described by the Kärger model (solid lines) in each tumor (C) and the data averaged over all tumors (D)

TABLE 3.

Summary of tDKI data measured in the cortical ribbon of C57BL/6 and BALB/c mouse brains using a linear fit to D(t) and the Kärger model to K(t) for t = 100–800 ms. A linear model of D(t) is defined as D(t) = At+D₀ with diffusion time t in milliseconds for consistency with the unit of D. The reported values are medians with interquartile ranges in parentheses

Mouse		A (10−4 μm2/ms2)	D0 (μm2/ms2)	K0	τex (ms)	K∞
C57BL/6	1	−0.32 (0.30)	0.52 (0.01)	0.46 (0.28)	35 (29)	0.18 (0.09)
	2	−0.24 (0.43)	0.54 (0.01)	1.34 (0.85)	12 (38)	0.16 (0.12)
	3	−0.48 (0.36)	0.53 (0.01)	0.31 (0.19)	72 (32)	0.21 (0.13)
	4	−1.75 (0.41)	0.59 (0.01)	0.36 (0.24)	41 (43)	0.26 (0.11)
	5	−1.94 (0.58)	0.58 (0.01)	0.51 (0.24)	37 (32)	0.03 (0.10)
	6	−1.16 (0.23)	0.56 (0.01)	0.48 (0.21)	60 (44)	0.00 (000)
	7	−1.33 (0.14)	0.52 (0.01)	0.90 (0.32)	33 (19)	0.00 (0.00)
	8	−0.86 (0.24)	0.52 (0.01)	0.76 (0.25)	41 (31)	0.07 (0.11)
	Average	−1.01 (0.36)	0.55 (0.01)	0.64 (0.38)	41 (34)	0.11 (0.10)
BALB/c	9	−1.17 (0.33)	0.63 (0.04)	0.45 (0.08)	31 (22)	0.41 (0.07)
	10	−0.72 (0.15)	0.36 (0.01)	0.87 (0.27)	23 (19)	0.32 (0.13)
	11	−0.95 (0.28)	0.56 (0.01)	0.58 (0.08)	25 (13)	0.21 (0.09)
	12	−1.40 (0.32)	0.64 (0.02)	0.60 (0.08)	46 (19)	0.10 (0.09)
	13	−3.14 (0.44)	0.50 (0.02)	1.18 (0.44)	28 (14)	0.00 (0.00)
	Average	−1.48 (0.32)	0.54 (0.02)	0.74 (0.18)	30 (17)	0.21 (0.09)

3.4 |. T1 measurement

Figure 7 shows the decays of S₀ data depending on mixing time for tumor and cortical ribbon ROIs. In all cases, the decay patterns were found to be mono-exponential for the diffusion times used for estimation of τ_ex, as supported by significant (p < 0.0001) linear regression fits to the log(S₀) data in all cases. For the shorter mixing times that were not used for estimation of τ_ex, it appears that the T₁ relaxation is markedly faster in all tumor ROIs (Figure 7A and 7B). A similar observation was made with the cortical ribbon ROIs (Figure 7C and 7D), although the trend is not as clear with just one data point in this short mixing time range.

FIGURE 7.

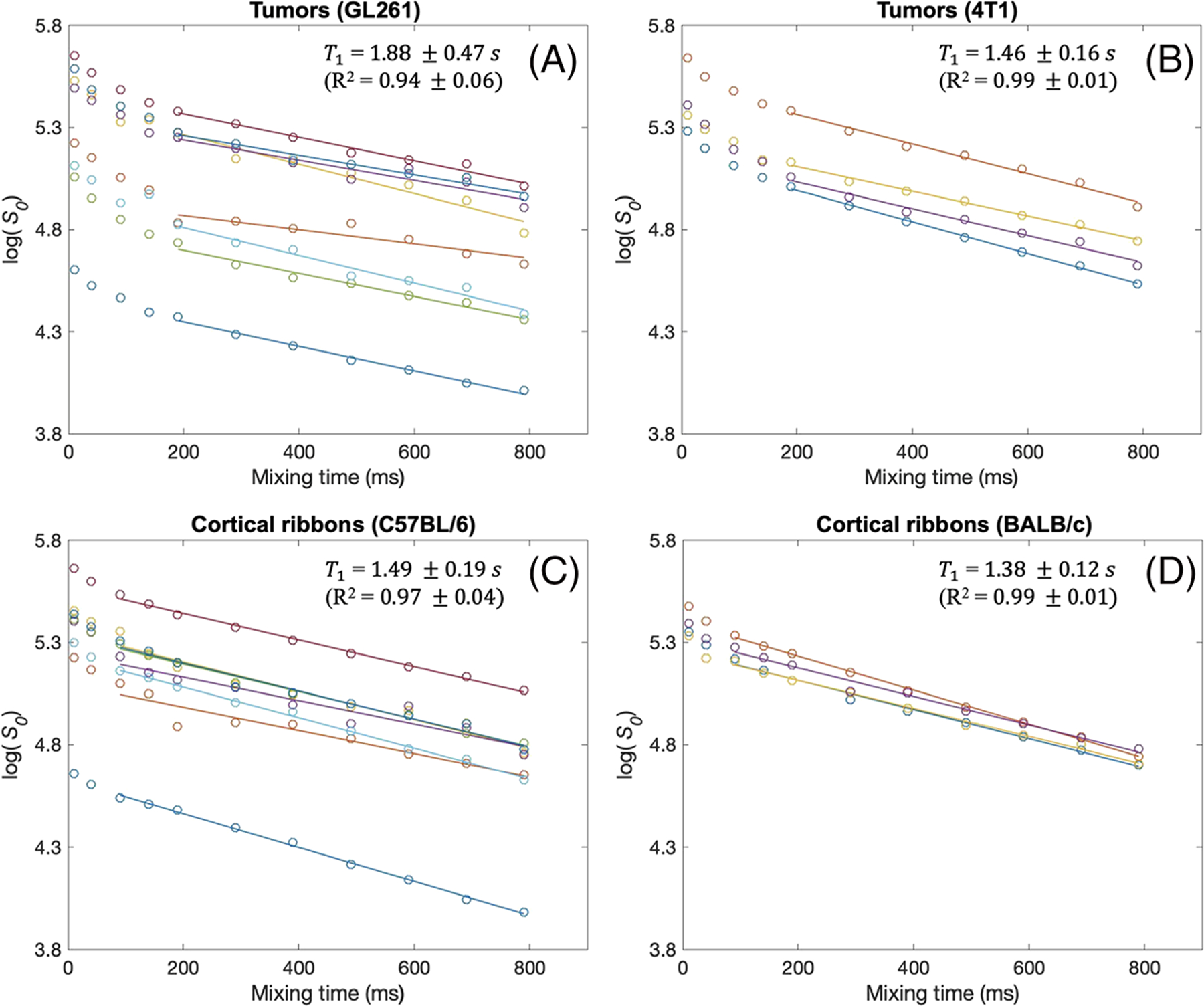
Estimation of T₁ from S₀ estimates at different mixing times used in this study for GL261 tumors (A), 4T1 tumors (B) and the cortical ribbons of C57BL/6 (C) and BALB/c mice (D). A linear model in the logarithmic scale (ie mono-exponential model) is fit to the S₀(t) values for t = 189–789 ms in tumor ROIs (A, B) and t = 89–789 ms in the cortical ribbon ROIs (C, D). These mixing time ranges correspond to the diffusion times used for the Kärger model fits in Figures 3–6. The T₁ values shown in the plots are from the slopes of the linear model fits. The R² values are close to 1.0 for all cases, supporting the view that the T₁ relaxation in all ROIs is mono-exponential

3.5 |. Breast cancer patients

Figure 8B and 8F shows diffusion-weighted images from the two breast cancer patients. The SNR was measured as the mean signal intensity of the tumor ROI divided by the standard deviation of background noise in the air. The SNR ranged from 10 to 335. The image for diffusion time t = 650 ms and b = 2000 s/mm² had the lowest SNR of 43 for Subject 1 and 10 for Subject 2. In the first case (Figure 8A–D), the post-contrast T₁-weighted images and diffusion-weighted images show a large mass of biopsy-proven invasive ductal carcinoma. As in the mouse tumor models, K(t) showed a monotonic decrease by about 30% with increasing diffusion time whereas D(t) did not show such a change. The model fit to K(t) using the bootstrapping approach estimated that the median and IQR are K₀ = 1.75 (IQR = 0.45), K_∞ = 0.55 (0.29) and τ_ex = 70 (94) ms. A similar trend was also observed with the second case shown in Figure 8E–H, where K₀ = 1.53 (0.45), K_∞ = 0.26 (0.22) and τ_ex = 106 (92) ms.

FIGURE 8.

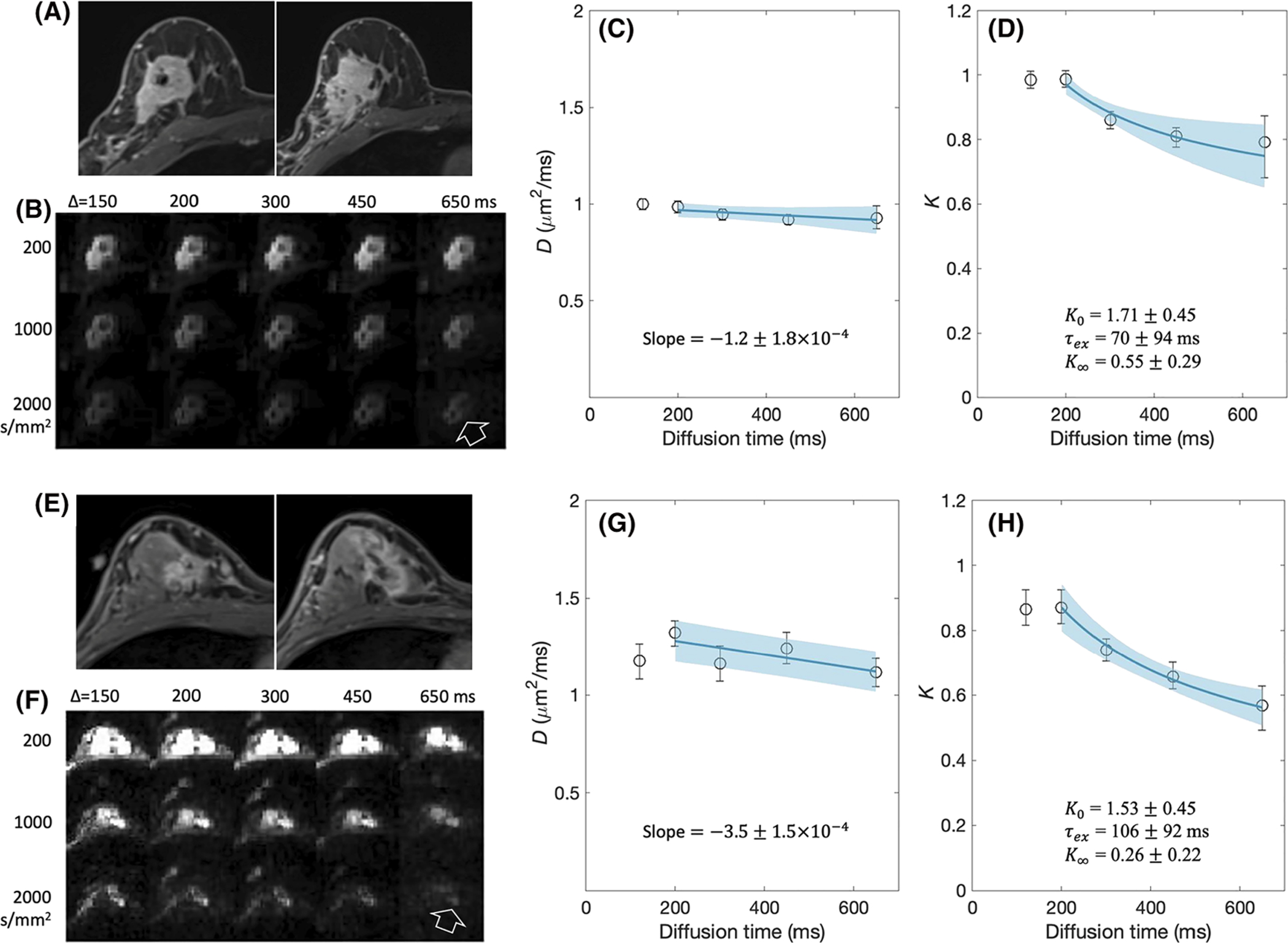
tDKI data of two biopsy proven invasive ductal carcinomas in a 35-year-old woman (A-D) and a 56-year-old woman (E-H). A, E, Post-contrast T₁-weighted images are angled oblique axial slices as per the clinical breast imaging protocol. Two adjacent slices are shown to roughly match the lesion on the axial diffusion-weighted images that are not angled. B, F, Diffusion-weighted images with multiple b-values and diffusion times for one slice with the cancer lesion shown in A, E. The lesion is shown clearly in these diffusion-weighted images with fat suppression (arrow). C, G, D(t) measured from the tumor is shown by a plot of the mean values with the error bars for the standard deviation. D, H, K(t) measured from the tumor is shown by a plot of the mean values with the error bars for the standard deviation. The solid lines are the linear model fits for D(t) and the Kärger model fits for K(t) with the standard deviations shown by the shaded areas

4 |. DISCUSSION

In this proof-of-concept study, we have demonstrated that the water exchange time, τ_ex, can be measured by the proposed tDKI method using data from two mouse tumor models and breast cancer patients. Our experimental results substantiate that the Kärger model can be considered as a valid model for a tumor tissue of which the cell membranes are permeable to water molecules, yet the exchange remains barrier limited, since the estimated exchange times τ_ex ~ 100 ms greatly exceed the characteristic times τ_c ~ 10 ms to diffuse across a cell. A similar observation, except with substantially shorter exchange times, about 34 ms, was also made with the tDKI data from the cortical ribbon of the mouse brain. Such short exchange times are close to previous observations in human gray matter with τ_ex ~ 10–30 ms,⁵⁰ and in mouse spinal cord with τ_ex ~ 10 ms.⁵¹ The present study results suggest that the tDKI can also be used to measure cellular water exchange rate in the gray matter when appropriate ranges of diffusion times and diffusion weightings are used.

The model used in our study is the Kärger model in a cumulant expansion representation to include the second- and fourth-order coefficients in the Taylor expansion of the powers of q of the magnetization logarithm. This cumulant expansion representation of the Kärger model provides an adequate description of the diffusion-weighted magnetization with a wide range of b-values used in this study (up to 3000 s/mm²). As shown by Fieremans et al,³⁵ the Kärger model can be applied in the long-time limit when the time is well beyond the characteristic time. In such a long-time regime, the diffusivity time dependence becomes negligible such that it cannot be used for estimation of relative fractions of the two exchanging compartments. In contrast, the diffusional kurtosis decreases in this long-time regime, which can be used to measure the exchange time. Estimation of the relative volume fractions would require diffusion times shorter than the long-time limit with a model appropriate for this time range in cancer tissue, as demonstrated by Reynaud et al.¹⁵

Fieremans et al³⁵ conducted Monte Carlo simulations with a tissue model consisting of a set of parallel randomly packed identical cylinders. This geometry was a model for axons in the white matter. However, the diffusion parameters measured in a plane perpendicular to the cylinders can be considered as a two-dimensional model for diffusion in spherical cells, such as tumor cells. The study demonstrated that the diffusion in the perpendicular direction is accurately described by the Kärger model for sufficiently long times (where the kurtosis decreases with time). In the barrier-limited regime, the diffusivity in the perpendicular direction is already constant at diffusion times close to τ_ex and longer, and the kurtosis decay can be used to estimate τ_ex. These observations in the Monte Carlo simulation study are in line with the results from our present in vivo imaging study of tumors as well as mouse brain.

The Kärger model regime that is used in the present study would not be valid if the cell membrane were impermeable, such as in the myelinated axons with the range of the diffusion times used in this study. This was clearly demonstrated by Jespersen et al⁴⁵ in their study of a spinal cord using diffusional kurtosis imaging acquired for 57 diffusion times ranging from 6 ms to 350 ms. Among the various findings on the diffusion time dependence of the microstructural diffusion parameters in a fixed spinal cord, the study showed that the diffusivities perpendicular to the spinal cord decreased continually in the range of diffusion times (the coarse-graining was not complete), and the corresponding diffusional kurtosis mostly increased. Such an increase of diffusional kurtosis is expected when the diffusion time is shorter than the exchange time.^34,35 In the case of an impermeable membrane, the exchange time is infinite, and therefore the diffusional kurtosis is not expected to decrease. Hence, the proposed tDKI method should be applied with an adequate range of diffusion times where the Kärger model is considered valid with respect to the expected water exchange time of the cells.

The present study demonstrates the feasibility of using the diffusion time dependence of the diffusional kurtosis to measure cellular-interstitial water exchange times in a tumor, which has not been reported to date. However, there have been several other dMRI methods used to measure water exchange between tissue compartments. One way is to use strong diffusion weighting gradients with a constant long diffusion time in between that can suppress the signal from extracellular space and enables us to monitor the change of intracellular signal depending on the diffusion time.³¹ This method is often referred to as the constant gradient (CG) method and has been demonstrated to measure water exchange rate in rat brains.^52,53 A variant of the double diffusion encoding method, also known as a filtered-exchange imaging (FEXI) method, has also been introduced to measure water exchange rate.⁵⁴ The FEXI method has been successfully used for breast cancer⁵⁵ and intracranial brain tumors.⁵⁶ A recent study using both CG and FEXI in perfused cells showed that both methods are sensitive to the changes in cell membrane permeability, while FEXI appears to overestimate the exchange rate compared with the CG method.²² While these methods are promising, they require suppression of the extracellular signal such that the SNR of the data can be lower than that of the tDKI method used in this study. Nevertheless, these dMRI methods could be used for cross-validation of each other in future studies.

The cellular-interstitial water exchange time, τ_ex, is closely related to the intracellular water lifetime (τ_i = τ_ex/v_e) that has been measured using dynamic contrast-enhanced (DCE) MRI in previous studies.^{3–5,57–60} With breast cancer patients undergoing neoadjuvant chemotherapy, it was observed that the lesions with pathological complete response showed a significant early increase of τ_i whereas the ones with non-pathological complete response did not show any noticeable change of τ_i.⁵ This result was interpreted as an effect of reduced metabolic activity of tumors responding well to the treatment. The time scale τ_i was also assessed as a prognostic biomarker in a study with a cohort of 72 patients with head and neck squamous cell carcinoma who underwent DCE-MRI scans prior to chemoradiation therapy.^4,59 It was found that patients with longer τ_i at pre-treatment had significantly prolonged overall survival at 5 years. Long τ_i (low exchange rate) corresponds to low cell metabolism, which may indicate less aggressive cancer. In contrast, short τ_i is an indication of high cellular metabolism that is a hallmark of aggressive cancer. These results suggest that τ_i can be a useful imaging marker for cancer cell metabolic activity. The τ_ex values estimated from the τ_i and v_e values reported in these previous studies are close to the values reported in the present study: τ_ex = 71 ± 33 ms for head and neck metastatic lymph nodes,³ 96 and 107 ms for head and neck cancer patients with partial and complete response respectively,⁵⁹ 62.5 ms as the median of 60 patients with head and neck squamous cancer,⁴ 228 and 591 ms for invasive ductal carcinoma,⁵ 30 and 150 ms for invasive ductal carcinoma⁵⁸ and 283 ms for the MDA-MB-231 breast cancer model.⁶⁰

While the feasibility of estimating τ_i from DCE-MRI data has been demonstrated by several studies,^{3–5,57–59} a concern has been raised regarding how difficult it is to measure τ_i accurately and precisely^12,13 considering the challenging requirements for quantitative DCE-MRI studies, such as data acquisition with an adequately high temporal resolution, determination of arterial input function, measurement of pre-contrast longitudinal relaxation time constant T₁ and RF transmit field B₁ inhomogeneity and selection of a proper kinetic model. In addition, it has also been shown that it is not trivial to separate the effect of τ_i on conventional DCE-MRI data from a combined effect of other kinetic parameters, particularly that of the vascular compartment.^13,61,62 Such inherent degeneracy of τ_i estimation in conventional DCE-MRI may be reduced by using an MRI scan protocol to give different sensitivities to the effect of water exchange within one imaging session.⁶³ In contrast, the proposed tDKI method is an attractive alternative to measure the cellular-interstitial water exchange more easily without using a contrast agent.

There are several limitations to be noted in this proof-of-concept study. One of them is the lack of validation of τ_ex measured by the tDKI method. There is apparently no pathological method to measure τ_ex and no in vivo imaging method has been established as a gold standard method. An alternative way could be to measure the water exchange rate with a complimentary dMRI method mentioned above, such as the CG or FEXI method. This possibility will be explored further in future studies. The diffusion times used in this study were selected to cover a wide enough range to assess whether the diffusion time dependence of D and K is in the Kärger model regime. The choice of diffusion times needs to be optimized for accurate estimation of τ_ex with a minimal scan time, in order to translate this method for clinical applications. One limitation in general is the lack of consensus on reference tissues with well documented information about exchange time. Availability of such reference tissue would be helpful to evaluate the results of the present study and others in future. Another limitation of the current study is that we assumed that the influence from the difference in the T₁ values of intra- and extracellular compartments on our diffusion-time-dependence study is negligible for the diffusion times used in this study. Further study is warranted to fully investigate the influence of T₁ in the cellular-interstitial water exchange measurement using the STEAM sequence and its dependence on the choice of scan parameters. While the current study demonstrates the feasibility of measuring τ_ex of tumors and the gray matter such as the cortical ribbon in the mouse brain, it could not fully address how to determine the lowest diffusion time for individual voxels of in vivo data. Particularly for the cortical ribbon, the lower bound of diffusion time was selected based on the observation of rapid decrease of kurtosis from the shortest diffusion time used in this study, while the diffusivity decrease was smaller to determine the lower bound. This could be further investigated in future studies with a sufficient number of short diffusion times around the characteristic diffusion time of the gray matter.

The purpose of this study was to assess the feasibility of using tDKI to measure τ_ex of tumors in both preclinical and clinical cases. Since we had a limited scan time of 5 min for the patient examinations, we could not have a sufficiently large number of diffusion times to investigate the time-dependent behavior of tDKI metrics. Hence, the animal studies with 11 diffusion times were used to measure the time-dependent changes to assess the feasibility of using it to measure τ_ex, as well as to determine the appropriate range of diffusion times for the measurement. Then, the human studies with five diffusion times were used to demonstrate that the τ_ex can be measured in human cancerous lesions as well. We believe that animal studies can also be used in future studies to investigate how the proposed tDKI approach for τ_ex measurement can be used with various therapeutic methods, prior to applying it to human studies, in addition to using it for any potential validation studies.

To conclude, in this proof-of-concept study, we found that the diffusion time dependence of diffusional kurtosis can be used to measure cellular-interstitial water exchange time τ_ex in tumors. This was successfully demonstrated with two mouse tumor models using a 7 T small animal scanner and with breast cancer patients at 3 T. The underlying mechanism of cellular-interstitial water exchange and its role in cancer cells are not fully understood to date. The results of this study suggest that the proposed tDKI method can be a useful tool to measure τ_ex relatively easily and to provide more insight into how the water exchange rate is associated with the aggressiveness of cancer and the treatment response in future clinical studies.

Abbreviations:

CG

constant gradient

DCE

dynamic contrast enhanced

dMRI

diffusion MRI

EPI

echo-planar imaging

FEXI

filtered-exchange imaging

IQR

interquartile range

RARE

rapid acquisition with relaxation enhancement

ROI

region of interest

SNR

signal-to-noise ratio

STEAM

stimulated-echo acquisition mode

tDKI

diffusion-time-dependent diffusional kurtosis imaging