Differential methylation analysis for bisulfite sequencing using DSS

Abstract

Bisulfite sequencing (BS-seq) technology measures DNA methylation at single nucleotide resolution. A key task in BS-seq data analysis is to identify differentially methylation (DM) under different conditions. Here we provide a tutorial for BS-seq DM analysis using Bioconductor package DSS. DSS uses a beta-binomial model to characterize the sequence counts from BS-seq, and implements rigorous statistical method for hypothesis testing. It provides flexible functionalities for a variety of DM analyses.

INTRODUCTION

Background

DNA methylation is an important epigenetic modification of the DNA molecule [1,2]. It has been shown to regulate biological processes such as cellular differentiation and genomic imprinting [3–6], and closely related to a number of diseases such as cancer [7–10]. There are several high-throughput technologies for measuring DNA methylation. Among them, bisulfite-conversion-based sequencing technologies (bisulfite sequencing, or BS-seq in short) offer single-nucleotide resolution DNA methylation profiling [11–14]. Depending on the genome coverage, BS-seq includes whole-genome bisulfite sequencing (WGBS), and reduced representation bisulfite sequencing (RRBS) that covers a small fraction of the genome with low cost. Due to the wide genomic coverage, single base-pair resolution and accurate measurement, BS-seq has quickly become the technology of choice in DNA methylation studies.

A key question in DNA methylation data analysis is to identify methylation changes associated with outcome of interest [15,16]. The differentially methylated loci/regions (DML/DMRs) can be detected by comparing methylation profiles from different conditions (e.g., case vs. control) [17]. There are a number of methods and tools serving this purpose. Here we provide a step-by-step tutorial for DML/DMR detection from BS-seq data using the Bioconductor package DSS (Dispersion Shrinkage for Sequencing).

Methods overview

A number of methods have been developed recently to detect DML/DMR from BS-seq data, along with our method DSS [18–20]. For example, MethylKit [15] adopts Fisher’s exact test or logistic regression to identify DML; Seqmonk incorporates Chi-square test and logistic regression results into a graphical analysis tool; bsseq [16] uses BSmooth method for methylome profile curve estimation and subsequent test for DMR; HMM-DM [21] and HMM-Fisher [22] utilize Hidden Markov Models along the genome to infer DMR; RnBeads [23] performs hierarchical linear models for DMR detection. Among these available methods, DSS is one of the most widely adopted software by researchers, with more than 11,000 downloads from Bioconductor in year 2018 alone.

BS-seq data carries its unique features. An important feature of BS-seq is that the data are sequence counts, which need to be modeled by discrete distributions. DSS uses a beta-binomial distribution for the BS-seq counts at each CpG site. To be specific, we use a beta distribution to model the unknown true methylation levels among biological replicates. Given the true methylation levels and total read count, the methylated counts are assumed to follow a binomial. With this model, differential methylation (DM) is performed for each CpG sites by testing whether the mean of beta-binomial distribution is related to the outcome. For example, in a simple two-group comparison case, we test whether the mean methylation levels in the two groups are the same.

In designing the BS-seq (or many other high-throughput technologies) experiment, larger sample size (biological replicates) is preferred because it generally result in high statistical power. However, due to budget concerns and the relatively high cost of BS-seq, the number of biological replicates is usually small. In some scenarios, there are even no biological replicates available (one sample per group-of-interest). The small or no biological replicates issue sets a major limitation in BS-seq experiment. The low sample size causes unstable estimation of within group variance, and subsequently undesirable hypothesis testing result. To overcome the problem, people often impose a prior on the biological variation to obtain a “shrinkage” estimation, which stabilizes the variance estimation and improves test results [24–26]. For BS-seq data, we reparameterize the beta-binomial distribution by a mean and a dispersion parameter, where the dispersion parameter is related to the biological variation among replicates. A key advantage of DSS is the improved estimation of dispersion, which is achieved by a shrinkage estimator based on a Bayesian hierarchical model. After obtaining the dispersion estimates, DSS performs DM detection by Wald statistical test at each CpG site. DSS provides functions for BS-seq DM analysis for two group comparisons [18], multi-factor design comparisons [20], and comparisons for data without biological replicates [19]. Below, we provide detailed instruction for all these functionalities, based on a publicly available BS-seq dataset.

MATERIALS

Software installation

DSS is a Bioconductor package. Users will first need to install R. At the R language webpage, choose your operating system (Linux/Mac/Windows) and follow the instructions on the webpage for R installation. To install DSS and dependency packages, go to the Bioconductor software package page for DSS at the website (www.bioconductor.org/packages/release/bioc/html/DSS.html).

Follow the instructions under the “Installation” section to install DSS by running several lines of R codes. After installation, load DSS into R environment by:

library(DSS)

BS-seq data preprocessing

Raw data generated from sequencing machines are usually in FASTQ format. Quality control (QC) and sequence trimming are recommended. After that, the FASTQ files need to be aligned to the reference genome. Aligner specifically designed for BS-seq such as bismark [27] is recommended. After alignment, methylation signal (counts) can be extracted for each CpG sites, using bismark again. More detailed instructions can be found at the Supplementary Materials. It includes code and suggestions for quality control, trimming, mapping and methylation signal calling. These steps prepare the necessary input files for DSS.

DSS requires input text files be in following format:

chr	pos	N	X
chr1	10497	48	45
chr1	10525	48	48
chr1	10542	48	47
chr11	10589	34	1

Here, each row represents one CpG site. Columns are chromosome name, genomic coordinates, total read count, and methylated read counts. To get more information for QC, trimmer, and aligner, please refer to instructions for specific software.

Example data

Throughout this tutorial, we will use a public dataset to demonstrate the analysis procedure using DSS. The data can be obtained from the Gene Expression Omnibus (GEO) under accession number GSE52140 [28]. This experiment used RRBS to profile the methylation levels in two lung cancer cell lines (A549 and HTB56) under two conditions (normal and metastatic). Thus, it is a typical 2×2 crossed experimental design. We pick two biological replicates for each combination of cell line and condition, so there are eight samples in total. To download data, go to the GEO website, search for GEO Accession number GSE52140 and download the 8 samples listed in Table 1.

Table 1.

Detailed sample information and experimental design of the eight illustrative BS-seq samples in this protocol

Index	Accession number	Cell line	Condition	Sample title	Download file name	R object
1	GSM1084238	A549	normal	A0R_d0_rep1	GSM1084238_A0R_d0_rep1.cpgs.txt	dat1
2	GSM1084239	A549	metastatic	A3R_d0_rep1	GSM1084239_A3R_d0_rep1.cpgs.txt	dat2
3	GSM1084244	HTB56	normal	H0R_d0_rep1	GSM1084244_H0R_d0_rep1.cpgs.txt	dat3
4	GSM1084245	HTB56	metastatic	H3R_d0_rep1	GSM1084245_H3R_d0_rep1.cpgs.txt	dat4
5	GSM1251236	A549	normal	A0R_d0_rep2	GSM1251236_A0R_d0_rep2.cpgs.txt	dat5
6	GSM1251237	A549	metastatic	A3R_d0_rep2	GSM1251237_A3R_d0_rep2.cpgs.txt	dat6
7	GSM1251238	HTB56	normal	H0R_d0_rep2	GSM1251238_H0R_d0_rep2.cpgs.txt	dat7
8	GSM1251239	HTB56	metastatic	H3R_d0_rep2	GSM1251239_H3R_d0_rep2.cpgs.txt	dat8

Here in sample names, “A” stands for A549 cells, “H” stands for HTB56 cells, “0” stands for normal cells, “3” stands for metastatic cells, “rep1” and “rep2” stand for first and second replicate, respectively. Their corresponding R objects are shown in the last column.

The downloaded data are in “.gz” compressed format. Unzip them to obtain the original “.txt” format. The data files are post-processed in plain text format, which has the methylation read count extracted from raw sequencing data. We will use this dataset to illustrate how to conduct different types of DM analysis:

• Two-group comparisons (normal A549 versus normal HTB56, two replicate each);

• Two-group comparisons without biological replicates (normal A549 versus normal HTB56, using only one sample each);

• Multi-factor design comparisons (all eight samples from this 2×2 crossed design).

PROTOCOL

Read in the data

DSS requires data from each BS-seq experiment to be summarized into four columns for each CpG site: chromosome number, genomic coordinate, total number of reads covering this position, and the number of reads showing methylation. In the following code, we read in the data and change them to follow the required format for DSS. Data for each sample will be represented as a data frame.

Reading in the data may take several minutes for each

fn = dir(pattern = “.cpgs.txt”)
for (i in 1:length(fn)){
       cat (“working on sample “, i, “\n”)
       #read in file
       dat.tmp = read.table (fn[i], header = T)
       #split the third column by the ‘/’ sign
       m.tmp = as.numeric(unlist(strsplit(as.character(dat.tmp[,3]), split = “/”)))
       #odd number indexes the methylated read counts
       #even number indexes the unmethylated read counts
       idx.even = (1:nrow(dat.tmp))*2
       idx.odd = idx.even- 1

       chr = dat.tmp$CHR
       pos = dat.tmp$POS
       N = m.tmp[idx.even] + m.tmp[idx.odd]
       X = m.tmp[idx.odd]

       #dat.s is a temporary object for one sample
       dat.s = data.frame(chr = chr, pos = pos, N = N, X = X)

       #save and name the object from one sample
       nam = paste(“dat”, i, sep = ““)
       assign(nam, dat.s)
}

sample. These R objects ‘dat1’, ‘dat2’, …, ‘dat8’ are data frames for the eight samples, each has four columns (chr, pos, N, and X), with each row representing one CpG site. Table 1 shows the correspondence between the R objects and the sample files.

DM analysis for regular two-group comparison

In this section, we provide detailed instruction for the most common DM analysis: comparing data from two conditions, with multiple replicates within each condition. Assume we are interested in finding DM between normal A549 cells and normal HTB56 cells, using two replicates for each cell line.

1. Create an object of class BSseq.

“BSseq” is a class defined to contain BS-seq data from multiple samples.

BSobj = makeBSseqData(list(dat1, dat5, dat3, dat7),
c(“A0R1”, “A0R2”, “H0R1”, “H0R2”))
[1:5000]

Based on Table 1, dat1 and dat5 are replicates derived from normal A549 cells, and dat3 and dat7 are replicates from normal HTB56 cells. For faster computation in this tutorial, we only use the first 5,000 CpG sites.

2. Perform statistical test for all CpG site using DMLtest function.

dmlTest = DMLtest(BSobj, group1 = c(“A0R1”, “A0R2”),
group2 = c(“H0R1”, “H0R2”), smoothing = FALSE)

Here the arguments group 1 and group 2 take the sample names for two groups under comparison. The DMLtest function performs the following steps: (i) estimate mean methylation levels for all CpG sites; (ii) estimate dispersion for each CpG site; (iii) conduct Wald test with estimated dispersion parameter. For the first step, there is an option for smoothing or not. Because the methylation levels show strong spatial correlations, i.e., nearby CpG sites have similar methylation levels, smoothing often helps to obtain better estimates of mean methylation. This is especially true when the CpG sites are densely spaced, as with whole-genome BS-seq. For data with sparsely spaced CpGs, such as from RRBS, smoothing might not help. To run the function DMLtest with smoothing, simply set smoothing = TRUE. If smoothing is requested, smoothing span is an important parameter which has non-trivial impact on DMR calling. We use 500 bp as default, and have observed that this default performs well in most data. The result from DMLtest is a data frame containing the hypothesis testing results for qualified CpG. Here, the qualified CpG sites are those with sufficient degree of freedom to carry out statistical test. The results will be feed into other functions for DML/DMR detection.

3. Call DML using the callDML function.

The callDML function takes the result object from DMLtest function and apply some user-specified criteria to define DML.

dmls = callDML(dmlTest, p.threshold = 0.001)

Here p.threshold is the p-values threshold for defining DML. By default, the p-values for the DM test is derived based on the null hypothesis that the methylation difference between two groups is 0. Additional threshold based on absolute differences in methylation levels can also be imposed through the “delta” parameter:

dmls = callDML(dmlTest, p.threshold = 0.001, delta = 0.1)

In the above line where delta is specified, the function will compute the posterior probabilities that the differences of the means greater than 0.1 for all CpG sites. In this case, sites with posterior probabilities greater than 1-p.threshold are deemed DML.

The result from callDML is a data frame for detected DML, sorted by the statistical significance. One can regard this result as the final output if there is no intention to combine DML into DMRs. Typing head(dmls) will show the first few lines of dmls as Figure 1.

Figure 1.

An example output of the first several lines of detected DML.

4. Call DMRs using the callDML function.

The callDML function works similarly as callDML. It takes the result object from DMLtest function and apply some user-specified criteria to define DMR. This function first detects statistically significant CpG sites (DML), then merges nearby loci into regions to form DMR.

dmrs = callDMR(dmlTest, p.threshold = 0.01)

Typing head(dmrs) to see the top DMRs detected from the line above (Figure 2).

Figure 2.

An example output of the first several lines of detected DMRs.

There are a number of additional parameters can be specified when merging loci into regions, including the minimum region length, minimum number of CpG sites, percentage of CpG sites required to be significant in the region, etc. Type ? callDMR to see detailed usages for these parameters.

The result from callDMR is a data frame, each row is a DMR. DMRs are sorted by the statistic areaStat, which was originally defined in the bsseq package as the sum of the test statistics of all CpG sites within the DMR. This quantity does not have a direct biological meaning. In ranking DMRs, it is not clear whether the length (number of CpG sites) or the height (methylation differences between two groups) is more important. areaStat is a combination of the two quantities. It is an ad hoc way to rank DMRs, but larger areaStat is more likely to be a DMR.

5. DMR visualization.

The DMRs can also be visualized using showOneDMR function.

With DMRs available in the object dmrs created in the previous step, enter the following to visualize the first DMR, for example.

showOneDMR(dmrs[1,], BSobj)

The result figure is shown in Figure 3. It displays the methylation levels as well as sequencing coverage depth information at each CpG site. The pink-shaded area is the detected DMR.

Figure 3.

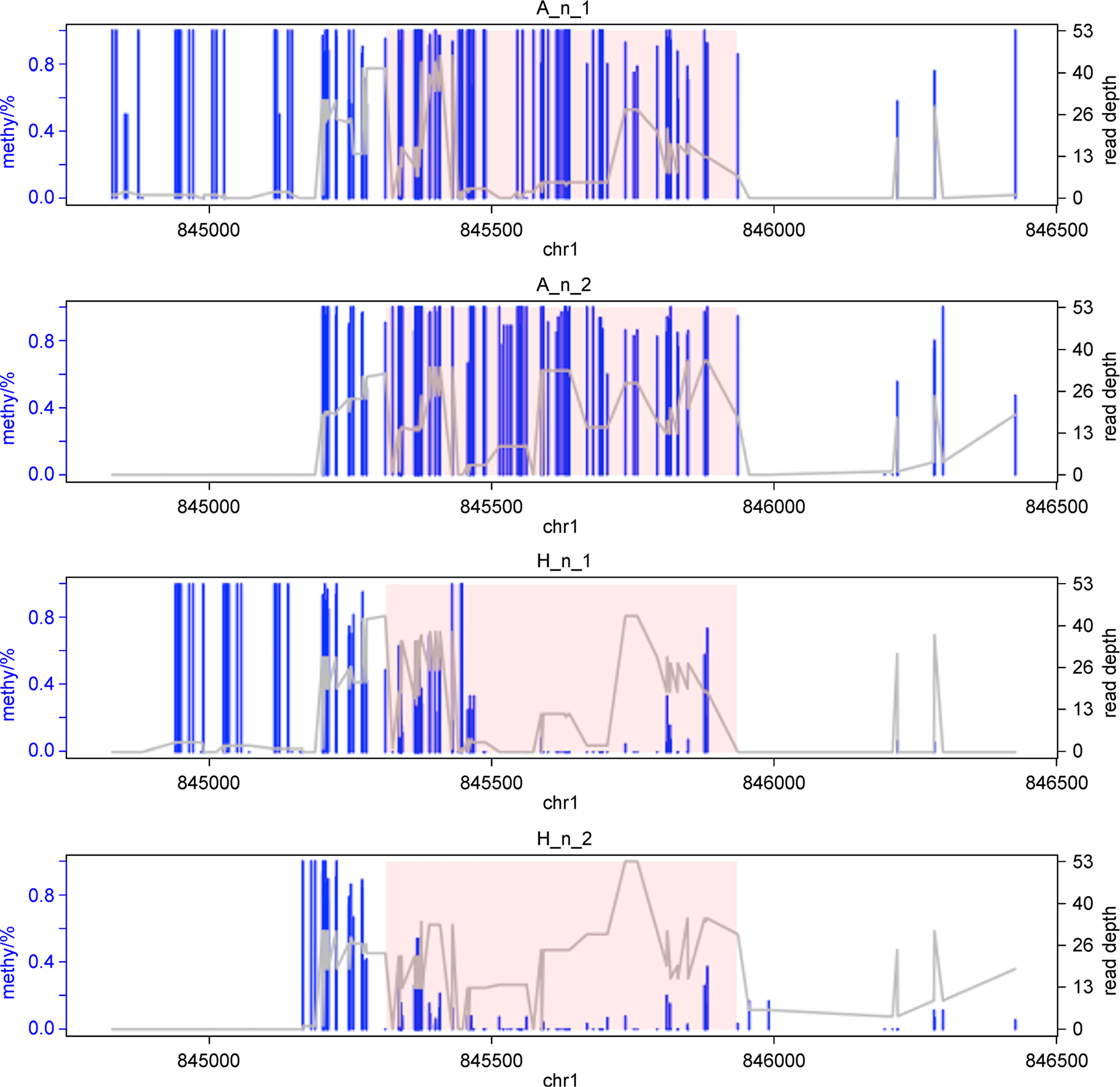
Visualization of one detected DMR.

Two-group DM analysis without replicate

Due to budget concerns and the relatively high cost, some BS-seq experiments have no biological replicates (one sample per group-of-interest). DSS can detect DML/DMRs from experiments without biological replicates. In statistical analysis, replicated data is necessary because one needs to estimate the within-group variance to quantify the uncertainty. In BS-seq data, we found that within-group variance can be reasonably estimated even without replicate, taking advantage of the spatial correlation of the methylation levels. Since nearby CpG sites have similar methylation levels, they can serve as “pseudo-replicates” for variance estimation. Our results show that this procedure provides much improved results than using methylation differences (which ignores the within-group variance) [19].

Here we conduct a two-group comparison to find DML/DMRs, with only one sample in each group. Assume we are still interested in finding the DML/DMRs between normal A549 cells and normal HTB56 cells, but only have one sample from each type of cell. The major difference from a regular two-group DM analysis that smoothing is now required in the DMLtest function.

1. Make BSseq object.

Use the following code to create an object of BSseq class, using one sample in each group:

BSobj = makeBSseqData(list(dat1, dat3), c(“A0R1”, “H0R1”))[1:5000]

In this BSseq object, dat1 is the only sample from normal A549 cells, and dat3 is the only sample from normal HTB56 cells. This mimics the situation where only one sample is obtained from case or control.

2. Perform statistical test for DML using the DMLtest function.

Here we compare group 1 with group 2 by indicating the sample names for each group. In the single-replicate case, smoothing is required for estimation of variance.

dmlTest = DMLtest(BSobj, group1 = c(“A0R1”), group2 = c(“H0R1”), smoothing = TRUE)

3. Call DML, DMRs, and visualization.

These steps are identical to previous steps from a regular two-group DM analysis.

dmls = callDML(dmlTest, p.threshold = 0.001)
dmrs = callDMR(dmlTest, p.threshold = 0.01)
showOneDMR(dmrs[1,], BSobj)

DM for general experimental design

The above examples are for simple two-group comparison. When the experimental design becomes more complex, for example, multiple groups, multiple factors crossed/nested, continuous covariates, one has to add these additional covariates into the model. For example, one may include gender, treatment status, or batch effect as additional covariates. In situations like these, one will resort to the generalized linear model (GLM) to handle the beta-binomial data. However, GLM is computationally intensive due to its iterative procedure. Based on our test, a RRBS dataset with 5 million CpG sites and 10 samples could take ~15 hours using GLM on a typical personal computer. In addition, the GLM procedure is numerically unstable when separation or quasi-separation happens in one or more covariates, which frequently occurs in many CpG sites, particularly when methylation levels are close to the boundaries (0 or 1).

DSS implements a rigorous and efficient algorithm for DM analysis under general experimental design. The key method is to use beta-binomial GLM with an arcsine link. The arcsine link breaks the variance-mean dependence in the beta-binomial data, which allows one to use a weighted least square to replace the computationally intensive iterative procedure in canonical GLM. This provides superior computational performance (50 times faster than GLM). Below we use all 8 samples in the example data to demonstrate the DM analysis procedure in a general design.

1. Make BSseq object

Use the following code to create an object of BSseq class, with all eight samples included:

BSobj = makeBSseqData(list(dat1, dat2, dat3, dat4, dat5, dat6, dat7, dat8),
c(“A0R1”, “A3R1”, “H0R1”, “H3R1”, “A0R2”, “A3R2”, “H0R2”, “H3R2”))

2. Create the experimental design.

The design is a data frame, each row for a sample. The columns are the experimental factors, which can be discrete or continuous. Orders of rows in the design need to match the samples in BSseq object. The column names of the design data frame will be used later for model fitting and hypothesis testing.

cell = c(rep(c(“A549”, “A549”, “HTB56”, “HTB56”),2))
condition = c(rep(c(“normal”, “metastatic”),4))
design = data.frame(cell, condition)

3. Fit a linear model.

The DM testing procedure is similar to that in a typical linear regression: fit a linear model and then test the coefficients in the model. The linear model fitting is done using DMLfit.multiFactor function, which takes a BSseq data object, a design data frame, and a model formula. The function will return the model fitting results that will be used later for DML/DMR calling. In the example below, we fit a model with cell, condition, and cell by condition interaction.

DMLfit = DMLfit.multiFactor(BSobj, design = design, formula = ~cell + condition + cell:condition)

4. Perform statistical test for DML.

With the linear model fitting results from DMLfit.multiFactor, we use DMLtest.multiFactor function to test the parameter(s) of interest. DMLtest.multiFactor provides flexible ways for testing the model parameters. User can specify one of the following parameters for testing: “coef”, “term”, or “Contrast”. Below we provide detailed description for each.

1. “coef” is used to test one parameter in the model. It can be an integer for the index of the parameter in the design matrix, or a character for the terms to be tested. When using character for coef, the character must match one of the column names in the design matrix. One can look at colnames(DMLfit$X) to obtain the column names. In our example, following lines are equivalent (to test the cell by condition interaction):

   DMLtest = DMLtest.multiFactor(DMLfit, coef = 4)
   DMLtest = DMLtest.multiFactor(DMLfit, coef =“cellHTB-56:conditionnormal”)
   

2. “term” is used to test a whole term in the model. If the term is continuous or a categorical variable with only two levels, it is equivalent to specifying ‘coef’ because it tests only one parameter in the model (one degree of freedom). However, when the term is a categorical variable with more than two levels, it will test multiple parameters at the same time so it is a compound hypothesis test, and a F-test will be performed. Another important distinction is that term needs to match one of the components of the input model formula, while coef needs to match one of the column names in the design matrix returned from DMLfit.multiFactor. In the example, we can use following code to test the cell by condition interaction:

   DMLtest = DMLtest.multiFactor(DMLfit, term = “cell: condition”)
   

3. “Contrast” is the most advanced option. It allows user to specify a contrast matrix for hypothesis testing. It can test any linear combination of the parameters by F-test. Let L be the contrast matrix. The hypothesis test performed is H₀ : L^T β=0. The number of rows in L must equal to the number of elements of β (which is the number of columns in the design matrix). Number of columns of L is the number of hypothesis tests. In the example, we can use following code to test the cell by condition interaction:

   L = matrix(c(0,0,0,1), ncol = 1)
   DMLtest = DMLtest.multiFactor(DMLfit, Contrast = L)
   

Here, those CpGs that have large proportion of missing values across samples (therefore disqualified for testing) will display NA’s in the DMLtest result.

5. Call DMR.

DMR can be identified using the callDMR function, as shown in the two-group comparison examples.

dmrs = callDMR(DMLtest, p.threshold = 0.2)

There are a few important distinctions in the DML/DMR calling for general design:

1. The “delta” parameter is not taken. In two-group comparison, delta represents a threshold for mean methylation difference. In general design, the coefficients from the linear model are not necessarily the methylation difference, so it is difficult to impose a threshold for the scale of the coefficient. Thus, in DML/DMR calling for general design, the only applicable threshold is the statistical significance (p-values).

2. The return data frame does not provide the mean and relative methylation levels for each experimental factor. This is because from a multiple regression, interpretation of the coefficient is in the form such as “the change of Y with 1 unit increase of X, adjusting for other covariates”. Considering X can be anything (even continuous), there is no clear definition of relative methylation level.

6. DMR visualization.

Similarly, one can use showOneDMR function to visualize a specific DMR

showOneDMR(dmrs[3,], BSobj)

If the figure cannot be seen in the R terminal directly (this could happen where there are too many samples to display), use the following to save the figure to a PDF document. The width and height are configurable by user.

pdf(“one_DMR.pdf”, width = 8, height = 12)
showOneDMR(dmrs[3,], BSobj)
dev.off()

Downstream analysis

After obtaining DML/DMR, one may conduct downstream analysis for functional or enrichment analysis. For example, the researcher may overlap DML/DMR with TSS/TES/gene/intron/exon and interpret these functional elements. Alternatively, the researcher may investigate the methylation profile change within a certain gene or region. For genome-wide analysis, as an example, the researcher may obtain the list of genes that overlap with DML/DMR, and conduct Gene Ontology (GO) analysis or Gene Set Enrichment Analysis (GSEA). Typically, Bioconductor software TopGO or GSEABase can be utilized for such downstream analysis purpose. Additionally, users may find Enrichr [29,30] helpful.

DISCUSSION

DSS provides comprehensive, flexible, and efficient functionalities for differential methylation analysis in BS-seq data. In this work, we provide step-by-step instructions for the use of DSS in different scenarios, including two-group comparison with and without biological replicates, as well as for general experimental design. For more detailed description of the functions, please refer to the function manuals and package vignette distributed with DSS.

There are still several scenarios that DSS does not handle. Paired-design experiment is one of them. Also, in general multi-factor experimental design, DSS will not incorporate spatial correlations from nearby CpG sites. In addition, if the experimental design is clustered, mixed effect models are more proper. Therefore, DSS will not be the ideal choice due to its fixed effect model design. Furthermore, DSS is not suitable for longitudinal data type. These are research topics we plan to implement in the near future.