A comprehensive survey of sine cosine algorithm: variants and applications

Abstract

Sine Cosine Algorithm (SCA) is a recent meta-heuristic algorithm inspired by the proprieties of trigonometric sine and cosine functions. Since its introduction by Mirjalili in 2016, SCA has attracted great attention from researchers and has been widely used to solve different optimization problems in several fields. This attention is due to its reasonable execution time, good convergence acceleration rate, and high efficiency compared to several well-regarded optimization algorithms available in the literature. This paper presents a brief overview of the basic SCA and its variants divided into modified, multi-objective, and hybridized versions. Furthermore, the applications of SCA in several domains such as classification, image processing, robot path planning, scheduling, radial distribution networks, and other engineering problems are described. Finally, the paper recommended some potential future research directions for SCA.

Introduction

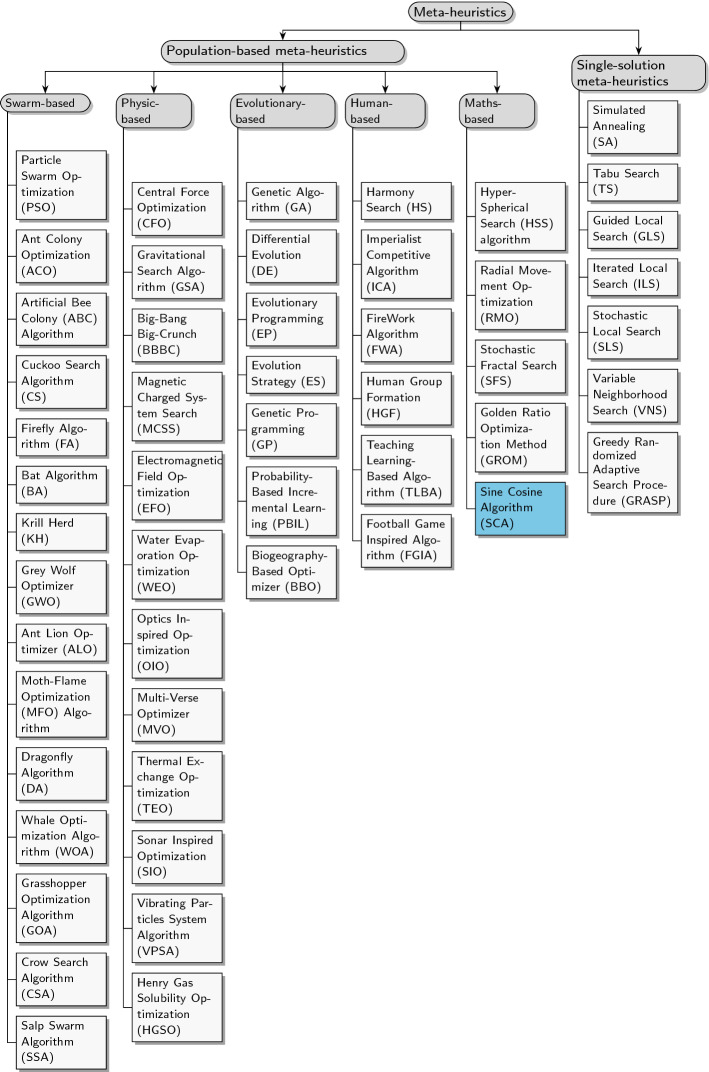
In the last three decades, researchers and scientific have given more attention to the field of optimization using meta-heuristics, so many meta-heuristics are being developed regularly for solving complex and real-world problems in various fields. According to BoussaïD et al. (2013), meta-heuristics can be classified into single solutions and algorithms with populations as shown in Fig. 1.

Fig. 1.

Classification of meta-heuristic algorithms

The generation of a single solution at each run is the main principle of single-based meta-heuristic algorithms, also known as trajectory algorithms. This solution is improved based on the neighborhood mechanism. Some of the popular single-based meta-heuristics are: Simulated Annealing (SA) (Kirkpatrick et al. 1983), Guided Local Search (GLS) (Voudouris and Tsang 1999), Tabu Search (TS) (Glover 1994; Glover and Laguna 1998), Variable Neighborhood Search (VNS) (Mladenović and Hansen 1997), Iterated Local Search (ILS) (Lourenço et al. 2003), Stochastic Local Search (SLS) (Hoos and Stützle 2004), and Greedy Randomized Adaptive Search Procedure (GRASP) (Feo and Resende 1989, 1995; Resende and Ribeiro 1998).

On the other side, population-based meta-heuristic algorithms requires the generation of a set of multiples solutions (population) at each run. It can be divided into five main classes: evolutionary-based, swarm intelligence-based, event-based, physics-based, and maths-based.

Evolutionary Algorithms (EA) is the first class of population-based algorithms which is inspired from the evolutionary phenomena in nature using 3 main operators (i.e. selection, recombination, and mutation). Some well-regarded evolutionary algorithms are: Genetic Algorithm (GA) (Holland 1992), Differential Evolution (DE) (Storn and Price 1997), Evolutionary Programming (EP) (Yao et al. 1999), Genetic Programming (GP) (Koza 1997), Evolution Strategy (ES) (Beyer and Schwefel 2002), and Biogeography-Based Optimizer (BBO) (Simon 2008; Ma et al. 2017).

The second category includes Swarm Intelligence (SI) approaches, in which the source of information is the collective behaviours in nature. (e.g. birds, ants, bees, etc.). The main strengths of these algorithms are their simplicity, flexibility, robustness, scalability, and self-organization (Meraihi et al. 2020b). The two most popular SI algorithms are Particle Swarm Optimization (PSO) (Eberhart and Kennedy 1995; Kennedy 2010), and Ant Colony Optimization (ACO) (Dorigo and Di Caro 1999). Other techniques in this class are: Artificial Bee Colony (ABC) Algorithm (Karaboga and Basturk 2007), Cuckoo Search Algorithm (CS) (Yang and Deb 2009; Shehab et al. 2017), Firefly Algorithm (FA) (Yang 2009; Fister et al. 2013), Bat Algorithm (BA) (Yang 2010, 2013), Krill Herd (KH) (Gandomi and Alavi 2012; Wang et al. 2019), Fruit Fly Optimization (FFO) algorithm (Pan 2012), Grey Wolf Optimizer (GWO) (Mirjalili et al. 2014; Faris et al. 2018; Hatta et al. 2019), Elephant Search Algorithm (ESA) (Deb et al. 2015), Ant Lion Optimizer (ALO) (Mirjalili 2015a; Abualigah et al. 2020), Moth-Flame Optimization (MFO) Algorithm (Mirjalili 2015b; Hussien et al. 2020), Dragonfly Algorithm (DA) (Mirjalili 2016a; Meraihi et al. 2020b), Whale Optimization Algorithm (WOA) (Mirjalili and Lewis 2016; Gharehchopogh and Gholizadeh 2019), Grasshopper Optimization Algorithm (GOA) (Saremi et al. 2017; Meraihi et al. 2021), Crow Search Algorithm (CSA) (Askarzadeh 2016; Meraihi et al. 2020a), and Salp Swarm Algorithm (SSA) (Mirjalili et al. 2017; Abualigah et al. 2019).

The third class is related the inspirations from different human-made events (Fausto et al. 2019). Some of the most well-regarded human-based algorithms are: Harmony Search (HS) (Geem et al. 2001; Manjarres et al. 2013; Zhang and Geem 2019), Imperialist Competitive Algorithm (ICA) (Atashpaz-Gargari and Lucas 2007), FireWork Algorithm (FWA) (Tan and Zhu 2010), Teaching Learning-Based Algorithm (TLBA) (Rao et al. 2011), and Football Game Inspired Algorithm (FGIA) (Fadakar and Ebrahimi 2016).

The fourth category is Physics-based Algorithms (PA) that imitate rules and principles in physics. Some examples of physics-based algorithms are: Central Force Optimization (CFO) (Formato 2007, 2008, 2009), Gravitational Search Algorithm (GSA) (Rashedi et al. 2009; Siddique and Adeli 2016; Rashedi et al. 2018), and Big-Bang Big-Crunch (BBBC) (Erol and Eksin 2006). Other recently developed physics-based algorithms are: Magnetic Charged System Search (MCSS) (Kaveh et al. 2013), Electromagnetic Field Optimization (EFO) (Abedinpourshotorban et al. 2016), Water Evaporation Optimization (WEO) (Kaveh and Bakhshpoori 2016), Optics Inspired Optimization (OIO) (Kashan 2015), Multi-Verse Optimizer (MVO) (Mirjalili et al. 2016; Abualigah 2020), Thermal Exchange Optimization (TEO) (Kaveh and Dadras 2017), Sonar Inspired Optimization (SIO) (Tzanetos and Dounias 2017), Vibrating Particles System Algorithm (VPSA) (Kaveh and Ghazaan 2017), and Henry Gas Solubility Optimization (HGSO) (Hashim et al. 2019).

The last category is Maths-based Algorithms (MA) that imitate mathematical rules. Some of the most well-known maths-based algorithms are: Hyper-Spherical Search (HSS) algorithm (Karami et al. 2014), Radial Movement Optimization (RMO) (Rahmani and Yusof 2014), Stochastic Fractal Search (SFS) (Salimi 2015), Golden Ratio Optimization Method (GROM) (Nematollahi et al. 2020), and Sine Cosine Algorithm (SCA) (Mirjalili 2016b).

SCA is one of the recent promising population-based meta-heuristic optimization algorithms introduced by Mirjalili in 2016. This algorithm is used to solve different optimization problems such as feature selection, image processing, robot path planning, scheduling, economic dispatch, radial distribution networks, and many others. It is based on the proprieties of the trigonometric sine and cosine functions and showed its performance and high efficiency compared to several well-regarded meta-heuristics existing in the literature.

This paper presents a survey of SCA, its variants (modified, multi-objective, and hybridized versions), and its applications in different domains. In order to collect published SCA articles, we consider various well-regarded publishers (i.e. Springer, IEEE, Elsevier, Taylor & Francis, Hindawi, and others) and we use Google scholar by employing the following search strings to build a database of SCA related articles:

• Sine Cosine Algorithm;

• Sine Cosine Optimization Algorithm;

• Improved Sine Cosine Algorithm;

• Sine Cosine meta-heuristics;

• Sine Cosine Algorithm applications;

• SCA.

The resulted papers are screened to retain only credible and original ones, using the combination of inclusion and exclusion criteria shown in Table 1. These criteria ensure that the selection process is objective and helps to limit irrelevant papers.

Table 1.

Inclusion and exclusion criteria

Inclusion criteria	Exclusion criteria
Papers presenting new propositions involving SCA algorithm	Papers published in predatory journals or predatory conferences
Papers presenting surveys on different SCA based approaches	Papers with less than 4 pages
Papers addressing at least one of the identified research questions	Papers written in a language other than English
Paper representing a complete version when several versions exist	Papers that do not provide details on the areas of interest of SCA algorithm
All available papers from 2016 to 2021	Papers published in the form of tutorial, abstract, poster, keynote, or a summary of a conference
	The full paper is not available for download
	Not peer-reviewed scientific papers

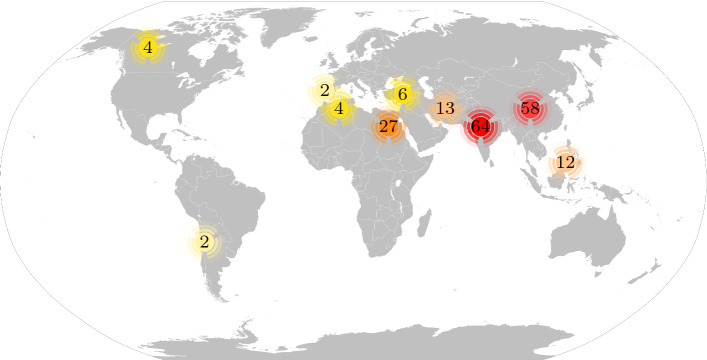
The statistics arisen from our study are presented in the figures below. Figure 2 shows the number of related SCA publications per publisher and per publication type. We can see that Springer and IEEE are those who published the most about SCA. The names of the concerned journals are detailed in the top 10 ranking shown in Table 2. Figure 3 presents the number of SCA publications per year and per publisher. We can see that SCA attracted a lot of interest over the last 3 years with a peak recorded in 2020. In fact, since the introduction of SCA in 2016, more than 210 works have been published on this algorithm. Figure 4 represents the top 10 countries ranked by the number of SCA publications where India and China are the most active countries in this area ahead of Egypt, Iran, Malaysia, Algeria, Turkey, Canada, Spain, and Chile. Finally, Fig. 5 shows the tag cloud of the top ten SCA-related keywords.

Fig. 2.

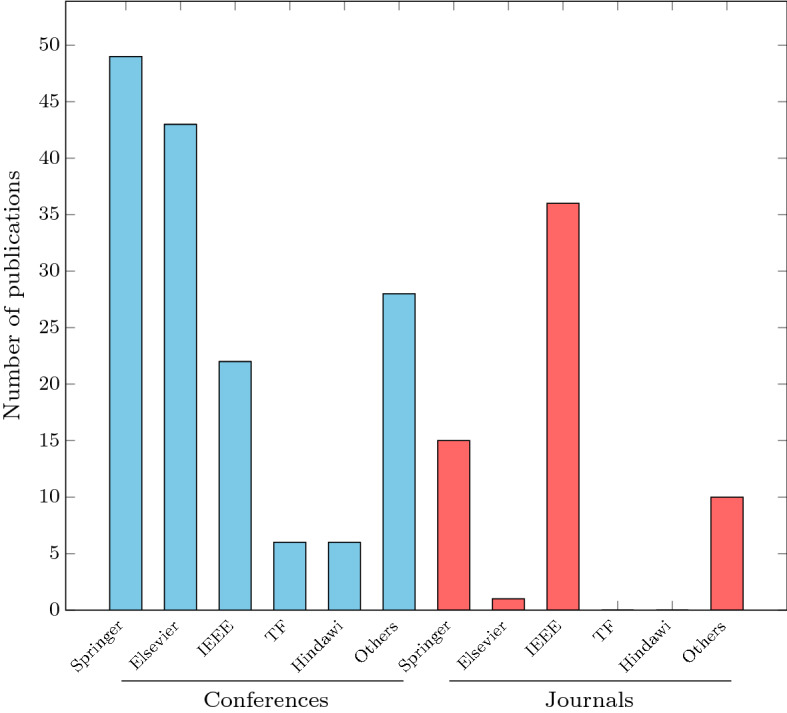
Number of SCA related publications by scientific databases

Table 2.

Top 10 journals ranked by number of SCA publications

Rank	Journal	Number of publication
1	IEEE Access	14
2	Expert Systems with Applications	13
3	Neural Computing and Applications	7
4	Applied Soft Computing	7
5	Arabian Journal for Science and Engineering	6
6	Soft Computing	6
7	Evolutionary Intelligence	5
8	Engineering with Computers	4
9	Knowledge-based Systems	3
10	Energy Conversion and Management	2

Fig. 3.

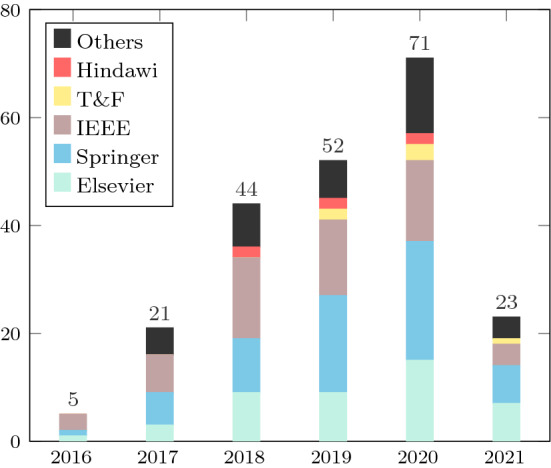
Number of publications on SCA per year

Fig. 4.

Top 10 countries ranked by number of publications on the SCA algorithm

Fig. 5.

Top 10 SCA-related keywords

To the best of our knowledge, there is only one survey (Abualigah and Diabat (2021)) analyzing the SCA-based papers in the literature. It covers around 100 research articles. However, the present SCA survey collects and discusses more than 210 articles published between 2016 and the beginning of 2021 which makes it different.

The rest of this paper is organized as follows. Section 2 describes the structure of the standard SCA. Section 3 presents the modified, multi-objective, and hybridized versions of SCA. The applications of SCA in various domains are discussed in Sect. 4. Section 5 gives comparisons and results of SCA with some well-regarded meta-heuristics. Discussion and some suggestions for further works are given in Sect. 6. In the end, Sect. 7 concludes the paper.

Sine Cosine Algorithm

The SCA algorithm was proposed by Seyedali Mirjalili in 2016 (Mirjalili 2016b) as a population-based meta-heuristic to solve optimization problems. This optimization algorithm uses the principle of trigonometric sine and cosine functions for updating the positions of individuals toward the optimal solution. The solutions in SCA are updated using the following equations (Mirjalili 2016b):

$$\begin{array}{c}\hfill X_{\mathit{ij}}^{t+1}=X_{\mathit{ij}}^t+r_1\ast sin(r_2)\ast |r_3{P}_{\mathit{ij}}^t-X_{\mathit{ij}}^t|\end{array}$$ 1

$$\begin{array}{c}\hfill X_{\mathit{ij}}^{t+1}=X_{\mathit{ij}}^t+r_1\ast cos(r_2)\ast |r_3{P}_{\mathit{ij}}^t-X_{\mathit{ij}}^t|\end{array}$$ 2

The effects of sine and cosine functions on Eqs. (1) and (2) are shown in Fig. 6

Fig. 6.

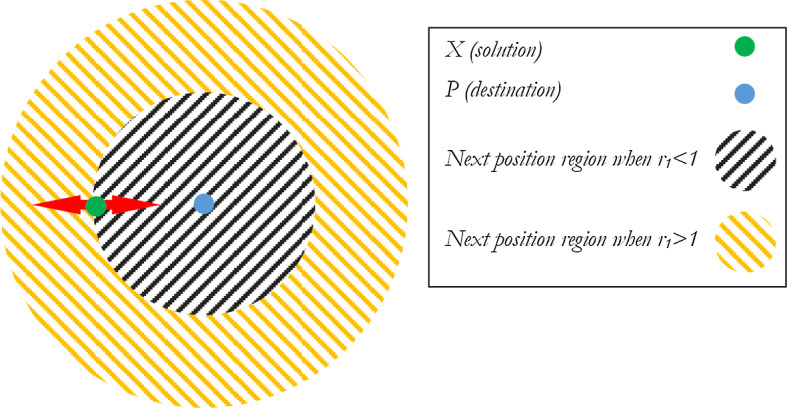
The effects of sine cosine functions in Eqs. (1) and (2) on the next position (Mirjalili 2016b)

In general, the aforementioned equations are combined to be used as follows:

$$\begin{array}{c}\hfill X_{\mathit{ij}}^{t+1}=\left\{\begin{array}{c}{X}_{\mathit{ij}}^t+r_1\ast cos(r_2)\ast |r_3{P}_{\mathit{ij}}^t-X_{\mathit{ij}}^t|,r_4\ge 0.5\hfill \\ X_{\mathit{ij}}^t+r_1\ast sin(r_2)\ast |r_3{P}_{\mathit{ij}}^t-X_{\mathit{ij}}^t|,r_4<0.5\hfill \end{array}\right)\end{array}$$ 3

where $X_{\mathit{ij}}^t$ represents the current individual i at iteration t in the $\mathit{d}$th dimension, $P_{\mathit{ij}}^t$ shows the best individual’s position at iteration t in the $\mathit{d}$th dimension, and $r_1,r_2,r_3,r_4$ are random parameters. These parameters are incorporated to avoid falling into local optima and balance exploratory and exploitative search patterns.

The parameter $r_1$ decides whether a solution updates its position towards the best solution $(r_1<1)$ or outwards it $(r_1>1)$. Note that $r_1$ decreases linearly from a preset constant (a) to 0 (Mirjalili 2016b; Attia et al. 2018) to balance exploratory and exploitative search patterns. It is updated using the following equation:

$$\begin{array}{c}\hfill r_1=a-t\frac{a}{T_{\mathit{max}}}\end{array}$$ 4

where a is a constant, t is the current iteration, and $T_{\mathit{max}}$ represents the maximum iterations allowed.

The parameter $r_2$ is set in the range of $[0,2\Pi ]$ that dictates how big the movement of a solution is towards or outwards of the destination. Another random parameter, $r_3$, assigns a random weighing to the destination. This allows emphasizing $(r_3>1)$ or de-emphasizing $(r_3<1)$ the impact of the destination of the position updating of other solutions. $r_3$ is in the range of [0, 2]. Finally, the last random parameter $r_4$ is in [0, 1] and acts as a switch to choose between the trigonometric functions of sine of cosine the Eq. 3 (Mirjalili 2016b; Attia et al. 2018).

The pseudo-code of the standard Sine Cosine Algorithm is illustrated in Algorithm 1 (Mirjalili 2016b). Its corresponding flowchart is illustrated in Fig. 7.

Fig. 7.

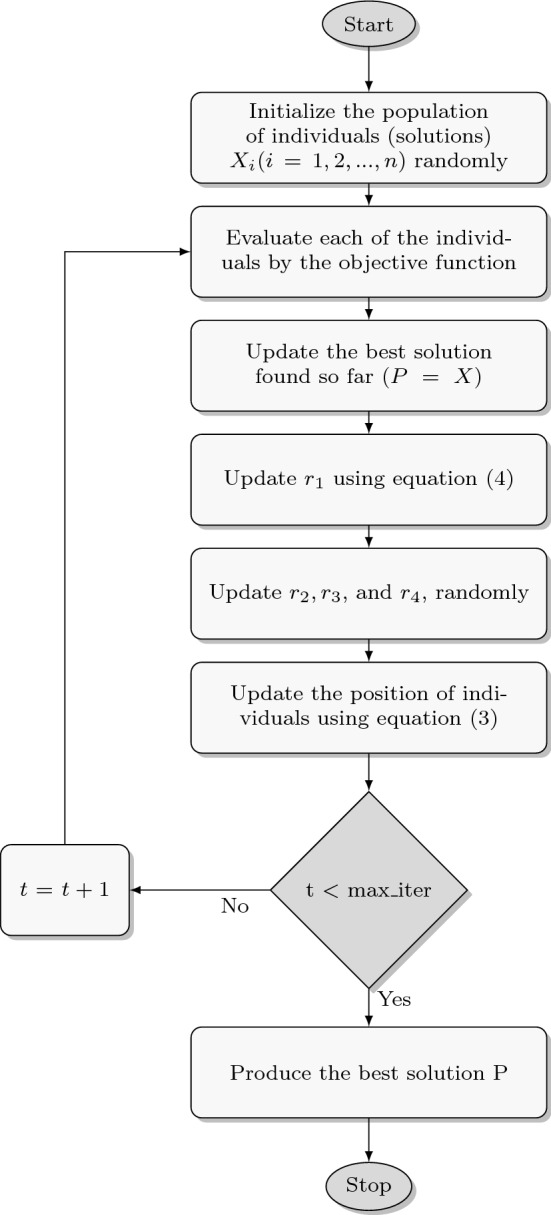
Flowchart of the Sine Cosine Algorithm

Recent variants of the Sine Cosine Algorithm

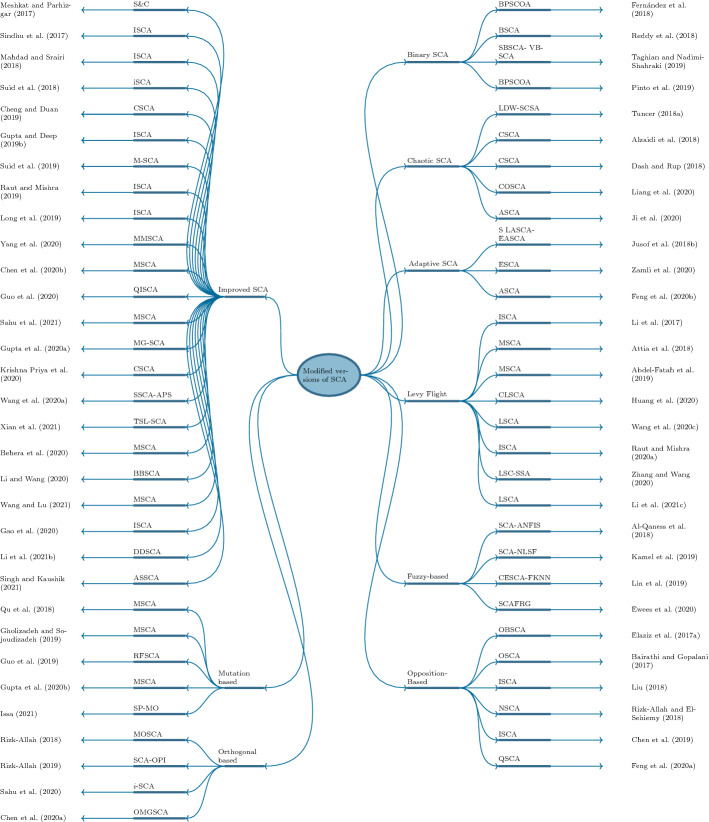
A wide range of SCA’s variants have been proposed in the literature, dividing into: modified, multi-objective, and hybridized versions. The variants of SCA are shown in Fig. 8.

Fig. 8.

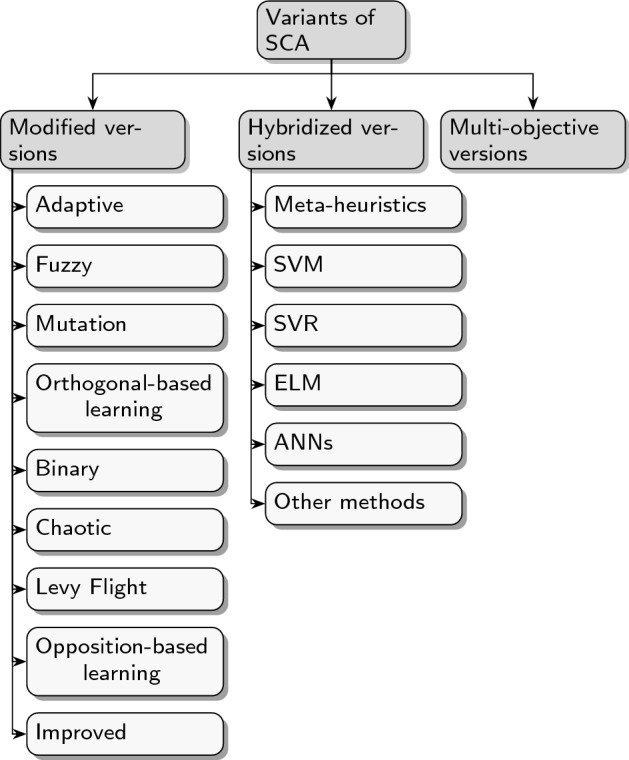
Variants of SCA

Modified versions of Sine Cosine Algorithm

As shown previously, there are nine modified versions of SCA in the literature. In each version, several approaches are proposed as it is represented in Fig. 9. In the following, the realization details of each approach are given and the summary of the main points to retain for each of them is provided in Table 3, where N represents the number of populations, D is the dimension, and T is the number of iterations.

Fig. 9.

Modified versions of SCA

Table 3.

Modified versions of SCA

Variant	Name	Complexity	Application	Results	Author (Ref.)
Binary SCA	BPSCOA	–	Set covering problem	BPSCOA achieves competitive results when compared with JPSO and MDBBH algorithms	Fernández et al. (2018)
	BSCA	$O(N\ast T\ast D)$	Unit commitment	Effectiveness of BSCA compared to the state-of-the-art algorithms in terms of solution quality and convergence	Reddy et al. (2018)
	SBSCA- VBSCA	$O(N\ast T\ast D)$	Feature selection	SBSCA provides better results compared to BBA, BGSA, BGWO, and BDA	Taghian and Nadimi-Shahraki (2019)
	BPSCOA	–	Knapsack problem	BPSCA obtains competitive results compared to BAAA and KMTR algorithms	Pinto et al. (2019)
Chaotic SCA	LDW-SCSA	–	Numerical functions	LDW-SCSA achieves better results compared to VS, PSO, and SCA	Tuncer (2018a)
	CSCA	–	Salient cryptographic features	Superiority of CSCA compared to some optimization-based S-box techniques	Alzaidi et al. (2018)
	CSCA	–	Block-based motion estimation	CSCA yields satisfactory and better results compared to other methods in terms of PSNR, DPSNR, and the number of search points	Dash and Rup (2018)
	COSCA	$O(N\ast 3\ast D\ast T)$	Global optimization problems	Efficiency of COSCA compared to other optimization methods	Liang et al. (2020)
	ASCA	$O(N\ast D)+2O(N)$+$T\ast (2O(N\ast D)+4O(N))$	Constrained and Unconstrained Optimization	Significant superiority of the ASCA compared to some well-regarded and advanced optimization approaches	Ji et al. (2020)
Adaptive SCA	LASCA-EASCA	–	Global optimization	Effectiveness of the adaptive versions compared to the original SCA in terms of accuracy and convergence speed	Jusof et al. (2018b)
	ESCA	–	Combinatorial testing problem	Superiority of ESCA compared to the original SCA, TLBO, and Jaya algorithms in terms of test suite sizes	Zamli et al. (2020)
	ASCA	$O(3\ast N\ast D\ast T)$	multiple hydropower reservoirs operation	Effectiveness and robustness of ASCA compared to other well-known algorithms in terms of convergence rate and solution quality	Feng et al. (2020b)
Levy Flight-Based SCA	ISCA	–	Complex nonlinear optimization problems	ISCA gives better performance when compared with GA, PSO, and SCA	Li et al. (2017)
	MSCA	$O(3\ast N\ast D\ast T)$	Optimal power flow	Effectiveness of MSCA compared to the original SCA and other published optimization techniques	Attia et al. (2018)
	MSCA	$O(2\ast N\ast D\ast T)$	Optimal Reactive Power Dispatch	Effectiveness and superiority of MSCA compared to other well-known meta-heuristics	Abdel-Fatah et al. (2019)
	CLSCA	$O(N\ast D+N^2)$+$T\ast (5O(N\ast D)$+$4O(N)+O(N^2))$	Benchmark functions	CLSCA achieves better results compared to PSO, GWO, SCA, SCADE, OBSCA, CSSA, CWOA, and FST_PSO	Huang et al. (2020)
	LSCA	–	Hyperspectral image	LSCA achieves better optimization results when compared with PSO, DE, GSA, CS, and SCA in terms of classification accuracy	Wang et al. (2020c)
	ISCA	$O(2\ast T\ast N\ast D)$	Distributed generators (DGs) allocation	Superiority of ISCA compared to HSA, GA, FWA, RGA, and FF algorithms	Raut and Mishra (2020a)
	LSC-SSA	$O((T\ast (N\ast D+N2-N)/2)$+$3+D+(N-1)\ast D)$	Training muti-layer perceptron neural network	LSC-SSA gives better results in terms of classification accuracy in comparison with PSO, FA, SSA, WOA, and SCA	Zhang and Wang (2020)
	LSCA	–	Global Optimization Problems	LSCA provides good convergence accuracy	Li et al. (2021c)
Fuzzy-Based SCA	SCA-ANFIS	–	Oil Consumption Forecasting	Effectiveness of SCA-ANFIS compared to the traditional ANFIS, GA-ANFIS, PSO-ANFIS, GWO-ANFIS, and WOA-ANFIS techniques	Al-Qaness et al. (2018)
	SCA-NLSF	–	Optimum capacitor allocation in distribution systems	Effectiveness of SCA-NLSF compared to DE and PSO algorithms in terms of power losses and energy cost	Kamel et al. (2019)
	CESCA-FKNN	$O(2\ast N+T+N\ast T(1+D))$	Predicting intentions of Students for master programs	CESCA-FKNN achieves better performance compared to RF, KELM, SVM, SCA-FKNN, DA-FKNN, and MFOFKNN	Lin et al. (2019)
	SCAFRG	–	Prediction of osteoporosis	SCAFRG achieves competitive results compared to other existing algorithms	Ewees et al. (2020)
Opposition-based SCA	OBSCA	$O(2\ast N\ast D\ast T)$	Global optimization problems	Effectiveness and performance of OBSCA compared to some well-known meta-heuristic algorithms in terms of convergence and time complexity	Elaziz et al. (2017a)
	OSCA	$O(2\ast N\ast D\ast T)$	Feed-forward neural network (FNN) training	Efficiency of OSCA compared to GA, DE, ES, ACO and PSO algorithms	Bairathi and Gopalani (2017)
	ISCA	–	Benchmark functions	ISCA has better performance compared to the original SCA, RLPSO, and wFIPS	Liu (2018)
	NSCA	–	Emission/economic load dispatch	Effectiveness and robustness of NSCA compared to other meta-heuristic algorithms existing in the literature	Rizk-Allah and El-Sehiemy (2018)
	ISCA	$O(3\ast N\ast D\ast T)$	Solar photo-voltaic parameter identification	ISCA gives superior and very competitive performance compared to ABC, ABSO, SA, PS, CPSO, GOTLBO, and GOFPANM	Chen et al. (2019)
	QSCA	–	Multiple hydropower reservoirs operation	QSCA produces better objective values compared to several existing evolutionary algorithms	Feng et al. (2020a)
Orthogonal-Based SCA	MOSCA	–	Design and manufacturing optimization problems	MOSCA outperforms other existing techniques in most cases	Rizk-Allah (2018)
	SCA-OPI	–	Global optimization problems	SCA-OPI gives competitive performance compared to some well-regarded optimization algorithms in terms of optimality and reliability	Rizk-Allah (2019)

Variant	Name	Application	Results	Author (Ref)
Mutation-Based SCA	i-SCA	$O(2\ast N\ast D\ast T)$	Optimal parameters control	Performance and supremacy of i-SCA compared to GA, PSO, and basic SCA	Sahu et al. (2020)
	OMGSCA	$O(N^2\ast D\ast T)$	Engineering design problems	Effectiveness and robustness of OMGSCA compared to some optimization algorithms	Chen et al. (2020a)
	MSCA	$O(N\ast 2\ast T\ast D)$	Benchmark functions	Effectiveness of MSCA compared toPSO, DE, BA, TLBO, GWO, and SCA in terms of searching precision and convergence speed	Qu et al. (2018)
	MSCA	–	Discrete sizing optimization of truss structures	Efficiency and robustness of MSCA compared to HPSO, HHS, AEDE, ECBO, IMBA, IGA, ESASS and SCA	Gholizadeh and Sojoudizadeh (2019)
	RFSCA	$O((2N+1)\ast D\ast T)$	Global optimization problems	Superior performance of RFSCA compared to SCA, OBSCA, PSO, OPSO, GWO, MFO, and SSA	Guo et al. (2019)
	MSCA	–	Global optimization problems	Efficiency and robustness of MSCA compared to the standard SCA, modified variants of SCA and some other meta-heuristics	Gupta et al. (2020b)
	SP-MO	–	Measuring similarity of COVID-19	Superiority of SP-MO over some relevant studies	Issa (2021)
Improved SCA	S&C	$O(N\ast T\ast D)$	Global optimization problems	Superiority of S&C compared to the classical SCA in terms of accuracy and convergence speed	Meshkat and Parhizgar (2017)
	ISCA	$O(2\ast N\ast T\ast D)$	Feature selection	Superiority of ISCA compared to well-known meta-heuristics by achieves the best classification accuracy	Sindhu et al. (2017)
	ISCA	–	Optimizing the loading margin stability	Effectiveness and superiority of ISCA compared to some well-known optimization algorithms in terms of solution quality and convergence speed	Mahdad and Srairi (2018)
	iSCA	–	Benchmark functions	iSCA provides competitive results when compared with SDA, MVO, ALO, and basic SCA	Suid et al. (2018)
	CSCA	–	Benchmark functions	Superiority of CSCA compared to the standard SCA, GA, SA, PSO, ACO, ABC, and SS	Cheng and Duan (2019)
	ISCA	$O(N\ast D\ast T)$	Global optimization problems	Robustness and efficiency of ISCA compared to the traditional SCA and other meta-heuristics	Gupta and Deep (2019b)
	M-SCA	–	Improving energy production of wind plant	M-SCA gives the highest total energy production when compared with other existing techniques	Suid et al. (2019)
	ISCA	$O(2\ast T\ast N\ast D)$	Power distribution network reconfiguration	Capability of ISCA to obtain global minimum results in most of the test distribution systems	Raut and Mishra (2019)
	ISCA	$O(N\ast T)$	Global optimization problems	ISCA gives competitive solutions compared to the original SCA and other population-based approaches	Long et al. (2019)
	MMSCA	–	Capacitated vehicle routing problem	Feasibility and efficiency of MMSCA compared to the original SCA	Yang et al. (2020)
	MSCA	$O(N\ast D\ast T)$	Global optimization and constrained engineering problems	Superiority of MSCA compared to other state-of- the-art methods in terms of quality of solutions and convergence speed	Chen et al. (2020b)
	QISCA	$O(N\ast D+3N\ast D\ast T)$	Global optimization and engineering problems	Effectiveness of QISCA in solving practical problems compared to 13 well-regarded optimization techniques	Guo et al. (2020)
	MSCA	–	Optimal parameters control	Effectiveness of MSCA in comparison with GA, PSO, and the traditional SCA	Sahu et al. (2021)
	MG-SCA	$O(N\ast D\ast T)$,	Global optimization problems	Effectiveness and ability of MG-SCA compared to other optimization approaches	Gupta et al. (2020a)
	CSCA	–	Multimedia content distribution in cloud environment	Superiority of CSCA compared to GA, PSO, and SCA	Krishna Priya et al. (2020)
	SSCA-APS	$O(N^2\ast D\ast T)$	Benchmark functions	Competitiveness of SSCA-APS compared to the original SCA and some SCA variants	Wang et al. (2020a)
	TSL-SCA	$O(T(8\ast N\ast D+2N))$	Global Optimization problems	Effectiveness of TSL-SCA compared to TLBO, CS, PSO, WOA, MFO, and SCA in terms of accuracy and convergence speed	Xian et al. (2021)
	MSCA	$O(N\ast D\ast T)$	Benchmark functions	MSCA gives better performance compared to the original SCA and other population-based meta-heuristics by obtaining the faster convergence	Behera et al. (2020)
	BBSCA	$O(2\ast N\ast D\ast T)$	Global optimization problems	DDSCA generates better results compared to several SCA algorithm variants	Li and Wang (2020)
	MSCA	$O(N^2\ast D\ast T)$	Engineering problems	MSCA provides superior efficiency as compared to some recent related approaches	Wang and Lu (2021)
	ISCA	$O(N\ast 2\ast T\ast D)$	Benchmark functions	ISCA performs better and faster than the classical SCA	Gao et al. (2020)
	DDSCA	–	Global optimization problems	DDSCA gives competitive results compared to other optimization algorithms	Li et al. (2021b)
	ASSCA	$O(2\ast T\ast N\ast D)$	Multi focus image fusion	ASSCA shows good results compared to other optimization algorithms by obtaining 40.625 of PSNR and 7.651 of RMSE	Singh and Kaushik (2021)

Binary Sine Cosine Algorithm

Fernández et al. (2018) proposed a Binary Percentile SCA (BPSCOA) for solving the Set Covering Problem (SCP). A percentile concept is used to perform the binarization process of SCA. The effectiveness of BPSCOA was evaluated based on different SCP instances in comparison with Jumping PSO (JPSO) and Multi Dynamic Binary Black Hole (MDBBH) algorithms. Simulation results showed that BPSCOA gives competitive results when compared with JPSO and MDBBH algorithms.

Reddy et al. (2018) proposed a new variant of binary SCA (BSCA) for solving the profit-based unit commitment (PBUC) problem. In BSCA, the modified sigmoidal transformation function was used for binary mapping of the continuous real-valued position to binary search space. The performance of BSCA was evaluated using 3 generic operations of the competitive electricity market and results demonstrated the effectiveness of BSCA compared to the state-of-the-art algorithms in terms of solution quality and convergence speed.

Taghian and Nadimi-Shahraki (2019) proposed two versions of binary SCA, called S-shaped binary SCA(SBSCA) and V-shaped binary SCA (VBSCA) as a seminal attempt to solve binary problems (specially feature selection). S-shaped and V-shaped transfer functions were used to map the continuous values into the binary position values. The performance of SBSCA and VBSCA were tested using 5 medical datasets taken from the UCI repository in comparison with Binary BA (BBA), Binary GSA (BGSA), Binary GWO (BGWO), and Binary DA (BDA). Numerical results demonstrated that SBSCA provides better results compared to BBA, BGSA, BGWO, and BDA on most of the medical datasets.

Pinto et al. (2019) proposed a binary SCA (BPSCOA) for solving the multidimensional backpack problem (MKP). The percentile technique was applied in the binarization process of SCA. The performance BPSCOA was evaluated using OR-Library benchmarks MKP and results showed that BPSCA obtains competitive results compared to Binary Artificial Algae (BAAA) and K-Means Transition Ranking (KMTR) algorithms.

Chaotic Sine Cosine Algorithm

Tuncer (2018a) proposed a novel chaotic weighted SCA (LDW-SCSA) based on the integration of chaos into SCA for numerical functions optimization. In LDW-SCSA algorithm, the logistic map was used to generate the weights dynamically. The performance of LDW-SCSA was evaluated based on 7 uni-modal and 6 multi-modal benchmark functions in comparison with the original SCA, PSO, and Vortex Search (VS) algorithm. Simulation results showed that LDW-SCSA achieves better results compared to VS, PSO, and SCA.

Alzaidi et al. (2018) introduced an enhanced SCA based on the incorporation of enhanced 1D chaotic map in SCA for building bijective substitution-boxes creating salient cryptographic features. Enhanced 1D chaotic map was introduced into the original SCA to explore and exploit the search space. Simulation results showed the superiority of the proposed approach compared to some optimization-based S-box techniques.

Dash and Rup (2018) proposed a chaotic-Based SCA with fitness approximation (FA) strategy for block-based motion estimation. FA was incorporated with SCA to maintain the balance between the exploration and exploitation. This approach was tested based on the widely used video sequences: Foreman, Carphone, Akiyo, Container, Football, and Stefan by considering only the luminance component of the sequences. Experimental results demonstrated that the proposed approach yields satisfactory and better results compared to other methods in terms of Peak-Signal-to-Noise-Ratio (PSNR), PSNR degradation ratio $(D_{\mathit{PSNR}})$, and the number of search points.

Liang et al. (2020) proposed a chaotic oppositional SCA (COSCA) for solving global optimization problems. Opposition-based learning method was used to optimize the exploration and exploitation capability of the original SCA. The effectiveness of COSCA was validated based on a set of 22 benchmark functions and 3 complex engineering problems including welded beam design, I-beam design, and pressure vessel design problems. Simulation results showed the efficiency and superiority of COSCA compared to the state-of-the-art optimization methods existing in the literature.

Adaptive Sine Cosine Algorithm

Jusof et al. (2018b) proposed two enhanced versions of SCA (LASCA, EASCA) based on the incorporation of Linear and exponential adaptive strategies (EASCA) into SCA for solving global optimization problems. The performance of LASCA and EASCA were evaluated on a wide range of test functions and compared with the original SCA. It was demonstrated that the effectiveness of the adaptive versions compared to original SCA in terms of accuracy and convergence speed.

Zamli et al. (2020) proposed an adaptive SCA for solving the combinatorial testing problem. A combination of linear and exponential magnitude update strategies was used for the search displacement. Simulation results demonstrated the superiority of the enhanced SCA compared to the original SCA, TLBO, and Jaya algorithms in terms of test suite sizes.

In the work of Feng et al. (2020b), an adaptive SCA (ASCA) based on elite mutation, neighborhood search, and simplex search strategies was proposed for optimizing the multiple hydro-power reservoirs operation. The Wu River cascade hydro-power system in southwest China was chosen to validate the performance of ASCA in comparison with GA, PSO, GSA, and original SCA. The superiority of ASCA compared to other well-known algorithms was demonstrated in terms of convergence rate and solution quality.

Lévy flight-based Sine Cosine Algorithm

An improved version of SCA based on Lévy Flight distribution was proposed in the work of Li et al. (2017) for solving the complex nonlinear optimization problems. The performance of the proposed SCA was evaluated based on five benchmark functions and compared to GA, PSO, and SCA. It was demonstrated that the proposed SCA gives better performance compared to GA, PSO, and SCA.

Attia et al. (2018) introduced a modified SCA (MSCA) based on the incorporation of Lévy flight in the original SCA to solve Optimal Power Flow (OPF) problems. The performance of MSCA was validated based on 2 standard benchmark networks namely IEEE-30 bus and IEEE 118-bus test systems under selected objective functions. MSCA was demonstrated to outperform all other comparative algorithms on this problem area.

Abdel-Fatah et al. (2019) introduced a modified SCA (MSCA) based on Lévy Flight distribution. The made of this modification to SCA in an attempt to solve the Optimal Reactive Power Dispatch (ORPD) problem. The performance of MSCA was tested based on IEEE 30-bus system taking into account 3 metrics including power loss reduction, voltage deviations minimization, and voltage stability enhancement. MSCA was demonstrated to outperform all other comparative algorithms on this problem area.

Huang et al. (2020) introduced an improved SCA (CLSCA) based on the combination of SCA with Lévy flight operator and chaotic local search mechanism. Another similar work was done by Wang et al. (2020c), in which an enhanced approach (LSCA) based on the integration of Lévy flight alternative distribution into SCA for HyperSpectral image (HSI).

Raut and Mishra (2020a) introduced an improved SCA (ISCA) based on Lévy Flight distribution for solving the problems of simultaneous distributed generators (DGs) allocation and network reconfiguration (NR). The performance of ISCA was evaluated based on 33-bus and 69-bus distribution systems and compared to HSA, GA, FWA, RGA, and FF algorithms. ISCA was demonstrated to outperform all other comparative algorithms on this problem area

Fuzzy-based Sine Cosine Algorithm

Al-Qaness et al. (2018) hybridized CA with Adaptive Neuro-Fuzzy Inference System (SCA-ANFIS) for Oil Consumption Forecasting. Another similar work was done by Kamel et al. (2019), in which a novel method based on combining SCA with Fuzzy Logic Control Normalized Loss Sensitivity Factor (NLSF) for optimum allocation of shunt capacitors in distribution systems. The efficiency of the proposed method was validated based on 15 bus and 69-bus distribution networks and was compared to DE and PSO algorithms.

Lin et al. (2019) introduced a hybrid optimization approach, called CESCA-FKNN, based on the hybridization of Chaos-Enhanced (CESCA) with Fuzzy K-Nearest Neighbor (FKNN) for predicting the college students’ intentions for master programs. The effectiveness of CESCA-FKNN was evaluated based on a real-life dataset collected from Wenzhou University in comparison with some classifier methods such as RF, KELM, SVM, SCA-FKNN, DA-FKNN, and MFO-FKNN. Experimental results demonstrated that the CESCA-FKNN algorithm achieves better performance compared to other classifier methods in terms of Matthews Correlation Coefficients (MCC), Classification Accuracy (ACC), sensitivity, and specificity.

Opposition-based learning Sine Cosine Algorithm

In the work of Elaziz et al. (2017a), an enhanced SCA called Opposition-Based Sine Cosine Algorithm (OBSCA) was proposed for solving global optimization problems. The Opposition-Based Learning (OBL) was integrated into SCA to enhance substantially its accuracy and performance. The effectiveness of OBSCA was evaluated based on several benchmark functions and engineering problems in comparison with the standard SCA and 13 well-known meta-heuristic techniques. OBSCA was demonstrated to outperform all other comparative algorithms on this problem area.

Opposition-Based Sine Cosine Algorithm (OSCA) was proposed in the work of Bairathi and Gopalani (2017) for learning enhancement of feed-forward neural network (FNN). The performance of OSCA was tested using eight different UCI datasets and compared to GA, DE, ES, ACO, and PSO algorithms. OSCA was demonstrated to outperform all other comparative algorithms in training FNNs.

Liu (2018) proposed an improved SCA (ISCA) based on the integration of OBL strategy and tent chaos search into SCA.In ISCA, the generation of individuals was made using OBL and Chaos strategies. ISCA was applied to six standard uni-modal and multi-modal benchmark functions in comparison with RLPSO, wFIPS, and classical SCA. Numerical results showed that ISCA has better performance compared to the original SCA, RLPSO, and wFIPS.

Chen et al. (2019) introduced a new improved opposition-based sine cosine technique, called ISCA, for solving the solar photovoltaic parameter identification problems. ISCA is based on the integration of OBL mechanism and Nelder-Mead simplex (NMs) strategy into SCA to enhance the diversification of the population. Experimental and statistical results demonstrated that ISCA gives superior and very competitive results compared to several well-known meta-heuristics such as ABC, ABSO, SA, PS, CPSO, GOTLBO, and GOFPANM.

Orthogonal-based Sine Cosine Algorithm

In the work of Rizk-Allah (2018), MOSCA was proposed hybridizing SCA with Multi-Orthogonal Search Strategy (MOSS). The application area was design and manufacturing optimization problem. The performance of MOSCA was evaluated based on 18 benchmark problems and 4 engineering design problems. Simulation results demonstrated that MOSCA outperforms other existing techniques in most cases.

Sahu et al. (2020) proposed an improved SCA (i-SCA) using the integration of multi-orthogonal search strategy into SCA for optimal design of robust Fractional Order-Multistage controller for frequency awareness of an islanded AC Micro-grid. The effectiveness of i-SCA was validated through different dynamic responses in comparison with GA, PSO, and basic SCA and results revealed the performance and supremacy of i-SCA.

An improved variant of the SCA algorithm, called OMGSCA, based on the incorporation of orthogonal learning mechanism, greedy selection strategy, and multi-population scheme into the basic SCA was proposed by Chen et al. (2020a). The performance of OMGSCA was tested based on 30 benchmark functions selected from the well-regarded IEEE CEC 2014 in comparison with the basic SCA, 6 improved SCA variants, and 10 well-known meta-heuristic algorithms. OMGSCA was also used to solve three constrained engineering design problems. It was demonstrated that OMGSCA is superior in this problem area.

Mutation-based Sine Cosine Algorithm

A new improved version of SCA (MSCA) based on greedy Levy mutation strategy and neighborhood search scheme was proposed in the work of Qu et al. (2018). MSCA was tested using 20 benchmark test functions including unimodal high-dimensional functions, multimodal high-dimensional functions, and multimodal low-dimensional functions. The MSCA algorithm was compared with PSO, DE, BA, TLBO, GWO, and SCA. The superiority of MSCA compared to these algorithms was demonstrated in terms of convergence rate and solution quality.

Gholizadeh and Sojoudizadeh (2019) proposed a modified SCA (MSCA) for discrete sizing optimization of truss structures. An efficient mutation operator is integrated into MSCA to reduce the probability of getting stuck in local optima. The performance of MSCA was assessed using benchmark truss optimization problems in comparison with HPSO, HHS, AEDE, ECBO, IMBA, IGA, ESASS, and SCA. Experimental results demonstrated the efficiency and robustness of MSCA compared to the mentioned optimization algorithms.

An enhanced SCA (RFSCA) based on Riesz fractional derivative mutation strategy was proposed in the work of Guo et al. (2019). In Gupta et al. (2020b), another improved SCA (MSCA) was propose using a mutation operator strategy and transition parameter for solving global optimization problems.

Other improved Sine Cosine Algorithms

Meshkat and Parhizgar (2017) proposed a novel SCA (S&C) based on a novel position update mechanism for solving global optimization problems. In S&C, the new position update mechanism is based on the coefficients of exploration rate (ExrR) and exploitation rate (ExtR). The effectiveness of S&C was evaluated based on CEC 2014 benchmark functions and results demonstrated the superiority of S&C over the original SCA in terms of accuracy and convergence speed.

Sindhu et al. (2017) proposed an improved SCA (ISCA) by combining SCA with new position update mechanism and elitism strategy for solving the feature selection problem. The effectiveness of ISCA was validated based on 10 medical and non-medical benchmark datasets. The superiority of ISCA was demonstrated compared to well-known meta-heuristics.

Mahdad and Srairi (2018) proposed an interactive SCA (ISCA) for optimizing the loading margin stability under contingency of practical power system. In ISCA, the random parameters $r_1,r_2,$ and $r_3$ are tuned dynamically to avoid the premature convergence of SCA. The performance of ISCA was evaluated based on IEEE 30-Bus and IEEE 118-Bus test systems.

Suid et al. (2018) proposed an improved SCA (iSCA) for solving the optimization problems. A nonlinear control strategy was introduced in order to synthesize the iSCA’s strength. The performance of iSCA was evaluated based on 23 classical well-known benchmark functions and compared to four other algorithms. Simulation results showed that iSCA provides competitive results.

Cheng and Duan (2019) proposed a Cloud model-based SCA (CSCA) for solving optimization problems. The cloud model was employed to tune the parameters of SCA adaptively. CSCA was validated using three benchmark function tests and results showed its superiority in comparison with GA, PSO, SA, ACO, ABC, and Scatter Search (SS) algorithms.

Gupta and Deep (2019b) proposed an improved SCA (ISCA) based on the incorporation of crossover, self-learning, and global search mechanisms into SCA for solving global optimization problems. The performance of ISCA was evaluated based on the classical, CEC 2014, and CEC 2017 benchmarks. ISCA was also used to solve 5 engineering problems and image thresholding problem.

Suid et al. (2019) proposed a modified SCA (M-SCA) for improving the energy production of wind plants. Two modifications i.e. the updated step size gain and the updated design variable were introduced into M-SCA to avoid the premature convergence condition and enhance the balance between exploration and exploitation rates. M-SCA was applied for maximizing energy production of a row of ten turbines and results showed that M-SCA gives the highest total energy production when compared with other existing techniques.

Raut and Mishra (2019) proposed an improved version of SCA (ISCA) for solving the Power Distribution Network Reconfiguration (PDNR) problem. In ISCA, the conversion parameter $r_1$ is defined using the nonlinear decreasing method, the simple branch exchange-based heuristic is also used to generate the initial population. The performance of ISCA was evaluated considering IEEE 33-bus, 69-bus, 84-bus, 119-bus, and 136-bus distribution systems and results showed the capability of ISCA to obtain global minimum results in most of the test distribution systems.

In (Long et al. 2019), an improved SCA (ISCA) was proposed based on the integration of nonlinear decreasing conversion parameter strategy and modified position update mechanism for solving global optimization problems. The effectiveness of ISCA was validated using 24 high-dimensional functions and several engineering design problems. Simulation results showed that ISCA gives competitive solutions compared to the original SCA and other population-based approaches.

Yang et al. (2020) proposed a Multi-group Multi-strategy SCA (MMSCA) for solving the capacitated vehicle routing problem (CVRP) in transportation. In MMSCA, multiple populations are executed in parallel and each population executes a different optimization strategy. The effectiveness of MMSCA was validated using 19 different types of test functions and results showed the feasibility and efficiency of MMSCA compared to the original SCA.

Chen et al. (2020b) introduced a multi-strategy enhanced SCA (MSCA) based on the incorporation of Cauchy mutation operator, chaotic local search mechanism, opposition-based learning, mutation, and crossover strategies into the original SCA for global optimization and constrained practical engineering problems. The performance of MSCA was evaluated based on 23 continuous benchmark tasks and three constrained practical engineering problems.

Guo et al. (2020) proposed an improved SCA (QISCA) based on the optimal neighborhood, quasi-opposition learning, and quadratic interpolation strategies for solving global optimization and engineering problems. QISCA was tested based on 23 benchmark functions, 30 latest CEC2017 test functions, and 3 constrained engineering problems. Simulation results showed the effectiveness of QISCA in solving practical problems compared to 13 well-regarded optimization techniques existing in the literature.

The percentage of modified versions of SCA is given in Fig. 10. As it is shown in this figure, improved SCA has more percentage.

Fig. 10.

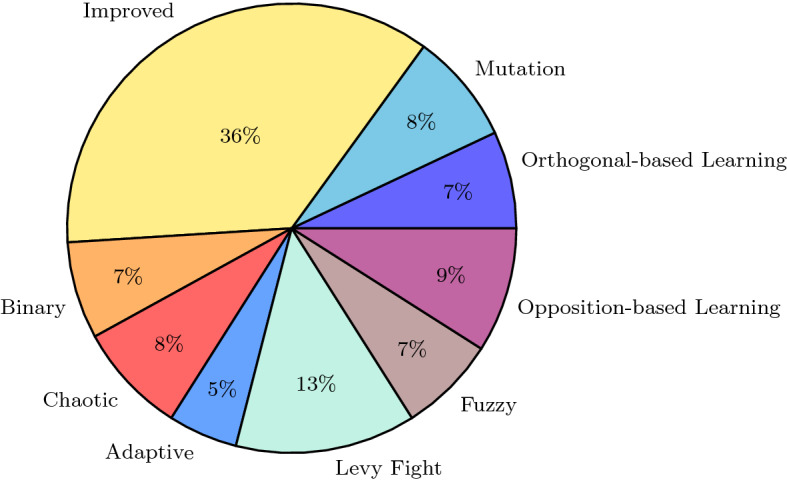
The modified versions of SCA

Multi-objective Sine Cosine Algorithm

There are some multi-objective versions of SCA that are proposed as shown in Table 4.

Table 4.

Multi-objective versions of SCA

Variant	Name	Application	Results	Author (Ref.)
Multi-objective SCA	MSCO	Non-smooth EELD problem	Robustness and efficiency of MSCO compared to other optimization techniques existing in the literature	Rizk-Allah et al. (2017)
	MO-SCA	Engineering design problems	Effectiveness and robustness of MO-SCA compared to other well-regarded algorithms in the literature	Tawhid and Savsani (2019b)
	MOSCA	Band selection of real HSI remote sensing images	Better performance of MOSCA compared to SFS, DSEBS, PSO, and SCA	Wan et al. (2019)
	MOSCA	Radial distribution networks	Effectiveness and robustness of MOSCA compared to LSA, BFOA, and MOPSO in terms of overall voltage profile and total power losses	Selim et al. (2019)
	MOSCA	Optimal DG allocation in radial distribution systems	Effectiveness of MOSCA compared to other well-known multi-objective algorithms	Raut and Mishra (2020b)
	EA-MSCA	Real-time task scheduling in multiprocessor systems	Superiority of EA-MSCA compared to some well-regarded optimization methods in most test cases	Abdel-Basset et al. (2021)

Rizk-Allah et al. (2017) proposed a multi-objective SCA (MSCO) for solving the non-smooth EELD problem. In MSCO, a pareto optimal concepts were used to find the set of non-dominated solutions. The MSCO algorithm was assessed based on 6-unit and 10-unit benchmarking test systems and results revealed the robustness and effectiveness of MSCO compared to other optimization techniques existing in the literature.

Tawhid and Savsani (2019b) introduced a multi-objective SCA (MO-SCA) for solving the multi-objective engineering design problems. Elitist non-dominated sorting approach and crowding distance strategy are introduced to determine non-domination levels and increase the coverage of Pareto optimal solutions obtained.

Wan et al. (2019) proposed a novel multi-objective SCA (MOSCA) for band selection of real HSI remote sensing images. The effectiveness of MOSCA was tested using two real HSI scenes such as the public Indian Pine HSI and the Unmanned Aerial Vehicle (UAV) HSI provided by the Intelligent Data Extraction and Analysis of Remote Sensing group (RSIDEA group). Simulation results showed the better performance of MOSCA compared to Sequential Forward Selection (SFS) algorithm, Dominant Set Extraction-Based Selector (DSEBS), PSO, and basic SCA.

Selim et al. (2019) proposed a multi-objective SCA (MOSCA) for optimum size and location of multiple Distribution STATic COMpensators (DSTATCOMs) in radial distribution networks. The performance of MOSCA was evaluated using IEEE 33-bus and IEEE 69-bus distribution systems taken into account 3 main objective functions such as total active power losses, total voltage deviation, and voltage stability index. Results showed the efficiency of MOSCA compared to LSA, BFOA, and MOPSO in terms of overall voltage profile and total power losses.

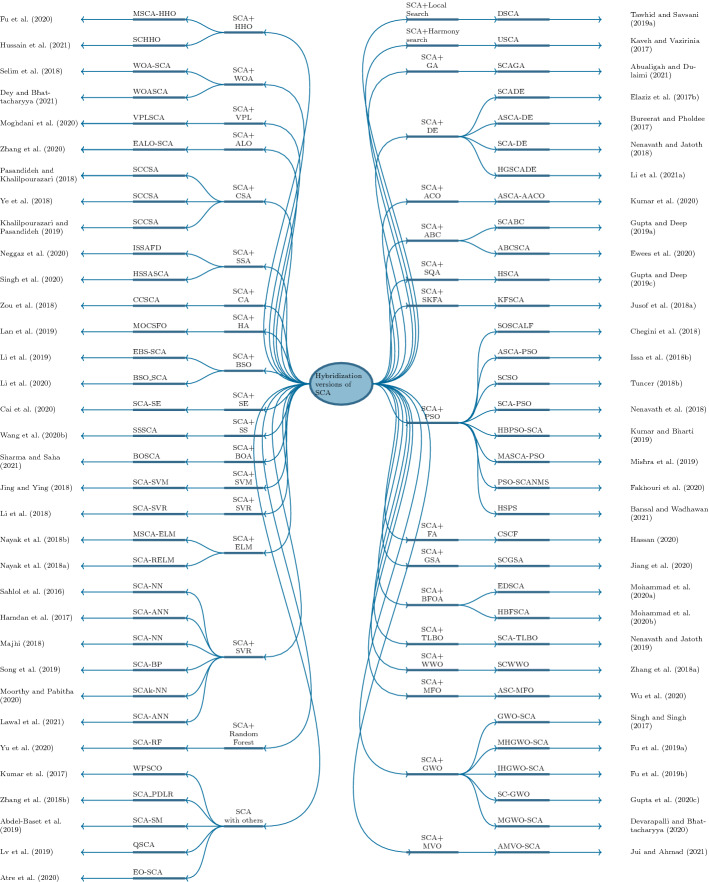
Hybridized versions of Sine Cosine Algorithm

This section describes the hybridized versions of SCA (Fig. 11). A summary of the main hybrid versions of SCA is illustrated in Table 5.

Fig. 11.

Hybridization versions of SCA

Table 5.

Hybridization versions of SCA

Variant	Name	Complexity	Application	Results	Author (Ref.)
SCA + Local Search	DSCA	$O(3\ast N\ast T\ast D)$	Traveling salesman problem	Performance of DSCA compared to other state-of-the-art algorithms	Tawhid and Savsani (2019a)
SCA + Harmony Search	USCA	$O(3\ast N\ast D\ast T)$	Tower crane selection and layout problem	Superiority of USCA compared to the original SCA, PSO, VPS, CBO, WOA, and SSA	Kaveh and Vazirinia (2017)
SCA + GA	SCAGA	–	Feature selection problem	SCAGA obtains good results compared to other related approaches existing in the literature	Abualigah and Dulaimi (2021)
SCA + DE	SCADE	–	Feature selection	SCADE gives better performance compared to ABC, SSO , and SCA	Elaziz et al. (2017b)
	ASCA-DE	$O(3N\ast D\ast T)$	Structural damage detection problem	Superiority of ASCA-DE compared to other meta-heuristics existing in the literature.	Bureerat and Pholdee (2017)
	SCA-DE	–	Visual tracking	Superiority of SCA-DE compared to PF, SIFT, PSO, and BA	Nenavath and Jatoth (2018)
	HGSCADE	$O(N+T\ast (N\ast D+2N+2))$	Global Optimization and Cylindricity Error Evaluation	Superiority of HGSCADE to other state-of-the-art approaches	Li et al. (2021a)
SCA + ACO	ASCA-AACO	–	Robot path planning	Efficiency of ASCA-AACO when compared with other existing optimization methodologies	Kumar et al. (2020)
SCA + ABC	SCABC	–	Image segmentation	SCABC showed its efficacy in determining the optimal thresholds of gray images	Gupta and Deep (2019a)
	ABCSCA	–	Multi-level thresholding image segmentation	Effectiveness of ABCSCA compared to ABC, SCA, WOA, SSA, GWO, SSO, FASSO, and WOAPSO	Ewees et al. (2020)
SCA + SQA	HSCA	–	Multilayer perceptrons	Superiority of HSCA compared to the classical SCA and other techniques	Gupta and Deep (2019c)
SCA + SKFA	KFSCA	$O(2\ast N\ast D\ast T)$	Global optimization problems	Effectiveness and superiority of KFSCA compared to the standard SCA in terms of accuracy and convergence speed	Jusof et al. (2018a)
SCA + PSO	SOSCALF	–	Global optimization problems	Superiority of SOSCALF compared to well-regarded optimization approaches	Chegini et al. (2018)
	ASCA-PSO	$O(2\ast N\ast D\ast T)$	Pairwise local sequence alignment	Good performance of ASCAPSO compared to the classical SCA and SW algorithm	Issa et al. (2018b)
	SCSO	–	Numerical functions optimization	SCSO has better results compared to ABC, KH, BBO, MFO, SCA, and HGWOSCA	Tuncer (2018b)
	SCA-PSO	–	Object tracking problems	SCA-PSO gives better capability to track an object when compared to MS, PF, PSO, BA, SCA, and HGSA	Nenavath et al. (2018)
	HBPSO-SCA	–	Feature selection	HBPSO-SCA provides better performance compared to BPSO, CBPSO, BMFO, BDFA, BWOA, SCA, and BABC	Kumar and Bharti (2019)
	MASCA-PSO	–	Brain tumor detection and classification	Effectiveness and superiority of MASCA-PSO compared to ABC, PSO, ASCA-PSO, SCA, SSA, GWO, WOA, and MFO	Mishra et al. (2019)
	PSO-SCANMS	$O(3N\ast D\ast T)$	Engineering design problems	Efficiency of PSO-SCANMS compared to PSO and other well-regarded techniques	Fakhouri et al. (2020)
	HSPS	–	Heterogeneous Fixed Fleet Vehicle Routing Problem	HSPS gives competitive results compared to other hybrid optimization algorithms in terms of convergence rate	Bansal and Wadhawan (2021)
SCA + FA	CSCF	–	Real-time engineering design problem	Efficiency and robustness of CSCF compared to ABC, PSO, FA, and SCA	Hassan (2020)
SCA + GSA	SCGSA	$O(N\ast D\ast T)$	Continuous optimization problems	Superiority of SCGSA compared to CGSA in terms of global optima and the speed of convergence	Jiang et al. (2020)
SCA + BFOA	EDSCA	–	Twin rotor system modeling	Better performance of EDSCA compared to the classical SCA	Mohammad et al. (2020a)
	HBFSCA	–	Global optimization problems	HBFSCA outperforms the classical SCA in terms of accuracy, convergence speed, and local optima avoidance	Mohammad et al. (2020b)
SCA + FOA	SCA_FOA	$O((N\ast D)+(T-N)\ast (N\ast D))$	Engineering problems	Efficiency of SCA_FOA compared to other competitive algorithms	Fan et al. (2020)
SCA + TLBO	SCA-TLBO	–	Visual tracking	Effectiveness of SCA-TLBO compared to other existing trackers	Nenavath and Jatoth (2019)
SCA + WWO	SCWWO	–	Global optimization problems	Efficiency of SCWWO compared to the original SCA, ABC, CS, DA, MFO, and WWO	Zhang et al. (2018a)
SCA + MFO	ASC-MFO	–	Parameter identification of hybrid active power filters	Better performance of ASC-MFO compared to some well-established algorithms	Wu et al. (2020)
SCA + GWO	GWO-SCA	–	Real life optimization problems	GWO-SCA yields highly competitive solutions compared to classical SCA, GWO, PSO, ALO, WOA, HAGWO, and MGWO	Singh and Singh (2017)
	MHGWO-SCA	$O(N\ast D\ast T)$	Fault diagnosis of rotating machinery	Superiority and availability of MHGWO-SCA compared to 7 relevant methods existing in the literature	Fu et al. (2019a)
	IHGWO-SCA	$O(3\ast N\ast D\ast T)$	Multi-step short-term wind speed prediction	Superiority and effectiveness of IHGWO-SCA compared to some relevant single and hybrid techniques	Fu et al. (2019b)
	SC-GWO	–	Engineering design problems	SC-GWO achieves competitive performance compared to other meta-heuristics existing in the literature	Gupta et al. (2020c)
	MGWO-SCA	$O(N\ast 2\ast D\ast T)$	Power system stabilizer parameters tuning	MGWO-SCA gives lesser overshoot values and faster settling time compared to the state-of-the-art optimization methods	Devarapalli and Bhattacharyya (2020)
SCA + MVO	AMVO-SCA	–	Continuous-time Hammerstein systems	AMVO-SCA achieves better performance in comparison with PSO, GWO, MVO, and SCA	Jui and Ahmad (2021)
SCA + HHO	MSCA-HHO	$O(3\ast N\ast D\ast T)$	SVM parameters tuning	Effectiveness and superiority of MSCA-HHO compared to other approaches	Fu et al. (2020)
	SCHHO	–	Feature selection problem	Efficiency of SCHHO compared to DA, SSA, GOA, GWO, WOA, SCA, and HHO	Hussain et al. (2021)
SCA + WOA	WOA-SCA	–	Voltage profile improvement	Superiority of WOA-SCA compared to WOA in minimizing the total power losses	Selim et al. (2018)
	WOASCA	–	Optimal scheduling in a micro-grid system	WOASCA provides robust and consistent results compared to SCA and WOA	Dey and Bhattacharyya (2021)
SCA + VPL	VPLSCA	$O(T\ast 5\ast N^2)+O(3\ast N\ast D)$	Global optimization problems	High performance of VPLSCA compared to CS, SSA, ALO, MFO, WOA, and SCA	Moghdani et al. (2020)
SCA + ALO	EALO-SCA	–	Abrupt motion tracking	Efficiency of EALO-SCA compared to other state-of-the-art optimization trackers	Zhang et al. (2020)
SCA + CSA	SCCSA	–	Global optimization problems	SCCSA gives competitive results in comparison with other state-of-the-art optimization algorithms	Pasandideh and Khalilpourazari (2018)
	SCCSA	–	Power joint optimal scheduling dispatch	Capability of SCCSA to control the voltage of nodes in micro-grid	Ye et al. (2018)
	SCCSA	$O(N\ast D\ast T)$	Global optimization problems	Superiority of SCCSA compared to other state-of-the-art optimization algorithms	Khalilpourazari and Pasandideh (2019)
SCA + SSA	ISSAFD	$O(N\ast D\ast T)$	Feature selection	ISSAFD provides better results compared to other well-regarded optimization techniques in terms of accuracy, sensitivity, and specificity	Neggaz et al. (2020)
	HSSASCA	$O(T\ast (N\ast D+Cost\ast N)+O(N\ast D\ast T)$	Engineering problems	Effectiveness and robustness of HSSASCA by providing the highest accuracies compared to other existing meta-heuristics	Singh et al. (2020)
SCA + CA	CCSCA	–	Optimal cascade hydropower stations	Efficiency of CCSCA in solving OOCHS	Zou et al. (2018)
SCA + HA	SCA-VNS	$O(N^2\ast D\ast T)$	Physicians and medical staff scheduling	Robustness and better performance of SCA-VNS compared to SCA, VNS, PSO, GA, and SA optimization algorithms	Lan et al. (2019)
SCA + BSO	EBS-SCA	$O(N\ast D\ast T)$	Global optimization problems	EBS-SCA yields better performance compared to other meta-heuristic algorithms in terms of global search ability and convergence speed	Li et al. (2019)
	BSO_SCA	–	Benchmark functions	BSO_SCA has considerable merit	Li et al. (2020)
SCA + SE	SCA-SE	–	Continuous Optimization Problems	Effectiveness of SCA-SE compared to other optimization approaches	Cai et al. (2020)
SCA + SS	SSSCA	–	Benchmark functions	SSSCA outperforms other states-of-the-art algorithms	Wang et al. (2020b)
SCA + BOA	BOSCA	$O(2\ast N\ast D\ast T)$	Benchmark functions and two real-world problems	Superiority of BOSCA compared to some other algorithms	Sharma and Saha (2021)
SCA + SVM	SCA-SVM	–	Fault diagnosis in analog circuit	Effectiveness of SCA-SVM compared to GS, GA, and PSO in terms of classification accuracy and iteration speed	Jing and Ying (2018)
SCA + SVR	SCA-SVR	–	Optimal SVR parameters tuning	Feasibility and reliability of SCA-SVR compared to other existing meta-heuristic methods	Li et al. (2018)
SCA + ELM	MSCA-ELM	–	Pathological brain detection	MSCA-ELM provides superior performance than conventional learning methods in term of classification accuracy	Nayak et al. (2018b)
	SCA-RELM	–	Automated diagnosis of pathological brain	Efficiency of SCA-RELM compared to state-of-the-art methods	Nayak et al. (2018a)
SCA + ANN	SCA-NN	–	Multi-Iayer perceptron	Superiority of SCA-NN compared to the basic NN by obtaining lower MSE and RMSE values	Sahlol et al. (2016)
	SCA-ANN	–	Load forecasting problem	Good performance and provides good fitting in both training and testing sets	Hamdan et al. (2017)
	SCA-NN	–	Breast cancer classification	Superiority of the SCA-NN compared to the recently reported classifiers in terms of accuracy and error rate	Majhi (2018)
	SCA-BP	$O(3\ast N\ast T\ast D)$	Image classification	SCA-BP provides better performance compared to some optimization algorithms in terms of classification accuracy	Song et al. (2019)
	SCAk-NN	–	Optimal detection of phishing attack	Effectiveness of SCAK-NN compared to Decision Tree and Naive Bayes in terms of accuracy, F-measure, and Mean Absolute Error	Moorthy and Pabitha (2020)
	SCA-ANN	–	Blast-induced ground vibration prediction	SCA-ANN gives better results compared to Gene expression programming (GEP) and adaptive neuro-fuzzy inference system (ANFIS) models	Lawal et al. (2021)
SCA + Random Forest	SCA-RF	$O(3\ast N\ast D\ast T)$	Determination of postblast ore boundaries	Predictive performance of the SCA-RF compared to SVR and ANN methods	Yu et al. (2020)
SCA with other methods	WPSCO	–	Maximum power point tracking	Reliability and robustness of WPSCO compared to state-of-the-art methods such as MFA and LIPSO	Kumar et al. (2017)
	SCA_PDLR	$O(N\ast 3\ast T\ast D)$	Benchmark functions	Effectiveness of SCA_PDLR compared with the classical SCA in terms of solution accuracy and convergence speed	Zhang et al. (2018b)
	SCA-SM	–	Numerical integration problems	Effectiveness and robustness of SCA-SM in calculating numerical value of definite integrals	Abdel-Baset et al. (2019)
	QSCA	$O(N\ast T\ast D)$	Benchmark functions	Superiority of QSCA compared to the classical SCA, ABC, PSO, BA, DA, and MFO	Lv et al. (2019)
	EO-SCA	–	Economic Load Dispatch	Robustness and aptness of EO-SCA in comparison with other well known optimization approaches	Atre et al. (2020)

Hybridization with local search

Tawhid and Savsani (2019a) proposed a discrete SCA (DSCA) based on the combination of SCA with 2-opt local search method as an attempt to solve TSP problems. The 2-opt local search method was used to update the solutions in each generation. The effectiveness of DSCA was tested based on 41 experimental benchmarks of symmetrical TSP taken from the TSPLIB library. The superiority of DSCA over the existing methods was demonstrated.

Hybridization with harmony search

Kaveh and Vazirinia (2017) proposed an Upgraded SCA (USCA) based on the hybridization of SCA with harmony search algorithm for solving the Tower Crane Selection and Layout Problem (TCSLP). Harmony search-based operator was used to deal with variable constraints and enhance the exploration, simultaneously. The performance of USCA was evaluated on several benchmark functions and results revealed the superiority of USCA compared to the original SCA and other state-of-the-arts optimization algorithms such as: PSO, VPS, CBO, WOA, and SSA.

Hybridization with differential evolution

Elaziz et al. (2017b) hybridized SCA and DE for the first time in the literature. DE operators were used to avoid the search from local optima stagnation. The performance of SCADE was assessed using eight datasets taken from the UCI machine learning site and compared to ABC, SSO, and SCA. It was demonstrated that SCADE gives better performance compared to other well-known techniques in terms of performance measures and statistical tests.

Bureerat and Pholdee (2017) introduced another hybridization of SCA and DE, called (ASCA-DE), for tackling the structural damage detection problem. The mutation operator of differential evolution and an adaptive strategy were integrated into SCA to avoid falling into local optima. The effectiveness of ASCA-DE was evaluated using several test problems for structural damage detection in comparison with DE, ABC, ACOR, ChSS, LCA, SA, TLBO, CMAES, ES, PSO, JADE, and classical SCA. The superiority of ASCA-DE was evident in their results.

Nenavath and Jatoth (2018) proposed a combined method, called SCA-DE, by hybridizing SCA with DE for solving single-objective optimization problems and visual tracking. In SCA-DE, SCA was used to emphasize the diversification, while DE was employed to focus on the intensification. The performance of SCA-DE was evaluated based on 23 uni-modal, multi-modal, and fixed dimension multi-modal benchmark functions and results showed that SCA-DE gives competitive results compared to the state-of-the-art meta-heuristics. SCA-DE was also applied for object tracking as a real thought-provoking case study and results showed its merits.

Hybridization with Ant Colony Algorithm

Kumar et al. (2020) hybridized an advanced SCA (ASCA) and advanced ACO (AACO) for solving the mobile robot path planning problem. SCA is used to find global best positions, while ACO is applied to find the next stand-point. The proposed ASCA-AACO was validated based on an unknown environment with static and dynamic obstacles. The results demonstrated its efficiency when compared with other existing optimization algorithms in this problem area.

Hybridization with artificial Bee Colony Algorithm

Gupta and Deep (2019a) developed a combined approach, called SCABC algorithm, using SCA and ABC for global optimization and image segmentation. The aim of this hybridization is to enhance the level of exploitation and exploration. The performance of SCABC was validated based on 23 benchmark functions and results showed its efficacy and robustness. Moreover, SCABC also used to solve the multilevel thresholding problem and results showed its efficacy in determining the optimal thresholds of gray images.

Ewees et al. (2020) introduced a hybrid method (ABCSCA) based on the hybridization of SCA with ABC for multi-level thresholding image segmentation. ABC was applied to reduce the search region, while the SCA algorithm was used to find the global optimal solution. The performance of ABCSCA was assessed using 19 images in low and high threshold levels in comparison with WOA, SSA, GWO, SSO, FASSO, WOAPSO, ABC, and SCA. The effectiveness of ABCSCA compared to other well-regarded methods was demonstrated by the authors in terms of PSNR and Structural Similarity Index (SSIM).

Hybridization with simulated quenching algorithm

Gupta and Deep (2019c) proposed a hybrid algorithm (HSCA) based on the hybridization of SCA with Simulated Quenching Algorithm (SQA) for global optimization and multilayer perceptrons.The leading guidance and simulated quenching algorithm were used to improve the search mechanism of SCA. HSCA was evaluated on 23 classical benchmark functions, standard and complex benchmark sets (IEEE CEC 2014 and CEC 2017), and 4 engineering optimization problems. It was also used for training multilayer perceptrons. Simulation results showed the superiority of HSCA compared to the classical SCA and other comparative optimization algorithms.

Hybridization with simulated Kalman filter algorithm

Jusof et al. (2018a) proposed a combined technique (KFSCA) based on the combination of SCA with Simulated Kalman Filter (SKF) algorithm for solving global optimization problems. SKF was integrated into SCA to provide a good balances between the exploration and exploitation. KFSCA was evaluated based on five benchmark functions and results showed its effectiveness and superiority compared to SCA and SKF in terms of accuracy and convergence speed.

Hybridization with particle swarm optimization algorithm

In the work of Issa et al. (2018b), an improved version of SCA (ASCA-PSO) is proposed for solving pairwise local sequence alignment problem. PSO was hybridized with SCA to enhance the exploitation of the search space. The performance of ASCA-PSO was tested based on biological protein sequences taken from the Swiss-Prot database with various lengths. Experimental results showed the good performance of ASCA-PSO compared to the classical SCA and Smith-Waterman (SW) alignment algorithm in terms of accuracy and computational time.

Tuncer (2018b) proposed a hybrid technique (SCSO) based on combining SCA with PSO for numerical functions optimization. The effectiveness of SCSO was evaluated using 14 well known unimodal and multimodal numerical benchmark functions in comparison with ABC, KH, BBO, MFO, SCA, and HGWOSCA. Simulation results showed that SCSO has better results in numerical functions optimization compared to other existing meta-heuristic approaches.

In the work of Nenavath et al. (2018), hybrid approach (SCA-PSO) based on the hybridization of SCA with PSO was proposed for solving global optimization problems. SCA-PSO combines the exploitation capability of PSO and exploration capability of SCA to obtain optimal global solutions. SCA-PSO was tested using 23 classical, CEC 2005 and CEC 2014 benchmark functions and results showed its efficiency compared to the state-of-the-art meta-heuristics. SCA-PSO was also applied to solve object track as a real thought-provoking case study and results demonstrated that SCA-PSO gives better capability to track an object when compared to other trackers such as Mean-shift (MS), PF, PSO, BA, SCA, Hybrid GSA (HGSA).

Kumar and Bharti (2019) proposed a hybrid method (HBPSOSCA) based on the hybridization of SCA with binary Binary PSO for feature selection problem. A cross breed approach of binary PSO was used to enhance the convergence performance of SCA. The performance of HBPSOSCA was validated based on seven real-life scientific datasets taken from the UCI machine learning repository and gene expression model selector (GEMS). Experimental results revealed that HBPSOSCA provides better performance compared to some competitive methods such as BPSO, C-BPSO, BMFO, BDFA, BWOA, SCA, BABC.

Mishra et al. (2019) proposed a modified adaptive SCA integrated with PSO (MASCA-PSO) based local linear radial basis function neural network (LLRBFNN) model. The application area of this paper was tumor detection and classification. PSO was combined with Adaptive SCA to provide a good balance between the exploitation and exploration. The performance of MASCA-PSO was tested using Dataset-160 and Data-255 taken from Harvard medical school of architecture.

In (Chegini et al. 2018), a hybrid algorithm (SOSCALF) was proposed combining SCA, PSO, and Lévy flight distribution for solving optimization problems. The effectiveness of SOSCALF was evaluated using 23 standard benchmark functions and 8 real constrained engineering problems in comparison with other PSO variants and well-known algorithms proposed in recent years. Simulation results demonstrated the superiority and effectiveness of SOSCALF when compared with well-regarded optimization approaches.

In (Fakhouri et al. 2020), PSOSCANMS was proposed hybridizing SCA, PSO, and Nelder–Mead simplex (NMS) optimization technique for solving engineering design problems. The mathematical formulations of both PSO and NMS were applied to make the search space more effective and ensure a good balance between the exploitation and exploration. The performance of PSOSCANMS was evaluated using 23 well-known unimodal and multimodal benchmark functions and 2 engineering design problems (compression spring design and welded beam design).

Hybridization with gravitational search algorithm

Jiang et al. (2020) proposed a hybrid method (SCGSA) by hybridizing SCA with Chaotic SGA (CGSA) for solving continuous optimization problems. Chaotic gravitational constants of CGSA were used to enhance the exploration ability and escape from local optima stagnation. The performance of SCGSA was tested based on 30 benchmark functions (CEC 2014) and results showed its efficiency compared to CGSA in terms of global optima and speed of convergence.

Hybridization with bacterial foraging algorithm

Mohammad et al. (2020a) proposed an improved SCA, called Elimination-Dispersal SCA (EDSCA), based on the combination of SCA with Bacterial Foraging Algorithm (BFA) for dynamic modeling of a twin-rotor system. The ED phase of BFA was integrated into the classical SCA to help search agents for solving the local optima problem. The performance of EDSCA was evaluated based on various CEC2014 benchmark functions with different fitness landscapes and features. Simulation results revealed the better performance of EDSCA compared to the classical SCA by obtaining less modeling error and better dynamic response.

Hybridization with teaching–learning-based optimization algorithm

Nenavath and Jatoth (2019) proposed SCA–TLBO method using SCA and TLBO for solving global optimization problems and visual tracking. The idea of TLBO was integrated into SCA to escape from local optima and enhance its search ability. SCA-TLBO was evaluated based on 23 eminent test functions and results showed its performance compared to other existing algorithms. Additionally, SCA-TLBO was used for visual tracking as a real thought-provoking case study and results revealed its effectiveness when compared to other existing trackers.

Hybridization with water wave optimization algorithm

Zhang et al. (2018a) proposed a hybrid method (SCWWO) using SCA and Water Wave Optimization (WWO) algorithm for global optimization. WWO was combined with SCA to obtain global optimal solutions. The effectiveness of SCWWO was evaluated using 14 benchmark test functions in comparison with the original SCA, ABC, CS, DA, MFO, WWO. Simulation results demonstrated the feasibility and efficiency of SCWWO compared to other well-regarded meta-heuristics existing in the literature.

Hybridization with Grey Wolf optimizer

In (Singh and Singh 2017), a hybrid method (GWO-SCA) was proposed for solving the classical and real-life optimization problems. Another hybrid of these two algorithms was done by Fu et al. (2019a), in which MHGWOSCA benefiting from search capabilities of SCA, GWO, and mutation operator for fault diagnosis of rotating machinery. The effectiveness of MHGWOSCA was tested using vibration signals with different fault locations and sizes taken from Bearings Data Center of Case Western Reserve University. Experimental results showed the superiority and availability of MHGWOSCA compared to a number of other algorithms.

Another similar work can be found in Fu et al. (2019b), in which IHGWOSCA was proposed. The IHGWOSCA algorithm was used for multi-step short-term wind speed prediction. IHGWOSCA was investigated to optimize the parameters of Phase Space Reconstruction (PSR)and Extreme Learning Machine (ELM) successfully. The performance of IHGWOSCA was evaluated based on 7 data sets from Sotavento Galicia and Inner Mongolia and results showed its effectiveness compared to some relevant single and hybrid techniques.

In Gupta et al. (2020c), SC-GWO was proposed using SCA with GWO for solving engineering design problems. The social and cognitive components of GWO were integrated into SCA to maintain a good balance between exploration and exploitation. The performance of SC-GWO was validated based on 13 well-known benchmark functions. SC-GWO was also used to determine the optimal setting for over-current relays. Another similar work was done by Devarapalli and Bhattacharyya (2020), in which MGWO-SCA was proposed for tuning the power system stabilizer parameters of an interconnected multi-machine power system. The effectiveness of MGWO-SCA was evaluated based on benchmark model of two area four generator multi-machine system. Simulation results showed that MGWO-SCA gives lesser overshoot values and faster settling time compared to the state-of-the-art optimization methods.

Hybridization with Harris Hawks optimization algorithm

In the work of Fu et al. (2020), MSCAHHO was proposed using SCA, HHO, and mutation operator to tune the parameters of Support Vector Machine (SVM) for fault classification. MSCAHHO was evaluated using vibration signals collected from Bearings Data Center of Case Western Reserve University and results showed its effectiveness and superiority when compared with some relevant techniques existing in the literature.

Hybridization with Whale optimization algorithm

WOA-SCA was proposed by Selim et al. (2018) for voltage profile improvement in active distribution networks. WOA was combined with SCA to raise its convergence. The performance of WOA-SCA was evaluated with the basic WOA based on IEEE 33-bus and 69-bus distribution systems. Simulation results demonstrated the superiority of WOA-SCA compared to the traditional WOA in minimizing the total power losses.

Hybridization with volleyball premier league algorithm

In Moghdani et al. (2020) VPLSCA was proposed hybridizing SCA with Volleyball Premier League (VPL) algorithm. SCA operators were used in the learning phase to obtain global optimal solutions. The effectiveness of VPLSCA was evaluated using 25 benchmark function and several engineering problems. Simulation results indicated the high performance of VPLSCA compared to some well-known meta-heuristics such as CS, SSA, ALO, MFO, WOA, and classical SCA.

Hybridization with ant lion optimizer algorithm

Zhang et al. (2020) developed a hybrid approach, called EALO-SCA, based on the hybridization of SCA with Extended ALO (EALO) for abrupt motion tracking. EALO was integrated into SCA to enhance the global exploration ability. The robustness of EALO-SCA was evaluated based on 12 video sequences and results showed its efficiency compared to other state-of-the-art optimization trackers.

Hybridization with Salp Swarm Algorithm

In Neggaz et al. (2020), a novel feature selection method, called ISSAFD, was proposed combining SSA, SCA, and Disrupt operator (DO). The efficiency of ISSAFD was validated based on 2O datasets in comparison with GA, PSO, ALO, GWO, and, SSA, SCA. It was demonstrated that ISSAFD is superior compared to other well-regarded optimization techniques in terms of accuracy, sensitivity, specificity, and the number of selected features. Another similar hybrid can be found in Singh et al. (2020) called HSSASCA.

Hybridization with cultural algorithm

Zou et al. (2018) proposed a hybrid method (CCSCA) based on the hybridization of SCA with Cultural Algorithm (CA) for solving optimal operation of cascade hydropower stations (OOCHS). CA which includes three components (i.e. population space, belief space, and communication protocol) is adopted as the evolution process of the population. The effectiveness of CCSCA was validated using as case study 5 hydropower stations located in the lower reaches of Yalong river. Simulation results showed the efficiency of CCSCA in solving OOCHS.

Hybridization with Hungarian algorithm

Lan et al. (2019) proposed a combined optimization algorithm (SCA-VNS) based on the incorporation of variable neighborhood search (VNS) of Iterated Hungarian Algorithm (IHA) into SCA for solving the physicians and medical staff scheduling problem in outpatient department of large hospitals with multiple branches. The performance of SCA-VNS was evaluated based on 22 instances with different number of physicians and branches. Experimental results demonstrated the robustness and better performance of SCA-VNS compared to SCA, VNS, PSO, GA, and SA algorithms.

Hybridization with brain storm optimization algorithm

Li et al. (2019) developed an enhanced hybrid technique (EBS-SCA) based on the hybridization of SCA with Brain Storm Optimization Algorithm for solving global optimization problems. EBS strategy is introduced in EBS-SCA to enhance the diversity of the population and the balance between exploration and exploitation.

Hybridization with support vector machine

In the work of Jing and Ying (2018), SCA-SVM was proposed for fault diagnosis in analog circuits. The performance of SCA-SVM was evaluated using four-op amp biquad high-pass filter circuit in comparison with Grid Search (GS), GA, and PSO. Simulation results revealed the effectiveness of SCA-SVM compared to GS, GA, and PSO in terms of classification accuracy and iteration speed.

Hybridization with support vector regression

In Li et al. (2018), SCA-SVR was proposed for optimal tuning of the penalty and kernel parameters in SVR. The performance of SCA-SVR was evaluated based on commonly used benchmark datasets in comparison with Grid Search-SVM (GS-SVR), PSO-SVR, ABC-SVR, KHA-SVR, GWO-SVR, FPA-SVR, SSO-SVR, ALO-SVR, and MVO-SVR. Computational results showed SCA-SVR’s feasibility and reliability compared to other existing meta-heuristic methods.

Hybridization with extreme learning machine

Nayak et al. (2018a) proposed a hybrid classification technique (SCA-RELM) based on the hybridization of SCA with Regularized ELM for automated diagnosis of pathological brain. The performance of SCA-RELM was evaluated using 3 well-studied datasets and results showed its efficiency and superiority compared to state-of-the-art methods.

Hybridization with neural network

In Sahlol et al. (2016) SCA-NN was proposed hybridizing SCA and NN for optimizing the multi-layer perceptron neural network. Another similar work was done by Hamdan et al. (2017), in which a combined method based on the combination of SCA with ANN was proposed for solving the load forecasting problem. The effectiveness of the combined method was tested using data of Temperature (${}^{\circ }$C), relative humidity (%) and electricity load demand (MW) collected for 3 years, i.e. 2014, 2015, and 2016 from Sharjah Electricity and Water Authority (SEWA). Experimental results showed that the combined method provides good fitting in both training and testing sets.

In Majhi (2018), another hybrid SCA-NN was proposed for breast cancer classification. The performance of SCA-NN was evaluated based on Wisconsin Hospital data set taking into account 2 metrics including Correct Classification Rate (CCR) and Average Squared Classification Error (ASCE). Experimental results demonstrated the superiority of the SCA-NN compared to the recently reported classifiers in terms of accuracy and error rate.

Song et al. (2019) proposed the hybrid SCA-BP for images classification. The performance of SCA-BP was evaluated using a bunch of real images in comparison with GA-BP and PSO-BP. Simulation results demonstrated that SCA-BP provides better performance compared to some optimization algorithms in terms of classification accuracy.

Hybridization with other algorithms

Kumar et al. (2017) proposed WPSCO hybridizing SCA with Weibull distribution method and Pareto distribution function for the maximum power point tracking (MPPT) problem. The performance of WPSCO was evaluated over the PV fed battery load by using a boost converter and results showed its reliability and robustness compared to state-of-the-art methods such as MFA and LIPSO.

In the work of Zhang et al. (2018b), an efficient algorithm (SCA_PDLR) based on the hybridization of SCA with population diversity based local refinement strategy (PDLR) was proposed. The performance of SCA_PDLR was validated based on CEC’17 benchmark functions and results showed its effectiveness when compared with the classical SCA in terms of solution accuracy and convergence speed.

Abdel-Baset et al. (2019) proposed a combined optimization approach (SCA-SM) based on the combination of SCA with Simpson method (SM) for solving numerical integration problems. The performance of SCA-SM was tested using several examples (single and multiples) and results showed the effectiveness and robustness of SCA-SM in calculating numerical value of definite integrals.

The percentage of hybridized versions of SCA with meta-heuristics, SVM, SVR, ELM, ANN, and other algorithms is given in Fig. 12. As it is shown in this figure, meta-heuristics have more percentage.

Fig. 12.

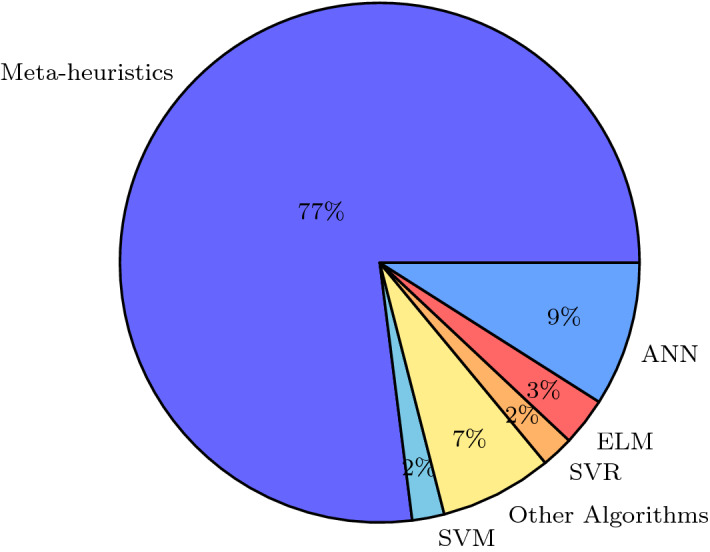
The hybridized versions of SCA

Applications of the Sine Cosine Algorithm

Since the proposal, SCA has been employed to solve diverse problems in both science and industry. As application areas, we can find electrical engineering (e.g. economic load dispatch, optimal power flow, distributed generators allocation, optimal load frequency control), computer engineering (e.g. wireless sensor nodes localiser, clustering, optimal camera placement, capacitated vehicle routing problem), classification (e.g. feature selection, image classification, Sonar target classification, pathological brain detection), and many others ( e.g. higher-order continuous systems, measuring similarity of COVID-19, oil consumption forecasting, block-based motion estimation, visual tracking, conceptual design of automobile components). Some of SCA applications are summarized in Table 6 and their details are given below.

Table 6.

SCA applications areas

Class	Problem	Author (Ref.)
Electrical	Economic Load Dispatch	Rizk-Allah and El-Sehiemy (2018)
Engineering		Gonidakis and Vlachos (2019), citeabdel2019optimal
		Guesmi et al. (2020), Atre et al. (2020)
		Rizk-Allah (2021)
	Distributed generators allocation	Kamel et al. (2019), Raut and Mishra (2020a)
	Optimal power flow	Attia et al. (2018)
	Photo-voltaic Power System	Sahu et al. (2019), Chen et al. (2019)
	Radial Distribution Networks	Ismael et al. (2017), Ang and Leeton (2019)
		Abdelsalam (2020), Raut and Mishra (2019)
		Raut and Mishra (2021)
	Optimal Load Frequency Control	Mishra et al. (2018) , Babaei and Safari (2020)
	Optimal PMU Placement	Laouamer et al. (2018)
	Hybrid Power Generation System	Algabalawy et al. (2018)
	Unit Commitment	de Oliveira et al. (2018), Reddy et al. (2018)
		Bhadoria et al. (2019)
	Optimal Reach Setting of Quadrilateral Relays	Shukla et al. (2020)
	Bend Photonic Crystal Waveguides	Mirjalili et al. (2020)
	Optimal Allocation of Capacitor Banks	Abdelsalam and Mansour (2019)
	Short-Term Hydrothermal Scheduling	Das et al. (2018)
	Partial shading detection	Chandrasekaran et al. (2020)
Control	Optimal parameters control	Ghayad et al. (2019), Bhookya and Jatoth (2019),
Engineering		Hekimoğlu (2019), Bhuyan et al. (2019)
		Sahu et al. (2020), Gorripotu et al. (2020)
		Mehra et al. (2020), Wu et al. (2020)
		Devarapalli and Bhattacharyya (2020), Fu et al. (2020)
		Devarapalli and Bhattacharyya (2021), Sahu et al. (2021)
		Li et al. (2018),
Computer	Lifetime Enhancement of Wireless Sensor Networks	Pandey et al. (2018)
Engineering	Optimal Re-Entry Trajectory Planning	Banerjee and Nabi (2017)
	Optimal Camera Placement	Fatlawi et al. (2018)
	Wireless sensor nodes localiser	Hamouda and Abohamama (2020)
	Cross layer resource allocation in wireless network	Praveena and Nagaraja (2021)
	Combinatorial Testing	Altmemi et al. (2020), Zamli et al. (2020)
	Optimal virtual machine placement	Gharehpasha and Masdari (2020)
	Capacitated vehicle routing problem	Yang et al. (2020), Bansal and Wadhawan (2021)
	Clustering	Kuo et al. (2021)
	Robot path planning	Kumar et al. (2020)
Classification	Feature Selection	Hafez et al. (2016), Elaziz et al. (2017b)
		Kumar and Bharti (2019), Belazzoug et al. (2019)
		Taghian and Nadimi-Shahraki (2019), Neggaz et al. (2020)
		Abualigah and Dulaimi (2021), Hussain et al. (2021)
	Image classification	Song et al. (2019)
	Sonar target classification	Wang et al. (2020d)
	Brain tumor detection and classification	Mishra et al. (2019)
	Pathological brain detection	Nayak et al. (2018b), Nayak et al. (2018a)
	Breast cancer classification	Majhi (2018)
Image	Manuscript Image Binarization	Elfattah et al. (2016)
Processing	Curve Fitting	Amat et al. (2019)
	Image segmentation	Gupta and Deep (2019a), Ewees et al. (2020)
		Chouksey and Jha (2020), Khrissi et al. (2021)
	Hyperspectral image	Wang et al. (2020c)
	Multi focus image fusion	Singh and Kaushik (2021)
Other	Global Sequence Alignment	Issa et al. (2018a)
Applications	Higher-Order Continuous Systems	Singh (2017)
	Conceptual design of automobile components	Yıldız et al. (2020)
	Multimedia content distribution in cloud environment	Krishna Priya et al. (2020)
	Improving energy production of wind plant	Suid et al. (2019)
	Measuring similarity of COVID-19	Issa (2021)
	Discrete sizing optimization of truss structures	Gholizadeh and Sojoudizadeh (2019)
	Design and manufacturing optimization problems	Rizk-Allah (2018)
	Multiple hydro-power reservoirs operation	Feng et al. (2020a), Feng et al. (2020b)
	Feed-forward neural network (FNN) training	Bairathi and Gopalani (2017)
	Prediction of osteoporosis	Ewees et al. (2020)
	Predicting intentions of Students for master programs	Lin et al. (2019)
	Oil Consumption Forecasting	Al-Qaness et al. (2018)
	Block-based motion estimation	Dash and Rup (2018)
	Set covering problem	Fernández et al. (2018)
	Knapsack problem	Pinto et al. (2019)
	Structural damage detection problem	Bureerat and Pholdee (2017)
	Visual tracking	Nenavath and Jatoth (2018), Nenavath and Jatoth (2019)
	Benchmark Functions	Tuncer (2018b), Tuncer (2018a)
		Liu (2018), Zhang et al. (2018b)
		Suid et al. (2018), Cheng and Duan (2019)
		Rizk-Allah (2019) , Lv et al. (2019)
		Li et al. (2019), Khalilpourazari and Pasandideh (2019)
		Guo et al. (2019), Gupta et al. (2020b)
		Li et al. (2020), Cai et al. (2020)
		Wang et al. (2020a), Wang et al. (2020b)
		Behera et al. (2020), Gao et al. (2020)
		Sharma and Saha (2021), Xian et al. (2021)

Electrical engineering

Economic load dispatch

Gonidakis and Vlachos (2019) used SCA for solving the Combined Economic and Emission Dispatch (CEED) in power system. The performance of SCA was tested using 3 test systems with different characteristics in comparison with Lagrange’s Method (LM), SA, and PSO. Simulation results showed that SCA provides high-quality results and outperforms other well-known optimization methods existing in the literature.

Photovoltaic power system

Sahu et al. (2019) applied SCA to optimize the factors of PID and FOPID controllers in photovoltaic (PV) system. Oscillation, time response, settling time, voltage, current and power of the system parameters were used to evaluate the performance of SCA and results demonstrated its effectiveness compared to P&O and PID methods by achieving the maximum power.

Radial distribution networks

Abdelsalam (2020) used SCA for optimal locations and sizes of distributed energy resources (DERs) in various configurations of radial distribution networks. The effectiveness of SCA was evaluated based on IEEE 33-bus and IEEE 69-bus radial distribution networks in comparison with Improved Analytical (IA) method. Simulation results showed the better performance of SCA in comparison with other methods by achieving the maximum saving and maximum reduction of power losses of 61.3% and 69.2% for IEEE 33-bus and 69-bus networks, respectively.

Ang and Leeton (2019) used SCA for optimal size and placement of Distributed Generation (DG) in radial distribution networks. The performance of SCA was tested based on 15 bus system, 33 bus system, 69 bus system, and 85 bus system by considering single and double DG units. Simulation results showed the performance and robustness of SCA compared to ABC, Voltage Sensitivity Index (VSI), and Index Vector (IV) methods in terms of power loss reduction and voltage profile improvement. SCA was also used for solving the problem of optimal selection of conductors in Egyptian radial distribution networks in Ismael et al. (2017).

Optimal load frequency control

Babaei and Safari (2020) used SCA for optimizing the parameters of fractional-order proportional-integral-derivative (FOPID) controller for the load frequency control (LFC) system. The performance of GOA was validated in single and two-area LFC system with EV aggregators with time-varying delays. Experimental results showed the superiority of SCA compared to PSO algorithm by obtaining fewer frequency variations.

Mishra et al. (2018) applied SCA-based PID controller for the LFC of power system. The performance of SCA was validated using different test scenarios with random load perturbations and results showed the robustness and superiority of SCA-PIDN controller compared to other controller methods.

Optimal PMU placement

Laouamer et al. (2018) used SCA for solving the optimal Phasor Measurement Unit (PMU) placement problem. The performance of SCA was evaluated based on 3 standards IEEE-9,14 and 30-buses and results revealed its effectiveness to obtain optimal number and placement of PMU.

Hybrid power generation system

Algabalawy et al. (2018) used SCA Optimal Design of Hybrid Power Generation. The performance of SCA was evaluated using 2 scenarios under different weather conditions. Simulation results revealed the efficiency and performance of SCA compared to CS, FA, and WOA in terms of total annual cost and system emissions.

Unit commitment

de Oliveira et al. (2018) used SCA for solving the Thermal Unit Commitment (TUC) problem. The performance of SCA was evaluated using two test systems of 4 and 10 units and results showed the effectiveness and applicability of SCA for solving the TUC problem.

Bhadoria et al. (2019) employed SCA for solving the unit commitment problem of the electric power system. The effectiveness of SCA was evaluated based on various small and medium level power systems including 4, 5, 6, 7, 10, 19, 20 and 40 unit test systems. Simulation results showed the efficacy and feasibility of SCA when compared with GWO, PSO, DE, FEP, and WOA. Another similar work in the area of Optimal Reach Setting of Quadrilateral Relays can be found in Shukla et al. (2020).

Bend photonic crystal waveguides

Mirjalili et al. (2020) used SCA for solving the Bend Photonic Crystal Waveguides (PCW) designing problem. Experimental results showed the efficiency and robustness of SCA compared to the classical method by providing optimal design of bend PCW. Another similar work in the area of Optimal Allocation of Capacitor Banks can be found in Abdelsalam and Mansour (2019).

Short-term hydrothermal scheduling

Das et al. (2018) employed SCA for solving the short-term hydrothermal scheduling problem in power system. The performance of SCA was evaluated using six different test systems with different cost functions in comparison with CSA, MCSA, IMO, QRIMO, MFO,DA, WOA, and ALO algorithms. Experimental results demonstrated that SCA provides superior results compared to state-of-the-art.

Control engineering

Optimal parameters control

Ghayad et al. (2019) used SCA and GSA for optimal parameters of PI controller under different disturbances. The performance of SCA and GSA were validated using 3 different disturbances namely three phase fault, step-change in AC voltage of system, and step-change in reference values. Experimental results showed that SCA has better results than GSA in terms of reactive power deviation, but GSA has better performance in terms of settling time.

Bhookya and Jatoth (2019) used SCA for tuning the PID controller parameters of an Automatic Voltage Regulator (AVR) system. The effectiveness of SCA was tested taking into account the overshoot, rising time, settling time, and steady-state error of the system as performance metrics. Experimental results revealed the performance and robustness of GOA compared to other FOPID and PID controller design methods for AVR system. Another similar work can be found in Hekimoğlu (2019).

Gorripotu et al. (2020) used a SCA-based PD-PID controller for frequency control of hybrid power system. The performance of SCA-based PD-PID controller was evaluated under 3 different cases: step load disturbance, band-limited noise, and step disturbance with noise at the wind system. Simulation results demonstrated the effectiveness of SCA-based PD-PID controller compared to other standard techniques.

A comparative analysis of an autonomous hybrid microgrid (AHM) system with controllable loads for demand-side management (DSM) using SCA based PID controller was presented in the work of Bhuyan et al. (2019). The performance of SCA based PID controller was validated using three different scenarios of the renewable source and load variations and results showed that SCA based PID controller gives better performance compared to PSO based PID controller in most of the scenarios.

Mehra et al. (2020) used SCA-based PID controller for level control design of three-tank system by minimizing the integral-of-squared error (ISE). Experimental results showed the efficiency of SCA-based PID controller compared to other controller methods.

Computer engineering

Lifetime enhancement of wireless sensor networks

Pandey et al. (2018) SCA for maximizing the lifetime of Wireless Sensor Networks (WSNs) in routing and clustering. The performance of SCA was evaluated by varying the number of sensors from 100 to 800 and moving the base station at different locations in comparison with GA, PSO, and least distance clustering (LDC) algorithms. Experimental results showed that SCA enhances the lifetime of sensors more than other algorithms and works better when moving the base station at different locations.

Optimal re-entry trajectory planning

Banerjee and Nabi (2017) used SCA for solving the re-entry trajectory problem for space shuttle vehicle. Maximizing the cross-range along with satisfying certain boundary conditions is selected for the problem. Simulation results showed that SCA gives good results in terms of simplicity and computational complexity.

Optimal pamera placement

Fatlawi et al. (2018) applied SCA for obtaining optimal placement of cameras. The effectiveness of SCA was validated in several scenarios and results showed the superiority of SCA compared to GA and PSO in terms of maximum coverage and better placement of cameras.

Classification

Feature selection

Hafez et al. (2016) used SCA for solving the channels feature selection problem. The classification accuracy and feature size reduction were used as evaluation metrics to validate the performance of SCA. The performance of SCA was evaluated based on 18 datasets from the UCI machine learning repository and results showed the effectiveness and robustness of SCA compared to GA and PSO algorithms by providing minimum selected features set with maximum classification accuracy.

Belazzoug et al. (2019) proposed an improved SCA (ISCA) for feature selection in text categorization. ISCA takes into account the position of the best solution found so far and a given random position from the search space to generate a new solution. The effectiveness of ISCA was validated using 9 text datasets in comparison with GA, ACO, MFO, original SCA and some of its variants and results showed its high performance in solving the text categorization problem.

Image processing

Manuscript image binarization

Elfattah et al. (2016) used SCA for Arabic manuscript image binarization. The algorithm was compared with Otsu’s and Niblack’s methods. Computational results demonstrated the robustness and superiority of SCA compared to the famous binarization methods existing in the literature.

Curve fitting

Amat et al. (2019) used SCA for solving the curve fitting problem. The main objective of SCA is to find the best middle control points by minimizing the sum square errors (SSE) which is considered as objective function. Simulation results showed a better performance of SCA compared to least square method (LSM).

Other applications

Global sequence alignment

Issa et al. (2018a) used SCA for solving pairwise global sequence alignment problem. The performance of SCA was tested based on the sequence of protein in humans and mice. It was shown that SCA gives better results compared to Dynamic Programming (DP) approach in terms of accuracy and execution time.

Higher-order continuous systems

In the work of Singh (2017), SCA was applied to derive a reduced-order model (ROM) of higher-order continuous system (HOCS). The performance of SCA was evaluated using the ninth-order boiler system and results showed that SCA outperforms some existing algorithms such as PSO, Elephant herding optimizations (EHO), Luus–Jaakola (LJ), and Nelder-Mead Simplex (NMS) algorithms.

The percentage of applications of SCA for solving different optimization problems is given in Fig. 13. As it is shown, SCA has been mostly used in the field of Electrical Engineering with 25%.

Fig. 13.

The applications of SCA

Results and comparisons

In this section, the SCA algorithm is evaluated and compared with six well-known meta-heuristics such as GA, PSO, FA, PFA, BA, and GSA. Three groups of mathematical test functions (i.e. uni-modal, multi-modal, and composite) are selected in the experiments. Each of the test functions is solved using 30 search agents and 500 iterations. As presented in Table7, the simulation results revealed that the SCA algorithm gives very competitive results on the majority of the test cases. Firstly, the SCA algorithm gives better performance on 3 out of 7 uni-modal test functions (F1, F2, and F7). Considering the proprieties and characteristics of the uni-modal functions, these results demonstrated that SCA benefits from high exploitation ability and convergence. Secondly, for the multi-modal test functions, it can be observed that SCA provides excellent results on 4 out of 6 test functions (F9, F11, F12, and F13). These results demonstrate the efficiency of SCA to avoid the search from local optima stagnation during optimization. Finally, the SCA algorithm gives better results on the composite test functions with challenging search spaces. SCA algorithm ensures a good balance between intensification and diversification.

Table 7.

The average results for solving benchmark functions

Function	GA	PSO	FA	PFA	BA	GSA	SCA
F1	0.8078	0.0003	0.0004	0.2111	1.0000	0.0000	0.0000
F2	0.5406	0.0693	0.0177	0.9190	1.0000	0.0100	0.0000
F3	0.5323	0.0157	0.0000	0.2016	1.0000	0.0016	0.0371
F4	0.8837	0.0936	0.0000	0.8160	1.0000	0.1177	0.0956
F5	0.6677	0.0000	0.0000	0.0813	1.0000	0.0000	0.0005
F6	0.7618	0.0004	0.0004	0.2168	1.0000	0.0000	0.0002
F7	0.5080	0.0398	0.0009	0.3587	1.0000	0.0021	0.0000
F8	1.0000	1.0000	1.0000	1.0000	0.0000	1.0000	1.0000
F9	1.0000	0.3582	0.0190	0.8714	0.4248	0.0222	0.0000
F10	0.8323	0.1045	0.0000	1.0000	0.8205	0.1569	0.3804
F11	0.7679	0.0521	0.0074	0.2678	1.0000	0.4011	0.0000
F12	0.4573	0.0000	0.0000	0.0008	1.0000	0.0000	0.0000
F13	0.6554	0.0000	0.0000	0.0187	1.0000	0.0000	0.0000
F14	0.4201	0.1816	0.0000	0.3786	1.0000	0.0961	0.3908
F15	0.0000	0.3016	0.4395	0.2235	1.0000	0.2926	0.0230
F16	0.0000	0.0427	0.5298	0.2652	0.3572	1.0000	0.0497
F17	0.1093	0.0249	0.7093	0.5197	0.8189	0.7887	0.0000
F18	0.0000	0.1772	0.0723	0.1310	1.0000	0.8018	0.0129
F19	0.0192	0.7727	0.8176	0.3192	1.0000	0.9950	0.0000

To confirm and decide about the significance of the results, a non-parametric statistical Wilcoxon test is used at 5% significance level and the P-values obtained are presented in Table 8. Note that N/A is written for the best algorithm in each test function which means Not Applicable. These results demonstrate strongly that the efficiency of SCA is statistically significant in comparison with other optimization algorithms.

Table 8.

The P-values of the Wilcoxon ranksum test over all runs

Function	GA	PSO	FA	PFA	BA	GSA	SCA
F1	0.002165	0.002165	0.002165	0.002165	0.002165	0.002165	N/A
F2	0.002165	0.002165	0.002165	0.002165	0.002165	0.002165	N/A
F3	0.002165	0.002165	N/A	0.002165	0.002165	0.008658	0.004329
F4	0.002165	0.002165	N/A	0.002165	0.002165	0.002165	0.002165
F5	0.002165	0.002165	0.002165	0.002165	0.002165	0.681818	N/A
F6	0.002165	0.002165	0.002165	0.002165	0.002165	N/A	0.002165
F7	0.002165	0.002165	0.240260	0.002165	0.002165	0.002165	N/A
F8	0.002165	0.002165	0.002165	0.002165	N/A	0.002165	0.002165
F9	0.002165	0.002165	0.484848	0.002165	0.002165	0.818182	N/A
F10	0.002165	0.002165	N/A	0.002165	0.002165	0.093074	1.000000
F11	0.002165	0.002165	0.002165	0.002165	0.002165	0.002165	N/A
F12	0.002165	0.015152	0.064935	0.002165	0.002165	0.064935	N/A
F13	0.002165	0.002165	N/A	0.002165	0.002165	0.393939	0.002165
F14	0.064935	0.588745	N/A	0.064935	0.002165	0.132035	0.064935
F15	N/A	0.064935	0.008658	0.008658	0.002165	0.002165	0.179654
F16	N/A	0.937229	0.002165	0.002165	0.002165	0.002165	0.818182
F17	0.015152	1.000000	0.002165	0.002165	0.002165	0.002165	N/A
F18	N/A	0.393939	0.699134	0.002165	0.002165	0.025974	0.818182
F19	0.699134	0.064935	0.041126	0.041126	0.002165	0.002165	N/A

Discussion and future works

SCA is a recent population-based optimization algorithm. It was quickly adopted in various fields to solve optimization problems thanks to two main criteria. It has the reputation of finding the global optimum. It considers the problem as a black box which make it possible to be applied in any king of optimization problem. The finding from this study can be summarized as follow:

• SCA attracted a lot of interest over the last 3 years. Since its introduction in 2016, more than 210 works have been published. The peak of publications is recorded in 2020 with 71 articles.

• India is the country that shows the most interest for SCA with total publications of 64.

• SCA has been applied to solve various optimization problems in different fields. Electrical engineering is the most addressed one. The part of applications developed with SCA in this area is estimated to 25%.

• Several modified versions of SCA are proposed. Improved SCA has the higher percentage with 36%.

• SCA is also hybridized with many other methods where 77% of contributions join SCA with other meta-heuristics especially PSO (18%) and GWO (13%).

• SCA is even applied to address multi-objective problems. Five variants are already available in the literature.

This focus on SCA is due to its many advantages. Some of them are given in Table 9. However, it suffers from the No Free Lunch (NFL) theorem which states that there is no optimization technique that can solve all optimization problems Wolpert and Macready (1997). Moreover, SCA may be getting stuck in local optimal.

Table 9.

Advantages and disadvantages of SCA

Advantages	Disadvantages
Easy to implement in many different programming languages	Suffers from premature convergence in some real-world optimization problems
Simplicity, robustness, adaptability, flexibility, and scalability are fundamental features found	Parameter tuning in SCA
Combination with other meta-heuristics and techniques	No theoretical analysis of convergence properties
Small number of control parameters that need to be adjusted
Lower stuck in local optima
Reasonable execution time
Suitable for a wide variety of difficult optimization problems
Good solutions

Despite this positive, there are still possible future directions such as:

• Combining SCA with other meta-heuristics like GA, CS, FA, KH, and DA.

• Investigating a systematical theoretical analysis of the running time, robustness, and stability of SCA.

• Comparing the effectiveness of SCA with other optimization techniques such as KH, MVO, FPA, CFO, and WEO.

• Extending multi-objective variants of SCA for tackling many-objective optimization problems.

• Enhancing SCA to be applied on some complex and real-world optimization problems such as self-driving cars, data analysis, and big data analysis.

• Applying SCA to solve other optimization problems in different fields such as computer science (Network and linear antenna array, multi-cast routing, intrusion detection, graph coloring), electrical engineering (renewable energy system, visible light communication, voltage source inverters, annual energy loss), civil engineering (fiber-reinforced polymer sheets, optimal sizing of skeletal structures, soil stability analysis), mechanical engineering (permanent magnet synchronous motor, steel making, parameter calibration), and real-world applications (timetabling, self-driving cars).

Conclusion

In this paper, we provide the first comprehensive survey of SCA according to the modifications, hybridizations, and applications. Since the development of SCA in 2016, more than 210 SCA papers have been published by several academics and researchers. These related papers proved the effectiveness, robustness, scalability, and efficiency of SCA to solve a large variety of optimization problems in different fields. This success is due to its simple implementation, its good convergence speed, its reasonable execution time, and its ability to be easily hybridized with other optimization algorithms. Despite the success of SCA, there are still several suggestions for future works. The modifications of the standard SCA needs more research by investigating new strategies and operators. Additional studies need to propose other SCA variants by combining it with other meta-heuristics and techniques. In addition, a systematical theoretical analysis of the running time, robustness, and stability of SCA needs to be investigated. Also, another interesting research area is the application of SCA to solve other optimization problems, especially complex, dynamic, and large-scale optimization problems.