Combination of network and molecule structure accurately predicts competitive inhibitory interactions

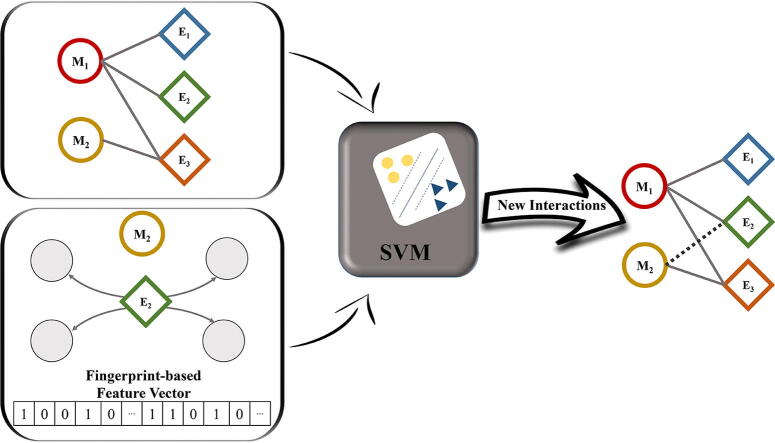
Graphical abstract

Abstract

Mining of metabolite-protein interaction networks facilitates the identification of design principles underlying the regulation of different cellular processes. However, identification and characterization of the regulatory role that metabolites play in interactions with proteins on a genome-scale level remains a pressing task. Based on availability of high-quality metabolite-protein interaction networks and genome-scale metabolic networks, here we propose a supervised machine learning approach, called CIRI that determines whether or not a metabolite is involved in a competitive inhibitory regulatory interaction with an enzyme. First, we show that CIRI outperforms the naive approach based on a structural similarity threshold for a putative competitive inhibitor and the substrates of a metabolic reaction. We also validate the performance of CIRI on several unseen data sets and databases of metabolite-protein interactions not used in the training, and demonstrate that the classifier can be effectively used to predict competitive inhibitory interactions. Finally, we show that CIRI can be employed to refine predictions about metabolite-protein interactions from a recently proposed PROMIS approach that employs metabolomics and proteomics profiles from size exclusion chromatography in E. coli to predict metabolite-protein interactions. Altogether, CIRI fills a gap in cataloguing metabolite-protein interactions and can be used in directing future machine learning efforts to categorize the regulatory type of these interactions.

1. Introduction

The flux of biochemical reactions, as the ultimate outcome of transcription, translation, and post-translational modifications, is determined not only by the concentration of substrates and active enzymes, but also by other metabolites that can alter the activity of enzymes via regulatory interactions, e.g. competitive inhibition or allosteric activation [1], [2]. The role of metabolite-protein regulatory interactions goes beyond modulating metabolic responses, since metabolites can also interact with proteins of non-enzymatic faction, such as transcription factors [3], [4]. Therefore, recent systems biology efforts have been directed at assembling and systematically analyzing small molecular regulatory networks (SMRNs), comprising the entirety of documented regulatory interactions between small molecules and proteins [5], [6]. In parallel, advances in high-throughput technologies have resulted in the development of in vitro and in vivo approaches to identify and verify metabolite-protein interactions [7], [8], [9].

The systems biology studies of SMRNs are based on combining the resources distributed across different databases (e.g. BRENDA [7], STITCH [10]). Metabolite-protein regulatory interactions can be divided into activating and inhibitory (however, see [11], for the subtle effects of single-molecules on this categorization). The inhibitory interactions can be further subdivided into competitive, noncompetitive, uncompetitive, suicide, and product [1]. Mining of the resulting SMRNs has led to the observations that: (1) inhibitory interactions are the most prevalent metabolite-protein interactions, with domination of competitive inhibition [5], [6]; (2) the competitive and allosteric inhibitory interactions are largely due to structural similarity between the substrate and competitive inhibitor (CI) and are, therefore, found in the network vicinity of the regulated enzyme [5], [6]; and (3) metabolite-protein regulatory interactions are non-randomly distributed in the network, but the pattern cannot be explained by thermodynamics principles or preservation of resources (via prevention of futile cycling) [6]. Therefore, it appears that a large fraction of SMRNs may be explained by structural similarity between metabolites that act as substrates and inhibitors, leading to the so-called self-inhibitory nature of metabolic networks.

However, not all metabolites that are structurally similar to the substrates of a regulated enzyme act as inhibitors. Moreover, not all inhibitors are structurally similar to the substrates of the regulated enzyme. While molecular docking approaches provide one means to narrow down the set of metabolites that can act as CIs [12], [13], [14], they are limited to proteins with resolved crystal structure [15]. Therefore, this approach is currently unfeasible for genome-scale studies of competitive inhibitory regulatory interactions. Therefore, despite the prevalence of such regulatory interactions across kingdoms of life [5], [6], the presented statistical findings and computational approaches do not provide a precise means to pinpoint metabolites that can act as CIs of a given enzyme.

Here we devise a supervised machine learning approach, called CIRI that determines whether or not a metabolite is involved in a competitive inhibitory regulatory interaction with an enzyme, provided information about the reactions that the enzyme can catalyze. To this end, we employ a machine learning procedure to identify metabolite-reaction, and thereby metabolite-enzyme, pairs that are not involved in competitive inhibitory interactions [16]. We validate the performance of CIRI on several unseen data sets and databases of metabolite-protein interactions not used in the training [10], [17]. Finally, we show that CIRI can be used to refine predictions about metabolite-protein interactions from PROMIS, an approach which employs metabolomics and proteomics profiles from size exclusion chromatography [18].

2. Results

2.1. Gold standard of competitive inhibitory interactions

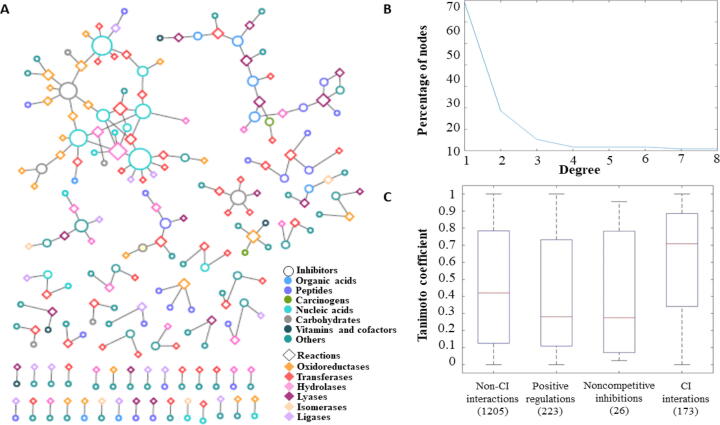
As a supervised learning approach, CIRI relies on high-quality gold standard to determine whether or not a metabolite-enzyme regulatory interaction is of competitive inhibitory nature. The gold standard is based on the computationally reconstructed SMRN of E. coli that includes 1926 unique interactions, between 454 metabolites and 365 reactions [6]. This SMRN contains 183 competitive inhibitory interactions, between 113 competitive inhibitors (CIs) and 116 reactions (Supplementary Table 1). Large-scale metabolic networks include gene-protein-reaction (GPR) rules that specify which enzymes catalyze a reaction along with the genes that code for them [19]. Therefore, metabolite-reaction interactions reported in the gold standard can be readily transformed into metabolite-enzyme and metabolite-gene interactions, used in the following analyses. As a result, the gold standard of competitive inhibitory interactions can be represented as a bipartite network (Fig. 1A), in which ADP acts as a CI in interaction with eight enzymes, while 69% of CIs have only one interaction (see Fig. 1B). We note that the inhibitors that are included in the gold standard can be classified into seven classes, including: organic acids, peptides, carcinogens, nucleic acids, carbohydrates, vitamins and cofactors, and others. The reactions in the gold standard are catalyzed by six enzyme classes, including: oxidoreductases, transferases, hydrolases, lyases, isomerases, and ligases (see Fig. 1A and Supplementary Table 1).

Fig. 1.

Gold standard of competitive inhibitory interactions. The bipartite network in (A) represents the gold standard of competitive inhibitory interactions. Node colors indicate the category to which the reaction/metabolite belongs. The categories for metabolites and reactions are retrieved from KEGG [20] and BRENDA [7]. The radius of the circle that represents a node is proportional to the node’s degree. The degree distribution of nodes in the gold standard network is illustrated in (B). The structural similarity between CIs and the reactants, measured by Tanimoto coefficients is shown in (C) and is compared with the Tanimoto coefficients over the other types of regulatory interactions (left-most boxplot) and the specific types of positive regulation and noncompetitive inhibition, included in the gold standard. The means of the Tanimoto coefficients of the regulator-substrate pair over the other types of regulatory interactions significantly differ from the mean of the Tanimoto coefficients of the CI-substrate pairs (p-value = ), as do the means for subtypes of positive regulation (p-value = ) and noncompetitive inhibition (p-value = ). The numbers below the boxplots denote the number of instances (pairs of regulator - substrate) included in the specific types of regulatory interactions.

2.2. Feature engineering based on metabolic reaction networks and structural similarity of metabolites

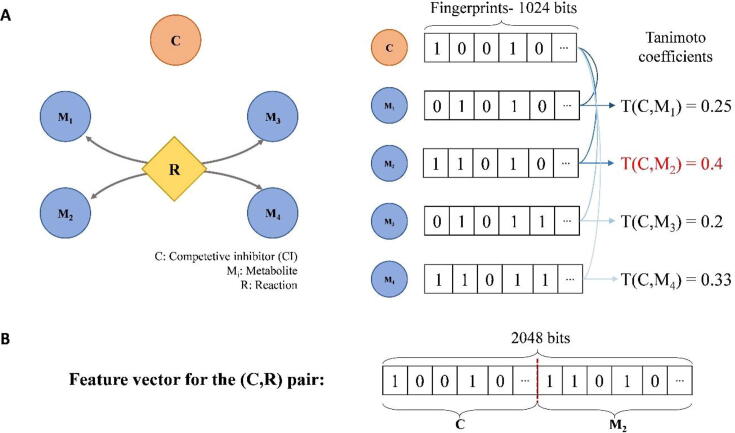
To study the structural similarity of CIs and substrates involved in competitive inhibitory interactions, we make use of interactions included in the SMRN of E. coli. For each competitive inhibitory interaction between a CI and an irreversible reaction, we extract all substrates of the reaction, and we calculate their structural similarities with the CI using the Tanimoto coefficient; if the reaction is reversible, we also consider the structural similarity of the products to the CI (see Methods). Finally, we use the maximum structural similarity over all reactants (i.e. substrates and/or products) as a score for the competitive inhibitory interactions (Fig. 2A). We employ the iJO1366 genome-scale metabolic model of E. coli [21] to obtain information about reversibility and reactants of reactions participating in the gold standard of competitive inhibitory interactions. Following this approach, we arrive at fingerprints for 107 CIs and for the substrates of 115 reactions involved in 173 (94.5%) competitive inhibitory interactions in the gold standard. Other types of regulations in the SMRN of E. coli includes 1205 unique interactions, between 429 regulators and 359 reactions. The fingerprints are available for 369 regulators and for the substrates of 249 reactions participating in 1152 interactions.

Fig. 2.

A visual illustration of CIRI. (A) A schematic representation of the fingerprints for a CI (C) and the reactants of reaction R are depicted. The structural similarities between C and all reactants of R are calculated using the Tanimoto coefficient. The reactant with the maximum structural similarity (M₂) is selected as the potential competitive reactant to C.  (B) The feature vector for the (C,R) pair in CIRI is constructed by concatenating the fingerprint of the C and that of the reactant with the maximum Tanimoto coefficient (M₂).

The comparison of the resulting scores indicate that CIs have higher similarity to the reactants of the reactions they inhibit in comparison to the metabolites involved in other types of regulations, namely positive regulation (p-value = $2.5\bullet {10}^{-9}$), noncomptetitive inhibition (p-value = $1.8\bullet {10}^{-8}$) and collectively (p-value = $1.8\bullet {10}^{-8}$), in the SMRN of E. coli (Fig. 1C). The other types of regulatory interactions do not contain enough instances in the employed gold standard to facilitate statistical testing. While this finding supports existing observations [5], [6], it also points out that there are cases of metabolite-reaction pairs where this statistical finding does not provide effective classification of competitive inhibitory interactions. For instance, following the described procedure (Fig. 2), NADP is an inhibitor of pyrroline-5-carboxylate reductase, but exhibits the smallest value for the Tanimoto coefficient of zero with the substrates of the reaction catalyzed for this enzyme; the same holds for THR and fumarate hydrates (see Supplementary Table 1 for additional examples). If we used the calculated Tanimoto coefficients to create a naïve classifier by simply using a threshold value (considering all pair above the threshold as competitive inhibitory interactions), we find that the area under the receiver operating characteristic curve (AUC) and area under the precision-recall curve (AUPR) of 0.78 and 0.07, respectively. We would like to stress that these findings are over a set of thresholds needed to derive the aforementioned curves. The question that then arises is: Can the performance of this naïve classifier be improved following a supervised machine learning approach?

2.3. Identification of metabolite-reaction pairs not involved in competitive regulatory interactions

Having established that CIs tend to show higher structural similarity to at least one of the reaction substrates, here we propose CIRI, a supervised machine learning approach based on support vector machine (SVM), to predict competitive inhibitory interactions. While one can envision that this strategy can be expanded by incorporating more than one of the highly similar substrates, here we test the simplest scenario of considering the most similar substrate to the inhibitor of an enzyme to build the features of the SVM.

For any pair of a metabolite and a reaction, CIRI predicts whether or not the metabolite can act as a CI for the reaction. The features in CIRI is constructed by concatenating the fingerprint of the CI and that of the reactant (i.e. substrate and/or product) that maximizes the score of the interaction, as explained above (Fig. 2). A reaction can be catalyzed by more than one enzyme (e.g. isoenzymes), so that the metabolites that act as CIs may differ between them. Since the assembled gold standard specifies whether a metabolite act as a CI to a reaction, rather than an enzyme, CIRI is designed to classify interactions between metabolites and reactions. However, by using the GPR rules, we can readily transfer the information from reactions to the underlying enzymes and genes, respectively.

To apply a supervised machine learning approach, we also need to specify a gold standard of negative instances (i.e. metabolite-enzyme pairs that are not involved in competitive inhibitory interactions). While instances that represent CI-reaction interactions are available from the gold standard described above, specifying metabolite-reaction pairs that are not involved in competitive inhibitory interactions is not straightforward due to the lack of information about absence of competitive inhibitions between a metabolite and a reaction. To overcome this issue, CIRI applies the strategy proposed by [16] to identify such instances.

Using the CIs from the gold standard of competitive inhibitory interactions, we construct feature vectors for the respective CI-reaction pairs (i.e. 107 × 115). The 12,132 ($=107\times 115-173$) uncharacterized pairs of metabolites and reactions are then divided into several subsets of size equal to that of positive instances in the gold standard. At each iteration, one of the subsets of uncharacterized pairs is treated as the negative class, and together with the positive class form a training set based on which an iteration-specific SVM is built (following a 10-fold cross-validation). All the remaining uncharacterized pairs are in turn treated as a test set and classified as positive or negative by the iteration-specific SVM. As a result, we train as many as $\frac{|\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{d}\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}|}{|\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}|}=\frac{12312}{173}70$ iteration-specific SVMs whose assessments of the uncharacterized pairs are finally aggregated, and the uncharacterized pairs can be ranked based on the number of iterations in which they are classified as positive. Clearly, a higher rank for a metabolite-reaction pair indicates a higher likelihood that it belongs to the positive class. Pairs with zero final score comprise the negative class of the training data.

From the 12,132 uncharacterized metabolite-reaction pairs, 4,626 (38.1%) receive a score of zero and are treated as instances that do not represent competitive inhibitory interactions. The results show that 364 (out of 12132) uncharacterized pairs receive the highest score of 69 which are cross-examined with the STITCH database [10]. Form the pairs with the highest score, we find out that 39% are included in STITCH database. To assess the significance of this finding, a null distribution of 1000 sets of 364 random uncharacterized pairs is generated and their interactions in STITCH are examined. The maximum percentage of interactions among the 1000 random sets is 24%. This indicates that pairs with the highest score of 69 are significantly enriched for interactions (p-value < 0.001)—demonstrating the validity of the employed procedure.

2.4. CIRI accurately predicts metabolite-reaction pairs involved in competitive inhibitory interaction

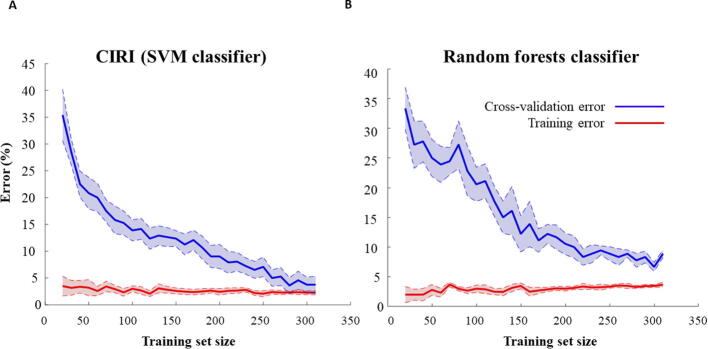
We note that the number of negative instances identified is considerably larger than the number of positive instances, leading to a class imbalance problem. To address this issue, at each iteration, a balanced subset of data is selected containing all positive instances and a subset of same size composed of negative instances sampled uniformly at random (100 repetitions). Ten percent of positive and negative instances from the selected data set for this iteration are then selected as test data, and the rest are used as iteration-specific training set, on which cross-validation is performed (see Methods). The best model obtained from the cross-validation with hyperparameter tuning is then validated on the unseen test data (see Methods). Our findings indicate that CIRI has area under the ROC curve (AUC) and the area under the precision-recall curve (AUPR) values of 0.90 and 0.85, respectively, indicating a 15% increase in comparison to the naïve classifier, described above, based on a threshold value for a metabolite-reaction score. The analysis of the learning curve demonstrates that the cross-validation error approaches the training error as the training set size increases, suggesting that the training set is representative and the classifier is not expected to suffer from overfitting issues (Supplementary Figure 1A).

A similarly constructed balanced data set, containing all positive instances and a subset of negative instances, is employed to train the final SVM classifier model. This SVM model is then used to predict whether or not any given CI could have a competitive inhibitory role for a given reaction. Since the choice of negative subset may influence the predictions, 100 different negative subsets of the same size are randomly selected from the negative class and independently used to train different classifier models. All trained models are in turn used to predict the class labels for all possible CI-reaction pairs (see Data section). The results of all models are at the end aggregated to assign a final score to each pair, which reflects the number of times the pair is classified as positive, i.e. forming a competitive inhibitory interaction.

From the 2,583 reactions included in the genome-scale metabolic model of E. coli, fingerprints are available for at least one reactant of 1,007 reactions. Using the CIs from the SMRN of E. coli, we construct feature vectors for $107,749(=107\times 1007)$ pairs. Further, all 100 trained model are applied to predict the class labels of every possible pairs, and the final score from the predictions are used to construct the predicted competitive inhibitory network of this study (see Supplementary Table 2). In the resulting network, we find that five CIs, including: adenosine, nicotinate D-ribonucleotide, NAD, AMP and NADP, have competitive inhibitory interactions with more than 70% of reactions in the network. Enzymes responsible for pentosyltransferases and hexosyltransferases and the ones with NAD⁺ or NADP⁺ as acceptor, are the most regulated enzymes in the predicted competitive inhibitory network. Furthermore, we use Tanimoto coefficient to calculate the structural similarity between all pairs of CIs in the network of predicted competitive inhibitory interactions. The average structural similarity of all pairs of CIs in the network is 0.21, which is significantly lower than that of for the five metabolites with the highest number of competitive inhibitory interactions (0.69, p-value = 1e-6). This shows that CIs with higher tendency to inhibit reactions, share more structural fragments.

The similarity of CIs in the predicted network is also measured by the Jaccard index. The Jaccard index for two given CIs calculates the proportion of shared reactions between the two CIs, relative to the total number of reactions which they regulate. Having established that the interaction between CIs and reactions are due to the high structural similarity of CIs to at least one of the reaction substrates, it is expected that CI pairs with higher number of shared reactions, have relatively higher structural similarity. Therefore, we investigate whether a correlation exists between the Jaccard indices of the CI pairs and their structural similarities. In the result network of this study, the two similarity measures for the CI pairs show a positive Pearson correlation coefficient of 0.41 (p-value = 1.2e-202). This finding further corroborates the validity of the large-scale predictions for the E. coli network of competitive inhibitory interactions.

2.5. Robustness analysis for the performance of CIRI

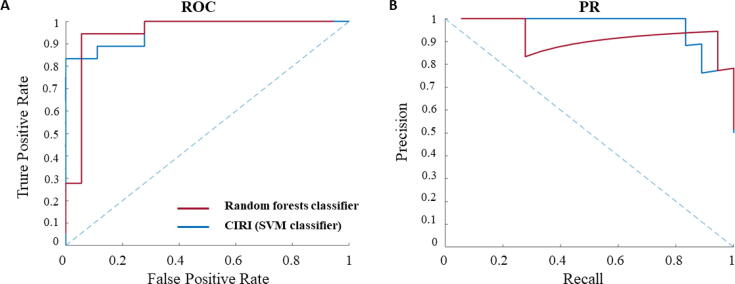
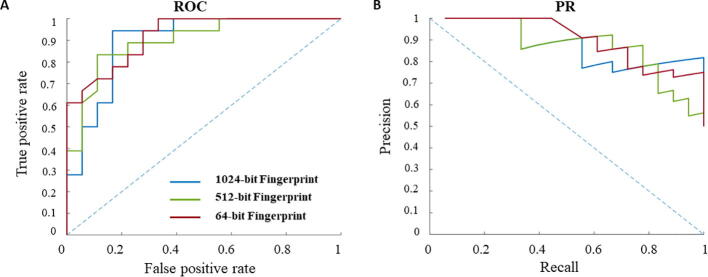
Here we examine the extent to which the choice of machine-learning technique, choice of negative instances, as well as the feature extraction impacts the performance of the prediction model. To assess the choice of machine-learning technique, we train random forests on the same feature vectors and compare the results with those obtained from an SVM-based classifier. Our findings show that the classifiers based on random forests perform similarly well with respect to the AUC and AUPR (Fig. 3). However, the learning curves for the classifiers based on random forests indicate that the training size is not sufficient for effective construction of this type of classifier (Supplementary Fig. 1Supplementary Figure 1B). These findings demonstrate that SVM-based classifiers are better suited for applications in CIRI.

Fig. 3.

The performance of CIRI and random forest classifier. In (A) and (B) the ROC and PR curves for CIRI and for the classifier based on random forests are shown, respectively.

We also tested the extent to which the findings depend on the type of molecular descriptor used. Since molecular descriptors, like atom pairs, result in features with different sizes for different molecules, they are not readily applicable in solving machine learning problems like that in CIRI. For this reason, we next assess the effect of reducing the number of features in the fingerprints, to 64 and 512, and determined the measures of performance. We find that the performance is not affected for both AUC and AUPR, indicating that smaller fingerprints are already sufficiently informative (Supplementary Figure 2).

Furthermore, we treat the activating interactions from E. coli’s SMRN as negative instances to probe whether the choice of negatives instances in CIRI to determine if this strategy has an impact on the performance. The performance of the resulting SVM is 0.76 and 0.70 with respect to the AUC and AUPR. Therefore, we conclude that the features themselves are appropriate to distinguish between the two classes of interactions, but that the choice of negatives affects the final predictions made.

Finally, to check the effect of reaction reversibility, we generate a null distribution of 100 metabolic models with the same set of reactions present in the E. coli metabolic model but with randomly set reaction reversibility. We then determine and compare the performance of CIRI on each of the generated models. Our results point out that the performance of CIRI is insensitive to the choice of reaction reversibility. The reason is that the scores for a CI and the two irreversible reactions obtained by splitting a reversible one on average differ slightly (see Supplementary Figure 3), explaining the robustness of performance. This is also in line with the expectation that the structural similarity of metabolites in a vicinity of a reaction is high.

2.6. Validation of the predictions from CIRI

Two independent interaction sources are employed to validate the competitive inhibitory network predicted by CIRI. The first source of interactions is retrieved from Piazza et al. [17] which provide 60 competitive inhibitory interactions on 15 CIs and 49 genes. Furthermore, the STITCH database is used to extract all known metabolite-protein interactions in E. coli. Since competitive inhibitory interactions are the most prevalent metabolite-protein interactions [5], [6], the validation here is conducted under the assumption that most metabolite-protein interactions in STITCH database are competitive inhibitory. In total, the E. coli metabolite-protein interaction network includes more than 2.2 million interactions on 88,044 metabolites and 1,028 genes. In addition, the STITCH database provides confidence score for each recorded interaction and in this study we apply two different thresholds of medium confidence (cutoff 0.5) and high confidence (cutoff 0.7). Applying the score cutoff of 0.5, yields 207,439 interactions on 29,556 metabolites and 3,800 genes, while the score cutoff 0.7 results in 79,156 interactions on 7,288 metabolites and 2,682 genes.

While these sources provide information about competitive inhibitory relations between pairs of metabolites and genes, the predicted network of this study comprises CI-reaction interactions. Therefore, to validate the predicted network, we first transform the included metabolite-reaction interactions in terms of metabolite-gene interactions following the GPR rules from the metabolic model used. There are 922 genes associated with 1,007 reactions in the predicted competitive inhibitory network, of which 285 are in one-to-one relation. Two different approaches are adopted to tackle this issue: In the first, we focus only on those reactions and genes that are in one-to-one correspondence (i.e. reactions which are catalyzed only by a single gene in the E. coli metabolic model, and for which the corresponding gene catalyzes no other reaction). Therefore, these metabolite-reaction pairs can be easily transformed into metabolite-gene pairs. In the second approach, we consider all reactions from the predicted network that are associated to at least one gene in the metabolic model. The scores assigned to the metabolite-reaction pairs in the predicted network are used to determine a unique score for a metabolite-gene pair. Three different schemes, i.e. taking the minimum, maximum, or mean over the reactions associated with a gene, are used to calculate the unique score for a metabolite-gene pairs.

Based on the first approach, the predictions of CIRI show an AUC of 0.66 when considering interactions retrieved from Piazza et al. [17] and AUC of 0.63 and 0.65 based on the STITCH interactions with medium confidence and high confidence, respectively. The results of using the second approach are summarized in Table 1, demonstrating that the performance of CIRI on unseen data sets can reach AUC score as high as 0.75, indicating that CIRI provides good performance on unseen data sets.

Table 1.

The AUC results from predictions of CIRI. To determine a unique score for a metabolite-gene interaction, three different schemes, i.e. taking the minimum, maximum, or mean over the reactions associated with the gene is used to transform metabolic-reaction interactions to metabolic-gene interaction. Here the predictions of CIRI are validated by employing two interaction sources from Piazza et al. [17] and STITCH database [10] with different confidence levels.

	Minimum score	Maximum score	Mean score
Piazza et al., 2018	0.74	0.75	0.75
STITCH (medium confidence)	0.63	0.64	0.64
STITCH (high confidence)	0.66	0.67	0.67

2.7. CIRI can be used to refine the predictions of other approaches

Here, we first use the PROMIS method to predict metabolite-protein interactions in E. coli. It has been shown that when metabolite and gene elution profiles are available from size exclusion chromatography data, the Pearson correlation cut-off of 0.7 between metabolite and protein elution profiles are indicative of interaction [18]. Using PROMIS, we collected a data set comprising 64 metabolites and 925 genes that can be mapped to genes in the genome-scale metabolic model of E. coli. Out of 64 × 925 possible metabolite-protein pairs, 18,270 have Pearson correlation coefficient larger than 0.7 and are identified as potential candidates for interactions.

Like for the interactions in STITCH, not all identified metabolite-protein interactions identified following PROMIS are competitive inhibitory. Therefore, having established that CIs tend to show higher structural similarity to at least one of the reaction substrates, we propose a filtering strategy to retrieve the competitive inhibitory interactions among all metabolite-gene interactions identified by PROMIS. To this end, for each identified protein metabolite interaction, we consider all reactions from the genome-scale metabolic model of E. coli that are associated to the protein (and respective gene) participating in the interaction. For the selected set of reactions, the structural similarities of corresponding reactants with the metabolite participating in the interactions are calculated using the Tanimoto coefficient. Finally, we take the maximum structural similarity over the reactants (i.e. substrates and/or products) of all reactions that are catalyzed by the same protein, to score the identified metabolite-protein (i.e. metabolite-gene) interactions. From the identified interactions from PROMIS, interactions with score larger than a given cut-off are considered as competitive inhibitory interactions.

Since each cut-off value on the Tanimoto coefficient results to different number of competitive inhibitory interactions from PROMIS, we first investigate this number for different cut-off values (Table 2). This number expectedly decreases with higher values for the applied cut-off. The competitive inhibitory interactions retrieved from PROMIS are then considered as an independent interaction source to validate the competitive inhibitory network predicted by CIRI. Using different cut-off values, we see that the sensitivity (or true positive rate) of CIRI can go as high as 0.94. The highest sensitivity is obtained with the cut-off value of 0.8 for the Tanimoto coefficient. We observe that higher values of AUC are associated with larger cut-off values for all three different schemes, i.e. taking the minimum, maximum, or mean over the reactions associated with the gene is used to transform metabolite-reaction interactions to metabolic-gene interaction (Table 2). This is also in line with the higher structural similarity of CIs and substrates involved in competitive inhibitory interactions. Using the filtering strategy, we show that the performance of CIRI on the retrieved networks can reach AUC score as high as 0.88 (Table 2).

Table 2.

The impact of different threshold for Tanimoto coefficient values on the retrieved competitive inhibitory network from PROMIS. The cut-off values of 0.6, 0.7, 0.8 and 0.9 are used to filter metabolite-protein interactions predicted by PROMIS method. Different cut-offs result in different number of competitive inhibitory interactions. The table also shows the performance of CIRI for different cut-offs and the three different schemes of transforming metabolite-reaction interactions to metabolite-gene interactions.

Cut-off values	0.6	0.7	0.8	0.9
# Competitive inhibitory interactions	898	692	200	66
The Pearson correlation coefficient between Jaccard index and structural similarity	0.49	0.44	0.37	0.74
AUC- using the minimum score	0.58	0.57	0.82	0.74
Sensitivity- using the minimum score	0.35	0.30	0.80	0.68
AUC- using the maximum score	0.59	0.58	0.88	0.85
Sensitivity- using the maximum score	0.39	0.35	0.94	0.82
AUC- using the mean score	0.59	0.58	0.86	0.82
Sensitivity- using the mean score	0.36	0.31	0.85	0.68

Using different cut-off values, we see that in the retrieved competitive inhibitory networks from PROMIS, NAD, AMP, NADP, FAD, cAMP, acetyl-CoA, isoleucine, leucine and adenosylhomocysteine are in the union set of the top five CIs with respect to the number of interactions in the retrieved networks. The pairwise structural similarity of all CI pairs are calculated in the retrieved networks, using Tanimoto coefficient. Moreover, the Jaccard index is used to quantify the degree of sharing association between two CIs in the retrieved competitive inhibitory networks. The Pearson correlation coefficient between the Jaccard indices of the CI pairs and their structural similarities is calculated for each retrieved network (Table 2). In all result networks using different cut-off values, the two similarity measures show positive correlations, which indicates that CI pairs with higher number of shared reactions, have relatively higher structural similarity, as for the analysis based on the network predicted based on E. coli’s genome-scale metabolic network in Section 2.4.

The same filtering strategy is used to retrieve the competitive inhibitory interactions among interactions in STITCH database. Similarly to the results shown in Table 2, here we also observe that higher values of AUC are associated with larger cut-off values for all three different schemes (Table 3). Using the filtering strategy, the performance of CIRI on the interactions retrieved from STITCH database improves for both thresholds of medium and high confidence (Table 3). The sensitivity of CIRI in recovering the competitive inhibitory interactions of STITCH depends on the cut-off value for the Tanimoto coefficient. The cut-off value of 0.8 results in the highest percentage of recovery, which is consistent with the results shown in Table 2.

Table 3.

The impact of different threshold for Tanimoto coefficient values on the retrieved competitive inhibitory network from STITCH. The cut-off values of 0.6, 0.7, 0.8 and 0.9 are used to filter metabolite-protein interactions from STITCH with medium and high confidence. Different cut-offs result in different number of competitive inhibitory interactions. The table also shows the performance of CIRI for different cut-offs and the three different schemes of transforming metabolite-reaction interactions to metabolite-gene interactions.

	Cut-off values		0.6	0.7	0.8	0.9
Medium confidence	# Competitive inhibitory interactions		2199	1884	1378	1106
	using the minimum score	AUC	0.76	0.79	0.81	0.81
		Sensitivity	0.79	0.83	0.88	0.88
	using the maximum score	AUC	0.78	0.81	0.83	0.82
		Sensitivity	0.86	0.91	0.94	0.93
	using the mean score	AUC	0.78	0.81	0.83	0.82
		Sensitivity	0.79	0.84	0.88	0.88
	Cut-off values		0.6	0.7	0.8	0.9
High confidence	# Competitive inhibitory interactions		1856	1628	1280	1059
	using the minimum score	AUC	0.77	0.80	0.81	0.81
		Sensitivity	0.80	0.85	0.88	0.88
	using the maximum score	AUC	0.79	0.82	0.83	0.82
		Sensitivity	0.87	0.92	0.94	0.93
	using the mean score	AUC	0.79	0.82	0.83	0.83
		Sensitivity	0.81	0.85	0.88	0.88

2.8. Universality of competitive inhibitory interactions

Features used in CIRI contain the information on the structures of two molecules, which can potentially compete for attachment to the same binding site. Since chemical structures and the corresponding fingerprints are the same across all organisms, the features used in CIRI do not represent organism-specific information. This indicates at the universality of the proposed prediction scheme, which may be applicable across different species. To test this hypothesis, we evaluate the performance of CIRI, where the SVM classifier is trained on data from one organism and tested on another.

To this end, we utilize the competitive inhibitory interaction data from human to construct the feature vectors for the SVM classifier [5]. The data set includes 295 competitive inhibitory interactions on 153 CI and 113 substrates, and fingerprints are available for all molecules participating in interaction set. Therefore, using the human data set, it is straightforward to form feature vector for a given pair of CI-substrate, by simply concatenating the fingerprints of the two. The extracted features are then provided as input to train a human-based SVM classifier, which is then applied on E. coli labeled test data to evaluate its performance. The E. coli test data includes all positive instances from the E. coli gold standard together with the negative instances identified by the abovementioned labelling strategy. The performance of human-based SVM classifier on the E. coli test data (AUC of 0.74) confirms that the proposed prediction scheme can be applied across species.

3. Conclusions

Recent mounting evidence has indicated the prominent role that metabolite-protein interactions play in regulating the activity of different cellular process in in shaping the overall functionality of cellular networks. However, it is paramount to get access to high-quality networks of metabolite-protein interactions before attempting to look for patterns that relate their structure to the functionality of other cellular networks (e.g. those in metabolism and gene regulation). Advances in supervised machine learning can employ these accumulated evidences to develop classifiers for metabolite-protein pairs that are involved in regulatory interactions. However, this approach is challenging due to the different (sub)classes of metabolite-protein interactions (e.g. activating and inhibitory). Due to the different underlying mechanisms that the different types of regulatory interactions are based on, it is not plausible that same machine learning approaches will be able to show equally good performance across all.

Here, we focused on the most prominent metabolite-protein interactions, namely of the competitive inhibitory type, and used a recently assembled gold standard along with a procedure for predicting metabolite-protein pairs not involved in such interaction to build an SVM based classifier in an approach we termed CIRI. In the simplest form, the CIRI uses features given by the fingerprints of a CI and the most similar substrate of a reaction catalyzed by the protein inhibited by the CI. We showed that the so-designed supervised approach outperforms the naïve classifier, based on the usage of a simple threshold of similarity of structures, by 20%. Thorough comparative analyses show that the choice of SVM supervised learning approach offers advantages over random forests, with respect to the size of the set of instances needed for training. Particularly, we observed that the random forest classifiers would require a larger gold standard, which is the reason for opting to use SVM-based classifiers.

In addition, extensive validation analyses with unseen data sets that document competitive inhibitor interactions, like that of Piazza et al. [17], and those, for which the multitude of included interactions can be assumed to be predominantly of this type (e.g. STITCH and PROMIS), demonstrate that CIRI shows equally good performance. Further, the validity of the predicted interactions was further supported by the correlation between the structural similarity of two metabolites and similarity of reactions/protein sets in which they act as CIs. Hence, the high-quality predictions from CIRI can next be validated in customized experiments.

To guide the follow-up experimental efforts, we highlighted metabolites and proteins which are predominantly involved in competitive inhibitory interactions. For instance, predictions bases on CIRI in multiple data sources in E. coli indicated that NAD, AMP, and NADP repeatedly appear as metabolites that act as CIs. We expect that ideas from CIRI can be extended to other types of metabolite-protein interactions as long as gold standards of sufficiently large size are assembled. However, these extensions would likely have to include additional structural information about proteins and/or consider only specific parts of the regulatory small molecule. The present formulation of CIRI would have to be adjusted for such applications. Nevertheless, our findings demonstrated that CIRI fills a gap in cataloguing metabolite-protein interactions and can be used in directing future experimental efforts to demonstrate the functional relevance of this type of interactions.

4. Methods

4.1. Molecular fingerprints and similarity

In chemoinformatics, molecular fingerprint is a way to represent molecular structure and chemical information of a molecule by a binary vector, in which each bit indicates the presence or absence of a structural fragment in the molecule [22]. Fingerprints are commonly used to measure the structural similarity of two molecules as a function of the number of fragments they share [5]. We use the R package Chemminer [23] to generate the fingerprints from structure-data files (SDF).

Among several similarity metrics to quantify the molecular similarity in the field of chemoinformatics, the well-known Tanimoto coefficient is confirmed as one of the most reliable metrics [22]. The Tanimoto coefficient for two molecules $A$ and $B$ is defined by

$$T\left(A,B\right)=\frac{N_{A\cap B}}{N_A+N_B-N_{A\cap B}}$$

where $N_A$ and $N_B$ are the number of 1 bits in the fingerprints $A$ and $B$, respectively, and $N_{A\cap B}$ is the number of 1 bits shared by the fingerprints of both molecules. The Tanimoto coefficient ranges from zero, when two fingerprints have no 1 bits in common, to one, when the two fingerprints are identical.

4.2. Support vector machine and random forest classifiers

Having a labelled training set of both positive and negative instances, with associated feature vectors formed by the concatenation of the fingerprints, an SVM can be trained to find the optimal hyperplane separating the two classes. Once the SVM classifier is trained, it can classify any new CI-reaction pair ($p$) based on a scoring function of the form $f\left(p\right)={\sum }_{i=1}^n{\alpha }_{i}K(p_i,p)$, where $n$ is the number of instances in the training set. Here, ${\alpha }_i$ are Lagrange multipliers optimized by the SVM to respectively enforce large positive and negative scores for the pairs in the positive and negative class. The kernel function $K\left(p_i,p\right)$ gives a measure of similarity between two pairs of $p_i$ and $p$. In CIRI, the SVM classifier is trained with a Gaussian (RBF) kernel function [24], as implemented in fitcsvm function of MATLAB. Bayesian optimization was used to perform hyperparameter optimization within cross-validation for the SVM parameters. In the case of random forests, we also used Bayesian optimization to tune the values of the minimum leaf size and the number of predictors to sample at each node. The entire code for training of the classifiers is available on GitHub under https://github.com/MonaRazaghi/CIRI.

4.3. Performance measures

AUC and AUPR are most commonly used measures for evaluating the performance of classifiers. In ROC curve, the true positive rate ($\mathrm{T}\mathrm{P}\mathrm{R}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}$) is plotted against the false positive rate ($\mathrm{T}\mathrm{P}\mathrm{R}=\frac{\mathrm{F}\mathrm{P}}{\mathrm{F}\mathrm{P}+\mathrm{T}\mathrm{N}}$), where TP and FN indicate the number of true positives and false negatives respectively, and FP and TN respectively show the number of false positives and true negatives. AUC is the area under ROC curve, and the closer AUC measure for a model comes to 1, the more accurate it is. Precision-recall curve shows a plot of the precision ($=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}$) and the recall ($=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}$) for different thresholds, and similar to AUC, higher values of AUPR indicates better performance for a classifier.

4.4. PROMIS on E. Coli size exclusion chromatography data

PROMIS is a method for studying protein-small molecule interactions in a non-targeted, proteome and metabolome-wide manner. This approach is based on size exclusion chromatography combined with LC-MS proteomics and metabolomics analysis of the collected fractions, assuming that small molecules bound to proteins would co-fractionate together as a complex [18].

The E. coli strain K12 was cultivated at 37 °C with moderate shaking until it reached the logarithmic phase (OD600 = 0,8). E. coli cells were harvested by centrifugation (RT, 4000g) and snap frozen in liquid nitrogen. PROMIS experiment was performed as described previously in [25]. Briefly, E. coli native lysate containing endogenous protein- protein and protein-metabolites complexes corresponding to 40 mg of protein, was separated using a Sepax SRT SEC-300 21.2 × 300 mm column (Sepax Technologies, Inc., Delaware Technology Park, separation range 1.2 mDa to 10 kDa) connected to an ÄKTA explorer 10 (GE Healthcare Life Science, Little Chalfont, UK). 40 1-mL protein containing fractions were collected, snap frozen in liquid nitrogen and lyophilized. Further proteins and metabolites from the lyophilized fractions were extracted using a methyl-tert-butyl ether (MTBE)/methanol/water method [26], where, molecules are simultaneously separated into organic phase (lipids), aqueous phase (polar and semi-polar metabolites) and protein pellets. Aqueous phase and protein pellets were dried in a SpeedVac and subjected metabolomic and proteomic analysis as described by Sokolowska et al. [25].

Briefly, the dried aqueous phase was suspended in 100 µL water. Samples were analysed by ACQUITY UPLC (Waters) coupled with Exactive mass spectrometer (Thermo Fisher Scientific) in positive and negative ionization modes. The mobile phases consisted of 0.1% formic acid in water (Solvent A) and 0.1% formic acid in acetonitrile (Solvent B) and the gradient ramped as fallows: 1 min 1% B, 11 min 1% to 40% B, 13 min 40% to 70% buffer B, then 15 min 70% to 99% B, followed 2 min washout with 99% B. Mass spectra were acquired using following settings: mass range from 100 to 1500 m/z, resolution set to 25,000, loading time restricted to 100 ms, AGC target set to 1e6, capillary voltage to 3 kV with a sheath gas flow and auxiliary gas value of 60 and 20, respectively. The capillary temperature was set to 250 °C and skimmer voltage to 25 V. Protein pellets obtained after MTBE extraction were resuspended in 50 µL denaturation buffer (6 M urea, 2 M thiourea in 40 mM ammonium bicarbonate). Reduction of cysteines, alkylation and enzymatic digestion using LysC/Trypsin Mix (Promega Corp., Fitchburg, WI) followed by desalting of a digested peptide was performed according to the protocol described in [40]. Dried peptides were resuspended in MS loading buffer (3% ACN, 0.1% FA) and measured with Q Exactive HF (Thermo Fisher Scientific) coupled to a reverse-phase nano liquid chromatography ACQUITY UPLC M−Class system (Waters). Equivalent of 1ug of proteins was injected per run and the gradient ramped from 3.2% ACN to 7.2% ACN over 20 min, then to 24.8% ACN over next 70 min and to 35.2% ACN over next 30 min, followed by a 5 min washout with 76% ACN. The MS was run using a data dependent acquisition method. Full scans were acquired at a 120,000 resolution, m/z ranging from 300.0 to 1600.0, a maximum fill time of 50 ms and an AGC target value of 3e6 ions. Each dd-MS2 scan was recorded at the resolution of 15,000 with an AGC target of 1e5, maximum injection time 100 ms, isolation window 1.2 m/z, normalized collision energy 27 and the dynamic exclusion of 30 sec.

Analysis of the metabolite and protein elution profiles was performed as describe before Sokolowska et al. [25], Gorka M [27], and included data filtering, normalization and deconvolution. Obtained data were integrated together using Pearson correlation assuming that what correlates, and hence co-eluates, together is potentially in the complex. Pearson correlation coefficient greater than 0.7 was used for delineate putative protein-metabolite interactions. Altogether, we identified 30.70% of metabolite-protein Pearson correlations to exhibit values larger than 0.7.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article:

Supplementary figure 1.

Supplementary figure 2.

Supplementary figure 3.