Abstract
Developing countries scramble to contain and mitigate the spread of coronavirus disease 2019 (COVID-19), and world leaders demand equitable distribution of vaccines to trigger economic recovery. Although numerous strategies, including education, quarantine, and immunization, have been used to control COVID-19, the best method to curb this disease is vaccination. Due to the high demand for COVID 19 vaccine, developing countries must carefully identify and prioritize vulnerable populations and rationalize the vaccine allocation process. This study presents a mixed-integer linear programming model for equitable COVID-19 vaccine distribution in developing countries. Vaccines are grouped into cold, very cold, and ultra-cold categories where specific refrigeration is required for their storage and distribution. The possibility of storage for future periods, facing a shortage, budgetary considerations, manufacturer selection, order allocation, time-dependent capacities, and grouping of the heterogeneous population are among the practical assumptions in the proposed approach. Real-world data is used to demonstrate the efficiency and effectiveness of the mathematical programming approach proposed in this study.
Keywords: Vaccine supply chain, Coronavirus vaccine, Equitable distribution, Location-inventory problem, Mixed-integer linear programming model, COVID-19
Introduction
The Developing Countries Vaccine Manufacturers Network (DCVMN) is a public-health agency representing vaccine manufacturers from emerging countries. The DCVMN is committed to protecting all people through research and development activities and manufacturing and distributing coronavirus disease 2019 (COVID-19) vaccines to developing countries (Pagliusi et al., 2020). COVID-19 has stressed the importance of preventing pulmonary infections and stopping the pandemic with vaccinations (Dinleyici et al., 2020). The World Health Organization (WHO) statistics show that nearly 84,000,000 cases of the virus have been identified worldwide by the end of 2020, and about 1,800,000 people have lost their lives (https://coronavirus.jhu.edu). The coronavirus outbreak has drastically changed global social norms and has brought about disruptions in health services provision (Chandir et al., 2020). Since the beginning of the disease outbreak, various strategies such as border closure, social distance, widespread testing, and homestay have been proposed by statesmen, the WHO, and other relevant centers to reduce the virus’s spread and cut its transmission chain (Coudeville et al., 2020). Some researchers, such as Govindan et al. (2020), have tried to reduce this disease’s prevalence by classifying people in the community and offering solutions to each class of people. Although these protective measures are crucial to managing this disease, vaccination is a critical defensive behavior to control and eradicate it (Reiter et al., 2020). More than 100 companies are developing the COVID-19 vaccine worldwide, some of which are placed in phase III trials (Degeling et al., 2020). With the mass production of the vaccine, demand is expected to outstrip supply in the early stages. Therefore, the vaccine distribution process will be of great importance. Government budget constraints, cold supply chain management, prioritization of people in the community, and waiting time for receiving vaccines are essential factors affecting vaccine distribution worldwide. Therefore, this study develops a mixed-integer linear programming (MILP) model for equitable COVID-19 vaccine distribution considering the factors mentioned above.
Duijzer et al. (2018) examined the literature on the vaccine supply chain. They categorized these studies into the product, production, allocation, and distribution modeling groups by combining the WHO’s priorities for creating a robust and flexible vaccine supply chain with an operations research perspective. Similarly, De Boeck et al. (2019) studied the vaccine distribution studies in low- and middle-income countries. They identified several problems that had received little or no attention in the operations research literature. They found operations researchers heavily concentrate on the strategic decisions in vaccine distribution chains and, to a lesser extent, tactical and operational decisions. Hovav and Tsadikovich (2015) used mathematical programming and proposed an optimization model to design a healthcare supply chain to control influenza vaccines’ distribution and inventory control. Saif and Elhedhli (2016) developed a cold supply chain for the distribution and inventory management of vaccines considering environmental issues. For this purpose, they proposed a mixed-integer programming (MIP) model to minimize total costs and used a Lagrangian decomposition algorithm to solve the proposed model. Lim et al. (2019) proposed a MIP model for redesigning a cold supply chain for vaccine distribution by considering the location problem and limitations. They developed a hybrid heuristic algorithm for large-scale problem-solving and validated their model using several African countries’ data. A bi-objective model was developed by Zandkarimkhani et al. (2020) to design a perishable pharmaceutical supply chain network and minimize total costs and lost demands. They used an integrated inventory-location-routing problem and developed a chain to distribute Avonex (prefilled syringe for multiple sclerosis disease).
One of the issues that should be considered in developing a vaccine distribution supply chain is the ambient temperature in which the vaccines are stored and transported. The transportation of vaccines at unfavorable temperatures has led to adverse events, especially in developing countries. Hence, Lin et al. (2020) proposed a model to solve this problem by implementing inspection strategies. Their intended chain includes distributors and retailers, and they analyze inspection policies of vaccines’ transportation in the cold supply chain. Gamchi et al. (2020) presented a novel bi-objective model using the susceptible-infected-recovered epidemic model and vehicle routing problem for vaccine distribution. Their model simultaneously minimizes social costs and the costs of operating vehicles and groups of people in the community. They validated their model using data from a cholera vaccine distribution chain. Yang et al. (2020) developed a MIP model for vaccine distribution in low- and middle-income countries in line with the WHO Expanded Program on Immunization (EPI). Their model aims to minimize total costs with validation using data from a vaccine distribution chain in African countries. Bulula et al. (2020) used a micro-costing approach to analyze costs in the vaccine supply chain. They showed the delegation of the vaccine supply chain’s responsibilities from the medical stores to the EPI would lead to a 27% reduction in the vaccine distribution and storage costs.
The trade-offs between the equitable allocation of resources have been studied in energy (Sasse & Trutnevyte, 2019), bicycle-sharing (Conrow et al., 2018), and food donation (Fianu & Davis, 2018; Orgut et al., 2016, 2017). Equitable distribution of resources must consider a fair sharing of the resources among recipients; however, studies emphasizing equitable distribution of resources are limited (Fianu & Davis, 2018). Equity and fairness are among the most critical issues to be considered in the vaccine distribution chain (Abila et al., 2020). In this regard, Enayati and Özaltın (2020) proposed a mathematical programming model for equitable influenza vaccine distribution. They divided the population into several subgroups and prevented the epidemic outbreaks by allocating the necessary vaccines to each subgroup equitably. Rastegar et al. (2021) went one step further and developed a MILP model for equitable influenza vaccine distribution by considering the location-inventory problem under pandemic COVID-19 conditions. The possibility of storage for future periods, being faced with a shortage, and budget constraints are among the practical assumptions considered in this research. They proposed a novel objective function to consider the concept of equitable distribution. They then evaluated their proposed model’s performance using data from an influenza vaccine distribution chain in Iran.
The remainder of this paper is organized as follows. In Sect. 2, we present our motivation and contributions. The proposed mathematical model is presented in Sect. 3. In Sect. 4, we present a case study to demonstrate the applicability of the method proposed in this study. A sensitivity analysis is conducted in Sect. 5 to exhibit the efficacy and robustness of our vaccine distribution method. We conclude the paper with our conclusions and future research directions in Sect. 6.
Motivation and contributions
A review of the vaccine distribution literature shows the research in this field is in its infancy. Some researchers, such as De Boeck et al. (2019) and Corey et al. (2020), have studied strategic and managerial approaches to vaccine distribution. Other researchers such as Gamchi et al. (2020), Yang et al. (2020), and Rastegar et al. (2021) have proposed mathematical models for vaccine distribution and supply chain network optimization. Supply chains for vaccine distribution require unique features. For example, some vaccine distribution requires a cold or very cold supply chain (i.e., Gamchi et al., 2020; Lim et al., 2019; Yang et al., 2020). Other vaccine distributions may require waiting time considerations in the supply chain (i.e., Gamchi et al., 2020). There is also the concern for fair and equitable access to vaccines. Sometimes it is impossible to provide vaccines for all members of society. Therefore, equitable distribution becomes a critical consideration and assumption in vaccine distribution networks (Enayati & Özaltın, 2020; Rastegar et al., 2021). Distribution of COVID-19 vaccines requires cold, very cold, and ultra-cold refrigeration. Waiting time to receive the vaccines from manufacturers also directly affects the delivery of vaccines to the public. This study presents the first mathematical model for equitable COVID-19 vaccine distribution considering time-dependent capacity and triple refrigeration requirement (i.e., cold, very cold, and ultra-cold).
Rastegar et al. (2021) proposed a mathematical model for equitable influenza vaccine distribution. The current study presents a MILP model for equitable distribution of the COVID-19 vaccines. The model proposed by Rastegar et al. (2021) is a single-product model. However, the current study addresses the need for a multi-product model for COVID-19 vaccine distribution requiring cold, very cold, and ultra-cold refrigeration. Moreover, this study considers multiple cold supply chains with varying refrigeration requirements. This capability does not exist in the model proposed by Rastegar et al. (2021). The ordering and delivery times of vaccines can vary in the current study because of the potential waiting time between ordering and receiving the vaccines. However, the model proposed by Rastegar et al. (2021) does not consider waiting time because vaccines are provided in the same period they are ordered.
In summary, the contributions of this study are to (i) introduce a location-inventory MILP model for a fair and equitable COVID-19 vaccine distribution in developing countries; (ii) propose a model to consider cold, very cold, and ultra-cold supply chain network design and; (iii) take into consideration an equitable vaccine distribution model capable of manufacturer selection, order allocation, capacity planning, and waiting time management; and (iv) validating the proposed model with real-world data.
Proposed model
Satisfying the global demand for COVID-19 vaccines is not a short-term problem due to limited production and supply. Consequently, vaccine delivery is subject to the waiting time. This study presents a MILP model for equitable COVID-19 vaccine distribution in developing countries by considering the location-inventory problem. In addition to limited production and supply constraints, the refrigeration requirement for the COVID-19 vaccine and the need for cold, very cold, and ultra-cold supply chains is a huge hurdle in developing countries. Furthermore, the need for grouping and prioritizing the population is another added complexity for the COVIS-19 vaccine distribution. The proposed model is considered a budget constraint and allows the applicant country to make the following customizations to the model: Which manufacturer should be selected? What period should the vaccine be ordered to the manufacturer, and how much? What is the waiting time for each manufacturer? Which distribution centers are needed? Which distribution centers need ultra-cold refrigeration equipment? How many vaccines should be transferred from distribution centers to warehouses in different states in each period? How many vaccines should be stored in the state warehouses in each period? How many vaccines should be allocated to each group in each state and period?
To better understand the problem under study, the assumptions of the proposed model are given as follows:
The proposed model is considered as multi-product and multi-period.
The model determines the location of distribution centers.
The established distribution centers can handle cold and very cold refrigeration.
Ultra-cold refrigeration can only be installed in previously established distribution centers equipped with very cold refrigeration.
An order can be placed after an existing order is received.
One order can be placed with each manufacturer in each period.
Time-dependent capacity is considered for the manufacturers.
Distribution centers are capacitated.
Each manufacturer produces only one type of vaccine.
The possibility of storage in the state warehouses for future periods is considered.
The possibility of facing a shortage is considered.
Mathematical model
| Indices | |
| Vaccine type | |
| Distribution center | |
| State | |
| Group type | |
| Period (ordering time) | |
| Period (delivery time) |
| Parameters | |
| The total demand of group g for COVID-19 vaccines in state s | |
| If vaccine i requires very cold or ultra-cold refrigeration | |
| Otherwise (vaccine i requires cold refrigeration) | |
| If vaccine i requires ultra-cold refrigeration | |
| Otherwise (vaccine i requires very cold refrigeration) | |
| The ordering cost to the manufacturer of vaccine i in period t | |
| The set-up cost of the distribution center d equipped with cold refrigeration | |
| The set-up cost of the distribution center d equipped with very cold refrigeration | |
| The additional cost required to convert very cold refrigeration to ultra-cold refrigeration in a distribution center | |
| The purchasing cost of two-doses of vaccine i | |
| The transportation cost of two-doses of vaccine i from manufacturer location to distribution center d | |
| The transportation cost of two-doses of vaccine i from distribution center d to the warehouse is state s | |
| The holding cost for two-doses of vaccine i in the state warehouse s | |
| The maximum vaccine i production capacity, if ordering and delivery time are in periods w and t, respectively | |
| The maximum distribution center d capacity for cold refrigeration vaccines | |
| The maximum distribution center d capacity for vaccines requiring ultra-cold refrigeration | |
| The maximum distribution center d capacity for vaccines requiring very cold refrigeration | |
| The minimum percentage coverage rate for group g | |
| Available budget | |
| A big number |
| Variables | ||
| Binary | ||
| Binary | ||
| Binary | ||
| Binary | ||
| Integer | The doses of vaccines i ordered in period w by distribution center d received in period t | |
| Integer | The doses of vaccines i allocated to distribution center d in period t | |
| Integer | The doses of vaccines i allocated to group g in state s in period t | |
| Integer | The doses of vaccines i stored in the warehouse of state s in period t | |
| Integer | The doses of vaccines i shipped from distribution center d to warehouse of state s in period t |
Objective function
| 1 |
The proposed model’s objective function is derived from the model presented by Rastegar et al. (2021) that focuses on the equitable distribution of the vaccine. In this objective function, vaccines are distributed based on maximizing the minimum delivery-to-demand ratio.
| 2 |
Constraint (2) ensures that each group receives the vaccine at least up to the coverage rate.
| 3 |
| 4 |
Constraints (3) and (4) are related to the inventory balance in the state warehouses in period 1 and the periods greater than one, respectively.
| 5 |
Not exceeding the capacity of vaccine manufacturers has been shown by constraint (5).
| 6 |
| 7 |
| 8 |
Not exceeding the distribution centers’ capacity of cold, very cold, and ultra-cold refrigeration is guaranteed in constraints (6) to (88), respectively.
| 9 |
The condition for the purchase of vaccines from manufacturers is that the order should be placed with the manufacturer. This condition is considered in constraint (9).
| 10 |
| 11 |
According to constraint (10), if a distribution center with proper equipment for cold refrigeration vaccines has not been set up, it will not receive orders from manufacturers. Similarly, based on the constraint (11), if a distribution center has not been equipped with very cold and ultra-cold refrigeration, it will not receive orders from manufacturers.
| 12 |
One order can be placed with each manufacturer in each period. This condition is satisfied by constraint (12).
| 13 |
| 14 |
| 15 |
| 16 |
According to the location conditions, if a distribution center with proper equipment for cold refrigeration vaccines has not been set up, it will not be allowed to send cold refrigeration vaccines to the states’ warehouses. This condition is considered in constraint (13). Also, if a distribution center equipped with very cold refrigeration has not been set up, it will not be allowed to send very cold refrigeration vaccines to the states’ warehouses. Similarly, suppose a distribution center equipped with ultra-cold refrigeration has not been set up. In that case, that distribution center will not send ultra-cold vaccines to the states’ warehouses. These conditions are considered in constraints (14) and (15), respectively. Moreover, there is no possibility of setting up the distribution centers equipped with ultra-cold refrigeration until the distribution centers equipped with very cold refrigeration are set up. This condition is also expressed by constraint (16).
| 17 |
| 18 |
The amount of vaccines delivered to each distribution center in each period is calculated by constraint (14). Constraint (15) is responsible for establishing the inventory balance in distribution centers.
| 19 |
As long as the order is being processed (i.e., it has not yet been delivered to the distribution center), it will not be possible to place a new order with that manufacturer. This condition is satisfied by constraint (16).
| 20 |
In all the constraints of the proposed model, the ordering time should always be less than or equal to the delivery time. Constraint (17) has been used to meet this condition.
| 21 |
In the end, constraint (18) states that the supply chain’s total costs should not exceed the available budget. These costs include ordering cost to manufacturers, set-up cost of distribution centers for cold refrigeration, very cold refrigeration, and ultra-cold refrigeration vaccines, purchasing cost of vaccines, transportation cost from manufacturers’ location to distribution centers, transportation cost from distribution centers to state warehouses, and holding cost at the state warehouses.
As can be seen, the objective function of the proposed model is nonlinear. To linearize it, we define a new free variable () and replace it with . Therefore, the following holds true:
| 19 |
Based on Eq. (19), the following formula always holds true:
| 20 |
Therefore, based on Eq. (19) and Eq. (20), the proposed nonlinear model is converted to a linear one as follows:
| 21 |
| 22 |
Case study
This section demonstrates the applicability of the model proposed in this study with the data obtained from the Ministry of Health and Family Welfare (MOHFW) in India. COVID-19 vaccines have been discovered not so long ago, and, thereby, adequate information and data on their distribution are not yet fully available and accessible. As a result, some data, including transportation costs, vaccine prices, and manufacturers’ capacities, are simulated based on the MOHFW’s preliminary estimations. As in the study carried out by Rastegar et al. (2021), the heterogeneous population in this study is also divided into eight groups. The group numbers are not representative of priorities. These group numbers simply identify a segment of the population:
Group (1): infants and toddlers ages 6–35 months,
Group (2): pregnant women with pre-existing medical conditions,
Group (3): adults aged 65 years and older with pre-existing medical conditions,
Group (4): critical healthcare providers and first responders,
Group (5): pregnant women without pre-existing conditions,
Group (6): adults aged 65 years and older without pre-existing medical conditions,
Group (7): people with pre-existing medical conditions, and
Group (8): other people.
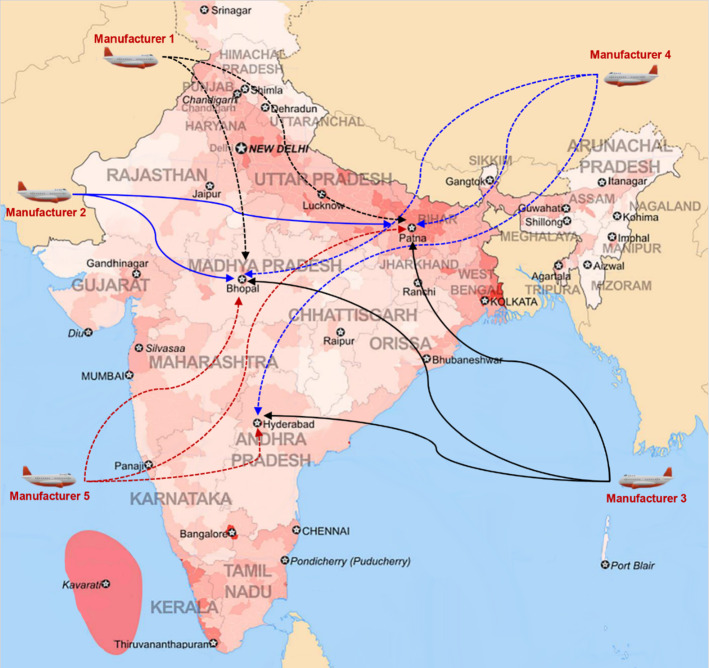
This study considers five vaccine types. Vaccine types 1 and 2 require ultra-cold refrigeration (− 70 °C ± 10 °C), vaccine types 3 and 4 require very cold refrigeration (− 25 °C to − 15 °C), and vaccine type 5 requires cold refrigeration (− 8 °C to − 2 °C). The vaccines are purchased from manufacturers outside India and are then transported to distribution centers. Afterward, vaccines are shipped to different distribution centers and distributed equitably among multiple warehouses in multiple states according to demand (See Fig. 1).
Fig. 1.
The vaccine distribution network
We should note data such as the demand for each group in each state, holding cost for the vaccines, coverage rate, and transportation cost between distribution centers and states have been extracted from historical data proposed by the MOHFW. Furthermore, the MOHFW’s estimated budget for vaccine purchase and distribution is 4.5 billion dollars. Table 1 presents the vaccine manufacturers’ capacities. Additional data is provided in Appendix A (Tables 8, 9, 10, 11, 12, 13, 14, 15 and 16).
Table 1.
The maximum delivery capacity of vaccine i for period t ordered in period w
| t | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| i | w | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1 | 0 | 0 | 7,500,000 | 10,000,000 | 15,000,000 | 19,000,000 | 25,000,000 | 30,000,000 |
| 1 | 2 | 0 | 0 | 3,000,000 | 7,000,000 | 11,000,000 | 15,000,000 | 20,000,000 | 25,000,000 |
| 1 | 3 | 0 | 0 | 0 | 5,000,000 | 9,000,000 | 13,000,000 | 18,000,000 | 22,000,000 |
| 1 | 4 | 0 | 0 | 0 | 0 | 5,000,000 | 9,000,000 | 15,000,000 | 20,000,000 |
| 1 | 5 | 0 | 0 | 0 | 0 | 0 | 7,500,000 | 12,500,000 | 17,500,000 |
| 1 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 6,000,000 | 10,000,000 |
| 1 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15,000,000 |
| 1 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2,500,000 |
| 2 | 1 | 0 | 6,000,000 | 15,000,000 | 20,000,000 | 28,000,000 | 32,000,000 | 40,000,000 | 60,000,000 |
| 2 | 2 | 0 | 0 | 10,000,000 | 14,000,000 | 20,500,000 | 27,000,000 | 35,000,000 | 42,000,000 |
| 2 | 3 | 0 | 0 | 0 | 8,000,000 | 13,500,000 | 20,000,000 | 27,500,000 | 34,000,000 |
| 2 | 4 | 0 | 0 | 0 | 0 | 12,000,000 | 18,000,000 | 25,500,000 | 32,000,000 |
| 2 | 5 | 0 | 0 | 0 | 0 | 0 | 9,500,000 | 16,000,000 | 30,000,000 |
| 2 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 10,000,000 | 25,000,000 |
| 2 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20,000,000 |
| 2 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 4,000,000 | 7,000,000 | 13,000,000 | 20,000,000 | 25,000,000 | 30,000,000 | 35,000,000 |
| 3 | 2 | 0 | 0 | 4,000,000 | 8,000,000 | 15,000,000 | 20,000,000 | 25,000,000 | 30,000,000 |
| 3 | 3 | 0 | 0 | 0 | 5,000,000 | 9,000,000 | 15,000,000 | 21,000,000 | 25,000,000 |
| 3 | 4 | 0 | 0 | 0 | 0 | 4,000,000 | 8,000,000 | 14,000,000 | 19,000,000 |
| 3 | 5 | 0 | 0 | 0 | 0 | 0 | 4,000,000 | 8,000,000 | 15,000,000 |
| 3 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 6,000,000 | 9,000,000 |
| 3 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5,000,000 |
| 3 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 0 | 4,000,000 | 7,000,000 | 11,000,000 | 17,500,000 | 21,000,000 | 27,500,000 | 34,000,000 |
| 4 | 2 | 0 | 0 | 1,500,000 | 3,000,000 | 6,000,000 | 8,750,000 | 11,250,000 | 15,500,000 |
| 4 | 3 | 0 | 0 | 0 | 2,000,000 | 3,750,000 | 6,000,000 | 8,750,000 | 11,500,000 |
| 4 | 4 | 0 | 0 | 0 | 0 | 1,500,000 | 3,000,000 | 4,500,000 | 6,000,000 |
| 4 | 5 | 0 | 0 | 0 | 0 | 0 | 5,000,000 | 8,000,000 | 11,000,000 |
| 4 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 2,000,000 | 5,250,000 |
| 4 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6,000,000 |
| 4 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 0 | 5,000,000 | 9,000,000 | 14,000,000 | 18,000,000 | 25,000,000 | 30,000,000 | 36,000,000 |
| 5 | 2 | 0 | 0 | 4,000,000 | 7,500,000 | 12,000,000 | 16,000,000 | 22,000,000 | 27,000,000 |
| 5 | 3 | 0 | 0 | 0 | 4,000,000 | 7,500,000 | 13,000,000 | 18,000,000 | 24,000,000 |
| 5 | 4 | 0 | 0 | 0 | 0 | 4,000,000 | 8,000,000 | 13,000,000 | 20,000,000 |
| 5 | 5 | 0 | 0 | 0 | 0 | 0 | 5,000,000 | 10,000,000 | 16,000,000 |
| 5 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 6,000,000 | 12,000,000 |
| 5 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7,000,000 |
| 5 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Table 8.
The demand for each group
| State | s | Group (g) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Uttar Pradesh | 1 | 17,370,453 | 136,901 | 1,189,945 | 1,165,607 | 1,232,233 | 2,210,133 | 610,884 | 213,966,569 |
| Bihar | 2 | 7,997,209 | 32,182 | 331,682 | 499,204 | 607,293 | 1,628,062 | 177,995 | 113,526,299 |
| Maharashtra | 3 | 9,309,824 | 38,385 | 684,242 | 480,298 | 531,381 | 2,047,686 | 220,520 | 109,831,887 |
| West Bengal | 4 | 10,574,496 | 47,384 | 366,198 | 547,857 | 510,432 | 1,682,009 | 209,009 | 85,671,917 |
| Madhya Pradesh | 5 | 13,984,533 | 35,530 | 267,620 | 495,085 | 272,592 | 1,021,796 | 137,209 | 69,144,601 |
| Rajasthan | 6 | 7,122,230 | 13,828 | 243,591 | 243,032 | 291,359 | 1,001,599 | 176,547 | 71,940,504 |
| Tamil Nadu | 7 | 6,200,806 | 36,331 | 158,305 | 233,510 | 332,000 | 849,269 | 239,867 | 69,791,179 |
| Karnataka | 8 | 5,665,246 | 23,414 | 92,349 | 405,377 | 373,408 | 978,112 | 180,654 | 59,844,125 |
| Gujarat | 9 | 5,440,436 | 23,251 | 293,834 | 185,263 | 206,762 | 957,655 | 182,568 | 56,582,632 |
| Andhra Pradesh | 10 | 6,417,458 | 29,164 | 122,473 | 204,846 | 306,568 | 703,711 | 115,883 | 46,003,290 |
| Odisha | 11 | 3,999,598 | 10,641 | 65,970 | 231,785 | 249,602 | 558,257 | 113,151 | 41,127,330 |
| Telangana | 12 | 3,200,720 | 19,292 | 83,460 | 177,136 | 226,847 | 616,784 | 73,655 | 34,964,837 |
| Jharkhand | 13 | 3,781,118 | 10,536 | 159,971 | 138,940 | 246,098 | 417,573 | 68,429 | 33,771,283 |
| Kerala | 14 | 2,257,706 | 9993 | 90,611 | 142,803 | 172,275 | 421,083 | 88,788 | 32,516,184 |
| Assam | 15 | 3,019,352 | 19,518 | 35,994 | 121,062 | 213,633 | 572,966 | 70,924 | 31,553,590 |
| Punjab | 16 | 3,790,538 | 15,739 | 179,620 | 84,395 | 203,320 | 428,190 | 57,741 | 25,381,830 |
| Chhattisgarh | 17 | 2,835,943 | 6468 | 103,989 | 147,179 | 123,582 | 369,434 | 64,755 | 25,784,881 |
| Haryana | 18 | 2,160,631 | 8392 | 154,933 | 112,818 | 148,955 | 401,139 | 83,545 | 25,134,279 |
| Delhi | 19 | 1,071,993 | 6964 | 42,554 | 84,195 | 115,861 | 205,254 | 48,186 | 17,135,916 |
| Jammu & Kashmir | 20 | 1,189,383 | 8989 | 18,020 | 40,819 | 48,076 | 161,670 | 42,380 | 12,096,984 |
| Uttarakhand | 21 | 1,050,549 | 2830 | 15,251 | 50,628 | 40,805 | 117,478 | 27,271 | 9,946,045 |
| Himachal Pradesh | 22 | 446,258 | 3248 | 8481 | 20,122 | 29,587 | 80,285 | 9042 | 6,854,931 |
| Tripura | 23 | 334,328 | 2205 | 22,485 | 12,093 | 17,280 | 41,963 | 7894 | 3,731,546 |
| Meghalaya | 24 | 300,049 | 2237 | 15,605 | 12,458 | 16,086 | 35,218 | 6792 | 2,978,266 |
| Manipur | 25 | 327,429 | 2041 | 15,333 | 12,366 | 9563 | 40,525 | 9727 | 2,674,562 |
| Nagaland | 26 | 157,490 | 492 | 11,525 | 6749 | 14,501 | 21,820 | 7172 | 2,029,945 |
| Goa | 27 | 128,919 | 545 | 4518 | 6821 | 10,570 | 15,934 | 4849 | 1,414,093 |
| Arunachal Pradesh | 28 | 104,451 | 248 | 4145 | 7067 | 8911 | 24,374 | 3647 | 1,417,614 |
| Puducherry | 29 | 119,550 | 672 | 5682 | 4240 | 5909 | 18,446 | 2037 | 1,257,004 |
| Mizoram | 30 | 111,794 | 184 | 1421 | 4957 | 5529 | 12,144 | 3769 | 1,099,447 |
| Chandigarh | 31 | 74,240 | 503 | 3320 | 5213 | 8087 | 11,362 | 2974 | 1,052,775 |
| Sikkim | 32 | 113,085 | 287 | 2164 | 4003 | 2204 | 8263 | 1110 | 559,134 |
| Dadra and Nagar Haveli and Daman and Diu | 33 | 54,118 | 105 | 1851 | 1847 | 2214 | 7611 | 1341 | 546,637 |
| Andaman and Nicobar Islands | 34 | 33,221 | 195 | 848 | 1251 | 1779 | 4550 | 1285 | 373,908 |
| Ladakh | 35 | 30,611 | 191 | 1433 | 1156 | 894 | 3789 | 909 | 250,040 |
| Lakshadweep | 36 | 6397 | 48 | 97 | 220 | 259 | 870 | 228 | 65,065 |
Table 9.
The ordering cost to the manufacturer of vaccine i in period t
| t | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 9100 | 9300 | 8200 | 9200 | 9300 | 8800 | 8800 | 8000 |
| 2 | 8200 | 8600 | 9100 | 9900 | 8900 | 10,000 | 9300 | 9000 |
| 3 | 9500 | 8400 | 8200 | 9400 | 9300 | 9200 | 8800 | 9900 |
| 4 | 9300 | 9300 | 9700 | 8700 | 9900 | 9600 | 8600 | 9000 |
| 5 | 9700 | 9600 | 9000 | 9200 | 8900 | 8400 | 9500 | 8400 |
Table 10.
The cost of setting up distribution centers equipped with cold refrigeration
| Distribution center | ||||
|---|---|---|---|---|
| Patna | Bhopal | New Delhi | Hyderabad | |
| 18,400,000 | 18,800,000 | 19,400,000 | 19,200,000 | |
Table 11.
The cost of setting up distribution centers equipped with very cold refrigeration
| Distribution center | ||||
|---|---|---|---|---|
| Patna | Bhopal | New Delhi | Hyderabad | |
| 46,000,000 | 47,000,000 | 48,500,000 | 48,000,000 | |
Amn
Table 12.
The coverage rate of each group
| Group | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Coverage rate () | 0.75 | 0.9 | 0.85 | 1 | 0.7 | 0.6 | 0.75 | 0.05 |
Table 13.
The purchasing cost for two doses of vaccine i
| Vaccine type | |||||
|---|---|---|---|---|---|
| 15.5 | 16.2 | 13.1 | 13.7 | 8.2 | |
Table 14.
Transportation cost for two doses of vaccine i from manufacturer’s location to distribution center d
| Distribution center | ||||
|---|---|---|---|---|
| i | Patna | Bhopal | New Delhi | Hyderabad |
| 1 | 8.25 | 9.08 | 8.91 | 9.8 |
| 2 | 7.6 | 8.36 | 8.21 | 9.03 |
| 3 | 8.32 | 9.15 | 8.99 | 9.89 |
| 4 | 7.69 | 8.46 | 8.31 | 9.14 |
| 5 | 6.89 | 7.58 | 7.44 | 8.18 |
Table 15.
The holding cost for two doses of vaccine i in the state s warehouse
| State (s) | i = 1 | i = 2 | i = 3 | i = 4 | i = 5 |
|---|---|---|---|---|---|
| 1 | 1.7 | 1.7 | 0.68 | 0.68 | 0.58 |
| 2 | 1.63 | 1.63 | 0.65 | 0.65 | 0.56 |
| 3 | 1.5 | 1.5 | 0.6 | 0.6 | 0.52 |
| 4 | 1.75 | 1.75 | 0.7 | 0.7 | 0.6 |
| 5 | 1.78 | 1.78 | 0.71 | 0.71 | 0.61 |
| 6 | 1.13 | 1.13 | 0.45 | 0.45 | 0.39 |
| 7 | 0.98 | 0.98 | 0.39 | 0.39 | 0.34 |
| 8 | 2.05 | 2.05 | 0.82 | 0.82 | 0.71 |
| 9 | 1.05 | 1.05 | 0.42 | 0.42 | 0.36 |
| 10 | 0.83 | 0.83 | 0.33 | 0.33 | 0.28 |
| 11 | 1.53 | 1.53 | 0.61 | 0.61 | 0.52 |
| 12 | 1.4 | 1.4 | 0.56 | 0.56 | 0.48 |
| 13 | 1.15 | 1.15 | 0.46 | 0.46 | 0.4 |
| 14 | 1.38 | 1.38 | 0.55 | 0.55 | 0.47 |
| 15 | 1.3 | 1.3 | 0.52 | 0.52 | 0.45 |
| 16 | 0.8 | 0.8 | 0.32 | 0.32 | 0.28 |
| 17 | 1.55 | 1.55 | 0.62 | 0.62 | 0.53 |
| 18 | 1.53 | 1.53 | 0.61 | 0.61 | 0.52 |
| 19 | 1.45 | 1.45 | 0.58 | 0.58 | 0.5 |
| 20 | 1.23 | 1.23 | 0.49 | 0.49 | 0.42 |
| 21 | 1.3 | 1.3 | 0.52 | 0.52 | 0.45 |
| 22 | 1.1 | 1.1 | 0.44 | 0.44 | 0.38 |
| 23 | 0.95 | 0.95 | 0.38 | 0.38 | 0.33 |
| 24 | 1.2 | 1.2 | 0.48 | 0.48 | 0.41 |
| 25 | 1.28 | 1.28 | 0.51 | 0.51 | 0.44 |
| 26 | 1.08 | 1.08 | 0.43 | 0.43 | 0.37 |
| 27 | 1.28 | 1.28 | 0.51 | 0.51 | 0.44 |
| 28 | 1.33 | 1.33 | 0.53 | 0.53 | 0.46 |
| 29 | 1.13 | 1.13 | 0.45 | 0.45 | 0.39 |
| 30 | 1.23 | 1.23 | 0.49 | 0.49 | 0.42 |
| 31 | 1.3 | 1.3 | 0.52 | 0.52 | 0.45 |
| 32 | 1.09 | 1.09 | 0.93 | 0.93 | 0.81 |
| 33 | 1.01 | 1.01 | 0.86 | 0.86 | 0.75 |
| 34 | 0.98 | 0.98 | 0.83 | 0.83 | 0.72 |
| 35 | 0.94 | 0.94 | 0.8 | 0.8 | 0.7 |
| 36 | 0.84 | 0.84 | 0.71 | 0.71 | 0.62 |
Table 16.
The distribution capacity of vaccines requiring cold, very cold, and ultra-cold refrigeration
| Distribution center | ||||
|---|---|---|---|---|
| Patna | Bhopal | New Delhi | Hyderabad | |
| 36,000,000 | 38,000,000 | 40,000,000 | 37,000,000 | |
| 90,000,000 | 90,000,000 | 97,500,000 | 87,000,000 | |
| 45,000,000 | 52,000,000 | 45,000,000 | 42,000,000 | |
The 7,500,000 in the first row of Table 1 indicates that if the order is placed to manufacturer 1 in period 1, the manufacturer will deliver a maximum of 7,500,000 doses of vaccines in period 3. The proposed model was run with the described data in GAMS software using CPLEX solver. The obtained results are as follows:
Distribution centers in Patna, Bhopal, and Hyderabad were set up to distribute the vaccines. Patna and Bhopal distribution centers can distribute vaccines requiring cold, very cold, and ultra-cold refrigeration, whereas Hyderabad distribution center can distribute vaccines requiring cold and very cold refrigeration.
Orders are placed with all five manufacturers. Patna and Bhopal distribution centers receive vaccines from all five manufacturers, but vaccines are purchased only from manufacturers 3, 4, and 5 for the Hyderabad distribution center.
With the available budget of 4.5 billion dollars, 186,096,615 doses of COVID-19 vaccines were purchased. The optimal doses of vaccines ordered to each manufacturer and the optimal doses of vaccines delivered by each distribution center are shown in Tables 2 and 3, respectively.
Table 2.
The optimal doses of vaccines delivered to distribution centers in each period
| t | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| i | d | w | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1 | 1 | 0 | 7,500,000 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 6 | 0 | 0 | 0 | 0 | 0 | 6,000,000 | 0 |
| 1 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 11,123,260 |
| 1 | 2 | 3 | 0 | 0 | 0 | 0 | 10,488,400 | 0 | 0 |
| 1 | 2 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 3,876,740 |
| 2 | 1 | 1 | 0 | 13,011,028 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 3 | 0 | 0 | 0 | 0 | 0 | 16,736,140 | 0 |
| 2 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 9,756,236 |
| 2 | 2 | 1 | 0 | 1,988,972 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 3 | 0 | 0 | 0 | 0 | 0 | 4,615,839 | 0 |
| 3 | 1 | 1 | 4,000,000 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 2 | 0 | 3,812,266 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 3 | 0 | 0 | 3,518,782 | 0 | 0 | 0 | 0 |
| 3 | 1 | 4 | 0 | 0 | 0 | 4,000,000 | 0 | 0 | 0 |
| 3 | 1 | 5 | 0 | 0 | 0 | 0 | 1,289,245 | 0 | 0 |
| 3 | 1 | 6 | 0 | 0 | 0 | 0 | 0 | 338,181 | 0 |
| 3 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 3,389,863 |
| 3 | 2 | 3 | 0 | 0 | 286,488 | 0 | 0 | 0 | 0 |
| 3 | 2 | 5 | 0 | 0 | 0 | 0 | 2,710,755 | 0 | 0 |
| 3 | 2 | 6 | 0 | 0 | 0 | 0 | 0 | 5,491,595 | 0 |
| 3 | 2 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1,610,137 |
| 3 | 4 | 2 | 0 | 187,734 | 0 | 0 | 0 | 0 | 0 |
| 3 | 4 | 3 | 0 | 0 | 1,194,730 | 0 | 0 | 0 | 0 |
| 3 | 4 | 6 | 0 | 0 | 0 | 0 | 0 | 170,224 | 0 |
| 4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 11,522,299 |
| 4 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 4,080,327 |
| 4 | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 18,397,374 |
| 5 | 1 | 2 | 0 | 3,690,682 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 3 | 0 | 0 | 1,405,615 | 0 | 0 | 0 | 0 |
| 5 | 1 | 4 | 0 | 0 | 0 | 529,233 | 0 | 0 | 0 |
| 5 | 1 | 5 | 0 | 0 | 0 | 0 | 4,492,539 | 0 | 0 |
| 5 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 5,553,466 |
| 5 | 2 | 1 | 4,999,780 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 2 | 2 | 0 | 309,318 | 0 | 0 | 0 | 0 | 0 |
| 5 | 2 | 3 | 0 | 0 | 170,980 | 0 | 0 | 0 | 0 |
| 5 | 2 | 4 | 0 | 0 | 0 | 3,154,955 | 0 | 0 | 0 |
| 5 | 2 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1,181,053 |
| 5 | 4 | 1 | 220 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 4 | 3 | 0 | 0 | 2,423,405 | 0 | 0 | 0 | 0 |
| 5 | 4 | 4 | 0 | 0 | 0 | 315,812 | 0 | 0 | 0 |
| 5 | 4 | 5 | 0 | 0 | 0 | 0 | 507,461 | 0 | 0 |
| 5 | 4 | 6 | 0 | 0 | 0 | 0 | 0 | 6,000,000 | 0 |
| 5 | 4 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 265,481 |
Table 3.
The optimal doses of vaccines delivered to distribution centers in each period
| t | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | d | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1 | 0 | 7,500,000 | 0 | 0 | 0 | 6,000,000 | 11,123,260 |
| 1 | 2 | 0 | 0 | 0 | 0 | 10,488,400 | 0 | 3,876,740 |
| 2 | 1 | 0 | 13,011,028 | 0 | 0 | 0 | 16,736,140 | 9,756,236 |
| 2 | 2 | 0 | 1,988,972 | 0 | 0 | 0 | 4,615,839 | 0 |
| 3 | 1 | 4,000,000 | 3,812,266 | 3,518,782 | 4,000,000 | 1,289,245 | 338,181 | 3,389,863 |
| 3 | 2 | 0 | 0 | 286,488 | 0 | 2,710,755 | 5,491,595 | 1,610,137 |
| 3 | 4 | 0 | 187,734 | 1,194,730 | 0 | 0 | 170,224 | 0 |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 11,522,299 |
| 4 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 4,080,327 |
| 4 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 18,397,374 |
| 5 | 1 | 0 | 3,690,682 | 1,405,615 | 529,233 | 4,492,539 | 0 | 5,553,466 |
| 5 | 2 | 4,999,780 | 309,318 | 170,980 | 3,154,955 | 0 | 0 | 1,181,053 |
| 5 | 4 | 220 | 0 | 2,423,405 | 315,812 | 507,461 | 6,000,000 | 265,481 |
For example, 7,500,000 in the first row of Table 2 indicates that distribution center 1 (Patna) has ordered type 1 vaccine in period 1 and received 7.5 million doses of vaccines in period 3.
The numbers included in Table 3 indicate the optimal doses of vaccines delivered to each distribution center in different periods. For example, 11,123,260 in the first row and last column of this table suggests that 11,123,260 doses of vaccine type 1 have been delivered to the Patna distribution center in period 8. Table 2 shows that this order has been placed in period 7.
The optimal doses of vaccines assigned to group 1 are given in Table 4. Similarly, in Appendix B (Tables 17, 18, 19, 20, 21, 22 and 23), the optimal doses of vaccines allocated to groups 2 to 8 are presented, respectively.
The optimal doses of vaccines shipped from distribution centers to the state warehouses in each period are shown in Table 5.
Finally, Table 6 presents the number of vaccine doses stored in the state warehouses in each period.
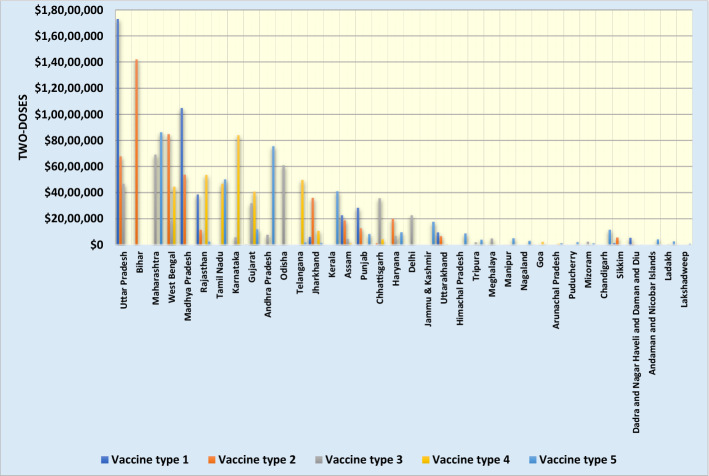
For example, 3,967,289 in the first row of Table 5 represents the number of type 1 vaccine doses shipped from Patna distribution center to state 1 (Uttar Pradesh) in period 3. Figure 2 presents the total doses of vaccines delivered to each state.
Table 4.
The optimal doses of vaccines assigned to group 1 in each period
| t | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| i | g | s | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 6,378,820 | |
| 1 | 1 | 5 | 0 | 0 | 0 | 0 | 10,488,400 | 0 | 0 | |
| 1 | 1 | 15 | 0 | 2,264,514 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 2,842,904 | |
| 1 | 1 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 945,494 | |
| 1 | 1 | 32 | 0 | 0 | 0 | 0 | 101,776 | 0 | 0 | |
| 2 | 1 | 1 | 0 | 6,649,020 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 5,997,907 | 0 | |
| 2 | 1 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 7,930,872 | |
| 2 | 1 | 13 | 0 | 2,835,839 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 1 | 18 | 0 | 0 | 1,620,474 | 0 | 0 | 0 | 0 | |
| 2 | 1 | 33 | 0 | 0 | 48,706 | 0 | 0 | 0 | 0 | |
| 3 | 1 | 10 | 0 | 0 | 778,223 | 0 | 0 | 0 | 0 | |
| 3 | 1 | 11 | 1,951,197 | 0 | 0 | 0 | 0 | 0 | 1,048,502 | |
| 3 | 1 | 17 | 0 | 0 | 0 | 2,126,958 | 0 | 0 | 0 | |
| 3 | 1 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 964,793 | |
| 3 | 1 | 24 | 0 | 0 | 0 | 0 | 0 | 270,044 | 0 | |
| 3 | 1 | 35 | 27,549 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 1 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 5,341,673 | |
| 4 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 4,650,605 | |
| 4 | 1 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 4,248,935 | |
| 4 | 1 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 4,080,327 | |
| 4 | 1 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 2,400,540 | |
| 4 | 1 | 27 | 0 | 0 | 0 | 0 | 0 | 0 | 116,027 | |
| 5 | 1 | 3 | 4,999,780 | 0 | 0 | 0 | 0 | 0 | 1,982,588 | |
| 5 | 1 | 10 | 0 | 0 | 0 | 0 | 0 | 4,034,871 | 0 | |
| 5 | 1 | 14 | 0 | 0 | 1,387,547 | 0 | 305,733 | 0 | 0 | |
| 5 | 1 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 892,038 | |
| 5 | 1 | 22 | 0 | 0 | 0 | 0 | 0 | 0 | 401,632 | |
| 5 | 1 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 300,895 | |
| 5 | 1 | 25 | 0 | 0 | 0 | 0 | 0 | 0 | 294,686 | |
| 5 | 1 | 26 | 0 | 0 | 0 | 0 | 0 | 0 | 141,741 | |
| 5 | 1 | 28 | 0 | 94,005 | 0 | 0 | 0 | 0 | 0 | |
| 5 | 1 | 29 | 0 | 0 | 0 | 0 | 0 | 0 | 107,595 | |
| 5 | 1 | 30 | 0 | 0 | 0 | 0 | 0 | 0 | 100,614 | |
| 5 | 1 | 31 | 0 | 0 | 0 | 0 | 66,816 | 0 | 0 | |
| 5 | 1 | 34 | 0 | 0 | 0 | 0 | 29,898 | 0 | 0 | |
| 5 | 1 | 36 | 0 | 0 | 0 | 0 | 0 | 0 | 5757 | |
Table 17.
The optimal doses of vaccines allocated to group 2 in each period
| t | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | g | s | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 9 | 0 | 0 | 0 | 0 | 0 | 22,785 |
| 1 | 2 | 27 | 0 | 0 | 0 | 0 | 0 | 534 |
| 1 | 2 | 32 | 0 | 0 | 0 | 0 | 281 | 0 |
| 2 | 2 | 1 | 134,162 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 2 | 0 | 0 | 0 | 0 | 31,538 | 0 |
| 2 | 2 | 5 | 0 | 34,819 | 0 | 0 | 0 | 0 |
| 2 | 2 | 13 | 10,325 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 17 | 0 | 0 | 0 | 0 | 6338 | 0 |
| 2 | 2 | 18 | 0 | 0 | 0 | 0 | 0 | 8224 |
| 2 | 2 | 21 | 2773 | 0 | 0 | 0 | 0 | 0 |
| 3 | 2 | 11 | 0 | 0 | 0 | 0 | 0 | 10,428 |
| 3 | 2 | 15 | 0 | 0 | 0 | 0 | 0 | 19,127 |
| 3 | 2 | 19 | 0 | 0 | 0 | 0 | 0 | 6824 |
| 3 | 2 | 24 | 0 | 0 | 0 | 0 | 0 | 2192 |
| 3 | 2 | 28 | 0 | 0 | 0 | 0 | 243 | 0 |
| 4 | 2 | 4 | 0 | 0 | 0 | 0 | 0 | 46,436 |
| 4 | 2 | 6 | 0 | 0 | 0 | 0 | 0 | 13,551 |
| 4 | 2 | 7 | 0 | 0 | 0 | 0 | 0 | 35,604 |
| 4 | 2 | 8 | 0 | 0 | 0 | 0 | 0 | 22,945 |
| 4 | 2 | 10 | 0 | 0 | 0 | 0 | 0 | 28,580 |
| 4 | 2 | 12 | 0 | 0 | 0 | 0 | 0 | 18,906 |
| 5 | 2 | 3 | 0 | 0 | 0 | 0 | 37,617 | 0 |
| 5 | 2 | 14 | 0 | 9793 | 0 | 0 | 0 | 0 |
| 5 | 2 | 16 | 0 | 0 | 0 | 0 | 0 | 15,424 |
| 5 | 2 | 20 | 0 | 0 | 0 | 0 | 0 | 8809 |
| 5 | 2 | 22 | 0 | 0 | 0 | 0 | 0 | 3183 |
| 5 | 2 | 23 | 0 | 0 | 0 | 0 | 0 | 2160 |
| 5 | 2 | 25 | 0 | 0 | 0 | 0 | 2000 | 0 |
| 5 | 2 | 26 | 0 | 0 | 0 | 0 | 0 | 482 |
| 5 | 2 | 29 | 0 | 0 | 0 | 658 | 0 | 0 |
| 5 | 2 | 30 | 0 | 0 | 0 | 0 | 0 | 180 |
| 5 | 2 | 31 | 0 | 492 | 0 | 0 | 0 | 0 |
| 5 | 2 | 33 | 0 | 102 | 0 | 0 | 0 | 0 |
| 5 | 2 | 34 | 0 | 0 | 0 | 0 | 0 | 191 |
| 5 | 2 | 35 | 0 | 0 | 0 | 0 | 0 | 187 |
| 5 | 2 | 36 | 0 | 0 | 0 | 0 | 0 | 47 |
Table 18.
The optimal doses of vaccines allocated to group 3 in each period
| t | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | g | s | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 3 | 1 | 0 | 0 | 0 | 1,011,454 | 0 | 0 |
| 1 | 3 | 32 | 0 | 0 | 0 | 2109 | 0 | 0 |
| 2 | 3 | 2 | 0 | 0 | 0 | 0 | 0 | 323,389 |
| 2 | 3 | 5 | 260,929 | 0 | 0 | 0 | 0 | 0 |
| 2 | 3 | 6 | 237,501 | 0 | 0 | 0 | 0 | 0 |
| 2 | 3 | 13 | 155,971 | 0 | 0 | 0 | 0 | 0 |
| 2 | 3 | 15 | 0 | 0 | 0 | 0 | 0 | 35,094 |
| 3 | 3 | 8 | 0 | 0 | 90,040 | 0 | 0 | 0 |
| 3 | 3 | 9 | 0 | 286,488 | 0 | 0 | 0 | 0 |
| 3 | 3 | 11 | 0 | 0 | 0 | 0 | 0 | 64,320 |
| 3 | 3 | 18 | 0 | 0 | 0 | 0 | 0 | 151,059 |
| 3 | 3 | 19 | 0 | 0 | 0 | 0 | 0 | 41,490 |
| 4 | 3 | 4 | 0 | 0 | 0 | 0 | 0 | 357,043 |
| 4 | 3 | 12 | 0 | 0 | 0 | 0 | 0 | 81,373 |
| 4 | 3 | 17 | 0 | 0 | 0 | 0 | 0 | 101,389 |
| 4 | 3 | 21 | 0 | 0 | 0 | 0 | 0 | 14,869 |
| 4 | 3 | 24 | 0 | 0 | 0 | 0 | 0 | 15,214 |
| 4 | 3 | 27 | 0 | 0 | 0 | 0 | 0 | 4405 |
| 4 | 3 | 28 | 0 | 0 | 0 | 0 | 0 | 4041 |
| 5 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 667,135 |
| 5 | 3 | 7 | 0 | 0 | 0 | 0 | 154,347 | |
| 5 | 3 | 10 | 0 | 0 | 0 | 0 | 0 | 119,411 |
| 5 | 3 | 14 | 0 | 0 | 0 | 0 | 0 | 88,345 |
| 5 | 3 | 16 | 0 | 0 | 0 | 0 | 0 | 175,129 |
| 5 | 3 | 20 | 0 | 0 | 0 | 0 | 0 | 17,569 |
| 5 | 3 | 22 | 0 | 0 | 0 | 0 | 0 | 8268 |
| 5 | 3 | 23 | 0 | 0 | 0 | 0 | 0 | 21,922 |
| 5 | 3 | 25 | 0 | 0 | 0 | 14,949 | 0 | 0 |
| 5 | 3 | 26 | 0 | 0 | 0 | 0 | 0 | 11,236 |
| 5 | 3 | 29 | 0 | 0 | 0 | 5539 | 0 | 0 |
| 5 | 3 | 30 | 0 | 0 | 0 | 0 | 1385 | 0 |
| 5 | 3 | 31 | 0 | 0 | 0 | 0 | 0 | 3237 |
| 5 | 3 | 33 | 0 | 1804 | 0 | 0 | 0 | 0 |
| 5 | 3 | 34 | 0 | 0 | 0 | 0 | 826 | 0 |
| 5 | 3 | 35 | 0 | 0 | 0 | 0 | 0 | 1397 |
| 5 | 3 | 36 | 0 | 0 | 0 | 0 | 0 | 94 |
Table 19.
The optimal doses of vaccines allocated to group 4 in each period
| t | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| i | g | s | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 4 | 32 | 0 | 0 | 0 | 0 | 4003 | 0 | 0 |
| 2 | 4 | 2 | 0 | 0 | 0 | 0 | 0 | 499,204 | 0 |
| 2 | 4 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 547,857 |
| 2 | 4 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 495,085 |
| 2 | 4 | 21 | 0 | 0 | 0 | 50,628 | 0 | 0 | 0 |
| 3 | 4 | 1 | 0 | 1,165,607 | 0 | 0 | 0 | 0 | 0 |
| 3 | 4 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 185,263 |
| 3 | 4 | 11 | 0 | 0 | 0 | 0 | 0 | 231,785 | 0 |
| 3 | 4 | 17 | 0 | 0 | 147,179 | 0 | 0 | 0 | 0 |
| 3 | 4 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 84,195 |
| 3 | 4 | 24 | 12,458 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 4 | 28 | 0 | 0 | 0 | 0 | 0 | 0 | 7067 |
| 3 | 4 | 30 | 0 | 0 | 0 | 0 | 0 | 0 | 4957 |
| 3 | 4 | 35 | 0 | 1156 | 0 | 0 | 0 | 0 | 0 |
| 4 | 4 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 405,377 |
| 4 | 4 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 121,062 |
| 5 | 4 | 3 | 0 | 0 | 480,298 | 0 | 0 | 0 | 0 |
| 5 | 4 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 243,032 |
| 5 | 4 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 233,510 |
| 5 | 4 | 10 | 0 | 0 | 0 | 0 | 204,846 | 0 | 0 |
| 5 | 4 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 177,136 |
| 5 | 4 | 13 | 0 | 0 | 0 | 138,940 | 0 | 0 | 0 |
| 5 | 4 | 14 | 0 | 0 | 0 | 0 | 0 | 142,803 | 0 |
| 5 | 4 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 84,395 |
| 5 | 4 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 112,818 |
| 5 | 4 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 40,819 |
| 5 | 4 | 22 | 0 | 0 | 0 | 0 | 0 | 0 | 20,122 |
| 5 | 4 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 12,093 |
| 5 | 4 | 25 | 0 | 0 | 12,366 | 0 | 0 | 0 | 0 |
| 5 | 4 | 26 | 0 | 0 | 0 | 0 | 0 | 0 | 6749 |
| 5 | 4 | 27 | 0 | 0 | 0 | 0 | 0 | 0 | 6821 |
| 5 | 4 | 29 | 0 | 0 | 0 | 0 | 4240 | 0 | 0 |
| 5 | 4 | 31 | 0 | 0 | 0 | 0 | 0 | 5213 | 0 |
| 5 | 4 | 33 | 0 | 0 | 0 | 1847 | 0 | 0 | 0 |
| 5 | 4 | 34 | 0 | 0 | 0 | 0 | 1251 | 0 | 0 |
| 5 | 4 | 36 | 220 | 0 | 0 | 0 | 0 | 0 | 0 |
Table 20.
The optimal doses of vaccines allocated to group 5 in each period
| t | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | g | s | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5 | 1 | 0 | 0 | 0 | 0 | 0 | 862,564 |
| 1 | 5 | 6 | 0 | 0 | 0 | 0 | 0 | 256,395 |
| 1 | 5 | 32 | 0 | 0 | 0 | 1939 | 0 | 0 |
| 2 | 5 | 2 | 0 | 0 | 0 | 0 | 0 | 534,417 |
| 2 | 5 | 5 | 0 | 0 | 0 | 0 | 239,880 | 0 |
| 2 | 5 | 13 | 0 | 216,566 | 0 | 0 | 0 | 0 |
| 2 | 5 | 15 | 0 | 0 | 0 | 0 | 187,997 | 0 |
| 2 | 5 | 17 | 0 | 0 | 0 | 0 | 108,752 | 0 |
| 2 | 5 | 25 | 0 | 0 | 0 | 0 | 0 | 8415 |
| 2 | 5 | 33 | 0 | 0 | 1948 | 0 | 0 | 0 |
| 3 | 5 | 8 | 0 | 0 | 0 | 0 | 328,599 | 0 |
| 3 | 5 | 9 | 0 | 0 | 0 | 181,950 | 0 | 0 |
| 3 | 5 | 11 | 0 | 0 | 0 | 0 | 0 | 219,649 |
| 3 | 5 | 19 | 0 | 0 | 0 | 0 | 0 | 101,957 |
| 3 | 5 | 24 | 14,155 | 0 | 0 | 0 | 0 | 0 |
| 4 | 5 | 4 | 0 | 0 | 0 | 0 | 0 | 449,180 |
| 4 | 5 | 12 | 0 | 0 | 0 | 0 | 0 | 199,625 |
| 4 | 5 | 21 | 0 | 0 | 0 | 0 | 0 | 35,908 |
| 4 | 5 | 27 | 0 | 0 | 0 | 0 | 0 | 9301 |
| 4 | 5 | 28 | 0 | 0 | 0 | 0 | 0 | 7841 |
| 5 | 5 | 3 | 0 | 0 | 467,615 | 0 | 0 | 0 |
| 5 | 5 | 7 | 0 | 0 | 0 | 0 | 292,160 | 0 |
| 5 | 5 | 10 | 0 | 0 | 0 | 0 | 0 | 269,779 |
| 5 | 5 | 14 | 0 | 0 | 0 | 0 | 151,602 | 0 |
| 5 | 5 | 16 | 0 | 0 | 0 | 0 | 0 | 178,921 |
| 5 | 5 | 18 | 0 | 0 | 0 | 0 | 0 | 131,080 |
| 5 | 5 | 20 | 0 | 0 | 0 | 0 | 0 | 42,306 |
| 5 | 5 | 22 | 0 | 0 | 0 | 0 | 0 | 26,036 |
| 5 | 5 | 23 | 0 | 0 | 0 | 0 | 0 | 15,206 |
| 5 | 5 | 26 | 0 | 0 | 0 | 0 | 0 | 12,760 |
| 5 | 5 | 29 | 0 | 0 | 0 | 0 | 0 | 5199 |
| 5 | 5 | 30 | 0 | 0 | 4865 | 0 | 0 | 0 |
| 5 | 5 | 31 | 0 | 0 | 0 | 7116 | 0 | 0 |
| 5 | 5 | 34 | 0 | 0 | 0 | 0 | 0 | 1565 |
| 5 | 5 | 35 | 0 | 0 | 0 | 0 | 0 | 786 |
| 5 | 5 | 36 | 0 | 0 | 0 | 0 | 0 | 227 |
Table 21.
The optimal doses of vaccines allocated to group 6 in each period
| t | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | g | s | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 6 | 1 | 0 | 0 | 0 | 0 | 1,326,080 | 0 |
| 1 | 6 | 32 | 0 | 0 | 0 | 6197 | 0 | 0 |
| 2 | 6 | 2 | 0 | 0 | 0 | 0 | 0 | 976,838 |
| 2 | 6 | 5 | 0 | 0 | 0 | 0 | 0 | 766,347 |
| 2 | 6 | 6 | 751,198 | 0 | 0 | 0 | 0 | 0 |
| 2 | 6 | 13 | 313,179 | 0 | 0 | 0 | 0 | 0 |
| 2 | 6 | 18 | 300,854 | 0 | 0 | 0 | 0 | 0 |
| 2 | 6 | 21 | 0 | 88,108 | 0 | 0 | 0 | 0 |
| 3 | 6 | 3 | 0 | 0 | 0 | 0 | 0 | 1,228,612 |
| 3 | 6 | 11 | 0 | 0 | 0 | 0 | 0 | 418,692 |
| 3 | 6 | 15 | 0 | 0 | 0 | 0 | 0 | 429,724 |
| 3 | 6 | 19 | 0 | 0 | 0 | 0 | 0 | 153,940 |
| 3 | 6 | 24 | 0 | 0 | 0 | 0 | 0 | 26,413 |
| 3 | 6 | 30 | 0 | 0 | 0 | 0 | 9108 | 0 |
| 4 | 6 | 4 | 0 | 0 | 0 | 0 | 0 | 1,009,206 |
| 4 | 6 | 8 | 0 | 0 | 0 | 0 | 0 | 733,584 |
| 4 | 6 | 12 | 0 | 0 | 0 | 0 | 0 | 462,588 |
| 4 | 6 | 17 | 0 | 0 | 0 | 0 | 0 | 277,075 |
| 4 | 6 | 27 | 0 | 0 | 0 | 0 | 0 | 11,950 |
| 5 | 6 | 7 | 0 | 0 | 0 | 0 | 636,951 | 0 |
| 5 | 6 | 9 | 0 | 0 | 0 | 0 | 0 | 718,241 |
| 5 | 6 | 10 | 0 | 0 | 0 | 527,783 | 0 | 0 |
| 5 | 6 | 14 | 0 | 0 | 315,812 | 0 | 0 | 0 |
| 5 | 6 | 16 | 0 | 0 | 0 | 0 | 0 | 321,142 |
| 5 | 6 | 20 | 0 | 0 | 0 | 0 | 0 | 121,252 |
| 5 | 6 | 22 | 0 | 0 | 0 | 0 | 0 | 60,213 |
| 5 | 6 | 23 | 0 | 0 | 0 | 0 | 0 | 31,472 |
| 5 | 6 | 25 | 0 | 0 | 0 | 0 | 0 | 30,393 |
| 5 | 6 | 26 | 0 | 0 | 0 | 0 | 0 | 16,365 |
| 5 | 6 | 28 | 18,280 | 0 | 0 | 0 | 0 | 0 |
| 5 | 6 | 29 | 0 | 0 | 0 | 0 | 0 | 13,834 |
| 5 | 6 | 31 | 0 | 0 | 0 | 0 | 8521 | 0 |
| 5 | 6 | 33 | 0 | 0 | 5708 | 0 | 0 | 0 |
| 5 | 6 | 34 | 0 | 0 | 0 | 0 | 0 | 3412 |
| 5 | 6 | 35 | 0 | 0 | 0 | 0 | 0 | 2841 |
| 5 | 6 | 36 | 0 | 0 | 0 | 0 | 0 | 652 |
Table 22.
The optimal doses of vaccines allocated to group 7 in each period
| t | |||||||
|---|---|---|---|---|---|---|---|
| i | g | s | 3 | 5 | 6 | 7 | 8 |
| 1 | 7 | 1 | 0 | 0 | 0 | 543,686 | 0 |
| 1 | 7 | 32 | 0 | 0 | 987 | 0 | 0 |
| 1 | 7 | 33 | 1193 | 0 | 0 | 0 | 0 |
| 2 | 7 | 2 | 0 | 0 | 0 | 0 | 158,415 |
| 2 | 7 | 5 | 0 | 0 | 0 | 0 | 122,116 |
| 2 | 7 | 6 | 157,126 | 0 | 0 | 0 | 0 |
| 2 | 7 | 13 | 60,901 | 0 | 0 | 0 | 0 |
| 2 | 7 | 15 | 0 | 0 | 0 | 63,122 | 0 |
| 2 | 7 | 18 | 0 | 0 | 0 | 0 | 74,355 |
| 2 | 7 | 21 | 24,271 | 0 | 0 | 0 | 0 |
| 3 | 7 | 3 | 0 | 0 | 0 | 0 | 196,262 |
| 3 | 7 | 8 | 0 | 160,782 | 0 | 0 | 0 |
| 3 | 7 | 9 | 0 | 0 | 162,485 | 0 | 0 |
| 3 | 7 | 11 | 0 | 0 | 0 | 0 | 100,704 |
| 3 | 7 | 19 | 0 | 0 | 0 | 0 | 42,885 |
| 3 | 7 | 24 | 0 | 0 | 0 | 6044 | 0 |
| 4 | 7 | 4 | 0 | 0 | 0 | 0 | 186,018 |
| 4 | 7 | 12 | 0 | 0 | 0 | 0 | 65,552 |
| 4 | 7 | 17 | 0 | 0 | 0 | 0 | 57,631 |
| 4 | 7 | 27 | 0 | 0 | 0 | 0 | 4315 |
| 4 | 7 | 28 | 0 | 0 | 0 | 0 | 3245 |
| 5 | 7 | 7 | 0 | 0 | 0 | 213,481 | 0 |
| 5 | 7 | 10 | 0 | 0 | 0 | 0 | 103,135 |
| 5 | 7 | 14 | 0 | 0 | 0 | 79,021 | 0 |
| 5 | 7 | 16 | 0 | 0 | 0 | 0 | 51,389 |
| 5 | 7 | 20 | 0 | 0 | 0 | 0 | 37,718 |
| 5 | 7 | 22 | 0 | 0 | 0 | 0 | 8047 |
| 5 | 7 | 23 | 0 | 0 | 0 | 0 | 7025 |
| 5 | 7 | 25 | 0 | 0 | 8657 | 0 | 0 |
| 5 | 7 | 26 | 0 | 0 | 0 | 0 | 6383 |
| 5 | 7 | 29 | 0 | 0 | 0 | 0 | 1812 |
| 5 | 7 | 30 | 0 | 3354 | 0 | 0 | 0 |
| 5 | 7 | 31 | 0 | 0 | 0 | 0 | 2646 |
| 5 | 7 | 34 | 0 | 0 | 0 | 1143 | 0 |
| 5 | 7 | 35 | 0 | 0 | 0 | 0 | 809 |
| 5 | 7 | 36 | 0 | 0 | 0 | 0 | 202 |
Table 23.
The optimal doses of vaccines allocated to group 8 in each period
| t | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | g | s | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 8 | 1 | 2,955,835 | 0 | 0 | 0 | 0 | 4,223,712 |
| 1 | 8 | 6 | 0 | 0 | 0 | 0 | 0 | 3,597,026 |
| 1 | 8 | 13 | 603,075 | 0 | 0 | 0 | 0 | 0 |
| 1 | 8 | 33 | 546,637 | 0 | 0 | 0 | 0 | 0 |
| 2 | 8 | 2 | 0 | 0 | 0 | 0 | 5,676,315 | 0 |
| 2 | 8 | 5 | 0 | 0 | 0 | 0 | 0 | 3,457,231 |
| 2 | 8 | 15 | 0 | 0 | 0 | 0 | 1,577,680 | 0 |
| 2 | 8 | 16 | 0 | 0 | 0 | 0 | 0 | 1,269,092 |
| 2 | 8 | 21 | 497,303 | 0 | 0 | 0 | 0 | 0 |
| 2 | 8 | 32 | 0 | 0 | 0 | 0 | 559,134 | 0 |
| 3 | 8 | 1 | 0 | 3,518,782 | 0 | 0 | 0 | 0 |
| 3 | 8 | 3 | 0 | 0 | 0 | 0 | 5,491,595 | 0 |
| 3 | 8 | 4 | 0 | 0 | 1,873,042 | 0 | 0 | 0 |
| 3 | 8 | 9 | 0 | 0 | 0 | 2,366,320 | 0 | 0 |
| 3 | 8 | 11 | 0 | 0 | 0 | 0 | 0 | 2,056,367 |
| 3 | 8 | 17 | 0 | 0 | 0 | 0 | 1,289,245 | 0 |
| 3 | 8 | 18 | 0 | 0 | 0 | 0 | 0 | 537,073 |
| 3 | 8 | 19 | 0 | 0 | 0 | 0 | 0 | 856,796 |
| 3 | 8 | 23 | 0 | 0 | 0 | 0 | 186,578 | 0 |
| 3 | 8 | 24 | 0 | 0 | 0 | 0 | 0 | 148,914 |
| 3 | 8 | 30 | 0 | 0 | 0 | 0 | 0 | 214,183 |
| 4 | 8 | 4 | 0 | 0 | 0 | 0 | 0 | 2,410,554 |
| 4 | 8 | 8 | 0 | 0 | 0 | 0 | 0 | 2,992,207 |
| 4 | 8 | 12 | 0 | 0 | 0 | 0 | 0 | 1,748,242 |
| 4 | 8 | 13 | 0 | 0 | 0 | 0 | 0 | 1,085,490 |
| 4 | 8 | 27 | 0 | 0 | 0 | 0 | 0 | 70,705 |
| 4 | 8 | 28 | 0 | 0 | 0 | 0 | 0 | 70,881 |
| 5 | 8 | 7 | 0 | 0 | 0 | 0 | 0 | 3,489,559 |
| 5 | 8 | 9 | 0 | 0 | 0 | 0 | 0 | 462,812 |
| 5 | 8 | 10 | 2,300,165 | 0 | 0 | 0 | 0 | 0 |
| 5 | 8 | 14 | 0 | 0 | 0 | 0 | 1,625,810 | 0 |
| 5 | 8 | 18 | 0 | 0 | 0 | 0 | 0 | 719,641 |
| 5 | 8 | 20 | 0 | 0 | 0 | 0 | 0 | 604,850 |
| 5 | 8 | 22 | 0 | 0 | 0 | 0 | 0 | 342,747 |
| 5 | 8 | 25 | 0 | 0 | 0 | 133,729 | 0 | 0 |
| 5 | 8 | 26 | 0 | 0 | 0 | 0 | 0 | 101,498 |
| 5 | 8 | 29 | 0 | 0 | 0 | 62,851 | 0 | 0 |
| 5 | 8 | 31 | 0 | 0 | 0 | 0 | 0 | 1,052,775 |
| 5 | 8 | 34 | 0 | 0 | 0 | 0 | 373,908 | 0 |
| 5 | 8 | 35 | 0 | 0 | 0 | 0 | 0 | 250,040 |
| 5 | 8 | 36 | 65,065 | 0 | 0 | 0 | 0 | 0 |
Table 5.
The optimal vaccine doses shipped from distribution centers to warehouses in each period
| t | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| i | d | s | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1 | 1 | 0 | 3,967,289 | 0 | 0 | 0 | 6,000,000 | 7,334,862 |
| 1 | 1 | 13 | 0 | 603,075 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 15 | 0 | 2,264,514 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 2,842,904 |
| 1 | 1 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 945,494 |
| 1 | 1 | 32 | 0 | 117,292 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 33 | 0 | 547,830 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 5 | 0 | 0 | 0 | 0 | 10,488,400 | 0 | 0 |
| 1 | 2 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 3,853,421 |
| 1 | 2 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 22,785 |
| 1 | 2 | 27 | 0 | 0 | 0 | 0 | 0 | 0 | 534 |
| 2 | 1 | 1 | 0 | 6,783,182 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 14,198,023 | 0 |
| 2 | 1 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 8,478,729 |
| 2 | 1 | 13 | 0 | 3,592,781 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 15 | 0 | 0 | 0 | 0 | 0 | 1,863,893 | 0 |
| 2 | 1 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 1,269,092 |
| 2 | 1 | 17 | 0 | 0 | 0 | 0 | 0 | 115,090 | 0 |
| 2 | 1 | 18 | 0 | 1,921,328 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 21 | 0 | 663,083 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 25 | 0 | 0 | 0 | 0 | 0 | 0 | 8415 |
| 2 | 1 | 32 | 0 | 0 | 0 | 0 | 0 | 559,134 | 0 |
| 2 | 1 | 33 | 0 | 50,654 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 5 | 0 | 843,147 | 0 | 0 | 0 | 4,533,260 | 0 |
| 2 | 2 | 6 | 0 | 1,145,825 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 18 | 0 | 0 | 0 | 0 | 0 | 82,579 | 0 |
| 3 | 1 | 1 | 1,165,607 | 0 | 3,518,782 | 0 | 0 | 0 | 0 |
| 3 | 1 | 4 | 0 | 0 | 0 | 1,873,042 | 0 | 0 | 0 |
| 3 | 1 | 11 | 1,951,197 | 3,812,266 | 0 | 0 | 0 | 338,181 | 0 |
| 3 | 1 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 448,851 |
| 3 | 1 | 17 | 147,179 | 0 | 0 | 2,126,958 | 1,289,245 | 0 | 0 |
| 3 | 1 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 688,132 |
| 3 | 1 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 2,252,880 |
| 3 | 1 | 24 | 480,220 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 30 | 228,248 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 35 | 27,549 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 2 | 3 | 0 | 0 | 0 | 0 | 0 | 5,491,595 | 1,424,874 |
| 3 | 2 | 9 | 0 | 0 | 286,488 | 0 | 2,710,755 | 0 | 185,263 |
| 3 | 4 | 8 | 0 | 0 | 409,197 | 0 | 0 | 170,224 | 0 |
| 3 | 4 | 10 | 0 | 0 | 778,223 | 0 | 0 | 0 | 0 |
| 3 | 4 | 23 | 0 | 186,578 | 0 | 0 | 0 | 0 | 0 |
| 3 | 4 | 28 | 0 | 0 | 7310 | 0 | 0 | 0 | 0 |
| 3 | 4 | 35 | 0 | 1156 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 4,458,437 |
| 4 | 1 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 5,355,224 |
| 4 | 1 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 1,085,490 |
| 4 | 1 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 121,062 |
| 4 | 1 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 436,095 |
| 4 | 1 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 50,777 |
| 4 | 1 | 24 | 0 | 0 | 0 | 0 | 0 | 0 | 15,214 |
| 4 | 2 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 4,080,327 |
| 4 | 4 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 4,686,209 |
| 4 | 4 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 8,403,048 |
| 4 | 4 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 28,580 |
| 4 | 4 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 4,976,826 |
| 4 | 4 | 27 | 0 | 0 | 0 | 0 | 0 | 0 | 216,703 |
| 4 | 4 | 28 | 0 | 0 | 0 | 0 | 0 | 0 | 86,008 |
| 5 | 1 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 243,032 |
| 5 | 1 | 10 | 0 | 2,300,165 | 0 | 529,233 | 4,492,539 | 0 | 238,053 |
| 5 | 1 | 13 | 0 | 0 | 138,940 | 0 | 0 | 0 | 0 |
| 5 | 1 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 826,400 |
| 5 | 1 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 963,539 |
| 5 | 1 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 1,765,361 |
| 5 | 1 | 22 | 0 | 0 | 0 | 0 | 0 | 0 | 870,248 |
| 5 | 1 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 390,773 |
| 5 | 1 | 25 | 0 | 496,780 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 26 | 0 | 297,214 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 28 | 0 | 112,285 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 30 | 0 | 0 | 110,398 | 0 | 0 | 0 | 0 |
| 5 | 1 | 31 | 0 | 0 | 1,146,816 | 0 | 0 | 0 | 0 |
| 5 | 1 | 33 | 0 | 0 | 9461 | 0 | 0 | 0 | 0 |
| 5 | 1 | 34 | 0 | 412,194 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 35 | 0 | 0 | 0 | 0 | 0 | 0 | 256,060 |
| 5 | 1 | 36 | 0 | 72,044 | 0 | 0 | 0 | 0 | 0 |
| 5 | 2 | 3 | 4,999,780 | 309,318 | 170,980 | 3,154,955 | 0 | 0 | 0 |
| 5 | 2 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 1,181,053 |
| 5 | 4 | 7 | 0 | 0 | 1,019,244 | 0 | 0 | 4,000,764 | 0 |
| 5 | 4 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 177,136 |
| 5 | 4 | 14 | 0 | 0 | 1,397,340 | 315,812 | 305,733 | 1,999,236 | 88,345 |
| 5 | 4 | 27 | 0 | 0 | 6821 | 0 | 0 | 0 | 0 |
| 5 | 4 | 29 | 0 | 0 | 0 | 0 | 201,728 | 0 | 0 |
| 5 | 4 | 36 | 220 | 0 | 0 | 0 | 0 | 0 | 0 |
Table 6.
The doses of vaccines stored in the state warehouses in each period
| t | |||||||
|---|---|---|---|---|---|---|---|
| i | s | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | 0 | 1,011,454 | 1,011,454 | 1,011,454 | 0 | 4,130,234 |
| 1 | 32 | 0 | 117,292 | 117,292 | 117,292 | 281 | 0 |
| 2 | 2 | 0 | 0 | 0 | 0 | 0 | 1,993,059 |
| 2 | 5 | 0 | 582,218 | 547,399 | 547,399 | 547,399 | 4,840,779 |
| 2 | 13 | 0 | 216,566 | 0 | 0 | 0 | 0 |
| 2 | 15 | 0 | 0 | 0 | 0 | 0 | 35,094 |
| 2 | 18 | 0 | 1,620,474 | 0 | 0 | 0 | 82,579 |
| 2 | 21 | 0 | 138,736 | 50,628 | 0 | 0 | 0 |
| 2 | 33 | 0 | 50,654 | 1948 | 0 | 0 | 0 |
| 3 | 1 | 1,165,607 | 0 | 0 | 0 | 0 | 0 |
| 3 | 8 | 0 | 0 | 409,197 | 158,375 | 158,375 | 0 |
| 3 | 11 | 0 | 3,812,266 | 3,812,266 | 3,812,266 | 3,812,266 | 3,918,662 |
| 3 | 17 | 147,179 | 147,179 | 0 | 0 | 1,289,245 | 0 |
| 3 | 23 | 0 | 186,578 | 186,578 | 186,578 | 186,578 | 0 |
| 3 | 24 | 467,762 | 453,607 | 453,607 | 453,607 | 453,607 | 177,519 |
| 3 | 28 | 0 | 0 | 7310 | 7310 | 7310 | 7067 |
| 3 | 30 | 228,248 | 228,248 | 228,248 | 228,248 | 228,248 | 219,140 |
| 5 | 3 | 0 | 309,318 | 0 | 2,687,340 | 2,687,340 | 2,649,723 |
| 5 | 7 | 0 | 0 | 1,019,244 | 1,019,244 | 1,019,244 | 3,723,069 |
| 5 | 10 | 0 | 0 | 0 | 529,233 | 4,289,143 | 254,272 |
| 5 | 13 | 0 | 0 | 138,940 | 0 | 0 | 0 |
| 5 | 25 | 0 | 496,780 | 484,414 | 484,414 | 327,079 | 325,079 |
| 5 | 26 | 0 | 297,214 | 297,214 | 297,214 | 297,214 | 297,214 |
| 5 | 27 | 0 | 0 | 6821 | 6821 | 6821 | 6821 |
| 5 | 29 | 0 | 0 | 0 | 0 | 128,440 | 128,440 |
| 5 | 30 | 0 | 0 | 110,398 | 102,179 | 102,179 | 100,794 |
| 5 | 31 | 0 | 0 | 1,146,324 | 1,146,324 | 1,072,392 | 1,058,658 |
| 5 | 33 | 0 | 0 | 7555 | 0 | 0 | 0 |
| 5 | 34 | 0 | 412,194 | 412,194 | 412,194 | 381,045 | 5168 |
| 5 | 36 | 0 | 6979 | 6979 | 6979 | 6979 | 6979 |
Fig. 2.
The total doses of vaccines allocated to each state
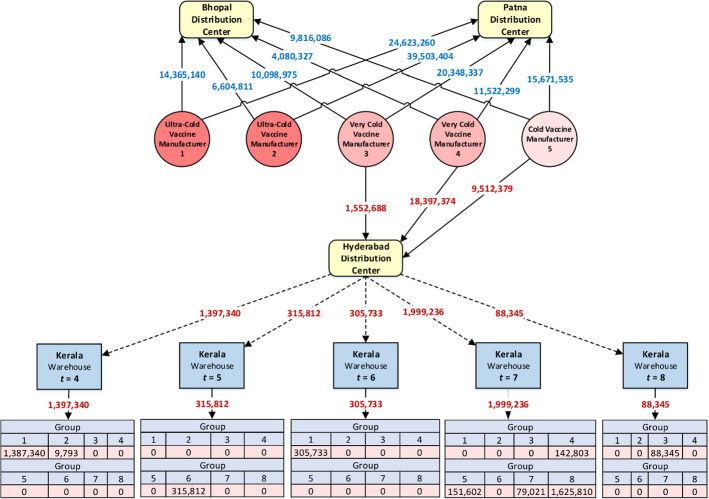
The following items have been depicted in Fig. 3 to provide a more accurate interpretation of the obtained result: the optimal doses of vaccines purchased from each manufacturer by the distribution centers, the optimal doses of vaccines assigned to the Kerala State to each group in each period, and the optimal doses of vaccines shipped from the Hyderabad distribution center to the Kerala State in each period.
Fig. 3.
Assigned vaccines to each group in each period in Kerala state
The results presented in Fig. 3 show that a total of 186,096,615 double-dose vaccines have been purchased from each of the five manufacturers, where 85,096,615 vaccines required ultra-cold refrigeration, 66,000,000 vaccines required very cold refrigeration, and the remainder required cold refrigeration. From the total purchased vaccine, 111,668,835 and 44,965,339 double-dose vaccines have been allocated to the Patna and Bhopal distribution centers, respectively. The remaining 29,462,441 double-dose vaccines have been allocated to the Hyderabad distribution center. In addition, the equitable vaccine distribution in Kerala State is depicted in this figure. 1,397,340 double-dose vaccines are transferred to this state from the Hyderabad distribution center in period 4, out of which 1,387,340 vaccines were assigned to group 1, and the remaining 9793 vaccines were allocated to group 2. Similarly, vaccines assigned to each group in periods 5 to 8 are shown in this figure. It is worth noting again some parameters, including transportation costs, vaccine prices, and manufacturing capacities, have been simulated based on preliminary estimates at MOHFW. In summary, this study demonstrated a practical, structured, and yet flexible scientific approach for equitable COVID-19 vaccine distribution in developing countries. The obtained results confirm the efficiency and effectiveness of the proposed model.
Sensitivity analysis
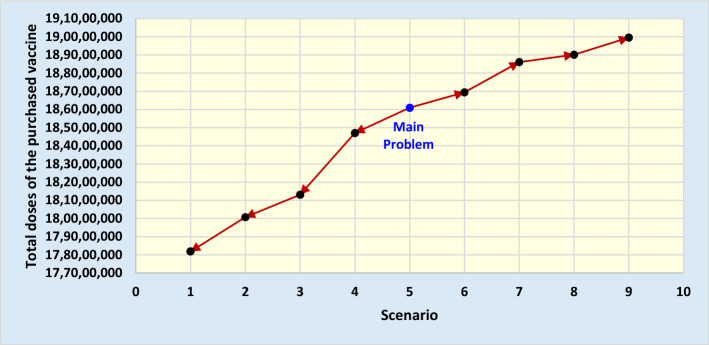
In this section, we study the performance of the model proposed in this study according to various budgetary constraints. We begin the sensitivity analysis by increasing (decreasing) the total budget and expect that the total doses of the purchased vaccine will increase (decrease) accordingly. For this purpose, we consider nine budgeting scenarios and calculate the total doses of the purchased vaccine for each scenario. The total doses of purchased vaccines for these scenarios are presented in Table 7 and Fig. 4.
Table 7.
Sensitivity analysis procedure using budget changes
| Scenario | Budget | Total doses of the purchased vaccine |
|---|---|---|
| 1 | 4,100,000,000 | 178,183,484 |
| 2 | 4,200,000,000 | 180,073,849 |
| 3 | 4,300,000,000 | 181,308,864 |
| 4 | 4,400,000,000 | 184,706,426 |
| 5 (main problem) | 4,500,000,000 | 186,096,615 |
| 6 | 4,600,000,000 | 186,943,712 |
| 7 | 4,700,000,000 | 188,607,348 |
| 8 | 4,800,000,000 | 189,013,640 |
| 9 | 4,900,000,000 | 189,956,071 |
Fig. 4.
Total doses of the purchased vaccine for each scenario
As shown in Table 7 and Fig. 4, as the budget amount increases (i.e., scenarios 6 to 9), the total doses of the purchased vaccine increase, and as the budget amount decreases (i.e., scenarios 4 to 1), the total doses of the purchased vaccine decreased. The results are logical and meet our expectations of the proposed model behavior. This sensitivity analysis confirms the applicability and logical performance of the model.
Conclusion
This study proposed a mathematical programming model for equitable COVID-19 vaccine distribution in developing countries in the context of a location-inventory problem, considering the concepts of equity and taking into account the needs for cold, very cold, and ultra-cold supply chains. This model is the general form of Rastegar et al.’s (2021) model that provides the possibility of distributing vaccines requiring cold, very cold, and ultra-cold refrigeration among heterogeneous populations. Budgetary considerations, manufacturer selection, and time-dependent capacities are considered some of the proposed model’s more general and practical assumptions. Data from a case study in India is used to validate the practical application of the proposed model. The results showed that with 4.5 billion dollars, the Indian government could purchase over 186 million double-dose COVID-19 vaccines, including over 85 million for ultra-cold, 66 million for very cold, and 35 million double-doses for cold supply chains. Finally, sensitivity analysis was used to confirm the applicability and logical performance of the model.
This study has proposed an operational model with strategic consideration under certainty for equitable COVID-19 vaccine distribution. Life is full of uncertainty, and failing to fully consider operational uncertainties can have detrimental consequences in any operations, including vaccination efforts in developing countries. Future research is needed to study some of our operational assumptions under uncertain conditions. In addition, more complex models with additional objective functions (i.e., emission reduction) can improve the real-world applicability of the vaccine distribution model proposed in this study. Future advanced analytics research is needed to coordinate manufacturing and distribution with healthcare providers and pharmacies to deploy vaccines more effectively and efficiently through specialized supply chain networks.
Acknowledgements
Dr. Madjid Tavana is grateful for the partial support he received from the Czech Science Foundation (GAˇCR19-13946S) for this research.
Appendix A
Appendix B
Declarations
Conflict of interest
The above authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Madjid Tavana, Email: tavana@lasalle.edu, http://tavana.us/.
Kannan Govindan, Email: kgov@iti.sdu.dk.
Arash Khalili Nasr, Email: khalilinasr@sharif.edu.
Mohammad Saeed Heidary, Email: saeed_heidary@atu.ac.ir.
Hassan Mina, Email: hassan.mina@ut.ac.ir.
References
- Abila DB, Dei-Tumi SD, Humura F, Aja GN. We need to start thinking about promoting the demand, uptake, and equitable distribution of COVID-19 vaccines NOW! Public Health in Practice. 2020;1:100063. doi: 10.1016/j.puhip.2020.100063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulula N, Mwiru DP, Swalehe O, Mori AT. Vaccine storage and distribution between expanded program on immunization and medical store department in Tanzania: A cost-minimization analysis. Vaccine. 2020;38(51):8130–8135. doi: 10.1016/j.vaccine.2020.10.088. [DOI] [PubMed] [Google Scholar]
- Chandir S, Siddiqi DA, Mehmood M, Setayesh H, Siddique M, Mirza A, Akhter MA. Impact of COVID-19 pandemic response on uptake of routine immunizations in Sindh, Pakistan: an analysis of provincial electronic immunization registry data. Vaccine. 2020;38(45):7146–7155. doi: 10.1016/j.vaccine.2020.08.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conrow L, Murray AT, Fischer HA. An optimization approach for equitable bicycle share station siting. Journal of Transport Geography. 2018;69:163–170. doi: 10.1016/j.jtrangeo.2018.04.023. [DOI] [Google Scholar]
- Corey L, Mascola JR, Fauci AS, Collins FS. A strategic approach to COVID-19 vaccine R&D. Science. 2020;368(6494):948–950. doi: 10.1126/science.abc5312. [DOI] [PubMed] [Google Scholar]
- Coudeville L, Gomez GB, Jollivet O, Harris RC, Thommes E, Druelles S, Mahé C. Exploring uncertainty and risk in the accelerated response to a COVID-19 vaccine: Perspective from the pharmaceutical industry. Vaccine. 2020;38(48):7588–7595. doi: 10.1016/j.vaccine.2020.10.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Boeck, K., Decouttere, C., & Vandaele, N. (2019). Vaccine distribution chains in low-and middle-income countries: A literature review. Omega, 102097.
- Degeling C, Williams J, Carter SM, Moss R, McVernon J. Priority allocation of pandemic influenza vaccines in Australia—Recommendations of 3 community juries. Vaccine. 2020 doi: 10.1016/j.vaccine.2020.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dinleyici EC, Borrow R, Safadi MAP, van Damme P, Munoz FM. Vaccines and routine immunization strategies during the COVID-19 pandemic. Human Vaccines & Immunotherapeutics. 2020;17:1–8. doi: 10.1080/21645515.2020.1804776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duijzer LE, van Jaarsveld W, Dekker R. Literature review: The vaccine supply chain. European Journal of Operational Research. 2018;268(1):174–192. doi: 10.1016/j.ejor.2018.01.015. [DOI] [Google Scholar]
- Enayati S, Özaltın OY. Optimal influenza vaccine distribution with equity. European Journal of Operational Research. 2020;283(2):714–725. doi: 10.1016/j.ejor.2019.11.025. [DOI] [Google Scholar]
- Fianu S, Davis LB. A Markov decision process model for equitable distribution of supplies under uncertainty. European Journal of Operational Research. 2018;264(3):1101–1115. doi: 10.1016/j.ejor.2017.07.017. [DOI] [Google Scholar]
- Gamchi NS, Torabi SA, Jolai F. A novel vehicle routing problem for vaccine distribution using SIR epidemic model. Or Spect. 2020;43:1–34. [Google Scholar]
- Govindan K, Mina H, Alavi B. A decision support system for demand management in healthcare supply chains considering the epidemic outbreaks: A case study of coronavirus disease 2019 (COVID-19) Transportation Research Part e: Logistics and Transportation Review. 2020;138:101967. doi: 10.1016/j.tre.2020.101967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hovav S, Tsadikovich D. A network flow model for inventory management and distribution of influenza vaccines through a healthcare supply chain. Operations Research for Health Care. 2015;5:49–62. doi: 10.1016/j.orhc.2015.05.003. [DOI] [Google Scholar]
- Lim J, Norman BA, Rajgopal J. Redesign of vaccine distribution networks. International Transactions in Operational Research. 2019 doi: 10.1111/itor.12758. [DOI] [Google Scholar]
- Lin Q, Zhao Q, Lev B. Cold chain transportation decision in the vaccine supply chain. European Journal of Operational Research. 2020;283(1):182–195. doi: 10.1016/j.ejor.2019.11.005. [DOI] [Google Scholar]
- Orgut IS, Ivy J, Uzsoy R. Modeling for the equitable and effective distribution of food donations under stochastic receiving capacities. IIE Transactions. 2017;49(6):567–578. [Google Scholar]
- Orgut IS, Ivy J, Uzsoy R, Wilson JR. Modeling for the equitable and effective distribution of donated food under capacity constraints. IIE Transactions. 2016;48(3):252–266. doi: 10.1080/0740817X.2015.1063792. [DOI] [Google Scholar]
- Pagliusi S, Dennehy M, Homma A. Two decades of vaccine innovations for global public good: Report of the developing countries’ vaccine manufacturers network 20th meeting, 21–23 october 2019, Rio de Janeiro, Brazil. Vaccine. 2020;38(36):5851–5860. doi: 10.1016/j.vaccine.2020.05.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rastegar M, Tavana M, Meraj A, Mina H. An inventory-location optimization model for equitable influenza vaccine distribution in developing countries during the COVID-19 pandemic. Vaccine. 2021;39(3):495–504. doi: 10.1016/j.vaccine.2020.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiter PL, Pennell ML, Katz ML. Acceptability of a COVID-19 vaccine among adults in the United States: How many people would get vaccinated? Vaccine. 2020;38(42):6500–6507. doi: 10.1016/j.vaccine.2020.08.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saif A, Elhedhli S. Cold supply chain design with environmental considerations: A simulation-optimization approach. European Journal of Operational Research. 2016;251(1):274–287. doi: 10.1016/j.ejor.2015.10.056. [DOI] [Google Scholar]
- Sasse JP, Trutnevyte E. Distributional trade-offs between regionally equitable and cost-efficient allocation of renewable electricity generation. Applied Energy. 2019;254:113724. doi: 10.1016/j.apenergy.2019.113724. [DOI] [Google Scholar]
- Yang Y, Bidkhori H, Rajgopal J. Optimizing vaccine distribution networks in low and middle-income countries. Omega. 2020;99:102197. doi: 10.1016/j.omega.2020.102197. [DOI] [Google Scholar]
- Zandkarimkhani S, Mina H, Biuki M, Govindan K. A chance constrained fuzzy goal programming approach for perishable pharmaceutical supply chain network design. Annals of Operations Research. 2020;295:1–28. doi: 10.1007/s10479-020-03677-7. [DOI] [Google Scholar]